Cicero predicts cis-regulatory DNA interactions from single cell chromatin accessibility data

Summary

Linking regulatory DNA elements to their target genes, which may be located hundreds of kilobases away, remains challenging. Here we introduce Cicero, an algorithm that identifies coaccessible pairs of DNA elements using single-cell chromatin accessibility data, and so connects regulatory elements to their putative target genes. We apply Cicero to investigate how dynamically accessible elements orchestrate gene regulation in differentiating myoblasts. Groups of Cicero-linked regulatory elements meet criteria of "chromatin hubs" — they are enriched for physical proximity, interact with a common set of transcription factors, and undergo coordinated changes in histone marks that are predictive of changes in gene expression. Pseudotemporal analysis revealed that most DNA elements remain in chromatin hubs throughout differentiation. A subset of elements bound by MYOD in myoblasts exhibit early opening in a PBX1- and MEIS1-dependent manner. This strategy can be applied to dissect the architecture, sequence determinants, and mechanisms of cis-regulation on a genome-wide scale.

Introduction

Chromatin accessibility is a powerful marker of active regulatory DNA. In eukaryotes, chromatin accessibility at both promoters and distal elements delineates where transcription factors (TFs) are bound in place of nucleosomes (Felsenfeld et al., 1996). Genome-wide analyses of chromatin accessibility as measured by DNaseI hypersensitivity have found that the repertoire of accessible regulatory elements constitutes a highly specific molecular signature of cell lines and tissues (Thurman et al., 2012). Furthermore, genome-wide association studies (GWAS) show that a substantial proportion of genetic risk for common disease falls within accessible regions in disease-relevant tissues or cell types (Gusev et al., 2014; Maurano et al., 2012).

Despite its importance, we continue to lack a quantitative understanding of how changes in chromatin accessibility relate to changes in the expression of nearby genes. A prerequisite for such an understanding is a map that links distal regulatory elements with their target genes. To this end, we developed Cicero, an algorithm that generates such linkages on a genome-wide basis based on patterns of coaccessibility in single cell data.

We demonstrate Cicero’s capabilities through an analysis of skeletal myoblast differentiation, which remains one of the best characterized models of gene regulation in vertebrate development. Myoblast differentiation is orchestrated by a core set of TFs, including MYOD and MEF2 (Molkentin et al., 1995), which regulate the expression of thousands of genes as cells exit the cell cycle, align, and fuse to form myotubes. Here we used single cell combinatorial indexing ATAC-seq (sci-ATAC-seq) on 13,367 cells to identify 329,020 accessible elements in myoblasts, nearly 22,000 of which open or close during differentiation. When applied to these data, Cicero linked most dynamic sites to one or more putative target genes. From the resulting cis-regulatory map, we can predict changes in gene expression based on the chromatin accessibility dynamics of the linked distal elements.

Design

In contrast with previous approaches that rely on a large compendium of bulk chromatin accessibility data generated across many cell lines or tissues (Thurman et al., 2012, Budden et al., 2015), we sought a method that would work with single cell chromatin accessibility data from a single experiment, and that was robust to the sparsity of that data. Cicero uses sampling and aggregation of groups of similar cells to adjust for technical confounders and to quantify correlations between putative regulatory elements. Based on these correlations, Cicero links regulatory elements to target genes using unsupervised machine learning. The algorithm can be applied to any cell type and organism for which a sequenced genome and single cell chromatin accessibility data are available. Because it accepts single cell data as input, Cicero can in principle work on complex mixtures of different cell types as are found in tissues.

Results

The trajectories of chromatin accessibility and gene expression during myoblast differentiation are highly similar

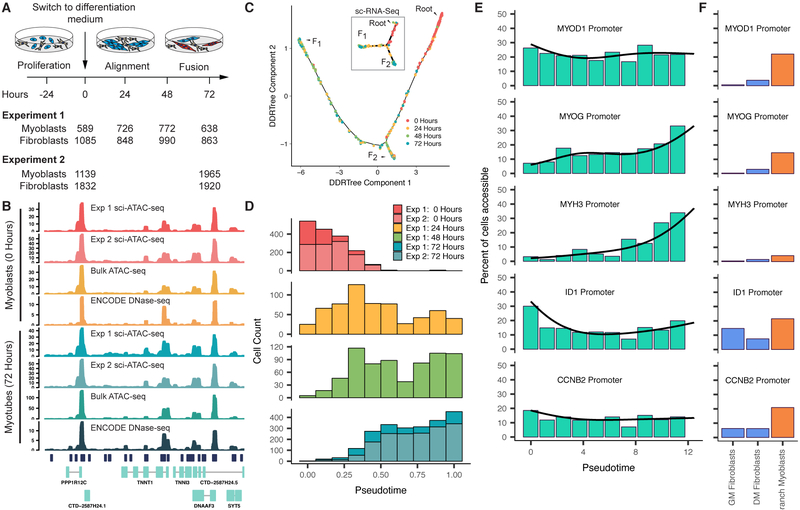
We performed a differentiation time course on human skeletal muscle myoblasts (HSMM), harvesting cells at 0, 24, 48 and 72 hours after the switch from growth media to differentiation media (Figure 1A). With optimized sci-ATAC-seq (Cusanovich et al., 2018), we profiled chromatin accessibility in 13,367 cells across 2 independent experiments. Aggregated single-cell ATAC-seq data was highly concordant with both bulk ATAC-seq and published DNaseI hypersensitivity data from myoblasts and myotubes (Figure 1B, Supplemental Figure 1A,B) (The ENCODE Project Consortium, 2012). To define accessible regions, we pooled reads from all cells from each experiment and called peaks with MACS 2 (Zhang et al., 2008). The vast majority of peaks were shared between experiments (Supplemental Figure 1B), so we used of a single merged set of peaks for all downstream analyses. After excluding 7,538 cells flagged as likely interstitial fibroblasts based on the absence of promoter accessibility in any of several known muscle markers (56%, a proportion similar to our estimate from single-cell RNA-seq in this system (Qiu et al., 2017a)), we identified 329,020 sites accessible in muscle cells. Each cell had reads overlapping with an average of 3,466 promoter-proximal accessible sites and 9,055 distal accessible sites (Supplemental Figure 1C).

Figure 1.

Differentiating myoblasts follow similar single cell chromatin accessibility and gene expression trajectories. A) Single cell chromatin accessibility profiles for human skeletal muscle myoblasts (HSMM) were constructed with sci-ATAC-seq. Contaminating interstitial fibroblasts (common in HSMM cultures) were removed informatically prior to further analysis. B) Aggregated read coverage from sci-ATAC-seq experiments in the region surrounding TNNT1 and TNNI3 in myoblasts (0 hours) and myotubes (72 hours). Bulk ATAC-seq prepared from the same wells as experiment 2 are shown alongside DNase-seq from ENCODE for comparison (ENCODE experiments ENCSR000EOO and ENCSR000EOP (The ENCODE Project Consortium, 2012)). C) The single cell trajectory inferred from 2,725 myoblast sci-ATAC-seq profiles from experiment 1 by Monocle (see Methods). In subsequent panels and throughout the paper, we exclude cells on the branch to outcome F₂ unless otherwise indicated. Inset shows the sc-RNA-seq trajectory reported for HSMMs (reproduced from Figure 2 of (Qiu et al., 2017a), cells were from the same lot and were cultured under identical conditions to those for sci-ATAC-seq). D) Distribution of cells in chromatin accessibility pseudotime from the root to trajectory outcome F₁. E) Percent of differentiating cells whose promoters for selected genes are accessible across pseudotime. Black line indicates the pseudotime-dependent average from a smoothed binomial regression. F) Percent of cells whose promoters for selected genes in E are accessible in fibroblasts collected in growth medium (GM) or differentiation medium (DM), as well as myoblasts localized to the branch to F₂. See also Figure S1.

We next sought to characterize changes in chromatin accessibility as myoblasts differentiated. However, analyzing differentiation from time series data is confounded by asynchronicity, i.e. Simpson’s Paradox (Simpson, 1951). To overcome this, we recently developed the technique of “pseudotemporal reordering” (or “pseudotime”) that uses machine learning to organize cells according to their progress through differentiation (Trapnell et al., 2014). Although our algorithm, Monocle 2, was designed for single cell transcriptomes (Qiu et al., 2017a), we were able to adapt it to sci-ATAC-seq data with straightforward modifications (see Methods).

Monocle independently placed the cells from each experiment along similar trajectories with two outcomes (denoted F₁ and F₂) (Figure 1C, Supplemental Figure 1D). These trajectories are similar to the trajectory constructed from single cell transcriptomes in our previous work (Qiu et al., 2017a) (Figure 1C inset). Cells harvested from growth media fell almost exclusively near the beginning of the trajectories, while cells from later time points were distributed over their length (Figure 1D). Over the path to F₁, promoters for well-known myogenic regulators and structural components of muscle opened (became more accessible), whereas the promoter of ID1, a well-characterized repressor of myoblast differentiation (Benezra et al., 1990), closed (Figure 1E). Similar to the single cell RNA-seq trajectory (Qiu et al., 2017a), a number of cells were positioned on a branch leading to the alternative outcome F₂. That these cells are accessible at the MYOD1 promoter, but not the MYH3 promoter, suggests they represent “reserve myoblasts” that did not fully differentiate (Yoshida et al., 1998) (Figure 1F). The similar trajectories constructed by Monocle from three independent experiments, as well as the close correspondence between the kinetics in expression and chromatin accessibility for key muscle genes, support the accuracy of Monocle’s pseudotime ordering.

Distal DNA elements are dynamically accessible during myoblast differentiation

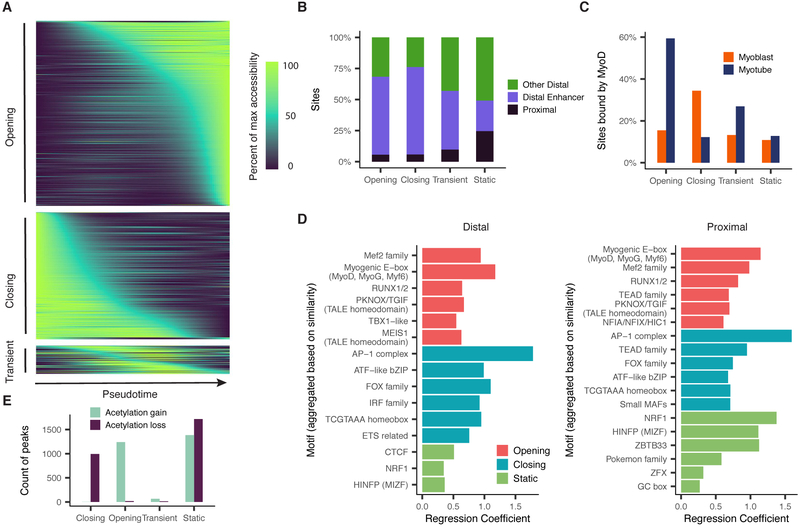
Differential analysis revealed significant pseudotime-dependent changes in accessibility at 21,678 of 329,020 (6.6%) sites during myoblast differentiation (Figure 2A, Supplemental Figure 2A). In addition, we conducted a similar differential analysis on previously published single-cell RNA-seq data from the same system (Trapnell et al., 2014). Of the “dynamic” accessible sites, only 1,324 (6.1%) were promoters (Figure 2B), of which 92 overlapped with 1,464 differentially expressed transcripts (FDR < 5%) by single-cell RNA-seq. Of the 64 of promoters with non-transient changes in both accessibility and gene expression, 62 (97%) were directionally concordant. Of the 20,354 distal, dynamically accessible sites, 68% were annotated as enhancers in myoblasts or myotubes (Libbrecht et al., 2016), as compared with only 36% of all accessible sites (Figure 2B).

Figure 2.

Thousands of DNA elements are dynamically accessible during myoblast differentiation. A) Smoothed pseudotime-dependent accessibility curves, generated by a negative binomial regression and scaled as a percent of the maximum accessibility of each site. Curve regressions are the same as regression for differential accessibility (see Methods). Each row indicates a different DNA element. Sites are sorted by the pseudotime at which they first reach half their maximum accessibility. B) Proportions of dynamic and static sites by site type. Color indicates whether a site is promoter-proximal (see Methods), a distal enhancer (defined as peaks that are not promoter-proximal, and are annotated by Segway as enhancers in either myoblasts or myotubes), or other distal (remaining sites). C) Percent of sites reported as bound by MyoD in either myoblasts or myotubes by (Cao et al., 2010). D) Motif enrichments in accessible sites. P-values result from logistic regression models that use the presence or absence of a given motif in each site to predict whether the site has a given accessibility trend (opening/closing/static). Plots show up to the top 6 Bonferroni-significant motifs by p-value. E) Counts of sites undergoing significant changes in H3K27 acetylation as measured by ChIP-Seq (Tang et al., 2015). See also Figure S2.

Using gene set enrichment analysis, we found that genes associated with contraction and other muscle-related functions were strongly enriched among genes with significantly opening promoter regions. In contrast, promoters for genes associated with the cell cycle, which are downregulated early in differentiation, were only marginally enriched among the differentially accessible sites (Supplemental Figure 2B). Most markers of actively proliferating cells did not show significant changes in promoter accessibility (Supplemental Figure 2C).

Comparison to ChIP-seq data (Cao et al., 2010) revealed that 59% of opening sites and 34% of closing sites are bound by MYOD in myotubes and myoblasts respectively (Figure 2C). In contrast, only 16% of static sites (those without significant changes in accessibility) were MYOD-bound in either myoblasts or myotubes. Dynamically accessible distal elements and promoters were also strongly enriched for binding motifs for MYOD, MYOG, and MEF2 family members and other TFs with central regulatory roles in myogenesis (Figure 2D).

Many TFs recruit enzymes that mark histones near regulatory DNA elements. For example, MYOD recruits p300, whose histone acetyltransferase activity is required for its role in activating gene expression (Dilworth et al., 2004; Puri et al., 1997; Sartorelli et al., 1997). A comparison with ENCODE data for myoblasts and myotubes showed overwhelming directional concordance between sites that were gaining or losing H3K27 acetylation (H3K27ac) vs. sites that were opening or closing in chromatin accessibility, respectively (Figure 2E). However, most changes in histone marks during differentiation occurred at sites that did not undergo significant changes in chromatin accessibility (Supplemental Figure 2D). Thus, myoblast differentiation is characterized by changes in H3K27ac at hundreds-of-thousands of sites, only a minority of which were accompanied by changes in their chromatin accessibility, at least to the extent that they are detectable by the methods employed here.

Cicero constructs genome-wide cis-regulatory models from sci-ATAC-seq data

We next sought to exploit patterns of coaccessibility between distal elements and promoters to build a genome-wide cis-regulatory map. This is challenging for several reasons. First, the raw correlations are driven in part by technical factors such as read depth per cell. Second, we have insufficient observations to accurately estimate correlations between billions of pairs of sites. Third, single cell ATAC-seq data is very sparse. Finally, while the accessibility of distal elements might be correlated with their target promoters, very distant or interchromosomal pairs of sites, will also be correlated by virtue of being part of the same regulatory program.

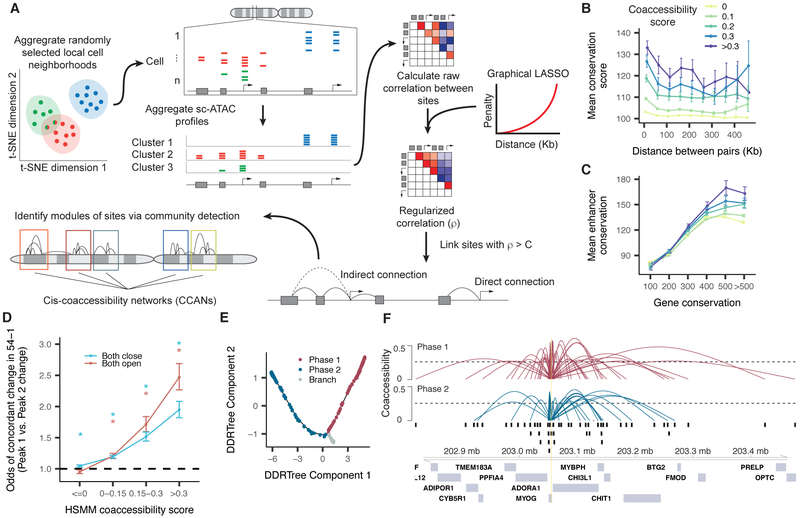
To address these challenges, we developed a new algorithm, Cicero, that subtracts technical and genomic distance effects while constructing a global cis-regulatory map from single cell chromatin accessibility profiles (Figure 3A). Briefly, the user provides Cicero with cells as input that have been clustered or pseudotemporally organized. The algorithm creates many groups of cells, each comprised of 50 cells similarly positioned in clustering or trajectory space. This helps to overcome the sparsity of the data while avoiding Simpson’s paradox (Simpson, 1951; Trapnell, 2015). It then aggregates accessibility profiles for cells in each group to produce counts that can be readily adjusted to subtract the effects of technical variables. Finally, it computes the correlations in adjusted accessibilities between all pairs of sites within 500 kb. To calculate robust correlations, we use Graphical LASSO (Friedman et al., 2008), which estimates regularized correlation matrices. Cicero penalizes correlations in a distant-dependent manner, preserving local patterns at the expense of very long-range ones. The output of Cicero consists of the coaccessibility scores for all pairs of sites within 500 kb of one another. Full details are provided in Methods.

Figure 3.

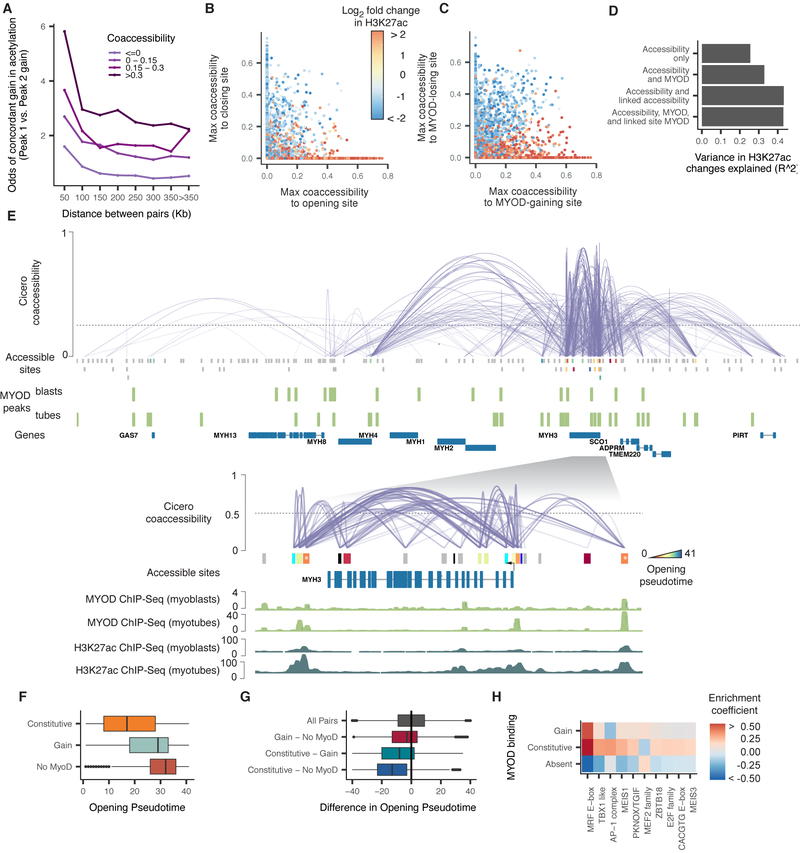
Cicero constructs cis-regulatory models genome-wide from sci-ATAC-seq data. A) An overview of the Cicero algorithm (see Methods for details) B) Mean phastCons 46-way placental conservation scores of distal peaks connected to promoters. Peaks were stratified by distance from the promoter and coaccessibility score between the promoter and the distal peak. C) Mean distal site conservation score versus connected gene conservation score stratified by coaccessibility score. D) Odds ratios of concordant accessibility dynamics across differentiation in 54-1 myoblasts between pairs of sites that are coaccessible in HSMM. For each bin of coaccessibility in HSMM, pairs of peaks that overlapped peaks in 54-1 non-targeting controls were assessed for concordant dynamics (>2 log2 fold change in both peaks or < −2 log2 fold change in both peaks). Error bars indicate 95% confidence intervals calculated using Fisher’s exact test. Asterisks represent estimates significantly different than 1 (p-values < 0.05 by Fisher’s exact test). E) Two “phases” of myoblast differentiation illustrated. F) A summary of the Cicero coaccessibility links between the MYOG promoter and distal sites in the surrounding region. The height of connections indicates the magnitude of the Cicero coaccessibility score between the connected peaks. The top set of (red) links were constructed from cells in phase 1, while the bottom (in blue) were built from phase 2. See also Figures S3 and S4.

We applied Cicero to generate a genome-wide cis-regulatory map from our myoblast sci-ATAC-seq data. As the first step, for example in experiment 1, Cicero aggregated differentiating myoblasts into 277 groups and identified 6.5M pairs of sites with positive coaccessibility scores, including 1.8M comprising a distal element and promoter. As the coaccessibility threshold is raised, promoters are connected to fewer regulatory elements with higher confidence. For example, at a cutoff of 0.25, promoters were connected to a median of 2 distal elements in experiment 1 (Supplemental Figure 3A). Distal sites that were highly coaccessible with promoters were more conserved across vertebrates (Figure 3B). This trend was more pronounced for sites linked to highly conserved genes, which tended to be coaccessible with more conserved distal elements (Figure 3C). To verify that coaccessibility between sites was not confined to our specific primary myoblast culture, we performed bulk ATAC-seq in myoblasts from another donor (“54-1”), before and after differentiation. Reassuringly, highly coaccessible sites were 2.2-fold more likely than unlinked sites to be undergoing directionally concordant changes in accessibility across differentiation in the 54-1 cells (Figure 3D). To explore how accessibility corresponded with gene regulation during differentiation, we devised a composite “gene activity score” of accessibility at both promoters and linked distal sites (Methods). Accessibility-based gene activity scores were positively correlated with expression (Supplemental Figure 3B-D).

As coaccessible elements tended to cluster, we post-processed Cicero’s output with a community detection algorithm to identify “cis-coaccessibility networks” (CCANs): modules of sites that are highly coaccessible with one another. The majority of dynamically accessible sites were included in CCANs even using a high coaccessibility threshold (Supplemental Figure 4A-E).

To assess the reproducibility of Cicero maps, we adapted a maximum weighted bipartite matching method to identify pairs of CCANs from the two experiments that share DNA elements in common (Methods). This algorithm matched 1,868 of the CCANs between the experiments, accounting for 84% and 91% of the sites in CCANs in experiments 1 and 2, respectively (Supplemental Figure 4F). Most pairs of sites linked in one experiment were also linked in the other (score > 0.25; 81% of expt. 1 sites also linked in expt. 2; 64% of expt. 2 sites also linked in expt. 1; Supplemental Figures 4G,H).

To further investigate chromatin dynamics during differentiation, we constructed Cicero maps on the two ‘phases’ of the pseudotime trajectory (before vs. after the F₂ branch) and computed CCANs for each map (Figure 3E). The general structure of Cicero connections was often maintained around genes of interest. For example, a similar set of distal elements are linked to the promoter of MYOG in both the early and late phases (Figure 3F). To identify CCANs that were maintained, gained or lost during differentiation, we applied our matching algorithm to compare CCANs between the first and second phases. For experiment 1, this algorithm matched 1,945 CCANs, accounting for 88% and 91% of the sites in CCANs in the first and second phases, respectively. However, although the general structure of CCANs was stable (few sites switched CCANs), many sites joined or left CCANs during differentiation (Supplemental Figure 4I,J). Intriguingly, we identified 60 sequence motifs that were predictive of whether a site would join, leave, or remain within a CCAN, including CTCF, which strongly predicted that an accessible site would remain within a CCAN (Supplemental Figure 4K).

We hypothesized that the CCANs identified by Cicero constitute “chromatin hubs”. Chromatin hubs, which are thought to involve looping interactions between distal regulatory elements and the genes they target, may act to coordinate the assembly of transcription complexes (de Laat and Grosveld, 2003; Tolhuis et al., 2002). To satisfy the definition of a chromatin hub, we expect CCANs should meet four criteria. First, they should exhibit greater physical proximity than expected based on their distance in the linear genome. Second, they should interact with a common set of protein complexes. Third, they should be epigenetically modified in concordant ways and at similar times. Finally, they should substantially contribute to regulating genes with promoters within the hub.

Coaccessible DNA elements exhibit physical proximity

To test whether coaccessible sites are closer together in the nucleus than unlinked sites at similar distances in the linear genome, we generated and applied Cicero to sci-ATAC-seq chromatin profiles from 889 human lymphoblastoid cells (GM12878), for which ChIA-PET and promoter-capture Hi-C data are available.

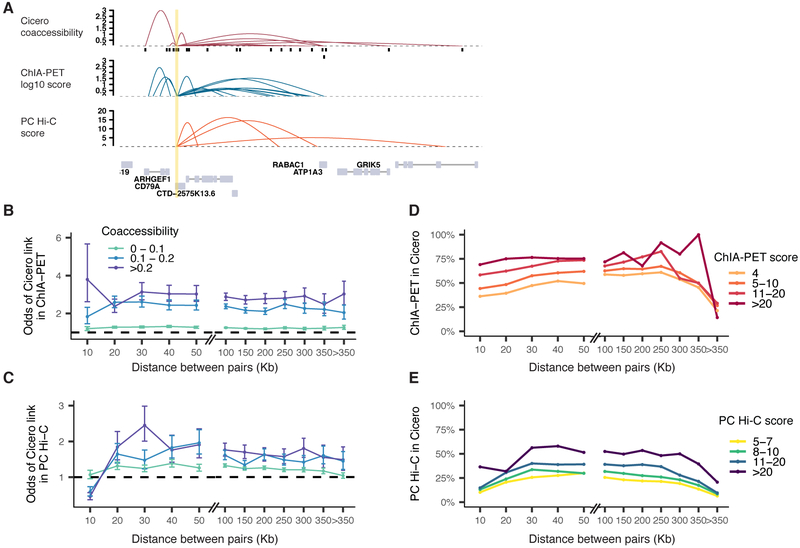
We observed strong concordance between Cicero-based linkages and DNA elements in RNA pol II-mediated contacts captured via ChIA-PET (Tang et al., 2015) as well as contacts found by promoter-capture Hi-C (Cairns et al., 2016; Mifsud et al., 2015), e.g. at the CD79A locus (Figure 4A). About half of DNA elements ligated via ChIA-PET (“anchors”) overlapped with accessible sites in our data, with greater overlap between anchors that were supported by multiple ChIA-PET reads and sites that were accessible in many cells (Supplemental Figures 5A,B). Pairs of sites reported by Cicero to be coaccessible were up to 2- to 3-fold more likely to be found in ChIA-PET and promoter-capture Hi-C than unlinked sites separated by similar distances (Figure 4B-C). Reciprocally, pairs of sites linked by many independent ChIA-PET or Hi-C ligation fragments were more likely to also be reported as coaccessible by Cicero (Figure 4D-E), e.g. ~75% of high-confidence ChIA-PET connections found in Cicero’s map. Although proximity ligation frequencies should not be taken as a direct measure of physical distance, these analyses show that Cicero-linked sites exhibit greater-than-expected physical proximity, even when very distant in the linear genome. We also found that Cicero connected sites were more likely to occupy the same topologically associated domain (TAD) than unlinked sites at the same distance (Fisher’s exact test, p-value < 2e-5 for all distance bins, TADs derived from 1kb-resolution Hi-C analysis of GM12878 (Rao et al., 2014)). Similarly, Cicero-linked sites were 1.5-fold more likely than unconnected pairs at the same distance to be found in the same A/B compartment (Supplemental Figures 5C,D).

Figure 4.

Coaccessible DNA elements linked by Cicero are physically proximal in the nucleus. A) Cicero connections for the CD79A locus compared to RNA pol-II ChIA-PET (Tang et al., 2015) and promoter capture Hi-C (Cairns et al., 2016). Link heights for ChIA-PET are log-transformed frequencies of each interaction PET cluster and for promoter capture Hi-C are soft-thresholded log-weighted p-values from the CHiCAGO software. B) Odds ratio of pairs of sites within a given coaccessibility and distance bin found in RNA pol-II ChIA-PET compared to pairs of sites with coaccessibility <= 0. Color represents the coaccessibility bin. Error bars indicate 95% confidence intervals calculated using Fisher’s exact test. All points shown were significantly different than 1 (p-values < 0.05 by Fisher’s exact test). C) Similar to panel B, but comparing Cicero links to sites ligated in promoter-capture Hi-C. All points shown were significantly different than 1 (p-values < 0.05 by Fisher’s exact test) except for at the 10 kb bin which may be impacted by the resolution of Hi-C consequent to the use of a 6-cutter restriction enzyme. For panels B and C, we fit a linear model which included coaccessibility score and overall accessibility and found in both cases that coaccessibility had a significant effect on presence in comparison datasets even after correcting for this potential confounder (see Methods for details). D) Fraction of ChIA-PET contacts found in Cicero connections as a function of distance, stratified by multiplicity of ligation product detections. E) Promoter-capture contacts detected in Cicero CCAN connections as a function of distance, stratified by CHiCAGO score. See also Figure S5.

Coaccessible DNA elements carry pairs of motifs for interacting TFs

We next investigated whether Cicero links might be mediated by interacting TFs. We searched for known sequence motifs within each peak in the HSMM data that could accurately predict whether Cicero would link other sites to it. Promoters with DNA binding motifs for one or more core myogenic TFs were significantly more likely to be connected (coaccessibility score > 0.25) to an opening distal site than promoters without them. For example, promoters containing at least one MYOD, MYOG or MYF6 motif were 3.6-fold more likely to be connected to an opening distal site than promoters with none of these motifs (p = 8.7 × 10⁻²⁷⁰; likelihood ratio test for logistic regression model).), and similarly, promoters with at least one MEF2 family motif were 2.8-fold more likely to be connected to an opening distal site (p = 7.9 × 10⁻¹¹⁹).

We hypothesized that these correlations resulted from direct, TF-mediated interactions. To explore this further, we focused on promoters linked to exactly one dynamically accessible distal site (coaccessibility score > 0.05) and used Graphical LASSO to identify pairs of motifs where the presence of a motif in the promoter predicted the presence of the paired motif in the dynamically accessible distal site (Methods). We identified a number of motif pairs corresponding to TFs known to physically interact. For example, opening distal elements were significantly more likely to have a MEF2 or RUNX1 motif if they were linked to a promoter with a MYOD motif (Supplemental Figure 6A). Myogenic regulatory factors (MRFs) are known to interact physically with MEF2 and RUNX1 (Knoepfler et al., 1999; Molkentin et al., 1995; Philipot et al., 2010).

MYOD coordinates histone modifications in cohorts of coaccessible sites

The physical proximity of coaccessible sites suggested that recruitment of histone-modifying enzymes to one site might induce changes in physically proximate sites. Indeed, pairs of sites were more likely to be undergoing significant, concordant gains in H3K27ac if they were linked by Cicero (Figure 5A). Sites that themselves exhibited static accessibility, but were linked to a dynamic, opening site, showed strong gains in H3K27ac, while static sites that were linked to dynamic, closing sites showed strong losses (Figure 5B). The gains in acetylation might be driven by de novo binding of MYOD at the opening site followed by recruitment of a histone acetyltransferase (e.g. p300). Supporting this, of the 2,050 sites with significant gains in H3K27ac but static accessibility, only 46% were bound by MYOD in myotubes. However, 97% were linked by Cicero to a MYOD-bound site (Figure 5C). Moreover, equipping a regression model with information about linked sites improved its accuracy in predicting changes in a site’s histone marks (Supplemental Figure 6B)

Figure 5.

Coaccessible DNA elements linked by Cicero are epigenetically co-modified. A) Odds ratio of a site gaining H3K27ac during myoblast differentiation, given that it is linked to a site that is doing so. Color indicates the strength of the Cicero coaccessibility links. The lightest color indicates pairs of sites that are unlinked by Cicero. B) Correspondence between a statically accessible site’s gain or loss of H3K27ac and its maximum coaccessibility score to a site that is opening (x axis) or closing (y axis). Sites that are not linked to an opening or closing site are drawn at x = 0 or y = 0, respectively. C) Similar to panel B, but describing the correspondence between a site’s gain or loss of H3K27ac and its maximum coaccessibility score to a site that is gaining or losing MYOD. D) The variance explained in a series of linear regression models in which the response is the log₂ fold change in H3K27ac level of each DNA element and the predictors are whether that site is opening, closing, or static, whether it gains or loses MYOD binding, and whether it is linked to neighbors that are doing so. See Methods for details on model specifications. E) The Cicero map for the 755 kb region surrounding MYH3 along with called MYOD ChIP-seq peaks from (Cao et al., 2010). Sites opening in accessibility are colored by their opening pseudotime (see Methods), sites not opening in accessibility are shown in grey. The inset shows the 60 kb region surrounding MYH3 along with MYOD ChIP-seq and H3K27ac ChIP-seq signal tracks from (Cao et al., 2010) and (The ENCODE Project Consortium, 2012). Only protein-coding genes are shown. F) Opening pseudotimes for all opening sites, subdivided by whether MYOD is bound in myoblasts and myotubes, myotubes alone, or neither. G) The difference in opening pseudotimes between pairs of linked DNA elements. The pairs are grouped based on whether one or both sites is constitutively bound by MYOD. H) TF binding motifs selected by an elastic net regression (alpha = 0.5), with a response encoding the MYOD binding status of each site. See also Figure S6.

We next considered whether gains in MYOD binding were concentrated in a few CCANs or widely distributed. Of the 2,323 hubs containing promoters, 74% contained at least one site undergoing a change in MYOD binding. For the subset of 431 hubs with a differentially expressed gene, 92% contained at least one site changing in MYOD binding. For example, within the single hub that includes myosin heavy chain isoforms 1, 2, 3, 4, 8, and 13 and numerous other genes, 15 sites underwent significant increases in accessibility. Of these, all were bound by MYOD in myotubes (Figure 5E). Interestingly, however, two sites very near MYH3 (marked with asterisks) opened substantially earlier in pseudotime than others and were bound by MYOD in myoblasts as well.

We wondered more generally whether sites bound by MYOD in myoblasts and throughout differentiation opened earlier than sites that gained MYOD binding during differentiation. A changepoint analysis using PELT (Killick et al., 2012) revealed that sites bound by MYOD throughout differentiation opened significantly earlier in pseudotime than those that gained MYOD (Mann-Whitney test p-value 1.2e-122) or were never bound by it (Mann-Whitney test p-value 8.0e-223) (Figure 5F). Moreover, rather than being enriched in whole hubs that open early as a group, constitutively MYOD-bound sites opened significantly earlier than sites linked to them that either gained MYOD (two-sided paired Student's t-test p-value = 1.0e-182) or were never bound by it (two-sided paired Student's t-test p-value =4.5e-318) (Figure 5G). Constitutively MYOD-bound sites were enriched for the MEIS1 and AP-1 motifs (Figure 5H) compared with sites that gain MYOD later in differentiation. Altogether, sites with MEIS1 motifs were linked to 69% of dynamically opening sites compared with only 16% of sites genome-wide (coaccessibility score > 0.25). Murine Meis1, in conjunction with Pbx1, has been reported to act as a complex required for the MYOD-mediated activation of the myogenin promoter, and mutations in MYOD that prevent interaction with PBX resulted in loss of many binding sites and regulatory targets (Berkes et al., 2004; Fong et al., 2015). Our results suggest MEIS1 recruitment of MYOD may be pervasive throughout the genome and could nucleate activation of other sites within a chromatin hub.

Sequence features of active chromatin hubs predict gene regulation

We wondered whether Cicero’s putative maps could be used to predict changes in gene expression. As a first test, we asked whether two genes with coaccessible promoters exhibited greater correlation in expression across individual cells than genes that were nearby but whose promoters were not linked by Cicero. Indeed, differentially expressed genes showed greater correlation in expression as a function of their coaccessibility score (Supplemental Figure 7F).

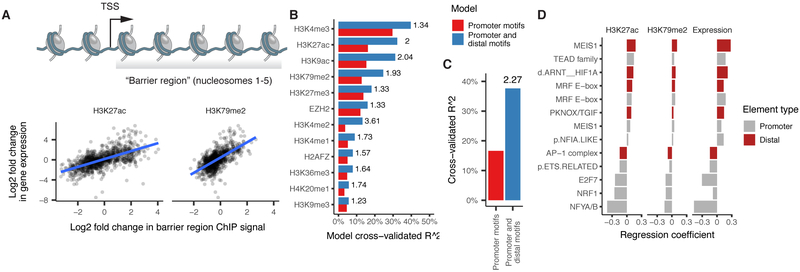
We next sought to develop a linear regression model to predict changes in either gene expression or changes in “barrier region” histone marks associated with promoter activation (Figure 6A). Our first model takes as input a binary map of the TF binding motifs present at the promoter upstream of each TSS. We then train it to predict how much of a gene’s observed expression change is attributable to each TF motif using elastic net regression and 50-fold cross-validation (Methods). The promoter-based model explained only 17% of the variance in expression and performed similarly in predicting a panel of histone marks (Figure 6B-C). Augmenting this model with TF motifs at linked distal sites improved its ability to explain changes in expression by 2.27-fold (Figure 6C). The TF motifs identified by the model included the MRF E-box, the MADS box bound by MEF2 family proteins, and the MEIS1 binding site, which were associated with upregulation, along with motifs for factors that drive cell proliferation such as AP-1, which were associated with downregulation (Figure 6D). Thus, when tasked with predicting which factors are important for gene regulation, our regression identified the major myogenic TFs using only the sequences in sites linked together by Cicero.

Figure 6.

Chromatin dynamics at distal DNA elements predicts gene regulation. A) Changes in histone acetylation in the first 1 kb downstream of each gene’s TSS, corresponding to the “barrier” to RNA pol II elongation posed by nucleosomes, are correlated with changes in its expression. B) Two regression models predict changes in the histone marks deposited throughout each gene’s barrier region. The first model predicts changes on the basis of TF binding motifs in gene promoters. The second model adds variables encoding the strength of coaccessibility with linked sites containing the motif. See Methods for details on the various models. Adjusted R^2 is computed as the fraction of null deviance explained. The number to the right of each bar indicates the ratio of variance explained between the first and second model. C) Similar to panel B, with changes in expression as the response. D) Coefficients from the model incorporating sequence at distal sites for each motif surviving model selection via elastic net. Note that the model considers each motif twice: once at promoters and again at distal sites, and both can be selected by elastic net. See also Figure S7.

MEIS1 and PBX1 are required for coordinated myoblast chromatin hub activation

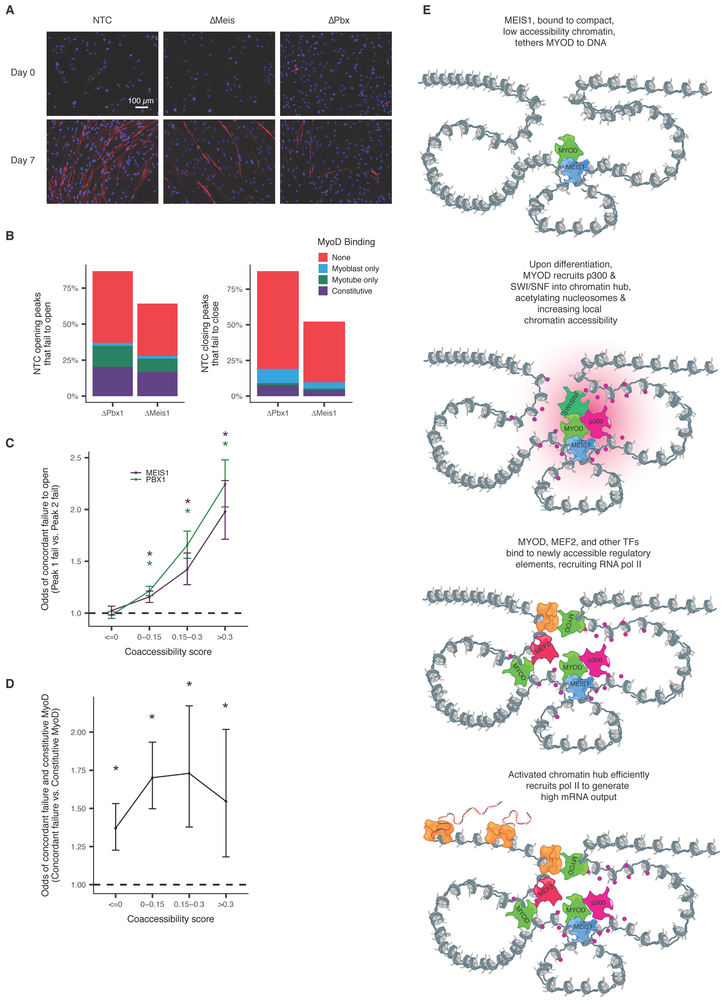
We hypothesized that MYOD, which recruits p300/PCAF and the BAF complex upon myoblast differentiation, might act to nucleate histone modification and nucleosome remodeling throughout a chromatin hub. To test this hypothesis, we genetically ablated MEIS1 or PBX1 (which forms a heterodimer with MEIS1) with CRISPR/Cas9 in 54-1 cells and then performed bulk ATAC-seq as they differentiated. Both ΔMEIS1 and ΔPBX1 myoblasts differentiated markedly less efficiently, with fewer and smaller myotubes than cells transduced with non-targeting control (NTC) sgRNAs (Figure 7A). Of 14,321 sites that underwent significant changes in accessibility in the 54-1 NTC, 7,868 (55%) and 12,520 (87%) failed to do so in ΔMEIS1 or ΔPBX1 cells respectively, and nearly 25% of sites that failed to open overlapped sites bound by MYOD in both normal myoblasts and myotubes (Figure 7B).

Figure 7.

MEIS1 and PBX1 knockout myoblasts fail to differentiate and show coordinated accessibility defects. A) Immunofluorescence microscopy images of non-template control, MEIS1 knockout and PBX1 knockout 54-1 cells at day 0 and day 7 post induction of differentiation. Nuclei are stained using DAPI, MYH3 is stained using anti-myosin MF20 and Alexa Fluor 594. B) Percent of peaks that open during differentiation in the NTC that fail to open in PBX1 and MEIS1 knockouts. Colors indicate the presence of MyoD binding in myoblasts and myotubes by ChIP-seq in HSMM. C) Odds ratios of concordant failure in accessibility gain across differentiation in 54-1 knockout myoblasts between pairs of sites that are coaccessible in HSMM. For each bin of coaccessibility in HSMM, pairs of peaks that overlapped peaks in 54-1 non-template controls were assessed for concordant failure to open (peaks that open in NTC but do not do so in knockouts). Color indicates knockout. Error bars indicate 95% confidence intervals calculated using Fisher’s exact test. Stars represent estimates significantly different than 1 (p-values < 0.05 by Fisher’s exact test). D) Similar to C. Odds ratios of concordant failure in accessibility gain given constitutive MyoD binding in one of the peaks. For each bin of coaccessibility in HSMM, pairs of peaks that overlapped peaks in 54-1 were assessed for presence of constitutive binding of MyoD in one or both of sites as well as coordinated failure to open. Only pairs of sites where both open in NTCs were included. Data is for MEIS1 knockout only due to a lack of sufficient power in PBX1. E) A model of how chromatin hub activation could be nucleated by a subset of “precociously” opening DNA elements. Such sites are occupied by TFs competent to bind relatively closed, inactive DNA elements, such as MEIS1, which may tether less competent factors such as MYOD to the hub. Subsequent recruitment of p300 and the BAF complex, possibly through intermediary factors (e.g. MYOD), leads to remodeling and acetylation of histones throughout the hub. These newly available sites are then bound by other transcriptional activators (e.g. MEF2), leading to the recruitment of Pol II. Moreover, acetylation of the histones downstream of assembled pre-initiation complexes reduces the barrier they pose to elongation, enhancing efficient transcription of genes within the hub.

Having observed that pairs of sites Cicero identified as highly coaccessible in HSMMs were more likely to open or close concordantly in the 54-1 cells upon differentiation (Figure 3D), we asked whether coaccessible pairs would be concordantly perturbed in the mutants. Indeed, pairs of sites that opened in the 54-1 NTC and were linked by Cicero tended to both fail to open in the mutants. For example, pairs of sites that Cicero linked with a coaccessibility score > 0.3 were 2.3-fold more likely to both fail to open in ΔPBX1 and 1.6-fold more likely in ΔMEIS1 than pairs of sites Cicero deemed not coaccessible, suggesting that coaccessibility is often maintained even when cells fail to differentiate (Figure 7C).

We next assessed whether constitutively MYOD-bound sites might nucleate changes throughout hubs by first dividing normally opening sites into those that were constitutively MYOD-bound, and those that were not. We then tested whether other sites linked to these groups at varying levels were more or less likely to coordinately fail to open in ΔMEIS1 (Figure 7D). Consistent with our hypothesis, highly coaccessible sites were 1.5-fold more likely to both fail to open in ΔMEIS1 myoblasts when one of the sites was constitutively bound by MYOD than when neither was constitutively bound by MYOD (p-value 0.0011, Fisher’s exact test). These findings suggest that MEIS1 may be important for proper MYOD-mediated recruitment of chromatin remodeling complexes to specific sites that subsequently act on others in 3D proximity.

Discussion

Despite their paramount importance, maps that comprehensively link distal regulatory sequences to their target genes are still lacking. Towards addressing this, we developed Cicero, which constructs putative cis-regulatory maps from single cell chromatin accessibility data. We anticipate these maps will guide downstream validation by other scalable methods such as massively parallel reporter assays and CRISPR-mediated (epi)genome editing. In contrast with other approaches like ChIA-PET and promoter-capture Hi-C, Cicero operates on single cell data and therefore avoids averaging effects that can confound bulk assays. As described here for a model of skeletal muscle differentiation, downstream analyses of Cicero-based links can advance our quantitative understanding of the eukaryotic gene regulation, and may also facilitate the identification of the target genes of noncoding variants underlying GWAS signals.

Pseudotemporal ordering of chromatin accessibility profiles from differentiating myoblasts revealed dynamic changes in thousands of DNA elements. Although changes in promoter accessibility were a poor predictor of gene expression dynamics, distal sites linked to genes by Cicero improved these models, particularly when sequence motifs were incorporated.

Our analyses show that the CCANs defined by Cicero meet the definition of chromatin hubs: they are physically close in the nucleus, their histone marks change in a coordinated fashion, and their interactions are likely mediated by a common set of TFs, some lineage-specific. For myogenesis, our results support a model of gene activation in which a subset of “precocious” enhancers recruit chromatin remodeling enzymes and other epigenetic modifiers to the hub, which mediate increases in accessibility of other binding sites (Figure 7E). For such a mechanism to work, chromatin hubs enclosing genes silent in myoblasts and activated during differentiation would need to be largely established prior to its onset. Indeed, Cicero linked more than half of activated or upregulated genes into such “pre-established” chromatin hubs. Sites that join or leave a hub are distinguished from those that remain part of it by specific TF motifs.

In differentiating myoblasts, MYOD is widely understood to recruit the BAF complex and p300/PCAF to activate enhancers of muscle genes (Serra et al., 2007; Simone et al., 2004). Although the role of MYOD in recruitment is well appreciated, how MYOD is itself recruited is less clear. We find that early-opening sites are enriched for MEIS1 motifs and constitutive MYOD binding. Meis1 has previously been reported to tether Myod to the inactive myogenin promoter prior to the onset of differentiation, and is required for myogenin activation and chromatin remodeling that permits the binding of MYOD to nearby MRF E-boxes that were previously inaccessible (Berkes et al., 2004; Maves et al., 2007; de la Serna et al., 2005). Whether MEIS1/PBX1 acts to tether MYOD to inactive chromatin more generally throughout the genome has remained an open question.

Our analyses suggest that MEIS1 and its cofactor PBX1 are required for chromatin remodeling at a large fraction of sites that normally open during myoblast differentiation by serving as initial recruitment sites for epigenetic remodeling enzymes. Binding of p300 to MEIS1/PBX1-tethered MYOD could then acetylate histones at all DNA elements physically nearby in the chromatin hub. This model may help explain the pervasive gains and losses of histone acetylation throughout the accessible genome, despite the smaller number of differentially accessible or MYOD-bound elements. Although we cannot exclude the possibility that some of the defects in chromatin remodeling are due to secondary effects downstream of MEIS1/PBX1, our genome-wide analysis taken together with biochemical and genomic data from previous studies support a direct role for MEIS1/PBX1 in recruiting factors that activate chromatin hubs.

Cicero provides an effective, genome-wide means of generating candidate links between regulatory elements and target genes in a tissue or cell type of interest using data from a single experiment. The chromatin hubs that it defines will facilitate the construction of quantitative models of epigenetic and gene expression dynamics, as well as the identification of genes whose dysregulation underlies GWAS associations. As the field pursues organism-scale cell atlases that comprehensively define each cell type and its molecular profile, such regulatory maps will be essential for understanding the epigenetic basis of each cell type’s gene expression program, in both health and disease.

Limitations

The primary limitation of Cicero is the putative nature of the regulatory connections it identifies. Determining whether a distal DNA element is necessary or sufficient to exert regulatory influence on the genes Cicero links to it requires downstream experimentation. We note that proximity ligation based methods for linking DNA elements to genes such as ChIA-PET or promoter capture Hi-C also have this limitation; proximity does not definitively mean regulatory interaction. Moreover, although we have found that our overall comparisons with available proximity ligation based data are concordant, some individual connections are missing from one or both sets of putative interactions, and it is not clear which should be considered more reliable. On the one hand, ligation is a molecular measurement (albeit an indirect one) of physical proximity, while Cicero’s links are based on computational inference. One the other, the ligation assays discussed here operate on bulk cell populations and are therefore subject to the artifacts introduced by averaging cells of different types or states, while Cicero operates at single-cell resolution.

STAR Methods Text

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Cole Trapnell (coletrap@uw.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Human Skeletal Muscle Myoblasts (HSMM)

HSMM derived from quadriceps biopsy (Lonza, catalog #CC-2580, lot #257130: healthy, age 17, female, of European ancestry, body mass index 19; cells were used within 5 passages of purchase) were cultured in skeletal muscle growth media (GM) using the SKGM-2 BulletKit (Lonza). The cells and differentiation protocol are those from Trapnell et al. (2014). Cells were seeded in 15 cm dishes, media was replenished every 48 hours and cells were allowed to reach 80-90% confluence. Differentiation was induced at time 0 via a switch to differentiation medium (DM) composed of alpha-mem (Thermo Fisher Scientific) and 2% horse serum. Cells in GM (time 0) or DM were then harvested at the specified times and processed as described below. HSMM tested negative for mycoplasma contamination within 3 weeks of the experiment.

GM12878

GM12878 (purchased from Coriell Cell Repository) was cultured in RPMI 1640 medium (Gibco 11875) supplemented with 15% FBS, 100U/ml penicillin and 100 μg/ml streptomycin. Cells were cultured in an incubator at 37C with 5% CO2 and were split to a density of 300,000 cells/ml three times a week.

54-1 Immortalized Human Myoblasts

54-1 human myoblasts (Krom et al., 2012; Snider et al., 2010) were a kind gift from Dr. Robert Bradley and Dr. Silvere van der Maarel. For expansion, 54-1 cells were cultured in high serum media containing 20% FBS, 1% penn-strep, 10 ng/mL recombinant human FGF and 1 μM dexamethasone in F-10 media. For myoblast differentiation, media was replaced with low serum media containing 1% horse serum, 1% penn-strep, 10 μg/mL insulin and 10 μg/mL transferrin in F-10 media.

METHOD DETAILS

Sci-ATAC-seq library construction

We prepared sci-ATAC-seq libraries using an improved version of the original protocol (Cusanovich et al., 2015), with improvements reported in (Cusanovich et al., 2017). Briefly, HSMM cells were harvested at defined times post switch to DM, washed and cells were lysed to obtain nuclei by resuspending cells in cold lysis buffer (CLB, 10 mM Tris HCL pH7.4, 10 mM NaCl, 3 mM MgCl2 and 0.1% IGEPAL CA-130) supplemented with protease inhibitors (Sigma). For each time point, 2.75 × 10⁵ nuclei were resuspended in a mix of 990 μL of CLB supplemented with protease inhibitors and 1.1 ml of Tagment DNA buffer (Illumina), and divided evenly amongst the wells of a 96 well LoBind plate (Eppendorf). 1 μL of uniquely barcoded Tn5 (Illumina) was added to each well followed by incubation at 55C for 30 minutes. Following Tn5 incubation, 20 μL of a solution containing 40 mM EDTA and 1 mM spermidine were added to each well and incubated at 37C for 15 minutes. Tagmented nuclei were pooled, stained by addition of DAPI to a final concentration of 3 μM and 25 DAPI positive nuclei were sorted into the wells of 96 well LoBind plates containing 12.5 μl of 0.8 mg/mL BSA and 0.04% SDS in EB buffer (Qiagen). Nuclei were lysed by incubation at 55C for 15 minutes. ATAC libraries were PCR amplified by addition of unique combinations of P5 and P7 primers for each well of sorted nuclei and PCR conditions were such that amplification did not reach saturation. For each sorted 96 well plate ATAC libraries were pooled and products cleaned using the Zymo Clean & Concentrator kit (Zymo). Libraries were quality controlled by analyzing on PAGE gels and quantified using the Qubit broad range DNA quantitation kit (Thermo Fisher Scientific).

Bulk ATAC-seq library construction

Bulk ATAC-seq experiments were performed as previously described (Buenrostro et al., 2013). Briefly, cells were trypsinized, washed with PBS and resuspended in cold-lysis buffer (CLB: 10 mM Tris-HCl pH 7.4, 10 mM NaCl, 3 mM MgCl₂ and 0.1% IGEPAL CA-630) supplemented with protease inhibitors (Sigma) to obtain nuclei. 100,000 nuclei were pelleted, resuspended in CLB and the equivalent of 20,000 nuclei were transferred, mixed with Tagment DNA buffer and Tn5 enzyme (Illumina). Reactions were incubated at 37C for 30 minutes and purified using the MinElute kit (Zymo). Sequencing adapters and indices were added via PCR using standard Nextera P5 and P7 primers with excess primers removed using a 1X Ampure cleanup (Agencourt). Libraries were quality controlled by examining on a PAGE gel and quantified using the Qubit broad range DNA assay (ThermoFisher Scientific).

54-1 knockout construction

Oligos containing sequences for small guide RNAs (sgRNAs) targeting PBX1, MEIS1 and non-targeting controls were designed as follows:

5’-tatcttGTGGAAAGGACGAAACACC[G]-[20bp sgRNA]-gttttagagctaGAAAtagcaagttaaaataagg-3

corresponding to the following form:

[U6 homology]-[sgRNA]-[sgRNA backbone homology]

The sgRNA sequences targeting Meis1, PBX1 and non-targeting controls are shown in Supplemental Table 1.

Oligos were ordered from IDT and made double stranded by PCR using primers that bind the U6 and sgRNA backbone homology sequences. Oligos corresponding to each sgRNA were then ligated using the In-Fusion HD kit (Clontech) into BsmBI and alkaline phosphatase digested lentiCRISPRv2-Blast (Addgene, #83480). Ligations were then transformed into Stellar Competent cells (Clontech), bacteria grown overnight in LB containing ampicillin and plasmids recovered using the Qiagen MiniPrep kit. Lentivirus was generated by transfection into HEK293T using the ViraPower packaging mix and viral containing supernatant was filtered using a 45 μm steriflip vacuum filter (Fisher Scientific). 54-1 cells were transduced with filtered virus, cultured for 48 hours and sgRNA containing cells selected by incubation with 5 μg/mL blasticidin. Cells were expanded for 21 days post-selection to allow for genome editing prior to myoblast differentiation experiments and bulk ATAC-seq.

Differentiation was induced in 54-1 lines as described for HSMM. Bulk ATAC-seq was conducted on day 0 and day 7 after induction.

54-1 staining

At various times along the differentiation protocol, 54-1 cells were washed with PBS, fixed by incubating for 20 minutes in 4% PFA (Electron Microscopy Sciences) in PBS and an additional 10 minutes in 100% methanol (Sigma). Samples were washed twice with IF buffer (0.2% triton X-100 and 5% w/v bovine serum albumin in PBS) and incubated with anti-myosin MF20 antibody (eBioscience) overnight at 4C with rotation. After primary antibody incubation, samples were washed twice with IF buffer and incubated with donkey anti-mouse Alexa Fluor-594 secondary antibody (Molecular Probes) and 5 μM DAPI. Finally, samples were washed twice with IF buffer, PBS added and myosin staining assessed by imaging on a Zeiss Axio Observer (Carl Zeiss Microimaging).

QUANTIFICATION AND STATISTICAL ANALYSIS

Processing of raw data

For sci-ATAC-seq, raw reads were processed identically to in Cusanovich & Hill et al. enclosed. Details are reproduced here for clarity. Briefly, BCL files were converted to fastq using bcl2fastq v2.16 (Illumina). Barcodes were corrected using a custom python script such that if a barcode component (tagmentation or PCR barcode separately) was within 3 edits from an expected barcode component, and the next best matching barcode component was at least 2 further edits away, the barcode component was corrected to the best match. Reads of barcode components that were not unambiguously assignable to an expected barcode were discarded.

Reads were mapped to the hg19 reference genome using bowtie2 with non-default options ‘-X 2000 -3 1’ (Langmead and Salzberg, 2012). Reads with mapping quality less than 10 were filtered. PCR duplicates were removed using a custom python script. Cells with low read counts were removed. The read count cutoff was determined by identifying the trough between the peaks of the bimodal distribution of read counts using the mclust package in R (Scrucca et al., 2016).

For the bulk ATAC-seq datasets, processing was done as above, but without barcode correction.

Defining accessible sites

To define peaks of accessibility across all sites, we used the MACS (version 2.1.1) (Zhang et al., 2008) peak caller. Specifically, we used macs2 callpeak, with the following non-default options: --nomodel --extsize 200 --shift −100 --keep-dup all. Reads from the encode blacklist (ENCFF001TDO) were excluded from peak-calling. Promoter peaks were further defined as the union of the annotated transcription start site (TSS) (Gencode V17) minus 500 base pairs, and MACS defined peaks upstream of the TSS. Cells were determined to be accessible at a given peak if a read from that cell overlapped the peak. Peaks were called as above for both of the HSMM experiments separately, and then the union of the two peak sets was used.

For the GM12878 and HL60 mixed dataset, preliminary peaks were called by MACS and used to separate the cell types using multi-dimensional scaling by Jaccard distance. The subset of reads from GM12878 cells was then used to recall peaks for GM12878 as above.

After accessible peaks were defined, a matrix was generated for each dataset with the count of reads from each cell or timepoint (in bulk) that overlapped each accessible peak.

Pseudotemporal ordering

For the HSMM dataset, contaminating interstitial fibroblasts were removed in silico based on the absence of promoter accessibility in any of several known muscle markers (MYOG, MYOD1, DMD, TNNT1, MYH1, MYH3, TPM2). In addition, cells with fewer than 1,000 accessible sites were excluded due to low assay efficiency. Finally, peaks present in less than 1% of cells were excluded during pseudotemporal ordering steps.

Despite improvements to the sci-ATAC-seq protocol that delivered a substantial increase in the number of sites detected per cell, sci-ATAC-seq data remains zero-inflated. The quality and efficiency of transposition, which varies between cells and across batches, is likely to be a major technical source of variation in the data. Simple dimensionality reduction techniques such as MDS show that a poorly-assayed cell is often more similar to other poorly-assayed cells of a different type than to well-assayed cells of the same type. In order to accurately group cells with similar chromatin accessibility profiles, we first clustered peaks that were within 1 kb and summed the reads overlapping them to create an integer-valued count matrix M.

To order the cells by progress through differentiation, we determined which aggregated peaks were relevant to the HSMM time course by fitting the following model:

$$\text{ln}(M_i)={\beta }_0+{\beta }_{T}T+{\beta }_{S}S$$

Where M_i is the mean of a negative binomially-distributed random variable for the number of reads overlapping the aggregate region i, T encodes the times at which each cell was harvested and S is the total number of accessible sites in each cell. We compared this full model to the reduced model:

$$\text{ln}(M_i)={\beta }_0+{\beta }_{S}S$$

by likelihood ratio test. This approach has been shown to improve power for single-cell RNA-seq transcript counts compared to simple two-group tests comparing cells at the beginning and the end of a trajectory (Qiu et al., 2017a, 2017b). Sites determined by this method to be time dependent and which were accessible in less than 10% of cells were then used to reconstruct the pseudotime trajectory using Monocle 2 (parameters ncenter and param.gamma set to 100, see (Qiu et al., 2017a)). To remove any bias created by different assay efficiency in different cells, total sites accessible was included as a covariate in the tree reconstruction. Each cell was assigned a pseudotime value based on its position along the trajectory tree. Cells that mapped to the F₂ branch were excluded from downstream analysis.

Differential accessibility analysis

When testing for differential accessibility across cells at a particular site, it is important to exclude technical variation due to differences in assay efficiency as discussed above. We first grouped cells at similar positions in pseudotime. We did this by k-means clustering along the pseudotime axis (k=10). These clusters were further subdivided such into groups containing at least 50 and no more than 100 cells. Next, we aggregated the binary accessibility profiles of the cells in each group into a matrix A, so that A_ij contains the number of cells in group j for which DNA element i is accessible. The average pseudotime ψ_j and average overall cell-wise accessibility S_j for cells in each group j were preserved for use during differential analysis.

To determine which peaks of accessibility were changing across pseudotime, we fit the following model to the binned data:

$$\text{ln}(A_i)={\beta }_0+{\beta }_{\tilde{\psi }}\tilde{\psi }+{\beta }_{\tilde{S}}\tilde{S}$$

Where A_i is the mean of a negative-binomial valued random variable of cells in which site i is accessible, and the tilde above ψ and S indicates that these predictors are smoothed with natural splines during fitting. This model was compared to the reduced model:

$$\text{ln}(A_i)={\beta }_0+{\beta }_{\tilde{S}}\tilde{S}$$

by the likelihood ratio test. Peaks with an adjusted p-value of less than 0.05 were determined to be dynamic across pseudotime.

Gene set enrichment analysis

Gene set enrichment analyses was conducted using the R package piano (Väremo et al., 2013) using a hypergeometric test. We tested against the Human GO Biological Processes gene set from (Merico et al., 2010).

Cicero

Cicero aims to identify all pairs of coaccessible sites. The algorithm takes as input a matrix of m by n binary accessibility values A, where A_mn is zero if no read was observed to overlap peak m in cell n and one otherwise. The algorithm also requires either a pseudotemporal ordering of the cells along a developmental trajectory (e.g. with Monocle 2) or the coordinates of the cells in some sufficiently low dimensional space (e.g. a t-SNE map) that the cells can be readily clustered. The algorithm then executes the following steps, which are detailed in the sections below: first, groups of highly similar cells are sampled using the clustering or pseudotemporal ordering, and their binary profiles are aggregated into integer counts. Second, these counts are optionally adjusted for user-defined technical factors, such as experimental batch. Third, Cicero computes the raw covariances between each pair of sites within overlapping windows of the genome. Within each window, Cicero estimates a regularized correlation matrix using the graphical LASSO, penalizing pairs of distant sites more than proximal sites. Fourth, these overlapping covariance matrices are “reconciled” to produce a single estimate of the co-accessibility across groups of cells. These co-accessibility scores are reported to the user, who can extract modules of sites that are connected in co-accessibility networks by first specifying a minimum co-accessibility score and then using the Louvain community detection algorithm on the subgraph induced by excluding edges below this score.

Grouping cells

In principle, Cicero could analyze the sample covariance computed between the vectors x_i and x_j of binary values encoding accessibility across cells for a pair of sites i and j. However, rather than working with the binary data directly, Cicero groups similar cells and aggregates their binary accessibility profiles into integer count vectors that are easier to work with in downstream steps. Under the grouping discussed below, the number of cells in which a particular site is accessible can be modeled with a binomial distribution or, for sufficiently large groups, the corresponding Gaussian approximation. Modeling grouped accessibility counts as normally distributed allows Cicero to easily adjust them for arbitrary technical covariates by simply fitting a linear model and taking the residuals with respect to it as the adjusted accessibility score for each group of cells.

In order to control for technical variation as discussed above, Cicero operates on a grouped cell count matrix, C. C is constructed by first mapping cells into low dimensions by either Monocle 2 or tSNE. Within this space, Cicero constructs a k-nearest neighbor graph, via the the FNN package (Beygelzimer et al., 2013), which is based on KD-trees and is highly efficient, scaling to large numbers of cells. Cicero then samples random cells and their k nearest neighbors (default k = 50) are grouped. Random cells continue to be chosen and grouped until no new group may be created that does does not overlap an existing group by less than 90% of members. Accessibility counts are then summed across all cells in a group to create count matrix C. Cicero’s grouping procedure can be viewed as a type of bootstrap aggregation, or “bagging” (Breiman, 1996), which has been shown to substantially improve the stability of a variety of algorithms in machine learning. Note that with these parameter settings in a typical experiment, a cell will be part of more than one group and therefore the groups will sometimes contain some of the same cells, which could in principle inflate co-accessibility scores across cells. However, in practice in our analyses of both GM12878 and HSMM, the median number of cells shared between pairs of groups is zero.

Adjusting accessibility counts for technical factors

To normalize for variations in assay efficiency across groups, matrix C is divided by a group-wise scaling factor (computed using the standard Monocle 2 method for library size calculations (estimateSizeFactors()) to create an adjusted accessibility matrix R. Because the entries of C are integer counts that can reasonably be approximated by Gaussian distributions, this matrix can be readily adjusted for arbitrary technical covariates (e.g. using the Limma package’s removeBatchEffect() function). In this study we did not adjust for factors beyond library size.

Computing co-accessibility scores between sites

Cicero next analyzes the covariance structure of the adjusted accessibilities in R. Given enough data, Cicero could in principle simply compute the raw covariance matrix U. However, because the number of possible pairs of sites is far larger than the number of groups of cells, Cicero uses the Graphical Lasso to compute a regularized covariance matrix to capture the co-accessibility structure of the sites. The Graphical LASSO computes the inverse of the sample covariance matrix, which encodes the partial correlations between those variables as well as the regularized covariance matrix (Friedman et al., 2008). These constitute a statistically parsimonious description of the correlation structure in the data: informally, two variables are partially correlated when they remain correlated even after the effects of all other variables in the matrix are excluded. The Graphical LASSO expects a small fraction of the possible pairs of variables to be partially correlated, preferring to select a sparse inverse covariance matrix over a dense one that fits the data equally well. Those pairs of sites that lack sufficient partial correlation to be worth the penalty term are assigned zero partial correlation in the inverse covariance matrix reported by Graphical LASSO. Formally, Cicero uses Graphical LASSO to maximize:

$$\log \text{det}\Theta -\text{tr}(U\Theta )-\Vert \Theta \ast \rho {\Vert }_1$$

Where Θ is the inverse covariance matrix capturing the conditional dependence structure of p accessible sites, and U is the sample covariance matrix computed from their values in R. In order to ensure stability of GLASSO, which can hang on poorly conditioned input, we add a small conditioning constant of 1e-4 to the diagonal of U prior to running it. The matrix ρ contains penalties that are used to independently penalize the covariances between pairs of sites, and * denotes component-wise multiplication.

In Cicero, we aim to find local cis-regulatory interactions, rather than global covariance structure that might be expected due to overall cell state. To achieve this, we set each penalty term in ρ such that peaks closer in genomic distance had a lower penalty term. Specifically, we used the following equation to determine ρ:

$${\rho }_{ij}=(1-d_{ij}^{-s})\alpha$$

Where d_ij is the distance in the genome (in kilobases) between sites i and j and s is a constant that captures the power-law distribution of contact frequencies between different locations in the genome as a function of their linear distance. A complete discussion of the various polymer models of DNA packed into the nucleus is beyond the scope of this paper, but we refer readers to (Dekker et al., 2013) for a discussion of justifiable values for s. We use a value of 0.75 by default in Cicero, which corresponds to the “tension globule” polymer model of DNA (Sanborn et al., 2015). The scaling parameter α controls the distance at which Cicero expects no meaningful cis-regulatory contacts, and its value is calculated automatically from the data. To calculate α, Cicero selects 100 random 500 kb genomic windows, and determines the minimum α value such that no more than 5% of pairs of sites at a distance greater than 250 kb (a user-adjustable value) had non-zero entries in Θ and less than 80% of all entries in Θ were nonzero. The mean of these values of α is then used to set the penalties for the whole genome. Cicero then applies Graphical LASSO to overlapping 500 kb windows of the genome (windows are spaced by 250 kb such that each region is covered by two windows).

Reconciling overlapping local co-accessibility maps

Cicero calculates correlation values (co-accessibility scores) from the resulting estimated sparse covariance matrix for each pair of peaks within 500 kb of each other. Because the genomic windows are overlapping, the majority of pairs of peaks have two calculations of co-accessibility. To consolidate these sites and create a genome-wide map of the accessible regulome, Cicero considers the co-accessibility scores for each pair of peaks to determine if they are in qualitative agreement (both calculated scores in the same direction). The qualitative agreement in our two test datasets were both >95%. Pairs of peaks not in qualitative agreement are considered undetermined. For peaks in qualitative agreement, the mean score of the two values is assigned.

Extracting cis-co-accessibility networks (CCANs)

Positive Cicero co-accessibility scores indicate that a pair of peaks is connected, with the magnitude of the co-accessibility corresponding to Cicero’s confidence in the link. To identify hubs of co-accessibility, Cicero can create a graph where each node is a peak of accessibility, and edges are the co-accessibility scores above a user-defined threshold. Communities within this genome-wide graph can be found using the Louvain community finding algorithm. Cicero can then assign peaks to cis-co-accessibility networks (CCANs) based on these communities.

Calculating gene activity scores

Cicero calculates an overall measure of the accessibility of sites linked to each gene k by first selecting rows of the binary accessibility matrix A that correspond to sites proximal to the gene’s transcription start sites or to distal sites linked to them. These rows, are weighted by their co-accessibility and then summed to produce a vector of accessibility scores R_k, where the overall accessibility of gene k in cell i is:

$$R_{ki}=\sum _{p\in P}\sum _{j\in D_p}{A}_{ij}\frac{u_{pj}}{{\sum }_{k\in D_p}{u}_{pk}}+A_{pi}$$

Where P indexes the promoter proximal sites of k, D_p indexes distal sites linked to proximal site p, and u is the Cicero co-accessibility score linking distal site j to proximal site p, and A is the binary score for accessibility at site j or p in cell i. In principle, D_p could include all distal sites linked to p, but here we restrict the set to distal sites that are differentially accessible (FDR < 1%) across pseudotime.

Because the magnitude of these aggregate accessibility values will depend on overall sci-ATAC-seq library depth in each cell, we capture this relationship via a linear regression:

$$\log \left(\sum _k{R}_k\right)={\beta }_0+{\beta }_A\log \left(\sum _j{A}_{ji}\right)$$

The aggregate accessibility for each gene k in cell i is then scaled using the output of this model r_i for cell i:

$${\tilde{R}}_{ki}=R_{ki}\cdot \frac{{\sum }_i{r}_i}{r_i}$$

Gene expression values measured by RNA-seq are typically approximately log-normally distributed. We therefore transform aggregate accessibility values to gene “activity” scores G_ki for each gene k in each cell i by simply exponentiating them. We also scale them by the total (exponentiated) gene accessibility values to produce “relative” activities:

$$C_{ki}=\frac{e^{{\tilde{R}}_{ki}}}{{\sum }_k{e}^{{\tilde{R}}_{ki}}}$$

Comparing two Cicero maps

Different Cicero CCAN maps were matched using the push-relabel algorithm for maximum matching in a weighted bipartite graph (Goldberg and Tarjan, 1986). Specifically, we used the maxmatching package in R to calculate the matching. Maximum matching in weighted bipartite graphs is a one-to-one matching such that the edge weights are maximized. In the case of comparing Cicero CCAN maps, the maximum matching is the one-to-one match of CCANs from map 1 to CCANs from map 2 such that the largest number of peaks is shared across the maps overall.

Analysis of 54-1 immortalized myoblasts

Bulk ATAC-seq libraries from 54-1 cells were processed as above. Data from the multiple guides at each timepoint and targeting each gene were merged for peak calling as described above. The resulting peaks were merged to create a master peak list. Reads per peak were then counted for each guide and time point separately. DESeq2 (Love et al., 2014) was used to test for differential accessibility between day 0 and day 7 across each of the three conditions (non-template control, MEIS1 targeted and PBX1 targeted). Two libraries (NTC guide 5 day 0 and PBX1 guide 4 day 7) were removed as major outliers by PCA. Peaks with a greater than 2-fold moderated fold change were considered to be dynamic. When comparing 54-1 peaks to HSMM peaks, overlap was determined by overlapping coordinates with a maximum gap of zero.

Motif enrichment analysis

Transcription factor motifs from the JASPAR 2016 database (Mathelier et al., 2016) were located in the sci-ATAC-seq peaks using FIMO (Grant et al., 2011). Motifs for TFs not expressed at ≥ 2 transcripts per million in bulk RNA-seq (HSMM myoblasts or myotubes) were excluded from downstream analysis. Many TF motifs are similar or identical to each other. To prevent this correlation from confounding regression analyses, we clustered motifs into motif families. For each pair of motifs A and B, we computed the conditional probability that given motif A is called at a genomic location with a FIMO p-value < 2e-5 (a stringent threshold), an overlapping instance of motif B will be called at p < 1e-4 (a permissive threshold). We constructed an undirected graph of motifs where there is an edge between motifs A and B if P(B at p < 1e-4 ∣ A at p < 2e-5) ≥ 0.5 or P(A at p < 1e-4 ∣ B at p < 2e-5) ≥ 0.5. Edges in this graph are assigned weights equal to the greater of these two conditional probabilities minus 0.5. We clustered the motifs on this graph using Louvain clustering (Blondel et al., 2008) and manually assigned names to each cluster. For downstream regression analyses, a genomic location is considered to have an instance of a motif family if any motif in the family is called at that location at p < 5e-5 (an intermediate threshold).

To generate the motif co-accessibility networks shown in Supplemental Figure 5A, we computed two sets of binary variables for each protein coding gene that had at least one sci-ATAC-seq peak in its promoter(s). The first set of variables are indicators of whether or not at least one instance of a motif family is present in any promoter peak for the gene. The second set of variables are indicators of whether or not at least one motif instance is present in any distal peak (excluding promoters of other genes) connected to the gene’s promoter(s) with a co-accessibility score greater than 0. We constructed a matrix where rows are genes and columns are these two sets of motif indicator variables. This matrix was provided as input to the Graphical LASSO subject to the constraint that partial correlations between two promoter motif variables or two distal motif variables are fixed to zero. The regularization parameter ρ for the Graphical LASSO was set as the smallest value that could achieve an estimated false discovery rate (FDR, the proportion of truly-zero partial correlations that are estimated as non-zero) of less than 5%. The FDR for a given value of ρ was estimated by running the Graphical LASSO with that value of ρ on versions of the motif indicator matrix with the distal variables row-shuffled (essentially assigning each gene to a random other gene’s set of distal motifs) and counting the proportion of motif pairs that are assigned a non-zero partial correlation (ideally, all should be zero in a shuffled matrix).

In Supplemental Figure 5A, an edge is drawn between a pair of motif families A and B if both 1) the co-accessibility of the indicator variable for A being at a distal site to the indicator variable of B being at a linked promoter site is > 0.02, and 2) the same is true if B is in the distal position and A is in the promoter.

Analysis of ChIA-PET and Hi-C data

To compare our Cicero connections to promoter-capture (PC) Hi-C, we used publicly accessible GM12878 data (Cairns et al., 2016). We used the provided ChICAGO score as our indicator of physical proximity.

To compare our data to PC Hi-C, we first overlapped our peaks with peaks from PC Hi-C. Peaks were considered to overlap if they were within 1 kb of each other. For this analysis, we only considered pairs of sci-ATAC-seq peaks where at least one was a promoter represented in the PC Hi-C data. In addition, we only considered pairs of peaks that were within the same A/B compartment to avoid potential confounding of cross-compartment connections (Fortin and Hansen, 2015). To check that the effect of a pair of peaks’ co-accessibility on presence in the dataset in Figure 4C was beyond the effect of the overall accessibility of the peaks, we ran a logistic regression predicting presence of the pair in PC Hi-C using binned co-accessibility and the geometric mean of the accessibility of the two peaks in the pair and found the coefficient for co-accessibility to be significant (p-value < 2e-16).

As a second comparison dataset, we used publicly accessible GM12878 polII ChIA-PET data (Tang et al., 2015) (GSE72816). To compare these data to Cicero’s connections, we first looked for overlap between our peaks, and ChIA-PET anchors. Because ChIA-PET anchors often overlap each other, we first merged overlapping anchors to create comparable ChIA-PET “peaks”. We considered accessible peaks within 1 kb of ChIA-PET peaks to be overlapping. To generate Figure 4B,D, we considered the subset of ChIA-PET and Cicero connections where the peaks were present in both datasets. Similarly as for PC Hi-C, to check that the effect of a pair of peaks’ co-accessibility on presence in the dataset in Figure 4B was beyond the effect of the overall accessibility of the peaks, we ran a logistic regression predicting presence of the pair in ChIA-PET using binned co-accessibility and the geometric mean of the accessibility of the two peaks in the pair and found the coefficient for co-accessibility to be significant (p-value < 2e-16).

Analysis of ChIP-Seq data (MYOD and histone)

To compare our accessible peaks to the known myogenesis master regulator MyoD, we used publicly accessible MyoD ChIP-seq in human myoblast and human myotube (MacQuarrie et al., 2013) (GSE50413). We considered our peaks to be bound by MyoD if they overlapped one of the annotated MacQuarrie et al. ChIP-seq peaks.

To compare our accessible peaks to histone modifications, we used publicly accessible ENCODE datasets in HSMM and HSMMtube (The ENCODE Project Consortium, 2012) (ENCFF000BKV, ENCFF000BKW, ENCFF000BMB, ENCFF000BMD, ENCFF000BOI, ENCFF000BOJ, ENCFF000BPL, ENCFF000BPM). We counted both HSMM and HSMMtube histone ChIP-seq reads in each accessible peak. To determine whether sites were changing in accessibility between HSMM and HSMMtube, we used DESeq2 differential analysis (Love et al., 2014) (FDR < 5%). To determine whether the barrier regions of genes were differentially histone modified, we similarly used DESeq2 to compare the read counts in the first 1000 base pairs of each GENCODE v17 transcript in HSMM and HSMMtube datasets.

To compare agreement between H3K27 acetylation marks of peaks connected by Cicero, we divided the odds of a site gaining acetylation if its connected site gained acetylation by the odds of a site gaining acetylation is it is connected to a site that is not gaining acetylation (Figure 5A).

Modeling H3K27 Acetylation Changes:

To model changes in acetylation among linked sites (Figure 5D), we compared four linear regression models:

$$\begin{gathered} \text{ln}(a_i)={\beta }_0+{\beta }_1{A}_{icl}+{\beta }_2{A}_{iop} \\ \text{ln}(a_i)={\beta }_0+{\beta }_1{A}_{icl}+{\beta }_2{A}_{iop}+{\beta }_3{m}_{ig}+{\beta }_4{m}_{il}+{\beta }_5{m}_{ic} \\ \text{ln}(a_i)={\beta }_0+{\beta }_1{A}_{icl}+{\beta }_2{A}_{iop}+{\beta }_3{\theta }_{op}+{\beta }_4{\theta }_{cl} \\ \text{ln}(a_i)={\beta }_0+{\beta }_1{A}_{icl}+{\beta }_2{A}_{iop}+{\beta }_3{m}_{ig}+{\beta }_4{m}_{il}+{\beta }_5{m}_{ic}+{\beta }_6{\theta }_{mg}+{\beta }_7{\theta }_{ml}+{\beta }_8{\theta }_{mc} \end{gathered}$$

where a_i is the log2 fold-change in H3K27 acetylation from myoblast to myotube at site i, A_icl and A_iop are indicator variables for whether site i is closing or opening across pseudotime, m_ig, m_il and m_ic are indicator variables for whether site i is gaining, losing, or constitutively bound by MYOD from myoblast to myotube according to ChIP-seq, θ_op and θ_cl are the highest Cicero co-accessibility scores that connect site i to another opening or closing site respectively, θ_mg and θ_ml, and θ_mc are the highest Cicero co-accessibility scores that connect site i to another MyoD gaining, MyoD losing or MyoD constitutive site. For each of the fitted models, we used elastic net regression (Zou and Hastie, 2005) to estimate the effect of each predictor.

Similarly, in Supplemental Figure 5B, we predict the log2 fold-change in each of the 12 ENCODE histone mark ChIP-seq datasets described above using only indicator variables for whether a site is gaining losing or constitutively bound by MYOD, or using these variables and the highest Cicero co-accessibility scores connecting a site to an opening or closing site.

Regression models for barrier region histone marks and gene expression:

For each of the 12 ENCODE histone mark ChIP-seq datasets described previously, we fit two regression models that predict, for each transcription start site, the log fold change in the number of reads from the given ChIP-seq dataset that fall in the barrier region of that TSS (first 1000 bp downstream) for myotubes vs. myoblasts. We exclude TSSs that do not have a significantly different number of barrier region reads in myotubes vs. myoblasts for any of the 12 datasets (p > 0.01), leaving 5,563 TSS included in the model.

In the first set of models (“promoter motifs”), the features are a set of binary indicator variables that have value 1 if any promoter sci-ATAC-seq peak for the TSS has at least one instance of a motif from a given motif family. In the second set of models (“promoter and distal motifs”), the features are the promoter motif indicator variables plus a second set of real-valued variables that encode the presence of distal sequence motifs. For a given motif family and TSS, the corresponding distal motif variable has a value equal to the highest co-accessibility score from any promoter sci-ATAC-seq peak for that TSS to any connected distal peak that has at least one instance of a motif from the motif family. If no such distal peak exists (the motif is absent in all connected distal sites), the distal motif variable is assigned a value of 0. The models were trained using elastic net regression.

We additionally fit models with the same features (“promoter motifs” and “promoter and distal motifs”) to predict the expression of the subset of the above TSSs (n = 937), that were additionally expressed in at least 4 cells in scRNA-seq and which were predicted by smoothed average across pseudotime to be expressed at above 1 copy per cell at some pseudotime.

DATA AND SOFTWARE AVAILABILITY

Data Availability

sci-ATAC-seq data is available on Gene Expression Omnibus (accession number GSE109828).

Code Availability

Cicero is available as an R package at http://cole-trapnell-lab.github.io/cicero/.