Global relationships among traditional reflectance vegetation indices (NDVI and NDII), evapotranspiration (ET), and soil moisture variability on weekly timescales

Abstract

Monitoring the effects of water availability on vegetation globally using satellites is important for applications such as drought early warning, precision agriculture, and food security as well as for more broadly understanding relationships between water and carbon cycles. In this global study, we examine how quickly several satellite-based indicators, assumed to have relationships with water availability, respond, on timescales of days to weeks, in comparison with variations in root-zone soil moisture (RZM) that extends to about 1 m depth. The satellite indicators considered are the normalized difference vegetation and infrared indices (NDVI and NDII, respectively) derived from reflectances obtained with moderately wide (20–40 nm) spectral bands in the visible and near-infrared (NIR) and evapotranspiration (ET) estimated from thermal infrared observations and normalized by a reference ET. NDVI is primarily sensitive to chlorophyll contributions and vegetation structure while NDII may contain additional information on water content in leaves and canopy. ET includes both the loss of root zone soil water through transpiration (modulated by stomatal conductance) as well as evaporation from bare soil. We find that variations of these satellite-based drought indicators on time scales of days to weeks have significant correlations with those of RZM in the same water-limited geographical locations that are dominated by grasslands, shrublands, and savannas whose root systems are generally contained within the 1 m RZM layer. Normalized ET interannual variations show generally a faster response to water deficits and enhancements as compared with those of NDVI and NDII, particularly in sparsely vegetated regions.

1. Introduction

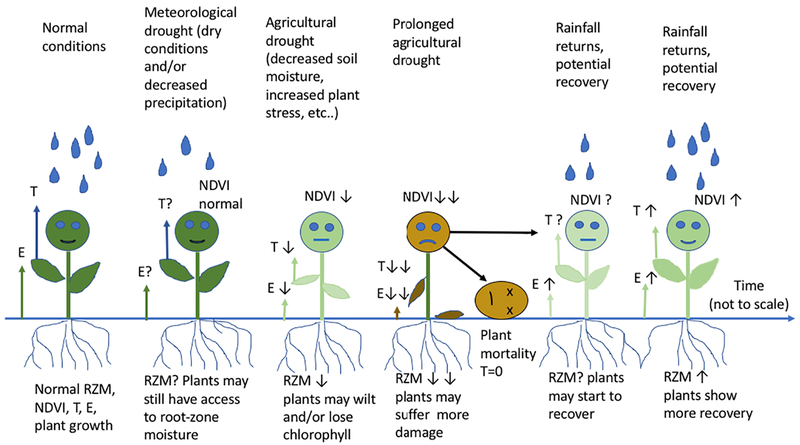
Drought monitoring is defined as tracking the severity, spatial extent, and impacts of drought. Use of that information to elicit an appropriate timely response is called early warning (Hayes et al., 2012). Drought monitoring and early warning are important components of proactive, risk-based strategies that are being developed to reduce the impact of droughts worldwide (Hayes et al., 2012). Early detection of water stress effects on vegetation is critical for decision making and drought preparedness in agricultural, ecological, and meteorological communities (e.g., AghaKouchak et al., 2015). A recent survey of stakeholders in the US noted potential benefits of having advanced notice (on the order of weeks) of worsening conditions that occur during the transition from meteorological drought (i.e., dry conditions and reduced precipitation) to agricultural drought (i.e., decreased soil moisture and impacts on vegetation) (Otkin et al., 2015). Such early warning could afford 1) ranchers the opportunity to move livestock to less susceptible pastures or to purchase supplemental feed; 2) farmers advanced notice to influence their marketing decisions or help them determine whether a cover crop might be beneficial to plant after harvest; and 3) government agencies the ability to best allocate equipment and personnel resources for mitigation, such as emergency haying (Otkin et al., 2015). In other regions of the world, such as sub- Saharan Africa, drought early warning systems have been shown to significantly increase food security and dietary diversity and may also be used to integrate pasture conservation (Akwango et al., 2017).

A drought indicator (DI) is a variable used to describe the physical characteristics of drought severity, spatial extent, and duration that along with specific trigger values may activate a drought response (Steinemann and Cavalcanti, 2006). Drought indicators may be related to hydrology (e.g., precipitation, soil moisture, snowpack), vegetation status (e.g., type, age, growth stage, and vigor including chlorophyll content and leaf area index that are related to vegetation indices), or both (e.g., evapotranspiration or ET). Satellite-based DIs have several advantages for drought monitoring and early warning, including global repeat coverage of spatially continuous and consistent spectral measurements and timely data distribution.

Satellite-derived reflectance-based vegetation indices (VI) and other parameters have been used for vegetation health and drought monitoring including drought assessment and drought early warning, particularly in savannas and ecosystems in semiarid regions (see e.g., the review of AghaKouchak et al., 2015, and references therein). NDVI has also been used to benchmark modern land-surface models for quantitative prediction of vegetation health (Crow et al., 2012). However, there remain several challenges in using satellite data for drought monitoring and early warning (WMO, 2006). For instance, satellite-derived DIs are sometimes inadequate for detecting early onset and end of drought and should be integrated with other climate, water, and soil parameters to fully characterize drought impacts and extents.

The use of satellite data for drought monitoring began in the 1980s with the launch of the Advanced Very High Resolution Radiometer (AVHRR) instruments on a series of operational meteorological satellites. The AVHRR contains two spectral bands that can be used to compute the normalized difference vegetation index (NDVI) (Tucker, 1979). The NDVI has been utilized in numerous studies involving drought early warning, agricultural monitoring, and other applications (see e.g., the review of Anyamba and Tucker, 2012, and references therein). This includes its use in the US Drought Monitor (USDM) (Svoboda et al., 2002) in the form of a vegetation health index that is based on anomalies (or deviations from climatological mean values) of NDVI (Kogan, 1995).

Many studies have also examined relationships among satellite-derived vegetation indices and variables related to water availability such as precipitation and soil moisture, sometimes in addition to other climate parameters (see e.g., Wang et al., 2007; Méndez-Barroso et al., 2009; Schnur et al., 2010; Karnieli et al., 2010; Swain et al., 2013; Zeng et al., 2013; Jamali et al., 2011; De Keersmaecker et al., 2015; AghaKouchak et al., 2015; Seddon et al., 2016, and references within). The timescales used in these studies have generally been monthly to yearly and the spatial extents have ranged from site level to global. Previous examinations of the time differences (e.g., leads or lags) between the expression of NDVI and responses of climate variables, such as temperature and water availability, have ranged from weeks to years (e.g., Braswell et al., 1997; Ahmed et al., 2017). The lags are sometimes computed using the native NDVI values (e.g., Owe et al., 1993) or their anomalies (i.e., first removing the average seasonal cycle) (e.g., Huber et al., 2011) depending on the particular application.

Evapotranspiration (ET) and, along with it, the ET-driven evaporative stress index (ESI) (Anderson et al., 2007, 2011a, 2013) are more recent satellite-derived data sets that can be used for early detection of water stress effects on vegetation as well as drought assessment (e.g., Courault et al., 2005; Anderson et al., 2007; Kalma et al., 2008; Yao et al., 2010; Mueller et al., 2011; Jiménez et al., 2011; Anderson et al., 2011a, 2013; Fisher et al., 2017; Vicente-Serrano et al., in press). ET includes both the loss of root zone soil water through transpiration (modulated by stomatal conductance) as well as evaporation from bare soil. This contrasts with NDVI and similar indices that are sensitive to structural parameters such as leaf area index (LAI) and/or to canopy chemical constituents such as relative chlorophyll content. Consequently, vegetation indices may have a delayed response or lower sensitivity to various forms of stress as compared with ET. ESI, defined as standardized anomalies in a normalized ET parameter, as well as the related rapid change index (RCI), derived from the accumulated magnitude of moisture stress changes occurring over multiple weeks, have been used to identify areas with increases in moisture stress that may precede rapid drought development or so-called flash droughts (Otkin et al., 2013, 2014). These products are used by a number of national and regional drought stakeholders including the USDM.

Many of the studies on the use of satellite-driven ET data sets for early drought detection and impacts such as on crop yields and terrestrial water budgets have focused regionally on the United States (e.g., Mishra et al., 2013; Otkin et al., 2013, 2014; Mladenova et al., 2017; Carter et al., 2018) and other individual countries (Anderson et al., 2016). Here, we expand on this work by comparing anomalies (or interannual variations) at the global scale of 1) a newly developed weekly normalized ET product from the Atmosphere-Land Exchange Inverse (ALEXI) approach that is driven by satellite and meteorological data (Hain and Anderson, 2017); 2) NDVI and NDII derived from MODIS reflectances; and 3) water availability as expressed by “root-zone ”(soil) moisture (RZM) in the top 1 m layer. Our focus is on the time leads/lags between short-term variations (i.e., daily to weekly timescales) in the RZM and satellite-based DIs that occur in water limited regions during the transition between meteorological and agricultural drought as depicted in the conceptual diagram in Fig. 1. Previous research with space-based observations has rarely focused on this short timescale. We conduct these comparisons using weekly averages at the native spatial resolution of a reanalysis RZM data set (0.5° latitude × 0.625° longitude), produced with a data assimilation system running with an unchanging model and analysis system using historical data streams; this is the lowest spatial resolution of the data sets used here. In combination, the prognostic model-based RZM data and diagnostic satellite-based ET estimates from ALEXI provide independent yet complementary assessments of the land-surface moisture status.

Fig. 1.

Conceptual diagram showing impacts of different stages of drought on vegetation as expressed by NDVI, transpiration (T), root-zone soil moisture (RZM), and evaporation (E).

One goal of this study is to use the new ALEXI-based ET data set (Hain and Anderson, 2017) to investigate whether it is possible to identify regions across the globe where normalized ET shows consistently faster short-term responses (on timescales of days to weeks) to anomalies in water availability as compared with NDVI or NDII. Another goal is to estimate the lead/lag times of these DIs with respect to each other and RZM over short timescales to determine how useful satellite-driven global ET-based data sets may be for the above-mentioned stakeholder needs.

2. Materials and methods

This section describes the data sets used in this study and how the interannual variability and time lags are computed. Additional details regarding the calculation of temporal lags and their associated uncertainties are provided in Appendix A.

2.1. Satellite drought indicator (DI) data sets

2.1.1. ALEXI-based ET estimates

With surface energy balance methods, estimates of ET are based on the thermal response of land surfaces containing vegetation as measured by thermal infrared (TIR) satellite retrievals of land-surface temperatures (Anderson et al., 2011b). The ALEXI method is a comprehensive set of algorithms to diagnose the surface energy balance with the aim of retrieving ET (Anderson et al., 1997, 2007; Mecikalski et al., 1999). ALEXI is based on the two-source energy balance (TSEB) approach (Kustas and Norman, 1999; Norman et al., 1995) in which the partitioning of turbulent fluxes is evaluated for the soil and the canopy (denoted with subscripts s and c, respectively). This is accomplished by 1) parameterizing the divergence of net radiation (R_net) between canopy and soil surface and 2) attributing the observed composite surface radiometric temperature (T_rad) into soil and canopy temperatures, T_s and T_c (note: uppercase T denotes temperature), respectively, based on the fraction of area covered with vegetation that is parameterized using LAI.

An initial guess for the canopy transpiration rate is based on the assumption that the green part of the canopy transpires at its potential maximum rate as estimated with a modified Priestley and Taylor (1972) approximation. The sensible heat flux for the two source components is then calculated in a set of equations that accounts for their different resistance to heat transfer and that satisfy the observation-based T_s and T_c and air temperature T_a (Norman et al., 1995). The final estimate of ET is determined in an iterative procedure in which soil evaporation is forced to be non-negative. ALEXI couples TSEB with an atmospheric boundary layer model to relate the morning rise in T_rad to the growth of the overlying planetary boundary layer and simulate an internally consistent T_a. This removes the need for T_a as an input data set and limits the sensitivity of the method to biases in instantaneous satellite-based temperature estimates, while allowing for regional and global implementations of the model (Anderson et al., 1997). Note that ALEXI does not make use of a soil moisture estimate.

The ALEXI model is run on the 0.05° (~5 km) Climate Modeling Grid (CMG) and provides the physical foundation to the ALEXI/DisALEXI modeling system that has been applied to many satellitebased thermal infrared (TIR) data streams from 30 m to 10 km (Anderson et al., 2011b). The data set used here is based on a recently developed global methodology to use twice-daily observations of land surface temperature from the US National Aeronautics and Space Administration (NASA) MODerate-resolution Imaging Spectroradiometer (MODIS) within the ALEXI framework (Hain and Anderson, 2017).

The data sources for this version of ALEXI are listed in Table 1. They include the two Terra and Aqua MODIS sensors, the NASA Clouds and the Earth’s Radiant Energy System (CERES), and the National Centers for Environmental Prediction (NCEP) Climate Forecast System Reanalysis (CFSR). The continuous 7-day totals are achieved by temporal interpolation of ALEXI ET retrievals on days with clear sky conditions by conserving the ratio of ET to daily insolation flux. The use of 7-day averages allows for filling in of most gaps in satellite coverage caused by incomplete coverage and cloud contamination. Our analysis method can determine leads and lags among different drought indicators at a timescale even finer than 7 days through the use of linear interpolation within the 7-day averages (see Appendix A).

Table 1.

Primary inputs for current global implementation of ALEXI.

Data	Purpose	Source	Spatial resolution	Temporal resolution
Land-surface temperature	Trad, Rnet	M0DISMYD11C11	0.05°	Daily, clear-sky
Surface shortwave and longwave	Rnet	CFSR2, CFSRv23	0.5°	Hourly
radiation fluxes		CERES SYNldeg4	1°	Daily
Albedo	Rnet	MODIS MCD43B35	0.05°	16-day
Leaf area index	Trad partitioning	MODIS MCD15A36	0.01°	4-day
Landcover type	Canopy characteristics	MODIS MCD12C17	0.01°	Fixed
Wind speed	Aerodynamic resistance	CFSR, CFSRv2	0.5°	Hourly
Lapse rate profile	Boundary layer growth model	CFSR, CFSRv2	0.5°	Hourly

¹Wan and Hulley (2015).

²Saha et al. (2010).

³Saha et al. (2011).

⁴Doelling (2012).

⁵Schaaf et al. (2002).

⁶Myneni et al. (2002).

⁷Friedl et al. (2010).

In order to remove inter-annual variation in available energy and to better focus on the drought signal, ET can be normalized by the potential ET (PET) (Anderson et al., 2007, 2011b). PET (or reference ET) was computed from the general form of the Penman-Monteith equation for a well defined reference surface (Allen et al., 1998). All necessary inputs needed for the computation of PET were taken from the same CFSR data set used in ALEXI. The fraction of potential ET (FPET) is then simply defined as FPET = ET/PET. Normalization by PET also serves to approximately rescale values between zero and one. Values above one do occur and may reflect local biases in PET or localized anomalous ET behavior.

The FPET data set, with native spatial resolution of FPET (0.05°), was aggregated to match that of the Modern-Era Retrospective analysis for Research and Applications 2 (MERRA-2) reanalysis data set described below. While this reduces spatial detail, multi-scale analyses of FPET suggest the generalized signals are not significantly impacted by aggregation (Yang et al., 2018).

2.1.2. Vegetation Indices

The satellite-derived vegetation indices examined are the NDVI and the normalized difference infrared index (NDII) that has been used to estimate equivalent water thickness of leaves and canopy (Yilmaz et al., 2008). We compute NDVI and NDII using atmospherically-corrected nadir BRDF-Adjusted Reflectance (NBAR) from the collection 6 Terra and Aqua MODIS MCD43D daily data set (Schaaf et al., 2002; Lucht et al., 2000; Schaaf, 2015). Our analysis spans the years 2003–2016 when both Terra and Aqua MODIS data are available. The native resolution of the MCD43D gridded data set is 0.0083°× 0.0083°. The nadir surface reflectance of each gridbox is derived using data acquired over a 16-day period at multiple angles for clear skies. A daily product is provided that weights the data according to quality and other factors. The daily reflectances are then averaged over the same spatial resolution as the MERRA-2 data set, as was done for ET and aggregated to the 7-day temporal resolution of the FPET data set. Using the averaged reflectances ρ from bands 1 (620–670 nm), 2 (841−876 nm), and 6 (1628–1652 nm), we compute NDVI = (ρ₂ − ρ₁)/(ρ₂ + ρ₁) and NDII = (ρ₂ − ρ₆)/(ρ₂ + ρ₆).

2.2. Soil moisture

We use fractional root-zone soil moisture (RZM), a dimensionless quantity, from the MERRA-2 reanalysis data product (Global Modeling and Assimilation Office (GMAO), 2015; Reichle et al., 2017a,b). The reanalysis process uses a numerical (weather) prediction model together with an analysis system to combine many different satellite-, ground-, and aircraft-based observations in a physically consistent way. The end product consists of gridded data sets of many variables. These include some two dimensional fields (i.e., latitude by longitude), like RZM, that are not directly observed. The choice of a model-based RZM for this study is driven by the fact that for the time periods considered here, only models can provide globally comprehensive RZM; there is no satellite data set that can remotely sense as deeply into the soil and in situ soil moisture measurements are sparse in coverage. The MERRA-2 RZM represents the moisture in the 0−1 m soil layer, independent of the actual vertical distribution of the plant roots.

In the course of the MERRA-2 integration, the component land model responds to observations-based meteorological forcing including gauge-based precipitation from the US National Oceanic and Atmospheric Administration (NOAA) Climate Prediction Center (CPC), and it generates estimates of numerous land states, including the RZM values used here. Reichle et al. (2017b) provide a detailed comparison of RZM with over 200 in situ measurement sites from several networks worldwide. The MERRA-2 results were significantly improved as compared with the predecessor MERRA system and generally better than the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA-Interim/Land reanalysis data set. The quality of the analyzed RZM depends strongly on the availability of gauge observations for the land surface precipitation forcing (Reichle et al., 2017a, see their Fig. 8).

We use the MERRA-2 data at their native spatial resolution of 0.5° latitude by 0.625° longitude. We refer to each element of the MERRA-2 two dimensional surface RZM field (at a single time step) as a gridbox. We evaluate all satellite-based DIs at the MERRA-2 gridboxes. The MERRA-2 RZM data set is the coarsest of the data sets considered here; therefore the spatial resolution of our study is driven by the MERRA-2 spatial resolution. The hourly MERRA-2 data were aggregated to the 7-day resolution of the FPET data set.

2.3. Calculation of interannual variations (IAV)

Interannual variations (IAV, also called anomalies) for satellite-based DIs and RZM at time t (note that lowercase t denotes time) in a given gridbox are normalized according to the min-max method, i.e.,

$$\text{DI}{\text{'}}_t=\left(\text{D}{\text{I}}_t-\text{D}{\text{I}}_t\right)/(\max \left(\text{DI}\right)-\min \left(\text{DI}\right)),$$ (1)

Where denotes that it is an IAV, is the climatological mean computed by averaging over the 14 years of data at the 7-day time period corresponding to t, and min(DI) and max(DI) and and refer to the average minimum and maximum climatological values, respectively, for a given gridbox. The min-max normalization does not affect the computed correlations or time lags; it expresses the IAV in terms of a fraction of the climatological range of values. For example, if the range of observed values of NDVI for a given gridbox is 0.5, then a positive anomaly of 0.25 will produce a (normalized) IAV of 0.25/0.5 = 0.5. The min-max normalization provides an alternative way to compare IAV values for various types of measurements that have different measurement/modeling errors as compared with the more commonly used standardized IAV or z-score in which native IAV values are divided by the standard deviation (Raschka, 2014). With z-scores, the standardized IAV would be effectively decreased for noisy measurements. Instead, for convenience we normalize the size of the IAV with respect to the range of observed values. This is also preferable to analyzing the IAV in native units which would tend to put less weight on smaller values that occur in regions with smaller ranges of observed values. Here, negative or decreasing IAV values of DIs tend to be associated with the effects of water or other types of stress. In other words, negative values are obtained when the indicator is lower than its mean value at a particular time of year, and decreasing IAV values mean that the DI values are decreasing with respect to their normal or mean values over time. To reduce the effects of random noise that impacts our analysis, we apply a six point boxcar smoothing filter to the IAV time series.

2.4. Calculation of time lags

To compute the lag (Δt) between two different DI′, DI′₁ and DI′₂, (for a given gridbox) we model DI′_1,t as the sum of a time shifted and scaled function of DI’_2,t and a residual term ϵ, i.e..,

$$D{I}_{1,t}^{\prime }=AD{I}_{2,t-\Delta t}^{\prime }+ϵ,$$ (2)

where Δt is the lag (in 7-day samples) of DI′₂ with respect to DI1. We solve for values of a scaling factor A, and offset ϵ, and Δt using a standard unconstrained non-linear (iterative) least-squares fitting approach (see Appendix A for details).

We restrict our analysis to regions with a substantial fraction of chlorophyll containing vegetation by using data only from 7-day time periods with a climatological mean NDVI > 0.15. We also remove time periods for which reanalysis surface temperature averages were ≤ 0°C. Finally, we only use gridboxes with ≥70 data points over the 14-year period.

When displaying correlations and leads/lags between the various DI’s, we focus on gridboxes having significant correlations after applying the fitting procedure (p-value < 0.00001). The choice of a higher p-value threshold, as may be expected, yields a number of gridboxes, that while meeting the p-value criteria, appear isolated and display relatively low correlations or precision. The choice of a very small p-value threshold eliminates most of these apparently spurious gridboxes while retaining those with higher correlations in the expected sensitive regions.

2.5. Processing and sampling of the satellite and soil moisture fields

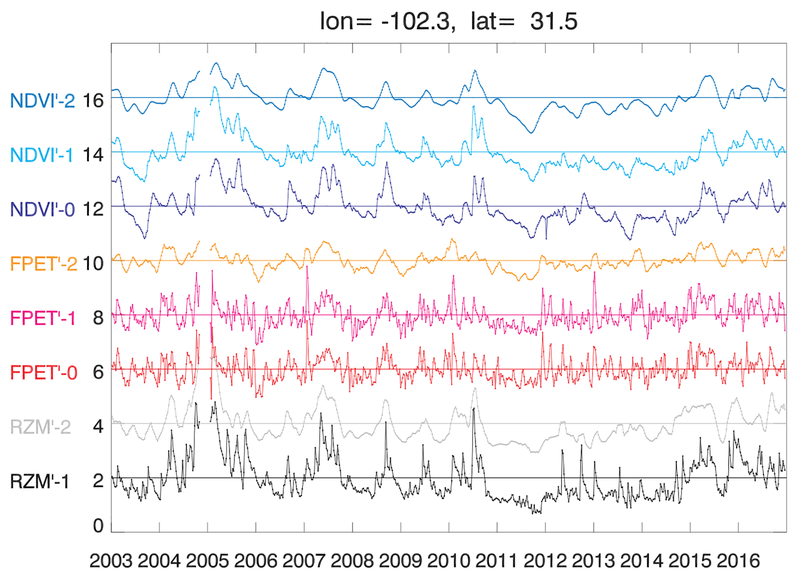
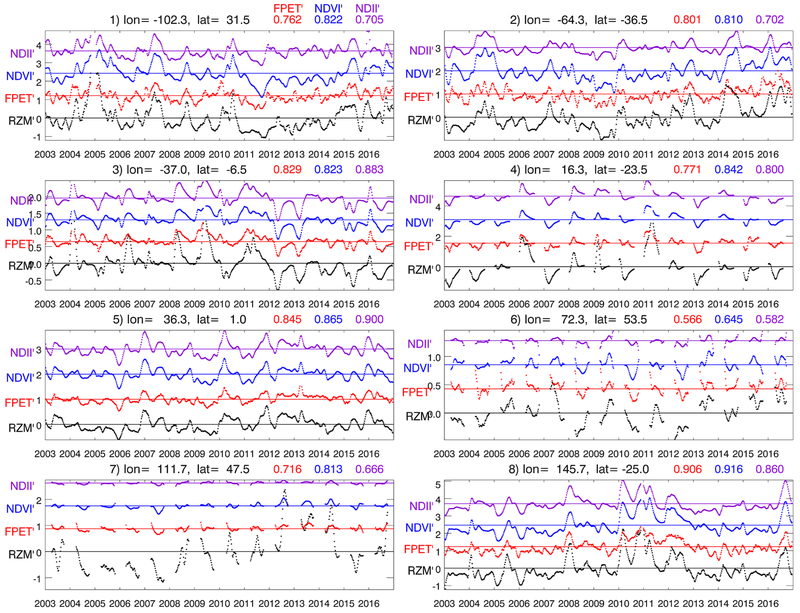
The satellite and soil moisture data sets are each averaged temporally and/or spatially in such a way as to put them all on similar scales. Fig. 2 shows an example of the data sets at different stages of processing at one location that will be used later (see Fig. 5, the “x” within box 1 for the mapped location). In this figure, the time series of NDVI′, FPET′, and RZM′ are shown first at the native spatial resolution at the point closest to the listed latitude and longitude at the native 7-day temporal resolution of the FPET data set (denoted with “−0 ”), then aggregated to the native 0.5°× 0.625° spatial resolution of the RZM data set(denoted with “−1 ”), and finally with temporal smoothing applied (denoted with “−2 ”). It is apparent that both FPET′ and RZM′ contain higher frequency structure as compared with NDVI′. The spatial averaging applied to NDVI′ and FPET′ does not appear to substantially alter the IAV values at this predominantly grassland location. The temporal smoothing, as expected, removes the high frequency structures in FPET′ and RZM′ which makes drought signals (prolonged negative anomalies), such as the Texas drought of 2011, more obvious and more similar to NDVI′.

Fig. 2.

Example of how the satellite and soil moisture anomaly data sets are processed; satellite data aggregated to the 7 day native period of the FPET data set at native spatial resolutions are denoted with “−0”; the data sets at 7 day temporal resolution at the native spatial resolution of the 0.5°× 0.625° RZM data set are denoted with “−1”; data sets with subsequent temporal smoothing applied are denoted with “−2”.

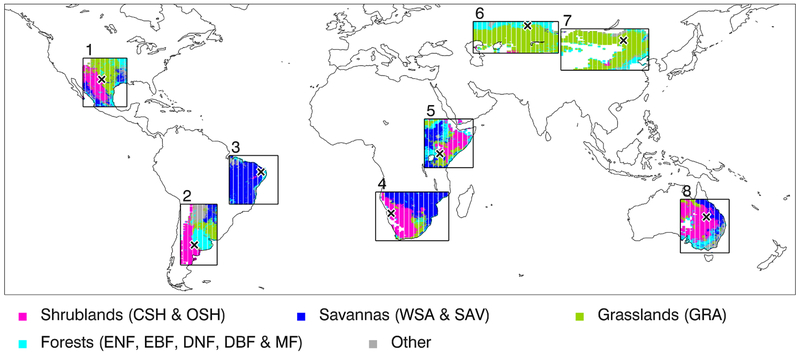
Fig. 5.

Vegetation types within water sensitive regions. The ‘x’ markers within each box denote locations for which time series will be further examined in detail below in Fig. 6.

It should be noted that there are sampling differences between the analyzed soil moisture and satellite data products considered here. These differences in sampling may lead to both random and systematic differences among the various data sets and can contribute to uncertainties in our analyses. For example, MERRA-2 data are averaged over all-sky conditions. In contrast, vegetation indices are averaged only over clear days. The FPET data are time composites of clear-sky values, to focus the signal on soil moisture controls of ET rather than insolation controls.

There are also time of day sampling differences. MERRA-2 data are averaged over all hours of the day and night. FPET is representative of mid-day conditions. The vegetation indices use both late morning and early afternoon data.

3. Results and discussion

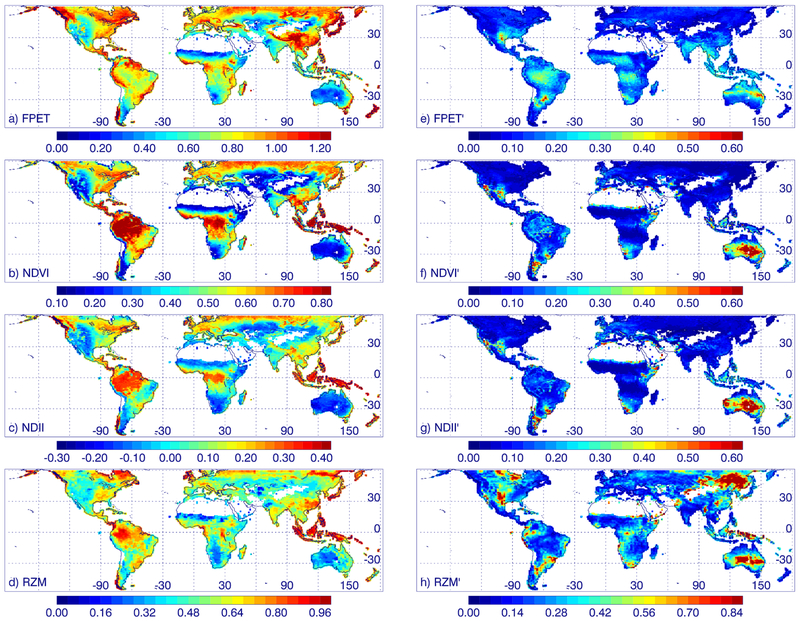
Fig. 3 shows maps of mean FPET, NDVI, NDII, and RZM (left column, a–d) and corresponding standard deviations of the IAV (right column, e–h) computed over the active growing season. All DIs show similar spatial patterns of means with generally higher values in forested regions such as the eastern US and northern Eurasia and lower values in semi-arid areas such as the western US, central and western Australia, northeast Brazil, southeast Argentina, and southern Africa as well as the horn of Africa and the Sahel. FPET is relatively lower in tropical rainforest regions (Amazon, tropical Africa, Indonesia) than other variables owing to few clear-sky samples during rainy season when all-sky FPET is high. The NDVI and NDII patterns for their mean values are the most similar to each other, of the four shown.

Fig. 3.

Left: means computed over the active growing season for a) FPET, (b) NDVI, (c) NDII, and (d) fractional “root-zone” soil moisture (RZM, in the top 1 m layer) from MERRA-2 (all quantities are dimensionless); Right: corresponding standard deviation of their weekly IAV (panels e–h). White areas with no data correspond to large deserts such as the Sahara, Arabian, and Gobi deserts.

The standard deviations of the IAV show areas where there are significant IAV values and also may give some indication of measurement noise and other errors. There are similar spatial patterns in the standard deviations of all DI′, with high values in semi-arid regions, particularly central Australia, Texas and northern Mexico, and southern Africa. The standard deviations of the DI′ values (as for the original mean DI values) are most similar for the NDVI′ and NDII′. However, there are also some differences. For example, higher standard deviations are shown for FPET′ as compared with the vegetation indices over tropical rain forest areas (Amazonia, central Africa, and the tropical Pacific). Relative to the VI′, FPET′ in these areas may be affected more by cloud contamination. In addition, there may also be some residual cloud contamination in the VI data. Cloud contamination should affect the NDVI more than the NDII since the band reflectance differences for NDVI are larger. This is consistent with the higher standard deviations of IAV seen for NDVI as compared with NDII in cloudy areas such as Amazonia.

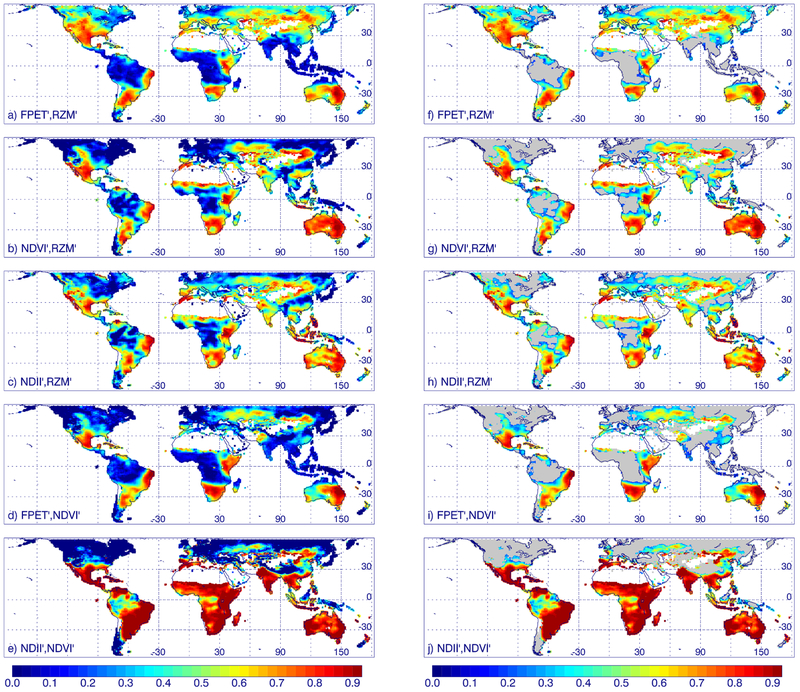
Fig. 4 shows mapped correlations between each DI′ and RZM′ and with respect to each other obtained during our fitting procedure (Eq. (2)) for all gridboxes (left) and only for those with p-values < 0.00001 (right). All satellite-based DI′s generally show similar correlations with respect to RZM′. NDVI′ generally displays the highest correlations with respect to RZM′ (panel b), but this only occurs in specific areas. In some areas, particularly the boreal forest areas at high northern latitudes (above 40°N) and parts of western Europe, FPET′ shows somewhat larger extents of areas significantly correlated with RZM′ as compared with the other satellite-based DI′. This indicates that FPET′ has higher sensitivity to water stress in these regions, although the correlations are in the moderate range, generally below 0.5.

Fig. 4.

Maps of Pearson’s correlation coefficient (r) between weekly satellite-based DI′ and RZM′ after fitting with Eq. (2); the first variable listed is the fitted parameter (fit by a scaled and shifted version of the second variable): a) FPET′ fitted using RZM′; b) NDVI′ fitted using RZM′; c) NDII′ fitted using RZM′. d) FPET′ fitted using NDVI′; and e) NDII′ fitted using NDVI′. Left: all gridboxes with valid data; Right (f–j): only for gridboxes with p-values < 0.00001 (all other gridboxes with valid data shown in gray).

In heavily forested regions such as Amazonia and other tropical rain forests and less drought-prone areas such as the NE US, there is less variability in the IAV values due to temporal stability of the vegetation itself. Therefore, the IAV values in these areas are likely dominated by measurement error (i.e., noise and cloud contamination). This results in mostly insignificant correlations of the satellite-based DI′s with respect to RZM′. An examination of fitting residuals (see Appendix B) provides additional insight into measurement errors. The correlations of FPET′ with respect to NDVI′ (panels d and i) show similar spatial patterns as with respect to RZM′ (panels a and f). Similar correlations have been shown at monthly timescales and for different months (Vicente-Serrano et al., in press) and empirical relationships between NDVI and ET have also been reported (Yao et al., 2010). NDVI′ and NDII′ are found to be highly correlated (panels e and j); they share a common reflectance band (NIR band 2) and so will have correlated measurement errors. However, the impact of cloud contamination will differ for NDVI and NDII with a larger expected effect on NDVI. This may explain the lower correlations in tropical regions that are frequently cloud covered. Appendix C provides additional statistical analyses and a summary of the correlations between the DI′s.

Fig. 5 shows vegetation types within eight large boxes that display high correlations between satellite-based DI′ and RZM′. The vegetation types are from the MODIS MCD12C1 2010 yearly land cover product gridded at 0.05°× 0.05° (Friedl et al., 2010). Table 2 lists the corresponding percentages of different vegetation types within these eight water-sensitive regions. These regions are dominated by grasslands, shrublands, and savannas that tend to have relatively shallow roots that lie within the top 1 m soil layer of the MERRA-2 RZM estimates. Vegetation systems with deeper roots, such as rain forests, may be able to extract water from deeper layers where moisture can be decoupled from the MERRA-2 RZM.

Table 2.

Percentages of different vegetation types within large boxes shown in Fig. 5. Shrublands include both open and closed shrublands; Savannas include woody savannas; Forests include evergreen broadleaf and needleleaf, deciduous broadleaf and needleleaf, mixed forests, and grass + mixed forests; Other includes water, urban, snow/ice, barren/sparsely vegetated, and wetlands. The last line (“all”) shows averages over the gridboxes within all the large boxes (i.e., not area-weighted).

Box #	Grasslands	Shrublands	Savannas	Croplands	Forests	Other
1	35.6	25.8	13.2	8.5	12.1	4.7
2	17.9	31.3	9.7	20.0	16.3	4.9
3	0.3	0.6	80.5	0.7	11.4	6.5
4	9.0	33.6	48.7	1.7	1.7	5.3
5	20.2	24.9	25.9	7.9	13.4	7.7
6	73.9	0.9	0.2	16.1	6.4	2.5
7	77.0	1.1	0.3	8.1	8.0	5.5
8	7.7	50.3	16.6	11.8	6.2	7.4
All	32.9	20.8	22.3	9.5	9.0	5.5

The areas with significant correlations between the satellite-based DI′ and RZM′ (and also between FPET′ and VI′) are similar to those found to have high correlations between NDVI and cumulative precipitation IAV (Zeng et al., 2013; Koster et al., 2014). These same areas were also found to have a significant drought resistance coefficient derived from NDVI at a bimonthly timescale (De Keersmaecker et al., 2015). It has been suggested that these regions play a major role in carbon cycle variability, particularly in the southern hemisphere (Poulter et al., 2014; Ahlström et al., 2015; Ma et al., 2016; Zhang et al., 2016).

Fig. 6 shows time series of smoothed IAV for several individual gridboxes from Fig. 5 (marked as an ‘x’ within the black boxes). From Fig. 6 it is immediately apparent that all satellite DI′ vary similarly in time, with timescales similar to those of RZM′. Well-known features, such as the 2011 Texas drought in box 1 (Sun et al., 2015; Wang et al., 2016) and 2010 Russian drought in box 6 (Yoshida et al., 2015) are shown as distinctly negative values in all DI′. Small time shifts of the order of a week to two weeks (i.e., 1–2 samples) between these different drought indicators are not readily apparent.

Fig. 6.

Time series of smoothed RZM′ (black) and DI′, the latter being offset (as indicated by the horizontal lines that indicate the zero level) for clarity with different colors as noted in the legend. Pearson’s correlation coefficients (r) with respect to RZM′ prior to the fitting are listed on the top right in the associated colors. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

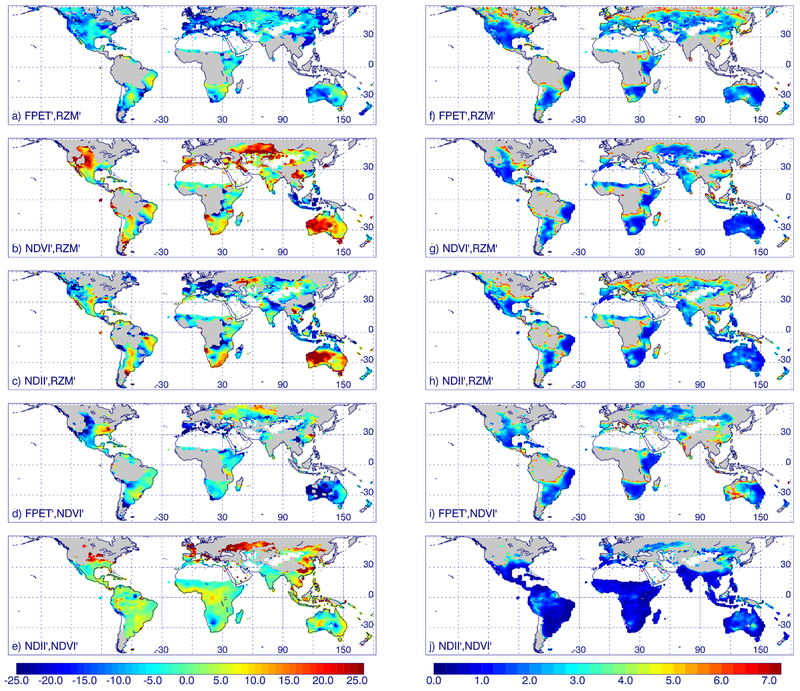
Fig. 7 shows computed time lags (Δt) and their estimated 2σ uncertainties for the same pairs of variables as in Fig. 4. These uncertainties are generally considered to be lower limits as explained in Appendix A. The lags of FPET′ with respect to RZM′ are generally smaller (~zero to a few weeks negative) than those of NDVI′ and NDII′. This means that FPET′ has a somewhat faster response to dry conditions than NDVI′ and NDII′. This is consistent with the results of Otkin et al. (2016) who showed that decreases in the ET-driven ESI anomalies (or IAV) preceded observed changes in crop conditions by up to one month during the 2012 US flash drought.

Fig. 7.

Left: Time lags (Δt, in days) between various drought indicators, where positive values indicate the lag of the first variable listed with respect to the second a) FPET′ and RZM′, b) NDVI′ and RZM′, c) NDII′ and RZM′; d) FPET′ and NDVI′; e) NDII′ and NDVI′; Right: Estimated 2σ uncertainty in lags computed with linear assumption for same parameter pairs.

The lags can take on negative values when IAV in the first parameter precedes that of the second variable. Fig. 7a shows some substantially negative values of Δt for FPET′ with respect to RZM′, for example on the Iberian Peninsula(meaning that FPET′ precedes RZM′). While this may seem counterintuitive at first, there are plausible explanations. In areas with sparse vegetation, ET is more sensitive to surface soil moisture through its direct connection to soil evaporation (E) and soil surface temperature. In these areas, reductions in FPET are more strongly tied to reductions in near-surface moisture than to reductions in moisture throughout the top 1 m (the “root zone” depth in the MERRA-2 system). An extended precipitation deficit will dry the top several centimeters of soil first (with concomitant impacts on FPET), while the full top meter of soil will take longer to dry. Similarly, a subsequent rainy period will allow near-surface moisture (and thus FPET) to recover more quickly than the full root zone. The net effect could be a negative time lag of FPET′ with respect to RZM′.

In fully vegetated areas, ET is dominated by vegetation transpiration (T), which is sensitive to the IAV in RZM through its link to vegetation water content, transpiration, and stomatal closure. For areas where transpiration is high and a negative time lag may occur between FPET′ and RZM′, such as in the southeastern US, negative lags could result if the MERRA-2 model underestimates the rate of depletion of soil water through ET or drainage. These areas generally have low correlations and high uncertainties in the computed lags owing to smaller IAV values and also fewer satellite land surface temperature retrievals in these frequently cloudy regions.

NDVI′ and NDII′ generally respond within about a week relative to RZM′ for most sensitive areas. We do not detect many significant leads or lags between NDVI′ and NDII′ (see Fig. 7e). The faster response, in general, of FPET′ as compared to the other satellite-based DI′ likely reflects surface processes (including soil evaporation and canopy interception) whose decline does not necessarily indicate long-term drought conditions.

The correlations and lags for NDVI′ with respect to RZM′ are generally consistent with those that have been found in more detailed studies at individual sites (e.g., Wang et al., 2007; Méndez-Barroso et al., 2009; Schnur et al., 2010; Swain et al., 2013; Jamali et al., 2011). For example, NDVI lags were found to vary with soil moisture at different depths ranging from a few days to several weeks (Jamali et al., 2011) and also varied with plant type (Swain et al., 2013). It should be noted that lags may vary with climatic or land-use changes (Ahmed et al., 2017) and that our approach derives a single lag value based on the wide range of conditions occurring over more than a decade.

4. Conclusions

Comparing global responses of FPET, NDVI, NDII, and RZM interannual variations, we show that they all feature the same basic spatial and temporal variability with respect to water stress in sensitive areas. These sensitive areas are dominated by grasslands, shrublands, and savannas. These vegetation types tend to have root systems contained within the 1 m defined root zone of the MERRA-2 RZM fields. Vegetation with deeper root systems, falling outside the top 1 m layer of the MERRA-2 root zone, such as trees within tropical rain forests, may be able to access water from deeper layers that can be decoupled from the MERRA-2 RZM. This effect, along with frequent cloud contamination of satellite retrievals in the same areas, may explain the low correlations between satellite drought indicators and RZM interannual variations in tropical regions. In moderately to highly vegetated areas of high northern latitudes such as in western Europe and North America, FPET′ shows larger areas with significant correlations with respect to RZM′ than NDVI′ or NDII′. Although the correlations in these areas are somewhat reduced (< ~ 0.5) as compared with more sensitive areas that correspond with semi-arid regimes (grasslands, shrublands, and savannas), our analysis indicates that FPET′ has higher sensitivity to water stress in these higher latitude regions.

FPET′ frequently leads RZM′ as well as NDVI′ and NDII′ in water sensitive regions by days, and by up to a week or more. The VI interannual variations typically lag those of RZM by days to a week or more. One explanation is that the bare soil evaporation component of FPET is a significant driver of interannual variations in these areas. Soil evaporation responds more quickly to soil conditions near the surface (top few cm) as compared with soil moisture throughout the top 1 m of the soil. Interannual variations in FPET′ therefore may show a rapid response to mild water stress, while NDVI′ and NDII′ respond primarily to more severe conditions throughout the root zone during a longer-term drought. This effect would tend to occur in more sparsely vegetated areas which is where FPET′ most frequently leads RZM′, NDVI′, and NDII′. In more fully vegetated areas, where correlations are generally lower, transpiration dominates over evaporation. In these areas, such as the eastern US and eastern China, negative lags of FPET′ interannual variations with respect to those of other indicators may result if the MERRA-2 model underestimates the rate of depletion of soil water through ET or drainage.

Our study suggests that the FPET and VI anomalies contain complementary information. While many drought-related parameters are produced on a monthly basis, these satellite data sets may also be useful at daily to weekly timescales. VI data, when processed carefully to remove the effects of sun-satellite geometry and clouds, provide relatively clean time series that show impacts of water availability changes in sensitive regions on timescales of the order of days to weeks. FPET anomalies, while somewhat more variable on daily timescales, may provide earlier detection of drought impacts as compared with VI anomalies owing to its sensitivity to changes in near-surface soil moisture that affects sparsely vegetated regions and stomatal conductance that plays more of a role in heavily vegetated area.

FPET, NDVI, and NDII can all be obtained at management level spatial resolutions (e.g., 1 km × 1 km or better) and with revisit times of the order of days with current satellites in low Earth orbit. In addition, NDVI can be derived at the field level (~30 m) with Landsat and Sentinel 2 that when combined is available at approximately weekly timescales. While our analyses were conducted at the scale of the global RZM data set, the approach of using IAV can be applied at the higher spatial resolution of the currently available satellite data sets. While both vegetation indices and FPET are currently used in the USDM, we have identified several regions of the world where these data may be useful in similar approaches.

We expect improvements in all data sets used here in the future, both in terms of data quality as well as spatial resolution. Reanalysis soil moisture will improve in the future as the input and assimilated data quality improves, for example through the addition of satellite-based rainfall estimates from the joint NASA and Japanese Aerospace Exploration Agency (JAXA) Global Precipitation Mission (GPM) and assimilation of radiometer observations from the NASA Soil Moisture Active Passive (SMAP) mission and the European Soil Moisture Ocean Salinity (SMOS) mission. We also expect higher spatial resolution in future reanalysis data sets.

Our approach of using IAV to estimate leads/lags between different satellite indicators is least effective in heavily vegetated areas owing in part to deeper root zones (deeper than 1 m) and less interannual variability in general. These aspects present inherent limitations of the method in more heavily vegetated areas. Particularly in the tropical rain forests, there is little interannual variability in the satellite indicators and there are larger observational errors due to cloud contamination. With respect to the cloud contamination issue, several next- generation geostationary Earth orbit (GEO) instruments including the Advanced Baseline Imager (ABI) may improve the data quality of the vegetation indices and FPET by increasing the number of potential observations with more frequent opportunities to see between clouds. Utilization of cloud tolerant microwave observations may improve the consistency and revisit time of sampling underpinning the ET retrieval. It also has the potential to reduce the noise, especially in areas with frequent cloud cover (Holmes et al., 2018). The ECOsystem Spaceborne Thermal Radiometer Experiment on (the international) Space Station (ECOSTRESS) since July 2018, is expected to provide the ESI for 1–2 years at a field level spatial resolution of tens of meters.

Appendix A. Details regarding the calculations of time lags

To compute the lag Δt between DI′₁ and DI′₂ according to Eq. (2), we solve for a state vector x consisting of A, ϵ, and Δt using an unconstrained non-linear least-squares approach, e.g., Rodgers (1990), i.e.,

$$\Delta x_i={\left(H_i^T{S}_y^{-1}{H}_i\right)}^{-1}{H}_i^T{S}_y^{-1}\left(y_{\text{obs}}-y_{\text{calc},i}\right),$$ (A,1)

where the subscript i denotes the iteration, H is the Jacobian matrix or linearized observation operator (∂ y/∂ x), superscript T denotes transpose, Sy is the observation error covariance, y_obs is the time series of DI′₁ (DI′_1,t) and y_calc is a vector of values computed using the forward model (Eq. (2)). In this formulation, Δt may take on non-integer values (i.e., fractions of the 7 day sampling interval); The shifted time series of DI′₂(DI′_{2,t Δt}) in Eq. (2) is calculated using linear interpolation. Hi is computed by finite differences (Eq. (2)), i.e., linearized about the current state estimate, using a Δt interval of 1 sample (7 days). The first guess for A and ϵ is computed using a linear (non-iterative) unconstrained least squares approach (Eqs. (2) and (A.1)) with Δt = 0. The retrieved Δt in samples can be converted to units of days by multiplication with 7 days/sample.

In Eq. (A.1), we assume that S_y is a diagonal matrix (σ²_yI), implying uncorrelated and constant errors for all observations. With these assumptions the Sy terms then cancel in Eq. (A.1) so that the state vector solution does not depend on the assumed measurement error variance. However, the measurement error variance is needed to estimate the retrieval error covariance. At convergence, the error covariance for x, S_x, is computed using

$$S_x={\left(H^T{S}_y^{-1}H\right)}^{-1}={\sigma }_y^2{\left(H^{T}H\right)}^{-1}$$ (A,2)

following Rodgers (1990). Here, we use the standard deviation of the residuals (y_obs −y_calc) at convergence as an estimate of σ_y.

We tested the approach with a Monte Carlo simulation and found that it worked very well for the case of random noise applied to DI′_1,t but noise free DI′_2,t. However, this standard linear error propagation technique may underestimate uncertainties when noise is added to DI′_2,t, because that noise is propagated into the Jacobian calculation and is not taken into account within the standard linear error estimation. A similar condition can occur if there are systematic differences between the two time series applied, i.e., when the model in Eq. (2) is imperfect. The Jacobian error may also produce a bias in the retrieval. To mitigate these issues, we always use the less noisy parameter for DI′_2,t. In addition, we apply a six point box car smoothing to all time series. This nearly eliminated the bias and underestimation of errors within the Monte Carlo simulator. However, with real data and imperfections in the assumed model, we must consider the error estimates as lower limits as they will tend to underestimate errors. In addition, intercomparison of lead/lags computed between different pairs of variables may not provide a perfect closure owing again to imperfections in the assumed models as well as nonlinearities.

We also found that in some cases, outliers (e.g., that may be present owing to undetected clouds for vegetation indices) can drive the fitting and produce unreliable shifts. We therefore undertook several measures to remove outliers as follows: 1) We compute standard deviations (σ) of DI′_1,t and DI′_2,t (DI₂ not time shifted) and assign a large error (i.e., resulting in a negligible weight, referred to as de-weighting) to any points with absolute values > 3.5σ; 2) We similarly de-weight any points where the absolute values of both DI′_1,tand DI′_2,t are > 2σ and DI′_1,t and DI′_2,tare of opposite sign; 3) To avoid extrapolation error, we de-weight the first and last points of a time series; 4) To avoid interpolation error, we de-weight any points that are adjacent to the points that are filtered out by checks (1) –(3) or missing data; 5) We de-weight any points with absolute values of residuals > 3σy;6) We de-weight any point for which the adjacent value of the IAV changes by more 4σ (continuity check).

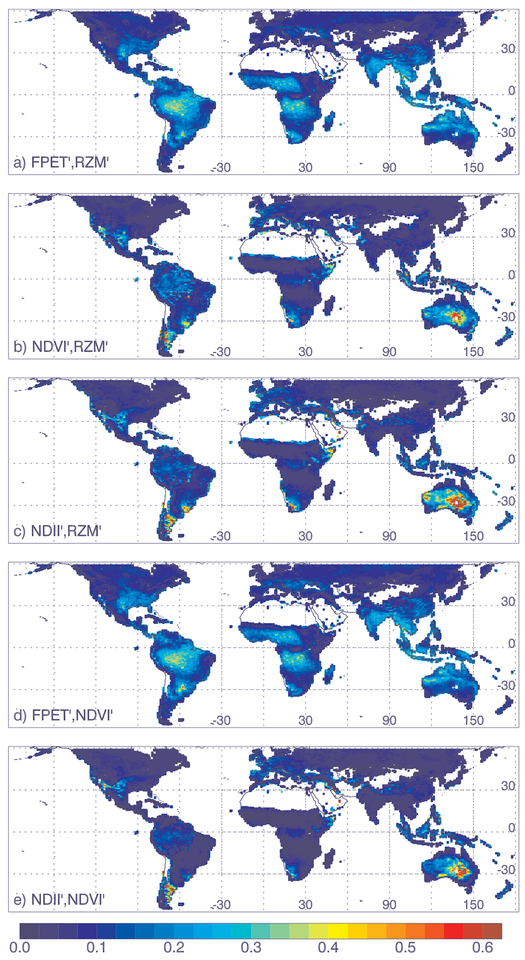
Appendix B. Fitting residuals

One way to assess the errors in the various DI measurements is to examine the fitting residuals (y_obs −y_calc) using Eq. (2) for different pairs of DI′. Fig. B.8 shows maps of the standard deviations of the fitting residuals. The units of the residuals are the fraction of the climatological range. In other words, a value of 0.3 means that the standard deviation of the fit is 30% of the range of climatological values observed during the growing season. In the ideal case, a perfect match exists between the noisy DI′ after accounting for a phase shift. Then, the standard deviation of the residual would be equal to the square root of the summed error variances of each DI′ used in Eq. (2). However, if there is an imperfect match between the DI′, then the residual will be increased. Note that the residuals are shown after quality control has been applied.

Fig. B.8.

Standard deviations of the fitting residuals for different pairs of gridded drought indicators using Eq. (2); the first variable listed is the fitted parameter (fit by a scaled and shifted version of the second variable): a) FPET′ fitted using RZM′; b) NDVI′ fitted using RZM′; c) NDII′ fitted using RZM′; d) FPET′ fitted using NDVI′; e)NDII′ fitted using NDVI′.

It is difficult to separate the effects of pure measurement error from model error in Eq. (2). Comparing the residuals computed with different pairs of DI′ and with the standard deviations of the interannual variations (IAV) may provide some clues. In places where residuals are not significantly reduced compared with the original standard deviations, this indicates measurement error and/or inability to fit one variable effectively with respect to another. For example, larger residuals are observed over Texas and northern Mexico as compared with surrounding regions for all DI′s. However, the residuals are reduced as compared with the standard deviations of the IAV indicating that there are significant yet imperfect relationships between the DI′ in this area.

In general, the fitting residuals are smallest for NDVI′ and NDII′ with respect to RZM′ and each other. NDVI and NDII benefit from relatively wide reflectance bands (e.g., 20 nm) with much higher SNR and larger signals.

The residuals involving FPET′ show large values over tropical rain forests where the range of the climatology (used for normalization) is small owing to limited seasonal variation. In these regions, known to be particularly cloudy, the effects of cloud contamination may be significant in comparison with the climatological range. A small climatological range may also explain the relatively high values of residuals in parts of sparsely vegetated Australia. At high northern latitudes where there is substantial seasonal variation during the growing season and in general small IAV values, the VI residuals are fairly small (standard deviations < ~ 0.2). Values are somewhat higher for FPET′ as compared with NDVI′ and NDII′.

Appendix C. Further analyses of correlations between DI′s

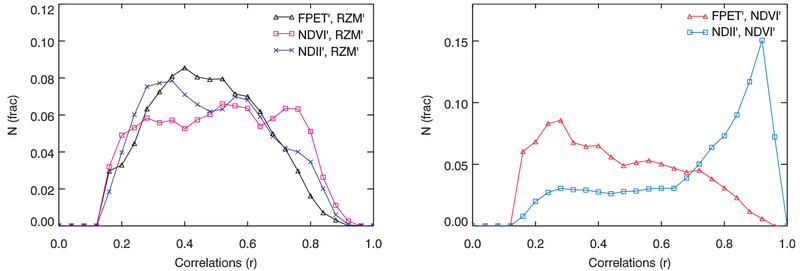
Fig. C.9 shows histograms of the correlations between the different satellite-based DI′ and RZM′. Table 3 summarizes statistics related to those distributions (means and standard deviations). It is apparent that FPET′ is better correlated with RZM′ than with NDVI′ indicating that it has a better relationship with water availability than vegetation structure.

Table 3.

Number of points meeting p-value criteria, means, modes, and standard deviations (σ) of the distributions of correlations between different pairs of DI′.

1st DI′	2nd DI′	# points	Mean	Mode	σ
FPET′	RZM′	20,520	0.49	0.40	0.17
NDVI′	RZM′	13,432	0.53	0.52	0.20
NDII′	RZM′	18,104	0.50	0.36	0.18
FPET′	NDVI′	11,613	0.47	0.28	0.20
NDII′	NDVI′	14,165	0.72	0.92	0.23

Fig. C.9.

Histograms of correlations between different satellite-based DI′ (left: satellite-based DI′ with RZM′; right: satellite-based DI′ with each other).