Seasonal to decadal variability in ice discharge from the Greenland Ice Sheet

Abstract

Rapid changes in thickness and velocity have been observed at many marine-terminating glaciers in Greenland, impacting the volume of ice they export, or discharge, from the ice sheet. While annual estimates of ice-sheet wide discharge have been previously derived, higher-resolution records are required to fully constrain the temporal response of these glaciers to various climatic and mechanical drivers that vary in sub-annual scales. Here we sample outlet glaciers wider than 1 km (N = 230) to derive the first continuous, ice-sheet wide record of total ice sheet discharge for the 2000–2016 period, resolving a seasonal variability of 6 %. The amplitude of seasonality varies spatially across the ice sheet from 5 % in the southeastern region to 9 % in the northwest region. We analyze seasonal to annual variability in the discharge time series with respect to both modelled meltwater runoff, obtained from RACMO2.3p2, and glacier front position changes over the same period. We find that year-to-year changes in total ice sheet discharge are related to annual front changes (r² = 0.59, p = 10⁻⁴) and that the annual magnitude of discharge is closely related to cumulative front position changes (r² = 0.79), which show a net retreat of > 400 km, or an average retreat of > 2 km at each surveyed glacier. Neither maximum seasonal runoff or annual runoff totals are correlated to annual discharge, which suggests that larger annual quantities of runoff do not relate to increased annual discharge. Discharge and runoff, however, follow similar patterns of seasonal variability with near-coincident periods of acceleration and seasonal maxima. These results suggest that changes in glacier front position drive secular trends in discharge, whereas the impact of runoff is likely limited to the summer months when observed seasonal variations are substantially controlled by the timing of meltwater input.

1. Introduction

Mass loss from the Greenland Ice Sheet (GrIS) is now the single largest cause of sea level rise (Vaughan et al. 2013; AMAP 2017), contributing approximately 1 mm a⁻¹ of global water equivalent over the 2010–2015 period (van den Broeke et al. 2016). Since the mid 1990’s, the GrIS has been losing ice at an increasing rate (Rignot et al. 2011; Sasgen et al. 2012; Hanna et al. 2013; Enderlin et al. 2014) due in part to increased discharge from marine-terminating outlet glaciers (Rignot and Kanagaratnam, 2006; Rignot et al. 2008; Enderlin et al. 2014; Andersen et al. 2015). Substantial increases in ice discharge are observed at large outlet glaciers over periods of months or less (e.g. Joughin et al., 2004; Howat et al. 2005), demonstrating short term sensitivity to external drivers, such as ocean circulation (Straneo et al. 2013; (Walsh et al. 2012) melt runoff (Joughin et al. 2008; Andersen et al. 2011), and sea ice/mélange conditions near the calving front (Howat et al. 2010; Carr et al. 2013; Moon et al. 2015; Bendtsen et al. 2017). Thus, understanding the dynamics of these glaciers requires measurements with a high temporal resolution.

Seasonal variability in the flow speed of marine-terminating glaciers in Greenland has been observed for small samples of glaciers (Howat et al. 2010; Howat et al. 2011; Hill et al. 2018) and for larger glacier inventories over short time periods (Howat et al. 2008; Moon et al. 2014; Moon et al. 2015). Previous ice sheet-wide estimates of discharge were largely based on summertime velocities and, therefore, may be biased toward higher values, demonstrating the need for decadal records of ice sheet-wide discharge that resolves seasonal to sub-monthly variability, potentially associated with surface meltwater runoff and calving. Here we present the first continuous record of daily estimates of net ice sheet discharge, derived over the 2000–2016 period. This record is used to resolve both distinct ice-sheet wide and regional patterns of seasonal variability and evaluate how seasonality has changed through time. We then compare these records to modelled meltwater runoff data and records of glacier front positions to assess how these terms impact discharge on seasonal to annual time scales.

2. Data and Methods

Following Howat et al. (2011), we derive time series of the rate of solid ice discharge (D) for 230 glaciers (Figure S4) with widths greater than 1 km by integrating the product of glacier thickness, ice velocity, and ice density across the glacier width at the grounded terminus. Observations are sampled along a static profile, i.e. fluxgate, oriented perpendicular to the direction of flow and located upstream of the grounding line, immediately inland of the most retreated grounding line during the 2000–2016 study period. We use the same flux gates as Howat et al. (2011) and Enderlin et al. (2014) except in cases where the grounding line had retreated inland of the gate location. Further, while Enderlin et al. (2014) used empirical relationships to estimate cross-sectional area and discharge at glaciers for which only along-flow profiles or no bed topography were available, we use the BedMachine version 3 gridded bed topography dataset (Morlighem et al. 2017), which uses ice thickness, flow speed observations and surface mass balance (SMB, i.e. the sum of the mass gained from accumulation and lost due to meltwater runoff, sublimation and snow drift erosion) to constrain a mass conservation model. As in prior studies, we assume that changes in the elevation of the glacier bed, due to erosion, deposition and/or lithosphere displacement, are small, as are variations in ice flow velocity with depth in fast flowing (> 1 km a⁻¹) glaciers. Bed topographic errors across our sampled flux gates average 70 ± 52 m. Thus, discharge is estimated from the bed topography and repeat measurements of surface elevation, the difference of which provides the time-variable ice thickness, and ice flow velocity. Additional information regarding the placement of flux gates and descriptions of the datasets are provided in the supplementary material.

Enderlin et al. (2014) derived annual discharge estimates from velocity data that were mostly collected between April and September. Increased data collection by SAR sensors (Terra/TandemSAR-X), low-light level functionality of Landsat 8 (Jeong and Howat, 2015; Fahnestock et al. 2016), and increased sampling density using image pairs between multiple sensors and/or acquired from crossing orbital tracks (Rosenau et al. 2015; Jeong et al. 2017), enable substantially better temporal resolution than available for Enderlin et al. (2014). Thus, we combine this increased velocity sampling with a Kalman filter approach to estimate D and it uncertainty as a continuous series. For each glacier, we first derive a standard seasonality curve by detrending the time series of monthly mean speeds and grouping mean speeds by the month of year, so that a 17-year time series would provide up to 17 estimates of mean speed for a given month. The standard seasonality is then obtained from the median value and covariance of the observations for each month and represents a “typical” pattern of change at each respective glacier. Months with fewer available observations will therefore tend to have a higher range of uncertainty. If no optical or radar data exist for a particular month throughout the time series, a standard monthly value is estimated by fitting a periodic function to the available monthly median values. The periodicity described here does not indicate that a symmetric, sinusoidal seasonality is assumed, but rather that by detrending the time series and isolating a mean seasonal pattern of change, we expect the endpoints of the curve to be the same (i.e. the 12-month curve would repeat). The seasonality curve is then normalized to yield an estimate of fractional change in speed between months, which informs a simple linear model. Within the Kalman filter framework, this linear model assimilates the observations to optimize estimates for missing months of the time series, with the errors equal to the combination of the observation and prediction errors. Uncertainty in the seasonality curves tend to exceed observational errors, resulting in formal errors that increase with distance from the observations. A more detailed description of this approach is provided in the supplementary material. Velocity measurements for the four northernmost glaciers (Steenby, C.H. Ostenfeld, Academy, and Hagen Brae) and several small glaciers near the central eastern margin were too sparse to derive a continuous time series and we instead estimate an annual D for these glaciers. This data sparsity occurs when months of missing data exceed the number of months containing reliable observations post-filtering, preventing a resolvable seasonality.

We use the same repeat ice surface elevation dataset as Enderlin et al. (2014), extended through 2016, and with the addition of stereoscopic digital elevation models produced from sub-meter resolution DigitalGlobe Inc. WorldView imagery for the ArcticDEM project (www.arcticdem.org). The DEMs are produced to 2 m resolution and coregistered over stationary (exposed rock) surfaces using the algorithm of Noh and Howat (2014). Following coregistration to remove biases, these data have an accuracy of better than ± 0.5 m (Noh and Howat, 2015). Elevation profiles are filtered for noise and smoothed as described in the supplementary material before subtracting the BedMachine V3 bed profiles from each surface elevation profile to give ice thicknesses. The series of ice thickness estimates were then linearly interpolated to the times of the series of velocity observations to obtain ice discharge rate, D. Errors in discharge at velocity observation times are calculated from propagation of measurement errors and uncertainties of interpolated values are determined from a Monte Carlo ensemble, as described in the supplementary material. We derive total ice sheet mass balance over the 2000–2016 period by combining our estimates of D with SMB data obtained a 5.5 km simulation of the Regional Atmospheric Climate Model, RACMO2.3 version 2 (RACMO2.3p2) statistically downscaled to 1 km, and compare these totals to monthly satellite gravimetry observations of ice sheet mass balance from the Gravity Recovery and Climate Experiment (GRACE). While RACMO2.3p2 applies the same model physics as described in Noël et al. (2018), a twice finer horizontal resolution (5.5 km instead of 11 km) better resolves SMB gradients over narrow glaciers at the ice sheet margins. Based on comparison with observations, the uncertainty in modelled basin-integrated runoff and snow accumulation (total precipitation minus sublimation) are, respectively, 20 % and 10%, which are combined to obtain an uncertainty in SMB by assuming the two are independent of each other (Noël et al., 2018; Van As et al., 2018).

We examine how D varies in response to meltwater runoff and changes glacier front position. Daily meltwater runoff estimates are also obtained from the RACMO2.3p2 product. Daily runoff values at each model grid point are summed over the ice sheet and within regional basins for comparison to D. We measure relative changes in glacier front position manually for the period 2000–2016 using all available imagery from ASTER and LANDSAT 4–8. This resulted in a measurement frequency of up to every few days during the summer, declining in frequency during the polar night, especially prior to 2012 (Landsat 8 launch). Due to the very large quantity of measurements, we used the efficient centerline methodology described in Walsh et al. (2012), who found a negligible difference in the temporal variation of front position between this and methods that involve digitization of the entire front. To enable comparison with discharge and runoff time series, we convert the irregular front position observations to daily rates of change and then resample the rates at 7-day intervals. The new resampled subset is then linearly interpolated to daily rates of front position change over the study period. Individual glacier records of frontal change are combined into regional and GrIS-wide records by first applying a discharge-dependent weighting function, so that retreat and advance events at larger glaciers are weighted more heavily, due to the proportionally larger impact of these glaciers on the discharge time series. We do not include front position measurements for Zachariæ Isstrøm and 79 North Glacier because the perennial mélange of tabular icebergs at their fronts make delineation of the front position arbitrary (e.g. Moon et al. 2008).

3. Results

3.1. Net Ice Sheet Discharge and Mass Balance

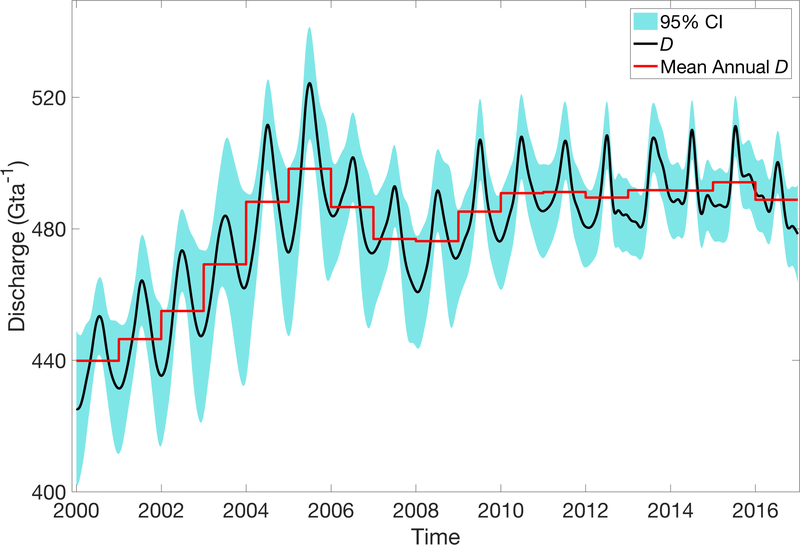
The net GrIS-wide D reveals a clear seasonality, typically characterized by an annual minimum in December and a maximum in mid-July (Figure 1), superimposed upon multi-year variability. Removing the linearly-interpolated annual means from the time series gives an average seasonal amplitude of 30 Gta⁻¹, or approximately 6 % of the mean annual discharge. The seasonal amplitude was largest in 2002, 2004, and 2005, reaching up to 46 Gta⁻¹, and, on average, higher before 2005 (35 ± 8 Gta⁻¹, where the uncertainty is 1−σ). This compares to an average seasonal amplitude of 27 ± 4 Gta⁻¹ after 2006, with overall trend of −0.7 Gta⁻¹ from 2000 to 2016. Beginning from a mean annual discharge of 440 ± 8 Gta⁻¹ in 2000, D increases to a maximum of 524 ± 9 Gta⁻¹ in late June 2005, primarily due to the accelerations of Kangerdlugssuaq and Helheim glaciers in the east (Howat et al. 2007; Joughin et al. 2008). In the following two years, the rapid decrease in D from these two glaciers resulted in the greatest seasonal decrease in GrIS D in 2006, declining to a minimum of 461 ± 9 Gta⁻¹ by January 2008. D then gradually increased, reaching the second-highest time series annual maximum of 494 ± 6 Gta⁻¹ in 2015, with a peak summertime value of 511 ± 6 Gta⁻¹ in July 2015. Annual D declined by 5 Gta⁻¹ in 2016 largely due to reductions in discharge observed at Køge Bugt and Jakobshavn (Figure S3). Thus, D has remained consistently between 10 to 12 % above the 2000 rates since 2010. Along with the annual mean quantities, the seasonal discharge signal varies throughout the study period. Prior to 2013, the seasonal variation in D is relatively symmetric, with a single distinct peak and little variability on sub-annual timescales. The final four years of the record are more variable, with minor peaks following the seasonal maxima. This pattern is predominantly due to changes observed in the NW region, addressed in detail in Sect. 3.2.

Figure 1:

Continuous estimates of discharge, D, for the GrIS for the 2000–2016 period, expressed as a rate of Gigatons per year (Gta⁻¹). Shading represents the 95 % confidence interval.

The ice sheet’s 20 largest glaciers account for over 50 % of the total D (Figure S4). Of these 20, the four largest glaciers (Fig. S3) together account for 25 % of the total D, and 56 % of the cumulative anomaly in GrIS-wide D relative to annual D in 2000. Variations in these four glaciers, therefore, dominate variability in total GrIS D. The secular trend of the combined D is substantially different with the four largest glaciers removed (Figure S5). Following the decline in D between 2005 and 2008, the combined D of the remaining glaciers, denoted here as D_s, continued to increase, reaching a maximum in 2011 before declining to another minimum 2012. The seasonal decline in D_s during the winter of 2013–2014 was anomalously reduced relative to other years, with speeds remaining elevated across the ice sheet. D_s then increased to a record maximum in July 2015, reaching an annual maximum of 374 ± 5 Gta⁻¹ in 2016. Thus, an overall continued increase in D_s since 2008 was largely offset in declines from the four largest glaciers over that period. Removing the four largest glaciers, however, does not change the relative seasonal amplitude of approximately 6 %, indicating that GrIS-wide seasonality is not dependent on the largest glaciers.

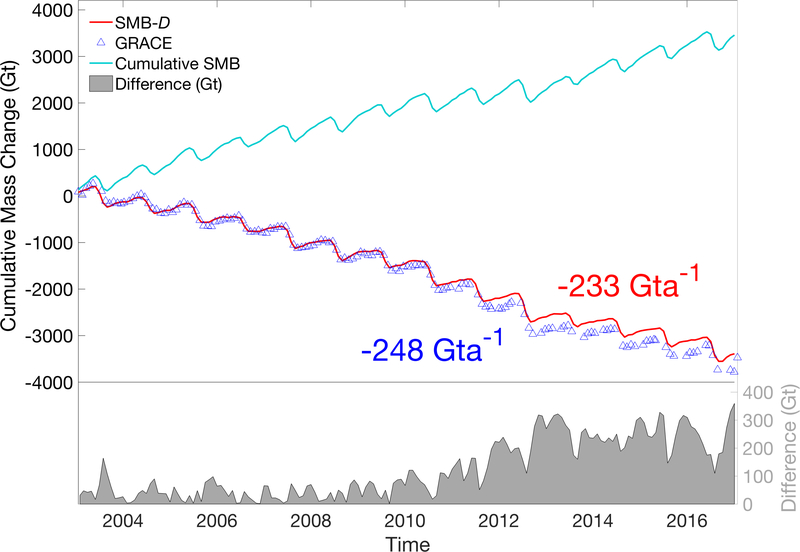
Our continuous estimates of D enable the first direct comparison to monthly satellite gravimetry observations of ice sheet mass balance from GRACE. We compute ice sheet mass balance by subtracting our estimates of net GrIS-wide D from daily 1 km² resolution SMB estimates obtained from RACMO2.3p2 (Noël et al., 2018). Following the methodology of van den Broeke et al. (2016), we incorporate SMB fluxes from the ice-free tundra and peripheral ice caps, which are included in the GRACE signal, into the ice-sheet mass balance calculations. Mass balance estimates of peripheral ice caps derived from laser altimetry (Bolch et al. 2013) found that areal averaged mass losses were similar for land-terminating and marine-terminating glaciers, and thus we assume D from peripheral glaciers and ice caps is small relative to the errors in other terms. We remove the SMB over ice shelves, downstream of the discharge flux gates, from the total. We use GRACE ice sheet mass updated from Wouters et al. (2013), corrected for glacial isostatic adjustment using the model of Khan et al. 2016. The cumulative mass losses estimated by SMB – D and GRACE, calculated by taking the difference between the annual mean cumulative losses in 2016 and 2003, are 3263 ± 259 and 3479 ± 280 Gt, respectively, over the 2003–2016 period (Figure 2). This 7 % difference equates to an integrated monthly bias of less than 1.5 Gt, nearly all of which is due to a greater loss estimated by GRACE in the anomalously severe 2011 and 2012 melt seasons. Extended to the beginning of the D time series, we estimate a total cumulative mass loss from 2000 through 2016 of 3730 ± 277 Gt. We also delineate individual glacier D records and SMB totals to align with the six regional basins used in Wouters et al. (2013) and compare these quantities to basin-scale GRACE estimates (Table 1, and Figures S6, S7). We find that while the seasonal variability in mass loss shown in GRACE is well resolved by SMB – D estimates for all basins, the level of agreement in magnitude of cumulative mass loss varies by basin. Estimates agree within their combined uncertainty (< ± 10 Gta⁻¹) for three basins, which together account for ~ 65% of the total mass loss. Annual mass loss rates from SMB – D in Basin 1 and 2 (northern regions) exceed GRACE estimates rates by more than 50 %, and mass loss rates from GRACE are approximately double those from SMB – D in Basin 4 (southeast). These differences largely cancel each other out, leading to the close agreement between estimates for the GrIS as a whole.

Figure 2:

Comparative cumulative GrIS mass change relative to 2003 between GRACE and monthly SMB-D. Cumulative SMB is also plotted, with cumulative differences between estimates plotted in the lower panel, associated with the right y-axis.

Table 1:

GrIS-wide and basin-scale (delineated in Fig. S6) cumulative mass changes in Gigatons over the 2003–2016 period, listed as the RACMO2.3p2 SMB component, SMB–D mass balance, and GRACE mass balance estimates. Cumulative mass changes here represent the difference between mean annual 2016 and mean annual 2003 estimates, with a negative value indicating net mass loss. The GrIS* domain includes SMB fields from tundra and detached ice caps.

	SMB	SMB-D	GRACE
Basin 1	−45 ± 31	−334 ± 32	−202 ± 5
Basin 2	155 ± 42	−266 ± 43	−159 ± 10
Basin 3	744 ± 42	−400 ± 43	−447 ± 38
Basin 4	1645 ± 46	−476 ± 48	−922 ± 34
Basin 5	502 ± 69	−869 ± 71	−841 ± 80
Basin 6	558 ± 27	−823 ± 28	−910 ± 44
GrIS*	3458±258	−3263 ± 259	−3479 ± 280

3.2. Regional Discharge Variability

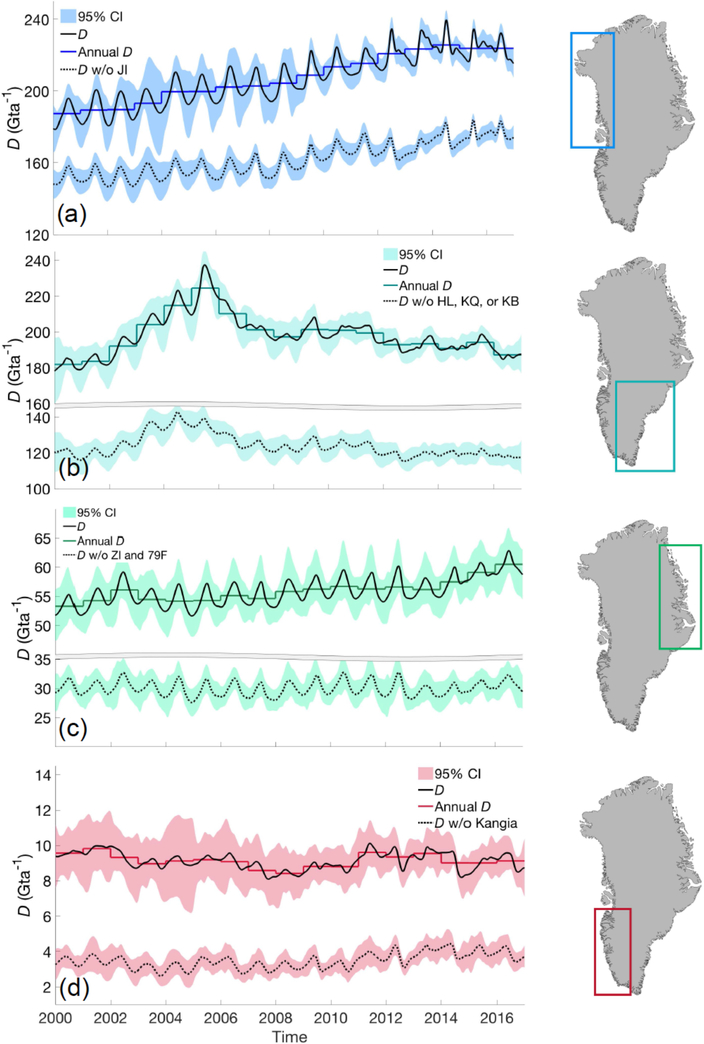
Partitioning D into the four quadrants used by Enderlin et al. (2013), we find significant spatial variability (Figure 3a), with regional D quantities summarized in Table 2. The northwestern (NW) region, which includes Jakobshavn northward to and including Petermann Glacier, has the highest combined discharge, averaging 207 Gta⁻¹, with a cumulative discharge anomaly, defined as the cumulative difference from the year 2000 D, of 343 ± 21 Gt. In the NW, we also find the highest seasonal amplitude in D of 18 ± 3 Gta⁻¹ or 9 %, with Jakobshavn Glacier (Figure S3a) alone contributing 7 ± 3 Gta⁻¹. Removing this glacier from the sample reduces the fractional seasonal amplitude to the GrIS-wide average of 6 % (10 ± 1.7 Gta⁻¹). On average, maximum D occurs on 12 July (day 192) with a uniform, sinusoidal seasonal cycle transitioning to an irregular, saw tooth pattern in 2012. This shift is also visible in the GrIS-wide time series and is primarily due to the emergence of a secondary, mid to late autumn peak in D at Jakobshavn (Figure S3a). We do not further investigate the cause of this secondary peak but note that previous work (Sundal et al. 2013; Bondizo et al. 2017) found that the majority of acceleration events at Jakobshavn are closely linked to changes at the calving front. On average, D at Jakobshavn reaches a seasonal maximum ~ 1 week later than the NW regionally averaged maxima. We find no significant trend in the timing of the seasonal maximum in the NW.

Figure 3:

Net regional D including (solid line) and excluding (dashed line) the dominant glaciers in each region, with shading representing the 95% confidence interval. From top to bottom these regions include: The northwest (a), plotted with and without Jakobshavn (JI), the southeast (b) with and without Helheim (HL), Kangerdlugssuaq (KQ), and the main trunk of Køge Bugt (KB), the northeast (c), with and without Zachariae Isstrøm (ZI) and 79 North (Fjorden) Glacier (79F), and the southwest (d) with and without Kangia Glacier.

Table 2:

Summary of D values for the total GrIS and four distinct regions (see Fig. 3), including the estimated mean annual D in 2000, the maximum D over the 2000–2016 period, and the cumulative D anomaly (ΔD₂₀₀₀) relative to the 2000 estimate. All values are described in units of Gta⁻¹. A negative value indicates a reduction in D relative to the 2000 value.

	2000 D	MAXIMUM D	ΔD2000
southwest	9.5 ± 1	10 ± 1	−7 ± 3
southeast	182 ± 6	238 ± 4	284 ± 17
northeast	53 ± 2	63 ± 2	47 ± 8
northwest	187 ± 5	240 ± 3	343 ± 21
GrIS	440 ± 8	524 ± 9	682 ± 31

The southeastern (SE) region, extending northward to and including Kangerdlugssuaq glacier, had a cumulative D anomaly of 284 ± 17 Gt since 2000 (Figure 3b). Approximately 60 % of the cumulative anomaly occurred at Helheim and Kangerdlugssuaq, due to the rapid 2004–2005 terminus retreat and subsequent acceleration (Howat et al. 2007), resulting in the SE reaching a period maximum rate of D of 238 ± 4 Gta⁻¹ in June 2005. Following this period of acceleration, regional D values steadily declined to an annual average of 187 ± 4 Gta⁻¹ in 2016, within the error of D observed in 2000 (182 ± 6 Gta⁻¹), prior to acceleration. As discovered by Enderlin et al. (2014), an overall decreasing trend in SE D of −1.7 Gta⁻² after 2005 has partially offset the overall increase of 2.7 Gta⁻² in the NW. Despite a large net regional D, there is substantially less seasonal variation in the SE, with an average seasonal amplitude of 9 ± 5 Gta⁻¹ or 5 %. The seasonal amplitude was greater during the 2000–2005 period of acceleration (14 ± 6 Gta⁻¹) than during the 2006–2016 period (7 ± 2 Gta⁻¹). The three largest glaciers in in this region (Køge Bugt, Helheim, and Kangerdlugssuaq) together contribute approximately 40 % of the net regional D. A seasonal signal is more visible after 2005 when excluding these three glaciers, with the remaining glaciers showing a slightly larger seasonal amplitude of approximately 6 %. On average, the summertime seasonal maxima in D occur approximately one week earlier in the SE than in the NW.

The NE and SW regions have fewer marine terminating outlet glaciers and contribute less to the total GrIS D. Discharge from the northeast (NE) region (Figure 3c), contributes approximately 12 % of the total ice sheet D, with the regional ice flux dominated by Zacharis Isstrøm and 79 North Glacier. This region exhibits a relatively consistent seasonal variability of 5 ± 1 Gta⁻¹, or 8 %. The seasonal maximum typically occurs at the end of June. Annual D increased by 4 Gta⁻¹ between 2013 and 2016, largely due to increased D observed at Zacharis Isstrøm (Mouginot et al. 2015; Choi et al. 2017). D in the NE shows a steady increase, accelerating from a rate of ~ 0.2 Gta⁻² during 2000–2012 to over 1 Gta⁻² during the 2013–2016 period, entirely due to acceleration of Zacharis Isstrøm and 79 North glaciers. Lastly, only 7 glaciers constitute the southwest (SW) (Figure 3d), where land-terminating glaciers dominate the margin. Kangia glacier alone accounts for over approximately 60 % of the total SW regional D. A doubling of the seasonal amplitude at Narssap Glacier, coinciding with rapid terminus retreat (Motyka et al. 2017), is responsible for the increase in regional variability after 2011.

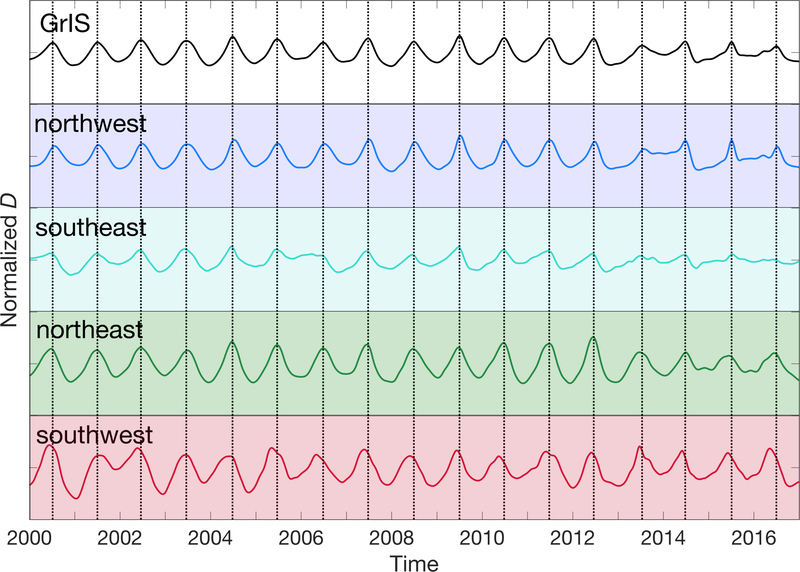
As mentioned above, variations in D may be due primarily to the largest glaciers, which may or may not represent typical glacier behavior. To assess seasonal glacier dynamics, we remove the impact of glacier size by first subtracting the secular trend from the series and then normalizing each glacier’s detrended D series by its maximum seasonal amplitude. This process effectively creates equally-weighted time series of D for individual glaciers, while isolating the seasonal signal. The averages of the normalized seasonal discharge for each region and the total GrIS are shown in Figure 4 and reveal that a distinct seasonal signal is a ubiquitous feature across the ice sheet, independent of glacier size. However, the timing of the seasonal maxima in the normalized data occurs approximately ten days earlier (late June, typically) than without normalization. As noted above, there is also a decrease in seasonal amplitude since 2013 of 20 % relative to earlier years. We observe a similar decrease in amplitude in the normalized series for the SE, NW and NE. This widespread reduction in seasonal amplitude corresponds with a period of relatively stable mean annual D, as shown in Fig. 1. As was noted from the raw regional D, the SE region exhibits the smallest seasonal variability. Unlike the raw time series, which showed the greatest seasonal amplitude in the NW, the NE region shows the largest seasonal amplitude in the normalized time series. This is likely due to the reduced impact of Jakobshavn on NW seasonality through the normalization. Fig. 4 also shows that the seasonal maxima occur coincidentally for the majority of glaciers over the majority of the GrIS, with the few glaciers in the SW reaching a seasonal maximum slightly earlier than the GrIS-wide average.

Figure 4:

Normalized, detrended D time series for the total GrIS (top), NW (blue), SE (cyan), NE (green) and SW (red) regions. The normalized discharge within each panel spans from −1 to 1. Vertical black lines align with the annual maximum D of the GrIS-wide series.

3.3. Variations in Annual Discharge, Front Position and Runoff

We expect that D will vary with both ice front position, due to changes in resistive stress at the terminus (e.g. Thomas et al. 2004; Howat et al. 2008), and with seasonal meltwater runoff, due to variations in basal water pressure (e.g. Joughin et al., 2012). We first test for broad, linear correlations between annual discharge, both over the entire GrIS and regionally, and annual changes in front position and total runoff. We calculate the GrIS-wide and regional annual runoff totals from daily RACMO2.3p2 outputs. Ice sheet-wide and regional front positions are the sum of each glacier’s change between 1 January each year, weighted by the fractional contribution of the glacier’s D to the GrIS or regional total. We then divide these sums by the total number of glaciers across the GrIS or region of interest and express the quantity as the mean weighted position change.

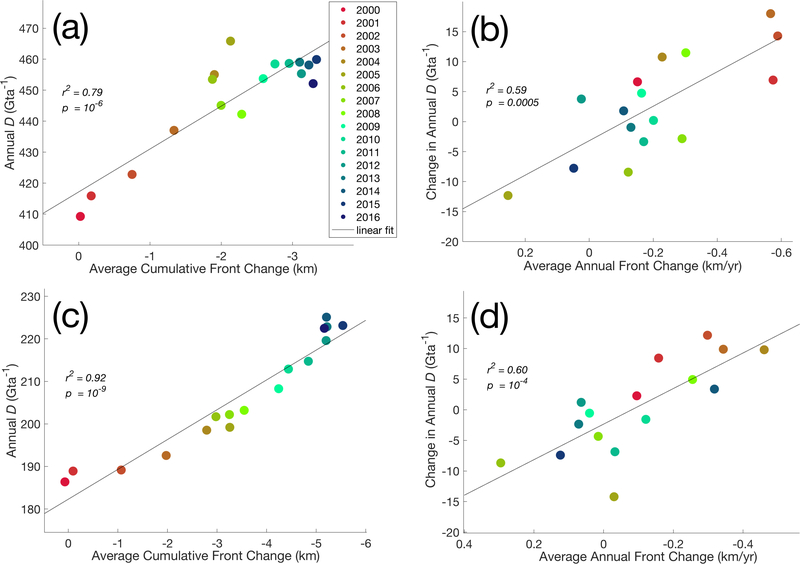
For the entire GrIS, we find the strongest relationship between annual D and the weighted, cumulative change in 1 January front position (r² = 0.79, p = 10⁻⁶) (Figure 5a). Note that the GrIS-wide weighted front position totals do not include 79 North Glacier and Zacharis Isstrøm for reasons described in Section 2, and thus the discharge contributions of those two glaciers are excluded from the annual D term. This correlation is slightly stronger than that obtained between annual D and the cumulative front position change from the previous year (r² = 0.68, p = 10⁻⁴). A weaker, but significant correlation is found between the change in annual D, defined here as the difference between the current and previous year’s annual D, and annual front position change during both the current year (r² = 0.59, p = 0.0005) (Figure 5b) and the previous year (r² = 0.50, p = 0.002). We test for these lagged relationships between retreat and annual D to account for the temporal grouping of the data. For example, front position may continue to retreat into the autumn, after the typical peak in D. If autumn/wintertime discharge rates remain elevated as a result of continued retreat through December of the previous year, we would anticipate the following springtime acceleration to be superimposed on a higher base discharge rate. These correlations are strengthened by excluding Petermann Glacier, where large retreats of its uniquely thin and fractured ice shelf in 2010 and 2012 had no resolvable impact on ice flow speed and, thus, D (Lemos et al. 2018; Münchow et al., 2014). In contrast, no significant correlation is found between annual D and total annual runoff. The addition of annual runoff as an independent variable also does not improve the correlations with front position described above.

Figure 5:

(a) Colored dots are GrIS-wide cumulative average front position change since 1 January 2000, with negative values indicating retreat, versus annual average discharge, D, for each year between 2000 and 2016. The black line is the linear best fit to the data points, with the variance (r²) and probability value (p) of the fit labelled. (b) The average rate of front position change, with negative values indicating retreat, for each year versus the change in average annual discharge between years. (c) Same relationship described in (a), but for glaciers in the NW region only. (d) Relationship between average front position change and the change in Annual D from the current to the following year (D_i+1 − D_i). Date color scale and statistics for (b), (c), and (d) are as described for (a).

Retreat was widespread over the study period in the NW, with glaciers there retreating, on average, 2.8 km from 2000 to 2016. The cumulative, weighted regional front position change shows a near-linear annual retreat with small interannual variation. A similarly strong linear trend is present in annual D, resulting in a nearly perfect correlation with annual cumulative front position change (r² = 0.92, p = 10⁻⁹) (Figure 5c). This relationship is slightly strengthened at a one-year lag, with a correlation of r² = 0.94 (p = 10⁻⁹) between annual D and cumulative front position up through the previous year. Only a weakly significant (r² = 0.25, p = 0.048) relationship exists between the change in NW annual D and the annual, rather than cumulative, front change during the previous year. Retreat also dominated in the SE region over the study period, averaging 1.7 km. Unlike in the NW, however, D in the SE correlated to the annual weighted change in front position, rather than cumulative change. Annual D is significantly correlated to the previous year’s annual front position change (r² = 0.28, p = 0.033). Even stronger is the correlation between the change in annual D and the annual front position change of the previous year, (r² = 0.60, p = 10⁻⁴) (Figure 5d and Figure S8). As with the complete GrIS, no significant correlations are found between D or interannual change in D and annual runoff in either the SE or NW regions.

3.4. Seasonal Variations in Discharge, Front Position and Runoff

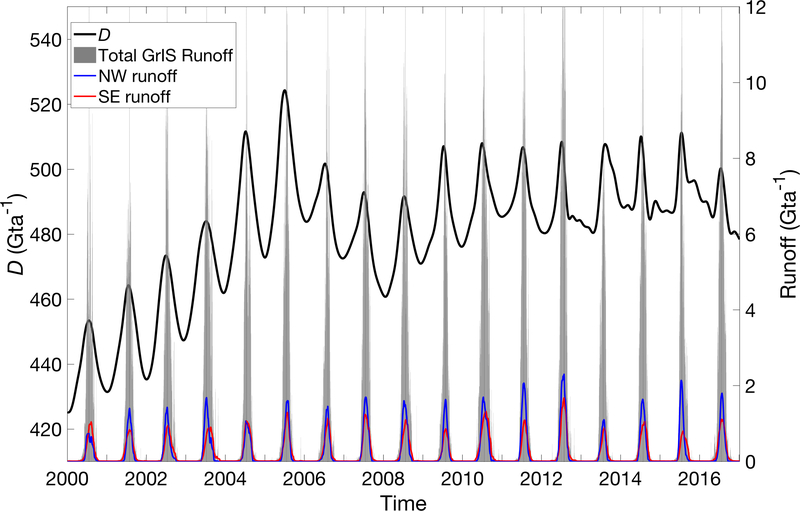
Runoff on the ice sheet typically begins in May and continues through September, reaching a maximum daily rate in July. Smoothing daily runoff values with a monthly (31-day) running mean results in a seasonal distribution with one or several distinct peak(s). Comparing GrIS-wide D to the smoothed runoff series (Figure 6), we find that seasonal acceleration of D is greatest at the onset of runoff, and reaches a seasonal maximum, on average, 13 ± 9 days after the greatest increase in runoff and 12 ± 7 days before the seasonal maximum in runoff. The only exception to this progression was in 2013, when the peak in D occurred after the seasonal maximum in runoff. The maximum D occurs, on average, 40 ± 8 days after the onset of significant runoff. Since the distribution of daily runoff includes a long tail of small values, we define the significant runoff onset as the day when runoff exceeds the 50^th percentile of daily runoff values between April 1 and November 1. We use this threshold to delineate the onset of significant runoff by separating days with negligible runoff contributions from those with non-negligible runoff contributions. We find a significant correlation between the date of runoff onset and the date of maximum D (r² = 0.33, p = 0.015), indicating that a later-occurring peak D may be related to later onset of runoff. However, despite the near synchronous timing between seasonal peaks in runoff and D, we find no other significant relationships between the timing of runoff and discharge, nor between the magnitude of runoff and the magnitude of the seasonal maximum D, or total annual D.

Figure 6:

Cumulative GrIS D (black, left y-axis) plotted with raw daily runoff totals (gray bars, right y-axis). The timing of the seasonal maximum runoff is emphasized by vertical dotted lines. Regional runoff totals, smoothed by a 31-day running mean, are shown for the NW and SE region.

There is regional variability in the timing and amplitude of runoff. The NW region reaches an average maximum of 2.6 ± 0.5 Gt day⁻¹ on day 199 (± 8), totaling 82 ± 21 Gt annually. Significant runoff onset occurs in early June (day 160 ± 7), one week later than runoff in the SE (day 15 ± 8) and preceding the timing of the regional maximum D by approximately one month (32 ± 10 days). There is a significant relationship in the NW region between the timing of runoff onset and the timing of the seasonal maximum in D (r² = 0.46 p = 0.003). In the SE, there is a similar magnitude of total annual runoff (75 ± 16 Gt), but a substantially lower maximum daily rate of 1.7 ± 0.5 Gt day⁻¹ which occurs, on average, on day 208 (± 10). There is also a greater interannual variability in the temporal separation between onset of runoff and maximum D (33 ± 22 days) in the SE region and, as a result, there is no significant correlation in their timing. As with the GrIS as a whole, we find no significant relationships between the magnitudes of runoff and D, or total annual D, in either region.

Front position also varies seasonally. Integrated over the GrIS, net weighted retreat begins in early April (day 92 ± 33) and continues through the end of September (day 265 ± 17). Daily rates of retreat increase most rapidly in early June (day 153 ± 41), reaching, on average, a maximum retreat rate on day 180 (± 35). We test for linear relationships between the timing of initial retreat and greatest increase in retreat, and timing and magnitude of maximum daily rate of retreat with the same seasonal D metrics described above (e.g. magnitude and timing of maximum D and timing of greatest increase in D). We find no significant relationships between the timing or magnitude of seasonal frontal change quantities with seasonal D. The seasonal progression of retreat and advance occurs earlier in the NW relative to the GrIS-wide average. In this region, total weighted front change rates show the greatest increase in retreat in mid-May, on average, (day 135 ± 46), and reach a peak retreat rate in mid-June (day 167 ± 38). In the SE region, by contrast, retreat accelerates the most in mid-June (day 169 ± 46) and reaches a maximum rate on day 200 (± 23). As with the GrIS-wide results, we find no significant correlations between the seasonality of retreat and D at the regional scale.

4. Discussion

Our GrIS-wide estimate of D in 2000 (440 ± 8 Gta⁻¹) is approximately 5 % and 20 % lower than annual estimates derived for 2000 in Enderlin et al. (2014) and Rignot et al. (2011), respectively. Our 2003–2010 mean D of 484 ± 9 Gta⁻¹ agrees within margins of uncertainty to estimates by Kjeldsen et al. (2015) over the same time period (465 ± 65.5 Gta⁻¹) with a bias of less than 20 Gta⁻¹. Annual D estimates for 2007 and 2011 are approximately 5 % and 7 % lower than those estimated in Andersen et al. 2015, but also within margins of uncertainty. Approximately half of the difference from Enderlin et al. (2014) can be explained by the bias resulting from the study’s use of, mostly, summertime median velocities and therefore higher discharge values. Other differences are likely due to a combination of observational error, uncertainties associated with empirical assumptions made in the absence of ice thickness data, methodological differences in the processing and filtering of surface elevation data, and uncertainties associated with ice thickness derivations using hydrostatic equilibrium assumptions (Rignot et al. 2011). The higher temporal resolution of D presented here also avoids nonuniform temporal sampling biases, and, once combined with SMB data from RACMO2.3p2, is in close agreement with independent estimates of ice sheet mass balance from GRACE. Significant discrepancies, however, between the SMB – D and GRACE estimates still exist at the regional scale (Figure S6), with SMB – D predicting nearly twice the loss in north of the ice sheet, but approximately half the loss of GRACE in the southeast. The difference in the SE may be due to an underestimation of either runoff, partly from the high slope of the ablation zone, overestimated accumulation rates, or ice thickness for glaciers lacking radio echo sounding measurements near the terminus. The differences in the north may be due to unrealistically low net SMB predicted there by RACMO2.3p2, with some years showing zero or negative SMB, and cumulative SMB loss in region 1 (Figure S7).

The seasonal variation in D of 6 % is significantly less than the ~ 10 % typically assumed for the GrIS (e.g. Rignot and Kanagaratnam, 2006; Andersen et al. 2015). While individual regions have larger relative seasonal variations, differences in the timing of their peaks cause them to offset each other in total. For instance, the GrIS-wide seasonal amplitude would be 60 Gta⁻¹, or nearly 13 %, if the seasonal signals expressed at individual glaciers were exactly in-phase. This effect of offsetting variability was especially strong in 2013, where early increases in D in the SE region dampened the winter minimum. The seasonal amplitude of GrIS has also declined since 2013 due to the widespread, 20 % reduction in the discharge seasonality of SE glaciers.

Changes in glacier discharge are due to changes in both ice flow speed and thickness, with less known about short-term (seasonal to interannual) variations in the latter. Consistent with numerous studies (e.g. Helm et al. 2014; Csatho et al. 2014; Kjeldsen et al. 2015), 89 % of the glaciers, including the 25 largest, thinned over the study period. Holding ice thickness constant, so that the change in discharge is due entirely to changes in flow speed, results in an increase in D of 110 Gta⁻¹ by 2016, or 60 Gta⁻¹ greater than estimated when including ice thickness change (Figure S9). Thus, ice thinning has offset the increase in D due to ice flow acceleration by over 50 % since 2000, and this fraction is steadily increasing with time since the initial, rapid acceleration in the SE in 2004 and 2005 (Figure S10b). Ice thickness changes on sub-annual timescales also reduce the seasonal amplitude of D. Holding thickness constant, as above, results in a seasonal variation that is, on average, 10% larger than if thickness changes are included. Thus, inclusion of ice thickness change on sub-annual to decadal timescales is essential for accurate estimates of D.

Changes in ice thickness also modulate the relationship between changes in D and ice front position. As described in Sect. 3.3, cumulative annual front change and annual D are uncorrelated in the SE region. However, holding ice thickness constant, as above, results in a strong correlation (r² = 0.79, p = 10⁻⁶), which is similar to that in the NW. Holding ice thickness constant (Figure S10b) also increases the strength of the correlation between annual changes in front position and the change in annual D the following year (r² = 0.75, p = 10⁻⁵). These increased correlations reflect the expected dependence of ice velocity on changes in ice front position (e.g. Howat et al. 2008; Nick et al. 2009; Vieli and Nick, 2011). The SE underwent a sudden, large increase in velocity and retreat in ice front position between 2002 and 2005, with another, smaller acceleration and retreat in 2010, but has since remained largely stable through 2016. Recent work by Bunce et al. (2018) describes increased interannual variability in SE front position, due to asynchronous retreat observed at glaciers in that region. This asynchrony may also contribute to the more recent muted seasonality in the SE region, as previously described. While velocity has remained stable, ice thinning has resulted in a declining D that is uncorrelated with cumulative ice front retreat. In contrast, both retreat and D have been increasing steadily in the NW throughout the record, indicating steadily increasing ice speeds, resulting in a high correlation between annual D and cumulative front position change (i.e. retreat).

Lastly, we expect glaciers to respond to changes in basal water pressure due to the seasonal input of runoff. Previous work focused on land-terminating glaciated regions of the GrIS (Sundal et al 2011; Tedstone et al. 2015) and work using modeled channelization processes (Schoof 2010) demonstrated that meltwater impacts on glacier velocities operate on narrow temporal windows and may even result in a net deceleration on seasonal to annual timescales. While both D and meltwater runoff show a similar pattern of seasonal variability, with a possible relationship between the timing of the onset of runoff and the seasonal peak in D, neither the seasonal maximum in runoff, nor the seasonally-integrated runoff, are significantly correlated to annual D. These indicate a more complex interaction between runoff, ice flow velocity and D, where the rate and distribution of runoff into the subglacial system are more relevant to glacier flow than total runoff (Stearns and van der Veen, 2018). For example, the sensitivity of D to runoff may vary throughout the melt season, with increased sensitivity early in the melt season when drainage channels are inefficient and unable to support the influx of runoff into the system (Chandler et al. 2013), thus increasing water pressure at the bed and enhancing basal flow (Palmer et al. 2011; Bartholomew et al. 2010). This is consistent with 13 ± 9 day average lag in timing between the fastest increase in runoff and the maximum GrIS-wide D, which is close to the 18-day average “residence time” between the production of melt runoff on the ice sheet and its transport to the margin estimated by van Angelen et al. (2014). Thus, taking this residence time into account, the seasonal maximum flow speed, and therefore D, occurs near the time we would expect maximum pressurization of the subglacial drainage system. Future work will build on these concepts by closely examining discharge rates of acceleration and deceleration in response to the distribution of runoff throughout the melt season, giving consideration to runoff residence times.

5. Conclusions

GrIS-wide D has remained near 490 Gta⁻¹ following a period of rapid acceleration before 2006, representing an 11 % increase from 2000. This apparent stabilization, however, is due to steady or declining flow speeds and ice thinning at the four largest glaciers, which dominate the ice sheet-wide total. Excluding these, the combined D of the remaining glaciers increased steadily over the time period, reaching a maximum in 2016, indicating that the largest glaciers are not representative of typical outlet glacier change. Trends in D vary regionally, increasing in the NW and NE and remaining steady in the SE, where sustained higher flow speeds are completely offset by ice thinning and D has returned to its year 2000 values. In total over the GrIS, ice thinning has offset the impact of increased ice flow speeds on D by over 50 % since 2000, substantially modulating the contribution of glacier dynamics on mass loss.

We find that annual changes in GrIS D can be mostly attributed to the cumulative, weighted change in glacier front position. This relationship is the strongest in the NW region, where continuous retreat has accompanied a near-linear increase in annual D and, therefore, changes in D are driven by changes in flow speed. In the SE, however, where speeds have remained relatively stable since 2005 while the glaciers have thinned, it is instead the annual changes in front position that correlate to changes in annual D the following year. In contrast, we find no correlations between annual D, or year-to-year changes in D, and modelled meltwater runoff. These results indicate that multi-year changes in D are dominated by changes in ice front position, through its impact to glacier dynamics, and that the magnitude of meltwater runoff has no consistent, discernible effect on total annual outlet glacier discharge.

We resolve a persistent, ubiquitous seasonal increase in D averaging 6 %. Regionally, this signal varies from 5 % in the SE to 9 % in the NW, with ± 1-month differences in timing resulting in an offsetting effect that decreases the combined total. There was also a marked decline in seasonality after the period of rapid ice flow accelerations in the SE, resulting in a ~ 23 % decrease in seasonality after 2006, and a near complete disappearance of a seasonal signal in the SE after 2013. While not correlated on an annual basis, seasonal variations in D do correspond to those of runoff. We observe that maximum D occurs ~ 2 weeks after maximum increases in runoff, which is similar to the expected time for runoff to reach the margin, and ~ 2 weeks before the seasonal maximum runoff. We also observe significant correlation between the onset of runoff and the timing of peaks in D, with earlier-occurring runoff onset corresponding to earlier peaks in D. This is consistent with the expected impact of increasing meltwater input to an inefficient subglacial drainage system at the start of the melt season, increasing the subglacial water pressure and glacier sliding velocity. This is followed by a decline in D before the peak in runoff is reached, attributed to the transition to efficient subglacial drainage. Such a transition also may explain the lack of correlation between the magnitudes of seasonal runoff and maximum D. Thus, while changes in front position, and their resulting persistent changes to the balance of forces at the glacier terminus, appear to dominant multi-year variability in regional and total GrIS D, seasonal variations are substantially controlled by the timing of meltwater input.

We have assessed the bulk behavior of ice sheet discharge and its broad relationships to possible external forcing, enabled by this first, complete estimate of continuous D over nearly two decades for all of Greenland’s large marine terminating glaciers. It is well established, however, that the behavior of glaciers in close proximity and under similar environmental forcing can vary substantially (e.g. McFadden et al. 2011; Moon et al. 2012; Carr et al. 2017). This is likely due to the sensitivity of outlet glacier dynamics to their particularly geometry (e.g. Enderlin et al. 2013; Porter et al. 2014; Carr et al. 2015; Bartholomaus et al. 2016; Catania et al. 2018) and we do not attempt to account for these differences here. However, detailed analysis of the relationships between particular glacier characteristics and their dynamics at a range of time scales using these data will be the subject of future work.