Optical-resolution photoacoustic microscopy of oxygen saturation with nonlinear compensation

Abstract

Optical-resolution photoacoustic microscopy (OR-PAM) of oxygen saturation (sO₂) offers high-resolution functional information on living tissue. Limited by the availability of high-speed multi-wavelength lasers, most OR-PAM systems use wavelengths around 532nm. Blood has high absorption coefficients in this spectrum, which may cause absorption saturation and induce systematic errors in sO₂ imaging. Here, we present nonlinear OR-PAM that compensates for the absorption saturation in sO₂ imaging. We model the absorption saturation at different absorption coefficients and ultrasonic bandwidths. To compensate for the absorption saturation, we develop an OR-PAM system with three optical wavelengths and implement a nonlinear algorithm to compute sO₂. Phantom experiments on bovine blood validate that the nonlinear OR-PAM can improve the sO₂ accuracy by up to 0.13 for fully oxygenated blood. In vivo sO₂ imaging has been conducted in the mouse ear. The nonlinear sO₂ results agree with the normal physiological values. These results show that the absorption saturation effect can be compensated for in nonlinear OR-PAM, which improves the accuracy of functional photoacoustic imaging.

1. Introduction

Optical-resolution photoacoustic microscopy (OR-PAM) converts absorbed optical energy into ultrasonic wave, offering optical absorption contrast at sub-cellular spatial resolutions [1–5]. Taking advantages of noninvasive and label-free imaging, OR-PAM has been widely applied to map functional parameters, e.g., blood flow, oxygen saturation (sO₂), and metabolic rate of oxygen, in living tissue [6–13]. When a laser impulse illuminates the blood vessel, the dominant absorbing molecules, deoxygenated hemoglobin (HbR) and oxygenated hemoglobin (HbO₂) generate photoacoustic (PA) signal, whose amplitude is a function of the molar extinction coefficients and the molecular concentrations [14–23]. PA measurements at two or more wavelengths allow the computation of the sO₂ [22–28].

Conventional sO₂ imaging assumes that the PA amplitude is a linear function of the absorption coefficient. However, when the absorption coefficient is high, the PA amplitude may become a nonlinear function of the absorption coefficient, referred to as the absorption saturation effect [29]. In such a case, the linear PA assumption will not be accurate and may lead to biased sO₂ measurements. The absorption saturation is related to the absorber’s thickness, the axial resolution, and the optical wavelength [30]. In in vivo imaging, the absorber’s thickness varies among different blood vessels. The axial resolution and the optical wavelengths usually compromise with other parameters, such as imaging depth, sensitivity, laser energy, and laser pulse repetition rate. For instance, to increase the imaging depth and detection sensitivity, OR-PAM usually uses a broadband ultrasound transducer with a central frequency of 50 MHz or lower, which limits the axial resolution to tens of microns. In high-speed OR-PAM, commercial high pulse-repetition-rate lasers with high pulse energy usually have a limited choice of wavelengths around 532nm [31, 32]. The absorption coefficient of 100% oxygenated blood at 532nm is ~237 cm^-1, which may cause absorption saturation in photoacoustic imaging. Therefore, compensation for the absorption saturation may improve the accuracy in OR-PAM sO₂ imaging.

Here, we develop a nonlinear OR-PAM technique to compensate for the absorption saturation in sO₂ imaging. We use a nonlinear model to compute the sO₂ from the PA measurements. We compare the nonlinear method with the linear one in numerical simulation. When absorption saturation exists, the nonlinear model can determine the sO₂ more accurately than the linear model. Solving the nonlinear model requires photoacoustic measurements at three or more optical wavelengths. We develop a three-wavelength pulsed laser to measure the sO₂. The laser has a 1-MHz pulse repetition rate at each wavelength, 150-ns wavelength-switching time, and 60-nJ or higher pulse energy at each wavelength. Phantom experiments on bovine blood and in vivo experiments in the mouse ear demonstrate the improved accuracy of nonlinear sO₂ imaging.

2. Methods

2.1 Absorption saturation

Under thermal and stress confinement, the PA amplitude from a voxel can be written as

$$PA=k\Gamma \eta F[1-\exp (-{\mu }_a\Delta z)],$$ (1)

where $k$ is a constant factor related to the PA detection sensitivity, $\Gamma$ is the local Grueneisen parameter, $\eta$ is the percentage of absorbed energy that converts into heat, $F$ is the fluence at the top surface of the voxel, ${\mu }_a$ is the absorption coefficient and is assumed as uniform in the voxel, and Δz is the voxel size in the axial direction.

If the absorption coefficient is low, and the axial resolution is high, i.e. ${\mu }_a\Delta z$ is close to zero, the PA amplitude can be approximated as

$$PA=k\Gamma \eta F{\mu }_a\Delta z,$$ (2)

In this case, the PA amplitude is a linear function of the absorption coefficient ${\mu }_a$. In the blood, ${\mu }_a$ is a linear function of the concentrations of HbO₂ and HbR. Thus, we can measure PA signals at two or more optical wavelengths and compute the sO₂ based on the approximated linear model in Eq. (2).

However, if the absorption is strong, or the axial resolution is low, i.e. ${\mu }_a\Delta z$ is not close to zero, the PA amplitude remains a nonlinear function of the absorption coefficient, which is referred to as absorption saturation. Most fast OR-PAM systems use wavelengths around 532nm, leading to strong absorption in the blood. In addition, the axial resolution is limited to tens of microns. In such a case, the use of linear PA model will cause a systematic error in the sO₂ calculation. In contrast, the nonlinear Eq. (1) shows an accurate relationship between the PA signal and the absorption coefficient even when the absorption saturation exists.

2.2 Nonlinear method for sO₂ measurement

To compensate for the saturation effect, the nonlinear model in Eq. (1) is used to measure the sO₂. The absorption coefficient of blood at one wavelength can be written as ${\mu }_a=r{C}_{HbT}[s{O}_2{\epsilon }^{oxy}+(1-s{O}_2){\epsilon }^{de}]$, where $r$ is a known constant coefficient [33,34], and $C_{HbT}$ is the total hemoglobin concentration, and ${\epsilon }^{oxy}$ and ${\epsilon }^{de}$ are the molar extinction coefficients of HbO₂ and HbR at the excitation wavelength. Substituting ${\mu }_a$ into Eq. (1), we can write the PA amplitude as a nonlinear function of sO₂ as

$$PA=k\Gamma \eta F[1-\exp (-r(s{O}_2{\epsilon }^{oxy}+(1-s{O}_2){\epsilon }^{de})C_{HbT}\Delta z)].$$ (3)

In superficial tissue, we assume that the local fluence F can be estimated from the fluence on the tissue surface. In the following text, the fluence is set to the unit and is not explicitly expressed in the equations. Equation (3) has three unknowns, sO₂, $r{C}_{HbT}\Delta z$, and $k\Gamma \eta$. To solve them, we measure the PA signals at three wavelengths, λ₁, λ₂, and λ₃, obtaining PA₁, PA₂, and PA₃.

An iterative algorithm is developed to solve the sO₂. Each iteration takes two steps. In the first step of the i^th iteration, we compute the ratio of PA_{1_i} to PA_{2_i} as

$$\frac{P{A}_{1-i}}{P{A}_{2-i}}=\frac{1-\exp [-u_i(s{O}_{2\_i}{\epsilon }_1^{oxy}+(1-s{O}_{2\_i}){\epsilon }_1^{de})]}{1-\exp [-u_i(s{O}_{2\_i}{\epsilon }_2^{oxy}+(1-s{O}_{2\_i}){\epsilon }_2^{de})]},$$ (4)

where $u_i=r{C}_{Hb{T}_i}\Delta z_i$. Substituting the sO₂ value from the previous iteration, i.e., $s{O}_{2\_i-1}$, into Eq. (4), we can solve the unknown $u_i$. In the second step, we compute the ratio of PA_{3_i} to PA_{2_i} as

$$\frac{P{A}_{3-i}}{P{A}_{2-i}}=\frac{1-\exp [-u_i(s{O}_{2\_i}{\epsilon }_3^{oxy}+(1-s{O}_{2\_i}){\epsilon }_3^{de})]}{1-\exp [-u_i(s{O}_{2\_i}{\epsilon }_2^{oxy}+(1-s{O}_{2\_i}){\epsilon }_2^{de})]},$$ (5)

Substituting $u_i$ into Eq. (5), we can solve an updated $s{O}_{2\_i}$.

The initial sO_{2_0} is estimated from the linear model in Eq. (2). After several iterations, the sO₂ value converges to a stable value. When the |sO_{2_i} - sO_{2_i-1}| is smaller than a threshold value (0.001 in this work), we terminate the iteration.

2.3 OR-PAM system

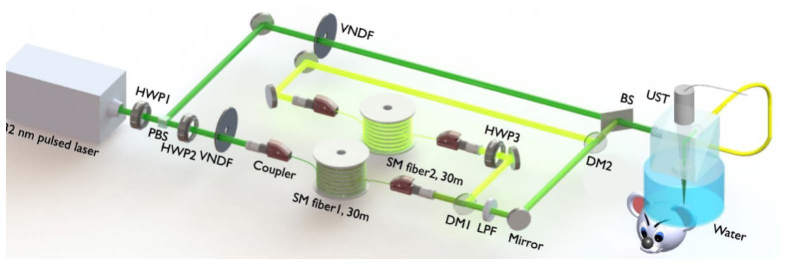
The nonlinear method requires PA measurements at three or more wavelengths. Here we develop an OR-PAM system with a 1-MHz three-wavelength pulsed laser. A schematic diagram of the OR-PAM system is illustrated in Fig. 1. A nanosecond pulsed laser (wavelength 532 nm, VPFL-G-20, Spectra-Physics) is used as a pump laser to generate another two wavelengths via stimulated Raman scattering (SRS). The highest pulse repetition rate of the pump laser is 1 MHz. The pulse width is set at 7 ns. The maximum pulse energy is 100 μJ, which is sufficient for inducing SRS in a single-mode fiber. The 532-nm pump beam is split into a direct path and a Raman path using a halfwave plate (HWP1) and a polarizing beamsplitter. The direct path is coupled into an OR-PAM probe without significant time delay. In the Raman path, the pump beam is coupled into a 30-meter polarization-maintaining single-mode fiber (SM fiber1, 30m, PM-S405-XP, NUFERN) through a fiber coupler (MBT621D, Thorlabs Inc). The coupling efficiency is ~55%. The 30-meter fiber will delay this path by 150 ns. A halfwave plate (HWP2) is placed before the fiber coupler to adjust the incident polarization state so that the SRS efficiency in the fiber is maximized. Via adjusting the incident power, the 30-meter fiber can generate 545 nm and 558 nm wavelengths via SRS effect. A dichroic mirror (DM1, 69-203, Edmund Optics Inc) is placed after the SRS fiber output to reflect the 558-nm light but transmit the 532-nm and 545-nm light. The 558-nm pulse further passes a halfwave plate (HWP3) and is coupled into another 30-meter polarization-maintaining single-mode fiber (SM fiber2, 30m, HB450-SC, FIBERCORE) for time delay. The halfwave plate adjusts the polarization state to suppress the SRS effect in the delay fiber. After the 30-meter delay, the 558-nm beam is combined with the 545-nm beam using another dichroic mirror (DM2, 69-203, Edmund Optics Inc). A long-pass filter (LPF, T540lpxr, CHROMA) is placed before dichroic mirror 2 to reject the remaining 532-nm light in the delay path. At the last stage, a 90/10 beam splitter combines the direct 532-nm beam with the delayed 545/558-nm beam. The three beams are coupled into the OR-PAM probe via a 2-meter single-mode fiber.

Fig. 1.

Schematic diagram of OR-PAM system with a three-wavelength pulsed laser. BS: beam splitter R/T: 90/10, DM1&DM2: dichroic mirror 550 nm short-pass, HWP1-3: half-wave plate, LPF: 540 nm long-pass filter, PBS: polarization beam splitter, SM fiber 1-2: single-mode fiber, UST: ultrasonic transducer, VNDF: variable neutral density filter.

In the OR-PAM probe, the pulsed laser beam is focused into the sample to induce photoacoustic waves. A 50-MHz ultrasound transducer (V214-BC-RM, Olympus-NDT) focuses on the sample and is confocally aligned with the optical focus to optimize the detection sensitivity. A low pass filter (SLP-50 + , Mini Circuits) is used to filter PA signal. The bandwidth of the filtered PA signal determines the axial resolution as 50 μm. Raster scanning the photoacoustic probe generates volumetric images. Detailed information of the OR-PAM probe can be referred to in the previous papers [16,27,35].

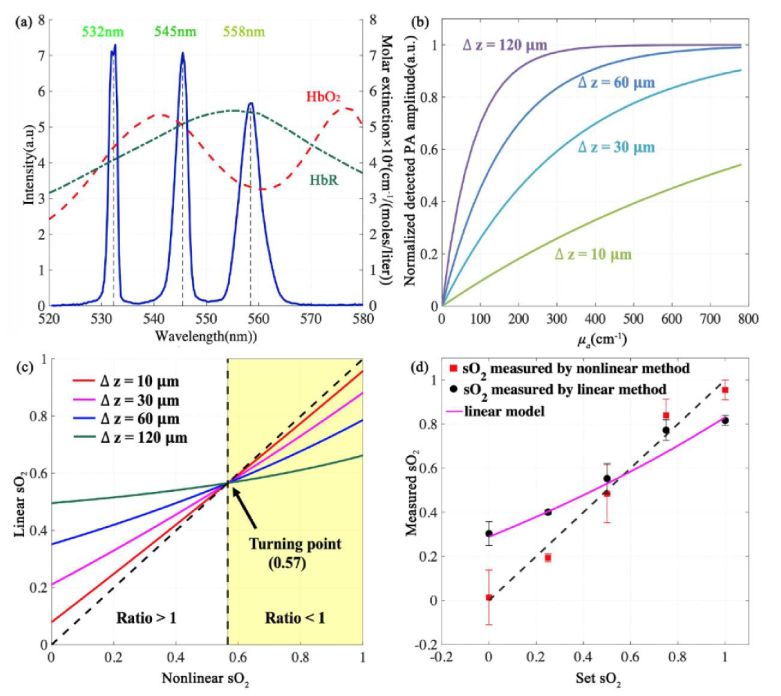
The pulse energy of each wavelength is about 60 $\mathrm{nJ}$ at the sample surface, which is comparable to the pulse energies used in other reported OR-PAM systems [16,27,35]. The time delays of the 532nm, 545nm, and 558nm pulses are 0, 150ns, and 300ns respectively, enabling temporal separation of the three PA signals. Figure 2 (a) shows laser spectrum measured with an optical spectrometer (USB 2000 + , Ocean Optics). The linewidths of the 532, 545, and 558 nm wavelengths are 1.6, 2.4, and 4.4nm, respectively. Normalized molar extinction coefficients of ${\mathrm{HbO}}_2$ and $\mathrm{HbR}$ are plotted in Fig. 2(a). The 532-nm wavelength is close to an isosbestic point, the 545-nm wavelength is an isosbestic point, and the 558-nm wavelength is more absorptive for HbR than HbO₂. The different absorption coefficients at the three wavelengths make it possible to implement the nonlinear sO₂ model.

Fig. 2.

(a) Spectrum of the three-wavelength stimulated-Raman-scattering laser. (b) Absorption saturation effect with different axial resolutions and absorption coefficients. (c) Impact of absorption saturation effect on sO₂ accuracy using linear method. The nonlinear sO₂ results is the same as the set values. The tilted dashed line represents an ideal case that the linear sO₂ results are unbiased. (d) In vitro sO₂ measurement of bovine blood samples using both linear and nonlinear models. Sample size = 5.

3. Results and discussion

3.1 Numerical simulation

We numerically evaluate the impact of absorption saturation on the accuracy of sO₂ measurement under different sO₂ values and different axial resolutions shown. The axial resolutions are set at 10 μm, 30 μm, 60 μm, and 120μm. Figure 2(b) shows that a lower axial resolution or a larger absorption coefficient may lead to stronger absorption saturation and nonlinearity. The total hemoglobin concentration is set at 160 g/liter. Using these parameters, we generate PA amplitudes at 3 wavelengths, 532 nm, 545 nm, and 558 nm by Eq. (1). The generated PA amplitudes at the three wavelengths are used to compute the sO₂ with the nonlinear method. The 532-nm and 558-nm PA amplitudes are used in the linear sO₂ computation. The nonlinear iterations converge after the second iteration. Because we use the same nonlinear model to generate simulation data and compute sO₂, in this simulation, all sO₂ results computed with the nonlinear method are the same as the set sO₂ values.

The linear sO₂ values are compared with the set sO₂, as shown in Fig. 2(c). When the set sO₂ value is greater than 0.57, the linear method underestimates the sO₂ value. When the sO₂ is smaller than 0.57, the linear method overestimates the sO₂ value. At sO₂ = 0.57, because the absorption coefficients at 532nm and 558nm are the same, the calculated sO₂ by linear method equals to the set value. In such a case, the saturation effect causes the same fractional PA changes at the two wavelengths and induces no errors to the linear sO₂ results. In other sO₂ values, the linear method leads to biased results due to absorption saturation. In contrast, the nonlinear method can compensate for absorption saturation.

3.2 In vitro validation of nonlinear method

We validate the nonlinear method on blood phantoms. Sealed anticoagulant bovine blood fills 5 transparent plastic bags. Each bag contains 10-ml blood. The sO₂ values of the blood samples are set via adding different dosages of sodium dithionite [36,37]. The minimum concentration of sodium dithionite to change sO₂ from 1 to 0 is 2.5 mg/ml. Via changing the chemical concentration, sO₂ of the samples are set to 0, 0.25, 0.5, 0.75, and 1. Nitrogen gas is used to remove air in the bag.

Figure 2(d) shows the sO₂ results of the in vitro experiments. Both linear and nonlinear methods are used to compute sO₂. Each sO₂ result was first averaged 100 times in one bag and then was averaged over 5 samples. For fully oxygenated blood samples, the linear method gives an averaged sO₂ value of 0.82 ± 0.02 (SD), and the nonlinear result is 0.95 ± 0.04(SD), showing an accuracy improvement of 0.13. For the set sO₂ of 0.75, 0.5, 0.25, 0, the nonlinear method can improve the linear results by 0.07, 0.08, 0.21, 0.28, respectively. The phantom results validate that the nonlinear method can compensate for the absorption saturation effect in the sO₂ measurement.

3.3 In vivo sO₂ imaging

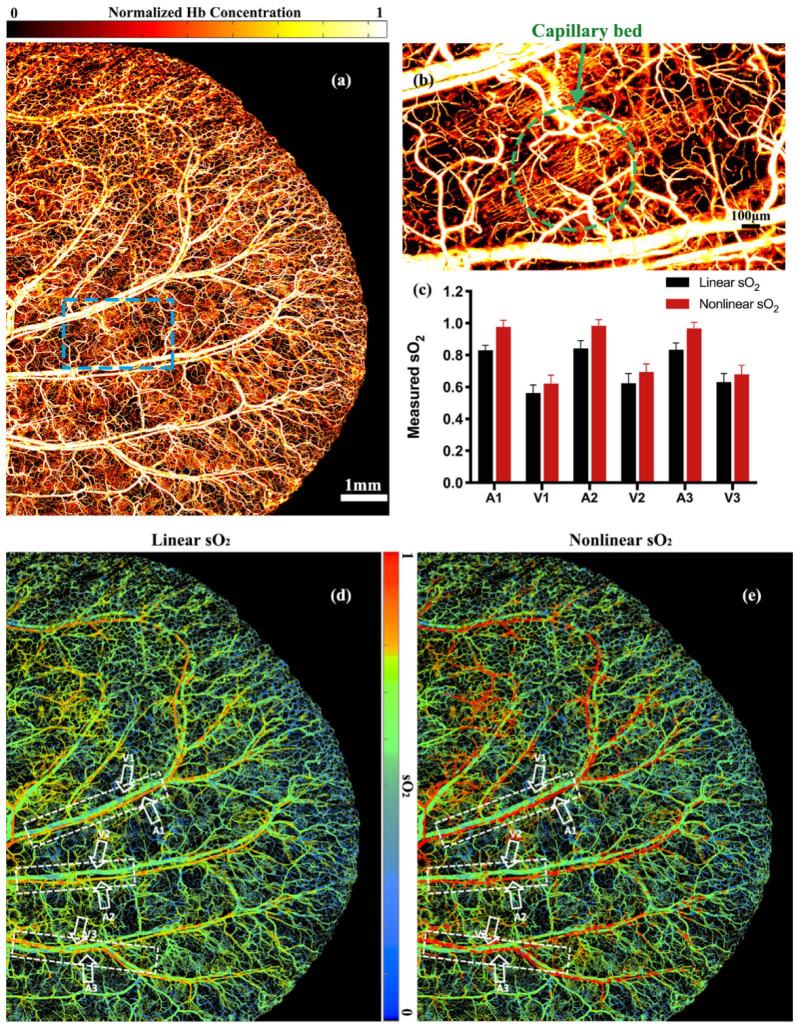
We compare the linear and nonlinear sO₂ imaging in the mouse ear. The protocol of animal experiments has been approved by the animal ethical committee of the City University of Hong Kong. PA images are acquired at three wavelengths, 532nm, 545nm, and 558nm. For each wavelength, the pulse energy is 60 nJ, the laser repetition rate is 4 kHz, and 4000 × 3500 A-lines are acquired for a 3D in vivo image. The step size in the lateral direction is 2.5 μm. The field of view of the acquired image is 10 × 8.75 mm² in the lateral plane. The time to acquire a 3D image is 3500 seconds. Figure 3(a) and (b) show a maximum-amplitude-projected image and a close-up image of the microvasculature acquired at 532nm. The capillaries can be resolved with a signal-to-noise ratio of 10.6 dB. The sO₂ values are calculated with the linear and nonlinear methods, as shown in Fig. 3(d) and (e). A 5 × 5-pixel moving-average filter is used to smooth the sO₂ images. In both the linear and nonlinear sO₂ images, the arteries and veins can be differentiated. In the arteries, the linear method gives results obvious lower than the nonlinear ones. To compare the linear and nonlinear results, we select the sO₂ values in three artery-vein pairs as labeled in the dashed boxes in Fig. 3(d) and (e). Figure 3(c) shows the averaged sO₂ values of each artery and vein. The sO₂ values by linear method are consistently smaller than the ones by nonlinear method. In Fig. 3(c), we only quantify trunk vessels. sO₂ values in those vessels are greater than 0.57. According to numerical simulation, when sO₂ is greater than 0.57, linear method underestimates sO₂. Thus, both the trunk arteries and veins show higher sO₂ in the nonlinear result than those in the linear one. We do find some small vessels have lower sO₂ (<0.57). However, if the vessel diameter is smaller than the axial resolution, the absorption saturation effect becomes not obvious. In those vessels, we do not observe significant difference between the nonlinear and the linear results.

Fig. 3.

(a) In vivo imaging of the total hemoglobin concentration in the mouse ear. (b) Close-up of the blue dashed box in (a). (c) Comparison of the linear and nonlinear sO₂ values in three artery-vein pairs as labeled in the white dashed boxes in (d) and (e). Error bars are standard derivations. (d) Linear sO₂ image of the mouse ear. (e) Nonlinear sO₂ image of the mouse ear.

The OR-PAM system has an axial resolution of 50 $\mathrm{\mu m}$. In the simulation results in Fig. 2(c), at an axial resolution of 50 $\mathrm{\mu m}$, the set sO₂ value is about 1.19 times of the one by linear method when the sO₂ is 1, and is 1.07 times of the one by linear method when the sO₂ value is 0.66. The in vivo results in Fig. 3(c) show a similar trend with the simulation results. The in vivo experiments demonstrate that the nonlinear method can compensate for the absorption saturation.

4. Conclusion

We develop a nonlinear method to compensate for the absorption saturation in OR-PAM sO₂ imaging. The absorption saturation effect is modeled and simulated with different sO₂ values and axial resolutions. Simulation results show that the linear sO₂ method may lead to systemic errors when the absorption saturation exists. In comparison, the nonlinear method can compensate for this error. Absorption saturation has been used to measure sO₂ based on saturation intensity or acoustic spectral analysis [38,39]. However, they may either require a high optical pulse energy or are not applicable to small blood vessels due to complicated acoustic spectrum. Our method is not limited by either the pulse energy or the vessel size. Conclusively, we develop an OR-PAM system with a three-wavelength pulsed laser to implement the nonlinear sO₂ imaging. Phantom experiments on bovine blood samples validate that the nonlinear method can improve sO₂ accuracy. We demonstrate nonlinear sO₂ imaging in the mouse ear. In normal physiological conditions, a literature reports the sO₂ values in the arteries are about 0.95~0.99 and the sO₂ values in the peripheral vein are about 0.70~0.80 [40]. The nonlinear sO₂ results are closer to these values than the linear results. The nonlinear sO₂ imaging method can reduce the systemic error caused by absorption saturation. We expect this technical advance in functional imaging may further expand the biomedical application of OR-PAM.

Funding

National Natural Science Foundation of China (NSFC) (81627805, 61805102); Research Grants Council of the Hong Kong Special Administrative Region (21205016, 11215817, 11101618); Science Technology and Innovation Commission of Shenzhen Municipality, China (JCYJ20160329150236426, JCYJ20170413140519030).

Disclosures

The authors declare that there are no conflicts of interest related to this article.