Improving visible light OCT of the human retina with rapid spectral shaping and axial tracking

Abstract

Visible light optical coherence tomography (OCT) theoretically provides finer axial resolution than near-infrared OCT for a given wavelength bandwidth. To realize this potential in the human retina in vivo, the unique technical challenges of visible light OCT must be addressed. We introduce three advances to further the performance of visible light OCT in the human retina. First, we incorporate a grating light valve spatial light modulator (GLV-SLM) spectral shaping stage to modify the source spectrum. This enables comfortable subject alignment with a red light spectrum, and image acquisition with a broad “white light” spectrum, shaped to minimize sidelobes. Second, we develop a novel, Fourier transform-free, software axial motion tracking algorithm with fast, magnetically actuated stage to maintain near-optimal axial resolution and sensitivity in the presence of eye motion. Third, we implement spatially dependent numerical dispersion compensation for the first time in the human eye in vivo. In vivo human retinal OCT images clearly show that the inner plexiform layer consists of 3 hyper-reflective bands and 2 hypo-reflective bands, corresponding with the standard anatomical division of the IPL. Wavelength-dependent images of the outer retina suggest that, beyond merely improving the axial resolution, shorter wavelength visible light may also provide unique advantages for visualizing Bruch’s membrane.

1. Introduction

While optical coherence tomography (OCT) is the clinical standard for high axial resolution imaging of retinal layers, important architectural features of the retina, which may play a role in early eye disease, cannot yet be assessed by current OCT instruments.

First, in glaucoma [1], loss of retinal ganglion cells (RGCs) [2,3] occurs along with thinning of retinal nerve fiber layer (RNFL), ganglion cell layer (GCL), and inner plexiform layer (IPL), reflecting axonal, somatic, and dendritic losses, respectively. While somatic (GCL) and axonal (RNFL) changes in glaucoma have been extensively studied with OCT, there are comparatively few studies on dendritic changes in human glaucoma [4]. The IPL is a layer of connections, where the dendrites of ganglion cells, axons of bipolar cells, and processes of amacrine cells converge to form 5 nominal bands or strata [5]. The IPL is also divided into on and off sublaminae [6–8], comprising the inner 3 and outer 2 bands, respectively. Recent fundamental research [9–12] in various animal models of optic nerve injury and hypertension [13] suggest that ganglion cell dendritic morphology changes early in glaucoma, and these changes may be most predictive in the off sublamina. However, aside from a few anecdotal reports [14,15], the in vivo visualization and quantification of IPL sublaminae remains challenging due to insufficient axial resolution.

Second, in age-related macular degeneration (AMD) [16], the earliest signs of AMD are assumed to be similar to changes observed histopathologically in older eyes [17]; namely, diffuse thickening of Bruch’s membrane (BM) [17–19] and deposits in the retinal pigment epithelium (RPE) basal lamina [20], the latter of which is considered one of the five layers of BM [21]. Discerning these two loci for deposits, in addition to a third subretinal locus for drusenoid deposits in the RPE [22], requires exquisite micron-level depth resolution. The ability to follow micron-scale disease processes in aging and early AMD in the human eye could lead to a better understanding of pathophysiology [23], and reveal new biomarkers for AMD progression [24]. However, even for high-end near infrared (NIR) OCT, direct observations of BM as distinct from the RPE in a morphologically normal retina are anecdotal [25–27].

Visible light OCT is an emerging technique that can perform structural and functional retinal imaging [28–37]. For a given wavelength bandwidth, visible light OCT improves axial image resolution compared to NIR OCT [38]. Recently ultrahigh axial resolution imaging was demonstrated with a fiber-based spectral / Fourier domain visible light OCT system with longitudinal chromatic aberration (LCA) correction [33], providing human retinal image quality that exceeded NIR OCT in some respects. Here, to further improve image quality, we incorporate a spectral shaping method to reduce sidelobes in the point spread function, to better assess subtle reflectance differences. In addition, we propose and implement a novel axial motion tracking algorithm to maintain optimal image sensitivity and resolution in the presence of eye motion. In contrast to previous algorithms [39–41], our method does not require a Fourier transform. We also implement spatially dependent dispersion compensation [42] in the in vivo human retina to for the first time. With these improvements, our human retinal images support the ability to clearly visualize the internal five-layered structure of the IPL and the hypo-reflective space between Bruch’s membrane and the Retinal Pigment Epithelium. Careful investigation of wavelength-dependent contrast in subband images suggests that beyond just improving the resolution, shorter visible OCT wavelengths provide key advantages for visualizing Bruch’s membrane.

2. Method

2.1 Visible light OCT system design for human imaging

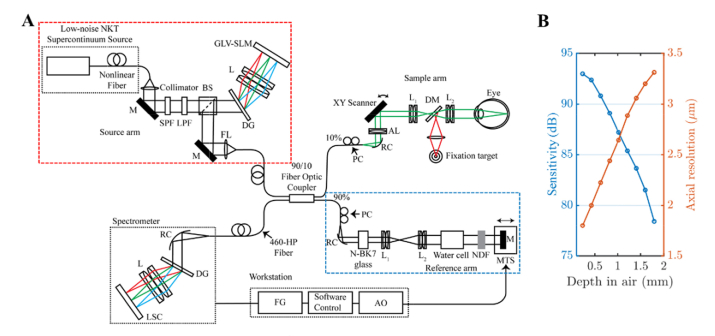
A fiber-based, LCA-corrected spectral / Fourier domain visible light OCT for human retinal imaging was built with a 156 MHz repetition rate, low noise, supercontinuum light source (NKT Photonics EXU3) as shown in the Fig. 1(A). To reduce axial point spread function (PSF) sidelobes and improve light safety margins, we developed a diffractive optical setup to rapidly shape the spectrum (red box). In addition, we developed a novel axial motion tracking algorithm, implemented in software, and incorporated a fast, magnetically actuated linear translation stage in the reference arm to compensate axial eye motion (blue box). The rest of the setup has been described previously [33,43]. Images from a single 38-year-old male subject are shown, though similar results were confirmed in three additional subjects. All procedures and protocols were approved by the UC Davis Institutional Review Board.

Fig. 1.

(A) Fiber-based visible light spectral / Fourier domain OCT system with spectral shaping (red box) and axial tracking (blue box) for imaging the human retina. SPF: short pass filter, LPF: long pass filter, BS: beam splitter, DG: diffraction grating, L: lens, GLV-SLM: grating light valve spatial light modulator, M: mirror, FL: focusing lens, PC: polarization controller, RC: reflective collimator, LSC: line-scan camera, AL: achromatizing lens, DM: dichroic mirror, NDF: neutral density filter, MTS: motorized translational stage, FG: frame grabber, AO: analog output. (B) The sensitivity roll-off (left) and the measured axial resolution (right) of the system versus depth. The sensitivity roll-off was ~5 dB and the measured axial resolution was < 2.8 µm in air over the first half of the axial imaging range.

2.2 Rapid spectral shaping

In spectral / Fourier domain OCT, the system axial resolution is determined by the coherence length of the light source, proportional to the ratio of center wavelength squared to the wavelength bandwidth. For a modulated or truncated source spectrum, sidelobes in the axial PSF degrade the image contrast. Here, we propose a new method that utilizes a grating light valve spatial light modulator (GLV-SLM) to rapidly and precisely shape the supercontinuum source spectrum.

The GLV-SLM (F1088, Silicon Light Machines, LLC) is a Micro-Electro-Mechanical Systems (MEMS) device with free-standing silicon nitride micro-ribbons attached to the surface of a silicon chip. The GLV-SLM has 1088 individual GLV pixels, with each pixel consisting of 3 ‘active’ ribbons and 3 ‘bias’ ribbons. The ‘active’ ribbons in a pixel are displaced, depending on the voltage applied to the pixel, to generate a square-well diffraction grating. The amplitude of reflected incident light is thus attenuated in that pixel. The update rate of our device is 108 kHz. We designed a diffractive optical setup (Fig. 1(A)), with a beam-splitter relaying light to the spectral filtering stage. Broadband light passes through the diffraction grating (DG) and the lens (L), which spectrally disperses and focuses on the GLV, respectively. The reflected and shaped spectrum retraces its path from the GLV-SLM, being reflected by the beam-splitter to the source arm of the OCT system. With this setup, the source spectrum can be rapidly shaped or neutrally attenuated within a single axial scan. The large number of degrees of freedom of the GLV enables compensating modulations in the supercontinuum spectrum.

2.3 Fourier transform-free axial motion tracking

Due to the curved focal plane in the spectrometer, the interference roll-off at the edge of the source spectrum is typically worse than the roll-off at the central portion. Therefore, in addition to the sensitivity roll-off with depth [44], the interference spectrum envelope narrows at higher path length mismatches, causing the axial resolution to also degrade with depth [45]. While our system has a nominal axial imaging range of ~2.24 mm; resolution and sensitivity are considered “near-optimal” over only about half this range [33,43]. Thus, we implemented axial tracking to maintain optimal resolution and sensitivity by maintaining an acceptable optical path length difference in the presence of eye motion.

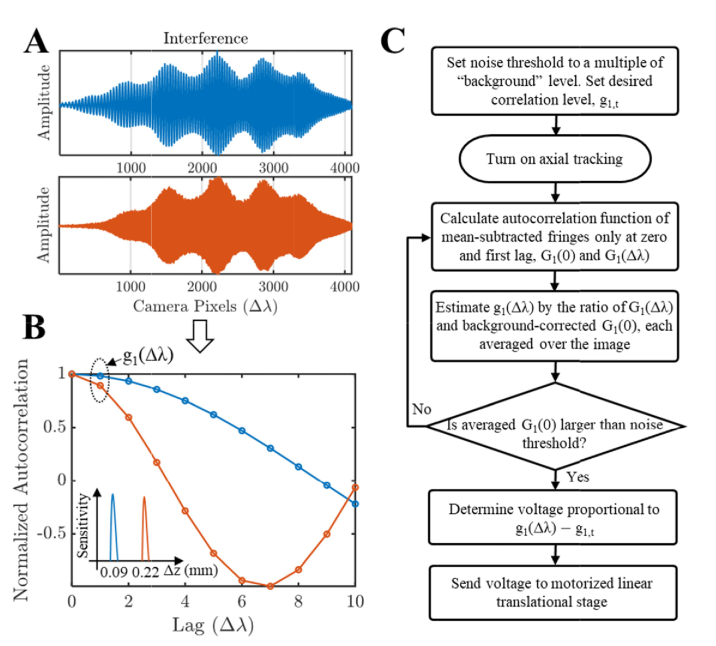
We developed a Fourier transform-free approach, based on the insight that larger path delays cause faster oscillations in the spectral interferogram (Fig. 2(A)). Thus, the path delay can be estimated from interferogram decorrelation, without needing a computationally expensive Fourier transform. Instead of tracking the axial position as in conventional algorithms, we track the normalized autocorrelation of the spectral interference, defined as:

Fig. 2.

Computationally simple axial tracking algorithm based on analysis of the interference spectrum. (A) Interference spectrum captured by the spectrometer at different path length mismatches. (B) The normalized autocorrelation, g₁, of the interference spectrum as a function of lag, in units of Δλ, representing the wavelength shift corresponding to one spectrometer pixel. Note that the smaller path difference has a slower decay rate, and the decay rate can be determined from the normalized autocorrelation at a single lag. (C) The workflow of axial motion tracking, based on the background noise-corrected, normalized autocorrelation. Note that this algorithm does not require a Fourier transform.

$$g_1(\Delta \lambda )=\frac{{\widehat{G}}_1\left(\Delta \lambda \right)}{{\widehat{G}}_1\left(0\right)-{\widehat{G}}_{1,noise}(0)}.$$ (1)

Here, Ĝ₁ represents the estimated spectral interference autocorrelation as a function of wavelength lag, which is estimated by averaging across interference spectra in an image frame. For simplicity, we assume that the spectral samples have a uniform spacing of Δλ. Conventional axial tracking requires resampling (~2N multiplies for linear interpolation), Fourier transformation (N/2 log N multiplies), and centroid calculation (N/2 multiplies), where N is the number of pixels on the camera. Our algorithm, as shown in Fig. 2(B), requires N multiplies for G₁(0) estimation and N-1 multiplies for G₁(Δλ) estimation (G_1,noise(0) is estimated once at the beginning of the session and does not affect the tracking algorithm complexity). The shorter computation time results in reduced latency, which is essential for tracking.

Qualitatively, we expect that larger path delays will cause faster oscillations in the spectral interferogram, S_int(λ), which leads to more decorrelation for a given Δλ. In the case uniform k (wavenumber) sampling (i.e., neglecting nonlinear sampling in k), we can derive a direct analytic expression for the spectral interference autocorrelation G₁(k) in terms of the complex OCT signal s(z). First, G₁(0) = _∫S_int(k)S^*_int(k)dk/2π = _∫s(z)s^*(z)dz = _∫|s(z)|²dz is the integral of the power spectrum. Note that G₁(0) is the energy in the interference spectrum, which is identical to the energy in the Fourier transform, by Parseval’s theorem [46]. Also, G₁(Δk) = ∫S_int(k + Δk)S*_int(k)dk/2π = _∫s(z)s*(z)e^-i2Δkzdz = 2_∫0^∞|s(z)|²cos(2Δkz)dz, since s(z) = s*(-z) by conjugate symmetry. Thus, for a single reflector located at z = z₀, g₁(Δk) = G₁(Δk)/G₁(0) = cos(2Δkz₀). Note that in this simple example, if Δk is the sampling interval, g₁(Δk) = 1 for z₀ = 0, g₁(Δk) = 0 for z₀ = π/4Δk (½ of the axial imaging range), and g₁(Δk) = −1 for z₀ = π/2Δk (the end of the axial imaging range). For uniform λ sampling (nonlinear sampling in k), g₁(Δλ) is similarly expected to decrease monotonically with increasing path delay, as shown experimentally in Fig. 2(B).

Our axial tracking algorithm is shown in Fig. 2(C). The computational simplicity results in reduced software latency, which is critical for good tracking performance. We incorporated a magnetically actuated stage (V-522, Physik Instrumente) with a maximum speed of 250 mm/s and 0.32 ms mechanical latency in the reference arm to track axial eye motion. The noise threshold was determined as the estimated “background” level, Ĝ_1,noise(0), multiplied by a constant, chosen empirically to avoid tracking during blinks while still tracking under low signal conditions. The input voltage was incremented proportional to g₁(Δλ) - g_1,t, where the constant of proportionality was empirically determined and g_1,t ≈ 0.8. The axial motion tracking algorithm was written in a C language dynamically linked library, called by Labview software, and the voltage control was achieved by an analog output on the PCIe-DAQ (6353, National Instruments).

2.4 Novel safe and light efficient scanning protocols with dynamic spectral shaping

To minimize light exposure, we custom designed our home-built OCT Labview acquisition software with alignment mode and acquisition mode. Alignment mode provides low incident power of ~0.01-0.02 mW at the cornea, yielding real-time images with sufficient contrast to optimize alignment. The beam diameter at the cornea was 1.6 mm. To minimize photochemical hazard, shorter wavelengths should be used only if necessary for resolution or functional contrast. Thus, in addition to lowering power, we used our shaping setup to shape the spectrum to longer wavelengths (600 nm – 650 nm) for alignment. Subsequently we shaped the spectrum to a broader bandwidth (475 nm – 650 nm), with an incident power of 0.08 mW, for image acquisition. Both cross-sectional xy and en face views were available to the operator during the alignment. These advances render visible light OCT scanning both safer and more comfortable for human retinal imaging.

2.5 Continuous small volume scanning protocol

Visualization of IPL lamination presents very specific challenges and thus requires careful optimization. The reflectance contrast of the hypo-reflective bands are on the order of ~10% with respect to the hyper-reflective bands in the IPL. As multiple backscattering neurites in the IPL are expected to be present within the coherence volume, the assumption of Gaussian statistics and fully developed speckle is reasonable for the complex field within each sublamina of the IPL. Given that the speckle contrast (standard deviation divided by the mean) of fully developed speckle is 100%, lamination is not visible in individual images, and averaging is required to reduce speckle. We developed a continuous small volume scanning protocol to generate a single cross-sectional image. In this protocol, we acquire consecutive volumes displaced along the fast (x) axis, where each volume contains multiple frames along the slow (y) axis. The spacing between frames along the y axis should be sufficiently large to ensure independent speckle averaging, but sufficiently small to avoid significant variations in retinal morphology. Our protocol included 13 consecutive volumes, consisting of 20 frames with 168 axial scans each per volume (10 kHz axial scan rate), where each frame was spaced by 2.5 µm along the slow axis. The field-of-view is ~2.6 mm along the fast axis and ~50 µm along the slow axis. Standard image reconstruction [45] with spatially-dependent dispersion compensation [42] is applied to all images. Then, two successive motion corrections are applied to generate the whole cross-section image. First, we estimate (via cross-correlation) and correct the axial eye motion in each volume individually and average over the multiple frames in a volume. Next, the axial motion between volumes is corrected, and then all the volumes are combined to generate one cross-sectional image.

3. Results

3.1 Rapid spectral shaping and performance comparisons

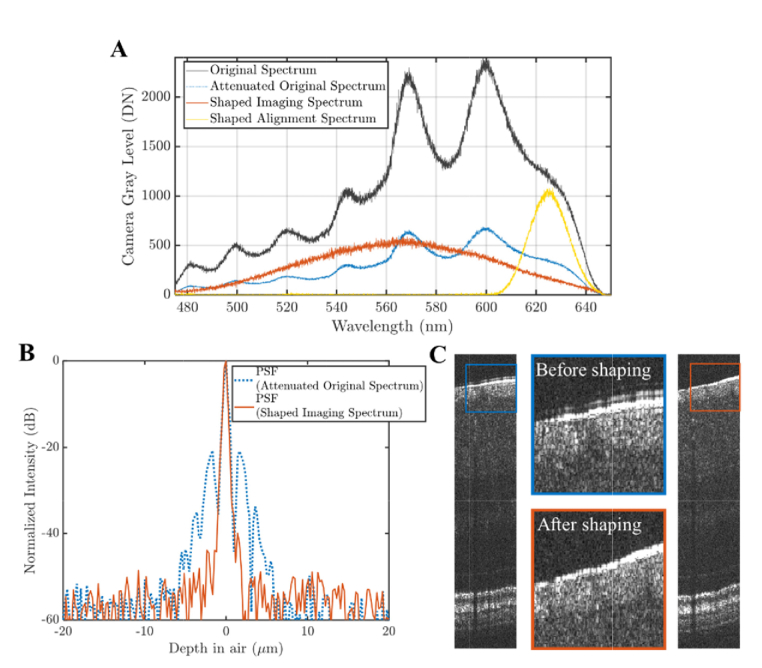
As shown in Fig. 3(A), our shaping setup enabled optimizing spectra for different tasks, such as ultrahigh resolution (UHR) imaging and alignment. The black curve is the original UHR spectrum from the light source. The yellow curve is the alignment spectrum (a Hamming function spectrum centered at 625 nm) for subject alignment to reduce bleaching, improve patient comfort, and reduce photochemical effects. The alignment spectrum reduces retinal luminous exposure by ~40% relative to the original spectrum with approximately equivalent power. Once aligned, the alignment spectrum is replaced by the shaped UHR imaging spectrum (orange curve) with 562.5 nm center wavelength and 110 nm full-width-at-half-maximum (FWHM) bandwidth for image acquisition.

Fig. 3.

Performance of spectral shaping. (A) Original spectrum (black) and shaped spectra, for UHR imaging (orange) and subject alignment (yellow). The spectral shaping setup was also used to neutrally attenuate the original spectrum (dotted blue) to the same exposure level as the shaped imaging spectrum, to provide a fair point spread function (PSF) comparison. (B) UHR PSFs for both the original (dotted blue) and the shaped (orange) spectrum with suppressed sidelobes. (C) In vivo UHR human retinal images demonstrate the benefits of shaping. The images are from consecutive frames in the same data set, where the spectrum was rapidly switched between frames to minimize motion artifacts and provide a fair comparison.

To evaluate shaping, we compared the axial point spread functions (PSFs) of the original UHR spectrum and the shaped UHR spectrum (Fig. 3(B)). The original spectrum was attenuated to have the same power as the shaped spectrum (to approximately maintain sensitivity). The PSFs were calculated as the Fourier transform of the interference spectra between sample and reference mirrors and processed by conventional OCT processing (re-sampling and dispersion compensation). The PSF acquired with the shaped spectrum demonstrates better sidelobe supression.

To examine effects of shaping in vivo, human UHR retinal imaging was performed (Fig. 3(C)). The left image was acquired with the shaped imaging spectrum, whereas the right image was acquired with the original spectrum. The original spectrum was attenuated to have the same power as the shaped imaging spectrum (to approximately maintain sensitivity), and the spectrum was switched during the acquisition (<10 microsecond switching time), ensuring near simultaneity. The middle figures are zooms of selected areas, showing reduced sidelobes in the shaped imaging spectrum image (orange box) compared to the original spectrum image (blue box). Importantly, when a digital post-processing method was applied instead to the original spectrum image to shape the spectrum, the reduction in sidelobes was accompanied by a 2 dB penalty in signal-to-noise ratio.

3.2 Axial tracking performance

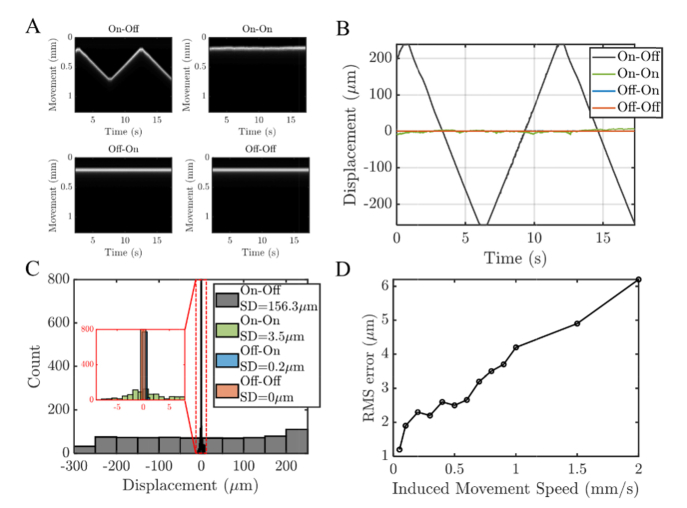
Characterization of axial motion tracking on a model eye is presented in Fig. 4. Performance was tested with a scan protocol of repeated frames at a 10 kHz axial scan rate and 48 Hz frame rate with ~190 axial scans per frame. The model eye consisted of a 25 mm bi-convex lens with a paper target in the focal plane. Different stages were employed in the reference arm to induce and compensate motion. The first motorized stage (Z825B, Thorlabs) was used to generate or induce movement, where the magnetically actuated stage was controlled by the tracking system (Fig. 1(A)) to compensate the induced motion. In Fig. 4(A)-(C), the induced movement is approximately a periodic triangle with 0.1 mm/s speed and an amplitude of 0.5 mm. Our results show that the induced motion can be compensated with low standard deviation. In Fig. 4(C), histograms of displacements relative to the mean position are shown. In Fig. 4(D), sub-10 micron RMS errors are shown for linear translation speeds up to 2 mm/s. Though axial tracking was sufficient to maintain an near-optimal path length difference in the presence of eye motion, additional motion correction was still needed in post-processing, to correct for micron-scale drift as well as intraframe motion.

Fig. 4.

Characterization of axial motion tracking for a model eye with induced motion during repeated imaging at a 48 Hz frame rate. (A). Axial scans from a single location in the frame in the model eye with induced reference movement (0.1 mm/s periodic triangle with 0.5 mm amplitude). Images represent different scenarios: with induced movement and without tracking (On-Off); with induced movement and with tracking (On-On); without induced movement and with tracking (Off-On); without induced movement and without tracking (Off-Off). (B-C) The displacements (determined by analysis of the OCT image time series) demonstrate that the motion can be tracked over a period of time with a standard deviation of 3.5 microns. (D) The root mean squared (RMS) errors of the sample positions relative to the mean position for different induced linear movement speeds with tracking.

3.3 Spatially dependent dispersion compensation in the human retina

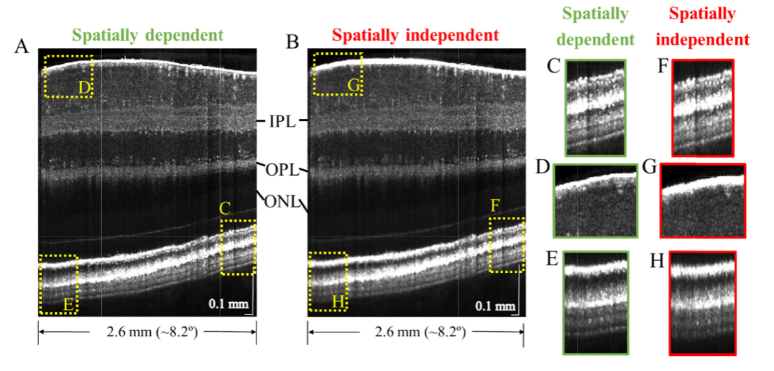
We next compared our recently-reported [42] spatially dependent dispersion compensation method (Fig. 5(A)) against a standard method (Fig. 5(B)) which compensates depth and transverse position independent dispersion up to third-order. The temporal edge of the retinal image is ~3.4° from the fovea. A side-by-side comparison illustrates that while the spatially independent method can achieve comparable image quality at a single position (Fig. 5(C),(F)), it is incapable of optimizing image quality at all positions simultaneously (Fig. 5(G)-(H)), and the spatially dependent method is needed (Fig. 5(D)-(E)).

Fig. 5.

Visible light OCT image with spatially dependent (A) and spatially independent (B) dispersion compensation. While the spatially independent method can perform comparably to the spatially dependent method at a particular image location (C,F), the spatially dependent method optimizes image sharpness at all locations (D,E), whereas the spatially independent method does not (G,H), enabling more consistent and clear visualization of lamination across the inner plexiform layer (IPL) and outer plexiform layer (OPL). A depth-dependent grayscale, transitioning in the outer nuclear layer (ONL), simultaneously highlights relevant contrast in both the inner and outer retina.

3.4 Inner retinal imaging and morphometry

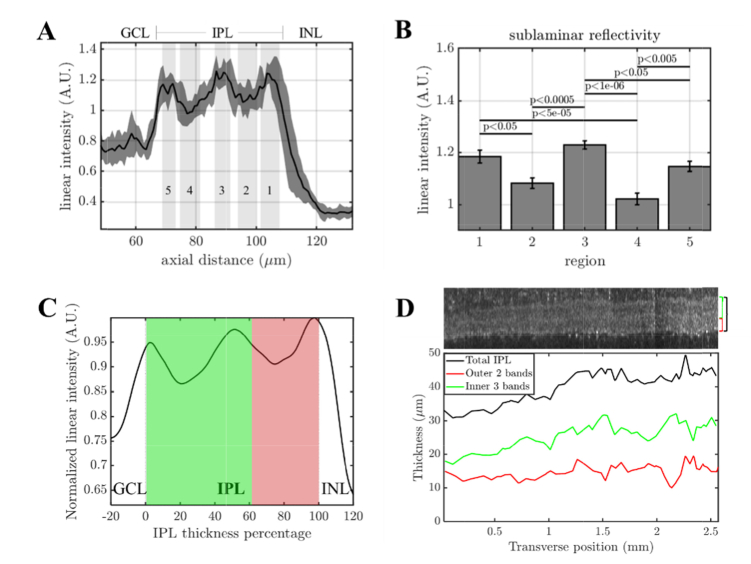
After optimizing dispersion compensation in visible light OCT, we proceeded to investigate IPL lamination. The linear signal intensity profile (mean ± standard deviation over ~0.15 mm transverse regions across a 1.5 mm field-of-view) in Fig. 6(A) illustrates that a hypo-reflective band (4) is resolved in the IPL on sublamina between two hyper-reflective bands (3 & 5). The reflectance of this band lies approximately midway between the reflectance of the ganglion cell layer and that of the rest of the inner plexiform layer. Our preliminary data also shows that the off sublamina includes a second hypo-reflective band (2) as well as a hyper-reflective band at the outer IPL edge (1). To generate reflectivity data for each band we background-corrected and normalized each axial scan to its median IPL intensity, then averaged over non-overlapping ~0.15 mm transverse regions along the fast axis. The mean and standard error (across regions) for each band are shown in Fig. 6(B) with p values determined by one-way ANOVA with Tukey’s Honest Significant Difference test. An alternative method of displaying IPL signal versus the IPL thickness percentage is also presented in Fig. 6(C), which accounts for proportional changes in the band thicknesses as the IPL thickness varies across the field-of-view (Fig. 6(D)).

Fig. 6.

Inner retinal morphometry and lamination in the inner plexiform layer (IPL) with visible light OCT. (A) The average linear signal intensity profile of the inner retina. The solid black line is the mean value over a 1.5 mm field-of-view, while the gray shaded region indicates the standard deviation over ~0.15 mm transverse regions. (B) IPL lamination is clearly visualized, with statistically significant differences in reflectivity between bands (ANOVA with Tukey’s Honest Significant Difference). (C) To account for IPL thickness changes over the 2.6 mm field-of-view, the normalized intensity is plotted versus IPL thickness percentage. The on sublamina (green) exhibits deeper troughs in band 4 than the off sublamina (red) does in band 2. (D) As the IPL thickness changes, the outer 2 bands (off sublamina) and inner 3 bands (on sublamina) appear to change in proportion.

3.5 Wavelength-dependent contrast

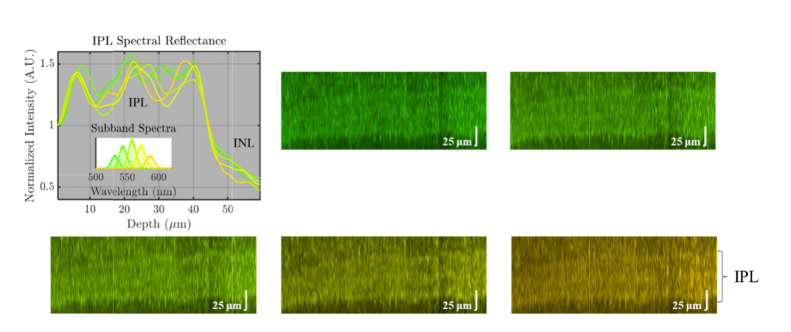
Spatially dependent dispersion compensation also enabled highly accurate investigation of wavelength-dependent contrast in visible light OCT. Figure 7 shows subband images of the outer retina, each in the true color of the subband center wavelength. Each subband spectrum was shaped to achieve an identical shape in wavenumber (k); thus the wavelength (λ) bandwidths increase quadratically with center wavelength. Each of the subband images, calculated by Fourier transformation of subband interference spectra, provides identical axial resolution. Close inspection of the outer retinal morphology in the subband images suggests that BM visibility increases markedly at shorter wavelengths, with a gap between BM and the RPE (white arrow) emerging at shorter visible wavelengths (Fig. 7), though the theoretical axial resolution does not change. On the contrary, visibility of IPL lamination does not appear to change significantly with wavelength (Fig. 8).

Fig. 7.

True color subband images of the outer retina with identical axial resolutions, obtained via digital spectral shaping. Axial line profiles were generated from flattened images with background correction and normalization proximal to the RPE. Note that the separation between the hyper-reflective Bruch’s membrane (BM) band and the hyper-reflective retinal pigment epithelium (RPE) band improves markedly at shorter wavelengths.

Fig. 8.

True color subband images of the inner plexiform layer (IPL) with identical axial resolutions, obtained via digital spectral shaping. Axial line profiles were generated from flattened images with background correction and normalization proximal to the IPL. Note that the IPL lamination contrast remains roughly the same across wavelengths, particularly in the on sublamina.

4. Discussion

In this work, we incorporated rapid spectral shaping, axial motion tracking, and spatially dependent dispersion compensation to improve the quality of visible light OCT human retinal images.

First, our results demonstrate the ability to image the internal structure of the IPL vis-à-vis reflectivity. The 3 hyper-reflective bands and 2 hypo-reflective bands observed with visible light OCT correspond well with the standard anatomical division of the IPL into 5 layers [5]. Synapse density or neurite orientation, size, and density, which vary across sublaminae [5], may generate this reflectivity contrast. Broadly, experimental animal studies [9–12] predict that the internal dendritic morphology of ganglion cells and possibly their synaptic partners change in early glaucoma, and more specifically, that these changes might be earliest and most predictive in the off sublamina. Our preliminary results suggest IPL sublamina thickness, reflectivity, and contrast (the variation between layers) as potential biomarkers for these early subtle morphological changes. Our accurate subband image comparison, enabled by the correction of spatially dependent dispersion [42], reveals that IPL lamination contrast is similar across the visible light OCT spectrum in the on sublamina (Fig. 8).

Second, our results confirm and expand upon the surprising finding that Bruch’s membrane is clearly and consistently visualized with visible light OCT [33]. We assume that the BM band comprises the inner collagenous layer (ICL), elastic layer (EL), and outer collagenous layer (OCL), which are highly scattering. The hypo-reflective space above BM and below the RPE then would correspond to the RPE basal lamina (BL) and the basal RPE cell body which contains fewer melanosomes. The hyper-reflective RPE band likely corresponds to melanosomes localized in the apical RPE. Our accurate subband image comparison (Fig. 7) revealed that the hypo-reflective space above the BM band is more prominent at shorter visible light OCT wavelengths. Regardless of the reason, our results suggest that shorter visible light OCT wavelengths improve BM visualization through a mechanism that is independent of axial resolution. Consistent with this finding, a previous NIR OCT study with a stated resolution comparable to ours reported IPL lamination, but did not clearly visualize BM [15]. In further support of this finding, we observed a similar improvement in BM visibility at shorter visibility wavelengths in pigmented mice, but not albino mice (data not shown). While further investigation is required, melanosome attenuation and shadowing may contribute to this intriguing result.

Finally, in this study, the incident power at the cornea was ~50x less than commercial NIR OCT during alignment, and ~10x than commercial NIR OCT during acquisition. Future work will investigate the ability of our shaping method increase the power and axial scan rate during acquisition, while still maintaining an acceptable margin of safety relative to thermal and photochemical hazards. Pending assessment of repeatability and reproducibility, visible light OCT imaging of the inner and outer retina may help to assess the earliest putative changes in both glaucoma and AMD.

5. Conclusion

In this work, several technical advances were implemented to improve the performance of visible light OCT in the human retina. Images revealed both inner plexiform layer lamination and a clear hypo-reflective space between Bruch's membrane (BM) and the retinal pigment epithelium (RPE). Spatially dependent dispersion compensation enabled precise investigation of wavelength-dependent contrast within individual subband images with identical axial resolution. The outer retinal contrast improved dramatically at shorter wavelengths, while the inner plexiform layer contrast showed no obvious improvement. These observations suggest that the IPL visualization is mainly improved by the axial resolution, whereas the improvement in BM visualization is further aided by the shorter visible wavelengths.

Funding

Glaucoma Research Foundation Catalyst for a Cure; National Institutes of Health (R01NS094681, R03EB023591, R21NS105043, R01EY028287, T32EY015387, and R01EY030361).

Disclosures

VJS: Optovue Inc. (P).