A tutorial on Dirichlet Process mixture modeling

Abstract

Bayesian nonparametric (BNP) models are becoming increasingly important in psychology, both as theoretical models of cognition and as analytic tools. However, existing tutorials tend to be at a level of abstraction largely impenetrable by non-technicians. This tutorial aims to help beginners understand key concepts by working through important but often omitted derivations carefully and explicitly, with a focus on linking the mathematics with a practical computation solution for a Dirichlet Process Mixture Model (DPMM)—one of the most widely used BNP methods. Abstract concepts are made explicit and concrete to non-technical readers by working through the theory that gives rise to them. A publicly accessible computer program written in the statistical language R is explained line-by-line to help readers understand the computation algorithm. The algorithm is also linked to a construction method called the Chinese Restaurant Process in an accessible tutorial in this journal (Gershman & Blei, 2012). The overall goals are to help readers understand more fully the theory and application so that they may apply BNP methods in their own work and leverage the technical details in this tutorial to develop novel methods.

1. Introduction

Bayesian nonparametric (BNP) methods address model complexity in fundamentally different ways than conventional methods. For example, in conventional cluster analysis (e.g., k-means) the analyst fits several models with varying degrees of complexity (k = 1, 2, … , K clusters) and then chooses the desired model based on model comparison metrics. The number of parameters is always fixed in the conventional analytics. BNP methods, however, are based on a statistical framework that contains in principle an infinite number of parameters. One such statistical framework is a stochastic process called the Dirichlet Process (DP). This tutorial aims to explain DP to the curious non-technicians.

We write primarily for a student who wants to learn BNP but finds most academic papers at a level of abstraction beyond his or her current reach. The DP is often described in abstract concepts in the literature, as a stochastic process that generalizes the Dirichlet distribution from being the conjugate prior for a fixed number of categories into the prior for infinitely many categories. The term nonparametric in this broad context basically means that the model has in principle an infinite number of parameters. Austerweil et al. (2015) describe this definition. A BNP model defined in this framework is not restricted to a specific parametric class. There are minimal assumptions of what models are allowed. An emergent property of this flexibility in model parameterization is that the structural complexity of a model can grow as data accrue. DP is also characterized as a distribution over distributions (e.g., Teh, 2017; Jara et al., 2011; Jara, 2017; Escobar & West, 1995). A student reading these materials may absorb all these concepts perfectly fine, but he or she may only have a vague impression as to the origin of these somewhat abstract concepts. This tutorial aims to make these concepts more concrete, explicit, and transparent.

Articles with a focus on applications of BNP methods offer limited technical details (e.g., Navarro et al., 2006; Karabatsos, 2017; Karabatsos & Walker, 2009). More technical papers, such as several recent sources (Orbanz & Teh, 2011; Jara, 2017; Müller et al., 2015; Hjort et al., 2012; Ghoshal & van der Vaart, 2015) explain the DP by Measure Theory, a concept that non-technicians are probably not familiar with. Classic papers (e.g., Ferguson, 1973; Blackwell & MacQueen, 1973; Antoniak, 1974) and a recent overview (Jara, 2017) are also abstract. To minimize these abstract concepts, DP is often explained using several construction methods, metaphors that help explain how the computation is actually implemented at a more intuitive level (Gershman & Blei, 2012). However, important details and derivations are typically not covered. There is, we believe, a need to bridge the gaps between these approaches in order to help non-technical readers understand more fully how DP is actually implemented in a self-contained how-to guide.

There has been a rapid growth in applications involving BNP methods, including in human cognition (Anderson, 1991; Austerweil & Griffiths, 2013; Collins & Frank, 2013), modeling individual variability (Navarro et al., 2006; Liew et al., 2016), and psychometric (Karabatsos & Walker, 2009, 2008). DP is one of the simplest and most widely-used methods that support BNP. There are already many tutorials and how-to guides (e.g., Gershman & Blei, 2012; Houpt, 2018; Orbanz, 2018; Kourouklides, 2018). This tutorial offers something different. We aim to make the technical details more accessible to non-technicians. Thus, the details are described much more explicitly than what is typically available in elementary introductions. We aim to describe in great detail exactly how a DP cluster analysis spawns a new cluster. Does DP somehow calculate a fit between an observation and its cluster? The omitted technical details are the focus of this tutorial, covered in an illustrative cluster analysis using DP mixture modeling. As we proceed along this tutorial, we will interject explanations of the omitted derivations. The intended readers are advanced graduate students in a quantitative psychology program or a related field, someone who is familiar with probability theory and conditional probability but unfamiliar with Measure Theory. Familiarity with R programming and Bayesian statistics is needed (e.g., at the introductory level in Lee, 2012). However, the required programming skills are no more complicated than writing simple functions in R and carrying out random sampling from standard probability distributions.

This tutorial is organized as follows. To establish a basic framework, we begin with a straightforward finite Gaussian mixture model with the number of clusters K fixed and known. Then we explain in detail how DP extends it to an infinite mixture model. Next, the construction method called the Chinese Restaurant Process (CRP) is explained (Aldous, 1985; Blackwell & MacQueen, 1973). We then introduce a computer program written in the statistical language R to demonstrate what the DP “looks like” in action, when it spawns new clusters as data accrue. The R program is adapted from the tutorial by Broderick (2017), an implementation of the Gibbs sampling algorithm in Neal (2000, algorithm 3). Our exposition may also be useful for technical experts as a refresher of the omitted derivations in Neal (2000) and other academic papers.

2. Finite Mixture Model

2.1. Hypothetical Data

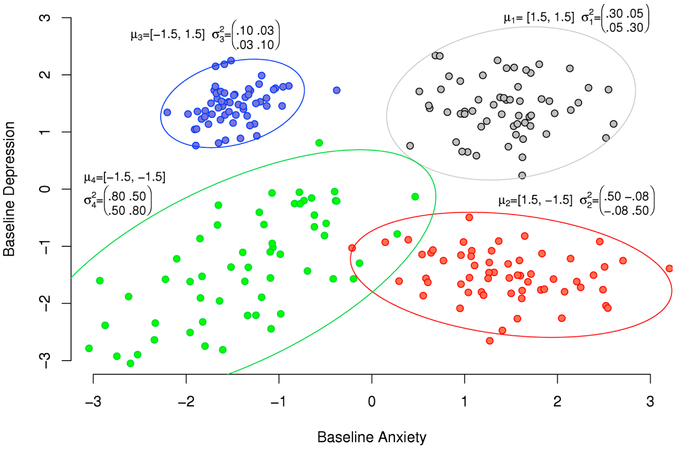
The hypothetical dataset in Figure 1 will be used throughout this tutorial to make the explanations more explicit and concrete. Each observation consists of two assessments, both normalized onto a z-scale. Each dot represents one participant’s two measurements, e.g., on anxiety (y₁) and depressive symptoms (y₂), respectively. The observations are simulated from K = 4 known clusters, each represented by a bivariate Gaussian distribution with mean μ_k and covariance matrix ${\sigma }_k^2$. The presumed known parameters for all 4 clusters are shown in Figure 1. DPMM is expected to find a 4-cluster solution without being explicitly told so.

Figure 1:

A hypothetical example of psychological assessment scores from 240 individuals divided into four known clusters. From each cluster, a random sample of 60 individuals is drawn from a bivariate Gaussian distribution with specified mean and covariance matrix. Also plotted are the 95th percentile ellipsoids for the underlying distributions.

2.2. Model Likelihood Function in a Finite Mixture Model

We begin with a straightforward finite mixture model with the number of clusters K fixed and known to establish the basic framework. The likelihood of the model is defined as a mixture of Gaussian distributions.

$$p(y_i\mid {\mu }_1,\dots ,{\mu }_k,{\sigma }_1^2,\dots ,{\sigma }_k^2,{\pi }_1,\dots ,{\pi }_k)=\sum _{k=1}^K{\pi }_k\mathcal{N}(y_i;{\mu }_k,{\sigma }_k^2),$$ (1)

where an observation y_i is evaluated according to a Gaussian distribution with the specified mean (μ_k ) and covariance (${\sigma }_k^2$) of each cluster, and then weighted by the mixing proportions π_k (weights assigned to the clusters, must sum to one).

Next, we introduce an indicator variable c_i to represent the ith participant’s cluster membership, where c_i takes on discrete values 1, … , K, so that c_i = k denotes that the ith observation is assigned to the kth cluster. Indicators such as c_i in mixture models are latent variables. Their specific values are stochastic realizations of the mixture probabilities π_k (think casting a die). For reasons that will become clearer later on, c_i is introduced here because it plays an important role in simplifying the calculations. If we know which cluster each observation belongs to, then each person’s data likelihood is calculated from his/her cluster mean and covariance:

$$p(y_i\mid c_i=k)=\mathcal{N}(y_i\mid {\mu }_k,{\sigma }_k^2).$$

2.3. Joint Posterior Distribution by Bayes’ Theorem

Bayes’ Theorem is then applied to obtain the joint posterior distribution of the model parameters:

$$p(\mu ,{\sigma }^2,\mathit{c}\mid y)=\frac{p(y\mid \mu ,{\sigma }^2,\mathit{c})p(\mu ,{\sigma }^2,\mathit{c})}{p(y)}\propto p(y\mid \mu ,{\sigma }^2,\mathit{c})p(\mu )p({\sigma }^2)p(\mathit{c}).$$ (2)

On the left hand side we have the joint posterior distribution of the cluster parameters and cluster assignment, which we want to estimate. On the right we have p(y∣μ, σ², c), the data likelihood function in Equation (1), multiplied by the priors. Bold font is used to represent vectors (e.g., cluster means μ_k as μ). This derivation shows an important concept in Bayesian statistics—“post is prior times likelihood” (Lee, 2012, section 2.1.2). From the joint posterior distribution we can derive the distribution for each parameter. The joint probability of p(μ, σ², c) turns into p(μ)p(σ²)p(c) because the three parameters are presumed mutually independent. Here p(μ)p(σ²)p(c) is the product of three prior distributions, described next.

2.3.1. Priors

We need to specify priors on μ, σ² and π. We use a normal prior common for all cluster means, $p({\mu }_k)~\mathcal{N}({\mu }_0,{\sigma }_0^2)$, specified with the covariance ${\sigma }_0^2$. If we set, for example, $p({\mu }_k)~\mathcal{N}({\mu }_0=0.0,{\sigma }_0^2=1.0)$, then we are explicitly expressing a standard normal prior for the cluster means. If an analyst has limited prior knowledge on the cluster means, then a wider margin of error may better reflect the uncertainty, e.g., $\mathcal{N}({\mu }_0=0.0,{\sigma }_0^2=16)$. Here μ₀ and ${\sigma }_0^2$ are hyperparameters of the parameter μ_k.

An inverse-Wishart prior distribution is appropriate for the covariance of multivariate normal data. The simplest multivariate normal data follows a bivariate normal such as the clusters in Figure 1. Using the notation in Gelman et al. (2003, Table A.1), the Inv-Wishart(S⁻¹, v) prior may be set at v = 2 degrees of freedom and a scale matrix S. For example, on clustering bivariate normals we may use an inverse scale matrix $S^{-1}=\left(\begin{array}{cc}\hfill 10\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 10\hfill \end{array}\right)$, which represents a high degree of uncertainty in the variances (diagonal entries) and zero covariation (off diagonal), which will be updated by data.

When modeling univariate normal, the inverse-Wishart distribution simplifies into the inverse-Gamma distribution with a shape parameter γ and rate parameter β.

$$p({\sigma }_k^2\mid \gamma ,\beta )\sim {\mathcal{G}}^{-1}(\gamma ,\beta )\propto (1∕{\sigma }_k^2{)}^{\gamma -1}\text{exp}(-\beta ∕{\sigma }_k^2).$$

The derivations in Appendix A.3 will be based on the univariate case to keep them simple. Note that hyperparameters (μ₀, τ₀) and (γ, β) can have priors of their own. Priors on hyperparameters are called hyperpriors. We are not using hyperpriors for simplicity.

The mixing proportions, π_k, are given a symmetric Dirichlet distribution prior with parameter α/K:

$$p({\pi }_1,\dots ,{\pi }_k\mid \alpha )\sim \text{Dirichlet}(\alpha ∕K,\dots ,\alpha ∕K)=\frac{\Gamma (\alpha )}{\Gamma (\alpha ∕K{)}^K}\prod _{k=1}^K{\pi }_k^{\alpha ∕K-1},$$ (3)

where α/K = 1 is for a flat Dirichlet distribution for simplicity. Γ(·) is the gamma function, represented by the capital Greek alphabet Γ. The gamma function is defined by an integral (e.g., Hogg & Craig, 1995, section 3.3). When the input of the gamma function is a positive integer, the output is just the familiar factorial function, offset by one, Γ(n) = (n – 1)!, which is used in this tutorial (e.g., Γ(7) = 6 × 5 × … × 2 × 1 = 720). The gamma function should not be confused with the gamma distribution defined above. A reader may notice that the shape of the distribution is only affected by α because K is a fixed and known constant in a finite mixture model. Thus, K is not a parameter per se. However, α/K plays a critical role later, when we extend the Dirichlet prior to accommodate an infinite mixture model in which the number of clusters is no longer fixed, it varies and may approach infinity.

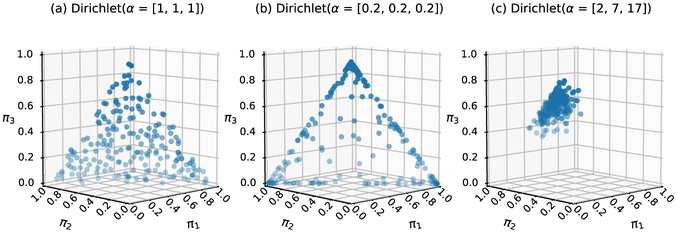
Readers unfamiliar with the Dirichlet distribution may find Figure 2 helpful. The Dirichlet distribution is the conjugate prior for a categorical and/or multinomial distribution. From a Dirichlet distribution with three clusters we may draw a sample of proportions [π₁, π₂, π₃] = [0.5, 0.3, 0.2], which would be the weights used in Equation (1). Figure 2 (a), with α = [1, 1, 1], shows a flat prior with weights evenly distributed (the dots represent potential realizations from the prior). Subplot (b), with α = [0.2, 0.2, 0.2], shows a prior with weights near the edges (e.g., [π₁, π₂, π₃] = [0.50, 0.49, 0.01]). Subplot (c), with α = [2, 7, 17], represents a prior belief that the third cluster has the highest weight (e.g., [π₁, π₂, π₃] = [0.2, 0.1, 0.6]). The values in α can be conceptualized as prior sample sizes (e.g., α = [2, 7, 17], a prior sample of 26 distributed in 3 subgroups). Elements of α are not required to take on the same value. Additional visual explanations can be found in Li et al. (2018).

Figure 2:

Examples of Dirichlet priors for a hypothetical mixture model with 3 components. The Dirichlet distribution is the conjugate prior distribution for a categorical variable such as the mixing proportions [π₁, π₂, π₃], plotted on a 3-dimensional simplex. Each symbol represents one possible realization of [π₁, π₂, π₃] arising from the underlying Dirichlet prior. The length of the α parameter defines the number of clusters and the specific parameter values affect how the mixing proportions are distributed. Subplot (a) shows a prior belief that [π₁, π₂, π₃] can take on any triplet seen evenly distributed on the 3-d simplex. Subplot (b) shows a prior belief that the mixing proportions are mostly at the edges of the 3-d simplex, where one mixing proportion is near zero (e.g., [π₁, π₂, π₃] = [0.50, 0.49, 0.01]). Subplot (c) shows a concentration of samples on π₃ when α = [2, 7, 17].

2.4. Conditional Posterior Distributions

From the joint posterior distribution in Equation (2) we can work out the conditional posterior distributions analytically for μ_k, ${\sigma }_k^2$, and π_k for Gibbs sampling. All you need to do is to reorganize Equation (2) such that you recognize the result as a known distribution from which you can draw samples. However, these algebraic manipulations are simpler if we work with the reciprocal of the variance instead of the variance. The reciprocal of the variance in a univariate normal distribution is called the precision. Similarly, the precision of a multivariate normal distribution is the inverse covariance matrix. See Gelman et al. (2003, section 2.6) for a discussion on the roles of precision in Bayesian statistics. These algebraic manipulations are shown with cluster precisions in Appendix A.

Cluster means.

Next we introduce the precision of the cluster covariance, τ_k, as the inverse covariance matrix. The conditional posterior distribution for the kth cluster mean is

$$\begin{gathered} p({\mu }_k\mid \mathit{y},c=k)\propto p(\mathit{y},c=k\mid {\mu }_k)p({\mu }_k) \\ \sim \mathcal{N}\left(\frac{{\stackrel{‒}{y}}_k{n}_k{\tau }_k+{\mu }_0{\tau }_0}{n_k{\tau }_k+{\tau }_0},n_k{\tau }_k+{\tau }_0\right). \end{gathered}$$ (4)

Detailed step-by-step derivations are provided in Appendix A.2. This equation may look confusing and intimidating at first. But we can approach it via known facts in normal conjugacy. Here we are trying to determine the probability distribution of the mean of the kth cluster with several normally-distributed data points, where p(y, c = k∣μ_k)p(μ_k) is based on Bayes’ rule. We have a prior of ${\mu }_k~\mathcal{N}({\mu }_0,{\tau }_0)$, with ${\tau }_0=1∕{\sigma }_0^2$ representing the precision about the mean in the prior. We also have some observed data points y, with an average of ${\stackrel{‒}{y}}_k=\frac{1}{n_k}\sum _{k[i=1]}^{n_k}{y}_i$, where k[i] represents summing over ith persons nested within the kth cluster and divided by n_k, the number of persons in that cluster. We can represent this information on data as $y~\mathcal{N}({\stackrel{‒}{y}}_k,{\tau }_k)$, where τ_k represents a residual uncertainty about the data around the cluster mean when it takes on a specific estimated value of ${\stackrel{‒}{y}}_k$. In this setting (when we have normal conjugacy with several normal observations and a normal prior), the following is known to be true. The posterior distribution of the sample mean μ_k has a precision that is the prior precision plus the sample precision multiplied by the number of observations in the sample, exactly n_kτ_k + τ₀ as above. Note that the manipulation is simpler if we work with precision instead of the covariance.

This fact can be found in introductory textbooks (e.g., Lee, 2012, section 2.3) as well as in more advanced textbooks (e.g., Gelman et al., 2003, section 2.6). We can think of n_kτ_k + τ₀ as the combined uncertainty about the cluster mean in the prior precision plus the residual uncertainty about the data around the cluster mean when it is known, which makes intuitive sense. In the cited textbooks you will also find the derivations of the mean of the posterior distribution. It is the prior mean weighted by the prior precision plus the sample average weighted by the number of observations and the sample precision, and this sum divided by the sum of the weights, exactly $\frac{{\stackrel{‒}{y}}_k{n}_k{\tau }_k+{\mu }_0{\tau }_0}{n_k{\tau }_k+{\tau }_0}$.

Cluster precisions.

The posterior precisions are:

$$\begin{gathered} p({\tau }_k\mid \mathit{y})\propto {\tau }^{n_k∕2}\text{exp}\left(-n_k\sum _{[i]c=k}(y_i-{\stackrel{‒}{y}}_k{)}^2\right)\times {\tau }^{\alpha -1}\text{exp}(-\beta \tau ) \\ ={\tau }^{\alpha -1+n_k∕2}\text{exp}\left(-\tau (\beta +\frac{1}{2}\sum _{[i]c=k}^K(y_i-{\stackrel{‒}{y}}_k{)}^2)\right), \end{gathered}$$ (5)

where the prior gamma distribution $\mathcal{G}(\gamma ,\beta )$ is combined with data to yield a posterior gamma distribution that has an updated shape parameter of α – 1 + n_k/2 and a rate parameter of $\beta +\frac{1}{2}\sum _{[i]c=k}^K{(y_i-{\stackrel{‒}{y}}_k)}^2$. Details can be found in Appendix A.3. Detailed derivations for Equations (4) and (5) may help beginners better understand why conjugate models take on specific forms.

Latent cluster membership.

The joint distribution of the indicators c₁, c₂, … , c_k is a multinomial realization of the mixing proportions π_k raised to n_k, the number of people in each of the K clusters.

$$p(c_1,\dots ,c_k\mid {\pi }_1,\dots ,{\pi }_k)=\prod _{k=1}^K{\pi }_k^{n_k}.$$ (6)

Recall that π_k follows a Dirichlet distribution with its density function controlled by the parameter α (Equation (3)), and also that the c_k indicators are realizations of π_k. Thus, the posterior Dirichlet distribution has the updated parameters n₁ + α/K – 1, … , n_k + α/K – 1.

When K is finite and known, the sampling model is relatively straightforward. We can turn Equations (3) – (6) into an algorithm for Gibbs sampling:

$$\begin{gathered} {\pi }_k^{(t)}\sim \text{Dirichlet}(n_1+\alpha ∕K-1,\dots ,n_k+\alpha ∕K-1), \\ {\mu }_k^{(t)}\mid {\mathit{c}}^{(t-1)},\mathit{y},{\tau }_k^{(t-1)}\sim \mathcal{N}\left(\frac{{\stackrel{‒}{y}}_k{n}_k{\tau }_k^{(t-1)}+{\mu }_0{\tau }_0}{n_k{\tau }_k^{(t-1)}+{\tau }_0},n_k{\tau }_k^{(t-1)}+{\tau }_0\right), \\ {\tau }_k^{(t)}\mid {\mathit{c}}^{(t-1)},\mathit{y},{\mu }_k^{(t-1)}\sim \text{Gamma}(\alpha -1+n_k∕2,\beta +\frac{1}{2}\sum _{[i]c=k}(y_i-{\stackrel{‒}{y}}_k{)}^2), \\ {\mathit{c}}_i^{(t)}\sim \text{Multinomial}(2,{\pi }_1^{(t)}\mathcal{N}(y_i\mid {\mu }_1^{(t)},{\tau }_1^{(t)}),\dots , \\ {\pi }_k^{(t)}\mathcal{N}(y_i\mid {\mu }_k^{(t)},{\tau }_k^{(t)})). \end{gathered}$$

We use the superscripts (t) and (t – 1) to index, respectively, the most recently sampled parameters and the parameters immediately preceding. In the last equation, the latent cluster membership is a multinomial realization of the underlying mixture proportions, weighted by the data likelihood of the corresponding cluster (e.g., c_i, = (0, 1, 0) arising from π = (0.4, 0.5, 0.1)). We omit some details such as the normalizing constant in the last line because it is not our immediate goal to explain how to assemble a finite mixture model. Rather, this exercise highlights the challenges in extending these results to infinite mixtures. The main point is to show the various probability distributions, what they look like, and how they can be derived through iteratively sampling. Readers who are interested in the details of Gibbs sampling can read our tutorial on a model with finite components (Li et al., 2018).

What if K is not finite and known? The algorithm above no longer works because it requires a fixed K. More challenging still, what if K approaches infinity? It would be impossible to sample from a Dirichlet distribution with an infinite vector of π’s. This seems hopeless. However, Ferguson (1973) solved the problem by working out the Dirichlet Process prior, a prior distribution that does not depend on the infinite π’s. This is described next.

3. Infinite Mixture Model

In this section we tackle the problem of infinite number of clusters. We aim to make the mathematical expositions explicit and concrete. After the derivations of the equations are worked out, they will be linked to a metaphor called the Chinese Restaurant Process (CRP, Aldous, 1985; Blackwell & MacQueen, 1973), a more intuitive representation of the DP. Readers researching the topic may encounter the CRP, but not necessarily the equations which explain why the CRP works. We aim to connect them to provide a fuller, more complete understanding of the DP. CRP is not the only representation of the DP. Other representations also exist (e.g., stick-breaking by Sethuraman (1994) and Pólya urn by Blackwell & MacQueen (1973)), whiCh are equivalent to the CRP.

3.1. Tackling the Problem of Infinite Number of Clusters

The first issue to address is the infinite vector of mixing proportions. Recall that π is a function of α (Equation (3)) and that C_i is a function of the vector π (Equation (6)). If we combine the two functions and integrate out π, then we can get C_i to arise directly from α. Here is what is shown in Rasmussen (2000):

$$\begin{gathered} p(c_1,\dots ,c_k\mid \alpha )=\int p(c_1,\dots ,c_k\mid {\pi }_1,\dots ,{\pi }_k)p({\pi }_1,\dots ,{\pi }_k\mid \alpha )d{\pi }_1\cdots d{\pi }_k \\ =\frac{\Gamma (\alpha )}{\Gamma (\alpha ∕K{)}^k}\int \prod _{k=1}^K{\pi }_k^{n_k+\alpha ∕K-1}d{\pi }_k \\ =\frac{\Gamma (\alpha )}{\Gamma (n+\alpha )}\prod _{k=1}^K\frac{\Gamma (n_k+\alpha ∕K)}{\Gamma (\alpha ∕K)}. \end{gathered}$$ (7)

The lowercase k is used as an index for a particular cluster. The uppercase K is used to represent the total number of clusters. In the next section we will see that DP allows K to represent a varying number of clusters, whether finite or infinite. A fixed K is no longer required in the DP. This notation is used throughout the tutorial.

Note that π disappears from the last equation. An important insight here is that a problematic parameter can be addressed by integrating it out of the model. The transition from line 1 to 2 is relatively straightforward. The symmetric Dirichlet prior in Equation (3) is multiplied with the multinomial mixing proportions in Equation (6). Since both equations involve π_k, a multiplication means adding the exponents together, and $\frac{\Gamma (\alpha )}{\Gamma {(\alpha ∕K)}^k}$ is a constant so it is moved to the front of the integral sign. However, the transition between lines 2 and 3 is not at all obvious. The omitted steps may be considered trivial by technical experts, but they are needed for a beginner to achieve a fuller understanding of the DP prior. Rasmussen (2000) explained that it is simply a “standard Dirichlet integral” and offered no further explanation. Neal (2000) skipped this entirely and went straight to Equation (8) below. Navarro et al. (2006) offered more details but not at an easily accessible level. Thus, we work them out explicitly in Appendix A.4 (Equations (A.6) – (A.7) specifically). Readers are encouraged to follow them step by step to understand the origin of Equation (7).

Equation (7) brings us one step closer to completely resolving the problem of sampling from an infinite number of mixture proportions. However, it still requires the total number of clusters K to take on a specific value. If K is to be allowed to approach infinity, then we will need a way to work around it. The next few steps are probably the most challenging to follow. We will be extremely explicit in working through the details in the exposition and notation, much more specific in explaining the steps than what is typically available in introductory texts.

3.2. When K Approaches Infinity

Equation (7) can be further leveraged to produce a complete workaround of K. We have a work out the conditional prior for a single indicator C_i given all other indicators except c_i.

$$p(c_i=k\mid c_{-i},\alpha )=\frac{n_{-i,k}+\alpha ∕K}{n-1+\alpha },$$ (8)

where the subscript −i in c_−i represents all indicators except the ith and n_−i,k represents the number of observations nested within the kth cluster excluding y_i. The n in the denominator is the total number of observations. Detailed derivations are long so that they are described in Appendix A.4 (Equations (A.7) – (A.8)). Readers are encouraged to follow the steps carefully to understand why Equation (8) is true.

3.3. Exchangeability

A direct result of Equation (8) is the exchangeability property—the probability of cluster assignment being invariant of the order of the individual data points. Each data point can be considered the last one in this conditional distribution. It does not matter which data entry is assigned to which cluster. Nothing on the right hand side of the equation is affected by the order of observations. The probability is primarily affected by the number of observations nested within the kth cluster. The cluster membership is determined one data entry at a time, in any order (conditional on the existing clustering arrangements). It also implies that two clustering arrangements will have the same probability so long as they have identical cluster sizes n_−i,k. Exchangeability is critically important in DP because it solves the problem of sampling from a Dirichlet distribution with infinitely many categories.

If we let K → ∞ in Equation (8), then the α/K in the numerator approaches the limit of zero and thus disappears.

$$\text{clusters where}(n_{-i,k}>0:p(c_i\mid c_{-i},\alpha )=\frac{n_{-i,k}}{n-1+\alpha }.$$ (9)

Suppose, in a hypothetical example, the first 10 observations have already been clustered into two clusters with 3 and 7 observations, respectively. The 11th observation is assigned to either cluster with a probability proportional to the number of observations already occupying the respective clusters, i.e., a 3:7 ratio. If we sum up the n_−i,k across the already occupied clusters, we get $\frac{10}{10+\alpha }$, The probability that the 11th observation being assigned to any of the already occupied clusters. Note that, if we add $\frac{\alpha }{10+\alpha }$ to $\frac{10}{10+\alpha }$, then we get $\frac{10+\alpha }{10+\alpha }$, which is exactly 1. What is $\frac{\alpha }{10+\alpha }$? It is the probability of the 11th observation not belonging to any of the already occupied clusters. It is the probability that the 11th observation being assigned a new, previously empty cluster. Generally, if we sum up n_−i,k in the numerator across the already occupied clusters, we get n − 1, the total number of observations excluding the last one. Similar to the hypothetical example above, $1-\frac{n-1}{n-1+\alpha }=\frac{\alpha }{n-1+\alpha }$ gives us the probability that the last observation being assigned a new cluster.

We dwell on this important point to make sure that it is absolutely clear. For any individual observation y_i, it can either be placed into one of the existing clusters or it can be the first member of a new, initially empty cluster. There are only these two scenarios so their probabilities must sum to 1. Scenario one involves placing the ith observation into one of the existing clusters (where n_−i,k > 0). The probability of attracting a new member in an already occupied cluster is proportional to n_−i,k, the number of observations already in each of the clusters. The total probability for scenario one is $\frac{{\sum }_{k=1}^K{n}_{-i,j}}{n-1+\alpha }$. Notice the numerator, n_−i,1 + n_−i,2 + · · · + n_−i,K adds up to n − 1, the total number of observations aggregated across all existing clusters except the single observation yet to be categorized. Thu the total probability for scenario one is $\frac{n-1}{n-1+\alpha }$. If the ith observation is not placed in any of the already occupied clusters, then a new cluster has to be created. This is scenario two. But what is the probability of a new cluster being created? It is exactly 1 minus the probability for scenario one. As we mentioned above, the probabilities of scenarios one and two sum to exactly 1. Thus the probability for the second scenario is

$$1-\frac{{\sum }_k{n}_{-i,k}}{n-1+\alpha }=\frac{n1+\alpha }{n-1+\alpha }-\frac{n-1}{n-1+\alpha }=\frac{(n-1+\alpha )-(n-1)}{n-1+\alpha }=\frac{\alpha }{n-1+\alpha }.$$

Therefore, putting everything together, the probabilities of cluster assignment are:

$$\begin{gathered} \text{clusters where}{n}_{-i,k}>0:p(c_i\mid {\mathit{c}}_{-i},\alpha )=\frac{n_{-i,k}}{n-1+\alpha }, \\ \begin{array}{c}\hfill \text{all other clusters}\\ \hfill \text{combined}\end{array}:p(c_i\ne c_k\forall j\ne i\mid {\mathit{c}}_{-i},\alpha )=\frac{\alpha }{n-1+\alpha }. \end{gathered}$$ (10)

An important property of the DP is captured in these equations. The probability that a new cluster is created is proportional to the concentration parameter α (Neal, 2000), shown in the second line. A greater value of α tends to encourage the creation of new clusters, especially if a cluster size is small. For example, if α = 3 and n_−i,k = 3, then the two probabilities are equal. If the mixture weights are given a symmetric Dirichlet prior of Dirichlet(α/K,…, α/K), then the Dirichlet posterior yields exchangeability, which in turn allows an iterative process of spawning new clusters, one observation at a time. An equivalent proof is given in Gershman & Blei (2012, their Equation (8)).

3.4. The Chinese Restaurant Process

The DP is often explained with a culinary metaphor called the Chinese Restaurant Process (CRP, explained in Gershman & Blei, 2012), using a diagram similar to that in Figure 3.

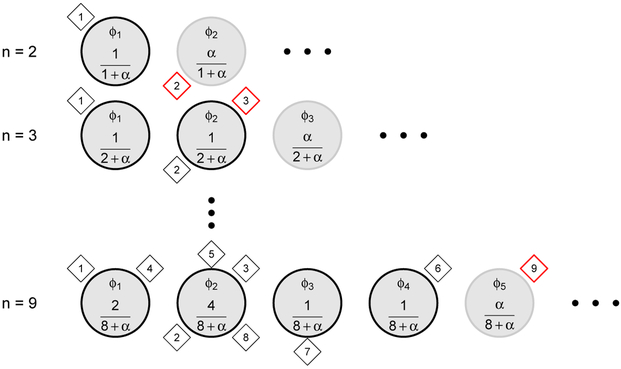
Figure 3:

An illustration of the Chinese Restaurant Process. In the CRP metaphor, imagine a Chinese restaurant with an infinite number of tables. Customers (individual data entries, shown as diamonds) enter into the restaurant one by one and are seated at tables (discrete clusters, shown as circles), in the order in which they enter into the restaurant. There are parameters associated with the clusters, represented as φ_k = [μ_k, τ_k] for the cluster means and precisions. The first customer who enters into the restaurant always sits at the first table. The second customer enters and sits at the first table with probability 1/(1 + α), and the second table with probability α/(1+α), where α is a positive real number (top row, where i = 2). When the third customer enters the restaurant, he or she sits at each of the occupied table with a probability proportional to the number of previous customers already sitting there, and at the next unoccupied table with probability proportional to α.

Imagine a Chinese restaurant with an infinite seating capacity. Customers (data entries, shown as diamonds) are seated at tables (clusters, shown as circles). The tables are identified with parameters ϕ_k = [μ_k, τ_k], the mean and precision of a cluster (we use their notation for ease of comparison). The first customer enters into the restaurant, he or she sits at an initially empty table. When the second customer arrives, he or she can either sit with the first customer at an already occupied table, or at an unoccupied table. Suppose that she sits at an unoccupied table. Now we have two tables occupied. When the third customer arrives, she sits at tables 1 and 2 with a probability proportional to the number of customers already seated there, and at an unoccupied table with probability proportional to the concentration parameter α. The same iterative process loops through the customers one at a time until all customers are assigned a table. The CRP begins with (in principle) an infinite number of tables. However, within a finite dataset, model complexity is determined by the DP. Not all of the infinitely many tables are realized given the data.

Table 1:

A comparison between the key equations in DP and how they can be implemented in R. The last column covers the primary R functions that carry out the calculations. The newly observed data entry is evaluated by the dmvnormO function to obtain its log density, given appropriate input parameters for the predictive distributions. Readers who prefer a different computer programming language may use these to guide their implementation.

Equations for DP	Line(s)	R code
$\frac{n_{-i,k}}{n-1+\alpha }\mathcal{N}\left({\tilde{y}}_i;\frac{{\stackrel{‒}{y}}_k{n}_k{\tau }_k+{\mu }_0{\tau }_0}{n_k{\tau }_k+{\tau }_0},\frac{1}{n_k{\tau }_k+{\tau }_0}+{\sigma }_y^2\right)$ Equation (12)	108 – 110	mean_p <- sig_p %*% (tau_y %*% sum_data + tauO %*% t(muO)) logp[c_i] <- log(n_k[c_i]) + dmvnorm(data[n,], mean = mean_p, sigma = sig_p + sigma_y, log = TRUE)
$\frac{\alpha }{n-1+\alpha }\mathcal{N}({\tilde{y}}_i;{\mu }_0,{\sigma }_0^2+{\sigma }_y^2)$ Equation (13)	117 – 118	logp[ Nclust+1 ] >- log(alpha) + dmvnorm(data[n,] , mean mu0, sigma = sigma0 + sigma_y, log = TRUE)

Table 2:

Results of classification under various model assumptions to recover a simulated 4 clusters of 60 each. Down the rows we have an increasing α, which should encourage the creation of new clusters. Across the columns from left to right we have an increasing measurement error of ${\sigma }_y^2$, which should discourage the creation of new clusters.

		${\sigma }_y^2=0.50$					${\sigma }_y^2=1.00$				${\sigma }_y^2=1.50$				${\sigma }_y^2=3.00$
α = 0.01	ci	1	2	3	4	5	1	2	3	4	1	2	3		1
	nk	64	33	63	60	20	79	67	35	59	145	30	65		240
α = 1.00	ci	1	2	3	4	5	1	2	3	4	1	2	3	4	1
	nk	65	60	30	22	63	60	36	68	76	87	30	66	57	240
α = 3.00	ci	1	2	3	4	5	1	2	3	4	1	2	3	4	1
	nk	66	60	24	27	63	68	60	34	78	36	63	74	37	240
α = 5.00	ci	1	2	4	5		1	2	3	4	1	3	5	6	1
	nk	75	61	33	71		84	61	64	31	33	79	113	15	240

For the CRP to work, the order of customers entering into the restaurant must not matter. This is the exchangeability property mentioned above. The CRP metaphor is appealing because it is intuitive and it maps nicely onto the equations and the iterative sampling one observation at a time. However, a closer inspection of Neal (2000) and Rasmussen (2000) shows that the CRP is not complete. The cluster assignment probabilities have to be further processed. Here we digress to cover an important Bayesian concept called the Posterior Predictive Distribution.

3.5. prior and Posterior Predictive Distributions

In Bayesian statistics, there are two types of predictive distributions. We first turn to the posterior predictive distribution, or PPD for short. The PPD is the posterior probability of newly observed values based on the data you have already seen (Christensen et al., 2011). A newly observed value from the ith person is commonly denoted as ${\tilde{y}}_i$. Intuitively, the probability of a new observation belonging to a cluster should be low if it is very far from the cluster and vice versa. Note that Equation (10) is conditional on all cluster indicators excluding that of ${\tilde{y}}_i$, it does not take into consideration how well the new observation fits any of the already occupied clusters. Thus, we need to incorporate the PPD of ${\tilde{y}}_i$ with respect to each of the kth cluster.

PPDs for Already Occupied Clusters.

PPDs are typically introduced in the following general setting (e.g., Gelman et al., 2003, section 3.6; Lee, 2012, section 2.3; and Novick & Jackson, 1974, section 6.4). Suppose a variable y is normally distributed with an unknown mean of μ and a measurement error in the form of a fixed and known variance ${\sigma }_y^2$, that is,

$$y\sim \mathcal{N}(\mu ,{\sigma }_y^2).$$

Also, if the unknown mean μ is expressed with a prior belief of

$$\mu \sim \mathcal{N}({\mu }_0,{\sigma }_0^2),$$

then the posterior predictive distribution of a newly observed $\tilde{y}$ given the data you have already seen is

$$\tilde{y}\sim \mathcal{N}({\mu }_0,{\sigma }_y^2+{\sigma }_0^2).$$

The density of a newly observed data point $\tilde{y}$ is evaluated by a normal distribution with mean μ₀ and variance ${\sigma }_y^2+{\sigma }_0^2$. The intuition here is that the combined covariance is the sum of two sources of variabilities, the variance due to measurement error, ${\sigma }_y^2$, and the variance around the unknown mean, ${\sigma }_0^2$. It is important to understand this point before we proceed. If it is still somewhat confusion, then a concrete example in Lee (2012, section 2.3) may help explain the difference between the posterior distribution and the posterior predictive distribution after several normal observations with a normal prior.

We are now ready to apply the general case of PPD to a new observation in the kth cluster. We already know from Equation (4) that the conditional posterior distribution for the kth cluster mean is normal with a mean of ${\mu }_p=\frac{{\stackrel{‒}{y}}_i{n}_k{\tau }_k+{\mu }_0{\tau }_0}{n_k{\tau }_k+{\tau }_0}$ and a precision of τ_p = n_kτ_k + τ₀. Thus, the variance for the unknown mean is ${\sigma }_p^2=1∕(n_k{\tau }_k+{\tau }_0)$. In other words, a cluster mean follows a distribution $\mathcal{N}({\mu }_p,{\sigma }_p^2)$. Furthermore, if we assume that the observations are measured with a fixed and known error of ${\sigma }_y^2$, then we can infer from the general case the PPD for a new observation in the kth cluster:

$$\begin{gathered} \tilde{y}\sim \mathcal{N}({\mu }_p,{\sigma }_p^2+{\sigma }_y^2), \\ =\mathcal{N}\left(\frac{{\stackrel{‒}{y}}_i{n}_k{\tau }_k+{\mu }_0{\tau }_0}{n_k{\tau }_k+{\tau }_0},\frac{1}{(n_k{\tau }_k+{\tau }_0)}+{\sigma }_y^2\right). \end{gathered}$$ (11)

Similar to the general case, the combined variance is the sum of the measurement error ${\sigma }_y^2$ and the variance around the unknown cluster mean, ${\sigma }_p^2$. Here we have assumed that the measurement error ${\sigma }_y^2$ is known and identical in each latent cluster, a crude but pragmatic approximation to make the example easier to follow. A catalog of posterior predictive distributions under various conjugacy can be found in Bernardo & Smith (2000). An electronic source can be conveniently located at https://enwikipedia.org/wiki/Conjugate_prior.

Prior Predictive Distribution.

A concept related to the PPD is the prior predictive distribution (Gelman et al., 2004, Chapter 1; Lee, 2012; Chapter 2; Novick & Jackson, 1974, p.142). Suppose a variable y follows a normal distribution with an unknown mean μ, and a fixed and known measurement error of ${\sigma }_y^2$. Additionally, μ follows a prior distribution with mean μ₀ and variance ${\sigma }_0^2$. The prior parameter μ₀, ${\sigma }_0^2$ and the uncertainty about the data, ${\sigma }_y^2$, are assumed known. Novic & Jackson (1974) show that the prior predictive distribution of $\tilde{y}$ follows a normal distribution with mean μ₀ and combined variance of ${\sigma }_0^2+{\sigma }_y^2$. In essence, the uncertainty about a future observation $\tilde{y}$ is the combined uncertainty about the cluster mean (${\sigma }_0^2$) and the residual uncertainty about the data around the cluster mean when it is known (${\sigma }_y^2$).

Before a new cluster is realized, its mean and precision is not defined. Thus, the likelihood of a newly observed ${\tilde{y}}_i$ arising from the prior has to be evaluated by the prior predictive distribution. We are now ready to weave together the two essential results: 1) the CRP to guide the cluster assignment; and 2) the prior and posterior predictive distributions to evaluate the probability of a single observation arising from the clusters. Next we combine the two to complete the DP mixture model.

Conditional Posterior Distribution of c_i.

The CRP assignment probabilities, when combined with the posterior and prior predictive distributions, turn Equation (10) into the following conditional posterior distributions for the indicators:

• clusters where n_−i,k > 0 :

$$\begin{gathered} p(c_i\mid {\mathit{c}}_{-i},{\mu }_k,{\tau }_k,\alpha )\propto p(c_i\mid {\mathit{c}}_{-i},\alpha )p({\tilde{y}}_i\mid {\mu }_k,{\tau }_k,{\mathit{c}}_{-i}) \\ \propto \frac{n_{-i,k}}{n-1+\alpha }\mathcal{N}\left({\tilde{y}}_i;\frac{{\stackrel{‒}{y}}_k{n}_k{\tau }_k+{\mu }_0{\tau }_0}{n_k{\tau }_k+{\tau }_0},\frac{1}{n_k{\tau }_k+{\tau }_0}+{\sigma }_y^2\right). \end{gathered}$$ (12)

• all other clusters combined :

$$\begin{gathered} p(c_i\ne c_k\forall j\ne i\mid {\mathit{c}}_{-i},{\mu }_0,{\tau }_0,\gamma ,\beta ,\alpha )\propto \\ p(c_i\ne c_k\forall j\ne i\mid {\mathit{c}}_{-i},\alpha )\int p({\tilde{y}}_i\mid {\mu }_k,{\tau }_k)p({\mu }_k,{\tau }_k\mid {\mu }_0,{\tau }_0,\gamma ,\beta )d{\mu }_{k}d{\tau }_k \\ \propto \frac{\alpha }{n-1+\alpha }\mathcal{N}({\tilde{y}}_i;{\mu }_0,{\sigma }_0^2+{\sigma }_y^2). \end{gathered}$$ (13)

Equation (12) incorporates the PPD of already occupied clusters. The density of a newly observed ${\tilde{y}}_i$ (i.e., last data entry to be categorized) is evaluated by the means and precisions of the corresponding PPDs. Equation (13) incorporates the prior predictive distribution into the creation of a new cluster as per CRP.

Equation (13) contains a seemingly intimidating integral. However, it can be divided into simpler components. First, p(μ_k, τ_k∣μ₀, τ₀, γ, β) represents values of cluster means and precision matrices that may arise from the priors. Next, with each realization of cluster parameters μ_k, τ_k, calculate the corresponding $p({\tilde{y}}_i\mid {\mu }_k,{\tau }_k)$, the probability of a newly observed $\tilde{y}$. This is repeated over all possible clusters arising from the priors. Finally, the integral sums the results over all possible realizations of clusters. This is also how the prior predictive distribution is formally defined (Gelman et al., 2003, section 1.3). This summing over all stochastic realizations of clusters is sometimes expressed in other tutorials (Neal, 2000; Rasmussen, 2000) as $\int \mathcal{N}({\tilde{y}}_i;\varphi )G_0(\varphi )d\varphi$, where ϕ = (μ_k, τ_k), is an abbreviated form of the same concept, where G₀(ϕ) represents a function of the prior distributions from which all cluster means and covariances may arise.

A more concrete example may help explain the equations. In Figure 3, when the 9th customer enters into the restaurant, he or she has a probability of sitting at the already occupied tables 1 – 4 proportional to a vector n_−i,j = (2, 4, 1, 1), respectively. Additionally, we need to consider how well the 9th customer fits the means of already occupied tables. If, for example, this customer is found nearest to table 2 (hypothetically, (y₁, y₂) = (1.3, −1.1), closest to μ₂ = (1.5, −1.5) in Figure 1), then it makes intuitive sense to assign him/her to table number 2. The proximity of this new customer to each of the already occupied tables is also a vector, evaluated by the PPDs given 8 previous observations as per Equation (12). The product of the two vectors is the probability of the 9th customer’s sitting at an already occupied table. However, as it turned out, the 9th customer is shown to be seated at a new table in Figure 3. That probability is governed by Equation (13), by a product of α/(n − 1 + α) and the prior predictive distribution. It is important to bear in mind that the CRP is a stochastic process so that a specific seating arrangement is a probabilistic realization of the DP. It is not fixed.

3.6. Relationship between DP, CRP, and DPMM

Equations (12) – (13) conclude the necessary derivations for the DPMM. We are ready to implement these results in a working computer program. However, this is a good point to explain the relationship between DP, CRP, and DPMM. The DP is described in the Introduction as a distribution over distributions because it extends an ordinary Dirichlet distribution with a fixed number of categories into infinitely many distributions with varying k categories (recall the steps between Equations (7) and (10)). The CRP can be understood as a distribution over partitions (how the sample is partitioned up), without incorporating the predictive distributions. And the DPMM is a mixture model that uses a DP prior to account for a theoretically infinite number of mixture components with the predictive distributions included (Equations (12) and (13)). Next they are implemented in a working computer program.

4. DPMM Algorithm

Algorithm 1 repeatedly samples the probability of cluster assignment one data entry at a time. It is equivalent to algorithm 3 in Neal (2000). The algorithm begins with the initial parameters and the maximum number of iterations. Then it enters a CRP-like process, in which y_i, the ith observation, is first removed from its cluster because a new value will be sampled in the current iteration. Next, Equations (12) – (13) are applied to calculate the probability of y_i belonging to one of the K + 1 clusters, with K + 1 denoting a newly created cluster. Note that the sampling algorithm is different from the usual Gibbs sampling because the sampling is done one data entry at a time. Also, a person can sit at a different CRP table from one iteration to the next. The algorithm ends when it reaches the maximum number of iterations. The cluster memberships over the iterations are returned. We can then calculate the posterior probability distribution of the ith observation belonging to clusters 1, … , k over the iterations. We may choose to use the cluster with the highest probability to represent the cluster membership for the ith observation. Note that lines 8 – 9 are based on Equaions (12) and lines 10 – 11 are based on Equation (13).

This raises a question. If, for example, an observation is assigned to cluster 2 on iteration 100 and then again on cluster 2 on iteration 800, is that really the same cluster? Generally, it is. Here is an intuitive explanation using the CRP metaphor. Because the CRP is applied to only one customer at a time, the other customers sitting at the same table offer stability over the table membership assignments. As more customers go through the CRP, tables with more customers tend to attract additional customers. Additionally, if a customer has a high posterior predictive probability of belonging to a specific group, and if there are already many customers in that group, then it is relatively unlikely for one single customer to be placed in a completely different group, conditional on all the other customers’ group membership assignments. Observations that are near the border of two overlapping clusters may switch between them across iterations. But cluster designations should still be stable. There are exceptions, of course. The CRP assignments may be unstable in the beginning, when only the first few customers are seated. The probability of being assigned to tables 1, 2, and 3 may be roughly comparable. The order of the table assignment can take on a different permutation and the overall probability distributions are not affected. These few initial observation may run into a problem that resembles the well-known label switching problem in Bayesian mixture models (Stephens, 2000; Jasra et al., 2005; Richardson & Green, 1997). However, this becomes less likely later on, when more customers go through the CRP. The PPDs offer additional stability. Obviously, a meager sample size aggravates the problem. Then the problem is really due to insufficient data and not an inherent limitation in the algorithm.

5. Implementation of DPMM Computation

5.1. R Program Line-by-Line

Appendix B shows how algorithm 1 can be implemented in R, modified from example 7 given by Broderick (2017). Variable names in the original program are changed to match our notation. The point of this exercise is to make the equations concrete and explicit. It also shows how computer programming complements methodology development. We will thus focus on the most sub-stantively important lines of code. Annotations added throughout this example should make the programming code easier to follow.

The first 28 lines cover the license information. Line 29 defines a function called crp_gibbs() and the input parameters it accepts. It accepts the raw data, the concentration parameter α, the prior mean and variance for the unknown cluster means (${\mu }_0,{\sigma }_0^2$), the measurement error variance (${\sigma }_y^2$, assumed fixed and known), initial cluster assignment, and the maximum number of iterations. The next line of substantive importance is line 63, where the CRP begins. Next on line 64, we begin the CRP one customer at a time, starting with the for(n in 1:N) loop. We next remove y_i from its cluster because we are going to draw a new sample of c_i for y_i. If this causes the table to become empty, then we replace the new empty cluster with the last cluster (lines 75 – 79) so that Nclust always points to already occupied tables and the next cluster (Nclus + 1) always points to the next new table to be created if necessary. These are described in the DPMM algorithm 1. The next line of substantive importance is line 89, where we calculate τ_p = (n_kτ_k + τ₀) as per Equation (11). We then inverse τ_p to get ${\sigma }_p^2$ to be used later.

Line 107 calculates the posterior means mean_p. Note that mean_p would be a vector of length 3 if Nclust contained 3 already occupied clusters. The posterior means are entered into lines 108 – 109 to calculate the CRP weights (log(n_k[c_i])) and multiply them by the log posterior predictive density using the dmvnorm() function with appropriate input parameters as per Equation (12). Logarithms make the computation easier because they turn multiplication into addition. Lines 116 – 117 calculate the probabilities for a newly created cluster as per Equation (13). Finally, line 124 draws a sample of which cluster this new customer should belong to, using the probabilities we just calculated. This customer can belong to any of the 1:(NClust+1) clusters. The remaining lines collect and return the results.

We can then use the next few lines to fit the model and find the Maximum A Posteriori (posterior mode) of the class membership estimates.

> library("MASS")     # mvrnorm() for multivariate normal
> set.seed(11)        # random seed set for reproducibility
> n <- 60              # sampling 60 each from 4 separate distributions
> m1 <- c(1.5, 1.5)   # upper right x, y means
> S1 <- matrix(c(0.3, 0.05, 0.05, 0.3), ncol = 2) # variance of c1
> # sampling n from each cluster as per its mean mu and variance Sigma
> clus1 <- mvrnorm(n = n, mu = m1, Sigma = S1)
> m2 <- c(1.5, −1.5)  # lower right
> S2 <- matrix(c(0.5, −0.08, −0.08, 0.2), ncol = 2)
> clus2 <- mvrnorm(n = n, mu = m2, Sigma = S2)
> m3 <- c(−1.5, 1.5)  # upper left
> S3 <- matrix(c(0.1, 0.03, 0.03, 0.1), ncol = 2)
> clus3 <- mvrnorm(n = n, mu = m3, Sigma = S3)
> m4 <- c(−1.5, −1.5) # lower left
> S4 <- matrix(c(0.8, 0.50, 0.50, 0.8), ncol = 2)
> clus4 <- mvrnorm(n = n, mu = m4, Sigma = S4)
> datc <- rbind(clus1, clus2, clus3, clus4) # 240 observations altogether
> # run the CRP Gibbs function in Appendix B.
> alpha <- 0.01
> mu0 <- matrix(rep(0, 2), ncol = 2, byrow = TRUE)
> sigma0 <- diag(2) * 3^2
> sigma_y <- diag(2) * 1
> c_init <- rep(1, nrow(datc))
> results <- crp_gibbs(data = datc, alpha = alpha, mu0 = mu0,
     sigma0 = sigma0, sigma_y = sigma_y, c_init = rep(1, nrow(datc)))
> #####
> # Gibbs sampling iterations are saved in ‘results’. Each row contains
> # the latent class membership distribution of one person over MCMC
> # iterations. A person is deemed a member of c=2 if, e.g., s/he
> # gets assigned most often to c2. So we tabulate the frequency
> # counts and whichever cluster with highest frequency is that
> # person’s latent class.
> #####
> tab <- apply( results, 1, FUN = function(x) {
     tab <- table(x)
     ans <- names(tab[which.max(tab)])
     return(ans)    } )
> table(tab)
tab
 1 2 3 4
76 39 65 60

Table 1 provides a side-by-side comparison between Equations (12) and (13) and the corresponding R commands. The last data entry is evaluated by the predictive distributions of the appropriate normal densities and weighted by the CRP assignment probabilities. The parameters for the appropriate predictive distributions are entered into the dmvnorm() function to obtain predictive log densities, which in turn are weighted by the CRP assignment probabilities to yield the multinomial probabilities of up to K + 1 clusters. Matrix multiplication (%*%) is used so that tau_y, a 2 by 2 matrix, conforms to the 2 by 1 matrix of sum_data to yield the correct x-y coordinates for the posterior cluster means. This is then left multiplied by sig_p, the inverse of τ_p = n_kτ_k + τ₀, which yields the same result as dividing by τ_p. The computation does not have to be implemented in R. Python programmers may use the numpy.random.normal() function and by setting input parameters loc = mean_p, scale = sig_p + sigma_y.

5.2. A Simulation Exercise

A beginner often learns a great deal more about how a model behaves by playing with its settings. Two input parameters, α and ${\sigma }_y^2$, play important roles in DPMM. We will investigate how they affect the clustering. Recall that the hypothetical data was constructed using 60 simulated observations each from four different multivariate normal distributions (totaling 240 data points). While this program has successfully recovered four different clusters without being instructed so, the differing membership sizes of each cluster indicate misclassifications. Misclassifications are due in part to the probabilistic nature of the algorithm. Other factors also play a role. For example, the value of α affects the probability of creating a new cluster. A larger value tends to encourage the creation of a new cluster. The measurement error in each cluster, ${\sigma }_y^2$, currently set to an identical 1.0 for all clusters, also affects the clustering (explained in section 3.5). Data points are more likely to be misclassified if they are more distant from the cluster centers than the prior variance and near the overlapping boundaries of the distributions. Although the current program is simple, it will be able to classify samples from distributions that are distinct and far part. Below we illustrate how a reader can try different settings to see how they affect the clustering. The most important idea to illustrate here is that the implementation is not prohibitively difficult. The resemblance between the R syntax and the mathematics also facilitates a fuller understanding of the theory.

Table 2 shows how the input values of parameters affect the CRP results. The next few lines loop over all combinations of α = (0.01, 1.00, 3.00, 5.00) and measurement error ${\sigma }_y^2$ = (0.50, 1.00, 1.50, 3.00) to examine how they affect the clustering.

> set.seed(11)
> alpha <- c(0.01, 1.00, 3.00, 5.00)
> sigma_y <- c(0.50, 1.00, 1.50, 3.00)
> for (i in 1:length(alpha))
+    for (j in 1:length(sigma_y))
+    {
+    results <- crp_gibbs(data = datc, alpha = alpha[i],
+         mu0 = matrix (rep (0, 2), ncol = 2, byrow = TRUE),
+         sigma0 = diag(2) * 3^2, sigma_y = diag(2) * sigma_y[j],
+         c_init = rep(1, nrow(datc)))
+    tab <- apply( results, 1, FUN = function(x)
+              { tab <- table(x)
+                ans <- names(tab[which.max(tab)])
+                return(ans) })
+    cat("alpha = ", alpha[i], "sigma_y = ", sigma_y[j], "\n")
+    print(table(tab))
+    }

The chosen values of input parameters offer a glimpse of how the algorithm behaves in real data analysis. The values of α are chosen so that we have a range of large and small values. An α = 1.0 is neutral in the creation of new clusters and thus may be a good default value. Larger α values tend to encourage the creation of new clusters.

The largest ${\sigma }_y^2=3.0$ is chosen because it is approximately the observed variance of the entire sample of 240 observations in the direction of either the x- or y-axis in Figure 1. It reflects a worst-case scenario in which the entire sample is presumed to fall within the inherent measurement error of 3.0—effectively treating the whole sample as one single cluster. It also implies that clusters cannot be distinguished unless (roughly speaking) they are separated by more than a measurement error or 3.0. Thus, the value of ${\sigma }_y^2$ can be thought of as the presumed precision in discovering discernible clusters. A ${\sigma }_y^2=1$ is approximately the variance of the cluster with the widest spread in Figure 1. The smallest measurement error of ${\sigma }_y^2=0.50$ is near the observed variances in the first two clusters in Figure 1, the middle-sized clusters. We are expressing an anticipated precision using the size of the middle-sized clusters as a guide. Here we use a crude by pragmatic visual inspection to guide the settings. However, an analyst should strive to use a reliable source to estimate the measurement error (e.g., the radioactive dating example in Lee, 2012, section 2.2).

Turning to Table 2, we begin by looking at the rightmost column. When ${\sigma }_y^2=3.0$ is set, we get only one cluster because that is what we instruct the model to do, regardless of the value of α. As we half the measurement error to 1.5, we begin to extract 3 to 4 clusters across different α values. However, misclassifications are common. If we set ${\sigma }_y^2=1.0$, then we get more consistent extraction of 4 clusters with fewer misclassifications across different α values. For ${\sigma }_y^2=0.50$ we tend to get five clusters. A closer inspection (not shown) indicates that some members of cluster 4 (widest spread) are grouped into a fifth cluster We observe skipped class memberships in c_i = 1, 3, 5, 6 when we set α = 5.00 and ${\sigma }_y^2=1.50$, likely due to a tendency to create up to 6 clusters during the iterations, but ultimately only 4 emerged in the end. Overall, Table 2 shows that the current implementation is sensitive to ${\sigma }_y^2$, and a ${\sigma }_y^2=1$ (near the observed variance in the cluster with visibly widest spread) appears to offer the most desirable result. An analyst may be able to use visual inspections or other observed, empirical characteristics in the clusters to guide the settings.

The following lines of code illustrate how we can obtain more information on the misclassifications. The variable c_true below contains the true class membership. Assuming that we set ${\sigma }_y^2=1$ and α = 1.0, we run the crp_gibbs() program and obtain the variable c_modal which contains the most likely cluster membership over the DP iterations. The apply() function takes the results (a matrix of 240 persons by 1000 iterations) and tabulates, one row at a time, each person’s most likely cluster membership assignment over 1000 iterations.

> set.seed(11)
> results <- crp_gibbs(data = datc, alpha = 1.0,
+   mu0 = matrix(rep(0, 2), ncol = 2, byrow = TRUE),
+   sigma0 = diag(2) * 3^2, sigma_y = diag(2) * 1.0,
+   c_init = rep(1, nrow(datc)))
> c_modal <- apply(results, 1, FUN = function(x)
    {
      tab <- table(x)
      ans <- names(tab[which.max(tab)])
      return(ans)
    } )
> c_true <- rep(1:4, each = 60)
> table(c_true, c_modal)
     c_modal
c_true  1  2  3  4
     1 60  0  0  0
     2  0 60  0  0
     3  0  0  0 60
     4  0  7 36 17

This cross-tabulation reminds us that: 1) the stochastic nature of the DP yields a distribution of c_modal that differs slightly from a previous solution done for Table 2; 2) the order of cluster carries no special importance, they are simply discrete labels (the true cluster 1, 2, 3, and 4 are labeled differently as 1, 2, 4, and 3); and 3) misclassifications occur in the 4th cluster (recall that cluster 4 is the lower left ellipsoid in Figure 1), in which 7 individuals are misclassified into cluster 2 (lower right in Figure 1) and 17 misclassified into cluster 3 (upper left). However, misclassifications in cluster 4 should not be surprising because of its high variability and its proximity to the neighboring clusters 2 and 3. Note the overlapping clusters 2 and 4 ellipsoids in Figure 1. For data points in the overlapping region, their cluster memberships are inherently uncertain. The point of this exercise is to show that overall distributions presented in Table 2 only provide limited information on how the DPMM program performs. It makes sense to break down the misclassifications to greater details.

5.3. Estimating Cluster Means and Covariances

Users of the DPMM may be interested in the cluster characteristics (e.g., means and covariances). Cluster means μ_k are straightforward to calculate using Equation (4). Cluster covariances are slightly more involved in part because Equation (5) only applies in the univariate normal. Fortunately, we can look up the formula for calculating a bivariate normal covariance (see Bernardo & Smith (2000) and https://en.wikipedia.org/wiki/Conjugate_prior).

The first 5 lines below carry out the necessary preparations for the prior means, the prior covariances and the prior precisions. Next, we use a for() loop to calculate the posterior means and covariances one cluster at a time. Note that we reuse some of the R code in Appendix B to calculate mean_p, the mean of the posterior distribution for the kth cluster, μ_k. Then we turn to the cluster covariance. According to the Wikipedia page above, if the prior covariance follows an inverse-Wishart distribution with v = 2 degrees of freedom and a scale matrix S₀ = σ₀, then the posterior inverse-Wishart distribution has n_k + v degrees of freedom and a posterior scale matrix of $S_0+{\sum }_{i=1}^{n_k}(y_i-{\mu }_k)(y_i-{\mu }_k{)}^T$. The ${\sum }_{i=1}^{n_k}(y_i-{\mu }_k)(y_i-{\mu }_k{)}^T$ term is the sum of squared deviations from the cluster mean, calculated by first taking the deviations (subtracting the mean from y₁ and y₂ with the sweep() function) so that they can be squared and summed using the crossprod() function. Furthermore, an inverse-Wishart distribution has a mean of $\frac{S_p}{{\nu }_p-p-1}$, where S_p, v_p are the scale matrix and degrees of freedom, respectively, and p = 2 because it is two-dimensional (bivariate) normal. Below we get S_p = ( sigma0 + crossprod(y_ss) ) and v_p = n_k[c_i] + 2, and the rest should be straightforward.

mu0     <- matrix(rep(0, 2), ncol = 2, byrow = TRUE)
sigma0  <- matrix(c(3, 1, 1, 3), ncol = 2)
sigma_y <- matrix(c(1, 0.2, 0.2, 1), ncol = 2)
tau0    <- solve(sigma0)     # inverse prior covariance
tau_y   <- solve(sigma_y)    # inverse measurement error
n_k <- table(c_modal)        # number of people in each cluster

for (c_i in 1:length(n_k))
  {
   tau_p <- tau0 + n_k[c_i] * tau_y      # R program line 89
   sig_p <- solve(tau_p)
   y <- datc[which(c_modal == names(n_k)[c_i]), ]
   sum_data <- colSums(y)                # R program line 95
   mean_p <- sig_p %*% (tau_y %*% sum_data + tau0 %*% t(mu0)) # 108
   y_ss <- sweep(y, MARGIN = 2, STATS = mean_p, FUN = "-")
   covariance <- ( sigma0 + crossprod(y_ss) ) / (n_k[c_i]+2−2−1)
   cat("\n cluster ", names(n_k)[c_i], "\n")
   print(round(mean_p, 3))
   print(round(covariance, 3))
  }

The results (available by running the code) are crude but reasonably close to the true parameter values in Figure 1, considering the short and accessible computer program. Accuracy may be enhanced with a greater number of iterations, or in a later version of the comput program to include, for example, a step to update the measurement error σ_y which is currently fixed. Other steps may be included. We can add these lines of code into Appendix B and have the parameter values returned. However, doing so not only adds complexity in the programming code, it may slow down the program considerably because of the additional computation and memory storage. That of course does not prohibit a reader from modifying the code and settings to see how they affect the results. In fact, we encourage tinkering with the computer program—arguably the best way to learn any computation algorithm.

6. Discussion

This tutorial aims to cover four themes: 1) rigorous derivations of the Dirichlet Process prior; 2) link the DP to the Chinese Restaurant Process construction method; 3) a hypothetical example on how the DP can be implemented in a bivariate mixture model; and 4) a simple simulation study to show readers the characteristics of the DP. Below we discuss the extent to which these aims have been achieved and if not, what a reader can do to remedy the limitations.

A complex and technical topic is inherently difficult to make accessible. An internet search of “Bayesian nonparametric” produces numerous tutorials, videos, web pages and blogs on this topic. This literature is so large that they are overwhelming and possibly paralyzing for a beginner who wishes to learn the DP prior. Where can he/she begin? Tutorials that cater to novices tend to focus primarily on an intuitive introduction, using visual explanations similar to our Figure 3. The statistical rigor is kept at a level of sophistication similar to our Equation (10), often with intermediate derivations omitted. Important concepts such as the exchangeability property are explained. However, there is usually limited discussion on how a beginner can extend these topics to novel models. We need a deeper understanding of BNP, e.g., Equations (12) – (13) with detailed explanations on how to put these concepts into practice. Some introductions go beyond these elementary explanations as an attempt to fill the first gap in the literature. More advanced expositions (e.g., Neal (2000); Rasmussen (2000); Broderick (2017); Gershman & Blei (2012)) cover these. They help readers penetrate the statistical rigor step by step. However, many critical derivations are either omitted, not explained in sufficient detail, or simply assumed understood. This is another important gap, and perhaps a barrier particularly difficult to overcome for behavioral scientists. There are other, still more challenging introductions that invoke Measure Theory (Teh, 2017; Orbanz & Teh, 2011; Jara, 2017; Müller et al., 2015; Hjort et al., 2012; Ghoshal & van der Vaart, 2015), which may be impenetrable for non-technicians.

This tutorial helps to fill all these gaps. Statistical rigor is gradually escalated step by step and aided by visual explanations. Elementary concepts are given statistical rigor, particularly on the recovered derivations in Appendix A. Some of the derivations may appear intimidating at first, such as the integration over the Dirichlet density in Equation (A.6). However, they are not impenetrable after all. We show that it is not necessary to labor through an integration. These derivations provide a thorough explanation of the CRP metaphor. A beginner may be able to go beyond the basics by knowing how the equations are derived and how they are implemented in a computer program. We hope that we have achieved aims 1 and 2 to the readers’ satisfaction. For technical experts, our detailed derivations and explanations may seem superfluous and possibly pedantic. However, we hope they agree with us that such a tutorial is useful in addressing gaps in the literature.

A deeper understanding may also help readers better appreciate other tutorials. For instance, a beginner who first read the Austerweil et al. (2015) chapter may not fully understand their definition of Bayesian nonparametrics. BNP is viewed from a general statistical perspective, where “nonparametric” refers to models not being restricted to some fixed parametric class (e.g., a finite mixture of normals). This tutorial shows that BNP extends a finite mixture model to a theoretically infinite number of parameters. A finite set of parameters may emerge as a result of applying BNP to a specific dataset, giving the property that a BNP model grows in complexity as data accrue.

Aim 3 is addressed through explaining the R program (Broderick, 2017) line by line. In so doing we connect the equations with the corresponding computation algorithm and apply the program to recover the known clusters of the hypothetical data in Figure 1. Programming forces the learner to be crystal clear because all steps must be clearly spelled out precisely and explicitly. We recognize the slight complication in the CRP. A cluster may become empty as the simulation proceeds. Steps must be taken to account for this. This exercise offers a critical insight in BNP by way of the DP prior. It is noteworthy that novel methods can be developed from only two essential ingredients: 1) the CRP seating probabilities in Equations (12) - (13); and 2) the prior and posterior predictive distributions according to the model. BNP is not as insurmountable as it first appears. Of course, a fully-fledged computation tool requires intensive work. Our Aim 3 has not provided a fully-fledged tool. However, we hope that readers are encouraged by seeing the example R program—a program can begin to take shape fairly easily. The required skills are not substantially more complicated than writing loops and calling stock functions to sample from conjugate distributions. Equipped with this insight (only two ingredients are needed), an advanced graduate student in quantitative psychology may be able to extend a simple program to a full solution, or to extend it to an entirely new clustering technique.

We are aware of the availability of several powerful computation tools for DP (Jara et al., 2011; Pedregosa et al., 2011; Eisentein, 2012; Christensen et al., 2011). A researcher who only wants a quick solution needs not bother with writing the Gibbs sampling code. However, we believe that the programming exercise facilitates a deeper understanding of BNP in general. This tutorial does not offer any methodological novelty. Another limitation is that we do not examine the known difficulties in the conjugate inverse-Wishart distribution for the covariance matrix (Gelman et al., 2003, section 19.2). Interested readers may find an alternative in Lewandowski et al. (2009). These limitations notwithstanding, we fill important gaps in the literature that limit the wider acceptance of BNP methods in behavioral sciences. We hope that students and their professors will find our pedagogy helpful in their research and teaching, especially in making complex concepts such as DPMM more accessible to methodologists in training. They may be able to extend the basic skills and a deep understanding into the development of new methods.

The DP mixture model is but an example of a large class of flexible BNP methods. This tutorial offers behavioral scientists entry into BNP by laying down the knowledge and mathematical derivations that make BNP possible to account for individual differences.

Highlights.

• Mathematical derivations essential to the development of Dirichlet Process are provided.

• An accessible pedagogy for complex and abstract mathematics in DP modeling.

• A publicly accessible computer program in R is explained line-by-line.

• Psychotherapy for patients with advanced cancer works differently depending on the psychosocial profiles identified by a DP mixture model.

Appendix A. Derivation of Technical Details

This Appendix summarizes the mathematical derivations of essential equations in DPMM, derivations that are typically omitted in other tutorials. The overall plan is to supplement the main text with details. We show that the DP can be explained rigorously using basic Bayesian statistics found in introductory texts. We work around Measure Theory, which tends to elude beginners. The hope is that a graduate student in a quantitative field in psychology may use this tutorial to first gain a clear understanding of the DP before tackling the mainstream literature using Measure Theory,

This appendix is divided into 4 subsections. We first describe the data likelihood function in Gaussian mixtures because it will be used to prove other equations. Then we provide detailed derivations to prove all the essential equations, starting with the posterior distribution of the cluster means (Appendix A.2). Following the flow of the main text, we next explain other equations one by one. We address the posterio precisions (Appendix A.3) and other details. We end with the latent cluster membership indicators in the Chinese Restaurant Process (Appendix A.4).

Appendix A.1. Data likelihood function in Gaussian mixtures

The probability density of the normal distribution is a function of its mean μ and standard deviation σ:

$$\frac{1}{\sqrt{2\pi {\sigma }^2}}\text{exp}\left(-\frac{y_i-\mu }{2{\sigma }^2}\right),$$

when multiplied across independent observations nested within each latent cluster, we get the data likelihood function:

$$l(\mathit{y}\mid {\mu }_k,{\sigma }_k^2)\propto \frac{1}{(\sqrt{{\sigma }^2}{)}^{n_k}}\text{exp}\left(-\frac{{\sum }_{i=1}^{n_k}(y_i-{\mu }_k{)}^2}{2{\sigma }_k^2}\right),$$

where, if the standard deviations are swapped with precisions by τ_k = 1/σ², then we get

$$l(\mathit{y}\mid {\mu }_k,{\tau }_k)\propto {\tau }^{n_k∕2}\text{exp}\left(-\frac{{\tau }_k{\sum }_{i=1}^{n_k}(y_i-{\mu }_k{)}^2}{2}\right).$$ (A.1)

This data likelihood function by cluster precisions is used throughout this section to update the priors of other parameters. Note that the notation above is based on the univariate Gaussian density because it is much simpler to work with. However, the same applies in the multivariate Gaussian density.

Appendix A.2. Posterior density for the cluster means μ_k

The data likelihood in Equation (A.1), when combined with the Gaussian prior for the latent cluster means, $\mathcal{N}({\mu }_0,{\tau }_0)$, yields the posterior distribution for the means μ_k.

$$\begin{gathered} p({\mu }_k\mid \mathit{y})\propto p(\mathit{y}\mid {\mu }_k)p({\mu }_k) \\ \propto \text{exp}\left(-\frac{{\tau }_k{\sum }_{i=1}^{n_k}(y_i-{\mu }_k{)}^2}{2}\right)\times \text{exp}(-\frac{{\tau }_0({\mu }_k-{\mu }_0{)}^2}{2}), \end{gathered}$$ (A.2)

where the first term is the data likelihood evaluated at the kth cluster mean and precision. The second term is the probability of μ_k evaluated at the prior. Note that

$$\begin{gathered} \sum _1^n(y_i-{\mu }_k{)}^2=\sum _1^n(y_i-\stackrel{‒}{y}+\stackrel{‒}{y}-{\mu }_k{)}^2=\sum _1^n(y_i-\stackrel{‒}{y}{)}^2+n(\stackrel{‒}{y}-{\mu }_k{)}^2 \\ \text{because}2(\stackrel{‒}{y}-{\mu }_k)\sum _1^n(y_i-\stackrel{‒}{y})=0, \end{gathered}$$

thus Equation (A.2) becomes (the subscript _k removed to make the equations easier to follow):

$$\begin{gathered} p(\mu \mid \mathit{y}) \\ \propto \text{exp}\left(-\frac{1}{2}[\tau (\sum _i^n(y-\stackrel{‒}{y}{)}^2+n(\stackrel{‒}{y}-\mu {)}^2)+{\tau }_0({\mu }^2-2{\mu }_0\mu +{\mu }_0^2)]\right) \\ \propto \text{exp}\left(-\frac{1}{2}[\tau n({\stackrel{‒}{y}}^2-2\stackrel{‒}{y}\mu +{\mu }^2)+{\tau }_0({\mu }^2-2{\mu }_0\mu )]\right) \\ \propto \text{exp}\left(-\frac{1}{2}[-2\tau n\stackrel{‒}{y}\mu +\tau n{\mu }^2+{\tau }_0{\mu }^2-2{\tau }_0{\mu }_0\mu ]\right) \\ \propto \text{exp}\left(-\frac{1}{2}[{\mu }^2(\tau n+{\tau }_0)]-\mu (2\tau n\stackrel{‒}{y}+2{\tau }_0{\mu }_0)\right) \\ \propto \text{exp}\left(-\frac{1}{2}[{\mu }^2(\tau n+{\tau }_0)+\mu (\tau n\stackrel{‒}{y}+{\tau }_0{\mu }_0)\right). \end{gathered}$$ (A.3)

If we call the posterior mean and precision μ_p and τ_p, respectively, and write

$$\begin{gathered} {\tau }_p=\tau n+{\tau }_0 \\ {\mu }_p=\frac{1}{{\tau }_p}(\tau n\stackrel{‒}{y}+{\tau }_0{\mu }_0), \end{gathered}$$ (A.4)

and we plug these back into the last line of Equation (A.3), we get

$$p(\mu \mid \mathit{y})\propto \text{exp}(-\frac{1}{2}{\mu }^2{\tau }_p+\mu {\mu }_p{\tau }_p).$$

Adding to the exponent $-\frac{1}{2}{\mu }_p^2{\tau }_p$, which is a constant as far as μ is concerned, we see that

$$p(\mu \mid \mathit{y})\propto \text{exp}(-\frac{1}{2}{\mu }^2{\tau }_p-\frac{1}{2}{\mu }_p^2{\tau }_p+\mu {\mu }_p{\tau }_p).$$

Rearranging the terms, the exponent is now

$$\text{exp}(-\frac{1}{2}({\mu }^2-2\mu {\mu }_p+{\mu }_p^2){\tau }_p),$$

thus

$$p(\mu \mid \mathit{y})\propto \text{exp}(-\frac{1}{2}(\mu -{\mu }_p{)}^2{\tau }_p).$$

Therefore, the posterior distribution for the cluster means is a Gaussian distribution with the updated mean and precision in Equation (A.4). Importantly, these parameters are exactly the ones shown earlier in Equation (4).

We have the familiar form of posterior precision equals prior precision plus data precision and the posterior mean equals the weighted average of prior mean and the data mean (Gelman et al., 2003, section 2.6).

Appendix A.3. Posterior density for the cluster precisions τ_k

The cluster precisions are given Gamma priors with the common shape parameter γ and rate parameter β, $p({\tau }_k\mid \gamma ,\beta )=\mathcal{G}(\gamma ,\beta )\propto {\tau }_k^{\gamma -1}\text{exp}(-\beta \tau )$. The data likelihood in Equation (A.1) is combined to get

$$\begin{gathered} p({\tau }_k\mid \mu ,\mathit{y},\gamma ,\beta )\propto {\tau }_k^{\gamma -1}\text{exp}(-\beta {\tau }_k)\times {\tau }_k^{n_k∕2}\text{exp}\left(-\frac{{\tau }_k{\sum }_{i=1}^{n_k}(y_i-{\mu }_k{)}^2}{2}\right) \\ ={\tau }_k^{\gamma +n_k∕2-1}\text{exp}\left(-{\tau }_k\left(\beta +\frac{{\sum }_{i=1}^{n_k}(y_i-{\mu }_k{)}^2}{2}\right)\right). \end{gathered}$$ (A.5)

Thus, with the data likelihood incorporated, the cluster precisions follow a Gamma posterior distribution with a shape parameters γ + n_k/2 and a rate parameter $\beta +\frac{{\sum }_{i=1}^{n_k}(y_i-{\mu }_k{)}^2}{2}$.

Appendix A.4. Posterior density for latent clusters

Here we work out the omitted derivations in Equation (7), which begins by integrating the mixing proportions π_k out:

$$\begin{gathered} p(c_1,\dots ,c_k\mid \alpha )=\int p(c_1,\dots ,c_k\mid {\pi }_1,\dots ,{\pi }_k)p({\pi }_1,\dots ,{\pi }_k)d{\pi }_1\cdots d{\pi }_k \\ =\int \underset{\text{Eq}.6}{\underbrace{\prod _{k=1}^K{\pi }_k^{n_k}}}\underset{\text{Eq}.3}{\underbrace{\frac{\Gamma (\alpha )}{\Gamma (\alpha ∕K{)}^k}\prod _{k=1}^K{\pi }_k^{\alpha ∕K-1}}}d{\pi }_1\cdots d{\pi }_k \\ =\frac{\Gamma (\alpha )}{\Gamma (\alpha ∕K{)}^k}\int \prod _{k=1}^K{\pi }_k^{n_k+\alpha ∕K-1}d{\pi }_1\cdots {\pi }_k, \end{gathered}$$ (A.6)

where the two product terms ${\prod }_{k=1}^K{\pi }_k^{n_k}$ and ${\prod }_{k=1}^K{\pi }_k^{\alpha ∕K-1}$ are combined into one with the exponents of π_k simply added together; $\frac{\Gamma (\alpha )}{\Gamma (\alpha ∕K{)}^k}$ is a constant and thus placed outside the integral (because it does not involve π_k). However, $\int \prod _{k=1}^K{\pi }_k^{n_k+\alpha ∕K-1}d{\pi }_1\cdots d{\pi }_k$ is difficult to integrate because it involves the product of K terms. But notice how it resembles the Dirichlet density. If we add a constant before it so that it becomes

$$\frac{\Gamma \left({\sum }_{k=1}^K(n_k+\alpha ∕K)\right)}{{\prod }_{k=1}^K\Gamma (n_k+\alpha ∕K)}\prod _{k=1}^K{\pi }_k^{n_k+\alpha ∕K-1},$$

then this new formula is precisely the density of a Dirichlet distribution with parameters n_k + α/K.

If we integrate this Dirichlet density over π_k,

$$\int \frac{\Gamma \left({\sum }_{k=1}^K(n_k+\alpha ∕K)\right)}{{\prod }_{k=1}^K\Gamma (n_k+\alpha ∕K)}\prod _{k=1}^K{\pi }_k^{n_k+\alpha ∕K-1}d{\pi }_1\cdots d{\pi }_k,$$

we know that it integrates to exactly 1 because of a basic fact that a proper probability density must integrate to 1. Thus,

$$\frac{\Gamma \left({\sum }_{k=1}^K(n_k+\alpha ∕K)\right)}{{\prod }_{k=1}^K\Gamma (n_k+\alpha ∕K)}\int \prod _{k=1}^K{\pi }_k^{n_k+\alpha ∕K-1}d{\pi }_1\cdots d{\pi }_k=1.$$

Notice that the formula above can be divided into two pieces, a constant term $\frac{\Gamma \left({\sum }_{k=1}^K(n_k+\alpha ∕K)\right)}{{\prod }_{k=1}^K\Gamma (n_k+\alpha ∕K)}$ and an integral $\int \prod _{k=1}^K{\pi }_k^{n_k+\alpha ∕K-1}d{\pi }_1\cdots d{\pi }_k$. Because they give you exactly 1 when multiplied together, the latter term must be the reciprocal of the former. Thus,

$$\int \prod _{k=1}^K{\pi }_k^{n_k+\alpha ∕K-1}d{\pi }_1\cdots d{\pi }_k=\frac{{\prod }_{k=1}^K\Gamma (n_k+\alpha ∕K)}{\Gamma \left({\sum }_{k=1}^K(n_k+\alpha ∕K)\right)}.$$

We have avoided a complicated integration entirely. Plugging this back into Equation (A.6), we get

$$\begin{gathered} p(c_1,\dots ,c_k\mid \alpha )=\frac{\Gamma (\alpha )}{\Gamma (\alpha ∕K{)}^k}\int \prod _{k=1}^K{\pi }_k^{n_k+\alpha ∕K-1}d{\pi }_1\cdots d{\pi }_k \\ =\frac{\Gamma (\alpha )}{\Gamma (\alpha ∕K{)}^k}\frac{{\prod }_{k=1}^K\Gamma (n_k+\alpha ∕K)}{\Gamma \left({\sum }_{k=1}^K(n_k+\alpha ∕K)\right)},\text{and because} \\ \Gamma (\alpha ∕K{)}^k=\prod _{k=1}^K\Gamma (\alpha ∕K),\text{and also} \\ \Gamma \left(\sum _{k=1}^K(n_k+\alpha ∕K)\right)=\Gamma (n+\alpha ),\text{we get} \\ p(c_1,\dots ,c_k\mid \alpha )=\frac{\Gamma (\alpha )}{\Gamma (n+\alpha )}\prod _{k=1}^K\frac{\Gamma (n_k+\alpha ∕K)}{\Gamma (\alpha ∕K)}, \end{gathered}$$ (A.7)

which is exactly Equation (7). Note that $\Gamma \left({\sum }_{k=1}^K(n_k+\alpha ∕K)\right)=\Gamma (n+\alpha )$ because individual cluster sizes, n_k, add up to the total number of data points n. Also, summing individual α/K over K simply yields α.

Now we turn to Equation (8) to work out the omitted derivations. We need the probability of latent cluster membership for the ith person given that the latent class memberships of all others are fixed and known. This goes back to the CRP metaphor, in which all previous i − 1 customers have been seated, and then the ith customer enters the restaurant and needs a table. This customer can either sit at an already occupied table, or at a new table. The equation below prescribes how a customer should be assigned to an already occupied table k.

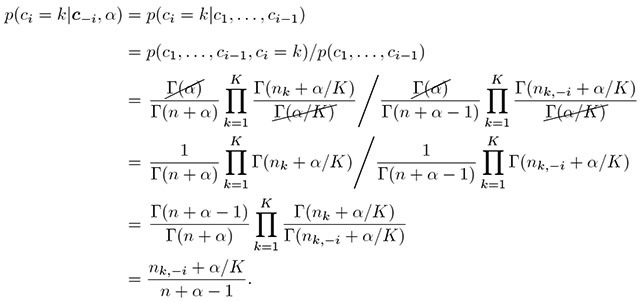(A.8)

Identical terms cancel each other out in the second line, and after rearranging the terms, we get the last line. It is based on the recurrence property of the Gamma function, Γ(x + 1) = x Γ(x), so that

$$\prod _{k=1}^K\frac{\Gamma (n_k+\alpha ∕K)}{\Gamma (n_{k,-i}+\alpha ∕K)}=\frac{(n_{k,-i}+\alpha ∕K)\Gamma (n_{k,-i}+\alpha ∕K)}{\Gamma (n_{k,-i}+\alpha ∕K)}=\frac{n_{k,-i}+\alpha ∕K}{1}.$$

A more intuitive explanation is that because Γ(x) = (x − 1)! so that

$$\Gamma (n+\alpha -1)∕\Gamma (n+\alpha )=(n+\alpha -2)!∕(n+\alpha -1)!=\frac{1}{n+\alpha -1}.$$

By working out the complex terms in a seemingly impenetrable equation, a simple pattern emerges in Equation (A.8)—the probability of the ith customer sitting at table k is influenced primarily by n_k,−i, the number of other customers alreay sitting in each of the kth table.

Appendix B. R Code

  1 #
  2 # Dirichlet Process Mixture Model example.
  3 # Last modified on Apr 19, 2018 by Yuelin Li from an example given by
  4 # Tamara Broderick, whose original source code is available at:
  5 # https://raw.githubusercontent.com/tbroderick/bnp_tutorial
  6 #      /2016mlss/ex7_sampler.R
  7 ###### Below are headers in the original source code file ######
  8 # A Gibbs sampler for a CRP Gaussian mixture model
  9 # Algorithm 3 in Neal 2000
 10 # Copyright (C) 2015, Tamara Broderick
 11 # www.tamarabroderick.com
 12 #
 13 # This program is free software: you can redistribute it and/or modify
 14 # it under the terms of the GNU General Public License as published by
 15 # the Free Software Foundation, either version 3 of the License, or
 16 # (at your option) any later version.
 17 #
 18 # This program is distributed in the hope that it will be useful,
 19 # but WITHOUT ANY WARRANTY; without even the implied warranty of
 20 # MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
 21 # GNU General Public License for more details.
 22 #
 23 # You should have received a copy of the GNU General Public License
 24 # along with this program. If not, see <-ttp://www.gnu.org/licenses/>.
 25 # useful for working with multivariate normal distributions
 26 #
 27 ##### Below are modified by YL. Variable names are changed from
 28 # the original to match the best we can the notation in the tutorial.
 29 crp_gibbs <- function(data,alpha=0.01,mu0,sigma0,sigma_y,c_init,maxIters=1000)
 30 {
 31 # data: an N by D matrix of data points
 32 # A small alpha encourages fewer clusters
 33 #    alpha <- 0.01
 34 # sigma_y: measurement error of data y, assumed known, same for all clusters.
 35 #    sigma_y <- diag(data_dim) * 1
 36 # mu0, sigma0: prior mean and variance around unknown mean mu
 37 #    mu0 <- matrix(rep(0, data_dim), ncol = data_dim, byrow = TRUE)
 38 #    sigma0 <- diag(data_dim) * 3^2
 39 # c_init: initial assignments of data points to clusters
 40 #
 41 require(mvtnorm)
 42 # dimension of the data points
 43 data_dim <- ncol(data)
 44 # number of data points
 45 N <- nrow(data)
 46 #####
 47 # Priors
 48 #####
 49 # prior precision on the unknown mean mu.
 50 tau0 <- solve(sigma0) # prior precision on $mu$, inverse of prior covariance
 51 # cluster-specific precision, assumed known, all clusters are assumed to
 52 # share identical measurement error of y ~ N(mu, sigma_y).
 53 tau_y <- solve(sigma_y)
 54 # initialize the CRP Gibbs sampler
 55 z <- c_init # initial cluster membership assignments
 56 n_k <- as.vector(table(z)) # initial data counts at each cluster, Eq (4).
 57 Nclust <- length(n_k) # initial number of clusters
 58 ##
 59 # Chinese Restaurant Process (CRP) Gibbs sampler begins
 60 ##
 61 res <- matrix(NA, nrow = N, ncol = maxIters) # cluster membership storage
 62 pb <- txtProgressBar(min = 0, max = maxIters, style = 3)
 63 for(iter in 1:maxIters) { # maxIters also prevents endless loops
 64 for(n in 1:N) { # one data point (customer) at a time
 65 # when nth customer enters the Chinese restaurant, we need to first
 66 # un-assign his/her initial cluster membership, then use Eq (12)
 67 # [already occupied table] and (13) [new table] to calculate the
 68 # updated probability of table assignment.
 69 c_i <- z[n] # what is the nth persons table assignment?
 70 n_k[c_i] <- n_k[c_i] - 1 # remove the nth person from table
 71 # if the table becomes empty when the nth person is removed,
 72 # then that table/cluster is removed.
 73 if( n_k[c_i] == 0 )
 74 {
 75   n_k[c_i] <- n_k[Nclust]  # last cluster to replace this empty cluster
 76   loc_z <- ( z == Nclust ) # who are in the last cluster?
 77   z[loc_z] <- c_i          # move them up to fill just emptied cluster
 78   n_k <- n_k[ -Nclust ]    # take out the last cluster, now empty
 79   Nclust <- Nclust - 1     # decrease total number of clusters by 1
 80 }
 81 z[n] <- −1 # ensures z[n] doesnt get counted as a cluster #####
 82 ##
 83 # Now we are ready to update table assignment by Eqs (12) and (13).
 84 ##
 85 # log probabilities for the clusters, add previously unoccupied table
 86 logp <- rep( NA, Nclust + 1 )
 87 # loop over already occupied tables 1:J and calculate pr as per Eq (13).
 88 for( c_i in 1:Nclust ) {
 89   tau_p <- tau0 + n_k[c_i] * tau_y # cluster precision as per Eq (4)
 90   sig_p <- solve(tau_p) # cluster variance, inverse of tau_c
 91   # find all of the points in this cluster
 92   loc_z <- which(z == c_i)
 93   # sum all the points in this cluster
 94   if(length(loc_z) > 1) {
 95     sum_data <- colSums(data[z == c_i, ]) }
 96   else {
 97     sum_data <- data[z == c_i, ]
 98   }
 99 #
100 # We need to use the predictive distribution of each already
101 # occupied table to predict the next customer sitting there.
102 #
103 # Use Eq (4) to find the conditional posterior distribution for
104 # the cluster means, (y * n_k * tau_j + mu0 * s0) /tau_p,and
105 # then use the predictive distribution of y_j in Eq (11) to
106 # predict new data value c_i from c-i.
107 #
108 mean_p <- sig_p %*% (tau_y %*% sum_data + tau0 %*% t(mu0))
109 logp[c_i] <- log(n_k[c_i]) +
110 dmvnorm(data[n,], mean = mean_p, sigma = sig_p + sigma_y, log = TRUE) }
111 #
112 # We are done looping over already occupied tables. Next, we use
113 # Eq (12) to calcualte the log probability of a previously
114 # unoccupied, 'new' table. Essentially,it is the prior predicitive
115 # distribution of the DP.
116 #
117 logp[ Nclust+1 ] <- log(alpha) +
118     dmvnorm(data[n,], mean = mu0, sigma = sigma0 + sigma_y, log = TRUE)
119 # transform unnormalized log probabilities into probabilities
120 max_logp <- max(logp)
121 logp <- logp - max_logp
122 loc_probs <- exp(logp)
123 loc_probs <- loc_probs / sum(loc_probs)
124 # draw a sample of which cluster this new customer should belong to
125 newz <- sample(1:(Nclust+1), 1, replace = TRUE, prob = loc_probs)
126 # spawn a new cluster if necessary
127 if(newz == Nclust + 1) {
128   n_k <- c(n_k, 0)
129   Nclust <- Nclust + 1
130   }
131 z[n] <- newz
132 n_k[newz] <- n_k[newz] + 1 # update the cluster n_k
133 }
134 setTxtProgressBar(pb, iter) # update text progress bar after each iter
135 res[, iter] <- z     # cluster membership of N observations
136 }
137 close(pb)            # close text progress bar
138 invisible(res)       # return results, N by maxIters matrix
139 }