Brain connectivity-informed regularization methods for regression

Abstract

One of the challenging problems in brain imaging research is a principled incorporation of information from different imaging modalities. Frequently, each modality is analyzed separately using, for instance, dimensionality reduction techniques, which result in a loss of mutual information. We propose a novel regularization-method to estimate the association between the brain structure features and a scalar outcome within the linear regression framework. Our regularization technique provides a principled approach to use external information from the structural brain connectivity and inform the estimation of the regression coefficients. Our proposal extends the classical Tikhonov regularization framework by defining a penalty term based on the structural connectivity-derived Laplacian matrix. Here, we address both theoretical and computational issues. The approach is first illustrated using simulated data and compared with other penalized regression methods. We then apply our regularization method to study the associations between the alcoholism phenotypes and brain cortical thickness using a diffusion imaging derived measure of structural connectivity. Using the proposed methodology in 148 young male subjects with a risk for alcoholism, we found a negative associations between cortical thickness and drinks per drinking day in bilateral caudal anterior cingulate cortex, left lateral OFC and left precentral gyrus.

1 Introduction

In vivo brain imaging studies typically collect multiple imaging data types, but most often the analysis is done for each data type separately, which does not adequately take into account the brain’s complexity. Statistical methods that simultaneously utilize and combine multiple data types can provide a more holistic view of brain (dys) function. We propose a novel statistical methodology that combines imaging data to derive a more complete picture of disease markers. In particular, we rigorously model associations between scalar phenotypes and imaging data measures while incorporating prior scientific knowledge. Specifically, we incorporate structural connectivity measures to model the association between the brain’s cortical thickness and alcoholism-related phenotypes. However, our methodology is more general and applicable to a variety of continuous outcomes and connectivity measures.

We work with a linear regression model where the scalar outcome for each subject i, y_i (vector of outcomes y) is modeled as a linear combination of covariates x₁,…, x_m (matrix of covariates, X) whose contribution is not penalized and predictors z₁,…, z_p (matrix of predictors, Z) whose contribution is penalized. Optimization problem for the parameter estimation can be written as

$$\underset{\beta ,b}{\text{argmin}}\left\{{\Vert \mathbf{y}-X\beta -Zb\Vert }_2^2+\lambda b^{\top }Qb\right\},$$ (1.1)

where the estimates of β and b are the best linear unbiased estimators (BLUE) and the best linear unbiased predictors (BLUP), respectively; Q incorporates the penalization information and λ is regularization parameter.

The general idea of incorporating structural information into regularized methods is well established (see e.g. Bertero and Boccacci (1998), Engl et al (2000), Phillips (1962)). Such information is provided by a matrix that is inserted into the penalty term and constructed depending on the application. Among the most commonly used matrices are the second–difference matrices, which impose smoothness on the estimates (Huang et al 2008). Hastie et al (1995) note that under the situation with many highly correlated predictors it is “efficient and sometimes essential to impose a spatial smoothness constraint on the coefficients, both for improved prediction performance and interpretability.” A more general approach to the problem is to assume that the modified penalty should take into account some presumed structure (a priori association) in the signal (Tibshirani and Taylor 2011; Slawski et al 2010). Such presumed structure can be represented mathematically in terms of an adjacency matrix, which shows strength of connections between variables (corresponding to nodes of the graph), and is reflected in the penalty term via a Laplacian (Chung 2005). This procedure constitutes the basis for approaches presented by Li and Li (2008) and Randolph et al (2012).

Prior information represented by a matrix Q may be incorporated into a regression framework using various types of penalty terms. Tikhonov regression (Tikhonov 1963) and PEER (Partially Empirical Eigenvectors for Regression) (Randolph et al 2012), employ the penalty of the form λb^TQb, with a symmetric semipositive definite matrix Q. The choice Q = I results in an ordinary ridge regression, which is the most commonly used method of regularization of the ill–posed problems. The connection of this type of penalty with ℓ₁ norm was analyzed by Li and Li (2008) and Slawski et al (2010). The penalized version of a linear discriminant analysis (LDA) was considered by Hastie et al (1995), while Tibshirani and Taylor (2011) proposed the ℓ₁ norm imposed on the matrix Q times the coefficient vector. In each of these, different choices of Q give rise to a variety of well–known models, including the fused lasso (Tibshirani et al 2005).

The natural problem that arises when applying penalized methods is the selection of a regularization parameter. Standard techniques to address this issue include the L–curve criterion and either cross-validation (CV) or generalized cross-validation (GCV) (see Craven and Wahba (1979), Hansen (1998), Brezinski et al (2003)). In Randolph et al (2012), authors take an advantage of the equivalence between the considered optimization problem and the Restricted Maximum Likelihood (REML) estimation (Ruppert et al 2003; Maldonado 2009) in the linear mixed model (LMM) framework. GCV and REML proceed by optimizing function of λ. According to experiments performed by P. T. Reiss (2009), GCV more likely finds a local, rather than global, optimum of this function as compared to REML. Better performance of REML was also confirmed in simulations performed in this work and, consequently, the equivalence with LMM was chosen as a technique for selection of regularization parameters in our proposal.

The linear mixed model equivalence with the penalized problem of Tikhonov type, with penalty λb^TQb, leads to the assumption that the prior distribution of b is of the form $\mathcal{N}(0,{\mathrm{\sigma }}_b^2{Q}^{-1})$, for some ${\mathrm{\sigma }}_b^2>0$. This assumption shows also a connection with the Bayes approach (see e.g. Maldonado (2009)) and raises the interpretation problem in the situation when Q is a singular matrix, which may be the case in some applications. It is important to address this concern because the reduction to the ridge regression, which is the first step in λ selection procedure via REML, requires the invertibility of Q. One possible solution is to use the Z-weighted generalized inverse of Q, (Elden 1982; Hansen 1998), which is comprised of both the penalty matrix Q and the design matrix Z. This solution produces the assumed distribution for b, which is not “purely prior” due to its dependence on a specific dataset.

Methods introduced in this work provide an alternative approach of handling the non-invertibility of the matrix Q. We take an alternative point of view for the prior distribution of b by assuming that the unknown true or optimal variance–covariance, ℚ, of b is (potentially) non-singular and that a singular matrix Q, defined by the user, and ℚ are “close”. In line with this argument, we acknowledge that an entire set of matrices that carry information about the true correlation structure of b exists (i.e., a set of informative matrices) and by using any of them we should be able to obtain a more accurate estimation and prediction than when the signal structure is unknown.

In Section 3 on regularization methods, we first present two simple and natural approaches that can be used to deal with the non-invertibility of the matrix Q. The first approach, called “AIM” (Adding Identity Matrix), removes the singularity of Q by adding the identity matrix multiplied by a relatively small constant, while the second, “VR” (Variable Reduction), builds the estimate from eigenvectors of Q, penalizing only eigenvectors corresponding to non-zero singular values. Then, we present our preferred method, ridgified Partially Empirical Eigenvectors for Regression (riPEER), which automatically selects two parameters in the penalty term simultaneously. riPEER handles the non-invertibility problem and also produces the desired adaptivity property.

riPEER can be viewed as a special case of the extension of the general-form Tikhonov regularization, known as the multi-parameter Tikhonov problem(Belge et al 2002; Brezinski et al 2003; Lu and Pereverzev 2011). Multi-parameter Tikhonov problem considers k matrices, Q₁,…, Q_k, together with k parameters λ₁,…,λ_k, and defines the penalty as ${\sum }_{i=1}^k{\lambda }_i{b}^T{Q}_{i}b$. Previous works proposed a higher dimension L– curve (Belge et al 2002), the discrepancy principle (Lu and Pereverzev 2011), and an extension of GCV (Brezinski et al 2003) to select the set of k regularization parameters. To the best of our knowledge, our work is the first to use the equivalence of the multi–parameter Tikhonov problem with the linear mixed model framework to estimate the regularization parameters.

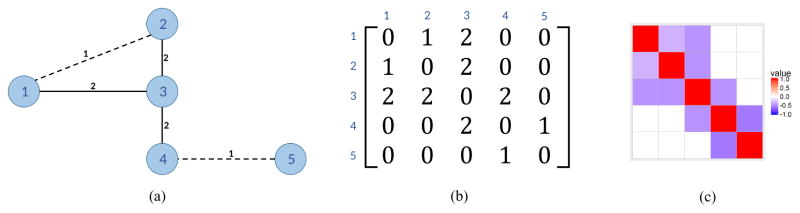
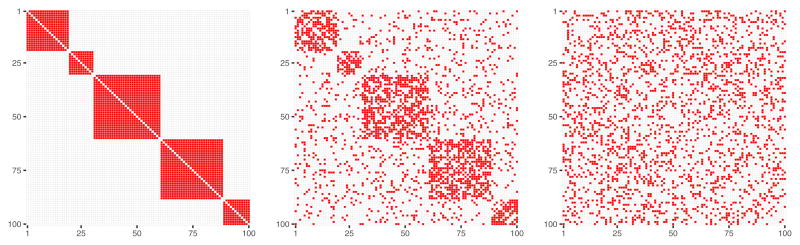
To define the measure of similarity between the brain regions, we used the density of connections calculated from the measurements acquired by diffusion imaging. The similarity measure between the regions i and j constitutes the (i, j)-entry in the symmetric adjacency matrix 𝒜, which is used to construct the normalized Laplacian, as detailed in Section 2.2. We exploit this structure as a prior scientific knowledge in our proposed regularization methodology. A sample graph, its corresponding adjacency matrix, and a heatmap of the normalized Laplacian are presented in Figure 1.

Fig. 1.

(a) Connectivity graph with five nodes and node similarity expressed as edge weights; (b) the corresponding adjacency matrix 𝒜; and (c) the heatmap of the normalized Laplacian.

The concept of utilizing normalized Laplacian matrix to define the penalty term was previously used by Li and Li (2008). However, substantial differences exist between their approach and our proposal. Firstly, in Li and Li (2008) the ℓ₁ norm of the coefficients is used as a second penalty term, which induces sparse solutions and serves as a variable selector. In contrast, riPEER employs ℓ₂ norm of coefficients as a second penalty term, and uses the confidence intervals to find the statistically significant predictors. The choice of ℓ₂ term is primarily motivated by the method’s application to the neuroimaging data, where we generally expect many variables to have small effects on the response rather than a few variables to have medium or large effects on the response. Secondly, with ℓ₂ norm used as a second penalty term, we are able to take an advantage of the equivalence between the riPEER optimization problem and an equivalent linear mixed model to simultaneously estimate both regularization parameters. This implies an important property of riPEER – robustness to an incomplete prior information, as shown in the simulations. In contrast to the simultaneous estimation via linear mixed model framework, Li and Li (2008) employs cross-validation procedure to select the two regularization parameters.

The remainder of this work is organized as follows. In Section 2, we formulate our statistical model, propose the estimation procedure, and discuss their main properties. We also describe the penalty term construction employing graph theory concepts and regularization parameter selection. Our new methods are described in Section 3 and their validation on simulated data is reported in Section 4. Finally, in Section 5, we apply our methodology to study the association of the brain’s cortical thickness and alcoholism phenotypes. The conclusions and a discussion are summarized in Section 6.

2 Statistical Model and Penalization

Motivated by the brain imaging data application, we consider a situation where the covariates and penalized predictors are distinct. For example, information about the structural connectivity of cortical brain regions is used to penalize only the predictors corresponding to cortical measurements, whereas other variables, such as demographic covariates and overall intercept, are included in the regression model as unpenalized terms.

2.1 Statistical model

Consider the general situation, where we have n observations of a random variable, stored in vector y, and the design matrix, [Z X], is given, where Z and X are n× p and n×m design matrices, respectively. Here, p denotes the number of all penalized variables and m is a number of unpenalized covariates. We assume that the unknown vectors b and β satisfy the multiple linear regression model,

$$y=[ZX]\left[\begin{array}{c}b\\ \beta \end{array}\right]+\epsilon =Zb+X\beta +\epsilon ,$$ (2.1)

where ε ~ 𝒩 (0,σ²I_n) is the vector of random errors.

Here, X is the n by m design matrix containing unpenalized covariates or, equivalently, columns corresponding to variables for which the connectivity information is not given. The standard procedure is to mean-center all columns in the design matrix to remove the intercept. In such case, X can be an empty matrix (i.e. the situation with m = 0 is taken into consideration) and then model (2.1) takes the form y = Zb+ε. The matrix Z corresponds to the predictors for which the connectivity information is available. Such information is given by a p by p symmetric matrix 𝒜 (also known as the connectivity matrix) that can be treated as a prior knowledge and employed in the estimation, e.g. via a Laplacian matrix Q (see Section 2.2), which can then be incorporated into the penalty term.

2.2 Defining Q as a normalized Laplacian

In this work, we use the normalized Laplacian matrix, see Chung (2005). Let 𝒜 = [a_ij], 1 ≤ i, j ≤ p be an adjacency matrix (symmetric matrix with non-negative entries and zeros on the diagonal), which defines the strength of the connections between nodes. The diagonal entries of the (unnormalized) Laplacian are d_i := Σ_j≠i a_ij, representing the sum of all weighted edges connected to node i.

The normalized Laplacian is defined as the p× p matrix Q:

$$Q(i,j):=\{\begin{array}{ll}1-a_{ii}/d_i,\hfill & \text{if}i=j\text{and}{d}_i\ne 0\hfill \\ -a_{ij}/\sqrt{d_i{d}_j},\hfill & \text{if}i\text{and}j\text{are}\text{connected}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$

It is worth noting that a Laplacian is a symmetric matrix. The justification why a matrix constructed in such a way could be incorporated in the penalty term is explained by the following property (see e.g. Li and Li (2008)). If we let Q to be the normalized Laplacian then

$$b^{T}Qb=\sum _{i,j:a_{ij}\ne 0}{\left(\frac{b_i}{\sqrt{d_i}}-\frac{b_j}{\sqrt{d_j}}\right)}^2{a}_{ij}.$$

The result above shows that defining penalty as λb^TQb implies that vectors that differ too much over linked nodes get more penalized. Scaling by $\sqrt{d_i}$ allows a small number of nodes with large d_i to have more extreme values. The proposition above also implies that for any adjacency matrix 𝒜, Laplacian is a positive semi-definite matrix. To determine that Q has zero as the smallest eigenvalue, it is enough to consider a p dimensional vector, b̃, defined as ${\stackrel{\sim }{b}}_i:=\sqrt{d_i}$. Then b̃^TQb̃ = 0.

The true structure of structural dependencies in a human brain is complicated and unknown. By defining Q via the adjacency matrix, we assume that coefficients in our model, corresponding to cortical thickness of different brain regions, are linked proportionally to the number of streamlines connecting them. Such an assumption may not be completely realistic. However, even if such a belief provides imperfect information, riPEER still uses some part of it to increase the estimation accuracy. At the same time, additional ordinary ridge penalty protects the method against utilizing prior knowledge which is not accurate. There is a wide literature on the approaches where some predefined (not estimated) structure information is used, e.g. Tibshirani and Taylor (2011), Li and Li (2008), ? and ?.

2.3 Estimate and its properties

If Q is a symmetric and positive definite matrix (hence invertible), we can use the estimate obtained as the solution to a convex optimization problem of the general-form Tikhonov regularization, i.e.,

$$\left[\begin{array}{c}{\widehat{b}}^{\text{Q}}\\ {\widehat{\beta }}^{\text{Q}}\end{array}\right]:=\underset{b,\beta }{\text{argmin}}\left\{{\Vert y-Zb-X\beta \Vert }_2^2+\lambda b^{\top }Qb\right\}.$$ (2.2)

Here λ > 0 is a tuning parameter which can be estimated using the equivalence with a corresponding linear mixed model. This estimation procedure is implemented in Randolph et al (2012). In our case, there is clear distinction between the penalized (i.e. Z) and unpenalized (i.e. X) covariates. By defining $Q_E:=\left[\begin{array}{cc}Q& 0\\ 0& 0\end{array}\right]$, the minimization procedure (2.2) is equivalent to

$$\left[\begin{array}{c}{\widehat{b}}^{\text{Q}}\\ {\widehat{\beta }}^{\text{Q}}\end{array}\right]:=\underset{\beta ,b}{\text{argmin}}\left\{{\Vert y-[ZX]\left[\begin{array}{c}b\\ \beta \end{array}\right]\Vert }_2^2+\lambda {\left[\begin{array}{c}b\\ \beta \end{array}\right]}^{\top }{Q}_E\left[\begin{array}{c}b\\ \beta \end{array}\right]\right\}.$$ (2.3)

The analytical solution to the above problem is given by

$$\left[\begin{array}{c}{\widehat{b}}^{\text{Q}}\\ {\widehat{\beta }}^{\text{Q}}\end{array}\right]={\left({[ZX]}^{\top }[ZX]+\lambda Q_E\right)}^{-1}{[ZX]}^{\top }y.$$ (2.4)

Randolph et al (2012) describe how the generalized singular value decomposition (GSVD) (see also Hansen (1998), Golub and Van Loan (2013), Bjorck (1996), Paige and Saunders (2006)) is a useful tool for understanding the role played by the ℓ₂ penalization terms in a regularized regression model. In particular, GSVD provides a tractable and interpretable series expansion of the estimate in (2.4) in terms of the generalized eigenvalues and eigenvectors.

2.4 Regularization parameter selection

We consider two parameter selection procedures, cross-validation and REML. Simulations performed in Section 4 show the advantage of the later over the former. Therefore, in our final procedure, the equivalence with linear mixed model is used to obtain λ.

We briefly review here the basics of the LMM theory necessary for this work (see e.g. Demidenko (2004) and C. E. McCulloch (2008)). Here, we consider the multiple linear regression model, y = Xβ + Zb+ε, with uncorrelated random vector ε, i.e., we assume that 𝔼(ε_i,ε _j) = 0 for i ≠ j. Let us first assume that Q has an inverse that matches (up to a multiplicative constant) the variance-covariance matrix of random effects:

• A.1β is the vector of fixed effects and b is vector of random effects,
• A.2𝔼(b) = 0 and 𝔼(ε) = 0,
• A.3 $\mathit{Cov}(b)={\mathrm{\sigma }}_b^2{Q}^{-1}$ and Cov(ε) =σ²I_n, for some unknown ${\mathrm{\sigma }}_b^2>0$ and σ² > 0,
• A.4b and ε are uncorrelated.

As noted above, a known Q implies the correlation matrix of b is known up to the multiplicative constant, ${\mathrm{\sigma }}_b^2$, which can be interpreted as a measure of signal amplitude. By assuming two-, three- and higher parameter families, one can generalize this to scenarios in which knowledge about the correlation is less rich. In the extreme case, no additional conditions for Cov(b) are assumed, other than that it is a symmetric, positive definite matrix, which results in (p²+ p)/2-parameter family of matrices.

Under the model (2.1) with assumptions A.1–A.4, it can be shown that $V:=\mathit{Cov}(y)={\mathrm{\sigma }}_b^{2}Z{Q}^{-1}{Z}^{\top }+{\mathrm{\sigma }}^2{I}_n$. The best linear unbiased estimator (BLUE) of β and best linear unbiased predictor (BLUP) of b are given by the following equations

$$\text{BLUE}(\beta )={(X^{\top }{V}^{-1}X)}^{-1}{X}^{\top }{V}^{-1}y,\text{BLUP}(b)={\mathrm{\sigma }}_b^2{Q}^{-1}{Z}^{\top }{V}^{-1}\left(y-X\text{BLUE}(\beta )\right).$$ (2.5)

Equivalently the expressions in (2.5) can also be obtained as the solution to an optimization problem. Assume that b has multivariate normal distribution: y|b ~𝒩 (Xβ +Zb, σ²I_n) and $b~\mathcal{N}(0,{\mathrm{\sigma }}_b^2{Q}^{-1})$. If ${\mathrm{\sigma }}_b^2$, σ² are known, this yields the following log-likelihood function

$$l(b,\beta )=-\frac{1}{2}\left({\mathrm{\sigma }}^{-2}{\Vert y-X\beta -Zb\Vert }_2^2+{\mathrm{\sigma }}_b^{-2}{b}^{\top }Qb\right)+c_1(Q,{\mathrm{\sigma }}_b^2,p)+c_2(n,{\mathrm{\sigma }}^2),$$

where functions c₁ and c₂ do not depend on either b or β. Looking for the maximum likelihood estimates simply leads to the problem(2.2), with $\lambda :={\mathrm{\sigma }}^2/{\mathrm{\sigma }}_b^2$. It can be shown that the optimal values of β and b are exactly given by BLUE and BLUP defined in (2.5). Our proposal provides an objective and statistically rigorous way to choose the tuning parameter λ in (2.2) when Q is a symmetric and positive definite matrix. Indeed, we can use REML to obtain the estimates of σ² and ${\mathrm{\sigma }}_b^2$ in the model characterized by A.1–A.4 and define λ̂ as ${\widehat{\mathrm{\sigma }}}^2/{\widehat{\mathrm{\sigma }}}_b^2$.

The first step is the conversion of the optimization problem to the ordinary ridge regression. Since Q is a symmetric, positive-definite matrix it can be decomposed as Q = L^⊤L, where L is an invertible matrix. Now

$${\Vert y-X\beta -Zb\Vert }_2^2+\lambda b^{\top }Qb={\Vert y-X\beta -Z{L}^{-1}Lb\Vert }_2^2+\lambda {(Lb)}^{\top }Lb={\Vert y-X\beta -\stackrel{\sim }{Z}\stackrel{\sim }{b}\Vert }_2^2+\lambda {\Vert \stackrel{\sim }{b}\Vert }_2^2,$$

for Z̃:= ZL⁻¹ and b̃ := Lb, which allows us to assume that Q = I in A.3 without loss of generality. This conversion procedure changes the general Tikhonov formulation to the ordinary ridge regression. One of the clear advantages of the the ordinary ridge is that it is easily implemented in a variety of existing software packages that support the LMM framework.

2.5 Statistical inference

We utilize a testing framework proposed in Ruppert et al (2003) to test for the significance of the penalized regression coefficients b and provide the (1−α) confidence intervals for b̂^Q for problems of form (2.2) via

$${CI}_Q={\widehat{b}}^{\text{Q}}\pm z_{\alpha }\times \sqrt{\frac{{\Vert y_{\mathcal{P}}-{\widehat{y}}_{\mathcal{P}}\Vert }_2^2}{n-p_{tr}}}\times \sqrt{\mathit{diag}[{(Z_{\mathcal{P}}^{\top }{Z}_{\mathcal{P}}+{\lambda }_{Q}Q)}^{-1}{Z}_{\mathcal{P}}^{\top }{Z}_{\mathcal{P}}{(Z_{\mathcal{P}}^{\top }{Z}_{\mathcal{P}}+{\lambda }_{Q}Q)}^{-1}]},$$ (2.6)

where z_α is the inverse of CDF of the standard normal distribution evaluated at (1−α/2) and p_tr is the trace of a “hat” matrix, H_Q, given by:

$$H_Q=Z_{\mathcal{P}}{(Z_{\mathcal{P}}^{\top }{Z}_{\mathcal{P}}+\lambda Q)}^{-1}{Z}_{\mathcal{P}}^{\top },$$ (2.7)

where y_℘,Z_℘ are given by $y_{\mathcal{P}}:={\mathcal{P}}_X^{c}y$ and $Z_{\mathcal{P}}:{\mathcal{P}}_X^{c}Z$, for ${\mathcal{P}}_X^c:=I_n-X{(X^{\top }X)}^{-1}{X}^{\top }$.

2.6 Goodness of fit

In Section 5 summarizing the brain imaging analysis, we use the adjusted R² to measure the goodness of fit of considered methods. The adjusted R² (which we denote by R̄²) was defined as

$${\overline{R}}^2:=1-\frac{{\sum }_{i=1}^n(y_i-{\widehat{y}}_i)/\mathit{redf}}{{\sum }_{i=1}^n(y_i-\overline{y})/(n-1)},$$ (2.8)

where red f stands for the residual effective degrees of freedom, given by

$$\mathit{redf}:\text{tr}\left({(I-H_E)}^{\top }(I-H_E)\right)\text{for}{H}_E:=[ZX]{\left({[ZX]}^{\top }[ZX]+\lambda Q_E\right)}^{-1}{[ZX]}^{\top }$$ (2.9)

where Q_E was introduced in Section 2.3.

3 Regularization Methods

The standardization procedure described in Section 2 can be applied when Q is a symmetric positive definite matrix. However, the normalized Laplacian is always a singular matrix. Thus, the methods described cannot be readily applied.

Suppose that Q in (2.2) is non-invertible and has rank equal to r with r < p. Since matrix Q is singular, we can not simply assume that $b~\mathcal{N}(0,{\mathrm{\sigma }}_b^2{Q}^{-1})$, as in A.3. However, it is reasonable to assume the existence of an unknown matrix ℚ such that $b~\mathcal{N}(0,{\mathrm{\sigma }}_b^2{\mathbb{Q}}^{-1})$, which is not identical, but, in some sense, close to Q. The intuition is that by making a “small modification” to Q, targeted to remove the singularity, one may produce an invertible matrix which is still “close” to ℚ and can use the information that it carries as described Section 2.

In this section, we first present two rather natural approaches dealing with the non-invertibility of matrix Q. In the first approach, we add the identity matrix multiplied by relatively small constant to the normalized Laplacian matrix Q in order to remove its singularity. In the second approach, we reduce the number of variables to be equal to the rank of matrix Q by considering an equivalent optimization problem expressed in the form of (1.1), but with the invertible matrix in the penalty term. In the second part of this section, we present our proposed method, riPEER, which addresses not only the non-invertibility problem, but is also fully automatic with the desired adaptivity property.

3.1 Handling the non-invertibility of matrix Q

The simple and natural idea of removing the singularity is by considering Q̃ := Q+λ₂I_p, rather than Q, for some fixed parameter λ₂. We refer to this method as Adding the Identity Matrix (AIM), where specific steps are presented below

Algorithm 1.

AIM procedure

input: matrices Z, X, positive semi-definite matrix Q, λ2 > 0

1: define Q̃ := Q+λ2Ip;

2: decompose Q̃ as Q̃ = L⊤L;

3: find REML estimates σ̂2 and ${\widehat{\mathrm{\sigma }}}_b^2$, of σ2 and ${\mathrm{\sigma }}_b^2$, in LMM with X as matrix of fixed effects, ZL−1 as matrix of random effects, $b~\mathcal{N}(0,{\mathrm{\sigma }}_b^2{I}_p)$ and ε ~ 𝒩(0,σ2In);

4: define $\lambda :={\widehat{\mathrm{\sigma }}}^2/{\widehat{\mathrm{\sigma }}}_b^2$ and find estimates β̂AIM and b̂AIM by applying formula (2.4) with matrix Q̃.

The value of λ₂ is a fixed small number. In our work, we tested several values of λ₂ to assess the solutions’ stability. Based on the simulation results, we set λ₂ to be equal to 0.001. The lack of the automatic procedure for choosing λ₂ in AIM is undoubtedly one of its main disadvantages.

The second idea considered in this section, Variable Reduction (VR), also produces the optimization problem with invertible matrix in the penalty, but without introducing arbitrary parameters. VR reduces the number of penalized predictors in the optimization problem by moving a subset of penalized predictors to the unpenalized matrix X. The VR method is based on the property stating that for any vector b ∈ℝ^p, b^⊤Qb can be expressed as c^⊤diag(s₁,…, s_r)c for nonzero singular values s₁,…, s_r of Q and some c from the r-dimensional subspace spanned by the singular vectors corresponding to s₁,…, s_r. In the next step, we proceed with the variable rearrangement.

We start with the optimization problem (2.2). Matrix Q has an eigen decomposition of the form

$$Q=U\left[\begin{array}{cc}\mathit{\sum }& 0\\ 0& 0\end{array}\right]U^{\top },\mathit{\sum }:\mathit{diag}(s_1,\dots ,s_r),s_i>0.$$ (3.1)

Using the notation b̃ :=U^⊤b and b̃_[1:r] for the first r coefficients of b̃, we get the equivalent optimization problem with the objective function ${\Vert y-X\beta -ZU\stackrel{\sim }{b}\Vert }_2^2+\lambda {\stackrel{\sim }{b}}_{[1:r]}^{\top }\mathit{\sum }{\stackrel{\sim }{b}}_{[1:r]}$. Matrix ZU is separated column-wise into A which is a submatrix of ZU created by the last p−r columns and ℤ which is a submatrix of ZU created by the first r columns. Let c := b̃_[r+1:p] be the regression coefficients corresponding to the columns in matrix A and d := b̃_[1:r] the regression coefficients corresponding to the new penalized variables in the matrix ℤ. Now, the optimization criterion can be written as,

$$\underset{\beta ,c,d}{\text{argmin}}\left\{{\Vert y-[XA]\left[\begin{array}{c}\beta \\ c\end{array}\right]-\mathbb{Z}d\Vert }_2^2+\lambda d^{\top }\mathit{\sum }d\right\}.$$ (3.2)

Optimization problem (3.2) is in the ordinary PEER optimization form (2.2) with an invertible penalty matrix Σ. Thus, an equivalent LMM can be easily derived. In summary, for a singular matrix Q some directions, corresponding to the singular vectors with zero singular values in ℝ^p, are not penalized. After changing the basis vectors, we can move the corresponding variables to the unpenalized part. All the steps are summarized in the Algorithm 2.

Algorithm 2.

VR procedure

Input: matrices Z, X, positive semi-definite matrix Q with rank r < p;

1: Let U be orthogonal matrix from (3.1) and define matrix of nonzero singular values, Σ := diag(s1,…, sr);

2: Denote by A last p−r columns of ZU and by ℤ first r columns of ZU;

3: Put 𝕏 := [X A] and consider minimization problem with the objective ${\Vert y-\mathbb{X}\stackrel{\sim }{\beta }-\mathbb{Z}d\Vert }_2^2+\lambda d^{\top }\mathit{\sum }d$, for β̃ ∈ ℝm+p−r and d ∈ ℝr ;

4: Estimate σ2 and ${\mathrm{\sigma }}_d^2$ in equivalent LMM, i.e. the model y = 𝕏β̃ +ℤd +ε, where $d~\mathcal{N}(0,{\mathrm{\sigma }}_d^2{\mathit{\sum }}^{-1})$ and ε ~𝒩(0,σ2In), and define $\lambda :={\widehat{\mathrm{\sigma }}}^2/{\widehat{\mathrm{\sigma }}}_d^2$;

5: Find estimates β̂VR and b̂VR by applying formula (2.4).

3.2 riPEER

In this section we present our main method – riPEER. The idea is to use two penalty parameters in the optimization problem – main penalty parameter λ_Q and a ridge adjustment parameter λ₂. This time, however, in contrast to AIM, both parameters are estimated via an equivalent LMM formulation. Specifically, the optimization problem is written as,

$$\left[\begin{array}{c}{\widehat{b}}^{\text{rP}}\\ {\widehat{\beta }}^{\text{rP}}\end{array}\right]:=\underset{\beta ,b}{\text{argmin}}\left\{{\Vert y-X\beta -Zb\Vert }_2^2+{\lambda }_Q{b}^{\top }(Q+{\lambda }_2{I}_p)b\right\}$$ (3.3)

or equivalently as

$$\left[\begin{array}{c}{\widehat{b}}^{\text{rP}}\\ {\widehat{\beta }}^{\text{rP}}\end{array}\right]=\underset{\beta ,b}{\text{argmin}}\left\{{\Vert y-X\beta -Zb\Vert }_2^2+{\lambda }_Q{b}^{\top }Qb+{\lambda }_R{\Vert b\Vert }_2^2\right\},$$ (3.4)

where λ_R = λ_Qλ₂. The latter formulation, with an additional ridge penalty, justifies the name of the method. Without loss of generality, in the first step we can reduce the problem by excluding the X matrix. It can be shown that

$$\{\begin{array}{l}{\widehat{b}}^{\text{rP}}={\text{argmin}}_b\{{\Vert {\mathcal{P}}_X^{c}y-{\mathcal{P}}_X^{c}Zb\Vert }_2^2+{\lambda }_Q{b}^{\top }Qb+{\lambda }_R{\Vert b\Vert }_2^2\}\hfill \\ {\widehat{\beta }}^{\text{rP}}={(X^{\top }X)}^{-1}{X}^{\top }(y-Z{\widehat{b}}^{\text{rP}})\hfill \end{array},$$ (3.5)

where ${\mathcal{P}}_X^c:=I_n-X{(X^{\top }X)}^{-1}{X}^{\top }$ is the projection onto orthogonal complement to the subspace spanned by columns of X. Denote $y_{\mathcal{P}}:={\mathcal{P}}_X^{c}y$ and $Z_{\mathcal{P}}:={\mathcal{P}}_X^{c}Z$. For the ease of computation, we perform an additional step; let USU^⊤ be the SVD of the matrix Q, with the orthogonal matrix U and the diagonal matrix S with nonnegative numbers on the diagonal. After the variable change via the transformation b̄ :=U^⊤b, the final form of problem becomes

$$\underset{\overline{b}}{\text{argmin}}\left\{{\Vert y_{\mathcal{P}}-Z_{\mathcal{P}}U\overline{b}\Vert }_2^2+{\overline{b}}^{\top }({\lambda }_{Q}S+{\lambda }_R{I}_p)\overline{b}\right\}.$$ (3.6)

Now the LMM equivalent to (3.6) can be characterized as follows:

• B.1we consider model y_℘ = Z̃b̄+ε, with Z̃ := Z_℘U and b̄ being the vector of random effects,
• B.2ε ~𝒩 (0,σ²I_n),
• B.3 $\overline{b}~\mathcal{N}(0,{\mathrm{\sigma }}^2{D}_{\lambda }^{-1})$, where D_λ :=λ_QS+λ_RI_p.

To the best of our knowledge, there is no existing R package that can be used to estimate the parameters based on the equation (3.6) in a straightforward way. Thus, we have focused on deriving and optimizing the LMM log-likelihood function. Following Demidenko (2004), maximizing the log-likelihood is equivalent to minimizing the expression

$$h(\lambda )=nln\left[{\Vert y_{\mathcal{P}}\Vert }_2^2+y_{\mathcal{P}}^{\top }\stackrel{\sim }{Z}{\left(D_{\lambda }+{\widehat{Z}}^{\top }\stackrel{\sim }{Z}\right)}^{-1}{\stackrel{\sim }{Z}}^{\top }{y}_{\mathcal{P}}\right]+ln\mid D_{\lambda }+{\stackrel{\sim }{Z}}^{\top }\stackrel{\sim }{Z}\mid -ln\mid D_{\lambda }\mid .$$

Specifically, the maximum likelihood estimator (mle) for σ², λ_Q and λ_R can be found as

$$\{\begin{array}{l}\mathbf{mle}(\lambda )={\text{argmin}}_{\lambda \succcurlyeq 0}h(\lambda )\hfill \\ \mathbf{mle}({\mathrm{\sigma }}^2)=n^{-1}{\lambda }_{\mathcal{P}}^{\top }{\left(\stackrel{\sim }{Z}{D}_{\mathbf{mle}(\lambda )}^{-1}{\widehat{Z}}^{\top }+I\right)}^{-1}{y}_{\mathcal{P}}\hfill \end{array},$$ (3.7)

where λ ⪰ 0 denotes the conjunction λ_Q ≥ 0 and λ_R ≥ 0. To find the solution to the above optimization problem we utilized sbplx function from the nloptr R software package (Ypma 2014), which is an R interface to NLopt (Johnson 2016) – a free/open-source library for nonlinear optimization. sbplx function implements Subplex algorithm (Rowan 1990) to estimate the parameters of an objective function to be minimized.

The method can be summarized as

Algorithm 3.

riPEER

input: matrices Z, X, positive semi-definite matrix Q

1: find SVD of Q, i.e. Q =USU⊤;

2: define projection matrix ${\mathcal{P}}_X^c$ as ${\mathcal{P}}_X^c:=I_n-X{(X^{\top }X)}^{-1}{X}^{\top }$;

3: denote $y_{\mathcal{P}}:={\mathcal{P}}_X^{c}y,Z_{\mathcal{P}};={\mathcal{P}}_X^{c}Z,\stackrel{\sim }{Z}:={\mathcal{P}}_X^{c}ZU$;

4: find estimates of λQ and λR by solving optimization problem in (3.7);

5: define ${\widehat{b}}^{\text{rP}}:={(Z_{\mathcal{P}}^{\top }{Z}_{\mathcal{P}}+{\lambda }_{Q}Q+{\lambda }_R{I}_P)}^{-1}{Z}_{\mathcal{P}}^{\top }{y}_{\mathcal{P}}$, β̂rP := (X⊤X)−1X⊤(y−Z)b̂rP.

In Section 4, we study the empirical performance of the proposed extensions to PEER. Namely, we conduct an extensive simulation study using data-driven connectivity matrices to evaluate the estimation performance of AIM, VR and riPEER. In addition, we compare the results from our proposed methods with the ordinary ridge regression.

4 Simulation experiments

In this section, we study the empirical behavior of the proposed method, riPEER, in a number of simulation experiments. We employ ordinary ridge, AIM and VR methods as comparators.

4.1 Simulation scenarios

We aim to evaluate the methods’ behavior assuming that given (“observed”) connectivity information describing connections between variables is at least partially informative. In the first simulation scenario considered, we assume that given connectivity information accurately reflects the true connectivity structure. In the second scenario, we investigate the effect of decreasing the amount of information contained in a connectivity matrix by permuting the “true” connections and using the permuted matrix version in a model estimation. Finally, we study the effect of false positives and false negatives present in a connectivity matrix by randomly adding or removing connections, respectively, in the “true” connectivity information, and employing the resulting matrix in a model estimation.

Each simulation scenario, we consider, is based on the following procedure. We first generate a matrix of p correlated features, Z ∈ ℝ^n×p, where the rows are independently distributed as 𝒩_p(0, Σ) with Σ_ij = exp{−k(i − j)²}, i = 1, …, p; j = 1, …, p. We then generate a vector of true coefficients $b~\mathcal{N}(0,{\mathrm{\sigma }}_b^2{Q}_{\mathit{true}}^{-1})$, b ∈ ℝ^p. Here, Q_true denotes the normalized Laplacian of an adjacency matrix 𝒜_true that represents assumed true connectivity between the variables (see Section 2.2). A coefficient vector b obtained via such procedure reflects the structure represented by 𝒜_true. We further generate an outcome y assuming the model y = Zb + ε, where ε ~ 𝒩(0, σ²I_n).

In simulation scenarios, we consider the following choices of the experimental settings:

1. number of predictors: p ∈ {50, 100, 200},

2. number of observations: n ∈ {100, 200},

3. signal strength: ${\mathrm{\sigma }}_b^2\in \{0.001,0.01,0.1\}$,

4. strength of correlation between the variables in the Z matrix: k ∈ {0.01, 0.004},

5. information in the given (observed) adjacency matrix 𝒜_obs: complete information or partial information.

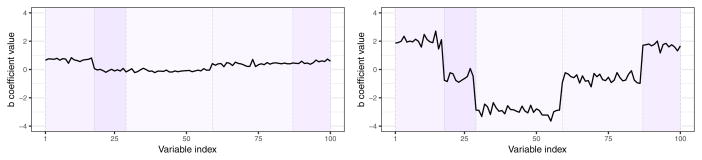
All these settings affect the estimation accuracy of the coefficient vector, b ∈ R^p, representing the association between the p variables in Z and outcome y in the model y = Zb + ε, ε ~ 𝒩(0, σ²I_n). In particular, using various values of ${\mathrm{\sigma }}_b^2$ may be viewed as defining signal strength for a fixed value of error variance σ² = 1 (see Figure 3).

Fig. 3.

Examples of b values simulated from $b~\mathcal{N}(0,{\mathrm{\sigma }}_b^2{Q}^{-1})$ distribution for ${\mathrm{\sigma }}_b^2=0.01$ (left panel) and ${\mathrm{\sigma }}_b^2=0.1$ (right panel), for Q being the Laplacian of 100×100 dimensional modularity graph adjacency matrix. Higher ${\mathrm{\sigma }}_b^2$ parameter value yields stronger signal. Colors of the background rectangular shades correspond to the color scale of the Laplacian matrix modules in Figure 2 (right panel), denoting the groups of nodes (variables) of common assigment to one of the five connectivity modules.

The 𝒜_true and 𝒜_obs adjacency matrices are based on an established modularity connectivity matrix obtained by Sporns (2013) (see also Cole et al (2014); Sporns and Betzel (2016)) in which each node belongs to one of five modules (communities) as displayed in Figure 12 in the Appendix. These five modules were identified by employing the the Louvain method (?) for extracting communities in networks (see Section 5.1).

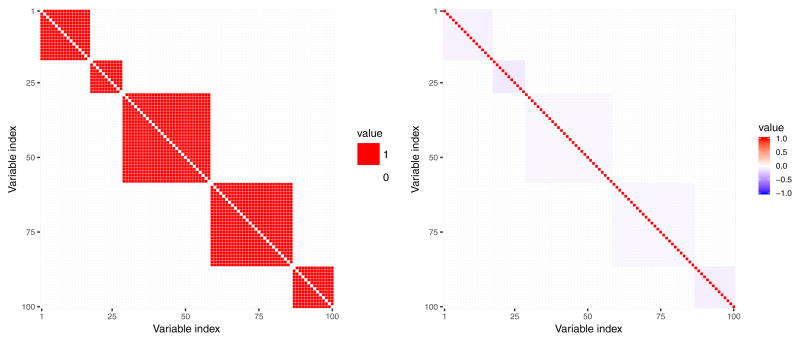
In all simulations conducted, we obtain 𝒜_true matrix by rescaling the original modularity matrix so as the number of nodes 𝒜_true matches the number of features p we assume in particular simulation setting (see Figure 2). As a result of rescaling the original modularity connectivity matrix, density of 𝒜_true matrix (here: proportion of non-zero entries of the matrix) varies slightly depending on the dimension of 𝒜_true; it equals 0.21, 0.22 and 0.23 for p = 50, p = 100 and p = 200, respectively. Construction of a given adjacency matrix 𝒜_obs is specific for each simulation scenario, which we describe in detail in Section 4.2.

Fig. 2.

Left panel: 100×100 dimensional adjacency matrix 𝒜 that represents assumed connectivity between 100 nodes (variables). Adjacency matrix entries colored with red are equal 1 and denote common assigment of the two nodes to one of the five connectivity modules. Adjacency matrix entries colored with white are equal 0 and denote that the two nodes are not connected with each other. Right panel: corresponding normalized Laplacian matrix.

In each simulation scenario, for particular values of number of predictors (p), number of observations (n), signal strength ( ${\mathrm{\sigma }}_b^2$), strength of correlation between the variables in the matrix Z (k) and 𝒜_obs, we perform 100 simulation runs. In each run, we generate objects Z_n,p, b_σb and the outcome via y = Z_n,pbσb + ε, ε ~ 𝒩(0, I_n). Finally, we assess the performance of all considered methods by comparing relative mean squared error (MSE) of the estimated coefficients b via $\mathit{MSEr}={\Vert \widehat{b}-b\Vert }_2^2/{\Vert b\Vert }_2^2$, where ||x||₂ denotes the ℓ₂-norm of a vector x = (x₁, …, x_p). Motivated by the applications to the brain imaging data, we focus on the accuracy of the regression parameters estimation.

4.2 Construction of a graph adjacency matrix 𝒜_obs

Accurate 𝒜_obs connectivity information

In the first simulation scenario we assume that a given graph adjacency matrix 𝒜_obs accurately reflects the true structure of model coefficients. We therefore set 𝒜_obs = 𝒜_true, which yields the normalized graph Laplacian matrix used in model estimation, Q_obs, carrying the same information about connections between model coefficients as Q_true used in the generation of “true” model coefficient vector b.

𝒜_obs connectivity information with the permuted “true” connections

To express misspecified connectivity information in the second simulation setting, we construct normalized graph Laplacian matrices Q_obs based on the 𝒜_{obs (diss)} which is a permuted version of the connectivity matrix 𝒜_true. Parameter diss in the definition of the 𝒜_{obs (diss)} describes the dissimilarity between 𝒜_obs and 𝒜_true, defined as

$$\mathit{diss}:=\left(\sum _{0\le i,j\le p}\mathbb{I}\{\mid {\mathcal{A}}_{\mathit{obs}}(i,j)-{\mathcal{A}}_{\mathit{true}}(i,j)\mid >0\}\right)/\left(2\sum _{0\le i,j\le p}\mathbb{I}\{{\mathcal{A}}_{\mathit{true}}(i,j)>0\}\right).$$

Entries of 𝒜_true are permuted (rewired) using one of the following methods.

1. A randomization procedure which preserves the original graph’s density, degree distribution and degree sequence, as implemented by keeping_degseq function from igraph R package (Csardi and Nepusz 2006). The algorithm chooses two arbitrary edges in each step, (a, b) and (c, d), and substitutes them with (a, d) and (c, b), if they do not already exists in the graph. In the 𝒜_obs construction we apply the keeping_degseq function iteratively until a predefined level of dissimilarity (parameter diss) between 𝒜_true and 𝒜_obs is reached.

2. A randomization procedure that preserves the original graph’s density, as implemented by each_edge function from igraph R package. The function rewires the endpoints of the edges with a constant probability uniformly randomly to a new vertex in a graph. In the 𝒜_obs construction we apply the each_edge function iteratively until a predefined level of dissimilarity (parameter diss) between 𝒜_true and 𝒜_obs is reached.

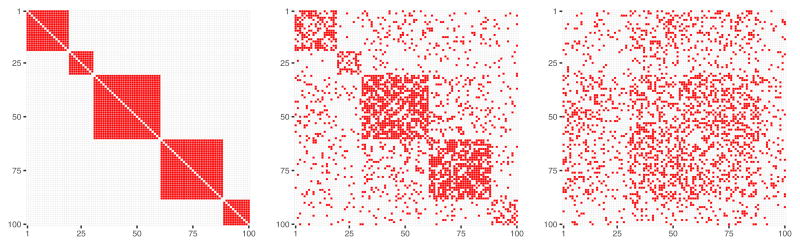
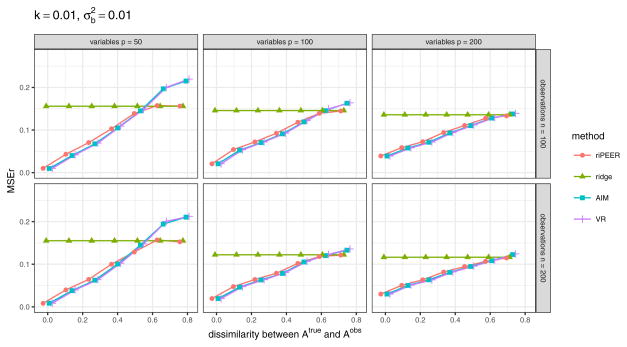
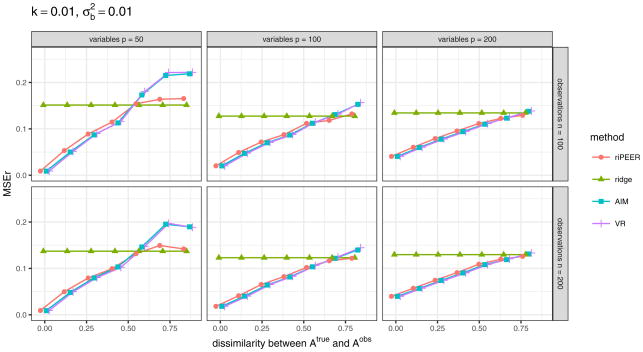
The two rewiring methods have different properties. Rewiring while preserving the original graph’s degree distribution yields 𝒜_obs matrix that reflects the initial modules size proportions even for relatively high values of diss value (Figure 4, right panel), while rewiring with a constant probability for a graph edge to be rewired yields completely random distribution of connections across a graph (Figure 5, right panel).

Fig. 4.

𝒜_obs matrices obtained by a graph rewiring with while preserving the original degree distribution, for a number of nodes p = 100 and dissimilarity between 𝒜_obs and 𝒜_true equal to diss = 0 (left panel), diss = 0.37 (central panel), diss = 0.74 (right panel).

Fig. 5.

𝒜_obs matrices obtained from a graph rewiring with a constant probability for a graph edge to be rewired, for a number of nodes p = 100 and dissimilarty between 𝒜_obs and 𝒜_true equal to diss = 0 (left panel), diss = 0.41 (central panel), diss = 0.81 (right panel).

Note that depending on 𝒜_true matrix density and the permutation procedure choice, the maximum attainable value of dissimilarity between 𝒜_obs and 𝒜_true varies slightly; for example, for the number of variables equal to p = 100 we obtained maximum dissimilarity between 𝒜_obs and 𝒜_true equal to diss = 0.74 for randomization procedure which preserves the original graph’s density, degree distribution and degree sequence, and diss = 0.81 for randomization procedure which preserves the original graph’s density only.

𝒜_obs connectivity information with a presence of false negatives and false positives

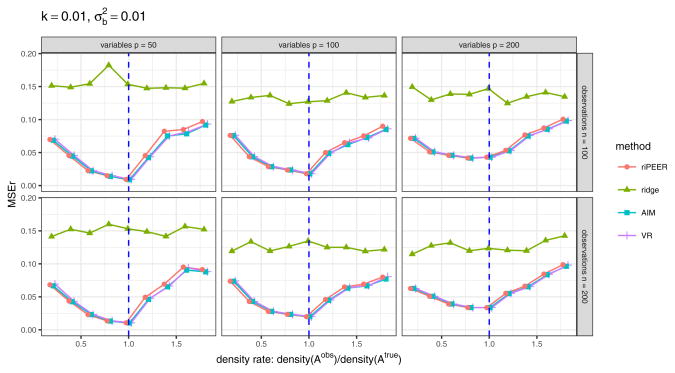
In the third simulation setting, we construct a collection of matrices 𝒜_obs by either randomly removing or adding connections to a graph represented by 𝒜_true in order to obtain 𝒜_obs of lower or higher density than 𝒜_true, respectively. As a result, 𝒜_obs of higher density than 𝒜_true corresponds to the presence of false positive entries (false positive connections) in a connectivity graph represented by 𝒜_obs whereas 𝒜_obs of lower density than 𝒜_true corresponds to the presence of false negative entries in a connectivity graph represented by 𝒜_obs. The procedure of randomly removing or adding connections to a graph represented by 𝒜_true is continued until a predefined ratio of 𝒜_obs matrix density and 𝒜_true matrix density is reached (here: between 0.2 and 1.8), see Figure 6.

Fig. 6.

𝒜_obs matrices obtained by randomly removing or adding connections to a graph represented by 𝒜_true until a predefined ratio of 𝒜_obs matrix density and 𝒜_true matrix density is reached, for the ratio density(𝒜_obs)/density(𝒜_true) equal 0.2 (left panel), 0.6 (middle left panel), 1.4 (middle right panel), 1.8 (right panel).

4.3 Parameter estimation

In the first scenario of the simulation study, we compare the following methods of fitting a linear regression model: ordinary ridge using two approaches to penalty parameter choice – CV and REML, and riPEER using two approaches to penalty parameter choice – CV and REML. In the second and third simulation scenarios we compare riPEER, ordinary ridge, AIM and VR, using REML approach for the penalty parameter choice.

We utilize mdpeer R package (Karas 2016) for the parameter estimation for all the methods except for two cases. For an ordinary ridge with λ_R regularization parameter chosen by cross-validation we use the implementation from glmnet R package (Friedman et al 2010). Specifically, we perform 10-fold cross-validation (CV) where a loss function is a squared-error of response variable’s predictions. We use the default setting from the glmnet::coef.glmnet which selects λ_R to be the largest value of λ such that the CV error is within 1 standard error of the minimum CV. For riPEER with λ_R and λ_Q regularization parameters chosen by cross-validation we use a function that is not included in the current version of the mdpeer R package. Specifically, regularization parameters (λ_Q, λ_R) are chosen in 10-fold cross-validation procedure over a fixed 2-dimensional grid of (λ_Q, λ_R) parameter values: ${\{\mathit{exp}(l_i)\}}_{i=1}^{12}$, where ${\{l_i\}}_{i=1}^{12}$ is a sequence of equally spaced values between −4 and 9. We select a pair of values (λ_Q, λ_R) which yields the minimum squared prediction errors averaged over the 10 folds.

4.4 Simulation results

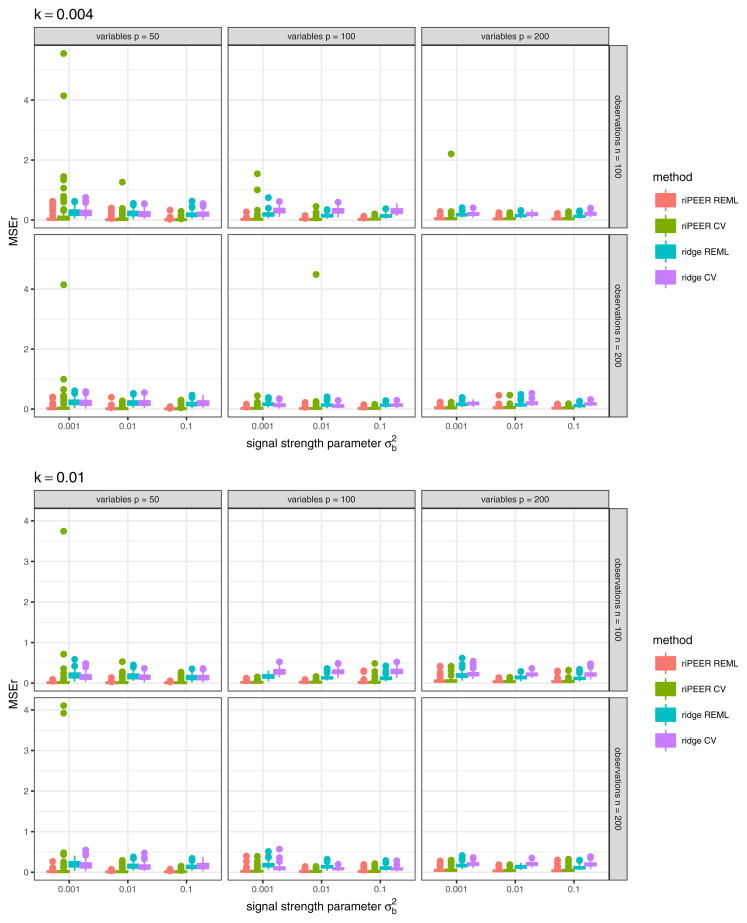
4.4.1 Accurate 𝒜_obs connectivity information

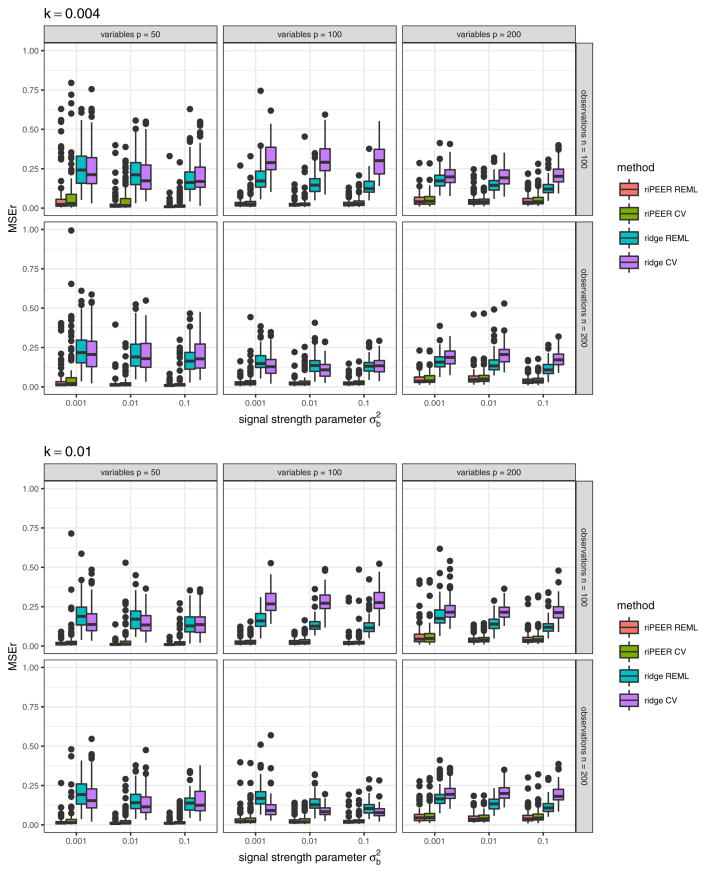
In the first simulation scenario we compare riPEER and ordinary ridge methods and we use both CV and REML to estimate the penalty parameter(s). We assume that a given connectivity matrix, 𝒜_obs, is fully informative. We consider various simulation parameter settings: number of predictors: p ∈ {50, 100, 200}, number of observations: n ∈ {100, 200} signal strength: ${\mathrm{\sigma }}_b^2\in \{0.001,0.01,0.1\}$, strength of correlation between the variables in the matrix Z: k ∈ {0.01, 0.004}.

Table 1 summarizes the relative mean squared error of estimation $\mathit{MSEr}(\widehat{b})={\Vert \widehat{b}-b\Vert }_2^2/{\Vert b\Vert }_2^2$ by a median based on 100 simulation runs for each simulation setting and each method considered. We also report Eff values for Eff defined as

Table 1.

b estimation relative error $\mathit{MSEr}={\Vert \widehat{b}-b\Vert }_2^2/{\Vert b\Vert }_2^2$, summarized by a median value over 100 simulation runs in case of informative connectivity information input. MSEr values are summarized for each combination of the simulation parameters (number of observations n, number of variables p, strength of correlation k between the variables in the matrix Z, signal strength ${\mathrm{\sigma }}_b^2$) and each estimation method considered. Eff values are reported, for Eff defined as Eff (method A, method B) = (MSEr of method B - MSEr of method A)/(MSEr of method B) × 100 %.

	n	p	k	${\mathrm{\sigma }}_b^2$	MSEr riPEER REML	MSEr riPEER CV	MSEr ridge REML	MSEr ridge CV	Eff (riPEER REML, riPEER CV)	Eff (ridge REML, ridge CV)	Eff (riPEER REML, ridge REML)
1	100	50	0.004	0.001	0.023	0.030	0.242	0.212	23%	−14%	90%
2	100	50	0.004	0.01	0.011	0.017	0.211	0.173	35%	−22%	95%
3	100	50	0.004	0.1	0.009	0.011	0.163	0.169	18%	4%	94%
4	100	50	0.01	0.001	0.013	0.017	0.189	0.137	24%	−38%	93%
5	100	50	0.01	0.01	0.010	0.013	0.171	0.134	23%	−28%	94%
6	100	50	0.01	0.1	0.009	0.013	0.128	0.137	31%	7%	93%
7	100	100	0.004	0.001	0.023	0.026	0.172	0.289	12%	40%	87%
8	100	100	0.004	0.01	0.019	0.022	0.146	0.291	14%	50%	87%
9	100	100	0.004	0.1	0.022	0.028	0.124	0.301	21%	59%	82%
10	100	100	0.01	0.001	0.019	0.021	0.160	0.268	10%	40%	88%
11	100	100	0.01	0.01	0.020	0.024	0.127	0.272	17%	53%	84%
12	100	100	0.01	0.1	0.018	0.021	0.116	0.276	14%	58%	84%
13	100	200	0.004	0.001	0.040	0.044	0.173	0.198	9%	13%	77%
14	100	200	0.004	0.01	0.038	0.041	0.144	0.192	7%	25%	74%
15	100	200	0.004	0.1	0.037	0.041	0.120	0.202	10%	41%	69%
16	100	200	0.01	0.001	0.045	0.048	0.176	0.215	6%	18%	74%
17	100	200	0.01	0.01	0.035	0.038	0.140	0.215	8%	35%	75%
18	100	200	0.01	0.1	0.036	0.041	0.120	0.213	12%	44%	70%
19	200	50	0.004	0.001	0.014	0.021	0.218	0.206	33%	−6%	94%
20	200	50	0.004	0.01	0.011	0.014	0.190	0.179	21%	−6%	94%
21	200	50	0.004	0.1	0.009	0.011	0.164	0.178	18%	8%	95%
22	200	50	0.01	0.001	0.012	0.014	0.193	0.154	14%	−25%	94%
23	200	50	0.01	0.01	0.009	0.011	0.141	0.115	18%	−23%	94%
24	200	50	0.01	0.1	0.010	0.012	0.138	0.125	17%	−10%	93%
25	200	100	0.004	0.001	0.022	0.025	0.148	0.128	12%	−16%	85%
26	200	100	0.004	0.01	0.019	0.021	0.136	0.108	10%	−26%	86%
27	200	100	0.004	0.1	0.020	0.024	0.131	0.134	17%	2%	85%
28	200	100	0.01	0.001	0.021	0.023	0.169	0.091	9%	−86%	88%
29	200	100	0.01	0.01	0.017	0.019	0.128	0.083	11%	−54%	87%
30	200	100	0.01	0.1	0.017	0.019	0.104	0.078	11%	−33%	84%
31	200	200	0.004	0.001	0.037	0.038	0.157	0.187	3%	16%	76%
32	200	200	0.004	0.01	0.047	0.050	0.133	0.205	6%	35%	65%
33	200	200	0.004	0.1	0.034	0.038	0.108	0.171	11%	37%	69%
34	200	200	0.01	0.001	0.045	0.046	0.165	0.194	2%	15%	73%
35	200	200	0.01	0.01	0.035	0.039	0.133	0.200	10%	34%	74%
36	200	200	0.01	0.1	0.038	0.044	0.108	0.182	14%	41%	65%

$$\mathit{Eff}(\text{method}\text{A},\text{method}\text{B})=(\mathit{MSEr}\text{of}\text{method}\text{B}-\mathit{MSEr}\text{of}\text{method}\text{A})/(\mathit{MSEr}\text{of}\text{method}\text{B})\times 100\%,$$

where “MSEr of method X” refers to an aggregated value of MSEr we report alongside in Table 1. Therefore, positive value of Eff (method A, method B) is the percentage reduction of an aggregated value of MSEr obtained by method A compared to method B whereas negative value of Eff (method A, method B) is the percentage gain of an aggregated value of MSEr obtained by method A compared to method B.

We can observe that riPEER method that uses REML for the selection of the tuning parameters outperforms riPEER that uses CV. More precisely, Eff (riPEER REML, riPEER CV) ranges from 2%to 35%, meaning we observe between 2%and 35% percentage reduction of an aggregated value of MSEr obtained by riPEER REML compared to riPEER CV, depending on the simulation setting. Notably, relatively high values of Eff (riPEER REML, riPEER CV) are obtained in simulation settings with the smallest number of predictors considered, p = 50. Also, for riPEER CV we observe a number of outliers in MSEr. These outliers are more numerous and more severe than for the corresponding riPEER REML method (see Figures 14 and 15 in the Appendix A). This is consistent with the work of P. T. Reiss (2009), where the authors noted that in their simulations cross-validation failed to find the global optimum of corresponding optimization problem more often than REML.

We do not observe any consistent dominance of ordinary ridge that uses REML for the selection of the tuning parameter over ordinary ridge that uses CV. The values of Eff (ridge REML, ridge CV) statistic range from −86% to 59% and mean of these values is 8%. Since the mean of Eff (ridge REML, ridge CV) values obtained is positive, we continue to use REML procedure for the selection of the tuning parameter for ordinary ridge later in the simulations.

Finally, in this experiment we observe that using a penalty term based on the connectivity information is more beneficial than using ordinary ridge penalty term. Specifically, we can see that Eff (riPEER REML, ridge REML) ranges from 65% to 95%, meaning we observe 65% to 95% percentage reduction of an aggregated value of MSEr obtained by riPEER REML compared to ridge REML.

4.4.2 𝒜_obs connectivity information with the permuted “true” connections

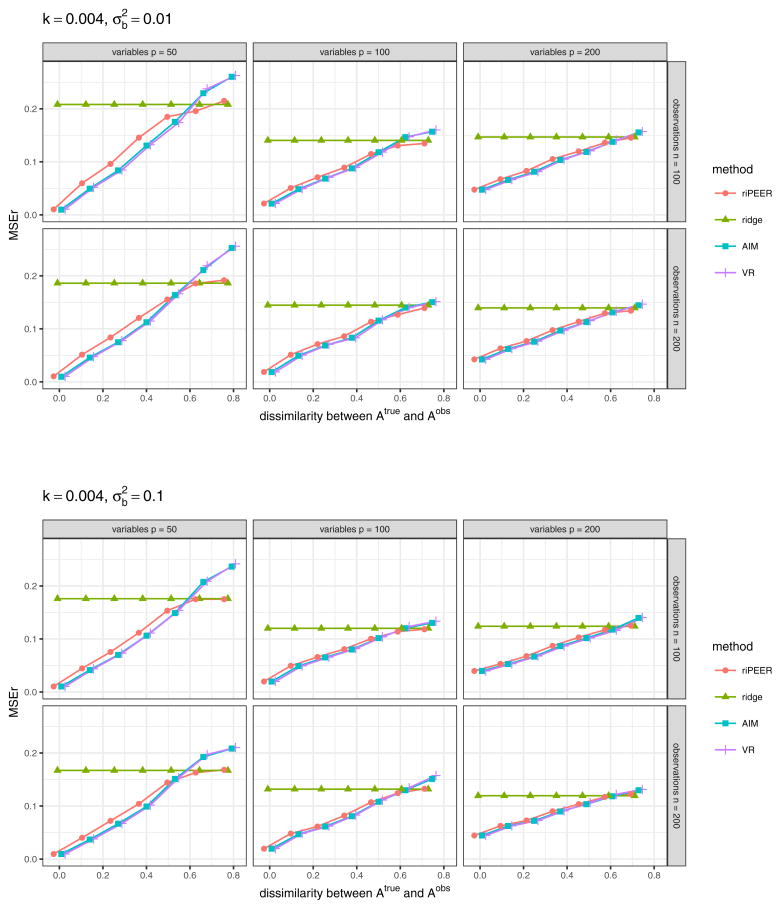
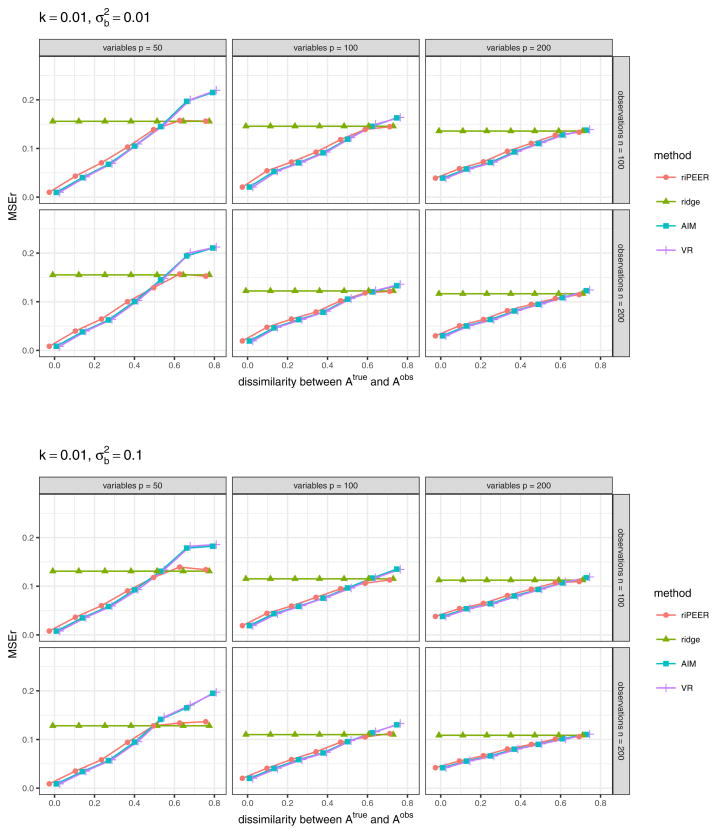
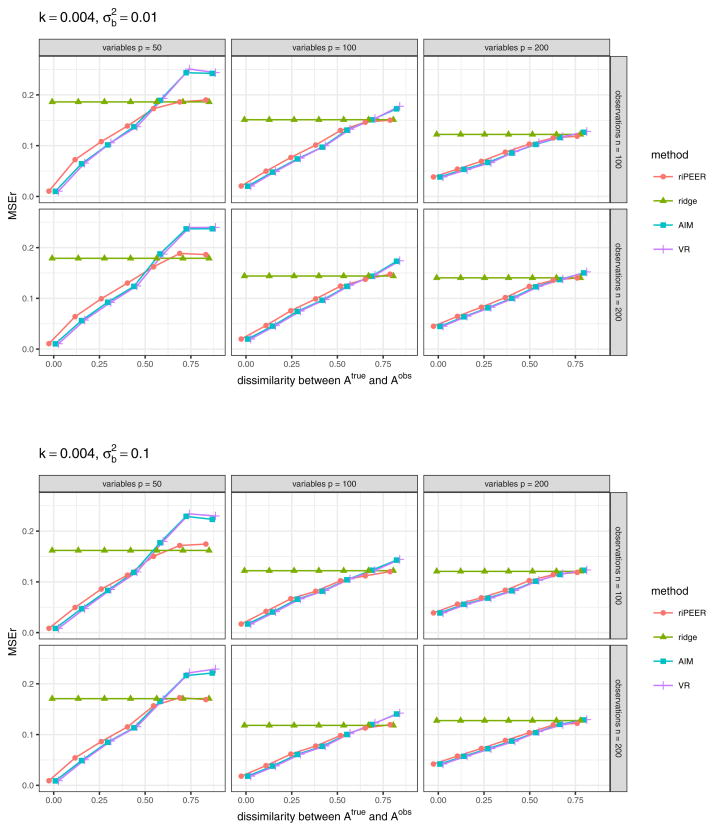
In the second simulation scenario, we investigate the behavior of riPEER in the case of decreasing amount of “true” information contained in the connectivity matrix 𝒜_obs. We construct 𝒜_obs by permuting the “true” connections from 𝒜_true, as described in the second paragraph of Section 4.2. We compare riPEER method with the ordinary ridge, AIM and VR methods. For all methods considered in the experiment, REML approach is used to select regularization parameter(s). We consider the following simulation parameter settings: number of predictors p ∈ {50, 100, 200}, number of observations n ∈ {100, 200}, signal strength ${\mathrm{\sigma }}_b^2\in \{0.01,0.1\}$, strength of correlation between the variables in the Z matrix k ∈ {0.004, 0.01}, different values of dissimilarity between 𝒜_true and 𝒜_obs (marked by the x-axis labels).

Figure 7 displays the aggregated (median) values of the relative estimation error based on the 100 simulation runs in a case when 𝒜_obs matrix used in model estimation is obtained via randomization procedure which preserves the original graph’s density, degree distribution and degree sequence, for experiment setting parameters k = 0.01, ${\mathrm{\sigma }}_b^2=0.01$. The results for other combinations of experiment setting parameters k and ${\mathrm{\sigma }}_b^2$ are presented in Figures 16 and 17 (Appendix A).

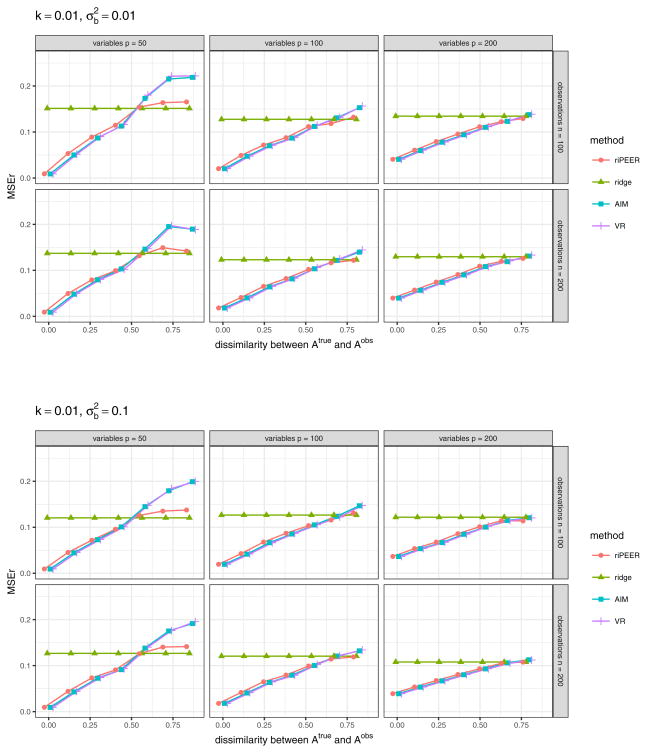
Fig. 7.

b estimation relative error $\mathit{MSEr}={\Vert \widehat{b}-b\Vert }_2^2/{\Vert b\Vert }_2^2$ values obtained in numerical experiments with the partially informative connectivity information input (graph rewiring with the original graph’s degree distribution preserved) for REML estimation methods: riPEER, ridge, AIM, VR. Error values are aggregated (median) out of 100 experiment runs for different combinations of simulation setup parameters: number of variables p ∈ {50, 100, 200} (left, central and right panels, respectively), number of observations n ∈ {100, 200} (top and bottom panels, respectively), level of dissimilarity between 𝒜_true and 𝒜_obs diss marked by x-axis labels, strength of correlation between the variables in the Z matrix k, signal strength ${\mathrm{\sigma }}_b^2$ . Here, k = 0.01, ${\mathrm{\sigma }}_b^2=0.1$

Figure 8 displays aggregated (median) values of the relative estimation error based on 100 simulation runs in a case when 𝒜_obs matrix used in model estimation is obtained via randomization procedure which preserves the original graph’s density only, for experiment setting parameters k = 0.01, ${\mathrm{\sigma }}_b^2=0.01$. The results for other combinations of experiment setting parameters k and ${\mathrm{\sigma }}_b^2$ are presented in Figures 18 and 19 (Appendix A).

Fig. 8.

b estimation relative error $\mathit{MSEr}={\Vert \widehat{b}-b\Vert }_2^2/{\Vert b\Vert }_2^2$ values obtained in numerical experiments with the partially informative connectivity information input (graph rewiring with a constant probability for a graph edge to be rewired) for REML estimation methods: riPEER, ridge, AIM, VR. Error values are aggregated (median) out of 100 experiment runs for different combinations of simulation setup parameters: number of variables p ∈ {50, 100, 200} (left, central and right panels, respectively), number of observations n ∈ {100, 200} (top and bottom panels, respectively), level of dissimilarity between 𝒜_true and 𝒜_obs diss marked by x-axis labels, strength of correlation between the variables in the Z matrix k, signal strength ${\mathrm{\sigma }}_b^2$. Here, k = 0.01, ${\mathrm{\sigma }}_b^2=0.1$

Plots in Figures 7 and 8 present very similar trends in the estimators’ behavior. Specifically, we can observe that when the connectivity information is exploited in estimation, riPEER, AIM and VR outperform or behave no worse than the ordinary ridge estimation method in simulation scenarios with low and moderate values of dissimilarity between 𝒜_true and 𝒜_obs (dissimilarity between 0 and 0.5). For the extreme values of dissimilarity between 𝒜_true and 𝒜_obs (dissimilarity approaching 0.8), AIM and VR start to perform slightly worse than the ordinary ridge. riPEER exhibits the adaptiveness property to the amount of true information contained in the penalty matrix; it results in like AIM or VR estimators in simulation scenarios with low and moderate dissimilarity between 𝒜_true and 𝒜_obs and yields results similar to ridge for the extreme values of dissimilarity between 𝒜_true and 𝒜_obs. Note that AIM and VR yield almost identical results for each combination of the simulation parameters considered.

Similar trends of estimation methods performance are observed for other combinations of simulation parameter values. in the case with 𝒜_obs matrix used in model estimation obtained via randomization procedure which preserves the original graph’s density, degree distribution and degree sequence, a complete set of aggregated MSEr values obtained is presented in Figures 16 and 17 (Appendix A). In the case with 𝒜_obs matrix used in model estimation obtained via randomization procedure which preserves the original graph’s density only, a complete set of aggregated MSEr values obtained is presented in Figures 18 and 19 (Appendix A).

4.4.3 𝒜_obs connectivity information with a presence of false negatives and false positives

In the third simulation scenario, we investigate the behavior of riPEER in the presence of false negative and false positive connections in the given graph adjacency matrix 𝒜_obs. We express the presence of false negatives and false positives by decreasing or increasing density of 𝒜_obs compared to 𝒜_true graph adjacency matrix, as described in the last paragraph of Section 4.2. We compare riPEER method with the ordinary ridge, AIM and VR methods. For all methods considered in the experiment, REML approach is used to select regularization parameter(s). We consider the following simulation parameter settings: number of predictors p ∈ {50, 100, 200}, number of observations n ∈ {100, 200}, signal strength ${\mathrm{\sigma }}_b^2=0.01$, strength of correlation between the variables in the Z matrix k = 0.01.

Figure 9 shows values of aggregated MSEr (median aggregation) based on 100 simulation runs. Clearly, the methods which use regularization based on the adjacency matrix 𝒜_obs – riPEER, AIM and VR – indicate relatively lower estimation error compared to the ordinary ridge, for the whole range of ratios of 𝒜_obs density to 𝒜_true density we consider.

Fig. 9.

The effect of using 𝒜_obs of lower and higher density than 𝒜_true density in model estimation. b estimation relative error $\mathit{MSEr}={\Vert \widehat{b}-b\Vert }_2^2/{\Vert b\Vert }_2^2$ values are aggregated (median) out of 100 experiment runs for methods: ridge, AIM, VR, riPEER (with REML used in all cases). The following simulation parameters are considered: number of variables p ∈ {50, 100, 200} (left, middle and right panels, respectively), number of observations n ∈ {100, 200} (top and bottom panels, respectively). Strength of correlation between the variables in the Z matrix is set as k = 0.01, signal strength ${\mathrm{\sigma }}_b^2=0.01$. On x-axis we denote the ratio of 𝒜_obs density to 𝒜_true density. Vertical blue lines denote the point where 𝒜_true and 𝒜_obs are the same.

Surprisingly, even in the case of 20% of the true connections contained in 𝒜_obs matrix, using either riPEER, AIM or VR yields a decrease of the aggregated estimation error by approximately 50% of the aggregated estimation error we obtain with the ordinary ridge. In addition, riPEER, AIM and VR outperform ordinary ridge also in the case where false positive connections are present in 𝒜_obs matrix. This indicates that using riPEER, AIM or VR is beneficial for estimation accuracy even in a case when small amount of true information is contained in a given 𝒜_obs matrix.

As expected, the lowest aggregated MSEr value corresponds to the situation when 𝒜_true and 𝒜_obs are the same (the x-axis point for which the ratio of 𝒜_obs density to 𝒜_true density is equal to one in Figure 9, marked by a vertical line). We observe this behavior in each experiment setting considered.

Note that for all ratios of 𝒜_obs density to 𝒜_true density considered, riPEER, AIM and VR yield similar estimates. This effect is caused by the fact that there is always some information about the true modularity connectivity structure preserved in the adjacency matrices used in model estimation in this experiment. It seems that forcing the usage of such 𝒜_obs in estimation – as in AIM and VR approaches – is beneficial here, as opposed to fully uninformative scenarios.

The numerical experiments conducted show that with an informative connectivity information input, riPEER method yields lower MSEr value than the ordinary ridge method. Results show that riPEER is adaptive to the level of information present in a connectivity matrix. This property stems from the data-driven estimation of the regularization parameters for the ordinary ridge and PEER penalty terms. More precisely, riPEER estimator’s performance is similar to AIM and VR estimators when the connectivity matrix is informative, whereas for an uninformative connectivity matrix riPEER behaves like ordinary ridge.

5 Imaging data application

Using the proposed methods, we model the associations between alcohol abuse phenotypes and structural cortical brain imaging data. Specifically, we utilize cortical thickness measurements obtained using the FreeSurfer software (Fischl 2012) to predict alcoholism-related phenotypes while incorporating the structural connectivity between the cortical regions obtained by Sporns (2013); see also Cole et al (2014); Sporns and Betzel (2016).

Our results for the cortical thickness association were obtained in a large sample of young, largely nonsmoking drinkers. This male-only at risk for alcoholism sample is very different from the studies of older alcoholic subjects recently reported in several articles (Momenan et al 2012; Nakamura-Palacios et al 2014; Pennington et al 2015). The number of reported morphometric differences found in these studies tended to involve the frontal lobe, with the effects considerably weaker in men only and after accounting for substance use. There is no consensus about the laterality of the cortical thinning effects in alcoholics, albeit some of the findings are medial (anterior cingulate cortex, ACC), while others could be explained by more prominent right hemisphere effects of lifetime alcohol exposure (Momenan et al 2012) not yet evident in this younger population.

5.1 Data and preprocessing

Study sample

The sample consisted of 148 young (21–35 years) social-to-heavy drinking male subjects from several alcoholism risk studies. Structural imaging data from 88 subjects were included in the study relating externalizing personality traits and gray matter volume (Charpentier et al 2016), with a subset of these 88 subjects also reported in the studies of dopaminergic responses to beer (Oberlin et al 2013, 2015, n=49 and 28, respectively), and regional cerebral blood flow (Weafer et al 2015, n=44). Subjects’ demographic and a risk for alcoholism-related characteristics are summarized in Table 2.

Table 2.

Study sample subjects’ characteristics.

Study variables	Min	Max	Mean	Median	StdDev
Age	21.0	35.0	24.0	23.0	3.2
Education	11.0	20.0	15.2	15.0	1.5
AUD relativesa	0.0	7.0	1.2	1.0	1.5
AUDITb	3.0	28.0	10.9	10.0	4.9
Drinks per weekc,d	0.4	62.0	16.3	14.9	10.6
Drinks per drinking dayc,d	1.3	23.9	5.9	5.5	3.4
Heavy drinking days per weekc,d	0.0	4.4	1.4	1.4	1.1
Years since first drinkc	2.0	24.0	7.7	7.0	4.1
Years since regular drinkingc	0.0	17.0	5.2	4.0	3.6
Years since first intoxicationc	2.0	24.0	6.9	6.0	3.9
Study variables	Proportion
Smoker	0.09

^aNumber of first or second degree relatives with Alcohol Use Disorder by self-report.

^bAlcohol Use Disorders Identification Test.

^cDrinking data are from the Timeline Followback Interview.

^dDrinking frequency data from past 35 days of a subject’s history.

MRI data acquisition

Brain imaging was performed using the following Siemens 3TMRI scanners/head coils: Trio-Tim/12-channel, Skyra/20-channel and Prisma/20&64-channel at the Indiana University School of Medicine Center for Neuroimaging. For all configurations, whole-brain high resolution anatomical MRI was collected using a 3D Magnetization Prepared Rapid Acquisition Gradient Echo (MP-RAGE) with imaging parameters optimized according to the ADNI (Alzheimer’s Disease Neuroimaging Initiative) protocol (Prisma/Skyra, 5.12 min, 1.05 × 1.05 × 1.2 mm³; Trio-TIM; 9.14 min, 1.0 × 1.0 × 1.2 mm³ voxels).

Cortical measurements

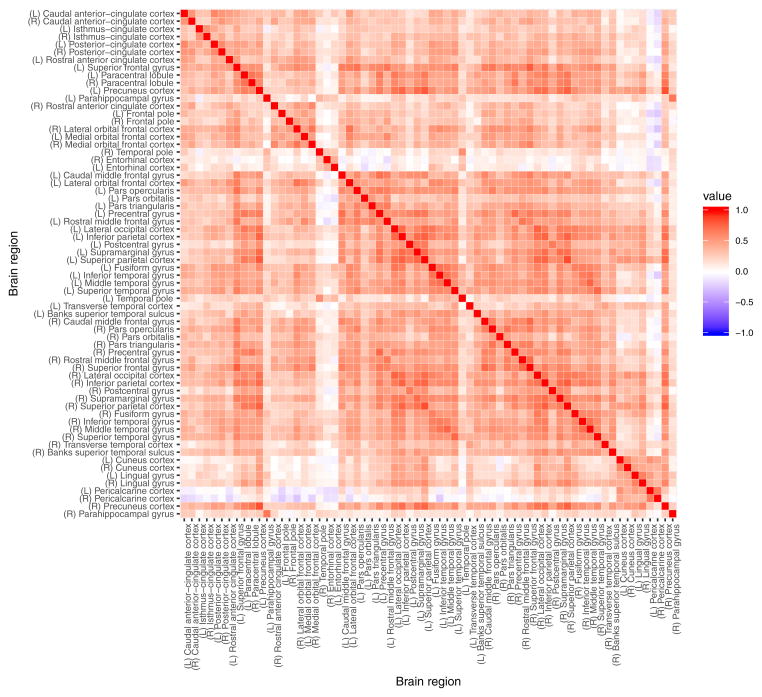
The FreeSurfer software package (version 5.3) was used to process the acquired structural MRI data, including gray-white matter segmentation, reconstruction of cortical surface models, labeling of regions on the cortical surface and analysis of group morphometry differences. The resulting dataset has cortical measurements for 68 cortical regions with parcellation based on Desikan-Killiany atlas (Desikan et al 2006). The subset of 66 variables describing average gray matter thickness (in millimeters) of gray matter brain regions did not incorporate left and right insula due to their exclusion from the structural connectivity matrix. It is important to note that the cortical measurement variables exhibit multicollinearity as evident in the high values of pairwise Pearson correlation coefficient (Figure 20 in the Appendix A).

Structural connectivity information

The established modularity connectivity matrix (see Sporns (2013); Cole et al (2014); Sporns and Betzel (2016)) in which each node belongs to one of five modules (communities) was used in the analysis. To obtain the matrix, structural connectivity weighted network is estimated based on a model proposed by Hagmann et al (2008) using a diffusion map to construct 3D curves of the maximal diffusion coherence. Louvain method (?), a greedy optimization procedure for extracting communities in networks, was then used to identify communities (modules) present in that network. The information about the five communities obtained was coded in a binary modularity matrix, where each entry is 1 for pairs of brain regions belonging to the same module and is 0 for pairs of brain regions belonging to different modules. The resulting 66×66 matrix 𝒜 was used to represent similarities between all brain region pairs. This matrix, illustrated in Figure 12 in the Appendix A, played the role of a structural connectivity adjacency matrix that was used to define Q, illustrated in Figure 13 in the Appendix A.

5.2 Estimation methods

We employed ordinary ridge, AIM, riPEER and VR with REML estimation of the regularization parameter(s) to quantify the association of imaging markers with the drinking frequency. In addition, we fitted both simple and multiple linear regression models to compare the unpenalized regression estimates to the estimates obtained from the regularized regression approach. We used the derived cortical thickness measures from 66 brain regions as predictors of the outcome y = Number of drinks per drinking day and connectivity matrix-derived Laplacian was used as a penalty matrix for AIM, riPEER and VR. For each of the four regularized regression estimation methods, we included Age, Smoker, and Years since the start of regular drinking as non-penalized adjustment variables. Both outcome and predictors were standardized to mean zero and variance equal to one.

5.3 Results

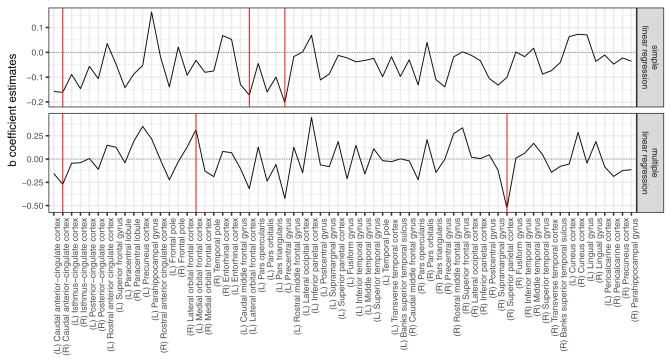
The regression coefficient estimates obtained from both simple and multiple linear regression are presented as black solid lines in Figure 10 in the top and bottom panel, respectively. Statistically significant coefficients (at a nominal level equal to 0.05) are marked with solid red vertical lines.

Fig. 10.

b̂ coefficient estimates obtained from linear regression: simple (upper panel) and multiple (bottom panel). Estimates’ values are denoted with a solid black line. Statistically significant (with a significance level of 0.05) coefficients are denoted with solid red vertical lines.

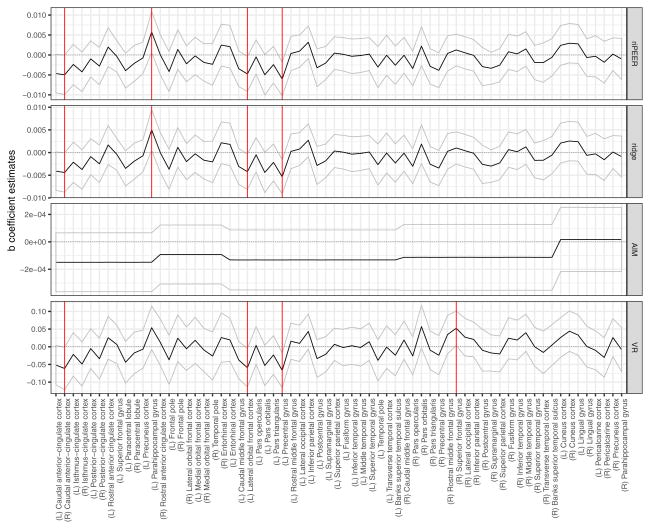
The regression coefficient estimates obtained from the ordinary ridge, AIM, riPEER and VR are presented as black solid lines in Figure 11, top to bottom, respectively. The uncertainty in the estimation of the regression model coefficients is expressed in the form of 95% confidence intervals, indicated by a gray ribbon area around the black solid line. Statistically significant variables are marked with solid red vertical lines. The goodness of fit measured by an adjusted R² was 0.06, 0.05, 0.09 and 0.06 for ridge, AIM, VR and riPEER, respectively. Under considered form of adjacency matrix, VR method works substantially different than others approaches - five modules implied five zero singular values in normalized Laplacian and, consequently, five additional unpenalized variables.

Fig. 11.

b̂ coefficient estimates obtained from riPEER, ridge, AIM and VR linear regression estimation methods. Estimates’ values are denoted with a black solid line. 95% confidence intervals are marked with a ribbon area. Statistically significant variables are denoted with red vertical solid lines.

Simple and multiple linear regression models without regularization both yielded negative association between recent drinking and the right caudal ACC thickness (Figure 10). However, other significant areas differed between simple and multiple regression models with one of the regions (left medial orbital frontal cortex, OFC) exhibiting the positive association with recent drinking. Incorporating the structural connectivity matrix information resulted in three negatively associated regions - right caudal anterior ACC (R-caudACC), left lateral orbitofrontal cortex (L-latOFC), and left precentral gyrus (L-PreCG) for ridge, riPEER and VR estimators (Figure 11). In addition, the cortical thickness of left pars orbitalis showed a trend-level negative association with recent drinking (p-value = 0.06 for ridge and riPEER, p-value = 0.07 for VR). By excluding the ridge penalty, the VR method identified a positive association of recent drinking and the right superior frontal gyrus (R-SFG) thickness.

With three regularization models (ridge, riPEER, VR), we found a negative association between cortical thickness of the right caudal ACC and recent drinking, the same region reported by Pennington et al (2015). A trend-level (p-value=0.06 for Ridge and riPEER; p-value =0.07 for VR) negative association was present in the left caudal ACC thickness. Our finding that the left lateral OFC cortical thickness and recent drinking were negatively related was in agreement with a trend-level cortical thinning of the left OFC in alcohol-only dependent subjects (Pennington et al 2015). We also observed a negative association of recent drinking and the left precentral gyrus thickness, albeit this area was more posterior than the left middle frontal cortex finding in alcoholics (Nakamura-Palacios et al 2014), but was homologous to the right precentral gyrus area found to show age effects in alcoholics (Momenan et al 2012).

None of the brain regions showed positive associations of cortical thickness and recent drinking across all regularization models. The female binge drinkers in Squeglia et al (2012) exhibited an increased cortical thickness in several frontal areas. The positive association of recent drinking and the SFG cortical thickness in the VR model could reflect a similar relationship in our slightly older male sample. The left parahippocampal gyrus finding in ridge and riPEER models was in unexpected direction although the gray matter volume of that area is known to be affected by the smoking status.

For simplicity, the application of our models was restricted to cortical thickness. It is possible that a more comprehensive picture of the brain morphometry deficits would emerge by also examining other measures, such as cortical surface and gray matter volume. Our regression approach is optimized to model predictors across a wide range of risk for alcoholism rather than focusing on well-defined groups, making direct comparisons more challenging. Finally, we excluded the insula because its structural connectivity information was not available in this analysis.

Importantly, the riPEER estimate mirrors that obtained from ridge. Due to the adaptive properties of riPEER, this result suggests that there is limited information relevant to alcohol consumption in the modularity connectivity graph and its influence in the estimation process is not substantial. From a different perspective, in the AIM with a predefined ordinary ridge regularization parameter, the estimation depends predominantly on the structure imposed by the modularity connectivity graph. This structure can be seen in Figures 11 and 12.

6 Discussion

We provided a statistically tractable and rigorous way of incorporating external information into the regularized linear model estimation. Our starting point was a generalized ridge or Tikhonov regularization termed PEER Randolph et al (2012). Here, we analyzed multi-modal brain imaging data with structural cortical information from a high resolution anatomical MRI and structural connectivity information inferred from diffusion imaging scan. Our main goal was to incorporate the structural connectivity information via the Laplacian-matrix-informed penalty in the Tikhonov regularization framework.

A graph Laplacian matrix is singular and the mixed model equivalency framework requires the invertibility of the penalty matrix. To account for this when using a graph Laplacian-derived penalty term in the PEER framework, we introduced three approaches. Specifically, VR reduces the number of penalized variables by excluding those in the null space of Q, while AIM adds a small user-defined multiple of the identity matrix to Q. riPEER similarly adds a multiple of the identity to Q, but the tuning parameter (i.e., the weight given to the this ridge term) is chosen automatically. Consequently, only riPEER is fully adaptive to the amount of information in Q that is relevant to the association between the predictors Z and outcome y.

Although VR and AIM are more computationally efficient, extensive simulations show that riPEER not only performs better when Q contains relevant information, it also performs no worse than ordinary ridge regression when Q is not informative.

The proposed methods to study the associations between the alcohol abuse phenotypes and highly correlated cortical thickness predictors using the structural connectivity information resulted in new clinical findings. By using structural connectivity among 66 cortical regions to define Q the proposed methodology found predictive structural imaging markers for the number of drinks per drinking day measure. Negative associations between cortical thickness and Drinks per drinking day were most evident in left and right caudal ACC, left lateral OFC and left precentral gyrus.

Our future work will incorporate additional brain connectivity information arising from other measures of structural brain connectivity including the fractional anisotropy values and fiber length as well as functional connectivity information. We will also combine more than one type of predictor, i.e. use multiple anatomical measures of cortical regions simultaneously.

A Appendix

Fig. 12.

Adjacency matrix of modularity graph connectivity information, derived from the connectivity of the brain cortical regions (Sporns 2013; Cole et al 2014; Sporns and Betzel 2016). Each node (cortical region) belongs to one of five connectivity modules.

Fig. 13.

Laplacian matrix of modularity graph connectivity information, derived from the connectivity of the brain cortical regions (Sporns 2013; Cole et al 2014; Sporns and Betzel 2016). Each node (cortical region) belongs to one of five connectivity modules.

Fig. 14.

Boxplots of b estimation relative error $\mathit{MSEr}={\Vert \widehat{b}-b\Vert }_2^2/{\Vert b\Vert }_2^2$ values obtained in numerical experiments with the informative connectivity information input, for estimation methods riPEER and ridge, for REML and cross-validation approach to regularization parameter(s) selection. Error values are summarized for different combinations of simulation setup parameters: number of observations n ∈ {100, 200}, number of variables p ∈ {50, 100, 200}, strength of correlation between the variables in the Z matrix k ∈ {0.004, 0.01}, signal strength ${\mathrm{\sigma }}_b^2\in \{0.001,0.01,0.1\}$.

Fig. 15.

Boxplots of b estimation relative error $\mathit{MSEr}={\Vert \widehat{b}-b\Vert }_2^2/{\Vert b\Vert }_2^2$ values obtained in numerical experiments with the informative connectivity information input, for estimation methods riPEER and ridge, for REML and cross-validation approach to regularization parameter(s) selection. Error values are summarized for different combinations of simulation setup parameters: number of observations n ∈ {100, 200}, number of variables p ∈ {50, 100, 200}, strength of correlation between the variables in the Z matrix k ∈ {0.004, 0.01}, signal strength ${\mathrm{\sigma }}_b^2\in \{0.001,0.01,0.1\}$. The y-axis is limited to values between 0 and 1 in order to depict differences in MSEr median values more clearly.

Fig. 16.

b estimation relative error $\mathit{MSEr}={\Vert \widehat{b}-b\Vert }_2^2/{\Vert b\Vert }_2^2$ values obtained in numerical experiments with the partially informative connectivity information input (graph rewiring with the original graph’s degree distribution preserved) for REML estimation methods: riPEER, ridge, AIM, VR. Error values are aggregated (median) out of 100 experiment runs for different combinations of simulation setup parameters: number of variables p ∈ {50, 100, 200} (left, central and right panels in each plot, respectively), number of observations n ∈ {100, 200} (top and bottom panels in each plot, respectively), level of dissimilarity between 𝒜_true and 𝒜_obs diss marked by x-axis labels, strength of correlation between the variables in the Z matrix k, signal strength ${\mathrm{\sigma }}_b^2$. Here, k = 0.004 (both upper and bottom plot), ${\mathrm{\sigma }}_b^2=0.01$ (upper plot) and ${\mathrm{\sigma }}_b^2=0.1$ (bottom plot).

Fig. 17.

b estimation relative error $\mathit{MSEr}={\Vert \widehat{b}-b\Vert }_2^2/{\Vert b\Vert }_2^2$ values obtained in numerical experiments with the partially informative connectivity information input (graph rewiring with the original graph’s degree distribution preserved) for REML estimation methods: riPEER, ridge, AIM, VR. Error values are aggregated (median) out of 100 experiment runs for different combinations of simulation setup parameters: number of variables p ∈ {50, 100, 200} (left, central and right panels in each plot, respectively), number of observations n ∈ {100, 200} (top and bottom panels in each plot, respectively), level of dissimilarity between 𝒜_true and 𝒜_obs diss marked by x-axis labels, strength of correlation between the variables in the Z matrix k, signal strength ${\mathrm{\sigma }}_b^2$. Here, k = 0.01 (both upper and bottom plot), ${\mathrm{\sigma }}_b^2=0.01$ (upper plot) and ${\mathrm{\sigma }}_b^2=0.1$ (bottom plot).

Fig. 18.

b estimation relative error $\mathit{MSEr}={\Vert \widehat{b}-b\Vert }_2^2/{\Vert b\Vert }_2^2$ values obtained in numerical experiments with the partially informative connectivity information input (graph rewiring with constant probability for an edge to be rewired) for REML estimation methods: riPEER, ridge, AIM, VR. Error values are aggregated (median) out of 100 experiment runs for different combinations of simulation setup parameters: number of variables p ∈ {50, 100, 200} (left, central and right panels in each plot, respectively), number of observations n ∈ {100, 200} (top and bottom panels in each plot, respectively), level of dissimilarity between 𝒜_true and 𝒜_obs diss marked by x-axis labels, strength of correlation between the variables in the Z matrix k, signal strength ${\mathrm{\sigma }}_b^2$. Here, k = 0.004 (both upper and bottom plot), ${\mathrm{\sigma }}_b^2=0.01$ (upper plot) and ${\mathrm{\sigma }}_b^2=0.1$ (bottom plot).

Fig. 19.

b estimation relative error $\mathit{MSEr}={\Vert \widehat{b}-b\Vert }_2^2/{\Vert b\Vert }_2^2$ values obtained in numerical experiments with the partially informative connectivity information input (graph rewiring with constant probability for an edge to be rewired) for REML estimation methods: riPEER, ridge, AIM, VR. Error values are aggregated (median) out of 100 experiment runs for different combinations of simulation setup parameters: number of variables p ∈ {50, 100, 200} (left, central and right panels in each plot, respectively), number of observations n ∈ {100, 200} (top and bottom panels in each plot, respectively), level of dissimilarity between 𝒜_true and 𝒜_obs diss marked by x-axis labels, strength of correlation between the variables in the Z matrix k, signal strength ${\mathrm{\sigma }}_b^2$ . Here, k = 0.01 (both upper and bottom plot), ${\mathrm{\sigma }}_b^2=0.01$ (upper plot) and ${\mathrm{\sigma }}_b^2=0.1$ (bottom plot).

Fig. 20.

Pairwise Pearson correlation coefficient for cortical average thickness measurements of 66 brain regions in 148 at risk for alcoholism male subjects.