Thermophysical characterisation of VO₂ thin films hysteresis and its application in thermal rectification

Abstract

Hysteresis loops exhibited by the thermophysical properties of VO₂ thin films deposited on either a sapphire or silicon substrate have been experimentally measured using a high frequency photothermal radiometry technique. This is achieved by directly measuring the thermal diffusivity and thermal effusivity of the VO₂ films during their heating and cooling across their phase transitions, along with the film-substrate interface thermal boundary resistance. These thermal properties are then used to determine the thermal conductivity and volumetric heat capacity of the VO₂ films. A 2.5 enhancement of the VO₂ thermal conductivity is observed during the heating process, while its volumetric heat capacity does not show major changes. This sizeable thermal conductivity variation is used to model the operation of a conductive thermal diode, which exhibits a rectification factor about 30% for small temperature differences (≈70 °C) on its terminals. The obtained results grasp thus new insights on the control of heat currents.

Introduction

The need of controlling and optimizing the performance of electronic devices with enhanced rates of operations has promoted the search for new materials with tailored physical properties¹. Phase change materials (PCMs) characterized by the ability to significantly change their properties in a narrow interval of temperatures², have attracted a lot of interest in electronics because of their ability to guide, rectify, and amplify electrical currents or thermal fluxes^3–7. Vanadium dioxide (VO₂) is one of these PCMs that is currently under intense research due to its reversible metal-insulator transition (MIT) occurring on a picosecond time scale^8–11 for temperatures around 68 °C^12–14. One of the innovative applications of VO₂ consists in using it as one of the terminals of radiative thermal diodes (TDs)^3,4,15,16 operating with a heat flux rectification ratio of 63%¹⁷, which is higher than 29% and 7% obtained for diodes based on carbon¹⁸ and boron nitride nanotubes¹⁹, respectively. In general, the ability of TDs to rectify heat fluxes can be defined by the following rectification factor²⁰ R:

$$R=\left|q_F-q_B\right|/\max \left(q_F,q_B\right)$$ 1

where q_F and q_B are the heat fluxes in the forward and backward configurations of the TDs, respectively. For the case of a radiative TDs, the values of these two heat fluxes are driven by the temperature variations of the VO₂ emissivity, which was already measured and studied^21,22. The sizeable contrast of the values of this property between the insulating and metallic phases of VO₂ also drives the amplification performance of radiative thermal transistors^23–26. By contrast, the thermal performance of conductive TDs and conductive thermal transistors based on VO₂ are determined by its thermal conductivity (k) and volumetric heat capacity (C_v)^27,28, which are not well quantified yet, especially during the heating and cooling processes of VO₂ around its MIT. Previous works focused on the heating process, reported that the effective thermal conductivity (k_eff) of thin films^29,30 and nanobeams³¹ of VO₂ increases during the insulator-to-metal transition; while the heat capacity of VO₂ pellets exhibits a well-defined peak for temperatures within this phase transition^32–34. Taking into account that both the optical^13,35,36 and electrical^37–40 properties of VO₂ exhibit a hysteresis behaviour (i.e., do not yield the same values during the heating and cooling processes at a given temperature within the MIT), its thermal properties are also expected to present this thermal hysteresis. However, this phenomenon has not yet been experimentally neither observed nor quantified on the thermophysical properties of VO₂.

In this work, the hysteresis of the thermophysical properties of VO₂ thin films deposited on either a r-sapphire or silicon substrate are measured along with the film-substrate interface thermal boundary resistance (TBR) R_th (Kapitza thermal resistance)^41,42 by means of a high-frequency photothermal radiometry (PTR)^43–46 technique. The thermal diffusivity (a) and thermal effusivity (e) were directly measured experimentally via the PTR method, and then they were used to determine both k and C_v of the thin films during their heating and cooling processes for temperatures within the VO₂ MIT. In addition, the obtained k are applied to model the operation of a conductive TD and to estimate its rectification factor.

Results

Sample characterisation

VO₂ thin films were deposited on r-sapphire (single crystal of Al₂O₃ cut through the orientation $1\overline{1}02$) and silicon (100) covered by an amorphous native oxide layer (of ∼3–5 nm thickness) substrates through pulsed laser deposition (PLD). The sample made of VO₂ and r-sapphire will be named sample H.1, while the second one H.2. Taking into account that the sapphire substrate and VO₂ films are semi-transparent to the visible light (pump beam of the PTR), a 30 nm-thick Ti layer was deposited on top of the VO₂ films of both samples. For sample H.1, the deposition of Ti (with a purity of 99,99%) was made long after the VO₂ deposition by using an electron-beam physical vapor deposition (EB-PVD, EVA 300 Alliance Concept device) at 5 10⁻⁴ Pa. Whereas, the deposition of the Ti layer on sample H.2 was made after the deposition of the VO₂ film inside another secondary PLD chambers.

The crystallinity and the structural characterisation revealing the microstructure of both samples H.1 and H.2 were carried out by means of an X-ray diffraction (XRD), a field emission scanning electron microscope (FESEM) and an atomic force microscope (AFM), whose patterns/images are shown in Figs S1 and S2 of the supplementary information (SI), respectively. The crystalline structure of samples H.1 and H.2 (Fig. S1) are found strongly depended on their substrates, a r-cut-sapphire monocrystalline (H.1) in one side, and a native amorphous oxide silicon layer on a Si substrate (H.2) on the other side. The SiO₂ amorphous layer is definitively a source of random individual grain organisation having varieties in shapes with grains enlargement in x, y and z directions, leading to a rough film (Fig. S2(f)), meanwhile the r-sapphire substrate tends to organise the grains and lead to low roughness (Fig. S2(e)). The results of the crystalline and structural characterisations of both samples are grouped in Table S1 in the SI.

Thermophysical properties

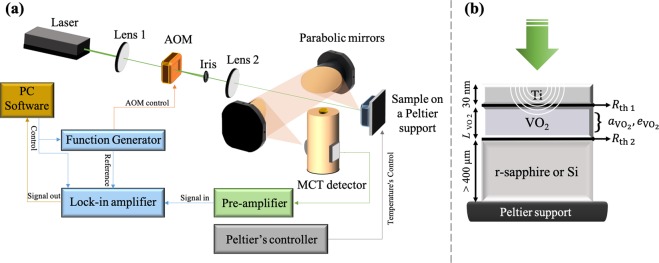
The thermophysical properties of the VO₂ samples were measured by using their infrared emissions recorded after being heated via a laser for modulation frequencies up to 10 MHz, through a high frequency PTR experimental setup shown in Fig. 1(a) (details present in the method section).

Figure 1.

(a) Diagram of the used frequency domain photothermal radiometry (FD-PTR) experimental setup. (b) 1D heating propagation model with TBR and volumetric heat absorption in the first layer of the studied sample placed on a Peltier element with controlled temperature. The white circles in the Ti and VO₂ layers represent the thermal waves induced by the laser heating (green arrow). R_{th 1} is the TBR between the Ti metallic film and the VO₂ while R_{th 2} is the TBR between the VO₂ and the substrate.

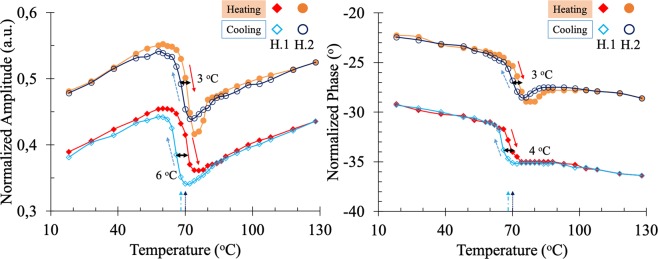
The experimental amplitude and phase of the alternative temperature field recorded on the surface of both samples during their heating and cooling with temperatures from 20 °C to 130 °C, are shown in Fig. 2, for the constant modulation frequency of 1 MHz. The temperature values of the horizontal axis stand for the sample temperature resulting from the sum of the Peltier’s and the laser’s heating temperatures (an additional steady (DC) temperature raise of 8 °C has been experimentally observed and added to the sample temperature due to the laser’s heating). Note that both the amplitude and phase exhibit a clear hysteresis loop formed between the heating and cooling processes. The temperature variations of the amplitudes before and after the MIT is mainly due to the non-linearity of the PTR measurement⁴⁷ and to the variation of the emissivity of the samples^21,22, and therefore only the phase reflects the variation of thermophysical properties of the sample. Note that the phases of both samples change about 4° across their MIT at a transition temperature of 68 °C and 70 °C for sample H.1 and H.2, respectively. This suggests that the thermophysical properties of the VO₂ thin films will also exhibit similar variations between the insulating and metallic phases.

Figure 2.

Experimental amplitude and phase of the temperature field recorded on the samples surface by using PTR at 1 MHz. The solid red and dashed blue arrows represent the heating and cooling processes of samples, respectively. Meanwhile the dashed-doted and doted arrows in the temperature axis represent the MIT temperature for sample H.1 and H.2, respectively.

In order to extract the thermophysical properties of the VO₂ films, a frequency scan from 20 KHz to 10 MHz has been performed for various temperatures during their heating and cooling across the MIT, as shown in Fig. S3 of SI. A 1D thermal characterization of the VO₂ films has been applied by analysing the amplitude and phase of the PTR signals recorded at each temperature, through a 1D quadrupole based model^48,49 that takes into account a volumetric heat absorption in the first layer, as detailed in the theoretical section, below.

Afterwards, sensitivity calculations⁵⁰ on the most significant parameters were performed. According to these sensitivities shown in Figs S4 and S5 of the SI, the amplitude and phase of the PTR signal are sensitive to the VO₂ thermophysical properties for high modulation frequencies up to 10 MHz. The influence of the Ti coating through the Ti/VO₂ interface TBR (R_{th 1}) is generally negligible compared to that of the substrates through the VO₂/substrate TBR (R_{th 2}). The thermal diffusivity (a), thermal effusivity (e) of VO₂ along with R_{th 2} were treated as fitting parameters and extracted from frequency scans of the PTR signals (example in Fig. S3) using a Gauss-Newton algorithm. The input parameters (thermophysical properties of Ti, r-sapphire, and Si) for this algorithm were taken from literature^51,52, while R_{th 1} was modelled with a decay law described by P. Hopkins⁵³ and E.T. Swartz & R.O. Pohl⁵⁴. This law considers that the TBR of a metal-dielectric interface decreases as temperature increases, which is confirmed by the acoustic^42,55 and diffusion⁵⁶ mismatch models as well as molecular dynamics simulations⁵⁷.

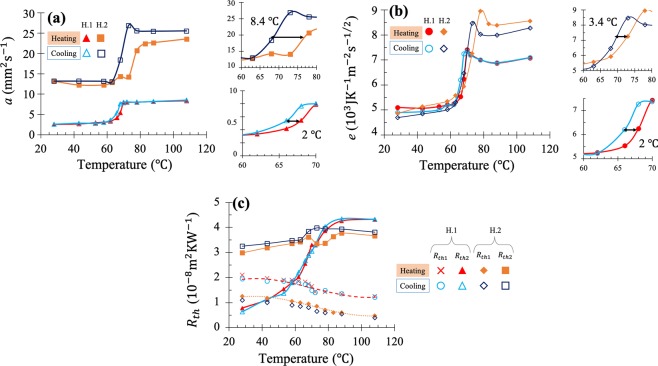
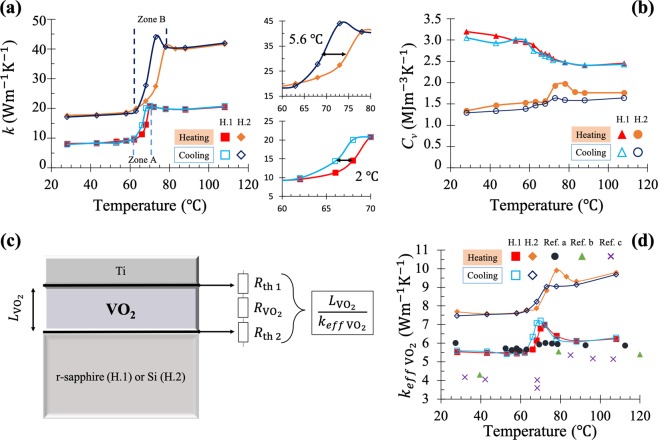
The temperature evolution of the VO₂ thermophysical properties a and e fitted for samples H.1 and H.2 are shown in Fig. 3(a,b), respectively; while the obtained values for both TBRs are displayed in Fig. 3(c). Both k and C_v were then determined through the relations: $k=e\sqrt{a}$ and $C_v=e/\sqrt{a}$, whose results are shown in Fig. 4(a,b), respectively. In addition, the effective thermal conductivity k_eff of the VO₂ films with thickness L, taking into account the effect of both TBRs R_{th 1} and R_{th 2}, has also been calculated through the well-known relation of thermal resistances in series⁴² (Fig. 4(c)): $L/k_{eff}=L/k_{{\mathrm{VO}}_2}+R_{\mathrm{th}1}+R_{\mathrm{th}2}$, and its values are reported in Fig. 4(d). The uncertainties over all properties were then computed using a least square algorithm⁵⁸ which considers the uncertainties of the experimental noise and the input parameters in the model, as detailed in the SI. Their values were found equal to ±30% for a, ±10% for e, ±15% for R_{th 2}, and ±18% for both k and C_v.

Figure 3.

Temperature evolution of the (a) thermal diffusivity and (b) thermal effusivity of both VO₂ films along with their (c) TBRs with the Ti layer and their substrates, obtained from the PTR measured signals. Dashed and dotted lines in (c) stand for the decay law used for R_{th 1}. The insets at the right in (a) and (b) show closeups of the zone of the transition.

Figure 4.

(a) Thermal conductivity and (b) volumetric heat capacity of the two VO₂ films, as functions of their temperature. (c) Circuit of the two TBRs in series with the thermal resistance of the VO₂ layer and its corresponding (d) effective thermal conductivity. Zone A and B in the thermal conductivity plot (a) represents the MIT phase transition zone of each sample. While in (d) Ref. a represent the results of Lee et al.³¹ for k_effof VO₂ nanobeam; Ref. b the k_eff of thin VO₂ film deposited on c-sapphire substrate (0001) by Oh et al.²⁹; and Ref. c the k_eff of thin VO₂ film deposited on quartz glass substrate by Kizuka et al.³⁰.

Discussion

Before discussing the thermophysical properties determined for the two VO₂ films, the assumed decaying law for R_{th 1} is going to be examined. This decaying of R_{th 1} as temperature raises (dashed and dotted lines in Fig. 3(c)) was taken because numerous studies on metal-dielectric and metal-metal interfaces reported this behaviour associated to the electron-electron coupling, which favours the interfacial heat transport through metal-metal interfaces^45,53,59. The difference between the absolute values of R_{th 1} of the two samples are not the same because the Ti layer on sample H.1 was made long after the VO₂ one, while for H.2 the Ti was shortly deposited after the VO₂, as pointed out in the previous section. Because of this assumption, a 15% of uncertainty has been added to R_{th 1} of sample H.1, through the least square algorithm used in our calculations. The impact of this error on the uncertainties of the other parameters is small, because its variation between 10-20% only changes by 2% the uncertainties of a and e.

Contrary to the Ti/VO₂ TBR R_{th 1}, the VO₂/substrate TBR R_{th 2} of both samples increases with temperature across the MIT (Fig. 3(c)), such that R_{th 2} becomes higher than R_{th 1} in the metallic phase. This fact is reasonable because of the atomic modification of the interface after the transition degrade its quality to conduct heat through the VO₂/substrate boundary. The significant difference between the values of R_{th 2} for samples H.1 and H.2 is due not only to their different substrates, but also to the presence of the very thin layer of native SiO₂ between the VO₂ film and its Si substrate.

Meanwhile, Fig. 3(a,b) display the influence of the MIT on a and e of both VO₂ films. Both a and e follow a similar temperature evolution with narrow hysteresis loops, at transition temperatures around 65 and 68 °C for samples H.1 and H.2 respectively (slightly different from the temperatures of the experimental phase transition shown in Fig. 2). Interestingly, the VO₂ films on samples H.1 and H.2 have practically the same e in the insulating phase (low temperature), while in the metallic phase the thermal effusivity of sample H.2 is higher than that of H.1. It is thus clear that silicon enables the growth of VO₂ films with a higher e variation than r-sapphire, across the MIT. This is also the case of the VO₂ a shown in Fig. 3(a) and therefore of the VO₂ k displayed in Fig. 4(a).

For the VO₂ film of sample H.1, k varies from 8.2 Wm⁻¹K⁻¹ in the insulating phase to 20.5 Wm⁻¹K⁻¹ in the metallic one, while for sample H.2, it goes from 16.9 to 42.2 Wm⁻¹K⁻¹, which represents a 2.5 enhancement of k through the MIT. These sizeable increases of k can be attributed to the complex redistribution and interactions of electrons (charge) and phonons (lattice) as well as to the spin and orbital degrees of freedom appearing during the MIT of VO₂ which is a highly correlated electronic material^9,10,60–62. At high temperatures, in this kind of non-Fermi liquids, the charge and heat are independently transported by distinct diffusive modes rather than carried by quasiparticles or momentum relaxation^63,64. Thus, the increase of k is attributed to the presence of a new heat transport channel in the VO₂ metallic phase associated to electronic interactions. This is explained by the fact that before the MIT (in the insulator phase) the heat conduction is dominated mainly by the lattice (phonon)^31,65, whereas in the metallic phase both the electronic and lattice contributions are interconnected due to a redistribution and interactions of charges^30,31,65,66. Hence, the difference between the absolute values of $k_{{\mathrm{VO}}_2}$ for samples H.1 and H.2 is mainly due to the phonon mean free path which is linked to their crystallinity driven by their substrates, as shown by the XRD patterns in Fig. S1^67,68. Furthermore, the presented differences in the hysteresis loops width is mainly linked to the nature of the substrate and the granularity of the VO₂, as reported in the literature^21,69,70. In a VO₂ single crystal, during the MIT, physical properties present strong variations (a variation of electrical resistivity of five orders of magnitude and more than 80% of optical transmission in the near IR range) in a very narrow temperature range (less than 1 K) around the transition temperature. In this paper, the two PLD VO₂ thin films are composed by a collection of grains Fig. S2. Each grain can be a single small crystal and the global behavior of the films can be explained on one hand by each intrinsic VO₂ single crystal properties combined on the other hand to the collective grain effect due to the microstructure of such particular thin films. Considering both samples, an approach can be based on heterogeneous nucleation⁷¹ and the grain size, shape, orientation and coupling would be crucial on the overall properties⁷².

The various shapes present in the VO₂ thin film, grown on Si/SiO₂ (sample H.2) are a consequence of the multitude of cristalline orientations linked to the SiO₂ native amorphous surface. VO₂ grains developed on Si/SiO₂ substrate present various shapes and a high rugosity (root mean square deviation (AFM) Rq = 40 nm) and peak to peak value (161 nm). These disorganized grains with 3D random shape (average size x = 320 nm, y = 350 nm and z = 161 nm) are decoupled to each other, increasing the density of grain boudaries and porosity.

It has been demonstrated that VO₂ grown on r-sapphire (sample H.1) induces a good coupling between grains (x = 200 nm, y = 650 nm and z = 28.6 nm). The single-crystal-substrate induces the growth of partially ordered grains which contributes to qualitatively improve the coupling between the substarte and the VO₂⁷³. The rugosity (Rq = 4 nm) and peak to peak values are lower than those presented for VO₂ on SiO₂/Si (divided respectively by 2 and 10). As a result, the density of grain boundaries, porosity and associated defects decreased leading to a stronger and sharper transition. Consequently, VO₂ thin films synthesized on SiO₂/Si (sample H.2) present wider thermal conductivity hysteresis equal to 5.6 °C compared to 2 °C (for sample H.1 using r-sapphire), and it has a longer phase transition (the MIT transition zone for sample H.2(zone B)) larger than the one of sample H.1 (zone A) in (Fig. 4(a)), similar to the emissivity hysteresis loops of analogous VO₂ systems²¹.

Moreover, the values of k_eff for sample H.1 (Fig. 4(d)) are close to the previous ones reported in the literature^29–31, for the heating process of VO₂ nanobeams and thin films. This consistence of the literature values with k_eff and not with k is explained by the fact that the TBR between the VO₂ film and its substrate was not explicitly considered in those previous works, which leads them to determine the effective thermal conductivity of their VO₂ samples. Besides, as shown in the same figure (Fig. 4(d)), k_eff found by Oh et al.²⁹ (green triangles) for thin VO₂ films deposited on c-sapphire substrate is lower than the one obtained in this study using r-sapphire substrate (red squares). Hence, knowing that both c-(0001) and r-($1\overline{1}02$) cut-sapphire are ideal substrates for VO₂ growth, due to their relatively small lattice mismatch, this difference in k_eff is linked to the orientation and nature of the VO₂ thin films grown on either sapphire single crystals⁷⁴.

The volumetric heat capacity C_v shown in Fig. 4(b) for the VO₂ film in sample H.2 exhibits a characteristic peak within the MIT, especially during the heating process, as was observed in previous works^32–34, while it keeps nearly constant for most temperatures outside the MIT. By contrast, the C_v for sample H.1 tends to decrease as the temperature increases without a clear peak for neither the heating nor the cooling processes. The significant differences on the values and temperature behaviour of the volumetric heat capacity of both VO₂ films is associated to their differences in crystallinity (Fig. S1) and grain structure (Fig. S2), as was elucidated in previous studies^37,39,75, as well as to a possible VO₂ thermal dilatation (volume expansion)⁷⁵, which is not taken into account in the used model. On the other hand, according to the sensitivity analysis (Figs S4 and S5) and the Gauss-Newton fitting procedure, it is possible to say first that the thermal effusivity results are more reliable, than the thermal diffusivity and thermal resistance ones. Secondly, the sensitivities of the PTR measurements on the VO₂ thermophysical properties and especially on R_{th 2} are higher for sample H.2 (Figs S4,S5). Consequently, the VO₂ thermophysical properties for sample H.2 are more accurate and reasonable than those for sample H.1 due to a more conductive substrate (k_r−sapphire ≈ 31.9 Wm⁻¹K⁻¹ and k_{intrinsic Si} ≈ 148 Wm⁻¹K⁻¹)^51,52. Therefore, they can be taken as a reference of the thermal characterization of VO₂ films.

Another important point is the anomalous behaviour in the form of a small peak in the k results of the VO₂ (Fig. 4(a)). The peaks that results from those appearing in the a and e (Fig. 3(a,b)) are similar to the ones observed in the behaviour of the emissivity^21,22, thermal conductivity^29,30, electrical conductivity³¹ and optical properties³⁶ of VO₂, and are not very well understood. VO₂, as mentioned in this discussion section, is a correlated electronic material in which the change in the comportment of electrons and phonons that occur with a change of the crystalline structure of VO₂ during the phase transition is still not well comprehended. Further investigations are hence necessary to shed more light on this anomalous behaviour.

Application in thermal rectification

The measured temperature variations of the VO₂ thermal conductivity $k_{{\mathrm{VO}}_2}(T)$ is now applied to assess R (Equation 1) of a conductive TD with VO₂ terminal (PCM) exchanging heat by conduction with a non-PCM, as shown in Fig. 5. In the forward bias (Fig. 5(a)), the steady-state heat flux q_F flows from the VO₂ terminal toward the non-PCM, while in the backward bias, an opposite direction heat flux q_B occurs. The values of q_F and q_B are determined by the respective thermal conductivities of the VO₂ ($k_{{\mathrm{VO}}_2}(T)$) and the non-PCM (k₂), and their difference (q_F ≠ q_B) is driven by the temperature dependence of $k_{{\mathrm{VO}}_2}(T)$ inside the VO₂ phase transition (zones A and B in Fig. 4(a))⁷⁶. For the sake of simplicity, we consider that inside these zones, k₂ is independent of temperature and remains constant for both the forward and backward biases. The asymmetry of $k_{{\mathrm{VO}}_2}(T)$ around its transition temperature T₀ allows hence to optimize the difference q_F−q_B by setting T_c < T₀ < T_h.

Figure 5.

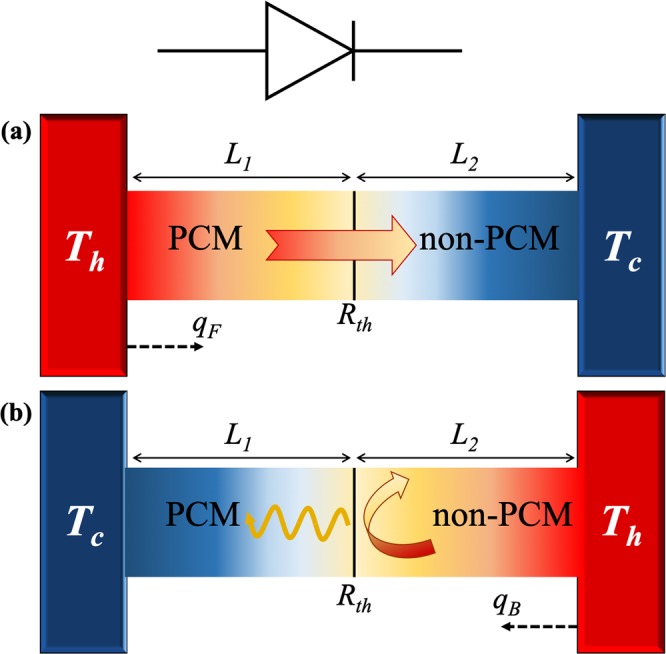
Scheme of a conductive thermal diode made up from a PCM and non-PCM in the (a) forward and the (b) backward configurations. Hot and cool thermal baths are set at temperatures T_h and T_c, respectively. The combined effect of the local transitions of the VO₂ puddles^13,37 is taken into account through the overall transition temperature T₀ in Eq. (3).

Taking into account that k of a material is defined by the Fourier’s law of heat conduction, the experimental values of k_VO2 shown in Fig. 4(a) indicates that we can apply this law to describe the heat conduction in VO₂. According to this law and Fig. 5(a), the heat flux q_F is given by

$$q_F=-k_{{\mathrm{VO}}_2}\left(T_1\right)\frac{d{T}_1}{dx}=-k_2\frac{d{T}_2}{dx},$$ 2

with T₁(x) and T₂(x) the VO₂ (for 0 < x < L₁) and the non-PCM (for L₁ < x < L₁ + L₂) temperatures, respectively. Based on Fig. 4(a), the measured $k_{{\mathrm{VO}}_2}$ can be modelled as follows

$$k_{{\mathrm{VO}}_2}\left(T\right)=k_d+\frac{k_m-k_d}{1+e^{-\beta (T-T_0)}},$$ 3

using k_d and k_m as the thermal conductivities in the insulating/dielectric (low temperature) and metallic (high temperature) phases, respectively. While T₀ represents the transition temperature and β the phase-transition slope of $k_{{\mathrm{VO}}_2}\left(T\right)$at T = T₀. The values of these parameters were calculated by fitting Equation (3) to the experimental data shown in Fig. 4(a) and are summarized in Table 1. The integration of Equation (2) under the usual boundary conditions of the temperature discontinuity (T₁(L₁) − T₂(L₁) = −R_thk₂dT₂/dx) and heat flux continuity (−k_VO2(T₁)dT₁/dx = −k₂dT₂/dx) at the interface x = L₁, yields

$$q_F=-\frac{1}{\beta \lambda {\rho }_m}\ln \left[\frac{f(T_h)}{f(T_c+\rho q_F)}\right],$$ 4

where ρ_m = L₁/k_m, λ = k_m/(k_m − k_d), f(T) = [1 + Z(T)]/Z(T)^λ, Z(T) = exp(−β(T − T₀)), and ρ = L₂/k₂ + R_th, with R_th being the TBR between the diode terminals. On the other hand, the heat flux (q_B) in the backward configuration (Fig. 5(b)) can be determined following a similar procedure and the final result can be written as

$$q_B=-\frac{1}{\beta \lambda {\rho }_m}\ln \left[\frac{f(T_h-\delta T+\rho q_B)}{f(T_c+\delta T)}\right],$$ 5

where δT = 2 °C (or 4.5 °C) is the hysteresis undergone by the VO2 thermal conductivity, as the terminal deposited on r-sapphire (or silicon) is cooled down from T_h in the forward configuration, to T_c in the backward one, as shown in Fig. 5. Note that the thermal resistance L₂/k₂ of the non-PCM influences both q_F and q_B through the total resistance ρ, which is symmetric in R_th and L₂/k₂. This fact indicates that the impact of interface TBR between the diode terminals can be neglected by choosing a non-PCM, such that L₂/k₂ ≫ R_th ~ 10⁻⁸m²KW⁻¹(see Fig. 3(c)), as will be considered in this work.

Table 1.

Materials properties of VO₂ deposited on r-sapphire and silicon substrates.

Material	km(Wm−1K−1)	kd(Wm−1K−1)	β(°C−1)	T0(°C)
VO2/Sapphire	20.5	8.2	0.4	67.5
VO2/Silicon	41.7	17.5	0.3	72.5

The plots in Fig. 6(a,b) represent the variation of R as a function of the temperature T_h of the hotter terminal for both conductive TD operating with terminals of VO₂/r-sapphire as well as VO₂/Si. Calculations were done with the numerical solutions of Equations (4) and (5) for q_F and q_B, in combination with Equation (1).

Figure 6.

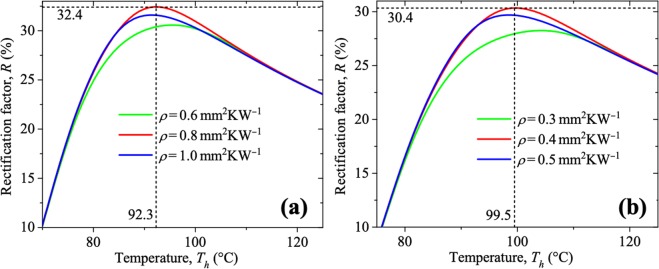
Dependence of the rectification factor on the temperature of the hot side of a conductive thermal diode with a terminal of VO₂ deposited on a substrate of (a) r-sapphire and (b) Silicon. Calculations were done for three representative values of the thermal resistance ρ, L₁ = 10 μm and T_c = 25 °C.

One can note that the TDs operating with VO₂/r-sapphire and VO₂/Si reach their optimal rectification factors R_opt = 32.4% and R_opt = 30.4% at the temperatures T_h = 92.3 °C and T_h = 99.5 °C, and thermal resistances ρ = 0.8 mm²KW⁻¹ and ρ = 0.4 mm²KW⁻¹, respectively. Higher and lower values of ρ and T_h yield lower rectification factors. Even though both diodes have practically the same highest rectification factor, the TD operating with terminals of VO₂/r-sapphire and a blackbody requires a terminals’ temperature difference (T_h − T_c =  67.3 °C) that is smaller than the corresponding one (T_h − T_c = 74.5 °C) for the diode composed of terminals of VO₂/Si and a blackbody. This difference is due to the fact that the first VO₂ sample has a smaller transition temperature T₀ and faster phase transition (higher β) than the latter one, as reported in Table 1. Additionally, the evidence that these temperature differences between the diode terminals (T_h − T_c) are larger than the equivalent phase transition zones of both samples shown in Fig. 6 is acceptable, given that the maximization (minimization) of the forward (backward) heat flux q_F (q_B) associated to R_opt occurs when T_h (T_c) is high (low) enough to ensure that most of the VO₂ terminal is in its metallic (insulating) phase, as established by the Fourier’s law of heat conduction. This fact suggests that VO₂ samples with sharper k slopes require smaller temperature intervals to reach the maximum R of a conductive TD, as was theoretically demonstrated in the literature⁷⁷. Moreover, R_opt values determined for VO₂/r-sapphire and VO₂/Si are higher than the corresponding one (R_opt = 19.7%) reported in the literature for another VO₂ sample⁷⁷, because their thermal conductivity contrasts k_m/k_d = 2.5 are larger than that (k_m/k_d = 1.7) of the latter sample. Thus, it is suggested that PCMs with higher k deviations, within their MIT, are expected to generate a more conductive TD with higher R that can even exceed that obtained using graphene (26%)⁷⁸.

The obtained outcomes lay down a novel methodology to study the thermophysical properties of VO₂ thin films and other PCMs with potential applications in the control of heat currents. As shown in this and previous works^21,79,80, the substrate plays a key role on the growth and thermal properties of VO₂ films, and therefore the detailed study of its impact with a wider variety of substrate materials, film thicknesses and deposition temperatures is a pending task.

Conclusion

In this study, experimental thermal characterisation of vanadium dioxide thin films were achieved using a PTR setup up to 10 MHz. The reported measurement of the VO₂ thermophysical properties ($a_{{\mathrm{VO}}_2}$, $e_{{\mathrm{VO}}_2}$ and R_{th 2}) was made. The hysteresis loops of these properties have been observed and quantified by performing all measurements for both the heating and cooling processes of samples with different temperatures within their MIT. It has been shown that: i) the a, e and k of both VO₂ films in their insulating phase, are lower than the corresponding ones in their metallic phase. The k of both VO₂ films exhibits a substantial enhancement of 2.5 during the MIT, whereas, their C_v display smaller variations. ii) MIT reduces the heat transmission at the interface through the phase changing. iii) This high k contrast of VO₂ allows to drive a conductive TD with a rectification factor as high as 30%, for a relatively small temperature difference between its two terminals of VO₂ and another non-PCM. The obtained results are thus expected to guide the fabrication of VO₂ films and other PCMs with thermal properties tailored for the control of the heat conduction in many technological applications.

Methods

Sample preparation

VO₂ thin films were deposited on substrates of r-sapphire ($1\overline{1}02$) and silicon (100) wafers through a pulsed laser deposition (PLD) process. This well-adapted method for the deposition of complex multi-element materials and oxides consists in using a pulsed high-power laser beam to evaporate a small amount of matter from a solid target within a stainless-steel ultra-high vacuum chamber²¹. During some hundreds or thousands of laser pulses, the evaporated matter condensed on a substrate forms a thin film. A KrF pulsed excimer laser with wavelength λ = 248 nm, pulse width of 25 ns, and repetition rate ranging from 3 Hz up to 25 Hz was employed to grow VO₂ films on both types of substrates set at the temperature of 600 °C. The oxygen pressure used for the deposition of all samples was of 2.2 Pa. The thicknesses of the VO₂ thin films of samples H.1 and H.2 were measured by a profilometer (KLA Tencor, Alpha-Step IQ) and their values were found to be of 500 nm and 400 nm (± 20 nm), respectively.

PTR measurements

The photothermal radiometry (PTR) technique detects the infrared signals emitted by a material after being heated up with a frequency modulated laser beam and analyses them to find the material’s thermophysical properties^43–45. The standard PTR setup used in our experiments uses an optical excitation provided by a continuous diode-pumped solid-state laser (DPSS, Dream Lasers Technol. Co., model SDL-532-300T) with an intensity of 300 mW, visible wavelength of 532 nm and a diameter of 0.6 mm at 1/e. Modulation frequencies up to 10 MHz were achieved by an acousto-optical modulator (AOM model AA.MTT.AR 05) placed between two lenses in their confocal plane. The laser beam spot inside the AOM driver controlled by a frequency generator (model FI5350GA) is thus minimized and the upper limit of the modulation frequency was determined by the transit time of the acoustic carrier frequency across the laser beam spot. An iris was used to select the zero-order diffracted beam. The intensity of the laser beam arriving on the sample surface is around 55% of the initial power after its passage through all the involved optics. The VO₂ samples were mounted on a Peltier support equipped with a temperature controller (Newport temperature controller Model 6100) via a Pt100 probe. The surface temperature of the samples was measured with a small thermocouple probe (YCT RS-232 Data Logger, YC-747D Thermometer, probe diameter = 85 µm) and was found to be equal to that registered by the Peltier support. An additional steady (DC) temperature raise of 8 °C has been experimentally observed and added to the sample temperature due to the laser’s heating. The infrared (IR) radiations generated from the sample heating are collected by two parabolic off-axis Au-coated mirrors (Edmund Optics) and transferred to a liquid-nitrogen cooled HgCdTe photoconductive detector sensitive to the IR radiation wavelengths between 5 and 12 µm (Kolmar Technologies, KMPV 11-1-J1/DC) with 1 mm² active area and antireflection-coated Ge window. The amplitude and phase of the detector electrical signal are then recorded and amplified through heterodyne lock-in amplifiers (Stanford Research Systems: SR844). The function generator used to modulate the AOM driver was also used as base reference of the lock-in frequency. A schematic representation of the used PTR system is shown in Fig. 1 and more details about it can be found elsewhere⁴⁵.

Theoretical calculations

Using such experimental setup configuration, the heating is considered to be one-dimensional. This can be explained by the relation between the laser spot size, the detector opening and the excitation source frequency. I.e., knowing that when the thermal diffusion length defined as μ = (a/πf)^1/2 (where a and f are the thermal diffusivity and the laser modulation frequency respectively) in meters is smaller than the opening of the detector, the heating is considered 1D (with a laser beam spot size equal to 0.6 mm at 1/e). Consequently, at enough high frequencies, the VO₂ layer is considered as thermally thick, because under these conditions, the penetration depth of the thermal wave (defined as μ) (whites circles in Fig. 1(b)) is small, in such a way that the thermal waves remain in the first two layers (Ti and VO₂) of the samples. For that reason, a quadrupole based model^48,49 including a volumetric heat absorption in the first layer (50 10⁶ for Ti) is used to fit the experimental data (normalized amplitude and phase simultaneously). This modelling was used to simultaneously fit the experimental data for the amplitude and phase of the PTR signal analysed by the lock-in amplifier. A sensitivity calculation⁵⁰ is also made to check which are the parameters that can be extracted, sensitive to this experimental measurement (details in section 3 of the SI). Subsequently, these sensitivities were used to compute the total uncertainties of the extracted parameters, using a least square algorithm as explained by another study⁵⁸. This method calculates the total error on an experimental parameter using both, the uncertainties related to the experimental noise and the input parameters (the fixed parameters in the model).

Author Contributions

G.H. performed the PTR experimental measurements, retrieved the VO₂ properties and wrote the manuscript along with N.H. and J.O.M.; M.C. & N.H. conceived the PTR experimental setup; M.C., N.H. & G.H. improved the PTR setup; C.C. & F.D.-B. developed and analyses the samples whose structural characterization was done by C.L.G.-H. & J.A.R.-R.; J.O.M. developed the conductive thermal diode application and interpreted the results with the help of J.J.A.-G., Y.E. & K.J.; G.H., N.H., M.C. & J.O.M. analysed the data, discussed the final results and edited the manuscript with the help of all the other authors. All authors approved the last version of the manuscript.

Data Availability

The datasets generated and/or analysed during the current study are available on request to the corresponding author.

Competing Interests

The authors declare no competing interests.

Supplementary information

Supplementary information accompanies this paper at 10.1038/s41598-019-45436-0.