Gregarious suspension feeding in a modular Ediacaran organism

Simulations show fossil Ernietta (548 Ma ago) lived gregariously to aid feeding, providing one of the oldest examples of commensalism.

Abstract

Reconstructing Precambrian eukaryotic paleoecology is pivotal to understanding the origins of the modern, animal-dominated biosphere. Here, we combine new fossil data from southern Namibia with computational fluid dynamics (CFD) to test between competing feeding models for the Ediacaran taxon Ernietta. In addition, we perform simulations for multiple individuals, allowing us to analyze hydrodynamics of living communities. We show that Ernietta lived gregariously, forming shallow marine aggregations in the latest Ediacaran, 548 to 541 million years (Ma) ago. We demonstrate enhanced vertical mixing of the water column above aggregations and preferential redirection of current into body cavities of downstream individuals. These results support the reconstruction of Ernietta as a macroscopic suspension feeder and also provide a convincing paleoecological advantage to feeding in aggregations analogous to those recognized in many extant marine metazoans. These results provide some of the oldest evidence of commensal facilitation by macroscopic eukaryotes yet recognized in the fossil record.

INTRODUCTION

The Ediacara biota [571 to 539 million years (Ma) ago] is an enigmatic group of soft-bodied organisms that represents the first major radiation of complex, macroscopic, and eukaryotic life. Although some of these organisms represent animals [Metazoa; e.g., (1, 2)], others do not appear to share any synapomorphies with extant metazoan clades and thus may represent extinct groups with no modern representatives (3). Reconstructing the paleobiology and paleoecology of these organisms has long been complicated by their non-analog body plans, which have no counterparts in the present day. Despite these difficulties, cutting-edge quantitative analyses and modeling techniques have provided a back door into understanding Ediacaran organisms, allowing us to better constrain their place in the eukaryotic tree of life (4–8). In particular, spatial analyses (4), inference of population-level habitat competition and partitioning (7, 8), modeling of feeding mode (5), and modeling of facultative motility [supported by field observations (6, 9–12)] in enigmatic taxa have provided new insights into their affinities, as well as nutrient cycling and the overall complexity of Ediacaran ecosystems. Here, we use computational fluid dynamics (CFD) to reconstruct the feeding ecology of the enigmatic Ediacaran taxon Ernietta plateauensis Pflug 1966. Although CFD has previously been used to study the paleobiology and paleoecology of individual fossils (5, 6), in this study, we use this method to test hypotheses surrounding the functioning of Ediacaran ecological communities for the first time.

Ernietta is a late Ediacaran (~548 to 538 Ma ago) sack-like organism with a modular architecture consisting entirely of tubular elements alternatingly stitched along a basal medial seam (Fig. 1B and fig. S1) (13, 14). Ernietta likely maintained a sessile and semi-infaunal lifestyle, with some portion of the body cavity buried beneath the sediment-water interface, leaving, at minimum, an upper frill exposed in the water column (14). Ernietta is one of the youngest Ediacaran taxa, with examples known right up until the Precambrian-Cambrian boundary (15), and therefore may provide insights into the character of Ediacaran ecosystems immediately before the second pulse of end-Ediacaran extinction (3). In this study, we analyze accumulations of Ernietta from the Witputs subbasin (Fig. 1A), Namibia, where disparate spatial aggregations of relatively undeformed individuals (fig. S1 and table S1) are found with the ventral portion (i.e., the suture) facing down into the sediment (Fig. 1B and fig. S1). This consistent orientation and lack of deformation suggests that these individuals were preserved in situ and hence indicates a gregarious ecology similar to many modern marine invertebrates.

Fig. 1. Study locality.

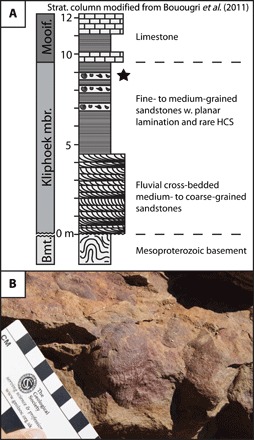
(A) Generalized stratigraphic section of Hansburg, Namibia, showing the distribution of Ernietta-bearing units [redrawn from (34)]. Bmt, Basement; Kliphoek mbr, Kliphoek member; Mooif, Mooifontein. (B) Close-up photograph of an overturned slab containing exceptionally preserved Ernietta with detailed suture and individual tube elements. Photo credit: Marc Laflamme, University of Toronto.

Ediacaran feeding modes

Modern shallow marine settings are home to a wide variety of organisms with varied feeding modes, including photoautotrophy, chemoautotrophy, suspension feeding, grazing, predation, and deposit feeding. Previous work (15, 16) has proposed that most members of the Ediacara biota were restricted to one of two possible feeding modes: osmotrophy or suspension feeding. Deposit feeding and predation is limited because of little evidence for movement or sediment disruption (17), indirect evidence of facultative mobility in some taxa notwithstanding (6, 9, 17). Furthermore, these two feeding modes can be discounted because the Ediacaran soft-bodied fossil record is almost entirely devoid of definitive body fossils with specialized feeding structures. The probable bilaterian Kimberella is alone among the Ediacara biota in being found associated with scratch marks, representing surficial grazing (10–12, 18), while Dickinsonia likely fed saprophytically via its ventral sole (19). Photoautotrophy can be discounted as a possible feeding ecology for Ernietta based on the presence of Erniettomorpha in deeper-water settings below the photic zone (20). Given the highly consistent and relatively simple body plans in this clade (21), it is unlikely that species within the erniettomorphs used completely different feeding modes. Chemoautotrophy is also unlikely as an Ediacaran feeding ecology, because the necessary levels of methane and hydrogen sulfide for chemosynthesis, such as near deep-sea vent communities (22), are not supported by geochemical studies (23). In Namibia, in particular, there is no geological evidence for the types of deposits that would support a dense chemoautrophic ecosystem. Consequently, osmotrophy and suspension feeding are the most plausible feeding modes for sessile members of the Ediacara biota, including Ernietta.

Osmotrophy is most often invoked as a potential feeding ecology on the basis of surface area–to–volume (SA/V) ratios similar to those of modern organisms that feed via passive absorption of dissolved organic matter (15). The potential for suspension feeding has been suggested for some of the frondose taxa (24) and demonstrated in the triradial taxon Tribrachidium (5). Rahman et al. (5) used computer simulations of fluid flow to establish robust criteria for testing between suspension feeding and osmotrophy in Ediacaran organisms. Macroscopic osmotrophs rely on passive absorption of organic matter through membranes and thus maximize feeding by distributing flow evenly across all exposed exterior surfaces (24). An osmotrophic feeding model for Ernietta would therefore predict that the flow would be evenly distributed over the entire surface of the organism. In contrast, suspension feeders obtain nutrients by transporting water through, or past, structures specialized to entrap organic particles (25–27). Thus, if Ernietta was a suspension feeder, then we would expect water flow to be directed to specific parts of the anatomy, which presumably represented sites of specialized feeding structures in the living organism. CFD allows us to test between these two hypothesized feeding modes by simulating fluid flows around three-dimensional (3D), semi-infaunal digital models of Ernietta in a virtual flume tank. Furthermore, we use fluid-structure interaction (FSI) simulations to assess how the rigidity of the Ernietta model might affect fluid flow and thus feeding efficiency. Last, we carry out an independent test of osmotrophy by calculating the SA/V ratio of our 3D models, comparing these to the SA/V ratios of extant osmotrophic organisms (15).

Gregarious behavior and feeding ecologies

Ernietta fossils are found aggregated in life position (e.g., presumed ventral sutures all facing down; Fig. 1B) in assemblages, which is highly suggestive of a gregarious lifestyle. Modern organisms aggregate for many reasons, including predator avoidance, reduced exposure to nutrient-depleted water (via tiering), or as a by-product of reproduction and recruitment. Ghisalberti et al. (28) demonstrated the importance of tiering within Ediacaran tiered frondose communities for developing canopy flow and enhancing vertical mixing of the water column, although recent analyses have proposed this to be less common than previously assumed (7). Enhanced vertical mixing offsets any depletion of nutrients from upstream individuals, as well as diluting possible waste products. While Ernietta communities do not demonstrate similar vertical size variations, their gregarious behavior would most likely affect individual feeding efficiency and ecology.

Many extant sessile marine invertebrates have evolved gregarious benthic ecologies to help with aspects of nutrient acquisition. For example, mussels and oysters form dense benthic accumulations that provide measurable benefits to suspension feeding (29, 30). Studies have demonstrated increased success in particle capture rates when living in aggregated populations (31); however, it has also been shown that some down current individuals (or those situated toward the center of patches) may receive fewer nutrients due to depletion from higher competition (32–34). In addition, both advection-diffusion models and experimental flume studies demonstrate that increasing the number of individuals generates turbulence near the bed, thickening the turbulent boundary layer, and thus playing an important role in nutrient delivery (34, 35). Topography created by accumulations of mussels increases the size of the turbulent boundary layer around the overall populations (34, 36, 37), and this produces vertical and horizontal mixing of nutrients over the length of the bed, thereby increasing the concentration of nutrients within the water column above the living populations (34). Many passive suspension feeders rely on this increased turbulence, as it mixes the water column and delivers more nutrients than simple laminar flow (37). Consequently, if gregarious living in Ernietta was an adaptation to aid feeding, then this would therefore predict the redirection of fluid flow toward areas of nutrient acquisition for all individuals in a population, and this redirection should be equally as strong as that seen in solitary individuals. We test this hypothesis through CFD simulations of flow for multiple individuals in spatial groupings.

RESULTS

Flow patterns

In all the CFD simulations performed, fluid velocity decreased rapidly where the flow first encountered the model(s), with a steep velocity gradient developed close to the bottom of the computational domain (Fig. 2 and figs. S5 to S7). A region of recirculating flow, characterized by much lower velocities than ambient flow, formed within the central cavity of the Ernietta model, as well as directly downstream of the model (Fig. 2 and figs. S5 and S7).

Fig. 2. CFD results.

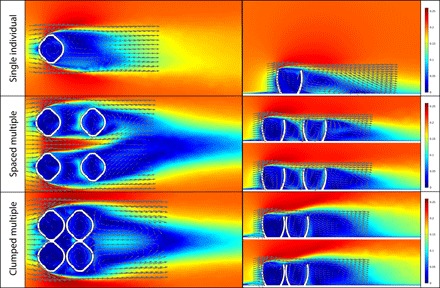
Results of CFD simulations in horizontal (left column) and vertical (right column) cross-sections. All models oriented parallel to flow, at moderate burial depth, and simulations were performed using an inlet velocity of 0.2 m/s. (Top) Single-model simulation results. (Middle) Spaced multiple-model simulation results. (Bottom) Clumped multiple-model simulation results.

In the single-model CFD simulations (fig. S5), downstream flow patterns were conserved between simulations with models in the same orientation, but recirculation became stronger with increasing velocity. Comparing simulations with models at different orientations (0° and 90°), overall water velocity downstream of perpendicularly oriented individuals was consistently slower compared to those in parallel orientation. Recirculation was generated for all simulated burial depths. In both orientations, downward vertical velocity in the cavity was consistently strongest at the downstream internal face, while upward vertical velocity was strongest at the upper tip of the upstream external face of the Ernietta model. Turbulence was always strongest for perpendicularly oriented individuals and increased with faster velocities.

In the multiple-model CFD simulations, the flow patterns produced for each of the individual Ernietta models were generally similar to the other individuals within the same row, as well as to those obtained for individuals in the single-model simulations in the same orientation. In particular, the region of recirculation developed within the central cavity was observed in all the simulations but was typically enhanced in downstream individuals (Fig. 2 and fig. S6). In each multiple-model simulation, the row of individuals furthest from the inlet typically experienced slightly higher flow velocities on their downstream internal face compared to velocities experienced by upstream models. Downstream models also experienced more strongly negative vertical velocity than upstream ones at these same downstream internal faces, indicative of greater fluid flow downwards into the cavity. This downward velocity is balanced by a faster than ambient upward velocity at the upstream internal face of these same downstream individuals. Velocities for upstream individuals were comparable to those in the single-model simulations, and cavity recirculation patterns among individuals of the same orientation were typically mirrored row-wise. Multiple-model simulations with mixed orientations in up- and downstream individuals did not exhibit mirrored recirculation patterns row-wise, but in simulations of well-spaced, mixed-orientation individuals, the individual patterns were similar to single-model simulations of the same respective orientations. Plots of turbulent kinetic energy for the well-spaced multiple-model simulations (Fig. 3 and fig. S6) show some weak turbulence around the sides of Ernietta individuals and near the top of the cavities, with stronger turbulence above downstream individuals where models were placed in perpendicular orientation (fig. S6).

Fig. 3. CFD results.

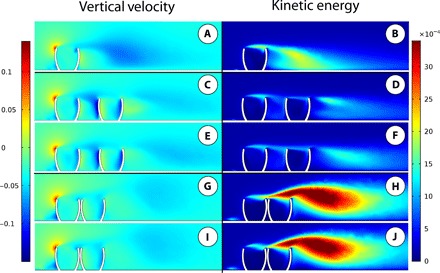
Results of CFD simulations in vertical cross-sections showing vertical velocity (left column) and kinetic energy (right column). All models oriented parallel to flow, at moderate burial depth, and simulations were performed using an inlet velocity of 0.2 m/s. (A and B) Single-model simulation. (C to F) Spaced multiple-model results, where (C) and (D) show left column of individuals and (E) and (F) show right column of individuals with respect to flow. (G to J) Clumped multiple-model results, where (G) and (H) show left column of individuals and (I) and (J) show right column of individuals with respect to flow.

In the clumped multiple-model CFD simulations (Fig. 2 and fig. S6), all vertical velocity patterns were enhanced compared to the well-spaced multiple-model simulations (fig. S6), and downstream individuals experienced much stronger recirculation compared to upstream individuals. Compared to the well-spaced multiple-model simulations, downstream individuals in the clumped multiple-model simulations experienced slower overall flow velocities and lower recirculation within their cavities. This was not conserved in the clumped-mixed orientation simulations, where overall recirculation patterns and flow velocities were stronger for downstream individuals. In the turbulent kinetic energy plots for the clumped individuals, a much stronger turbulence was created above and downstream of downstream individuals, as indicated in fig. S6.

In the FSI simulation (movies S1 and S2), flow patterns were generally conserved throughout the 10-s duration of the simulation, with recirculation within the cavity observed once the flow had reached steady state. There was a very small displacement (<0.2 mm) of the upper part of the Ernietta model during the first 0.1 s of the simulation; however, no additional displacement was observed under steady-state flow.

Drag calculations

Drag forces increased and the coefficients of drag decreased with increasing inlet velocity (Table 1 and fig. S8). In addition, drag forces and their coefficients increased with decreasing burial depth (increased relative height in the water column) and were greatest when individuals were oriented perpendicular to the flow. In multiple-model simulations, drag was typically close to zero for downstream individuals but more similar to that seen in the single-model simulations for upstream individuals. The exception to this pattern was the mixed-orientation multiple-model simulation, in which downstream individuals are offset from upstream ones (fig. S7). In the multiple-model simulations, drag forces and their coefficients were greater in the clumped simulations than in the well-spaced ones, which, in turn, produced slightly more drag than single-model simulations with individuals in the same orientation (Table 1 and fig. S8).

Table 1. Drag results.

Results of CFD simulations for single- and multiple-model simulations of Ernietta, varying the current velocity (0.1, 0.2, and 0.5 m/s), burial depth (shallow, moderate, and deep), and orientation with respect to flow (parallel and perpendicular).

Density of fluid (kg/m3)	Dynamic viscosity of fluid [kg/(s·m)]
1000	0.001
Model	Burial depth	Orientation	Characteristic dimension (m)	Reference area (m2)	Velocity (m/s)	Reynolds number	Drag force (N)	Drag coefficient
Single individual	Shallow	Parallel	0.059	0.0032	0.10	5,900	0.01115498717230990	0.697186698269369
					0.20	11,800	0.04435156048105120	0.692993132516425
					0.50	29,500	0.27451391432455000	0.686284785811375
	Shallow	Perpendicular	0.064	0.0038	0.10	6,400	0.01640526727730790	0.863435119858310
					0.20	12,800	0.06556131975167460	0.862648944100981
					0.50	32,000	0.40547097969682800	0.853623115151217
	Moderate	Parallel	0.059	0.0024	0.10	5,900	0.00780989011491970	0.650824176243308
					0.20	11,800	0.03095450738813410	0.644885570586127
					0.50	29,500	0.19148327641114800	0.638277588037160
	Moderate	Perpendicular	0.064	0.0028	0.10	6,400	0.01097594350218370	0.783995964441693
					0.20	12,800	0.04385177326839820	0.783067379792825
					0.50	32,000	0.27217976318145000	0.777656466232714
	Deep	Parallel	0.059	0.0016	0.10	5,900	0.00510221637973906	0.637777047467382
					0.20	11,800	0.02002824322207540	0.625882600689856
					0.50	29,500	0.12240245033436900	0.612012251671845
	Deep	Perpendicular	0.064	0.0018	0.10	6,400	0.00665568976802439	0.739521085336043
					0.20	12,800	0.02659742614565730	0.738817392934925
					0.50	32,000	0.16418447680940500	0.729708785819578
Four individuals
Top left	Moderate	Parallel	0.059	0.0024	0.20	11,800	0.0337107511642232	0.702307315921317
Bottom left	Moderate	Parallel	0.059	0.0024	0.20	11,800	0.0336249551239988	0.700519898416642
Top right	Moderate	Parallel	0.059	0.0024	0.20	11,800	0.0039417469198683	0.082119727497256
Bottom right	Moderate	Parallel	0.059	0.0024	0.20	11,800	0.0030375563506614	0.063282423972112
Four individuals
Top left	Moderate	Perpendicular	0.064	0.0028	0.20	12,800	0.0504436221184845	0.900778966401509
Bottom left	Moderate	Perpendicular	0.064	0.0028	0.20	12,800	0.0491364809391965	0.877437159628509
Top right	Moderate	Perpendicular	0.064	0.0028	0.20	12,800	−0.0008403062351596	−0.015005468484993
Bottom right	Moderate	Perpendicular	0.064	0.0028	0.20	12,800	−0.0056891902315857	−0.101592682706888
Four individuals
Top left	Moderate	Perpendicular	0.064	0.0028	0.20	12,800	0.0498790059537312	0.890696534888057
Bottom left	Moderate	Parallel	0.059	0.0024	0.20	11,800	0.0332994715036173	0.693738989658694
Top right	Moderate	Parallel	0.059	0.0024	0.20	11,800	−0.0011524043075931	−0.024008423074855
Bottom right	Moderate	Perpendicular	0.064	0.0028	0.20	12,800	0.0043642874977630	0.077933705317196
Four individuals, clumped
Top left	Moderate	Parallel	0.059	0.0024	0.20	11,800	0.0426060103328862	0.887625215268462
Bottom left	Moderate	Parallel	0.059	0.0024	0.20	11,800	0.0426196085320831	0.887908511085065
Top right	Moderate	Parallel	0.059	0.0024	0.20	11,800	−0.0074879970079540	−0.155999937665708
Bottom right	Moderate	Parallel	0.059	0.0024	0.20	11,800	−0.0027149188517437	−0.056560809411327
Four individuals, clumped
Top left	Moderate	Perpendicular	0.064	0.0028	0.20	12,800	0.0580070614238671	1.035840382569060
Bottom left	Moderate	Perpendicular	0.064	0.0028	0.20	12,800	0.0565483085671746	1.009791224413830
Top right	Moderate	Perpendicular	0.064	0.0028	0.20	12,800	−0.0085171293959361	−0.152091596356002
Bottom right	Moderate	Perpendicular	0.064	0.0028	0.20	12,800	−0.0084508226386397	−0.150907547118565
Four individuals, clumped
Top left	Moderate	Perpendicular	0.064	0.0028	0.20	12,800	0.0580510254958707	1.036625455283410
Bottom left	Moderate	Parallel	0.059	0.0024	0.20	11,800	0.0418699175305886	0.872289948553929
Top right	Moderate	Parallel	0.059	0.0024	0.20	11,800	−0.0040699100616795	−0.084789792951656
Bottom right	Moderate	Perpendicular	0.064	0.0028	0.20	12,800	−0.0071175827072387	−0.127099691200690
Five individuals
Top left	Moderate	Perpendicular	0.064	0.0028	0.20	12,800	0.0491217229681063	0.877173624430470
Bottom left	Moderate	Parallel	0.059	0.0024	0.20	11,800	0.0328310384436475	0.683979967575990
Top right	Moderate	Parallel	0.059	0.0024	0.20	11,800	0.0261873415135867	0.545569614866390
Middle right	Moderate	Perpendicular	0.064	0.0028	0.20	12,800	0.0161636012318585	0.288635736283187
Bottom right	Moderate	Parallel	0.059	0.0024	0.20	11,800	0.0275210268558887	0.573354726164348

SA/V ratios

SA/V ratios of the exposed model (e.g., above the sediment-water interface; fig. S4) increased with increasing burial depth of the organism (fig. S8). The whole model (e.g., epibenthic or entirely above the sediment-water interface) had an SA/V ratio of 0.59 mm²/mm³, and the deeply buried model (e.g., sediment-water interface halfway between midline suture and top most portion of the model) had the highest SA/V ratio of 0.77 mm²/mm³ (fig. S8).

DISCUSSION

Competing feeding models for Ernietta

The results of the CFD simulations show that the flow was not distributed evenly over the entire surface of the organism, as predicted if Ernietta was feeding osmotrophically (15, 24). Instead, our simulations reveal that there was consistent and strong recirculation within the central cavity of the organism, regardless of the burial depth (deeply buried to midway between the suture and top of the model or shallowly buried to the midway point between the bottom and midline suture of the model), current velocity, and orientation with respect to flow (Fig. 2 and figs. S5 to S7), as expected if Ernietta was a suspension feeder (27). Even when the model was allowed to deform under fluid flow in the FSI simulation, recirculation was still apparent once the flow reached steady state. The ubiquity of recirculation in the presence of these varying conditions indicates that Ernietta would have been capable of functioning as a passive suspension feeder in an environment with variable current velocities and directions, regardless of the burial depth and variously interpreted endobenthic lifestyles (i.e., fully endobenthic or semi-endobenthic or surficial epibenthic). Evidence for recirculation within the central cavities of individual Ernietta is also apparent in fossil material; slow recirculation of fluid would likely lead to settling of sediment particles within the body cavity, which matches observations of graded sediment fill within Ernietta fossils (14). Recirculation would have cycled nutrient-depleted fluid out of the cavity, providing access to new, nutrient-rich flow. The observed recirculation indicates that the internal cavity of Ernietta was the likely site of nutrient acquisition, although the precise mechanism of particle capture and processing remains uncertain, given the lack of specialized feeding structures preserved in fossils.

We also analyzed the SA/V ratios of our models as an independent test for osmotrophy. SA/V ratios for the three burial depths and whole model lie in a tight range (0.59 to 0.77 mm²/mm³) that falls far below the values exhibited by extant deep-sea osmotrophs [typical ranges of 8 to 20,000 mm²/mm³; (38)] and modeled SA/V for the Ediacaran frond Fractofusus [1 to 10,000 mm²/mm³; (15)]. Coupled with the inference of a semi-infaunal life habit for Ernietta (13, 14), these SA/V ratios suggest that an osmotrophic feeding ecology was unlikely. Even if a solitary Ernietta individual was capable of absorbing nutrients from the surrounding porewater as well as the water column, it would likely deplete nutrients from the surrounding porewater within the sediment rapidly. These nutrients, in turn, would have a low replenishment rate due to the overlying microbial mat acting as a diffusive boundary. Depletion of the surrounding porewaters would have been further enhanced if we consider the inferred gregarious life habit of these organisms (13, 14, 39), indicating that only the exposed portions of the organism would likely be absorbing nutrients. Furthermore, our Ernietta model comprised only a single layer of tubes, while some fossils show evidence for two layers (13, 14). Incorporating this additional layer of tubes into the model would likely increase volume without drastically increasing surface area, thus lowering SA/V values even further (or at minimum maintain SA/V values if the inner tubes were not in direct contact with the other tubes). The only means by which Ernietta could have attained the high SA/V necessary for osmotrophy is by limiting the active tissue in each tubular unit to a very thin layer surrounding an empty vacuole (15), which is improbable given the structural rigidity necessary for the inferred semi-infaunal lifestyle.

Gregarious behavior

Our well-spaced multiple-model simulations (Fig. 3 and fig. S6) show that downstream individuals were exposed to comparatively faster flow velocities than upstream ones while maintaining stronger patterns of recirculation within the internal cavity compared to upstream individuals. Moreover, the strength of recirculation within the cavity in upstream individuals in the multiple-model simulations is very similar to that seen in the single-model simulations (fig. S5). Having Ernietta individuals grouped in tighter aggregates (i.e., clumped arrangements; Figs. 2 and 3 and fig. S5) preserves the increased recirculation within the cavities in the downstream individuals and additionally creates increased turbulence above downstream individuals, both factors that would have likely enhanced nutrient delivery. This nutrient delivery to downstream individuals is further enhanced by the strong downward velocity at the downstream internal faces of their cavities in conjunction with the increased turbulence above downstream individuals. This turbulence remixes flow sourced from the cavities of upstream individuals with the surrounding ambient flow; some of this fluid is then redirected into the cavity of downstream individuals. This indicates that the nutrient-depleted flow from upstream cavities would be mixed with more nutrient-rich ambient flow above the aggregated individuals and then preferentially transported into the feeding cavities of the downstream organisms. These results provide a paleoecological and paleobiological explanation for the observation that Ernietta lived gregariously within aggregated populations (Fig. 1 and fig. S1). The enhancement of recirculation within downstream cavities coupled with the hypothesized benefits of gregarious living for feeding, such as vertical mixing of nutrients in the water column and enhanced turbulence within the boundary layer (34, 36, 37), strongly suggests that a gregarious lifestyle would have aided feeding in Ernietta.

There are several alternative explanations for gregarious behavior in extant marine invertebrates, but these can be dismissed for Ernietta. For example, many extant aquatic organisms aggregate as a consequence of reproduction. If this was the sole driver, then we might expect to see smaller individuals in close association with larger individuals, as seen in the Ediacaran organism Fractofusus [(4); though see (40)]. However, in nearly all the studied assemblages of Ernietta, there is no reported evidence of such a size distribution, and our beds show no such distribution (table S1). Moreover, under the velocity conditions in which Ernietta likely lived (41), offspring would have been transported substantial distances (meters to kilometers) from their parents (42), which would likely result in more dispersed colonization sites. Even if their settling rate was exceedingly fast, we would anticipate a degree of current alignment within the offspring (43), which we do not observe in the fossil communities preserved at Farm Hansburg (42). Thus, while the initial placement of these organisms is likely influenced by dispersal from reproduction, their ecological success in aggregations was likely driven by factors other than reproductive dispersal alone. Avoidance of predation is another possible explanation for aggregating, but there is currently no evidence for any predation within the soft-bodied Ediacara biota (9, 17). A final possibility involves aggregation as a means of elevating oneself within the water column, thereby partitioning feeding among individuals at different tiering heights, as has been documented in barnacles (44) and oysters (45). While this arrangement has been demonstrated in a single community of older age (7, 28, 46), none of these features were observed at Farm Hansburg and Kuibis Farm, Namibia, or in our individual size data (table S1). We do note a large size range within collected Ernietta, but we do not see defined size classes such as what might be observed in tiering. Furthermore, we see no evidence for attachment to other individuals for tiering as often seen in modern organisms (44).

Consequently, we infer that the gregarious lifestyle of Ernietta was primarily an adaptation to aid in feeding, and more specifically a commensal interaction. Our CFD results demonstrate that downstream individuals consistently experienced less drag than upstream individuals, which would buffer fluid-derived strain on downstream organisms. The minimization of drag bestows a number of protective benefits to the organism, including decreased chance of tissue tears from faster water velocities, reduced chance of abrasion from larger particles within the water, and the ability to capture nutrients in less stressful conditions. However, increased turbulence from overall topography generated by aggregated individuals (Fig. 3 and fig. S6), as also outlined above for some modern mussels (34, 36, 37), would disrupt fluid flow around them and aid in transporting organic particles from microbial mats into the water column. While this is not explicitly observed in our simulations, one limitation in assessing this feature in our simulations is that the virtual seafloor is not characterized by any degree of surface topography or roughness. At all other locations of nonuniform topography (e.g., where the models are located), we do see mixing and turbulent energy, indicating that this mixing would likely occur but is not accurately portrayed because of limitations in the experimental design. This vertical mixing would replenish water currents depleted in nutrients following feeding by upstream individuals, ensuring that downstream individuals had access to nutrient-rich currents. In modern epibenthic mussels, this phenomenon is pivotal for communities (34), and survival of downstream individuals has been hypothesized to be unlikely without this flow characteristic (37).

Last, our CFD analyses provide a convincing mechanism for the accumulation of layered sediments seen inside fossil Ernietta (14). Simulations illustrate significant recirculation of current around communities of Ernietta, as well as lower-velocity recirculation inside the cavities of individual organisms. In a tidally and storm-influenced paleoenvironment (14, 41), the suspended sediment would therefore have settled out over Ernietta populations, forming layered deposits inside cavities and accumulating around the outside of individuals. Hence, these communities of Ernietta would likely have contributed to forming low-relief mounds on the seafloor (in support of this, in situ Ernietta accumulations on Farm Hansburg often form discrete clumps). Further, the gregarious nature of these organisms and associated benefits for feeding represents one of the oldest examples of commensal facilitation, which emphasizes that Ediacaran ecosystems were much more complex than has been previously imagined, and provides a paleoecological link to the animal-dominated ecosystems of the Paleozoic (47).

MATERIALS AND METHODS

Geological setting

Fossil outcrops at Farm Hansburg (Fig. 1B) preserve communities of Ernietta within 20- to 30-cm-thick medium- to fine-grained planar-bedded sandstones (39). Ernietta was restricted to storm-influenced muddy tidal flats, suggesting that these organisms thrived in environments with periodic sediment supply, fluctuating salinity, and medium- to low-flow velocities (41). Although these fossiliferous horizons were thought to belong to the Kanies Member of the Kuibis Formation (39), new chemostratigraphic data instead suggest that they belong to the Kliphoek Member (41), thus placing them as stratigraphically equivalent to the iconic fossil horizons preserved at Farm Aar (Fig. 1A) (41). Within the fossiliferous horizons, the vast majority of Ernietta that we found are in disparate spatial aggregations (fig. S1 and table S1), although we cannot discount the presence of rare, isolated individuals. Most individuals within communities are found preserved in a common orientation, with the ventral portion (i.e., the suture) facing down into the sediment (Fig. 1B and fig. S1). This common orientation and relative lack of deformation comprise strong evidence that Ernietta were preserved in life position, rather than transported. Typical accumulations consist of 5 to 15 closely spaced individuals (fig. S1), with rare larger slabs preserving less dense populations.

Ernietta model construction

A 3D digital model of Ernietta was constructed in COMSOL Multiphysics v. 5.3a through box modeling. The model was built from multiple cylindrical elements, which were iteratively added, moved, rotated, and scaled to approximate the modular shape of the organism (fig. S2). The model was scaled on the basis of measurements reported for published fossil material (14) and incomplete specimens collected during fieldwork from Namibia (fig. S3). To avoid adding additional interpretive biases, the model was based solely off fossil material and not previous artistic reconstructions. Hence, some smaller features, such as specialized feeding structures, are likely missed because of taphonomic overprint. Surface area and volume measurements were obtained using VGStudio Max 2.2.

Computational fluid dynamics

CFD simulations were carried out using COMSOL Multiphysics v. 5.3a. The Ernietta model was fixed to the lower surface of the computational domain, which consisted of a cuboid (fig. S3). Models were oriented upright in/on the sediment; this decision was based both on observations made in the field on Farm Hansburg (where the overwhelming majority of our specimens were found in an upright orientation) and the nature of sediment infill reported by Ivantsov (12), who inferred that the sediment accumulated inside Ernietta cavities during life (and so also supported an upright orientation). Portions of the model considered to be buried were subtracted from the domain, leaving only the exhumed regions of the model, thereby approximating different burial depths possible for a semi-infaunal lifestyle. An inlet with a normal inflow velocity boundary condition was assigned to one end of the domain, with a zero-pressure boundary condition assigned to the opposing end. Slip boundary conditions were assigned to the top and sides of the domain, allowing inviscid flow along the walls, and a no-slip boundary condition was assigned to the lower surface of the domain and the surfaces of the fossil, fixing the fluid velocity at zero. The fluid properties of water [density = 1000 kg/m³; dynamic viscosity (μ) = 0.001 kg/(s⋅m)] were assigned to the model. The domain was meshed using free tetrahedral elements, which varied in size according to the distance from the fossil (larger elements used in regions further away from the fossil). We conducted a sensitivity analysis to identify the optimal mesh size (table S2) and, based on this, selected COMSOL’s “normal” mesh parameter for use in all the simulations. Simulations were run using the shear stress transport turbulence model, which solves the Reynolds-averaged Navier-Stokes equations, and a stationary solver was used to compute the steady-state flow patterns.

CFD simulations were carried out with inlet velocities of 0.1, 0.2, and 0.5 m/s (Reynolds numbers, 5900 to 32,000) (Table 1 and section S1), which encompass typical current velocities in shallow marine conditions on modern continental shelves (48). Because the orientation of Ernietta with respect to the current is poorly constrained based on the fossil record, we ran simulations with models oriented at both 0° and 90° to the inlet (figs. S3 and S4). The life mode of Ernietta is debated, and it has been interpreted as fully endobenthic (49), surficial epibenthic (50), and semi-endobenthic (13, 14, 51). To address the different interpretations of burial depths of Ernietta, we performed simulations at three positions relative to the sediment-water interface, all of which correspond to semi-infaunal lifestyles, with the most shallowly buried model closely resembling an epibenthic lifestyle (fig. S4).

We carried out a series of simulations using multiple Ernietta individuals to evaluate the impact of a gregarious lifestyle on fluid flow. Six of these simulations were set up, with four individuals arranged in a square in different orientations and positions relative to the inlet, walls, and other individuals (fig. S6). These six simulations were divided into “clumped” (fig. S6) and “spaced” (fig. S6) arrangements, where interindividual distances were adjusted. The fifth simulation included five individuals, which were arranged with a row of three individuals downstream of a row of two individuals (fig. S7). All of these simulations were conducted using an inlet velocity of 0.2 m/s and with Ernietta individuals at a “moderate” burial depth (Table 1). This allowed us to assess the impact of orientation and spacing on flow patterns in multi-individual assemblages.

Last, we conducted an FSI simulation (movies S1 and S2) to evaluate the extent to which the Ernietta model was deformed by fluid flow. The material properties of silicone rubber [density = 1100 kg/m³; Poisson’s ratio = 0.47; Young’s modulus = 1,000,000 Pa; (52)] were assigned to a single individual of Ernietta oriented at 90° to the inlet with a moderate burial depth, and an FSI simulation was carried out using a normal mesh size and a simple algebraic yPlus turbulence model. A time-dependent simulation was run over a period of 10 s, with the inlet velocity increased from 0 to 0.2 m/s during the first 0.1 s of the simulation.

Simulation results were visualized as 2D plots showing overall flow velocity magnitude (U), flow velocity in the vertical axis (w), and turbulent kinetic energy magnitude (k) at horizontal and vertical cross-sections through the domain to characterize flow patterns. In addition, drag forces and their coefficients were calculated to quantify the forces exerted by the fluid on Ernietta in different positions (fig. S4).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/6/eaaw0260/DC1

Section S1. Reynolds number and drag coefficient calculations for characterizing flow regimes

Fig. S1. Field photographs of Ernietta aggregations likely representing bioherms.

Fig. S2. Ernietta model construction for CFD analyses.

Fig. S3. Select examples of CFD simulation setup.

Fig. S4. Frontal surface area at respective burial depth for calculations.

Fig. S5. CFD results for single-individual model.

Fig. S6. CFD results for multiple-individual model.

Fig. S7. CFD results for offset multiple-individual model.

Fig. S8. CFD drag results and SA/V values for all models.

Table S1. Size measurements of Ernietta from Farm Hansburg and Farm Kuibis in Namibia, collected summer 2016.

Table S2. Sensitivity analyses for meshing.

Movie S1. 2D FSI simulation of Ernietta in perpendicular orientation.

Movie S2. 3D FSI simulation of Ernietta in parallel orientation.