A Review of Cell-Based Computational Modeling in Cancer Biology

Abstract

Cancer biology involves complex, dynamic interactions between cancer cells and their tissue microenvironments. Single-cell effects are critical drivers of clinical progression. Chemical and mechanical communication between tumor and stromal cells can co-opt normal physiologic processes to promote growth and invasion. Cancer cell heterogeneity increases cancer’s ability to test strategies to adapt to microenvironmental stresses. Hypoxia and treatment can select for cancer stem cells and drive invasion and resistance. Cell-based computational models (also known as discrete models, agent-based models, or individual-based models) simulate individual cells as they interact in virtual tissues, which allows us to explore how single-cell behaviors lead to the dynamics we observe and work to control in cancer systems. In this review, we introduce the broad range of techniques available for cell-based computational modeling. The approaches can range from highly detailed models of just a few cells and their morphologies to millions of simpler cells in three-dimensional tissues. Modeling individual cells allows us to directly translate biologic observations into simulation rules. In many cases, individual cell agents include molecular-scale models. Most models also simulate the transport of oxygen, drugs, and growth factors, which allow us to link cancer development to microenvironmental conditions. We illustrate these methods with examples drawn from cancer hypoxia, angiogenesis, invasion, stem cells, and immunosurveillance. An ecosystem of interoperable cell-based simulation tools is emerging at a time when cloud computing resources make software easier to access and supercomputing resources make large-scale simulation studies possible. As the field develops, we anticipate that high-throughput simulation studies will allow us to rapidly explore the space of biologic possibilities, prescreen new therapeutic strategies, and even re-engineer tumor and stromal cells to bring cancer systems under control.

INTRODUCTION

Cancer is a complex systems problem that involves interactions between cancer cells and their tissue microenvironments.^1-3 Therapeutic approaches that narrowly focus on cancer cells frequently lead to disappointing outcomes, including resistance, tissue invasion, and treatment failure. Such failures are partly due to the unexpected behaviors that emerge from the dynamical systems of cancer tissues. Therapies act as selective pressures, even while cancer cells use increased genetic variability to broadly sample survival strategies and adapt.^3,4 Chronic hypoxia, another selective pressure, leads to metabolic changes, selection for cancer stem cells that resist treatment, invasion, and angiogenesis.^4-6 Tumor cells communicate biochemically and biomechanically with stromal cells, which allows them to co-opt normal physiologic processes.^1-3,7,8 Mathematical models can serve as "virtual laboratories" with fully controlled conditions where scientists and clinicians can investigate the emergent clinical behaviors that result from basic cell hypotheses and can evaluate new therapeutic strategies.^1,9

This review surveys cell-based methods for simulating cancer. Also known as discrete models, agent-based models, or individual-based models, cell-based models simulate individual cell behaviors within tissue environments. These models have several advantages. Each cell agent can track a fully independent state with individual parameters that reflect heterogeneity in cancer. Modelers can directly implement cell rules that reflect observations of single-cell behavior and cell-cell interactions, which allow us to translate biologic hypotheses to mathematical rules quickly; run simulation experiments that explore the emergent behaviors of these hypotheses; and compare against new data to confirm, reject, or iteratively improve the underlying hypotheses.^1,9,10

A SURVEY OF CELL-BASED MODELING METHODS

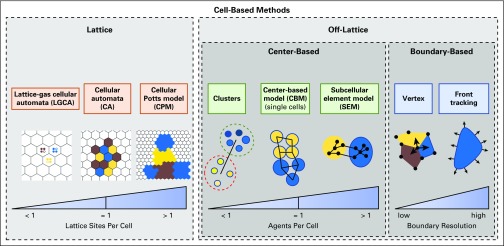
Cell-based models represent individual cells with two main paradigms—lattice-based models that track cells along a rigid grid and off-lattice models that have no such restriction. Figure 1 classifies most cell-based modeling approaches. Table 1 lists major open source modeling packages.

FIG 1.

A schematic classification of cell-based modeling approaches.

TABLE 1.

Computational Methods and Open Source Toolkits

Lattice-Based Methods

Lattice-based models can use regular structured meshes (eg, Cartesian¹¹ [two- or three-dimensional [2D/3D], dodecahedral [3D])¹² or unstructured meshes.¹³ Structured meshes are simpler to implement, visualize, and combine with partial differential equation (PDE) solvers, but their structure can lead to grid biases.¹³ Unstructured meshes can avoid these issues¹³ but with greater complexity.

We can further categorize lattice-based methods by their spatial resolution. In cellular automaton (CA) models, each lattice site can hold a single cell.^14-17 At each time step, each cell is updated with discrete lattice-based rules: remain, move to a neighboring lattice site, die (free a lattice site), or divide to place a daughter cell in a nearby site.^14-17 These methods usually update the lattice sites in a random order to reduce grid artifacts.^14,15

In lattice gas CA (LGCA) models, a single lattice site can contain multiple cells.^14,15,17,18 LGCA models track the number of cells that move through channels between individual lattice sites rather than the motion of each individual cell. They can simulate very large numbers of cells efficiently over long periods while also connecting to statistical mechanics theory; this facilitates analysis and provides a bridge to continuum methods that model cell densities or populations instead of single cells.^17,18

Some problems may require resolution of individual cell morphologies. Cellular Potts models (CPMs) use multiple lattice sites to represent each cell.^14,15,19 At each time step, CPMs visit each pixel (2D) or voxel (3D), test a random swap with a neighboring pixel/voxel, and accept or reject the swap (probabilistically) on the basis of whether it would reduce a global energy. Although CPMs can model cell morphologies and mechanics that cannot be incorporated in CA models, they are much more computationally intensive. Also, the calibration of Monte Carlo steps to physical time can be challenging.²⁰

Off-Lattice Methods

We can divide off-lattice models into center-based models (CBMs) that focus on cell volumes (or masses) and models that focus on cell boundaries. We can further classify these approaches by level of morphologic detail.

CBMs.

CBMs track each cell’s center of mass or volume, typically by using a single software agent per cell.^13-15,21 Some CBMs represent cells as points, whereas others explicitly model cell volumes. CBMs typically update the cells’ positions by explicitly formulating the adhesive, repulsive, locomotive, and drag-like forces exchanged between cell centers.^13-15,21 Most CBMs approximate cells as spheres; however, some approximate cells as deformable ellipsoids to better represent their morphologies.^22,23

CBMs can model cell morphology in greater detail by breaking cells into subcellular elements^24,25: Each cell is represented by multiple center-based agents that interact with adhesive and repulsive forces. These models better approximate cell biomechanics but at increased computational cost. Conversely, cells can be organized into clusters or functional units (eg, breast glands or colon crypts) that are simulated as agents that interact by mechanical forces or other rule-based motions^26,27; this allows modelers to incorporate heterogeneous details into individual clusters of cells but with greater computational efficiency than traditional CBMs.

Boundary-tracking models.

Vertex-based methods (eg, Fletcher et al²⁸) model cells as polygons (2D) or polyhedra (3D) and compute the forces that act on their vertices; they are particularly useful for modeling confluent tissues.²⁹ For greater spatial resolution, front-tracking methods, such as the immersed boundary method (IBM), solve PDEs for fluid flow inside and between cells and then advect boundary points along the cells’ membranes in this flow.³⁰ Level set methods have been applied to implicitly track the movement of cell boundaries,³¹ and VCell (see Connecting to Molecular Effects) recently added front-tracking capabilities.^32,33 These are among the most computationally intensive cell-based methods, but they are useful for coupling detailed cell mechanics to fluid and solid tissue mechanics.

Connecting to Molecular Effects

Most cell-based models are hybrid discrete-continuum; they couple a discrete cell model to continuum models of the microenvironment.^1,14,15 In general, these models use reaction-diffusion PDEs to simulate biotransport of oxygen, growth factors, and drugs. Ghaffarizadeh et al³⁴ developed BioFVM to solve diffusive transport of tens to hundreds of chemical substrates in 3D tissues; it is the underlying PDE solver for PhysiCell (a center-based simulation framework).²¹ In this framework, modelers write rules to relate individual cell phenotypes to local chemical substrate conditions.²¹

Many discrete models include systems of ordinary differential equations (ODEs) to model molecular processes in individual cells.^35,36 VCell can simulate reacting flows of many proteins within a single detailed cell,^32,33 and many modeling packages (eg, Chaste,³⁷ CompuCell3D,³⁸ and EPISIM³⁹) support systems biology markup language (SBML) to include systems of ODEs that simulate molecular effects in individual cells. Others use discrete models within individual agents: Gerlee and Anderson⁴⁰ used small neural networks to simulate individual cell phenotypic "decisions" on the basis of microenvironmental inputs, whereas PhysiBoSS⁴¹ combines the Boolean network modeling approach of MaBoSS^42,43 with PhysiCell²¹ to simulate molecular processes in individual cells.

EXAMPLES OF CELL-BASED MODELING IN CANCER BIOLOGY

We now explore a series of modeling themes that illustrate the use of cell-based modeling in cancer biology. Although we cannot comprehensively review all cell-based modeling in cancer (or even sample all major use cases for cell-based modeling), these themes are drawn from across the field to demonstrate scientific problems with significant cell-scale effects where cell-based models can yield new insights.

Hypoxia in Breast Cancer

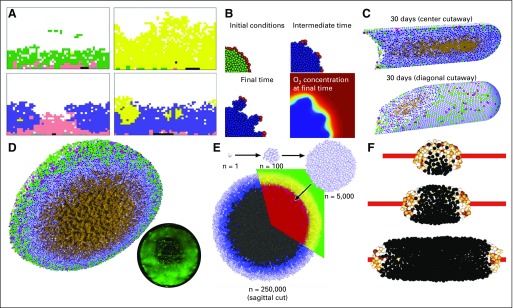
Many groups have used cell-based models to investigate tumor growth in hypoxic tissues and more generally, the effect of diffusive transport limits. Gatenby et al⁴⁴ and Smallbone et al⁴⁵ used CAs to examine hypoxia-driven switching to invasive phenotypes in ductal carcinoma in situ (DCIS). They incorporated cellular metabolic adaptations to hypoxia, which allowed them to study early tumor invasion (Fig 2A). Anderson and colleagues^46,47 extended earlier CA results by adapting IBCell³⁰ (an IBM) to mouse mammary (EMT6/Ro) tumor cell proliferation in hypoxic tissues. As before, they found that hypoxic gradients could drive tissue invasion, but IBCell’s improved modeling of cell adhesion and biomechanics predicted more rounded invasive tips⁴⁷ (Fig 2B).

FIG 2.

Cell-based models of hypoxia in breast cancer. (A) A cellular automaton model of breast cancer that explores cellular metabolic changes and early development of invasion. Reprinted with permission from Gatenby et al.⁴⁴ (B) An immersed boundary model to simulate cancer invasion under hypoxic gradients. Adapted with permission from Anderson et al.⁴⁷ (C) PhysiCell (a center-based model [CBM]) simulation of ductal carcinoma in situ as it advances in breast ducts under diffusive growth limits. Note the brown necrotic core. Adapted with permission from Ghaffarizadeh et al.²¹ (D) Adapted PhysiCell simulation of hanging-drop tumor spheroids. Oxygen diffusive limits lead to hypoxic gradients, greatest proliferation on the outer edge, an interior quiescent region, and an central necrotic core (brown). Note the network of fluid-filled pores that emerges from the necrotic core mechanics. These are observed in experiments. The inset shows a fluorescent image of a hanging-drop tumor spheroid. Adapted with permission from Ghaffarizadeh et al.²¹ (E) CBMs of tumor spheroids pioneered by Drasdo and Höhme produced similarly layered structures. Reprinted with permission from Drasdo and Höhme.⁴⁸ (F) A CBM of tumor cords growing around a blood vessel and showing a reversed structure with viable tissue in the interior. Adapted with permission from Szymańska et al.⁴⁹

Macklin et al⁵⁰ and Hyun and Macklin⁵¹ applied a CBM to study oxygen-driven proliferation and necrosis in solid-type DCIS with comedonecrosis. After calibrating to individual patient pathology data (tissue specimens immunostained for the Ki67 protein to detect cycling cells, cleaved caspase 3 to detect apoptosis, and annotated with viable rim sizes and cell density⁵⁰), they were able to simulate comedonecrosis and microcalcifications as emergent properties of the simulations along with realistic, constant rates of tumor advancement along the breast ducts. Ghaffarizadeh et al²¹ refined the DCIS model and extended it to 3D as well as simulated the hypoxic interiors of hanging drop spheroids calibrated to match MCF-10A birth and death kinetics in culture (Figs 2C and D). As in early 3D work by Drasdo and Höhme⁴⁸ on EMT6/Ro cells (Fig 2E), they predicted a layered structure—an outer proliferative rim surrounding a quiescent perinecrotic region and an interior necrotic core. They were the first to predict networks of fluid-filled pores in the necrotic cores that emerge from the competing effects of necrotic cell shrinking and adhesion; these structures are observed in experimental models (Fig 2D inset). Szymańska et al⁴⁹ used a CBM of EMT6 cells to simulate a growing tumor cord—a solid tumor that grows around a blood vessel. They predicted a similar three-layer structure but in reverse order—a proliferating core nearest the blood vessel, quiescent interior, and necrotic exterior (Fig 2F).

Tumor-Induced Angiogenesis and Drug Delivery

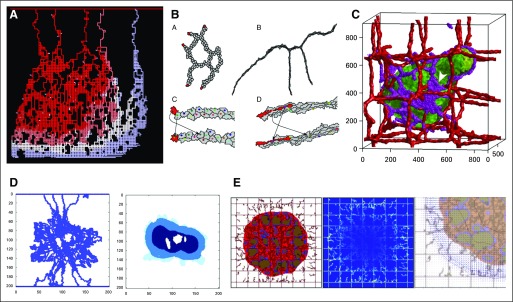
Tumor-induced angiogenesis allows lesions to grow to clinically detectable sizes.³ McDougall and colleagues^52,53 modeled sprouting angiogenesis with a CA model of vessel tip migration: Sprout tip agents followed chemotactic and haptotactic signals to migrate toward hypoxic tumor regions and left a trail of functional vessels. They incorporated a detailed vascular network flow model, including dynamic wall shear stress rules for vessel branching and anastomosis (vessel looping), and used this framework to explore therapeutic delivery from tumor-associated vasculatures (Fig 3A). Bauer et al⁵⁴ used a CPM to simulate tumor-induced angiogenesis, by adding a detailed microenvironment, including extracellular matrix (ECM) and multiple vascular endothelial growth factor isoforms; they concluded that variations in the spatial distributions of proangiogenic factors greatly affect capillary morphology and that inhomogeneities in nonvascular tissue naturally lead to capillary anastomosis. Boas and Merks⁵⁵ used a CPM to investigate novel hypotheses on cell overtaking: Cell-cell biomechanical and chemical communication can cause endothelial cells in the stalk to assume the role of migrating tip cells by migrating to the front of an advancing vessel (Fig 3B). Shirinifard et al⁵⁶ used a CPM to investigate tumor growth with angiogenesis and showed that tumor size increases with increasing angiogenesis and that the tumors grow along the vasculature (Fig 3C).

FIG 3.

Tumor-associated angiogenesis and vascular flow. (A) A two-dimensional (2D) cellular automaton model of sprouting angiogenesis used to study drug delivery from tumor vasculatures. Reprinted with permission from McDougall et al.⁵³ (B) A 2D cellular Potts model of angiogenesis. Stalk cells can overtake tip cells to become new tip cells. The arrows show these role swaps. Reprinted with permission from Boas and Merks.⁵⁵ (C) A 3D cellular Potts model of sprouting angiogenesis driven by vascular endothelial growth factor released by hypoxic tumor cells. Adapted with permission from Shirinifard et al.⁵⁶ (D) A 2D cellular automaton model (left) to investigate drug delivery to simulated tumors (right). Adapted with permission from Cai et al.⁵⁷ (E) A discrete angiogenesis model of McDougall et al⁵³ combined with a continuum tumor growth model⁵⁸ used to investigate the effect of interstitial fluid pressure and lymphatic drainage on therapeutic delivery. Shown are tumor and the discrete vasculature (left); fluid extravasation from blood and lymphatic vessels (middle); and interstitial fluid velocity (right), which hinders drug delivery. Adapted with permission from Wu et al.⁵⁹

Cai et al⁵⁷ used a CA model of tumor cells in a continuous ECM coupled with a discrete angiogenesis model that included flow effects and substrate perfusion from the vasculature (Fig 3D). They showed that the final vessel configuration depends on emergent, dynamic feedback mechanisms in vascular remodeling rather than on initial conditions. Wu et al⁵⁹ extended an earlier hybrid discrete-continuum model⁵⁸ (that was based on that of McDougall and colleagues^52,53) to investigate the influence of interstitial fluid pressure, interstitial fluid flow, and lymphatic drainage on drug delivery in growing tumors.⁵⁹ They found that elevated interstitial hydraulic conductivity and high interstitial fluid pressure limit the transvascular delivery of nutrients and therapeutics (Fig 3E).

Cancer Stem Cells

Models of cancer stem cells (CSCs) offer valuable insights into the driving forces of cancer biology. Fletcher and colleagues^37,60,61 developed a 3D CBM of colonic crypts to explore the role of stem cells (in the bottom of the crypt) in colorectal carcinogenesis. Neighboring cells were connected by linear springs, and stem-cell division and differentiation were driven by Wnt gradients along the crypt axis. The geometry of the stem-cell hierarchy (proliferation at the crypt base, expansion and differentiation along the middle and top) created an overall base-to-top proliferative cell flux. This flux has an anticancer protective effect wherein it pushes any mutated cell and its progeny out of a crypt before they can spread throughout a crypt, unless the mutation occurs in a stem-cell niche (Fig 4A).

FIG 4.

Cancer stem cells, invasion, and the "go or grow" hypothesis. (A) Top view of a three-dimensional (3D) center-based model of colon crypts (left plots) where the stem-cell niche is in the center. A nonstem mutation (blue cells) is swept out of the crypt by the proliferative cell flux. On the right, is a 3D view of four such ducts that feed cells to a central villus, which is based on the same simulation model. Adapted with permission from Fletcher et al⁶¹ (left) and Mirams et al³⁷ (right). (B) A 3D cellular automaton (CA) model (with stem-cell effects) of how chemical signaling with fibroblasts and macrophages can drive triple-negative breast cancer. Among these findings, if stromal cells can promote increased cancer cell migration, the overall tumor grows. Reprinted with permission from Norton et al.⁶² (C) A 2D CA model to investigate the spread of traits in growing tumors, when cancer cells and their progeny could carry four tumor traits. Traits disseminate largely radially, with clear implications for tumor needle biopsies. Adapted from Poleszczuk and Enderling.¹¹ (D) A 2D cellular Potts model of stem cells in glioblastoma that shows their role in building resistance to radiotherapy. Reprinted with permission from Gao et al.⁶³ (E) Lattice gas CA models of the "go or grow" hypothesis in glioblastoma multiforme. As cells spend more time proliferating, they contribute to better growth up to a critical transition point; beyond this point, decreased migration is insufficient to open space for cell division. Adapted with permission from Hatzikirou et al.⁶⁴ (F) A center-based model to explore the "go or grow" hypothesis in glioblastoma multiforme. Here, G₀ is the models' growth rate parameter. Adapted with permission from Kim et al.⁶⁵

Norton et al⁶² built a 3D CA model to examine the interaction between triple-negative breast cancer and stromal cells. Stem cells proliferated and differentiated into progenitor cells, and cancer cells exchanged chemical signals with fibroblasts and infiltrating macrophages. Among their results, they found that increasing the stromal effect on cancer cell proliferation decreased overall tumor size, whereas increasing the stromal effect on cancer cell migration increased tumor size (Fig 4B).

Poleszczuk et al⁶⁶ developed a 2D CA model of CSCs and nonstem cancer cells, which tracked four traits in each individual cell: migration rate, apoptosis, symmetric CSC division, and cancer cell proliferation potential. They found that increasing the cancer cell proliferation potential could reduce tumor growth because the increased cancer cell population competed with CSCs for space and inhibited CSC division. They also found that traits propagated radially from the centers of growing tumors; this has implications for biopsies of tumor heterogeneity (Fig 4C). Gao et al⁶³ used a CPM to investigate the role of glioma stem cells (GSCs) in glioblastoma growth and radiation therapy response (Fig 4D). They found that switching from asymmetric to symmetric division or fast GSC cycling was necessary to explain clinical observations of glioma repopulation after radiotherapy and that the expanded GSC fraction could reduce radiosensitivity.

Alfonso et al⁶⁷ also explored radiotherapy treatment paradigms with respect to a heterogeneous population of CSCs and cancer cells using a 3D CA model. They found that CSCs, which are typically more radioresistant, segregated to the center of the tumor across a range of proliferation and death parameters. This emergent phenomenon is due to the faster cycling time of the cancer cells compared with CSCs. When these cell arrangements were subjected to radiotherapy, they found that radiotherapy is more effective at tumor control when it is concentrated on the tumor center where CSCs are located rather than when it is spread homogeneously across the entire tumor.

The "Go or Grow" Hypothesis for Glioblastoma Multiforme

Tektonidis et al⁶⁸ examined the "go or grow" (GoG) hypothesis in gliomas, where tumor cells must make a "decision" between migration (go) or proliferation (grow). They modeled data from 3D spheroid cell cultures with a 2D LCGA model and attempted to recapitulate three experimental observations: nonidentical spreading rates of the invasive rim and central core, radially persistent and symmetric cell motion, and a highly proliferative central core compared with the remaining tumor. Tektonidis et al evaluated the emergent model behavior under a variety of cell phenotype rule sets to determine which rules were required to predict the three observations. They found that a proliferative-motility dichotomy (the GoG hypothesis), cell-cell repulsion, and density-dependent switching between the proliferative and motile states were required to match experimental observations. They concluded that disruption of the GoG mechanism to favor proliferation could limit the required tumor resection volume in surgical interventions.

Hatzikirou et al⁶⁴ investigated the GoG hypothesis in glioblastoma multiforme (GBM) using a 2D LGCA model. In their work, cells could divide, re-orient, migrate, or apoptose on the basis of local oxygenation conditions. They modeled the GoG hypothesis by switching hypoxic cells to a motile phenotype and reverting to a proliferative phenotype after escaping hypoxia. They found that increasing the cell bias toward proliferation increases overall tumor growth, but crossing a threshold could decrease overall tumor growth when motility is insufficient to open new space for cell division (Fig 4E). Comparable results were obtained by Gerlee and Nelander⁶⁹ using stochastic switching between the two phenotypes (migrate or proliferate). From their CA model, they derived a system of coupled PDEs to investigate further the relationships between cell-level parameters and tumor-scale dynamics.

In related work, Böttger et al⁷⁰ explored a 2D LGCA GoG model for GBM to provide a more quantitative parameter space analysis of a tumor’s invasive dynamics. Systematically varying model parameters for proliferation and motility led to counterintuitive results about invasion. Specifically, invasion speed depended on two competing processes: emptying space as a result of cell migration and filling space as a result of cell proliferation. In later work, Böttger et al⁷¹ used similar techniques to find that if cell motility decreases with increased cell density, then small tumors self-extinguish. On the other hand, increasing cell motility with increasing cell density leads to self-sustaining growth, similar to the Allee effect frequently observed in ecology.

Kim et al⁶⁵ used a CBM to explore GBM using miR-451 as an intracellular detector of glucose, with an ODE model of miR-451 as the effector for selecting migration versus proliferation for glioma cells (Fig 4F). They found that cell migration depended not only on glucose, but also on mechanical spacing between cells. They also predicted that the placement of chemoattractants at the edges of a resected tumor could reduce GBM cell migration from the resection site. These GoG examples highlight the key role played in single-cell decisions in GBM and the potential for cell-based models that explore the clinical behaviors that emerge from single-cell effects.⁷²

Cancer Invasion and Epithelial-Mesenchymal Transition

Cancer invasion is essential to metastatic progression.^3,72-74 Cancer cells acquire a motile phenotype to escape primary tumors and invade nearby tissues (as conceptually modeled in epithelial-to-mesenchymal transition [EMT]⁷⁵), invade and travel within blood and lymphatic vessels,^76,77 and finally colonize distant metastatic niches.⁷⁸ Because single-cell effects are critical, many cell-based models have investigated cancer invasion with or without explicit modeling of EMT.

Reher et al⁷⁹ developed a 2D LGCA model to simulate the effects of a heterogeneous cell-cell adhesion in an epithelial layer, with decreased cell-cell adhesion representing one of the effects of EMT. Cell-cell adhesion was modeled by varying the initial and maximum number of adhesion receptors for each virtual cell. They found that increased adhesion heterogeneity as well as decoupling receptor number from environmental signals (cell-cell contact) lead to increased dissemination.

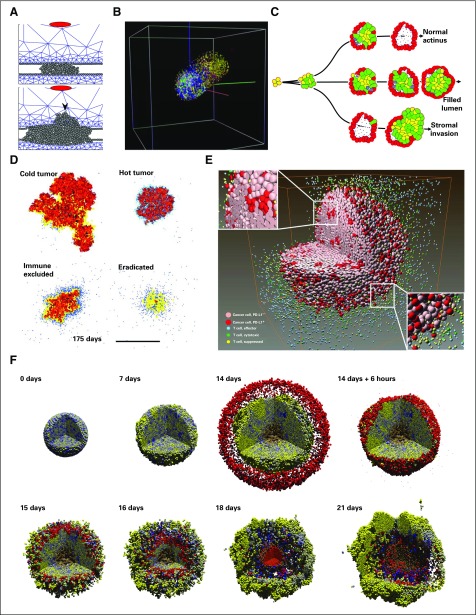
Kim and Othmer⁸⁰ developed a center-based model with a continuous ECM description to investigate the interactions of tumor cells, signal-secreting stromal cells, and the ECM. Stromal levels of fibroblast-secreted protein initiated EMT, which switches cells to an invasive, motile phenotype. Invasive cells also secreted a tumor-associated protease, which degrades the basement membrane and ECM. Degradation of the basement membrane results in more cell exposure to fibroblast-secreted protein, which results in more phenotypic switching; more invasion; more ECM degradation; and ultimately, collective cell invasion (Fig 5A). These results suggest that inhibiting fibroblast secretions could affect invasive potential.

FIG 5.

Cancer invasion and immunosurveillance. (A) In a center-based model, signals secreted by stromal cells (red) induce tumor cells (gray) to degrade the basement membrane and invade the stroma (blue mesh). Adapted with permission from Kim et al.⁸⁰ (B) A three-dimensional (3D) cellular automaton (CA) model to study selection in heterogeneous brain cancers. Cells could mutate their signaling network parameters, which leads to more invasive clones. Adapted with permission from Zhang et al.⁸¹ (C) An immersed boundary method of contact-based signaling and polarization in breast acini.^82,83 Cells with altered signaling could fill the lumen or invade the stroma. Adapted with permission from Anderson et al.⁸² (D) A 2D CA model of tumor-immune interactions. Immune cells (blue dots) become exhausted after too many successful tumor cell kills and create fibrotic tissue (yellow). Tumor encapsulation, tumor elimination, and chronic response are observed in the model. Adapted with permission from Kather et al.⁸⁴ (E) A sophisticated 3D CA model of treatments targeting programmed cell death-1 (PD-1) and programmed death ligand 1 (PD-L1) in cancer cells. (PD-L1⁺ cells express PD-L1; PD-L1⁻ cells do not.) Reprinted with permission from Gong et al.⁸⁵ (F) A 3D center-based model of immune responses to an immunostimulatory factor in a heterogeneous tumor (shaded by immunogenicity; yellow cells are most immunogenic). Immune cells (red) seek and adhere to cancer cells, test for immunogenicity, and induce apoptosis. The immune response failed after immune cells aggregated near a local maximum in the signaling factor, which allows the tumor to repopulate. Adapted with permission from Ghaffarizadeh et al.²¹ This work was explored further with high-performance computing.¹⁰

Zhang et al⁸¹ used a 3D CA model to investigate tissue invasion and tumor cell heterogeneity in glioma. Using a subcellular signaling network, cells divide and move on the basis of external concentrations of nutrients and signaling molecules. They acquire oncogenic mutations upon division to produce new clones. Each successive clone is more proliferative and nutrient seeking, which increases overall invasive potential. By starting with a sphere of the least oncogenic cells in the center of the simulation, Zhang et al found that heterogeneity increased in all regions of the simulation followed by a decrease in heterogeneity in the regions that contain the nutrient source and eventual recovery of heterogeneity. The decrease was attributed to an outgrowth of the most oncogenic subclone, which potentially explains the asymmetric invasive growth seen in experimental and clinical reports (Fig 5B).

Anderson et al⁸² used an IBM to investigate morphologic changes in breast acini as a result of variation in cell polarization and anoikis behaviors in response to cell contact with other cells and the basement membrane. In this, and additional work by Rejniak et al,⁸³ Anderson et al showed that atypical behavior in a single cell can lead to eventual intraductal and stromal invasion (Fig 5C).

In a sophisticated investigation of metastatic colonization, Araujo et al⁸⁶ developed a hybrid CA model of prostate cancer (PCa) bone metastasis. In their work, mesenchymal stromal cells differentiated into osteoblasts that created bone material, whereas osteoclasts degraded bone. In the absence of tumor cells, these cell populations coordinated through transforming growth factor-β and receptor activator of nuclear factor kappa beta ligand (RANKL) signaling to maintain healthy bone tissue. When PCa cell agents were introduced into the bone, tumor-secreted transforming growth factor-β promoted osteoblast activity, but osteoblast-osteoclast feedbacks simultaneously degraded bone to release new growth factors that could drive additional PCa proliferation and invasion. Araujo et al studied the model to compare potential improvements of RANKL inhibitors and bisphosphonates (two standard-of-care treatments for bone metastases). They found that additional refinements to bisphosphonates would yield little clinical improvement over current treatments, whereas improvement of RANKL inhibitors from the current (model-estimated) 40% inhibition closer to a theoretical maximum 100% inhibition could dramatically improve outcome.

Tumor Immunosurveillance

Individual interactions between tumor cells and immune cells are critical to immunosurveillance.^3,7,87 Cell-based models are uniquely capable of examining these while considering the roles of stochasticity and heterogeneity.

Kather et al⁸⁴ developed a CA model to study complex interactions between tumor cells and immune cells. In their model, immune cells could randomly appear (an influx model), migrate toward tumor cells, and kill them. Immune cells were assumed to be exhausted after killing a maximum number of times and would induce tissue fibrosis that impaired cell migration. Tumor cells could proliferate, die, remain stationary, or migrate on the basis of the number of open neighboring lattice sites and their distance to the nearest open lattice site (a phenomenologic model of necrosis). Depending on the relative migration and proliferation parameters for tumor and immune cells, this model could exhibit diverse tumor-immune interactions, including successful immunosurveillance (eradicated), tumor encapsulation by fibrotic tissue (immune excluded), and ongoing immune responses (Fig 5D). Gong et al⁸⁵ recently developed a 3D CA model to investigate the tumor-immune responses to programmed cell death-1 and programmed death-ligand 1 inhibition (Fig 5E).

Ghaffarizadeh et al²¹ developed a 3D off-lattice model of an immune attack on a tumor with a heterogeneous oncoprotein (mutations increased both proliferation and immunogenicity). After simulating initial growth, they added simulated immune cells that chemotaxed toward tumor-released immunostimulatory factors. Each immune cell tested for mechanical collision with cells, formed an (Hookean) adhesion, tested for immunogenicity, and stochastically attempted to induce tumor cell apoptosis. Attached immune cells eventually would succeed in killing the tumor cell and detach or continue the attempt before detaching and continuing their search for new targets. Their simulations showed initial tumor regression but eventual tumor regrowth when immune cells passed some tumor cells and formed large clumps near maxima of the immunostimulatory factor (Fig 5F). The authors have expanded their investigation to supercomputers to explore further the effect of stochastic migration on the overall efficacy of the immune response¹⁰; this work showcases the potential for using supercomputers to explore large therapeutic design spaces in high throughput.

ADDITIONAL RESOURCES

As companions to this review, we maintain three online curated collections:

1. Cloud-hosted examples of cell-based cancer models: https://www.scienceopen.com/collection/online-cancer-simulators

2. Open source cell-based simulation frameworks: https://www.scienceopen.com/collection/open-source-agent-frameworks-biology

3. Additional reviews of mathematical modeling in cancer: https://www.scienceopen.com/collection/math-modeling-in-cancer-reviews

DISCUSSION

Cell-based methods can track single-cell traits and individual behaviors, which make them well suited for problems where single-cell effects are important, such as stem-cell hierarchies, heterogeneity, invasion, and tumor-immune interactions. They are ideal for hypothesis-driven computational experiments because biologic observations of single-cell behavior can be directly translated to agent rules.

Lattice-based methods are straightforward to implement and fast, which makes them useful for quickly testing new ideas. We show how lattice-based methods have yielded insights on cancer metabolism, cancer stem cells, angiogenesis, the GoG hypothesis, invasion, and cancer immunosurveillance. CA methods remain the most common method for modeling vascular networks, whereas CPMs have investigated the finer details of angiogenesis.

Lattice-based methods are at risk for grid-based artifacts, and their biomechanical realism is limited; off-lattice models can readily incorporate biomechanics and off-lattice cell-cell interactions. As the hypoxia and immunosurveillance examples show, novel structures can arise from the interplay of stochasticity, transport limitations, mechanics, and single-cell characteristics. However, off-lattice models often are computationally demanding, and they generally have many parameters to calibrate. Ultimately, no single method is best for all problems. Modelers should reproduce findings with multiple approaches to avoid algorithm-dependent biases.⁸⁸

This is an exciting time to apply cell-based modeling to cancer. Increases in computational power are allowing larger simulation studies with greater sophistication, and high-throughput computing is enabling exploration of high-dimensional parameter spaces.¹⁰ Open source platforms have lowered the barrier to entry for using sophisticated techniques (Table 1). In the future, we envision that cell-based modeling software will be increasingly user friendly, cloud hosted, and open to modular contributions from the community,⁸⁸ which would potentiate a community-driven ecosystem of interoperable tools that together exceed the sum of their parts.¹ We are excited to imagine the new insights that are on the horizon.

AUTHOR CONTRIBUTIONS

Conception and design: John Metzcar, Paul Macklin

Financial support: Paul Macklin

Collection and assembly of data: John Metzcar, Yafei Wang, Randy Heiland

Manuscript writing: All authors

Final approval of manuscript: All authors

Accountable for all aspects of the work: All authors

AUTHORS’ DISCLOSURES OF POTENTIAL CONFLICTS OF INTEREST

The following represents disclosure information provided by authors of this manuscript. All relationships are considered compensated. Relationships are self-held unless noted. I = Immediate Family Member, Inst = My Institution. Relationships may not relate to the subject matter of this manuscript. For more information about ASCO's conflict of interest policy, please refer to www.asco.org/rwc or ascopubs.org/jco/site/ifc.

Paul Macklin

Patents, Royalties, Other Intellectual Property: Patent in review for machine learning in digital pathology

No other potential conflicts of interest were reported.