Absolute Quantification of Phosphor‐Containing Metabolites in the Liver Using ³¹P MRSI and Hepatic Lipid Volume Correction at 7T Suggests No Dependence on Body Mass Index or Age

Abstract

Background

Hepatic disorders are often associated with changes in the concentration of phosphorus‐31 (³¹P) metabolites. Absolute quantification offers a way to assess those metabolites directly but introduces obstacles, especially at higher field strengths (B₀ ≥ 7T).

Purpose

To introduce a feasible method for in vivo absolute quantification of hepatic ³¹P metabolites and assess its clinical value by probing differences related to volunteers' age and body mass index (BMI).

Study Type

Prospective cohort.

Subjects/Phantoms

Four healthy volunteers included in the reproducibility study and 19 healthy subjects arranged into three subgroups according to BMI and age. Phantoms containing ³¹P solution for correction and validation.

Field Strength/Sequence

Phase‐encoded 3D pulse‐acquire chemical shift imaging for ³¹P and single‐volume ¹H spectroscopy to assess the hepatocellular lipid content at 7T.

Assessment

A phantom replacement method was used. Spectra located in the liver with sufficient signal‐to‐noise ratio and no contamination from muscle tissue, were used to calculate following metabolite concentrations: adenosine triphosphates (γ‐ and α‐ATP); glycerophosphocholine (GPC); glycerophosphoethanolamine (GPE); inorganic phosphate (P_i); phosphocholine (PC); phosphoethanolamine (PE); uridine diphosphate‐glucose (UDPG); nicotinamide adenine dinucleotide‐phosphate (NADH); and phosphatidylcholine (PtdC). Correction for hepatic lipid volume fraction (HLVF) was performed.

Statistical Tests

Differences assessed by analysis of variance with Bonferroni correction for multiple comparison and with a Student's t‐test when appropriate.

Results

The concentrations for the young lean group corrected for HLVF were 2.56 ± 0.10 mM for γ‐ATP (mean ± standard deviation), α‐ATP: 2.42 ± 0.15 mM, GPC: 3.31 ± 0.27 mM, GPE: 3.38 ± 0.87 mM, P_i: 1.42 ± 0.20 mM, PC: 1.47 ± 0.24 mM, PE: 1.61 ± 0.20 mM, UDPG: 0.74 ± 0.17 mM, NADH: 1.21 ± 0.38 mM, and PtdC: 0.43 ± 0.10 mM. Differences found in ATP levels between lean and overweight volunteers vanished after HLVF correction.

Data Conclusion

Exploiting the excellent spectral resolution at 7T and using the phantom replacement method, we were able to quantify up to 10 ³¹P‐containing hepatic metabolites. The combination of ³¹P magnetic resonance spectroscopy imaging data acquisition and HLVF correction was not able to show a possible dependence of ³¹P metabolite concentrations on BMI or age, in the small healthy population used in this study.

Level of Evidence: 2

Technical Efficacy: Stage 1

J. Magn. Reson. Imaging 2019;49:597–607.

Liver disorders often manifest in changes of concentrations of numerous phosphorus‐31 (³¹P) metabolites.1 in vivo ³¹P magnetic resonance spectroscopy (MRS) offers the possibility to assess many of these metabolites and help in the diagnosis of some diffuse liver disorders,1 such as viral,2 alcoholic3, 4 and nonalcoholic fatty liver disease (NAFLD),5, 6 cirrhosis,7, 8, 9 liver metastases,10, 11 and diabetes.12, 13

In experiments at clinical magnetic fields (B₀ ≤ 3 T), it is possible to detect only a limited amount of metabolites, namely, adenosine triphosphates (γ‐, α‐, and β‐ATP), inorganic phosphate (P_i), grouped phosphomonoesters (PMEs), and grouped phosphodiesters (PDEs).7, 11, 14, 15, 16, 17, 18, 19, 20, 21, 22 The improvement in spectral resolution and the increased signal‐to‐noise ratio (SNR) that can be achieved by the use of higher fields (B₀ ≥ 7T),23 or, at lower fields, utilizing methods such as proton decoupling and the nuclear Overhauser effect (NOE).24, 25 Such improvements are of potential benefit in determining possible biomarkers. The application of higher fields allows the resolution and discrimination of phosphocholine (PC) and phosphoethanolamine (PE) from PMEs and glycerol phosphocholine (GPC), glycerol phosphoethanolamine (GPE), and phosphatidylcholine (PtdC) from PDEs, as well as nicotinamide adenine dinucleotide (NADH) from α‐ATP, and also, a peak that originates from uridine diphosphoglucose (UDPG).1, 23, 26

The disadvantage of MR experiments at 7T is the increased inhomogeneity of the excitation field (B₁).27 This can be tackled by a phantom replacement technique where the map of B₁ distribution and coil sensitivity is acquired on a phantom object with an experimental setup identical to the in vivo measurements. This method is applicable only if the organ of interest is homogeneous enough, as the phantom itself is a homogeneous mixture. Custom simulations of transmitted (${\mathrm{B}}_1^{+}$) and received (${\mathrm{B}}_1^{-}$) field distribution and their combination to B₁, as provided by measurements from both in vivo and phantom experiments, are an approach with which to validate and justify the use of the phantom replacement technique to correct for field inhomogeneity in certain tissues.

At 7T, a larger spectral bandwidth leads to increased chemical shift displacement errors (CSDEs) and shorter spin–spin relaxation times (T₂), yielding a faster decrease of the observable signal. Therefore, CSDE‐insensitive, free‐induction decay (FID)‐based sequences, such as chemical shift imaging (CSI) or CSDE‐reduced Image Selected in vivo Spectroscopy (ISIS),1, 23, 27 are preferred for proper localization. To avoid contamination by adjacent subcutaneous tissue (e.g., muscle or adipose tissue), multidimensional approaches (2D, 3D) are favored. In addition, 3D‐CSI offers the possibility to map the metabolites in all three dimensions23 and select the signal from the appropriate anatomical regions during postprocessing. This enables the use of a single phantom dataset for B₁ correction of all in vivo measurements. The relatively long measurement times of 3D‐CSI can still be kept to an acceptable time due to short spin‐lattice relaxation times (T₁) at 7T,26 and, therefore, reduced repetition times (TRs).

The output of many previous ³¹P MRS studies were relative quantities, which provided ratios of metabolite signals or their groups,7, 11, 15, 16, 17, 18 whereas only a few studies have performed absolute concentrations.19, 20, 22, 24, 25 These absolute concentrations provide more specific and precise information, since each metabolite can be investigated individually and the readout does not rely on possible changes in other metabolites. Frequently, ATP serves as an internal reference for quantifications, assuming ATP to be constant within populations,14, 26 and thus, calculated concentrations are not true absolute, but rather, relative quantities. The assumption of constancy might not necessarily be valid, as a recently published study reported food intake‐dependent γ‐ATP levels in the liver.28 The questions of whether there are differences in metabolite concentrations between lean and overweight people and whether those differences are dependent on age are of great interest.

Determining the hepatocellular content of lipids (HCL) results in additional information about the condition of the liver29 and can be used to correct assessed metabolite concentrations for the volume captured by lipid droplets.13 This might be of importance for a possible dependency of hepatic ³¹P metabolite content on body mass index (BMI).

The purpose of this study was to implement and validate a method for absolute quantification of ³¹P metabolites at 7T. Unlike other studies, we aimed to quantify hepatic metabolites without the use of an internal reference, which may be subject to metabolic fluctuations. In addition, using the recently published T₁ times of ³¹P metabolites in hepatic tissue at 7T,26 we approached the quantification of low‐concentration ³¹P metabolites, such as PtdC, NADH, and UDPG. Furthermore, a second aim was to investigate possible concentration dependencies on BMI and age, as well as the influence of correction for hepatic lipid volume fraction (HLVF).

Materials and Methods

All measurements were performed on a 7T whole‐body MR system MAGNETOM (Siemens Healthineers, Erlangen, Germany) using a double‐tuned ¹H/³¹P surface coil (RAPID Biomedical, Rimpar, Germany) with diameters of 9.5 cm for the ¹H and 10.5 cm for the ³¹P channel. For coil load correction, a small, cylindrical glass vial (diameter: 10 mm, height: 13 mm, volume: 1 mL) containing triphenylphosphate (TTP) diluted in chloroform was placed at the same position relative to the coil, and fixed by foam material. This calibration reference sample had a stable ³¹P resonance signal at –11 ppm with respect to phosphocreatine (PCr), and therefore, did not overlap with any other liver signals. It was also used as orientation to place the field of view (FOV) of the 3D‐CSI.

Written, informed consent was obtain from each individual subject for in vivo measurements. The study was approved by the local Institutional Review Board. Measurements were performed after overnight fasting.

Prior to all measurements, localized shimming was performed on a manually selected volume in the phantom/liver by the automated procedure provided by the vendor, with additional manual adjustments. A linewidth of the water peak of around 80 Hz (magnitude spectrum) in a 100 cm³ volume with free‐breathing was typically achieved.

Phantom Preparation

For the initial method‐testing and calibration experiments, two cylindrical phantoms (diameter: 17 cm, height: 9 cm, volume: 2 L) were prepared. They contained 15 mM and 25 mM ³¹P in the form of KH₂PO₄ dissolved in distilled water. Table salt (NaCl) was added to reach an electrical conductivity of about 6.5 mS/cm, which is in the range of physiological conditions. The 15 mM ³¹P concentration served as a method calibration phantom, whereas the 25 mM ³¹P phantom was used to validate the experiment. T₁ times of the phantoms were determined with an inversion recovery sequence with a TR of 40 seconds and 18 inversion times (TI), and with durations from 20 to 20,000 msec. Gadoteric acid (Gd‐DOTA, trade name Dotarem) was added to both phantoms in order to shorten the T₁ times to a convenient length of 1 to 2 seconds.

Calibration Reference Signal

The main experiments consisted of a sequence of 2000 μsec rectangular (RECT) pulses (TE = 1.1 msec, TR = 1.5 sec) (WIP #546A by Dr. Tiejun Zhao, Siemens Healthineers) to determine the flip angle‐dependence on the pulse voltage in the calibration reference influenced by the coil load of the measured subject. These pulses were centered on the resonance frequency of the reference sample. A nonlocalized 600 μsec RECT pulse sequence was used, with the calculated voltage to flip magnetization by a 90° angle in the calibration reference and on its resonance frequency with a TE of 0.4 msec, a TR of 20 sec, and 4 averages.

3D‐CSI Sequence

Spectra were acquired with 12 phase‐encoding gradients by elliptically reduced k‐space sampling in all three spatial directions in a FOV of 20 × 20 × 20 cm³. Spatial zero‐filling was applied to interpolate the data to a 16 × 16 × 16 matrix. Each spectrum was recorded, with a spectral width of 5000 Hz, as 1024 complex data points and originated from a volume with a nominal voxel size of about 1.95 cm³. To minimize voxel bleeding, a Hamming filter was applied over the full k‐space. The "real" voxel size of unfiltered and filtered data was experimentally determined.

Assuming the calibration reference to be a point source, the spatial response function (SRF)30 was recorded as a signal profile through the source. The 64% level of the SRF was used to estimate the voxel volume. An imaging sequence of the same FOV was run for spatial orientation.

The necessary voltage to achieve a 90° flip angle for a distance of about 5.8 cm in the axial direction from the coil center, which is a typical distance of the liver parenchyma, was calculated with the Biot‐Savart law for the 600 μsec RECT pulses (TR = 1.8 sec, TE = 0.9 msec) of a 3D‐CSI sequence.

To calculate the B₁ correction matrix, the calibration phantom was measured with the 3D‐CSI sequence seven times with different frequency offsets to compensate for pulse profile variations in dependence on frequency. The offsets were: the resonance frequency of the phantom's ³¹P signal (0 Hz); –800 Hz; –615 Hz; –385 Hz; +300 Hz; +915 Hz; and +1150 Hz. The resonance peak of each voxel's spectrum was fitted with a single Lorentzian‐shaped line in a java‐based graphical magnetic resonance user interface (jMRUI)31, 32 using the Advanced Method for Accurate, Robust, and Efficient Spectral fitting (AMARES).33 The resulting amplitude distribution was proportional to the B₁ field.

Phantom Verification

To validate the method (accuracy and precision), 3D‐CSI data from the 25 mM phantom were measured and analyzed. A volume of voxels in a region where the liver was expected to be located was used to calculate the ³¹P concentration. Therefore, the single spectra of 148 voxels (enclosing a volume of 289.1 cm³ based on the nominal voxel size of 1.95 cm³, not corrected for voxel bleedings due to the point spread function and the applied Hamming filter) were quantified in the same way as the 15 mM calibration phantom. The result of this measurement was compared with the known concentration of the solution.

Radiofrequency Simulations

To evaluate B₁ field similarity between the homogeneous phantom and the situation in vivo, radiofrequency (RF) simulations of ${\mathrm{B}}_1^{+}$ and ${\mathrm{B}}_1^{-}$ sensitivity were calculated on a liquid phantom using XFdtd software (v. 7.3, Remcom, State College, PA, USA), as well as on a human model ("Duke," provided by IT'IS Foundation, Zürich, Switzerland)34 with a finite‐difference, time‐domain method. The data were then combined and visualized in MatLab (v. R2016a, MathWorks, Natick, MA, USA). To correct for different coil loads, a factor proportional to the amplitude of the excitation pulse was introduced in the simulation and empirically adapted to reach a similar transmission depth. The color scaling for both the phantom and the in vivo simulation was adjusted.

Measurement Procedure

Figure 1 depicts the basic setup for the phantom (Fig. 1a) and in vivo measurements (Fig. 1b). The latter were obtained after overnight fasting in a right lateral position with the liver on top of the coil analogous to the phantom positioning. After assessment of the 3D‐CSI data, additionally the HCL was measured in vivo using ultrashort‐echo time ¹H MRS (TE = 6 msec, TR = 5 sec, 16 averages) on a single voxel (3 × 3 × 3 cm³) placed well within the hepatic parenchyma and corrected for both T₁ and T₂.29 The total measurement time took about 40 minutes.

Figure 1.

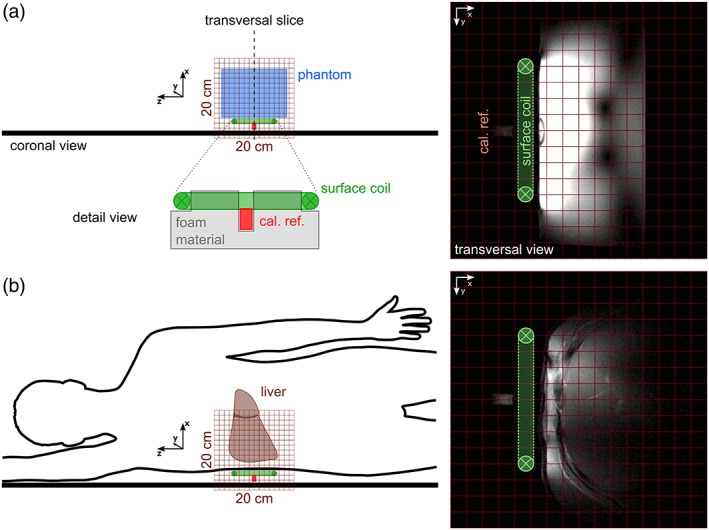
Basic experimental setup: Coronal sketches of the phantom (a) and in vivo (b) experiment on the left and the transversal localizer images through the coil center rotated 90° clockwise on the right. Note the calibration reference (cal. ref.) fixed relative to the coil (detail view, a) on the same position.

Data Processing and Analyzing

In vivo data were processed using an in‐house‐developed MRS imaging (MRSI) software tool20 adapted for 7T data according to the workflow, with the following criteria for representative hepatic voxel selection: 1) located in the liver according to the localizer images; 2) spectra showed a sufficient SNR of above 8 of at least one peak; and 3) muscle contamination was avoided, as demonstrated by the absence of a PCr signal (possible present peak smaller than twice the maximum of the noise signal). An automatic, self‐programmed selection algorithm was used on the magnitude spectra and additionally, manual inspection was performed on the real and imaginary part of the spectra. The spectra of these voxels were sent to and quantified in jMRUI using AMARES with the following parameters: 12 peaks (γ‐ATP and α‐ATP with each two equal peaks (16 Hz distant due to J‐coupling, same linewidth and amplitude), and P_i, PE, PC, GPC, GPE, PtdC, NADH, and UDPG) with a Lorentzian line shape and soft constraints on the expected resonance frequencies. For all resonance lines, except for ATP signals, the linewidth was limited to 50 Hz. The results were then reimported to the MRSI software tool and the absolute concentration of each metabolite (index m) and voxel with coordinates x, y, and z (indices [x,y,z]) was then calculated according to the following formula:

$$c_{m\left[x,y,z\right]}=c_p\cdot \frac{I_{m\left[x,y,z\right]}}{I_{p\left[x,y,z\right]}}\cdot \frac{S_p}{S_m}\cdot \frac{I_{ref\hspace{0.17em}p}}{I_{ref}}$$

where c _m and c _p describe the concentrations of a metabolite in vivo and in the phantom, respectively, I _m and I _p are the signal integrals, S _m and S _p are the saturation correction factors calculated from corresponding T₁ times (for α‐ and γ‐ATP, GPC, GPE, P_i, PC, and PE from Ref. 23, for PtdC, NADH, UDPG from Ref. 26, and I _ref and I _{ref p} are the signal integrals of the calibration reference. The latter were not received from the 3D‐CSI data, but from the nonlocal sequence run on the resonance frequency of the calibration reference by jMRUI‐fitting of that peak.

In addition, the calculated concentrations were corrected for the volume captured by lipid droplets, as suggested by Szendroedi et al.13:

$$HLVF=\frac{HCL}{\left(1.138-0.339\cdot HCL\right)}$$

with the assessed HCL used to calculate hepatic lipid volume fraction (HLVF) and correct the mean ³¹P metabolite concentrations, $\overline{c_m}$, as the adapted concentrations, $\overline{c_m{}_{{}_a}}$:

$$\overline{c_m{}_{{}_a}}=\frac{\overline{c_m}}{\left(1-HLVF\right)}$$

In Vivo Reproducibility Testing

Four young healthy volunteers (age: 26–32 years) with varying BMI (21.9–29.6 kg m⁻²) were measured twice in one session with complete repositioning and shimming between the measurements. This was repeated on another day with the exception of one volunteer where only one second‐day measurement was performed.

In Vivo Measurements for Biological Variability

Nineteen healthy human volunteers were recruited for in vivo measurements. Subjects were arranged into three subgroups by age (20–35 years vs. 45+ years) and BMI, with a threshold of 25 kg m⁻², into young lean (YL) (3m/2f, age: 27 ± 3 years, BMI: 22.2 ± 0.8 kg m⁻²), elderly lean (EL) (4m/3f, age: 61 ± 8 years, BMI: 21.5 ± 1.2 kg m⁻²), and elderly overweight (EO) (5m/2f, age: 57 ± 7 years, BMI: 28.5 ± 2.2 kg m⁻²). ³¹P concentrations were assessed with and without HLVF correction.

Statistical Analysis

The coefficient of variation (CV) of each ³¹P metabolite concentration was calculated for each session of the two consecutive measurements of the reproducibility testing. The mean values of the CVs represent the goodness of the test–retest reproducibility. Day‐to‐day analysis was performed by computing the CVs of the metabolite concentrations of two single measurements on different days of each volunteer. The mean values of these CVs are a measure for the day‐to‐day variability. The biological variability was investigated by a group comparison on the metabolites using analysis of variance (ANOVA) with Bonferroni correction for multiple comparisons. In addition, a Student's t‐test was used to assess differences between γ‐ and α‐ATP levels within each group.

Results

Setup and Method Validation

The measured signal distribution in a transversal slice through the coil center and phantom, the corresponding simulated data, and the in vivo RF simulation is visualized in Fig. 2. Figure 2a shows the received signal from the 15 mM phantom with the signal integral of each voxel mapped to the CSI‐grid with cubic interpolation. A similar pattern was achieved with the simulation. The signal distribution in a homogeneous phantom with the mask of the human model is shown in Fig. 2b and an in vivo model with the liver marked out is in Fig. 2c.

Figure 2.

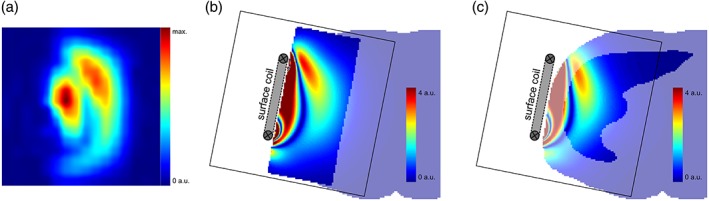
Distribution of the raw MRS signal in the phantom measurement and numerical simulations: Measured and quantified voxel signal distribution of the 15 mM phantom through a central transversal slice with cubic interpolation (a); visualized simulations of a homogeneous cylindrical phantom underlaid with a semi‐transparent human body mask (b); and an in vivo model with the liver enhanced (c); by the combination of both transmit and receive sensitivity with adjusted transmission depth and amplitude scaling (cutoff at 4 a.u.).

Absolute quantification of the 25 mM phantom yielded an average ³¹P concentration of 24.4 ± 2.1 mM (mean ± standard deviation [SD]). The corresponding concentration distribution was relatively homogeneous, with single voxels varying about 20% from the expected value (Fig. 3a). The metabolic map from the liver, with its mean concentration of γ‐ATP from one volunteer from the YL group, is depicted in Fig. 3b. The voxel selection process can be explained in more detail by Fig. 3c, which shows the magnitude spectra in the orange rectangle of Fig. 3b. The red‐marked PCr peak originated from muscles and does not usually appear in the liver tissue of healthy volunteers. These voxels and voxels with low SNR were discarded and only the yellow‐framed spectra were further processed. The green‐encircled spectrum of Fig. 3c is explicitly shown in Fig. 3d (original, middle), with its fitted spectrum using jMRUI (estimate, top) and the residual signal (residue, bottom) to visualize the goodness of the fit. Note that there is almost no PCr contamination (0 ppm), and, due to elliptical reduced acquisition in k‐space, the "real" shape of a voxel is not cubical but spherical. Its diameter, based on the 64% SRF level of the calibration reference, was estimated to be around 2.59 cm for the unfiltered and 2.99 cm for the Hamming‐filtered CSI that covered a volume of 9.11 cm³ and 14.05 cm³, respectively.

Figure 3.

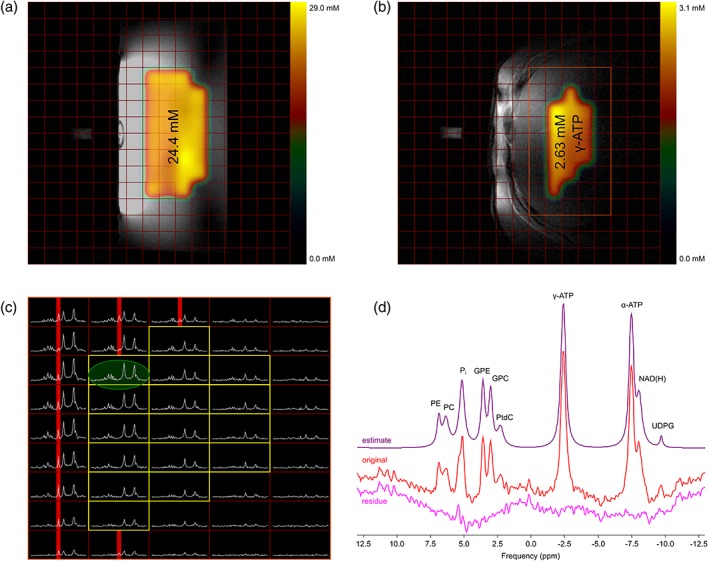
Absolute quantification: phantom validation experiment and example of an in vivo measurement: central scout images of the 25 mM phantom (a), and a hepatic region from in vivo measurement (b) with the 3D‐CSI grid and the calculated total ³¹P and γ‐ATP concentration distribution of selected voxels, respectively, as well as the mean value overlaid; in vivo magnitude spectra from the voxels within the orange rectangle of (b) with the yellow‐framed voxels used for absolute quantification and the voxels that fulfilled the criterion for the exclusion of a too‐high PCr signal enhanced in red (c); original spectrum of the green encircled voxel of c (red), its estimated AMARES metabolite fit (purple), and its residue (pink) (d).

Reproducibility Testing

For the reproducibility testing, 15–75 (mean ± SD: 45.5 ± 18.5) voxels incorporating a nominal volume of 89.0 ± 36.2 cm³ fulfilled the criteria for quantification. The test–retest evaluation resulted in mean CVs of less than 13% when focusing on metabolites, which gave rise above a certain SNR (excluding UDPG, NADH, and PtdC). The mean CVs of UDPG and NADH were both close to 20%. PtdC's mean CV was about 42%. The mean day‐to‐day CVs of the ATP‐metabolites were both beyond 7%, while all other metabolites with exception of PtdC did not exceed 17%. The latter reached slightly beyond 35% (Table 1).

Table 1.

Mean CVs as a Result of the Reproducibility Measurements

	[γ‐ATP]	[α‐ATP]	[GPC]	[GPE]	[Pi]	[PC]	[PE]	[UDPG]	[NADH]	[PtdC]
Test‐retest mean CV (n =  7)	5.6%	10.5%	8.7%	10.1%	11.8%	12.9%	11.6%	19.9%	19.0%	42.2%
Day‐to‐day mean CV (n =  4)	4.5%	6.4%	10.3%	8.6%	9.5%	12.7%	16.1%	16.3%	10.3%	34.3%

Test‐retest CVs state the variability of the metabolite concentrations of two successive measurements of a volunteer in one session, while day‐to‐day CVs represent the variation of metabolite concentrations of two single measurements on different days of a volunteer. Mean values of CV were calculated as arithmetical average over the measurement sessions and volunteers for test‐retest and day‐to‐day comparison, respectively.

Biological Variations

Based on the quantification criteria the number of voxels included in the analysis for the YL group ranged from 31–60 covering a nominal volume of 85.2 ± 22.5 cm³. For the other two groups, EL and EO, the quantified volume reached 93.2 ± 45.7 cm³ (16–79 voxels) and 95.7 ± 28.2 cm³ (22–68 voxels), respectively.

The mean and SD of the calculated metabolite concentrations without correcting for HLVF of each group is given in Table 2, top. Significant differences between groups were found in γ‐ and α‐ATP, as well as in P_i (P < 0.05), and PC showed a P‐value smaller than 0.1. Using the Bonferroni correction for multiple comparisons, these significances held only between the EL and EO groups for ATP metabolites (γ‐ATP: P = 0.019, α‐ATP: P = 0.009). In addition, P‐values below 0.1 appeared in P_i between these groups (P = 0.057) and in PC between YL and EL (P = 0.085). The correction for HLVF (Table 2, bottom) resulted in no significant differences, but the P‐value in PC between the YL and EL groups was still below 0.1 (P = 0.098). Figure 4 shows the grouped distribution with boxplots of a few metabolites with and without correction for HLVF.

Table 2.

Absolute ³¹P Concentrations (mM) in the Different Groups

	[γ‐ATP]	[α‐ATP]	[GPC]	[GPE]	[Pi]	[PC]	[PE]	[UDPG]	[NADH]	[PtdC]
YL	2.56 ± 0.10	2.42 ± 0.15	3.31 ± 0.27	3.38 ± 0.87	1.42 ± 0.20	1.47 ± 0.24†	1.61 ± 0.20	0.74 ± 0.17	1.21 ± 0.38	0.43 ± 0.10
EL	2.92 ± 0.39*	2.68 ± 0.33*	3.60 ± 0.93	3.59 ± 0.83	1.47 ± 0.17†	1.00 ± 0.32†	1.42 ± 0.64	0.81 ± 0.34	1.22 ± 0.36	0.44 ± 0.12
EO	2.38 ± 0.34*	2.15 ± 0.28*	4.03 ± 0.90	3.58 ± 0.59	1.17 ± 0.26†	1.05 ± 0.40	1.46 ± 0.19	0.74 ± 0.25	1.22 ± 0.17	0.39 ± 0.27
YLcorr	2.63 ± 0.10	2.48 ± 0.18	3.40 ± 0.27	3.48 ± 0.93	1.46 ± 0.20	1.51 ± 0.23†	1.65 ± 0.20	0.76 ± 0.18	1.24 ± 0.38	0.44 ± 0.10
ELcorr	3.00 ± 0.42	2.75 ± 0.37	3.70 ± 0.98	3.69 ± 0.89	1.51 ± 0.18	1.02 ± 0.33†	1.46 ± 0.67	0.83 ± 0.34	1.25 ± 0.37	0.46 ± 0.12
EOcorr	2.68 ± 0.61	2.44 ± 0.45	4.24 ± 1.10	3.93 ± 1.02	1.33 ± 0.28	1.11 ± 0.45	1.65 ± 0.18	0.82 ± 0.35	1.38 ± 0.29	0.44 ± 0.32

The asterisks (*) indicate significant differences (P < 0.05) and the daggers (†) indicate P‐values below 0.1 in a metabolite concentration between the two marked groups (separately without and with HLVF correction) according to ANOVA, with post‐hoc Bonferroni multiple comparisons test.

Mean and SD of the calculated ³¹P metabolite concentrations of each group both not corrected and corrected for HLVF (Indicated by the index ‘corr’)

Figure 4.

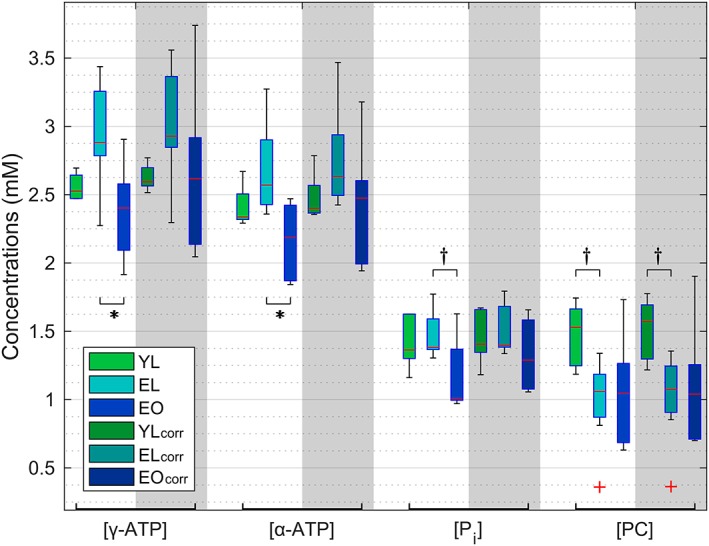
Grouped boxplots of metabolic concentrations: comparison of selected metabolites between the three groups with and without correction for HLVF (index 'corr'). Significant differences between the two groups are marked with an asterisk (*) and P‐values below 0.1 are marked with a dagger (†). The red plus signs (+) indicate outliers of corresponding groups (more distant than 1.5 times the interquartile range), but these were not excluded from statistical calculations.

A comparison of the ATP levels (γ‐ vs. α‐ATP) did not result in significant differences in the YL group (either with or without HLVF correction, P = 0.218 and P = 0.213, respectively), but showed significances within the EL and EO groups for HLVF uncorrected (EL: P = 0.019, EO: P = 0.014), as well as for corrected metabolite concentrations (EL: P = 0.019, EO: P = 0.048).

The comparison of the results of our measurements with previous studies using external references19, 20, 24, 25 or an internal reference26 giving the mean values of the YL group corrected for HLVF is depicted in Fig. 5. For this purpose, the PME concentration from our study was calculated from the sum of PC and PE and PDE as the sum of GPC and GPE, as well as PtdC. The latter was included since it was most likely fitted together with both GPC and GPE in previous studies that had poorer spectral resolution.

Figure 5.

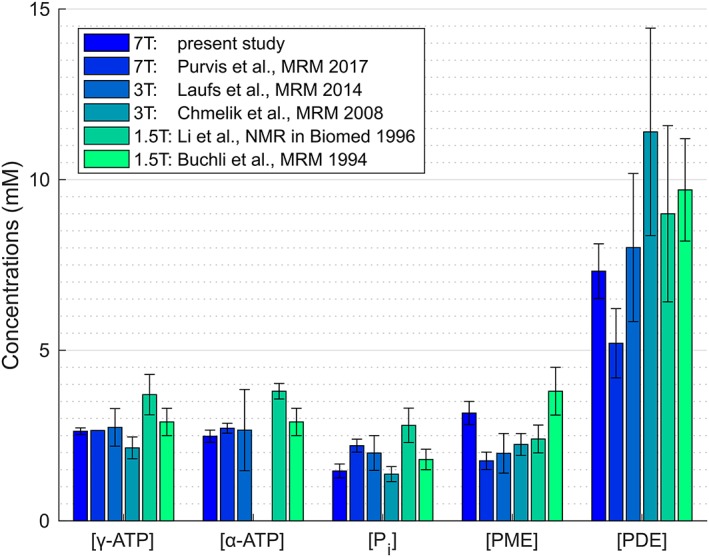
Numerical comparison with reported values: mean values of absolute concentrations of the YL group of this study corrected for HLVF compared with the results of other studies, with PME as the sum of PC and PE, and PDE as the sum of GPC, GPE, and PtdC.

Discussion

This study shows the feasibility of absolute quantification of hepatic ³¹P metabolites performed at 7T using an external reference. This method ensures that the results are independent from the assumption of a constant internal reference metabolite. Due to the excellent spectral resolution at 7T, and with the support of recently reported T₁ values,26 we could quantify even less abundant metabolites, such as UDPG, NADH, and PtdC, but, due to the limited pulse bandwidth, we did not approach quantification of β‐ATP.

Several obstacles had to be solved for the experimental setup using a surface Tx/Rx coil at a magnetic field strength of 7T. Although excitation with RECT pulses shows less homogeneity on the resonance frequency of a metabolite than excitation with adiabatic half‐passage pulses,35 the use of RECT pulses yields a better off‐center frequency excitation profile. With the robust automated flip angle calculation, the voltage necessary to achieve a 90° flip angle in the calibration reference was calculated and used to gain the maximum amplitude of a nonlocalized spectrum in the resonance peak of the calibration reference. This signal had sufficient SNR and was always clearly distinguishable from other metabolites. Its signal integral is used as a measure for the coil load.

The comparison of the simulated data of the phantom and the human model showed similar signal distribution in a wide area of the sensitive volume covering the liver. The relatively high homogeneity of the hepatic tissue and the isotropic liquid phantom are the basis to this similarity. Thus, the simulation supports the feasibility and results of our method. The measured in vitro data of the phantom also showed a similar asymmetric pattern, as is visible in the simulation, which confirms the validity of the measured data. Only in the area close to the coil the simulation showed high variations compared with the recorded phantom data. Considering that the resolution of the CSI data is much lower (12 phase‐encoding steps for 20 cm in each direction), signals from different locations contribute to one voxel and might also decrease the signal due to opposite phases. Thus, the region close to the coil cannot be used for quantification, but is not of relevance since it is occupied by fat and muscle tissue that border the liver. In addition, the positioning of the coil in the simulation might not represent the exact same location as was actually performed.

The phantom validation experiment resulted in a widely homogeneous distribution of the calculated absolute concentrations and the mean value of 24.4 mM (CV: 8.5%) was close to the real value of 25 mM. The deviation of single voxels from the expected concentration is not a discrepancy in our method since the assessed concentration was averaged over all selected voxels. The physiologically based inhomogeneity of in vivo metabolite distribution can be seen, particularly for PtdC, which is very abundant in bile.36 Thus, the high PtdC amplitude suggested signal contamination by the gallbladder and the affected voxels might have been excluded for this hepatic tissue‐specific evaluation. The frequency‐dependent signal variation was countered by using phantom correction maps at various frequency offsets. For greater precision, this could be done for the resonance frequencies of each metabolite. We limited it to seven offsets: at –800 Hz (PE, PC); –615 Hz (P_i); –385 Hz (GPE, GPC, PtdC); 0 Hz (PCr); +300 Hz (γ‐ATP); +915 Hz (α‐ATP, NADH); and +1150 Hz (UDPG). Signals of each metabolite were corrected by the map closest to their frequency offset, as indicated in brackets.

The signals of γ‐ and α‐ATP both originate from the same molecule, and thus, calculated concentrations are supposed to be equal. Due to curve‐fitting, adjacent metabolites (e.g., adenosine diphosphates [ADP]37, 38, which cannot be distinguished as separate signals, were also (partly) covered by the ATP fitting lines and slightly contaminated the resulting values. Contrary to our results, many studies show higher α‐ATP than γ‐ATP content due to greater signal overlaps in the α‐ATP frequency range. An explanation for the differences in this study (significance only within the EL and EO groups) could be the high spectral resolution at 7T, which might have decreased these signal overlaps, and the additional possible overfitting of NADH, which could have led to a decrease of the calculated α‐ATP concentration.

Analyzing the reproducibility measurements day‐to‐day CVs showed mostly slightly lower variability than the test–retest results. The reason, therefore, was one measurement that was not used for the day‐to‐day variability calculation. This one yielded only 15 voxels, which met the requirements for quantification and unexpectedly low metabolite concentrations. Treating this measurement as an outlier the mean CVs for the test–retest evaluation of γ‐ATP and α‐ATP improved from 5.6% to 2.8% and from 10.5% to 6.5%, respectively. The quantitation of other metabolites (excl. PtdC) resulted in mean CVs of less or equal 14%, while values for PtdC in hepatic tissue reached a CV of 31%. The high variability of PtdC can be caused by the contamination from bile due to voxel bleeding. Overall, both test–retest and day‐to‐day CVs showed relatively low variabilities for in vivo quantification.

Looking more closely at the EO group, it could be assumed that, due to a higher BMI, and thus, the often thicker fat tissue layer, the selected voxels were further away from the coil, which may have introduced a bias in the calculation. Nevertheless, in our study and our approach, 1) the number of quantified voxels was comparable in all three groups and the pulse penetration depth was similar, meaning that the selection range in depth cannot be substantially further away from the coil for one group, and 2) the volunteers were positioned on top of the coil on the right lateral side where the body mass of the subjects pushed superficial tissue partly aside; thus, tissue layers that covered the liver did not appear too thick. Overall, the selection process showed, in most cases, the majority of voxels that fulfilled the selection criterion lay in the same slabs parallel to the coil.

The group analysis showed significant differences in γ‐ and α‐ATP concentrations for BMI comparison (EL vs. EO). This might suggest that the signal, which is often used as an internal reference, underlies substantial fluctuations due to a possible dependence on HCL. Care must be taken, especially when comparing healthy volunteers with patient groups whose pathologies result in higher BMIs. Correcting for the volume captured by lipid droplets can compensate for such differences, but can also introduce another possible source of errors due to uncertainties in the HLVF assessment. A recent study also reported differences in γ‐ATP depending on dietary fat intake.28 Other findings with low P‐value (P < 0.1) were seen in the BMI comparison in P_i (EL vs. EO) and in the age comparison in PC concentrations (YL vs. EL). The latter could not be confirmed through a comparison of the YL and EO groups, and may just have occurred by chance.

We are well aware that BMI is an insufficient biomarker for fat content in the tissue, but as it is easy to achieve without complex and time‐demanding measurements, it was the method of choice for probing possible dependencies suggested previously.13 Its low informative value was also a reason why we separated the volunteers only into subgroups with low and high BMI.

When we compare our HLVF corrected result from the YL group to previous reports, we have to be aware that Buchli et al. (19) reported only NTP concentration, which was plotted both for γ‐ and α‐ATP. In our study, γ‐ATP was calculated to be very close to the literature value of 2.65 mM, which was used by Purvis et al.26 as a concentration reference for quantification. It is also in good agreement with Buchli et al.19 and Laufs et al.25 The latter overlaps with our calculated α‐ATP concentration within one SD, where other studies show higher values. The assessed hepatic P_i concentration was very close to published values by Chmelik et al.,20 whereas other studies have reported higher values.

In our study, the PME concentration was higher than that reported in more recent studies, but lower than that reported by Buchli et al. The single contributions of PC and PE to the total PME signal in our findings are both higher compared with what Li et al.24 and Purvis et al.26 reported. PDE concentrations vary the most across the literature. Previous studies at lower field strengths reported higher values than ours, which are within one SD of those of Laufs et al.25 and Li et al.24 In this case, differences can probably be attributed to the lower spatial resolution, as well as different localization schemes (single voxel vs. CSI) and fitting routines, and thus, possible contamination by PtdC. The recently published study by Purvis et al.26 at 7T showed a relatively low PDE concentration that our study could not confirm.

Different T₁ times used for saturation correction could give an explanation for our concentration deviations from Purvis et al.26 (Table 3). After applying their correction factors, ATP, GPC, and PC concentrations result in almost equal values. Other metabolites such as GPE, P_i, and PE do not match as well. The concentrations of less‐abundant metabolites, such as UDPG, NADH, and PtdC, were saturation corrected using the T₁ times exclusively published by Purvis et al.26 In their study these metabolites were reported with higher concentrations (2.03 ± 0.20 mM, 2.35 ± 0.21 mM, and 1.37 ± 0.35 mM, respectively) than our evaluation results. Li et al.24 found a concentration similar to what we found for NADH of 1.1 ± 0.1 mM, but estimated a higher value of 1.4 ± 0.9 mM for PtdC, which was not a specified metabolite by that time. The differences in PtdC in their study could have resulted from contamination by bile from the gallbladder, which we avoided. In the future, special care should be taken for the quantification of UDPG and NADH. NADH is a potential marker for the redox state of the various biochemical processes.39

Table 3.

Influence of Different T₁ Times Used for Saturation Correction on the Calculated Concentrations

	[γ‐ATP]	[α‐ATP]	[GPC]	[GPE]	[Pi]	[PC]	[PE]
T1 by Chmelík et al.23	0.50	0.46	5.94	6.19	0.70	3.74	4.41
T1 by Purvis et al.26	0.57	0.56	3.90	4.38	1.34	2.26	3.92
Current results using T1‐correction from Ref. 23 (mean)	2.56	2.42	3.31	3.38	1.42	1.47	1.61
Current results using T1‐correction from Ref. 26 (mean)	2.67	2.53	2.40	2.61	1.83	1.05	1.50
Results by Purvis et al.26 (mean)	2.65	2.72	2.35	1.50	2.21	1.03	0.74

T₁ times provided by Chmelík et al. (as used in our study for the listed metabolites) and Purvis et al. (both in sec); calculated metabolite concentrations of our study and T₁s by Chmelík et al.; calculated metabolite concentrations of our study and T₁s by Purvis et al.; and Purvis et al.'s findings (all in mM).

At this point, we would like to state that we are aware of some limitations of our study. The analyses of differences between young vs. old and lean vs. overweight population are limited by a rather small number of subjects per group (five to seven subjects), and therefore, data from larger populations would be necessary to confirm our findings concerning the possible BMI‐dependent ATP concentrations. This is even more critical for statistical evaluations after correction for HLVF due to higher SDs and lower effects on the mean values. Focusing on α‐ATP and assuming the calculated SDs of a sample as equal to the SDs of a population (s = σ), at least 35 to 40 volunteers would be needed for each group to detect a possible difference in the concentrations with a power of more than 90% (calculation based on Piface40 using a two‐sample t‐test). Such a high sample number would go beyond the scope and possibilities of this study. Furthermore, even though the MRS‐based measurement of HCL is robust enough (CV < 10%), possible errors introduced further uncertainties due to the HLVF correction. Additional limitations arise from the magnetic field inhomogeneities: Although localized shimming was performed within a defined volume in the liver, no further B₀ corrections over the CSI matrix were applied. B₁ imperfections were compensated by phantom correction maps generated at seven different frequency offsets. Ideally, each metabolite should have its own correction map according to its offset from the reference frequency. The SNR criterion for quantification is fulfilled if at least one peak reaches a certain value. That means that in accepted voxels with poorer spectral quality peaks of less abundant metabolites cannot be clearly distinguished from noise but were still quantified and thus might not resemble the true concentration. A metabolite‐dependent SNR requirement could solve this issue. Moreover, the quantification is based on the assumption that the composition of the phantom regarding its ³¹P content, conductivity, and permittivity resembles in vivo conditions in the organ of interest.

In conclusion, this study showed that an elaborate method of measuring and calculating absolute concentrations from the 3D ³¹P MRSI experiments can overcome the experimental limitations and fully use the advantage of increased SNR and spectral resolution at 7T. Due to the use of an external reference, the method does not depend on the assumption of a constant reference metabolite. The high precision of assessed concentrations makes the quantification feasible for even less‐abundant metabolites, such as UDPG, NADH, and PtdC in hepatic tissue. The combination of ³¹P MRSI data acquisition and hepatic lipid volume correction based on ¹H MRS data minimizes the effect of BMI or age on ³¹P metabolite concentrations in a healthy population beyond the level of detection.