Abstract
There is a theoretical disagreement in the working memory literature, with some proposing that the storage and processing of information rely on distinct parts of the cognitive system and others who posit that they rely, to some extent, on a shared attentional capacity. This debate is mirrored in the literature on working memory and aging, where there have been mixed findings on the ability of older adults to perform simultaneous storage and processing tasks. We assess the overlap between storage and processing and how this changes with age using a procedure in which both tasks have been carefully adjusted to produce comparable levels of single-task performance across a sample (N = 164) of participants aged 18–81. By manipulating incentives to perform one task over the other, this procedure was also capable of disentangling concurrence costs (single-versus dual-task performance) from prioritization costs (relative payoffs for storage versus processing performance) in a theoretically meaningful manner. The study revealed a large general cost to serial letter recall performance associated with concurrent performance of an arithmetic verification processing task, a concurrence cost that increased with age. For the processing task, there was no such general concurrence cost. Rather, there was a prioritization effect in dual-task performance for both tasks, irrespective of age, in which performance levels depended on the relative emphasis assigned to memory versus processing. This prioritization effect was large, albeit with a large residual in performance. The findings place important constraints on both working memory theory and our understanding of how working memory changes across the adult lifespan. (257 words)
Keywords: Working Memory, Adult Lifespan, Storage, Processing
Working memory is a broad construct that means subtly different things to different researchers (see Cowan, 2017). As such, it is difficult to give an all encompassing definition, but generally the term working memory is used to refer to the system that supports the temporary storage of information as well as the ongoing processing of incoming information or the manipulation of the contents of memory. There is a longstanding debate in the literature as to how this simultaneous storage and processing is achieved and how this changes across the lifespan. A major theoretical divide can be seen between modular theories that have separate, specialized resources that can be devoted to the storage or processing of information (e.g. Baddeley & Hitch, 1974; Logie, 2011), and other theories with some kind of general resource that can be shared between competing demands (for example, an attentional bottleneck or limited capacity focus of attention; Barrouillet & Camos, 2015; Cowan, 2010; Kane et al., 2004; Oberauer, Lewandowsky, Farrell, Jarrold, & Greaves, 2012). Findings like the cognitive load function, the linear function relating memory span to the concentration of processing events within complex span tasks, have been taken as strong evidence that storage and processing compete for a common resource (Barrouillet, Bernardin, & Camos, 2004; Barrouillet, Bernardin, Portrat, Vergauwe, & Camos, 2007; Vergauwe, Barrouillet, & Camos, 2010). Nevertheless, it has been proposed by multiple component theorists that there are certain conditions under which the parallel performance of storage and processing, without cost, can be observed (Baddeley & Hitch, 1974; Doherty & Logie, 2016; Logie, Cocchini, Della Sala, & Baddeley, 2004; Logie, 2011). We outline these two sides of the debate more thoroughly below and derive detailed predictions that allow us to contrast these theories of how storage and processing interact.
The debate regarding the cost associated with simultaneous storage and processing is mirrored in the literature on aging. Here the question is whether any dual task cost associated with combining the two demands is exacerbated in older adults. Age differences tend to be larger for tasks combining storage and processing demands (Bopp & Verhaeghen, 2005) but, under arguably more controlled conditions, there have been studies reporting little-to-no differential dual task cost with age (e.g. M. Anderson, Bucks, Bayliss, & Della Sala, 2011; Baddeley, Logie, Bressi, Della Sala, & Spinnler, 1986; Logie et al., 2004; Belleville, Rouleau, & Caza, 1998; Myerson, Hale, Rhee, & Jenkins, 1999). Whether we assume modularity or some degree of conflict between storage and processing has obvious influence on how we interpret change in working memory performance with age. Further, how working memory performance changes with age places important constraints on theories of working memory. For example, the suggestion that age affects the ability to divide attention between storage and processing (e.g. Craik, 1977; Mayr & Kliegl, 1993) relies on the shared resource view of working memory, whereas the finding that they can be performed simultaneously with little to no cost to either memory or processing seems to align well with the multicomponent view (e.g. Baddeley, 2012; Logie, 2016). Thus, in the present work we take a relatively novel approach to assessing the conflict, if any, between storage and processing performance in a large lifespan sample spanning ages 18 to 81 recruited simultaneously at two laboratories (one in the UK and one in the US).
Most of the work on the overlap of storage and processing, and its change with age, has focussed on manipulations of the difficulty of one task (e.g. the speed with which items must be processed) on the performance of the other (e.g. Barrouillet et al., 2007; Chen & Cowan, 2009; Logie et al., 2004). This has resulted in evidence consistent with either side of the theoretical divide (see the examples above). The present study aims to look at this issue from another vantage point. Specifically, we use the method of assessing the trade-off, if any, between two tasks as participants are incentivized to attend to one over the other (for other descriptions and applications of this general method, see N. D. Anderson, Craik, & Naveh-Benjamin, 1998; Craik, Govoni, Naveh-Benjamin, & Anderson, 1996; Navon & Gopher, 1979; C. C. Morey, Cowan, Morey, & Rouder, 2011; Sperling & Melchner, 1978). To our knowledge this method has not been applied to the assessment of whether or not storage and processing compete for a common limited attentional capacity. Further, as we argue below, this approach allows us to separate two conceptually distinct sources of dual task cost: those under volitional control of the participant and those that occur due to the concurrence of the two demands.
Prior to describing the present study we outline the theoretical divide between modular and resource sharing conceptions of working memory storage and processing. Following this we detail some of the mixed findings in the literature regarding how the ability to coordinate storage and processing tasks changes with age.
Storage and Processing in WM: The Theoretical Divide
Given the importance of the construct of working memory, a number of broad theoretical frameworks have been built to attempt to understand its function. These differ in many respects, including the extent to which storage and processing are presumed to interfere under various experimental settings. At a general level, theories on this topic can be split into those that assume independence of components contributing to storage and processing, and those that assume some degree of competition between the two for a common attentional capacity.
Storage and processing as drawing upon distinct components
As an example of the former position, the multiple component model of working memory, first conceptualized by Baddeley and Hitch (1974) (for modifications, see Baddeley, 1986, 2000; Baddeley & Logie, 1999; Logie, 2011), proposes separate modules dedicated to the storage of verbal and visual material, as well as a central executive that facilitates the processing of information. In addition, much like other accounts of working memory, the multiple component model also allows for major contributions to memory performance from long-term memory (episodic and semantic). Thus, according to this modular account, there should be conditions where storage and processing can run in parallel, with little-to-no conflict between the demands. Leveraged in support of this proposal are studies which find no significant conflict between storage and processing tasks. For example, Cocchini, Logie, Della Sala, MacPherson, and Baddeley (2002) found no significant decline in performance for digit span combined with a visuospatial tracking task within a 15 second retention interval relative to when these tasks were performed individually (see also Logie et al., 2004). Also cited in support of the idea of multiple components are studies finding what is claimed as ‘small’ dual task costs. Duff and Logie (2001, Experiment 2) examined simple span for words and verification of arithmetic problems and compared this to complex span where the to-be-remembered words and arithmetic problems were presented simultaneously. Expressing dual task performance as a proportion of single task, they found an approximately 10% drop in performance combined across the two tasks (with most of the decrement occurring for the word recall task). Focusing on the substantial residual performance, even under high memory and processing demands, Duff and Logie labelled this drop ‘small’ in comparison and interpreted it as possibly reflecting the need to switch between the demands of encoding the word and processing the equation, rather than a conflict between storage and processing, per se (see also Duff & Logie, 1999; Logie & Duff, 2007). The cost to coordination has been expanded upon in articles arguing that the original proposal of a single central executive to control cognition could effectively be replaced by a range of executive functions, one of which being the ability to coordinate the functions of different components during dual tasks (e.g., Barnard, 1999; Logie, 2016; Miyake et al., 2000; Vandierendonck, 2016).
A crucial condition for minimizing the conflict between storage and processing, according to this position, is that the capacity of the individual components should not be overloaded. As suggested by Logie (2011), a reduction in dual task compared with single task performance may only be observed when domain-specific components are pushed beyond capacity. Therefore, when assessing the overlap of storage and processing in working memory, it is important to ensure that individual task demand is adjusted for each participant, or titrated such that each component is functioning within its limits (see Doherty & Logie, 2016). Thus, according to this view, a major determinant of whether simultaneous storage and processing comes at a cost in individuals of different ages is the extent to which the demand of each task has been titrated to account for age differences in single task performance (for a similar argument, see Somberg & Salthouse, 1982; Salthouse, Rogan, & Prill, 1984). Indeed, it has been observed, at least in some research with small numbers of participants, that there are no age differences in the ability to simultaneously store and process information, provided each task has been titrated to individual ability (M. Anderson et al., 2011; Baddeley et al., 1986; Baddeley, Baddeley, Bucks, & Wilcock, 2001; Belleville et al., 1998; Logie et al., 2004; although see Bier, Lecavalier, Malenfant, Peretz, & Belleville, 2017; Logie, Della Sala, MacPherson, & Cooper, 2007), a point to which we return below.
As noted above, the multiple component position does not completely rule out storage+processing dual task costs. Instead it has proposed that when they occur it is not due to conflict between storage and processing for a common resource. Thus it is also important to minimize other potential sources of interference, such as the requirement to switch between the encoding of stimuli and the processing task, as is the case in complex span tasks such as those used by Duff and Logie (2001, 1999). In the present experiment we adopted a pre-load procedure in which the memory items were presented prior to a retention interval containing the processing task. This approach arguably does a better job of separating the demand of storage of the memory load, which is of primary interest here, from its initial encoding. Another potential source of conflict that would not necessarily challenge the assumption of multiple components is that of conflict between input and output modalities. Having to perform the necessary transformation of a auditory-verbal code for a manual response would appear to require operations that would conflict with concurrent processing (see Hazeltine, Ruthruff, & Remington, 2006; Stephan & Koch, 2010; Thalmann & Oberauer, 2017). Thus in the present study we presented the to-be-remembered letters either visually for typed recall, or aurally for oral recall. When memoranda are presented visually and the concurrent processing task is also presented visually there may be some interference as participants may also be relying on visual codes (Logie, Della Sala, Wynn, & Baddeley, 2000; Logie, Saito, Morita, Varma, & Norris, 2016). This interference is not assumed to be modifiable by the participant such that incentivizing them to perform more accurately on the memory task, and placing less emphasis on processing, is not expected to modulate the extent of the dual task cost. To test this, in the present study we presented memoranda either visually or auditorily, whereas the processing task was always presented visually.
Storage and processing as competing for attention
In contrast to theories that have strictly separate components contributing to processing and storage, shared-resource theories propose that the two functions draw upon the same capacity-limited attentional system. The embedded processes model of Cowan (1988, 2010) is an example of such an account, where the central limitation of working memory is in the number of items that can be simultaneously held in the focus of attention. Activities demanding of attention, like concurrent processing tasks, trade-off with the storage of information within the focus of attention (Chen & Cowan, 2009). Similarly, the time-based resource sharing model (TBRS; Barrouillet et al., 2004, 2007; Barrouillet & Camos, 2015) proposes that there is attentional time sharing between the storage (or active refreshing) of memory representations and the processing of incoming information. The primary evidence for this time sharing is the linear function relating memory span to the proportion of time spent on a concurrent processing task (also termed cognitive load; e.g., Barrouillet et al., 2004, 2007).
It is important to point out that neither of these accounts are ‘pure’ resource sharing models, in that they each allow for both attentional modes of maintenance in working memory (such a refreshing) and non-attentional mechanisms, such as subvocal rehearsal and activated long-term memory (Cowan, 1992; Camos, Lagner, & Barrouillet, 2009; Rhodes & Cowan, 2018; see Oberauer, 2009a; Unsworth & Engle, 2007 for similar proposals). Nevertheless, these two accounts clearly predict that measures of storage and processing should compete and that more accurate performance of one should come at the expense of performance on the other. This prediction is shared with other accounts of working memory that include a general capacity limit (e.g. J. R. Anderson, Reder, & Lebiere, 1996; Kane et al., 2004; Oberauer et al., 2012) and even a modification to the multiple component model which allows for a domain general storage buffer that is intimately tied to the central executive (Baddeley, 2000; Baddeley, Allen, & Hitch, 2011).
In summary, a clear theoretical divide exists between working memory frameworks that see storage and processing as drawing on a general attention, and those arguing for relative independence of the two functions. The question of whether there is conflict between storage and processing is mirrored in the aging literature, where the question is whether older participants exhibit a greater level of conflict than younger adults when the two demands must be performed simultaneously. Below we outline the mixed findings regarding age-related change in dual task performance and how they relate to the broader debate outlined above.
Aging and Simultaneous Storage and Processing
It is well established that performance on tasks requiring short-term storage declines across the adult lifespan (e.g., Dobbs & Rule, 1989; Foos, 1989; Johnson, Logie, & Brockmole, 2010; Park et al., 2002). However, early studies noted that this age-related decline in short-term storage was exacerbated when concurrent processing was required (e.g. Broadbent & Heron, 1962; Parkinson, Lindholm, & Urell, 1980; Wingfield, Stine, Lahar, & Aberdeen, 1988; Wright, 1981). For example, age differences in the ability to recall information after a short delay were exacerbated when that delay was filled by a requirement to process or manipulate information. This supported the notion that older adults experience greater difficulty when tasked with coordination of simultaneous cognitive activities (Salthouse, 1990; Mayr & Kliegl, 1993). Accordingly, the performance deficit observed in older adults for tasks assessing storage and processing, as opposed to short-term storage only, could be attributed to specific difficulty in division of attention between maintenance and processing (Craik, 1977). This clearly brings to mind a shared resource conception of working memory, where time or capacity must be shared between the demands and this becomes more restricted with age.
However, subsequent research has been more equivocal on the ability of older relative to younger adults to coordinate storage and processing requirements. Much of this work has focused on the complex span task, in which study events are intermixed with processing events. Jenkins, Myerson, Hale, and Fry (1999) performed a meta-analysis of studies from their lab, with a total of over 400 participants, using both verbal and spatial memoranda and found no evidence that age effects were larger for complex span relative to simple span paradigms (see also Hale et al., 2011). On the other hand, in their meta-analysis of the broader literature Bopp and Verhaeghen (2005) found that the age-difference between younger and older adults on complex span was approximately twice that of the effect of age on simple span. This is in line with other reports suggesting a greater age deficit when storage and processing must be performed concurrently compared with storage or processing alone (Bier et al., 2017; Holtzer, Stern, & Rakitin, 2004).
Importantly, there have been a number of reports that have attempted to adjust for age-differences in single task ability, by titrating or adjusting the difficulty of each task to a common performance level before they are combined as a dual task. This allows dual task performance to be compared to a common baseline (for discussion of the importance of this, see Somberg & Salthouse, 1982) and these experiments have largely found no evidence for a disproportionate dual task cost as a function of age (M. Anderson et al., 2011; Baddeley et al., 1986, 2001; Belleville et al., 1998; Logie et al., 2004; Kilb & Naveh-Benjamin, 2014). These findings line up with the suggestion that there is little-to-no dual task cost when the individual tasks have been titrated (Logie, 2011). Further, the disproportionate dual task cost observed in patients with Alzheimer’s disease has been used to argue for a specific coordination function as one of a range of executive functions (Baddeley et al., 1986, 2001; Logie et al., 2004; Logie, 2016). This is clearly different from the earlier suggestion that age might impair the ability to divide attention (Craik, 1977), as this conception of working memory doesn’t have a single attentional system to divide.
However, these studies that have failed to find disproportionate dual task costs with age have typically used small samples and there have been contrary reports in the literature (e.g. Bier et al., 2017; Logie et al., 2007). Given the importance of this question for the understanding of working memory theory and how working memory changes with age, the present study recruited a larger sample of participants than has been common in previous studies that have addressed these issues (N = 164) sampled from across the adult lifespan (18–81 years old) and treated age as a continuous rather than a grouping variable. In addition, as we describe below, we took a slightly different approach to previous studies which allows us to identify two conceptually distinct sources of dual task conflict.
A Different Approach to Assessing Conflict Between Storage and Processing
Much of the previous work on storage and processing in working memory has examined the effect of varying the difficulty of one task while assessing performance on the other. For example, the speed or concentration of processing decisions within a certain delay may be varied and the resulting accuracy or memory span examined (e.g. Barrouillet et al., 2004, 2007). These manipulations have resulted in data that have been interpreted in favor of both the shared and independent viewpoints outlined above. As an example of the former, Vergauwe, Camos, and Barrouillet (2014) varied memory load (e.g. the number of to-be-remembered letters or spatial locations) and examined reaction times to processing events presented during a retention interval. Examining only trials on which recall was 100% correct, Vergauwe et al. found a steady increase in reaction times to the processing task with each additional memory item. Reaction times only increased for the first item, but this is a strong demonstration of an effect of memory load on processing performance (see also Chen & Cowan, 2009).
On the other hand, load manipulations have yielded different findings leading to differing theoretical interpretations. Doherty and Logie (2016) separately adjusted the number of to-be-remembered digits and the number of spatial judgements (is a box above or below the center of the screen) presented within a 5 second retention interval. In the dual task phase of their experiments they then manipulated the load of these tasks around span including measurements at, below (−1), and above (+1, +2) the titrated level. They found no effect of the processing task on memory performance and no effect of manipulating the load of the processing task around their pre-identified span level. Performance of the spatial processing task, however, did show a drop but only when the memory load was set above the participants’ span. The interpretation offered was that, within the span of individual components of the multiple component account, storage and processing demands can be effectively handled by the independent components (see also Logie et al., 2004). Once storage demands exceeded capacity, however, participants were said to engage additional components, such as the use of visuospatial or semantic codes, which may impede performance of concurrent processing depending on the material used for that task. A related finding was reported by Baddeley and Hitch (1974) who showed that with a memory load of three verbal items, there was no impact on memory performance or on a demanding verbal reasoning task when the latter was performed during a retention interval. However, a preload of six items resulted in systematic slowing of the interpolated reasoning task.
As the above discussions show, a variety of interpretations have been offered for findings from dual task studies. At this point it is important to discuss an awkward aspect of the extant literature. As we have noted, some studies leveraged in support of the multiple component position, that different components support storage and processing, have found no dual task costs to combining storage and processing (Cocchini et al., 2002; Logie et al., 2004; Doherty & Logie, 2016), whereas other studies within the multiple component framework have found dual-task costs (e.g. Duff & Logie, 1999, 2001). However, for the latter studies, it has been argued that these costs are ‘small’, especially when expressed as a proportion of single task performance. Instead multiple component theorists tend to focus on ‘residual’ performance levels, which are often fairly high despite the heavy load imposed by dual tasking, and argue that this is out of step with the expectations of accounts with a general attention shared between maintenance and processing. However, the TBRS and embedded processes models (as well as other similar accounts in the field) are not pure resource sharing models. They too have other sources that can support performance without placing a great demand on attention, such as rehearsal for verbal material (Cowan, 1992; Camos et al., 2009) or activated long-term memory for items displaced or removed from the focus of attention (Oberauer, 2009a, 2005; Rhodes & Cowan, 2018; Unsworth & Engle, 2007). Thus, the multiple component model is not distinguished from the other accounts by having multiple ‘components’. Rather it differs in the assumptions as to what the components are presumed to achieve (i.e. storage or processing) and how they are deployed to support performance. More important than this realization, however, is the need for a common criteria for characterizing a dual task cost as ‘small’.
In the present work we adopt a measure of effect size which scales effects in terms of expected differences in performance between individuals, and ask proponents of resource sharing and multiple component theories to state predictions on this basis. In addition we adopt a different approach to previous studies addressing this issue that may help in distinguishing these accounts of storage and processing in working memory. The approach we use is to manipulate the incentive to perform one task over the other, rather than manipulate the demand of the storage and processing tasks. In the present study the storage task required serial ordered recall of consonants following an 11 second delay, whereas the processing task required the speeded verification of single digit additions presented on screen during a period of 10 seconds (see Figure 1). Crucially, prior to the dual-task phase, participants’ span for each of these separate tasks was assessed and this measure was used to set the demand for the rest of the experiment. This span level was chosen such that participants could perform the single task competently, but were away from ceiling level performance (~ 80% accuracy). The cut-off used is the same as that used in studies that have found dual task conflict between storage and processing (Barrouillet et al., 2004, 2007) as well as those that have found no evidence of conflict, provided task demand was kept at or below this span level (Doherty & Logie, 2016).
Figure 1 .
The general trial procedure.
Following this initial titration, the two tasks were combined to create several dual task conditions in which the relative emphasis on the two tasks was varied by differentially awarding points for accuracy on each task and informing the participants that points would be converted to monetary reward at the end of the session. Each trial was awarded 100 points with the proportion of points allocated to each task varying between blocks. Participants were given trial-by-trial feedback on the number of points earned from each task which also served to reinforce the weighting.
Distinguishing concurrence costs from prioritization
Such a comparison of single task performance to dual task performance under different conditions of emphasis to each task allows us to assess two conceptually distinct sources of dual task conflict (see Navon & Gopher, 1979). The first reflects the change in performance on a given task as less emphasis is placed on it. If this is concomitant with an increase in performance on the other task, we can claim to have observed a prioritization trade-off. We term any decrease in accuracy as emphasis is shifted away from a given task as a prioritization cost (equivalently we could call any increase in performance with more emphasis a prioritization benefit). The second source of potential conflict reflects any drop in performance in dual task conditions relative to single task conditions that applies regardless of the emphasis placed on a given task. Such a concurrence cost, in addition to any decline in performance with lowering emphasis, would be associated with an additional drop in performance seen in all dual task conditions relative to single task. It is important to distinguish the so called concurrence cost from the dual task cost often measured in studies like this. The dual task cost (i.e. the difference between single and dual task performance) potentially reflects both of the sources mentioned above: any interference between tasks that is obligatory (i.e. not under volitional control of the participant), and the differential allocation of a more general attention resource, if there is one, between the two tasks. This is important for the reasons outlined earlier. A dual task cost can be accommodated by multiple components as reflecting something other than competition between storage and processing, such as the recruitment of the processing resource to support high demands on memory (e.g. Doherty & Logie, 2016). A prioritization cost, on the other hand, is much harder to accommodate and is naturally predicted by a shared attentional resource under volitional control (i.e. an attentional bottleneck or focus of attention).
Of course, like any manipulation, we must make a few assumptions for this distinction between the prioritization cost and the concurrence cost to work, especially with regards to the comparison of participants of different ages. For example, the reward used to incentivize performance should motivate participants regardless of age. Thus, in the present case we used both trial-by-trial feedback and monetary reward to encourage participants. Older adults, who are probably more fiscally secure than younger adults, would then have constant reinforcement on every trial of the weighting of each task. Provided we assume that participants are motivated to maximize their performance (i.e. points), which is a tacit assumption of most studies like this one, we should observe a prioritization trade off if the two tasks compete for a common resource (Navon & Gopher, 1979; Norman & Bobrow, 1975, 1976).
We must also make the distinction between the possession of a shared resource and the ability to effectively share that resource between tasks. It may be that older adults are less efficient at allocating priority to one demand over another, in which case what appears as a prioritization cost in younger groups would appear as a concurrence cost in older groups. In this case we would be wrong to conclude that storage and processing compete less for a common resource with age. In other words, age differences in these two conceptually distinct sources of dual task conflict must be interpreted in reference to each other. Despite these caveats, this general method has been used effectively in studies of both younger (e.g. C. C. Morey et al., 2011; Sperling & Melchner, 1978) and older adults (e.g. N. D. Anderson et al., 1998; Salthouse et al., 1984; Somberg & Salthouse, 1982).
Deriving predictions from multiple component, time-based resource sharing, and embedded processes accounts
Our primary motivation for using this approach is that, granting the aforementioned assumptions, they lead to clear differential predictions from the embedded processes, time-based, and multi-component frameworks. The view of working memory outlined by Logie and colleagues (Logie, 2011; Logie et al., 2004; Cocchini et al., 2002) does not predict any prioritization cost associated with shifting emphasis away from a task when task demand is titrated, nor does it predict a differential impact of age on prioritization performance. It does, however, allow for other kinds of conflict to occur, such as visual interference when both the to-be-remembered items and the processing task are presented on screen (Logie et al., 2000, 2016; Saito, Logie, Morita, & Law, 2008). Alternatively, conflict between input and output modalities may contribute to dual task interference (see Hazeltine et al., 2006; Stephan & Koch, 2010; Thalmann & Oberauer, 2017), but crucially this should be reflected only in a concurrence cost that applies to all dual task conditions. With respect to age, the extant literature suggest that age differences in dual task coordination are minimal when single task demand has been titrated (M. Anderson et al., 2011; Baddeley et al., 1986, 2001; Logie et al., 2004). However, as noted earlier, these studies have typically included small samples. Thus it is not possible to rule out the possibility that there is a small age-related increase in dual task costs that would become apparent with a sufficiently large sample. According to the multiple component model any age differences in dual task performance would be expected to apply in all dual task conditions, regardless of the particular emphasis placed on the tasks. These predictions are summarized in the first row of Table 1.
Table 1.
A summary of predictions for the current experiment and their rationale from three working memory frameworks. A summary of the results of the experiment is given in the bottom row.
| Theory - plus brief description | Concurrence Cost (CC) | Prioritization Cost (PC) | Concurrence Cost × Age | Prioritization Cost × Age |
|---|---|---|---|---|
| Multiple Components – Storage and processing rely on separate components and do not compete | No CC for auditory lists. Possibly a small CC for visual memory lists due to use of visual codes interfered with by the visually presented processing task. No CC for the processing task. | None as storage and processing do not compete for a shared resource | None or small. A small CC for older adults cannot be ruled out on the basis of existing literature. | None |
| Time Based Resource Sharing - Attention is switched on a temporal basis between processing and storage | Large CC for the memory task given large increase in cognitive load from single to dual task. | Large PC for each task reflecting attentional time sharing between storage and processing with the time allocated to each demand approximately related to the emphasis placed on it. | None. Titration is assumed to produce a constant cognitive load across participants so no age differences are expected. | None. See Concurrence Cost × Age. |
| Embedded Processes - Limited capacity focus of attention coordinates and switches between storage and processing demands | Small CC for both tasks due to demand of coordinating the switching of attention between maintenance and processing. | Large PC for each task through direction of the focus of attention in accordance with task emphasis. Smaller PC for auditory lists due to support from the auditory store. | At least a small age effect on CC for both tasks. Age is assumed to impair coordination functions required to switch between tasks | Possibly a slightly reduced PC for each task with age. A smaller proportion of older adults’ span is assumed to reflect central storage. |
| Findings of the present experiment | Large CC for memory and no clear evidence of CC for processing. | Large PC for both memory and processing tasks. PC for memory is slightly smaller for auditory letters and oral recall than for visual letters and typed recall. | CC increased linearly with age. | No evidence of age-related change to PC for ether task. |
Note: Effect size predictions are made on the scale of expected differences between individuals. For more detail on predictions, see https://osf.io/b2epe/
Turning to the shared resource frameworks, there is a clear prediction of a trade-off between storage and processing; shifting emphasis away from one task should result in a prioritization cost with a concurrent prioritization benefit for the task receiving the greater emphasis. Given the well known effects of aging on speed of processing (Cerella, 1985; Salthouse, 1996), according to TBRS we may predict a greater prioritization trade-off between storage and processing with age, as processing events take longer to complete. There is some evidence to suggest that the refreshing of memory representations is less effective in older adults (e.g. Fanuel, Plancher, Monsaingeon, Tillmann, & Portrat, 2018; Loaiza & McCabe, 2013; although see Loaiza & Souza, 2017; Souza, 2016 for conflicting evidence from a cued refreshing paradigm). That being said, by adjusting task demand for each individual to a common single task accuracy level, it may be argued that age-differences in prioritization cost will not appear. While cognitive load has not been previously conceived of as an individual differences variable within the TBRS framework, titration is assumed to produce the same effective cognitive load across individuals. Therefore, unlike the multiple component account, TBRS predicts a prioritization trade-off between storage and processing, but, like multiple components, anticipates no additional trade-off as a function of age. Developmental studies in children have already shown that the way in which memory accuracy is impacted by variations in cognitive load of a concurrent task is proportional to mean level of performance (i.e., older children who are better performers are more affected by variations in cognitive load, but when mean performance levels are equated, slopes of cognitive load functions no longer differ across age; Barrouillet, Gavens, Vergauwe, Gaillard, & Camos, 2009). With regards to the concurrence cost, the time-based resource sharing approach naturally predicts one for the memory task due to the addition of a processing component that requires attention, thereby disrupting refreshing activities. This increase in cognitive load from single to dual task is expected to produce a performance cost to memory performance that applies in all dual task conditions (see second row of Table 1).
The embedded processes account shares some features with the TBRS account, namely the use of attention in refreshing (e.g. Cowan, 1992), and assumes that there are additional factors at play (see third row of Table 1). Cowan (1984) reviewed evidence for two phases of auditory storage; an initial phase, typically aligned with the concept of echoic memory, lasting up to 350 ms and a longer form of storage in activated long-term memory (see Cowan, 1988) capable of representing auditory sequences for up to 20 seconds (e.g. Balota & Duchek, 1986; Watkins & Watkins, 1980). Auditory lists are presumed to receive support from this longer auditory storage and, thus, the prioritization trade-off between storage and processing should be less pronounced for auditorily than for visually presented information. With reference to the effects of aging, the embedded processes framework posits two opposing factors. Specifically, aging is predicted to affect the executive ability to coordinate and switch between processes (see Mayr, 2001; Wasylyshyn, Verhaeghen, & Sliwinski, 2011), leading to a disproportionate age-related detriment in dual task settings (i.e. a greater concurrence cost) and possibly greater difficulty adhering to the priority instructions. Further, the titrated level of difficulty will reflect both the combination of central and peripheral contributions to short-term memory ‘span’ (Cowan, Saults, & Blume, 2014). As aging is primarily thought to affect the central capacity of the focus of attention in working memory (e.g. Naveh-Benjamin et al., 2014), a greater proportion of older adults’ span is thought to rely on peripheral components that do not compete for attention. Therefore, perhaps paradoxically, the embedded processes position may expect the trade-off between storage and processing to actually decrease with age. That is, older adults may be expected to show less of a change in performance between conditions where little priority is placed on a given task to where the most priority is placed on that task (i.e. less of a prioritization cost). Given these different factors, with somewhat opposing effects, the embedded processes account does not make as clear predictions for aging as the other accounts.
The predictions for the present experiment from the multiple component, time-based resource sharing, and embedded processes accounts are presented in Table 1. It should be noted that our aim here is not to identify the ‘true’ conception of working memory. Rather our purpose here is to test a specific instance in which we have identified a clear theoretical difference: the multiple component framework adopted for the current study assumes that, once demand is titrated, dual task conflicts should be small or non-existent and not indicative of competition for a limited capacity general attention. A related claim is that age differences in dual task performance are eliminated for storage and processing tasks once task demands have been titrated, both for overall dual task performance and for the effects of prioritization. Even under titrated conditions, resource sharing theories, such as embedded processes and time-based resource sharing, still expect storage and processing to compete for a limited attention capacity and, thus, still expect the hallmarks of resource sharing, but differ in their predictions regarding the impact of age. So far these proposals have not received adequate empirical scrutiny with a method more suited to discriminating between the different theoretical proposals with regard to dual task performance and how it varies across the adult lifespan.
The Present Study
We recruited participants from two sites, one in the UK (Edinburgh, Scotland) and one in the US (Columbia, Missouri), whose ages at each site cover most of the adult lifespan (18–81). These participants were asked to simultaneously retain arbitrary sequences of consonants in mind (the storage/memory task) while performing an arithmetic verification task that required the speeded processing of single digit additions (the processing task). Crucially, prior to the dual-task phase, each participant’s span for each of these tasks was assessed and this measure was used to set the demand level for the rest of the experiment. To address the important issue of task prioritization, we manipulated this directly through both task feedback and financial reward such that participants were motivated to attend more to one task or the other. This method has been effectively applied in previous studies but, to our knowledge, it has not been applied to studying the overlap, or lack thereof, between storage and processing with respect to age. Participants were awarded points in return for performance, with 90, 70, 50, 30, or 10% of these points going to one task over the other. These dual-task measures were compared to single task measures in which all emphasis (points) was placed on one task. The proportion of the total points earned by the participant was converted to a monetary reward. Finally, to ensure that input-output modality conflict was minimized, the memory task was either presented visually and participants recalled by typing responses on a keyboard, or, the to-be-remembered letters were presented auditorily and recall was oral.
Method
Participants
The final sample was made up of 164 participants aged 18 to 81 (Mean = 49.52, SD = 18.91), with 84 from the Edinburgh site and 80 from the site in Columbia. At the UK site, 2 further participants were excluded for taking medication for anxiety or depression, 3 participants withdrew from the experiment, and a final participant was excluded for scoring below a preset cutoff on the background cognitive measures (see below). At the US site, 2 participants withdrew from the experiment and 1 participant did not return for the second session due to illness. Basic participant characteristics for the final sample are presented in Table 2 with participants grouped into 5 approximately equal size age-groups.
Table 2.
Participant characteristics and background cognitive test scores (means and standard deviations in parenthesis) collapsed across testing site.
| Age Group | |||||
|---|---|---|---|---|---|
| 18–30 | 31–43 | 44–56 | 57–70 | 71–81 | |
| N | 33 | 33 | 32 | 33 | 33 |
| female | 14 | 21 | 21 | 21 | 16 |
| age | 23.24 (3.52) | 35.91 (3.35) | 50.12 (3.54) | 63.64 (3.56) | 74.73 (3.01) |
| YoE | 15.98 (2.29) | 18.85 (5.00) | 16.88 (2.76) | 17.39 (3.23) | 15.64 (3.42) |
| VC (T) | 54.82 (8.48) | 56.45 (8.68) | 58.22 (6.80) | 60.70 (9.27) | 58.94 (8.60) |
| VC (raw) | 40.42 (4.65) | 42.70 (5.19) | 44.16 (3.61) | 44.76 (5.48) | 42.73 (5.26) |
| MR (T) | 56.76 (9.37) | 55.21 (8.62) | 55.06 (6.75) | 57.70 (9.01) | 60.33 (7.44) |
| MR (raw) | 23.15 (2.98) | 22.76 (2.46) | 21.09 (3.05) | 20.55 (4.00) | 19.33 (3.48) |
| MoCA | 28.73 (1.23) | 27.64 (1.75) | 28.06 (1.68) | 27.42 (2.21) | 26.52 (1.97) |
Note: YoE = years of education, VC (T) = vocabulary T score, VC (raw) = vocabulary raw score, MR (T) = matrix reasoning T score, VC (raw) = matrix reasoning raw score, MoCA = Montreal Cognitive Assessment score
Participants were tested individually on two occasions on separate days, no more than two weeks apart. In one session participants completed the auditory-oral (AO) version of the experiment and in the other they performed the visual-typed (VT) version (see below for more detail). At the UK site participants were recruited from the student population of the University of Edinburgh, the Psychology Research volunteer panel, and the wider community of Edinburgh. At the US site participants were recruited from the student population of the University of Missouri-Columbia and the Subject Pool of the Memory and Cognitive Aging laboratory. Participants received a flat rate of compensation (£12/ $15) for their participation in each session, which lasted approximately 1.5 hours, and had the chance to earn an extra amount in each session that was commensurate with their performance on the main experimental tasks (£4/ $5; see below). The experiment protocol was approved by the institutional review board of the University of Missouri and the ethics committee of the University of Edinburgh.
Prior to the main experimental task participants completed either the Montreal Cognitive Assessment (MoCA; Nasreddine et al., 2005) or the two-subscale version of the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 2011), which includes the vocabulary (VC) and matrix reasoning (MR) assessments. The MoCA was completed prior to the AO session, whereas the WASI was completed prior to the VT session. Raw scores are given along with T scores for each subtest, each of which is scaled to have an age adjusted mean of 50 and standard deviation of 10.
Our sample appears to be typical for studies such as these (see Table 2). The youngest group scored slightly lower on the vocabulary subscale relative to the other groups and there is a general drop in matrix reasoning performance and scores on the MoCA with increasing age. The testing site did not appear to have an effect with the exception of the vocabulary measure, for which a site by age-group interaction was observed. The raw score of the youngest group in the UK was particularly low (~ 37) relative to the other groups (~ 43). This difference seems inconsequential so the scores are presented collapsed across site in Table 2 (scores split by site are available in the supplement to this article).
As there are known issues with the standard cut-off score used to establish cognitive impairment with the MoCA (it appears to have a high false-positive rate as shown by Rossetti, Lacritz, Cullum, & Weiner, 2011), participants were excluded from the study if they scored less than the recommended cut-off of 26 on the MoCA in conjunction with poor performance on a subtest of the WASI (defined as performing within the bottom 5% or a T score < 34). An alternative criterion for exclusion was a score of less than 20 on the MoCA (Waldron-Perrine & Axelrod, 2012). As mentioned above, 1 participant was excluded from the final analysis due to poor performance on the background cognitive measures.
Stimuli and Apparatus
Memory stimuli consisted of a pool of 18 consonants, excluding ‘w’, ‘y’, and ‘z’. For auditory presentation with oral response conditions (AO) the audio recordings of letters were taken from the Mac OS X in the voice ‘Allison’ that simulates a standard North American accent. The recordings have an average duration of 385 ms (range: 206–523) and were presented to participants at a comfortable listening level over Fostex T40RP MK3 headphones. For visual presentation with typed response conditions (VT), letters were presented one at a time in the Lucida Console font with a height of 1.3° of visual angle at an approximate viewing distance of 60 cm.
Visual stimuli were presented on a grey background (R = G = B = 128) via a 23” Lenovo ThinkVision T2324p monitor with a 60 Hz refresh rate. Single digit additions in the processing task were also presented in the Lucida Console font with a height of 1.3° of visual angle at an approximate viewing distance of 60 cm. Participants responded to the processing task via a button box (www.blackboxtoolkit.com). The experimental procedure was programmed using PsychoPy (Peirce, 2007, 2009).
Design and Procedure
Before describing the structure of each session of the experiment we will describe the general trial procedure shown in Figure 1.
Trial Procedure.
Single Task Memory.
Participants initiated each trial by pressing one of two keys on the response box, an event that initiated a 2 second blank interval prior to the presentation of the first memory item. In the AO condition letters were presented over headphones at a rate of 1 per second, with a period of silence following each letter. In the VT condition letters were also presented at a rate of 1 per second with the letter presented at the center of the screen for 250 ms followed by a 750 ms blank interval. The presentation continued until the appropriate number of letters was presented, determined by the titration procedure (see below). Following the last letter there was a 1 s blank interval prior to the processing part of the trial. For conditions in which there was no memory requirement, placeholders were presented instead. In the AO condition, the memory task placeholder consisted of five 300 Hz tones presented for 250 ms followed by a silent interval of 750 ms. In the VT condition the memory task placeholder consisted of 5 filled diamond characters (subtending 1.5° visual angle) each presented for 250 ms and followed by a 750 ms blank screen.
In single task memory blocks the final memory item was followed by a 1 second blank interval and then an additional 10 seconds during which a placeholder was presented (to fill in for the processing task presented during dual task blocks). This placeholder was a solid circle (1.5°) appearing on the screen five times for 1750 ms with an interstimulus interval of 250 ms.
Immediately following the final placeholder a 400 Hz tone was played. This signified to participants that they should recall the letters in their correct serial order. In the VT condition the participant used the keyboard to enter responses. To acknowledge responses, each recalled item appeared on the screen for 500 ms or until another key was pressed at which point the most recently recalled item appeared in its place. Participants were informed that they could not correct mistakes and if they were unsure about a particular item, given that the task involved recalling letters in order, they could type ‘0’ (zero) to skip an item. In the AO condition the participant would respond orally and the researcher entered the participants’ responses on the laptop running the experiment. In this condition, if the participant was unsure of a given item they were instructed to respond ‘pass’. Researchers were able to correct typing errors and confirmed the recalled sequence by pressing the Enter key. To allow for later checking on the possibility of experimenter errors, audio recordings of recall were also taken for each trial in the AO condition. There was no time limit for response and accuracy for the memory task was the number of letters recalled in their correct serial position out of the number of letters presented.
Single Task Processing.
Again the trial was initiated by the participant and began with a 2 second blank screen. Following that, a placeholder was presented in lieu of the memory letters. In the AO condition, the memory task placeholder consisted of five 300 Hz tones presented for 250 ms followed by a silent interval of 750 ms. In the VT condition the memory task placeholder consisted of 5 filled diamond characters (subtending 1.5° visual angle) each presented for 250 ms and followed by a 750 ms blank screen. The final placeholder was followed by a 1 second blank interval prior to the onset of the processing task, which took place in a 10 second period.
Participants were required to verify single digit additions (e.g., 6 + 7 = 13) as quickly and as accurately as possible (see Figure 1). The sum was either correct or deviated by ±1 (e.g., 6 + 7 = 14 or 6 + 7 = 12). Participants responded by either pressing a button marked with a check symbol (right hand), to indicate that the sum was correct, or by pressing a button marked with a cross (left hand), to indicate that it was incorrect. Depending on the number of processing items to be presented, as determined by titration (see below), during the 10 s processing phase, each sum appeared on the screen for (10 − N/4)/N seconds, where N is number of sums to verify, with a 250 ms blank interval in between items. Participants were able to respond to a given item from its onset right up until the onset of the next processing item. Accuracy for the processing task was the number of sums correctly verified out of the number given within the 10 s period.
Dual Task Memory+Processing.
The combination of the memory and processing tasks is shown in Figure 1. In this case no placeholders were presented.
Structure of Sessions.
The two sessions differed in the nature of the memory task. Half of the participants in each of the 5 age groups in Table 2 completed the auditory presentation and oral recall version in the first session, whereas the other half completed the visual presentation and typed recall version. Otherwise the sessions were made up of the same three sections described below.
Letter Identification.
At the start of each session participants completed a letter identification task. Participants were presented with a single letter at a time (either auditorally for the duration of the recording in the AO session or visually for 250 ms in the VT session) and were required to respond by typing the perceived letter using the keyboard. Following response there was a 500 ms blank interval before the next letter was presented. Participants cycled through the letter set in a random order twice. The purpose of this task was to ensure that participants were able to accurately discriminate between the letter stimuli. Errors on the pretest phase of the experiment were extremely rare (approximately 2.14% of responses), so these data are reported in the supplementary material.
Titration of Each Task.
Following this initial pre-test, the purpose of the second section of each experimental session was to obtain a measure of each individual’s ability to perform the memory and processing tasks in isolation, with placeholders presented in place of the omitted task. Participants completed a staircase procedure, which began with five items (i.e., either five letters to memorize or five sums to verify). Each level consisted of two trials with a given number of items. At the first level, five items were presented. If participants were able to achieve 80% accuracy or greater across these two trials they were deemed to have passed and an additional item was added for the next level. Otherwise an item was taken away in order to reduce difficulty. This proceeded until the participant had completed at least 8 levels (16 trials). If the 8th level was passed and it was the highest level passed by the participant, additional levels were run until the participant failed. The resulting span for the given task was the highest level passed by the participant during the titration procedure. This titration procedure occurred in each session and the order in which memory and processing were titrated was counterbalanced in line with the main priority manipulation, see below.
Single and Dual Task Blocks.
The third section of the experiment required participants to differentially prioritize memory and processing performance. This was incentivized by offering a reward of 100 points per trial distributed between the tasks. Let P be the number of points given to memory and 100 − M the number of points given to processing, P could take on the values 90, 70, 50, 30, and 10 in this experiment. Participants were instructed that they could obtain up to P points for wholly accurate performance (correct serial recall) on the memory task and up to 100 − M points for wholly correct processing responses. At the end of each session the proportion of the total number of points obtained by the participant determined the financial reward to the nearest whole. Two memory-and-processing counterbalancing conditions differed based on whether P increased or decreased from block to block.
To obtain a measure of performance on these tasks at span levels, ‘pure’ single task measures were completed before and after the priority blocks. Participants starting with M = 90 began with a pure memory measure and ended with a pure processing measure, whereas participants starting with M = 10 started with pure processing and ended with pure memory. In these pure blocks placeholders were presented for the omitted task and participants were awarded up to 100 points for the task at hand.
Participants completed eight trials in each of the seven blocks (two pure and five different values of P). Prior to each block they were also given two practice trials to familiarize themselves with the current weighting. There were 4 counterbalancing conditions crossing (1) the aforementioned order of memory and processing in both the titration and priority phases of the experiment (i.e., memory-processing, processing-memory), and (2) the order of presentation/recall formats across sessions 1 and 2 (i.e., AO-VT, VT-AO). These orders were equally distributed across the five age-groups described above.
To motivate participants, in addition to the base payment for taking part (£12 per session in the UK and $15 per session in the US), they could earn up to 1/3 more (£4 or $5) by collecting as many points as they possibly could. Feedback on the number of points obtained was given following each trial via bar plots that filled up to indicate the number of points, out of the total available, that the participant obtained for each task. A running total of points, out of the number possible to obtain, in that block was also presented at the bottom of the screen. Participants were only given feedback in terms of points as the amount of money awarded for each trial was quite small, and the points were converted to money at the end of the experiment (rounded to the nearest whole). This general approach to motivating participants has been effectively applied in several previous studies (C. C. Morey et al., 2011; Somberg & Salthouse, 1982; Salthouse et al., 1984). To avoid the potential that participants may match their level of performance on each task to the perceived demands of the experimenter, thereby producing a spurious trade-off (see Navon, 1984), participants were informed that in order to gain the most points—and therefore the most money—they would have to be 100% accurate on both tasks. Thus, if participants were able to perform both tasks without cost this feedback should have motivated them to do so. However, if they were able to shift attention between the tasks to mitigate any cost associated with simultaneous performance of the storage and processing tasks these instructions and feedback should have incentivized this. The materials for this experiment can be found here: https://osf.io/b2epe/.
Analysis
In the present study our primary interest was accuracy across the single task and varying priority levels of the dual task conditions. While it is typical practice in much of cognitive psychology to aggregate correct and incorrect responses into a proportion (i.e., N correct/N total) and submit these to an ANOVA, this is an inappropriate treatment of accuracy data (see Agresti, 2002). Analysis of aggregate proportions, or even transformations thereof (e.g., arcsine square root), is liable to producing spurious interactions (Dixon, 2008), which is of particular concern in research on cognitive aging (Salthouse, 2000). Rather, analysis using generalized linear mixed models is appropriate in the present case. In particular, we use the logit link function to model the log odds of a correct response on a given task. This scale is more appropriate when modeling accuracy, as it is bounded between 0 and 1, and it accounts for the fact that proportions are inherently more variable in the mid range of accuracy (i.e., around 0.5). Therefore it should be noted that while we plot data on its observed scale the modeling is done on log odds, a more appropriate latent scale (see Dixon, 2008, for further detail on the appropriateness of this scale).
Although we present the data binned into 5 age groups for communication purposes in tables and figures, age was treated as a continuous variable. The age variable was scaled into z-scores prior to modeling and we considered both linear and non-linear (quadratic) age terms during model selection (see below), as both have been reported in the wider literature (e.g. Johnson et al., 2010; Verhaeghen & Salthouse, 1997). For the factor of presentation-recall format (and other binary factors) we used effects coding, such that AO was coded −1 and VT was coded +1. For condition (i.e. the manipulation of task priority) we used ‘backwards difference coding’ to compare successive levels to each other. With this coding scheme the first contrast compares the single task measure (e.g., pure memory) to the first dual task condition (e.g., 90 points to memory) and the second contrast compared that condition to the next level of allocation (e.g., 70 points to memory) and so on. This coding scheme allows us to address the issue of most interest to us; specifically, does the manipulation of priority result in a prioritization cost in performance as fewer points are allocated to a particular task and, if so, does the extent of that prioritization cost vary with age. A clear trade-off would be consistent with the sharing of a central resource between the two tasks. Additionally, we were interested in whether there are sources of dual task interference that are not modifiable by instructions to prioritize one task over another. With this coding scheme this would be evident in a disproportionately large coefficient for the first contrast (i.e. between the single task condition and the first dual task condition). On the other hand, values around zero for each of these contrasts would be consistent with separate resources being deployed in parallel. We consider other ways of distinguishing these two factors later in the article.
The data were analyzed using the lme4 package in R (Bates, Maechler, Bolker, & Walker, 2014; R Core Team, 2015).1 Our analysis proceeded by fitting a full model, including main effects of condition, presentation-recall format (AO, VT), both linear and quadratic age terms, and interactions between these variables (interactions only included one of the age terms). We also included testing site to examine whether patterns of performance differed between labs. All models contained a random participant intercept, which modeled individual differences between participants in overall accuracy. This led to an unwieldy model that was difficult to interpret. Therefore, we proceeded to simplify the model in the following fashion. The highest order (in this case three-way) interaction was removed and the resulting model was compared to the full model via the Bayesian information criterion (BIC; Schwarz, 1978), which penalizes the fit of a model for the number of parameters it has. If the BIC was lower for the reduced model this was considered evidence against the removed effect, in which case it was taken out for subsequent stages in the model comparison. This continued in a similar fashion through to the two-way interactions and then main effects. We did not consider removing interactions or main effects if they were subsumed by retained higher order interactions. For example, if the presentation-recall format by testing site interaction had been retained, we would not consider removing either format or site as main effects later in the model simplification procedure. For interactions or effects involving age, we considered removing the quadratic age term prior to the linear one. If the non-linear effect was retained we would not remove the linear effect. This process continued until all effects not receiving support from the model comparison were eliminated and the final model was determined.2
The span data, arising from the titration procedure described above, were analyzed in a similar manner using a standard linear mixed model (using the identity link function). We report the results of the final models here and the results of the full models can be found in the Supplementary Material.
An important step we take in the present work is to place predictions from the resource sharing and resource independent accounts on a common scale. Specifically, as all models contained a random participant effect, we used the estimated standard deviation to scale coefficients of interest. Thus, where reported, the effect sizes we refer to give the magnitude of the effect in terms of expected differences between individuals. Coefficients in Tables are presented with z or t-values which are used to assess the significance of the coefficients.3 For the thresholds of determining whether a given coefficient is significantly different from 0 we use two criteria. The reason for this is that we have a mix of tests for which either a directional or non-directional hypothesis is appropriate. For example, there is no reasonable expectation that reducing the number of points allocated to a particular task would reliably improve performance or that older participants will outperform younger participants. For such one-sided tests a z-value greater than 1.65 in the predicted direction may be considered significant. For two-way hypotheses, such as the effect of presentation-recall format, in which no particular direction is predicted, a z-value exceeding 1.96 can be used to denote significance (α= 0.05).
Results
Spans
In the present study ‘span’ for each of the tasks was established using a modified staircase procedure (see above) to find a level (number of letters or arithmetic problems) at which the participant was approximately 80% accurate or more. Accuracy for the memory task was defined as recalling the correct letter in the correct serial position, whereas accuracy for the arithmetic task was defined as responding correctly to a sum within the allowed response window. These values were used to set the difficulty of each task in the main section of the study.
Memory Span.
Figure 2 displays span values for the memory task split by the presentation and recall formats with the data binned into five age groups for visualization purposes. In the analysis of memory span, which started with effects of format, site, age (linear and quadratic), and their interactions, the final model retained the linear effect of age only. The intercept term suggested a mean span of approximately 6 (β = 6.01 (0.07), t = 85.01) and the linear effect of age suggests a drop in span of around 0.5 for each standard deviation increase in age (β = −0.49 (0.07), t = −6.86). This is comparable to meta-analytic estimates of the effect of age on simple span (Bopp & Verhaeghen, 2005). The BIC comparison was against main effects of modality ( BIC = 10.37), as the mean spans were very similar across formats (AO = 5.99, VT = 6.03; see the bottom panel of Figure 2). The evidence was also against an effect of site (ΔBIC = 9.21). As a guide to interpreting differences in BIC (ΔBIC) between models, Raftery (1995, Table 6) suggests that a difference of 0–2 be considered weak, 2–6 positive, 6–10 strong, and > 10 very strong.
Figure 2 .
Span estimates for the memory task split by presentation/recall format across 5 age-groups. Points are individual scores (jittered within groups to reduce overlap) with means and within subjects 95% confidence intervals overlaid. Note: Age Group 1 = 18–30; 2 = 31–43; 3 = 44–56; 4 = 57–70; 5 = 71–81.
Processing Span.
Spans for the arithmetic verification task are presented in Figure 3. This task was identical across the two sessions (see Figure 1), so rather than include the main effect of format the full model included session (1 or 2) along with site and age. The final model in this case included the linear age term and the main effect of session. The intercept term suggests an average span on this task of around 9 (β = 8.85 (0.14), t = 62.62) and the linear age effect again pointed towards a drop of around 0.5 per SD increase in age (β = −0.56 (0.14), t = −3.93). Between session 1 and 2 processing spans increased by approximately 1.2 (β = −0.61 (0.05), t = −12.06). The age by session interaction was rejected (ΔBIC = 9.03) suggesting the gain in session 2 was similar across age (see bottom panel of Figure 3).
Figure 3 .
Span estimates for the processing (arithmetic verification) task split by session across 5 age-groups. Points are individual scores (jittered within groups to reduce overlap) with means and within subjects 95% confidence intervals overlaid. Note: Age Group 1 = 18–30; 2 = 31–43; 3 = 44–56; 4 = 57–70; 5 = 71–81.
Memory and Processing Accuracy
Figure 4 presents both the memory and processing accuracy data from this study across the two presentation-recall modalities and the different allocation conditions. The grey lines trace out data points from each individual and display considerable variability in performance across all conditions, an issue to which we return later in the results. These data are also presented split into five age groups in Figure 5, although it is important to reiterate that age was treated as a continuous variable in the analyses presented below.
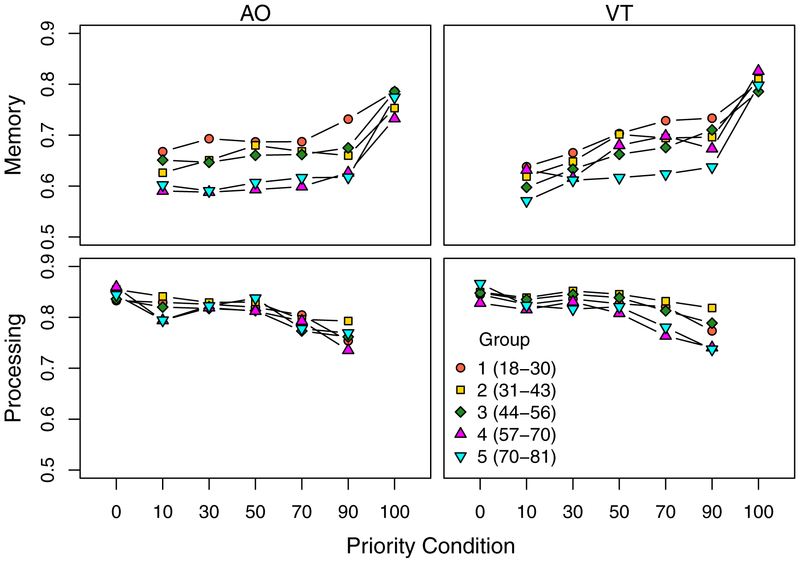
Figure 4 .
Accuracy on memory and processing tasks across point allocation for the two presentation and recall formats. Lines from individual participants are given with means and 95% CIs. Condition numbers refer to the number of points allocated to the memory task (P) in that condition with the number of points allocated to processing being 100 − M. The 0 condition is the single task processing measure and the 100 condition is single task memory.
Figure 5 .
Mean accuracy on memory and processing tasks binned into 5 age groups. See Figure 4 for an explanation of condition numbers.
Memory Accuracy.
As described in the Analysis section, our approach was to fit a full model and then simplify it by removing components and assessing change to model fit via BIC. The final model in the analysis of memory accuracy is presented in Table 3. The full model and description of steps taken in simplifying it can be found in the Supplementary Material. There were no indications that testing site modulated any of these patterns, as including this factor did not change the final model. Thus, the patterns reported below can be considered to have been replicated across two independent labs.
Table 3.
Final model for the analysis of memory accuracy. See the main text for description of the analysis approach.
| Parameter | β | Std. Err | z |
|---|---|---|---|
| (Intercept) | 0.761 | 0.035 | 21.913 |
| C1. 100 vs 90 | −0.587 | 0.026 | −22.256* |
| C2. 90 vs 70 | −0.045 | 0.025 | −1.847* |
| C3. 70 vs 50 | −0.038 | 0.024 | −1.565 |
| C4. 50 vs 30 | −0.127 | 0.024 | −5.251* |
| C5. 30 vs 10 | −0.073 | 0.024 | −3.086* |
| Format (VT vs AO) | 0.065 | 0.007 | 9.075** |
| z(Age) | −0.132 | 0.035 | −3.775* |
| C1 × Format | −0.044 | 0.026 | −1.683 |
| C2 × Format | 0.01 | 0.025 | 0.41 |
| C3 × Format | −0.04 | 0.024 | −1.633 |
| C4 × Format | −0.041 | 0.024 | −1.692 |
| C5 × Format | −0.046 | 0.024 | −1.932 |
| C1 × z(Age) | −0.181 | 0.026 | −6.823** |
| C2 × z(Age) | 0.004 | 0.025 | 0.167 |
| C3 × z(Age) | −0.003 | 0.025 | −0.108 |
| C4 × z(Age) | 0.008 | 0.024 | 0.311 |
| C5 × z(Age) | 0.06 | 0.024 | 2.524** |
Note:
= p < 0.05 for a one-tailed test (i.e. one where we expect a direction apriori),
= p < 0.05 two-tailed test. C components refer to specific contrasts between priority conditions (100 = single task memory).
Starting with main effects, the factor of priority condition (100, 90, 70, …) had a clear effect on performance. Contrast 1 (C1) compares the single task memory condition to the first dual task condition (with 90% of points allocated to memory) and demonstrates a pronounced drop in accuracy (also visible in Figures 4 and 5). The participant standard deviation was estimated as 0.435 (recall that this is on log odds scale) so scaling this effect gives an effect size of −1.35 (see Analysis section). The drop in performance seen in the contrasts of 90-with-70 (C2) is significant in a one tailed test (z < −1.65), whereas the contrast of 70-with-50 (C3) is not (scaled effect sizes of −0.1 and −0.09, respectively). Significant drops in accuracy were observed between the 50 and 30 (C4; scaled effect = −0.29) and 30 and 10 conditions (C5; scaled effect = −0.17).
To bolster the claim that the first contrast is disproportionate we can look at 96% confidence intervals (CIs) for each of the coefficients. The CIs for the contrast between single task memory and the first dual task condition ([−0.639, −0.536]) do not overlap with the CIs for all of the other contrasts (C2 = [−0.093, 0.003], C3 = [−0.086, 0.01], C4 = [−0.174, −0.079], C5 = [−0.12, −0.027]). This is arguably a conservative test of the concurrence cost given that the change in emphasis, as operationalized through points, is smaller for the first contrast relative to the others. We consider an alternative model for identifying the concurrence cost apart from any prioritization below.
Presentation and recall format also resulted in a small effect, with the VT condition being slightly more accurate overall, relative to AO (scaled effect size = 0.3). The linear effect of age was also significant, with a scaled effect size, per each standard deviation increase in age, of −0.3.
Turning to interactions, both the condition × format, and the condition × (linear) age interactions were retained in the final model. The coefficients associated with the condition × format interaction are all small and non-significant (see Table 3), but the retention of this factor in the model suggests that overall this interaction is contributing to model fit. The inclusion of this interaction in the final model suggests, a greater drop in performance with fewer points allocated to memory, a greater prioritization cost, in the VT condition (scaled effect sizes in the region of −0.19 with the exception of the contrast between 90 and 70. See Table 3).
The age × condition interaction was more pronounced, but specifically for the first contrast (C1) comparing the 100 (single task memory) and 90 conditions. This suggests a greater performance drop between the single task condition and the first dual-task condition with age. The scaled effect size for this comparison suggested that this drop was −0.42 units (i.e. expected difference between individuals) larger with each SD increase in age. The remaining contrasts are negligible and the final contrast between the 30 and 10 point conditions suggests a smaller drop in accuracy with age (scaled effect = 0.14). Once again, we looked at CIs to test whether the age by condition interaction was specific to the first contrast. Indeed, the 95% CI for the first interaction contrast did not include zero and did not overlap with the other interaction contrasts, suggesting the memory concurrence cost is accentuated by age (C1 = [−0.233, −0.129], C2 = [−0.044, 0.053], C3 = [−0.051, 0.046], C4 = [−0.04, 0.055], C5 = [0.013, 0.107]). Note that the final contrast between conditions 30 and 10 points to memory is significant in the positive direction. This suggests a smaller difference in this contrast with age but given that the other coefficients do not strongly show this same trend we cannot claim that the prioritization trade-off is reduced with age.
In summary, performance on the storage task declines as fewer points are allocated to it, a prioritization cost, and the disproportionate first contrast between the single task condition and the 90 points-to-memory condition suggests a concurrence cost for the memory task irrespective of priority. Further, this concurrence cost appears to increase linearly with age. The remaining contrasts suggest that change in dual task memory performance with fewer points appears to be more or less constant with age but is less pronounced with auditory presentation and oral recall.
Processing Accuracy.
The results of the final model from the analysis of processing accuracy are presented in Table 4. Once again, there was no indication that the pattern of performance varied by testing site. This final model was made up of a main effect of condition, main effects of format and age (linear), as well as their interaction. For the main effect of condition, the first contrast in Table 4 compares the first dual tasking condition (90 points to processing; M = 10) to the single task processing measure (M = 0). As the random participant intercept standard deviation was estimated at 0.361, the scaled effect size for this contrast is −0.33. There is no significant drop in performance between the 90 and 70 points to processing conditions (C2; scaled effect = 0). Accuracy then drops, but not significantly, between the 70 and 50 conditions (C3; scaled effect = −0.08), and then to a greater (and significant) degree between the 50 and 30 (C4; scaled effect = −0.52), and 30 and 10 conditions (C5; scaled effect = −0.35). The 95% CI for the first contrast ([−0.17, −0.07]) overlaps with 3 of the other 4 contrasts (C2 = [−0.048, 0.049], C3 = [−0.078, 0.02], C4 = [−0.236, −0.142], C5 = [−0.172, −0.082]). Thus, there is no evidence for a disproportionate drop in performance from single to dual task. Unlike the memory task, there is no clear concurrence cost for the processing task, but, like the memory task, there is a clear prioritization effect that does not differ with age.
Table 4.
Final model for the analysis of processing accuracy. See the main text for description of the analysis approach.
| Parameter | β | Std. Err | z |
|---|---|---|---|
| (Intercept) | 1.536 | 0.029 | 52.711 |
| C1. 0 vs 10 | −0.12 | 0.025 | −4.714* |
| C2. 10 vs 20 | 0 | 0.025 | 0.013 |
| C3. 30 vs 50 | −0.029 | 0.025 | −1.167 |
| C4. 50 vs 70 | −0.189 | 0.024 | −7.863* |
| C5. 70 vs 90 | −0.127 | 0.023 | −5.526* |
| Format (VT vs AO) | 0.033 | 0.007 | 4.631** |
| z(Age) | −0.06 | 0.029 | −2.054* |
| Format (VT vs AO) × z(Age) | −0.023 | 0.007 | −3.239** |
Note:
= p < 0.05 for a one-tailed test (i.e. one where we expect a direction apriori),
= p < 0.05 two-tailed test. C components refer to specific contrasts between priority conditions (0 = single task processing).
The main effect of format suggests that, as in the memory analysis, overall performance on the processing task was marginally better for VT than AO (scaled effect size = 0.18). The linear effect of age points towards a small overall drop in processing accuracy with age (scaled effect size = −0.17 per SD increase). The age × format interaction was very slight and suggests that the overall effect of age on processing accuracy is somewhat larger in the VT condition than the AO condition (scaled effect size = −0.12).
In summary, the main finding is that processing performance declines as fewer points are allocated to it. Crucially, the drop between the single task condition and the first dual task block is not disproportionately larger than the other contrasts, unlike the memory data.
Addressing Potential Objections
It is important to address a potential objection that could be raised from the multiple component perspective. Both the analyses of memory and processing accuracy yielded overall effects of age and, thus, it may be argued that our titration procedure was ineffective. The disproportionate age effect of going from single task to dual may have occurred because the older adults were pushed beyond span, particularly in the memory task (cf. Logie, 2011). As Figure 4 shows, there is a considerable amount of variability around 80% accuracy in the single task condition. Accordingly, those performing below this level may be said to be overloaded, whereas those performing over 80% might be considered under span. Thus, we conducted additional analyses to examine whether those pushed beyond span show a larger dual task cost (as suggested by Logie, 2011). We focused on the 100 and 90 conditions only and, in the model, allowed for participants to differ not only in their baseline level of performance but also in the extent to which their accuracy changed in going from memory alone to memory+processing. The correlation between these random effects was negative (−.57, 95% CI = [−.69, −.42]), suggesting that those who performed better in single task actually showed a greater drop going to dual task.4 This is the opposite of what would be expected if participants pushed beyond span were recruiting more domain general resources. Including this random effect also did not affect the interaction between age and single vs dual task.
There were effects of age in the final models for both the memory and the processing data. Thus the slight age differences in single task performance may complicate our interpretation of the memory concurrence cost. In situations like this it is common to scale the dual task cost by single task accuracy (i.e. [single - dual]/single) (e.g. M. Anderson et al., 2011; Logie et al., 2004, 2007). This puts the age groups on a similar scale, where a proportion of 1 reflects no cost at all (i.e. perfect dual task performance). We analyzed this measure and it reproduced the pattern of findings presented above. For memory there was a main effect of age, reflecting the concurrence cost, and no age by priority allocation condition interaction, reflecting the consistency of the prioritization trade-off across age. For processing there was no main effect of age nor an age by condition interaction. These results are presented in full in the Supplementary Material.
A further issue we must address is the possibility that a subset of participants gave up on a particular task (e.g. stopped responding), when it was not sufficiently rewarded, and that the apparent trade-off was driven by participants deliberately not performing the task. There is suggestion that a handful of participants may have taken this tack in Figure 4, where some lines drop considerably when the points were not weighted towards a given task. To address this we performed an additional analysis excluding participants scoring 10% or less on the memory task (recalling, on average less than 1 letter) in the 30 and 10 conditions or participants scoring 50% (chance) or less on the processing task in the 70 and 90 conditions. Twelve participants were omitted from these analyses; one for falling below both criteria and the remaining for appearing to give up on the processing task (4 were in the two youngest age groups, 8 in the two oldest groups). Removing these participants did not change the pattern of results from those presented in Tables 3 and 4. Therefore, it does not appear that the prioritization cost we observed is being driven by a subset of the participants ‘giving up’. We discuss other potential interpretations of these data from the multiple component perspective in the Discussion section.
Finally, another potential criticism may concern the specific analysis we used. In particular the analysis of the priority condition variable which only allowed the comparison of successive conditions. It is important to ask to what extent our particular choice of coding scheme influenced the findings. In particular the backwards difference coding we used for the priority variable does not result in orthogonal contrasts. However, when the analysis is conducted with an orthogonal contrast matrix the same final model is recovered for both the memory and processing data. Further, there are alternative models that may prove useful. In the Supplementary Material we discuss one such model which more parsimoniously splits the priority condition variable into the effects of single versus dual task (to examine the concurrence cost) and a linear effect of points allocated to a particular task (to examine the prioritization cost). As shown in the supplement, this analysis does not challenge any of the results presented here and we argue that the coding scheme used here was more appropriate given that we had no reason a priori to constrain the effect of priority (or points) to be linear. Also this assumption appears to be inappropriate for the processing data (see Supplementary Material).
Discussion
In this study we have examined the extent to which a memory task and a processing task conflict with each other when performed together compared to when they are performed separately, and how this changes with age. Specifically, we were interested in assessing whether conflict occurred despite the demands of each task being adjusted to a common accuracy level for each individual before they were combined. Further, by varying the priority weighting of the tasks when the two tasks were performed simultaneously we were able to distinguish concurrence costs from prioritization costs in a theoretically meaningful way. These factors taken together, we would argue, are of use in addressing the differential assumptions of the three different theoretical perspectives being considered here regarding how storage and processing interact in working memory and how this changes across the adult lifespan.
The results can be summarized as follows: For memory performance there is a large drop in performance between single task and dual, regardless of the priority weighting. This concurrence cost gets larger, in a linear fashion, from age 18 to 81. For the processing task a concurrence cost was not clearly observed. Rather, processing performance gradually dropped as emphasis was shifted away from this task and towards memory. Thus, for the dual task data, there does appear to be a prioritization trade-off between the memory and processing tasks, which does not appear to differ by age. This priority shift is such that the difference between the highest priority to lowest priority conditions was approximately 0.65 in standard deviation units (see Analysis section) for the memory task and 0.95 for the processing task. For the memory data, there was evidence that the prioritization cost was somewhat attenuated when presentation was auditory and recall was oral relative to visual presentation and typed recall (see Table 3). Overall performance was reliably better with visual presentation and typed recall relative to auditory presentation and oral recall, most likely due to the contribution of phonological confusion errors in the latter condition. Importantly, these patterns were replicated across two testing sites (one in the UK, one in the US).
We first discuss our findings with regard to how storage+processing dual task performance changes across the adult lifespan. Some aspects of these results were unanticipated by the predictions made in Table 1, and it is clear that none of the three theoretical perspectives correctly predicted all of the results obtained. We discuss what these findings could indicate in reference to the wider literature on aging and working memory. We also suggest some possible follow ups on the present findings to further probe the nature of the age related concurrence cost that we observed. Following that we discuss the present findings in relation to the working memory frameworks that motivated our study. We discuss where predictions were correct and where they missed the mark. Where there are discrepancies between expectations and findings we discuss what modifications could be made to each of the three frameworks to reduce the discrepancy.
Storage and Processing Across the Adult Lifespan
What do our findings tell us about storage and processing across the adult lifespan? Recall that there are mixed results regarding whether age-differences in performance are typically larger on working memory measures that require some form of concurrent processing or manipulation (Belleville et al., 1998; Bopp & Verhaeghen, 2005; Jenkins et al., 1999). Some studies have suggested that older adults have a specific problem in coordinating joint storage and processing demands (Craik, 1977; Mayr & Kliegl, 1993; Salthouse, 1990), whereas others have presented conditions under which there are no such significant conflicts (M. Anderson et al., 2011; Baddeley et al., 1986; Logie et al., 2004; although see, Bier et al., 2017; Logie et al., 2007). Given that the evidence for this proposition has been mixed and it was hoped that the present manipulation of task incentives would shed new light on this.
Our findings clearly contrast with several previous studies that have titrated single task demand on different combinations of tasks and have found no clear evidence of a differential storage+processing dual task cost with age (M. Anderson et al., 2011; Logie et al., 2004; Baddeley et al., 1986, 2001; Belleville et al., 1998). The present work recruited a much larger sample than these previous studies from a much wider range of ages. Therefore, it may very well be the case that we had greater power to detect an aging effect. Further, unlike previous studies, we assessed dual task performance over a range of priority allocation conditions. This revealed a general concurrence cost for the memory task with age but no differences across age in response to the priority manipulation. With this in mind, it may be that in previous studies older adults have been able to prioritize task performance for memory to the extent that a cost does not appear strongly on combined measures that aggregate over both tasks (see, e.g., M. Anderson et al., 2011; Logie et al., 2004) or only appears on the secondary task (N. D. Anderson et al., 1998; Bier et al., 2017; Logie et al., 2007).
Indeed, when age-related dual task costs have been found on concurrent processing tasks they typically have been for tasks without a response deadline. For example, Logie et al., 2007 used a simple reaction time task and found that older adults were slower to respond when retrieving a digit load and N. D. Anderson et al. (1998) found similar age-related slowing in a task requiring retrieval after a longer delay. More recently Bier et al. (2017) combined a digit span task with visuospatial tracking (tasks that have previously revealed no significant age differences; Logie et al., 2004; Baddeley et al., 1986) and found that, while the demand of both tasks had been titrated, older adults showed a much greater degree of slowing in the tracking task with a concurrent memory load. In addition they found that the drop in digit span performance from single to dual task was comparable across the two age groups. Of relevance to the present work, Bier et al. (2017, Experiment 1) also manipulated the relative degree of emphasis placed on the digit recall and tracking tasks and found no consistent effects of emphasis in either age group. We suspect that these different findings may have something to do with the nature of our processing task. In the present study each processing event fell within a predetermined interval and the task advanced even if a response was not given (i.e. there was a response deadline). If, in those previous experiments, older adults had been delaying responses to the processing task in order to protect performance on the memory task then this would explain the slowing of responses (and possibly the failure to adhere to priority instructions in Bier et al., 2017). It would also explain the age-related concurrence cost for memory in the present experiment where processing responses could not be slowed. Thus our findings may actually not be out of step with previous reports of age-related dual task effects in the working memory literature.
The lack of age-difference in the prioritization cost is interesting, particularly in light of the large concurrence cost for memory. It contrasts with the prediction from the embedded processes account which suggested that prioritization cost might get smaller with increasing age (though that prediction is not central to the embedded processes approach and the rationale was formulated on demand for the present study). However, the finding is in line with one of the predictions from multiple components and from time based resource sharing. From both latter perspectives, the result can be interpreted by suggesting that titration effectively corrected for age-differences in processing speed and produced an equivalent cognitive load for participants of different ages. Therefore, according to these accounts, while older adults may be slower or less efficient than younger adults at using the gaps between processing items to perform memory maintenance (cf. Fanuel et al., 2018; Loaiza & McCabe, 2013) they are just as efficient in shifting priority between storage and processing in accordance with task incentives once demands have been more or less corrected for these baseline differences. This seems comparable to recent findings in visual working memory tasks showing equivalent benefits of retro-cueing, which occurs at a relatively slow experimenter-set pace, for younger and older adults (Loaiza & Souza, 2017; Souza, 2016). Our findings are also similar to those of Salthouse et al. (1984) who, in three experiments, found an age-related concurrence cost when two titrated short-term recall tasks, one using letters and the other digits, were combined but an equivalent equivalent performance trade-off in response to task incentives.
In summary, the present study suggests an age-related difficulty in maintaining verbal information in mind while performing a concurrent processing task. This finding may be related to other previous reports of age-effects which have been seen in slowing of processing responses in tasks without a strict response deadline (Bier et al., 2017; Logie et al., 2007), although this awaits direct testing. Our findings are also consistent with a preserved ability of older adults to shift priority between conflicting tasks that are titrated to individual ability (Somberg & Salthouse, 1982; Salthouse et al., 1984). While these findings are not without precedent (cf. Salthouse et al., 1984) they were not anticipated by any of the sets of predictions we gathered (see Table 1). So in the next section we consider some possible sources of the age-related concurrence cost seen in the memory task.
Possible causes of the age-related concurrence cost.
One way to narrow down the possible origins of the memory concurrence cost and its increase with age is to consider how our findings may have differed given minor variations in our paradigm. Several studies have found that providing a delay following the presentation of a memory item and prior to the onset of a distracting processing task reduces the effect of processing on storage (e.g. Bayliss, Bogdanovs, & Jarrold, 2015; De Schrijver & Barrouillet, 2017; Klapp, Marshburn, & Lester, 1983). In the case of Klapp et al. (1983), a delay of 5 seconds or more following the presentation of to-be-remembered letters in a Brown-Peterson task eliminated the effect of a processing task on recall. Using the alternative approach described in the introduction Vergauwe et al. (2014) estimated that each additional memory item slowed first item processing responses by approximately 250 ms per item (see also Camos et al., in press; Jarrold, Tam, Baddeley, & Harvey, 2011).
It may be that the formation and implementation of a rehearsal program takes time and is initially disrupted by a concurrent task (Naveh-Benjamin & Jonides, 1984); therefore, the extra time may facilitate performance through more effective rehearsal. However, there is also evidence for benefits of additional free time following memory items under articulatory suppression (Bayliss et al., 2015; De Schrijver & Barrouillet, 2017) and the strongest effects of memory load on processing times in Vergauwe et al. (2014) were found under suppression. This suggests the existence of an additional consolidation of memory representations that occurs after their presentation. One interpretation is this may be closely linked to the concept of removal of items from the focus of attention to the activated portion of long-term memory in embedded processes type accounts (e.g. Oberauer, 2005; Rhodes & Cowan, 2018). Within the time-based resource sharing account, the additional time may be used for refreshing the contents of memory. Within the multiple components account, this additional time could be used to transfer verbal information from the phonological loop into long-term episodic memory.
In short, it is possible that our delay of 1 s between the final list item and the start of the processing task may not have been sufficient even for our younger adults. If older adults take longer to form a stable representation, then we may expect their recall to be more affected by the presence of the processing task in all conditions that it is present, as was observed here. Further, we would also expect them to delay processing operations when the task allows, as has been observed in previous experiments (e.g. Bier et al., 2017; Fanuel et al., 2018; Logie et al., 2007).
There is some work that bears on this issue. Oberauer (2005) used two tasks in which two lists had to be retained and at different points in the trial one of the lists would be cued as relevant for a particular response (hence the other list was temporarily irrelevant but could become relevant later in the trial). In one task, requiring memory for words, the required response was to a recognition probe that had either been present in the relevant list or not, whereas the other task, requiring memory for digits, required that an item from the relevant list be recalled and an arithmetic operation performed on it. The cue of which list would be relevant appeared at various intervals before the onset of the to-be-performed task. The underlying logic was that if the length of the irrelevant list affected reaction times to the task it could be said that the irrelevant list was taking up space in the focus of attention. While the full results of these experiments were very complex, Oberauer (2005) found that irrelevant list effects were largely eliminated after approximately 3 seconds and that there were no clear differences between younger and older adults (see also Oberauer, 2001). More recently, Fanuel et al. (2018) assessed the influence of memory load on older adults’ response times to a parity task (using the method of Vergauwe et al., 2014). While the authors had a limited number of observations for older adults and could only focus on small memory loads, as they focused only on trials where recall was perfect, they found that the introduction of a memory load slowed their responses to the first processing item to a greater degree than it did for the younger group. This would seem to suggest that more time to consolidate memory representations prior to switching to the processing task may be beneficial for older adults. Nevertheless, given the relatively scant, and somewhat contradictory, data bearing on this issue, it would be interesting to assess whether providing more time prior to the onset of processing in the present task set up 1) reduces the memory concurrence cost and 2) reduces age-differences in this concurrence cost.
There are other possible mechanisms underlying this age-related effect that may not necessarily predict a beneficial effect of increasing the amount of time given prior to the processing task. For example, even if older adults are as quick to consolidate items into working memory their representations may still be more susceptible to interference from distraction (Hedden & Park, 2001; Oberauer & Kliegl, 2001) or proactive interference from previously studied memory lists (May, Hasher, & Kane, 1999; Lustig, May, & Hasher, 2001). It is possible that the age-related concurrence cost could be modulated by varying the featural overlap between the storage and processing tasks (although see Myerson et al., 1999). Alternatively, given well established age-differences in the effect of proactive interference on working memory span (May et al., 1999; Lustig et al., 2001), it is possible that the age-difference in the concurrence cost could be eliminated in conditions that allow release from proactive interference (Emery, Hale, & Myerson, 2008). We discuss a potential interpretation of our data from an interference standpoint in more detail below.
Implications for Theories of Working Memory
Distinguishing shared-resource and multiple-resource accounts of working memory (and cognition more generally) is notoriously difficult (Navon & Gopher, 1979). Typically studies manipulate the difficulty of one task while assessing performance levels on another. However, with regards to the overlap of storage and processing in working memory, these manipulations have provided data claimed in support of both attention based (e.g. Barrouillet et al., 2004; Vergauwe et al., 2014; Chen & Cowan, 2009) and multiple-component (e.g. Doherty & Logie, 2016; Duff & Logie, 1999, 2001) theories. In the present study we attempted to gain a different vantage point on these questions. The alternative viewpoint offered by manipulation of task priorities, which has been very informative in previous studies (e.g. Craik et al., 1996; Navon & Gopher, 1979; C. C. Morey et al., 2011; Sperling & Melchner, 1978) and its combination with titration of task demand allowed us to derive differential predictions from three accounts of working memory (see Table 1).
Implications for storage and processing as drawing upon different components.
The present experimental conditions were contrived to maximize our chance of observing parallel functioning of storage and processing, and to minimize age-differences in dual task performance. It has previously been suggested that conflict between storage and processing may be observed when individual task demands are pushed beyond the capacity of participants (Logie, 2011) and previous experiments manipulating demands above a titrated level have supported this (Doherty & Logie, 2016). This led to the prediction that there would be no prioritization trade-off between memory and processing performance. This account does, however, allow for other sources of dual task interference which would apply regardless of the emphasis placed on a given task. For example, for visually presented letters observers may use visual codes that may be interfered with by the visually presented processing task (Logie et al., 2000, 2016; Saito et al., 2008). Thus this version of the multiple component account predicted a small concurrence cost for the VT condition. The present manipulation of task priorities, however, revealed a clear prioritization trade-off even though task demand was adjusted to where participants were fairly proficient with each task individually. In addition, memory task performance took a particular hit when combined with a processing demand. This was the case for both visually and auditorally presented letters. Importantly, as the additional analyses presented above show, there was no indication that those participants who were perhaps ‘overloaded’ (i.e. their single task performance was below the desired titration level) exhibited a larger cost to dual task performance. In fact the opposite appeared to be the case, with participants who performed lower at single task exhibiting less of a dual task drop in accuracy.
One potential argument could be that our tasks were not sufficiently pure to separately identify storage and processing functions. For example, it is possible that the processing task affected memory performance as it acted as an articulatory suppressor, which prevented active rehearsal of the material. In a separate series of experiments with younger adults (Doherty et al., under review), we assessed this by titrating task difficulty under articulatory suppression. The rationale is that, in this case, span reflects the ability of the individual to perform the tasks without the aid of articulation. If a subvocal requirement of the processing task is causing the concurrence cost we observed, it should be greatly attenuated under these circumstances. However, dual task costs were even larger in this case when the single and dual tasks were performed under suppression. Thus this appears to reflect a central limit for this pairing of tasks, regardless of the availability of articulatory rehearsal.
These findings, as well as other findings of dual task costs in younger adults even under titrated demands with different tasks to ours (M. Anderson et al., 2011; Bier et al., 2017) or low memory loads (Chen & Cowan, 2009; Vergauwe et al., 2014), are difficult to reconcile with the notion that trade-off between storage and processing is only observed when individual components are overloaded (Logie, 2011). So in what way can we accommodate these findings within the multiple component model? The pattern of results, in particular the asymmetrical concurrence cost for memory that did not appear significantly for processing, may be accounted for by assuming that span in the memory task reflects the combination of a limited capacity memory store and additional strategies that require a component also co-opted for processing (see also Doherty & Logie, 2016). When a concurrent processing demand is introduced memory performance drops as the co-opted component is no longer available. This would lead to the concurrence cost that we observed here for the memory task. Further, assuming that the amount to which observers engage in additional strategies that serve to supplement maintenance can be discounted in favor of performing the processing task could also account for the observed prioritization trade-off between the tasks. With this interpretation, however, it becomes a legitimate question to ask to what extent this account of storage and processing is functionally distinct from a resource sharing account. This could then lead to interesting questions as to what kind of resource is being shared.
A major challenge for the multiple component model, therefore, is a precise specification of what ‘span’ actually comprises, as previous interpretation of experimental data has relied on the assumption that titrated span reflects the capacity limit of individual components (Baddeley et al., 1986; Cocchini et al., 2002; Doherty & Logie, 2016; Logie et al., 2004). One way of dealing with this difficult issue for the multiple component account may be to conduct detailed analyses of error patterns that may be indicative of the use of several components in span (e.g. visual errors in verbal recall tasks Logie et al., 2000; Saito et al., 2008). In addition detailed reports of strategy use may also provide an important source of information, as what ‘span’ reflects can be influenced by the approach taken by the participant (e.g. Bailey, Dunlosky, & Hertzog, 2009; Logie, Della Sala, Laiacona, Chalmers, & Wynn, 1996). Whether or not this additional information can clearly distinguish multiple components from attention based accounts remains to be tested.
Implications for storage and processing as competing for attention.
The fairly substantial prioritization trade-off between the memory and processing tasks (see effect sizes above) in dual task conditions with differing allocation of priority to each task is consistent with theories that propose some sharing of limited capacity attention (e.g., J. R. Anderson et al., 1996; Cowan, 1988; Baddeley, 2000; Barrouillet et al., 2004; Kane et al., 2004; Oberauer et al., 2012). Both the embedded processes and time-based resource sharing accounts assume that a limited capacity focus of attention serves to refresh memory representations, which decay during the portions of time occupied by the processing task. The former allows for several items to be refreshed at once, whereas the latter assumes serial refreshing of an item at a time. While we are not able to distinguish multi-item from single-item refreshing (indeed this has also proven difficult in computational simulations; Portrat & Lemaire, 2015) the present findings support the natural prediction from these accounts (see Table 1) that participants can focus on maintenance at the expense of processing and vice versa. Importantly, this prioritization effect was observed even though the demand of individual tasks was adjusted to account for individual differences in single task performance.
Further, there was evidence that this prioritization effect was attenuated for auditory memoranda, which is clearly in line with the embedded processes prediction that a particularly strong trace for auditory features in activated long-term memory would bolster performance in this condition and reduce reliance on central capacity (Cowan, 1984, 1988, see Table 1). While the TBRS account did not make any predictions with regard to modality differences it does allow for the maintenance of verbal memoranda through the use of rehearsal in addition to refreshing (Camos et al., 2009). The finding of a slightly larger prioritization trade-off for visual lists can be accommodated by the assumption that they were less efficiently rehearsed, relative to auditory lists, as they had to go through an additional recoding process from a visual to an auditory or phonological code (Baddeley, Thomson, & Buchanan, 1975). Less efficient maintenance through rehearsal would mean a greater reliance on refreshing and, hence, greater trade-off with the processing task.
The memory concurrence cost is also in line with the prediction from the time-based resource sharing account that the sudden increase in cognitive load from single to dual task would have a large effect on recall. However, it is it not easy to explain why the concurrence cost simultaneously increased with age. Recall that it is the assumption that titration resulted in a common cognitive load across participants of different ages that led to the prediction from time-based resource sharing that the prioritization cost would not increase with age. The TBRS model could account for this effect of age by assuming that, as discussed above, older adults have a deficit in initiating refreshing activities (Fanuel et al., 2018) or have a general deficit in switching between cognitive demands regardless of priority (Salthouse et al., 1984; Verhaeghen, 2011; Mayr & Kliegl, 1993).
The embedded processes account expected that having to coordinate the two demands would come at a cost that would be disproportionate for older adults. However, what was not predicted was the asymmetrical nature of this concurrence cost, which appeared strongly for the memory task and was not at all clear for the processing task. As we discussed above this may be attributable to the processing task chosen, a possibility that could be explored in future studies. Some studies using a processing task without a strict response deadline have found that older adults are slower under dual task situations (e.g Bier et al., 2017). Further, simple arithmetic problems such as these are typically solved by participants by direct retrieval of the solution from long-term memory (Geary & Wiley, 1991). To the extent that this retrieval captures attention and is automatic (see Craik et al., 1996; Schneider & Shiffrin, 1977) a switching cost may not be seen for a processing task such as ours. Rather participants, and specifically older participants, may have been slowed in switching back to maintenance activities. This is similar to the interpretation offered by Jarrold et al. (2011) who suggested that participants may become ‘entrained’ by the processing block in the Brown-Peterson task and neglect maintenance. Of course this post hoc interpretation will require systematic testing with other processing tasks that do not engender such automatic retrieval from long-term memory.
Finally, the embedded processes account predicted, perhaps counterintuitively, that the prioritization cost would be attenuated with increasing age. This was based on the assumption that a greater proportion of older participant’s span would reflect peripheral storage relative to central storage due to a presumed reduction in capacity of the focus of attention. The present results suggest a rethink of that proposal which is based on largely indirect evidence of a smaller focus of attention in older adults (e.g. Naveh-Benjamin et al., 2014). Cowan et al. (2014) have proposed a method of measuring the contributions of central and peripheral storage to working memory performance and have applied this to childhood development (Cowan, Li, Glass, & Scott Saults, 2017). Application of this approach in the context of aging would be useful in light of the present findings which point to the conclusion that the proportion of storage span that competes with the processing task is equivalent across age.
An alternative account based on interference.
It is important to consider what an interference account of the present data might look like as these accounts are often able to account for the same phenomena as the three accounts under consideration despite having quite different principles at their foundation (see, e.g., Oberauer et al., 2012; Nairne, 1990). There are several possible sources of interference, some of which may play a role in the current context. A major source in the computational model of complex span proposed by Oberauer et al. (2012) is superposition, where the representation of serial order is distorted by the interleaved processing items. In a pure interference model, where no decay occurs, this necessitates a process of removal which is assumed to take place during periods of free time between processing items. In the present Brown-Peterson type task memory items were presented prior to the onset of the processing task, distinguishing the order of the memory items from the processing items and, therefore, minimizing the effects of superposition (see Jarrold et al., 2011). Another possible source of interference is that of response competition (see Oberauer, 2009b) where processing distractors enter the set of recall candidates. We can rule this out in the current context as the processing items (numbers) were distinct from the memory items (letters), and could easily be excluded from the set of recall candidates, but more importantly our task did not allow the entering of digits during the recall phase. This leaves similarity between the memory and processing items as perhaps the major source of interference in the task used here. Similarity is hard to operationalize as items can differ in a range of ways and it also depends on the way in which items are coded by the observer. For example, if participants used visual features to code items in the VT condition (Logie et al., 2000, 2016; Saito et al., 2008), in addition to phonological features, an interference account would presumably predict interference with the visually presented processing task, as basic visual features are shared between letters and numbers. However, given that no difference in the memory concurrence cost was found between the VT and AO conditions it may be argued that the mode of presentation did not really affect the mode of representation.
This leaves the interference account of the prioritization trade-off. There are two main ways that the interfering effects of processing items on the representations of memory items can be modified by the participant. Assuming that processing items must be encoded into working memory in order to complete the necessary operations one could filter the processing items so that they are encoded less strongly. Weaker encoding of the processing items would benefit memory performance and degrade processing performance. A second possible mechanism for explaining the trade-off with prioritization is that of removal. As there is typically no form of decay in these interference accounts, once processing items have been encoded they must then be removed or inhibited so that they can no longer distort the representations of the memory items. If more time is spent removing the representations of processing items then memory performance would benefit from the reduced interference but, assuming removal and processing cannot co-occur, this would slow responses to subsequent processing items. Given the argument that age-differences arise primarily as older adults are less efficient at inhibiting previously relevant but now irrelevant information (e.g. Hasher & Zacks, 1988) this may lead to the prediction of a smaller prioritization trade-off with age, which was not observed. However, the titration of the two tasks may have offset differences in rates of removal across age, in the same way that titration may have eliminated differences in refreshing speed according to the TBRS interpretation.
Both of these mechanisms, modulation of distractor encoding and varying the pace of removal, could produce the observed prioritization cost. What is more difficult to explain, however, is the difference in the extent of this prioritization cost between the AO and VT conditions. Assuming that auditory representations were less susceptible to interference and therefore less in need of filtering or removal would complicate the interpretation above of the equivalent concurrence cost between the two conditions.
Summary.
The three accounts of working memory that we have most closely considered here operate at a broad level. One may ask if it is possible, or worthwhile, to compare predictions from the accounts that we have considered. Why not focus on refining each of the models in pursuit of versions that can make actual quantitative predictions? We absolutely see the merit in this approach. However, we think that in certain situations comparing specific proposals of these models is useful too. The literature has reached something of a stalemate on the issue of storage and processing in working memory. Shared resource theorists can point to the many instances of conflict between the two demands (Barrouillet et al., 2007; Chen & Cowan, 2009; Vergauwe et al., 2010), whereas multiple component theorists can instead point to boundary conditions which appear to support their position (Cocchini et al., 2002; Doherty & Logie, 2016; Logie et al., 2004). Failing to contrast these proposals directly, we believe, stunts theoretical development in the field and contributes to a literature that is often contradictory.
Here we identified a clear difference between the predictions of working memory accounts that posit that maintenance is achieved in part by a general attention that conflicts with processing (e.g. Barrouillet et al., 2007; Cowan, 2010) and a version of the multiple component account in which storage and processing only compete when individual components are overwhelmed (Logie, 2011). Our experiment was a particularly strict test of these proposals. Our method of varying priority weighting to one task over another allowed us to look for evidence of trade-off between the two tasks in addition to other sources of interference that may be less indicative of competition for attention. We also recruited a larger sample from a range of ages than previous studies on this question.
Comparing the predictions to the results it is clear that none of the accounts got everything correct (see Table 1), which would have been surprising. These findings place important constraints on each of these theories and we have described how each could be modified in response to these data. To account for these findings, and other findings of dual task conflict even under titrated conditions (M. Anderson et al., 2011; Bier et al., 2017), the assumption of the multiple component model must be that many components contribute to span measures and that tasks conflict to the extent to which they overlap in the components that drive span. This is a sensible suggestions but, without an explanation of what components contribute in what situations, it makes the multiple component model functionally equivalent to a resource sharing model. We see this as part of a growing, and perhaps reassuring, trend for these accounts of working memory to become more similar (see Baddeley, 2012; Logie & Cowan, 2015; Cowan et al., 2014, for discussion of this). The approach applied here, of pitting the frameworks against each other on a specific area of disagreement and then attempting to resolve these differences through integrating theories, might be more fruitful for genuine theoretical progress in understanding working memory rather than the more common approach of demonstrating that one existing theory is superior to any other existing theory. What have been interpreted as ‘small’ dual task effects within the multiple component framework suggested that theories with a general attention contribution to storage should predict more of a performance cost. However, when proponents of each theory are asked to make their predictions on a common scale, the data line up well with the idea of some competition for a limited capacity attention.
We have described the ways in which the theories could be modified in light of findings that did not match the predictions going in and how this serves to bring them closer together. Most importantly, whereas the multicomponent approach made some predictions of no prioritization trade-off for tasks that have been individually titrated, such costs were obtained. All three theoretical camps agree that some sort of resource is needed to account for the trade-offs. The embedded-processes approach (Cowan, 1988, 2010) considers the resource to be a capacity-limited focus of attention shared between tasks, whereas the TBRS approach (Barrouillet & Camos, 2015; Barrouillet et al., 2007) considers the resource to be a matter of a time limit in switching between tasks to use attention to refresh the materials before they decay. The multicomponent approach attempts to avoid the concept of attention, given fears of the concept being no clearer than an unexplained homunculus (Baddeley & Logie, 1999; Logie, 2016). It might, however, account for the trade-off by relying on some specific kind of processing as a resource shared between tasks. One such resource would be phonological processing including, but not limited to verbal rehearsal, a kind of process discussed on all three approaches (Baddeley et al., 1975; Cowan, 1992; Camos et al., 2009), but our other ongoing research (Doherty et al., under review) shows tradeoffs even in the presence of articulatory suppression. Another, seemingly more suitable candidate may be the contribution of long-term memory, including retrieval of math information and perhaps new long-term episodic learning of the materials to be recalled (cf. Unsworth & Engle, 2007). These uses of long-term memory may account for the residual performance in the two tasks but, also, a version of the multicomponent model could include a proposal that semantic retrieval is needed to support both storage (through known letter representations) and processing (through known arithmetic facts) and has a bottleneck limiting the retrieval needed to support the two tasks at once. Whether this bottleneck must be characterized as a general attention factor or not is still a matter of debate among us. All of the approaches strive for parsimony but differ in whether parsimony consists of limiting the number of modules as in the embedded-process and TBRS approaches, avoiding the concept of general attention as in the multicomponent approach, or both as in the interference approach (for which other complexities must be substituted, such as generalized interference).
To progress further towards reconciliation of these accounts, the field will need better, independent indices of which components of a multicomponent system, or aspect of attention, are coming into play for a given procedure. The data also require changes in all of the accounts regarding the nature of the aging process, softening the expectation of the multicomponent account that there would be no increase in the concurrence cost in normal aging and restraining the embedded-process account in which an age change in the prioritization cost reasonably could be expected. Considerable progress is made in constraining all of the models to become more alike, though additional work must now be focused on exploring the basic concepts on which the models differ, namely modularity and attention.
Conclusion
The present work addressed two primary questions: 1) Does a concurrent arithmetic processing task trade-off with storage of letters in working memory in response to task incentives, even if those tasks have been titrated to individual ability? 2) Are there differences in storage+processing dual task performance across the adult lifespan under titrated conditions?
Taking the questions in reverse, there was a specific cost to the storage of letters when combined with the concurrent processing task and this increased linearly with age. Despite this age-related concurrence cost, there were no age differences in response to the manipulation of task priority. This precise combination of results was not predicted ahead of time but is consistent with an age related deficit in switching between the encoding of memory items and the processing task or general susceptibility to interference from the processing task and/or previous trials. These findings contrast with previous smaller studies that have not found a significant difference between older and younger participants but are consistent with other reports of age-related slowing on processing tasks without a strict response deadline.
In response to the first question we observed a considerable prioritization trade-off as participants were instructed to prioritize one task over the other. This was in addition to the concurrence cost observed in memory performance. The prioritization trade-off, which didn’t differ by age, was less pronounced for auditorally presented letters, suggesting additional domain specific support for this material. These findings place important constraints on working memory theory. In particular these findings would appear inconsistent with suggestions from multiple component theorists that storage and processing rely only on independent components when task demand is set within the bounds of their capacity. The prioritization cost is more easily accommodated by theories with some general resource split between storage and processing demands, although these theories need to make some additional assumptions about the effects of aging to account for the full set of findings.
Supplementary Material
Acknowledgments
This work was funded by the Economic and Social Research Council (ESRC) grant ‘Working memory across the adult lifespan: an adversarial collaboration (WoMAAC)’ ES/N010728/1.
Footnotes
This paper was written using the R package knitr (Xie, 2016) and also made use of plyr (Wickham, 2011).
This analysis plan was specified before we began data collection. More detail is available here: https://osf.io/b2epe/.
Note that in this case the z value is a test statistic (coefficient divided by its standard error) and not a transformation of the data as was done for the age variable
Similar conclusions are reached if this analysis is done comparing single task to the average of all dual task conditions (−.67, 95% CI = [−.76, −.55])
Part of this work was presented at the 2017 meeting of the Psychonomic society in Vancouver, BC, and at the 2018 Cognitive Aging Conference in Atlanta, GA.
References
- Agresti A (2002). Categorical data analysis (2nd ed.). Hoboken, NJ: John Wiley & Sons. [Google Scholar]
- Anderson JR, Reder LM, & Lebiere C (1996). Working memory: Activation limitations on retrieval. Cognitive psychology, 30 (3), 221–256. [DOI] [PubMed] [Google Scholar]
- Anderson M, Bucks RS, Bayliss DM, & Della Sala S (2011). Effect of age on dual-task performance in children and adults. Memory & cognition, 39 (7), 1241–1252. [DOI] [PubMed] [Google Scholar]
- Anderson ND, Craik FIM, & Naveh-Benjamin M (1998). The attentional demands of encoding and retrieval in younger and older adults: I. evidence from divided attention costs. Psychology and Aging, 13 (3), 405–423. [DOI] [PubMed] [Google Scholar]
- Baddeley A (1986). Working memory. New York: Oxford University Press. [Google Scholar]
- Baddeley A (2000). The episodic buffer: a new component of working memory? Trends in Cognitive Sciences, 4 (11), 417–423. [DOI] [PubMed] [Google Scholar]
- Baddeley A (2012). Working memory: theories, models, and controversies. Annual Review of Psychology, 63 , 1–29. [DOI] [PubMed] [Google Scholar]
- Baddeley A, Allen RJ, & Hitch GJ (2011). Binding in visual working memory: The role of the episodic buffer. Neuropsychologia, 49 (6), 1393–1400. [DOI] [PubMed] [Google Scholar]
- Baddeley A, Baddeley H, Bucks R, & Wilcock G (2001). Attentional control in alzheimer’s disease. Brain, 124 (8), 1492–1508. [DOI] [PubMed] [Google Scholar]
- Baddeley A, & Hitch G (1974). Working memory In Bower G (Ed.), Recent advances in learning and motivation (Vol. 8, p. 47–90). Academic Press. [Google Scholar]
- Baddeley A, Logie R, Bressi S, Della Sala S, & Spinnler H (1986). Dementia and working memory. The Quarterly Journal of Experimental Psychology, 38 (4), 603–618. [DOI] [PubMed] [Google Scholar]
- Baddeley A, & Logie RH (1999). Working memory: The multiple-component model In Miyake A & Shah P (Eds.), Models of working memory: Mechanisms of active maintenance and executive control (pp. 28–61). New York, NY: Cambridge University Press. [Google Scholar]
- Baddeley A, Thomson N, & Buchanan M (1975). Word length and the structure of short-term memory. Journal of verbal learning and verbal behavior, 14 (6), 575–589. [Google Scholar]
- Bailey H, Dunlosky J, & Hertzog C (2009). Does differential strategy use account for age-related deficits in working-memory performance? Psychology and aging, 24 (1), 82–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balota DA, & Duchek JM (1986). Voice-specific information and the 20-second delayed-suffix effect. Journal of Experimental Psychology: Learning, Memory, and Cognition, 12 (4), 509. [DOI] [PubMed] [Google Scholar]
- Barnard P (1999). Interacting cognitive subsystems In Miyake A & Shah P (Eds.), Models of working memory: Mechanisms of active maintenance and executive control (pp. 298–339). New York, NY: Cambridge University Press. [Google Scholar]
- Barrouillet P, Bernardin S, & Camos V (2004). Time constraints and resource sharing in adults’ working memory spans. Journal of Experimental Psychology: General, 133 (1), 83–100. [DOI] [PubMed] [Google Scholar]
- Barrouillet P, Bernardin S, Portrat S, Vergauwe E, & Camos V (2007). Time and cognitive load in working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 33 (3), 570–585. [DOI] [PubMed] [Google Scholar]
- Barrouillet P, & Camos V (2015). Working memory: Loss and reconstruction. Psychology Press. [Google Scholar]
- Barrouillet P, Gavens N, Vergauwe E, Gaillard V, & Camos V (2009). Working memory span development: a time-based resource-sharing model account. Developmental psychology, 45 (2), 477–490. [DOI] [PubMed] [Google Scholar]
- Bates D, Maechler M, Bolker B, & Walker S (2014). lme4: Linear mixed-effects models using Eigen and S4 [Computer software manual]. Retrieved from http://CRAN.R-project.org/package=lme4(R package version 1.1-7)
- Bayliss DM, Bogdanovs J, & Jarrold C (2015). Consolidating working memory: Distinguishing the effects of consolidation, rehearsal and attentional refreshing in a working memory span task. Journal of Memory and Language, 81 , 34–50. [Google Scholar]
- Belleville S, Rouleau N, & Caza N (1998). Effect of normal aging on the manipulation of information in working memory. Memory & Cognition, 26 (3), 572–583. [DOI] [PubMed] [Google Scholar]
- Bier B, Lecavalier NC, Malenfant D, Peretz I, & Belleville S (2017). Effect of age on attentional control in dual-tasking. Experimental Aging Research, 43 (2), 161–177. [DOI] [PubMed] [Google Scholar]
- Bopp KL, & Verhaeghen P (2005). Aging and verbal memory span: A meta-analysis. The Journals of Gerontology Series B: Psychological Sciences and Social Sciences, 60 (5), P223–P233. [DOI] [PubMed] [Google Scholar]
- Broadbent D, & Heron A (1962). Effects of a subsidiary task on performance involving immediate memory by younger and older men. British Journal of Psychology, 53 (2), 189–198. [DOI] [PubMed] [Google Scholar]
- Camos V, Lagner P, & Barrouillet P (2009). Two maintenance mechanisms of verbal information in working memory. Journal of Memory and Language, 61 (3), 457–469. [Google Scholar]
- Camos V, Mora G, Oftinger A-L, Mariz Elsig S, Schneider P, & Vergauwe E (in press). Does long-term memory affect refreshing in verbal working memory? Journal of Experimental Psychology: Learning, Memory, and Cognition. [DOI] [PubMed] [Google Scholar]
- Cerella J (1985). Information processing rates in the elderly. Psychological Bulletin, 98 (1), 67–83. [PubMed] [Google Scholar]
- Chen Z, & Cowan N (2009). How verbal memory loads consume attention. Memory & cognition, 37 (6), 829–836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cocchini G, Logie RH, Della Sala S, MacPherson SE, & Baddeley A (2002). Concurrent performance of two memory tasks: Evidence for domain-specific working memory systems. Memory & Cognition, 30 (7), 1086–1095. [DOI] [PubMed] [Google Scholar]
- Cowan N (1984). On short and long auditory stores. Psychological Bulletin, 96 (2), 341–370. [PubMed] [Google Scholar]
- Cowan N (1988). Evolving conceptions of memory storage, selective attention, and their mutual constraints within the human information-processing system. Psychological Bulletin, 104 (2), 163–191. [DOI] [PubMed] [Google Scholar]
- Cowan N (1992). Verbal memory span and the timing of spoken recall. Journal of Memory and Language, 31 (5), 668–684. [Google Scholar]
- Cowan N (2010). The magical mystery four: How is working memory capacity limited, and why? Current Directions in Psychological Science, 19 (1), 51–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N (2017). The many faces of working memory and short-term storage. Psychonomic Bulletin & Review, 24 (4), 1158–1170. [DOI] [PubMed] [Google Scholar]
- Cowan N, Li Y, Glass BA, & Scott Saults J (2017). Development of the ability to combine visual and acoustic information in working memory. Developmental science. doi: 10.1111/desc.12635 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Saults JS, & Blume CL (2014). Central and peripheral components of working memory storage. Journal of Experimental Psychology: General, 143 (5), 1806–1836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craik FIM (1977). Age differences in human memory In Birren JE & Schaie KW (Eds.), Handbook of the psychology of aging (pp. 384–420). New York, NY: Van Nostrand Reinhold. [Google Scholar]
- Craik FIM, Govoni R, Naveh-Benjamin M, & Anderson ND (1996). The effects of divided attention on encoding and retrieval processes in human memory. Journal of Experimental Psychology: General, 125 (2), 159–180. [DOI] [PubMed] [Google Scholar]
- De Schrijver S, & Barrouillet P (2017). Consolidation and restoration of memory traces in working memory. Psychonomic bulletin & review, 24 (5), 1651–1657. [DOI] [PubMed] [Google Scholar]
- Dixon P (2008). Models of accuracy in repeated-measures designs. Journal of Memory and Language, 59 (4), 447–456. [Google Scholar]
- Dobbs AR, & Rule BG (1989). Adult age differences in working memory. Psychology and Aging, 4 (4), 500–503. [DOI] [PubMed] [Google Scholar]
- Doherty JM, Belletier C, Rhodes S, Jaroslawska AJ, Camos V, Barrouillet P, … Logie RH (under review). Dual-task costs in working memory: An adversarial collaboration. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doherty JM, & Logie RH (2016). Resource-sharing in multiple-component working memory. Memory & Cognition, 44 (8), 1157–1167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duff SC, & Logie RH (1999). Storage and processing in visuo-spatial working memory. Scandinavian Journal of Psychology, 40 (4), 251–259. [DOI] [PubMed] [Google Scholar]
- Duff SC, & Logie RH (2001). Processing and storage in working memory span. The Quarterly Journal of Experimental Psychology: Section A, 54 (1), 31–48. [DOI] [PubMed] [Google Scholar]
- Emery L, Hale S, & Myerson J (2008). Age differences in proactive interference, working memory, and abstract reasoning. Psychology and Aging, 23 (3), 634–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fanuel L, Plancher G, Monsaingeon N, Tillmann B, & Portrat S (2018). Temporal dynamics of maintenance in young and old adults. Annals of the New York Academy of Sciences. [DOI] [PubMed] [Google Scholar]
- Foos PW (1989). Adult age differences in working memory. Psychology and Aging, 4 (3), 269–275. [DOI] [PubMed] [Google Scholar]
- Geary DC, & Wiley JG (1991). Cognitive addition: Strategy choice and speed-of-processing differences in young and elderly adults. Psychology and aging, 6 (3), 474–483. [DOI] [PubMed] [Google Scholar]
- Guttentag RE (1989). Age differences in dual-task performance: Procedures, assumptions, and results. Developmental Review, 9 (2), 146–170. [Google Scholar]
- Hale S, Rose NS, Myerson J, Strube MJ, Sommers M, Tye-Murray N, & Spehar B (2011). The structure of working memory abilities across the adult life span. Psychology and Aging, 26 (1), 92–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasher L, & Zacks RT (1988). Working memory, comprehension, and aging: A review and a new view. Psychology of Learning and Motivation, 22 , 193–225. [Google Scholar]
- Hazeltine E, Ruthruff E, & Remington RW (2006). The role of input and output modality pairings in dual-task performance: Evidence for content-dependent central interference. Cognitive Psychology, 52 (4), 291–345. [DOI] [PubMed] [Google Scholar]
- Hedden T, & Park D (2001). Aging and interference in verbal working memory. Psychology and Aging, 16 (4), 666–681. [DOI] [PubMed] [Google Scholar]
- Holtzer R, Stern Y, & Rakitin BC (2004). Age-related differences in executive control of working memory. Memory & Cognition, 32 (8), 1333–1345. [DOI] [PubMed] [Google Scholar]
- Jarrold C, Tam H, Baddeley AD, & Harvey CE (2011). How does processing affect storage in working memory tasks? Evidence for both domain-general and domain-specific effects. Journal of Experimental Psychology: Learning, Memory, and Cognition, 37 (3), 688–705. [DOI] [PubMed] [Google Scholar]
- Jenkins L, Myerson J, Hale S, & Fry AF (1999). Individual and developmental differences in working memory across the life span. Psychonomic Bulletin & Review, 6 (1), 28–40. [DOI] [PubMed] [Google Scholar]
- Johnson W, Logie RH, & Brockmole JR (2010). Working memory tasks differ in factor structure across age cohorts: Implications for dedifferentiation. Intelligence, 38 , 513–528. [Google Scholar]
- Kane MJ, Hambrick DZ, Tuholski SW, Wilhelm O, Payne TW, & Engle RW (2004). The generality of working memory capacity: a latent-variable approach to verbal and visuospatial memory span and reasoning. Journal of Experimental Psychology: General, 133 (2), 189–217. [DOI] [PubMed] [Google Scholar]
- Kilb A, & Naveh-Benjamin M (2014). The effects of divided attention on long-term memory and working memory in younger and older adults: Assessment of the reduced attentional resources hypothesis In Logie RH & Morris RG (Eds.), Working memory and ageing (pp. 48–78). Hove, UK: Psychology Press. [Google Scholar]
- Klapp ST, Marshburn EA, & Lester PT (1983). Short-term memory does not involve the “working memory” of information processing: The demise of a common assumption. Journal of Experimental Psychology: General, 112 (2), 240. [Google Scholar]
- Loaiza VM, & McCabe DP (2013). The influence of aging on attentional refreshing and articulatory rehearsal during working memory on later episodic memory performance. Aging, Neuropsychology, and Cognition, 20 (4), 471–493. [DOI] [PubMed] [Google Scholar]
- Loaiza VM, & Souza AS (2017). Is refreshing in working memory impaired in older age? evidence from the retro-cue paradigm. Annals of the New York Academy of Sciences. [DOI] [PubMed] [Google Scholar]
- Logie RH (2011). The functional organization and capacity limits of working memory. Current Directions in Psychological Science, 20 (4), 240–245. [Google Scholar]
- Logie RH (2016). Retiring the central executive. The Quarterly Journal of Experimental Psychology, 69 (10), 2093–2109. [DOI] [PubMed] [Google Scholar]
- Logie RH, Cocchini G, Della Sala S, & Baddeley A (2004). Is there a specific executive capacity for dual task coordination? evidence from Alzheimer’s disease. Neuropsychology, 18 (3), 504–513. [DOI] [PubMed] [Google Scholar]
- Logie RH, & Cowan N (2015). Perspectives on working memory: introduction to the special issue. Memory & Cognition, 43 (3), 315–324. [DOI] [PubMed] [Google Scholar]
- Logie RH, Della Sala S, Laiacona M, Chalmers P, & Wynn V (1996). Group aggregates and individual reliability: The case of verbal short-term memory. Memory & Cognition, 24 (3), 305–321. [DOI] [PubMed] [Google Scholar]
- Logie RH, Della Sala S, MacPherson SE, & Cooper J (2007). Dual task demands on encoding and retrieval processes: Evidence from healthy adult ageing. Cortex, 43 (1), 159–169. [DOI] [PubMed] [Google Scholar]
- Logie RH, Della Sala S, Wynn V, & Baddeley A (2000). Visual similarity effects in immediate verbal serial recall. The Quarterly Journal of Experimental Psychology: Section A, 53 (3), 626–646. [DOI] [PubMed] [Google Scholar]
- Logie RH, & Duff SC (2007). Separating processing from storage in working memory operation span In Osaka N, Logie RH, & D’Esposito M (Eds.), The cognitive neuroscience of working memory (pp. 119–135). Oxford, UK: Oxford University Press. [Google Scholar]
- Logie RH, Saito S, Morita A, Varma S, & Norris D (2016). Recalling visual serial order for verbal sequences. Memory & Cognition, 44 (4), 590–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lustig C, May CP, & Hasher L (2001). Working memory span and the role of proactive interference. Journal of Experimental Psychology: General, 130 (2), 199. [DOI] [PubMed] [Google Scholar]
- May CP, Hasher L, & Kane MJ (1999). The role of interference in memory span. Memory & cognition, 27 (5), 759–767. [DOI] [PubMed] [Google Scholar]
- Mayr U (2001). Age differences in the selection of mental sets: the role of inhibition, stimulus ambiguity, and response-set overlap. Psychology and aging, 16 (1), 96–109. [DOI] [PubMed] [Google Scholar]
- Mayr U, & Kliegl R (1993). Sequential and coordinative complexity: age-based processing limitations in figural transformations. Journal of Experimental Psychology: Learning, Memory, and Cognition, 19 (6), 1297–1320. [DOI] [PubMed] [Google Scholar]
- Miyake A, Friedman NP, Emerson MJ, Witzki AH, Howerter A, & Wager TD (2000). The unity and diversity of executive functions and their contributions to complex “frontal lobe” tasks: A latent variable analysis. Cognitive Psychology, 41 (1), 49–100. [DOI] [PubMed] [Google Scholar]
- Morey CC, Cowan N, Morey RD, & Rouder JN (2011). Flexible attention allocation to visual and auditory working memory tasks: Manipulating reward induces a trade-off. Attention, Perception, & Psychophysics, 73 (2), 458–472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morey RD, & Rouder JN (2015). BayesFactor: Computation of Bayes Factors for Common Designs [Computer software manual]. Retrieved from http://CRAN.R-project.org/package=BayesFactor(R package version 0.9.11-1)
- Myerson J, Hale S, Rhee SH, & Jenkins L (1999). Selective interference with verbal and spatial working memory in young and older adults. The Journals of Gerontology Series B: Psychological Sciences and Social Sciences, 54 (3), P161–P164. [DOI] [PubMed] [Google Scholar]
- Nairne JS (1990). A feature model of immediate memory. Memory & Cognition, 18 (3), 251–269. [DOI] [PubMed] [Google Scholar]
- Nasreddine ZS, Phillips NA, Bédirian V, Charbonneau S, Whitehead V, Collin I, … Chertkow H (2005). The Montreal Cognitive Assessment, MoCA: a brief screening tool for mild cognitive impairment. Journal of the American Geriatrics Society, 53 (4), 695–699. [DOI] [PubMed] [Google Scholar]
- Naveh-Benjamin M, & Jonides J (1984). Maintenance rehearsal: A two-component analysis. Journal of Experimental Psychology: Learning, Memory, and Cognition, 10 (3), 369–385. [Google Scholar]
- Naveh-Benjamin M, Kilb A, Maddox GB, Thomas J, Fine HC, Chen T, & Cowan N (2014). Older adults do not notice their names: A new twist to a classic attention task. Journal of Experimental Psychology: Learning, Memory, and Cognition, 40 (6), 1540–1550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Navon D (1984). Resources—a theoretical soup stone? Psychological Review, 91 (2), 216–234. [Google Scholar]
- Navon D, & Gopher D (1979). On the economy of the human-processing system. Psychological review, 86 (3), 214–255. [Google Scholar]
- Norman DA, & Bobrow DG (1975). On data-limited and resource-limited processes. Cognitive psychology, 7 (1), 44–64. [Google Scholar]
- Norman DA, & Bobrow DG (1976). On the analysis of performance operating characteristics. Psychological Review, 83 (6), 508–510. [Google Scholar]
- Oberauer K (2001). Removing irrelevant information from working memory: a cognitive aging study with the modified sternberg task. Journal of Experimental Psychology: Learning, Memory, and Cognition, 27 (4), 948–957. [PubMed] [Google Scholar]
- Oberauer K (2005). Control of the contents of working memory–a comparison of two paradigms and two age groups. Journal of Experimental Psychology: Learning, Memory, and Cognition, 31 (4), 714–728. [DOI] [PubMed] [Google Scholar]
- Oberauer K (2009a). Design for a working memory. Psychology of learning and motivation, 51 , 45–100. [Google Scholar]
- Oberauer K (2009b). Interference between storage and processing in working memory: Feature overwriting, not similarity-based competition. Memory & Cognition, 37 (3), 346–357. [DOI] [PubMed] [Google Scholar]
- Oberauer K, & Kliegl R (2001). Beyond resources: Formal models of complexity effects and age differences in working memory. European Journal of Cognitive Psychology, 13 (1–2), 187–215. [Google Scholar]
- Oberauer K, Lewandowsky S, Farrell S, Jarrold C, & Greaves M (2012). Modeling working memory: An interference model of complex span. Psychonomic Bulletin & Review, 19 (5), 779–819. [DOI] [PubMed] [Google Scholar]
- Park DC, Lautenschlager G, Hedden T, Davidson NS, Smith AD, & Smith PK (2002). Models of visuospatial and verbal memory across the adult life span. Psychology and Aging, 17 (2), 299–320. [PubMed] [Google Scholar]
- Parkinson SR, Lindholm JM, & Urell T (1980). Aging, dichotic memory and digit span. Journal of Gerontology, 35 (1), 87–95. [DOI] [PubMed] [Google Scholar]
- Peirce JW (2007). PsychoPy—psychophysics software in Python. Journal of Neuroscience Methods, 162 (1), 8–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peirce JW (2009). Generating stimuli for neuroscience using PsychoPy. Frontiers in Neuroinformatics, 2 , 10. doi: 10.3389/neuro.11.010.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Portrat S, & Lemaire B (2015). Is attentional refreshing in working memory sequential? a computational modeling approach. Cognitive Computation, 7 (3), 333–345. [Google Scholar]
- R Core Team. (2015). R: A Language and Environment for Statistical Computing [Computer software manual]. Vienna, Austria: Retrieved from http://www.R-project.org/ [Google Scholar]
- Raftery AE (1995). Bayesian model selection in social research. Sociological Methodology, 25 , 111–163. [Google Scholar]
- Rhodes S, & Cowan N (2018). Attention in working memory: Attention is needed but it yearns to be free. Annals of the New York Academy of Sciences. doi: 10.1111/nyas.13652 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossetti HC, Lacritz LH, Cullum CM, & Weiner MF (2011). Normative data for the Montreal Cognitive Assessment (MoCA) in a population-based sample. Neurology, 77 (13), 1272–1275. [DOI] [PubMed] [Google Scholar]
- Rouder JN, Morey RD, Speckman PL, & Province JM (2012). Default Bayes factors for ANOVA designs. Journal of Mathematical Psychology, 56 , 356–374. [Google Scholar]
- Saito S, Logie RH, Morita A, & Law A (2008). Visual and phonological similarity effects in verbal immediate serial recall: A test with kanji materials. Journal of Memory and Language, 59 (1), 1–17. [Google Scholar]
- Salthouse TA (1990). Working memory as a processing resource in cognitive aging. Developmental Review, 10 (1), 101–124. [Google Scholar]
- Salthouse TA (1996). The processing-speed theory of adult age differences in cognition. Psychological Review, 103 (3), 403–428. [DOI] [PubMed] [Google Scholar]
- Salthouse TA (2000). Methodological assumptions in cognitive aging research In Craik FIM & Salthouse TA (Eds.), The handbook of cognitive aging (2nd ed., pp. 467–498). Mahwah, NJ: Erlbaum. [Google Scholar]
- Salthouse TA, Rogan JD, & Prill KA (1984). Division of attention: Age differences on a visually presented memory task. Memory & Cognition, 12 (6), 613–620. [DOI] [PubMed] [Google Scholar]
- Schneider W, & Shiffrin RM (1977). Controlled and automatic human information processing: I. detection, search, and attention. Psychological review, 84 (1), 1–66. [Google Scholar]
- Schwarz G (1978). Estimating the dimension of a model. The Annals of Statistics, 6 (2), 461–464. [Google Scholar]
- Somberg BL, & Salthouse TA (1982). Divided attention abilities in young and old adults. Journal of Experimental Psychology: Human Perception and Performance, 8 (5), 651–663. [DOI] [PubMed] [Google Scholar]
- Souza AS (2016). No age deficits in the ability to use attention to improve visual working memory. Psychology and Aging, 31 (5), 456–470. [DOI] [PubMed] [Google Scholar]
- Sperling G, & Melchner MJ (1978). The attention operating characteristic: Examples from visual search. Science, 202 (4365), 315–318. [DOI] [PubMed] [Google Scholar]
- Stephan DN, & Koch I (2010). Central cross-talk in task switching: Evidence from manipulating input–output modality compatibility. Journal of Experimental Psychology: Learning, Memory, and Cognition, 36 (4), 1075–1081. [DOI] [PubMed] [Google Scholar]
- Thalmann M, & Oberauer K (2017). Domain-specific interference between storage and processing in complex span is driven by cognitive and motor operations. The Quarterly Journal of Experimental Psychology, 70 (1), 109–126. [DOI] [PubMed] [Google Scholar]
- Unsworth N, & Engle RW (2007). The nature of individual differences in working memory capacity: active maintenance in primary memory and controlled search from secondary memory. Psychological review, 114 (1), 104–132. [DOI] [PubMed] [Google Scholar]
- Vandierendonck A (2016). A working memory system with distributed executive control. Perspectives on Psychological Science, 11 (1), 74–100. [DOI] [PubMed] [Google Scholar]
- Vergauwe E, Barrouillet P, & Camos V (2010). Do mental processes share a domain-general resource? Psychological Science, 21 (3), 384–390. [DOI] [PubMed] [Google Scholar]
- Vergauwe E, Camos V, & Barrouillet P (2014). The impact of storage on processing: How is information maintained in working memory? Journal of Experimental Psychology: Learning, Memory, and Cognition, 40 (4), 1072–1095. [DOI] [PubMed] [Google Scholar]
- Verhaeghen P (2011). Aging and executive control: reports of a demise greatly exaggerated. Current Directions in Psychological Science, 20 (3), 174–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verhaeghen P, & Salthouse TA (1997). Meta-analyses of age–cognition relations in adulthood: Estimates of linear and nonlinear age effects and structural models. Psychological Bulletin, 122 (3), 231–249. [DOI] [PubMed] [Google Scholar]
- Waldron-Perrine B, & Axelrod BN (2012). Determining an appropriate cutting score for indication of impairment on the Montreal Cognitive Assessment. International journal of geriatric psychiatry, 27 (11), 1189–1194. [DOI] [PubMed] [Google Scholar]
- Wasylyshyn C, Verhaeghen P, & Sliwinski MJ (2011). Aging and task switching: a meta-analysis. Psychology and Aging, 26 (1), 15–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watkins OC, & Watkins MJ (1980). The modality effect and echoic persistence. Journal of Experimental Psychology: General, 109 (3), 251–278. [DOI] [PubMed] [Google Scholar]
- Wechsler D (2011). Wechsler Abbreviated Scale of Intelligence–Second Edition (WASI-II). San Antonio, TX: NCS Pearson. [Google Scholar]
- Wickham H (2011). The split-apply-combine strategy for data analysis. Journal of Statistical Software, 40 (1), 1–29. Retrieved from http://www.jstatsoft.org/v40/i01/ [Google Scholar]
- Wingfield A, Stine EA, Lahar CJ, & Aberdeen JS (1988). Does the capacity of working memory change with age? Experimental Aging Research, 14 (2), 103–107. [DOI] [PubMed] [Google Scholar]
- Wright RE (1981). Aging, divided attention, and processing capacity. Journal of Gerontology, 36 (5), 605–614. [DOI] [PubMed] [Google Scholar]
- Xie Y (2016). knitr: A general-purpose package for dynamic report generation in r [Computer software manual]. Retrieved from http://yihui.name/knitr/(R package version 1.15.1)
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.