Abstract
Thermodynamic analysis is an important part of chemical engineering. However, its application in biotechnology has been hampered by lack of data on thermodynamic properties of microorganism biomass. In this paper, a review was made of methods for estimation of thermodynamic properties of biomass, including standard enthalpy of combustion hC⁰, enthalpy of formation hf⁰, entropy s⁰, and Gibbs free energy of formation gf⁰. These parameters were calculated on molar and mass specific basis for 32 microorganism species, including 14 bacteria, 7 yeast and 11 algae species. It was found that hf⁰, s⁰, gf⁰ are, respectively, similar for all the analyzed species, due to the fact that all living organisms have a common ancestor and thus a similar chemical composition. Furthermore, all the analyzed microorganisms have negative hf⁰, originating from partial oxidation of all other elements by oxygen and nitrogen. A brief review was given of microorganism endogenous and growth metabolic rates. Finally, based on the determined thermodynamic properties, entropy of individual E. coli and Pseudomonas cells were determined and entropy of a Pseudomonas colony during its lifespan was calculated and analyzed. Three periods can be distinguished in the existence of a microorganism colony: (a) accumulation period when cell number, mass and entropy increase, (b) steady state period when they are approximately constant, and (c) decumulation period when they decrease.
Keywords: Chemical Engineering, Thermodynamics, Physical chemistry
1. Introduction
Animate matter represents a highly organized, self-assembled amount of substance clearly separated by a semipermeable membrane from its environment (inanimate matter) (Morowitz, 1992). In biological terms, an organism is characterized by cellular structure that corresponds to a thermodynamic system (Morowitz, 1955; Schrödinger, 2003; von Bertalanffy, 1950; Balmer, 2010; Popovic, 2017a, 2018, Demirel, 2014). Animate matter represents an open system (von Bertalanffy, 1950). Moreover, the seven fundamental characteristics of life are: (1) ordered cell structure, (2) reproduction, (3) growth and development, (4) energy utilization, (5) response to the environment, (6) homeostasis, and (7) evolutionary adaptation (Campbell and Reece, 2002). Thus, an organism also represents a growing open system due to accumulation of matter and energy (Popovic, 2017b). Thus, animate matter performs thermodynamic processes corresponding to biological (life) processes.
Thermodynamics is widely applied in chemical engineering, but its full potential is still unexploited in biotechnology. Thermodynamics has played a fundamental role in the development of chemical industry, facilitating design of new technologies, enabling optimization of existing processes and avoiding difficult measurements. Therefore, there are three kinds of information that one must have for chemical engineering: balances, kinetics and thermodynamics. However, in biotechnology, a new and rapidly developing field of engineering, there is still a lack of information for thermodynamic analysis, forcing process development to be based on expensive measurements and making their optimization difficult (von Stockar, 2010). Therefore, it would be beneficial to have better means to predict thermodynamics of biotechnological processes.
Many biotechnological processes utilize growth of microorganisms, which can be represented by a chemical reaction, also known as growth reaction (von Stockar, 2010). Growth reactions, like all other reactions, have thermodynamic parameters that can be calculated as the difference of products and reactants. Since a major product in microorganism growth are new microorganisms, to find reaction thermodynamics, it is necessary to have standard thermodynamic properties of biomass.
The goal of this paper is to determine standard thermodynamic parameters of microorganism biomass and based on them make an analysis of microorganism growth. Section 2 reviews the methods used for determining biomass thermodynamic parameters, including enthalpy of combustion, enthalpy of formation from elements, entropy and Gibbs free energy of formation from elements. Section 3 gives the results and indicates general trends. Finally, section 4 gives explanations for the trends in the results, discusses microorganism metabolic rates and applies the results to growth of a Pseudomonas colony. Entropy of a Pseudomonas cell is calculated, and entropy change during growth of the entire colony is presented and discussed.
2. Methods
This section reviews methods to estimate thermodynamic parameters of microorganism biomass. First, enthalpy of combustion estimation methods are reviewed and compared to experimental microorganism biomass combustion data. Based on the determined enthalpies of combustion, a method is shown how to find enthalpies of formation of microorganisms. The discussion then turns to estimating entropy of dry microorganism biomass from its elemental composition, using the Battley equation.
Animate matter (a living organism) consists of water and dry biomass. The methods reviewed in this section are used to find thermodynamic properties of dry microorganism biomass. Once these are known, they are added to corresponding thermodynamic properties of water to find thermodynamic properties of animate matter, that is of the living organism (section 4).
Empirical formulas have been collected from the literature for 32 microorganism species, including 14 bacteria, 7 yeast and 11 algae species. They are given in Tables 1 and 2. From Tables 1 and 2, it can be seen that the most abundant elements in all microorganisms are C, H, O and N, which can be used to roughly represent their composition. Thus, the average chemical formula of dry bacterial biomass was found from data in Table 1 to be CH1.7O0.4N0.2, for fungi it is CH1.7O0.5N0.1 and for algae CH1.7O0.5N0.1. All other elements are present in amounts a magnitude lower or less.
Table 1.
Standard enthalpy of formation , entropy , and Gibbs free energy of formation normalized per mole of carbon atoms (UCF formula) of dry bacteria, fungi and algae biomass. To appreciate the size of a cell, a single Magnetospirillum gryphiswaldense cell can be described by C2.31 × 1010H4.68 × 1010O2.93 × 10⁹N6.56 × 1099Fe4.00 × 10⁷. The thermodynamic parameters for entire cells are given by the equation X⁰cell = nbio · + nw · where X⁰cell is thermodynamic parameter (Hf, S, or Gf) for a single cell, thermodynamic parameter for biomass from this table, nbio number of moles of dry matter, thermodynamic parameter for water and nw number of moles of water in the cell (Section 4.3).
| Name | Formula | Reference | (kJ/mol) | (J/mol K) | (kJ/mol) |
|---|---|---|---|---|---|
| BACTERIA | |||||
| Bacteria (general) | CH1.666O0.270N0.200 | Abbott and Clamen (1973) | −61.90 ± 3.32 | 30.15 ± 5.94 | − 22.82 ± 5.09 |
| Aerobacter aerogenes | CH1.830O0.550N0.250 | Naresh et al. (2011) | − 129.35 ± 6.93 | 38.42 ± 7.57 | − 79.55 ± 9.19 |
| Brevibacterium flavum | CH1.80O0.33N0.19 | Duboc et al. (1999), Table 9 | − 79.50 ± 4.26 | 32.76 ± 6.45 | − 37.04 ± 6.19 |
| Bacillus cereus | CH1.49O0.43N0.22 | Duboc et al. (1999), Table 9 | − 91.88 ± 4.92 | 31.43 ± 6.19 | − 51.14 ± 6.77 |
| Corynebacterium glutamicum | CH1.78O0.44N0.24 | Duboc et al. (1999), Table 9 | − 103.31 ± 5.54 | 35.52 ± 7.00 | − 57.27 ± 7.62 |
| Escherichia coli | CH1.770O0.490N0.240 | Bauer and Ziv (1976) | − 114.11 ± 6.12 | 36.36 ± 7.16 | − 66.98 ± 8.25 |
| E. coli | CH1.74O0.34N0.22 | Duboc et al. (1999), Table 9 | −79.81 ± 4.28 | 32.75 ± 6.45 | −37.36 ± 6.20 |
| E. coli K-12: grown on Acetic acid | CH1.54O0.4N0.21 | Battley (1992), Table 3 | −86.80 ± 4.65 | 31.28 ± 6.16 | −46.25 ± 6.49 |
| E. coli K-12: grown on glucose | CH1.74O0.464N0.26 | Battley (1992), Table 3 | −107.38 ± 5.76 | 35.85 ± 7.06 | −60.91 ± 7.86 |
| E. coli K-12: grown on glucose | CH1.81O0.40N0.22 | Battley (1992), Table 3 | −95.37 ± 5.11 | 34.76 ± 6.85 | −50.32 ± 7.15 |
| E. coli K-12: grown on glucose | CH1.73O0.53N0.235 | Battley (1992), Table 3 | −121.73 ± 6.52 | 36.54 ± 7.20 | −74.36 ± 8.67 |
| E. coli K-12: grown on glucose | CH1.78O0.511N0.237 | Battley (1992), Table 3 | −119.09 ± 6.38 | 36.83 ± 7.25 | −71.36 ± 8.55 |
| E. coli K-12: grown on glucose | CH1.81O0.49N0.234 | Battley (1992), Table 3 | −115.38 ± 6.18 | 36.74 ± 7.24 | −67.76 ± 8.34 |
| E. coli K-12: grown on glucose | CH1.54O0.34N0.24 | Battley (1992), Table 3 | −73.46 ± 3.94 | 30.67 ± 6.04 | −33.71 ± 5.74 |
| E. coli K-12: grown on Succinic acid | CH1.56O0.36N0.23 | Battley (1992), Table 3 | −78.54 ± 4.21 | 31.12 ± 6.13 | −38.20 ± 6.04 |
| E. coli W: grown on glucose | CH1.698O0.427N0.250 | Battley (1992), Table 3 | −97.82 ± 5.24 | 34.45 ± 6.79 | −53.17 ± 7.27 |
| E. coli W: grown on glycerol | CH1.698O0.427N0.250 | Battley (1992), Table 3 | −97.82 ± 5.24 | 34.45 ± 6.79 | −53.17 ± 7.27 |
| Flavobacterium dehydrogenans | CH1.63O0.40N0.21 | Duboc et al. (1999), Table 9 | −89.66 ± 4.81 | 32.38 ± 6.38 | −47.68 ± 6.71 |
| Klebsiella aerogenes | CH1.750O0.430N0.220 | Naresh et al. (2011) | −100.14 ± 5.37 | 34.60 ± 6.82 | −55.28 ± 7.40 |
| Klebsiella aerogenes | CH1.730O0.430N0.240 | Naresh et al. (2011) | −99.50 ± 5.33 | 34.72 ± 6.84 | −54.50 ± 7.37 |
| Klebsiella aerogenes | CH1.750O0.470N0.170 | Naresh et al. (2011) | −109.03 ± 5.84 | 34.47 ± 6.79 | −64.34 ± 7.87 |
| Klebsiella aerogenes | CH1.730O0.430N0.240 | Naresh et al. (2011) | −99.50 ± 5.33 | 34.72 ± 6.84 | −54.50 ± 7.37 |
| Lactobacillus helveticus | CH1.58O0.39N0.23 | Duboc et al. (1999), Table 9 | −85.84 ± 4.60 | 31.94 ± 6.29 | −44.45 ± 6.48 |
| Magnetospirillum gryphiswaldense | CH2.060O0.130N0.280Fe0.00174 | Naresh et al. (2011) | −44.02 ± 2.36 | 33.72 ± 6.64 | −0.31 ± 4.34 |
| Methanobacterium thermoautotrophicum | CH1.63O0.43N0.22 | Duboc et al. (1999), Table 9 | −96.32 ± 5.16 | 33.14 ± 6.53 | −53.37 ± 7.11 |
| Methylococcus capsulatus | CH2.000O0.500N0.270 | van Dijken and Harder (1975) | −123.64 ± 6.63 | 39.90 ± 7.86 | −71.93 ± 8.97 |
| Paracoccus denitrificans | CH1.510O0.460N0.190 | Shimizu et al. (1978) | −99.18 ± 5.32 | 31.71 ± 6.25 | −58.08 ± 7.18 |
| Paracoccus denitrificans | CH1.810O0.510N0.200 | Stouthamer (1977) | −119.83 ± 6.42 | 36.51 ± 7.19 | −72.50 ± 8.57 |
| Pseudomonas C12B | CH2.000O0.520N0.230 | Mayberry et al. (1968) | −128.09 ± 6.87 | 39.56 ± 7.79 | −76.80 ± 9.19 |
| Saccharopolyspora erythraea (a) | CH1.61O0.47N0.19 | Duboc et al. (1999), Table 9 | −104.58 ± 5.61 | 33.12 ± 6.52 | −61.65 ± 7.55 |
| Saccharopolyspora erythraea (b) | CH1.68O0.47N0.16 | Duboc et al. (1999), Table 9 | −106.80 ± 5.72 | 33.44 ± 6.59 | −63.46 ± 7.69 |
| YEAST | |||||
| Saccharomyces cerevisiae | CH1.613O0.557N0.158P0.012S0.003K0.022Mg0.003Ca0.001 | Battley, 1999a,b | −131.99 ± 7.07 | 34.66 ± 6.83 | −87.07 9.11 |
| Saccharomyces cerevisiae | CH1.640O0.520N0.160 | Harrison (1967) | −116.65 ± 6.25 | 33.91 ± 6.68 | −72.69 ± 8.24 |
| Saccharomyces cerevisiae | CH1.830O0.560N0.170 | Kok and Roels (1980) | −131.58 ± 7.05 | 37.18 ± 7.32 | −83.38 ± 9.24 |
| Saccharomyces cerevisiae | CH1.810O0.510N0.170 | Wang et al. (1976) | −119.83 ± 6.42 | 35.97 ± 7.09 | −73.19 ± 8.54 |
| Saccharomyces cerevisiae Whi 2+ | CH1.65O0.57N0.14 | Duboc et al. (1999), Table 9 | −128.08 ± 6.86 | 34.63 ± 6.82 | −83.19 ± 8.90 |
| Saccharomyces cerevisiae Whi 2− | CH1.64O0.5N0.18 | Duboc et al. (1999), Table 9 | −112.20 ± 6.01 | 33.88 ± 6.68 | −68.28 ± 8.00 |
| Saccharomyces cerevisiae CBS 426a | CH1.56O0.52N0.16 | Duboc et al. (1999), Table 9 | −114.10 ± 6.12 | 32.93 ± 6.49 | −71.42 ± 8.05 |
| Saccharomyces cerevisiae CBS 426b | CH1.52O0.51N0.19 | Duboc et al. (1999), Table 9 | −110.61 ± 5.93 | 32.79 ± 6.46 | −68.11 ± 7.85 |
| Candida utilis | CH1.830O0.540N0.100 | Herbert (1976) | −127.13 ± 6.81 | 35.54 ± 7.00 | −81.06 ± 8.90 |
| Candida utilis | CH1.870O0.560N0.200 | Naresh et al. (2011) | −132.85 ± 7.12 | 38.20 ± 7.53 | −83.32 ± 9.36 |
| Candida utilis | CH1.830O0.460N0.190 | Naresh et al. (2011) | −109.35 ± 5.86 | 35.62 ± 7.02 | −63.18 ± 7.95 |
| Candida utilis | CH1.870O0.560N0.200 | Naresh et al. (2011) | −132.85 ± 7.12 | 38.20 ± 7.53 | −83.32 ± 9.36 |
| Candida utilis ATCC 9950 | CH1.66O0.56N0.07 | Duboc et al. (1999), Table 9 | −126.17 ± 6.76 | 33.31 ± 6.56 | −83.00 ± 8.72 |
| Candida kefyr NCYC 1441 | CH1.66O0.44N0.12 | Duboc et al. (1999), Table 9 | −99.50 ± 5.33 | 31.90 ± 6.28 | −58.15 ± 7.21 |
| Debaryomyces hansenii | CH1.71O0.6N0.10 | Duboc et al. (1999), Table 9 | −136.65 ± 7.32 | 35.22 ± 6.94 | −90.99 ± 9.39 |
| Debaryomyces nepaliensis CBS 5921 | CH1.77O0.63N0.09 | Duboc et al. (1999), Table 9 | −145.23 ± 7.78 | 36.35 ± 7.16 | −98.10 ± 9.92 |
| Kluyveromyces marxianus NRRL 665 | CH1.73O0.53N0.17 | Duboc et al. (1999), Table 9 | −121.73 ± 6.52 | 35.38 ± 6.97 | −75.87 ± 8.60 |
| Zygosaccharomyces bailii NCYC 563 | CH1.63O0.55N0.13 | Duboc et al. (1999), Table 9 | −123.00 ± 6.59 | 33.83 ± 6.66 | −79.15 ± 8.58 |
| FILAMENTOUS FUNGI | |||||
| Aspergillus niger | CH1.60O0.55N0.10 | Duboc et al. (1999), Table 9 | −122.04 ± 6.54 | 32.92 ± 6.49 | −79.37 ± 8.48 |
| Aspergillus niger (spores) | CH1.50O0.53N0.12 | Duboc et al. (1999), Table 9 | −114.42 ± 6.13 | 31.67 ± 6.24 | −73.36 7.99 |
| Mucor rouxii | CH1.79O0.43N0.07 | Duboc et al. (1999), Table 9 | −101.41 ± 5.44 | 32.40 ± 6.38 | −59.40 ± 7.34 |
| Neurospora crassa | CH1.80O0.45N0.13 | Duboc et al. (1999), Table 9 | −106.17 ± 5.69 | 33.98 ± 6.69 | −62.12 ± 7.69 |
| Penicillium chrysogenum | CH1.87O0.22N0.08 | Duboc et al. (1999), Table 9 | −57.27 ± 3.07 | 29.53 ± 5.82 | −18.99 ± 4.80 |
| ALGAE | |||||
| Algae (general) | CH2.481O1.038N0.151P0.00943 | Wang et al. (2017) | −260.31 ± 13.95 | 54.03 ± 10.64 | −190.27 ± 17.13 |
| Chlamydomonas | CH1.65O0.39N0.12 | Duboc et al. (1999), Table 9 | −88.07 ± 4.72 | 30.82 ± 6.07 | −48.12 ± 6.53 |
| Chlorella | CH1.719O0.404N0.175P0.0105 | Manahan and Manahan (2009) | −95.34 ± 5.11 | 33.00 ± 6.50 | −52.56 7.05 |
| Chlorella a sp. MP-1 | CH1.793O0.608N0.121 | Phukan et al. (2011) | −141.17 ± 7.57 | 36.78 ± 7.25 | −93.49 ± 9.73 |
| Chlorella minutissima | CH1.714O0.286N0.143 | Prajapati et al. (2014) | −66.93 ± 3.59 | 30.02 ± 5.91 | −28.02 ± 5.35 |
| Chlorella pyrenoidosa | CH1.625O0.250N0.125 | Prajapati et al. (2014) | −56.15 ± 3.01 | 27.92 ± 5.50 | −19.96 ± 4.65 |
| Chlorella vulgaris | CH1.667O0.222N0.111 | Prajapati et al. (2014) | −51.30 ± 2.75 | 27.65 ± 5.45 | −15.47 ± 4.37 |
| Chrorella sp. ATCC 7516 (medium 5) | CH1.76O0.35N0.09 | Duboc et al. (1999), Table 9 | −82.67 ± 4.43 | 30.86 ± 6.08 | −42.67 ± 6.24 |
| Chlorella Spain sp. ATCC 7516 (medium S) | CH1.78O0.36N0.12 | Duboc et al. (1999), Table 9 | −85.53 ± 4.58 | 31.83 ± 6.27 | −44.27 ± 6.45 |
| Rocan 1 | CH1.40O0.50N0.04 | Duboc et al. (1999), Table 9 | −104.58 ± 5.61 | 28.44 ± 5.60 | −67.71 ± 7.28 |
| Rocan BUV 2 | CH1.56O0.59N0.05 | Duboc et al. (1999), Table 9 | −129.66 ± 6.95 | 32.30 ± 6.36 | −87.79 ± 8.85 |
| Scenedesnus obtusiusculus | CH1.64O0.44N0.11 | Duboc et al. (1999), Table 9 | −98.86 ± 5.30 | 31.48 ± 6.20 | −58.06 ± 7.15 |
| Selenastrum capricornutum | CH1.60O0.43N0.08 | Duboc et al. (1999), Table 9 | −95.37 ± 5.11 | 30.26 ± 5.96 | −56.14 ± 6.89 |
Table 2.
Standard specific (per gram) enthalpy of formation hf⁰, entropy s⁰, and Gibbs free energy of formation gf⁰ of dry bacteria, fungi and algae biomass. Empirical formulas reflect elemental composition of microorganisms and are normalized per mole of carbon atoms. To appreciate the size of a cell, a single Magnetospirillum gryphiswaldense cell can be described by C2.31 × 1010H4.68 × 1010O2.93 × 10⁹N6.56 × 1099Fe4.00 × 10⁷. The thermodynamic parameters for entire cells are given by the equation X⁰cell = mbio · x⁰bio + mw · xw⁰ where X⁰cell is thermodynamic parameter (Hf, S, or Gf) for a single cell, x⁰bio thermodynamic parameter for biomass from this table, mbio mass of the cell dry matter, xw⁰ thermodynamic parameter for water and mw mass of water in the cell (Section 4.3).
| Name | Formula | Reference | hf⁰ (kJ/g) | s⁰ (J/g K) | gf⁰ (kJ/g) |
|---|---|---|---|---|---|
| BACTERIA | |||||
| Bacteria (general) | CH1.666O0.270N0.200 | Abbott and Clamen (1973) | −2.97 ± 0.16 | 1.45 ± 0.29 | −1.10 ± 0.24 |
| Aerobacter aerogenes | CH1.830O0.550N0.250 | Naresh et al. (2011) | −4.95 ± 0.27 | 1.47 ± 0.29 | −3.04 ± 0.35 |
| Brevibacterium flavum | CH1.80O0.33N0.19 | Duboc et al. (1999), Table 9 | −3.65 ± 0.20 | 1.50 ± 0.30 | −1.70 ± 0.28 |
| Bacillus cereus | CH1.49O0.43N0.22 | Duboc et al. (1999), Table 9 | −3.91 ± 0.21 | 1.34 ± 0.26 | −2.18 ± 0.29 |
| Corynebacterium glutamicum | CH1.78O0.44N0.24 | Duboc et al. (1999), Table 9 | −4.27 ± 0.23 | 1.47 ± 0.29 | −2.37 ± 0.31 |
| Escherichia coli | CH1.770O0.490N0.240 | Bauer and Ziv (1976) | −4.57 ± 0.24 | 1.45 ± 0.29 | −2.68 ± 0.33 |
| E. coli | CH1.74O0.34N0.22 | Duboc et al. (1999), Table 9 | −3.58 ± 0.19 | 1.47 ± 0.29 | −1.68 ± 0.28 |
| E. coli K-12: grown on Acetic acid | CH1.54O0.4N0.21 | Battley (1992), Table 3 | −3.79 ± 0.20 | 1.37 ± 0.27 | −2.02 ± 0.28 |
| E. coli K-12: grown on glucose | CH1.74O0.464N0.26 | Battley (1992), Table 3 | −4.32 ± 0.23 | 1.44 ± 0.28 | −2.45 ± 0.32 |
| E. coli K-12: grown on glucose | CH1.81O0.40N0.22 | Battley (1992), Table 3 | −4.09 ± 0.22 | 1.49 ± 0.29 | −2.16 ± 0.31 |
| E. coli K-12: grown on glucose | CH1.73O0.53N0.235 | Battley (1992), Table 3 | −4.77 ± 0.26 | 1.43 ± 0.28 | −2.91 ± 0.34 |
| E. coli K-12: grown on glucose | CH1.78O0.511N0.237 | Battley (1992), Table 3 | −4.71 ± 0.25 | 1.46 ± 0.29 | −2.82 ± 0.34 |
| E. coli K-12: grown on glucose | CH1.81O0.49N0.234 | Battley (1992), Table 3 | −4.62 ± 0.25 | 1.47 ± 0.29 | −2.72 ± 0.33 |
| E. coli K-12: grown on glucose | CH1.54O0.34N0.24 | Battley (1992), Table 3 | −3.28 ± 0.18 | 1.37 ± 0.27 | −1.51 ± 0.26 |
| E. coli K-12: grown on Succinic acid | CH1.56O0.36N0.23 | Battley (1992), Table 3 | −3.48 ± 0.19 | 1.38 ± 0.27 | −1.69 ± 0.27 |
| E. coli W: grown on glucose | CH1.698O0.427N0.250 | Battley (1992), Table 3 | −4.07 ± 0.22 | 1.43 ± 0.28 | −2.21 ± 0.30 |
| E. coli W: grown on glycerol | CH1.698O0.427N0.250 | Battley (1992), Table 3 | −4.07 ± 0.22 | 1.43 ± 0.28 | −2.21 ± 0.30 |
| Flavobacterium dehydrogenans | CH1.63O0.40N0.21 | Duboc et al. (1999), Table 9 | −3.90 ± 0.21 | 1.41 ± 0.28 | −2.07 ± 0.29 |
| Klebsiella aerogenes | CH1.750O0.430N0.220 | Naresh et al. (2011) | −4.22 ± 0.23 | 1.46 ± 0.29 | −2.33 ± 0.31 |
| Klebsiella aerogenes | CH1.730O0.430N0.240 | Naresh et al. (2011) | −4.15 ± 0.22 | 1.45 ± 0.29 | −2.27 ± 0.31 |
| Klebsiella aerogenes | CH1.750O0.470N0.170 | Naresh et al. (2011) | −4.61 ± 0.25 | 1.46 ± 0.29 | −2.72 ± 0.33 |
| Klebsiella aerogenes | CH1.730O0.430N0.240 | Naresh et al. (2011) | −4.15 ± 0.22 | 1.45 ± 0.29 | −2.27 ± 0.31 |
| Lactobacillus helveticus | CH1.58O0.39N0.23 | Duboc et al. (1999), Table 9 | −3.72 ± 0.20 | 1.38 ± 0.27 | −1.93 ± 0.28 |
| Magnetospirillum gryphiswaldense | CH2.060O0.130N0.280Fe0.00174 | Naresh et al. (2011) | −2.18 ± 0.12 | 1.67 ± 0.33 | −0.02 ± 0.22 |
| Methanobacterium thermoautotrophicum | CH1.63O0.43N0.22 | Duboc et al. (1999), Table 9 | −4.08 ± 0.22 | 1.40 ± 0.28 | −2.26 ± 0.30 |
| Methylococcus capsulatus | CH2.000O0.500N0.270 | van Dijken and Harder (1975) | −4.79 ± 0.26 | 1.55 ± 0.30 | −2.79 ± 0.35 |
| Paracoccus denitrificans | CH1.510O0.460N0.190 | Shimizu et al. (1978) | −4.21 ± 0.23 | 1.35 ± 0.27 | −2.47 ± 0.30 |
| Paracoccus denitrificans | CH1.810O0.510N0.200 | Stouthamer (1977) | −4.83 ± 0.26 | 1.47 ± 0.29 | −2.92 ± 0.35 |
| Pseudomonas C12B | CH2.000O0.520N0.230 | Mayberry et al. (1968) | −5.01 ± 0.27 | 1.55 ± 0.30 | −3.00 ± 0.36 |
| Saccharopolyspora erythraea (a) | CH1.61O0.47N0.19 | Duboc et al. (1999), Table 9 | −4.39 ± 0.24 | 1.39 ± 0.27 | −2.59 ± 0.32 |
| Saccharopolyspora erythraea (b) | CH1.68O0.47N0.16 | Duboc et al. (1999), Table 9 | −4.55 ± 0.24 | 1.43 ± 0.28 | −2.70 ± 0.33 |
| YEAST | |||||
| Saccharomyces cerevisiae | CH1.613O0.557N0.158P0.012S0.003K0.022Mg0.003Ca0.001 | Battley, 1999a,b | −5.04 ± 0.27 | 1.32 ± 0.26 | −3.32 ± 0.35 |
| Saccharomyces cerevisiae | CH1.640O0.520N0.160 | Harrison (1967) | −4.82 ± 0.26 | 1.40 ± 0.28 | −3.00 ± 0.34 |
| Saccharomyces cerevisiae | CH1.830O0.560N0.170 | Kok and Roels (1980) | −5.22 ± 0.28 | 1.48 ± 0.29 | −3.31 ± 0.37 |
| Saccharomyces cerevisiae | CH1.810O0.510N0.170 | Wang et al. (1976) | −4.92 ± 0.26 | 1.48 ± 0.29 | −3.00 ± 0.35 |
| Saccharomyces cerevisiae Whi 2+ | CH1.65O0.57N0.14 | Duboc et al. (1999), Table 9 | −5.17 ± 0.28 | 1.40 ± 0.28 | −3.36 ± 0.36 |
| Saccharomyces cerevisiae Whi 2− | CH1.64O0.5N0.18 | Duboc et al. (1999), Table 9 | −4.64 ± 0.25 | 1.40 ± 0.28 | −2.82 ± 0.33 |
| Saccharomyces cerevisiae CBS 426a | CH1.56O0.52N0.16 | Duboc et al. (1999), Table 9 | −4.73 ± 0.25 | 1.36 ± 0.27 | −2.96 ± 0.33 |
| Saccharomyces cerevisiae CBS 426b | CH1.52O0.51N0.19 | Duboc et al. (1999), Table 9 | −4.54 ± 0.24 | 1.35 ± 0.27 | −2.80 ± 0.32 |
| Candida utilis | CH1.830O0.540N0.100 | Herbert (1976) | −5.32 ± 0.29 | 1.49 ± 0.29 | −3.39 ± 0.37 |
| Candida utilis | CH1.870O0.560N0.200 | Naresh et al. (2011) | −5.18 ± 0.28 | 1.49 ± 0.29 | −3.25 ± 0.36 |
| Candida utilis | CH1.830O0.460N0.190 | Naresh et al. (2011) | −4.58 ± 0.25 | 1.49 ± 0.29 | −2.65 ± 0.33 |
| Candida utilis | CH1.870O0.560N0.200 | Naresh et al. (2011) | −5.18 ± 0.28 | 1.49 ± 0.29 | −3.25 ± 0.36 |
| Candida utilis ATCC 9950 | CH1.66O0.56N0.07 | Duboc et al. (1999), Table 9 | −5.34 ± 0.29 | 1.41 ± 0.28 | −3.51 ± 0.37 |
| Candida kefyr NCYC 1441 | CH1.66O0.44N0.12 | Duboc et al. (1999), Table 9 | −4.44 ± 0.24 | 1.42 ± 0.28 | −2.60 ± 0.32 |
| Debaryomyces hansenii | CH1.71O0.6N0.10 | Duboc et al. (1999), Table 9 | −5.52 ± 0.30 | 1.42 ± 0.28 | −3.68 ± 0.38 |
| Debaryomyces nepaliensis CBS 5921 | CH1.77O0.63N0.09 | Duboc et al. (1999), Table 9 | −5.78 ± 0.31 | 1.45 ± 0.28 | −3.90 ± 0.39 |
| Kluyveromyces marxianus NRRL 665 | CH1.73O0.53N0.17 | Duboc et al. (1999), Table 9 | −4.95 ± 0.27 | 1.44 ± 0.28 | −3.08 ± 0.35 |
| Zygosaccharomyces bailii NCYC 563 | CH1.63O0.55N0.13 | Duboc et al. (1999), Table 9 | −5.07 ± 0.27 | 1.39 ± 0.27 | −3.26 ± 0.35 |
| FILAMENTOUS FUNGI | |||||
| Aspergillus niger | CH1.60O0.55N0.10 | Duboc et al. (1999), Table 9 | −5.12 ± 0.27 | 1.38 ± 0.27 | −3.33 ± 0.36 |
| Aspergillus niger (spores) | CH1.50O0.53N0.12 | Duboc et al. (1999), Table 9 | −4.83 ± 0.26 | 1.34 ± 0.26 | −3.10 ± 0.34 |
| Mucor rouxii | CH1.79O0.43N0.07 | Duboc et al. (1999), Table 9 | −4.68 ± 0.25 | 1.49 ± 0.29 | −2.74 ± 0.34 |
| Neurospora crassa | CH1.80O0.45N0.13 | Duboc et al. (1999), Table 9 | −4.65 ± 0.25 | 1.49 ± 0.29 | −2.72 ± 0.34 |
| Penicillium chrysogenum | CH1.87O0.22N0.08 | Duboc et al. (1999), Table 9 | −3.09 ± 0.17 | 1.59 ± 0.31 | −1.02 ± 0.26 |
| ALGAE | |||||
| Algae (general) | CH2.481O1.038N0.151P0.00943 | Wang et al. (2017) | −7.77 ± 0.42 | 1.61 ± 0.32 | −5.68 ± 0.51 |
| Chlamydomonas | CH1.65O0.39N0.12 | Duboc et al. (1999), Table 9 | −4.08 ± 0.22 | 1.43 ± 0.28 | −2.23 ± 0.30 |
| Chlorella | CH1.719O0.404N0.175P0.0105 | Manahan and Manahan (2009) | −4.15 ± 0.22 | 1.44 ± 0.28 | −2.29 ± 0.31 |
| Chlorella a sp. MP-1 | CH1.793O0.608N0.121 | Phukan et al. (2011) | −5.59 ± 0.30 | 1.46 ± 0.29 | −3.70 ± 0.39 |
| Chlorella minutissima | CH1.714O0.286N0.143 | Prajapati et al. (2014) | −3.30 ± 0.18 | 1.48 ± 0.29 | −1.38 ± 0.26 |
| Chlorella pyrenoidosa | CH1.625O0.250N0.125 | Prajapati et al. (2014) | −2.89 ± 0.16 | 1.44 ± 0.28 | −1.03 ± 0.24 |
| Chlorella vulgaris | CH1.667O0.222N0.111 | Prajapati et al. (2014) | −2.73 ± 0.15 | 1.47 ± 0.29 | −0.82 ± 0.23 |
| Chrorella sp. ATCC 7516 (medium 5) | CH1.76O0.35N0.09 | Duboc et al. (1999), Table 9 | −4.00 ± 0.21 | 1.49 ± 0.29 | −2.07 ± 0.30 |
| Chlorella Spain sp. ATCC 7516 (medium S) | CH1.78O0.36N0.12 | Duboc et al. (1999), Table 9 | −4.03 ± 0.22 | 1.50 ± 0.30 | −2.08 ± 0.30 |
| Rocan 1 | CH1.40O0.50N0.04 | Duboc et al. (1999), Table 9 | −4.76 ± 0.25 | 1.29 ± 0.25 | −3.08 ± 0.33 |
| Rocan BUV 2 | CH1.56O0.59N0.05 | Duboc et al. (1999), Table 9 | −5.47 ± 0.29 | 1.36 ± 0.27 | −3.70 ± 0.37 |
| Scenedesnus obtusiusculus | CH1.64O0.44N0.11 | Duboc et al. (1999), Table 9 | −4.44 ± 0.24 | 1.42 ± 0.28 | −2.61 ± 0.32 |
| Selenastrum capricornutum | CH1.60O0.43N0.08 | Duboc et al. (1999), Table 9 | −4.41 ± 0.24 | 1.40 ± 0.28 | −2.60 ± 0.32 |
2.1. Enthalpy of combustion
Standard molar enthalpy of combustion of microorganism biomass can be calculated from their elemental composition, using empirical relations. The empirical relations predict enthalpy of biomass combustion, from which enthalpy of formation can be estimated using simple thermochemical relations. In the literature there are at least 40 empirical equations for estimating enthalpy of combustion of biomass (Kiang, 2012). This section reviews and compares using experimental data the most widely used methods, including Patel-Erickson, Boie, Dulong, Mason-Gandhi and Channiwala-Parikh equations (Annamalai et al., 2018).
Dulong was the first to propose, in the 19th century, that heat of combustion of coal can be empirically correlated with its chemical composition (Kiang, 2012). Dulong's equation is still in use today and its success has inspired many to look for similar equations applicable to a wide range of fuels, an example being the widely used Boie equation (Annamalai et al., 2018; Kiang, 2012). The underlaying mechanism of the correlation was discovered by Thornton (1917), who realized that the heat of combustion is proportional to number of oxygen atoms used to burn the fuel. Thornton's work was generalized and extended by Patel and Erickson (1981), who realized that enthalpy of combustion – a redox reaction – is proportional to the number of electrons transferred from the fuel to oxygen.
The Patel-Erickson equation states that the standard molar enthalpy of combustion of organic matter is proportional to the number of electrons that it transfers to oxygen during combustion (Patel and Erickson, 1981). The proportionality is expressed through the equation (Patel and Erickson, 1981; Battley, 1998)
| (1) |
where E is the number of electrons transferred to oxygen during combustion to CO2(g), H2O(l), N2(g), P4O10(s) and SO3(g) (Patel and Erickson, 1981; Battley, 1998).
There are two conventions about sulphur oxidation: SO2 and SO3 conventions. The first is used in the combustion literature (van Loo and Koppejan, 2008) and is based on sulphur oxidation to SO2
| (2) |
This convention is due to the fact that in most combustion processes sulphur is oxidized to SO2. The second convention is used in the calorimetry literature (Battley, 1992; 1999b; Minas da Piedade, 1999, p. 38) and considers sulphur oxidation to SO3
| (3) |
The second convention is due to the fact that sulphur is oxidized to SO3, H2SO4 or sulphates in bomb calorimeters (Battley, 1992; 1999b; Minas da Piedade, 1999, p. 38). Boie, Dulong, Mason-Gandhi, and Channiwala-Parikh equations, which will be discussed below, use the S→SO2 convention. The Patel-Erickson equation can be used with both conventions. The S→SO2 convention implies the coefficient 4 multiplying nS in Eq. (4), since an S atom gives 4 electrons when it is oxidized to SO2. The S→SO3 convention requires multiplying nS by 6, since an S atom gives 6 electrons when it is oxidized to SO3. However, regardless of which convention is chosen, the results do not change significantly. The difference between Patel-Erickson equation enthalpies of combustion calculated using the two conventions is 0.13%.
Thus, during combustion, a C atom gives its 4 valence electrons, H gives 1, N gives none since it is converted to N2, P gives 5 and S gives 6. Inorganic ions, like Na+ and Mg2+ are not included, since they are already in their highest oxidation state and cannot transfer any electrons to oxygen (Battley, 1998). Thus, E is calculated through the equation
| (4) |
where nC, nH, nO, nN, nP and nS are the number of C, H, O, N, P and S atoms in the biomass empirical formula (Patel and Erickson, 1981; Battley, 1998). If any of these atoms are not present, they are just neglected during the calculation (Battley, 1998). An example calculation of biomass using the Patel-Erickson equation is given in the section 2.5.
The Boie equation is a widely used model for estimating standard specific enthalpy of combustion hC⁰ of fuels of known elemental composition
| (5) |
where wC, wH, wO, wN and wS are mass fractions of carbon, hydrogen, oxygen, nitrogen and sulphur in the fuel, respectively (Annamalai et al., 2018). The method of converting standard enthalpy of combustion from molar to mass specific hC⁰ basis is described in section 3.
The Dulong equation gives standard molar enthalpy of combustion hC⁰ of fuels as a function of their composition as (Annamalai et al., 2018)
| (6) |
The Mason-Gandhi equation gives standard specific enthalpy of combustion as
| (7) |
where wAsh is the mass fraction of ash in the sample (Annamalai et al., 2018).
The Channiwala-Parikh equation gives standard specific enthalpy of combustion as (Annamalai et al., 2018)
| (8) |
The five models were compared to experimental heat of combustion data, reported by Duboc et al. (1999) and Battley (1999b). Microorganism compositions in the form of mass fractions and empirical formulas (UCF) were taken from Duboc et al. (1999) and Battley (1999b). They are given in Table 3. The mass fraction data was used to calculate enthalpies of combustion of the microorganisms, using the Boie, Dulong, Mason-Gandhi, and Channiwala-Parikh equations. The empirical formulas were used to calculate the enthalpies of combustion using the Patel-Erickson equation. The results are presented in Table 4. Based on the results from Table 4, average absolute deviations were calculated and are presented in Table 5. As can be seen from Table 5, the best results were obtained from the Channiwala-Parikh equation and the Patel-Erickson equation. This result is in agreement with that of Cordier et al. (1987), who found the Patel-Erickson equation to be among the most precise models for estimating enthalpy of combustion of microbial biomass.
Table 3.
Elemental composition of dry microorganism biomass: element mass fractions, elemental empirical formulas and empirical formula molar masses. Data taken from taken from Duboc et al. (1999) and Battley (1999b). wAsh, wC, wH, wO and wN represent mass fractions of ash, C, H, O and N, respectively, while Mr is the empirical formula molar mass, which can be calculated through the equation: Mr = 12.0107 / wC (Duboc et al. (1999)).
| Name | wAsh | wc | wH | wO | wN | Empirical formula | Mr (g/mol) |
|---|---|---|---|---|---|---|---|
| Bacteria | |||||||
| Lactobacillus helveticus | 0.0903 | 0.4754 | 0.0625 | 0.2439 | 0.1279 | CH1.58O0.39N0.23 | 25.26 |
| F. dehydrogenans | 0.1353 | 0.4516 | 0.0615 | 0.2429 | 0.1087 | CH1.63O0.40N0.21 | 26.60 |
| Saccharopolyspora erythraea (a) | 0.0932 | 0.4586 | 0.0616 | 0.2861 | 0.1005 | CH1.61O0.47N0.19 | 26.19 |
| Saccharopolyspora erythraea (b) | 0.0483 | 0.4848 | 0.068 | 0.3067 | 0.0922 | CH1.68O0.47N0.16 | 24.77 |
| B. flavum | 0.3023 | 0.3854 | 0.0578 | 0.1698 | 0.0847 | CH1.80O0.33N0.19 | 31.16 |
| Escherichia coli | 0.1127 | 0.4783 | 0.0695 | 0.2165 | 0.123 | CH1.74O0.34N0.22 | 25.11 |
| Bacillus cereus | 0.0998 | 0.4605 | 0.0573 | 0.2626 | 0.1198 | CH1.49O0.43N0.22 | 26.08 |
| Corynebacterium glutamicum | 0.3209 | 0.3365 | 0.05 | 0.1993 | 0.0933 | CH1.78O0.44N0.24 | 35.69 |
| Methanobacterium thermoautotrophicum | 0.1865 | 0.412 | 0.0558 | 0.239 | 0.1067 | CH1.63O0.43N0.22 | 29.15 |
| Algae | |||||||
| Rocan 1 | 0.0615 | 0.5118 | 0.0596 | 0.3405 | 0.0266 | CH1.40O0.50N0.04 | 23.47 |
| Rocan BUV 2 | 0.1167 | 0.4452 | 0.0578 | 0.3519 | 0.0284 | CH1.56O0.59N0.05 | 26.98 |
| Chlamydomonas | 0.042 | 0.5326 | 0.0734 | 0.2795 | 0.0725 | CH1.65O0.39N0.12 | 22.55 |
| Chrorella sp. ATCC 7516 (medium 5) | 0.0543 | 0.5505 | 0.0806 | 0.2599 | 0.0547 | CH1.76O0.35N0.09 | 21.82 |
| Chlorella Spain sp. ATCC 7516 (medium S) | 0.0431 | 0.539 | 0.08 | 0.2604 | 0.0775 | CH1.78O0.36N0.12 | 22.28 |
| Selenastrum capricornutum | 0.0565 | 0.5238 | 0.07 | 0.3028 | 0.0469 | CH1.60O0.43N0.08 | 22.93 |
| Scenedesnus obtusiusculus | 0.0522 | 0.5104 | 0.0697 | 0.3011 | 0.0666 | CH1.64O0.44N0.11 | 23.53 |
| Filamentous fungi | |||||||
| Neurospora crassa | 0.0848 | 0.4817 | 0.0722 | 0.2899 | 0.0714 | CH1.80O0.45N0.13 | 24.93 |
| Penicillium chrysogenum | 0.2113 | 0.5114 | 0.0795 | 0.15 | 0.0478 | CH1.87O0.22N0.08 | 23.49 |
| Mucor rouxii | 0.0957 | 0.5035 | 0.0752 | 0.2865 | 0.0391 | CH1.79O0.43N0.07 | 23.85 |
| Aspergillus niger | 0.0877 | 0.4618 | 0.0617 | 0.3372 | 0.0516 | CH1.60O0.55N0.10 | 26.01 |
| Aspergillus niger (spores) | 0.0318 | 0.4915 | 0.0614 | 0.3483 | 0.067 | CH1.50O0.53N0.12 | 24.44 |
| Yeast | |||||||
| Candida kefyr NCYC 1441 | 0.047 | 0.5118 | 0.0713 | 0.2992 | 0.0707 | CH1.66O0.44N0.12 | 23.47 |
| Candida utilis ATCC 9950 | 0.0968 | 0.4597 | 0.0639 | 0.342 | 0.0376 | CH1.66O0.56N0.07 | 26.13 |
| Debaryomyces hansenii | 0.0874 | 0.4441 | 0.0636 | 0.3522 | 0.0527 | CH1.71O0.6N0.10 | 27.05 |
| D. nepaliensis CBS 5921 | 0.0451 | 0.4567 | 0.0678 | 0.383 | 0.0474 | CH1.77O0.63N0.09 | 26.30 |
| Saccharomyces cerevisae | 0.0502 | 0.4588 | 0.0621 | 0.3403 | 0.0847 | CH1.613O0.557N0.158P0.012S0.003K0.022Mg0.003Ca0.001 | 26.18 |
| S. cerevisiae Whi 2+ | 0.0704 | 0.4516 | 0.0627 | 0.3412 | 0.0741 | CH1.65O0.57N0.14 | 26.60 |
| S. cerevisiae Whi 2- | 0.0864 | 0.4544 | 0.0624 | 0.3022 | 0.0946 | CH1.64O0.5N0.18 | 26.43 |
| S. cerevisiae CBS 426a | 0.0955 | 0.4505 | 0.0589 | 0.31 | 0.0851 | CH1.56O0.52N0.16 | 26.66 |
| S. cerevisiae CBS 426b | 0.0306 | 0.4777 | 0.0611 | 0.3268 | 0.1038 | CH1.52O0.51N0.19 | 25.14 |
| Kluyveromyces marxianus NRRL 665 | 0.1005 | 0.4385 | 0.0635 | 0.3107 | 0.0868 | CH1.73O0.53N0.17 | 27.39 |
| Zygosaccharomyces bailii NCYC 563 | 0.065 | 0.4626 | 0.0632 | 0.3372 | 0.072 | CH1.63O0.55N0.13 | 25.96 |
Table 4.
Standard specific enthalpy of combustion of dry microorganism biomass. The experimental values were taken from Duboc et al. (1999) and Battley (1999b). The theoretical values were calculated using the Patel-Erickson, Boie, Dulong, Mason-Gandhi and Channiwala-Parikh equations.
| Name | hC⁰ (kJ/kg) |
|||||
|---|---|---|---|---|---|---|
| Experiment | Patel-Erickson | Boie | Dulong | Mason-Gandhi | Channiwala-Parikh | |
| Lactobacillus helveticus | −21274.9881355791 | −21115.55 | −22077.49 | −20683.25 | −21576.84 | −21055.00 |
| F. dehydrogenans | −19540.6196141774 | −20183.81 | −21014.97 | −19752.67 | −20670.87 | −20050.70 |
| Saccharopolyspora erythraea (a) | −19824.416561899 | −19817.69 | −20742.13 | −19225.27 | −20417.14 | −19961.37 |
| Saccharopolyspora erythraea (b) | −21279.9054176692 | −21263.91 | −22126.58 | −20662.22 | −21951.56 | −21524.40 |
| B. flavum | −15777.6965539061 | −18330.61 | −18917.30 | −18298.94 | −18847.27 | −17743.41 |
| Escherichia coli | −21106.0970634518 | −22395.10 | −23266.12 | −22284.06 | −22996.41 | −22224.50 |
| Corynebacterium glutamicum | −19469.4647272848 | −19729.35 | −20690.98 | −19093.08 | −20132.78 | −19720.95 |
| Methanobacterium thermoautotrophicum | −15061.7699218197 | −15257.49 | −16018.28 | −14990.16 | −15769.12 | −14759.97 |
| Rocan 1 | −16235.4900213976 | −18185.18 | −18990.84 | −17662.80 | −18605.51 | −17931.94 |
| Rocan BUV 2 | −20232.1796398212 | −20837.95 | −21312.80 | −19754.89 | −21327.68 | −21198.91 |
| Chlamydomonas | −19845.6443004987 | −18043.94 | −18646.82 | −17038.92 | −18779.24 | −18424.74 |
| Chrorella sp. ATCC 7516 (medium 5) | −24553.1584337299 | −24001.16 | −24612.78 | −23546.40 | −24616.19 | −24153.66 |
| Chlorella Spain sp. ATCC 7516 (medium S) | −26735.0487481995 | −25775.67 | −26184.54 | −25542.49 | −26466.41 | −25830.52 |
| Selenastrum capricornutum | −25323.8945273797 | −25237.21 | −25848.10 | −25058.29 | −25983.07 | −25342.39 |
| Scenedesnus obtusiusculus | −22935.0845496099 | −22974.49 | −23489.04 | −22339.00 | −23593.81 | −23212.97 |
| Neurospora crassa | −24791.8406087905 | −22481.21 | −23125.60 | −21873.46 | −23115.95 | −22706.73 |
| Penicillium chrysogenum | −25543.4512559634 | −21841.11 | −22561.42 | −21465.60 | −22649.96 | −22039.17 |
| Mucor rouxii | −22890.3094740523 | −25695.83 | −25857.40 | −26042.63 | −26371.04 | −25151.44 |
| Aspergillus niger | −20897.595477366 | −22969.34 | −23511.44 | −22696.16 | −23852.61 | −23214.62 |
| Aspergillus niger (spores) | −16098.6170664491 | −19229.52 | −19992.47 | −18427.07 | −20003.47 | −19641.94 |
| Candida kefyr NCYC 1441 | −21565.8121508322 | −20193.36 | −20975.47 | −19187.68 | −20793.86 | −20623.34 |
| Candida utilis ATCC 9950 | −21902.570208231 | −22637.59 | −23407.60 | −22185.66 | −23406.67 | −22968.56 |
| Debaryomyces hansenii | −20591.5225590515 | −19312.23 | −20033.18 | −18586.74 | −20206.41 | −19780.16 |
| D. nepaliensis CBS 5921 | −19412.0659078988 | −18533.58 | −19431.52 | −17832.42 | −19529.54 | −19091.78 |
| Saccharomyces cerevisae | −18784.067539777 | −19391.25 | −20323.05 | −18670.34 | −20221.32 | −19863.70 |
| S. cerevisiae Whi 2+ | −19288.7009083567 | −19059.42 | −19987.83 | −18308.76 | −20204.24 | −19805.32 |
| S. cerevisiae Whi 2− | −19597.4589324519 | −18846.58 | −19847.00 | −18154.39 | −19745.52 | −19364.85 |
| S. cerevisiae CBS 426a | −19841.8493509954 | −19510.05 | −20471.83 | −18908.53 | −20212.59 | −19765.80 |
| S. cerevisiae CBS 426b | −20085.2989417769 | −18842.36 | −19781.76 | −18131.62 | −19510.87 | −19131.74 |
| Kluyveromyces marxianus NRRL 665 | −19970.484651186 | −19891.61 | −20924.93 | −19065.40 | −20507.95 | −20275.50 |
| Zygosaccharomyces bailii NCYC 563 | −19440 | −18949.10 | −19897.39 | −18376.51 | −19756.97 | −19234.48 |
Table 5.
A comparison of five predictive enthalpy of combustion models, based on absolute average deviations from experimental data.
| Equation | AAD (%) |
|---|---|
| Channiwala-Parikh | 5.00 |
| Patel-Erickson | 5.36 |
| Mason-Ghandi | 6.15 |
| Boie | 6.56 |
| Dulong | 6.65 |
The Patel-Erickson equation was chosen as the method to calculate enthalpies of combustion of microorganisms presented in this study for three reasons:
-
1.
It is among the most precise equations for estimating microorganism enthalpy of combustion.
-
2.
It is the most widely applicable equation for animate matter, since it includes phosphorus, which is present in all living organisms. Phosphorus in living organisms is oxidized during combustion to P4O10, which has a very negative enthalpy of formation (()P4O10 = −2984.0 kJ/mol, compared with ()CO2 = −393.51 kJ/mol (Atkins and de Paula, 2006). Thus, phosphorus has a great influence on calculated enthalpy of formation of microorganisms, on which it affects through Eq. (10).
-
3.
It can be used with any kind of elemental analysis, even those that do not determine ash content of a sample. Such methods are often used in biomedical studies, an example being in vivo neutron activation analysis, a noninvasive method that allows determination of elemental compositions of living organisms (Heymsfield et al., 1993).
Thus, based on the Patel-Erickson equation, enthalpies of combustion of microorganisms were calculated, and then converted into enthalpies of formation.
2.2. Enthalpy of formation
Once is determined, standard molar enthalpy of formation of microorganism biomass ()bio can be calculated as enthalpy of the first reactant in the oxidation reaction (Battley, 1998)
| CnCHnHOnONnNPnPSnSKnKMgnMgCanCaFenFe + (nC + ¼ nH + 1¼ nP + 1½ nS + ¼ nK + ½ nMg + ½ nCa + ¾ nFe - ½ nO) O2 → nC CO2 + ½ nH H2O + ½ nN N2 + ¼ nP P4O10 + nS SO3 + ½ nK K2O + nMg MgO + nCa CaO + ½ nFe Fe2O3 | (9) |
that is, using the formula
| (10) |
More details on how to calculate biomass enthalpy of formation in practice and an example calculation of ()bio for E. coli can be found in section 2.5.
As was shown above, the error in enthalpy of combustion estimated through Patel's rule is 5.36% ()bio is calculated using and of the oxides. The oxide values have been accurately determined by experiment and have a negligible compared to the error in . Thus, the absolute error in ()bio is equal to that of estimated from the Patel-Erickson equation.
2.3. Entropy
Composition of dry biomass can be used to calculate its standard molar entropy , through the Battley equation (Battley, 1999a)
| (11) |
where ni is the number of atoms of element i in the empirical formula of the biomass, is standard molar entropy of element i and ai is the number of atoms per molecule of element i in its standard state elemental form. For example, the standard state elemental form of carbon is graphite, which is simply written as C, which makes aC = 1. On the other hand, hydrogen, oxygen and nitrogen are in their standard state elemental forms all diatomic gasses H2, O2 and N2, respectively, which implies that aH = aO = aN = 2. The summation is over all elements constituting the dry biomass. More details on how to practically apply the Battley equation and an example calculation of for E. coli can be found in section 2.5.
The Battley equation simply states that standard molar entropy of biomass equals a constant 0.187 times the standard molar entropy of its constituent elements – the sum term. In the sum term, /ai represents entropy per mole of atoms of an element. The entropy per mole of atoms of the element is then multiplied by the number of moles of that element in the biomass ni, giving the contribution of that element to the entropy of the biomass. Finally, when contributions of all elements are summed, they are multiplied by the constant 0.187, which takes into account the fact that the elements are no longer in their standard state pure forms, but are a part of the biomass. The Battley equation is a consequence of additivity of entropy: entropy of biomass is a sum of contributions of all its constituent elements.
The Battley equation can be used to predict standard specific entropy of a wide range of organic substances. It has been shown to be applicable to dry microorganism biomass, proteins, amino acids, nucleotides and fatty acids (Battley, 1999a). The error of predicting entropy of dry biomass using the Battley equation is 2% (Battley, 1999a). In case of hydrated biomass, the entropy of hydration is the greatest source of error and increases it to 19.7% (Battley, 1999a).
The Battley equation can also be used to find standard molar entropy of formation of dry biomass from elements (Battley, 1999a). In this case, it takes the form (Battley, 1999a)
| (12) |
Eq. (12) is based on the definition of entropy of formation and the Battley equation. The formation of biomass from elements can be, in a very simplified way, represented by the chemical equation
| (13) |
Thus the entropy of formation of biomass is = . As was explained above, is the sum term in the Battley equation: = Σi (/ai)·ni (Battley, 1999a). The entropy of biomass is = 0.187 . Taking the difference between and results in the Eq. (12) (Battley, 1999a).
Since is based on experimentally highly accurately determined element entropies, the error in originates from error in . Thus the error in is equal to the error in given by the Battley equation.
2.4. Gibbs free energy
From ()bio and , it is possible to calculate the standard molar Gibbs free energy of formation of microorganisms from elements , using the Gibbs equation
| (14) |
where under standard conditions T = 298.15 K. The error in , σG can be estimated from error in ()bio, σH, and , σS, using the equation σG = σH + T σS.
2.5. An example of estimation of thermodynamic properties of microorganisms
This section gives a practical example, on dry E. coli biomass, of estimation of standard specific enthalpy of combustion, enthalpy of formation and entropy.
2.5.1. Standard specific enthalpy of combustion and enthalpy of formation
Enthalpy of formation can be estimated from elemental composition of dry microorganisms using the Patel-Erickson equation. First, elemental composition will be used to find enthalpy of combustion through the Patel-Erickson equation. Then enthalpy of combustion will be used to find enthalpy of formation of dry E. coli biomass through classical reaction thermochemistry.
The Patel-Erickson equation is first used to determine the standard specific enthalpy of combustion for dry E. coli biomass. From Table 1, the empirical formula of dry E. coli biomass is CH1.770O0.490N0.240. It contains nC = 1 carbon atoms, nH = 1.770 hydrogen atoms, nO = 0.490 oxygen atoms and nN = 0.240 nitrogen atoms. The number of electrons transferred to oxygen during combustion, E, can be determined through Eq. (4). Substituting the actual amounts of C, H, O and N gives
| (15) |
| (16) |
This result is now substituted into the Patel-Erickson equation (Equation 1) to find for dry E. coli biomass
| (17) |
| (18) |
| (19) |
Now that has been determined, the second step is to find the standard specific enthalpy hf⁰ of dry E. coli biomass. The complete combustion of the dry biomass can be represented by reaction (9). Having in mind that hf⁰ for N2 and O2 is zero, the enthalpy change for this reaction is and is given by the equation
| (20) |
which can be manipulated to give the enthalpy of microorganism formation ()bio
| (21) |
For dry E. coli biomass Eqs (9) and (21) become
| (22) |
| (23) |
The enthalpies of formation of the inorganic compounds are ()CO2 = −393.51 kJ/mol and ()H2O = −285.83 kJ/mol (Atkins and de Paula, 2006). Substituting these values into Eq. (23), along with the previously calculated = −532.36 kJ/mol gives
| (24) |
| (25) |
Thus the standard specific enthalpy of formation of dry E. coli biomass is ()bio = −114.11 kJ/mol. Standard specific enthalpy of formation per unit mass (hf⁰)bio can be found through the equation
| (26) |
where (Mr)bio is the molar mass of the E. coli empirical formula CH1.770O0.490N0.240: (Mr)bio = 25.00 g/mol. Thus,
| (27) |
| (28) |
Thus, the standard specific enthalpy of formation of dry E. coli biomass is (hf⁰)bio = −4.57 kJ/g.
2.5.2. Standard specific entropy
Biomass composition can be used to calculate its standard molar entropy through the Battley equation (equation 11). A general microorganism empirical formula is CnCHnHOnONnNPnPSnSKnKMgnMgCanCaFenFe. In their standard elemental states C, P, S, K, Mg, Ca and Fe are all solids and are represented by a single atom unit formula (e.g. C(graphite) or K(s)) (Atkins and de Paula, 2006). Thus, aC = aP = aS = aK = aMg = aCa = aFe = 1. On the other hand, H, O and N come in the form of diatomic molecules H2, O2 and N2, thus aH = aO = aN = 2. The Battley equation now becomes
| (29) |
The E. coli biomass has the empirical formula is CH1.770O0.490N0.240. Since there are only 4 elements in the empirical formula, Eq. (29) becomes
| (30) |
Since the empirical formula contains nC = 1 carbon atoms, nH = 1.770 hydrogen atoms, nO = 0.490 oxygen atoms and nN = 0.240 nitrogen atoms
| (31) |
The standard molar entropies are = 5.51 J/mol K, = 130.68 J/mol K, = 205.15 J/mol K and = 191.61 J/mol K (Atkins and de Paula, 2006). Thus,
| (32) |
| (33) |
| (34) |
Thus, the standard molar entropy of dry E. coli biomass is 36.36 J/mol K. The standard specific entropy s⁰bio can be found through the equation
| (35) |
where (Mr)bio is the molar mass of the E. coli empirical formula: (Mr)bio = 25.00 g/mol. Thus
| (36) |
| (37) |
Thus, the standard specific entropy of dry E. coli cells is 1.45 J/g K.
3. Results
Standard molar thermodynamic parameters of dry microorganism biomass have been calculated, as described in section 2, including enthalpy of formation from elements ()bio, entropy and Gibbs free energy of formation from elements . They are given in Table 1. From the standard molar thermodynamic properties, it is possible to calculate standard specific (per gram) thermodynamic properties using the equation x⁰ = /Mr, where x⁰ is standard property (hf, s, or gf) per gram, is the corresponding property per mole and Mr is molar mass of the biomass empirical formula. Thus, standard specific enthalpy of formation from elements (hf⁰)bio, specific entropy s⁰bio and specific Gibbs free energy of formation from elements (gf⁰)bio of dry biomass were calculated and are given in Table 2.
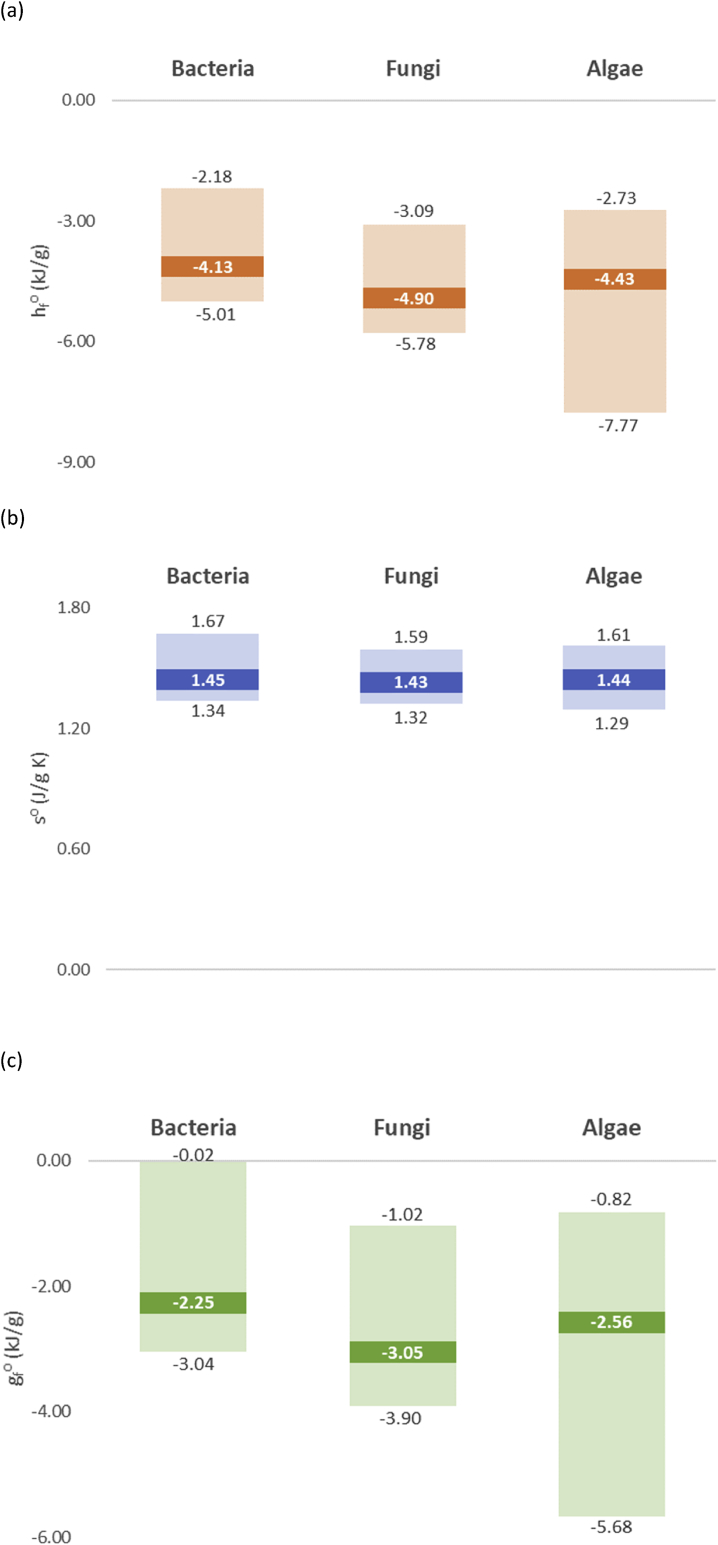
The thermodynamic parameters have very similar values for the three classes, as would be expected. They are shown in Fig. 1. Interesting trends can be seen among the standard thermodynamic properties. For all the studied microorganisms (hf⁰)bio < 0, s⁰bio > 0 and (gf⁰)bio < 0. The (hf⁰)bio < 0 trend means that formation of biomass from elements is exothermic. The s⁰bio > 0 trend is a consequence of the third law of thermodynamics, stating that entropy cannot have a negative value. Finally, the (gf⁰)bio < 0 implies that formation of biomass from elements is a spontaneous process for all the studied microorganism species.
Fig. 1.
A comparison between average (a) enthalpy of formation from elements, (b) entropy and (c) Gibbs free energy of formation of bacteria, fungi and algae. The top number represents maximal value, middle number is the average value, while the bottom number is the minimal value for the group.
The thermodynamic properties in Tables 1 and 2 are at standard conditions, implying a temperature of 25 °C (298.15 K). To find their values at 37 °C (310.15 K), a correction must be made. Thus, specific enthalpy of formation from elements at 37 °C, hf37C, and specific entropy at 37 °C, s37C, are (Atkins and de Paula, 2006)
| (38) |
| (39) |
where cp is specific heat capacity, while hcor and scor are corrections that need to be made from 298.15K to 310.15K. The specific heat capacity of dry yeast biomass is 1.308 J/g K (Battley et al., 1997). Based on these values, hcor = 0.0157 kJ/g and scor = 0.0516 J/g K. Both of these corrections are lower than the error values reported in Table 2 (0.27 and 0.26, for yeast hf⁰ and s⁰, respectively). Thus, for calculations at 37 °C it is an acceptable approximation to use the standard thermodynamic parameter values reported in Tables 1 and 2.
4. Discussion
This section begins with a discussion of the general trends in the results from section 3 and attempts to give explanations for these trends. Then microorganism metabolic rates are discussed. Finally, a thermodynamic analysis of microorganism growth is made. The analysis first determines entropy of individual E. coli and Pseudomonas cells, and then entropy of a Pseudomonas colony during its lifespan.
4.1. Trends in microorganism thermodynamic parameters
Most living cells constitute of similar classes of molecules and thus have similar thermodynamic properties. All the analyzed microorganisms have very similar (hf⁰)bio, s⁰bio and (gf⁰)bio values, respectively (Fig. 1). The reason is that most living organisms share a very similar molecular structure: they are made mostly of water, lipids, proteins, carbohydrates and nucleic acids (Alberts et al., 2002). These compounds are major components of all living cells, because all existing life forms have evolved from a single common ancestor (last universal common ancestor, LUCA). The differences in cell phenotypes arise from the expressed proteins and distribution of constituent molecules. However, as can be seen from the general empirical formulas of bacteria (CH1.7O0.4N0.2), fungi (CH1.7O0.5N0.1) and algae (CH1.7O0.5N0.1), the general chemical constituents of all the three groups of organisms are very similar, resulting in similar elemental compositions and similar values of (hf⁰)bio, s⁰bio and (gf⁰)bio.
Formation of biomass from elements is always exothermic because there is partial oxidation of less electronegative elements in the biomass by oxygen and nitrogen. All analyzed microorganism species have very similar (hf⁰)bio which are all negative. The reason can be seen from the chemical equation representing biomass formation from elements:
| nc C + ½ nH H2 + ½ nO O2 + ½ nN N2 + nP P + nS S + nK K + nMg Mg + nCa Ca + nFe Fe → CnCHnHOnONnNPnPSnSKnKMgnMgCanCaFenFe | (40) |
Oxygen is the second most electronegative atom in the periodic table, after fluorine. Since there are no oxygen-fluorine compounds in the biomass and peroxides are not present in a high concentration, the oxidation state of oxygen is -2. Similarly, nitrogen is in the biomass mostly present in the form of amines, making its oxidation state -3. Thus, during formation of biomass from elements, oxygen and nitrogen change their oxidation states from 0 in their elemental forms to -2 and -3, respectively, in the biomass. This implies that there is partial oxidation of the other elements that constitute the biomass. This partial oxidation process, like all other oxidations, is exothermic and makes the enthalpy of formation of biomass from elements negative. This is in agreement with the results of Erickson et al. (1978, p. 1598), who found that microbial biomass synthesis from organic substrates (such as glucose) is exothermic, due to partial oxidation of the substrate by oxygen.
4.2. Microorganism metabolic rates
Metabolic rate of a living organism is the amount of energy it uses to sustain itself for a period of time and is expressed in watts. Specific metabolic rate is the metabolic rate of an organism divided by its mass and is expressed in watts per kilogram of body weight. For microorganisms, there are two metabolic rates of interest: endogenous metabolic rate and growth metabolic rate (Makarieva et al., 2005). Endogenous metabolic rate is the metabolic rate of nongrowing unicellular organisms in nutrient-free suspensions (Makarieva et al., 2008). It is the microorganism analog of basal or standard metabolic rate in animals (Makarieva et al., 2008). On the other hand, growth metabolic rate is the metabolic rate of microorganisms growing on a medium (Makarieva et al., 2005). Specific endogenous metabolic rates of some of the microorganisms in this study are given in Table 6.
Table 6.
Specific endogenous metabolic rates of microorganisms. The data was taken from Makarieva et al. (2008).
| Name | q (W/kg-wet mass) | mcell (pg) |
|---|---|---|
| Aerobacter aerogenes | 8.71 | 0.4 |
| Bacillus cereus | 21.92 | 3.7 |
| Escherichia coli | 5.22 | 0.7 |
| Escherichia coli K-12 | 14 | 0.7 |
| Escherichia coli W | 4.2 | 0.7 |
| Klebsiella aerogenes | 7.07 | 0.3 |
| Paracoccus denitrificans | 5.87 | 0.16 |
| Chlamydomonas reinhardtii | 15 | 19.4 |
| Chlorella pyrenoidosa | 7.7 | 30 |
| Selenastrum capricornutum | 21 | 22.432 |
Basal metabolic rates of many organisms can be predicted using Kleiber's law, which states that basal metabolic rate of an organism Q is proportional to its mass m: Q = 293 m3/4 (Kleiber, 1947; Balmer, 2010). This implies that the specific basal metabolic rate q is q = 293 m−1/4 (Balmer, 2010). Kleiber's law has been found to give good predictions of metabolic rates of animals (Balmer, 2010). However, Hemmingsen found that Kleiber's law does not hold for microorganisms (Blaxter, 1989, page 126). This result was confirmed in a later study by Makarieva et al. (2005), which involved 80 prokaryote species, and by Makarieva et al. (2008), involving 3006 species from all kingdoms. Thus, for microorganisms it is best to use their experimental metabolic rates. A comprehensive database with basal metabolic rates of many living organisms, including endogenous metabolic rates of microorganisms, can be found in the supplemental material of Makarieva et al. (2008). Growth metabolic rates of microorganisms are given in the supplemental material of Makarieva et al. (2005).
4.3. Thermodynamic analysis of microorganism growth
In this section, the results from section 3 will be applied to bacterial colony growth. Entropy of a single E. coli cell and a single Pseucomonas cell will be calculated, and entropy change of a growing Pseudomonas colony will be analyzed. The following analysis is based on two axioms:
-
1.
Microorganisms grow and multiply, making colonies, through cell division.
-
2.
Growth is caused by import and accumulation of substances taken from the surroundings, resulting in change in mass and volume of a colony.
Growth of microorganisms occurs in five phases, during time and culture aging: (1) lag, (2) exponential, (3) declining growth rate, (4) stationary and (5) death phase. Duration of the phases depend on availability of nutrients in the environment. The exponential phase is the period when growth is the most intense. The number of microorganisms is described as a function of time by the equation
| (41) |
where Ncells,0 is the initial cell number and td is division time (Widdel, 2010). A cell or a colony, as growing open systems, are characterized by thermodynamic parameters, including entropy (Battley, 1999a; von Stockar and Liu, 1999).
Entropy of a single E. coli cell was calculated using data from Table 2. A cell consists of dry biomass and water. Therefore, the total entropy of a cell, Scell, is
| (42) |
where s⁰bio is standard specific entropy of dry biomass (Table 2), mbio mass of dry biomass, mw mass of water in the cell, and sw⁰ standard specific entropy of water, which is 3.886 J/g K (Cox et al., 1984). Eq. (42) also contains entropy of hydration of biomass, (SP)hid. However, there is no method to accurately predict (SP)hid. Thus, (SP)hid was included into the error of s⁰bio given in Table 2, as is described in section 2.3, and (SP)hid was set to zero in Eq. (42). Finally, a single Escherichia coli cell weighs 9.5 · 10−13 g, containing 2.8 · 10−13 g (30%) of dry mass and 6.7 · 10−13 g (70%) of water (Neidhardt, 1996). Therefore, according to Eq. (42) the entropy of a single E. coli cell is (3.01 ± 0.05) · 10−12 J/K. A similar reasoning can be applied to a Pseudomonas cell. A Pseudomonas cell has a mass of 8 · 10−13 g, of which 70% is water (Makarieva et al., 2008). Using data from Table 2, entropy of a single Pseudomonas cell is (2.55 ± 0.04) · 10−12 J/K.
Based on entropy of a single cell and bacterial growth data, entropy of an E. coli colony was calculated as a function of time. Microorganisms live in colonies. The entropy of a colony is the sum of entropies of all microorganisms that comprise it
| (43) |
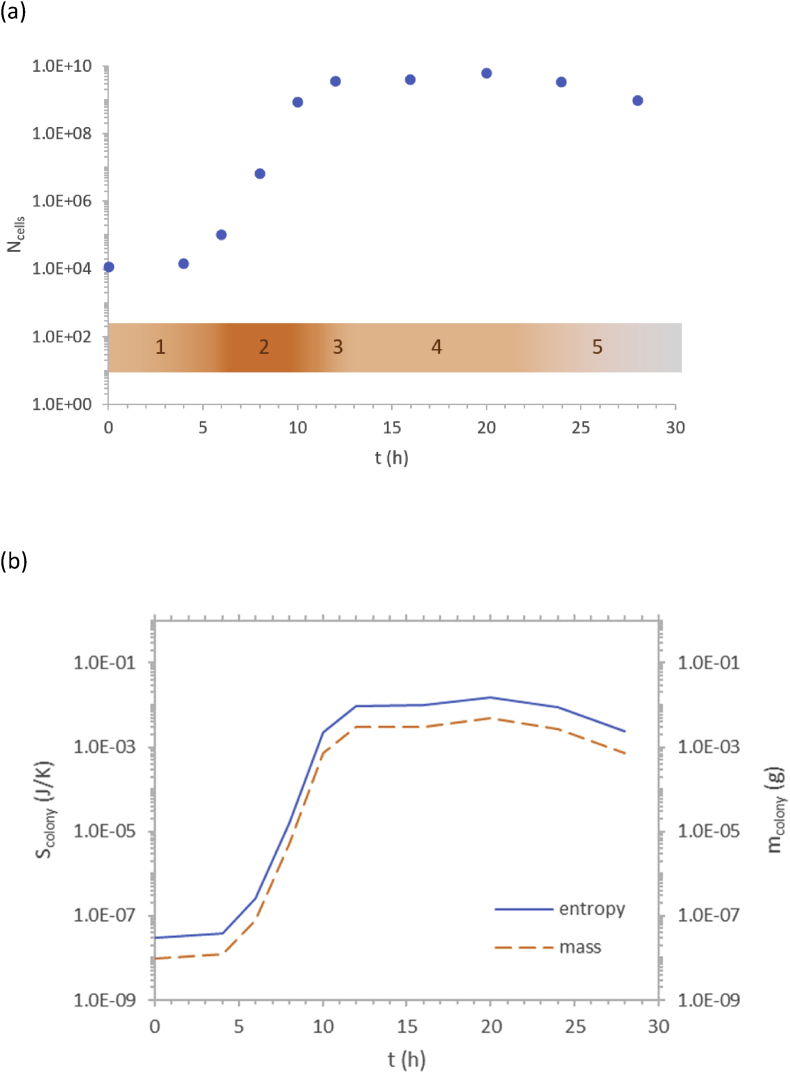
where Ncells is the initial number of cells in the colony. Since a colony grows during time through increase in cell number, its entropy changes. Therefore, using Eq. (43) and growth data, entropy of a microorganism colony can be determined as a function of time. Using growth data from Maier et al. (2009), entropy of a Pseudomonas colony throughout its lifespan was calculated and is shown in Fig. 2.
Fig. 2.
Thermodynamics of growth of a Pseudomonas colony. (a) Cell number versus time - growth curve data taken from Maier et al. (2009). The orange gradient line represents growth intensity, while the numbers on it indicate the growth phases: (1) lag, (2) exponential, (3) declining growth rate, (4) stationary and (5) death phase. (b) Colony entropy Scolony and mass mcolony as a function of time. Colony entropy was calculated through Eq. (43), using the previously calculated single cell entropy of (2.55 ± 0.04) ∙ 10−12 J/K. Colony mass was calculated as cell mass multiplied by number of cells. The entropy curve is represented by the full blue line, while the dashed orange line represents the mass curve.
As can be seen from Fig. 2, there is an exponential increase in both the number of cells and in entropy of the colony during the exponential phase of colony growth. This is a general trend, according to Eq. (43), since standard specific entropy of any substance, including living organisms, can only be positive due to the third law of thermodynamics, as discussed in section 3. Therefore, any growing organism increases its mass and entropy.
Three periods can be distinguished in the existence of a microorganism colony: (a) accumulation period when cell number, mass and entropy increase, (b) steady state period when they are approximately constant, and (c) decumulation period when they decrease. The Pseudomonas colony begins growth with 1.2 · 104 cells and an initial entropy of 3.1 · 10−8 J/K. Then, through import, accumulation of matter from the environment and cell division, the colony grows, and increases its mass and entropy to 9.4 · 10−3 J/K, after 12 hours. It is obvious that entropy of microorganisms, during colony life and aging, increases during the first three phases (lag, exponential and declining growth rate), corresponding to the accumulation period. During the fourth phase (stationary), cell number and entropy remain approximately constant in time, making the steady state period. Only in the last phase (death), due to lack of nutrients, the entropy of the colony begins to decrease due loss of living cells and the colony enters the death period. Finally, once the last cell has decomposed, the colony ceases to exist.
5. Conclusions
Elemental compositions have been collected and presented for 32 microorganism species, including 14 bacteria, 7 yeast and 11 algae species (Tables 1 and 2). All three classes have very similar average elemental compositions: bacteria CH1.7O0.4N0.2, fungi CH1.7O0.5N0.1 and algae CH1.7O0.5N0.1.
Enthalpy of combustion experimental data was used to compare five widely used predictive models: Patel-Erickson, Boie, Dulong, Mason-Gandhi and Channiwala-Parikh equations (Table 5). It was found that Patel-Erickson and Channiwala-Parikh equations give the most accurate predictions for microorganism biomass. The Patel-Erickson model was chosen to perform the calculations in this work, since it is the most appropriate for microorganism biomass composition data. Based on standard enthalpies of combustion of microorganism biomass, standard enthalpies of formation from elements were calculated.
Standard entropy of biomass was found from its elemental composition using the Battley equation, a model that can give accurate predictions for a wide range of organic compounds. Based on standard enthalpy of formation from elements and entropy, standard Gibbs free energy of formation from elements was calculated. Thermodynamic properties were calculated for the 32 microorganism species (Tables 1 and 2).
Trends in microorganism thermodynamic parameters were discussed. Each thermodynamic property has very similar values for all the analyzed microorganisms (Fig. 1). This is due to the fact that all living organisms share a universal common ancestor and thus have similar chemical compositions. Standard enthalpies of formation from elements of all analyzed microorganisms are negative, due to the fact that during hypothetical formation of biomass from elements oxygen and nitrogen partially oxidize other elements in the biomass. All microorganisms have positive standard specific entropy, due to the third law of thermodynamics. Gibbs energies of formation from elements of all the microorganisms are negative.
A brief review was made of microorganism endogenous and growth metabolic rates (Table 6). It has been found that it is best to use experimental values, since the subject literature shows that microorganism metabolic rates cannot be correlated using Kleiber's law.
Entropy a single E. coli cell has been found to be (3.01 ± 0.05) · 10−12 J/K, while entropy of a single Pseudomonas cell is (2.55 ± 0.04) · 10−12 J/K. Based on this value, entropy of a Pseudomonas colony was calculated during its lifespan (Fig. 2). During the log, exponential and declining growth rate phases entropy and mass of the colony both increase, in the stationary phase they are approximately constant, while in the death phase they decrease. Thus, three periods can be distinguished in the existence of a microorganism colony: accumulation period, steady state period, and decumulation period.
Declarations
Author contribution statement
Marko Popovic: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- Abbott B.J., Clamen A. The relationship of substrate, growth rate, and maintenance coefficient to single cell protein production. Biotechnol. Bioeng. 1973;15:117–127. doi: 10.1002/bit.260150109. [DOI] [PubMed] [Google Scholar]
- Alberts B., Johnson A., Lewis J., Raff M., Roberts K., Walter P. fourth ed. Garland Science; New York: 2002. Molecular Biology of the Cell. [Google Scholar]
- Annamalai K., Thanapal S.S., Ranjan D. Ranking renewable and fossil fuels on global warming potential using respiratory quotient concept. J. Combust. 2018;2018:16. Article ID 1270708. [Google Scholar]
- Atkins P., de Paula J. eighth ed. W. H. Freeman and Company; New York: 2006. Physical Chemistry. [Google Scholar]
- Balmer R.T. Academic Press; Burlington: 2010. Modern Engineering Thermodynamics. [Google Scholar]
- Battley E.H. An empirical method for estimating the entropy of formation and the absolute entropy of dried microbial biomass for use in studies on the thermodynamics of microbial growth. Thermochim. Acta. 1999;326:7–15. [Google Scholar]
- Battley E.H. The thermodynamics of microbial growth. In: Kemp E.B., editor. Handbook of Thermal Analysis and Calorimetry, vol. 4: From Macromolecules to Man. Elsevier; Amsterdam: 1999. pp. 219–235. [Google Scholar]
- Battley E.H. The development of direct and indirect methods for the study of the thermodynamics of microbial growth. Thermochim. Acta. 1998;309:17–37. [Google Scholar]
- Battley E.H., Putnam R.L., Boerio-Goates J. Heat capacity measurements from 10 to 300 K and derived thermodynamic functions of lyophilized Saccharomyces cerevisiae including the absolute entropy of formation at 298.15 K. Thermochim. Acta. 1997;298:37–46. [Google Scholar]
- Battley E.H. On the enthalpy of formation of Escherichia coli K-12 cells. Biotechnol. Bioeng. 1992;39:5–12. doi: 10.1002/bit.260390103. [DOI] [PubMed] [Google Scholar]
- Bauer S., Ziv E. Dense growth of aerobic bacteria in a bench-scale fermentor. Biotechnol. Bioeng. 1976;18:81–94. doi: 10.1002/bit.260180107. [DOI] [PubMed] [Google Scholar]
- Blaxter K. Cambridge University Press; Cambridge: 1989. Energy Metabolism in Animals and Man. [Google Scholar]
- Campbell N.A., Reece J.B. sixth ed. Benjamin Cummings; New York: 2002. Biology. [Google Scholar]
- Cordier J.L., Butsch B.M., Birou B., von Stockar U. The relationship between elemental composition and heat of combustion of microbial biomass. Appl. Microbiol. Technol. 1987;25:305–312. [Google Scholar]
- Cox J.D., Wagman D.D., Medvedev V.A. Hemisphere Publishing Corp; New York: 1984. CODATA Key Values for Thermodynamics. [Google Scholar]
- Demirel Y. third ed. Elsevier; Amsterdam: 2014. Nonequilibrium Thermodynamics: Transport and Rate Processes in Physical, Chemical and Biological Systems. [Google Scholar]
- Duboc P., Marison I., von Stockar U. Quantitative calorimetry and biochemical engineering. In: Kemp R.B., editor. Handbook of Thermal Analysis and Calorimetry Vol. 4: from Molecules to Man. Elsevier; Amsterdam: 1999. pp. 267–365. [Google Scholar]
- Erickson L.E., Minkevich I.G., Eroshin V.K. Application of mass and energy balance regularities in fermentation. Biotechnol. Bioeng. 1978;20:1595–1621. [PubMed] [Google Scholar]
- Harrison J.S. Aspects of commercial yeast production. Process Biochem. 1967;2:41–45. [Google Scholar]
- Herbert D. Stoichiometric aspects of microbial growth. In: Dean A.C.R., Ellwood D.C., Evans C.G.T., Melling J., editors. Continuous Culture 6: Applications and New fields. Ellis Horwood; Chichester, England: 1976. pp. 1–30. [Google Scholar]
- Heymsfield S.B., Wang Z., Baumgartner R.N., Dilmanian F.A., Ma R., Yasumura S. Body composition and aging: a study by in vivo neutron activation analysis. J. Nutr. 1993;123(2-Suppl):432–437. doi: 10.1093/jn/123.suppl_2.432. [DOI] [PubMed] [Google Scholar]
- Kiang Y. 2012. An universal method to predict higher heating values of fuel compounds.https://www.researchgate.net/publication/304717597_An_universal_method_to_predict_higher_heating_values_of_fuel_compounds [online] Research Gate. Available at. [Google Scholar]
- Kleiber M. Body size and metabolic rate. Physiol. Rev. 1947;27(4):511–541. doi: 10.1152/physrev.1947.27.4.511. [DOI] [PubMed] [Google Scholar]
- Kok H.E.D., Roels J.A. Method for the statistical treatment of elemental and energy balances with application to steady-state continuousculture growth of Saccharomyces cerevisiae CBS 426 in the respiratory region. Biotechnol. Bioeng. 1980;22:1097–1104. [Google Scholar]
- Makarieva A.M., Gorshkov V.G., Li B.L., Chown S.L., Reich P.B., Gavrilov V.M. Mean mass-specific metabolic rates are strikingly similar across life’s major domains: evidence for life’s metabolic optimum. Proc. Natl. Acad. Sci. U.S.A. 2008;105(44):16994–16999. doi: 10.1073/pnas.0802148105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makarieva A.M., Gorshkov V.G., Li B.L. Energetics of the smallest: do bacteria breathe at the same rate as whales? Proc. R. Soc. B. 2005;272:2219–2224. doi: 10.1098/rspb.2005.3225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manahan S., Manahan S.E. ninth ed., ninth ed. CRC Press; Boca Raton: 2009. Environmental Chemistry. [Google Scholar]
- Mayberry W.R., Prochazka G.J., Payne W.J. Factors derived from studies of aerobic growth in minimal media. J. Bacteriol. 1968;96:1424–1426. doi: 10.1128/jb.96.4.1424-1426.1968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maier R.M., Pepper I.L., Gerba C.P. second ed. Elsevier; Amsterdam: 2009. Environmental Microbiology. [Google Scholar]
- Minas de Piedade M.E. Oxygen bomb combustion calorimetry: principles and applications to organic and organometallic compounds. In: Minas de Piedade M.E., editor. Energetics of Stable Molecules and Reactive Intermediates. Springer; Berlin: 1999. pp. 29–54. [Google Scholar]
- Morowitz H.J. Yale University Press; New Haven: 1992. Beginnings of Cellular Life: Metabolism Recapitulates Biogenesis. [Google Scholar]
- Morowitz H.J. Some order-disorder considerations in living systems. Bull. Math. Biophys. 1955;17:81–86. [Google Scholar]
- Naresh M., Das S., Mishtra P., Mittal A. The chemical formula of a magnetotactic bacterium. Biotechnol. Bioeng. 2011;109(5):1205–1216. doi: 10.1002/bit.24403. [DOI] [PubMed] [Google Scholar]
- Neidhardt F.C. Vol. 1. ASM Press; 1996. p. 14. (Escherichia coli and Salmonella: Cellular and Molecular Biology). [Google Scholar]
- Patel S.A., Erickson L.E. Estimation of heats of combustion of biomass from elemental analysis using available electron concepts. Biotechnol. Bioeng. 1981;23:2051–2067. [Google Scholar]
- Phukan M.M., Chutia R.S., Konwar B.K., Kataki R. Microalgae Chlorella as a potential bio-energy feedstock. Appl. Energy. 2011;88:3307–3312. [Google Scholar]
- Popovic M. 2018. Thermodynamic Mechanism of Life and Aging. arXiv, arXiv:1801.08073 [q-bio.OT] [Google Scholar]
- Popovic M. 2017. Researchers in an Entropy Wonderland: A Review of the Entropy Concept. arXiv, arXiv:1711.07326. [Google Scholar]
- Popovic M. Living organisms from Prigogine’s perspective: an opportunity to introduce students to biological entropy balance. J. Biol. Educ. 2017;52(3):294–300. [Google Scholar]
- Prajapati S.K., Malik A., Vijay V.K. Comparative evaluation of biomass production and bioenergy generation potential of Chlorella spp. through anaerobic digestion. Appl. Energy. 2014;114:790–797. [Google Scholar]
- Schrödinger E. The Physical Aspect of the Living Cell. Cambridge university press; Cambridge: 2003. What is life? 10th printing. [Google Scholar]
- Shimizu T., Furuki T., Waki T., Ichikawa K. Metabolic characteristics of denitrification by Paracoccus denitrificans. J. Ferment. Technol. 1978;56:207–213. [Google Scholar]
- Stouthamer A.H. Theoretical calculations on the influence of the inorganic nitrogen source on parameters for aerobic growth of microorganisms. Antonie Leeuwenhoek. 1977;43:351–367. doi: 10.1007/BF02313762. [DOI] [PubMed] [Google Scholar]
- Thornton W.M. The relation of oxygen to the heat of combustion of organic compounds. Philosophical Magazine Series 6. 1917;33(194):196–203. [Google Scholar]
- van Dijken J.Pv., Harder W. Growth yields of microorganisms on methanol and methane. A theoretical study. Biotechnol. Bioeng. 1975;17:15–30. [Google Scholar]
- van Loo S., Koppejan J. Earthscan; London: 2008. The Handbook of Biomass Combustion and Co-firing. [Google Scholar]
- von Bertalanffy L. The theory of open systems in physics and biology. Science. 1950;111(2872):23–29. doi: 10.1126/science.111.2872.23. [DOI] [PubMed] [Google Scholar]
- von Stockar U., Liu J. Does microbial life always feed on negative entropy? Thermodynamic analysis of microbial growth. Biochim. Biophys. Acta. 1999;1412(3):191–211. doi: 10.1016/s0005-2728(99)00065-1. [DOI] [PubMed] [Google Scholar]
- von Stockar U. Biothermodynamics of live cells: a tool for biotechnology and biochemical engineering. J. Non-Equilib. Thermodyn. 2010;35:415–475. [Google Scholar]
- Wang H.Y., Mou D.G., Swartz J.R. Thermodynamic evaluation of microbial growth. Biotechnol. Bioeng. 1976;18:1811–1814. [Google Scholar]
- Wang L., Wang X., Jin X., Xu J., Zhang H., Yu J., Sun Q., Gao C., Wang L. Analysis of algae growth mechanism and water bloom prediction under the effect of multi-affecting factor. Saudi J. Biol. Sci. 2017;24:556–562. doi: 10.1016/j.sjbs.2017.01.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Widdel F. 2010. “Theory and Measurement of Bacterial Growth” Grundpraktikum Mikrobiologie, 4. Sem. (B.Sc.)https://www.mpi-bremen.de/Binaries/Binary307/Wachstumsversuch.pdf Available at: [Google Scholar]