DL-3-Aminoisobutyric acid: vibrational, NBO and AIM analysis of N–H⋯O bonded-zwitterionic dimer model

Abstract

A zwitterionic dimer model constructed of inter-molecular –N–H⋯O bonding has been proposed for the solid sample of DL-3-Aminoisobutyric acid consistent with IR absorption and Raman spectral features measured in the 3500–400/50 cm⁻¹. This zwitterionic dimer model in water as solvent has been computed at B3LYP/6–311++G(d,p) and B3LYP-D3/6–311++G(d,p) levels including Grimme's dispersion correction associated with the –N–H⋯O interaction and SCRF-SMD method. Of the several possible monomer and dimer conformational structures, the most stable dimer constructed of two zwitterion monomer units has produced vibrational modes due to the –NH₃⁺ cation and –CO₂‾ anion involved in the –N–H⋯O bonding in fair agreement with the observed broad but composite IR modal features near the 3500–2000 cm⁻¹. Except for the frequency of asymmetric stretching mode of the –NH₃⁺ cation, its symmetric and bending modes agree with the observed values. As for the –CO₂‾ anion, the frequencies of all of its modes are in good agreement with the experiment. Natural bond orbital (NBO), molecular electrostatic potential (MEP), atoms-in-molecules (AIM) and non-covalent interaction (NCI) analyses have been used to understand electronic characterization of the –N–H⋯O bonding.

1. Introduction

Amino acids are the building blocks of polypeptides and proteins with diverse structural and functional properties. They have been and still are of fundamental importance because of their vital role in the vast biological landscape. Lately non-proteinogenic amino acids, also called unnatural amino acids, have also aroused interest for similar reasons including pharmaceutical applications [1, 2]. Biochemical activities in biological species primarily involve non-covalent interactions, say, among amino acids and other molecular fragments, for example, in bases in DNA and RNA; the interactions include H-bonding and stacking. The common H-bonds are O–H⋯O, N–H⋯O, C–H⋯O, and so on [3]. Invariably the amino acids or unnatural amino acids have the neutral structures (NE) in the gas phase and zwitterionic structure (ZW) in the condensed phase. They are categorized as α, β, γ and δ-amino acids depending on the position of amino group (−NH₂) in the carbon chain [4, 5, 6]. Although β-amino acids are less abundant than their α-analogues, they occur in nature both in free and peptide-bound species [7, 8]. The oligomers containing β-amino acids have emerged as promising tools in medicinal chemistry with higher stability toward common peptides as they possess the potential to fold into secondary structures consisting of helices, turns and pleated sheets [7, 8, 9, 10]. The title molecule, DL-3-Aminoisobutyric acid (for short 3AIBA) being synonymous with α-Methyl-β-alanine, is a β-amino acid which occurs naturally in all living organisms. In humans and animals, 3AIBA can be formed from the nucleotide thymine and also from the amino acid valine [11, 12]. Since 3AIBA is structurally similar to β-alanine, it can also be called as α-methyl-β-alanine having one additional methyl group on α-carbon atom. In their free form, β-alanine and 3AIBA are found as metabolites in the mammals and also as moieties in several pharmacologically active compounds such as antibiotics, antitumor agents and antifungal agents [7, 8, 10, 13].

Among the non-covalent interactions, namely, H-bonding, π-stacking, van der Waals and electrostatic types, the landscape for H-bonding interactions is vast with implications across diverse supramolecular systems, nanostructures and nano-biomaterials [14, 15]. The nearest competitor to H-bonding is π-stacking interaction. Both H-bonding and π-stacking interactions are proved determinants in DNA-protein interactions for molecular recognition. The van der Waals and hydrophobic interactions, of course, play their role as well but as secondary determinants [16]. In a combined theoretical and experimental study, Krylov et al. have shown that H-bonding, among non-covalent interactions, influence ionization energies (IEs) of the dimers of nucleic acid bases: adenine-adenine, thymine-thymine and adenine-thymine dimers [17]. In a detailed theoretical and experimental study on the nine possible 2-pyridone-n-fluorobenzene dimer species, Leutwyler et al. have shown that H-bonding and π-stacking compete with small energy differences, both of which being accounted satisfactorily by the coupled-cluster model comprising single and double excitations with a perturbative corrections for triple excitations (CCSD(T)) [18]. In constructing 2D supramolecular networks, the role of multiple H-bonds has been ascertained in the structural polymorphism at the solid-liquid interface [19, 20, 21, 22, 23, 24]. In particular, the role of multiple H-bonds in inducing chirally different morphologies in a series of self-assembled nanostructures of 2-hydroxyl-7-pentadecyloxy-fluorenone has been demonstrated by Wenli Deng et al [25]. Some experimental vibrational studies and electronic structure calculations have also been reported for NE and ZW species of amino acids and aminophosphates [26, 27, 28].

Experimental and theoretical vibrational spectroscopy are proved techniques for investigating structural and/or conformational aspects of H-bonded molecular systems and their complexation with other molecules with potential implications for understanding the role of H-bonding in diverse material and biological phenomena [29, 30, 31, 32]. In the present work we study the role of inter-molecular –N–H⋯O bonding in building dimer species of 3AIBA and characterize dimerization on the basis of the structural, spectral and electronic properties. H-bond-induced dimer structures are of interest in decoding molecular vibrational structures since it is reasonable to assume the dimer species as basic units of intermolecular association in condensed phases [33, 34]. It is profitable to correlate structural, electronic and vibrational characterization with observed vibrational IR and Raman spectral features. Electronic structure calculations from density functional theory (DFT) codes provide an opportunity to model electronic and vibrational properties corresponding to different stable NE conformers in gas phase and ZW conformers in solvent media which are otherwise experimentally difficult to realize. Experimental IR spectrum of 3AIBA shows a very broad composite band structure across 3500–2000 cm⁻¹, making assignments of the bands untenable. It calls for the construction of possible ZW dimer species defined by H-bonding between –NH₃⁺and –CO₂‾ groups and such dimer species would yield vibration modes for the satisfactory characterization of the observed IR and Raman spectral features and provide enhanced understanding of the involvement of electronic molecular orbital in –N–H⋯O bonding. We have carried out this proposed work using DFT modeling and NBO analysis. The NBO provides a satisfactory understanding of the stability of the H-bonded dimer species in terms of perturbative interaction energies resulting from the overlap integral between the lone-pair orbital of the donor and the anti-bonding orbital of the acceptor in the –N–H⋯O bonding. All these aspects constitute the principal aim of the present work.

Experimental and computational studies of NE form of β-alanine crystals and its ZW form in the aqueous media have been reported [35, 36]. The XRD structural studies of H-bonding in a series of amino-substituted carboxylic acids have been investigated [37, 38, 39]. The first among the series is γ–aminobutyric acid (GABA). The room and low temperatures structural studies of monoclinic phase of GABA have been carried out by different workers [40, 41, 42]. In monoclinic phase, the molecule is observed as partially folded zwitterion in gauche conformation. The ZW form of GABA is again observed in the tetragonal phase [37]. The three hydrogen atoms of –NH₃⁺ form three strong H-bonds as in the monoclinic phase, but there is additional fourth weaker H-bond resulting in a two-centre bifurcated bond. Also the evidence suggests that there is an intramolecular –N–H⋯O bridge bond. The three strong H-bonds are similar in both monoclinic and tetragonal phases. There are infinite chains of H-bonded molecules running in one dimension that are cross-linked by the remaining H-bonds to form a three dimensional network. The major difference in both phases is that monoclinic structure shows gauche conformation while the tetragonal structure shows trans conformation of CH₂–CH₂ groups. Subsequent XRD study on another member of the series, 8-Aminocaprylic acid (8ACA) has been shown to crystallize inthe centrosymmetric space group P2₁/n in the extended ZW form upon dissolving in water [38]. It forms five intermolecular H-bonds, two of which are bifurcated. Each molecule is linked to six neighbouring molecules by a total of ten H-bonds in the monoclinic phase. DL-3-Aminoisobutyric acid monohydrate (DL-3-AIBA·H₂O) whose structure is comparable with the afore-mentioned molecules crystallizes in the orthorhombic with centrosymmetric space group Pbca as a partially folded ZW. With this structure each acid molecule and its associated water molecule are directly H-bonded to five acid molecules and two water molecules. The three hydrogens in the –NH₃⁺ group form inter-molecular H-bonding with the two –CO₂‾ groups of the neighboring molecules and one water molecule. The N⋯O distances range from 2.758 to 2.809 Å and –N–H⋯O angles from 149 to 171^° [39]. It is therefore reasonable to assume that the 3AIBA has also ZW form with affinity for inter-molecular –N–H⋯O bonding as is true for DL-3-Aminoisobutyric acid monohydrate. This is borne out by the fact that in the present work, some strong IR absorptions in the region 1675-1400 cm⁻¹ are presumably produced by the –NH₃⁺ and –CO₂‾ groups as characteristic vibrational modes and a medium weak but highly characteristic band at 2139 cm⁻¹ is the signature of the sum of the frequencies of asymmetric bending and torsional modes of –NH₃⁺ group. This sum mode is the most reliable characteristic band for the identification of the –NH₃⁺ cation in all the amino acids with ZW structure [43, 44]. In our previous study, it was satisfactorily explained the observed vibrational spectral features of L-β-Homoserine in terms of ZW dimer structures characterized by inter-molecular –N–H⋯O and –O–H⋯O bonding [45]. To account for the vibrational structure of 3AIBA, we computed seven –N–H⋯O bonded ZW dimer structures, of which the most stable one has produced a molecular structure and vibrational bands, namely, due to the –NH₃⁺, –CO₂‾ groups and –N–H⋯O bonding, in fair agreement with the experimental IR and Raman spectral features. Overall, the computed structural parameters of this dimer species are in fair agreement with the experimental crystal structure of 3AIBA monohydrate within 4%. A detailed NBO analysis has provided such properties as molecular orbital occupancies, charges on the atoms and the second order perturbative energies which support the strong –N–H⋯O bonding in the most stable dimer species (D₁) referred to above. Further, topological AIM and NCI analyses have been performed to characterize the H-bonding in D₁ and its MEP surface has been plotted to understand the reactivity of the molecule.

2. Experimental

2.1. Experimental measurements

The solid sample of DL-3-Aminoisobutyric acid was purchased from Sigma Aldrich Chemical Company and used without further purification. FT-IR spectra of the pellets made up of solid sample were recorded on a Nicolet 6700 FT-IR spectrometer that uses an Alum standard ETC Ever-Glo IR source, Deuterated Triglycine Sulphate (DTGS) detector equipped with KBr window. Pellets were prepared by taking the sample and KBr in 1:100 ratio and the spectra were recorded with 4 cm⁻¹ resolution in the region 4000 − 400 cm⁻¹ for 50 scans. Raman spectra of solid sample were recorded without sample preparation on the Nicolet NXR-FT-Raman Module spectrometer that uses a Nd:YVO₄ (1064 nm) laser as a source of excitation, CaF₂ beam splitter and liquid nitrogen cooled Ge detector. The spectra were recorded with 4 cm⁻¹ resolution in the region 4000–100 cm⁻¹ for 500 scans.

2.2. Computational modeling

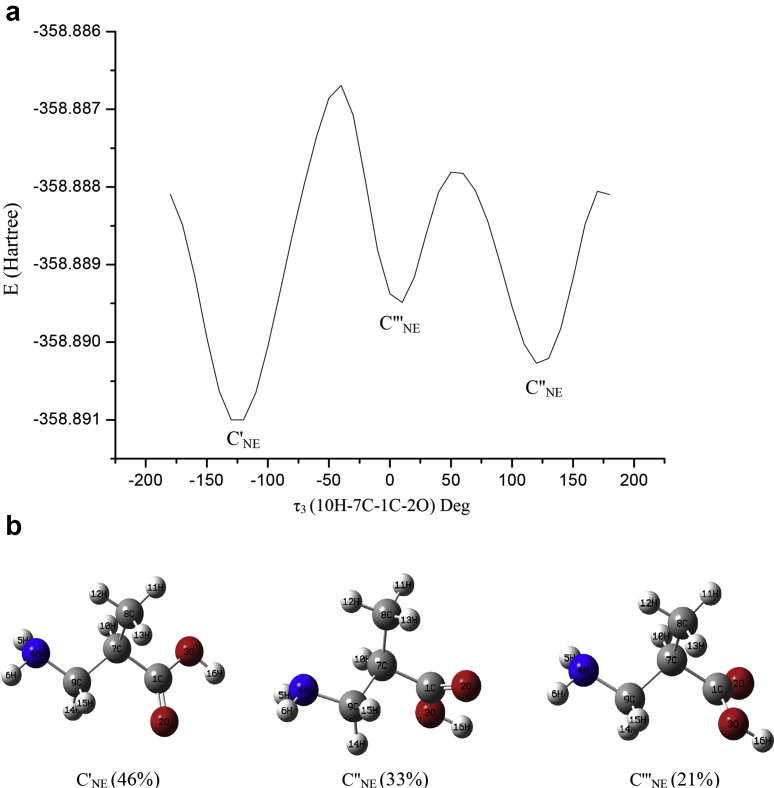
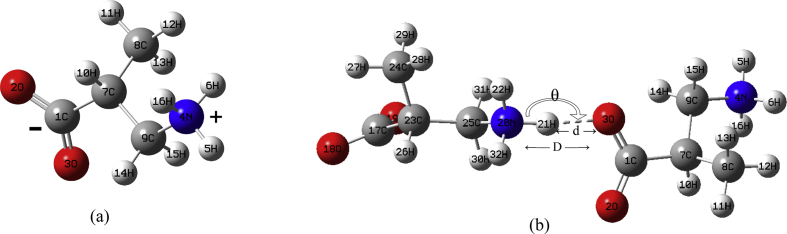
The electronic structure calculations have been performed using the Gaussian 09W and GaussView5 suite of programs [46, 47]. In order to minimize the computational cost, we did two jobs in tandem, firstly Restricted Hartree-Fock (RHF)/3-21G level of calculation followed by a second calculation at B3LYP/6–311++G(d,p) level [48]. To reduce the computational cost, the most stable NE conformers in gas phase were searched by a relaxed potential energy surface (PES) scan at the RHF/3-21G level. Initially, the dihedral angles, τ₁ (16H–3O–1C–2O) and τ₂ (14H–9C–4N–6H) were varied simultaneously with 10^° interval from -180° to 180° and from 0° to 360° (refer Fig. 1 for τ_1, τ_2, τ₃ and 2(b) for atom numbering). During the relaxed scan, all the internal coordinates were relaxed while the dihedral angles τ₁ and τ₂ were fixed at the specified values. The PES for this scan shows three minimum energy structures (Fig. 2(a)). The full optimization of these structures followed by frequency calculation was performed at B3LYP/6–311++G(d,p) level. Among the optimized structures, the one with lowest energy is considered to be more stable. This stable structure in NE form is shown in Fig. 2(b). In order to fix the orientation of carboxylic group for this minimum energy structure, we further scanned the dihedral angle τ₃ (10H–7C–1C–2O) from -180° to 180°. This relaxed PES scan resulted in three minima (Fig. 3(a)). Further optimization of these structures followed by frequency calculations at B3LYP/6–311++G(d,p) level yielded three true structures with no imaginary harmonic frequencies. These three NE conformers we call C'_NE, C″_NE, C‴_NE are presented in Fig. 3(b) and their optimized dihedral angles, geometrical parameters, Gibbs free energies and relative Boltzmann populations are presented in Tables 1 and 2. Further optimization of the conformers to search for ZW forms was performed using the Self-Consistent Reaction Field implicit Solvation Model based on Charge Density (SCRF-SMD) in water medium [35, 49, 50]. The optimization yielded only one stable ZW monomer, say, C_ZW, shown in Fig. 4 and its geometrical parameters are given in Table 2. Next we considered building possible dimer structures as a combination of C'_NE, C″_NE, C‴_NE and C_ZW, inter-linked by –N–H⋯O bonding. We ran calculations at RHF/3-21G level, giving rise to seven ZW dimer structures, say, D₁, D₂,….,D₇, that are collected in Fig. 5. The Gibbs free energies and Boltzmann populations of all the dimers are presented in Table 3. Consecutive differences in Boltzmann populations of D₁ to D₇ show that structurally and energetically D₁ is the most stable structure. Further, the five dimer species, D₁–D₅, are close to one another with respect to their energies and vibrational frequencies and all of their Boltzmann populations add up to 98%. Accordingly, as a reasonable approximation, we chose D₁ as a representative species for further optimization, harmonic frequency calculation and NBO analysis at B3LYP/6–311++G(d,p) level and its results will be used in the forthcoming discussion. The resultant geometrical structure of D₁ is shown in Fig. 4 and H-bonding parameters are presented in Table 2. In order to include Grimme's dispersion correction associated with the –N–H⋯O interaction, we ran calculation at B3LYP-D3/6–311++G(d,p) level. We found that both the optimized dispersion-corrected energies and frequencies hardly differed from the results without dispersion correction [51, 52]. We have based vibrational mode analysis on potential energy distributions (PED) computed from VEDA program [54]. The AIM analysis has been carried out using Multiwfn software and the isosurfaces are visualized using VMD software package [55, 56].

Fig. 1.

Molecular structure of DL-3-Aminoisobutyric acid showing the dihedral angles τ₁, τ₂, τ₃ used for PES scan.

Fig. 2.

(a). PES scan curve of DL-3-Aminoisobutyric acid showing three minima for the dihedral angles τ₁ = 16H– 3O–1C–2O and τ₂ = 14H–9C–4N–6H at RHF/3-21G level. (b). Optimized structure of DL-3-Aminoisobutyric acid obtained by PES scan for τ₁ and τ₂ in NE form at B3LYP/6–311++G(d, p) level.

Fig. 3.

(a). PES curve for the dihedral angle τ₃ = 10H–7C–1C–2O yielding the stable conformers C'_NE, C″_NE and C‴_NE of DL-3-Aminoisobutyric acid at RHF/3-21G level. (b). Optimized structures (C'_NE, C″_NE and C‴_NE) of DL-3-Aminoisobutyric acid in NE form at B3LYP/6–311++G(d, p) level (values given in paranthesis are their Boltzmann populations).

Table 1.

Optimized dihedral angles, Gibbs free and relative energies, Boltzmann population of the NE monomers of DL-3-Aminoisobutyric acid in gas phase.

Monomers	Dihedral angles (in deg)∗			Gibbs free energy G (Hartree)	ΔG (kcal/mol)	% Population
	τ1	τ2	τ3
C'NE	-1.3	72.3	-145.3	-363.0746	0	46
C″NE	0.8	73.5	157.0	-363.0743	0.201	33
C‴NE	0.3	71.8	4.8	-363.0738	0.483	21

^∗τ₁, τ₂, τ₃ as shown in Fig. 1.

Table 2.

Optimized geometrical parameters of NE monomers (C'_NE ₋ C‴_NE), ZW monomer (C_ZW) and dimer (D₁) of DL-3-Aminoisobutyric acid.

Parameters	C'NE	C″NE	C‴NE	CZW	D1	Expta
Bond length (Å)
1C–2O	1.206	1.206	1.206	1.264	1.256	1.247
1C–3O/17C–19O∗	1.358	1.359	1.360	1.264	1.272/1.263∗	1.251
1C–7C	1.514	1.516	1.515	1.544	1.540	1.520
3O–16H	0.969	0.969	0.969	--	--	--
9C–4N/25C–20N∗	1.467	1.465	1.465	1.507	1.507/1.499∗	1.484
9C–7C	1.538	1.550	1.544	1.527	1.527	1.522
9C–14H	1.098	1.099	1.100	1.088	1.088	1.000
9C–15H	1.092	1.093	1.092	1.088	1.088	1.020
4N–5H/20N–21H∗	1.015	1.014	1.015	1.023	1.022/1.063∗	0.960
4N–6H/20N–22H∗	1.013	1.013	1.013	1.023	1.023/1.022∗	1.050
4N–16H/20N–32H∗	--	--	--	1.023	1.023/1.022∗	0.970
8C–7C	1.542	1.530	1.538	1.539	1.539	1.528
8C–11H	1.091	1.092	1.092	1.092	1.092	0.970
8C–12H	1.090	1.090	1.090	1.094	1.093	1.060
8C–13H	1.093	1.092	1.092	1.093	1.093	1.010
7C–10H	1.095	1.094	1.093	1.094	1.094	0.980
RMSD	0.0700	0.0704	0.0704	0.0619	0.0649
Bond angle (in deg)
2O–1C–3O	122.0	121.9	121.8	125.2	124.8	124.3
2O–1C–7C	125.9	125.9	125.8	118.0	117.6	118.0
3O–1C–7C	111.9	111.9	112.2	116.7	117.4	117.6
1C–3O–16H	107.0	107.0	107.0	--	--	--
4N–9C–7C/20N–25C–23C∗	110.3	110.3	110.1	111.3	111.3/111.9∗	112.3
4N–9C–14H	113.4	113.2	113.2	105.9	106.0	104.5
4N–9C–15H	108.3	108.2	108.2	106.5	106.5	106.5
7C–9C–14H	109.0	109.1	109.0	111.4	111.3	112.5
7C–9C–15H	108.8	108.4	108.9	112.2	112.2	111.0
15H–9C–14H	106.5	107.2	107.0	108.9	108.9	109.0
9C–4N–5H	111.1	111.1	111.1	110.9	110.5	108.0
9C–4N–6H	110.9	111.1	111.0	110.5	111.6	106.7
9C–4N–16H	--	--	--	111.7	111.0	112.6
5H–4N–6H	107.1	107.4	107.3	107.9	107.6	106.0
5H–4N–16H	--	--	--	107.7	107.9	111.0
6H–4N–16H	--	--	--	107.7	107.9	110.0
7C–8C–11H	111.2	111.2	111.1	110.2	110.3	110.0
7C–8C–12H	109.0	109.3	109.1	111.9	111.6	112.0
7C–8C–13H	110.5	110.4	110.8	110.8	110.8	109.0
11H–8C–12H	109.1	108.8	108.7	107.1	107.1	107.0
11H–8C–13H	108.5	107.9	108.3	108.3	108.4	110.0
12H–8C–13H	108.2	108.9	108.5	108.1	108.2	106.0
1C–7C–9C	110.4	108.1	110.7	110.4	110.5	113.2
1C–7C–8C	109.3	111.4	111.1	109.0	109.1	108.6
1C–7C–10H	107.2	107.2	104.9	107.1	106.7	109.4
9C–7C–8C	112.3	112.1	112.2	112.8	112.9	109.6
9C–7C–10H	109.1	107.4	108.3	108.4	108.5	108.1
8C–7C–10H	108.2	110.2	109.1	108.7	108.6	109.8
RMSD	3.4560	3.5830	3.5062	1.7860	1.8596
Dihedral angle (in deg)
16H–3O–1C–2O	-1.3	0.8	0.3	--	--	--
14H–9C–4N–6H	72.3	73.5	71.8	-60.1	-60.84	--
10H–7C–1C–2O	-145.3	157.0	4.8	-149.6	-146.5	--
Hydrogen bonding parameters
20N–21H (r)	--	--	--	--	1.063	1.050
21H⋯3O (d)	--	--	--	--	1.663	1.730
20N⋯3O (D)	--	--	--	--	2.721	2.758
20N–21H⋯3O (θ)	--	--	--	--	172.9	166.0

^aXRD data of DL-3-Aminoisobutyric acid monohydrate [39].

Fig. 4.

Optimized (a) C_ZW, (b) D₁ structures of DL-3-Aminoisobutyric acid showing the hydrogen bonding parameters d, D, θ (parameter values are given in Table 2).

Fig. 5.

Optimized structures of zwitterionic dimers D₁ to D₇ computed at RHF/3-21G level.

Table 3.

Gibbs free and relative energies of seven ZW dimers with their Boltzmann population.

Dimer	Gibbs free energy G(Hartree)	Relative Energy ΔG (kcal/mol)	Population (%)
D1	-717.601533	0	35.56
D2	-717.600996	0.337	20.20
D3	-717.600917	0.387	18.59
D4	-717.600594	0.589	13.23
D5	-717.600318	0.762	9.89
D6	-717.598533	1.883	1.51
D7	-717.598126	2.138	0.98

3. Results and discussion

3.1. Structural analysis

The computed C_ZW and D₁ species with the –N–H⋯O bonding are shown in Fig. 4. The optimized geometrical parameters of NE monomers C'_NE, C″_NE, C‴_NE, ZW monomer C_ZW and dimer D₁ compared with the XRD data of DL-3-Aminoisobutyric acid monohydrate by means of root-mean-square-deviation (RMSD) values are presented in Table 2. The low RMSD values of C_ZW and D₁ for bond lengths (0.0163 and 0.0231 Å) and bond angles (0.8093 and 0.3905^°) show the good agreement with XRD data than NE monomers (0.0487–0.0498 Å for bond lengths and 5.0272–5.1152^° for bond angles). From Table 2, we note that the –N–H bond lengths are 1.023 Å in C_ZW as well as in D₁ where the –N–H bonds are free. But the r = N–H bond length at the H-bonded region is 1.063 Å showing the elongation of the bond up to 4%. The bond angle Ɵ = N–H⋯O is 173^°. The d = H⋯O distance is 1.663 Å, being shorter than the sum of the van der Waals radii of H and O, D = 2.721 Å and the –N⋯O distance is 2.726 Å, apparently indicating rather a strong H-bonding [3, 57]. Elongation in r causes decrease in both force constant and stretching frequency in D₁. For example, the 20N–21H bond vibrates at the frequency, 2612 cm⁻¹, which is lower than the frequencies, 3399 and 3349 cm⁻¹ of the 20N–22H and 20N–32H bonds. The bonds adjacent to the –N–H⋯O, namely, the –C=O corresponding to the 1C–3O bond and the –C–N corresponding to the 25C–20N bond have respectively also shown a small increase and decrease in their values from C_ZW to D₁. These changes are consistent with NBO analysis to be discussed in the following sections.

3.2. NBO analysis

NBO analysis has originated as a method for studying hybridization and covalency effects in polyatomic wave functions associated with, among other factors, intermolecular associations [58, 59, 60, 61, 62]. NBO analysis was performed for the monomer C_zw and dimer D₁ of 3AIBA using NBO Version 3.1 implemented in the Gaussian 09 package at B3LYP/6–311++G(d,p) level and the results are presented in Tables 4 and 5. The Tables show the occupancies, description of NBOs, polarization coefficients c_A², c_B² (in %) and the contribution of s character (in %) on each atom forming a bond in the monomer C_zw and dimer D₁. The following features are observed from the NBO results:

• (i)The σ(1C–2O), π(1C–2O) and σ(1C–3O) are strongly polarized towards the oxygen atom in both the C_zw and D₁. The occupancies of these bond orbitals are less in the D₁ compared to those in the C_zw.
• (ii)Again in both C_zw and D_1, the σ*(1C–2O) and σ*(1C–3O) are polarized towards the carbon atom while π*(1C–2O) is still more polarized towards the carbon atom. Occupancies of σ* and π* orbitals of the 1C–2O bond are less in the D₁ whereas that of σ*(1C–3O) is large.
• (iii)In both C_zw and D₁ for σ(1C–2O), σ(1C–3O), σ*(1C–2O) and σ*(1C–3O), natural hybrids on the carbon and oxygen atoms are sp² hybridized as expected with sufficiently large p character on both the atoms compared to the s character (in Tables 4 and 5, only s contributions on the atoms are given). The hybrid orbitals of π and π* of 1C–2O exhibit p character.
• (iv)The σ(N–H) bond orbitals are polarized more towards the nitrogen atom and σ*(N–H) are polarized towards hydrogen. In σ*(N–H) orbitals, the NHO on N are sp³ hybridized and NHO on H is completely of s character.
• (v)The nonbonding type of NBOs which are due to lone-electron pair orbitals, n₁(2O), n₁(3O) are of sp^0.65, sp^0.61 hybridized in C_ZW and sp^0.64, sp^0.82 in D₁. The remaining lone pair orbitals, n₂(2O), n₂(3O) and n₃(3O) exhibit pure pcharacter both in C_ZW and D₁ thus favoring the π delocalization at –CO₂‾ site.

Table 4.

Computed NBO parameters for some of the important natural bond orbitals in C_ZW.

NBOs Ω/Ω∗ (A-B)	Occupancy q	Polarization coefficients (%)		Description of NBO	Contribution of s character (%)		ΔqΩΩ*
		cA2	cB2		A	B
σ(1C–2O)	1.99624	34.31	65.69	0.5858 (sp2.10) C1 + 0.8105 (sp1.55)O2	32.23	39.15	1.94647
σ∗(1C–2O)	0.04977	65.69	34.31	0.8105 (sp2.10)C1 - 0.5858 (sp1.55)O2
π(1C–2O)	1.99334	22.75	77.25	0.4769 (p)C1 + 0.8789 (p)O2	0.45	0.15	1.61977
π∗(1C–2O)	0.37357	77.25	22.75	0.8789 (p)C1 - 0.4769 (p)O2
σ(1C–3O)	1.99484	34.15	65.85	0.5843 (sp2.14)C1 + 0.8115 (sp1.69)O3	31.74	37.09	1.93103
σ∗(1C–3O)	0.06381	65.85	34.15	0.8115 (sp2.14) C1 - 0.5843 (sp1.69) O3
σ(4N–5H)	1.99316	72.96	27.04	0.8542 (sp3.38)N4 + 0.5200 (s)H5	22.83	99.93	1.98787
σ∗(4N–5H)	0.00529	27.04	72.96	0.5200 (sp3.38) N4 - 0.8542 (s)H5
σ(4N–6H)	1.99371	72.82	27.18	0.8533 (sp3.31)N4 + 0.5214 (s)H6	23.20	99.93	1.98535
σ∗(4N–6H)	0.00836	27.18	72.82	0.5214 (sp3.31)N4 - 0.8533 (s)H6
σ(4N–16H)	1.99380	72.81	27.19	0.8533 (sp3.34)N4 + 0.5214 (s)H16	23.03	99.93	1.98549
σ∗(4N–16H)	0.00831	27.19	72.81	0.5214 (sp3.34)N4 - 0.8533 (s)H16
n1(2O)	1.97923			sp0.65	60.73
n2(2O)	1.90320			p	0.01
n1(3O)	1.98025			sp0.61	61.95
n2(3O)	1.90938			p	0.10
n3(3O)	1.62882			p	0.92

Note: Δq_ΩΩ* = Difference in occupancies q_Ω – q_Ω*. Where Ω - bonding and Ω^∗ - antibonding orbitals on A and B.

Table 5.

Computed NBO parameters for some of the important natural bond orbitals in the H-bonding region in D₁.

NBOs Ω/Ω∗ (A-B)	Occupancy q	Polarization coefficients (%)		Description of NBO	Contribution of s character (%)		ΔqΩΩ*
		cA2	cB2		A	B
σ(1C–2O)	1.99575	34.37	65.63	0.5862 (sp2.15)C1 + 0.8101 (sp1.57)O2	31.64	38.86	1.94797
σ∗(1C–2O)	0.04778	65.63	34.37	0.8101 (sp2.15)C1 - 0.5862 (sp1.57)O2
π(1C–2O)	1.98812	23.06	76.94	0.4802 (p)C1 + 0.8772 (p)O2	1.45	0.25	1.63194
π∗(1C–2O)	0.35618	76.94	23.06	0.8772 (p)C1 - 0.4802 (p)O2
σ(1C–3O)	1.98748	32.45	67.55	0.5697 (sp2.20)C1 + 0.8219 (sp2.05)O3	31.15	32.77	1.88137
σ∗(1C–3O)	0.10611	67.55	32.45	0.8219 (sp2.20)C1 - 0.5697 (sp2.05)O3
σ(20N–21H)	1.99045	76.22	23.78	0.8730 (sp2.84)N20 + 0.4877 (s)H21	26.03	99.89	1.90924
σ∗(20N–21H)	0.08121	23.78	76.22	0.4877 (sp2.84)N20 - 0.8730 (s)H21
σ(20N–22H)	1.99275	72.06	27.94	0.8489 (sp3.50)N20 + 0.5286 (s)H22	22.19	99.94	1.98324
σ∗(20N–22H)	0.00951	27.94	72.06	0.5286 (sp3.50)N20 - 0.8489 (s)H22
σ(20N–32H)	1.99277	72.07	27.93	0.8489 (sp3.55)N20 + 0.5285 (s)H32	21.96	99.94	1.98385
σ∗(20N–32H)	0.00892	27.93	72.07	0.5285 (sp3.55)N20 - 0.8489 (s)H32
n1(2O)	1.97908			sp0.64	60.93
n2(2O)	1.90125			p	0.01
n1(3O)	1.96243			sp0.82	54.98
n2(3O)	1.86544			p	7.70
n3(3O)	1.61485			p	4.56

Note: Δq_ΩΩ* = Difference in occupancies q_Ω – q_Ω*. Where Ω - bonding and Ω^∗ - antibonding orbitals on A and B.

According to the NBO procedure, the strength of concerned bonds is computed by considering the difference in occupancies of bonding and antibonding NBOs. From Tables 4 and 5, it is evident that in D₁, the 1C–2O bond is strong and in the C_zw stronger bond is 1C–3O. The difference in occupancies of bonding and antibonding σ and π components of 1C–2O are 1.94647 and 1.61977 in C_ZW, 1.94797 and 1.63194 in D₁. The σ component of 1C–2O has slightly more occupancy in the D₁ than in C_zw. The total occupancies (σ + π) are 3.566 in C_ZW and 3.579 in D₁ showing that 1C–2O carbonyl bond is stronger in the dimer than in the monomer.

The atomic charges are useful in evaluating the electronic structure of bonds [63]. The charge distribution among the atoms in C_ZW and D₁ has also been calculated by the natural population analysis (NPA) and is presented in Table 6. It is noted from Table 6 that, the charges on the atoms 21H, 22H and 32H in D₁ are 0.460, 0.435 and 0.435 respectively while on the 2O and 3O are −0.825 suggesting the strong electrostatic interaction between 21H and 3O. Charge transfer between the proton donor –NH₃⁺ group and the proton acceptor –CO₂‾ group elongate the –N–H bond length and hence weaken the –N–H bond. The difference in natural atomic charges between 5H in C_zw and 21H in D₁ and proton acceptor 3O are 0.004 and −0.035 respectively, suggesting that the dimer is stabilized by the red-shifted H-bonding. This is consistent with the increase in occupancy (see Tables 4 and 5) from 0.00529 in the monomer (σ*(4N–5H)) to 0.08121 in dimer (σ*(20N–21H)).

Table 6.

Natural atomic charges of C_ZW and D₁ computed by NBO analysis.

CZW		D1
Atom	Charge (a.u)	Atom	Charge (a.u)	Atom	Charge (a.u)
1C	0.796	1C	0.815	17C	0.795
2O	-0.842	2O	-0.825	18O	-0.855
3O	-0.860	3O	-0.825	19O	-0.850
4N	-0.673	4N	-0.672	20N	-0.707
5H	0.456	5H	0.456	21H	0.460
6H	0.450	6H	0.451	22H	0.435
7C	-0.332	7C	-0.329	23C	-0.329
8C	-0.582	8C	-0.582	24C	-0.582
9C	-0.167	9C	-0.167	25C	-0.171
10H	0.222	10H	0.225	26H	0.219
11H	0.216	11H	0.217	27H	0.215
12H	0.206	12H	0.208	28H	0.204
13H	0.207	13H	0.208	29H	0.206
14H	0.227	14H	0.227	30H	0.221
15H	0.224	15H	0.225	31H	0.217
16H	0.450	16H	0.451	32H	0.435

The second order perturbation energies (E⁽²⁾) were computed at B3LYP/6–311++G(d,p) level. The energy associated with each donor and acceptor is estimated using second order perturbation theory as,

$$E_{i\to j}^{\left(2\right)}=-n\frac{{\left|F_{ij}\right|}^2}{\left({\epsilon }_j-{\epsilon }_i\right)}$$ (1)

where n is the population of the donor orbital, Fij is the Fock matrix element between the i and j NBOs, ${\epsilon }_i={\text{Ω}}_i\text{|}F{\text{|Ω}}_i$ and${\epsilon }_j={\text{Ω}}_j^{\ast }\text{|}F{\text{|Ω}}_j^{\ast }$, where ${\text{Ω}}_i$ and ${\text{Ω}}_j$ are donor and acceptor NBOs.

The mixing coefficients${\lambda }_{i\to j}$ can be estimated as, ${\lambda }_{i\to j}=\frac{F_{ij}}{{\epsilon }_i-{\epsilon }_j}$ and the occupancy transfer (charge transfer) $Q_{i\to j}$ from ${\Omega }_i\text{to}{\Omega }_j^{\ast }$ as, $Q_{i\to j}=2{\lambda }_{i\to j}^2$.

Larger the $E^{\left(2\right)}$ value, more intensive is the interaction between donor and acceptor. Fig. 6 shows the interaction of the filled orbital with the unfilled non-Lewis orbital [64]. The E⁽²⁾ values corresponding to –N–H⋯O interaction in the dimers D₁, D_2, D_3, D_4, D_5, D₆ and D_7, are 35.01, 23.70, 27.42, 20.85, 2.53, 19.08 and 27.13 kcal/mol respectively, suggesting that more charge transfer interactions exist in the case of D₁. These intermolecular –N–H⋯O bonds are formed by the orbital overlap between lone pair (n) of oxygen (O) and antibonding orbital (σ*) of N–H. Lone pair of oxygen and antibonding orbitals of N–H are identified as electron donor and acceptor NBO species. The H-bonding between n(O) and σ^∗(N–H) results in charge transfer causing stabilization of the dimer species. This –N–H⋯O intermolecular bonding increases the electron density which leads to the elongation of the N–H bond lengths and hence lowering the corresponding stretching vibrational frequencies in D₁. For the D_1, the intermolecular interactions between some of the important donor-acceptor NBO pairs such as n(3O) and σ*(20N–21H) give rise to the energies 28.46, 6.10 and 0.45 kcal/mol which are presented in Table 7 and the graphical electron density maps of NBOs corresponding to these interactions are presented in Fig. 7.

Fig. 6.

Second order perturbative donor-acceptor interaction involving a filled orbital i and an unfilled orbital j.

Table 7.

Computed mixing coefficients (λ), charge transfer (Q) giving NBOs with stabilization energy corresponding to –N–H⋯O interaction in D_1.

NBOs Ωi→Ω*j	Mixing coefficient λi→j	Charge transfer Qi→j	E(2)a kcal/mol
n1(3O)→σ*(20N₋21H)	0.1853	0.03433	28.46
n2(3O)→σ*(20N–21H)	0.0696	0.00969	6.10
n3(3O)→σ*(20N–21H)	0.0266	0.001411	0.45
CR(3O)→σ*(20N–21H)	0.0043	0.000037	0.43
σ(1C–3O)→σ*(20N–21H)	0.0156	0.000488	0.37

Note: Ω_i, Ω_j^∗ = donor, acceptor NBOs, σ^∗ = antibonding orbital, n = lone pair on oxygen atom, CR = core.

^aEnergy of hyperconjugative interaction (stabilization energy).

Fig. 7.

Electron density maps of selected NBOs involved in –N–H⋯O bonding in D₁. Donor (lone pair orbital of 3O) and acceptor (antibonding orbital of 20N–21H) NBOs are shown separately in left columns and their overlapping due to H-bonding is shown in right columns. Green and yellow colours of the orbitals correspond to positive and negative signs respectively.

From this analysis, we can conclude the following. The decreased occupancy of σ component of 1C–3O bond from C_zw to D₁ is consistent with the increase in the 1C–3O bond length value from 1.264 Å in C_zw to 1.272 Å in D₁. Similarly, the difference in atomic charges 5H in C_zw, 21H in D₁ and 3O suggest that the dimer is stabilized by the red-shifted H-bonding. This is in agreement with the increase in occupancy from 0.00529 in the C_ZW (σ*(4N–5H)) to 0.08121 in D₁ (σ*(20N–21H)). The computed second order perturbative energies also suggest that the strong H-bonding exist in D_1.

3.3. AIM analysis

The –N–H⋯O bonding in D₁ species of 3AIBA has been studied through AIM analysis. According to AIM theory, a chemical bond including hydrogen bond is characterised by the presence of a bond critical point (BCP). The topological parameters like electron density ρ(r) and their Laplacian $\nabla$²ρ(r) computed at BCP are useful tools to characterize the strength of a bond between donor and acceptor atoms [65, 66, 67, 68, 69]. The important topological parameter values obtained for D₁ species include the electron density (0.0519 a.u), its corresponding Laplacian (0.1326 a.u), potential energy density (V(r) = -0.0486 a.u). Interaction energy (E_int = 15.2 kcal/mol) of the –N–H⋯O bond has been calculated at BCP using the relation E_int = V(r)/2. The low value of ρ(r) and positive value of $\nabla$²ρ(r) and the value of interaction energy satisfy the criteria for existence of medium H-bond according to Rozas et al [70]. With all these values we can conclude that, a medium strong –N–H⋯O inter-molecular bond exist in D₁.

Non-covalent interactions (NCI) in the molecular systems can be visualized using reduced density gradient (RDG) [71, 72]. The RDG is given by:

$$s=\frac{1}{2{\left(3{\pi }^2\right)}^{1/3}}\left(\frac{\left|\nabla \rho \left(r\right)\right|}{\rho {\left(r\right)}^{4/3}}\right)$$ (2)

where ρ(r) is the electron density and $\nabla$ρ(r) is its gradient. NCI isosurfaces illustrate the nature of the interactions in real space through colour codes. Blue, green, red colours are used to represent attractive hydrogen bond, weak van der Waals and steric interactions respectively. The NCI isosurface for the D₁ species is shown in Fig. 8. A blue patch between the hydrogen atom of –NH₃⁺ group from one ZW monomer and oxygen atom of –CO₂‾ group from another ZW monomer unit in Fig. 8 is attributed to –N–H⋯O bonding. Green and red patches between –NH₃⁺, CH₃ and –CO₂‾, CH₂ groups within the monomer units represent the van der Waals and repulsive steric interactions respectively.

Fig. 8.

Reduced density gradient isosurface for D₁ of DL-3-Aminoisobutyric acid. Blue, green, red colours are used to represent attractive hydrogen bond, weak van der Waals and steric interactions respectively.

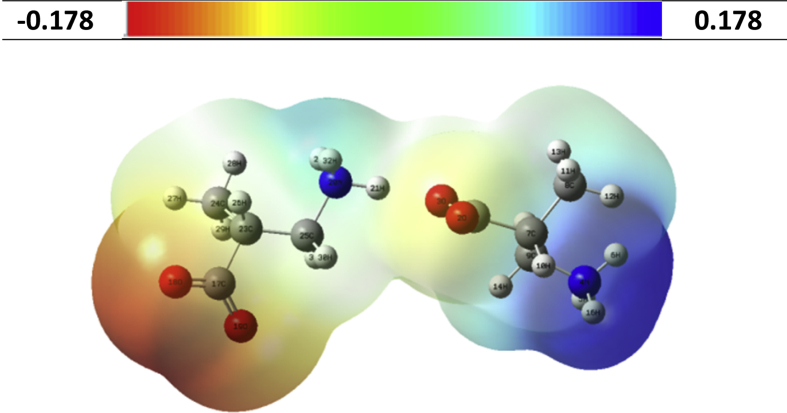
3.4. MEP analysis

The molecular electrostatic potential (MEP) serves as a useful quantity to explain H-bonding and reactivity of molecules [73]. The MEP surface of the D₁ species was calculated from the optimized molecular structure discussed in section 2.2 and shown in Fig. 9. The different values of electrostatic potentials at the MEP surface are represented by different colors: red, blue and green represent the regions of most negative, most positive and zero electrostatic potential respectively. The negative region is localized over –CO₂‾ group indicating the most reactive site for electrophillic attack and positive region is localized over –NH₃⁺ group which is reactive site for nucleophillic attack. The loss of red and blue colors on –CO₂‾ and –NH₃⁺ groups in the bonding region of the D₁ species is attributed to –N–H⋯O donor-acceptor interaction.

Fig. 9.

Molecular electrostatic potential surface for D₁ of DL-3-Aminoisobutyric acid (in the range between -0.178 to 0.178 a.u).

3.5. Vibrational analysis

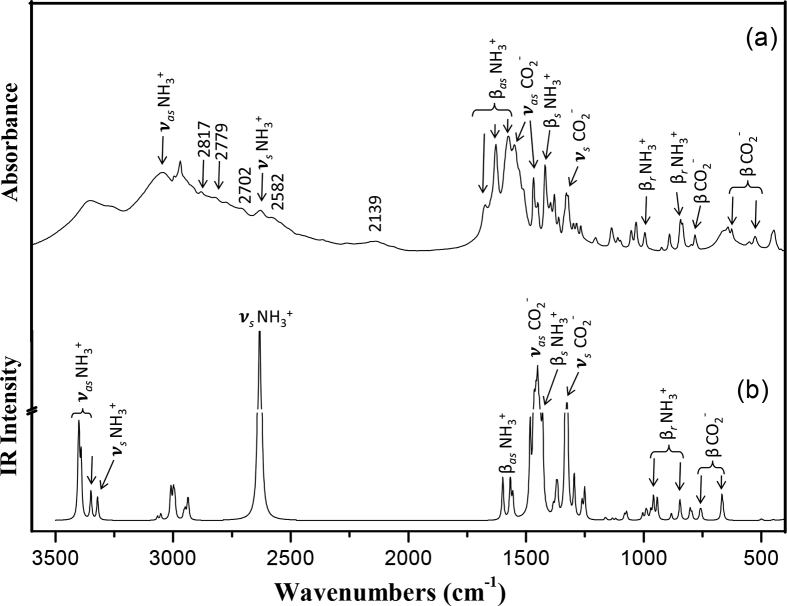
The experimental IR and Raman spectra of 3AIBA and their comparison with the simulated spectra of D₁ are shown in Figs. 10 and 11. The IR spectrum marked by a broad composite band structure in the region 3500 − 2000 cm⁻¹ with FWHM 700 cm⁻¹ is indicative of inter-molecular interactions of which we assume H-bonding. A series of multiple peaks on this broad band and, medium to strong bands in the 1675 − 1400 cm⁻¹ are characteristic modes of –NH₃⁺ and –CO₂⁻ groups, strongly suggesting the ZW nature of the 3AIBA. However, the Raman spectrum has not shown these bands since the Raman modes are generally weak for ionic group vibrations. The strong bands it has shown are due to –CH, –CH₂ and –CH₃ groups in the 3000 − 2850 cm⁻¹. In other regions, the 1675 − 1400 cm⁻¹ is marked by very sharp IR bands readily assigned to the stretching and bending modes of –CO₂⁻ and –NH₃⁺ groups. The Raman bands are weak in this region. We now present a detailed vibrational analysis of the observed and computed bands of the C_ZW monomer and D₁ dimer species. We refer to modes arising from H-bonded vibrations as ‘bonded modes’; otherwise, they will be referred to as ‘free modes’.

Fig. 10.

(a) Experimental and (b) simulated dimer (D₁) IR spectra of DL-3-Aminoisobutyric acid. Frequency values corresponding to vibrational modes are given in Table 8. Only the stretching, bending vibrations of –NH₃⁺, –CO₂⁻ and their combinations are assigned in the above spectra. Ordinate in Dimer spectrum (b) is broken to adjust the bands from overshooting because of their largest intensity.

Fig. 11.

(a) Experimental and (b) simulated dimer (D₁) Raman spectra of DL-3-Aminoisobutyric acid. Frequency values corresponding to vibrational modes are given in Table 8. Only the stretching, bending vibrations of –NH₃⁺, ₋COO¯ and their combinations are assigned in the above spectra. Ordinate in Dimer spectrum (b) is broken to adjust the bands from overshooting because of their largest intensity.

3.5.1. NH₃⁺ modes

In the IR spectrum no absorption is observed in the usual N–H stretching region, 3500 − 3300 cm⁻¹; instead a broad absorption of medium intensity at 3044 cm⁻¹ is identified as asymmetric stretching mode of –NH₃⁺ as against the predicted band at 3391 cm⁻¹ in C_ZW and at 3399 cm⁻¹ in D₁ [74,75]. Second asymmetric stretching mode has not been observed near 3383 cm⁻¹ but is computed in C_ZW and it is at 3390 cm⁻¹ in D₁ (bonded mode is at 3349 cm⁻¹). The symmetric stretching mode is not seen in the Raman spectrum since this band is apparently obscured by the more intense –C–H stretching band, but is predicted at 3321 cm⁻¹ [76]. As for the bonded mode we identify a medium weak absorption at 2629 cm⁻¹, which is correlated to a predicted band at 2612 cm⁻¹ [77]. Bonded asymmetric bending mode identified as a medium weak absorption at 1675 cm⁻¹ with its Raman band at 1689 cm⁻¹ is correlated to the predicted band at 1599 cm⁻¹; the free mode is predicted at 1568 cm⁻¹. The second bonded mode is assigned to a very strong absorption at 1627 cm⁻¹ (Raman band at 1616 cm⁻¹) is correlated to a predicted band at 1566 cm⁻¹, the free mode is predicted at 1556 cm⁻¹. Another asymmetric mode appearing as a very strong absorption at 1574 cm⁻¹ with its weak Raman band at 1584 cm⁻¹ is correlated to a predicted band at 1482 cm⁻¹. The symmetric bending mode observed as a medium weak absorption at 1400 cm⁻¹ is correlated to a predicted band at 1431 cm⁻¹. As for the rocking modes, weak and medium weak absorptions observed at 995 and 844 cm⁻¹ are correlated to the predicted bands at 970 and 843 cm⁻¹ respectively.

3.5.2. CO₂⁻ modes

As for the –CO₂⁻ modes, the asymmetric stretching bonded mode is identified as a very strong absorption at 1546 cm⁻¹ with its Raman mode at 1544 cm⁻¹ and is computed at 1458 cm⁻¹; the free mode is predicted at 1465 cm⁻¹. The second asymmetric mode predicted at 1450 cm⁻¹ is correlated to a strong absorption and medium strong Raman band near 1468 cm⁻¹. Symmetric stretching mode identified as a medium strong absorption at 1329 cm⁻¹ is computed at 1332 cm⁻¹. Another symmetric stretching mode predicted at 1325 cm⁻¹ is correlated to the medium strong Raman band at 1312 cm⁻¹. Weak to medium absorptions at 782, 642 and 526 cm⁻¹ are identified as deformation modes of –CO₂⁻ and are predicted at 761, 668 and 502 cm⁻¹ respectively.

3.5.3. Combination bands

Further, some bands appeared only in the IR spectrum in the region 2700 − 2000 cm⁻¹ as a substructure on the broad absorption are assigned to a combination of asymmetric bending of –NH₃⁺ with –C–N stretching or torsional modes of –NH₃⁺ [10, 57]. The weak to medium absorptions at 2702 and 2629 cm⁻¹ may arise due to the –N–H⋯O bonding, and it is reasonable to assign them to a combination of –NH₃⁺ asymmetric stretch and deformation of the –C–N bond [78]. The band at 2139 cm⁻¹ being a combination of –NH₃⁺ asymmetric stretch and –C–N torsional mode is identified as a marker band for the identification of cation –NH₃⁺ moiety in amino acids [10, 11]. Similarly, the weak absorptions at 2817, 2779 and 2582 cm⁻¹ are combinations of –NH₃⁺ asymmetric stretch with –C–N deformation and stretching vibrations.

3.5.4. C–H, C–C and C–N bands

All the other bands, which are not influenced by the H-bonding, have appeared in their usual region. As for methyl vibrations, the Raman spectra shows distinct, intense bands assigned to asymmetric and symmetric stretching vibrations in the region 3000 − 2850 cm⁻¹ whereas the IR bands in this region appeared as weak bands or sometimes as shoulder to the other bands. The scissoring and deformation modes appear in the region 1450 − 1360 cm⁻¹. The –C–N bending modes are assignedto the coupled vibrations with−C–C bending and stretching vibrations in the region 1300 − 800 cm⁻¹. Medium weak Raman bands at 1033 and 891 cm⁻¹ are identified as –C–C skeletal vibrations suggesting that the carbon chain is not perturbed due to the H-bonding. A detailed assignments of all the modes compared with the assignments of β-alanine are presented in Table 8.

Table 8.

Experimental and computed frequencies (cm⁻¹) of C_ZW and D₁ structures with assignments for DL-3-Aminoisobutyric acid.

Observed Frequenciesd		β-alaninee		Computed Frequenciesa		Assignmentsc
IR	Raman	IR	Raman	CZW	D1
3044 s	--			3391	3399	Vas (NH3+, 90)
--	--			3383	3390 (3349)b	Vas (NH3+, 98)
2629 mw	--			3313	3321 (2612)	Vs (NH3+, 100)
2988 sh	2991 vs	3017	3016	3066	3066	Vas (CH2, 99)
2969 s	--	--	2936	3012	3011	Vas (CH2, 99)
--	2949 vs			3011	3009	Vas (CH3, 96)
--	2908 vvs			2993	2993	Vas (CH3, 95)
--	2889 sh			2945	2948	V(CH, 96)
2879 mw	--			2936	2935	Vs (CH3, 99)
2817 w	--			--	--	1675 + 1136
2779 w	--			--	--	1627 + 1136
2702 w	--			--	--	1627 + 1053
2629 mw	--			--	--	1574 + 1053
2582 w	--			--	--	1574 + 923
2139 w	--			--	--	1675 + 447
1675 mw	1689 w	1653	1686	1561	1568 (1599)	δas (NH3+, 86)
1627 vs	1616 w			1554	1556 (1566)	δas (NH3+, 90)
1574 vvs	1584 w	1573	1556	--	1482	δas (NH3+, 71)
1546 vs	1544 w	1633	1630	1463	1465 (1458)	Vas (CO2‾, 64)
1468 s	1468 ms			1452	1450	Vas (CO2‾, 18), δs (CH3, 26)
1452 mw	1445 mw	1466	1473	1441	1441	δsc (CH2, 73)
1419 s	--			1436	1435	δas (CH3, 63)
1400 w	1399 w			1423	1431	δs (NH3+, 56), δas (CH3, 27)
1379 mw	1386 w	1447	1434	1383	1384	Ω (CH2, 46)
1360 w	1365 w			1371	1371	δ (CH3, 34), δ (CH2, 14)
1329 ms	1331 mw	1403	1395	1330	1332	V (CO2‾, 17), δ (CN, 34), δt (CH2, 19)
--	1312 ms			1320	1325	V (CO2‾, 36), δ (CN, 28)
1299 w	--			1290	1294	δ (CC, 39), δ (CH, 15)
1272 w	1267 s			1248	1251	δ (CH, 49), (CO2‾, 12)
1136 mw	1134 w			1160	1159	δ (CC, 30), δ (CN, 10)
1108 w	1107 mw			1121	1119	V (CC, 33), δ (CN, 14)
1053 mw	1051 mw			1072	1072	δ (CC, 13), δ (CN, 11), δ (CO, 11)
1032 mw	1033 mw			990	991	Δ (CC, 36), (CC, 28)
995 w	1003 w	1061	1068	965	970	ρ (NH3+, 30), δ (CC, 10), δ (CO, 10)
923 vw	921 w			937	943	V (CN, 64), (CC, 11)
891 w	891 w			877	882	V (CC, 33), (CN, 17)
844 mw	837 ms	991	998	838	843	Ρ (NH3+, 15), δ (CC, 24)
799 vw	--			794	794	V (CC, 38), δ (CO2‾, 14)
782 w	773 w			753	761	δ (CO2‾, 59), δ (CC, 10)
642 mw	632 w	654	659	654	668	δ (CO2‾, 35)
526 w	539 w	538	541	490	502	Δ (CO2‾, 37), (CC, 10)
447 w	445 w			--	450	Δ (N–H⋯O, 27), δ (CN, 40)
--	--			357	358	Δ (CN, 27), τ (CC, 11), τ (OH, 12)
--	--			345	346	Τ (CO, 12), τ (CC, 34)
--	296 w		327	326	321	Τ (CC, 43), τ (CN, 20)
--	252 vw		224	250	275	Τ (CC, 36), τ (CN, 11)
--	--			218	227	Τ (CC, 35), (O…H, 10)
--	170 w		167	197	202	Τ (CC, 78)
--	126 mw		112	119	119	Τ (CCN, 77)
--	--			--	107	τ (CN, 11), τ (CO, 11), τ (O⋯H, 45)
--	--			--	76	Δ (H...OC, 41), τ (CN, 19)
--	--			53	46	τ (CN, 23), τ (NCO, 10), τ (CO, 22)

ν = stretching; δ = bending; ω = wagging; ρ = rocking, δ_t = twisting, τ = torsional vibration below 400 cm⁻¹; as = antisymmetric; s = symmetric.

^aFrequencies are scaled by 0.9688 [53].

^bA dimer frequency shown in bracket belongs to bonded mode.

^cThe quantities given in brackets are PED contribution (in %).

^dOur experimental results.

^eRef [4].

4. Conclusions

A satisfactory zwitterionic dimer model at B3LYP/6–311++G(d,p) level and SCRF-SMD method, constructed of inter-molecular –N–H⋯O bonding between –NH₃⁺ group of one zwitterionic monomer unit and –CO₂⁻ group of another identical zwitterionic monomer unit, has been proposed for DL-3-Aminoisobutyric acid. The vibration modal features predicted by the model are in fair agreement with the IR and Raman modes in 3040–3000 cm⁻¹ and 1680–1460 cm⁻¹. The Grimme's dispersion correction associated with the –N–H⋯O interaction computed at B3LYP-D3/6–311++G(d,p) level which yielded both the optimized dispersion-corrected energies and frequencies hardly differed from the results without dispersion correction. As for the NBO characterization of the –N–H⋯O bonding, it has been shown that it is formed by the orbital overlap between lone pair (n) of oxygen (O) as electron donor and antibonding orbital (σ*) of N–H bond as acceptor. The stabilization of the dimer species has been shown to arise from the hyperconjugation interaction between n(O) and σ^∗(N–H) that has explained both structural aspects of DL-3-Aminoisobutyric acid and its empirical IR red spectral shift. The AIM analysis has shown the intermolecular –N–H⋯O bondingin D₁ of 3AIBA. The values of ρ(r) and $\nabla$²ρ(r) and hydrogen bond energy at bond critical points indicate a strong intermolecular –N–H⋯O bonding. The same result has been deduced from the NCI analysis as well. Overall all the DFT, NBO, AIM and NCI calculations mutually support each other. It may be said that the stretching modes of –NH₃⁺ and –CO₂⁻ groups might have been predicted more accurately perhaps for a trimer model.

Declarations

Author contribution statement

Shashikala Yalagi: Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Jagdish Tonannavar: Conceived and designed the experiments; Analyzed and interpreted the data.

Jayashree Tonannavar: Conceived and designed the experiments; Analyzed and interpreted the data; Wrote the paper.

Funding statement

This work was supported by the Department of Physics under the Centre of Advanced Study at Level II (Grant no: No.F.530/9/CAS-II/2015(SAP-I)) funded by University Grants Commission, New Delhi. Jayashree Tonannavar was supported by the University Grants Commission, New Delhi by the Major Research Programme grant (F.37–243/2009(SR)).

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.