A new analysis approach for T₂ relaxometry myelin water quantification: Orthogonal Matching Pursuit

Abstract

Purpose

In vivo myelin quantification can provide valuable noninvasive information on neuronal maturation and development, as well as insights into neurological disorders. Multiexponential analysis of multiecho T₂ relaxation is a powerful and widely applied method for the quantification of the myelin water fraction (MWF). In recent literature, the MWF is most commonly estimated using a regularized nonnegative least squares algorithm.

Methods

The orthogonal matching pursuit algorithm is proposed as an alternative method for the estimation of the MWF. The orthogonal matching pursuit is a greedy sparse reconstruction algorithm with a low computation complexity. For validation, both methods are compared to a ground truth using numerical simulations and a phantom model using comparable computation times. The numerical simulations were used to measure the theoretical errors, as well as the effects of varying the SNR, strength of the regularization, and resolution of the basis set. Additionally, a phantom model was used to estimate the performance of the 2 methods while including errors occurring due to the MR measurement. Lastly, 4 healthy subjects were scanned to evaluate the in vivo performance.

Results

The results in simulations and phantoms demonstrate that the MWFs determined with the orthogonal matching pursuit are 1.7 times more accurate as compared to the nonnegative least squares, with a comparable precision. The remaining bias of the MWF is shown to be related to the regularization of the nonnegative least squares algorithm and the Rician noise present in magnitude MR images.

Conclusion

The orthogonal matching pursuit algorithm provides a more accurate alternative for T₂ relaxometry myelin water quantification.

1. INTRODUCTION

MRI is a helpful technique to detect abnormalities in the cerebral white matter (WM). For instance, T₂‐weighted imaging techniques grant excellent contrast to identify WM abnormalities, and DWI provides information on the integrity of the WM tracts.1 Although these methods are invaluable in the ongoing research and clinical diagnosis of WM disorders, they fail to provide more specific information on one of the most characteristic components of the WM, the myelin.

Myelin is a layered, fatty substance wrapped around the axons that is comprised of lipids and proteins. The myelin acts as an electrical insulator, accelerating the transport of electrical signals along the axons. In addition to the dry mass, the myelin volume is roughly made up of 40% water, which is trapped between the lipid bilayers of the myelin sheath.2 Myelin is vital to healthy neuronal development and can therefore provide valuable information regarding neuronal maturation and development as well as insights into disintegration as part of several neurological disorders.3 Therefore, MRI techniques that yield specific information on the myelin content can provide information on WM that complements structural T₂‐weighted and DWI techniques.

White matter is relatively bright on T₁‐weighted images, which is related to myelin‐bound cholesterol, whereas the T₂‐weighted contrast of WM is low due to motion‐restricted protons in the myelin water. Previously, both the T₁‐ and T₂‐weighted images were combined to enhance myelin contrast by calculating the ratio of T₁‐ and T₂‐weighted image intensities.4 Despite the enhanced myelin contrast, the T₁‐to‐T₂ ratio fails to provide information that is specific to the myelin. Besides conventional imaging methods, DWI is often used to study the WM. However, whereas DWI measures can provide information on changes in myelin, they are not suitable for absolute quantification of myelin content.5 Another technique that is used to detect abnormalities in myelin content is magnetization transfer imaging via the magnetization transfer ratio.6 Whereas the magnetization transfer ratio is sensitive to the interaction of water molecules with the macromolecules in the myelin sheath, it is not specific enough to distinguish between myelin abnormities and, for example, inflammatory processes.7 Contrary to these indirect measures of myelin, UTE imaging can be used to image the myelin sheath directly.8 Although the MR signal of the myelin sheath dephases too quickly (10 µs < T₂ < 1 ms) to be visible on conventional T₂‐weighted images, it can be visualized using UTE sequences. Although UTE measurements are promising in the field of myelin quantification, they remain challenging on clinical MR systems due to hardware limitations.9

Because water is a significant part of the myelin volume, many studies have focused on the quantification of myelin water as an indirect measure of myelin content. Myelin water can be quantified using either the multicomponent driven equilibrium single pulse observation of T₁ and T₂ 10 or the analysis of T₂ relaxometry. In the current study, T₂ relaxometry is used to quantify the myelin water. The rationale for using T₂ relaxometry to quantify myelin content is that trapped and motion‐restricted water particles between the lipid layers of the myelin sheath have a faster T₂‐weighted signal decay (10 ms < T₂ < 40 ms) compared to more freely moving water in the intra‐ and extracellular spaces (80 ms < T₂ < 100 ms) and CSF (T₂ > 2 s).11 Due to these differences in T₂ relaxation time, MR imaging can provide surrogate markers of myelin content via the myelin water, whereas the T₂ relaxation profile of a single voxel is a superposition of myelin water, intra‐ and extracellular water, and CSF components. The signal attributed to each of these components can then be determined by separating the measured signal into its constituting relaxation components. From the resulting relaxation components, the fraction of myelin water signal to the total water signal, the myelin water fraction (MWF), can be determined. Biexponential fitting methods are typically unsuitable for the extraction of the constituting components because they are unstable; furthermore, they assume that only 2 components are present, which is not guaranteed. Alternatively, the constituting components can be extracted using multiexponential analysis.

In literature, the multiexponential analysis is most commonly performed with the nonnegative least squares (NNLS) algorithm.12, 13, 14, 15, 16 Opposed to biexponential fitting methods, the NNLS algorithm makes no assumptions on the number of underlying components and does not require an estimation of the solution to start the optimization algorithm. Instead, the NNLS reconstructs the signal from a predefined overcomplete basis set of T₂ relaxation decay curves, the so‐called dictionary.

In the current study, we propose the orthogonal matching pursuit (OMP) algorithm17 as an alternative to estimate the MWF using T₂ relaxation MRI. Common applications of the OMP are wavelet decomposition, denoising of images, and reconstruction of images or signals (e.g., NMR spectroscopy spectra).18, 19, 20, 21 Similar to the NNLS, the OMP uses an overcomplete dictionary to estimate the corresponding weights of each element from the dictionary. However, in contrast to the NNLS, the OMP is a greedy algorithm that aims to model as much of the current residuals in each step rather than working toward the global optimum.22

In the following, we compare the performance of the OMP and NNLS algorithms on estimating the MWF using T₂ relaxometry. To investigate the theoretical errors for varying SNR of both methods, numerical simulations are used. A phantom model is employed to assess errors related to the MR acquisition, and lastly, the 2 methods are compared in healthy volunteers.

2. THEORY

2.1. Nonnegative least squares

Introduced by Lawson and Hanson,23 and extensively investigated and applied to T₂ relaxation data by Whittall and MacKay16 for the first time, the NNLS uses a predefined basis set $\mathbf{A}$ with $M$ elements of discrete $T_{2j}$ relaxation decay curves to characterize the measured signal $y_i$ as

$$y_i=\sum _{j=1}^M{s}_j\mathrm{e}\mathrm{x}\mathrm{p}(-t_i/T_{2j})=\sum _{j=1}^M{\mathbf{A}}_{\mathit{ij}}{s}_j,\text{for}i=1,2,\cdots ,N,$$

where $s_j$ is the amplitude corresponding to the $T_{2j}$ relaxation time, $t_i$ is the measurement time of data point $i$, and $N$ represents the total number of data points. Now, the NNLS problem can be written as

$${\chi }_{\mathrm{m}\mathrm{i}\mathrm{n}}^2=\underset{s\ge 0}{\min }\left(\sum _{i=1}^N{\left|\sum _{j=1}^M{\mathbf{A}}_{\mathit{ij}}{s}_j-y_i\right|}^2\right),$$

where ${\chi }_{\mathrm{m}\mathrm{i}\mathrm{n}}^2$ represents the misfit that is minimized by the NNLS algorithm. Typically, in T₂ relaxation analysis the number of data points is smaller compared to the elements in the basis set (N < M), making the NNLS an ill‐posed problem. To provide a more stable solution, a regularized version of the NNLS is used, adding a smoothing constraint,

$${\chi }_{\mathrm{r}\mathrm{e}\mathrm{g}}^2=\underset{s\ge 0}{\min }\left(\sum _{i=1}^N{\left|\sum _{j=1}^M{\mathbf{A}}_{\mathit{ij}}{s}_j-y_i\right|}^2+\mu \sum _{j=1}^M{\left|s_{j+2}-{2s}_{j+1}+s_j\right|}^2\right),$$

where $\mu$ is the regularization parameter and ${\chi }_{\mathrm{r}\mathrm{e}\mathrm{g}}^2$ is the regularized misfit. Because the regularization term represents a numerical derivative, a larger $\mu$ results in a smoother amplitude distribution ($s$) at the cost of a larger misfit (${\chi }_{\mathrm{r}\mathrm{e}\mathrm{g}}^2$). The NNLS is a convex algorithm with a unique solution. However, the regularized NNLS has a high computational complexity, limiting the number of elements in the basis set. Typically, 120 logarithmically spaced elements ranging from 15 to 2000 ms are used.24, 25, 26, 27

2.2. Orthogonal Matching Pursuit

The OMP algorithm, introduced by Davis et al.,17 builds a sparse representation to estimate the measured signal $y$ by iteratively selecting that element from a predefined basis set $\mathbf{A}$, which correlates most with the current residual (i.e., greedy optimization).20 To initialize the algorithm, the measured signal serves as the first (artificial) residual. To ensure positive weights, Bruckstein et al. proposed a nonnegative implementation of the OMP by solving an unconstrained nonnegative least squares problem for a subset of $\mathbf{A}$ with the current selection of $K$ elements, ${\widehat{\mathbf{A}}}_K$, in each iteration,28

$${\chi }_{\mathrm{m}\mathrm{i}\mathrm{n}}^2=\underset{s\ge 0}{\min }\left(\sum _{i=1}^N{\left|\sum _{j=1}^K{\widehat{\mathbf{A}}}_{\mathit{Kij}}{s}_j-y_i\right|}^2\right).$$

Note that the weights of previously selected elements can become 0, which means that not all the selected elements are necessarily represented in the final signal representation. From this point on, we will refer to the aforementioned nonnegative implementation of the OMP simply as OMP. The OMP iterates until 1 of 2 stopping criteria is met: 1) either a user defined number of elements ($n$) is selected from $\mathbf{A}$, or 2) there is no new element from the dictionary that positively correlates with the last residual. Thus, the OMP algorithm combines the low computational complexity of a greedy algorithm with the stability of a least‐squares solver. The OMP algorithm is shown in pseudocode (algorithm 1).29 Greedy algorithms such as the OMP have a low computational complexity, thus allowing a higher resolution (e.g., 1000 or more basis set elements).

Algorithm 1: Nonnegative Orthogonal Matching Pursuit
Input: signal y, Dictionary A, sparsity n, x = 0
Output: signal weights x
1: initialize r0 = y, s = ∅, i = 0
2: while i < n & max(Atri) > 0 do
3: k = argmax(Atri)
4: s = s U k
5: xs = argminθ>0 ||y ‐ Asθ||2
6: ri+1 = y ‐ Asxs
7: i = i + 1
8: End while
9: x(s) = xs

2.3. Myelin water fraction

For both methods, the MWF is subsequently defined as the amplitude fraction of the T _{2 j} relaxation elements associated with myelin water to all T _{2 j} relaxation water elements, for which the myelin water component is expected to have a T₂ relaxation time in the range of 15 to 40 ms at 3.0 tesla.14

3. METHODS

3.1. Numerical simulations

To estimate the numerical errors of the NNLS and OMP algorithms, multiexponential relaxation curves were computationally synthesized. To also include effects of stimulated echoes caused by B₁ inhomogeneities, the extended phase graph (EPG) algorithm30 was used to synthesize relaxation data with an imperfect refocusing FA of 150°31, 32 and 32 TEs with an echo spacing of 12 ms (range 12–384 ms). The relaxation rates used for the water components in the simulations were T₁ = 1000 ms, T_2long = 100 ms, and T_2myelin = 30 ms, corresponding to healthy WM tissue. Furthermore, additional data was synthesized simulating a WM lesion using T₁ = 600 ms, T_2lesion = 200 ms, and T_2myelin = 30 ms.33, 34 However, the shape of the underlying in vivo T₂ distribution is unknown and might behave more like a continuous distribution instead of a discrete distribution. Therefore, to study the potential effects of the underlying distribution on the MWF estimation of both algorithms, a continuous Gaussian distribution consisting of 2 pools (T_2long: mean 100 ms and SD 10 ms, T_2lesion: mean 200 ms and SD 20 ms, T_2myelin: mean 30 ms and SD 3 ms) also was reconstructed.35, 36

To estimate the effects of myelin water content and SNR on the analysis, 1000 Rician noise realizations were calculated for varying MWF (range 0%–30%, with 1% increment) and SNR (100, 200, and 350). Additionally, the effects of a smaller echo spacing of 8 ms (range 8–256 ms) and a lower T_2myelin peak time of 15 ms were also assessed for an SNR of 200. Rician noise was simulated as the magnitude of the signal with additive complex‐valued Gaussian noise, and SNR was defined as the signal at the first echo (TE = 12 ms) divided by the SD of the added complex‐valued Gaussian noise. Rician‐distributed noise is nearly Gaussian for high SNR values (> 3); however, we still need to take the Rician‐distributed noise into account because the SNR decreases exponentially for increasing TE.

3.2. Phantom model

To estimate errors in MWF estimation due to the signal acquisition, 2 vials with manganese (II) chloride solutions were prepared with concentrations of 0.07 mM and 0.25 mM, resulting in monoexponential T₂ relaxation curves with T_2long ≈ 110 ms and T_2myelin ≈ 30 ms, and T₁ relaxation values of T_1long ≈ 1300 and T_1myelin ≈ 500, respectively. Ideally, the T_1myelin should be closer to 1000 ms; however, it is still sufficiently long (T₁ >> T₂) to have no substantial effect in subsequent EPG analyses.37 Multiexponential decays were synthesized by summing 2 randomly chosen voxels from each vial and weighing them such that a varying MWF (range 0%–30%, with 1% increment) is obtained. This process was repeated 1000 times. SNR of the phantom model was estimated as the mean signal of a region of interest (ROI) located in the vials at the first echo (TE = 12 ms) divided by the SD measured in 4 ROIs in the air placed in each corner of the image. As the measured noise is Rician‐distributed, a correction is applied such that $\frac{{\sigma }_{R\mathrm{i}\mathrm{c}\mathrm{e}}}{\sqrt{2-\pi /2}}={\sigma }_{\mathrm{G}\mathrm{a}\mathrm{u}\mathrm{s}\mathrm{s}}$ is used.38

3.3. In vivo data

Four healthy adult volunteers (age, range 26–30 years, 3 males) were scanned, and a single transverse slice MWF map was determined for each individual using both quantification methods. Additionally, a fifth healthy adult volunteer (age 29, female) was scanned using a 3D GRASE sequence. The SNR of the in vivo data was determined as the mean signal in the genu and splenium of the corpus callosum divided by the SD measured in 4 ROIs in the air placed in each corner of the image. All volunteers gave written permission, and the study was conducted with the approval of the institutional review board.

3.4. MRI acquisition

The vials and healthy volunteers were scanned on a 3.0 tesla unit (Philips Achieva, Best, the Netherlands) with an 32‐element head coil using a single transverse slice multispin‐echo (MSE) sequence (TR = 3000 ms, 32 echoes with the shortest possible echo spacing for this sequence of 12 ms, range 12–384 ms, FOV 240 × 198 × 4 mm, reconstruction matrix size 160 × 160, voxel size 1.5 × 1.5 × 4 mm, and 2 signal averages).39 In vivo, the slice is positioned through the genu and splenium of the corpus callosum and angulated parallel to the inferior edges of the corpus callosum. A single healthy volunteer was scanned using a 3D GRASE sequence (TR = 611 ms, 32 echoes with echo spacing of 13 ms, range 13–416 ms, FOV 240 × 198 × 128 mm, reconstruction matrix size 160 × 160 × 32, voxel size 1.5 × 1.5 × 4 mm, EPI factor = 3, turbo factor = 32, SENSE = 2). For anatomical reference, T₁‐weighted 3D turbo field echo images were acquired for all healthy volunteers (TR = 8.2 ms, TE = 3.7 ms, TI = 1010 ms, FA = 8°, 1‐mm thick slices).

3.5. Analysis

3.5.1. Modifications to the Orthogonal Matching Pursuit algorithm

The OMP algorithm was slightly modified to better suit the current problem of MWF estimation from MR relaxation data. Because the relaxation signal and dictionary are strictly positive, the highest correlation of the signal with the dictionary is always found for the longest T₂ relaxation time present in the dictionary (assuming all dictionary elements have unit amplitude). Therefore, the first iteration depends on the dictionary defined by the user and does not necessarily converge to a meaningful answer. To improve the result of the OMP algorithm, 2 random elements are selected from the dictionary for initialization of the iteration process. One initialization element corresponds to a myelin water associated relaxation time (T₂ < 40 ms), and the other element is one of the slower components (T₂ ≥ 40 ms). Note that this initialization makes no assumption on the final number of components. The OMP tries to explain as much of the current residual as possible in each iteration, and therefore does not necessarily converge to the global optimum. Furthermore, due to the random initialization, the output of the algorithm can vary for identical inputs. Therefore, the stability of the algorithm can be enhanced by running with multiple random initializations per voxel. Because OMP is approximately 20 times faster than NNLS, we ran the OMP algorithm 20 times for each voxel. For the averaging of these results, an exponentially decaying quadratic weighting is applied such that those MWFs with a larger fitting residual have a lower weighing because they are likely the result of less optimal fitting due to the greedy nature of the OMP algorithm (Figure 1). Furthermore, the effect of the number of random initializations is investigated using the synthetic data by also running the OMP algorithm 1, 5, 10, and 50 times.

Figure 1.

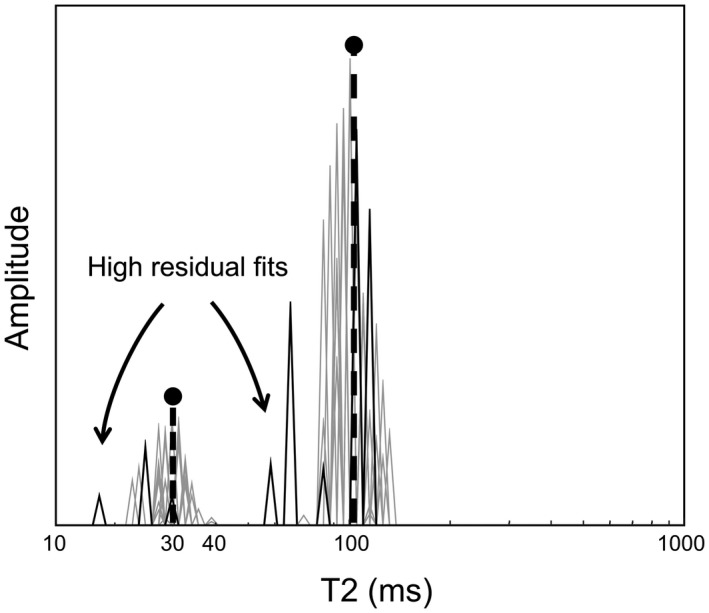
Example of a typical T₂ distribution reconstructed using 20 iterations of the OMP. High residual fits (solid black lines) will contribute less to the final result in comparison to lower residual fits (gray lines). The 2 dashed black lines represent the original T₂ distribution OMP, orthogonal matching pursuit.

The modified algorithm stops when the residual of the current iteration is larger than the residual of the previous iteration, in other words, when the next selected element does not provide a better fit.

These aforementioned modifications were added to the MatLab (MathWorks, Natick, MA, version 8.4, R 2014b) implementation of the OMP algorithm by Yaghoobi,29 which is available on GitHub (https://github.com/GSDrenthen/Non-Negative-OMP).

3.5.2. Data preprocessing

A singular value decomposition filter was used to reduce noise in the measured multiecho data.40 Furthermore, the EPG algorithm was used to correct for B₁‐inhomogeneities.30 To this end, for each voxel the corresponding refocusing FA is calculated by solving the multiexponential problem for a range of FAs and subsequently selecting the FA that corresponds to the lowest residual. A refocusing FA range of 100 to 180° was used. For the construction of the T₂ basis functions using the EPG, the T₁ relaxation was assumed to be 1000 ms in all cases.

For the multiexponential analysis, dictionaries of 120 and 1000 logarithmically spaced relaxation basis functions with a range of T₂ relaxation times of 15 to 3500 ms were used for the NNLS and OMP methods, respectively. An upper bound of 3500 ms was chosen such that contribution from free water content (T₂ > 2 s) could also be fitted. Previously, it was shown that reliable fits could also be obtained using a 40‐element basis set.32 However, because we use a high‐resolution (1000 elements) basis set for the OMP algorithm, we compare it to a relatively high‐resolution (120 elements) NNLS. Furthermore, to investigate if the increased number of elements in the basis set effects the MWF estimation, the OMP was also run with the same basis set of 120 functions as the NNLS. The curvature of the NNLS amplitude spectrum was minimized using a standard regularization, allowing a misfit of $1.020\le {\chi }_{\mathrm{r}\mathrm{e}\mathrm{g}}/{\chi }_{\mathrm{m}\mathrm{i}\mathrm{n}}\le 1.025$.11 Previously, regularization of the NNLS was associated with an underestimated MWF.41 Therefore, to investigate the effect of the regularization strength, an additional numerical simulation with 2 extra smoothing constraints ($1.005\le {\chi }_{\mathrm{r}\mathrm{e}\mathrm{g}}/{\chi }_{\mathrm{m}\mathrm{i}\mathrm{n}}\le 1.010$ and $1.040\le {\chi }_{\mathrm{r}\mathrm{e}\mathrm{g}}/{\chi }_{\mathrm{m}\mathrm{i}\mathrm{n}}\le 1.045$) was performed.

3.5.3. Validation

For the numerical simulations and phantom model, the accuracy of the MWF estimation by the OMP and NNLS methods was evaluated using the absolute bias, defined as the mean absolute deviation from the ground truth MWF,

$$\mathrm{A}\mathrm{b}\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{t}\mathrm{e}\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}=\frac{{\sum }_1^N\left|\mu -{\mathrm{M}\mathrm{W}\mathrm{F}}_{\mathrm{i}\mathrm{n}}\right|}{N},$$

where $\mu$ is the mean estimated MWF, ${\mathrm{M}\mathrm{W}\mathrm{F}}_{\mathrm{i}\mathrm{n}}$ is the ground truth MWF (range 0%–30%, with 1% increments), and $N$ is the number of MWF values ($N=31$ in this case).

The precision of both methods is evaluated by the relative standard deviation (RSD),

$$\mathrm{R}\mathrm{S}\mathrm{D}\left(\%\right)=100\%·\frac{\sigma }{\mu },$$

where $\sigma$ is the SD and $\mu$ is the calculated mean. The RSD is determined for a ${\mathrm{M}\mathrm{W}\mathrm{F}}_{\mathrm{i}\mathrm{n}}$ of 15% (RSD_15%) because an MWF of 15% is a commonly reported MWF in normal WM. 12, 14, 42

Because the in vivo data cannot be validated with a ground truth measurement, we compare the 2 methods with respect to each other. To this end, the WM was segmented from the T₁‐weighted images and coregistered to the MSE space using the SPM12 MatLab package (https://www.fil.ion.ucl.ac.uk/spm/software/spm12/). Thereafter, 2 major WM structures, the genu and splenium of the corpus callosum, were manually delineated; and 2 subcortical structures, the thalamus and the caudate, were segmented using the FreeSurfer software (version 5.3, https://surfer.nmr.mgh.harvard.edu).43 These ROIs are important structures and have often been studied in previous MWF research.32, 44

4. RESULTS

4.1. Numerical simulations

The mean estimated MWF of the NNLS and OMP methods for the simulated data with an SNR of 200 at the first echo (TE = 12 ms) is shown with respect to the supplied MWF in Figure 2. Additionally, the absolute bias of the MWF estimation is depicted in the same figure. Both methods systematically underestimate the ground truth MWF. However, over the whole MWF range, the MWF values estimated with the OMP are closer to the ground truth MWF compared to those estimated with the NNLS. This results in a 1.8 times smaller average absolute bias of the OMP method compared to the NNLS (NNLS: 4.4% vs. OMP: 2.5%). The 2 methods have a comparable RSD_15% (NNLS: 29% vs. OMP: 32%).

Figure 2.

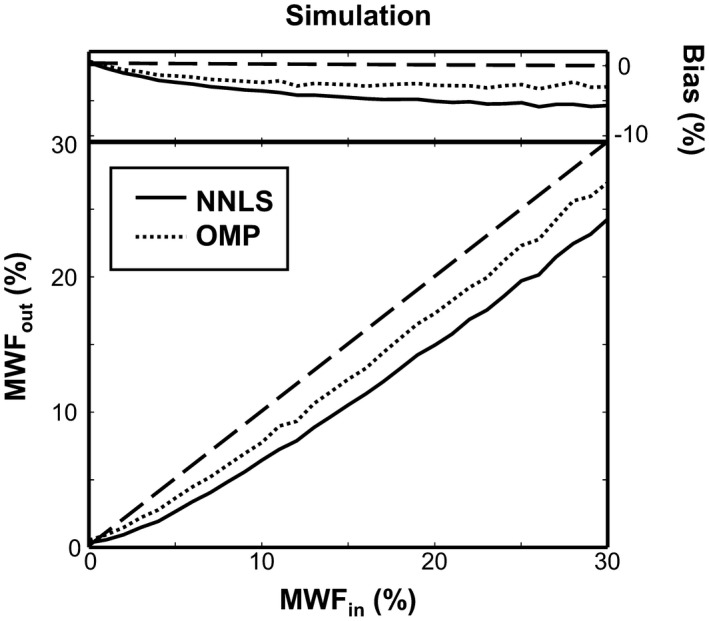
The estimated MWF from the numerical simulations using the NNLS (solid line) and the OMP (dotted line) is plotted against the supplied MWF. The dashed black line depicts the ground truth MWF, whereas the top of the figure shows the absolute bias of the estimated MWF MWF, myelin water fraction; NNLS, nonnegative least squares.

The effect of SNR on the absolute bias and RSD_15% of the MWF estimation for both methods is shown in Table 1 for healthy WM tissue and for WM lesions. The absolute bias and RSD_15% increased for the simulations with lower SNR. For nearly all SNR levels, the OMP has a smaller absolute bias and similar RSD_15% compared to the NNLS.

Table 1.

Absolute bias and RSD_15% of the MWF estimation of healthy WM tissue and a WM lesion using the NNLS and OMP algorithms with varying SNR

		Healthy WM			WM lesion
		NNLS	OMP	NNLS/OMP	NNLS	OMP	NNLS/OMP
	SNR
Absolute bias	100	6.4	3.9	1.6	2.9	2.1	1.4
	200	4.4	2.5	1.8	1.7	1.3	1.3
	350	3.0	1.6	1.9	1.0	0.7	1.4
RSD15%	100	57%	49%	1.2	34%	31%	1.1
	200	29%	32%	0.9	17%	20%	0.9
	350	19%	22%	0.9	10%	14%	0.7

Abbreviations: MWF, myelin water fraction; NNLS, nonnegative least squares; OMP, orthogonal matching pursuit; RSD, relative standard deviation; WM, white matter.

The effect of echo spacing and T_2myelin is shown in Table 2. A decreased T_2myelin of 15 ms greatly improves the MWF estimation for both methods. The large improvement is most likely due to the 2 T₂ peaks being further apart and thus more easily distinguished. Reducing the echo spacing to 8 ms allows for a better characterization of the fast myelin decay; however, it also decreases the total T₂ range (up to 256 ms), possibly hampering the correct characterization of slower decaying signals.

Table 2.

Absolute bias and RSD_15% of the MWF estimation for varying ESP and T_2myelin peak using the NNLS and OMP algorithms with an SNR of 200

		NNLS	OMP	NNLS/OMP
	ESP/T2myelin
Absolute bias	8/30 ms	5.9	3.0	2.0
	8/15 ms	0.8	0.3	2.7
	12/15 ms	1.1	0.5	2.0
RSD15%	8/30 ms	27%	33%	0.8
	8/15 ms	8%	8%	1.0
	12/15 ms	12%	11%	1.1

Abbreviation: ESP, echo spacing.

Using a continuous T₂ distribution instead of 2 distinct discrete peaks did not have a strong or meaningful effect on the results. The changes in absolute bias were <0.1% for both methods, whereas the RSD_15% did not deviate more than 1%. Reducing the basis set of the OMP algorithm to 120 elements showed similar changes in absolute bias (<0.1%) and RSD_15% (<1%). Furthermore, in Figure 3 the effect of computational time on the estimation of the MWF is shown for the OMP method, where the absolute bias decreases with running more instances of the algorithm.

Figure 3.

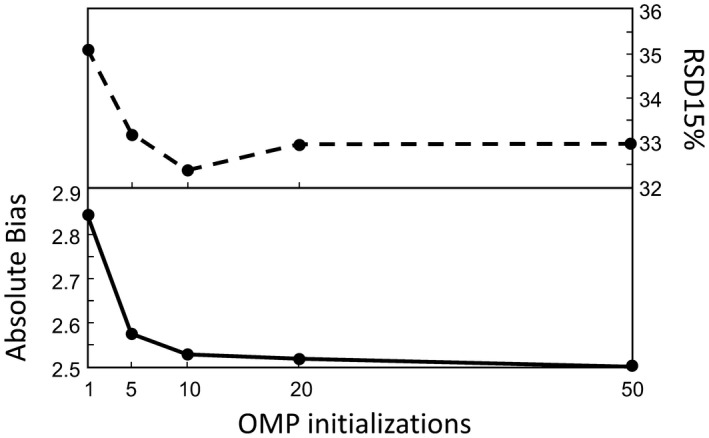
The effect that the number of random initializations has on the MWF estimation of the OMP method. Dashed line represents RSD_15% , and the solid line depicts the absolute bias RSD, relative standard deviation

Lastly, the effect of the NNLS smoothing constraint is shown in Figure 4. It is observed that a stronger regularization (i.e., higher smoothing constraint) shifts the peaks of the T₂ distribution slightly to the lower T₂ values. Additionally, the estimated MWF is lower for stronger smoothing (e.g., the total myelin‐related amplitude decreases).

Figure 4.

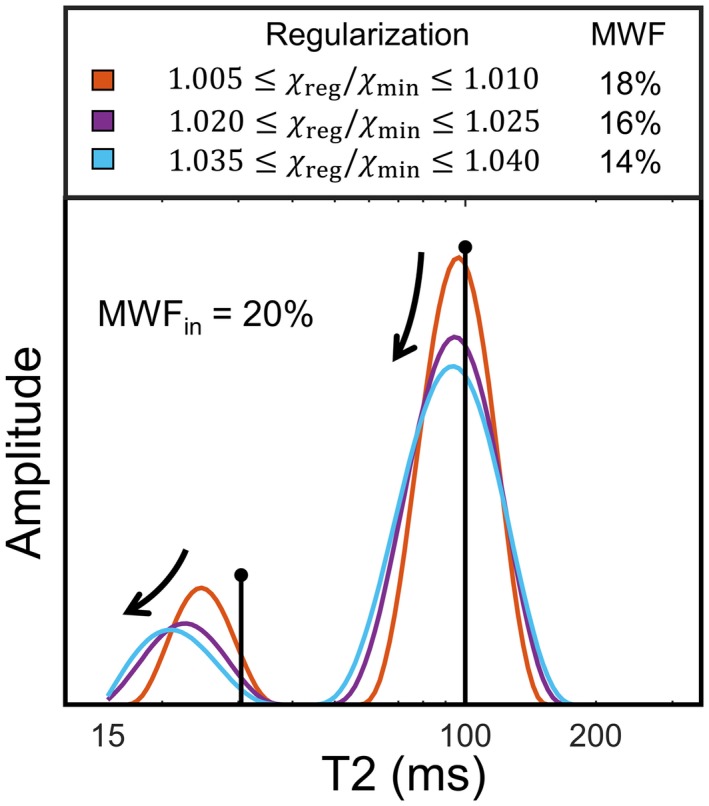
The effect of NNLS regularization using a smoothing constraint. The colored lines depict the reconstructed T₂ distribution for different regularization strengths, whereas the black lines represent the original T₂ distribution

4.2. Phantom model

The SNR of the phantom measurement at the first TE (TE = 12 ms) was 340 ± 34 (mean ± SD). The mean estimated MWF of the NNLS and OMP methods for the phantom measurements is shown in Figure 5 with respect to the defined MWF. Additionally, the absolute bias of the MWF estimation is shown for both methods in the same figure. From this we observe that, over almost the whole MWF range, both methods systematically underestimate the ground truth MWF, and that the MWF values estimated with the OMP are closer to the ground truth MWF. The absolute bias of the OMP method is on average 1.7 times smaller compared to the NNLS (NNLS: 3.4% vs. OMP: 2.0%), whereas the 2 methods have a comparable RSD_15% (NNLS: 25% vs. OMP: 18%).

Figure 5.

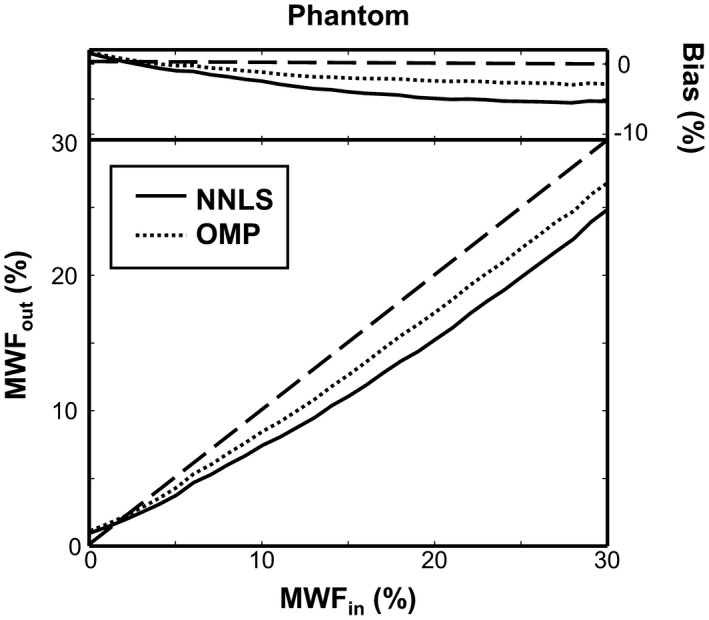
The estimated MWF from the phantom model using the NNLS (solid line) and the OMP (dotted line) is plotted against the defined MWF. The dashed black line depicts the ground truth MWF, whereas the top of the figure shows the absolute bias of the estimated MWF

4.3. In vivo

The SNR of the in vivo measurements at the first TE (TE = 12 ms) was 363 ± 193 (mean ± SD) measured in the genu and splenium of the corpus callosum. In Figure 6A, the MWF maps of a single representative healthy subject calculated with both the NNLS and OMP method are shown. In Figure 6B, the T₁‐weighted image with the ROIs is shown, and in Figure 6C a scatter plot of voxel‐wise MWF values in the ROIs as well as all the WM voxels is shown. Mean MWF values obtained in the ROIs and WM with the OMP algorithm were on average slightly higher by approximately 2% (actual MWF units) in comparison to the NNLS (Table 3). In addition, previously reported MWF values in the genu, splenium, thalamus, and caudate using the MSE acquisition and NNLS with EPG correction, as in the current study, are also given in the table.

Figure 6.

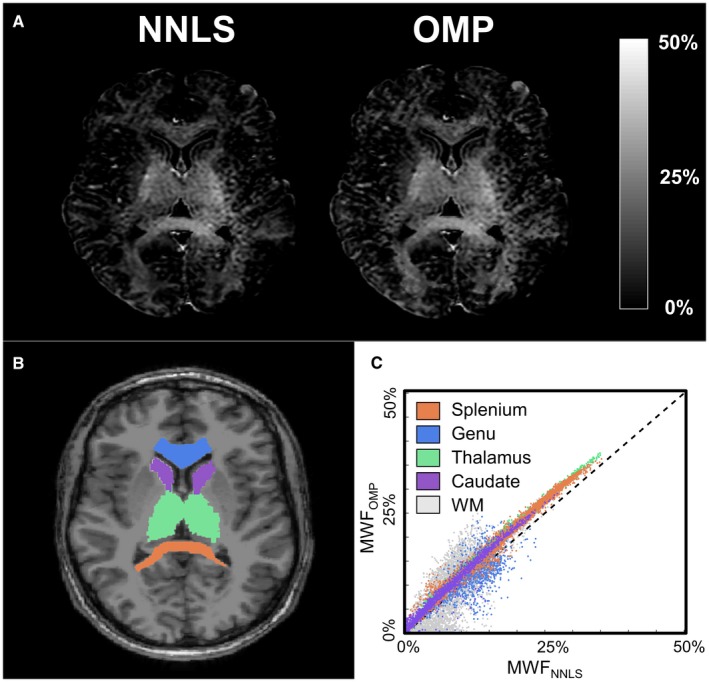
The results of the MSE sequence of a single representative subject (male, 28 year). The MWF map estimated with the NNLS and OMP methods (A), the T₁‐weighted image with the delineated ROIs (B), and a scatter plot of the MWF values in the ROIs and all WM (C) are shown ROI, region of interest; WM, white matter

Table 3.

The MWF estimated with the NNLS and OMP algorithms in the 2 ROIs (genu and splenium of the corpus callosum) as well as all WM. For reference, previously reported MWF values are added. Means and SDs are given

	Average MWF (%)		Literature Values
	NNLS	OMP	Prasloski32	Prasloski12	Mädler44
Splenium	18.8 ± 5.6	21.1 ± 5.6	15.2 ± 2.2a	14.5 ± 2.0a	10.8 ± 5.6
Genu	11.4 ± 5.2	13.2 ± 5.3	10.5 ± 2.4a	10.6 ± 3.6a	9.0 ± 4.0
Thalamus	14.3 ± 3.8	17.0 ± 3.9	–	3.4 ± 2.1a	3.1 ± 0.7
Caudate	5.6 ± 1.7	7.1 ± 1.8	–	1.8 ± 1.2a	2.4 ± 0.1
All WM	11.3 ± 6.2	13.0 ± 6.7	–	–	9.9 ± 3.6

Abbreviation: ROI, region of interest.

^aData obtained by digitizing plots.

Using the 3D GRASE sequence, whole brain MWF maps are calculated with the NNLS and OMP. Figure 7A shows the MWF map estimated using the OMP algorithm. In Figure 7B, a scatter plot of voxel‐wise MWF values in the ROIs as well as all the WM voxels is shown. On average, the MWF values obtained with the OMP algorithm were slightly higher by approximately 1% to 2% (actual MWF units) in comparison to NNLS.

5. DISCUSSION

5.1. Current findings

In the current study, the OMP algorithm is introduced as an alternative method for the determination of the MWF from multiexponential T₂ relaxation data and is compared with the most commonly applied method in literature, NNLS. The estimation of the MWF using both methods is validated using a ground truth from numerical simulations and an in vitro phantom model. It is shown that the OMP yields a more accurate MWF estimation compared to the NNLS, whereas a comparable precision (in terms of RSD_15%) is obtained. Furthermore, the in vivo results are in line with the numerical simulations and the phantom model, showing on average that the MWF calculated with the OMP is higher compared to the NNLS.

5.2. Effect of SNR

For each of the 3 SNR levels studied, the OMP outperforms the NNLS algorithm in terms of a smaller absolute bias. As to be expected, a lower SNR is found to be associated with a larger overall absolute bias as well as a less precise measurement (i.e., higher RSD_15%) of the MWF. The multiecho sequence used in this study has an approximate SNR of 350. Therefore, we would expect that the simulations with an SNR of 350 would best represent the phantom and in vivo results. Indeed, the phantom model shows an accuracy and precision comparable to the simulations with SNR 350. The absolute bias is, however, higher in the phantom model. Most likely this is caused by the B₁ inhomogeneities and subsequent error correction using the EPG algorithm, which induces additional errors difficult to model in the simulations.

5.3. Underestimation of MWF

The MWF is systematically underestimated by an absolute bias of approximately 1% to 5% in the simulations as well as the phantom model. One possible explanation for this phenomenon might be the effect of Rician noise present in magnitude images. Although the Rician noise can be considered near‐Gaussian for higher SNRs, it tends toward the Rayleigh distribution for images with low SNR. Because the SNR in multiecho measurements decreases exponentially for longer TEs, the Rician noise in the low SNR measurements could be misinterpreted for a slow decaying component. This artificial slow‐decaying component adds to the total water amplitude and therefore reduces the MWF.15

Previously, the regularization of the NNLS algorithm was also found to cause MWF underestimation.41 In this study, it is observed that the peak of the underlying T₂ distribution shifts to a shorter T₂. Because the regularization introduces a smoothing constraint, more elements from the basis set will be used to obtain an optimal result. To provide a result with the lowest misfit, elements that are close to the original peak will be preferred. Because the basis set is logarithmically spaced, the shorter T₂ times are closer to the original peak, shifting the peak to the left in the spectrum. To compensate for this shift, the amplitude of the peak is reduced. This effect is stronger for the myelin peak because in this region the basis functions are more densely distributed, thus underestimating the MWF. Using NNLS with weaker regularization, or even unregularized, would suffer less from this underestimation41; however, it would decrease the stability of the algorithm because it is well established that the ill‐posed NNLS requires strong regularization.

The OMP is not regularized with a smoothing constraint; instead, the OMP algorithm is repeated 20 times to provide more stable results. Therefore, the OMP does not suffer from an underestimated MWF due to a smoothing constraint. Because the OMP has a (roughly 20 times) lower computational complexity, it results in a computational time comparable to the NNLS with 120 basis functions. However, the NNLS is commonly used with fewer basis functions, resulting in a lower computational time (e.g., the 40 basis functions case is roughly 1.5 times faster). Therefore, the comparison of computational times presented here should be interpreted with caution.

5.4. In vivo applicability

The in vivo results are in line with the numerical simulations and phantom measurements because we found that the in vivo MWF estimated with the OMP yielded somewhat higher values compared to the NNLS. More specifically, because the in vivo data have an SNR of approximately 350, we would expect a similar increase of the OMP as measured in the simulations with SNR 350. Indeed, we found that the mean MWF values determined with the OMP in the genu and splenium of the corpus callosum, thalamus, caudate, and all the WM show a similar increase of MWF compared to those estimated with the NNLS. Furthermore, the MWF values reported in the genu and splenium of the corpus callosum using the NNLS method are within normal limits compared to previous studies,32, 44 whereas the MWF values reported in the thalamus and caudate are much higher. However, whereas the values are not specifically reported, some other studies have also observed a relatively high MWF in these structures.41, 45 Therefore, these discrepancies between the MWF values reported in our study and the values of previous literature might be explained by differences in age of the healthy volunteers and different scanning parameters.

5.5. Study considerations

In this study, we used healthy volunteers without WM abnormalities. However, our simulations have indicated that the OMP algorithm outperforms the NNLS in healthy tissue as well as in WM lesions. This implies that the OMP algorithm can be a useful tool in future patient studies. The single‐slice MSE sequence that was used in this study limits the comparison of the MWF estimation methods to specific brain regions. Furthermore, the MSE sequence is a relatively slow sequence (~13 min for a single slice) and therefore not optimal for patient studies. However, the MSE is considered as the reference method for MWF estimation,11 and is therefore suitable for comparative studies as the current study. The performance of the OMP algorithm to determine the MWF should be further evaluated on accelerated multiecho sequences. Recently, several studies have already focused on fast acquisition of multiecho data for the purpose of MWF mapping. For instance, Prasloski et al. showed that whole brain MWF mapping was possible under 15 min using a gradient‐spin echo sequence with 32 TEs,12 whereas Nguyen et al. showed that even faster whole brain MWF mapping was possible acquiring 6 TEs in 4 min using a modified T₂prep sequence.46 In this study, we already showed the applicability of the OMP algorithm for multiecho data acquired using a 3D GRASE sequences. Furthermore, the OMP algorithm could also prove valuable in other MR modalities that require multiexponential analysis, such as intravoxel incoherent motion.47, 48

6. CONCLUSION

We have applied the OMP for the multiexponential T₂ relaxation component analysis to estimate the MWF and compared it to the most commonly applied algorithm in literature, the NNLS. Using numerical simulations and an in vitro phantom model, it was demonstrated that the OMP is a more accurate method for the estimated MWF. The bias of the MWF estimation using the OMP was roughly reduced by a factor of 2, whereas the precision was comparable to the NNLS. In vivo results show similar findings as the simulations and phantom model, proving that OMP can be a preferred alternative to conventional methods for its accuracy and low computational complexity.

7.

Figure 7.

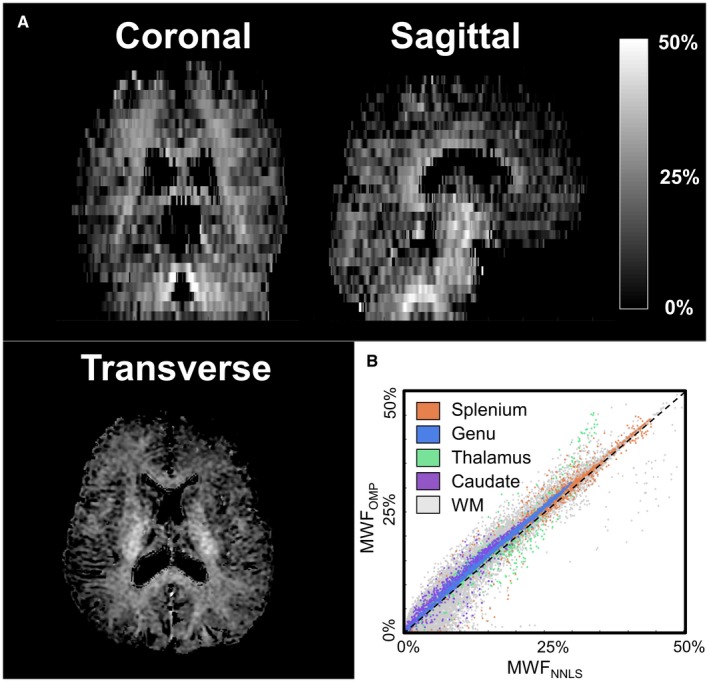
The results of the 3D GRASE sequence of a single subject (female, 29 year). A coronal, sagittal, and transverse slice of the MWF map estimated with the OMP method (A) and a scatter plot of the MWF values in the ROIs and all WM (B) are shown

Drenthen GS, Backes WH, Aldenkamp AP, Op ’t Veld GJ, Jansen JFA. A new analysis approach for T₂ relaxometry myelin water quantification: Orthogonal Matching Pursuit. Magn Reson Med. 2019;81:3292–3303. 10.1002/mrm.27600