Elasticity as the Basis of Allostery in DNA

Abstract

Allosteric interactions in DNA are crucial for various biological processes. These interactions are quantified by measuring the change in free energy as a function of the distance between the binding sites for two ligands. Here, we show that trends in the interaction energy of ligands binding to DNA can be explained within an elastic birod model, which accounts for the deformation of each strand as well as the change in stacking energy due to perturbations in position and orientation of the bases caused by the binding of ligands. The strain fields produced by the ligands decay with distance from the binding site. The interaction energy of two ligands decays exponentially with the distance between them and oscillates with the periodicity of the double helix in quantitative agreement with experimental measurements. The trend in the computed interaction energy is similar to that in the perturbation of groove width produced by the binding of a single ligand, which is consistent with molecular simulations. Our analysis provides a new framework to understand allosteric interactions in DNA and can be extended to other rod-like macromolecules whose elasticity plays a role in biological functions.

Graphical Abstract

INTRODUCTION

When a ligand binds to DNA, it induces conformational changes at the binding site, which could propagate to regions tens of base-pairs away, thereby encouraging or inhibiting the binding of a second ligand in those places. Such interactions between two binding agents are called allosteric interactions. Our focus here is on a mechanism for allostery based on the elasticity of long molecules. Although we will illustrate our theory using DNA as an example, long-range allosteric interactions have been documented in actin, microtubules, and helical peptide chains. For example, myosin binds to actin filaments leading to the suppression of the formation of cofilin clusters via allosteric signaling.¹ Long-range structural changes induced by taxol binding to microtubules inside a cell prevents cell division, thus making it a potent antitumor agent.² The transfer of chiral stimulus triggered by a binding agent across a helical peptide chain gives the molecule an overall chiral character and is yet another instance of allostery.³ Instances of allostery in DNA have been known for decades.^4,5 Antitumor drug actinomycin D binds to DNA by intercalating between the adjacent base pairs⁵ containing a guanine base. However, in the presence of daunomycin, another antitumor drug, actinomycin, is observed to bind to poly(dAT) DNA oligomers too. This is due to the allosteric stabilizing influence exerted by the already bound daunomycin molecule near its binding site. We will analyze allostery in ds-DNA because detailed experimental and simulation results are available for it,^6-8 thus allowing quantitative comparisons with our theory.

We define the allosteric interaction energy $\Delta G=E_{12}^{\{0,p\}}-E_1^0-E_2^p$, where $E_{12}^{\{0,p\}}$ is the free energy of the protein–DNA complex consisting of two proteins separated by distance p and $E_1^0$ and $E_2^p$ are the free energies of the protein–DNA complexes consisting of one protein. Kim et al.⁷ have conducted single-molecule experiments using fluorescence techniques to measure allosteric interaction energy ΔG between two proteins on a DNA oligomer. In their paper,⁷ DNA-binding proteins are categorized as (a) proteins that bend DNA such as LacR and T7-RNAp and (b) proteins that bind to straight DNA such as GRDBD and BamHI. Here, we deal with the latter category.

We use the theory of elastic birods⁹ to develop a mechanical model for investigating protein–DNA interactions. A birod consists of two elastic strands joined by an elastic web. We represent the sugar-phosphate backbone of DNA using the outer strands and the complimentary base pairing is modeled using the elastic web. A birod model of DNA has different properties than a homogeneous rod model at short length scales; however, as the length of the birod increases, the elastic properties of both models become indistinguishable.¹⁰

We discuss key features that distinguish our model from the state-of-the-art⁸ worm-like chain model for DNA allostery.

1. Helical geometry: Kim et al.¹¹ discovered that the interaction energy ΔG between two proteins on DNA decays exponentially while oscillating with the periodicity of the DNA double helix. It is thereby imperative that we account for the double helical geometry of DNA, which is conveniently incorporated in a birod model,⁹ but is absent in a worm-like chain model of DNA.

2. Elasticity of base pairs: Proteins interact with DNA by altering the geometry of the double helix, such as changing the width of major/minor groove.^6,12 The elasticity of the base pairs, represented by the elastic web in a birod model is essential to accurately model these local deformations.

3. Stacking energy: Stacking energy penalizes the change in orientations of the base pairs with respect to each other. We use a stacking energy quadratic in the twist and stretch of the DNA-double helix.

In an existing model⁸ of allostery, tension in the worm-like polymer chain to which the two proteins are bound plays an important role in the decaying oscillatory behavior of the interaction energy ΔG. However, in the experiments of Kim et al.⁷ and simulations of Dršata et al.,⁶ the oscillatory exponentially decaying allosteric interactions on DNA are present even in the absence of tension. Here, we use an analytical model to show that decaying oscillatory behavior of the interaction energy can arise from the interplay between the double helical geometry and the elasticity of the base pairs.

Our model provides key insights into the structural deformations of the DNA helix, changes in the groove width when a ligand binds to DNA, and the allosteric interaction energy ΔG between two proteins on DNA. We compute the correlations between the displacement variables at the two sites of protein binding and establish their connection to the interaction energy between the two proteins. Our results are in excellent quantitative agreement with the experimental data in Kim et al.⁷ and Kopka et al.¹²

Numerical simulations^6,13 have been used to propose mechanical models for DNA allostery. These papers describe DNA using three sets of coordinates: intra-base-pair coordinates buckle, propeller, opening, shear, stretch and stagger, inter-base-pair coordinates tilt, roll, twist, shift, slide, and rise, and major and minor groove widths. The DNA-binding protein fixes some (or all) of the degrees of freedom at the site of binding, resulting in deformations away from it. The energy of binding can therefore be computed. The approach is comprehensive, but computationally expensive. Drawing upon the know-how from Dršata et al.,^6,13 we allow for the bending, twisting, stretching, and shearing of the base pairs. Furthermore, we go beyond their numerical models by considering the mechanics of the outer strands, which, as pointed out later, is crucial to getting the correct twist–stretch coupling for double-stranded DNA.

THEORY

DNA comprises of two helical strands held together via complementary base pairing. When a ligand, such as a protein or a drug, binds to DNA, it exerts forces and moments on the double helix^14,15 causing deformations at the base-pair level. We use the theory of birods⁹ to investigate these deformations. A birod consists of two elastic strands that interact through an elastic web. This construction makes it suitable for investigating the deformations at the base-pair level in a DNA molecule, which a homogeneous rod model cannot capture.¹⁶ The latter ignores the double-helical structure and the elasticity of the base pairs, both of which are crucial to the problem under consideration. In the following (·)_x denotes $\frac{\partial (\cdot )}{\partial x}$. Lower case letters such as a, r, β^± are scalars, bold lower case letters such as t⁺, b⁻ are vectors, whereas bold upper case letters such as R⁻, ${\mathbf{R}}_0^{+}$, Z are 3 × 3 tensors.

We assume the phosphate backbones comprising of phosphodiester bonds, represented by outer strands in our model to be inextensible and unshearable. Our assumption of inextensibility can be justified by examining the elastic properties of ssDNA. The stretch modulus of ssDNA, at high ion concentration, is about 1000 pN,¹⁷ which is about twice that of the largest modulus (K_e = 600 pN) used in our model. At low ion concentrations, under which the experiments reported in Kim et al. are conducted, ssSDNA shows an even stiffer response.¹⁸ The assumption of unshearability is justified if the cross-sectional dimensions are much smaller than the length of a rod,¹⁹ which is indeed true for DNA molecules. Because these backbones consist of consecutive single bonds that allow free rotation about the bond, we assume that they cannot resist twisting moments. The base pairing is represented by the elastic web, which is capable of extending, shearing, bending, and twisting. In addition to the elastic energy, we consider contributions from the stacking energy, which is associated with the change in orientations of the successive base pairs.

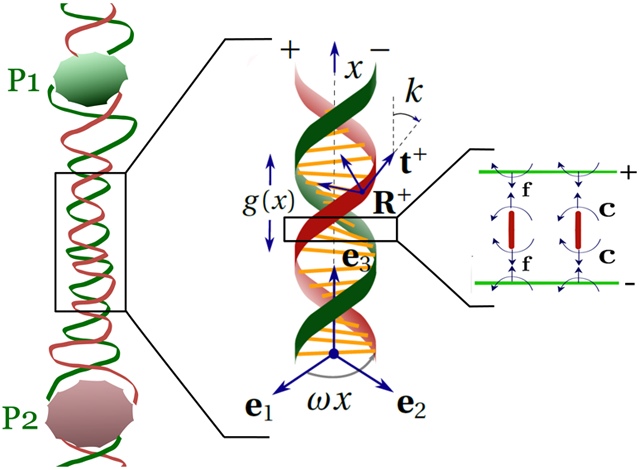
In this paper, we consider the proteins that do not bend DNA. Kim et al.⁷ report experimental data for allosteric interaction energy using a DNA-binding protein pair: GRDBD and BamHI, both of which do not bend DNA.^20,21 Kim et al.⁷ have also experimented with proteins that bend DNA, and they have been theoretically treated elsewhere.^22,23 We denote the helical strands as ±; their positions in the reference state are denoted by ${\mathbf{r}}_0^{\pm }$. We use arclength parameter x to parametrize the double helix (Figure 1). Thus,

$$\begin{gathered} {\mathbf{r}}_0^{+}=a(\cos \omega x{\mathbf{e}}_1+\sin \omega x{\mathbf{e}}_2)+x{\mathbf{e}}_3, \\ {\mathbf{r}}_0^{-}=a(\cos (\omega x+\alpha ){\mathbf{e}}_1+\sin (\omega x+\alpha ){\mathbf{e}}_2)+x{\mathbf{e}}_3 \end{gathered}$$ (1)

where a = 1 nm is the radius of the DNA helix, p = 3.4 nm is the pitch, $\omega =\frac{2\pi }{p}$, and α is the phase difference between the helices. Here, we assume α = π to make the computations analytically tractable. We consider a deformed configuration where the double helix extends and twists about e₃, and its radius and phase angle also change due to binding of ligands. The deformed state of the ± strands is denoted by r^±(x), where

$$\begin{gathered} {\mathbf{r}}^{+}(x)=(a+r)(\cos (\omega x+{\beta }^{+}){\mathbf{d}}_1+\sin (\omega x+{\beta }^{+}){\mathbf{d}}_2) \\ +(x+{\int }_{-\infty }^{x}a{\xi }^{+}\mathrm{d}x){\mathbf{e}}_3, \\ {\mathbf{r}}^{-}(x)=-(a+r)(\cos (\omega x+{\beta }^{-}){\mathbf{d}}_1+\sin (\omega x+{\beta }^{-}){\mathbf{d}}_2) \\ +(x+{\int }_{-\infty }^{x}a{\xi }^{-}\mathrm{d}x){\mathbf{e}}_3 \end{gathered}$$ (2)

such that d_1x = k₃d₂ and d_2x = −k₃d₁. To gain a better physical insight, we give a visual representation of the deformation described in the above equation in Figure 2. We only show the deformation for the + strand for clarity and indicate the strain variables r (change in radius), β (change in phase angle), and ξ (stretch of the center-line). We assume all the displacement and strain parameters r, β^±, and ξ^± vanish at x = ±∞ because the deformations caused by the proteins are local. The change in radius r, change in the phase angle β^±, stretches ξ^±, and the twist k₃ are assumed to be small (~O(ε)) such that second-order terms such as r² and ξβ⁻ are negligible. However, there could be finite rotations resulting from k₃.

Figure 1.

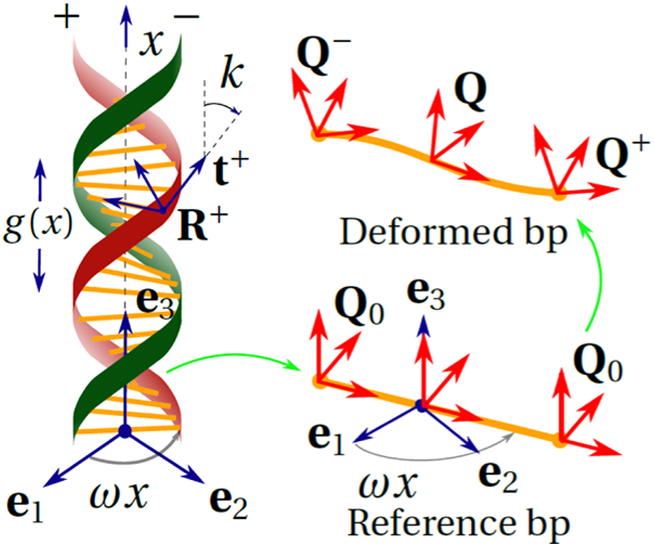
Birod model of DNA. The angle between the tangent t⁺ and e₃ is k. A base pair in reference and deformed state is shown. The director frames attached to ± ends of the base pair change from Q₀ to Q^±, respectively. The rigid rotation of the strand Q = (Q⁺Q^−T)^1/2Q⁻ and microrotation P = (Q⁺Q^−T)^1/2.

Figure 2.

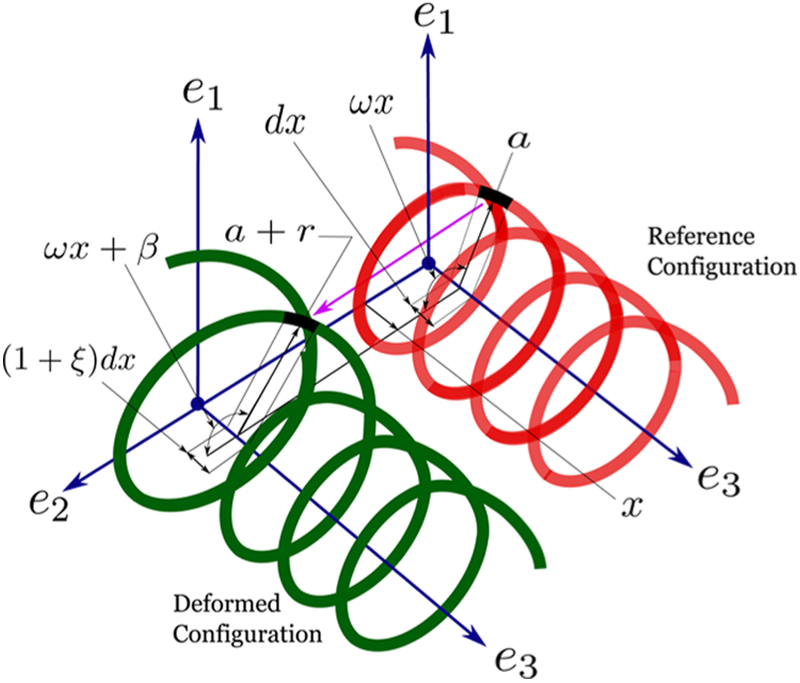
Distortions to the helical geometry of the + strand. We assume that the DNA remains straight after the binding of proteins. Therefore, the axis e₃ remains undisturbed. The radius of the helix a changes to a + r, the phase angle ω x changes to ω x + β, and the length of the infinitesimal element dx, shown in black, changes to (1 + ξ) dx.

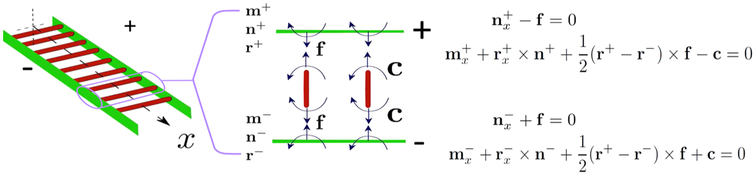
As shown in Figure 3, the birod consists of two elastic strands joined by an elastic web. We show a straight elastic ladder for easy visualization of the key forces and moments. The + strand exerts a body force l and a body moment c on the − strand via the elastic web. The balance laws for the two outer strands constitute the governing equations for the birod.⁹ The deformation of the elastic web can be calculated once the deformation of the outer strands is known. We need to solve the following balance equations for a helical birod,

$$\begin{gathered} {\mathit{n}}_x^{\pm }\mp \mathit{f}+\mathit{l}=0, \\ {\mathit{m}}_x^{\pm }+{\mathbf{r}}_x^{\pm }\times {\mathit{n}}^{\pm }+\frac{1}{2}({\mathbf{r}}^{+}-{\mathbf{r}}^{-})\times \mathit{f}\mp \mathit{c}+\mathit{h}=0 \end{gathered}$$ (3)

where m^± and n^± are the contact moment and contact force, respectively, in ± strands. f and c are the distributed force and distributed moment exerted by the + strand on the − strand. l and h are the body force and body moment exerted by the base pairs onto both ± strands. In what follows, we use the position vectors for the deformed helix r^±(x) (eq 2) to compute these quantities. The constitutive relations for the forces n^±, moments m^±, and the force l and moment c transferred by the web, are discussed in the relevant subsections.

Figure 3.

Free-body diagrams that establish the connection between an elastic rod and an elastic birod. We deliberately show a straight ladder instead of helical birod to illustrate the mechanics. An elastic birod comprises two elastic rods + and −. The + strand exerts a moment c and force f on the − strand through an elastic web. This transfer of moment and force leads to deformation of the web. In the figure, r^± denotes the position vector for ± strands and n^± and m^± denote the contact forces and contact moments in ± strands, respectively. The force and moment balance for + and − strand constitute the governing equations (eq 3) for the elastic birod. For further discussion, see Moakher and Maddocks.⁹

Contact Forces in the Outer Strands (n^±).

The outer strands are inextensible, which means $\mid {\mathbf{r}}_x^{\pm }\mid =\mid {\mathbf{r}}_{0x}^{\pm }\mid$ yielding

$${\omega }^{2}r+a\omega (k_3+{\beta }_x^{\pm })+{\xi }^{\pm }=0$$ (4)

We use the above equation to eliminate ξ^± from eq 2. Due to the constraint in eq 4, the contact forces n^± enter as Lagrange multipliers.

Contact Moments in the Outer Strands (m^±).

We attach a director frame ${\mathbf{R}}^{\pm }=\left[{\mathbf{n}}_0^{\pm }{\mathbf{b}}_0^{\pm }{\mathbf{t}}_0^{\pm }\right]$ to each cross section of the ± strands, where ${\mathbf{n}}_0^{\pm }$, ${\mathbf{b}}_0^{\pm }$, and ${\mathbf{t}}_0^{\pm }$ are the normal, binormal, and tangent in the reference state to ± strand, respectively. n^±, ${\mathbf{b}}_0^{\pm }$, ${\mathbf{t}}_0^{\pm }$, and the curvature in the reference configuration ${\Omega }_0^{\pm }$ are computed using eq 1 as follows

$$\begin{gathered} {\mathbf{t}}_0^{\pm }=\frac{{\mathbf{r}}_{0x}^{\pm }}{\mid {\mathbf{r}}_{0x}^{\pm }\mid }=\pm \sin k(-\sin \omega x{\mathbf{e}}_1+\cos \omega x{\mathbf{e}}_2)+\cos k{\mathbf{e}}_3, \\ {\mathbf{n}}_0^{\pm }=\frac{{\mathbf{t}}_x^{\pm }}{\mid {\mathbf{t}}_x^{\pm }\mid }=\mp (\cos \omega x{\mathbf{e}}_1+\sin \omega x{\mathbf{e}}_2), \\ {\mathbf{b}}_0^{\pm }={\mathbf{t}}_0^{\pm }\times {\mathbf{n}}_0^{\pm } \\ =\mp \cos k(-\sin \omega x{\mathbf{e}}_1+\cos \omega x{\mathbf{e}}_2)+\sin k{\mathbf{e}}_3, \\ {\Omega }_0^{\pm }={\Omega }_0=({\mathbf{t}}_0^{\pm }.{\mathbf{t}}_0^{\pm }{)}^{1∕2}=\omega \sin k \end{gathered}$$ (5)

Similarly, we use eq 2 to compute the Frenet–Serret frame R^± = [n^± b^± t^±] and curvature Ω^± in the deformed state. We neglect terms higher than first order, such as rβ⁺, ξ⁻ r~O(ε²), and get

$$\begin{gathered} {\mathbf{R}}^{\pm }=[{\mathbf{n}}^{\pm }{\mathbf{b}}^{\pm }{\mathbf{t}}^{\pm }]={\mathbf{ZR}}_0^{\pm }(1+{\Theta }^{\pm }), \\ \mathbf{Z}={\mathbf{d}}_1\otimes {\mathbf{e}}_1+{\mathbf{d}}_2\otimes {\mathbf{e}}_2+{\mathbf{e}}_3\otimes {\mathbf{e}}_3, \\ {\Theta }^{\pm }=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill -{\theta }_3^{\pm }\hfill & \hfill {\theta }_2^{\pm }\hfill \\ \hfill {\theta }_3^{\pm }\hfill & \hfill 0\hfill & \hfill -{\theta }_1^{\pm }\hfill \\ \hfill -{\theta }_2^{\pm }\hfill & \hfill {\theta }_1^{\pm }\hfill & \hfill 0\hfill \end{array}\right] \\ {\theta }_1^{\pm }=r\omega +a({\beta }_x^{\pm }+k_3),{\theta }_2^{\pm }=-r_x\cos k+{\beta }^{\pm }\sin k, \\ {\theta }_3^{\pm }=\frac{-\omega r_x-a({\beta }_{xx}^{\pm }+k_{3x})}{\omega \sin k}-\frac{(r_x\cos k-{\beta }^{\pm }\sin k)\cos k}{\sin k} \end{gathered}$$ (6)

The bending moment in the outer strands m^± is proportional to the change in curvature ${\kappa }^{\pm }={\Omega }^{\pm }-{\Omega }_0^{\pm }$ and is directed along the binormal b^± such that m^± = EIκ^±b^±, where EI is the bending modulus of the strand. Note that the twisting moment is zero because the phosphate backbone consists of single bonds that permit free rotations.

Force and Moment Transferred by the Web (f, c).

Now, we compute the bending and twisting of the web, which represents base pairing. We attach a director frame Q₀ to both + and − end of the base pair (Figure 1).

$${\mathbf{Q}}_0=[{\mathbf{e}}_r{\mathbf{e}}_{\theta }{\mathbf{e}}_3]$$ (7)

where e_r = cos ωxe₁ + sin ωxe₂ and e_θ = −sin ωxe₁ + cos ωxe₂. As the birod deforms, these frames respectively get mapped to Q^±. We compute Q^± using the deformation of R^± from eq 6 keeping in mind that the angles between the columns of ${\mathbf{R}}_0^{\pm }$ and ${\mathbf{Q}}_0^{\pm }$ should remain constant during deformation implying (${\mathbf{R}}_0^{\pm \mathrm{T}}{\mathbf{Q}}_0={\mathbf{R}}^{\pm \mathrm{T}}\mathbf{Q}$), thus

$${\mathbf{Q}}^{\pm }={\mathbf{ZR}}_0^{\pm }(\mathbf{I}+{\Theta }^{\pm }){\mathbf{R}}_0^{\pm T}{\mathbf{Q}}_0,{\Theta }^{\pm }\sim O(\epsilon )$$ (8)

Now, we can compute the rigid rotation Q and microrotation P for each base pair. The microrotation contains information about the “difference” between the rotations Q^±.⁹ This is related to the moment transferred by the base pair c via an elastic constitutive relation for the web

$$\mathbf{P}=({\mathbf{Q}}^{+}{\mathbf{Q}}^{-\mathrm{T}}{)}^{1∕2}=\mathbf{Z}(\mathbf{I}+{\Phi }^{\mathrm{c}}){\mathbf{Z}}^{\mathrm{T}}$$ (9)

Here, ${\Phi }^c=\frac{{\mathbf{R}}^{+}{\Theta }^{+}{\mathbf{R}}^{+\mathrm{T}}-{\mathbf{R}}^{-}{\Theta }^{-}{\mathbf{R}}^{-\mathrm{T}}}{2}$ is a skew symmetric tensor. The moment transferred by the base pair is directly proportional to the Gibbs vector of $P.\eta =\tan \frac{\lambda }{2}\widehat{\mathbf{k}}$ is a Gibbs rotation vector for a rotation matrix T if $\mathbf{T}\widehat{\mathbf{k}}=\widehat{\mathbf{k}}$ and 1 + 2 cos λ = tr T. In our case, the Gibbs vector of P is $2\eta =2\mathbf{Z}\stackrel{‒}{\eta }=\mathbf{Z}{\varphi }^c$, where ϕ^c is the axial vector of skew symmetric tensor Φ^c. Note that in the reference state, η₀ = 0 because P₀ = (Q₀Q^T)^1/2 = I. The rigid rotation of the base pair Q = PQ⁻. Here,

$$\mathbf{Q}=\mathbf{Z}(1+\Phi ){\mathbf{Q}}_0$$ (10)

and $\Phi =\frac{{\mathbf{R}}^{+}{\Theta }^{+}{\mathbf{R}}^{+\mathrm{T}}+{\mathbf{R}}^{-}{\Theta }^{-}{\mathbf{R}}^{-\mathrm{T}}}{2}$ is a skew symmetric matrix. The moment exerted by + strand on the − strand by means of the elastic web, c, is computed using c = QHQ^Tη, where H = diag[H₁, H₂, H₃] are the elastic moduli.⁹ Now, we shift our focus to the extension and shear of the web. In the reference configuration, the displacement between the two strands ${\mathbf{w}}_0=\frac{{\mathbf{r}}_0^{+}-{\mathbf{r}}_0^{-}}{2}=a{\mathbf{e}}_r,$ which, in deformed configuration, changes to $\mathbf{w}=\frac{{\mathbf{r}}^{+}-{\mathbf{r}}^{-}}{2}$. The force f exerted by + strand on the − strand is computed using $\mathit{f}=\mathbf{QL}({\mathbf{Q}}^{\mathrm{T}}\mathbf{w}-{\mathbf{Q}}_0^{\mathrm{T}}{\mathbf{w}}_0)$, where L = diag [L₁, L₂, L₃] are the elastic moduli, $\beta =\frac{{\beta }^{+}+{\beta }^{-}}{2}$ and ${\beta }^c=\frac{{\beta }^{+}-{\beta }^{-}}{2}$.

$$\begin{gathered} \mathit{c}={\mathbf{QHQ}}^{\mathrm{T}}\eta \\ =H_1(-a{k}_3-\omega r_x-a{\beta }_x){\mathbf{f}}_1+H_2\frac{(-a{k}_{3x}-\omega r_{xx}-a{\beta }_{xx})}{\omega }{\mathbf{f}}_2 \\ +H_3\left({\beta }^c-\frac{a\text{cot}k}{\omega }{\beta }_{xx}^c\right){\mathbf{e}}_3, \\ \mathit{f}=\mathbf{QL}({\mathbf{Q}}^{\mathrm{T}}\mathbf{w}-{\mathbf{Q}}_0^{\mathrm{T}}{\mathbf{w}}_0) \\ =L_{1}r{\mathbf{f}}_1+a{L}_2\text{cot}k\frac{a{k}_{3x}+2\omega r_x+a{\beta }_{xx}}{\omega }{\mathbf{f}}_2 \\ -a^2{L}_3\frac{{\omega }^2{\beta }^c+{\beta }_{xx}^c}{\omega }{\mathbf{e}}_3 \end{gathered}$$ (11)

Contributions from the Stacking Energy (l, h).

We now consider the contributions from the stacking energy. The center line of the double helix e₃ undergoes both twist k₃ and extension $\xi =\frac{{\xi }^{+}+{\xi }^{-}}{2}$. We associate a quadratic stacking energy $E_{\mathrm{s}}=K_{\mathrm{c}}{k}_3^2+K_{\mathrm{e}}{\left(\frac{{\xi }^{+}+{\xi }^{-}}{2}\right)}^2$ to penalize this change in the orientation of successive base pairs. Due to this energy, the base pairs exert a body force l and a body moment h on both ± strands, which are given by

$$\mathit{l}=K_{\mathrm{e}}\left(\frac{{\xi }^{+}+{\xi }^{-}}{2}\right){\mathbf{e}}_3,\mathit{h}=K_{\mathrm{c}}{k}_3{\mathbf{e}}_3$$ (12)

RESULTS

Now we have all the ingredients for solving the governing differential equations of a birod. Substituting these quantities in the balance laws (eq 3) gives us a set of 12 differential equations. The complete procedure for solving those equations is in the supplement; however, we highlight crucial points here. It follows from the governing equations that β⁺ = β⁻ (= β, say), $n_3^c=n_1=n_2=0$. β⁺ = β⁻ implies ξ⁺ = ξ⁻ (= ξ, say), thereby reducing 12 equations to 6 equations in 6 unknowns r, β, k₃, $n_{1,2}^c$, n₃. We look for solutions of the form

$$\begin{gathered} r(x)=r_0{\mathrm{e}}^{-\lambda x},\beta (x)={\beta }_0{\mathrm{e}}^{-\lambda x},\xi (x)={\xi }_0{\mathrm{e}}^{-\lambda x}, \\ {n}_1^{\mathrm{c}}(x)=n_{10}^{\mathrm{c}}{\mathrm{e}}^{-\lambda x},n_2^{\mathrm{c}}(x)=n_{20}^{\mathrm{c}}{\mathrm{e}}^{-\lambda x},n_3(x)=n_{30}{\mathrm{e}}^{-\lambda x} \end{gathered}$$ (13)

We substitute this form into the governing equations (eq 3) and obtain an eigenvalue problem in λ. To make further progress, we need the values of the elastic constants. We use K_c = 80 pNnm², K_e = 600 pN, L₁ = L₂ = L₃ = H₁ = H₂ = H₃ = 10 pN. In the supplement, we show that these values yield the correct twist, stretch, and twist–stretch coupling moduli for double-stranded B-DNA.²⁴ Solving for the eigenvalues, λ we get

$$\lambda =\pm \zeta \pm \mathrm{i}\omega ,\zeta =0.32{\text{nm}}^{-1}$$ (14)

and the solution for the strain parameters y₁ = r, y₂ = k₃, and y₃ = β is of the form

$$\begin{gathered} y_i(x)=A_1{\mathbf{V}}_1(i){\mathrm{e}}^{(-\zeta -\mathrm{i}\omega )x}+A_2{\mathbf{V}}_2(i){\mathrm{e}}^{(-\zeta +\mathrm{i}\omega )x} \\ +B_1{\mathbf{V}}_3(i){\mathrm{e}}^{(\zeta -\mathrm{i}\omega )x}+B_2{\mathbf{V}}_4(i){\mathrm{e}}^{(\zeta +\mathrm{i}\omega )x} \end{gathered}$$ (15)

where V_j(i) is the ith component of the eigenvector corresponding to the eigenvalue j in the exponent. Clearly, the decay length ζ is only a function of the elastic parameters of ds-DNA, in agreement with the conclusion of Kim et al.⁷ Note that the strain parameters are exponentially decaying while oscillating with the period ω of the double helix. We impose the boundary conditions on r and β, remembering that the displacements of the strands must be continuous. For a protein binding at x = p

$$\begin{gathered} \text{as}x\to \pm \infty ,r(x),\beta (x)\to 0 \\ \text{at}x=p,r(0)=r_0,\beta (0)={\beta }_0 \end{gathered}$$ (16)

We present the variation of r, k₃, and β for a protein binding at x = 0 for two different sets of boundary conditions in Figure 4. Notice the sinusoidal correlation between the local deformation of base pairs that is in agreement with earlier work that used Monte Carlo simulations.^22,23

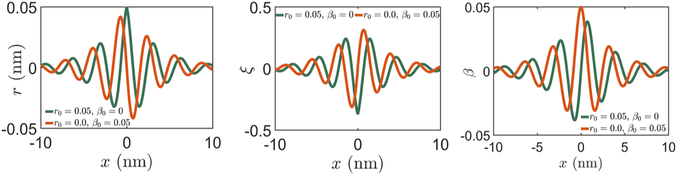
Figure 4.

Variation of r, k₃, ξ, and β⁺ = β⁻ = β for a single protein. The red curve corresponds to the boundary conditions β₀ = 0, r₀ = 0.05 nm, and the green curve to r₀ = 0, β₀ = 0.05. Even if r₀ = 0, i.e., the protein does not change the radius of the molecule at the binding site, a change in the phase angle β₀ ≠ 0 can cause the radius to change at locations away from the binding site. Similar coupling exists among other strain parameters. The magnitudes r₀ and β₀ chosen here ensure that the change in the groove width, a parameter whose magnitude is known,¹² is in the correct range (3 Å). The decay length is l_d = ζ⁻¹ ≈ 10 bp, which is close to the one documented in literature.^7,23

We show the deformed shapes of the helices in Figure 5 for three cases: first when one protein binds at x = 0, second when two proteins bind at x = ±1.5 nm, and third when two proteins bind at x = ±3.5 nm. The boundary condition for each protein is r₀ = 0.2 nm, β₀ = 0. We deliberately choose large values for r₀ and β₀ to distinguish the deformed shape from the reference shape. The large configuration changes near the site of protein binding (x = 0) decay exponentially with distance. Note, there is a strong overlap in the deformation fields when the distance between two proteins is 3 nm compared to 7 nm. This overlap results in an interaction energy between the two proteins, which we subsequently quantify using eq 18.

Figure 5.

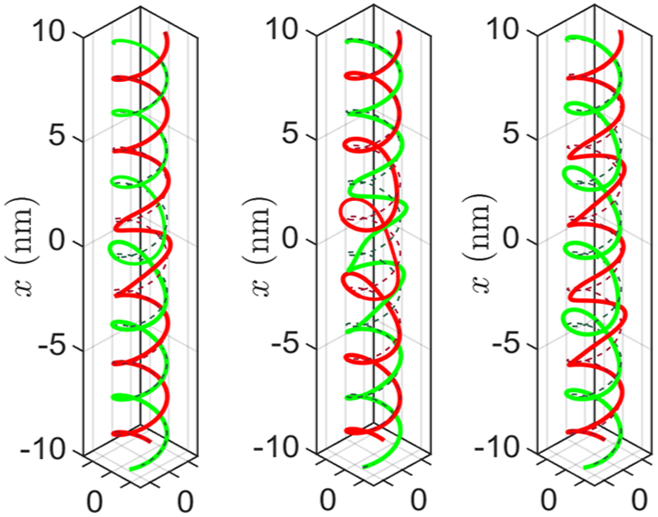
We show the deformed configuration of the double helix, with red and green colors corresponding to + and − strand, respectively. In the first figure, one protein binds at x = 0 with r₀ = 0.2 nm and β₀ = 0. The magnitudes are chosen to be artificially large to make the deformations discernible in the figure. In the second figure, two proteins bind at x = ±1.5 nm. In the third figure, two proteins bind at x = ±3.5 nm. Notice the overlap of deformations in the second figure, which is absent in the third one. We use eqs 19, 20, and 21 to demonstrate how this overlap leads to an interaction energy between the two proteins. The dotted lines denote the corresponding undeformed configuration.

We now compute the interaction energy ΔG for two proteins. The energy functional of the double-helical rod is

$$\begin{gathered} E[r,\beta ,k_3]=\frac{1}{2}EI({\kappa }^{+}{)}^2+\frac{1}{2}EI({\kappa }^{-}{)}^2+\sum _{i=1}^3\frac{1}{2}(L_i\Delta {\mathbf{w}}_i^2 \\ +H_i{\widehat{\eta }}_i^2)+K_{\mathrm{c}}{k}_3^2+K_{\mathrm{e}}{\xi }^2 \end{gathered}$$ (17)

where $\widehat{\eta }={\mathbf{Q}}^{\mathrm{T}}\eta$ and $\Delta \mathbf{w}={\mathbf{Q}}^{\mathrm{T}}\mathbf{w}-{\mathbf{Q}}_0^{\mathrm{T}}{\mathbf{w}}_0$. Consider two proteins, P₁ and P₂ binding at x = 0 and x = p. The interaction energy ΔG is defined as

$$\Delta G(p)=E_{12}^{\{0,p\}}-E_1^0-E_2^p$$ (18)

where $E_{12}^{\{0,p\}}=E\left[r_{12},{\beta }_{12},{(k_3)}_{12}\right]$ is the energy of two proteins binding onto DNA at x = 0 and x = p, whereas $E_1^0=E\left[r_1,{\beta }_1,{(k_3)}_1\right]$ and $E_2^p=E\left[r_2,{\beta }_2,{(k_3)}_2\right]$ are the energies of a single protein binding at x = 0 and x = p, respectively. We linearly superimpose the strain fields from each protein (r₁ and r₂, etc.) to get the resultant strain field (r₁₂, etc.) caused by two proteins simultaneously binding to DNA.

$$r_{12}(x)=r_1(x)+r_2(x-p)$$ (19)

We obtain β₁₂ and (k₃)₁₂ similarly. We compute the interaction energy ΔG(p) as a function of the distance between two proteins p and plot it in Figure 6 together with experimental data from Kim et al.⁷ In excellent agreement with experiment⁷ and numerical simulations,²² ΔG decays exponentially while oscillating with the period of the double helix (~10 bp).

Figure 6.

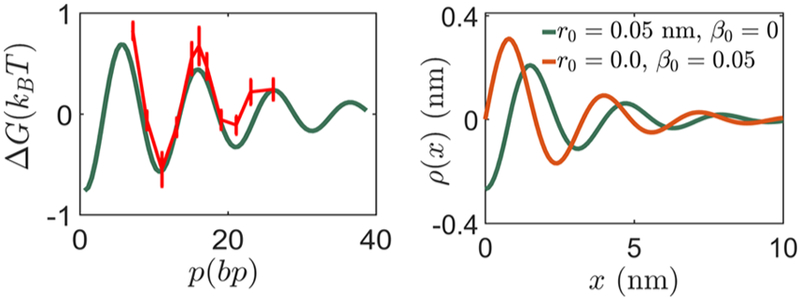
The first figure shows the variation of interaction energy ΔG with distance p between the two proteins P₁ and P₂. The boundary conditions r₁ = 0.001 nm, β₁ = 0.0045 for P₁ and r₂ = 0.001 nm, β₂ = −0.0045 for P₂ give the best fit to the experimental data for ΔG.⁷ In the second figure, we show the variation of change in groove width $\rho (x)=g(x)-\frac{p}{2}$ when a protein with boundary conditions r₀, β₀ binds at x = 0. The decaying sinusoidal character is documented in previous work.^7,22 The magnitude of the change in groove width (~3 A) is consistent with estimates in ref 12.

We justify this variation of interaction energy for a simple case as follows. Consider a strain parameter δ(x) and the associated quadratic energy potential $\epsilon [\delta (x)]={\int }_{-\infty }^{\infty }\frac{{\delta }^2(x)}{2}\mathrm{d}x$. Similar to our strain parameters in eq 15, let us assume δ(x) = A e^−bx cos(μx), then

$$\mathcal{E}[\delta (x)]={\int }_{-\infty }^{\infty }\frac{{\delta }^2(x)}{2}\mathrm{d}x=\frac{A^2(2b^2+{\mu }^2)}{4b(b^2+{\mu }^2)}$$ (20)

ℇ[δ(x – p)] = ℇ[δ(x)]. Now, the strain obtained by superposing two strain sources a distance p apart are δ₂(x) = δ(x) + δ(x – p). The energy functional corresponding to δ₂(x) is

$$\begin{gathered} \mathcal{E}[{\delta }_2(x)]=\frac{A^2(2b^2+{\mu }^2)}{2b(b^2+{\mu }^2)}+A^2{c}_1{\mathrm{e}}^{-bp}\sin (\mu p) \\ +A^2{c}_2{\mathrm{e}}^{-bp}\cos (\mu p) \\ =\mathcal{E}[\delta (x)]+\mathcal{E}[\delta (x-p)]+\Delta G \end{gathered}$$ (21)

where $c_1=\frac{b^3}{2b\mu (b^2+{\mu }^2)}$, and $c_2=\frac{\mu ({\mu }^2+2b^2+p{b}^3+pb{\mu }^2)}{2b\mu (b^2+{\mu }^2)}$. It is notable how the decaying sinusoidal behavior of the interaction energy ΔG follows naturally from the functional form of the strain parameters and their eventual superposition. A cartoon illustrating this key point is presented in Figure 7.

Figure 7.

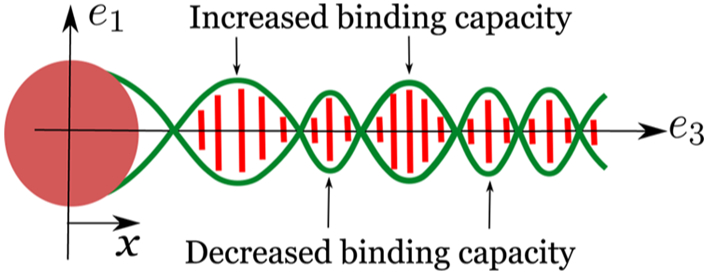
Equation 15 shows that the strain parameters r, β, and ξ decay exponentially while oscillating with the periodicity of the double helix. Let us assume that the protein binding at x = 0 increases the radius of the double helix from a to a + r₀. This change in radius at x = 0 decays exponentially while oscillating with the periodicity of the double helix, away from the binding site. Similar behavior is observed for other strain parameters, β and ξ. Due to this sinusoidal modulation of the geometry, the binding of the second protein is facilitated at some locations, while inhibited at others; this manifests as an exponentially decaying oscillatory behavior observed in the allosteric interaction energy (ΔG).

Next, we focus on the width of the groove because many proteins are known to change the width of the major/minor groove of DNA.^7,12,25 We define the width of the groove, g(x), as follows (we do not have a major/minor groove because α = π for simplicity):

$$g(x)={\mathbf{r}}^{-}.{\mathbf{e}}_3\left(x+\frac{\pi }{2\omega }\right)-{\mathbf{r}}^{+}.{\mathbf{e}}_3\left(x-\frac{\pi }{2\omega }\right)$$ (22)

Note that in the reference configuration, the groove width $g_0=\frac{\pi }{\omega }=\frac{p}{2}$. We consider a protein binding at x = 0 and compute the change in groove width ρ(x) = g(x) – g₀ for two sets of boundary conditions, r₀ = 0, β₀ = 0.02 and r₀ = 0.02 nm, β = 0 (see Figure 6). The groove width ρ decays exponentially with increasing distance from the binding site while oscillating with the periodicity of the double helix. This characteristic decaying sinusoidal oscillation is documented in refs 22, 23 and is also observed experimentally.⁷ It has been proposed that this change in groove width could explain the sinusoidally decaying interaction energy (notice the similarity of the two panels in Figure 6) between two proteins bound to DNA because the binding energy of a protein binding to DNA could potentially depend on the groove width.^22,23 However, we have arrived at the decaying sinusoidal variation of the interaction energy by computing the elastic energy stored in the birod without assuming any connection to the groove width. Thus, we argue that the characteristic variation in groove width and the characteristic variation of the interaction energy have the same underlying cause—the geometry and elasticity of helical DNA at the base-pair level.

To make the above point more concrete, we give another analytical argument. Consider two proteins P1 and P2 binding at x = 0 and x = p, respectively. Kim et al.⁷ argue that when a protein binds to DNA, it alters the groove width, which leads to $\Delta G\propto {\rho }_0^1{\rho }_0^2+{\rho }_p^1{\rho }_p^2$, where ${\rho }_p^1$ is the change in the groove width caused by protein P1 at x = p, and so on. On the other hand, we assume that the protein binds to DNA by fixing the radius r and phase angle β at the binding site. Let us examine whether ΔG ∝ α₁r₁₂(p) + α₂β₁₂(p), where $r_{12}(p)=r_0^1{\mathrm{r}}_0^2+r_p^1{r}_p^2$, ${\beta }_{12}(p)={\beta }_0^1{\beta }_0^2+{\beta }_p^1{\beta }_p^2$, for some constants α₁ and α₂. Here, $r_0^1$ is the change in radius caused by protein P1 at x = 0. Other quantities ($r_0^2$, $r_p^1$, $r_p^2$, ${\beta }_0^1$, ${\beta }_0^2$, ${\beta }_p^1$, ${\beta }_p^2$) are defined similarly. For simplicity, assume α₁ = α₂ and define q(p) = r₁₂(p) +β₁₂(p). We plot $\Delta G_n=\frac{\Delta G}{{\mid \Delta G\mid }_{\max }}$ and $q_n=\frac{q(p)}{{\mid q(p)\mid }_{\max }}$ versus the distance between the two proteins p in Figure 8a. We observe that while the location of peaks and valleys for ΔG_n and q(p)_n coincides, the magnitudes are not identical.

Figure 8.

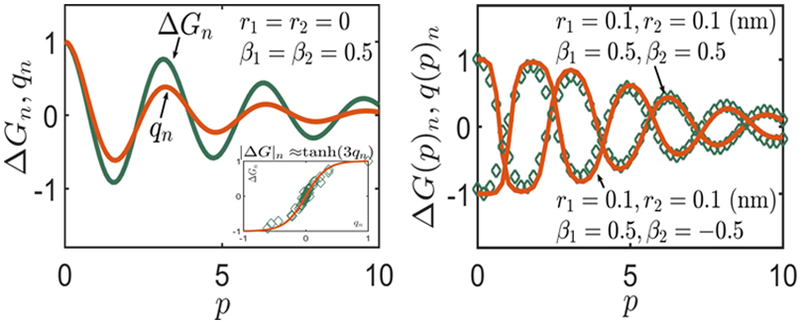
Consider two proteins P1 and P2 binding at x = 0 and x = p, respectively. The first figure shows the variation of normalized free energy $\Delta G{(p)}_n=\frac{\Delta G}{{\mid \Delta G\mid }_{\max }}$ and correlation function $q{(p)}_n=\frac{q(p)}{{\mid q\mid }_{\max }}$ with the distance between the two proteins p. The correlation function $q(p)=(r_0^1{r}_0^2+r_p^1{r}_p^2)+({\beta }_0^1{\beta }_0^2+{\beta }_p^1{\beta }_p^2)$ where $r_p^1$ is the change in radius caused by protein P1 at x = p. The boundary conditions for the two proteins are given in the figure. We find that the peaks and valleys of ΔG_n and q_n coincide; however, the magnitudes are not identical. We find that the magnitudes are related as ΔG_n ≈ tanh(3q_n), as shown in the inset. We test this empirical relation for two different sets of boundary conditions and find a remarkable match. The diamonds denote the free energies computed using eq 18 and the solid line denotes the free energy computed using the normalized correlation function q(p)_n. This exercise shows that the correlation functions can be used as a surrogate for free energies.

Our next step is to relate the magnitudes of two quantities ΔG_n and q_n. Assume an empirical relation ΔG_n = y(q_n). We plot ΔG_n versus q_n in Figure 8 and find that the resultant profile looks akin to y(x) = tanh(ax), a ≈ 3.0 gives the best fit. Thus, ΔG_n ≈ tanh(3q_n). Note that for large values of p (p > 10 nm), the correlation function q_n is small, thence tanh(3q_n) ≈ 3q_n, and we recover the form similar to that used in Kim et al.⁷ (but with different strain variables) ΔG_n ∝ q_n. Note that we used a particular set of boundary conditions to extract the relation ΔG_n ≈ tanh(3q_n). Now, we test this relation to compute interaction energies for other sets of proteins, which apply different boundary conditions in Figure 8b. We observe a remarkable agreement with the free energies computed using eq 18. Thus, we have shown that the correlation function q(p) can be used as a surrogate for the interaction energy as Kim et al.⁷ did. Evaluating the correlation function q(p) involves measuring displacement variables at two binding sites, which can in turn be related to the free energy using the above scheme.

To conclude, we have demonstrated that the theory of elastic birods can provide useful insights into the allosteric interactions between two proteins binding to a DNA molecule. Our analysis ties together the continuum theory,⁹ experiments,⁷ and numerical simulations.^6,22 Our computations indicate that the interaction energy (eq 18) for two proteins bound to DNA decays exponentially while oscillating with the period of the DNA double helix. The decay length depends only on the elastic characteristics of the web, whereas the oscillatory behavior is inherited from the underlying doublehelical geometry. We have shown that the strong correlation of interaction energy with the changes in groove widths caused by the proteins are rooted in elasticity and geometry of DNA. However, our model suffers from some shortcomings. Existing models^6,23 rely on numerical simulations, possibly accounting for the stacking energy in a more comprehensive way compared to our approach, which assumes it is quadratic in the twist and stretch of the centerline. Also, these models^6,23 can account for a wider variety of boundary conditions applied by a protein, owing to more variables describing the DNA structure. Besides, we made various simplifying assumptions such as assuming the outer strands to be inextensible and unshearable. These assumptions could break down close to the binding site where DNA structure might be drastically altered. Some studies¹² shed light on the kinematics of a protein binding to DNA, but an analysis of the deformations at the binding site is beyond the scope of our model. While the results from our model agree with the experimental observations, the outcomes from the existing models in literature such as^22,23 agree as well. The main strength of our model compared to the existing models is twofold: (i) we account for the mechanics of the outer strands and (ii) our model provides useful insights into the phenomenon at a modest computational cost. Our techniques based on a helical birod model could potentially be applied to other molecules, which have a double helical geometry such as dsRNA, and coiled-coil intermediate filaments.