Coherently broadened, high-repetition-rate laser for stimulated Raman scattering–spectroscopic optical coherence tomography

Abstract

We present a novel light source specifically tailored for stimulated Raman scattering–spectroscopic optical coherence tomography (SRS-SOCT), which is, to the best of our knowledge, a novel molecular imaging method that combines the molecular sensitivity of SRS with the spatial and spectral multiplexing capabilities of SOCT. The novel laser consists of an 8 W, 450 fs Yb:KGW oscillator, with a repetition rate of 40 MHz, which delivers the Stokes beam for SRS-SOCT and also pumps and amplifies an optical parametric oscillator (OPO). The output of the amplified OPO is then frequency doubled and coherently broadened using a custom-made tapered fiber that generates bandwidth pulses >40 nm, compressible to <50 fs, with the average power over 150 mW, near the shot-noise limit above 250 kHz. The broadened and compressed pulse simultaneously serves as the pump beam and SOCT light source for SRS-SOCT. This light source is assessed for SRS-SOCT, and its implications for other imaging methods are discussed.

Stimulated Raman scattering–spectroscopic optical coherence tomography (SRS-SOCT) is a recently developed molecular imaging technique that leverages the spatial and spectral multiplexing capabilities of SOCT with the molecular sensitivity and specificity of SRS for fast, tomographic, and label-free molecular imaging [1,2]. To date, SRS-SOCT, as well as other nonlinear, dispersion-based methods [1-4], have relied on a low repetition (rep.) rate, regeneratively amplified laser source to generate (1) a low-coherence, broadband pulse for low-coherence interferometric detection with (S)OCT and wide coverage of the Raman spectral regions of interest, and (2) a narrowband pulse to coherently drive the nonlinear vibrational interactions with a high spectral resolution. However, low-rep. rate, amplified lasers are not well suited for biological imaging as their high peak powers can easily cause sample damage [5], and the low rep. rate can limit imaging speed. To this end, we develop a high-rep. rate laser system that fulfills the unique requirements for SRS-SOCT, including a narrowband Stokes beam and a broadband pump, which also serves as the SOCT beam, both bandwidth limited and with sufficient intensities for nonlinear imaging.

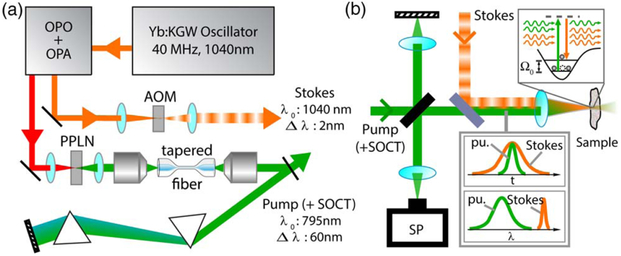
The system (Fig. 1) consists of a 40 MHz, 8 W, 450 fs, solid state Yb:KGW oscillator, fixed at 1040 nm (Stuttgart Instruments) [6]. The oscillator output is then used to pump a recently developed compact optical parametric oscillator (OPO), which exhibits a high parametric gain and is robust to intracavity losses [7,8]. Further, synchronization of the OPO cavity with the pump laser is not critical, and active stabilization of the cavity length is not required, thus providing high shot-to-shot and long-term stability [8,9]. The tunable OPO output seeds a single-stage, optical parametric amplifier that is also pumped by the Yb:KGW oscillator (Stuttgart Instruments). The amplified 1.4 to 2 μm tunable output of the OPO is then frequency doubled to 795 nm (tunable from 740 to 975 nm), using a periodically poled LiNbO₃ crystal exhibiting a fan-out poling structure. Here we generate pulses with >500 mW power, 0.3 ps duration, and 2.5 nm bandwidth at 795 nm. A fraction of the oscillator output (e.g., 200 mW) is also used directly as the Stokes beam for SRS-SOCT.

Fig. 1.

Schematic of the SRS-SOCT. (a) Light source that produces a narrowband Stokes beam and a broadband pump beam. (b) Michelson interferometer where the Stokes and pump beams are recombined at the sample arm. SP, spectrometer.

The frequency-doubled output is well suited for nonlinear microscopy (e.g., SRS when combined with the Stokes beam) [6,8], but its narrowband properties are not suitable for OCT, which relies on a broad spectrum for coherence gating to recover depth information. Further, the narrow bandwidth of the doubled, 795 nm pulse does not provide sufficient coverage of the spectral regions of interest, 2700 cm⁻¹–3200 cm⁻¹. With the Stokes beam set to 1040 nm, the SOCT beam (also the pump) must span from ~780 to 812 nm to cover this spectral region. Finally, SRS-SOCT relies on the nonlinear interaction between the Stokes and pump beams in the sample; thus, the pulses must be temporally short (ideally, bandwidth limited) and overlapped.

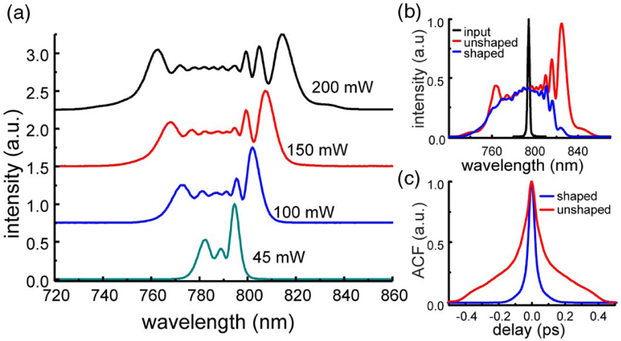
To achieve the aforementioned requirements for the SOCT beam (also the pump) in SRS-SOCT, we coherently broaden the 795 nm pulse using a SMF28 single-mode fiber tapered down to 4 μm, over a length of 9 cm, with a tapering angle of 0.8°. The fiber was tapered by heating and stretching, producing a thin thread of silica in air, which guides light at the outer boundary. The large refractive-index mismatch between silica and air allows light to concentrate into a small area, increasing its intensity and driving nonlinear effects. Dumais et al. [9] showed that the nonlinear interactions in tapered fibers are largely driven by self-phase modulation, along with soliton formation [10]. Because the broadening occurs in the short, tapered region, the total fiber length can be kept short (~20 cm), which minimized normal group-velocity dispersion (GVD). The short tapered area is mounted in a protective housing, and the rest of the SMF28 fiber is used to guide light into the tapered region, allowing easy handling and stable in-coupling compared to photonic crystal fibers (which give comparable spectral broadening) [11]. Figure 2(a) shows the broadened spectrum using different input powers. The specific diameter has been chosen to shift the zero-dispersion wavelength close to the required center wavelength, while still operating in the normal dispersion regime. Consequently, moderate but sufficient broadening is achieved [12].

Fig. 2.

Coherently broadened 795 nm pulse using a custom-made tapered fiber. The initial pulse is 0.25 ps with a 2.7 nm bandwidth. (a) shows broadening. (b) The spectrum at 795 nm center wavelengths is shaped to remove solitons. (c) Temporal profile of broadened and compressed pulse. ACF: Autocorrelation function.

Since broadening is primarily achieved through self-phase modulation, and GVD is minimized, pulses can be efficiently compressed using a conventional prism compressor. Figure 2(b) shows that pulses can be compressed to below 100 fs when the fiber output is ~250 mW. But the resulting spectra exhibit an asymmetry with relatively strong modulation on both spectral edges; these features can result from a temporal asymmetric pump pulse and/or soliton formation. Removing this portion of the beam at the distal end of the compressor using a knife edge enables further compression of the output [13], down to below 50 fs [Figs. 2(b) and 2(c); output power ~150 mW]. This also results in a smoother, less structured spectrum, which is also beneficial for SOCT. Broadband spectra with other center wavelengths can be achieved using different taper diameters, which could yield access to other spectral regions (including the fingerprint region).

Next, the broadened and compressed pump beam is sent to a Michelson interferometer, and the Stokes beam is recombined with the pump at the sample arm using a dichroic mirror [see Fig. 1(b)]. Light is focused onto the sample using a 35 mm lens, and light back-reflected from the sample and reference mirror is detected with a high-resolution spectrometer (resolution δλ = 074 nm; BaySpec). In the experiments presented below, the Stokes beam is amplitude modulated at f₀ = 20 kHz using an acousto-optic modulator, spectra are acquired at 50 kHz, and a total of 2048 spectra are acquired to generate an SRS-SOCT A-scan.

As an initial demonstration of the use of this, light source for SRS-SOCT, we use two synthetic samples consisting of poly-dimethylsiloxane (PDMS) and poly-methyl methacrylate (PMMA), which contain peaks in the high wavenumber region at 2900 cm⁻¹ and 2950 cm⁻¹, respectively. Initially, we use the reflection of the back surface of a slab (2 mm thick) of each material.

After the Stokes and pump beam interact with the sample, the back-reflected sample field can be described as

$$E_S(\omega )=r\cdot E_0(\omega )\times \exp [-i\cdot {\tilde{n}}_{\mathrm{NL}}(\omega )\cdot \omega z_0∕c],$$ (1)

where ${\tilde{n}}_{\mathrm{NL}}\propto {\chi }^{(3)}(\Omega )\cdot I_{\text{Stokes}}$ is the complex nonlinear refractive index, r is the reflectivity of the sample, z₀ is the region of interaction, I_Stokes is the Stokes intensity, and Ω = ω – ω_Stokes; is the wavenumber. The detected interferometric signal between the sample and reference arm, after removing the DC component (which can be achieved digitally) and assuming a single reflector, can be described as [1,2]

$$\tilde{I}(\omega )=r{I}_0(\omega )e^{-i\cdot \frac{\omega }{c}\cdot 2z}\times \exp \left[\frac{z_0{\beta }_0\omega }{2c}\cdot \mathrm{Im}\{{\chi }^{(3)}(\Omega )\}\cdot I_{\text{Stokes}}\right]\times \exp \left[-i{z}_0{\beta }_0\frac{\omega }{c}\cdot \mathrm{Re}\{{\chi }^{(3)}(\Omega )\}\cdot I_{\text{Stokes}}\right],$$ (2)

where I₀(ω) = ∣E₀(ω)∣² and ${\beta }_0=3∕(2n_0^{2}c{\epsilon }_0)$ is a real-valued constant. Equation (2) contains three components: the first term contains the slowly varying envelope, I₀(ω), as well as the carrier frequency that depends on the delay, z, between the sample and reference fields. The second and third terms describe the nonlinear amplitude changes (∣ΔI∣) and phase changes (∣Δ∠I∣) that occur when the Stokes beam is present.

$$\mid \Delta I\mid (\Omega )\propto r\times I_0\times I_{\text{Stokes}}\times \mathrm{Im}\{{\chi }^{(3)}(\Omega )\},$$ (3)

$$\mid \Delta \angle I\mid (\Omega )=\mid \Delta \varphi \mid (\Omega )\propto \omega \times I_{\text{Stokes}}\times \mathrm{Re}\{{\chi }^{(3)}(\Omega )\}.$$ (4)

Note that the amplitude change depends on the initial intensity of the pump, I₀, and the reflectivity, r, unlike the phase signal.

Nonlinear changes are obtained by filtering the complex OCT signal from a specific depth, using a Gaussian filter, and taking a Fourier transform (FT), which reveals the complex spectrum. This process is repeated for multiple acquisitions in the same location (2048 in this case), during which the Stokes beam is modulated at a frequency f₀ (20 kHz). Then, any changes in the amplitude and phase of the spectrum that occur at f₀, correspond to the nonlinear signal. Then the digital window is swept across depth similarly to a short-time FT.

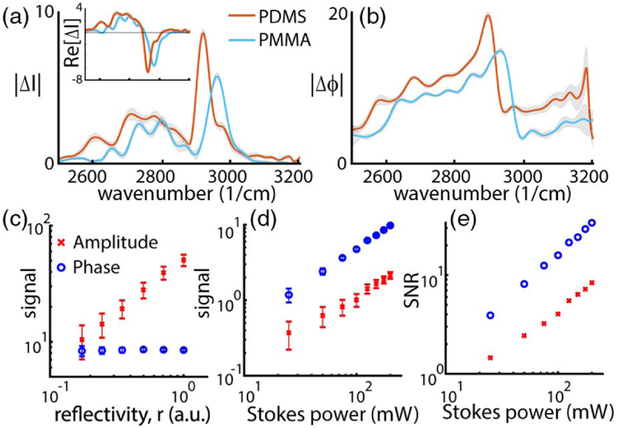
Figures 3(a) and 3(b) show representative amplitude and phase spectra from PDMS and PMMA. For the amplitude changes, PDMS and PMMA each show one strong peak, with centers around 2900 cm⁻¹ and 2950 cm⁻¹, respectively, while the changes in phase yield the characteristic dispersive “S-shape,” each shifted by approximately 50 cm⁻¹, as expected. This clearly indicated that the measured signal corresponds to the vibrational modes of the samples. The amplitude spectra also possess an unexpected background signal below the SRS peaks, which exhibit a broader spectral nonlinear response. Interestingly, this component is 180° out-of-phase with the sharp spectral SRS features, both relative to the Stokes modulation [inset of Fig. 3(a)]. Hence these nonrandom deviations may be estimated and potentially removed via phase-locked detection or by varying the pump-Stokes delay. (Future work could incorporate phase-lock-in-detection to account for these effects.) This interaction, with a broad spectral response, does not show an appreciable effect on the dispersive signal.

Fig. 3.

(a) Amplitude and (b) phase spectra from PDMS and PMMA. Amplitude spectra show the expected peaks at 2900 and 2950 cm⁻¹, respectively. Inset shows changes in-phase with the Stokes modulation. (b) Dispersive spectra show their characteristic shape with a 50 cm⁻¹ shift between PMMA and PDMS. Signal scaling with (c) reflectivity and (d) the Stokes power. (e) Signal-to-noise scaling with the Stokes power.

We also perform a power-scaling experiment to verify the expected response of the signals with power, as described in Eqs. (3) and (4). First, we attenuate the sample arm of the interferometer, while keeping a constant reference and Stokes beam power [see Fig. 3(c)], which we use here to simulate effective changes in the reflectivity, r [see (Eq. 1)]. As expected, the amplitude signals vary linearly with the reflectivity of the field, with a slope of the log–log plot of 0.92. On the other hand, the phase signal remains constant (slope of 0.01), as it does not depend on either the reflectivity or the initial intensity of the pump beam I₀.

Next, we vary the Stokes beam power [Fig. 3(d)]. Here we see that both signals scale linearly with I_Stokes, where the slope for the amplitude and phase signals in the log–log plot are 0.92 and 1.01, respectively. Figure 3(e) shows the signal-to-noise ratio (SNR) scaling with the Stokes beam, which also exhibits a linear dependence (slope of amplitude and phase are 0.91 and 1.02, respectively). Further, the phase shows a factor of 4 better SNR compared to the amplitude signal, which is consistent with previous findings where the phase yields a higher SNR due to its insensitivity to r · I₀ [2,3]. In these experiments, the signal and noise are given by the average absolute value and standard deviation, respectively, of 10 measurements. The sample arm (pump) power was 20 mW.

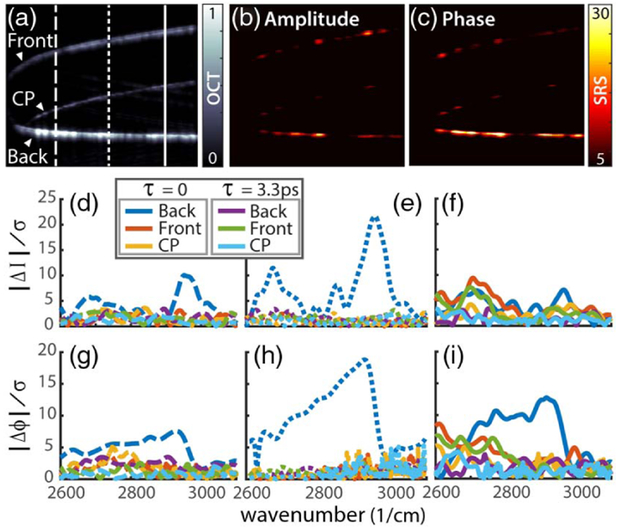
Figure 4(a) depicts an OCT image of a PMMA slab that has been cut with a milling machine to ca. 1 mm, where the rough edges produced by the cut are used to generate scattering (instead of using a strong reflection, as in the previous experiment). Both the front and back surfaces of the slab are clearly visible in the OCT image [Fig. 4(a)] along with their common path (CP) signal. Molecular images derived from the average SRS amplitude and phase signals (normalized by the noise) are displayed in Figs. 4(b) and 4(c), where we observe that most of the signal is detected from the back surface. This is primarily due to the Rayleigh range of the objective lens, which is ~300 μm, plus the focus was set on the back surface. Figures 4(d)-4(i) show the nonlinear amplitude and phase spectra extracted from the front surface, back surface, as well as the CP signal form three different regions as demarcated by the lines in Fig. 4(a).

Fig. 4.

(a) OCT image of a thin PMMA slab. 2 mm × 4 mm (z—x-plane). Nonlinear (b) amplitude and (c) phase changes. (d)–(f) Amplitude and (g)–(i) phase spectra from the front surface, back surface, and the common path signal from three different regions as demarcated by the lines in (a). Stokes-pump delay set to τ = 0 and 3.33 ps.

Again, the SRS spectral response is only observed from the back surface, and both the amplitude and phase spectra are in good agreement with the results presented in Fig. 3 (using a reflection). Further, these results again show that the phase signal provides a higher SNR compared to the nonlinear amplitude changes.

To confirm that the detected nonlinear signal is generated from an SRS interaction and not a thermal response, we change the delay of the Stokes beam by 1 mm (τ = 3.33 ps) such that it precedes the pump. In this scenario, the fields are no longer temporally overlapped, and thus an SRS signal cannot be generated; however, a thermal response—if present—would persist. Figures 4(d)-4(i) show that the spectra from all surfaces with a Stokes-pump delay of τ = 3.33 ps are in the noise floor, that is, no significant thermal signal is observed. This further confirms that the signal produced form the back surface with τ = 0 ps is from an SRS interaction.

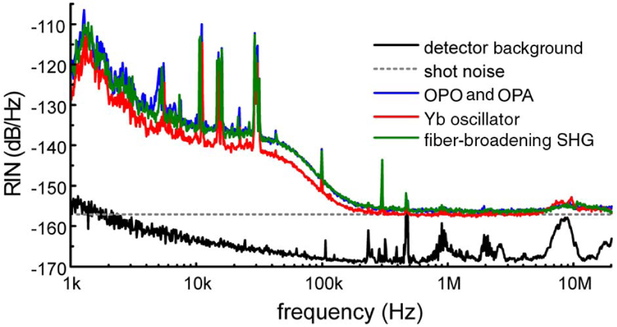
While this novel light source has been specifically tailored for SRS-SOCT, we find its noise properties to also be well suited for more traditional multiphoton microscopy, including SRS and coherent anti-Stokes Raman spectroscopy (CARS). Figure 5 depicts the relative intensity noise, for both the 1040 nm oscillator (Stokes beam) and the frequency doubled and broadened, 795 nm pump beam. Remarkably, all beams exhibit near-shot-noise limited characteristics above 250 kHz. Such characteristics can enable, for example, rapid spectral tuning, modulation multiplexing [14,15], spectral tailoring [16], or broadband SRS as well as CARS [17], without requiring balanced detection, even though fiber broadening has been implemented.

Fig. 5.

Relative intensity noise (RIN) of the different conversion stages measured at a photocurrent of 1.5 mA.

Stable fiber broadening has previously been demonstrated for high-resolution OCT using a long (80 cm) single-mode fiber [18]. In their work, Wang et al. reported on light broadened by self-phase modulation in a single-mode fiber, which resulted in no noise amplification, unlike that of a continuum light from a microstructure fiber (more on this below) [18]. However, no attempts were made to compress the output to obtain bandwidth-limited pulses, as this is not necessary for OCT. In the work presented here, the tapered fiber design also shows no noise amplification, and it allows for the total fiber length to be kept short (<20 cm), thus enabling compression with a SF11 glass prism pair with a small footprint (~50 cm separation between prisms). For longer fiber lengths or more complicated dispersion profiles, more sophisticated compression techniques are necessary [14-16].

Fiber broadening and supercontinuum generation for nonlinear microscopy have also been extensively explored [14,15]. However, for the most part, solid-state lasers are still preferred as supercontinuum light suffers from quantum noise that amplifies the amplitude and phase noise [16,17], and ultimately deteriorates image quality. Recently, a polarization-maintaining, all-normal dispersion photonic crystal fiber that produces predictable and stable pulses was demonstrated [19,20]. Combined with arbitrary pulse shaping and “local compression” techniques [21], Tu et al. achieved high-quality, multi-modality, multiphoton imaging using supercontinuum light [20]. For SRS-SOCT, however, supercontinuum generation is not desirable, as much of the light would not contribute to the SRS signal of interest (a 30 nm bandwidth from 780 to 810 nm is sufficient to cover the high-wavenumber region and achieve <10 μm axial sectioning with OCT). Further, with the tapered fiber, we obtain high-power spectral density: >150 mW over 40 nm bandwidth. Finally, a strong (>200 mW), narrowband (<3 nm) Stokes beam is needed to coherently drive the vibrational modes of the molecules with a high spectral resolution in SRS-SOCT—such strong power spectral density cannot be obtained from a supercontinuum but is available with the source presented here.

In summary, we have developed, to the best of our knowledge, a novel light source specifically tailored for SRS-SOCT. The light source consists of a high-rep. rate (40 MHz) Yb:KGW oscillator and an amplified OPO system that is frequency doubled, broadened with a tapered fiber, and compressed with a prism pair. The dual beam output provides a narrowband Stokes beam with high powers to drive the SRS interactions, and a broadband pump beam that is used for coherence gating with SOCT and that covers the high wavenumber Raman region. Basic experiments using synthetics samples were used to demonstrate the utility of the source for SRS-SOCT. Finally, we demonstrated that the light source has near-shot noise characteristics above 250 kHz. Reaching the shot-noise limit above 250 kHz may be possible with SRS-SOCT using faster line cameras or optical lock-in techniques [22], but they are not necessary given the robustness of the phase signal to laser noise. Nevertheless, such low-noise capabilities also make this source a viable candidate for multiphoton photon microscopy, including SRS and CARS. Future work will focus on biomedical applications of SRS-SOCT using this light source.