Blinded continuous monitoring in clinical trials with recurrent event endpoints

Abstract

In studies with recurrent event endpoints, misspecified assumptions of event rates or dispersion can lead to underpowered trials or overexposure of patients. Specification of overdispersion is often a particular problem as it is usually not reported in clinical trial publications. Changing event rates over the years have been described for some diseases, adding to the uncertainty in planning. To mitigate the risks of inadequate sample sizes, internal pilot study designs have been proposed with a preference for blinded sample size reestimation procedures, as they generally do not affect the type I error rate and maintain trial integrity. Blinded sample size reestimation procedures are available for trials with recurrent events as endpoints. However, the variance in the reestimated sample size can be considerable in particular with early sample size reviews. Motivated by a randomized controlled trial in paediatric multiple sclerosis, a rare neurological condition in children, we apply the concept of blinded continuous monitoring of information, which is known to reduce the variance in the resulting sample size. Assuming negative binomial distributions for the counts of recurrent relapses, we derive information criteria and propose blinded continuous monitoring procedures. The operating characteristics of these are assessed in Monte Carlo trial simulations demonstrating favourable properties with regard to type I error rate, power, and stopping time, ie, sample size.

1. INTRODUCTION

The determination of the number of patients to be recruited is a key step in the planning of any clinical trial. However, considerable uncertainty often exists with regard to nuisance parameters needed for sample size calculation. Recurrent event counts such as relapses in multiple sclerosis (MS) or exacerbations in chronic obstructive pulmonary disease (COPD) are commonly modelled by negative binomial distributions. With such endpoints, the nuisance parameters necessary for the sample size calculation are the event rate in the control group or overall and a parameter describing the overdispersion or extra‐Poisson dispersion, ie, the inflation of the variance above the mean. In these settings, specification of the overdispersion is often a particular problem as it is usually not reported in clinical trial publications.1, 2 Changing event rates over the years have been described for some diseases including relapsing MS3, 4 and COPD,5 adding to the uncertainty in the planning of such trials. To mitigate the risks of inadequate sample sizes, internal pilot study designs have been proposed.6 The preference is for blinded procedures, as they generally do not affect the type I error rate and maintain trial integrity, which is of particular importance in confirmatory trials.7, 8 For recurrent events methods for blinded sample size, reestimation/review are available.9, 10, 11, 12, 13, 14

In a design with a sample size review, the sample size is adapted based on accruing data. Hence, the sample size is not fixed but is a random variable. The larger the variance in the sample size is, the larger the uncertainty in the planning with regard to budget and drug supply, for instance. Therefore, there is a clear practical interest in minimizing the variation in the adapted sample size. For normally distributed endpoints, Friede and Miller15 demonstrated that the variance in the resulting sample size can greatly be reduced if not one but repeated sample size reviews are conducted. Taking it to the extreme by assessing the variance in the outcomes continuously based on blinded data, they introduced the concept of blinded continuous monitoring where recruitment is stopped once sufficient information has been gathered. The concept is not entirely new as event numbers are commonly monitored in event driven trials with time‐to‐event endpoint.16 In this article, we apply the concept of blinded continuous monitoring to trials with recurrent event endpoints, assuming negative binomial distributions.

Our investigations are motivated by a randomized controlled trial in paediatric MS, a rare neurological condition in children. There is a need for robust and efficient designs, in particular in small populations and rare diseases. In the following section, we provide some background on the paediatric MS trial, highlighting the ethical as well as the practical constraints of running a confirmatory clinical trial of considerable size in a rare disease.

The manuscript is organized as follows. We first provide a brief overview of randomized controlled clinical trials in paediatric MS and introduce the example study mentioned above. In Section 3 the statistical model considered is described, and Wald‐type tests for the hypotheses of interest are given. Furthermore, a sample size formula is derived. In Section 4 methods for blinded continuous monitoring are proposed. Their operating characteristics are explored by Monte Carlo simulations in Section 5. We close with a brief discussion.

2. A CLINICAL TRIAL IN PAEDIATRIC MULTIPLE SCLEROSIS

Multiple sclerosis is a chronic, immune‐mediated disorder of the central nervous system, characterized by inflammation, demyelination, and irreversible axonal/neuronal loss, which ultimately leads to cognitive decline and severe disability. MS currently affects approximately 2.3 million people worldwide.17 Although MS is not a rare disease, the paediatric onset of MS is. It is estimated that approximately 5% (different estimates range from 0.4% to 10.5%) of all MS patients manifest the disease already in childhood or adolescence and that less than 2% do so before the age of 10 years.18, 19, 20 In children with MS, at least 98% present relapsing‐remitting MS (RRMS) at the onset of the disease,21 which is characterized by acute, recurrent episodes of neurological abnormalities called relapses.

At the time of writing, no double‐blind randomized controlled clinical trial (RCT) had been reported in children with MS,22 but a number of RCTs were ongoing.23 Recruitment to RCTs in children is generally challenging. This is mainly due to the burden placed onto the children and their carers by study procedures and also due to ethical concerns. Also, RCTs are still relatively rare in paediatric settings, and therefore clinical investigators sometimes lack necessary experience with this type of design. In paediatric MS, the situation is further complicated by the fact that a number of trials are initiated simultaneously, competing for the same type of patients.

Study FTY720D2311 (in the following referred to as the paediatric fingolimod trial) was planned as a 2‐year, double‐blind, double‐dummy study evaluating the efficacy and safety of fingolimod (oral) versus IFN beta‐1a (injection) in paediatric MS patients aged 10 to less than 18 years. The study is registered in clinicaltrials.gov under NCT01892722. The primary endpoint is the annual relapse rate (ARR), which is the most commonly used primary clinical outcome for studies in RRMS. Standard analyses of this endpoint include negative binomial regressions and Poisson regression with appropriate adjustment for potential overdispersion. In the case of the paediatric fingolimod trial, the primary analysis model assumes a negative binomial distribution of relapses.

At the time of planning the paediatric fingolimod trial, no controlled paediatric MS trial had been completed. Hence assumptions for sample size calculations for the primary endpoint (ARR) were made based on adult data from the fingolimod Phase 3 programme, and specifically the TRANSFORMS study which compared fingolimod with interferon beta‐1a in adult patients.24 The uncertainty about the relapse rates in children and the appropriate dispersion was high. Children with MS may relapse more frequently compared with adults.25 Blinded sample size recalculation9, 10, 11, 12, 13, 14 could mitigate the risks associated with misspecified assumptions, making the trial more robust.

Although the standard designs in RRMS are RCTs with fixed follow‐up,26 trials in MS could be conducted more efficiently if patients, once recruited, were observed until sufficient statistical information has accumulated in all patients to provide the desired statistical power. To limit the burden to individual patients and to gather sufficient safety information (eg, International Conference on Harmonisation27), minimum and maximum follow‐up times might be imposed, but otherwise the follow‐up time could be flexible to optimize the efficiency of the trial.

Informed by adult data, the original plan was to follow‐up a total of 190 patients (95 per group) for 2 years. To make the trial more robust to misspecifications of nuisance parameters and to gain efficiency in this vulnerable population, a design was adopted that includes blinded monitoring of the information and flexible follow‐up. The statistical aspects of this approach will be described below.

3. STATISTICAL MODEL, HYPOTHESIS TESTING, AND SAMPLE SIZE CALCULATION FOR RECURRENT EVENT ENDPOINTS

We consider a clinical trial where patients are randomized to a test or control treatment and where the primary endpoint is a recurrent event, for example relapses in MS. We assume that the number of events follows a negative binomial distribution, which is a common assumption in MS trials. More specifically, the available data for patient i in treatment arm j are the number of events Y _ij in follow‐up time T _ij, for i = 1, …, n _j and j = 1,2 (1 = test, 2 = control). The negative binomial model is written as Y _ij~NegBin(λ _j T _ij,κ), with event rate λ _j (>0) and overdispersion parameter κ (>0). With this parametrization, E(Y _ij) = μ _ij and Var(Y _ij) = μ _ij(1 + κμ _ij), where μ _ij = λ _j T _ij. For very small values of κ, expectation and variance are almost identical, and the negative binomial distribution is close to a Poisson distribution. The treatment effect of interest is the event rate ratio θ = λ ₁/λ ₂, and we consider two estimators for θ based on method of moments (MM) and maximum likelihood (ML).

The MM estimator of the event rate λ _j is given by $\widehat{\lambda }$ _j = Y _j/T _j, where Y _j = Σ_i Y _ij and T _j = Σ_i T _ij, ie, the estimate is the total number of relapses divided by the total follow‐up time. Using the delta method,28 a normal approximation for the MM estimator of the logarithm of the event rate ratio is

$$\mathsf{log}\left({\widehat{\theta }}_{\mathsf{MM}}\right)~\mathsf{N}\left(\mathsf{log}\left({\mathsf{\lambda }}_{\mathsf{1}}/{\mathsf{\lambda }}_{\mathsf{2}}\right),\mathsf{1}/\left({\mathsf{\lambda }}_{\mathsf{1}}{\mathsf{T}}_{\mathsf{1}}\right)+\mathsf{1}/\left({\mathsf{\lambda }}_{\mathsf{2}}{\mathsf{T}}_{\mathsf{2}}\right)+\mathsf{\kappa }\left\{{\mathsf{\Sigma }}_{\mathsf{i}}{{\mathsf{T}}_{\mathsf{i}\mathsf{1}}}^{\mathsf{2}}/{{\mathsf{T}}_{\mathsf{1}}}^{\mathsf{2}}+{\mathsf{\Sigma }}_{\mathsf{i}}{{\mathsf{T}}_{\mathsf{i}\mathsf{2}}}^{\mathsf{2}}/{{\mathsf{T}}_{\mathsf{2}}}^{\mathsf{2}}\right\}\right).$$ (1)

In the following, we will use the information of the MM estimator, ie, the reciprocal of its variance

$${\mathsf{I}}_{\mathsf{MM}}={\left[\mathsf{1}/\left({\mathsf{\lambda }}_{\mathsf{1}}{\mathsf{T}}_{\mathsf{1}}\right)+\mathsf{1}/\left({\mathsf{\lambda }}_{\mathsf{2}}{\mathsf{T}}_{\mathsf{2}}\right)+\mathsf{\kappa }\left\{{\mathsf{\Sigma }}_{\mathsf{i}}{{\mathsf{T}}_{\mathsf{\text{i1}}}}^{\mathsf{2}}/{{\mathsf{T}}_{\mathsf{1}}}^{\mathsf{2}}+{\mathsf{\Sigma }}_{\mathsf{i}}{{\mathsf{T}}_{\mathsf{i}\mathsf{2}}}^{\mathsf{2}}/{{\mathsf{T}}_{\mathsf{2}}}^{\mathsf{2}}\right\}\right]}^{-\mathsf{1}}.$$ (2)

For cases of equal follow‐up times (T _ij = T) and equal patient numbers in both groups (n _j = n), the information is

$$\mathsf{I}=\mathsf{n}/\left\{\mathsf{1}/\left({\mathsf{\lambda }}_{\mathsf{1}}\mathsf{T}\right)+\mathsf{1}/\left({\mathsf{\lambda }}_{\mathsf{2}}\mathsf{T}\right)+\mathsf{2}\mathsf{\kappa }\right\}.$$ (3)

The ML estimates are obtained by an iterative procedure as implemented in commonly available software (eg, procedure GENMOD in SAS; or the function glm.nb in the R package MASS29). A normal approximation for the ML estimator of the logarithm of the relapse rate ratio is given by

$$\mathsf{log}\left({\widehat{\theta }}_{\mathsf{ML}}\right)~\mathsf{N}\left(\mathsf{log}\left({\mathsf{\lambda }}_{\mathsf{1}}/{\mathsf{\lambda }}_{\mathsf{2}}\right),\mathsf{1}/{\mathsf{I}}_{\mathsf{1}}+\mathsf{1}/{\mathsf{I}}_{\mathsf{2}}\right),$$ (4)

where I ₁ and I ₂ is the expected Fisher information for test and control, respectively. As described in Lawless,30 the information of the ML estimator is

$${\mathsf{I}}_{\mathsf{ML}}=\mathsf{1}/\left\{\mathsf{1}/{\mathsf{I}}_{\mathsf{1}}+\mathsf{1}/{\mathsf{I}}_{\mathsf{2}}\right\},$$ (5)

with I ₁ = Σ_iT_i1 λ ₁/(1 + κT _i1 λ ₁) and I ₂ = Σ_i T _i2 λ ₂/(1 + κT _i2 λ ₂). For the case of equal follow‐up times and equal patient numbers in both groups, Equation 5 is identical to Equation 2 and given by Equation 3. If the follow‐up times are unequal, the information in Equation 5 is typically larger than in Equation 2, as the ML estimator is more efficient than the MM estimator.

The Wald test can be used to test the null hypothesis H₀: θ ≥ 1 against the alternative H₁: θ < 1 at one‐sided significance level α. The null hypothesis is rejected if the one‐sided upper confidence limit for log(θ) is less than 0, ie, if log( $\widehat{\theta }$) + z _1‐α/ $\surd \widehat{I}$ < 0, where z _1‐α is the corresponding standard normal quantile and $\widehat{I}$ is an estimate of the information, typically obtained by replacing the unknown parameters in Equation 2 or Equation 5 by point estimates.

For a fixed design, the sample size of the clinical trial is decided at the planning stage. To attain power 1‐β at the alternative event rate ratio of θ* for the Wald test with one‐sided significance level α, the information must be

$${\mathsf{I}}^{*}={\left({\mathsf{z}}_{\mathsf{1}-\alpha }+{\mathsf{z}}_{\mathsf{1}-\beta }\right)}^{\mathsf{2}}/\mathsf{log}{\left({\mathsf{\theta }}^{*}\right)}^{\mathsf{2}};$$ (6)

see, for example, Jennison and Turnbull.31 To translate this requirement for the information to a sample size, additional assumptions are needed on the nuisance parameters (control event rate λ ₂ and overdispersion parameter κ) as well as on the follow‐up times T _ij as the information in Equations 2 and 5 depends on these. Trial and error may be used to calculate the required sample size. For a design with equal follow‐up time for each patient (T _ij = T) and equal randomization to both groups, the information in Equation 3 is proportional to the sample size, so that an analytical expression is obtained; see also Friede and Schmidli10 and Keene et al.32 By setting Equation 6 equal to Equation 3, the required sample size per group is the smallest integer n such that

$$\mathsf{n}\ge \left\{\mathsf{1}/\left({\mathsf{\theta }}^{*}{\mathsf{\lambda }}_{\mathsf{2}}\mathsf{T}\right)+\mathsf{1}/\left({\mathsf{\lambda }}_{\mathsf{2}}\mathsf{T}\right)+\mathsf{2}\mathsf{\kappa }\right\}{\left({\mathsf{z}}_{\mathsf{1}-\alpha }+{\mathsf{z}}_{\mathsf{1}-\beta }\right)}^{\mathsf{2}}/\mathsf{log}{\left({\mathsf{\theta }}^{*}\right)}^{\mathsf{2}}.$$ (7)

3.1. Application to paediatric fingolimod trial

The paediatric fingolimod trial introduced above was originally planned with fixed follow‐up time of 2 years (T = 2). Initial protocol assumptions for the nuisance parameters were that the ARR for interferon β‐1a is λ ₂ = 0.36 and that the overdispersion parameter is κ = 0.82 based on data in adults (Cohen et al24). The assumed treatment effect was θ* = 0.5, again based on adult clinical trials. Using Equation 7, a sample size of n = 95 patients per treatment group is required to attain at least 80% power (β = 0.2) with the Wald test at one‐sided significance level α = 0.025.

Applying Equation 6, one finds that the required information for the detection of 50% treatment effect is I* = 16.34. Applying Equation 3, one can verify that the paediatric fingolimod trial with the nuisance parameters as specified in the sample size calculation and with a sample size of n = 95 produces the required information I ⁰ = 16.36. The small numerical difference between I* and I ⁰ is explained by the rounding of n to integers before calculating the information in Equation 3.

Figure 1 illustrates the relationship between sample size and follow‐up times under various assumptions of the relapse rate and dispersion parameter. The initial design of the paediatric fingolimod trial assumed a fixed follow‐up of 2 years in 190 patients, which would provide information I ⁰ = 16.36. The same information (and hence the same power of 80%) could be attained with less patients if the follow‐up time T would be increased. Also, if the control ARR would be higher than assumed or the over‐dispersion κ lower than assumed, the follow‐up time could be shortened without negative impact on the power. Alternatively, the sample size could be reduced in these cases. If one could monitor the information in the blinded data of the ongoing trial, the follow‐up time or the sample size (or both) could be adjusted to provide just the right amount of data for the required power of the statistical test. A blinded monitoring of information would allow to protect patients from overexposure to experimental treatment, and it would ensure adequate power for the detection of the prespecified treatment effect at the end of the study.

Figure 1.

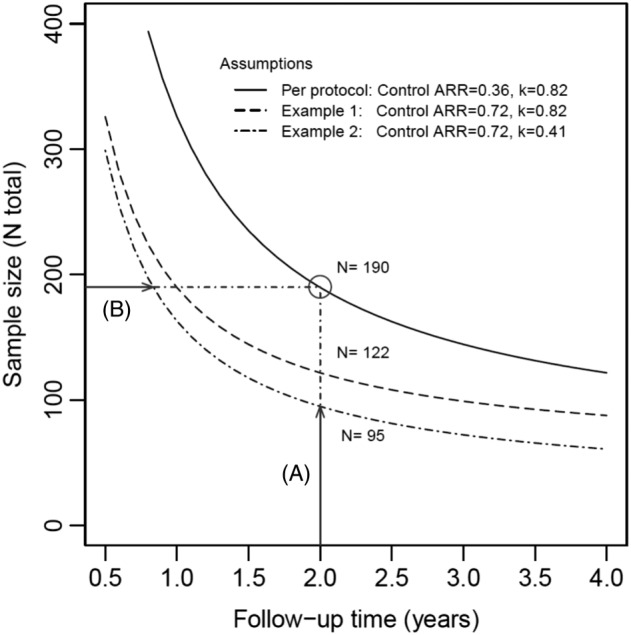
Total sample size required to attain 80% power at a one‐sided test of 2.5% for an assumed treatment effect of 50% (rate ratio 0.5), as a function of the follow‐up time. The solid line corresponds to protocol assumptions for the two nuisance parameter (control ARR, dispersion κ). For a two‐year study with fixed follow‐up, a sample size of 190 patients is required. Examples 1 and 2 show the impact of deviations from the initial assumptions on the nuisance parameters. If the ARR in the control group is higher or the overdispersion lower than initially anticipated, the same power can be achieved with A, a smaller sample size or B, a shorter follow‐up time

4. BLINDED CONTINUOUS MONITORING

In this section we propose methods for the blinded evaluation of the information. The information may be assessed once or continuously in clinical trials as proposed by Friede and Miller15 in the setting of continuous endpoints and as commonly applied in the setting of time‐to‐event outcomes when the total number of events is monitored. Since the trial is stopped once sufficient information is gathered, the application of such blinded continuous monitoring procedures will lead to varying follow‐up times across the study population. In this design the follow‐up times and with it summary statistics such as the total follow‐up time become random variables. If the monitoring starts before the preplanned number of patients is recruited into the study, also the sample size is a random variable.

To evaluate the information, estimates of the model parameters λ ₁, λ ₂, and κ are needed. Under an assumed treatment effect θ^*, the event rates λ ₁ and λ ₂ and the dispersion parameter κ can be estimated from blinded data. These estimates can then be used to evaluate the information. In the following we describe alternative blinded estimators of the model parameters before describing the evaluation of the information.

4.1. Blinded estimation of the parameters

The following approaches to estimating the nuisance parameters may be considered:

1. Lumping approach. As in a blinded sample size review,10 a negative binomial model could be fitted to the lumped data, ie, the pooled data of both treatment groups. This provides estimates $\widehat{\lambda }$ and $\widehat{\kappa }$ of the overall annual relapse rate λ and of the dispersion κ. For an assumed rate ratio θ^*, estimates of the annual relapse rates in the two groups are obtained through ${\widehat{\lambda }}_1^{\left(b\right)}=2\widehat{\lambda }{\theta }^{*}/\left(1+{\theta }^{*}\right)$ and ${\widehat{\lambda }}_2^{\left(b\right)}=2\widehat{\lambda }/\left(1+{\theta }^{*}\right)$. Estimators of the overall event rate λ and the dispersion κ can be obtained by MM or by ML. In Section 3, the MM estimator of the event rates λ _j was described. The MM estimator of the overall event rate is computed analogously on the lumped data. The MM estimator of the dispersion κ is obtained by solving numerically equation 2.10 in the article by Lawless.30 If the equation has no solution, the dispersion is set to 0 (Poisson case). No closed form exists for the ML estimators, which are obtained by numerical optimization.

2. Mixture model approach: The lumped data is a mixture of two negative binomial distributions with mixture weights of 0.5 in a balanced design (with 1:1 allocation ratio). For an assumed rate ratio of θ^*, estimates of the overall event rate λ and of the common dispersion κ can be obtained by maximizing the mixture likelihood.14, 33 This approach is different from the expectation‐maximization (EM) algorithm–based procedures, which would also estimate the treatment effect.11, 34 The properties of such EM algorithm–based procedures have been subject to some debate.12, 35, 36

4.2. Blinded estimation of the information

In the following we consider estimation of the information from the blinded data. First we consider assessments of the information based on the MM estimates before describing the corresponding assessment based on ML estimates.

In randomized controlled trials, it is reasonable to assume that the follow‐up times in the two groups are (at least approximately) the same, ie, that T ₁ = T ₂ = T _total/2, where T _total is the total of the follow‐up times at the review time. We further assume that the sum of the squared follow‐up times is the same in both groups, ie, that Σ_iT_i1 ² = Σ_iT_i2 ² = Σ_jΣ_i T _ij ²/2. Hence, the evaluation of the information in Equation 1 for the MM estimator based on blinded information is

$$\mathsf{I}={\left[\mathsf{2}/\left({\mathsf{\lambda }}_{\mathsf{1}}{\mathsf{T}}_{\mathsf{\text{total}}}\right)+\mathsf{2}/\left({\mathsf{\lambda }}_{\mathsf{2}}{\mathsf{T}}_{\mathsf{\text{total}}}\right)+\mathsf{\text{4κ}}\left({\mathsf{\Sigma }}_{\mathsf{j}}{\mathsf{\Sigma }}_{\mathsf{i}}{{\mathsf{T}}_{\mathsf{ij}}}^{\mathsf{2}}\right)/{{\mathsf{T}}_{\mathsf{\text{total}}}}^{\mathsf{2}}\right]}^{-\mathsf{1}},$$ (8)

where the reestimated values are plugged in for λ ₁, λ ₂, and κ at the blinded review. Note that if T _ij = T, n _j = n, then T _total = 2nT, and Σ_jΣ_i T _ij ² = 2nT ², and one obtains again Equation 2. If ML estimators are used instead of the MM estimators, the blinded estimates for I ₁ and I ₂ are

$$\mathsf{0}.\mathsf{\text{5}}{\Sigma }_m{T}_m{\mathrm{\lambda }}_{\mathsf{1}}/\left(\mathsf{1}+\mathrm{\kappa }{T}_m{\mathrm{\lambda }}_{\mathsf{1}}\right)\mathsf{\text{and}}\mathsf{0}.\mathsf{\text{5}}{\Sigma }_m{T}_m{\mathrm{\lambda }}_2/\left(\mathsf{1}+\mathrm{\text{κ}}{T}_m{\mathrm{\lambda }}_2\right),$$ (9)

respectively, assuming that the distribution of the follow‐up times is the same in both groups. Here the index m is for all observations from both treatment arms. Based on either Equation 8 or 9, using either the lumping approach or the mixture model approach, one can monitor the accumulation of information in the blinded data.

5. SIMULATION STUDY MOTIVATED BY THE PAEDIATRIC FINGOLIMOD TRIAL

The operating characteristics of the proposed blinded continuous monitoring design were assessed in a simulation study motivated by the paediatric fingolimod trial described in Section 2. In the planning of the study, annual relapse rates of λ ₁ = 0.18 and λ ₂ = 0.36 were assumed for fingolimod and interferon β‐1a, respectively, with a rate ratio of 0.5 (see Section 3.1). These assumptions were somewhat conservative, since they were informed by adult data while relapses occur more frequently in children and adolescents than in adults. Therefore, we also included in our simulation study scenarios with higher ARR: in one scenario we kept the rate ratio at 0.5 (λ ₁ = 0.36 and λ ₂ = 0.72), and in another one, the effect was set to be slightly larger with a rate ratio of 0.375 (λ ₁ = 0.27 and λ ₂ = 0.72). To assess the type I error rate, three scenarios were considered with λ ₁ = λ ₂ = 0.36, 0.54, and 0.72. The relapse counts were drawn from negative binomial distributions with dispersion parameter κ = 0.82 constant across the treatment groups, as this was the original planning assumption in the paediatric fingolimod trial.

For the purpose of the simulations, we assumed that 95 patients per group (190 in total) are recruited linearly over a period of 24 months, with three patients being recruited into each arm in the first month; this amounts to a monthly rate of four patients per group from month 2 to month 24. The blinded information monitoring starts in month 25 after completion of recruitment and consists of monthly blinded looks. Additionally, the design with blinded monitoring starting in month 13 was considered. The overall relapse rate and the dispersion are estimated from the blinded data using ML estimators and the lumping approach (see Section 4); the group specific rates are derived by assuming a rate ratio of 0.5 as in the original sample size calculation. The study is stopped once the information is estimated to be at least I ⁰ = 16.36, the information that would be obtained at the end of the trial based on protocol assumptions and fixed follow‐up of 2 years per patient (see Section 3), or the maximum length of the entire study of 48 months is reached, whatever comes first. For ethical reasons the double‐blind treatment period for a child or adolescent is typically limited. Therefore the maximum treatment and follow‐up period for each patient is restricted to 24 months in this simulation study. For each scenario 2000 trials were simulated so that the Monte Carlo standard error is about 0.009 for the power and 0.003 for the type I error rate.

First we consider the results for the design with the blinded information monitoring starting in month 25, ie, after completion of recruitment. Under the planning scenario (λ ₁ = 0.18 and λ ₂ = 0.36), the design with blinded continuous monitoring achieves a power of 0.785, close to the target and power in the fixed follow‐up design of 0.8. The stopping times are given in Figure 2. In only about 60% the trial runs to full completion, resulting in an average stop time of 44.3 months. This means there is a saving of about 4 months on the total duration of the trial compared with the fixed follow‐up design, which would take 48 months (24 months recruitment plus 24 months follow‐up time). In the scenario with higher rates but same rate ratio of 0.5 (λ ₁ = 0.36 and λ ₂ = 0.72), the trials are considerably shorter (see Figure 2) and stop on average at month 28.3, while the power is with 0.853, above the target of 0.8. In the scenario with the more pronounced treatment effect (λ ₁ = 0.27 and λ ₂ = 0.72), the power was simulated as 0.987. The trials stop on average in month 31.3; the distribution of the stop times is given in Figure 2.

Figure 2.

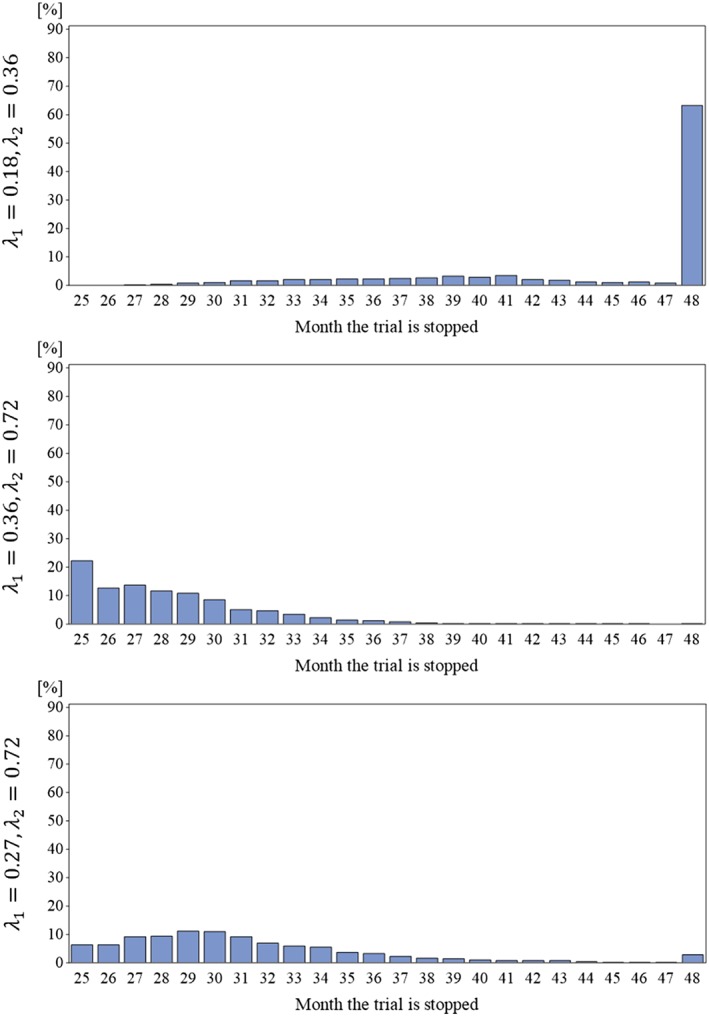
Distribution of the stop times of the trials with blinded continuous monitoring for the three scenarios under the alternative

Under the null hypotheses, the type I error rates of the one‐sided Wald‐type test of 0.0245, 0.0225, and 0.0250 were observed for the three scenarios with λ ₁ = λ ₂ = 0.36, 0.54, and 0.72, respectively, close to the nominal level of 0.025. The observed distributions of the stop times are depicted in Figure 3. As can be seen by comparing the panels of the figure, the trials tend to stop earlier with higher relapse rates. The average trial durations were 33.8, 27.1, and 25.4 for λ ₁ = λ ₂ = 0.36, 0.54, and 0.72, respectively, constituting substantial time savings compared with the fixed‐follow up design with 48 months.

Figure 3.

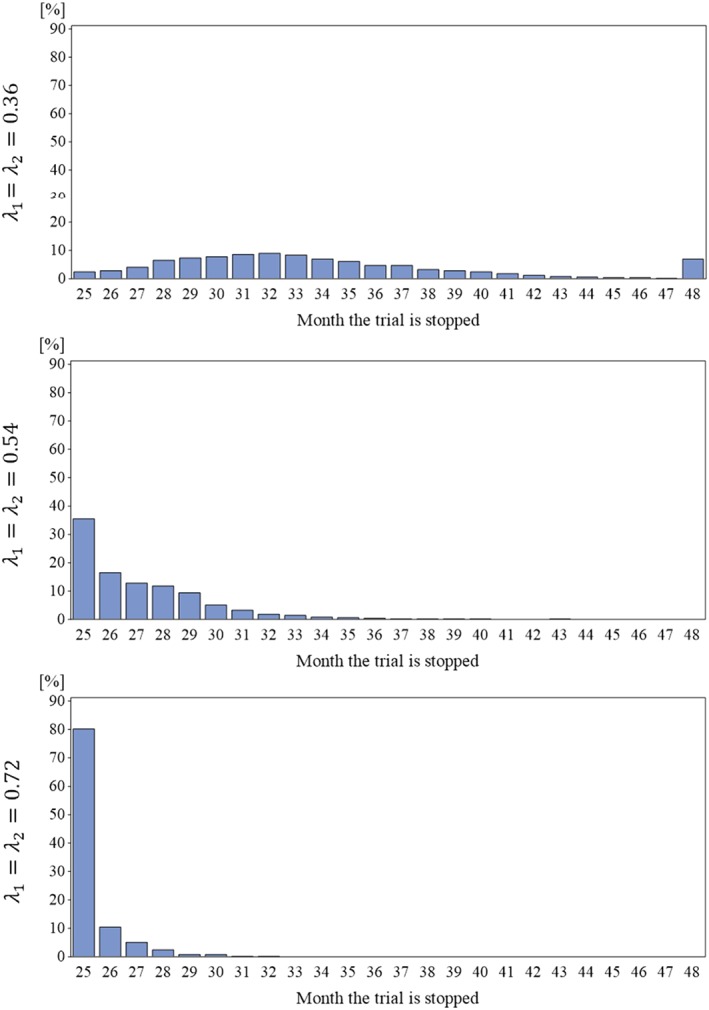
Distribution of the stop times of the trials with blinded continuous monitoring for the three scenarios under the null hypothesis

Now we turn to the design with blinded monitoring starting in month 13. Whereas in the design considered above always a total of 190 patients were recruited, the sample size is variable in this design and was limited to a maximum of 190 patients recruited over 25 months. Under the planning scenario (λ ₁ = 0.18 and λ ₂ = 0.36), 190 patients were recruited into the trial in all simulation runs, yielding a power of 0.805, close to the target of 0.8. The average duration was 44.2 months. These operating characteristics are similar to the design with later start of the monitoring. In the scenario with higher rates but same rate ratio of 0.5 (λ ₁ = 0.36 and λ ₂ = 0.72), the trials are considerably shorter and slightly smaller, stopping on average at month 28.1 with an average sample size of 188.3 while the power is with 0.843, above the target of 0.8. In the scenario with the more pronounced treatment effect (λ ₁ = 0.27 and λ ₂ = 0.72), a simulated power of 0.985 was observed. The trials stop on average in month 31.3 with mean sample size of 189.5.

Under the null hypotheses, one‐sided type I error rates of 0.0245, 0.0250, and 0.0255 were observed for the three scenarios with λ ₁ = λ ₂ = 0.36, 0.54, and 0.72, respectively. As with the design starting monitoring at month 25, the observed levels are close to the nominal level of 0.025. The average trial durations were 33.8, 26.6, and 23.7 for λ ₁ = λ ₂ = 0.36, 0.54, and 0.72, respectively. As for the design with monitoring from month 25, these are substantial savings compared with the fixed‐follow up design with 48 months: the larger the relapse rates, the larger the savings. In comparison with the design with the later start of the monitoring, the earlier start yields shorter trial durations, in particular with higher rates. The average total sample sizes were 189.9, 186.4, and 176.2 for λ ₁ = λ ₂ = 0.36, 0.54, and 0.72, respectively, which are modest savings in comparison with the 190 patients in the design with the later start of the monitoring, but they are an additional benefit given the shorter trial durations.

6. CONCLUSIONS AND DISCUSSION

In this article we proposed blinded continuous monitoring for clinical trials with recurrent outcomes. The concept of blinded continuous monitoring of the information is not entirely new. Continuous monitoring of blinded information has previously been suggested by Friede and Miller15 for continuous outcomes with a blinded estimator of the variance and is well established in time‐to‐event trials where the total number of events are monitored. Here we described alternative methods to estimate the relevant nuisance parameters in a blinded fashion assuming negative binomial distributions for the recurrent events. In a simulation study, we demonstrated that type I error rates in designs with blinded continuous monitoring are similar to those in fixed designs. This is not unexpected as this is in line with findings in Friede and Miller.15 The simulation study was motivated by a trial in paediatric MS and is therefore somewhat limited in scope. However, previous simulation studies considering a variety of combinations of event rates and levels of overdispersion demonstrated consistent results with blinded sample size reestimation across scenarios considered (eg, Friede and Schmidli9, 10 and Schneider et al12, 13, 14). Furthermore, the simulations showed that the blinded continuous monitoring applied to trials with recurrent outcomes has some favourable properties in that it leads to robust and efficient designs.

Our investigations were motivated by a randomized controlled trial in paediatric MS. In the meanwhile the trial was completed; it was stopped early with a positive result.37 Of course, the methods proposed are also relevant and of potential benefit to other indications and are not restricted to small populations or rare diseases. Examples include two large ongoing phase III trials with ofatumumab in adult patients with relapsing‐remitting MS (NCT02792218, NCT02792231).

Despite the statistical advantages, the implementation of continuous monitoring might be challenging logistically. In practice, rather than monitoring the information continuously, only a few data looks may be possible. However, this does not seem to be a major drawback: as can be seen from figure 7 in Friede and Miller15, the utility of additional looks diminishes rapidly beyond something like five data looks. For instance, in the two ongoing phase III trials with ofatumumab in adult patients with relapsing‐remitting MS mentioned above, blinded data are reviewed twice: once prior to completion of recruitment to decide whether the sample size should be increased and a second time to decide when the trial can be stopped early as sufficient information was already gathered.

For evaluating the information, we proposed a number of alternative blinded approaches to estimate the nuisance parameters. More specifically, we considered the simple lumping approach where all observations from both groups are lumped into one group and the mixture model approach where it is acknowledged that the observations come from two distributions, but it is unknown in the blinded data looks which observation comes from which group. The lumping approach is computationally simpler and was therefore preferred in the simulation study. However, the mixture distribution approach has some advantages over the lumping approach when the treatment difference is (very) large, since the mixture approach will yield estimates of the dispersion parameter that are less exaggerated than the lumping approach. Alternatively, one could correct the bias in estimating the dispersion parameter with the lumping approach. This would be similar to the so‐called adjusted variance in blinded reestimation designs with normal endpoints.38 Whereas we only considered ML estimators for the mixture model approach, we described for the lumping approach additionally MM estimators. The latter are easier to compute than the ML estimators but have generally larger variances under the assumed negative binomial model (eg, Schneider et al12).

For any constellation of nuisance parameters, blinded continuous monitoring assures that the trial has sufficient power to test the null against the alternative hypothesis as long as the true treatment effect is at least of the size assumed in the planning. Uncertainty regarding the effect size is not mitigated by blinded continuous monitoring. In situations where there is high uncertainty about the treatment effect, group sequential designs with unblinded interim analyses should be considered. We refer here to the fundamental paper by Scharfstein et al39 and some recent developments by Mütze et al.40, 41 Mütze et al40 develop group sequential designs for negative binomial outcomes, whereas more flexible semiparametric models for recurrent‐event endpoints are considered in their follow‐on paper.41 As argued in Friede and Miller,15 there is some promise in combining repeated sample size reestimation based on nuisance parameters with group sequential plans. They propose to use blinded estimators of the nuisance parameters to adjust the sample size although unblinded estimators are available in the data looks (interim analyses) of the group sequential design. This is mainly for two reasons. First, the use of blinded estimators can be understood as means to control type I and type II error rates. Secondly, it avoids potential issues with back‐calculating the treatment effect from the reestimated sample sizes.

Negative binomial regression is popular to model recurrent events. Examples include exacerbations in lung diseases such as asthma, chronic obstructive pulmonary disease, cystic fibrosis (CF), and non‐CF bronchiectasis, as well as hospitalizations in heart failure. Their widespread use motivated us to focus on these in our investigations. However, a number of alternatives exists including the Anderson‐Gill model42 and the so‐called LWYY model by Lin et al43, to name but a few. Further extensions include time trends in the event rates. Here we assumed constant rates, but it has been suggested that, for example, relapse rates in relapsing MS might decrease with follow‐up time.14, 44 To extend the blinded continuous monitoring approach to recurrent events with time trends in the rates is subject to ongoing research within our group.

CONFLICTS OF INTEREST

T.F. provided consultancies to Novartis Pharma AG regarding sample size reestimation strategies for the MS study that served as an example in this paper. D.H. and H.S. are employees of Novartis Pharma AG. 

Friede T, Häring DA, Schmidli H. Blinded continuous monitoring in clinical trials with recurrent event endpoints. Pharmaceutical Statistics. 2019;18:54–64. 10.1002/pst.1907