Virtual reality simulation of robotic transsphenoidal brain tumor resection: Evaluating dynamic motion scaling in a master‐slave system

Abstract

Background

Integrating simulators with robotic surgical procedures could assist in designing and testing of novel robotic control algorithms and further enhance patient‐specific pre‐operative planning and training for robotic surgeries.

Methods

A virtual reality simulator, developed to perform the transsphenoidal resection of pituitary gland tumours, tested the usability of robotic interfaces and control algorithms. It used position‐based dynamics to allow soft‐tissue deformation and resection with haptic feedback; dynamic motion scaling control was also incorporated into the simulator.

Results

Neurosurgeons and residents performed the surgery under constant and dynamic motion scaling conditions (CMS vs DMS). DMS increased dexterity and reduced the risk of damage to healthy brain tissue. Post‐experimental questionnaires indicated that the system was well‐evaluated by experts.

Conclusion

The simulator was intuitively and realistically operated. It increased the safety and accuracy of the procedure without affecting intervention time. Future research can investigate incorporating this simulation into a real micro‐surgical robotic system.

1. INTRODUCTION

Transsphenoidal surgery is a minimally invasive endonasal surgical procedure to remove pituitary tumours located behind the sphenoid bone in the brain.1 The surgery is performed through a small incision at the back of the nasal cavity at the sphenoid bone, by means of the manipulation of the endoscope and the microsurgical instruments across the nostrils. The surgery generally has a duration of 2 to 4 hours and is performed in different stages. (1) The preparation of the patient in the operating table. (2) Making an incision in the back of the nasal cavity across one nostril by removing a portion of the nasal septum dividing the left and right nostrils. (3) Opening the back of the sphenoid sinus by an osteotomy of the sella bone, until exposing the dura mater membrane. (4) Removing the dura mater and the tumour by progressively resecting and removing small pieces of soft tissue. (5) Finally, closing the incision in the sella by a portion of the septum wall or synthetic graft. Particular attention deserves the fourth step and must be performed cautiously for removing the tumour avoiding the risk of causing injuries to the surrounding nerves and vessels. The duration of this step is usually from 30 to 45 minutes approximately, depending on the tumour size.

The surgery leaves typically no visible scarring and allows short recovery time in patients but is difficult because it involves two critical implications: (1) highly constraining the operative space available in the brain; and (2) demanding high dexterity from the neurosurgeon to operate safely. For these reasons, there is an increasing interest in the development of new micro‐surgical robotic devices as advanced tools that enhance the accuracy and safety of such neurosurgical interventions.2, 3 However, the before mentioned difficulties have brought new challenges concerning the control and usability of these robotic devices in procedures with narrow space and indirect visibility. Therefore, it is necessary to develop new control algorithms for intuitive and robust manipulation of robotic tools. For example, the incorporation of collision avoidance and path planning algorithms into the control loop of robotic systems with multiple degrees of freedom, inside static and dynamic environments,4, 5 would reduce the risk of tools in contact with delicate tissue around the operative area. It would also prevent undesirable configurations of the robotic arms that otherwise would hinder the standard workflow of the neurosurgeon. Consequently, much work is in progress in developing new robotic manipulators6 and in incorporating additional features into the control loop. With the final objective of enhancing the surgeon's dexterity while working in operative conditions that have many spatial and visual restrictions, some valuable features can be incorporated into the control loop such as force feedback, tremor filtering, virtual fixtures, dynamic motion scaling (DMS), and collision avoidance.7, 8, 9, 10

On the other hand, the use of surgical simulators that traditionally have shown to be useful for training may have the capability to be used during the development of micro‐surgical robotic systems. Simulators could play an essential role in detecting potential problems and unexpected events derived from the integration of robots into the current intervention loops. Simulators offer flexibility and the possibility to test different operative conditions, and are, therefore, useful in evaluating the improvement in a surgeon's performance by including additional features to the robotic control loop. Hence, simulators become a more sophisticated option; they introduce new complex surgical gestures and tasks to reproduce actual procedures realistically. Further, they could also be used for surgical training purposes and pre‐operative planning of robotic surgeries.

For neurosurgery, some simulators have already been developed.11, 12, 13 A notable example, the NeuroTouch,13 an advanced simulator focused on the realistic behaviour of soft tissue and force feedback, leading to the development of realistic neurosurgical simulation, has been mainly applied for training and evaluation of surgical skills.14 The NeuroTouch system focuses on the off‐line simulation of the surgical procedure itself, employing standard surgical tools. However, it is not conceived to mimic robotic teleoperation surgery, and to the best of our knowledge, to date has not addressed the integration of robotic tools into the simulation.

Our team developed a virtual reality (VR) system that simulates the transsphenoidal procedure for resection of pituitary tumours in the brain. For the moment, we specifically focused on the fourth stage of the surgery, the dura mater and tumour resection, because this phase is considered the riskiest and critical step during the procedure.

The deformable behaviour of the soft tissue, including membranes, tumour, and brain, was modelled using position‐based dynamics, allowing for real‐time tissue resection. A pair of haptic interfaces was employed for the manipulation of the virtual robotic tools and for providing tactile sensation during the intervention. The haptic interfaces are also used for the physical robotic system.2 Thus, the transition from the simulation to physical robotic test would be facilitated.

We incorporated a region‐based DMS algorithm into the simulator to enhance accuracy while operating near critical tissue around the tumour. Although the effects of motion scaling on surgical task performance have been extensively discussed in the literature,15, 16, 17 DMS based on the distance to the target area and its inclusion inside a VR simulator is still a new feature. The simulation may play an essential role in evaluating the task performance and feasibility of the integration of a new algorithm with the physical robot. Expert neurosurgeons and residents participated in the experiment to evaluate the usability of the system. Like already developed simulators, our system can monitor and obtain useful data during the experimental sessions that cannot be measured in the operating room, and potentially apply those data for skills assessment.18 After analysing the data obtained during the experiments, we concluded that the integration of the DMS algorithm contributed to a reduction in collision occurrence of the tools against healthy brain tissue and in the percentage of healthy tissue removed, indicating an enhancement in the participants' accuracy.

2. MATERIALS AND METHODS

Existing simulators for neurosurgery predominantly employ standard surgical tools that in practice are manually operated; indeed, virtual tools are mainly modelled as straight rigid rods with limited mobility at the jaw of the forceps. In our simulator, we incorporated the model of a bending robotic forceps, based on the design of a previously developed surgical robot,2 named MM‐2, as depicted in Figure 1. The simulator focuses on allowing intuitive manipulation of the articulated tool via haptic interfaces, and on accurate tissue interaction while considering the real mechanism of the forceps.

Figure 1.

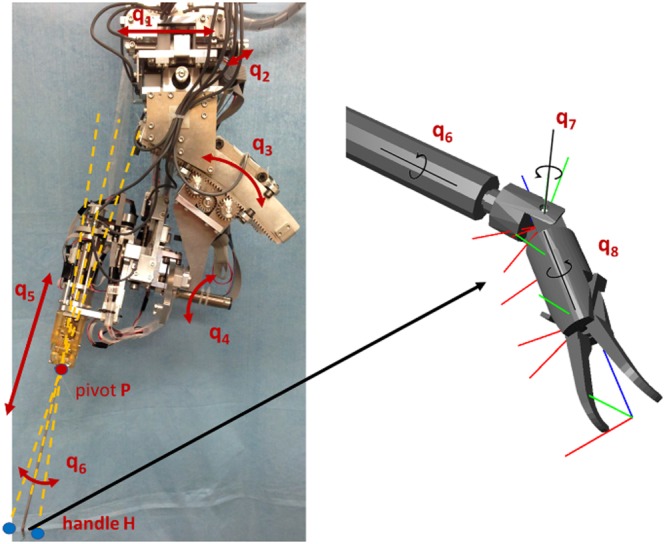
Neurosurgical robot system (left), and details of the forceps computer‐aided design showing the degrees of freedom (right)

The simulator was designed following the Master‐Slave scheme in robot‐assisted surgery, where the executed actions by the robotic system (Slave) are commanded in real time by the surgeon, who is provided with visual information of the ongoing process through a separate manually controlled user interface (Master). Such decoupling enhances the position accuracy and generates a smooth trajectory for the procedure.19 Analogously, the present simulation system comprises two software modules: (1) the Master program, responsible for monitoring the states of haptic interfaces and foot pedals; and (2) the VR simulator itself, playing the role of the Slave counterpart. The components communicate with each other via the User Datagram Protocol. The Master program is also responsible for computing the force to be exerted by the haptic interfaces depending on the simulation state; additionally, the graphical output of the simulator is streamed to a stereo‐monitor allowing for immersion of the user into the virtual environment (Figure 2).

Figure 2.

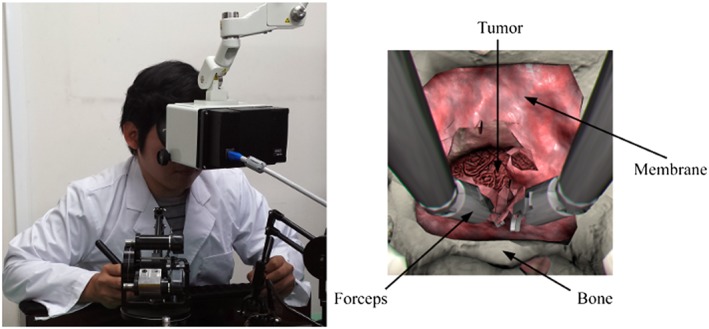
(left) User interacting with the simulator through two haptic interfaces and a stereo‐monitor; (right) screenshot of the simulation indicating virtual components

The simulator was developed by integrating two independent models, namely, the rigid‐body dynamics and the soft body deformation models. The first one is dedicated to collision detection and response to rigid objects, such as the collision of the robotic forceps and the skull; while the second model is responsible for simulating the interaction of the tools with the soft tissues, allowing for real‐time deformation, tearing, and resection of the virtual deformable structures. The physical and logical components of the simulator and the interaction flow with the user are shown in Figure 3, while the details of the simulation algorithm (Figure 4) will be addressed below.

Figure 3.

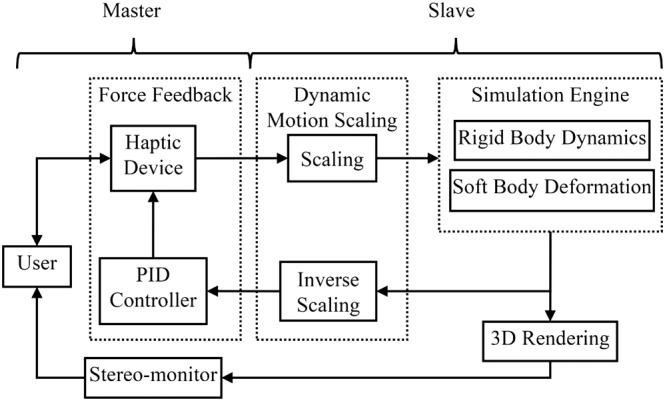
Simplified diagram of the system showing interaction flow

Figure 4.

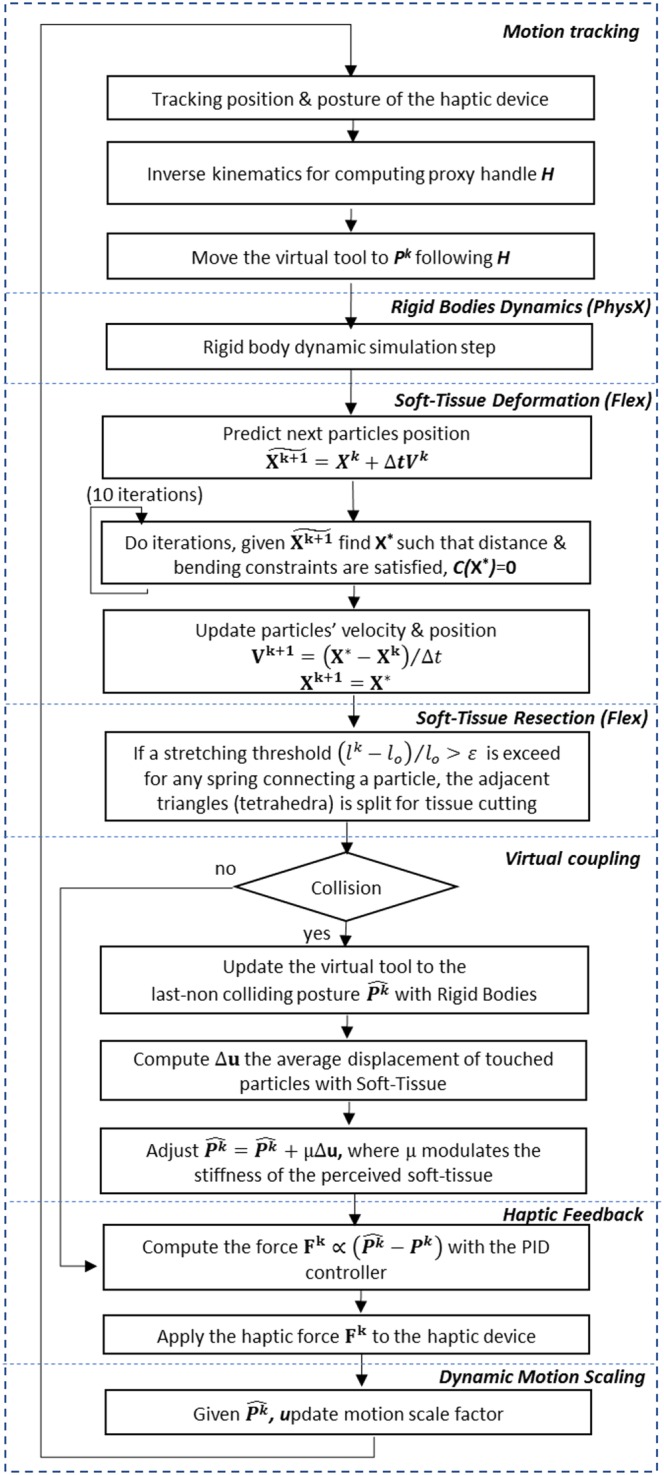
Scheme showing the overall algorithm of the simulator

2.1. Rigid‐body dynamics

A multi‐rigid bodies dynamic equation solver is responsible for simulating the behaviour of the rigid objects, in our case, the collision of the robotic forceps and the skull. For simplicity, the skull was considered as static, opposite to the dynamic behaviour of the tools. The dynamics computation loop is performed in the following way: first, the external forces such as gravity are applied to the virtual rigid objects; then, time integration is performed to obtain the new position of the objects. Next, the collision detection step is executed, followed by the collision response step which computes the reaction forces and obtains the non‐colliding configuration of the rigid objects, to be used in the next simulation cycle. To achieve this goal, we employed the NVIDIA PhysX engine,20 an impulse‐based physics engine, written in C++ language and designed for adding physics to video games; although PhysX runs on the CPU, it may take advantage of compatible GPU devices. This engine performed well and showed stability during robotic simulations when tested against other physics engines,21 and it has already been employed in the development of virtual surgery simulators.22, 23

Inside the PhysX engine, the geometries for the simulated objects can be approximated using solid primitives such as spheres or boxes; from the models, it is also possible to employ the triangle meshes directly. However, coding for collision detection between triangle meshes is computationally burdensome. To achieve real‐time simulation, we employed an approximated convex decomposition24 of the original geometries for the skull and the forceps, rather than working with high‐resolution meshes (Figure 5), speeding up the broad phase of the collision detection algorithm.

Figure 5.

Triangle meshes for the skull and details of the robotic tool (left), and their respective approximated decomposition into convex shapes (right)

2.2. Soft tissue deformation and resection

Several approaches for simulating the elastic behaviour of biological tissues have been proposed.25 The finite element method (FEM)26 has been widely applied in many virtual surgical simulations. FEMs are based on continuum mechanics, with a strong mathematical foundation and physical validity27, 28, 29; however, because of the high computational load, the real‐time response cannot be ensured, and changes in the mesh topology become prohibitive when a precomputed response is used to speed up the solution.30

In our work, we proposed to use position‐based dynamics,31 in which the shape of the anatomical structures is discretised into particles, each one containing information about its position, mass, and velocity. The properties of the elastic material are approximated by using distance constraints C that contain information about the rest length l _o (starting length of any spring in rest position) and a stiffness factor μ 32 (Figure 6). For our purposes, we integrated the NVIDIA FLEX Engine,33 a programming library for physics‐based simulation games using particles. With this approach, it is possible to simulate a wide range of materials, from solids to fluids, under the same framework, while allowing real‐time simulation by solving the system's equations in parallel on the GPU. An advantage of the method is that changes in the topology, due to tearing or cutting, can be easily handled by modifying the connectivity between the particles.

Figure 6.

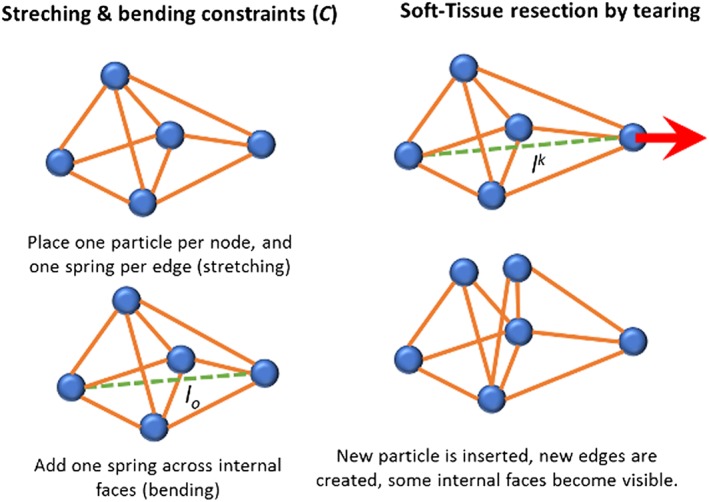
Graphical scheme of the particles' interaction during the simulation, illustrating the geometrical constraints (left) and the mesh subdivision mechanism for tissue cutting (right)

The simulated dura mater membrane covering the incision in the bone (Figure 2—right) was approximated using a mass‐spring network, starting from a non‐manifold mesh, and placing a particle for each vertex and one stretch constraint per edge. Additionally, bending constraints were placed across the edges, adding more control and stability to the elastic behaviour of the membrane. Volumetric tissue, such as the tumour, were approximated using the corresponding tetrahedral mesh of the geometries, placing a particle per vertex while adding stretch constraints along the edges, and bending constraints across the faces shared by two adjacent tetrahedrons (Figure 6—left). For simulating the resection of the membrane, we employed a previously described algorithm31 for cutting surface meshes as a result of the threshold exceeding the external forces applied to the deformable models, while tearing the material (Figure 6—right). Since this method has been proved to be stable, the same algorithm was extended for handling tearing operations on tetrahedral meshes for the simulation of a tumour (and brain) resections.

2.3. Haptic interaction

The main feature of the haptic interfaces is their capability to exert linear or angular force in one or more axes. By modulating the exerted force, in response to user actions inside the virtual environment, it is possible to mimic tactile sensation when interacting with the simulated objects and to emulate properties such as viscosity or roughness.34 We employed a pair of haptic interface devices (PHANTOM PREMIUM 1.0, Geomagic, USA) representing each hand, with 3 DOF of force output, and customised for allowing 7 DOF input: XYZ position, 3 gimbal angles for tool orientation, and a grip angle for modulating the forceps aperture.

2.3.1. Motion tracking

The simulator mimics the movements of the micro‐surgical forceps implemented in the MM‐2 neurosurgical robot (2), which is a redundant manipulator with 8 DoF for position and orientation, with 3 DoF for bending, rotation, and gripping with the forceps. We simplified the movement of the tool by assuming that once the tools are placed inside the nostrils, joints q₁ and q₂ remained fixed (Figure 1), which results in the workspace defined by the cone formed by the movements of joints q₃, q₄, and q₅, with origin in pivot point P. Thus, the tool position in the simulation is defined by the vector $\overrightarrow{\mathbf{PH}}$, given the tracked position in space of the end‐effector of the haptic interface H. On the other hand, the tool orientation (q₆, q₇, and q₈) and forceps aperture are considered absolute with a one‐to‐one correspondence with the real orientation of the gimbal and grip angle of the haptic interface.

As would occur in the robotic master‐slave scheme, the reachable workspace of the haptic interface is limited concerning the operative workspace within the simulation. For this reason, the translation of the end‐effector is relative with respect to the last position, established when pushing the foot pedal (setting the origin of the reachable workspace) and reset when the pedal is released.35

2.3.2. Virtual coupling

During the simulation, the simulated tool follows the tracked real posture of the haptic interface through a virtual coupling scheme, using a penalty‐based method through a previously modified version of the algorithm,36, 37 as explained below (Figure 7).

Figure 7.

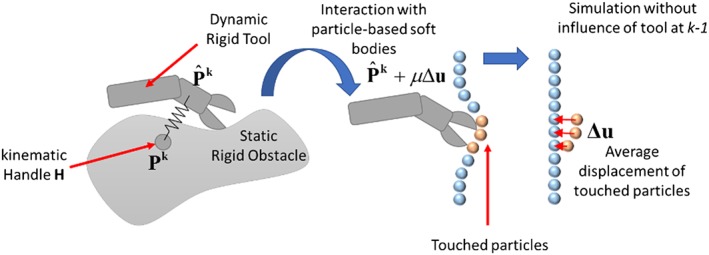
Virtual coupling scheme for interactions between the virtual tools and rigid‐bodies such as bones (left) and particles for soft‐tissue interaction (right). The virtual tool tries to reach the handle but without penetrating the objects. A force, depicted by an arrow, is exerted to enforce the user movement from the actual position towards the ideal non‐colliding configuration

First, the virtual tool posture P ^k is rigidly transformed to follow the haptic interface. To this aim, an auxiliary kinematic virtual rigid object (the proxy handle) is translated following the position of the end‐effector H of the haptic interface mapped to the space of the virtual environment, such that the proxy handle can penetrate the rigid objects in the scene. The virtual tools were approximated using a set of rigid convex shapes, for which the spatial configuration changes depending on the angles retrieved from the gimbals in the proxy handle of the haptic interface. Following the simulation, the virtual tool is attached to the proxy handle using a virtual spring, in such a way the virtual tool is always trying to reach the handle shape but without penetrating the rigid objects in the scene, thus adjusting the last non‐colliding position $\widehat{{\mathbf{P}}^{\mathbf{k}}}$ of the tool, obtained as result of the rigid‐body dynamics in the simulation.

To compute a stable collision response, we prevented the virtual tool from changing its orientation during the collision response phase (the second phase, or narrow phase of the collision algorithm when the fine contacts are detected). For this purpose, its inertia was adjusted to an arbitrarily large value (instantaneously during the time step that lasted the execution of the narrow phase), while its mass was kept low. Additionally, a damping factor was added contributing to the stability of the coupling, and for reducing the jittering movement of the virtual tool that could be induced by the manipulation of the haptic interface. When the tool is not colliding with an object, it moves along with the handle shape; however, when the tool enters into a colliding state, it stays in the last non‐colliding position solved by the physics engine.

2.3.3. Force feedback

Previous studies computed the exerted force F ^k proportional to interpenetration, it means to the error between the current position and the non‐penetrating position of the detected first contact.38 In our implementation, we adopted two different mechanisms for computing the force response due to the interaction with rigid‐bodies (between tools and bone), and with soft tissues (membrane and healthy brain).

For the force feedback due to rigid‐bodies contacts, we employed a PID controller, receiving input regarding the current position of the haptic interface P ^k, as reference value the ideal position of the tool $\widehat{{\mathbf{P}}^{\mathbf{k}}}$ (ie, the non‐colliding position) mapped to the workspace of the physical haptic interface.

With regard to force feedback during the interaction with soft tissue, the capabilities of the current implementation of the position‐based dynamics engine that we employed are limited in the sense that the reaction forces cannot be obtained directly from the position‐based dynamics solver. Thus, the ideal non‐colliding position of the tool with the soft‐tissue is estimated by compensating the last tool position at the time step before the collision with the displacement of the colliding particles after the collision at the next time step during the simulation. The compensation is computed in the following way (Figure 7). The last configuration of the particles is backed up; then, a second simulation step is performed without considering the influence of gravity and contact with the convex shapes from the tools, enforcing displacements due to distance constraints between particles. Finally, the average displacement of the particles Δu that were in contact with the tools is obtained (Figure 8). This average displacement is then applied to the target position for the tools, after multiplying it by a constant factor μ (stiffness of the contact); this value modulated the perceived stiffness of the soft tissue during force feedback and was manually tuned up during preliminary testing experiments, until achieving a suitable tactile perception according to the opinion an expert neurosurgeon.

Figure 8.

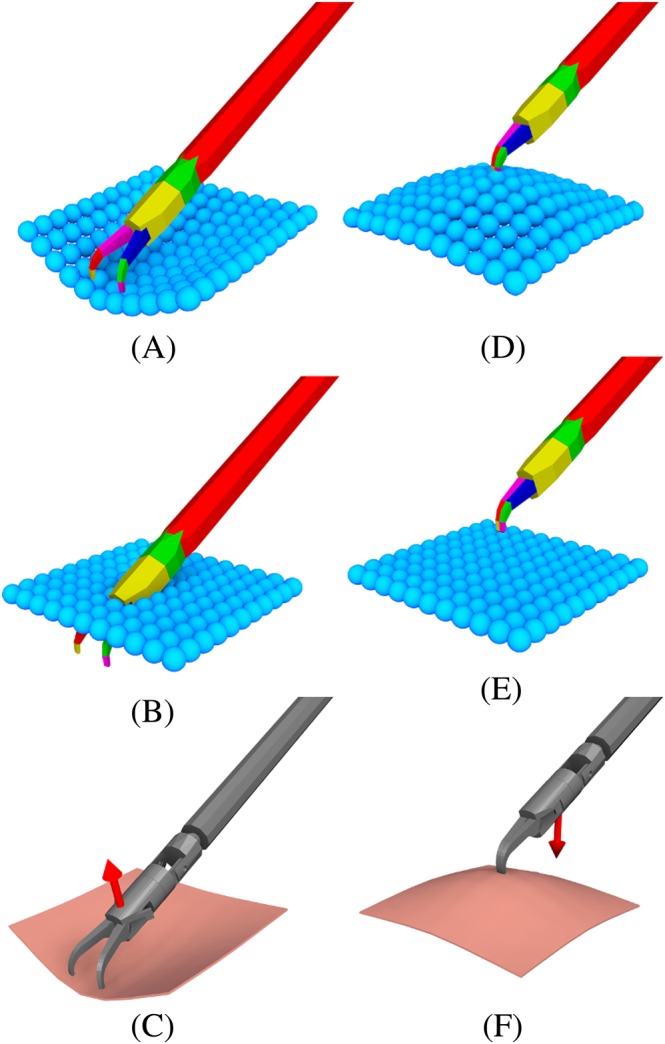
Particle‐based soft tissue pushing (A‐C) and pulling (D‐F). Convex decomposition of the tool interacting with particles (A, D). Second simulation step without the influence of the convex objects (B, E). The shaded scene with an arrow showing the average particle displacements (C, F)

2.4. Dynamic motion scaling

The DMS feature allows variation in the ratio of the tool's motion in the Master system to the operator's hand motion in the Slave system. The concept of motion scaling has been previously studied, and many approaches to achieving such an effect have already been proposed.16 The purpose of DMS is our new concept and consists of dynamically changing the motion scaling ratio according to the position of the robotic tools relative to the target area, to make the user's movements more accurate while approaching dangerous zones or handling delicate tissue. DMS would also allow coarse movements when the tools are moving in empty regions of the workspace. Therefore, it is imperative to choose adequate scaling factors and rules for changing the scale value in real time, depending on the context during the simulation. In other words, suitable DMS enhances surgical dexterity while improving safety during the operation, without unnecessarily increasing the required movements and time while performing the intervention.

In our simulator, we implemented a region‐based approach for motion scaling, in which each zone is represented as a triangular mesh with an associated scaling factor (Figure 9—left). The scaling factor is then decided based on the position of the end‐effector of the virtual tools amongst the meshes, by searching for the nearest mesh surface enclosing the point. The scaling factor is linearly interpolated between adjacent regions (ie, closed meshes), to avoid abrupt changes which could potentially lead to errors during the interaction, allowing smooth movement of the tools (Figure 9—right). The scaling regions were established by considering the proximity and shape of the delicate tissue: the scale factor is small when the tools are near the healthy brain tissue and increases when the tool moves away until reaching a maximum value at the entrance of the nasal cavity.

Figure 9.

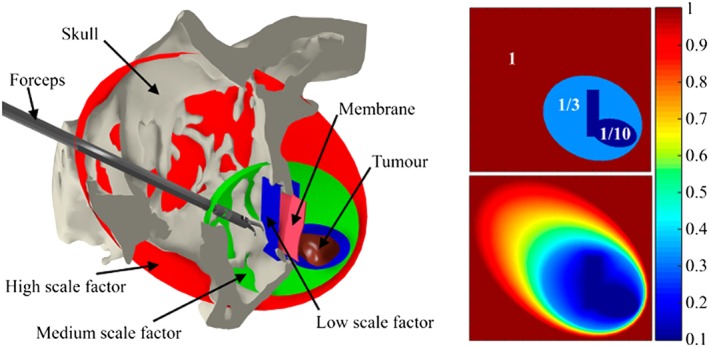
(Left) Sagittal slice of the skull that reveals the membrane, tumour, and forceps, where closed meshes represent the scaling zones. (Right) Colour map visualisation of the motion scaling factor sampled on the sagittal plane without interpolation (above), and with linear interpolation (below)

3. EXPERIMENTS

3.1. Objective of the study

To evaluate the reliability, usability, and acceptability of the simulator, we carried out an experimental study with volunteer participants. With the aim of determining to what extent the implemented region‐based DMS may contribute to improving the user performance, different experimental conditions were tested. To assess the effect of DMS for movement accuracy, we focused on the metrics for contact points and percentage of healthy and tumour tissue removed.

3.2. Participants

Personnel from the clinical staff from the Departments of Neurosurgery of three different hospitals were invited to participate in the study, at the University of Tokyo Hospital, Nippon Medical School Hospitals both in Japan, and General Hospital of Mexico “Dr Eduardo Liceaga,” Mexico. Participants were divided into two groups: five expert neurosurgeons (experts), and 11 surgical residents with no experience in the transsphenoidal intervention (novices).

3.3. Tumour removal task

The task in the experiments consisted of manipulating the virtual forceps controlled through the haptic interfaces to remove a transsphenoidal tumour. Participants were tasked with removing a simulated membrane covering the opening of the sphenoid bone, by approaching it through the nasal cavity, and then extracting the entire tumour while avoiding any damage to the surrounding healthy brain tissue (Figure 10). We tested two different conditions (constant motion scaling CMS, and DMS), with the two groups of participants (expert surgeons and novices residents). A scaling of 1/3 was applied for CMS, and three scales of 1, 1/3 and 1/10 for high, medium, and low scaling factors were applied for each DMS region, respectively (Figure 9).

Figure 10.

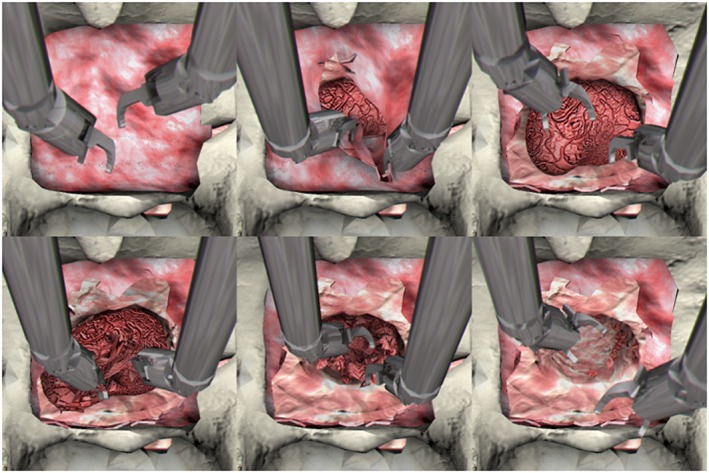
(From left to right and from above to below) Screenshots of VR simulator showing different moments as the task progresses from start to completion

Since all the participants had no previous knowledge about our simulator; they were verbally introduced to the functioning characteristics of the system. Participants were allowed to freely practice for 5 minutes at the beginning of the experiment. Since novices participants have no previous experience in tumour resection, we suspected that they were unable to finish the complete tumour removal with the system. For this reason, the experiment was designed to terminate after 3 minutes, regardless of the user progress in the task. This interval is a representative sampling time, considering that the real tumour resection phase typically last from 30 to 45 minutes and that the system focusses in tissue resection simulation with the forceps, but obviating the tasks of extracting the resected tissue, blood suction and lens cleaning (one‐third of the surgical gestures).

3.4. Measurements

One of the features implemented in our simulator during the intervention is the collision point reporting feature. We considered all contact pairs reported by the collision detection algorithm at each step of the simulation; these pairs included contact between (1) rigid body shapes of the skull and the convex shapes representing the virtual forceps; (2) both forceps; and (3) the particles representing the soft tissue and the tools.

Aside from collision information, our simulator also records the percentage of healthy and tumour tissue removed during the test time. The amount of tissue removed was determined by the accumulative integration of the area or volume from individual elements that have been disconnected from the main body and displaced to a different position. Triangle elements were used to approximate the membrane area, while tetrahedral elements were employed for the volume of the brain, including a tumour and healthy brain tissue since thin or flat geometry such as membranes are more convenient to describe using mesh surfaces while volumetric objects (eg, organs) are better modelled using tetrahedra. To determine the percentage of removed tissue of triangle elements, we take the ratio of the accumulated area of all triangles that have been disconnected due to the user interaction with respect to the original area of the unaltered geometry. The same stay for tetrahedrons elements, but in this case considering the computed volume of the tetrahedral elements.

The simulator provides additional useful information for assessing the performance and dexterity of the user during the interaction. This information includes the total time for completing the task, the full path and the path length of both virtual tools, the frequency of activating the foot pedal (ie, changes from released to pushed positions), and the frequency of grasping action by each forcep (ie, changes from opened to closed positions).

3.5. System assessment

To evaluate the system, at the end of the experiment, the participants were asked to answer a questionnaire inquiring about their experience and level of comfort while operating our system (Table 1). Each question was scored on a 5‐point Likert scale, where 1 stands for “strongly disagree” and 5 for “strongly agree.”

Table 1.

Applied questionnaire for assessing the usability of the system by the participants, reporting the perceived fidelity of the transsphenoidal brain tumour resection simulation

Question	Evaluated Feature	Item
1. The tool movement was consistent with my intention.	Usability	Motion consistency
2. The force feedback was not distracting while removing soft tissues.	Usability	Feedback helpful
3. Dynamic motion scaling was helpful during interaction with the soft tissue.	Usability	Motion scaling
4. The force feedback due to touching soft tissue was noticeable.	Fidelity	Feedback noticeable
5. The sensation of grasping the forceps was accurate.	Fidelity	Grasp accuracy
6. The behaviour of the soft tissue was natural.	Fidelity	Soft tissue realism

Six aspects were evaluated: three assessing the usability of the system, and three assessing the fidelity of the perceived realism of the tumour removal simulation. The usability questions assessed (1) how the participants perceived the motion of the virtual tools corresponded to their intention (motion consistency). (2) How useful participants perceived the tactile feedback to be (feedback helpful). (3) To what extent participants perceived the usefulness of the DMS effect for dexterity around soft tissue (motion scaling). On the other hand, the fidelity questions assessed (4) how realistic the participants perceived the tactile sensation of the haptic interfaces to be while interacting with the tissue (feedback noticeable). (5) Based on their experience, how accurately the participants perceived the grasping operation with the virtual forceps to be (grasp accuracy). And (6) how realistic they perceived the simulated soft‐tissue behaves in comparison to real tissue (soft tissue realism) (Table 2).

Table 2.

Kinematic performance of the executed gestures with the virtual tools by each group of participants under the two motion scaling conditions

	Novice		Expert Neurosurgeon		P
	DMS	CMS	DMS
Path length [cm]	173.87 ± 47.66	128.87 ± 55.22	174.46 ± 45.27	126.06 ± 60.09	0.001
Velocity [cm/s]	0.874 ± 0.265	0.668 ± 0.290	0.957 ± 0.308	0.603 ± 0.235	0.05
Acceleration [cm/s2]	26.394 ± 8.925	35.664 ± 19.419	29.916 ± 6.571	30.588 ± 7.913	NP
Jerk [cm/s3]	2007.34 ± 644.34	2582.25 ± 1347.99	2363.57 ± 597.86	2413.42 ± 685.98	NP

4. RESULTS

As visualised in Figure 11, the recorded 3D trajectories of the tip of the tools of both the virtual forceps showed evidence of differences in the motion patterns of both novice and expert surgeons for the two motion scaling conditions. In general, the experts' patterns showed less regular movements with both hands than the ones performed by the novices, and their interval of movements occurred in a wider range of directions. By comparing the paths between the two motion scaling conditions, it can be observed that DMS allowed participants to perform finer motions in a more compact target operative area (near the membrane and soft tissue of the tumour) (Figure 11). A multivariate analysis of variance (MANOVA) applied to the path of the tool's tips of both hands, following a design of 2 Hands × 2 motions scaling conditions (CMS vs DMS) × 2 levels of expertise (neurosurgeon vs novice), revealed a main factor effect for hands (F(1,56) = 9.392, P < 0.0035) and for motion condition (F(1,56) = 13.117, P < 0.001). In fact, the path of the tool's tips for both hands was smaller for the dynamic scaling motion condition (107.746 ± 11.637 cm) than for constant motion (154.592 ± 11.637), as seen in Figure 12A. Then, to confirm the effect of the motion scaling over the kinetics of the practitioners' gestures, another three series of MANOVA were applied to the mean velocity, acceleration, and jerk of their recorded motion paths. Main factor effect over the mean velocity was revealed for hands (F(1,56) = 8.653, P < 0.005) and motion condition (F(1,56) = 15.43, P < 0.001) as seen in Figure 12B, with lower velocity for left (0.671 ± 0.050 cm/s) than right hand (0.881 ± 0.050 cm/s), and more importantly lower velocity (0.916 ± 0.050 cm/s) for DMS than CMS (0.636 ± 0.050 cm/s). Table 2 summarises the observed kinematic performance of the participants for the executed surgical gestures during the tests.

Figure 11.

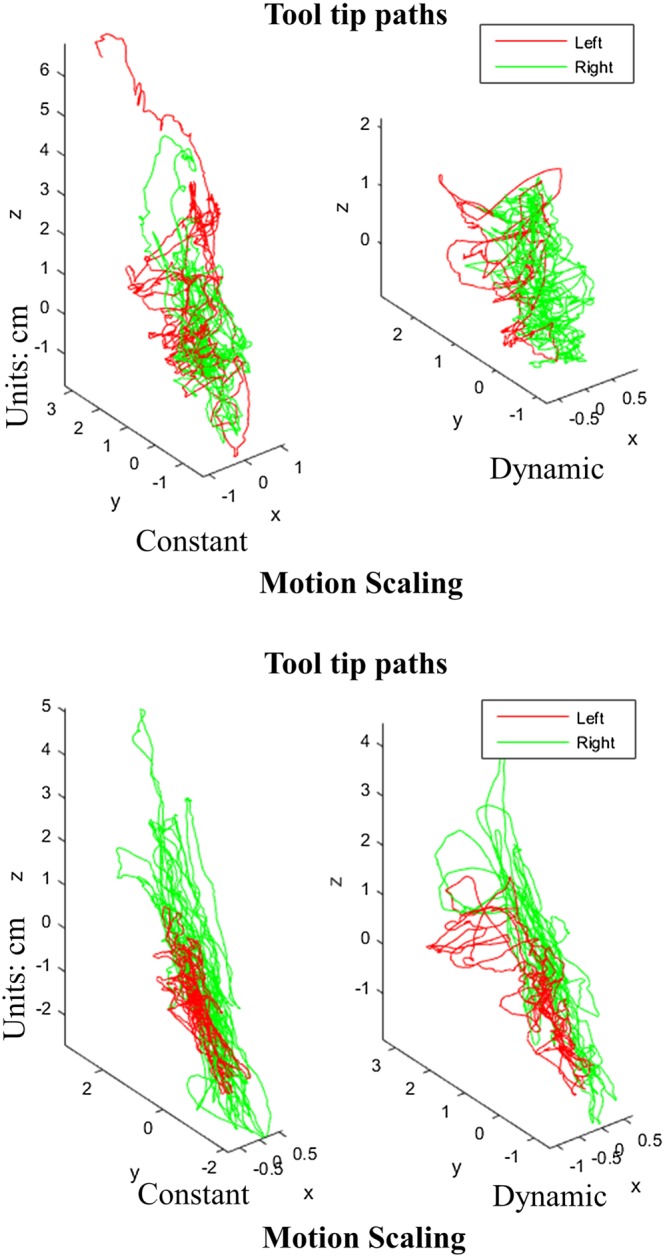
Visualization of the path of the tool's tip of two representative participants. A, An expert user. B, A novice. Paths exhibit more irregular patterns for experts and more compact and finer motions in the dynamic motion scaling condition

Figure 12.

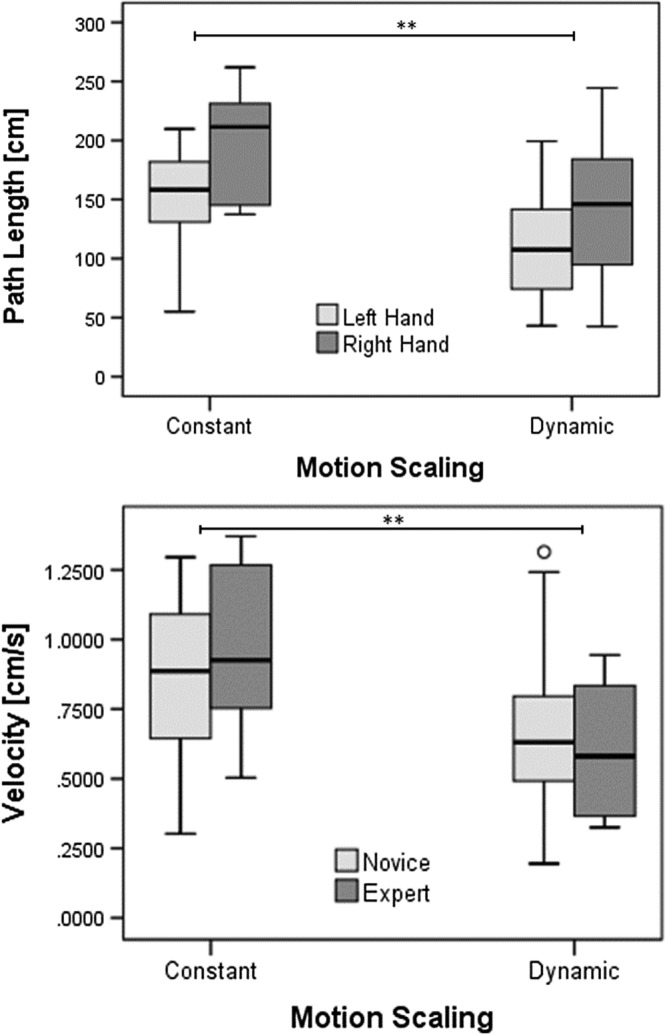
Boxplots indicating the path length and velocity of movements of participants. A, Significantly smaller path length was observed for both hands (P = 0.0035) and motion scaling condition (** P = 0.001). B, Significantly different velocity in the movements was observed between hands (P < 0.005) and slower velocity for dynamic than constant motion scaling condition (** P < 0.001)

The implemented DMS scheme was also helpful in improving interaction with different anatomical structures in the operation area, by reducing unnecessary contact for both groups of participants. As seen in (Table 3), the number of collisions was reduced during the interactions between (1) tool vs tool (3060 ± 2765 for CMS, 2318 ± 1720 for DMS). (2) Bones vs tools (21 469 ± 10 229 for CMS, 13 772 ± 9443 for DMS). (3) Tumor vs tools (178 249 ± 134 300 for CMS, 118 525 ± 92 044 for DMS). Moreover, especially (4) the healthy brain tissue vs tools (36 178 ± 32 681 for CMS, 212 130 ± 24 742 for DMS).

Table 3.

Total collisions as a result of the interaction with the virtual tools by each group of participants under the two motion scaling conditions

Collisions	Novice		Expert Neurosurgeon		P
	DMS	CMS	DMS
Tools	2663 ± 2784	2371 ± 1543	3935 ± 2813	2203 ± 1720	NP
Bones	20 350 ± 11 523	11 893 ± 9835	21 470 ± 10 229	13 772 ± 9443	0.065
Membrane	123 900 ± 129 073	114 719 ± 111 300	115 946 ± 122 515	309 841 ± 403 715	NP
Tumor	175 717 ± 101 635	129 905 ± 92 960	183 820 ± 204 346	93 491 ± 95 014	NP
Brain	38 190 ± 31 959	12 825 ± 28 250	31 753 ± 37 631	10 602 ± 17 213	0.051

A MANOVA applied to collisions with two factors, comparing motion condition CMS vs DMS, and neurosurgeons vs novices confirmed a main factor effect for healthy brain tissue (F(1,28) = 4.158, P = 0.051) at the limit of significance. This indicates that the DMS condition aids to reduce risky contacts in healthy soft tissue, and with less extent at bones (F(1,28) = 3.685, P = 0.065). In the graphs in Figure 13, we summarise the average number of collision points recorded during the experiments for each experimental condition, collision case, and participant group.

Figure 13.

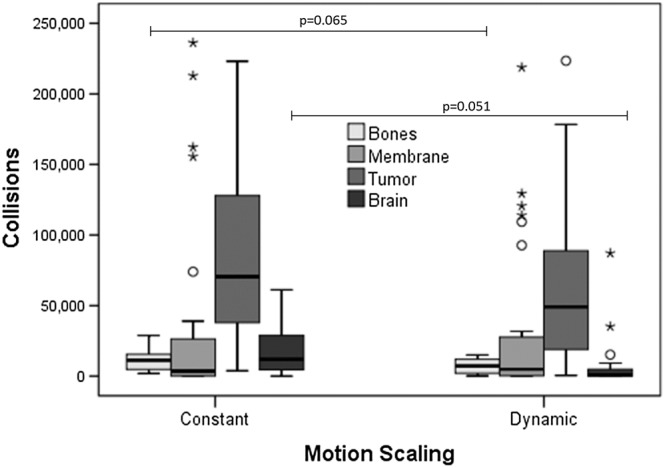
Boxplots indicating the number of collision points between tools and tissue element in the scene (bones, membrane, tumour, and brain), under each tested condition. Collisions with bones and brains resulted different among scaling conditions, and especially risky collisions with healthy brain tissue were lower in dynamic motion scaling than constant motion scaling, at the limit of significance (P = 0.051)

To evaluate the improvement in the participants' performance in completing the task under the two motion conditions, we focused on the percentage of removed tumour, and the percentage of healthy tissue removed (Table 4). As there was a time restriction on each test, the tumour was not completely removed. Thus, to normalise these values for the different conditions so we could compare the results, the ratio of the volume of tumour tissue removed to the volume of healthy brain tissue removed was also obtained. A smaller ratio indicated higher accuracy in the operation. During the DMS condition, the amount of the resected tissue was reduced (Figure 14): membrane tissue (26.77 ± 17.42% for CMS, 24.46 ± 18.19% for DMS); tumor tissue (58.24 ± 28.74% for CMS, 27.90 ± 27.01% for DMS); and healthy brain tissue (2.41 ± 2.43% for CMS, 0.12 ± 0.26% for DMS).

Table 4.

Percentage of tissue removed by each group of participants under the two motion scaling conditions

Resected Tissues	Novice		Expert Neurosurgeon		P
	DMS	CMS	DMS
Tumor tissues (%)	67.24 ± 25.43	32.34 ± 25.670	38.42 ± 27.69	18.12 ± 30.24	0.011
Healthy brain tissues (%)	2.95 ± 2.49	0.173 ± 0.26	1.23 ± 2.01	0.12 ± 0.26	0.005
Tumor/healthy brain tissue resection ratio	0.058 ± 0.068	0.004 ± 0.007	0.018 ± 0.027	0.001 ± 0.004	0.038

Figure 14.

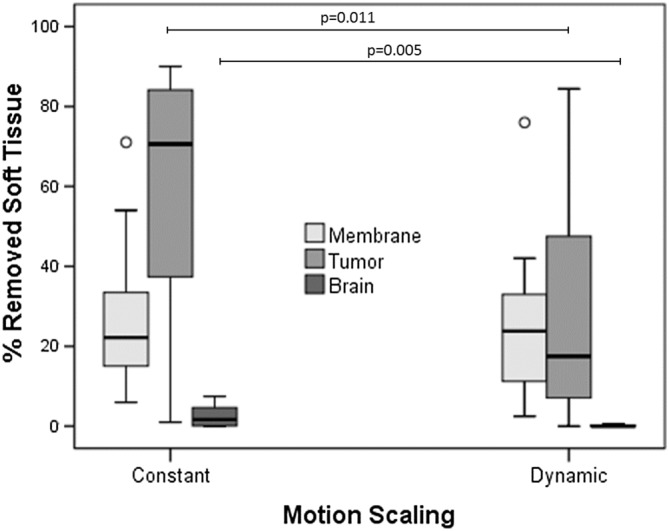
Boxplots indicating the mean percentage of tissue removed per participant group. A, Tumour tissue; B, healthy brain tissue; C, tumour/healthy brain tissue resection ratio

Two series of MANOVA applied to the amount of resected tissue, following a design of (CMS vs DMS) × (neurosurgeon vs novice), confirmed a main factor effect of motion scaling condition for tumor tissue (F(1,28) = 7.412, P = 0.011), and brain tissue (F(1,28) = 9.158, P = 0.005). The tumour/brain tissue resection ratio was reduced as well (0.045 ± 0.0607 for CMS, 0.0034 ± 0.0068 for DMS); a similar MANOVA test also confirmed main factor effect of motion scaling condition (F(1,28) = 4.768, P = 0.038).

Further, novices reduced the amount of resected healthy brain tissue from 2.95 ± 2.49% to 0.173 ± 0.26% in the DMS condition, while experts succeeded in reducing it from 1.23 ± 2.01% to 0.12 ± 0.27% with a tumour/healthy tissue resection ratio of 0.009 ± 0.020. Moreover, a subsequent MANOVA test revealed main factor effect for the level of expertise for the brain tissue (F(1,28) = 4.505, P = 0.043), with 49.79 ± 30.67% of resected tumour tissue by novices vs 28.27 ± 12.74% by neurosurgeons.

These findings indicate that the proposed DMS scheme may play an important role in robotic teleoperation surgeries by increasing dexterity and accuracy that could minimise the risk of resecting healthy brain tissue around the tumour.

As for the post‐experimental questionnaire, the novice group gave positive median scores (≥ 3.5) for all, except one, of the six items—the perceived level of realism of the soft‐tissue behaviour (soft tissue realism). This seems a reasonable opinion as the novices had lesser experience in in‐vivo manipulation of soft tissue through gestures with real surgical instruments. The expert group also gave higher positive median scores (≥ 4) for all. In any case, none of the items presented a negative median score, indicating that the simulator was well evaluated. The results for such questions are shown in Figure 15.

Figure 15.

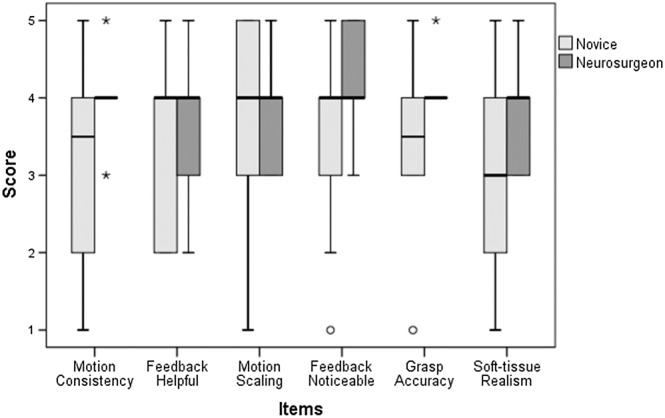
Boxplots showing the median scores of the post‐experimental questionnaire

5. DISCUSSION

In the graphs representing the percentage of tissue removed, regardless of the unbalanced number of participants per group and the high standard deviation of the data, it can be observed that in most of the cases, the novices removed a higher percentage of the tumour but also removed more healthy brain tissue. This observation could be explained considering that even when both novice and expert participants were conscious of dealing with simulation, the expert neurosurgeons tended to remove the tumour more moderately due to their experience and awareness of the complexity and risk regarding the task. Another remarkable difference between the experts and novices was observed in the trajectories of the tip of the tools. While the movements of the expert participants tended to be more pseudo‐random motions in a broader range of directions, the novices tended to make more deterministic and repetitive movements in preferred directions, given their lack of experience and dexterity.

In the graphs representing the average number of collision points, it can be observed that when DMS was enabled, the number of collisions of the tools against the bone and healthy brain tissue was successfully reduced. Additionally, DMS aid the practitioners to reduce the velocity of their movements during the surgical gestures. Both aspects show that smooth changes in motion scaling increased the dexterity of the participants, which was more noticeable in the experts' case. In other words, the induced DMS feature reduced mobility around lower scale regions near the soft tissue but positively enabled finer and safer movements especially near the tumour.

Although the percentage of the removed tumour was decreased with the introduction of DMS, to around of half of the amount of tumour tissue in comparison with constant motion scaling, the percentage of healthy brain tissue removed was almost negligible. In the case of expert neurosurgeons to 0.12% of resected healthy tissue under DMS. This was also observed by analysing the ratio of the volume of tumour tissue removed to that of healthy brain tissue, which practically vanished for both novice residents and expert neurosurgeons, achieving more safeness in the resection manipulation of tissue due to the more dexterous manipulations near the critical zone.

The increment in safeness comes at the cost of longer required time for completely removing the simulated tumour, because both groups of participants removed half of the tissue in the DMS condition, compared to the constant motion scaling, in the same given amount of time. In particular, the expert neurosurgeons resected approximately 30% of the tumour under the CMS condition within the 3 minutes that lasted the experiment, while approximately 18% of the tumour was removed in the DMS condition. Thus, the required time for fully completing the tumour removal task doubled the resection time from 8 to 16 minutes approximately in the simulation, for CMS and DMS correspondingly. Considering that the current simulation obviated the tasks of extracting the resected tissue, blood suction, and lens cleaning, we hypothesise that the tissue resection gestures would take one‐third of the 30 to 45 minutes of duration of the resection phase. Thus, in the longest case, this phase would extend from 45 to 58 minutes approximately (incrementing one‐third of the resection phase), so in total extending 5% to 10% the estimated time of the full surgery (for 2‐4 hours, respectively), which in any case would be still acceptable and moreover safer.

The evaluation of the usability of the system was discussed through the results of the post‐experimental questionnaire. In general, as we expected, the reported scores were higher for the experts than the novices. Due to their experience and familiarity with the surgical procedure, the experts' answers were considered to more consistently support the validity of our experiments, while the answers from the novices reflected a weaker opinion about the helpfulness of the proposed system.

Following the opinion from the experts, the movement of the virtual forceps was consistent with their movements on the haptic interface devices, which indicates that the proposed scheme to control the virtual tools was intuitive. In addition, the experts could notice the force feedback while touching or handling soft tissue, indicating that the proposed method for approximating the force exerted when touching particle‐based soft tissue was convincing. This feature is essential for VR simulators, as the simulator immerses the user in the virtual environment and increases the awareness of the user when manipulating delicate organs. The experts displayed a neutral opinion about if such a feature could be distracting during the simulation; however, we think this opinion would improve as experts become familiar with DMS with more training sessions. As for the accuracy of the simulation, after evaluating the opinion of the experts, the interaction of the virtual tools with the simulated soft tissue was considered accurate. They also considered that DMS was helpful, which is consistent with the analysis of the data obtained from the simulation. Even though we employed an approximated method for simulating the soft tissue interaction, the expert users considered that the behaviour of the soft tissue was natural, which supports our choice of using a position‐based dynamics method.

The present work presents some limitations that provide opportunities for further research. First, the position‐based dynamics method for simulating the soft‐tissue presents advantages over FEMs,26, 27, 28 such as easiness of implementation, real‐time computations, and the suitability to generate dynamic topology changes for simulating tissue resection. Unfortunately, like other common methods such as mass‐spring,39 this method also suffers some drawbacks, especially difficult to set material parameters and limited biophysical realism. For the moment, the biomechanical validity of the simulated tissues was out of the scope of this study so, rather than biophysically recreating the soft tissues properties, we experimentally calibrated the visuotactile feedback to plausible soft‐tissue deformations, based on the experience and opinion of the expert neurosurgeons. Surveys of experts showed that the behaviour of the simulated tissues is consistent with the user interactions. However, more work is needed towards the integration to our current development of other soft‐tissue deformable models, suitable for tissue resection but with biomechanical validity, such meshless methods,40 as future research.

Second, volunteers who participated in this study have no experience with real robotic transsphenoidal surgeries in patients. However, especially experts regularly collaborated as volunteers in experiments conducted for the design, development, and testing of new robotic and haptic systems at our research groups. For this reason, we consider their active participation in this work, and their opinion valuable to evaluate our VR system, as they are aware of the difficulties of the integration process of robot and simulation technologies into micro neurosurgery procedures.

Third, residents expressed lower scores in the survey than neurosurgeons, mainly because they do not have experience of transoperative interacting with living tissues. However, their opinions must not be neglected, because they have experience on interacting with synthetic silicon phantoms, or manually assisting by handling the microsurgical instruments such the endoscope, while the expert neurosurgeon is performing some surgical gestures during the nasal cavity opening stage. So, for the scope of this work, their experience is not negligible and serves as a reinforcement opinion for the evaluation of the current system, and as a baseline for the enhancement and incorporation of new features to the system.

6. CONCLUSIONS

In this work, we presented a novel approach of using an interactive VR simulator to mimic the procedure of robotic micro‐surgery for the resection of transsphenoidal brain tumours. By implementing continuous DMS inside the simulation loop, it was possible to improve the accuracy of finer movements around the target zone, reducing the number of undesired contacts with healthy brain tissue and consequently the amount of healthy tissue removed at the cost of increasing the procedure duration by an acceptable amount of time. Based on the assessment of the system through the post‐experimental questionnaire, DMS was considered helpful while handling the soft tissue. Moreover, essential characteristics of the simulator, including the behaviour of the soft tissue, the controlling mechanism of the tools, and grasping of the tissue were perceived as intuitive and natural according to the participants. In particular, expert neurosurgeons positively assessed the full system. Future work in this research contemplates (1) carrying out a more controlled and more extended studies that aim at designing new metrics for surgical skill assessment and learning strategies; (2) the incorporation of the simulator with a micro‐surgical robot as a tool for designing novel control and teleoperation algorithms; (3) the incorporation of other soft‐tissue deformable methods suitable for biophysical realism.

Heredia‐Pérez SA, Harada K, Padilla‐Castañeda MA, Marques‐Marinho M, Márquez‐Flores JA, Mitsuishi M. Virtual reality simulation of robotic transsphenoidal brain tumor resection: Evaluating dynamic motion scaling in a master‐slave system. Int J Med Robotics Comput Assist Surg. 2019;15:e1953 10.1002/rcs.1953