A Latent Transition Analysis of the Longitudinal Stability of Dual-Factor Mental Health in Adolescence

Abstract

Dual-factor models of mental health are increasingly supported but little is known about longitudinal trends in dual-factor mental health. The current study used latent profile analysis (LPA) to empirically identify dual-factor mental health classes at each of Grades 9 through 12 and latent transition analysis (LTA) to examine stability of classes over four academic years. A sample of 875 adolescents from two cohorts reported on their social-emotional strengths and psychological distress. Cross-sectional LPAs for each grade year resulted in four mental health classes: complete mental health, moderately mentally healthy, symptomatic but content, and troubled. An LTA model indicated that the complete mental health class exhibited the most stability, followed by moderately mentally healthy and symptomatic but content classes. The troubled class exhibited the least stability. Less than 24% of participants remained in the same mental health class across all years. Findings support regular monitoring of students’ dual-factor mental health to accurately inform mental health promotion, prevention, and intervention efforts.

Dual-factor models conceptualize mental health as the interaction between well-being and psychopathology and research supports the need to consider both in school-based mental health assessment, prevention, and intervention efforts (Greenspoon & Saklofske, 2001; Keyes, 2002; Suldo & Shaffer, 2008). The stability of psychopathology (e.g., Overbeek, Vollebergh, Meeus, Engels, & Luijpers, 2001) and well-being (e.g., Huebner, Funk, & Gilman, 2000) independently is well established; however, research examining the stability of dual-factor mental health is limited. Only three identified studies have examined the longitudinal stability of dual-factor mental health (Compton, 2016; Kelly, Hills, Heubner, & McQuillin, 2012; McMahan, 2012) — over five-month, seven-month, and one-year periods. It remains unknown to what degree adolescents’ dual-factor mental health status remains stable or changes beyond one year during this dynamic period of psychosocial development. The present study addresses gaps in dual-factor mental health research by examining the stability of adolescents’ dual-factor mental health across the high school years. Results of this study can inform efforts to identify and support youths’ mental health needs in schools.

Defining Mental Health

Traditional approaches to mental health assessment have defined mental health primarily as the absence of psychopathology (Greenspoon & Saklofske, 2001; Keyes, 2002). This approach places mental health and mental illness at opposite ends of a single continuum and assumes that mental health arises from the absence of mental illness. However, with the renewed interest in positive psychology, definitions of mental health began to include an explicit focus on the presence of positive health indicators, such as well-being (Seligman, 2002) or social-emotional assets/strengths (Scales, 1999). Contemporary mental health researchers increasingly conceptualize mental health as (a) being distinct from mental illness, and (b) including an explicit focus on psychosocial well-being (e.g., Seligman & Csikszentmihalyi, 2000).

Contemporary, dual-factor (e.g., Greenspoon & Saklofske, 2001) or two-continua (e.g., Westerhof & Keyes, 2010) models of mental health propose that positive (i.e., strengths, subjective well-being) and negative (i.e., distress, psychopathology) indicators of mental health lie on separate, related continua, and that each be considered when attending to youths’ mental health (Suldo & Shaffer, 2008). These models suggest that the absence of psychopathology may represent a necessary, but insufficient, condition for mental health (Jahoda, 1958). Using this framework, at least four discrete mental health groups have been reported across elementary (Compton, 2016; Greenspoon & Saklofske, 2001), middle (Antaramian, Huebner, Hills, & Valois, 2010; Suldo & Shaffer, 2008), and high school students (McMahan, 2012; Suldo, Thalji-Raitano, Kiefer, & Ferron, 2016), as well as across transition age adults (Eklund, Dowdy, Jones, & Furlong, 2011; Renshaw & Cohen, 2014). These groups have been defined as: (a) troubled (i.e., high psychopathology, low well-being), (b) complete mental health (i.e., low psychopathology, high well-being), (c) symptomatic but content (i.e., high psychopathology, high well-being), and (d) vulnerable or languishing (i.e., low psychopathology, low well-being).

Research supports the benefit of dual-factor over problem-focused approaches to mental health classification. Overall, a variety of positive outcomes are associated with complete mental health, with low levels of psychopathology proving insufficient for optimal development. Conversely, youth exhibiting low levels of well-being and high levels of psychopathology experienced the poorest outcomes across studies (Antaramian et al., 2010; Greenspoon & Saklofske, 2001; Renshaw & Cohen, 2014; Suldo & Shaffer, 2008; Suldo, Thalji, & Ferron, 2011). For example, middle school students with higher levels of complete mental health were found to have superior reading achievement, academic self-perceptions, motivation, attendance, engagement, and social relationships and functioning (e.g., peer and teacher support) compared to youth in the other three mental health groups (e.g., Antaramian et al., 2010; Suldo & Shaffer, 2008). Similarly, high school students with complete mental health experienced better academic attitudes, perceptions of physical health, social support, satisfaction with romantic relationships, and identity development (Suldo et al., 2016).

Meaningful variation along both the well-being and psychopathology dimensions has been related to differences in academic and social-emotional outcomes. For example, in comparison to vulnerable students, youth with complete mental health exhibited superior outcomes, indicating that merely the absence of psychopathology is insufficient for optimal functioning (Antaramian et al., 2010; Suldo & Shaffer, 2008; Suldo et al., 2016). In addition, for youth experiencing psychopathology, those with higher levels of well-being (i.e., symptomatic but content) had more positive outcomes when compared to youth with similar levels of psychopathology, but low levels of well-being (i.e., troubled; Suldo & Shaffer, 2008; Suldo et al., 2016). When youths’ mental health is examined within a dual-factor framework, it is possible to comprehensively understand their mental health functioning.

Longitudinal Stability of Dual-Factor Mental Health

Despite the growing evidence in support of dual-factor approaches, current research is limited by its cross-sectional nature. Although some variation is evident in stability estimates across various indicators of psychopathology and well-being when examined independently, research generally supports moderate levels of stability over periods of one year or more (e.g., r = .53 to .60 for internalizing problems, externalizing problems, and well-being indicators; Deković, Buist, & Reitz, 2004; Ferdinand, Verhulst, & Wiznitzer, 1995; Huebner, 2004; Huebner et al., 2000; Obradović et al., 2006). However, research examining the stability of dual-factor mental health is limited, despite its importance for informing recommendations about frequency of assessment and school-based prevention and intervention efforts.

Only three known studies have investigated the longitudinal stability of dual-factor mental health (Compton, 2016; Kelly et al., 2012; McMahan, 2012). Kelly and colleagues (2012) examined the stability of dual-factor mental health group membership among adolescents in Grades 7 and 8 and over a five-month period. Using norm-referenced cut-point criteria, participants were classified into four groups based on the intersection of high or low subjective well-being and psychopathology. Overall, 69% of the middle school students remained in the same mental health group at both Time 1 and Time 2, indicating moderate levels of stability across dual-factor mental health groups. Across the four groups, the complete mental health group exhibited the greatest stability, with 85% of those in the complete mental health group at Time 1 remaining in that group five months later.

McMahan (2012) further investigated the one-year stability of dual-factor mental health among high school students, and also identified adolescents in the complete mental health group to exhibit the greatest stability over time (80%), followed by the troubled group (36%), and the vulnerable group (27%). Overall, most adolescents (61%) remained in the same mental health group one year later, with 16% of adolescents exhibiting change only in levels of psychopathology and 14% exhibiting changes only in their levels of well-being. Only 9% of adolescents exhibited changes in their levels of both psychopathology and subjective well-being.

Most recently, Compton (2016) examined the stability of dual-factor metal health among early elementary aged students in kindergarten through second grade, and found that 71% of students remained in the same mental health group seven months later. Of those individuals who changed groups, 13% exhibited changes in psychopathology only, 11% exhibited changes in their well-being only, and 5% showed changes in both their levels of psychopathology and well-being (Compton, 2016). The complete mental health group exhibited the greatest stability over the seven-month period, with 86% remaining in this group from Time 1 to Time 2. Compton (2016) also used longitudinal trajectory modeling to examine the patterns in the stability of dual-factor mental health over four time points within 18 months. Creating one score reflective of standardized well-being and psychopathology, five trajectory groups were evident: persistently troubled, improving, declining, persistently moderate, and persistently flourishing. Most early-elementary-aged individuals were found to experience persistently flourishing (34%) or moderate mental health (39%) over a period of 18 months, with fewer youth represented in a declining (9%) or improving (11%) mental health trajectory.

Overall, the results of previous longitudinal research suggest that dual-factor mental health groups exhibit moderate stability, with the majority (61% – 71%) of youth remaining in the same mental health group after at most one year. Youth who exhibited patterns of complete mental health were most likely to remain mentally healthy across examinations. However, patterns of instability were evident among all groups, with either the vulnerable (Compton, 2016; Kelly et al., 2012) or symptomatic but content (McMahan, 2012) groups exhibiting the lowest levels of stability. In each longitudinal study of dual-factor mental health, youth were more likely to progress toward complete mental health than to regress toward troubled mental health over time. See Table 1 for a summary of the group-based stability and transition patterns observed in these studies.

Table 1.

Stability Patterns of Previous Longitudinal Dual-Factor Mental Health Research

Study	Group at Time 1	Proportion Remaining in Group at Time 2	Most Likely Transition Group at Time 2 (%)
Kelly et al. (2012)	Complete Mental Health	85%	Symptomatic but Content (9%)
	Symptomatic but Content	42%	Complete Mental Health (43%)
	Vulnerable	29%	Complete Mental Health (46%)
	Troubled	47%	Vulnerable (23%)
McMahan (2012)	Complete Mental Health	80%	Symptomatic but Content (10%)
	Symptomatic but Content	17%	Complete Mental Health (47%)
	Vulnerable	27%	Complete Mental Health (45%)
	Troubled	36%	Vulnerable (20%) or Symptomatic but Content (20%)
Compton (2016)	Complete Mental Health	86%	Symptomatic but Content (10%)
	Symptomatic but Content	44%	Complete Mental Health (38%)
	Vulnerable	24%	Complete Mental Health (52%)
	Troubled	61%	Symptomatic but Content (22%)

Although the existing longitudinal research offers an expanded understanding of dual-factor mental health, this literature is limited by the short-term longitudinal nature of each study (e.g., examining only five-month, seven-month, or one-year stability) and the classification approaches (e.g., logically derived cut scores) used to create groups. This study extends the available literature on longitudinal dual-factor mental health through an examination of stability over multiple years, including examination of one- and two-year stability, and comparison of transitions in mental health status measured at three time points. Given the dynamic nature of adolescence, which involves navigating various biological and developmental milestones, and the significance of the adolescent period for the onset and development of mental health challenges (e.g., Merikangas, Nakamura, & Kessler, 2009), the current study focuses on the high school period.

Classification Approaches for Dual-Factor Mental Health

In each of the three previous studies that examined the stability of dual-factor mental health, and in dual-factor mental health research more broadly, youth were placed into dual-factor groups based on logically-derived methods. Specifically, students were classified into mental health groups using dichotomous classification criteria determined via sample-specific (e.g., z-scores) or norm-referenced cut points at two time points. A limitation of the cut-point classification method is that it always produces four groups based on the binary (i.e., high versus low) cut-score method used, with proportions of youth classified into each group determined by the selected cut-point criteria. This approach is further problematic because criteria are often unclear regarding which cut points to use and the selection of cut points imposes differences between groups that might not be meaningful or might result in errors in group classification (e.g., Nylund, 2007). That is, variation within groups and similarities across groups are minimized. Moreover, replication of research using cut scores becomes more challenging when varied cut-score criteria are used across studies. In particular, when a standardized (e.g., use of z-scores) or sample-dependent approach is taken, as was used in each of the three previous longitudinal studies, youths’ mental health classification becomes dependent upon not only their own mental health experiences, but also on the variations in mental health among other youth in the sample (Nylund, Bellmore, Nishina, & Graham, 2007).

An alternative approach to dual-factor classification that merits consideration is latent profile analysis (LPA; Kim, Dowdy, Furlong, & You, 2017; Nylund, 2007). Classifying youths using cut scores necessitates logical decision-making about which cut-score values to use based on population-based or norm-referenced scores; however, LPA is a person-centered approach that allows for groups, or classes, to be created based on patterns in observed item responses that measure an underlying latent construct (Nylund, Bellmore, et al., 2007). Given the limitations of forming groups based on cut scores, LPA has been offered as a promising approach to better understand youths’ dual-factor mental health by classifying youth via empirical instead of logically derived means (Moffa, 2018).

The Present Study

The current study investigated the longitudinal stability of dual-factor mental health among a high school adolescent sample. Data collected once per year, over three years, among two cohorts of students were used to examine the stability of dual-factor mental health groups from Grades 9 to 12. After empirically identifying the emerging mental health groups in each grade year using LPA, latent transition analysis (LTA) was used to examine stability and patterns in transitions among mental health classes across the high school years. Specifically, the current study examined the following research questions:

1. How stable is adolescents’ dual-factor mental health from Grade 9 through Grade 12?

   1. How stable is mental health across one year?

   2. How stable is mental health across two years (e.g., does adolescents’ mental health in year 1 predict their mental health in year 3)?

2. Which mental health classes exhibit greater stability over time?

3. Are patterns in stability among mental health classes the same across transition points?

Method

Participants

Participants included students attending one high school in central California during the 2013–2015 academic years. A retrospective accelerated longitudinal design was used for the current study. Thus, participants included two cohorts of students: Cohort A consisted of students enrolled in ninth grade in 2013–2014, and Cohort B consisted of students enrolled in tenth grade in 2013–2014. A total of 497 students in Grade 9 (91% of those enrolled) and 466 students in Grade 10 (94% of those enrolled) participated in the universal screening in 2013–2014. Given the longitudinal nature of this study, individuals with at least two years of data across the three possible years when the survey was conducted were selected for inclusion. That is, individuals selected from Cohort A included students enrolled in ninth grade in 2013–2014 who also completed the survey in tenth grade in 2014–2015 and/or eleventh grade in 2015–2016 (n = 467; 94.0%). Individuals selected from Cohort B included students enrolled in tenth grade in 2013–2014 who also completed the survey in eleventh grade in 2014–2015 and/or twelfth grade in 2015–2016 (n = 408, 87.6%). Sample design and demographic information for the total sample and each cohort are presented in Tables 2 and 3, respectively.

Table 2.

Sample Size and Attrition Rate

	9th	10th	11th	12th
Cohort A	n = 467	n = 453 (3%)	n = 367 (19%)
Cohort B		n = 408	n = 391 (4%)	n = 306 (22%)
Total	n = 467	n = 861	n = 758	n = 306

Table 3.

Sample Demographic Characteristics

	Cohort A	Cohort B	Total Sample	County*	California*
Female	52.2%	48.8%	50.4%	--	--
Ethnicity
Latinx or Hispanic	51.2%	56.4%	53.5%	67.0%	53.5%
Non-Hispanic White	39.6%	35.0%	37.5%	25.1%	25.0%
Asian or Pacific Islander	6.4%	5.4%	5.9%	3.0%	11.6%
Black or African American	1.3%	2.0%	1.6%	1.3%	6.2%
American Indian or Alaska Native	0.9%	1.2%	1.0%	0.5%	0.6%
Special Education Eligible	11.8%	9.0%	10.3%	11.0%	11.3%
Eligible for Free or Reduced-Price Meal	50.7%	48.8%	47.9%	61.0%	59.4%

^*data reflect total student enrollment in the 2013–2014 school year

Demographic data for overall student enrollment within the county in which this research took place, as well as for the state of California (California Department of Education, 2014), are also presented in Table 3, and indicate that, overall, this sample is representative of these areas. Attrition rates, also presented in Table 2, were similar for each cohort across years of the study (e.g., from Year 1 to Year 2); however, cohort attrition rates vary across grade years. Patterns of missing data were examined for the transition from Grade 10 to Grade 11. The demographic characteristics of youth in both cohorts who were missing data in Grade 11 approximated what is seen in the overall sample. Additionally, independent samples t-tests of scores on the indicators used in this study for youth with missing data in Grade 11 for both cohorts did not support statistically significant differences when compared to youth with data in Grade 11.

Procedure

Student data were collected as part of an ongoing partnership between the researchers and the high school to investigate universal screening practices. The high school was interested in conducting a yearly student wellness survey to help inform prevention and early intervention activities. All students in Grades 9 through 12 were invited to participate in a universal screening survey each year for three consecutive years. Following approval by the university’s Institutional Review Board, district approval, passive parental consent, and student assent, school personnel administered the student surveys to participating students in a group format during one period of their regular school day. To ensure fidelity of survey administration across classrooms each year, administration scripts were provided to all classroom teachers. Data were collected within the first month of the fall semester of each of the 2013–2014 (Year 1), 2014–2015 (Year 2), and 2015–2016 (Year 3) academic years. Year 1 and 3 survey administration was completed electronically using an online survey system [i.e., SurveyMonkey ® (Year 1) and Qualtrics ® (Year 3)] whereas Year 2 administration was completed via paper-and-pencil at the request of the school administration. Students who were absent on their classroom’s initial screening day were provided with up to five additional opportunities to complete the survey within two weeks of initial data collection each year.

Measures

Well-being indicators

The Social Emotional Health Survey-Secondary (SEHS-S) consists of 36 items designed to measure positive psychological dispositions among students in middle and high school (Furlong, You, Renshaw, Smith, & O’Malley, 2014; You et al., 2014). Four second-order positive mental health domains were used as indicators of well-being in this study. These second-order domains are each made up of three first-order positive psychological traits measured by three items, resulting in nine-items measuring each domain (Furlong et al., 2014). The four domains include: belief-in-self (self-efficacy, self-awareness, persistence), belief-in-others (school support, peer support, family coherence), emotional competence (emotional regulation, empathy, self-control), and engaged living (optimism, gratitude, zest; Furlong et al., 2014; You et al., 2014). A five-point response scale is used on the gratitude and zest subscales (1 = not at all, 2 = very little, 3 = somewhat, 4 = quite a lot, 5 = extremely) whereas a four-point response scale is used for the other 10 subscales (1 = not at all true of me, 2 = a little true of me, 3 = pretty much true of me, 4 = very much true of me).

Mean scores for the nine items contributing to the four second-order mental health domains (belief-in-self, belief-in-others, emotional competence, and engaged living) were used as indicators of well-being. In the Year 3 survey, one item (“I understand why I do what I do”) on the self-awareness subscale of the belief-in-self domain was missing for all students due to survey procedure error. Given moderate significant correlations between items on the self-awareness subscale and the belief-in-self domain at each time point (r = .22 to .50), the mean belief-in-self score was computed without this item for Year 3 (Grade 11 for Cohort 1, Grade 12 for Cohort 2); thus, we do not feel it significantly influenced content balance.

In the current study, internal consistency reliability estimates ranged from .80 (Grade 9) to .82 (Grade 12) for belief-in-self, .80 (Grade 9) to .86 (Grade 12) for belief-in-others, .79 (Grade 9) to .85 (Grade 12) for emotional competence, and .87 (Grade 9) to .89 (Grade 11) for engaged living.

Distress indicators

The Strengths and Difficulties Questionnaire (SDQ) is a self-report measure designed to assess behavioral and emotional attributes in youth aged 4 to 17 years (Goodman, 1997, 1999). Although designed to consist of five subscales each with five items (Goodman 1997, 1999), psychometric investigations of the five-factor SDQ with youth in the United States have concluded that the original model has inadequate psychometric characteristics, particularly including low subscale internal consistency reliability (α = .47–.74 across difficulties subscales; Ruchkin, Jones, Vermeiren, & Schwab-Stone, 2008). A three-factor structure including emotional distress/withdrawal, behavioral reactivity/conduct problems, and prosocial behaviors/peer competence (Dickey & Blumberg, 2004; Ruchkin et al., 2008) has been found to have superior reliability estimates with youth in the U.S. than the original five-factor model (α = .68–.77 across difficulties subscales). Consistent with the partner school’s goal of efficiency in screening, select items from the SDQ were used as indicators of externalizing and internalizing distress. Factor loadings, which provide a measure of the strength of the relation between a given item and the underlying latent factor of interest, for all items on the Ruchkin et al. (2008) emotional distress/withdrawal and behavioral reactivity/conduct problems factors were examined prior to selecting items for the abbreviated measure used in this study. The five items with the highest loadings on each of the emotional distress/withdrawal (items 3, 6, 8, 13, and 16; λ = .47 to .60) and the behavioral reactivity/conduct problems factors (items 2, 5, 10, 15, and 22; λ = .56 to .62) were ultimately selected for use in this study, given the strength of their relation with the underlying latent construct of interest. The emotional distress/withdrawal items were used to measure internalizing distress whereas the behavioral reactivity/conduct problem items were used as a measure of externalizing distress. Factor analyses conducted on the administered SDQ items supported a two-factor model comprised of nine items: five measuring internalizing and four measuring externalizing problems (item 5 was removed; contact first author for additional information). Mean scores for the internalizing (i.e., emotional distress) and externalizing (i.e., behavioral reactivity/conduct problems) distress items were computed.

In the current study, reliability estimates for each of the internalizing (α =.71 to .78, ω = .80 to .86 in Grades 9 and 12, respectively) and externalizing (α = .61 in Grade 9 to .72 in Grade 12, ω = .73 in Grade 9 to .83 in Grade 11) composites were similar to what has been found in other research using the SDQ (e.g., Koskelainen, Sourander, & Vauras, 2001; Ruchkin et al., 2008).

Data Analytic Strategy

Recognizing the limitations in current classification methods that use a cut score approach, the current study examined dual-factor mental health across Grades 9, 10, 11, and 12 using an empirical, person-centered classification scheme, LPA. A longitudinal extension of LPA, LTA (Chung, Park & Lanza, 2005; Graham, Collins, Wugalter, Chung, & Hansen, 1991) was subsequently performed to examine the stability of dual-factor mental health across the high school years. LTA is a type of structural equation model that enables the examination and description of change in latent categorical variables (e.g., mental health groups) over time. As such, both measurement (i.e., LPA models at each time point) and structural (i.e., an autoregressive relation between latent class variables at each time point) model components are specified. The primary parameters of interest in LTA are transition probabilities, which are conditional probabilities that indicate the likelihood of an individual being in class k at time point t given that the individual was in latent class l at time point t-1 (Nylund, 2007). For example, transition probabilities provide information regarding the likelihood of an individual who is a member of Class 1 at Time 1 shifting to Class 2 at Time 2, and so on. Transition probabilities were examined to assess the degree of stability of dual-factor mental health over time.

The model building process for LTA includes examination of the cross-sectional measurement models followed by various structural specifications of the longitudinal regression model (e.g., stationary transitions, second-order effects, specification of covariates; Nylund, 2007). LTA models include multiple latent class variables from multiple time points; in the current study, four latent class variables for each grade (i.e., Grades 9, 10, 11, 12) were included. Given the accelerated longitudinal design of this study, data were missing for all participants in Cohort A in Grade 12 and for Cohort B in Grade 9. However, all analyses were conducted using Full Information Maximum Likelihood (FIML; Enders & Bandalos, 2001) estimation using the expectation-maximization (EM) algorithm (Dempster, Laird, & Rubin, 1977), which accounts for indicator-level and longitudinal-level missingness. A cohort covariate was included in the LTAs to account for data that were missing by design (Little, 2011). Using FIML and the EM algorithm, latent class membership was estimated for members of Cohort A in Grade 12 and Cohort B in Grade 9.

When specifying the LTA models, the latent class variable (c) for each cross-sectional measurement model is regressed onto the latent class variable from the previous time point (e.g., Grade 10 latent class “c10” is regressed onto Grade 9 latent class “c9”). In doing so, the latent classes for each measurement time point become conditioned on the previous time point. As with all mixture models, when structural features are jointly estimated, the measurement model of the emerging latent class can change in unintended ways and obscure their interpretation (Asparouhov & Muthén, 2013; Vermunt, 2010). Therefore, a three-step method was used to specify the LTA to prevent changes in emerging dual-factor mental health classes at each grade year (Asparouhov & Muthén, 2013; Nylund-Gibson, Grimm, Quirk, & Furlong, 2014). Doing this ensured that the class-sizes and proportions remained unchanged for each part of the measurement model when the structural parameters were included. Therefore, the steps used to build the LTA model in the current investigation differ slightly from other LTA investigations that did not use the three-step approach (e.g., Nylund, 2007). The steps used included (a) explore measurement model for each time point, (b) explore measurement invariance, (c) explore structural LTA model specifications, and (d) specify the final LTA model. A description of the model building process is embedded with the results presented below. All models were estimated using Mplus version 7.4 (Muthén & Muthén, 1998–2015), using a large number of random starts (ranging from “500 100” up to “2,000 500” for models with more classes) to ensure the solution was a global, rather than local, one.

Determining model fit

A combination of indicators, including statistical indicators and substantive theory, were used in determining fit of the LPA models (Masyn, 2013; Muthén, 2003). Statistical indicators include evaluations of relative fit which assess fit of the current model by comparing it to an alternative model that differs in the number of latent classes by one. Indices considered are Bayesian Information Criteria (BIC; Schwartz, 1978), adjusted BIC (ABIC), Bayes Factor (BF), correct model probability (cmP), Bootstrap Likelihood ratio Test (BLRT; McLachlan & Peel, 2000), and Vuong Lo Mendel Rubin LRT (VLMR-LRT; Vuong, 1989). Lower BIC and ABIC values indicate superior fit, though often the leveling off, or diminishing gain in BIC by adding one class, is used as a criterion when selecting class (Nylund, Asparouhov, & Muthén, 2007; Masyn, 2013). Nonsignificant BLRT and VLMR-LRT values offer support for the k-1 class solution, larger cmP values indicate a greater probability of the model being correct, and BF values greater than 10 offer strong evidence for a model (Masyn, 2013). Simulation studies have found that the most reliable estimates of model fit are provided by the BIC and BLRT indices (Nylund, Asparouhov, et al., 2007), thus these fit indices are given the most weight. When comparing fit of LTA models with various structural specifications, a log likelihood ratio chi-square test (LRT) was used to assess if significant differences exist in fit between the two models (Masyn, 2013; Nylund, 2007). Since none of these fit indices have been shown to work equally under all modeling conditions (Nylund, Asparouhov et al., 2007), and in practice the fit indices are not all congruent, it is also recommended that both statistical and substantive justification be considered when deciding on the number of classes (Muthén, 2003; Masyn, 2013).

Results

The results are presented methodically to represent the four primary LTA modeling steps used in this study. An explanation of the analytic process involved at each step is included prior to discussion of the associated results.

Step 1: Exploration of Measurement Model for Each Grade

LPA models for dual-factor mental health were independently specified for Grades 9, 10, 11, and 12 using four positive mental health domains (belief-in-self [BIS], belief-in-others [BIO], engaged living [EL], emotional competence [EC]) and two psychological distress domains (internalizing risk [INT] and externalizing risk [EXT]) as indicators. Both class-invariant (i.e., item variances are freely estimated but constrained to be equal across classes), diagonal (i.e., no within class indicator covariances), and class-varying (i.e., item variance are freely estimated for each class) diagonal LPA models were examined (Kam, Morin, Meyer, & Topolntsky, 2016; Masyn, 2013; Morin et al., 2011). Missing item-level responses on each indicator were examined prior to computing composites. Fewer than 1.3% of the sample evidenced missing data on any given item administered. Mean scores were computed for individuals who answered at least 75% of items on a given composite, resulting in less than 1% of the sample having indicator-level missingness on a given indicator across grade years. A model for each of Grades 9, 10, 11, and 12 was selected as the optimal model according to the statistical criterion described above and substantive dual-factor theory. The unconditional latent profile models serve as the measurement portion of the LTA model.

Descriptive statistics

Prior to specifying cross-sectional LPAs for each time point, descriptive information was examined for the overall sample and for each of Cohort A and Cohort B. Average responses on the mental health indicators for the whole sample as well as for each cohort are available in Table 4. Independent samples t-tests of the six indicators were performed to investigate whether differences existed among the two cohorts. Results indicated differences among the two cohorts primarily in Grade 10, with Cohort A having significantly higher self-reported levels of belief-in-self (d = 0.34), belief-in-others (d = 0.27), and emotional competence (d = 0.37) and lower levels of internalizing (d = −0.48) and externalizing distress (d = −0.43; p < .01) than Cohort B. In Grade 11, Cohort A had significantly lower self-reported externalizing distress (d = −0.19) than did Cohort B (p < .01). Differences in mean indicator scores between the two cohorts approximated small to medium effects (Cohen, 1988). However, average scores on the well-being indicators were in the average range for both cohorts, and average scores on the distress indicators were indicative of low levels of distress. These discrepancies in indicator scores for Grade 10, in particular, may be due to differences in survey administration method (paper and pencil for Cohort A versus online for Cohort B), although equivalence is generally observed for paper-pencil and online administration of measures of mental health (Eaton et al., 2010; Van de Looij-Jansen & de Wilde, 2008) or experience taking the survey (second year for Cohort A versus first year for Cohort B). Although the cause of these differences is unknown, a cohort covariate was included in the LTAs both to account for cohort level missing data as well as to control for cohort effects.

Table 4.

Means and Standard Deviations of Mental Health Indicators for the Total Sample, Cohort A, and Cohort B

	BIS	BIO	EC	EL	INT	EXT
Grade 9 (n = 467)
Total sample	2.88(.50)	3.11(.57)	2.96(.49)	3.28(.70)	1.67(.47)	1.76(.44)
Cohort A	2.88(.50)	3.11(.57)	2.96(.49)	3.28(.70)	1.67(.47)	1.76(.44)
Cohort B	—	—	—	—	—	—
Grade 10 (n = 861)
Total sample	2.96(.50)	3.20(.57)	3.10(.51)	3.29(.69)	1.63(.49)	1.62(.47)
Cohort A	3.04(.47)	3.32(.51)	3.19(.46)	3.34(.66)	1.52(.45)	1.52(.46)
Cohort B	2.87(.53)	3.07(.61)	3.00(.55)	3.24(.73)	1.75(.51)	1.72(.46)
Grade 11 (n = 758)
Total sample	3.03(.51)	3.28(.55)	3.22(.48)	3.32(.69)	1.56(.48)	1.53(.47)
Cohort A	3.03(.54)	3.27(.58)	3.22(.50)	3.34(.71)	1.55(.48)	1.48(.48)
Cohort B	3.02(.48)	3.28(.52)	3.23(.46)	3.30(.67)	1.57(.48)	1.57(.47)
Grade 12 (n = 306)
Total sample	3.10(.53)	3.31(.56)	3.26(.51)	3.39(.72)	1.60(.51)	1.48(.47)
Cohort A	—	—	—	—	—	—
Cohort B	3.10(.53)	3.31(.56)	3.26(.51)	3.39(.72)	1.60(.51)	1.48(.47)

Note. BIS = belief in self, BIO = belief in others, EC = emotional competence, EL = engaged living, INT = internalizing distress, EXT = externalizing distress. The mean-value range for BIS, BIO, and EC was 1 to 4; for EL was 1 to 4.67; and for INT and EXT was 1 to 3.

Cross-sectional LPA measurement models

Cross-sectional LPAs were run for each of Grades 9, 10, 11, and 12. Class enumeration began with a one-class solution, followed by exploration of additional models with more latent classes. Table 5 presents the information used to evaluate the fit of each LPA model of both the class-invariant diagonal and class-varying diagonal solutions for each grade level. Fit indices produced for the Grade 9 class-invariant diagonal models support a four-class solution as the optimal LPA model (BIC = 3754.55, p_LMRT = .40 comparing the five and four-class solutions, implying that the addition of a fifth class does not significantly improve model fit). Although the BIC does not reach an absolute minimum at four classes, a relative leveling off occurs after the four-class model. A four-class solution was also supported in the Grade 9 class-varying diagonal solution (BIC = 3750.57, cmP = .69, p_LMRT = .24 comparing five- and four-class solutions); however, 17% of the log likelihood starting values did not converge, indicating instability in the model solution. This pattern held true for each of the Grade 10, 11, and 12 class-varying diagonal solutions, with between 13% and 99% of log likelihood values not converging for three- to five- class class-varying diagonal models. Therefore, the four-class, class-invariant diagonal solution was selected as the optimal LPA model for Grade 9 and only results of class-invariant diagonal solutions are discussed for the Grade 10, 11, and 12 models.

Table 5.

Information Used to Evaluate Tested LPA Dual-Factor Mental Health Models

Model	Number of classes	Log likelihood	BIC	p-value of BLRT	p-value of LMRT	Entropy	BF	cmP	Class Prevalence
Grade 9 - Model 1 (n = 467)	1	−2154.43	4382.61	—	—	1.00	<.001	<.001	1.00
	2	−1919.37	3955.53	<.001	<.001	0.72	<.001	<.001	.50, .50
	3	−1831.09	3821.98	<.001	0.582	0.79	<.001	<.001	.10, .32, .58
	4	−1775.86	3754.55	<.001	0.018	0.77	<.001	<.001	.10, .20, .24, .47
	5	−1743.02	3731.90	<.001	0.401	0.80	0.002	0.002	.01, .12, .18, .22, .47
	6	−1715.46	3719.80	<.001	0.242	0.77	<.001	0.998	.01, .07, .14, .19, .20, .40
Grade 9 - Model 2 (n = 467)	1	−2154.43	4382.61	—	—	1.00	<.001	<.001	1.00
	2	−1879.02	3911.70	<.001	<.001	0.77	<.001	<.001	.41, .59
	3*	−1769.82	3773.21	<.001	0.021	0.77	<.001	<.001	.19, .30, .51
	4*	−1718.55	3750.57	NC	0.039	0.80	2.180	0.69	.14, .19, .21, .46
	5*	−1679.38	3752.13	NC	0.235	0.81	>10	0.31	.05, .12, .19, .22, .42
	6*	−1649.52	3772.31	NC	0.124	0.82	<.001	<.001	.03, .05, .13, .16, .23, .39
Grade 10 - Model 1 (n = 861)	1	−4099.00	8279.09	—	—	1.00	<.001	<.001	1.00
	2	−3555.22	7238.85	<.001	<.001	0.81	<.001	<.001	.31, .69
	3	−3356.31	6888.33	<.001	<.001	0.79	<.001	<.001	.14, .32, .53
	4	−3296.22	6815.45	<.001	0.438	0.78	<.001	<.001	.07, .19, .25, .49
	5	−3248.91	6768.15	<.001	0.163	0.79	<.001	<.001	.06, .07, .12, .28, .46
	6	−3210.04	6737.71	<.001	0.221	0.78	<.001	1.00	.04, .05, .12, .16, .24, .38
Grade 10 - Model 2 (N = 861)	1	−4099.00	8279.09	—	—	1.00	<.001	<.001	1.00
	2*	−3498.59	7166.14	<.001	0.002	0.75	<.001	<.001	.45, .55
	3*	−3238.72	6734.25	NC	0.006	0.81	<.001	<.001	.22, .23, .55
	4*	−3142.76	6630.17	NC	0.169	0.78	<.001	<.001	.13, .17, .25, .44
	5*	−3076.64	6585.80	NC	0.102	0.75	<.001	<.001	.10, .11, .21, .27, .31
	6*	−3024.31	6568.99	NC	0.142	0.77	<.001	1.00	.03, .09, .13, .19, .27, .29
Grade 11 - Model 1 (n = 758)	1	−3510.00	7099.56	—	—	1.00	<.001	<.001	1.00
	2	−3023.55	6173.09	<.001	<.001	0.79	<.001	<.001	.37, .63
	3	−2860.97	5894.33	<.001	0.040	0.80	<.001	<.001	.13, .33, .54
	4	−2791.14	5801.09	<.001	0.010	0.77	<.001	<.001	.06, .21, .29, .44
	5	−2720.24	5705.70	<.001	0.003	0.80	0.005	0.01	.05, .12, .17, 24, .42
	6	−2691.74	5695.13	<.001	0.192	0.82	<.001	0.99	.01, .06, .12, .17, .24, .41
Grade 11 - Model 2 (n = 758)	1	−3510.00	7099.56	—	—	1	<.001	<.001	1.00
	2*	−2950.43	6066.62	NC	<.001	0.77	<.001	<.001	.48, .52
	3*	−2712.38	5676.72	<.001	0.137	0.84	<.001	<.001	.11, .32, .57
	4*	−2611.28	5560.73	NC	0.310	0.79	<.001	1.00	.14, .20, .21, .45
	5	No Convergence
	6	No Convergence
Grade 12 - Model 1 (n = 306)	1	−1482.459	3033.601	—	—	1.00	<.001	<.001	1.00
	2	−1299.777	2708.302	<.001	0.017	0.76	<.001	<.001	.44, .56
	3	−1210.031	2568.875	<.001	0.001	0.84	<.001	<.001	.08, .38, .53
	4	−1165.242	2519.363	<.001	0.001	0.84	0.218	0.17	.08, .21, .34, .37
	5	−1143.689	2516.321	<.001	0.421	0.82	9.840	0.76	.08, .13, .19, .26, .34
	6	−1125.943	2520.894	<.001	0.115	0.84	<.001	0.08	.06, .07, .13, .14, .27, .33
Grade 12 - Model 2 (n = 306)	1	−1482.459	3033.601	—	—	1.00	<.001	<.001	1.00
	2*	−1262.427	2667.944	NC	<.001	0.95	<.001	<.001	.19, .81
	3*	−1171.73	2560.956	NC	0.063	0.84	<.001	1.00	.18, .24, .59
	4	No Convergence
	5	No Convergence
	6	No Convergence

Note. Bolded values indicate preferred model for a given fit index. Shaded rows indicate model selected for each year. NC = no convergence.

^*log likelihood starting and best-solution values did not converge, indicating model instability

Of the Grade 10 solutions, support was offered for each of a three- (BIC = 6888.33, p of LMRT = <.001) and four-class solution (BIC = 6815.45). Although the BIC began approaching a relative minimum at the three-class solution (i.e., leveling off), the value of the BIC was lower in the four-class solution and exhibited minimal decreases after the four-class solution. Given recommendations for consistency in LTA measurement models (e.g., Lanza, Flaherty, & Collins, 2003) and being mindful of the goals of the larger study, we further examined the four-class solution, noting that the additional fourth class meaningfully differed from the other three classes and that the four emerging classes were consistent with the four-class solution from the Grade 9 analyses. Therefore, after consideration of model fit information, substantive theory, and recommendations for specification of LTA models, the four-class class-invariant diagonal solution was selected as the optimal model for Grade 10 (Muthén, 2003).

LPAs in Grade 11 resulted in BIC values supporting three- to five- class solutions. The p_LMRT supported a five-class solution. Examination of the mean plots for each solution indicated the emerging fourth class to offer substantive meaning over a three-class solution, with the four emerging classes in the four-class solution being consistent with the four emerging classes in the Grade 9 and Grade 10 solutions. In the five-class solution, the fifth emerging class appeared to represent differentiation of a class in the four-class solution fitting a pattern of average well-being and average distress that comprised approximately 29% of the sample, which offered little additional substantive meaning. In addition, given the complexity of the modeling specifications for LTA, preference exists for parsimonious cross-sectional solutions that offer longitudinal consistency, when appropriate, across data points (e.g., Lanza et al., 2003). As the four-class solution produced in the Grade 11 solution paralleled the four-class solutions in the Grade 9 and 10 analyses, a four-class solution was selected as the optimal model for Grade 11 (Muthén, 2003).

In the Grade 12 solutions, although the BIC reached an absolute minimum in the five-class solution, the differences in the BIC with the four- and six- class solutions were negligible. The BF and cmP supported a five-class solution; however, these indices are computed based upon the BIC value for each class and thus reflect the absolute minimum of the BIC in the five-class solution. The p_LMRT, which is computed independently from the BIC, supported a four-class solution. Further, examination of the estimated means plot indicated the classes emerging in the four-class solution to be substantively similar to the four classes in the Grade 9, 10, and 11 solutions. Therefore, the four-class solution was selected as the optimal model for each of Grades 9, 10, 11, and 12.

Figure 1 presents the estimated mean plots for the four-class LPA solutions. Although varying slightly in indicator means over time, the four classes maintained a substantively similar pattern across the four grade years. Based on the pattern of mean scores across the well-being and distress domains, the following labels are offered for the four emerging classes across each grade: complete mental health (high well-being and low distress), moderately mentally healthy (high-average well-being and low distress), symptomatic but content (average to high-average well-being and average to above-average distress), and troubled (average to low-average well-being and above-average distress).

Figure 1.

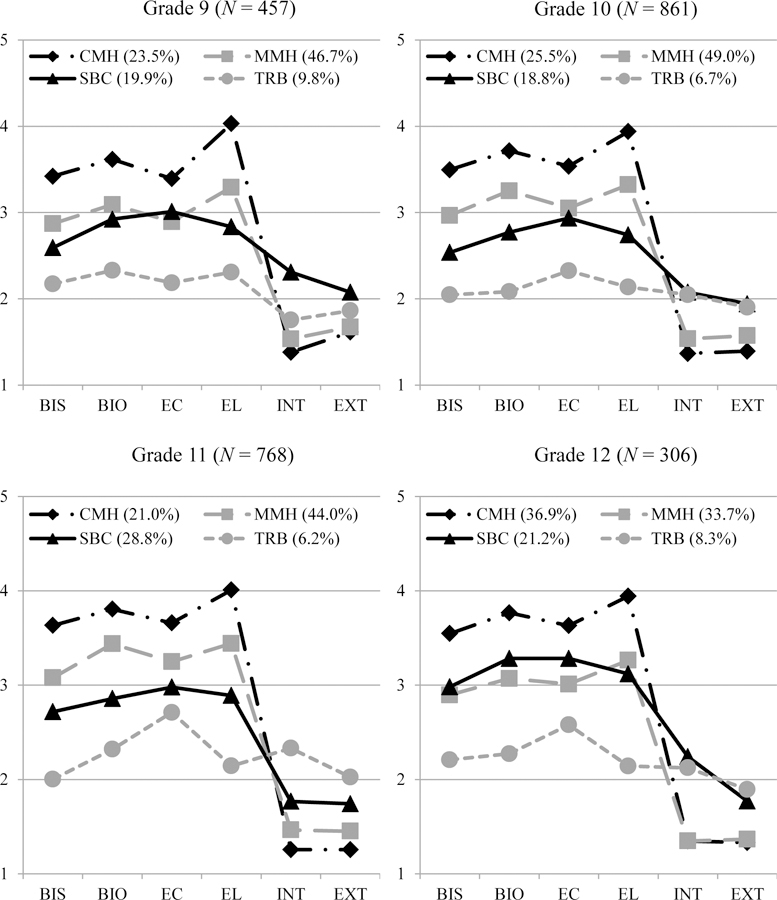
Dual-factor mental health profile plots displaying estimated means for the four-class solution for each of Grade 9 through Grade 12. Class size information is presented in the legend. Note. BIS = belief in self, BIO = belief in others, EC = emotional competence, EL = engaged living, INT = internalizing distress, EXT = externalizing distress. CMH = complete mental health class, MMH = moderately mentally healthy class, SBC = symptomatic but content class, TRB = troubled class. The mean-value range for BIS, BIO, and EC was 1 to 4; for EL was 1 to 4.67; and for INT and EXT was 1 to 3

Step 2: Examining Measurement Invariance

Given that a four-class solution was selected as the optimal model for each grade, measurement invariance constraints were explored. Using the three-step approach, measurement invariance was examined prior to including the latent regression paths of a LTA model (i.e., the four measurement models were specified simultaneously, but autoregressive relations between each latent class “c” variables were not included). Measurement invariance was examined by specifying (a) a model assuming full measurement non-invariance, such that all parameters were freely estimated and allowed to vary across each grade; and (b) a model assuming full measurement invariance, such that all measurement parameters are constrained to be equal across time (Lanza et al., 2003). The LRT was used to assess for significant differences in model fit when the invariance constraints were specified.

The model assuming full non-invariance exhibited improved fit over the model assuming full invariance, χ²_diff(72) = 310.15, p < .001. This result was expected given the large number of parameters that were constrained to be equal in the full invariance solution, thus increasing the degree of model misfit. However, assuming measurement invariance is recommended when the same number and type of classes emerges across measurement time points (Lanza et al., 2003). Assuming measurement invariance is also recommended to allow for clearer interpretation of the transition probabilities of interest (Nylund, 2007). That is, when measurement parameters are held equal at each time point, changes in mental health group membership are directly interpretable as related to developmental changes occurring over time rather than due to relations between the mental health indicators with each class (Lanza et al., 2003). Given that the same number of mental health profiles emerges in each grade year, and, as can be seen in Figure 1, the profile patterns of the mental health classes are similar across grade year, measurement invariance can be reasonably assumed. Therefore, the unconditional full measurement invariance model was selected for the following analyses.

Step 3: Exploration of Structural Model Specifications

Next, the LTA model was specified to include full measurement invariance to examine stability and transitions among mental health classes from Grade 9 to Grade 10, Grade 10 to Grade 11, and Grade 11 to Grade 12. Cohort was controlled for in the LTA model building process by specifying a cohort covariate regressed onto each latent class variable, thus transition probabilities are estimated controlling for any cohort effects.

Examination of transition probabilities

First, we tested the plausibility of stationary transition probabilities across the three transition periods (i.e., Grade 9 to Grade 10, Grade 10 to Grade 11, and Grade 11 to 12), which would indicate that the probability of changing mental health classes is equal for each transition point. We fit two models, one where the transition probabilities were constrained to be equal and compared this to one where they were freely estimated. It is important to note that when covariates are considered, the stationarity assumption is not appropriate (Nylund, 2007). However, given interests in examining whether changes in dual-factor mental health vary as a function of developmental time, we examined the stationarity assumption without the cohort covariate effect. Results of the LRT comparing the two models indicated a significant worsening in fit when holding the transition probabilities constant, χ²_diff (24) = 108.04, p < .001. Therefore, students’ probability of transitioning among the dual-factor mental health classes varied throughout high school and stationary transitions were not assumed in the models with additional structural specifications described below.

Second-order effects

Given the interest in examining stability of dual-factor mental health beyond a one-year period (research question 1b), second-order effects were also examined. A second-order effect implies a lasting effect of mental health status, for example, whether Grade 9 mental health predicts Grade 11 mental health above and beyond the indirect relation of Grade 11 mental health with Grade 9 mental health via Grade 10 mental health class membership. To test for second-order effects, two LTA models were run: the first specifying only first-order comparisons (i.e., Grade 9 to Grade 10, Grade 10 to Grade 11, Grade 11 to Grade 12) and the second including the second-order effects of mental health in Grade 11 with Grade 9 and Grade 12 with Grade 10. Each controlled for the cohort covariate. Results indicated that the second-order transition model significantly improved fit, χ²_diff (18) = 30.24, p = .022, which suggested that there was a lasting effect of students dual-factor mental health in Grade 9 and Grade 10 that affected their mental health in Grade 11 and 12, respectively.

Step 4: Specification of the Final LTA Model

Given the results of the LTA model building process described above, the final LTA model was specified to control for a cohort covariate effect and to include full measurement invariance, nonstationary transitions, and second-order effects. Table 6 presents the class proportions for each grade year after specification of the final conditional LTA model. The proportion of students classified into the complete mental health class grew from Grade 9 (19%) to Grade 12 (36%) whereas the proportion of students in the moderately mentally healthy class decreased from Grade 9 (50%) to Grade 12 (33%). The size of the symptomatic but content class was relatively consistent, with the smallest percentage of students classified into this class in Grade 10 (19%). Finally, the size of the troubled class grew from Grade 9 (3%) to Grade 10 (7%), but then remained consistent through Grade 12 (7%).

Table 6.

Percent of Students in Each of the Dual-Factor Mental Health Classes in Grades 9 through 12

Class	Grade 9	Grade 10	Grade 11	Grade 12
Complete Mental Health	19.14	25.74	20.52	35.75
Moderately Mentally Healthy	49.98	48.52	43.79	33.44
Symptomatic but Content	28.06	18.70	29.03	23.90
Troubled	2.80	7.04	6.67	6.91

Table 7 displays the transition probabilities for the first-order effects of the final LTA model. Overall, one-year stability in dual-factor mental health membership was the strongest from Grade 9 to Grade 10. For example, of students who were most likely to be classified into the complete mental health class in Grade 9, 79% remained in the complete mental health class in Grade 10. Similarly, 70% of students in the moderately mentally healthy class in Grade 9 remained in this class in Grade 10. The lowest levels of stability were evident for the symptomatic but content class, with 46% of students in this class in Grade 9 remaining in the class in Grade 10. The complete mental health class exhibited the highest levels of stability across two transition points (i.e., Grade 9 to 10 and Grade 11 to 12), whereas the troubled class exhibited the least stability across two transition points (i.e., Grade 10 to 11 and Grade 11 to 12). Overall, the Grade 11 to 12 comparison demonstrated the lowest levels of stability across each of the moderately mentally healthy, symptomatic but content, and troubled mental health groups, with less than 35% of participants classified in each class in Grade 11 remaining within the same class in Grade 12. Looking across the three one-year transition points (i.e., Grades 9 to 10, 10 to 11, and 11 to 12), the complete mental health class had the greatest average stability (77%), followed by the moderately mentally healthy class (56%), the symptomatic but content class (47%), and the troubled class (42%).

Table 7.

Conditioned Latent Transition Probability Estimates of First-Order Effects

Class	Complete Mental Health	Moderately Mentally Healthy	Symptomatic but Content	Troubled
Grade 9		Grade 10
Complete Mental Health	0.79	0.19	0.02	0.00
Moderately Mentally Healthy	0.20	0.70	0.10	0.00
Symptomatic but Content	0.02	0.33	0.46	0.19
Troubled	0.00	0.22	0.19	0.60
Grade 10		Grade 11
Complete Mental Health	0.61	0.39	0.00	0.00
Moderately Mentally Healthy	0.08	0.63	0.26	0.04
Symptomatic but Content	0.04	0.15	0.69	0.12
Troubled	0.04	0.06	0.51	0.40
Grade 11		Grade 12
Complete Mental Health	0.93	0.00	0.07	0.01
Moderately Mentally Healthy	0.38	0.34	0.24	0.12
Symptomatic but Content	0.00	0.62	0.26	0.12
Troubled	0.03	0.08	0.64	0.25

Note. Bolded values indicate the proportion of students who remained in the same mental health class across comparison points.

Of those students who exhibited instability across the one-year comparisons (see Table 7), students initially fitting a complete mental health class were, on average, most likely to transition to the moderately mentally healthy class followed by the symptomatic but content class. Students fitting a moderately mentally healthy class were, on average, similarly likely to transition into the complete mental health class (22%) or the symptomatic but content class (20%). Of those in a symptomatic but content class, students were, on average, more likely to transition into a moderately mentally healthy class (37%), followed by a troubled class (14%). Of those students who transitioned out of a troubled class, most transitioned into a symptomatic but content class followed by a moderately mentally healthy class. It was very unlikely for students to transition from the complete mental health class to the troubled class over a one-year period. Thus, students were more likely to transition into a healthier mental health class (i.e., characteristic of average- to above-average strengths and low to average distress) than into a less healthy class (i.e., characteristic of low-average strengths and average to above-average distress).

The second-order effects comparing two-year transitions from Grade 9 to Grade 11 and from Grade 10 to Grade 12 were indicative of similar patterns. Table 8 presents the transition probabilities for the second-order effects, while controlling for cohort-effects. Similar to the one-year comparisons, when comparing dual-factor mental health stability over two years, the complete mental health group exhibited the most stability (69%). The symptomatic but content class exhibited the second greatest stability (56%), followed by the moderately mentally healthy (52%) and troubled (36%) classes. Stability estimates for each class were similar across both two-year comparisons, with the troubled class showing stronger two-year stability from Grade 10 to 12 than from Grade 9 to 11.

Table 8.

Conditioned Latent Transition Probability Estimates of Second-Order Effects

Class	Complete Mental Health	Moderately Mentally Healthy	Symptomatic but Content	Troubled
Grade 9		Grade 11
Complete Mental Health	0.65	0.33	0.02	0.00
Moderately Mentally Healthy	0.13	0.58	0.27	0.02
Symptomatic but Content	0.05	0.36	0.59	0.20
Troubled	0.17	0.06	0.50	0.27
Grade 10		Grade 12
Complete Mental Health	0.73	0.03	0.23	0.01
Moderately Mentally Healthy	0.32	0.46	0.17	0.04
Symptomatic but Content	0.06	0.41	0.53	0.07
Troubled	0.04	0.44	0.06	0.46

Note. Bolded values indicate the proportion of students who remained in the same mental health class across comparison points.

With four classes across four time points, 256 (4⁴) transition patterns were possible based upon the estimated model. Of these possible patterns, 116 were observed. Twenty-five patterns were followed by 10 or more participants and comprised 78.2% of the sample. The patterns comprising the largest proportion of the sample were individuals who remained in the complete mental health (10.4%) and moderately mentally healthy (9.5%) classes across each of Grades 9, 10, 11, and 12. Approximately 3.7% of participants remained in the symptomatic but content class across each grade year, whereas only 0.4% of participants remained in the troubled class over the four years. Therefore, most students changed mental health class at least once over the four years. However, 42.3% of students were in either the complete mental health or moderately mentally healthy classes over each of the four years whereas 10.6% were in either the symptomatic but content or troubled classes over each of the four years. Figure 2 summarizes the four-year stability patterns for each of the complete mental health, moderately mentally healthy, symptomatic but content, and troubled classes based on the final estimated LTA model.

Figure 2.

Four-year stability patterns for each of the (A) complete mental health, (B) moderately mentally healthy, (C) symptomatic but content, and (D) troubled profiles, respectively, based on the final estimated LTA model from Grade 9 to Grade 12. Numbers in circles refer to percent of students in each mental health profile. Numbers above arrows indicate the percentage of students who transition from one mental health profile to another.

Discussion

Although mental health models describing the intersection of well-being and distress are increasingly recognized and empirically supported (e.g., Greenspoon & Saklofske, 2001; Suldo & Shaffer, 2008), a majority of the research examining dual-factor models has been cross-sectional. No research to date has examined the stability of dual-factor mental health over a period longer than one year within an adolescent population. Therefore, the current study contributed to the literature by examining the stability of adolescents’ dual-factor mental health across the high school years. Specifically, the current study used LTA to model transition patterns among emerging latent mental health classes across Grades 9 through 12, as well as probabilities of transitioning from, or remaining within, a class. Prior to specifying the longitudinal LTA models, cross-sectional LPA measurement models were tested for each of Grades 9 through 12. Four mental health classes emerged across each grade year: complete mental health, moderately mentally healthy, symptomatic but content, and troubled. Contrary to previous dual-factor research, a vulnerable or languishing group (i.e., low well-being and low distress) did not emerge when groups were formed via LPA rather than via rationally determined cut points.

Stability of Dual-Factor Mental Health

An LTA model building process was used to answer the first research question regarding (1a) how stable dual-factor mental health is from Grade 9 through 12 and (1b) if adolescents’ early mental health status is predictive of later mental health status. The final selected LTA model included first-order transitions (Grades 9 to 10, 10 to 11, and 11 to 12) and second-order transitions (Grades 9 to 11 and 10 to 12). The LTA model including second-order effects fit significantly better than a model that included only first-order effects, supporting a lasting impact of one’s current dual-factor mental health status. Results also indicated that current dual-factor mental health predicted mental health status two years later above and beyond an indirect relation between mental health status in the intermediate year.

The second research question, regarding which mental health classes exhibit the most stability over time, was answered by reviewing the resulting LTA transition patterns. Results across Grades 9 through 12 indicated that between 0.4% (troubled) and 10% (complete mental health) of students were classified into the same mental health class across the four-year period, with the strongest four-year stability observed for students in the complete mental health (10%) and moderately mentally healthy (9%) classes. Similar to Compton’s (2016) results, students experiencing persistent complete mental health and moderate mental health across the four years comprised the largest observed transition patterns. Youth fitting a persistently troubled pattern comprised the smallest stability pattern. In sum, results suggested that adolescence is characterized by fluid complete mental health status, when examined across a four-year period.

In previous research that examined stability of dual-factor mental health across shorter time periods (i.e., two time points within one year), most students were found to remain in the same mental health group over time (61% to 71%; Compton, 2016; Kelly et al., 2012; McMahan, 2012), and the complete mental health group was found to demonstrate the greatest stability (86%, Compton, 2016; 85%, Kelly et al., 2012; 80%, McMahan, 2012). Congruent with previous research, the complete mental health class exhibited the greatest stability, on average, across comparison points in the current study (73%). Greater stability was observed across one-year comparisons (77%) than across the two-year comparisons (69%). However, contrary to previous research, in this study the troubled class demonstrated the least stability (39%). Of students initially classified into a troubled class, 42% remained in this class one year later, and 36% remained two years later. The troubled group similarly had the poorest four-year stability, with less than 1% of students classified in the troubled class in Grade 9 remaining in that class in Grades 10, 11 and 12. Although the rank ordering of average stability estimates among groups differs from previous research, the proportion of youth who remained in the troubled group across one-year periods in the current study (25% from Grade 11 to 12, 40% from Grade 10 to 11, and 60% from Grade 9 to 10) is consistent with previous research examining stability over one year or less with middle school students (47%; Kelly et al., 2012), high school students (36%; McMahan, 2012), and early elementary school students (61%; Compton, 2016).

In addition, whereas McMahan (2012) found a symptomatic but content group to have the least stability for high school students over one year (17%), the symptomatic but content class in the current study exhibited moderate stability (52%) over one- (47%) and two-year (56%) comparisons. These results are consistent with estimates produced for early elementary (Compton, 2016) and middle-school (Kelly et al., 2012) students. The disparities in stability estimates among adolescents in the troubled and symptomatic but content groups in this study may reflect differences in measurement tools or classification method. Overall, in the current study, greater stability was observed for adolescents in mental health classes characteristic of average to above-average well-being (i.e., complete mental health [73%], moderately mentally healthy [54%], and symptomatic but content [52%]) than the troubled class (39%) who reported the lowest average levels of well-being.

The third research question was answered via the testing of stationary transition probabilities during the LTA model building process. Results did not support a stationary assumption, indicating that rate of change in dual-factor mental health varies across transition points. An examination of transition probabilities provided support for patterns observed in previous longitudinal research, such that youth were more likely to show an improvement in their levels of well-being and distress over time. Expanding upon previous research, in this investigation fewer than 5% of youth remained in the troubled and in the symptomatic but content classes across all grade years, suggesting that adolescents who report experiencing distress with limited well-being at the beginning of high school are unlikely to remain in this mental health state for the entirety of their high school experience. However, of the 25% to 35% of students experiencing distress in one grade, less than 8% were likely to transition into a complete mental health class over a one-year period, with fewer than 22% transitioning to a complete mental health class after two years. Overall, these results highlight the chronicity of distress in conjunction with average to low-average strengths (Compton, 2016; McMahan, 2012) as well as the need for intervention particularly with these youths. In contrast, students who were in the complete mental health class were most likely to remain in this class or to enter the moderately mentally healthy class.

Additional examination of patterns in stability among mental health classes, however, confirmed variability across transition points particularly across the one-year comparisons. For example, stability estimates over one year ranged from 61% (Grade 10 to 11) to 93% (Grade 11 to 12) for complete mental health, 34% (Grade 11 to 12) to 70% (Grade 9 to 10) for moderately mentally healthy, 26% (Grade 11 to 12) to 69% (Grade 10 to 11) for symptomatic but content, and 25% (Grade 11 to 12) to 60% (Grade 9 to 10) for troubled. Whereas stability from Grade 11 to 12 was lowest for the moderately mentally healthy, symptomatic but content, and troubled classes, stability for complete mental health was strongest across these two grades. Stability estimates similarly demonstrated variability across two-year comparisons. This finding is noteworthy as it highlights important limitations to previous longitudinal work in which dual-factor mental health group membership was examined only across two time points or within up to a one-year period. Although contributing greatly to the growing understanding of dual-factor mental health, caution is recommended in generalizing from the stability estimates provided in previous short-term longitudinal work examining only two time periods. Given the variability observed between comparison points in the current study, the stability estimates provided in previous research may also reflect age-specific information that may differ for youth at other age or grade levels. Additional longitudinal research is needed to replicate the results of the current and previous research, and to expand both the time frame for measurement and age levels of participants. Moreover, research examining individual or contextual characteristics associated with transition patterns (i.e., the influence of covariates on transition probabilities) can provide additional information important in understanding patterns in instability, which may then further inform intervention recommendations.

Implications for School-Based Mental Health Practice

The results of the current study offer continued support for the expanded, dual-factor conceptualization of mental health. At each grade level, variation was observed across levels of well-being and distress, resulting in four emerging LPA identified mental health groups that differed along both well-being and distress dimensions. The observed patterns of the four emerging groups (Figure 1), particularly the presence of a symptomatic but content class demonstrating average levels of both well-being and distress, indicate that the traditional, bipolar view of mental health is insufficient for describing youths’ mental health experiences. Findings from the present study also indicate the need to regularly monitor students’ mental health, with respect to both well-being and distress to accurately inform promotion, prevention, and intervention efforts. Although, on average, 73% of students within a complete mental health class maintained their mental health status one year later, up to 39% (Grade 10 to 11) of students declined from their complete mental health status one year later, with up to 35% (Grade 9 to 11) moving from a complete mental health class across two-year comparisons. Universal screening for complete mental health that targets both distress and well-being has been recommended to monitor students’ mental health needs to inform prevention and early intervention efforts (Moore et al., 2015). This focus on complete mental health moves the field beyond the historical, symptomatology perspective focused solely on indicators of distress. Future validation work on measures to be used in complete mental health screening, such as the SEHS-S used in this study, is needed for schools to easily access tools which can be used to efficiently screen for complete mental health.

Additionally, the longitudinal results of the current study can inform recommendations regarding frequency of universal screening. Previous research has yielded inconsistent recommendations regarding the frequency with which to monitor mental health via universal screening. Existing recommendations range from screening when students enter a new school (Stoep et al., 2005), to multiple times per year (Ennis, Lane, & Oakes, 2012; Severson, Walker, Hope-Doolittle, Kratochwill, & Gresham, 2007), to once per year (Dowdy, Furlong, Eklund, Saeki, & Ritchey, 2010; Dowdy et al., 2014), to only during key developmental time periods for a given problem (Stoep et al., 2005). Regarding screening at entry into a new school (i.e., in Grade 9), this study’s results indicated that the greatest average stability among the dual-factor mental health classes was from Grade 9 to 10; however, much movement occurred among the mental health classes following the Grade 9 screening assessment. On average, students in the healthiest group (i.e., complete mental health) exhibited the greatest stability across comparisons, suggesting that approximately 70% of adolescents maintain positive mental health over a two-year period. However, few students (10%) remained in the complete mental health class across each of four years, suggesting that screening for complete mental health only once during the high school period would be insufficient.

Given that less than one-quarter of students remained in the same mental health class across all time points, screening only once at entry into school limits a school’s ability to inform intervention for students beyond the current academic year. At the very least, the results of the current study indicate the need for screening at the start of high school and in Grade 12, where stability in dual-factor mental health from the previous year was the lowest across moderately mentally healthy, symptomatic but content, and troubled groups. However, observed variability across stability estimates and instability patterns across the one- and two-year transition periods indicate that in order to most accurately identify and refer students for intervention, screening may need to occur at least once per year.

As the screening data used for this study were collected at one-year intervals, our results are limited in their ability to determine if there is an added benefit of screening multiple times within an academic year versus screening only once per academic year. However, the moderate stability observed across one-year periods indicates that screening multiple times per year may be unnecessary. Overall, the results of the current study support recommendations to monitor students’ dual-factor mental health at least once per academic year (Dowdy et al., 2010, 2014).

Although variability was observed in stability of mental health groups, greater stability was observed among the more flourishing groups (i.e., adolescents who were in a complete mental health class tended to have most stability) with youth in a troubled class having the least stability. Therefore, screening yearly for both well-being and distress is critical for informing referral into interventions that can ameliorate distress as well as bolster well-being. In doing so, intervention may aid students to achieve a stable, complete mental health status and prevent those with complete mental health from declining (McMahan, 2012). Moreover, given recommendations to triage universal screening results with additional, second-gate assessments (Eklund, Tanner, Stoll, & Anway, 2014; Walker, Small, Severson, Seeley, & Feil, 2014), the mental health patterns observed in this study support the use of second-gate measures that further assess for psychosocial and coping resources, in addition to psychopathology. Given that youth in profiles characteristic of higher levels of well-being tended to remain in more flourishing mental health categories, it will be particularly important for practitioners to include wellness promotion in intervention programs for youth experiencing psychological distress, and for well-being to be monitored during the course of intervention to inform continued implementation or adaptation.

Limitations and Future Directions

Despite study strengths, important limitations warrant discussion. First, the current study used a retrospective accelerated longitudinal design including two cohorts of participants (Cohort A: Grades 9 to 11; Cohort B: Grades 10 to 12). Although this design allows for an examination of the stability of dual-factor mental health across the high school years, data were missing by design in Grades 9 and 12. Thus, information regarding participants’ dual-factor mental health was modeled using the EM algorithm that uses known information about class membership to estimate parameters for students with missing data and a cohort covariate was included in the structural LTAs. The cohort covariate was also used to control for the effect of observed differences between the two cohorts in overlapping grade years on study indicators. Furthermore, although attrition rates were comparable across years of this study, these rates varied for each cohort across grade years. The largest attrition rates were observed between Year 2 and Year 3 of the study, potentially due to differences in survey administration method (i.e., paper and pencil in Year 2 versus online in Year 3). Potential method/administration effects that may have influenced survey completion were also accounted for by the cohort covariate. Therefore, although this covariate was included within the LTA models, differences between the two cohorts and the accelerated nature of this study’s sampling involving the merging of two cohorts represent a limitation in this study’s sample. Replication is needed with independent, robust samples including youth with data across the high school years.

We also recognize that there were limitations to the measures used in this study and findings may be a result of the assessments used. In particular, although consistent with previous research using the full self-report SDQ with youth in the U.S., the SDQ indicators used in this study evidenced inadequate internal consistency estimates and reliability. Thus, despite its widespread use in clinical settings, there remain significant concerns regarding the psychometric properties of the SDQ (e.g., Twyford, Buckley, Moffa, & Dowdy, 2018). Moreover, although the items used in this study evidenced the strongest relation with the latent construct they were intended to measure, this approach to item selection did not guarantee that content balance was maintained in the abbreviated measure administered. Additional research and replication of this study’s findings with additional measures of internalizing and externalizing distress are needed.

Information was not available regarding whether participants received intervention following universal screening each year; thus, we are unable to identify the extent to which interventions may have impacted observed transition probabilities. Additional research that replicates the current findings within additional large samples of youth followed across all four years of high school while also controlling for intervention exposure is needed.

Additionally, although an LPA approach to classification and examination of stability of dual-factor mental health has several advantages over a rationally determined cut-score approach, LPA classification is not without its challenges. At the most basic level, it is important to consider how LPA could be used by practitioners, the vast majority of whom would be unfamiliar with this sophisticated, methodological approach. As it is not feasible or practical to train practitioners to use LPA and LTA, researchers need to utilize these approaches to make informed recommendations on how to classify and interpret classes so that practitioners can effectively work with youth (Moffa, 2018). We view these types of LPA and LTA examinations as an initial step needed to further inform classification approaches that are more easily used by practitioners. For example, following additional research, cut scores can be created based on latent profile group status so that practitioners would know what group or class a student is in based on their score profile. We see the field moving forward by providing information on group status of an individual as opposed to solely providing cut scores based on T-scores. In the meantime, practitioners are encouraged to be critical of the cut scores used in their universal screening practices and to recognize that forming groups using cut scores is inherently associated with some degree of error. Practitioners need to closely examine group membership, using multiple sources of data, gathered over time, to inform what follow-up may be appropriate for specific groups and their members.

Additional challenges include that a combination of empirical and substantive fit criteria are used during the class enumeration process to inform the selection of the optimal class solution. However, as evidenced in the current study, statistical indices are not always conclusive or in agreement regarding the number of latent classes in the optimal model. Most notably, in the Grade 10 and Grade 11 LPA solutions, empirical fit criteria supported models with either three (Grade 10) or five (Grade 11) classes in addition to a four-class solution. When empirical fit criteria do not clearly indicate a single solution, using substantive theory and considering parsimony of plausible solutions is recommended in further examining the appropriateness of different solutions (Masyn, 2013). Thus, these results should be considered as one possible solution and as an initial step in the examination of the longitudinal stability of dual-factor mental health in adolescents using LTA.

Replication of the current LPAs and LTAs with additional, large, and diverse student samples is needed. Replication is further indicated given that the number of latent dual-factor mental health groups is empirically identified based on the observed heterogeneity within a given sample, and that the current study used data from a single high school. Therefore, the inability to identify a vulnerable or languishing class in the current LPAs may reflect sample specific characteristics such that the number of individuals fitting a vulnerable profile was too few to be detected or that a languishing group is an artifact of a rational cut point approach to classification. Also recognizing that the high school years are characterized as a time of dynamic developmental changes, replication with elementary and middle school samples is needed to further understand patterns of stability and instability across development and transition points.

Finally, the longitudinal results of the current study yielded similarities with previously conducted dual-factor stability research; however, nontrivial differences were also observed. For example, paralleling previous work, the complete mental health class exhibited the greatest average stability across comparison points in the current study, with most students who transitioned across comparison points trending toward moderate or complete mental health. However, students fitting a troubled mental health pattern exhibited the lowest levels of stability in the current study, whereas previous research indicated students in a troubled group to have the second greatest stability estimates. These differences may reflect the different classification approaches used across studies (e.g., sample-dependent cut point criteria vs. LPA), discrepancies in measurement tools used, or sample specific characteristics. Overall, additional research is needed that examines stability of dual-factor mental health, specifically whether differences in classification approaches influence stability results. Future research investigating the relation of longitudinal dual-factor mental health trajectories to distal outcomes (e.g., graduation rates, development of psychological disorder) as well as individual and school-level predictors of stability can further inform school-based prevention and early intervention efforts for all students.