Agent-Based Modeling of Cancer Stem Cell Driven Solid Tumor Growth

Abstract

Computational modeling of tumor growth has become an invaluable tool to simulate complex cell–cell interactions and emerging population-level dynamics. Agent-based models are commonly used to describe the behavior and interaction of individual cells in different environments. Behavioral rules can be informed and calibrated by in vitro assays, and emerging population-level dynamics may be validated with both in vitro and in vivo experiments. Here, we describe the design and implementation of a lattice-based agent-based model of cancer stem cell driven tumor growth.

1. Introduction

Agent-based modeling has a long history in quantitative oncology [1–3], including stem cell dynamics [4–9], and heterogeneity [10–12]. Such models can help predict disease progression and make invaluable recommendations for therapeutic interventions [13, 14]. Agent-based models simulate the behavior and interaction of individual cells. Behavioral rules can be dependent on environmental conditions, which include chemicals in the extracellular environment [15–17], supporting structures in the extracellular matrix [18, 19], fluid dynamics [20], physical forces [21], or presence and interactions with other cells [22, 23]. Computer simulations are usually initialized with a single cell or a cluster of individual cells, and the status and behavior of each cell are typically updated at discrete time points based on their internal rules and current environmental conditions. Such models may help identify if cancer stem cells comprise a subpopulation of specific proportion in a tumor [24], and how to deliver radiotherapy doses efficiently to eradicate cancer stem cells [25].

2. Materials

Implement all classes and functions in a concurrent version system to allow shared programming and efficient debugging.

2.1. Lattice

A finite 2D (or 3D if necessary) lattice, where each site can be occupied by a single or a population of cells (crowding).

1. Lattice size. Simulations are commonly initialized with either (a) a small number of cells to observe emergent population-level behavior, or (b) a populated tissue architecture. Define lattice size to accommodate anticipated final cell number. Account for possible boundary effects in case of a growing population. Set the size of a single lattice site to the size of a cell.

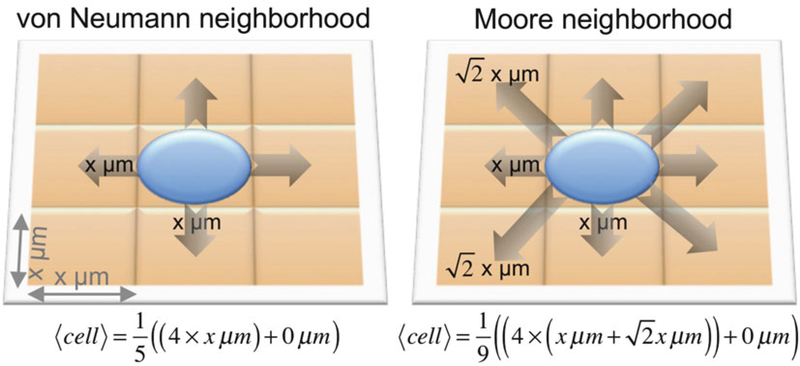
2. Neighborhood. Determine if cells interact with their four orthogonal neighbors (north, south, east, west; von Neumann neighborhood), or with the adjacent eight neighboring lattice points (northwest, north, northeast, east, west, southeast, south, southwest; Moore neighborhood) (Fig. 1).

3. Boundary conditions. Define behavior of cells on the boundary of the lattice, set to either periodic (the boundary “wraps”, so cells on the left edge interact with cells on the far right edge) or no-flux reflective (cells on the edge of the lattice only interact with interior and edge cells). Note that simulations with no-flux boundary conditions may introduce boundary effects, i.e., accumulation of cells near the boundary. For dynamically expanding arrays no boundary conditions are necessary.

Fig. 1.

Schematic of expected cell displacement, cell, in the von Neumann (left) and Moore (right) neighborhoods on a two-dimensional lattice with lattice sizes of x² μm²

2.2. Cell

Each cell is an individual entity with the following basic attributes:

1. Time to next division event (t_c).

2. Type of the cell—stem/non-stem (isStem).

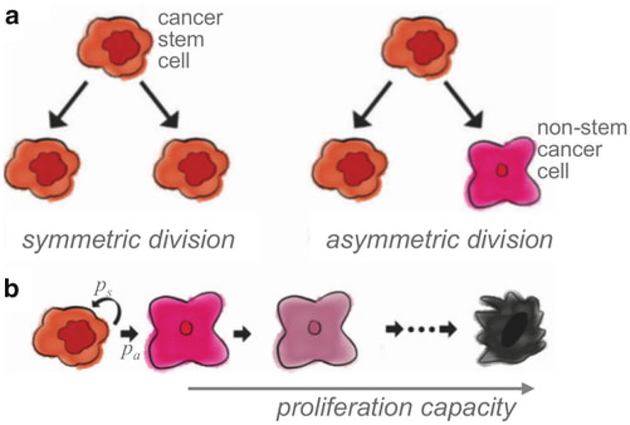
3. Probability of symmetric division (p_s). Cancer stem cells divide either symmetrically to produce two identical cancer stem cells, or asymmetrically to produce a cancer stem cell and a non-stem cancer cell [26]. In the case of cancer stem cell define probabilities of symmetric division, 0 < p_s ≤ 1, and asymmetric division p_a = 1 − p_s (Fig. 2).

4. Telomere length (p). Set the telomere length of the initial cell or cell population as a molecular clock [27–29], which is a quantification of the Hayflick limit [30].

5. Current cell cycle phase (if required). If information about specific cell cycle phases is required (such as for simulations of cell cycle specific chemotherapeutics) define cell cycle phases. Cell cycle length can be divided into fractions comparable to experimentally measured cell cycle distributions.

6. Probability of spontaneous death (α). Cancer cells (isStem = false) accumulate mutations that introduce genomic instability which may lead to premature cell death. Define a probability of spontaneous cell death, α ≥ 0, at which rate cells may die during cell division attempts. Cancer stem cells (isStem = true) have a superior DNA damage repair machinery [31–33] and, thus, the probability of spontaneous cell death can be set to zero. For more biological realism, define a cell death rate that is larger than zero, but less than the self-renewal rate to ensure net population growth.

Fig. 2.

(a) Schematic of cancer stem cell symmetric and asymmetric division. (b) Schematic representation of cancer stem cell symmetric (p_s) and asymmetric division (p_a) and non-stem cancer cell proliferation capacity. Adapted from [24]

Each cell is equipped with a set of basic functions:

1. Procedure advance time (input arguments = time increment Δt, list of available sites in the direct neighborhood).

   • Decrease time to next division (t_c) by Δt. If t_c < 0 set t_c = 0.
   • Update current cell cycle phase (if necessary).
   • If t_c ≤ 0 and there is available space, then perform division and generate new times to next division for both resulting cells.

2. Procedure divide (input argument = list of available sites in the direct neighborhood).

   Choose a random number 0≤n≤1 from the uniform distribution. If n < α, then simulate cell death, i.e., remove cell from the simulation and instantaneously make a corresponding lattice point available. If required, instead of instantaneous cell removal, site on the lattice can be made available for new cells after specified amount of time, e.g., in order to simulate duration of apoptosis process. Otherwise:

   • If the cell is not-stem (isStem = false) then decrease the proliferation capacity (p) by one, as non-stem cancer cells do not upregulate telomerase and are thus not long-lived and cannot initiate, retain, and reinitiate tumors [34, 35]. Simulate cell death by removing the cell from the simulation if the proliferation capacity is exhausted, i.e., less or equal to zero. Otherwise, new cell is a clone of the mother cell, i.e., non-stem cancer cell only produces non-stem cancer cell and decremented proliferation capacity is inherited by the daughter cell. Place new cell at vacant neighboring lattice point at random.
   • If the cell is cancer stem cell (isStem = true), then draw a number from uniform distribution to decide if the division is symmetric based on the probability p_s. If division is symmetric, new cell is a perfect clone of the mother cell; that is a cancer stem cells do not erode telomeres and retain identical proliferation capacity after mitosis. Otherwise, non-stem cancer cell offspring of a cancer stem cell inherit the current telomere length and determined proliferation capacity, i.e., new cell is identical except for attribute isStem, which set to false. Place new cell at vacant neighboring lattice point at random.

3. Procedure generate time to next division. Cells divide on average every 24 h. Derive specific cell cycle times t_c (hours), averages and standard deviations from proliferation rate calculations from clonogenic assays or live microscopy imaging [36].

4. Procedure random migration (input argument = list of available sites in the direct neighborhood). Cells may perform a random walk, and probabilities of migrating into adjacent lattice points can be obtained from a discretized diffusion equation [37, 38]. Assuming Moore neighborhood (see Sect. 2.1 above) and a cell at position (x₀,y₀): at time t can move based on available lattice points in the immediate eight-cell Moore neighborhood N_(x0,y0) with probabilities

   $$P\left(x_i^{t+1},y_i^{t+1}\right)=\frac{\mathrm{\Gamma }\left(x_i^t,y_i^t\right)}{1+{\sum }_{N\left(x_0,y_0\right)}\mathrm{\Gamma }\left(x_i^t,y_i^t\right)},i=1,\dots ,8$$

   With

   $$\mathrm{\Gamma }\left(x_i^t,y_i^t\right)=\{\begin{array}{c}1,\text{ if lattice point }{x}_i,y_i\text{ is unoccupied at time }t\\ 0,\text{ otherwise }\end{array}.$$

   With probability 1/(1+number of unoccupied neighboring lattice points) the cell remains temporarily stationary, and a cell that completely surrounded by other cells is not moving. Note that in this implementation, movement to all adjacent lattice points is equally weighted. This can be modified to account for increased distance to diagonal lattice points.

5. Procedure directed migration (if required) (input arguments = list of available sites in the direct neighborhood, function F whose gradient ∇F describes the migration stimulus, such as chemoattractant or chemorepellant). Vector $\overrightarrow{\mathrm{n}}$ describes the vector connecting the current cell position (x₀, y₀) to the center of one of the adjacent lattice points (x_i, y_i). Directed migration only occurs towards available lattice sites (S) when $\mathrm{\nabla }F·\overrightarrow{\mathrm{n}}>0$. Weight each available site S by the factor cos(θ), where θ is the angle between the gradient ∇F and the movement direction $\overrightarrow{\mathrm{n}}$ for each possible movement). (Notice that cos(θ) = 1 when ∇F and $\overrightarrow{\mathrm{n}}$ are parallel, and cos(θ) = 0 when they are perpendicular, to give greatest weight to travel along the chemoattractant gradient direction.)

Sum each cos(θ) over the S available sites to get the averaged cosine value AS. Define the probability of mobilization G through an arbitrary chemotactic/haptotactic responsiveness function via G = H(|∇F|AS/(AS + 1)), where H has the properties:

• H(0) = 0 (no directed motion when no lattice sites are available or the chemical gradient is zero),

• H is a (monotonically) increasing function (directed motility increases with the magnitude chemotactic signal and alignment with the lattice), and

• H tends to 1 as |∇F|AS/(AS + 1) approaches ∞(directed motility increases with the chemotactic signal, but saturates at a maximal level scaled to 1).

If a cell moves, its direction is weighted by the respective cosines for movement, so that cos(θ)G/(AS) is the probability of movement to the available site at angle θ. This method is explained in detail elsewhere [39].

3. Methods

3.1. Programming Environment

1. Define programming language. Agent-based models can be implemented and simulated in any programming language; most prominent languages including C++, Java, Julia, Python, and Matlab. Each of these languages offers different computational speed and coding feasibility. C++ is considered as the environment offering the best performance, but has a high programming complexity. Matlab offers a great number of built-in functions and is easy to code in, but has significantly lower performance (e.g., when using nested loops).

2. Define graphical output. Visualize simulation solutions of agent-based models using existing implementations of graphical programming or implement specific visualization tools.

3. Agent-based software packages. Utilize predeveloped agent-based software packages; most prominent include Netlogo [40, 41], CompuCell3D [36, 42], Chaste [43], or Swarm [44].

3.2. Simulation Procedure

1. Time step. Define the simulation time step, Δt, such that Δt is smaller than the fastest biological process that is being considered in the model. In a model of cell proliferation (~1/day) and cell migration (~1 cell width/h), set Δt ≤ 1 h.

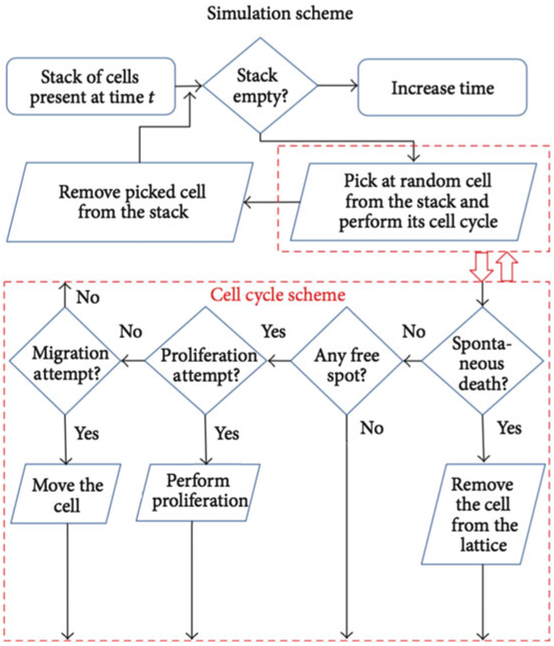
2. Develop a simulation flowchart to conceptualize and visualize the simulation procedure. At each defined discrete simulation time step, consider mutually exclusive processes that occur with lowest rate constant first. Let us assume that cell migration and cell proliferation are mutually exclusive (e.g., cells could migrate through most of G1, S, G2 phases). Check if maturation age is reached; if not, check if migration time is reached (Fig. 3).

3. Lattice update sequence. Update cells in random order to avoid lattice geometry effects. Maintain a list of “live” cell agents and select cells for update from this list at random.

4. Cell update sequence. Consider vacancy in cell neighborhood in random order to avoid lattice geometry effects. Maintain a list of vacant adjacent lattice sites for each cell agent and select for update from this list at random.

Fig. 3.

Sample simulation flowchart with cell cycle scheme

4. Notes

1. Homogenous populations. The presented model produces a heterogeneous population of stem and non-stem cancer cells. If p_s = 1, the population remains (if only initialized with cancer stem cells) or will become (if initialized with both stem and non-stem cancer cells) homogenous comprised of only cancer stem cells. If p_s = 0, only non-stem cancer cells are produced and the resulting population size oscillates around a dynamic equilibrium or, if the probability of cancer stem cell death is positive and non-zero, the population will inevitably die out [45].

2. Plasticity. The presented model considers cancer stemness a cell phenotype, whereas recent literature may suggest stemness to be a reversible trait [46, 47]. The model can be extended to simulate phenotypic plasticity through cancer stem cell differentiation (that is, the cancer stem cell phenotype is set to non-stem cancer cell) and non-stem cancer cell de-differentiation (that is, the non-stem cancer cell phenotype is set to cancer stem cell) [48].

3. Senescence. The presented model considers cell death after exhaustion of proliferation potential. Alternatively, cells may enter senescence [49] and, although mitotically inactive, continue to consume resources that influence the behavior of remaining cancer cells [50].

4. Evolution. The presented model considers fixed parameters or rate constants for each cell trait. Rate constants can change due to mutations and genetic drift [51], which allows for simulations of the evolution of cancer stem cell traits under different environmental conditions [12, 52].

5. Carcinogenesis. Such modeling framework can be adapted to model tissue homeostasis and mutation/selection cascades during cancer development [16, 53].

6. To ensure model results are reproducible, simulation inputs (parameters) and outputs should be recorded using open, standardized data formats, using biologically driven data elements that can be reused in independent models. The MultiCellDS (multicellular data standard) Project assembled a cross-disciplinary team of biologists, modelers, data scientists, and clinicians to draft a standard for digital cell lines, which record phenotype parameters such cell cycle time scales, apoptosis rates, and maximum proliferative capacity. Separate digital cell lines can represent cancer stem cells and non-stem cells. Similarly, standardized simulation outputs can record the position, cell cycle status, and other properties of simulated cells. Using standards will allow better software compatibility, facilitate cross-model validation, and streamline development of user-friendly software to start, modify, visualize, and analyze computational models. See MultiCellDS.org for further details.

7. Model assumptions (e.g., Fig. 3) should also be recorded with standardized data formats. The Cell Behavior Ontology (CBO) [54] provides a “dictionary” (ontology) of applicable stem cell behaviors, but it may not be able to fully capture the entire model logic in its present form. Extensions to the Systems Biology Markup Language (SBML) [55], such as SBML-Dynamic [56], are currently being developed to leverage the model structure of SBML and the ontology of CBO to annotate the mathematical structure of agent-based models, but the standards are not yet complete.

8. Treatment. The presented agent-based model can be extended to account for the effects of cancer therapy including radiation [57–59], chemotherapy [60], oncolytic viruses [61], or immunotherapy [62].

9. Analysis. Agent-based models can be rigorously analyzed for sensitivity and stability [63, 64]. Comparison of coarse-grained model behavior (e.g., growth curves) with known analytical results can quality-check calibration protocols and the computational implementation.

10. Dynamically expanding domains. Tradeoffs between lattice size and computing speed can be avoided using dynamically growing domains [65].

11. Hybrid models. The discussed model setup can be extended to a hybrid discrete-continuous framework where single cells are modeled as discrete agents, and environmental chemicals diffuse on a mapped continuum layer [66–68]. In those models cell cycle time may vary with environmental conditions (e.g., [16] and [69]).

12. Cell neighborhood. In more complex cases daughter cells can populate empty lattice sites within a given distance to approximate tissue deformability.