Categorizing a continuous predictor subject to measurement error

Abstract

Epidemiologists often categorize a continuous risk predictor, even when the true risk model is not a categorical one. Nonetheless, such categorization is thought to be more robust and interpretable, and thus their goal is to fit the categorical model and interpret the categorical parameters. We address the question: with measurement error and categorization, how can we do what epidemiologists want, namely to estimate the parameters of the categorical model that would have been estimated if the true predictor was observed? We develop a general methodology for such an analysis, and illustrate it in linear and logistic regression. Simulation studies are presented and the methodology is applied to a nutrition data set. Discussion of alternative approaches is also included.

1. Introduction

Fitting models by categorizing a continuous risk predictor is a common practice in epidemiology. Among many recent examples, see [20, 19, 1, 5, 10] and [25]. A look at current issues of epidemiology journals will uncover many more examples. An important issue is that, generally in these problems, there are many covariates other than the main risk predictor.

The appeal of categorization in interpreting results is clear. If we have a risk predictor X, and we categorize it into J levels (C₁, …, C_J), one can compare the highest level of the predictor, C_J, to the lowest level, C₁, and if they are statistically significantly different, one can then conclude that it is better to be in the class that has the lowest risk, and quantify how much better.

One important technical point is that categorization implicitly posits an induced model based on the categorized variable X. In some cases, the induced model actually fits the data, e.g., when the response Y actually depends on X only through its categorized version, or if there are no other covariates, see the next paragraph. In other cases, and generally, the induced model does not fit the data, and we call this model misspecified. In particular, suppose that there are other covariates than X, say Z. Consider a binary response, Y, let H(·) be the logistic distribution function, and suppose that the true risk model in ·the continuous scale is pr(Y = 1|X, Z) = H{m(X, Z, β)} for some continuous function m(·). Then, even if there is no measurement error, if any of the covariates Z are related to Y in this continuous model, or if there is an interaction of X and Z on Y, categorizing X into J levels and plugging that into m(X, Z, β) in place of X leads to a misspecified model as we have defined it. Measurement error in this context makes things even more difficult. When there is no measurement error, [26] gives a characterization of what is actually being estimated in misspecified models: while we do not emphasize it, our paper extends this characterization to the measurement error case. A relevant paper that first solved this particular problem is [14], which was also cited in [26].

This slightly different terminology is motivated by the following example. Suppose that Y is binary, there are no additional covariates Z, and simply define π_j = pr(Y = 1|X* = j), where X* is the categorized predictor. Then we can write, correctly, that pr(Y = 1|X* = j) = H{I(X* = j)θ_j} by making the obvious identifications. Thus, categorization does result in an induced correctly specified logistic model, just not the one in the continuous scale. A logistic regression analysis of Y on the categories of X* then will estimate θ_j consistently.

Our point is not to try to get epidemiologists to change their common practice. Instead, we study the effect of measurement error when a continuous predictor variable subject to measurement error is categorized. Our goal is to answer the question: with measurement error in this context, how can we (a) obtain consistent estimates of what epidemiologists would have obtained if X were actually observed; and (b) develop consistent standard errors.

We answer the question above in a general way. Section 2 gives basic technical background. Section 3 provides a general methodology for answering questions (a) and (b) above. Section 4 presents simulation studies for linear and logistic regression that show the good behavior of our methodology, both in terms of bias and confidence interval coverage. Section 5 shows applications of our approach by using data from the Eating at America’s Table Study [23]. Section 6 presents a discussion about other potential approaches to categorization and how those approaches compare to ours. Sketches of technical arguments are in the appendix.

Remark 1.

As discussed above, categorization leads to a misspecified model. It is also well-known that such categorization generally leads to differential measurement error [11, 13, 3], and thus additional complications over simply fitting a measurement error model. Chapters 6.1–6.2 of [13] has a detailed discussion when the continuous variable is dichotomized, calling the result differential by dichotomization. We are thus assuming that the true risk model in a continuous variable X is not categorical in X. If it were, consult [13] and [3], who also discuss the issue of doing a measurement error analysis in this case, especially the difficult complex issues of computation and identifiability both theoretical and practical.

2. Data generating mechanism and basic ideas

2.1. Illustration: A special case of linear regression

It is instructive to consider a special case, namely linear regression. Doing so will set the stage for our general method. The response is Y, the scalar predictor subject to error is X, the observed scalar predictor is W, there are predictors Z measured without error, and we define $\tilde{Z}={\left(1,Z^{\text{T}}\right)}^{\text{T}}$ to allow for an intercept. The regression model in the continuous predictor X is $Y=X{\beta }_1+{\tilde{Z}}^{\text{T}}{\beta }_2+ϵ$, where ϵ is mean zero independent of (W, X, Z). There are j = 1, …, J categories (C₁, …, C_J): the number of categories J is set by the investigator, and is generally 3 (tertiles), 4 (quartiles) or 5 (quintiles), depending on the scientific field and the investigator’s interests. Here M(X, Z) = {I(X ∈ C₁), …, I(X ∈ C_J), Z^T}^T. If X could be observed, then we would also immediately obtain an estimate of $\beta ={\left({\beta }_1,{\beta }_2^{\text{T}}\right)}^{\text{T}}$.

By [26], when X is observed, what epidemiologists estimate by using the categorized M(X, Z) is Θ, where, based on the normal equations for the categorized predictor, $\Theta ={\left({\theta }_1,\dots ,{\theta }_J,{\Theta }_{J+1}^{\text{T}}\right)}^{\text{T}}$ is the solution to

$$\begin{gathered} 0=E\left[M(X,Z)\left\{Y-M^{\text{T}}(X,Z)\Theta \right\}\right] \\ =E\left[M(X,Z)\left\{X{\beta }_1+{\tilde{Z}}^{\text{T}}{\beta }_2-M^{\text{T}}(X,Z)\Theta \right\}\right]. \end{gathered}$$ (1)

The estimate $\widehat{\mathbf{\Theta }}$ is the solution to $0=n^{-1}{\sum }_{i=1}^{n}M\left(X_i,Z_i\right)\left\{Y_i-M^{\text{T}}\left(X_i,Z_i\right)\Theta \right\}$, and this is a consistent estimate of Θ. Comparisons between categories j and k for j, k ≤ J, say, are ${\widehat{\theta }}_j-{\widehat{\theta }}_k$.

However, when X is not observable, estimating the solution to (1) has to be based solely on (Y, W, Z). In (1), it makes sense that if one believes the true regression model is linear in (X, Z), then, at some point, an estimate of β can be obtained via a measurement error analysis if there are sufficient data to do so.

Solving (1) based only on the observed W though is not so easy, and it is clear that some part of the relationship between W and X given Z is going to need to be specified, as it needs to be to do a general measurement error analysis. One way to do this is to define

$$\mathcal{G}(X,Z,\Theta ,\beta )=M(X,Z)\left\{X{\beta }_1+{\tilde{Z}}^{\text{T}}{\beta }_2-M^{\text{T}}(X,Z)\Theta \right\},$$ (2)

and then define $Q(W,Z,\Theta ,\beta )=E\{\mathcal{G}(X,Z,\Theta ,\beta )|W,Z\}$. Since 0 = E{Q(W, Z, Θ, β)}, Θ can be estimated by solving

$$0=n^{-1}{\sum }_{i=1}^n[E\left\{M(X,Z)\left(X{\beta }_1+{\tilde{Z}}^{\text{T}}{\beta }_2\right)|W_i,Z_i\right\}-E\left[\left\{M(X,Z)M^{\text{T}}(X,Z)\right\}|W_i,Z_i\right]\Theta ].$$

Hence, in this simple case, for j = 1, …, J we will need to be able to calculate expectations of XI(X ∈ C_j) given (W, Z) and the probability that X ∈ C_j given (W, Z). As we will see, in general problems, we will need to estimate the expectations of other functions of X given (W, Z).

So, to summarize, to get a general solution, it appears that we will need to estimate (β₁, β₂) by a measurement error analysis and estimate expectations of specified functions of X given (W, Z).

Remark 2.

Following on Remark 1, it is obvious that in the unlikely event that the true risk model is actually categorical in X, so that E(Y | X, Z) = M^T(X, Z)β, then model misspecification and differential measurement error both disappear, and one really needs just the probabilities that X is in the categories given (W, Z). As [13] and [3] discuss in detail, estimating such models is difficult because of model identifiability concerns. Often, papers dealing with this issue assume the existence of a validation data set, where X is actually observed on a subset of the data. [13] is a particularly good source for the difficulties we have mentioned and remedies using replication data. [3], page 314, who states that estimating the misclassification rates is “most likely coming from internal validation data” and also has a nice discussion.

2.2. Assumptions

Our work is very general, but even so, the algorithm is basically the same as in Section 2.1. Our methodology requires three basic assumptions, described below. We let X be the continuous predictor subject to measurement error, Z covariates measured exactly, W the mismeasured version of X, and Y the response.

Assumption 1.

When X is observed, the true response model in the continuous scale has parameters β, such that there is an estimating function, Φ_true(Y, X, Z, β) that identifies β and satisfies

$$0=E\left\{{\mathrm{\Phi }}_{\text{true}}(Y,X,Z,\beta )|X,Z\right\}.$$ (3)

Assumption 1 occurs in at least two circumstances.

Example 1.

(A) There are functions m₁(X, Z, β) and m₂(X, Z, β) such that E(Y|X, Z) = m₁(X, Z, β) and the unbiased estimating function that would be used if X were observable is

$${\mathrm{\Phi }}_{\text{true}}(Y,X,Z,\beta )=m_2(X,Z,\beta )\left\{Y-m_1(X,Z,\beta )\right\}.$$ (4)

(B) There is a parametric model for Y given (X, Z).

Example 1(A) is very general, in that it includes traditional quasilikelihood models, nonlinear regression, generalized linear models, probit regression, etc. Crucially, it does not require a fully parametric model for the distribution of Y given (X, Z).

In our approach, as in linear regression in Section 2.1, we may need to obtain information about moments of specified functions of X given (W, Z). To do this, we will consider the setting in which there may be an external data set of N observations giving information on one set of parameters of the joint distribution, Λ_ext: if there is no external study, N = 0 and Λ_ext does not exist. In addition, there is another set of the parameters, Λ_int, that is estimated from the n observations in the internal data set.

Assumption 2.

When X is not observed, either (a) the distribution of X given (W, Z) is known up to parameters Λ_ext and Λ_int as described above, or (b) there is a function, $\mathcal{G}(X,Z,\Theta ,\beta )$ defined at (11) below, whose conditional expectation given (W, Z) depends on parameters Λ_ext and Λ_int and can be estimated. The parameter Λ_ext cannot be estimated by internal data, while the parameter Λ_int can be estimated by internal data. For both, there are unbiased estimating functions V_ext,m(Λ_ext) for the external data and V_int,i(Λ_int, Λ_ext) for the internal data such that E{V_ext,m(Λ_ext)} = 0 and E{V_int,i(Λ_int, Λ_ext)} = 0.

For linear regression, $\mathcal{G}(X,Z,\Theta ,\beta )$ is given in (2).

If there are external data and N > 0, we estimate Λ_ext by solving the estimating equation

$$0=N^{-1}\sum _{m=1}^N{V}_{\text{ext},m}\left({\Lambda }_{\text{ext}}\right).$$ (5)

In the internal data set, we estimate Λ_int by solving an estimating equation

$$0=n^{-1}{\sum }_{i=1}^n{V}_{\text{int},i}\left({\Lambda }_{\text{int}},{\widehat{\Lambda }}_{\text{ext}}\right).$$ (6)

There is also a very subtle issue that needs to be made explicit.

Assumption 3.

If external data are necessary for model identification, the parameter Λ_ext is transportable in the sense that this parameter is the same in the external and internal data sets.

The issue of when parameters are transportable from an external data set to the internal data set is discussed in Chapter 2.2.4–2.2.5 of [4]. As they state, it is much better if there are sufficient internal data that external data need not be used, but this is not always the case.

2.3. General observations when X is observed

As argued in Section 1, the goal is to fit a model when X is categorized into J levels (C₁, …, C_J), and so we defined the dummy variables and Z together as M(X, Z) = {I(X ∈ C₁), …, I(X ∈ C_J), Z^T}^T: our formulation allows more complex forms, including interactions. Suppose there are i = 1, …, n subjects in the primary/main/internal study, and suppose further that we observe (Y_i, X_i, Z_i). If X is observed, the analysis done on these categories will be based on replacing (X, Z) in (3)–(4) by M(X, Z), and to make clear the categorization, we define a parameter Θ, set Φ_cat{Y_i, M(X_i, Z_i), Θ} = Φ_true{Y_i, M(X_i, Z_i), Θ}, and obtain $\widehat{\mathbf{\Theta }}$ by solving

$$0=n^{-1}{\sum }_{i=1}^n{\mathrm{\Phi }}_{\text{cat }}\left\{Y_i,M\left(X_i,Z_i\right),\Theta \right\}.$$ (7)

More complex forms of (7) are easily accommodated.

Unlike in Assumption 1 and (3)–(4), except in the rare case that the categorized model is actually true, 0 ≠ E[Φ_cat{Y, M(X, Z), Θ}|X, Z], a conditional expectation. This is a key part of the work in [26].

Despite the fact that the categorized model does not fit the data conditional on (X, Z), by standard estimating equation theory [26], the estimate formed by solving (7) has a limit as n → ∞, Θ, which is the solution to

$$0=E\left[{\mathrm{\Phi }}_{cat}\{Y,M(X,Z),\Theta \}\right].$$ (8)

It is important to observe that (8) is an unconditional expectation, not a conditional one.

If, instead of observing X, we observe its mismeasured version W, and if we replace X by W, we will of course generally inconsistently estimate both β and Θ.

2.4. Estimating the true parameter β

In our approach, as in Section 2.1 for linear regression, we must estimate β in (3). There is of course a large literature on how to do this [13, 4, 3, 27]. Borrowing on that literature, from Assumptions 1–2, for an estimating function Φ(Y, W, Z, β, Λ_int, Λ_ext), the estimate, $\widehat{\beta }$, is the solution to

$$0=n^{-1}{\sum }_{i=1}^n\mathrm{\Phi }\left(Y_i,W_i,Z_i,\beta ,{\widehat{\Lambda }}_{\text{int}},{\widehat{\Lambda }}_{\text{ext}}\right),$$ (9)

where $\left({\widehat{\Lambda }}_{\text{int}},{\widehat{\Lambda }}_{\text{ext}}\right)$ are obtained from equations (5) and (6), respectively. Of course, the details and the form of Φ(·) differ from case-to-case.

3. Methodology and asymptotic theory

3.1. Methodology: General case

The methodology is simple to explain at the general level. The target Θ is defined as the solution to (8). However, we can rewrite (8) as

$$0=E\left(E\left[{\mathrm{\Phi }}_{\text{cat}}\{Y,M(X,Z),\Theta \}|W,Z\right]\right).$$ (10)

Since the distribution of Y given (X, Z) depends on β, for notational completeness we define

$$\begin{gathered} \mathcal{G}(X,Z,\Theta ,\beta )=E\left[{\mathrm{\Phi }}_{\text{cat}}\{Y,M(X,Z),\Theta \}|X,Z\right] \\ =E\left[{\mathrm{\Phi }}_{\text{cat}}\{Y,M(X,Z),\Theta \}|X,Z,\beta \right]; \end{gathered}$$ (11)

$$Q\left(W,Z,\Theta ,\beta ,{\Lambda }_{\text{int}},{\Lambda }_{\text{ext}}\right)=E\{\mathcal{G}(X,Z,\Theta ,\beta )|W,Z\}.$$ (12)

Making the usual nondifferential measurement error assumption, i.e., that Y and W are independent given (X, Z),

$$0=E\left\{Q\left(W,Z,\Theta ,\beta ,{\Lambda }_{\text{int}},{\Lambda }_{\text{ext}}\right)\right\}.$$ (13)

Critically, (12) depends only on the observed covariates. Thus, if we have consistent estimates $\left(\widehat{\beta },{\widehat{\Lambda }}_{\text{int}},{\widehat{\Lambda }}_{\text{ext}}\right)$ of (β, Λ_int, Λ_ext), then a consistent estimate $\widehat{\Theta }$, of Θ solves

$$0=n^{-1}{\sum }_{i=1}^{n}Q\left(Z_i,W_i,\mathbf{\Theta },\widehat{\beta },{\widehat{\Lambda }}_{\text{int}},{\widehat{\Lambda }}_{\text{ext}}\right).$$ (14)

In some cases, we do not have external data. Thus, we do not have V_ext and Λ_ext, and V_int and Θ only depend on Λ_int.

Remark 3.

The key question is how to compute $\mathcal{G}(X,Z,\Theta ,\beta )$ in (11). In the fully general case (3), we require a parametric model for the distribution of Y given (X, Z), as in Example 1(B). However, in standard regression models of the form in (4) in Example 1(A), great simplification occurs, because in that case,

$${\mathrm{\Phi }}_{\text{cat}}\{Y,M(X,Z),\Theta \}=m_2\{M(X,Z),\Theta \}\left[Y-m_1\{M(X,Z),\Theta \}\right],$$

and thus

$$\mathcal{G}(X,Z,\Theta ,\beta )=m_2\{(X,Z),\Theta \}\left[m_1(X,Z,\beta )-m_1\{M(X,Z),\Theta \}\right].$$

C.3 gives detailed formulae for linear and logistic regression.

Remark 4.

Our method is closely related to the expectation-correction method of [27], Chapter 2.5.2, and less closely to the general corrected score methods first introduced by [17]. [27] has an excellent and comprehensive discussion of the correction methods in the literature. We do not have a score function per se, but we have a function, Φ_cat{Y, M(X, Z), Θ}, with the property that E[Φ_cat{Y, M(X, Z), Θ}] = 0: importantly, it is not true that the conditional expectation E[Φ_cat{Y, M(X, Z), Θ}|X, Z] ≡ 0. Instead of our (11)–(12), the expectation-correction method uses as its estimating equation E[Φ_cat{Y, M(X, Z), Θ}|Y, W, Z] = Q*(Y, W, Z, Θ, β, Λ_int, Λ_ext). The obvious distinction is that our function Q(·) does not involve Y explicitly, while the expectation-correction function Q*(·) does involve Y. We used Q(·) and (11) because our assumptions allow $\mathcal{G}(\cdot )$ to be calculated explicitly, especially in Example 1(A), so that implementation is somewhat easier. In addition, in Example 1(A), there does not need to be a full likelihood, as would be required in the expectation-correction method, so there are actual differences in the methods.

3.2. Asymptotic Theory

Asymptotic theory for the parameter estimates is easily derived. Let Ω = (Θ, β, Λ_int, Λ_ext) and let the true values of the parameters be denoted by Ω.

It is neater notation in this section to let i = 1, …, n denote the internal data, and i = n + 1, …, n + N denote the external data. For i > n, define ${\mathrm{\Psi }}_i(\Omega )={\left\{0,0,0,V_{\text{ext},i}^{\text{T}}\left({\Lambda }_{\text{ext}}\right)\right\}}^{\text{T}}$, while for i ≤ n define

$${\mathrm{\Psi }}_i(\Omega )=\{Q^{\text{T}}\left(W_i,Z_i,\Theta ,\beta ,{\Lambda }_{\text{int}},{\Lambda }_{\text{ext}}\right),{\mathrm{\Phi }}^{\text{T}}\left(Y_i,W_i,Z_i,\beta ,{\Lambda }_{\text{int}},{\Lambda }_{\text{ext}}\right),V_{\text{int},i}^{\text{T}}\left({\Lambda }_{\text{int}},{\Lambda }_{\text{ext}}\right),0{\}}^{\text{T}}.$$

If there are external data, the estimate $\widehat{\Omega }$ solves $0={\sum }_{i=1}^{n+N}{\mathrm{\Psi }}_i(\widehat{\mathbf{\Omega }})$. If there are no external data, then N = 0, Ω = (Θ, β, Λ_int) and the zero element and Λ_ext in the definition of Ψ_i(Ω) are removed.

By standard estimating equation results, we have the following results, which are shown in Appendices A.1 and A.2.

Lemma 1.

If there are external data, i.e., N > 0, make Assumptions 1–3. Suppose that N → ∞ and n → ∞ such that n/(n + N) → b_lim, where 0 < b_lim < 1. Then

$${(n+N)}^{1/2}(\widehat{\Omega }-\Omega )\to \text{Normal}\left\{0,A^{-1}B{\left(A^{-1}\right)}^{\text{T}}\right\},$$

where A = b_limE{∂Ψ₁(Ω)/∂Ω^T} + (1 − b_lim)E{∂Ψ_n+N(Ω)/∂Ω^T} and B = b_limcov{Ψ₁(Ω)} + (1 − b_lim)cov{Ψ_n+N(Ω)}. In the definitions A of and B, the expectation and covariance matrix for Ψ₁(Ω) are computed in the internal data, while the expectation and covariance matrix for Ψ_N+n(Ω) are computed in the external data. Let ${\widehat{C}}_{\text{ext}}$ be the sample covariance matrix of ${\mathrm{\Psi }}_i(\widehat{\Omega })$ for i = n + 1, …, n + N and let ${\widehat{C}}_{\text{int}}$ be the sample covariance matrix of ${\mathrm{\Psi }}_i(\widehat{\Omega })$ for i = 1, …, n. Consistent estimates of A and B are easily seen to be $\widehat{A}={(n+N)}^{-1}{\sum }_{i=1}^{N+n}\partial {\mathrm{\Psi }}_i(\widehat{\Omega })/\partial {\Omega }^{\text{T}}$ and $\widehat{B}=\{n/(n+N)\}{\widehat{C}}_{\text{int}}+\{N/(n+N)\}{\widehat{C}}_{\text{ext}}$.

Lemma 2.

If there are no external data, i.e., N = 0, make Assumptions 1–2. As n → ∞,

$$n^{1/2}(\widehat{\Omega }-\Omega )\to \text{Normal}\left\{0,A^{-1}B{\left(A^{-1}\right)}^{\text{T}}\right\},$$

where A = E{∂Ψ₁(Ω)/∂Ω^T} and B = cov{Ψ₁(Ω)}. In the definitions of A and B, the expectation and covariance matrix for Ψ₁(Ω) are computed in the internal data. Let ${\widehat{C}}_{\text{int}}$ be the sample covariance matrix of ${\mathrm{\Psi }}_i(\widehat{\Omega })$ for i = 1, …, n. Consistent estimates of A and B are easily seen to be $\widehat{A}=n^{-1}{\sum }_{i=1}^n\partial {\mathrm{\Psi }}_i(\widehat{\Omega })/\partial {\Omega }^{\text{T}}$ and $\widehat{B}={\widehat{C}}_{\text{ int }}$.

Remark 5.

While the calculations used in Lemmas 1–2 are standard, as a referee has pointed out, we are making the following kinds of assumptions to carry them through: weaker conditions can be constructed. All these conditions hold in our examples of linear and logistic regression with additive measurement error. There is a parameter which we have called in this subsection Ω = (Θ, β, Λ_int, Λ_ext). For i = 1, …, n + N, we have defined estimating functions Ψ_i(Ω), which we have defined in such a way that E{Ψ_i(Ω)} = 0 for i = 1, …, n + N: the expectations are unconditional, although in implementing the estimators we have exploited our Assumptions 1–3 to simplify the numerical calculations. Having done all this, we are now in the realm of estimating equation theory. Sufficient but not necessary conditions for our asymptotic theory to hold are the following.

• The parameter space is compact. This is not necessary but it is convenient for proving consistency.

• There is a unique Ω in the parameter space such that E{Ψ_i(Ω)} = 0 for all i = 1, …, n + N.

• The estimating equations Ψ_i(Ω) are 3-times continuously and boundedly differentiable in the parameter space.

• The estimating equation $0={\sum }_{i=1}^{n+N}{\mathrm{\Psi }}_i(\Omega )$ has a unique solution.

• The matrix E{∂Ψ_i(Ω)/∂Ω^T} is of full rank within a neighborhood of the true parameter value.

• For sufficiently large (n, N), within a neighborhood of the true parameter value, ${(n+N)}^{-1}{\sum }_{i=1}^{n+N}\partial {\mathrm{\Psi }}_i(\Omega )/\partial {\Omega }^{\text{T}}$ is of full rank with eigenvalues bounded away from 0 and ±∞.

Remark 6.

The major new item here in verifying the assumptions mentioned in Remark 5 are the differentiability assumptions having to do with Q(W, Z, Θ, β, Λ_int, Λ_ext) in (12). Let the conditional density/mass function of Y given (X, Z) be f_Y|X,Z (·, β, Λ_int, Λ_ext) and the conditional density/mass function of X given (W, Z) be f_X|W,Z(·, Λ_int, Λ_ext). Let dν(y) and dν(x) be integrals/counts as the case requires. Then (12) can be written out as

$$Q\left(W,Z,\Theta ,\beta ,{\Lambda }_{\text{int}},{\Lambda }_{\text{ext}}\right)=\int \left\{\int {\mathrm{\Phi }}_{\text{cat}}\{y,M(x,Z),\Theta \}{f}_{Y|X,Z}\left(y|x,Z,\beta ,{\Lambda }_{\text{int}},{\Lambda }_{\text{ext}}\right)d\nu (y)\right\}\times f_{X|W,Z}\left(x|W,Z,{\Lambda }_{\text{int}},{\Lambda }_{\text{ext}}\right)d\nu (x).$$

Then the non-standard differentiability assumptions in Remark 5 are really about the differentiability assumptions of Φ_cat{y, M(x, Z), Θ}, f_Y|X,Z(·, β, Λ_int, Λ_ext) and f_X|W,Z(·, Λ_int, Λ_ext) with respect to the parameters.

4. Simulations: Logistic and linear regression

4.1. Logistic regression

4.1.1. Scenarios

For simplicity, we do our simulations in the case that there is no Z. For logistic regression, we assume that the true model is

$$\text{pr}(Y=1|X)=H\left({\beta }_0+X{\beta }_1\right)=H\{(1,X)\beta \},$$ (15)

where H(·) is the logistic distribution function. Then we generate data as

$$W=X+U;X=\text{Normal}\left({\mu }_x,{\sigma }_x^2\right);U=\text{Normal}\left(0,{\sigma }_u^2\right),$$ (16)

where X and U are independent. We set β₀ = −0.42 and set β₁ = log(1.5) in Table 1. We set (μ_x = 0, ${\sigma }_x^2=1$, ${\sigma }_u^2=1$), so that the measurement error variance is the same as the variance of X, and the classical attenuation coefficient is $\lambda ={\sigma }_x^2/\left({\sigma }_x^2+{\sigma }_u^2\right)$. Solving (8) numerically, we find that Θ = (−0.98, −0.64, −0.42, −0.21, 0.14)^T. In both cases, the main study sample size is n = 500.

We used the quintiles of the distribution of X to define the categories. This is because, as stated in the introduction, we have our goal is to obtain consistent estimates of what epidemiologists would have obtained if X were actually observed, in this case, the quintiles of X.

We did simulations in two cases:

1. External-Internal Data: The internal data has no replicates and the external data set has size N = 300 and K = 2 replicates for each observation. The nuisance parameters are ${\Lambda }_{\text{ext}}={\sigma }_u^2$ and ${\Lambda }_{\text{int}}=\left({\mu }_x,{\sigma }_x^2\right)$. We estimated ${\sigma }_u^2$ from the external data with replicates, and estimated μ_x, ${\sigma }_x^2$ using the internal data without any replicates. Standard errors were computed as in Lemma 1.

2. Internal Data Only: The internal data has R = 2 replicates and there are no external data (K = 0). The nuisance parameters $\Lambda ={\Lambda }_{\text{int}}=\left({\mu }_x,{\sigma }_x^2,{\sigma }_u^2\right)$. We estimated (μ_x, ${\sigma }_x^2$, ${\sigma }_u^2$) from the internal data with replicates. Standard errors were computed as in Lemma 2.

C.3 provides details of implementation.

4.1.2. Results

The results given below are similar, and indeed even more impressive, when the main study sample size n increases to n = 1,000, 2,000 and 3,000, and thus these are not displayed here. The results are also similar when β₁ is either smaller or larger. The same qualitative results are also found for Θ = (θ₁, …, θ₅)^T individually (results not shown).

We fit the new approach and compare it with the naive method for the both cases described above. Our main interest is to estimate the log relative risk θ₅ − θ₁, which compares the effect of the category 5 with the effect of the category 1. In the two simulations, we computed (a) the log relative risk pretending that X is observed; (b) our method; and (c) the naive method that ignores measurement error. In the scenario of internal data with R = 2, the predictor used was the sample mean of the replicates.

Based on 1000 simulated data sets, in Table 1, we report the empirical average mean bias, asymptotic standard error, standard deviation, root mean squared error, and coverage rate of the nominal 95% confidence interval across the simulations.

From Table 1, we observe the following.

• The estimator using true X and our method both have little bias and provide near-nominal coverage.

• The naive estimator that ignores the measurement error is badly biased and attenuated towards zero. Consequently the coverage probabilities are near-zero and the root mean squared errors are quite inflated.

• With no internal replicates, i.e., R = 1, the root mean squared error of our method is naturally higher than if X had been observed, but not quite as high as would be expected in a continuous analysis. Indeed, in a continuous analysis with attenuation λ = 0.50, as in our simulation, one would expect a doubling of root mean squared error.

4.2. Linear regression

4.2.1. Scenarios

In this section, we do simulations based on simple linear regression with no Z, including homoscedastic and heteroscedastic cases.

We assume that the true model is

$$Y={\beta }_0+X{\beta }_1+ϵ=(1,X)\beta +ϵ,$$ (17)

Similarly, we generate data as

$$W=X+U;X=\text{Normal}\left({\mu }_x,{\sigma }_x^2\right);U=\text{Normal}\left(0,{\sigma }_u^2\right).$$

We set β₀ = 0 and set β₁ = 0.75 and studied two cases: (a) homoscedastic with ϵ ~ N(0, 1); and (b) heteroscedastic with ϵ ~ N(0, 0.2 + 0.5ײ). The classical attenuation coefficient and sample size are the same as in Section 4.1. Solving (8) numerically, we find that Θ = (−1.04, −0.40, 0.00, 0.40, 1.05)^T. C.2 provides implementation details.

4.2.2. Results

Similarly as before, our main interest is to estimate θ₅ − θ₁, which compares the effect of the category 5 with the effect of the category 1. In the two simulations, we computed θ₅ − θ₁ (a) pretending that X is observed; (b) our methods; and (c) the naive method that ignores measurement error. For the naive method, in internal data with R = 2, the predictor used is the sample mean of the replicates.

Based on 1000 simulated data sets, in Table 2, we report the empirical average mean bias, asymptotic standard error, standard deviation, root mean squared error, and coverage rate of the nominal 95% confidence intervals across the simulations.

From Table 2, we see that similar conclusions can be drawn as in Section 4.1. However, an interesting thing is in the heteroscedastic case, when noise ϵ has its variance related to X. Assuming that X is observed, the coverage rate of nominal 95% confidence intervals is low, because the heteroscedasticity is ignored. Using our method, we can get close to nominal coverage without knowing any information about the noise ϵ. Thus, this example shows that our method is very general as we stated in Example 1(A).

5. Empirical example

5.1. Data description

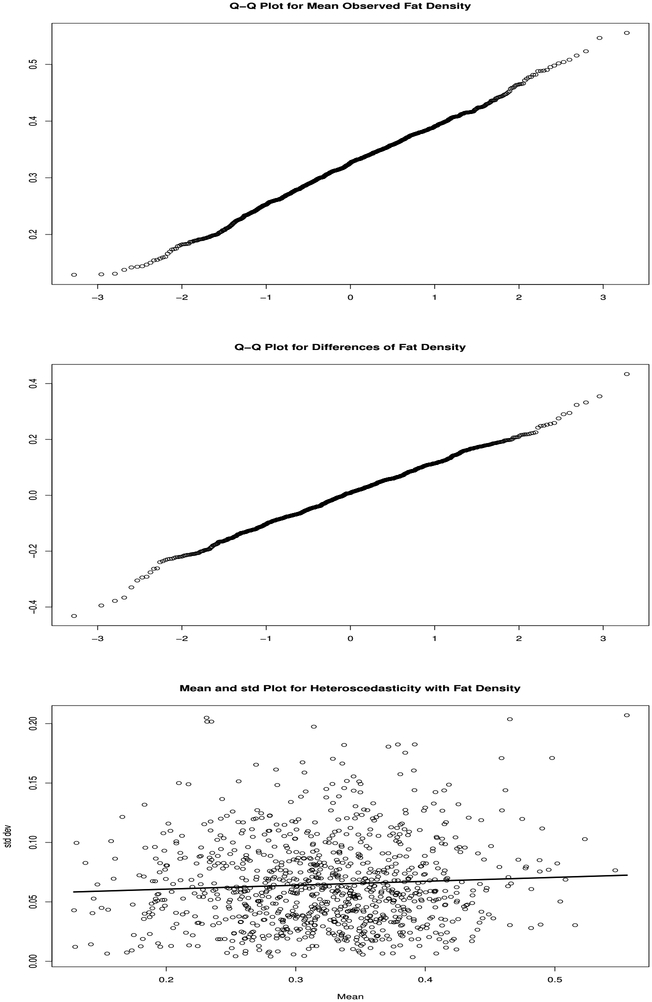
We illustrate our methods using data from the Eating at America’s Table (EATS) Study [23], in which 964 participants completed multiple 24-hour recalls of diet. We consider the variable Fat Density, which is the percentage of calories coming from Fat. The response Y is either (i) the indicator of obesity, which means that a subject’s body mass index (BMI, weight in kilograms divided by the square of height in meters) is 30 or greater. or (ii) the actual body mass index. We assume that W, is unbiased for usual intake X, and that W = X +U. It is reasonable in these data to take (a) X to be normally distributed, (b) that U is normally distributed; and (c) that X and U are independent, as we now describe. We used the methods described in [9] and Chapter 1.7 of [4], which also give the rationale for these methods. Specifically, for (a), as they suggest a qq-plot of the individual means for Fat Density looked acceptably normal, with skewness and kurtosis = −0.06 and 3.02, respectively, see the top panel of Figure 1. For (b), as they suggest, we took differences of the first and second Fat Density measurements, which had skewness (theoretically = 0) and kurtosis = −0.14 and 3.40, respectively: the somewhat higher kurtosis here is seen to be minor on the qq-plot, see the middle panel of Figure 1. Finally, for (c), they suggest analyzing the correlation between the individual-level mean and standard deviation = 0.06, and there was no obvious strong pattern when we plotted the data the latter against the former, see the bottom panel of Figure 1.

For numerical stability, our analysis in the continuous scale is uses centered and standardized W using $(15W-5)/\sqrt{0.5}$. To illustrate an example of an internal and an external study, we randomly selected N = 200 subjects as the external study to have the first two 24-hour recalls, while using the remaining data as the main internal study. As in the simulation, we either set the number of recalls R = 1, K = 2, meaning the external study data were used to estimate the measurement error variance, for R = 2, K = 0, in which case the external data were not used.

5.2. Results

5.2.1. Logistic regression

As described in Section 4.1, we assume the true model defined by (15)–(16), and the respective two cases. In this application we again estimate the log relative risk θ₅ − θ₁. We fit both our new approach and the naive model that ignores measurement error when external data is and is not used.

In Table 3, we observe that when using the external data and only 1 observation in the internal data the estimate of the log relative risk θ₅ − θ₁ from our approach is 108% greater than the naive estimate, while when using internal data with two replicates our estimate of our approach is 32% greater than the naive estimate. This makes sense because the second case uses the mean of two replicates, hence has smaller measurement error variance, and thus the naive estimate will be closer to our method.

In both cases, the asymptotic standard error from our new method is greater than the naive method, which led to wider confidence intervals. This makes sense, because with a scalar covariate measured with error, correcting for measurement error bias usually increases estimated standard errors, while of course reducing bias.

5.2.2. Linear regression

Next we consider the linear model with body mass index as the response. All assumptions for W, X and U are the same as in Section 5.1. Moreover, we maintain the standardization and sampling scheme in Section 5.1: the results are presented in Table 4.

From Table 4, we observe similar conclusions as in logistic regression case. One point of particular interest is that in both scenarios (external-internal or internal data only), our estimator converges theoretically to the same value, and this is seen in the results. The naive method that ignores measurement error estimates different parameters because the measurement error variance is twice as large in the external-internal case as it is in the internal-only case.

6. Other approaches and the assumptions

6.1. Other approaches

We emphasize once more that it is common practice in epidemiology to categorize a continuous predictor, and we have given numerous citations of this practice. Generally, this practice results in a misspecified model.

Our goal is to correct the analysis so as to reproduce, asymptotically, the estimators that would have been obtained if there were no measurement error. The problem has not been considered previously in the context that a continuous predictor has been categorized. Such categorization generally leads to differential measurement error [11, 13, 3], and thus additional complications over simply fitting a measurement error model.

While our paper is the first to consider the issue of how to correct an analysis to account for a continuous predictor that is categorized, there are of course other possible approaches, but none of them really avoids the basic issues we have discussed of what is needed to obtain consistent estimators with asymptotically correct inference in the case of measurement error.

• For example, one could assume that the true risk model is based upon the categorized truth, even if this is implausible in most contexts. One could further assume that the misclassification is nondifferential, which is incorrect if the true risk model is in the continuous scale [11, 13, 3]. There is a small literature on this problem. [13], especially Chapter 6.1, has remarks on the bias induced when a binary predictor is misclassified. [3], Chapter 6.7.7 and Chapter 6.14, has a detailed discussion of the issue, and provides a number of references to the problem. Both [13] and [3] show that a measurement error correction will require a distribution for the categorical X given (W, Z), sometimes called the reclassification rate, and both indicate that there are substantive issues, including identifiability, involved with estimating these models. For replication studies wherein W is measured repeatedly on a subset of the data, there is some evidence that 3 replicates will result in identifiability. However, both books emphasize the use of internal validation substudies, wherein one actually observes X in a substudy.

• If X_cat is the categorized truth, then one might attempt an analysis based on assuming a joint distribution of (Y, W, X_cat) given Z, but as in any measurement error model [4], the joint distribution requires (a) a distribution for Y given (X_cat, W, Z), and (b) the distribution of (W, X_cat) given Z. However, (a) actually depends on W, and thus that the modeling presents additional complications. In addition, (b) is no easier than ours, can be implausible and does not make fewer assumptions than we have done.

• Simulation-extrapolation, or SIMEX, [6, 22, 4] is a well-known approach to the creation of approximately, but not fully, consistent estimators for additive measurement error models of the form W = X +Z^Tα +U, where U is independent of Z and can be homoscedastic or heteroscedastic but has replicates [8], and is generally taken to be normally distributed. This literature attempts to dispense with distributional assumptions for X for the continuous case, but is at best approximately correct. The fact that a categorized risk model is implausible, leading to differential measurement error, may also cause complications, but the use of SIMEX in this context is a worthwhile topic for further study. We also mention the MCSIMEX procedure [16], which is appropriate for misclassified data where the misclassification probabilities can be estimated.

• It is also possible to change the paradigm entirely and avoid categorization, and all the issues related to categorization, by instead using Bsplines. Indeed, part of the reason sometimes given for categorizing a continuous predictor and not modeling a response linearly in the continuous X is that it could lead to unduly extreme comparisons for risk between the lowest and the highest values of X. The general thought is that this can be overcome by replacing the linear X by a Bspline in X. There are papers involving Bsplines and measurement error [2, 12, 18], and it appears that regression calibration can possible be used by calibrating each spline basis function. After the fitting, one could compare the Bspline fits at the 10^th, 30^th, 50^th, 70^th and 90^th percentiles of X to form versions of the tables found in epidemiology papers, but the interpretations are not fully comparable.

We showed how to solve this problem and given asymptotically consistent estimators with asymptotically correct standard errors. Assumption 2 is reasonable in other contexts than ours, for example, that X has a mixture-of-normals distribution and U is normally distributed [7].

6.2. Assumptions in the simulations and example

Readers of an initial version of this paper have noted that our simulations and data example use the assumption that the distribution of X given (W, Z) is normally distributed, but misinterpreted this fact into concluding that the approach is only applicable in that case. For the data example in Section 5, we justified the assumptions using known methods for model checking of measurement error models. Assumption 2 is widely used and reasonable in many other contexts than ours numerical work, for example, that X has a mixture-of-normals distribution and U is normally distributed [7]. Modeling via mixture distributions is a reasonable way to extend what we have done in the classical error case. See also [21] for the homoscedastic and heteroscedastic cases when the variance function and the distributions of X and U are modeled as mixture distributions.

Many papers in the literature also rely on the existence of validation data, where X is actually observed in a subset of the main data set. In that case, Assumption 2 is easily checked by model fitting and validation on the observed validation data subset.

6.3. Categorization

In Section 2.1, we stated that the number J of categories was set by the investigators, Usually, J = 3, 4 or 5, as seen by the examples cited in the introduction. In addition, setting the category limits is also an art, and may be based on (a) limits in the literature; (b) limits based on the error-prone instrument, such as the quintiles of a food frequency questionnaire or 24-hour recall; and (c) limits based on a measurement error analysis. Since our goal is to construct the analysis that would have been done if X could be observed, we use the latter.

Appendix A: Sketch of technical arguments

A.1. Argument for Lemma 1

We consider the case that there are external data used to estimate Λ_ext and that there are parameters Λ_int. As in Section 3.2, the data for i = 1, …, n are for the internal data, while, for i = n + 1, …, n + N, are for the external data if such external data exist and are used. The functions Ψ_i(Ω) are also defined in Section 3.2. By Taylor series,

$$\begin{gathered} {\left(n+N\right)}^{-1/2}{\sum }_{i=1}^{n+N}\left\{{\mathrm{\Psi }}_i(\widehat{\Omega })-{\mathrm{\Psi }}_i(\Omega )\right\}={\left(n+N\right)}^{-1/2}{\sum }_{i=1}^{n+N}\left\{\frac{\partial {\mathrm{\Psi }}_i(\Omega )}{\partial \Omega }\left(\widehat{\Omega }-\Omega \right)+o_p\left(\Vert \widehat{\Omega }-\Omega \Vert \right)\right\} \\ =\left\{{\left(n+N\right)}^{-1}{\sum }_{i=1}^{n+N}\frac{\partial {\mathrm{\Psi }}_i(\Omega )}{\partial \Omega }\right\}{\left(n+N\right)}^{1/2}\left(\widehat{\Omega }-\Omega \right)+o_p(1). \end{gathered}$$

For logistic regression and linear regression, the forms of Ψ_i(Ω) can be found in Appendix C. Thus,

$${(n+N)}^{1/2}(\widehat{\Omega }-\Omega )=-{\left\{{(n+N)}^{-1}\sum _{i=1}^{N+n}\partial {\mathrm{\Psi }}_i(\Omega )/\partial \Omega \right\}}^{-1}{(n+N)}^{-1/2}\sum _{i=1}^{N+n}{\mathrm{\Psi }}_i(\Omega )+o_p(1).$$

It is obvious that ${(n+N)}^{-1}{\sum }_{i=1}^{N+n}\partial {\mathrm{\Psi }}_i(\Omega )/\partial \Omega =A+o_p(1)$, and immediate that ${(n+N)}^{-1/2}{\sum }_{i=1}^{N+n}{\mathrm{\Psi }}_i(\Omega )\to \text{Normal}(0,B)$, where A and B are defined in Lemma 1.

A.2. Argument for Lemma 2

We consider the case that there are only parameters Λ_int. As in Section 3.2, the data for i = 1, …, n are for the internal data. The functions Ψ_i(Ω) are also defined in Section 3.2. Then

$$\begin{gathered} 0=n^{-1/2}\sum _{i=1}^n{\mathrm{\Psi }}_i(\widehat{\Omega }) \\ =n^{-1/2}\sum _{i=1}^n{\mathrm{\Psi }}_i(\Omega )+\left\{n^{-1}\sum _{i=1}^n\partial {\mathrm{\Psi }}_i(\Omega )/\partial \Omega \right\}{n}^{1/2}(\widehat{\Omega }-\Omega )+o_p(1), \end{gathered}$$

so that

$$n^{1/2}(\widehat{\Omega }-\Omega )=-{\left\{n^{-1}\sum _{i=1}^n\partial {\mathrm{\Psi }}_i(\Omega )/\partial \Omega \right\}}^{-1}{n}^{-1/2}\sum _{i=1}^n{\mathrm{\Psi }}_i(\Omega )+o_p(1).$$

As in A.1, $n^{-1}{\sum }_{i=1}^n\partial {\mathrm{\Psi }}_i(\Omega )/\partial \Omega =A+o_p(1)$, and ${(n+N)}^{-1/2}{\sum }_{i=1}^{N+n}{\mathrm{\Psi }}_i(\Omega )\to \text{Normal}(0,B)$, where A and B are defined in Lemma 2.

Appendix B: Tables for simulations and EATS data analysis

Table 1.

Simulation study for logistic regression in Section 4.1 with sample size n = 500 and, where applicable, the external study has sample size N = 300 and 2 replicates, while β₀ = −0.42, β₁ = log(1.5). The target parameter, Θ = (θ₁, …, θ₅)^T, where θ_j is the parameter for the j^th category. Displayed are results for the estimation of the log relative risk, θ₅ − θ₁. Ext-Int Data is the case that external data are used to estimate the measurement error variance. Int Data is the case that the internal data have 2 replicates, and the Ignore ME estimator ignores the measurement error and is based on the mean of these replicates. Coverage is the coverage rate of nominal 95% confidence intervals. RMSE is the square root of the mean squared error.</Table_Caption>

		Log Relative Risk Analysis
Data	Method	mean bias	Mean Estimated Std. Err.	Actual Standard Deviation	RMSE	Coverage
X observed		0.016	0.304	0.301	0.301	95.2%
Ext-Int Data
	Our Method	−0.005	0.41	0.402	0.402	94.5%
	Ignore ME	−0.453	0.251	0.256	0.520	0%
Int Data
	Our method	0.005	0.361	0.323	0.323	95.9%
	Ignore ME	−0.287	0.268	0.266	0.391	80.2%

Table 2.

Simulation study for linear regression in Section 4.2 with n = 500 and, where applicable, the external study has sample size N = 300 and 2 replicates, while β₀ = 0, β₁ = 0.75. The target parameter, Θ = (θ₁, …, θ₅)^T, where θ_j is the parameter for the j^th category. Displayed are results for the estimation of θ₅ − θ₁. Ext-Int Data is the case that external data are used to estimate the measurement error variance. Int Data is the case that the internal data have 2 replicates, and the Ignore ME estimator ignores the measurement error and is based on the mean of these replicates. Coverage is the coverage rate of nominal 95% confidence intervals. RMSE is the square root of the mean squared error.

		Results Analysis (θ5 − θ1)
Data	Method	mean bias	Mean Estimated Std. Err.	Actual Standard Deviation	RMSE	Coverage
			Homoscedastic ϵ ~ N(0, 1)
X observed		0.004	0.145	0.150	0.150	95.1%
Ext-Int Data
	Our Method	0.013	0.249	0.233	0.233	95.8%
	Ignore ME	−0.814	0.139	0.142	0.826	0.1%
Int Data
	Our method	−0.007	0.176	0.170	0.170	95.3%
	Ignore ME	−0.536	0.142	0.145	0.555	3.7%
			Heteroscedastic ϵ ~ N(0,0.2 + 0.5x2)
X observed		0.004	0.123	0.169	0.169	85.3%
Ext-Int Data
	Our Method	0.011	0.261	0.245	0.245	95.9%
	Ignore ME	−0.814	0.122	0.135	0.825	0.1%
Int Data
	Our Method	−0.010	0.197	0.189	0.189	95.9%
	Ignore ME	−0.537	0.123	0.141	0.555	1.8%

Table 3.

Data analysis for logistic regression in Section 5. The target parameter, Θ = (θ₁, …, θ₅)^T, where θ_j is the parameter for the j^th category. Displayed are results for the estimation of the log relative risk, θ₅ − θ₁. Ext-Int Data is the case that external data are used only to estimate the measurement error variance, and the external data have 2 replicates. Int Data is the case that the internal data have 2 replicates, and the Ignore ME estimator ignores the measurement error and is based on the mean of these replicates. Asymptotic Std. Err. is the standard error estimate from the theory. CI is the nominal 95% confidence interval for the log relative risk. p-value is the p-value for the test that the log relative risk = 0.</Table_Caption>

		Log Relative Risk Analysis
Data	Method	Estimate	Asymptotic Std. Err.	95% CI	p-value
Ext-Int Data
	Our Method	0.98	0.47	(0.06,1.90)	0.036
	Ignore ME	0.47	0.24	(0.00, 0.95)	0.049
Int Data
	Our Method	1.10	0.34	(0.43,1.77)	0.001
	Ignore ME	0.83	0.22	(0.39,1.26)	0.000

Table 4.

Data analysis in for linear regression Section 5. The target parameter, Θ = (θ₁, …, θ₅)^T, where θ_j is the parameter for the j^th category. Displayed are results for the estimation of θ₅ − θ₁. Ext-Int Data is the case that external data are used only to estimate the measurement error variance, and the external data have 2 replicates. Int Data is the case that the internal data have 2 replicates, and the Ignore ME estimator ignores the measurement error and is based on the mean of these replicates. Asymptotic Std. Err. is the standard error estimate from the theory. CI is the nominal 95% confidence interval for θ₅ − θ₁. p-value is the p-value for the test that θ₅ − θ₁ = 0.

		Results Analysis (θ5 − θ1)
Data	Method	Estimate	Asymptotic Std. Err.	95% CI	p-value
Ext-Int Data
	Our Method	0.59	0.18	(0.24, 0.95)	0.001
	Ignore ME	0.28	0.10	(0.09, 0.47)	0.004
Int Data
	Our Method	0.56	0.13	(0.30,0.81)	0.000
	Ignore ME	0.35	0.09	(0.18,0.52)	0.000

Fig 1.

EATS data of Section 5. Top panel: Normal qq-plot of the mean Fat Density over 4 recalls. This indicates that the mean Fat Density is approximately normally distributed and qualifies for the assumptions in our numerical example. Middle panel: Normal qq-plot of differences of observed Fat density, as a diagnosis that U is approximately normally distributed. Bottom panel: Mean and standard deviation plot to diagnose heteroscedasticity, showing that there is little heteroscedasticity in the measurement errors.

Appendix C: Estimating equations for linear and logistic regression

C.1. Estimating the nuisance parameter Λ

Here we only consider two cases among numerous possibilities. One is that the internal data consists of (Y_i, W_i, Z_i) for i = 1, …n and ${\sigma }_u^2$ is estimated from the external data using replicates W_ik for k = 1, …, K and i = n + 1, …, n + N. The second case is that the replicates are in the internal data.

C.1.1. External-internal data

For specificity, we consider the first case that the external data have no responses Y, are independent of the internal data. Suppose that we use external data only to estimate ${\sigma }_u^2$, and we observe W_ik = X_i + U_ik for k = 1, …, K and i = n+1, …, n+N. We use internal data to estimate μ_x, ${\sigma }_x^2$ without replicates. In the external data, let ${\overline{W}}_i=K^{-1}{\sum }_{k=1}^K{W}_{ik}$. Define ${\widehat{\sigma }}_{u,i}^2={(K-1)}^{-1}{\sum }_{k=1}^K{\left(W_{ik}-{\overline{W}}_i.\right)}^2$ to be the sample variance of the W_ik for a given i. Because $E\{\left(W_i-{\mu }_x\right){}^2)={\sigma }_x^2+{\sigma }_u^2$, unbiased estimating equations for $\left({\Lambda }_{\text{ext}},{\Lambda }_{\text{int}}\right)=\left({\mu }_x,{\sigma }_x^2,{\sigma }_u^2\right)$ are

$$\begin{gathered} \text{For\hspace{0.17em}}{\mu }_x:n^{-1}{\sum }_{i=1}^n\left(W_i-{\mu }_x\right)=0; \\ For{\sigma }_u^2:N^{-1}{\sum }_{i=n+1}^{n+N}\left({\widehat{\sigma }}_{u,i}^2-{\sigma }_u^2\right)=0; \\ \text{For\hspace{0.17em}}{\sigma }_x^2:n^{-1}{\sum }_{i=1}^n\left\{{\left(W_i-{\mu }_x\right)}^2-{\sigma }_x^2-{\sigma }_u^2\right\}=0. \end{gathered}$$

C.1.2. Internal data only

Suppose there is no external data, and we have replicates W_ir for r = 1, …, R in the internal data. Now we use internal data to estimate $\Lambda =\left({\mu }_x,{\sigma }_x^2,{\sigma }_{uR}^2\right)$, and we observe W_ir = X_i + U_ir for r = 1, …, R and i = 1, …, n.

Define ${\overline{W}}_i=R^{-1}{\sum }_{r=1}^R{W}_{ir}$. Define ${\widehat{\sigma }}_{u,i}^2$ to be the sample variance of the W_ir within subject i, and define ${\sigma }_u^2/R={\sigma }_{uR}^2$. The estimating equations are

$$\begin{gathered} \text{For\hspace{0.17em}}{\mu }_x:n^{-1}{\sum }_{i=1}^n\left({\overline{W}}_i.-{\mu }_x\right)=0; \\ For{\sigma }_{uR}^2:n^{-1}{\sum }_{i=1}^n\left({\widehat{\sigma }}_{u,i}^2/R-{\sigma }_{uR}^2\right)=0; \\ \text{For\hspace{0.17em}}{\sigma }_x^2:n^{-1}{\sum }_{i=1}^n\left\{{\left({\overline{W}}_i.-{\mu }_x\right)}^2-{\sigma }_x^2-{\sigma }_{uR}^2\right\}=0. \end{gathered}$$

Since the two cases we considered are the same as in linear regression and logistic regression, the way we estimate Λ_int and Λ_ext are exactly the same. Then we will only give details for the estimating equations about β and Θ below.

C.2. Details for linear regression

C.2.1. Background

Here we give full details of our methodology for linear regression. As in Lemma 1, Ω = (Θ, β, Λ_int, Λ_ext).

Let $\tilde{Z}={\left(1,Z^{\text{T}}\right)}^{\text{T}}$. Here we consider the simple case of linear regression with the classical measurement error model in both the external and internal data sets to be

$$\begin{gathered} Y=X{\beta }_1+{\tilde{Z}}^{\text{T}}{\beta }_2=\left(X,{\tilde{Z}}^{\text{T}}\right)\beta ; \\ W=X+U;X=\text{Normal}\left({\tilde{Z}}^{\text{T}}\alpha ,{\sigma }_x^2\right);U=\text{Normal}\left(0,{\sigma }_u^2\right). \end{gathered}$$

C.2.2. The forms of Φ(·)

In this linear model, denote the estimating equations for β as Φ(·), we consider

$$\mathrm{\Phi }\left(Y,W,Z,\beta ,{\Lambda }_{\text{int}},{\Lambda }_{\text{ext}}\right)={(1,W)}^{\text{T}}\left(Y-W{\beta }_1-{\tilde{Z}}^{\text{T}}{\beta }_2\right)+{\left(0,{\beta }_1{\sigma }_u^2\right)}^{\text{T}}.$$

C.2.3. The forms of Φ_cat(·) and Q(·)

Since we assume the true model is $Y=\left(X,{\tilde{Z}}^{\text{T}}\right)\beta$, it is easy to see that categorical estimating function

$${\mathrm{\Phi }}_{\text{cat}}\left\{Y,M^{\text{T}}(X,Z)\Theta \right\}=M(X,Z)\left[Y-M^{\text{T}}(X,Z)\Theta \right].$$

Hence, by simple calculations and following Remark 3, with Ω = (Θ, β, Λ_int, Λ_ext),

$$Q(W,Z,\Omega )=E\left[M(X,Z)\left\{\left(X,{\tilde{Z}}^{\text{T}}\right)\beta -M^{\text{T}}(X,Z)\Theta \right\}|W,Z\right].$$

We used the integrate function in the R package stats to compute the integrals.

The estimating function for β = (β₀, β₁) is

$$\mathrm{\Phi }(\beta ,\widehat{\Lambda })=n^{-1}{\sum }_{i=1}^{n}E\left(\left[Y_i-H\left\{m\left(X_i,\beta \right)\right\}\right]\partial m\left(X_i,\beta \right)/\partial {\beta }^{\text{T}}|W_i\right).$$

The estimating function for Θ is

$$Q\left(W_i,\Theta ,\widehat{\beta },\widehat{\Lambda }\right)=E\left[\begin{array}{c}m\left(X_i,\widehat{\beta }\right)I\left(X_i\in C_1\right)-{\Theta }_{1}I\left(X_i\in C_1\right)\\ ⋮\\ m\left(X_i,\widehat{\beta }\right)I\left(X_i\in C_J\right)-{\Theta }_{J}I\left(X_i\in C_J\right)\end{array}|W_i\right].$$

Asymptotic standard errors were estimated as in Lemma 1 and Lemma 2.

C.3. Details for logistic regression

C.3.1. Background

Here we give full details of our methodology for logistic regression. As in Lemma 1, Ω = (Θ, β, Λ_int, Λ_ext).

As before, let H(·) denote the logistic distribution function and let $\tilde{Z}={\left(1,Z^{\text{T}}\right)}^{\text{T}}$. Here we consider the special case of linear logistic regression with the classical measurement error model in both the external and internal data sets to be

$$\begin{gathered} pr(Y=1|X,Z)=H\left(X{\beta }_1+{\tilde{Z}}^{\text{T}}{\beta }_2\right)=H\left\{\left(X,{\tilde{Z}}^{\text{T}}\right)\beta \right\}; \\ W=X+U;X=\text{Normal}\left({\tilde{Z}}^{\text{T}}\alpha ,{\sigma }_x^2\right);U=\text{Normal}\left(0,{\sigma }_u^2\right). \end{gathered}$$

Different from the linear case in Section C.2, we consider the case where X depends on another covariate Z. There are numerous data structures possible, but we here present the external-internal and internal data only cases.

C.3.2. Settings

There are two settings of interest.

• There is no information about ${\sigma }_u^2$ in the internal data, so that the external parameter is the measurement error variance, ${\Lambda }_{\text{ext}}={\sigma }_u^2$, while the internal parameters are ${\Lambda }_{\text{int}}={\left({\alpha }^{\text{T}},{\sigma }_x^2\right)}^{\text{T}}$.

• There are no external data, so that Λ_ext is null, and the internal data with replicates allow estimation of ${\Lambda }_{\text{int}}={\left({\alpha }^{\text{T}},{\sigma }_u^2,{\sigma }_x^2\right)}^{\text{T}}$.

In both case, ${\sigma }_u^2$ (or ${\sigma }_{uR}^2$ in the internal data only case) are estimated the same as in C.1.1 and C.1.2, while the estimating function for (α, ${\sigma }_x^2$) is

$$V_{\text{int},i}\left({\Lambda }_{\text{int}},{\Lambda }_{\text{ext}}\right)=\left\{{\tilde{Z}}_i^{\text{T}}\left(W_i-{\tilde{Z}}_i^{\text{T}}\alpha \right),{\left(W_i-{\tilde{Z}}_i^{\text{T}}\alpha \right)}^2-{\sigma }_x^2-{\sigma }_u^2\right\},$$

where i = 1, …, n.

C.3.3. Estimating β

In this section, we implement our method and give all estimating equations in the case where we have both external and internal data. In another case, where we only use internal data with replicates, all results below are still valid by removing Λ_ext.

Define $\lambda ={\sigma }_x^2/\left({\sigma }_x^2+{\sigma }_u^2\right)$. Then, given (W, Z), X is normally distributed with mean $\mu \left(W,Z,{\Lambda }_{\text{ext}},{\Lambda }_{\text{int}}\right)={\tilde{Z}}^{\text{T}}\alpha +\lambda \left(W-{\tilde{Z}}^{\text{T}}\alpha \right)$ and variance $\lambda {\sigma }_u^2$. We write this conditional density as f_x|w,z(x, w, z, β, Λ_int, Λ_ext).

There are multiple ways to estimate β from the observed data. Here we describe two of them.

• The first is regression calibration, in which X is replaced by its mean given (W, Z) and the linear logistic model is fit. Thus the regression calibration method has

  $$\mathrm{\Phi }\left(Y,W,Z,\beta ,{\Lambda }_{\text{int}},{\Lambda }_{\text{ext}}\right)={\left\{\mu \left(W,Z,{\Lambda }_{\text{ext}},{\Lambda }_{\text{int}}\right),\tilde{Z}\right\}}^{\text{T}}\times \left[Y-H\left\{\mu \left(W,Z,{\Lambda }_{\text{ext}},{\Lambda }_{\text{int}}\right){\beta }_1+{\tilde{Z}}^{\text{T}}{\beta }_2\right\}\right].$$
• A second possibility, one that we used, is the following. By simple calculations, pr(Y = 1|W, Z) = p(W, Z, β, Λ_int, Λ_ext), where

  $$p\left(W,Z,\beta ,{\Lambda }_{\text{int}},{\Lambda }_{\text{ext}}\right)=\int H\left\{\left(x,{\tilde{Z}}^{\text{T}}\right)\beta \right\}{f}_{x|w,z}\left(x,W,Z,{\Lambda }_{\text{int}},{\Lambda }_{\text{ext}}\right)dx,$$

  a quantity that is easily computed in R using the integrate function in the R package stats. Denote p_i = pr(Y_i = 1|W_i, Z_i). Thus, the loglikelihood $\propto n^{-1}{\sum }_{i=1}^n{Y}_i\text{log}\left(p_i\right)+\left(1-Y_i\right)\text{log}\left(1-p_i\right)$. We then use optim function in the R package stats to minimize the negative loglikelihood to estimate β.

C.3.4. The forms of Φ_cat(·) and Q(·)

Since we assume the true model is $\text{pr}(Y=1|X,Z)=H\left\{\left(X,{\tilde{Z}}^{\text{T}}\right)\beta \right\}$, it is easy to see that categorical estimating function

$${\mathrm{\Phi }}_{\text{cat}}\left\{Y,M^{\text{T}}(X,Z)\Theta \right\}=M(X,Z)\left[Y-H\left\{M^{\text{T}}(X,Z)\Theta \right\}\right].$$

Hence, with Ω = (Θ, β, Λ_int, Λ_ext), by simple calculations and following Remark 3,

$$Q(W,Z,\Omega )=E\left(M(X,Z)\left[H\left\{\left(X,{\tilde{Z}}^{\text{T}}\right)\beta \right\}-H\left\{M^{\text{T}}(X,Z)\Theta \right\}\right]|W,Z\right).$$

We used the integrate function in the R package stats to compute the integrals.