Abstract
The effects of osmotic swelling on key cellular biomechanical properties are explored in this chapter. We present the governing equations and theoretical backgrounds of the models employed to estimate cell membrane tension and elastic moduli from experimental methods, and provide a summary of the prevailing experimental approaches used to obtain these biomechanical parameters. A detailed analysis of the current evidence of the effects of osmotic swelling on membrane tension and elastic moduli is provided. Briefly, due to the buffering effect of unfolding membrane reservoirs, mild hypotonic swelling does not change membrane tension or the adhesion of the membrane to the underlying cytoskeleton. Conversely, osmotic swelling causes the cell membrane envelope to stiffen, measured as an increase in the membrane elastic modulus.
1. INTRODUCTION
External mechanical forces and the biomechanical properties of extracellular environments are well recognized today to play major roles in numerous cell functions including proliferation, differentiation, cell—cell interactions and more. Multiple studies showed that cells respond to stretch, shear stress and stiffness of the extracellular matrix by activating mechano-sensitive signaling cascades which couple mechanical signals to cellular responses. Earlier studies traditionally assumed that since cells visibly swell when exposed to hypotonic solution, membrane stretch and increase in membrane tension should play the central role in the ability of cells to respond to hypotonic swelling and induce the regulatory volume decrease (RVD), a process responsible for cell volume homeostasis in hypotonic conditions. The general belief that cell swelling should result in membrane stretch and an increase in membrane tension was also used in multiple studies to determine whether a specific process is stretch-sensitive. However, several considerations led to questioning the assumption that cell swelling necessarily leads to an increase in membrane tension. Instead, accumulating evidence, including studies from our lab, suggest that osmotic swelling leads to stiffening of the cellular envelope with little or no effect on membrane tension. In this chapter, we will review and discuss the current state of knowledge about whether and how osmotic challenge affects membrane tension and elasticity.
1.1. Basic Considerations: Low Extensibility and Limits of Membrane Stretch before Lysis
Mechanically, membrane deformations can be defined by several different parameters: (1) an elastic modulus or an area expansion modulus that corresponds to membrane expansion without shearing or bending (2) a bending modulus corresponding to membrane bending without shearing or expansion; and (3) a shear modulus that corresponds to an elongation of the membrane without changing surface area or bending. For all three parameters, the greater the value of the modulus, the more resistant the membrane is to this particular form of deformation (Hochmuth & Waugh, 1987). Biological membranes were found to have high elastic moduli, indicating resistance to area expansion, low shear moduli, corresponding to the fluid nature of the membrane bilayer, and highly variable bending moduli, which depends on membrane composition and cytoskeleton attachment (Diz-Muñoz, Fletcher, & Weiner, 2013). These parameters suggest that cells have limited ability to increase membrane surface area via stretch in order to accommodate an increase in cell volume during cell swelling.
Consistent with these biomechanical considerations, early studies of the physical properties of the membranes of red blood cells established that these membranes are highly resistant to stretch (Evans & Fung, 1972; Evans & Leblond, 1973; Evans, Waugh, & Melnik, 1976). These studies showed that osmotic swelling of red blood cells resulted in little (up to 7%) or no detectable increase in the surface area. Furthermore, applying well-defined negative pressure to pre-swollen red blood cells, Evans et al. (1976) determined that the maximal area expansion that these cells can achieve before they undergo cell lysis ranges between 2 and 4% of the initial cell area in red blood cells that apparently do not have significant membrane reservoirs to unfold. Since cell swelling may result in a very significant increase in cell volume, the inability of the cell membrane to stretch indicates that swelling should be accompanied by recruiting membrane reservoirs, either from natural membrane unfolding or from fusion of intracellular vesicles (Clark, Wartlick, Salbreux, & Paluch, 2014; Dai & Sheetz, 1999; Sens & Turner, 2006).
1.2. Membrane Unfolding during Cell Swelling
Numerous studies showed that plasma membranes of mammalian cells are highly folded and include different types of invaginations, such as caveolae, clathrin-coated pits, and protrusions, such as microvilli (Vlahakis & Hubmayr, 2000). It is reasonable to assume, therefore, that cell swelling through water intake from the extracellular space during osmotic challenge should result in membrane unfolding, which would allow a significant increase in cell volume as water enters the cell, without stretching and lysing the plasma membrane, and without changing the total membrane surface area. Conceptually, this is a protective mechanism to accommodate acute cell swelling prior to the initiation of the regulatory volume decrease (RVD), a process of cell volume recovery. However, while membrane folds are clearly detected by scanning and TEM microscopy, it is difficult to quantify the unfolding process using microscopy techniques.
In our earlier study, we approached this question, therefore, by comparative analysis of an apparent surface area determined visually or electrically based on measuring cell capacitance (Fig. 1) (Levitan & Garber, 1997, pp. 245–267). The experiment was performed with human myeloma cells whose spherical shape allowed estimating their “visual” surface area by measuring their diameters. The capacitance based estimate of the area is based on the generally accepted assumption that membrane capacitance is directly proportional to the total membrane area and can be calculated using a typical specific capacitance of biological membranes of 1 µF/cm2 (Hille, 2001). It is also important to note that membrane area estimated from capacitance is expected to include all membrane folds unless they are electrically uncoupled from the membrane. Therefore, if membrane surface area increases because of the fusion of intracellular vesicles, membrane capacitance increases but if the membrane simply unfolds, capacitance should remain constant. Also, if significant stretching of the membrane were possible without lysis, this would be expected to increase cell capacitance as well. We observed that, as expected, exposing the cells to a hypotonic challenge resulted in a significant increase in the apparent “visual” surface area from below 500 µm2 to ~1500 ± 290 µm2, shown in Fig. 1A, corresponding to an increase in the cell diameter from ~30 to ~45 µm. However, the surface area of the cells estimated by measuring cell capacitance did not change during the swelling process (Fig. 1B and C). Furthermore, the “electrical” surface area measured prior to the osmotic challenge was 1590 ± 70 µm2, more than two fold higher than the “visual” area of the same cells. As the swelling developed, the two measurements converged, as the “visual” area increase and the “electrical” area remained constant. These observations, therefore, indicate that visual cell swelling of myeloma cells is a result of membrane unfolding.
Figure 1.
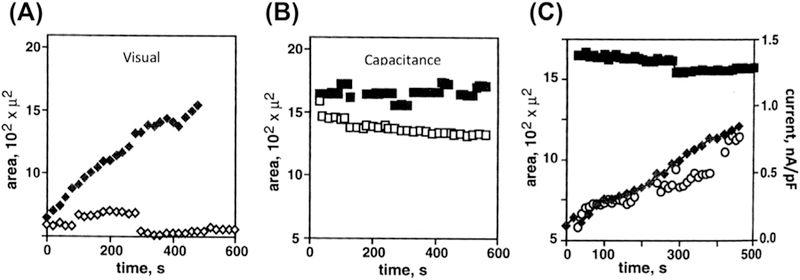
Cell membrane unfolding accompanies volume regulated ion channel (VRAC) activation. (A) The change in average cell surface area over time determined by visual measurement of cell radius using light microscopy with phase optics and a video camera. Data was analyzed using NIHImage software. Measurements made in isotonic solutions are shown with open symbols and those in 75% hypotonic solutions with solid symbols. (B) Average cell capacitance does not change in hypotonically-challenged (filled) or unchallenged (open) cells. For Panels A and B, each point represents n ≥ 3. (C) Simultaneous measurement of VRAC current amplitude (open circles) and surface area as determined from visual (solid diamonds) and capacitance (solid squares) measurements is shown for a representative cell in a hypotonic solution. Activation of VRAC correlates with an increase in surface area determined using visual but not electrical, measurement of cell surface area.
Consistent with these observations, we also observed no change in membrane capacitance during cell swelling in endothelial cells suggesting that these cells swell by unfolding membrane invaginations as well (Levitan, Christian, Tulenko, & Rothblat, 2000). These observations are also in agreement with earlier studies showing that while cell swelling in T-lymphocytes is accompanied by an increase in cell capacitance, presumably from the recruitment of intracellular membranes, there is no correlation between the time-courses of cell swelling and capacitance increase, indicating that swelling should involve membrane unfolding (Ross, Garber, & Cahalan, 1994). Similarly, another earlier study by Groulx, Boudreault, Orlov, and Grygorczyk (2006) used a 3D topography imaging technique to determine changes in cell volume and surface area for four mammalian cells types under hypotonic conditions. They found that cells could increase their volume about two fold by drawing on excess membrane from surface reservoirs. Moreover, the volume increased more than 10 fold and the surface area increased 3.6 times when intracellular membrane reserves were recruited, under extreme hypotonic conditions. Taken together, these studies indicate that cell swelling does not necessarily result in an increase in membrane tension because the process of membrane unfolding may accommodate significant cell swelling without any increase in tension. In the next part of this chapter, we will discuss the theoretical basis for estimating membrane tension and the experimental measurements of membrane tension during swelling (Part II. Membrane Tension).
Another important biomechanical parameter is the elastic modulus, which gives an indication of the stiffness or deformability of the material. Conceptually, it is important to discriminate between elastic moduli/deformability of the cellular membrane bilayer, the underlying sub-membrane cytoskeleton and the bulk cellular cytoskeleton. It is well-known that the thin lipid bilayer is much more deformable than the underlying cytoskeleton and as such does not contribute significantly to the stiffness of the cells. However, it may still play a significant role in the process of membrane unfolding described above, particularly if the unfolding is accompanied with detachment between the membrane and the sub-membrane cytoskeleton. If membrane unfolding occurs with the sub-membrane cytoskeleton still attached, the elastic properties of the membrane-bilayer/sub-membrane cytoskeleton complex, which together can be termed “cellular envelope,” are dominated by the cytoskeleton component. However, different cytoskeleton elements may also have very distinct elastic properties. Clearly, cellular biomechanical properties are highly heterologous and the values of the elastic moduli estimated experimentally may strongly depend on how exactly the deformability was measured. It is not surprising, therefore, that earlier studies produced controversial results for changes in membrane stiffness during osmotic swelling: The study of Zou et al. (2013) showed that cortical neurons undergo transient stiffening upon osmotic swelling, whereas Spagnoli, Beyder, Besch, and Sachs (2008) found significant softening in several cell types. In our recent study, we show that both significant stiffening and mild softening can be observed in the same cells at the same time depending on the depth of the mechanical perturbation used to estimate the stiffness (Ayee, LeMaster, Teng, Lee, & Levitan, 2018). In Part III of this chapter, we will discuss the theoretical considerations used to estimate cellular elastic moduli, experimental values for cell stiffening or softening obtained in different studies and their interpretations in terms of the underlying mechanisms (Part III. Elastic Modulus).
2. MEMBRANE TENSION
2.1. Theoretical Basis and Experimental Approaches of Measuring Membrane Tension
In the complex environment of a cell membrane, measuring membrane tension is not straightforward and frequently there is a lack of clarity about the interpretations of the measurements. In the next part of this chapter we will discuss the theoretical basis and experimental approaches that are currently used to estimate membrane tension in cell membranes and then discuss the current evidence to determine whether osmotic swelling results in an increase in membrane tension in different cell types and conditions.
The current experimental approaches to estimate membrane tension are based on changes in the free energy of the bilayer upon mechanical perturbation. The lipid bilayer is composed of two monolayers of amphiphilic phospholipid molecules forming a quasi-two-dimensional fluid structure. The thickness of this structure is on the order of a few nanometers (Edidin, 2003), while the lateral size can be several micrometers wide. The mechanical properties of this membrane structure make it highly resistant to lateral stretching or compression, while being very flexible (Lipowsky & Sackmann, 1995; Safran, 2003). These mechanical properties can be estimated by applying the principles of differential geometry and statistical mechanics to represent the lipid bilayer as a mathematical surface (Derényi et al., 2007; Farago & Pincus, 2004; Vaidya, Huang, & Takagi, 2008). Therefore, changes in membrane shape can be represented by associating the free energy of the bilayer with shape deformations caused by bending, surface tension, and changes in pressure. The-free energy of the lipid bilayer describes its energetic stability, with lower free energy values representing more favorable conformations (Canham, 1970). In many experimental studies of cell membrane biomechanics, simplified equations are used to estimate the elastic parameters of the membranes, often with the assumptions underlying the use of particular equations not explicitly stated. In this section, we will discuss the equation for determining membrane tension by beginning with the Helfrich expression for bilayer free energy (Helfrich, 1973). Furthermore, since, as discussed in detail below, membrane tension is estimated experimentally by measuring the force required to pull a membrane tether (nanotube), we discuss how the energy expression is simplified to describe the membrane tension obtained from a tether. We will then discuss the effects of the cytoskeleton on the tension measurements.
Specifically, the estimation of membrane tension is based on the equation that describes the free energy of a bilayer, the Helfrich Equation of Generalized Shape Energy (Bukman, Yao, & Wortis, 1996; Derényi et al., 2002, 2007; Deuling & Helfrich, 1976; Helfrich, 1973; Vaidya et al., 2008). The essential components that constitute the free energy of the bilayer membrane are: (1) surface tension, (2) pressure (3) elastic bending modulus and the spontaneous curvature of the membrane, (4) elastic modulus determining the directionality of bending, called the saddle-splay modulus, and (5) the point force that pulls a membrane tether away from the membrane. The values of these parameters depend on the composition and area density of lipids constituting the membrane and may be positive or negative as shown below in Eq. (1).
The various terms in the free energy equation can be defined as follows:
The membrane surface tension is defined as the force per unit length acting on a cross-section of membrane (Clark et al., 2014) and is obtained from: , where σ is the tensile stress (surface tension) and dA a surface area element.
The pressure term represents the pressure difference across the membrane (Bukman et al., 1996): , where ΔP is the pressure difference between the inner and outer membrane leaflets and dV is a volume element.
The bending term represents the energy required to deform the membrane from its intrinsic curvature, while the spontaneous curvature is the preferred curvature that the membrane assumes based on its heterogeneous composition (Dai & Sheetz, 1995; Deuling & Helfrich, 1976): , where κ is the bending modulus, H is the mean curvature, and c0 is the spontaneous curvature.
The saddle-splay term represents the Gaussian curvature (Powers, Huber, & Goldstein, 2002) describing the relative rigidity of the membrane with respect to deformations in Gaussian curvature: , where is the saddle-splay modulus and K is the Gaussian curvature.
The tether term, FL, represents the effect of the point force (F) that pulls a tether from the membrane to a tether length of L (Derényi et al., 2002).
Thus, taken together, these terms provide an estimate of the free energy of a bilayer membrane (Bukman et al., 1996; Derényi et al., 2002, 2007; Deuling & Helfrich, 1976; Helfrich, 1973; Vaidya et al., 2008):
| (1) |
As described briefly above, an experimental approach to estimate membrane tension involves pulling membrane tethers from the bilayer membrane using techniques such as atomic force microscopy (AFM) or laser optical tweezers (Dai & Sheetz, 1999; Dai, Sheetz, Wan, & Morris, 1998; Diz-Muñoz et al., 2010; Lieber, Yehudai-Resheff, Barnhart, Theriot, & Keren, 2013; Sheetz, 2001; Sinha et al., 2011; Sun et al., 2007). In these techniques, a section of membrane attached to a probe is pulled into the shape of a narrow cylindrical nanotube (tether). The force exerted on the probe by the tether (tether force) is recorded and used to estimate the membrane tension. The relationship between the tether force and membrane tension is based on a simplified version of the free energy equation above (Eq. 1). In the next part of this discussion, we will describe the assumptions that are typically made to eliminate the terms of this equation that are unnecessary for application to membrane tension estimation by tether force.
First, it is possible to eliminate the second term representing the pressure change component of the equation, . It is generally assumed that there is no pressure change across the section of membrane constituting the tether (i.e., ΔP = 0) (Powers et al., 2002). It is also possible to eliminate the saddle-splay term, the fourth term of Eq. (1), . This is based on the definition of the Gaussian curvature, K, in terms the two principal curvatures, cmax and cmin, which are the maximum and minimum values of the curvature at each given point on the membrane surface. Gaussian curvature is the product of the two principal curvatures at each point on the surface, and is an intrinsic measure of curvature: K = cmaxcmin. The sign of the Gaussian curvature characterizes the surface shape, with positive Gaussian curvature indicating an elliptic point, negative being a hyperbolic (saddle) point, and a Gaussian curvature of zero representing a parabolic point. Importantly, zero Gaussian curvature is observed in cylinders because one of the principal curvatures would be zero (Fig. 2). Therefore, K is assumed to be zero for membrane tethers. Thus, Eq. (1) can be simplified to give:
| (2) |
Figure 2.
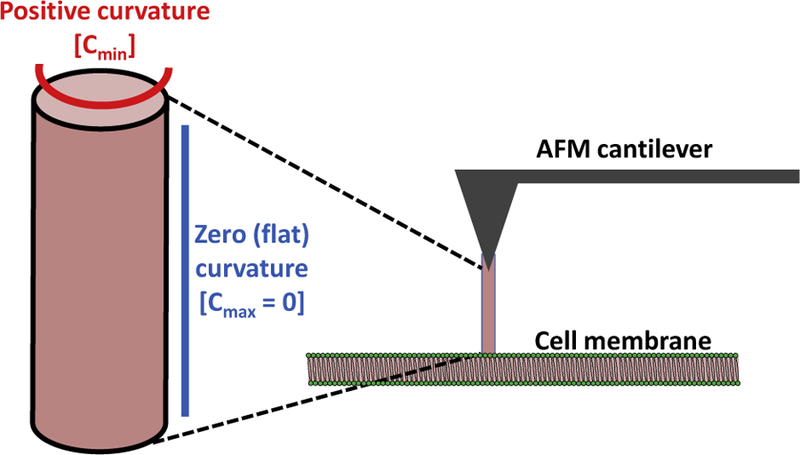
Schematic depicting the formation of a cylindrical membrane tether (nanotube) from a bilayer membrane by an atomic force microscope (AFM) cantilever tip. The cylinder has no Gaussian curvature because one principal curvature is positive while the other is zero (flat). The membrane tether is composed mainly of phospholipids derived from the membrane.
The first term on the right-hand side of Eq. (2) accounts for the surface tension within the membrane, while the second term represents the energetic cost of bending the membrane into a cylindrical tether. The final term (FL) characterizes the contribution of the tether force to the free energy. In other words, three main energy components contribute to the free energy of a tether: as a tether is pulled away from the cell membrane with a point force of F, there is competition between the stretching energy to pull a section of the membrane away from the bulk membrane into an elongated, cylindrical tether (membrane tension), and the bending energy needed to form the membrane into the narrow tubular shape of the tether (Derényi et al., 2007). Integrating Eq. (2) over the surface area (A) of the tether results in:
| (3) |
For a membrane tether of length L and radius R, the surface area is given as A = 2πRL, which is the surface area of a cylinder. The mean curvature, H, is the arithmetic mean (average) of the two principal curvatures, and is an extrinsic measure of curvature: . Since, as mentioned earlier, one of the principal curvatures for a cylinder is zero, the mean curvature becomes: , where c is the non-zero curvature. The principal curvature at each point on a curve is defined as the reciprocal of the radius of curvature at that point: . Thus, substituting and the surface area, A=2πRL into Eq. (3) results in:
| (4) |
It is often assumed that there is no difference between the two leaflets of the bilayer forming the tether and hence there is no spontaneous curvature (i.e., c0 = 0) (Deuling & Helfrich, 1976; Powers et al., 2002). Therefore the free energy expression in Eq. (4) further simplifies to:
| (5) |
An equilibrium radius (R0) results as the surface tension works towards reducing the tether radius. This equilibrium value is calculated by minimizing Eq. (5) through taking the partial derivative of the free energy with respect to tether radius, R (Derényi et al., 2002):
| (6) |
Hence, the equilibrium radius can be obtained as a function of surface tension and bending modulus:
| (7) |
This equation can be rearranged to obtain expressions for bending modulus and surface tension:
| (8) |
| (9) |
Similarly, the equilibrium tether force is obtained by taking the partial derivative of the free energy with respect to tether length from Eq. (5):
| (10) |
Substituting the expression for equilibrium radius from Eq. (7) for R in Eq. (10) and solving for F0 results in the equilibrium tether force being a function of surface tension and bending modulus:
| (11) |
Once again, this equilibrium equation can be rearranged to obtain expressions for the surface tension and bending modulus:
| (12) |
| (13) |
Substituting the equations for k and s from Eqs. (8) and (9) into Eqs. (12) and (13) provides expressions for the membrane surface tension and bending modulus at the equilibrium condition as functions of only equilibrium tether force and radius (Pontes et al., 2011, 2013). This allows these elastic constants of tension, σ, and bending modulus, κ, to be experimentally estimated by pulling membrane tethers to obtain the steady-state (equilibrium) tether force, F0 and the tether radius, R0 as shown in Eqs. (14) and (15):
| (14) |
| (15) |
These two equations are typically used in experimental studies to estimate membrane tension of lipid vesicles or cellular membranes from measurements of the tether force (F0) obtained either using atomic force microscopy (AFM) or optical tweezers (Dai & Sheetz, 1999; Dai et al., 1998; Diz-Muñoz et al., 2010, 2013; Hochmuth, Shao, Dai, & Sheetz, 1996; Lieber et al., 2013; Sheetz, 2001; Sinha et al., 2011; Sun et al., 2007). Both of these state-of-the-art techniques are valid to determine the tether force, however, the radius (R0) of tethers pulled from membranes using laser optical tweezers can be directly determined, whereas, it is not possible to measure the radii of tethers pulled using the AFM experimental technique. This is due to the fact that tethers are pulled in the same direction as the microscope optical axis in AFM measurements and, therefore, cannot be directly visualized. Consequently, with AFM measurements, when comparing different conditions without a change in membrane composition, it can be assumed that the tether radius will remain constant (Ayee et al., 2018). This allows comparison of the relative changes in membrane tension between different conditions.
It is important to note, however, that while these equations (Eq. 14 and 15)are applicable to lipid bilayer membranes such as those of vesicles, they do not take into account the fact that cellular membranes are attached to an underlying cytoskeleton network. This attachment has a major impact on the force required to pull membrane tethers (Dai & Sheetz, 1999; Sheetz, 2001). Indeed, a network of actin filaments forms the cortical cytoskeleton beneath the cell membrane, which is attached to this cortical network by linker proteins such as filamins (Razinia, Mäkelä, Ylänne, & Calderwood, 2012), myosin-1 motors (McConnell & Tyska, 2010; Nambiar, McConnell, & Tyska, 2009), and ezrin-radixin-moesin (ERM) family proteins (Fehon, McClatchey, & Bretscher, 2010). Numerous studies show that disruption of the cytoskeletal networks dramatically decreases the tether force measured in various cell types under different experimental conditions (Ayee et al., 2018; Dai & Sheetz, 1999; Pontes et al., 2011; Raucher et al., 2000; Sun et al., 2005, 2007). These differences in tether force in the presence or absence of the cortical cytoskeleton is attributed to the membrane-cortex adhesion energy (Diz-Muñoz et al., 2010). Consequently, for cells, the equilibrium tether force (Eq. 11) contains an additional term representing the adhesion energy density (γ0) between the cell membrane and the cytoskeleton (Brochard-Wyart, Borghi, Cuvelier, & Nassoy, 2006; Hochmuth et al., 1996).
| (16) |
The term (σ + γ0), also called σm, is the “apparent” membrane tension, which contains terms for both the in-plane bilayer tension and the membrane-cytoskeleton adhesion (Dai & Sheetz, 1999; Sheetz & Dai, 1996). This apparent membrane tension can be calculated from the results of a typical AFM experiment that measures tether force. The close similarity between the values for tether force in lipid vesicles that contain only lipids and in membranes of cells with disrupted cytoskeletons suggests that integral membrane proteins do not contribute significantly to the tether force.
In experimental contexts, tether force values (F0) have been found to range between approximately 30–40 pN for various cell types. Conversely, F0 values for the same cell types treated with actin depolymerization agents that significantly disrupt the cytoskeleton (such as Latrunculin-A or cytochalasin-D) are found to be reduced by approximately 50% to about 15 pN in most cases (Ayee et al., 2018; Pontes et al., 2011; Raucher et al., 2000; Sun et al., 2005, 2007). Similarly, the tether forces and membrane-cytoskeleton adhesion energy measured in membrane blebs, which do not contain cytoskeletal structures, have also been found to be significantly lower, by at least 50%, than those of control cells (Dai & Sheetz, 1999; Raucher et al., 2000). Therefore, with respect to the apparent membrane tension defined in Eq. (16), the experimental results above indicate that the attachment of the membrane to the cortical network is as important of a contributor to the tether force as the in-plane bilayer tension. Like-wise, the F0 values from cells with disrupted cytoskeletons are in close agreement with tether force values obtained from lipid vesicles composed of egg phosphatidylcholine combined with mPEG-DOPE and DSPE-PEG biotin. For these lipid vesicles, a static tether force of 16 pN was obtained using optical tweezers (Cuvelier, Chiaruttini, Bassereau, & Nassoy, 2005). This value is very similar to the tether forces of 15 pN for cytoskeleton disrupted cells discussed above. Hence, experimental measurements of tether forces in cells contain information about both the membrane tension and the energy of adhesion to the cytoskeleton.
In addition to tether pulling experiments, another mechanical method to independently probe cellular membrane properties, including the apparent membrane tension, σm, involves indenting cells with an AFM cantilever. In this technique, the cantilever is depressed into a cell and experiences a restoring force that resists this mechanical deformation. The restoring force that results from this indentation is the result of an isotropic tension (σiso), which is composed of the combined membrane and cortical cytoskeleton tension (σ0 = σm + σc) as well as the change in membrane surface area resulting from stretching the membrane during indentation (Evans, 1974; Kwok & Evans, 1981; Pietuch & Janshoff, 2013):
| (17) |
where KA is the area compressibility modulus of the membrane connected to the cortical layer and ΔA is the change in surface area as compared to the initial surface area, A0. The cortical cytoskeleton tension (σc) is generated by contractile stress of the actin network (Levayer & Lecuit, 2012; Salbreux, Charras, & Paluch, 2012), while the membrane tension term (σm = σ + γ0) is the apparent membrane tension, composed of the in-plane bilayer tension and the membrane-cytoskeleton adhesion, as explained above. Although this indentation method may theoretically be used to obtain an estimate of the apparent membrane tension, it should be used with caution, considering that determination of the surface area of cells is complicated by the fact that the membrane is folded and wrinkled, with excess membrane stored in reservoirs (Clark et al., 2014; Dai & Sheetz, 1999; Sens & Turner, 2006). Hence, a reasonable measurement of , particularly the small change in area upon indentation, would be difficult to obtain (Pietuch & Janshoff, 2013). The indentation approach is most reliable for measuring the cellular elastic modulus, whereas tether pulling is more reliable for estimating apparent membrane tension.
2.2. Osmotic Swelling has Little or No Effect on Membrane Tension
As mentioned previously, the question of the impact of osmotic swelling on membrane tension has been controversial. It was initially believed that an increase in membrane tension would result from hypo-osmotic cell swelling, and that this change in tension would lead to the activation of mechanosensitive ion channels, thus restoring the cellular osmotic equilibrium in the process known as regulatory volume decrease (RVD) (Hoffmann & Dunham, 1995; Okada et al., 2001). However, direct evidence to support the belief that cell swelling would lead to increased cell tension is scarce. A study by Dai et al. of osmotically challenged molluscan neurons observed an increase in the apparent membrane tension measured by membrane tethers pulled using optical tweezers (Dai et al., 1998), while a similar study of mammalian cells by Sinha et al. (2011) saw changes in the apparent tension only when the membrane folds and invaginations were pre-flattened by cholesterol depletion or genetic Caveolin-1 deficiency. As mentioned above, the apparent membrane tension measured in these studies would depend on both the in-plane bilayer tension and the membrane-cytoskeleton adhesion.
We recently undertook a study to simultaneously analyze the impact of a mild osmotic gradient of 20% on the membrane tension and elastic modulus of human aortic endothelial cells (HAECs) by using both AFM nanoindentation and measuring the force required to pull membrane tethers (Ayee et al., 2018). With regards to membrane tension under osmotic challenge, our experiments yielded tether forces in the range of 40 pN for HAECs under both isotonic and hypotonic conditions, while values for cells treated with F-actin disrupting agents were approximately 15 pN under both conditions (Fig. 3). Since there was no difference in the tether force values between the isotonic and hypotonic conditions, we concluded that mild hypotonic swelling did not affect membrane tension or the adhesion energy between the membrane and cortical cytoskeleton.
Figure 3.
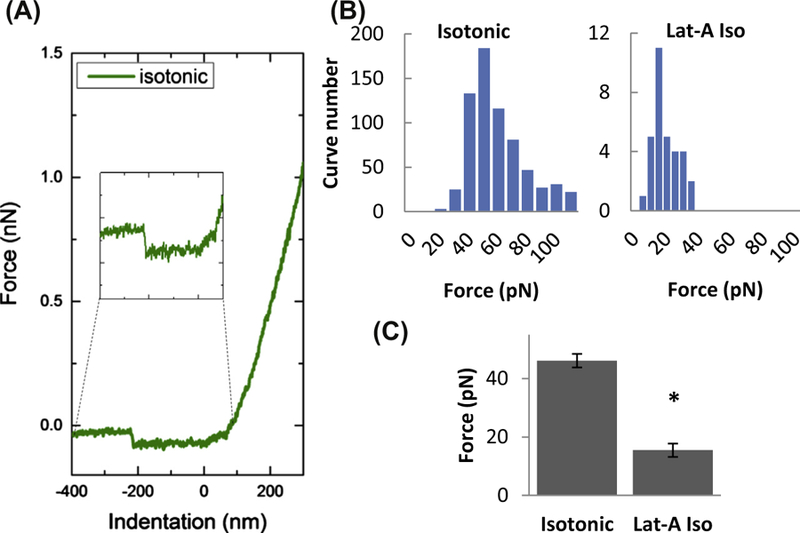
Effect of F-actin depolymerization on the force of membrane tether formation. (A) Representative traces of AFM retraction force curves for cells in isotonic solution with an inset of a representative force discontinuity (used to obtain the tether force). The force discontinuity represents the change in force experienced by the cantilever while retracting from the sample surface upon detachment of the tether. (B) Histograms of membrane tether forces measured in cells exposed to isotonic solution (left) and Latrunculin-A in isotonic medium (right). (C) Mean membrane tether forces of cells with and without exposure to Latrunculin-A (1 µM for 10 min). (Asterisk denotes statistically significant difference using an unpaired samples T-Test (n = 15–60 cells; P < 0.05) between Latrunculin-A treated and untreated cells).
This conclusion is consistent with the earlier studies both from our group (Levitan & Garber, 1997, pp. 245–267) and other investigators (Dai & Sheetz, 1999; Dai et al., 1997, 1998; Groulx et al., 2006; Raucher & Sheetz, 1999; Sens & Turner, 2006; Sinha et al., 2011), showing that there are significant membrane reservoirs in membrane folds and invaginations, which may accommodate an increase in cell volume and apparent increase in cell surface area without any membrane stretch, thus buffering membrane tension. Indeed, Morris (Morris, 2018) describes the concept of “membrane tension homeostasis” (MTH) as an essential process that works to prevent cellular plasma membranes from lysing under osmotic stress by employing a combination of multiple passive and active stochastic tension modulating steps to resist rupture.
3. ELASTIC PROPERTIES
3.1. Theoretical Basis and Experimental Approaches of Measuring Membrane and Cellular Elastic Modulus
The elastic modulus is another important biomechanical parameter that provides information about cell stiffness. This modulus can be estimated by probing cells with an AFM cantilever to obtain force/distance curves. The curves are obtained by recording the force applied and cantilever deflection at various vertical positions of the cantilever as it approaches, indents, and retracts from each cell (Kuznetsova, Starodubtseva, Yegorenkov, Chizhik, & Zhdanov, 2007). The experimental curves are then fitted to the Hertz model to obtain the Young’s elastic modulus of the cells. AFM cantilever tips of various geometries may be used, however, for a pyramidal cantilever tip geometry, the Hertz model gives the force (F) applied to the cantilever (loading force) as (Ayee et al., 2018; Lin, Dimitriadis, & Horkay, 2007):
| (18) |
where E is the Young’s elastic modulus, δ is the indentation depth, ν is the cellular Poisson’s ratio (assumed to be 0.5 for incompressible biological material, and 2ϕ is the angle of the tip (25°–45°). The exact form of the Hertz model depends on the geometry of the cantilever tip. Although this is the most commonly used model to estimate cellular elastic moduli from AFM experiments (Haase & Pelling, 2015; Schillers et al., 2017; Thomas, Burnham, Camesano, & Wen, 2013), the Hertz model was developed based on several assumptions regarding the material being tested, including sample homogeneity, isotropy, and a linear stress-strain response. These assumptions present a limitation to the model, given that cells are structurally heterogeneous and anisotropic. Therefore, during experiments to estimate the elastic modulus, it is essential to maintain small, uniform indentation depths and probe sizes relative to the sample size, as well as uniform analyses of resulting force/distance curves based on depth of indentation (Dokukin, Guz, & Sokolov, 2013; Lin et al., 2007).
Consequently, the force/distance curves obtained from AFM experiments may be analyzed in different ways to provide elastic modulus estimates that discriminate between the membrane/cortical cytoskeleton region and the whole cell, representing the stiffness of the deeper cytoskeleton (Askarova, Sun, Sun, Meininger, & Lee, 2013; Ayee et al., 2018). To quantify membrane stiffness and extract values of the elastic modulus, E, the force/distance curves can be analyzed from the point at which the AFM cantilever initially touches the cell surface to the point at which it reaches a depth of about 5 nm, representing the approximate thickness of the membrane lipid bilayer (Edidin, 2003). For the elastic modulus of the whole cell, on the other hand, the entire force/distance curve is fitted to the Hertz model. By analyzing force/distance curves in these two ways, the elastic modulus values for the membrane envelope and whole cell are found to be very different (Askarova et al., 2013; Ayee et al., 2018).
3.2. Osmotic Swelling has Differential Effects on Membrane and Cellular Elastic Moduli
Like membrane tension, the issue of the effect of osmotic swelling on cellular elastic moduli has been controversial. Spagnoli et al. (2008) found that osmotic swelling resulted in overall softening of cells measured by AFM using cantilevers with 15 µm polystyrene beads glued to the tips. In this study, the force/distance curves were fitted in their entirety to a version of the Hertz model for hard spheres indenting elastic solid surfaces, thus providing an estimate of the whole cell stiffness. The cell softening observed in this case may be explained in one two ways. First, the cellular cytoskeleton may be thought of as a cross-linked filamentous gel having a poroelastic structure, which has been likened to the structure of a sponge, and has therefore been termed the “sponge-effect” by Sachs et al. (Chao, Sivaselvan, & Sachs, 2018; Charras, Mitchison, & Mahadevan, 2009; Sachs & Sivaselvan, 2015). Another possibility is that the softening could be explained by mild disruption and reorganization of the cytoskeleton as a result of osmotic challenge (Hoffmann, 2000; Hoffmann, Lambert, & Pedersen, 2009; Jorgensen et al., 2003; Lambert, Hoffmann, & Pedersen, 2008; Levitan, Almonte, Mollard, & Garber, 1995; Pasantes-Morales, Cardin, & Tuz, 2000; Pedersen et al., 1999, 2001; Spagnoli et al., 2008; Sun & Levitan, 2003). It is not clear which of these possibilities would account for the observed mild softening of cells as a response to osmotic challenge. In contrast to this observed softening, however, Zou et al. (2013) found that osmotic challenge induced stiffening of cortical neurons. These results were obtained from AFM experiments using 20 µm borosilicate spherical glass beads mounted on the cantilever, and the force/distance curves were fitted to the Hertz model for spherical incompressible tips. Again, in this study, the entire force curves were fitted to the Hertz model to obtain estimates of the elastic moduli. The cortical neurons were briefly exposed to hypotonic shock, resulting in an increase in stiffness, which changed to softening when the solution medium was exchanged. In some cases, softening began even before the medium was changed.
Although both studies described above used whole cell analysis to determine cellular elastic moduli, the differences in their respective experimental methodologies may account for the different effects observed after osmotic challenge. Specifically, the exposure times employed may partly account for the different results obtained. The Spagnoli study exposed various cell types to a hypotonic solution of DMEM with mannitol for at least 10 min. On the other hand, in the Zou study, the cortical neurons were exposed to BPS with reduced NaCl for only 5 min, after which the solution was replaced by an isotonic BPS one. Interestingly, the elastic moduli of the cells in the Spagnoli study initially ranged between about 300 and 400 Pa before treatment, which decreased to about 100 Pa after the hypotonic challenge. Conversely, the elastic moduli of the neurons in the Zou study were initially at approximately 150 Pa, they rose to about 350 Pa within 1–2 min during the 5 min challenge, and then fell back down to the baseline of 150 Pa. Another difference between the two studies was the osmolality of their respective hypotonic solutions. The Spagnoli study used a strong hypotonic solution of 90 mOsm, while the Zou study used a milder osmotic gradient with a solution at 217 mOsm. The use of strong osmotic gradients to study the effects of swelling on cells is not unusual, with most previous studies subjecting cells to osmotic gradients of 50% and above (Dai et al., 1997, 1998; Groulx et al., 2006; Guo, Wang, Sachs, & Meng, 2014; Meng & Sachs, 2010; Pietuch, Brückner, & Janshoff, 2013; Raucher & Sheetz, 1999), some even exposing cells to pure distilled water. Such strong osmotic gradients, however, may not be relevant physiologically. For example, we previously showed that the plasma osmolality decreases by only about 10% in the extreme case of compulsive water drinking (Verghese et al., 1997), due to the tight physiological regulation of the osmolality of the plasma and extracellular fluids. Therefore, osmolality values within the physiological range may be more informative when examining the effects of osmotic swelling on cells. Also, as mentioned above, the manner in which the force/distance curves are analyzed provides information pertinent to different regions of the cell.
In our recent study of hypotonically swollen human aortic endothelial cells (HAECs), we employed a mild 20% osmotic gradient (Ayee et al., 2018). From our analysis of the two regions of the force/distance curves as described above, we concluded that the elastic modulus of the membrane/cortical cytoskeleton envelope was lower than that of the whole cell (deeper cytoskeleton) with about 10 kPa estimated for the membrane region and 20 kPa for the whole cell. Force curves are continuous; therefore, we distinguished between the membrane region and the whole cell by approximating that the membrane region extended about 5 nm from the cell surface. We found that the osmotic challenge resulted in a significant stiffening of the membrane region in endothelial cells, increasing the elastic modulus twofold (Fig. 4). These values are higher than those observed for cortical neurons and other cell types described above; however, they are in the same range as values for endothelial cells found in our earlier work (Ayee et al., 2017; Shentu et al., 2010, 2012). It is known that the elastic modulus of the cell membrane depends largely on the stiffness of the cortical cytoskeleton underlying the membrane (Fletcher & Mullins, 2010; Pourati et al., 1998; Rotsch & Radmacher, 2000; Sato, Theret, Wheeler, Ohshima, & Nerem, 1990; Wagner, Tharmann, Haase, Fischer, & Bausch, 2006; Wu, Kuhn, & Moy, 1998; Zhang, Long, Wu, & Yu, 2002). As expected, treating our cells with Latrunculin-A caused a significant decrease in the elastic modulus to 1.3 kPa. Unexpectedly, however, the stiffening effect induced by osmotic swelling was enhanced by the disruption of F-actin. Since it was shown previously that direct application of hydrostatic pressure to cells with a micropipette results in membrane stiffening (Beyder & Sachs, 2009), we propose that the stiffening of osmotically challenged endothelial cells should be attributed to an increase in internal hydrostatic pressure, originating from the influx of water into the cells due to the osmotic gradient. In contrast to the results obtained for the membrane region, although there was a slight reduction in stiffness of the deeper cytoskeleton, we saw no statistically significant change in the stiffness when cells we exposed to an osmotic challenge, with elastic modulus values remaining between 15 and 20 kPa. Indeed, previous work on Ehrlich ascites tumor cells by Pedersen et al. (1999) showed that osmotic challenge affected only F-actin in the cortical region and not in the deeper cytoskeleton. Consequently, we concluded that osmotic swelling with physiologically relevant hypotonic gradients resulted in depth-dependent changes in the elastic modulus of cells, a fact that should be considered when estimating cell stiffness in experimental settings. Moreover, it is also interesting to note that changes in cell stiffness were shown to affect activation of volume-regulated anion channels (VRAC), one of the major mechanisms of cell volume regulation (Byfield, Hoffman, Romanenko, Fang, Crocker, & Levitan, 2006).
Figure 4.
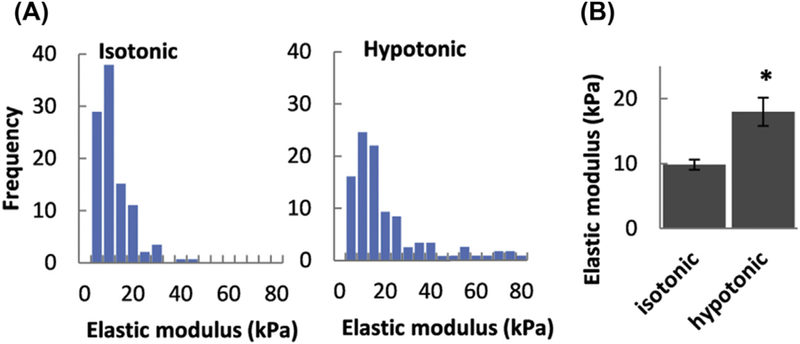
Effect of osmotic challenge on the elastic modulus of endothelial cells. (A) Histograms of elastic moduli measured in the membrane region of cells exposed to isotonic (left) and hypotonic (right) solutions. (B) Mean membrane region elastic moduli of cells in isotonic and hypotonic solutions. (Asterisk denotes significant difference using an unpaired samples T-Test (n = 15–60 cells; P < 0.05) between moduli measured under each condition).
4. CONCLUSIONS
In this chapter we provide a detailed analysis of the methodology used to estimate cell membrane tension and elastic moduli, specifically addressing the theoretical background surrounding the models used in these analyses, the governing equations employed in estimating these biomechanical parameters, and the key assumptions made. We include a summary of the prevalent experimental approaches and describe what is currently understood about how these parameters change during osmotic swelling. From our recent work (Ayee et al., 2018), we find that mild hypotonic swelling does not change membrane tension or the adhesion energy between the membrane and cortical cytoskeleton due to the buffering effect of unfolding membrane reservoirs. These findings challenge the general expectation that cell swelling should result in an increase in membrane tension. We conclude also that the cell membrane envelope stiffens during swelling (Fig. 5), and unexpectedly, stiffening is enhanced when the cytoskeleton was disrupted, indicating that the cytoskeleton has a dampening effect on the increase in stiffness. These conclusions have important implications to the field of membrane biomechanics and indicate that hypotonic swelling may not be a suitable method to determine the role of membrane tension in mechanosensitive processes.
Figure 5.
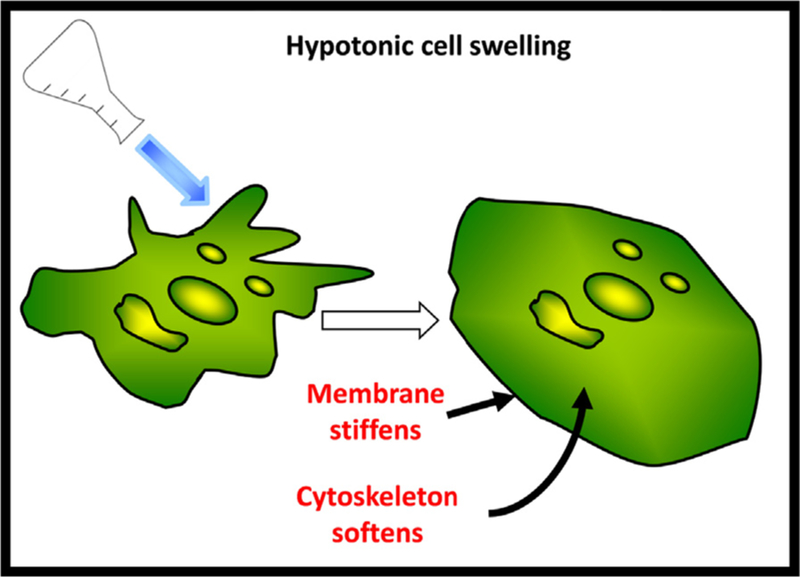
Schematic depicting cell swelling and membrane unfolding as a response to hypotonic challenge resulting in membrane stiffening and mild cytoskeleton softening.
ACKNOWLEDGMENTS
We are very grateful to Nicolas Barbera for the critical reading of this manuscript. We also thank Mr. Gregory Kowalsky for his help in designing Fig. 5. The work was supported by the National Institutes of Health (NIH) grants T32 HL-82547 (to M.A.A.A.), HL-083298, and HL-073965 (to I.L.).
REFERENCES
- Askarova S, Sun Z, Sun GY, Meininger GA, & Lee JC (2013). Amyloid-β peptide on sialyl-LewisX-selectin-mediated membrane tether mechanics at the cerebral endothelial cell surface. PLoS One, 8 e60972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayee MA, LeMaster E, Shentu TP, Singh DK, Barbera N, Soni D, Tiruppathi C, Subbaiah PV, Berdyshev E, & Bronova I (2017). Molecular-scale biophysical modulation of an endothelial membrane by oxidized phospholipids. Biophysical Journal, 112, 325–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayee MAA, LeMaster E, Teng T, Lee J, & Levitan I (2018). Hypotonic challenge of endothelial cells increases membrane stiffness with No effect on tether force. Biophysical Journal, 114, 929–938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beyder A, & Sachs F (2009). Electromechanical coupling in the membranes of Shaker-transfected HEK cells. Proceedings of the National Academy of Sciences, 106, 6626–6631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brochard-Wyart F, Borghi N, Cuvelier D, & Nassoy P (2006). Hydrodynamic narrowing of tubes extruded from cells. Proceedings of the National Academy of Sciences, 103, 7660–7663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bukman DJ, Yao JH, & Wortis M (1996). Stability of cylindrical vesicles under axial tension. Physical Review E, 54, 5463. [DOI] [PubMed] [Google Scholar]
- Byfield FJ, Hoffman BD, Romanenko VG, Fang Y, Crocker JC, & Levitan I (2006). Evidence for the role of cell stiffness in the modulation of volume-regulated anion channels. Acta Physiologica, 187, 285–294. [DOI] [PubMed] [Google Scholar]
- Canham PB (1970). The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. Journal of Theoretical Biology, 26, 61–81. [DOI] [PubMed] [Google Scholar]
- Chao P-C, Sivaselvan M, & Sachs F (2018). Cell softening due to osmotic swelling; extending the Donnan equilibrium In Press. [DOI] [PubMed]
- Charras GT, Mitchison TJ, & Mahadevan L (2009). Animal cell hydraulics. Journal of Cell Science, 122, 3233–3241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark AG, Wartlick O, Salbreux G, & Paluch EK (2014). Stresses at the cell surface during animal cell morphogenesis. Current Biology, 24, R484–R494. [DOI] [PubMed] [Google Scholar]
- Cuvelier D, Chiaruttini N, Bassereau P, & Nassoy P (2005). Pulling long tubes from firmly adhered vesicles. EPL (Europhysics Letters), 71, 1015. [Google Scholar]
- Dai J, & Sheetz MP (1995). Mechanical properties of neuronal growth cone membranes studied by tether formation with laser optical tweezers. Biophysical Journal, 68, 988e996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai J, & Sheetz MP (1999). Membrane tether formation from blebbing cells. Biophysical Journal, 77, 3363–3370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai J, Sheetz MP, Wan X, & Morris CE (1998). Membrane tension in swelling and shrinking molluscan neurons. Journal of Neuroscience, 18, 6681–6692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai J, Ting-Beall HP, & Sheetz MP (1997). The secretion-coupled endocytosis correlates with membrane tension changes in RBL 2H3 cells. The Journal of General Physiology, 110, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derényi I, Jülicher F, & Prost J (2002). Formation and interaction of membrane tubes. Physical Review Letters, 88, 238101. [DOI] [PubMed] [Google Scholar]
- Derényi I, Koster G, Van Duijn M, Czövek A, Dogterom M, & Prost J (2007). Membrane nanotubes. In Controlled nanoscale motion (pp. 141–159). Springer. [Google Scholar]
- Deuling H, & Helfrich W (1976). The curvature elasticity of fluid membranes: A catalogue of vesicle shapes. Journal de Physique, 37, 1335–1345. [Google Scholar]
- Diz-Muñoz A, Fletcher DA, & Weiner OD (2013). Use the force: Membrane tension as an organizer of cell shape and motility. Transfusion clinique et biologique, 23, 47–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diz-Muñoz A, Krieg M, Bergert M, Ibarlucea-Benitez I, Muller DJ, Paluch E, & Heisenberg C-P (2010). Control of directed cell migration in vivo by membrane-to-cortex attachment. PLoS Biology, 8 e1000544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dokukin ME, Guz NV, & Sokolov I (2013). Quantitative study of the elastic modulus of loosely attached cells in AFM indentation experiments. Biophysical Journal, 104, 2123–2131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edidin M (2003). Lipids on the frontier: A century of cell-membrane bilayers. Nature Reviews Molecular Cell Biology, 4, 414. [DOI] [PubMed] [Google Scholar]
- Evans EA (1974). Bending resistance and chemically induced moments in membrane bilayers. Biophysical Journal, 14, 923–931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans E, & Fung Y-C (1972). Improved measurements of the erythrocyte geometry. Microvascular Research, 4, 335–347. [DOI] [PubMed] [Google Scholar]
- Evans E, & Leblond P (1973). Image holograms of single red blood cell discocyte-spheroechinocyte transformations. In Red cell shape (pp. 131–140). Springer. [PubMed] [Google Scholar]
- Evans EA, Waugh R, & Melnik L (1976). Elastic area compressibility modulus of red cell membrane. Biophysical Journal, 16, 585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farago O, & Pincus P (2004). Statistical mechanics of bilayer membrane with a fixed projected area. The Journal of Chemical Physics, 120, 2934–2950. [DOI] [PubMed] [Google Scholar]
- Fehon RG, McClatchey AI, & Bretscher A (2010). Organizing the cell cortex: The role of ERM proteins. Nature Reviews Molecular Cell Biology, 11, 276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher DA, & Mullins RD (2010). Cell mechanics and the cytoskeleton. Nature, 463, 485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groulx N, Boudreault F, Orlov SN, & Grygorczyk R (2006). Membrane reserves and hypotonic cell swelling. The Journal of Membrane Biology, 214, 43–56. [DOI] [PubMed] [Google Scholar]
- Guo J, Wang Y, Sachs F, & Meng F (2014). Actin stress in cell reprogramming. Proceedings of the National Academy of Sciences, 111, E5252–E5261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haase K, & Pelling AE (2015). Investigating cell mechanics with atomic force microscopy. Journal of The Royal Society Interface, 12, 20140970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helfrich W (1973). Elastic properties of lipid bilayers: Theory and possible experiments. Zeitschrift für Naturforschung C, 28, 693–703. [DOI] [PubMed] [Google Scholar]
- Hille B (2001). Ion channels of excitable membranes MA: Sinauer Sunderland. [Google Scholar]
- Hochmuth F, Shao J-Y, Dai J, & Sheetz MP (1996). Deformation and flow of membrane into tethers extracted from neuronal growth cones. Biophysical Journal, 70, 358–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hochmuth R, & Waugh R (1987). Erythrocyte membrane elasticity and viscosity. Annual Review of Physiology, 49, 209–219. [DOI] [PubMed] [Google Scholar]
- Hoffmann EK (2000). Intracellular signalling involved in volume regulatory decrease. Cellular Physiology and Biochemistry, 10, 273–288. [DOI] [PubMed] [Google Scholar]
- Hoffmann EK, & Dunham PB (1995). Membrane mechanisms and intracellular signalling in cell volume regulation. International Review of Cytology, 161, 173–262. [DOI] [PubMed] [Google Scholar]
- Hoffmann EK, Lambert IH, & Pedersen SF (2009). Physiology of cell volume regulation in vertebrates. Physiological Reviews, 89, 193–277. [DOI] [PubMed] [Google Scholar]
- Jorgensen NK, Pedersen SF, Rasmussen HB, Grunnet M, Klaerke DA, & Olesen S-P (2003). Cell swelling activates cloned Ca2+-activated K+ channels: A role for the F-actin cytoskeleton. Biochimica et Biophysica Acta (BBA)-Biomembranes, 1615, 115–125. [DOI] [PubMed] [Google Scholar]
- Kuznetsova TG, Starodubtseva MN, Yegorenkov NI, Chizhik SA, & Zhdanov RI (2007). Atomic force microscopy probing of cell elasticity. Micron: the International Research and Review Journal for Microscopy, 38, 824–833. [DOI] [PubMed] [Google Scholar]
- Kwok R, & Evans E (1981). Thermoelasticity of large lecithin bilayer vesicles. Biophysical Journal, 35, 637–652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lambert I, Hoffmann E, & Pedersen S (2008). Cell volume regulation: Physiology and pathophysiology. Acta Physiologica, 194, 255–282. [DOI] [PubMed] [Google Scholar]
- Levayer R, & Lecuit T (2012). Biomechanical regulation of contractility: Spatial control and dynamics. Transfusion clinique et biologique, 22, 61–81. [DOI] [PubMed] [Google Scholar]
- Levitan I, Almonte C, Mollard P, & Garber S (1995). Modulation of a volume-regulated chloride current by F-actin. The Journal of Membrane Biology, 147, 283–294. [DOI] [PubMed] [Google Scholar]
- Levitan I, Christian AE, Tulenko TN, & Rothblat GH (2000). Membrane cholesterol content modulates activation of volume-regulated anion current in bovine endothelial cells. The Journal of General Physiology, 115, 405–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitan I, & Garber SS (1997). Volume regulated anion channels and cytoskeletal interaction. From ion channels to cell-to-cell Conversations Springer. [Google Scholar]
- Lieber AD, Yehudai-Resheff S, Barnhart EL, Theriot JA, & Keren K (2013). Membrane tension in rapidly moving cells is determined by cytoskeletal forces. Current Biology, 23, 1409–1417. [DOI] [PubMed] [Google Scholar]
- Lin DC, Dimitriadis EK, & Horkay F (2007). Robust strategies for automated AFM force curve analysis-I. Non-adhesive indentation of soft, inhomogeneous materials. Journal of Biomechanical Engineering, 129, 430–440. [DOI] [PubMed] [Google Scholar]
- Lipowsky R, & Sackmann E (1995). Structure and dynamics of membranes: I. From cells to vesicles/II. generic and specific interactions Elsevier. [Google Scholar]
- McConnell RE, & Tyska MJ (2010). Leveraging the membraneecytoskeleton interface with myosin-1. Transfusion clinique et biologique, 20, 418–426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meng F, & Sachs F (2010). Visualizing dynamic cytoplasmic forces with a compliance-matched FRET sensor. Journal of Cell Science, 124, 261–269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris CE (2018). Cytotoxic swelling of sick excitable cells - impaired ion homeostasis and membrane tension homeostasis in muscle and neuron. Current Topics in Membranes, 81, 457–496. [DOI] [PubMed] [Google Scholar]
- Nambiar R, McConnell RE, & Tyska MJ (2009). Control of cell membrane tension by myosin-I. Proceedings of the National Academy of Sciences, 106, 11972–11977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okada Y, Maeno E, Shimizu T, Dezaki K, Wang J, & Morishima S (2001). Receptor-mediated control of regulatory volume decrease (RVD) and apoptotic volume decrease (AVD). The Journal of Physiology, 532, 3–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasantes-Morales H, Cardin V, & Tuz K (2000). Signaling events during swelling and regulatory volume decrease. Neurochemical Research, 25, 1301–1314. [DOI] [PubMed] [Google Scholar]
- Pedersen SF, Hoffmann EK, & Mills J (2001). The cytoskeleton and cell volume regulation. Comparative Biochemistry and Physiology Part a: Molecular & Integrative Physiology, 130, 385–399. [DOI] [PubMed] [Google Scholar]
- Pedersen SF, Mills JW, & Hoffmann EK (1999). Role of the F-actin cytoskeleton in the RVD and RVI processes in Ehrlich ascites tumor cells. Experimental Cell Research, 252, 63–74. [DOI] [PubMed] [Google Scholar]
- Pietuch A, Brückner BR, & Janshoff A (2013). Membrane tension homeostasis of epithelial cells through surface area regulation in response to osmotic stress. Biochimica et Biophysica Acta (BBA) - Molecular Cell Research, 1833, 712–722. [DOI] [PubMed] [Google Scholar]
- Pietuch A, & Janshoff A (2013). Mechanics of spreading cells probed by atomic force microscopy. Open biology, 3, 130084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pontes B, Ayala Y, Fonseca ACC, Romão LF, Amaral RF, Salgado LT, Lima FR, Farina M, Viana NB, & Moura-Neto V (2013). Membrane elastic properties and cell function. PLoS One, 8 e67708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pontes B, Viana N, Salgado L, Farina M, Neto VM, & Nussenzveig H (2011). Cell cytoskeleton and tether extraction. Biophysical Journal, 101, 43–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pourati J, Maniotis A, Spiegel D, Schaffer JL, Butler JP, Fredberg JJ, Ingber DE, Stamenovic D, & Wang N (1998). Is cytoskeletal tension a major determinant of cell deformability in adherent endothelial cells? American Journal of Physiology - cell Physiology, 274, C1283–C1289. [DOI] [PubMed] [Google Scholar]
- Powers TR, Huber G, & Goldstein RE (2002). Fluid-membrane tethers: Minimal surfaces and elastic boundary layers. Physical Review E, 65, 041901. [DOI] [PubMed] [Google Scholar]
- Raucher D, & Sheetz MP (1999). Characteristics of a membrane reservoir buffering membrane tension. Biophysical Journal, 77, 1992–2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raucher D, Stauffer T, Chen W, Shen K, Guo S, York JD, Sheetz MP, & Meyer T (2000). Phosphatidylinositol 4, 5-bisphosphate functions as a second messenger that regulates cytoskeleton–plasma membrane adhesion. Cell, 100, 221–228. [DOI] [PubMed] [Google Scholar]
- Razinia Z, Mäkelä T, Ylänne J, & Calderwood DA (2012). Filamins in mechanosensing and signaling [DOI] [PMC free article] [PubMed]
- Ross PE, Garber SS, & Cahalan MD (1994). Membrane chloride conductance and capacitance in Jurkat T lymphocytes during osmotic swelling. Biophysical Journal, 66, 169–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rotsch C, & Radmacher M (2000). Drug-induced changes of cytoskeletal structure and mechanics in fibroblasts: An atomic force microscopy study. Biophysical Journal, 78, 520–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sachs F, & Sivaselvan MV (2015). Cell volume control in three dimensions: Water movement without solute movement. The Journal of General Physiology, 201411297. [DOI] [PMC free article] [PubMed]
- Safran S (2003). Statistical thermodynamics of surfaces, interfaces, and membranes Boca Raton: CRC Press. [Google Scholar]
- Salbreux G, Charras G, & Paluch E (2012). Actin cortex mechanics and cellular morphogenesis. Transfusion clinique et biologique, 22, 536–545. [DOI] [PubMed] [Google Scholar]
- Sato M, Theret DP, Wheeler LT, Ohshima N, & Nerem RM (1990). Application of the micropipette technique to the measurement of cultured porcine aortic endothelial cell viscoelastic properties. Journal of Biomechanical Engineering, 112, 263–268. [DOI] [PubMed] [Google Scholar]
- Schillers H, Rianna C, Schäpe J, Luque T, Doschke H, Wälte M, Uriarte JJ, Campillo N, Michanetzis GP, & Bobrowska J (2017). Standardized nanomechanical atomic force microscopy procedure (SNAP) for measuring soft and biological samples. Scientific Reports, 7, 5117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sens P, & Turner MS (2006). Budded membrane microdomains as tension regulators. Physical Review E, 73, 031918. [DOI] [PubMed] [Google Scholar]
- Sheetz MP (2001). OPINION: Cell control by membrane-cytoskeleton adhesion. Nature Reviews Molecular Cell Biology, 2, 392. [DOI] [PubMed] [Google Scholar]
- Sheetz MP, & Dai J (1996). Modulation of membrane dynamics and cell motility by membrane tension. Trends in cell biology, 6, 85–89. [DOI] [PubMed] [Google Scholar]
- Shentu TP, Singh DK, Oh M-J, Sun S, Sadaat L, Makino A, Mazzone T, Subbaiah PV, Cho M, & Levitan I (2012). The role of oxysterols in control of endothelial stiffness. Journal of Lipid Research, 53, 1348–1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shentu TP, Titushkin I, Singh DK, Gooch KJ, Subbaiah PV, Cho M, & Levitan I (2010). oxLDL-induced decrease in lipid order of membrane domains is inversely correlated with endothelial stiffness and network formation. American Journal of Physiology - cell Physiology, 299, C218–C229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinha B, Köster D, Ruez R, Gonnord P, Bastiani M, Abankwa D, Stan RV, Butler-Browne G, Vedie B, & Johannes L (2011). Cells respond to mechanical stress by rapid disassembly of caveolae. Cell, 144, 402–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spagnoli C, Beyder A, Besch S, & Sachs F (2008). Atomic force microscopy analysis of cell volume regulation. Physical Review E, 78, 031916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun A, & Levitan I (2003). Osmotic stress alters the intracellular distribution of non-erythroidal spectrin (Fodrin) in bovine aortic endothelial cells. Journal of Membrane Biology, 192, 9–17. [DOI] [PubMed] [Google Scholar]
- Sun M, Graham JS, Hegedüs B, Marga F. o., Zhang Y, Forgacs G, & Grandbois M (2005). Multiple membrane tethers probed by atomic force microscopy. Biophysical Journal, 89, 4320–4329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun M, Northup N, Marga F, Huber T, Byfield FJ, Levitan I, & Forgacs G (2007). The effect of cellular cholesterol on membrane-cytoskeleton adhesion. Journal of Cell Science, 120, 2223–2231. [DOI] [PubMed] [Google Scholar]
- Thomas G, Burnham NA, Camesano TA, & Wen Q (2013). Measuring the mechanical properties of living cells using atomic force microscopy. Journal of Visualized Experiments [DOI] [PMC free article] [PubMed]
- Vaidya N, Huang H, & Takagi S (2008). Correct equilibrium shape equation of axisymmetric vesicles. In Integral methods in science and engineering (pp. 267–276). Springer. [Google Scholar]
- Verghese C, Levitan I, Nair C, Abraham G, Garber SS, & Josiassen RC (1997). Impaired lymphocyte volume regulation in schizophrenic patients with polydipsiae—hyponatremia. Biological Psychiatry, 42, 733–736. [DOI] [PubMed] [Google Scholar]
- Vlahakis NE, & Hubmayr RD (2000). Invited review: Plasma membrane stress failure in alveolar epithelial cells. Journal of Applied Physiology, 89, 2490–2496. [DOI] [PubMed] [Google Scholar]
- Wagner B, Tharmann R, Haase I, Fischer M, & Bausch AR (2006). Cytoskeletal polymer networks: The molecular structure of cross-linkers determines macroscopic properties. Proceedings of the National Academy of Sciences, 103, 13974–13978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu H, Kuhn T, & Moy V (1998). Mechanical properties of L929 cells measured by atomic force microscopy: Effects of anticytoskeletal drugs and membrane crosslinking. Scanning, 20, 389–397. [DOI] [PubMed] [Google Scholar]
- Zhang G, Long M, Wu Z-Z, & Yu W-Q (2002). Mechanical properties of hepatocellular carcinoma cells. World Journal of Gastroenterology, 8, 243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou S, Chisholm R, Tauskela JS, Mealing GA, Johnston LJ, & Morris CE (2013). Force spectroscopy measurements show that cortical neurons exposed to excitotoxic agonists stiffen before showing evidence of bleb damage. PLoS One, 8 e73499. [DOI] [PMC free article] [PubMed] [Google Scholar]


