Hierarchical Fully Convolutional Network for Joint Atrophy Localization and Alzheimer’s Disease Diagnosis using Structural MRI

Abstract

Structural magnetic resonance imaging (sMRI) has been widely used for computer-aided diagnosis of neurodegenerative disorders, e.g., Alzheimer’s disease (AD), due to its sensitivity to morphological changes caused by brain atrophy. Recently, a few deep learning methods (e.g., convolutional neural networks, CNNs) have been proposed to learn task-oriented features from sMRI for AD diagnosis, and achieved superior performance than the conventional learning-based methods using hand-crafted features. However, these existing CNN-based methods still require the pre-determination of informative locations in sMRI. That is, the stage of discriminative atrophy localization is isolated to the latter stages of feature extraction and classifier construction. In this paper, we propose a hierarchical fully convolutional network (H-FCN) to automatically identify discriminative local patches and regions in the whole brain sMRI, upon which multi-scale feature representations are then jointly learned and fused to construct hierarchical classification models for AD diagnosis. Our proposed H-FCN method was evaluated on a large cohort of subjects from two independent datasets (i.e., ADNI-1 and ADNI-2), demonstrating good performance on joint discriminative atrophy localization and brain disease diagnosis.

1. Introduction

Alzheimer’s disease (AD), characterized by the progressive impairment of cognitive functions, is the most prevalent neurodegenerative disorder that ultimately leads to irreversible loss of neurons [1]. Brain atrophy associated with dementia is an important biomarker of AD and its progression, especially considering that the atrophic process occurs even earlier than the appearance of amnestic symptoms [2]. Structural magnetic resonance imaging (sMRI) can non-invasively capture profound brain changes induced by the atrophic process [3], based on which various computer-aided diagnosis (CAD) approaches [4], [5], [6] have been proposed for the early diagnosis of AD as well as its prodromal stage, i.e., mild cognitive impairment (MCI).

Existing sMRI-based CAD methods usually contain three fundamental components [4], i.e., 1) pre-determination of regions-of-interest (ROIs), 2) extraction of imaging features, and 3) construction of classification models. Depending on the scales of pre-defined ROIs in sMRI for subsequent feature extraction and classifier construction, these methods can be further divided into three categories, i.e., 1) voxel-level, 2) region-level, and 3) patch-level morphological pattern analysis methods. Specifically, voxel-based methods [7], [8], [9], [10], [11] attempt to identify voxel-wise disease-associated microstructures for AD classification. This kind of methods typically suffers from the challenge of over-fitting, due to the very high (e.g., millions) dimensionality of features/voxels compared with the relatively small (e.g., tens or hundreds) number of subjects/images for model training. In contrast, region-based methods [12], [13], [14], [15], [16], [17], [18] extract quantitative features from pre-segmented brain regions to construct classifiers for identifying patients from normal controls (NCs). Intuitively, this kind of methods focuses only on empirically-defined brain regions, and thus may fail to cover all possible pathological locations in the whole brain. To capture brain changes in local regions for the early diagnosis of AD, patch-based methods [19], [20], [21], [22], [23] adopt an intermediate scale (between the voxel-level and region-level) of feature representations for sMRI to construct classifiers. However, a critical issue for such patch-level pattern analysis is how to identify and combine discriminative local patches from sMRI [22].

On the other hand, the conventional voxel-, region-, and patch-based CAD methods have several common disadvantages. 1) Feature representations defined solely at a single (i.e., region- or patch-) level are inadequate in characterizing global structural information of the whole brain sMRI at the subject-level. 2) Hand-crafted features are independent of, and may not be well coordinated with, subsequent classifiers, thus potentially leading to sub-optimal diagnostic performance.

In recent years, deep convolutional neural networks (CNNs) are showing increasingly successful applications in various medical image computing tasks [24], [25], [26], [27], [28], [29], [30]. Capitalizing on task-oriented, high-nonlinear feature extraction for classifier construction, CNNs have also been applied to developing advanced CAD methods for brain disease diagnosis [31], [32], [33], [34]. However, considering that the early stage of AD could only cause subtle structural changes in the brain, it is difficult to train a conventional end-to-end CNN model without any guidance for AD classification. Therefore, relying on domain knowledge and experts’ experience, most existing CNN-based methods empirically pre-determine informative regions (e.g., hippocampus [31], [33]) or patches (e.g., located by certain anatomical landmark detector [34]) in sMRI to construct diagnostic models. That is, the stage of discriminative localization [35] of brain atrophy is methodologically independent of the latter stages of feature extraction and classifier construction, which may hamper the effectiveness of the deep neural networks in brain disease diagnosis.

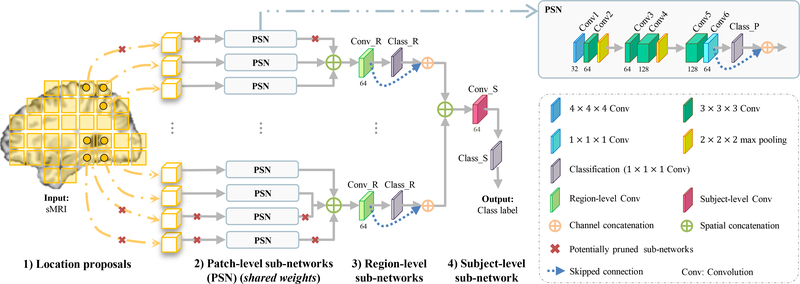
In this paper, we propose a deep learning framework to unify discriminative atrophy localization with feature extraction and classifier construction for sMRI-based AD diagnosis. Specifically, a hierarchical fully convolutional network (H-FCN) is proposed to automatically and hierarchically identify both patch- and region-level discriminative locations in whole brain sMRI, upon which multi-scale (i.e., patch-, region-, and subject-level) feature representations are jointly learned and fused in a data-driven manner to construct hierarchical classification models. Based on the automatically-identified discriminative locations in sMRI, we further prune the initial H-FCN architecture to reduce learnable parameters and finally boost the diagnostic performance. A schematic diagram of our H-FCN method is shown in Fig. 1. In the experiments, our proposed method was trained and evaluated on two independent datasets (i.e., ADNI-1 and ADNI-2) for multiple AD-related diagnosis tasks, including AD classification, and MCI conversion prediction. Experimental results demonstrate that our proposed H-FCN method can not only effectively identify AD-related discriminative atrophy locations in sMRI, but also yield superior diagnostic performance compared with the state-of-the-art methods.

Fig. 1.

Illustration of our hierarchical fully convolutional network (H-FCN), which includes four components: 1) location proposals, 2) patch-level sub-networks, 3) region-level sub-networks, and 4) subject-level sub-network.

The rest of the paper is organized as follows. In Section 2, we briefly review previous studies on sMRI-based CAD methods for AD diagnosis. In Sections 3 and 4, we introduce the studied datasets and our proposed H-FCN method, respectively. In Section 5, our proposed H-FCN method is evaluated and compared with the state-of-the-art methods. In addition, the components and parameters of our network are analyzed in detail. In Section 6, we discuss the relationship between our proposed method and previous studies and analyze the main limitations of the current study. The paper is finally concluded in Section 7.

2. Related Work

In this section, we briefly review previous work on sMRI-based CAD methods for AD diagnosis, including the conventional learning-based and deep-learning-based methods.

2.1. Conventional Learning-based Methods

In terms of the scales of adopted feature representations, the voxel-, region-, and patch-based methods are representative categories of sMRI-based CAD methods in the literature.

Typically, voxel-based methods extract voxel-wise imaging features from the whole brain sMRI to construct classifiers for distinguishing patients from normal controls (NCs). For example, Klöppel et al. [8] used gray matter (GM) density map of the whole brain, generated by voxel-based morphometry (VBM) [36], to train a linear support vector machine (SVM) [37] for identifying sMRI scans of AD. Hinrichs et al. [9] integrated a spatial regularizer into the linear programming boosting (LPboosting) model [38] for AD classification using GM density map. Li et al. [10] extracted both volumetric and geometric measures at each vertex on the cortical surface to construct a linear SVM for discriminating MCI from NC. The voxel-level morphological pattern analysis usually has to face the challenge of high-dimensional features, especially for the volumetric sMRI with millions of voxels. Hence, dimensionality reduction approaches [39], [40], [41] are desirable for dealing with the potential over-fitting issue caused by the high-dimensional, voxel-level feature representations. In another word, the diagnostic performance of voxel-based methods may largely rely on dimensionality reduction.

Region-based methods employ imaging features extracted from brain regions, while these regions are usually predetermined based on biological prior knowledge or anatomical brain atlases [42]. For example, Magnin et al. [43] and Zhang et al. [14] parcellated the whole brain into several non-overlapping regions by non-linearly aligning each individual sMRI onto an anatomically labeled atlas, and then extracted regional features to train the SVM classifiers for AD diagnosis. Fan et al. [12] adopted the watershed algorithm [44] to group sMRI voxels into an adaptive set of brain regions, from which regional volumetric features were extracted to perform SVM-based AD classification. Koikkalainen et al. [45] and Liu et al. [17] spatially normalized each individual sMRI onto multiple atlases, and then extracted regional features in each atlas space to construct ensemble classification models for AD/MCI diagnosis. Wang et al. [13] and Sørensen et al. [16] performed AD diagnosis based on sMRI hippocampal features, considering that the influence of the AD pathological process on the hippocampus has been biologically validated. Also, several studies performed AD diagnosis based on the fusion of complementary information provided by the hippocampus and other brain regions in sMRI. For example, in [46], features extracted from the hippocampus and posterior cingulate cortex were combined to learn SVM classifiers for AD/MCI diagnosis. In [47], the classifiers trained independently based on hippocampal and CSF features were combined, followed by another classifier to further refine the diagnostic performance.

It is worth mentioning that the early stage of AD would induce subtle structural changes in local brain regions, instead of isolated voxels or the whole brain [9], [22]. Accordingly, several previous studies proposed to perform AD diagnosis by using imaging features defined at the patch-level, i.e., an intermediate scale between the voxel-level and region-level. For example, Liu et al. [21] extracted both the patch-wise GM density maps and spatial-correlation features to develop a hierarchical classification model for AD/MCI diagnosis. Tong et al. [22] adopted local intensity patches as features to develop a multiple instance learning (MIL) model [48] for AD classification and MCI conversion prediction. Zhang et al. [23] first detected anatomical landmarks in sMRI, and then extracted morphological features from the local patches centered at these landmarks to perform SVM-based AD/MCI classification. The pre-selection and combination of local patches to capture global information of the whole brain sMRI is always a key step in these existing patch-based methods.

2.2. Deep-Learning-based Methods

The conventional learning-based methods adopt handcrafted features (e.g., GM density map [8], [9], cortical thickness [10], or hippocampal shape measurements [13]) to construct classifiers, which may yield sub-optimal diagnostic performance due to potential heterogeneities between independently-extracted features and subsequent classifiers.

Recently, CNN-based methods have been proposed to extract high-level region/patch-wise features in a data-driven manner for brain disease diagnosis. For example, Li et al. [31] and Khvostikov et al. [33] pre-extracted hippocampal region to train CNNs using sMRI and multimodal neuroimaging data, respectively. Liu et al. [34] extracted local image patches centered at multiple pre-defined anatomical landmarks to develop the CNN-based models for AD classification and MCI conversion prediction.

Apart from CNNs, some other deep learning methodologies have also been applied to developing CAD methods for AD diagnosis. For example, deep Boltzmann machine [49] was used by Suk et al. [50] to learn shared feature representations between patches extracted from sMRI and positron emission tomography (PET) images, based on which an ensemble SVM classifier was further trained for AD/MCI classification. Liu et al. [51] extracted hand-crafted features from pre-segmented brain regions, and further fed these low-level features into stacked auto-encoders [52] for producing higher-level features for AD classification. Lu et al. [53] developed a multi-scale deep neural network for early diagnosis of AD, where low-level patch-wise features extracted from PET images were used as network input.

However, similar to the conventional learning-based methods, these existing deep-learning-based methods still require the pre-determination of the ROIs prior to network training. That is, localization of discriminative brain regions in sMR images is still independent of feature extraction and classifier construction, which may hamper the corresponding diagnostic performance.

3. Materials

In this section, we introduce the sMRI datasets as well as the image pre-processing pipeline used in our study.

3.1. Studied Datasets

Two public datasets downloaded from Alzheimer’s Disease Neuroimaging Initiative¹ (i.e., ADNI-1 and ADNI-2) [54] were studied in this paper. Note, subjects that appear in both ADNI-1 and ADNI-2 were removed from ADNI-2. The demographic information of subjects in both ADNI-1 and ADNI-2 is presented in Table 1.

TABLE 1.

Demographic information of the subjects included in the studied datasets (i.e., the baseline ADNI-1 and ADNI-2). The gender is reported as male/female. The age, education years, and mini-mental state examination (MMSE) values [54] are reported as Mean ± Standard deviation (Std).

Dataset	Category	Gender	Age	Education	MMSE
ADNI-1	NC	127/102	75.8±5.0	16.0±2.9	29.1±1.0
	sMCI	151/75	74.9±7.6	15.6±3.2	27.3±1.8
	pMCI	102/65	74.8±6.8	15.7±2.8	26.6±1.7
	AD	106/93	75.3±7.5	14.7±3.1	23.3±2.0
ADNI-2	NC	113/87	74.8±6.8	15.7±2.8	26.6±1.7
	sMCI	134/105	71.7±7.6	16.2±2.7	28.3±1.6
	pMCI	24/14	71.3±7.3	16.2±2.7	27.0±1.7
	AD	91/68	74.2±8.0	15.9±2.6	23.2±2.2

ADNI-1:

The baseline ADNI-1 dataset consists of 1.5T T1-weighted MR images acquired from totally 821 subjects. These subjects were divided into three categories (i.e., NC, MCI, and AD) in terms of the standard clinical criteria, including mini-mental state examination scores and clinical dementia rating. According to whether MCI subjects would convert to AD within 36 months after the baseline evaluation, the MCI subjects were further specified as stable MCI (sMCI) subjects that were always diagnosed as MCI at all time points (0–96 months), or progressive MCI (pMCI) subjects that finally converted to AD within 36 months after the baseline. To sum up, the baseline ADNI-1 dataset contains 229 NC, 226 sMCI, 167 pMCI, and 199 AD subjects.

ADNI-2:

The baseline ADNI-2 dataset include 3T T1-weighted sMRI data acquired from 636 subjects. According to the same clinical criteria as those used for ADNI-1, the 637 subjects were further separated as 200 NC, 239 sMCI, 38 pMCI, and 159 AD subjects.

3.2. Image Pre-Processing

All sMRI data were processed following a standard pipeline, which includes anterior commissure (AC)-posterior commissure (PC) correction, intensity correction [55], skull stripping [56], and cerebellum removing. An affine registration was performed to linearly align each sMRI to the Colin27 template [57] to remove global linear differences (including global translation, scale, and rotation differences), and also to resample all sMRIs to have identical spatial resolution (i.e., 1 × 1 × 1 mm³).

4. Method

In this part, we introduce in detail our proposed H-FCN method, including the architecture of our network (Section 4.1), a specific loss function for training the network (Section 4.2), the network pruning strategy (Section 4.3), and the implementation details (Section 4.4).

4.1. Architecture

Our proposed hierarchical fully convolutional network (H-FCN) is developed in the linearly-aligned image space. As shown in Fig. 1, it consists of four sequential components, i.e., 1) location proposals, 2) patch-level sub-networks, 3) region-level sub-networks, and 4) subject-level sub-network.

Briefly, image patches widely distributed over the whole brain (Section 4.1.1) are fed into the patch-level sub-networks (Section 4.1.2) to produce the feature representations and classification scores for these input patches. The outputs of the patch-level sub-networks are grouped/merged according to the spatial relationship of input patches, which are then processed by the region-level sub-networks (Section 4.1.3) to produce the feature representations and classification scores for each specific region (i.e., a combination of neighboring patches). Finally, the outputs of the region-level sub-networks are integrated and processed by the subject-level sub-network (Section 4.1.4) to yield the classification score for each subject. The architecture of our proposed H-FCN is detailed as follows.

4.1.1. Location proposals

Our proposed H-FCN method adopts a set of local image patches as the inputs for the network. To generate location proposals for the extraction of anatomically-consistent image patches from different subjects, we first need to construct the voxel-wise anatomical correspondence across all linearly-aligned sMRIs (with each image corresponding to a specific subject). To this end, each linearly-aligned sMRI is further non-linearly registered to the Colin27 template. Based on the resulting deformation fields, for each voxel in the template, we find its corresponding voxel in each linearly-aligned sMRI, thus building the voxel-wise anatomical correspondence in the linearly-aligned image space.

After that, image voxels widely distributed over the whole template brain image are used as location proposals (i.e., yellow squares shown in Fig. 1). We further locate corresponding voxels in each linearly-aligned sMRI, and extract same-sized (e.g., 25 × 25 × 25) patches centered at these location proposals to construct our hierarchical network. Notably, the motivation of using location proposals that are widely distributed over the whole brain is to ensure that H-FCN can include and then automatically identify all discriminative locations in a data-driven manner. But, beyond that, there is no explicit assumption regarding the specific discriminative power of each location proposal. This is different from existing region- and patch-based methods (e.g., [16], [22], [34], [46]) in nature, as those previous studies select/rank ROIs according to their informativeness (usually pre-defined based on domain knowledge).

On the other hand, it is also worth mentioning that prior knowledge could also be included in our H-FCN model to reduce the computational complexity and boost the learning performance. The reason is that prior knowledge can help efficiently filter out obviously uninformative voxels from selected location proposals, especially considering that a volumetric sMR image usually contains millions of voxels. Therefore, in one of our implementations, we adopt anatomical landmarks defined in the whole brain image [23] as prior knowledge for generating location proposals. Under the constraint that the distance between any two landmarks is no less than 25, the number of location proposals is further reduced to 120 to control the number of learnable parameters. We denote this kind of implementation as with-prior H-FCN (wH-FCN for short) in this paper.

We also implement another version of H-FCN, where the template image is directly partitioned into multiple non-overlapped patches, and their central voxels are then warped onto the linearly-aligned subject as location proposals. We denote this variant implementation as no-prior H-FCN (nH-FCN for short). Note that wH-FCN and nH-FCN share the same number (i.e., 120) of input image patches, the same patch size (i.e., 25 × 25 × 25) and similar network structure. The difference is that they use different location proposals. Both wH-FCN and nH-FCN make no explicit assumption regarding the specific discriminative capacities of the input location proposals, which should be further determined by the network in a data-driven manner.

4.1.2. Patch-level sub-networks

As the PSN modules shown in Fig. 1, all patch-level sub-networks developed in our H-FCN (both wH-FCN and nW-FCN) have the same structure, i.e., fully convolutional network [58], for efficiency of training. In addition, in our implementation, all these PSN modules share the same weights to limit the number of learnable parameters, especially considering a relatively large number of input patches.

Specifically, each PSN module contains six convolutional (Conv) layers, including one 4×4×4 layer (i.e., Conv1), four 3×3×3 layers (i.e., Conv2 to Conv5), and one 1×1×1 layer (i.e., Conv6). The number of channels for Conv1 to Conv6 is 32, 64, 64, 128, 128, and 64, respectively. All Conv layers have unit stride without zero-padding, which are followed by batch normalization (BN) and rectified linear unit (ReLU) activations. Between Conv2 and Conv3, as well as between Conv4 and Conv5, a 2×2×2 max-pooling layer is adopted to down-sample the intermediate feature maps. At the end, a classification layer (i.e., Class P) is realized via 1 × 1 × 1 convolutions (with C channels, where C is the number of categories) followed by sigmoid activations.

As the result, each local image patch is processed by the corresponding PSN module to yield a patch-level feature representation (i.e., output of Conv6; size: 1×1×1×64), based on which a patch-level classification score (size: 1 × 1 × 1 × C) is further produced by the subsequent classification layer (i.e., Class P). Intuitively, the diagnostic/classification score accuracy of each PSN module indicates the discriminative capacity of the corresponding location proposal.

4.1.3. Region-level sub-networks

To construct the region-level sub-networks, we concatenate each patch-level feature representation with the corresponding patch-level classification score across channels, i.e., as a 1 × 1 × 1 × (64 + C) tensor. These patch-level outputs are then used as the inputs for the subsequent region-level sub-networks. In particular, here the classification scores for each specific patch can be regarded as high-level, task-oriented features, which is similar to the auto-context strategy used in image segmentation [59], [60]. That is, as complementary to the patch-level feature representations, the subsequent classification scores could potentially provide more direct and higher semantic information with respect to the diagnostic task. Also, using both of them as the inputs for the region-level sub-networks, the patch-level classification scores could be jointly optimized with the patch-level feature representations under multi-scale supervision (which will be detailed in Section 4.2).

Then, we group spatially-nearest patches, e.g., in a 2 × 2 × 2 neighborhood of each patch, to form a specific region (or second-level patch). Accordingly, the corresponding patch-level outputs are concatenated by taking into account their spatial relationship, e.g., as a 2×2×2×(64+C) tensor. As shown in Fig. 1, for each specific region, a region-level Conv layer (i.e., Conv R) is then applied on the concatenated tensor to generating a region-level feature representation (size: 1×1×1×64), based on which a region-level classification score is further produced by the subsequent classification layer (i.e., Class R). Similar to the patch-level sub-networks, the diagnostic score accuracy of each region-level sub-network indicates the discriminative capacity of the corresponding region. Notably, the specific regions (or second-level patches) described here are partially overlapped. The shapes of them are deformable, depending on the location proposals. Specifically, in nH-FCN, these regions are regular partitions of the template image, which are further deformed for each subject in the linearly-aligned image space. In nH-FCN, these regions have irregular shapes, determined by the locations of pre-defined anatomical landmarks.

4.1.4. Subject-level sub-network

Finally, all region-level feature representations (size: 1×1×1 × 64) and classification scores (size: 1 × 1 × 1 × C) are concatenated. They are further processed by the subject-level Conv layer (i.e., Conv S in Fig. 1) to obtain a subject-level feature representation (size: 1 × 1 × 1 × 64), based on which a subject-level classification score (size: 1×1×1×C) is produced by the ultimate classification layer (i.e., Class_S in Fig. 1).

It is worth noting that, in our proposed H-FCN method, the discriminative power of the sub-networks defined at different scales is expected to increase monotonously, as posterior sub-networks are trained to effectively integrate outputs of preceding sub-networks to produce higher-level features for the diagnostic task.

4.2. Hybrid Loss Function

We design a hybrid cross-entropy loss to effectively learn our proposed H-FCN, in which the subject-level labels are used as weakly-supervised guidance for the training of patch-level and region-level sub-networks. Specifically, let ${\left\{\left({\mathbf{X}}_n,{\mathbf{y}}_n\right)\right\}}_{n=1}^N$ be a training set containing N samples, where X_n and y_n ∈ {1, …, C} denote, respectively, the sMRI for the n^th subject and the corresponding class label. The learnable parameters for the patch-, region-, and subject-level sub-networks are denoted, respectively, as W^p, W^r, and W^s. Then, our hybrid cross-entropy loss is designed as:

$$\begin{gathered} \mathcal{L}\left({\mathbf{W}}^p,{\mathbf{W}}^r,{\mathbf{W}}^s\right)= \\ -\frac{{\lambda }^p}{N}\sum _{n=1}^N\frac{1}{C}\sum _{c=1}^C{\delta }_{n,c}\log \left({\mathcal{P}}^p\left({\widehat{\mathbf{y}}}_n=c|{\mathbf{X}}_n;{\mathbf{W}}^p,{\mathbf{W}}^r,{\mathbf{W}}^s\right)\right) \\ -\frac{{\lambda }^r}{N}\sum _{n=1}^N\frac{1}{C}\sum _{c=1}^C{\delta }_{n,c}\log \left({\mathcal{P}}^r\left({\widehat{\mathbf{y}}}_n=c|{\mathbf{X}}_n;{\mathbf{W}}^r,{\mathbf{W}}^s\right)\right) \\ -\frac{1}{N}\sum _{n=1}^N\frac{1}{C}\sum _{c=1}^C{\delta }_{n,c}\log \left({\mathcal{P}}^s\left({\widehat{\mathbf{y}}}_n=c|{\mathbf{X}}_n;{\mathbf{W}}^s\right)\right), \end{gathered}$$ (1)

where δ_n,c is a binary indicator of the ground-truth class label, which equals 1 iff y_n = c. Function ${\mathcal{P}}^p(\cdot |\cdot )$, ${\mathcal{P}}^r(\cdot |\cdot )$, and ${\mathcal{P}}^s(\cdot |\cdot )$ denote the probability obtained, respectively, by the patch-, region-, and subject-level sub-networks, in terms of a given subject (e.g., X_n) being diagnosed as a specific class (e.g., ${\widehat{\mathbf{y}}}_n=c$). Thus, given a training set ${\left\{\left({\mathbf{X}}_n,{\mathbf{y}}_n\right)\right\}}_{n=1}^N$, the first to the last terms of Eq. (1) denote, respectively, the average loss for all patch-level sub-networks, the average loss for all region-level sub-networks, and the loss for the subject-level subnetwork.

As can be inferred from the form of ${\mathcal{P}}^p(\cdot |\cdot )$ and ${\mathcal{P}}^r(\cdot |\cdot )$, the training loss from higher-level sub-networks are back-propagated and merged into lower-level sub-networks to assist the updating of their network parameters. Tuning parameters λ^p and λ^r control, respectively, the influences of patch-level and region-level training losses, which were empirically set as 1 in our experiments.

4.3. Network Pruning

After training the initial H-FCN model by minimizing Eq. (1) directly, the discriminative capabilities of input location proposals can be automatically inferred in a data-driven manner. Based on the resulting diagnostic/classification scores on the training set for each patch-level and region-level sub-networks, we further refine the initial H-FCN by pruning sub-networks to remove uninformative patches and regions. An illustration of such network pruning step is denoted by small red crosses in Fig. 1.

Specifically, we select the top T^r regions and T^p patches with the lowest diagnostic losses on the training set. Then, we delete those uninformative (i.e., not listed in the top T^r) region-level sub-networks, and hence the connections between those uninformative regions and the preceding patches are simultaneously removed. We further prune the uninformative (i.e., not listed in the top T^p) patch-level sub-networks that connect to the remaining (informative) region-level sub-networks. Finally, we remove the sub-networks for regions (as well as their corresponding patch-level connections) that are completely included in other regions to form the pruned H-FCN model.

The pruned H-FCN model yielded in the above manner contains much less learnable parameters than the initial H-FCN model. It is worth noting that those informative regions remained in the pruned H-FCN model may have different shapes and sizes, as they are constructed on the outputs of varying numbers of informative patches. Also, these regions are potentially overlapped. In our experiments, we selected top 10 regions (i.e., T^r = 10) and top 20 patches (i.e., T^p = 20) to prune the network.

4.4. Implementations

The proposed networks were implemented using Python based on the Keras package², and the computer we used contains a single GPU (i.e., NVIDIA GTX TITAN 12GB). The Adam optimizer with recommended parameters was used for training, and the size of mini-batch was set as 5. The networks were trained on one complete dataset (e.g., ADNI-1), and then tested on the other independent dataset (e.g., ADNI-2). We randomly selected 10% training samples as the validate set. The diagnostic models and the corresponding tuning parameters (e.g., the patch size) were chosen in terms of the validation performance.

In the training stage, the definition of the voxel-wise correspondence for the extraction of anatomically-consistent image patches requires about 10 minutes for each subject. We trained the networks for 100 epochs, which took around 14 hours (i.e., 500 seconds for each epoch). In the application stage, the diagnosis for an unseen testing subject only requires less than 2 seconds, based on its non-linear registration deformation field (for the definition voxel-wise correspondence) and trained networks.

4.4.1. Training strategy

For the task of AD classification (i.e., AD vs. NC), the initial wH-FCN model was trained from scratch by minimizing Eq. (1) directly. After identifying the most informative patches and regions, the pruned wH-FCN model was trained in a deep manner. That is, the sub-networks at each scale of the pruned network were first trained sequentially by freezing the preceding sub-networks (i.e., at finer scales) and minimizing the corresponding term in Eq. (1). After that, by using the learned parameters as initialization, all sub-networks were further refined jointly.

4.4.2. Transfer learning

Compared with the task of AD classification, the task of MCI conversion prediction is relatively more challenging, since structural changes of MCI brains (between those of NC and AD brains) caused by dementia may be very subtle. Considering that the two classification tasks are highly correlated, recent studies [19], [34] have shown that the supplementary knowledge learned from AD and NC subjects can be adopted to enrich available information for the prediction of MCI conversion. Accordingly, in our implementation, we transferred the network parameters learned for AD diagnosis (i.e., AD vs. NC classification) to initialize the training of the network for pMCI vs. sMCI classification.

4.4.3. Data augmentation

To mitigate the over-fitting issue, 0.5 dropout was activated for the Conv6, Conv R, and Conv S layers in Fig. 1. Also, the training samples were augmented on-the-fly using three main strategies, i.e., i) randomly flipping the sMRI for each subject, ii) randomly distorting the sMRI with a small scale for each subject, and iii) randomly shifting at each location proposal within a 5 × 5 × 5 neighborhood to extract image patches. It is worth mentioning that the operation of randomly shifting was designed specifically for our proposed method. When combined with the first two operations, it could effectively augment the number and diversity of available samples for training our H-FCN model. Moreover, as introduced in Section 4.1.2, the patch-level sub-networks shared weights across different patch locations in our implementations. This could also help reduce the over-fitting risk, considering the number of learnable parameters was effectively reduced and the input image patches were extracted at different brain locations with various anatomical appearances. In addition, based on identified discriminative locations, the network pruning strategy introduced in Section 4.3 further reduced the number of learnable parameters to tackle the over-fitting challenge.

5. Experiments and Analyses

In this section, we first compare our H-FCN method with several state-of-the-art methods. Then, we validate the effectiveness of the important components of our method, including the prior knowledge for location proposals, the network pruning strategy, and the transfer learning strategy. After that, we further evaluate the influence of the network parameters (e.g., the size and number of input image patches) as well as the training data partition on the diagnostic performance. Finally, we verify the multi-scale discriminative locations automatically identified by our H-FCN method.

5.1. Experimental Settings

Our H-FCN method was validated on both tasks of AD classification (i.e., AD vs. NC) and MCI conversion prediction (i.e., pMCI vs. sMCI). The classification performance was evaluated by four metrics, including classification accuracy (ACC), sensitivity (SEN), specificity (SPE), and area under receiver operating characteristic curve (AUC). These metrics are defined as $\text{ACC}=\frac{\text{TP}+\text{TN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}}$, $\text{SEN}=\frac{\text{TP}}{\text{TP}+\text{FN}}$, and $\text{SPE}=\frac{\text{TN}}{\text{TN}+\text{FP}}$, where TP, TN, FP, and FN denote, respectively, the true positive, true negative, false positive, and false negative values. The AUC is calculated based on all possible pairs of SEN and 1-SPE obtained by changing the thresholds performed on the classification scores yielded by the trained networks.

5.2. Competing Methods

The proposed wH-FCN method was first compared with three conventional learning-based methods, including 1) a method using region-level feature representations (denoted as ROI) [14], 2) a method using voxel-level feature representations, i.e., voxel-based morphometry (VBM) [36], and 3) a method using patch-level feature representations, i.e., landmark-based morphology (LBM) [23]. Besides, wH-FCN was further compared with a state-of-the-art deep-learning-based method, i.e., 4) deep multi-instance learning (DMIL) model [34].

1). Region-based method (ROI):

Following previous studies [14], the whole brain sMRI data were partitioned into multiple regions to extract region-scale features for SVM-based classification. More specifically, each sMRI was first segmented into three tissue types, i.e., gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF), by using the FAST algorithm [61] in the FSL package³. Then, the anatomical automatic labeling (AAL) atlas [62], with 90 pre-defined ROIs in the cerebrum, was aligned to each subject using the HAMMER algorithm [63]. Finally, the GM volumes in the 90 ROIs were quantified, and further normalized by the total intracranial volume (estimated by the summation of GM, WM, and CSF volumes), to train linear SVM classifiers.

2). Voxel-based morphometry (VBM):

In line with [36], all sMRI data were spatially normalized to the Colin27 template to extract local GM density in a voxel-wise manner. After that, a statistical group comparison based on t-test was performed to reduce the dimensionality of the high-dimensional voxel-level feature representations. Finally, linear SVM classifiers were constructed for disease diagnosis.

3). Landmark-based morphometry (LBM):

In the LBM method [23], morphological features (i.e., local energy pattern [64]) were first extracted from a local image patch centered at each pre-defined anatomical landmark. These patch-level feature representations were further concatenated and processed via z-score normalization process [65] to perform linear SVM-based classification.

4). Deep multi-instance learning (DMIL):

The DMIL method [34] adopted local image patches to develop a CNN-based multi-instance model for brain disease diagnosis. Specifically, multiple image patches were first localized by anatomical landmarks. Then, each input patch was processed by a CNN to yield the corresponding patch-level feature representations. These patch-level features were finally concatenated and fused by fully connected layers to produce subject-level feature representations for AD classification and MCI conversion prediction. In line with [34], totally 40 landmarks were selected to construct the classifier.

Notably, our implementation of wH-FCN shared the same landmark pool with the LBM and DMIL methods. However, the key difference between them is that, based on prior knowledge, both the LBM and DMIL methods first pre-selected the top 40 landmarks as inputs. In contrast, our wH-FCN method regarded all anatomical landmarks equally as potential location proposals, without explicit assumption concerning their discriminative capacities.

5.3. Diagnostic Performance

In this group of experiments, the baseline ADNI-1 and ADNI-2 datasets were used as the training and testing sets, respectively. Results of AD vs. NC and pMCI vs. sMCI classification obtained by the competing methods (i.e., ROI, VBM, LBM, and DMIL) and our wH-FCN method are presented in Table 2.

TABLE 2.

Results for AD classification (i.e., AD vs. NC) and MCI conversion prediction (i.e., pMCI vs. sMCI).

Method	AD vs. NC classification				pMCI vs. sMCI classification
	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC
ROI	0.792	0.786	0.796	0.867	0.661	0.474	0.690	0.638
VBM	0.805	0.774	0.830	0.876	0.643	0.368	0.686	0.593
LBM	0.822	0.774	0.861	0.881	0.686	0.395	0.732	0.636
DMIL	0.911	0.881	0.935	0.959	0.769	0.421	0.824	0.776
wH-FCN	0.903	0.824	0.965	0.951	0.809	0.526	0.854	0.781

Several observations can be summarized from Table 2. 1) Three patch-based methods (i.e., LBM, DMIL, and wH-FCN) yield better classification results than both the ROI method and VBM method. This shows that, as an intermediate scale between the region-level and voxel-level feature representations, the patch-level feature representations could provide more discriminative information regarding subtle brain changes for brain disease diagnosis. 2) For both diagnosis tasks, deep-learning-based methods (i.e., DMIL and wH-FCN) outperform other three traditional learning-based methods (i.e., the ROI, VBM, and LBM methods) with relatively large margins, demonstrating that learning task-oriented imaging features in a data-driven manner is beneficial for subsequent classification tasks. 3) Compared with the state-of-the-art DMIL method, our proposed wH-FCN method has competitive performance in the fundamental task of AD classification. More importantly, our wH-FCN method yields much better results on the more challenging task, i.e., MCI conversion prediction. Specifically, the performance improvements brought by our method with respect to ACC, SEN, and SPE are all statistically significant (i.e., p-values < 0.05) in pMCI vs. sMCI classification. The main reason could be that the integration of discriminative localization, feature extraction, and classifier construction into a unified deep learning framework is effective for improving diagnostic performance, since, in this way, the three important steps can be more seamlessly coordinated with each other in a task-oriented manner. The DMIL method slightly outperforms our wH-FCN method in the task of AD vs. NC classification, with p-values > 0.5 for both ACC and AUC. It perhaps due to the reason that the AD classification task has less strict requirement for task-oriented discriminative localization than the MCI conversion prediction task, considering the structural changes in brains with AD should be easier to be captured. Another reason could be that DMIL constructed specific CNNs (i.e., with different network parameters) for image patches extracted at different brain locations. Nevertheless, as a compromise, such kind of implementations inevitably increases the computational complexity, especially when a relatively large number of local patches are extracted as the network inputs.

5.4. Effectiveness of Prior Knowledge for Location Proposals

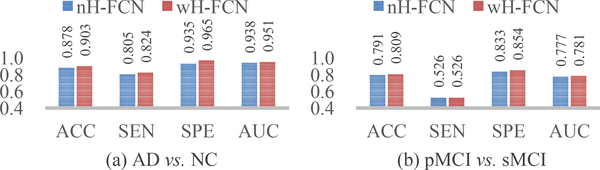
As introduced in Section 4.1.1, in the implementation of our wH-FCN method, the anatomical landmarks were used as prior knowledge to assist the definition of relatively informative location proposals, i.e., to efficiently filter out uninformative locations. To evaluate the effectiveness of this strategy, we also designed another version of our proposed network (i.e., nH-FCN) for comparison, in which the location proposals were defined without any prior knowledge.

In Fig. 2, the two variants of our method (i.e., nH-FCN and wH-FCN) are compared on both the tasks of AD classification and MCI conversion prediction. According to Fig. 2 and Table 2, we can have at least two observations. 1) Compared with the state-of-the-art method (i.e., DMIL), our nH-FCN and wH-FCN consistently lead to competitive performance, especially on the challenging task of MCI conversion prediction. For example, in the case of DMIL vs. nH-FCN, the ACC and SEN for MCI conversion prediction is 0.769 vs. 0.791 and 0.421 vs. 0.526, respectively. In some sense, this reflects the robustness of our proposed method in terms of location proposals. 2) Our wH-FCN outperforms nH-FCN on both tasks, e.g., the AUC for AD classification is 0.951 vs. 0.938, and for MCI conversion prediction is 0.781 vs. 0.777. It indicates that wH-FCN may include more informative patches as the initial inputs, compared with nH-FCN that does not consider any prior knowledge on discriminative locations in sMRI. Also, it potentially implies that, if we could initialize the network with more informative location proposals, the diagnostic performance of our proposed H-FCN method could be further improved.

Fig. 2.

Comparison between no-prior locations proposals (i.e., nH-FCN) and with-prior location proposals (i.e., wH-FCN). (a) and (b) show the classification results for AD diagnosis and MCI conversion prediction, respectively.

5.5. Effectiveness of Hierarchical Network Pruning

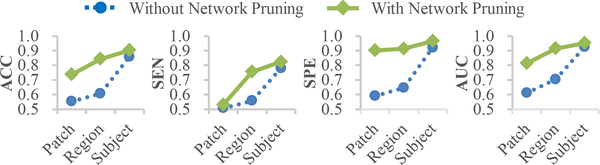
As introduced in Section 4.3, a key component of our proposed method is the network pruning strategy to hierarchically prune uninformative region-level and patch-level sub-networks, thereby reducing the number of learnable parameters and ultimately boosting the diagnostic performance.

In this group of experiments, we evaluated the effectiveness of the network pruning as well as the hierarchical architecture used in our proposed wH-FCN method. Specifically, using the task of AD diagnosis as an example, we performed a two-fold evaluation, including 1) the comparison between the initial network without network pruning and the refined network with network pruning, and 2) the comparison of classification performance for sub-networks defined at different (i.e., patch-, region-, and subject-) levels.

The corresponding experimental results are presented in Fig. 3, from which we can have the following observations. 1) Our network pruning strategy effectively improves the classification performance of the sub-networks defined at the three different scales, where the improvement for the patch-level and region-level sub-networks is especially significant. This implies that those uninformative patches and regions in the initial network were largely removed due to the network pruning strategy. 2) From the patch-level to the subject-level, the sub-networks defined at different scales lead to monotonously increased classification performance in terms of all the four metrics. This indicates that, capitalizing on the hierarchically integration of feature representations from lower-level sub-networks, our proposed method can effectively learn more discriminative feature representations for the diagnosis task at hand.

Fig. 3.

Results of AD classification produced by our wH-FCN method with and without the network pruning strategy, respectively. For each case, the average classification performance of the sub-networks defined at different scales are presented.

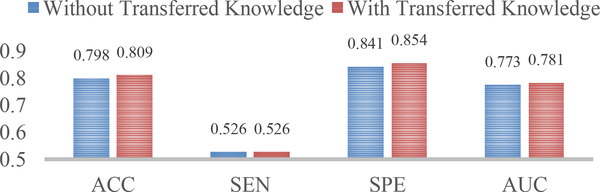
5.6. Effectiveness of Transfer Learning

As introduced in Section 4.4.1, we used the network parameters learned from the task of AD classification as initialization to train networks for the relatively challenging task of MCI conversion prediction, considering that the two tasks are highly correlated according to the nature of AD.

In this group of experiments, we verified the effectiveness of the transferred knowledge for the network training. To this end, we trained another network from scratch for MCI conversion prediction, and compared the resulting classification performance with that obtained by the previous network trained with transferred knowledge.

The corresponding results are presented in Fig. 4, based on which we can find that initialization of networks with transferred knowledge could further boost a little bit of diagnostic performance. This is intuitive and reasonable, especially under the circumstance that the two diagnosis tasks are correlated. The possible reason is that the training data in the task of pMCI vs. sMCI classification are implicitly enriched since the supplementary information of AD and NC subjects is also included.

Fig. 4.

Comparison between our wH-FCN models trained without and with transferred knowledge, respectively, for MCI conversion prediction. In the latter case, the parameters of the network for AD classification were transferred to initialize the training of the network for MCI conversion prediction.

5.7. Influence of the Number of Image Patches

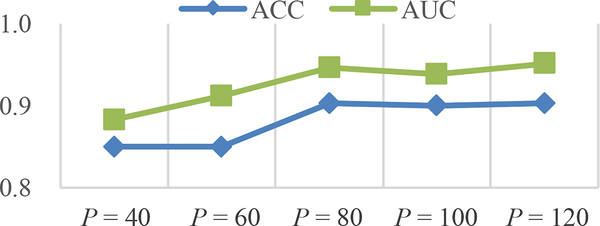
In this group of experiments, we investigated the influence of the number of input image patches (denoted as P) on the classification performances achieved by our wH-FCN method. Using AD classification as an example, we orderly selected P from {40, 60, 80, 100, 120} in wH-FCN and recorded the corresponding results. Experimental results quantified by ACC and AUC are summarized in Fig. 5.

Fig. 5.

Results of AD classification obtained by our wH-FCN method in terms of different numbers of input image patches (i.e., P = 40,60, …, 120).

From Fig. 5, we can observe that both the values of ACC and AUC are clearly increased when changing P from 40 to 80. For example, we have ACC = 0.850 and AUC = 0.883 when P = 40, while ACC = 0.903 and AUC = 0.946 when P = 80. This implies that less location proposals are not enough to yield satisfactory results, potentially because 1) limited number of local patches cannot comprehensively characterize the global information at the subject-level, and 2) limited number of location proposals may fail to include some actually discriminative locations at the very beginning. We can also observe that the performance of our method is relatively stable between P = 80 and P = 120, considering that the improvements of ACC and AUC are slow. The main motivation for choosing P = 120 in our implementations is to largely include potentially informative locations, as well as to account for the computational complexity and memory cost during the training.

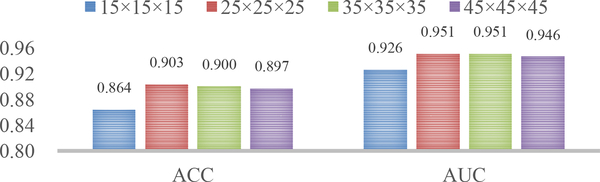
5.8. Influence of the Size of Image Patches

In previous implementations of our H-FCN method, the size of input image patches was fixed as 25×25×25. To evaluate the influence of patch size, in this group of experiments, we trained networks using local patches with the size of 15×15×15, 25×25×25, 35×35×35, and 45×45×45, one by one. Correspondingly, the classification results in terms of ACC and AUC are reported in Fig. 6.

Fig. 6.

Results of AD classification obtained by our wH-FCN method in terms of different sizes of input image patches (i.e., 15 × 15 × 15, 25 × 25 × 25, 35 × 35 × 35, and 45 × 45 × 45).

From Fig. 6, we can see that our proposed H-FCN method is not very sensitive to the size of input patch in a wide range (i.e., from 15 × 15 × 15 to 45 × 45 × 45), and the overall better result is obtained using patches with the size in the range of [25×25×25,35×35×35]. Also, H-FCN using relatively smaller image patches (i.e., 15 × 15 × 15) cannot generate good results, implying that too small image patches could not capture global structural information of the whole brain. On the other hand, the performance of H-FCN using larger image patches (i.e., 45×45×45) is also slightly decreased. It may be because too large image patches inevitably include more uninformative voxels, which could affect the identification of subtle brain changes in these large patches.

5.9. Influence of Data Partition

In all the above experiments, we trained and tested the classification networks on the baseline ADNI-1 and ADNI-2 datasets, respectively. To study the influence of training data as well as the generalization ability of our proposed method, in this group of experiments, we reversed the training and testing sets to train the network on ADNI-2, and then apply the learned network on ADNI-1 for AD classification.

Accordingly, the classification results on the testing set (i.e., ADNI-1) are summarized in Table 3, in which our proposed wH-FCN method is compared with a state-of-the-art patch-based method (i.e., LBM). We can observe that our proposed wH-FCN method still outperforms the competing method in this scenario. In addition, by comparing the results achieved by wH-FCN trained on ADNI-2 (Table 3) with the results achieved by wH-FCN trained on ADNI-1 (Table 2), it can be seen that the diagnostic results are comparable (e.g., 0.895 vs. 0.903 for ACC, and 0.945 vs. 0.951 for AUC). The network constructed on ADNI-1 is slightly better, possibly due to the fact that more training subjects are available in ADNI-1 than in ADNI-2. These experiments suggest that our proposed H-FCN model has good generalization capacity in sMRI-based AD diagnosis.

TABLE 3.

Results for AD classification (i.e., AD vs. NC) on the baseline ADNI-1, using the baseline ADNI-2 as the training set.

Method	ACC	SEN	SPE	AUC
LBM	0.820	0.824	0.817	0.887
wH-FCN	0.895	0.879	0.910	0.945

5.10. Automatically-Identified Multi-Scale Locations

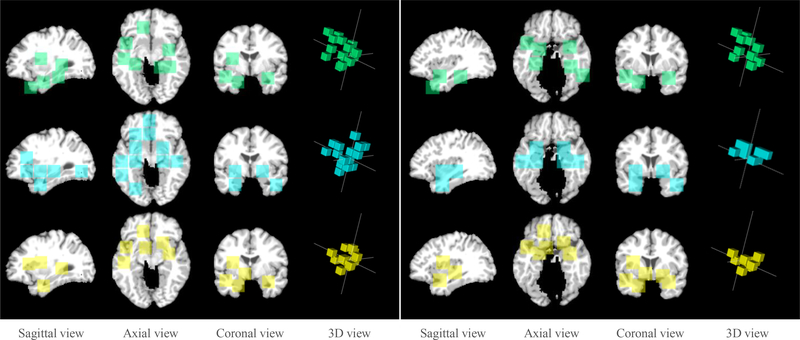
Our proposed H-FCN method can automatically identify hierarchical discriminative locations of brain atrophy at both the patch-level and region-level. In Fig. 7, we visually verify those automatically-identified locations in distinguishing between AD and NC as well as between pMCI and sMCI.

Fig. 7.

Discriminative locations automatically identified by our proposed method at the patch-level (i.e., the left panel) and region-level (i.e., the right panel). The first to third rows correspond, respectively, to our proposed wH-FCN model trained for AD classification, our proposed nH-FCN model trained for AD classification, and our proposed wH-FCN model trained from scratch for MCI conversion prediction.

Specifically, the first, second, and third rows of Fig. 7 present the discriminative atrophy locations identified, respectively, by the wH-FCN trained for AD classification, the nH-FCN trained for AD classification, and the wH-FCN trained from scratch for MCI conversion prediction. Also, the left and right panels of Fig. 7 denote, respectively, the patch-level and region-level discriminative atrophy locations identified by our method. From Fig. 7, we can have the following observations. 1) In all three different cases, our proposed H-FCN method consistently localized multiple locations at the hippocampus, ventricle, and fusiform gyrus. It is worth noting that the discriminative capability of these brain regions in AD diagnosis has already been reported by previous studies [7], [23], [31], [69], which implies the feasibility of our proposed method. 2) For AD classification, although different location proposals were used, the two different implementations of our proposed method (i.e., wH-FCN and nH-FCN) identified multiple patches and regions that are largely overlapped or localized at similar brain regions. 3) The patches and regions identified by our wH-FCN trained from scratch for MCI conversion prediction (i.e., the third row) were largely consistent with those identified by our wH-FCN trained for AD classification (i.e., the first row), although totally different subjects were used to train the networks in the two different but highly-correlated tasks. Statements in both 2) and 3) imply the robustness of our proposed method in identifying discriminative atrophy locations in sMRI for AD-related brain disease diagnosis.

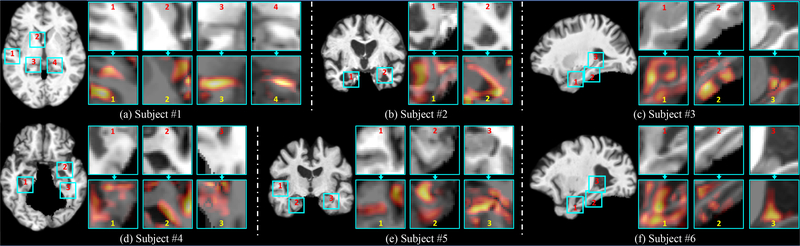
Also, based on the identified patch-level discriminative locations, it is intuitive to further localize AD-related structural abnormalities at a finer scale (i.e., voxel-level). As an example, Fig. 8 presents the discriminative patches localized by our wH-FCN method in six patients with AD, and the corresponding voxel-level AD heatmaps generated by the method proposed in [35] for these patches. To generate such voxel-level heatmaps, we used the identified patches to train a 3D FCN described in Fig. S3 of the Supplementary Materials. The architecture of this 3D FCN is similar to the PSN module used in our H-FCN, but with several essential modifications. Specifically, in this 3D FCN method, we removed the pooling layers and included zero-padding in the convolutional (Conv) layers to preserve the spatial resolution of the input patches for the following feature maps. We then used a global average pooling layer followed by a fully connected (FC) layer (without bias) to produce the classification score. After training, the voxel-level AD heatmaps were finally calculated based on the FC weights and the outputs of the last Conv layer, using the operation proposed in [35]. From Fig. 8, we can observe that, based on the discriminative patches localized by our H-FCN method, we could further identify more detailed discriminative locations at the voxel level, e.g., the hippocampus, and the corners and boundaries of the ventricle. Potentially, we may also replace the PSN module (shown in Fig. 1) with the above FCN to directly produce the voxel-level AD heatmaps in our H-FCN, while it will inevitably increase the computational complexity for training, due to the high spatial resolutions of intermediate feature maps.

Fig. 8.

Voxel-level AD heatmaps for the discriminative patches automatically-identified by our H-FCN method in six different subjects. The heatmaps and the image patches have the same spatial resolution (i.e., 25×25×25). Note that voxels with warmer (or more yellow) colors in these heatmaps have higher discrminative capacities.

Moreover, we further verified the effectiveness of another two strategies (i.e., the voxel-wise anatomical correspondence for location proposals and the hierarchical architecture) used in our H-FCN method, and also analyzed the influence of the size of regional inputs on the diagnostic performance. These experimental results can be found in Section 1 to Section 3 of the Supplementary Materials.

6. Discussion

In this section, we first summarize the main differences between our proposed H-FCN method and previous studies on AD-related brain disease diagnosis. We also point out the limitations of our proposed method as well as potential solutions to deal with these limitations in the future.

6.1. Comparison with Previous Work

Compared with the conventional region- and voxel-level pattern analysis methods [7], [8], [9], [10], [11], [12], [13], [14], [16], [17], [18], [41], [45], our proposed H-FCN method adopted local image patches (an intermediate scale between voxels and regions) as inputs to develop a hierarchical classification model. Specifically, multi-scale (i.e., patch-, region-, and subject-level) sub-networks were hierarchically constructed in our proposed method, by using outputs of preceding sub-networks as inputs. In this way, local-to-global morphological information was seamlessly integrated for comprehensive characterization of brain atrophy caused by dementia. Also, different from conventional patch-level pattern analysis methods [19], [21], [22], [23] using manually-engineered imaging features, our proposed H-FCN method can automatically learn high-nonlinear feature representations, which are more consistent with subsequent classifiers, leading to more powerful diagnosis capacity.

Our proposed H-FCN method is also different from existing deep-learning-based AD diagnosis methods in the literature [31], [33], [34], [50], [51], [66], [68]. First and foremost, in contrast to existing CNN-based methods that require the pre-determination of informative brain regions [31], [33] or local patches [34] for feature extraction, our proposed method integrated automatic discriminative localization, feature extraction, and classifier construction into a unified framework. In this way, these three correlated tasks can be more seamlessly coordinated with each other in a task-oriented manner. In addition, rather than using solely the mono-scale feature representations, our proposed method extracted and fused complementary multi-scale feature representations to construct a hierarchical classification model for brain disease diagnosis.

In Table 4, we briefly summarize several state-of-the-art results reported in the literature for AD classification and/or MCI conversion prediction using baseline sMRI data of ADNI, including seven conventional learning-based methods (i.e., voxel-level analysis [9], [41], region-level analysis [17], [45], and patch-level analysis [19], [21], [22]), and five deep-learning-based methods (i.e., [33], [50], [51], [66], [68]). It is worth noting that the direct comparison between these methods is impossible due to the utilization of different datasets. That is, the results in Table 4 are not fully comparable, since these studies were performed with the varying number of subjects, and also the varying partition of training and testing samples, and the definition of pMCI/sMCI may be partially different as well. However, by roughly comparing our study (i.e., the last row of Table 4) with these state-of-the-art methods, we can still have several observations. First, in contrast to the studies using only fractional sMRI data of ADNI-1, our proposed method was evaluated on a much larger cohort of 1,457 subjects from both ADNI-1 and ADNI-2, which should be more challenging but more fair. Second, using a more challenging evaluation protocol (i.e., independent training and testing sets), our method also obtained competitive classification performance, especially for MCI conversion prediction. Third, compared with [68] that constructed an end-to-end CNN model using the whole brain sMRI data and [33] that constructed a CNN model using hippocampal sMRI data, our proposed method yielded better diagnostic results. This implies that, due to the use of hierarchical architecture and automatic discriminative localization, our method is more sensitive to subtle structural changes in sMRI caused by dementia.

TABLE 4.

A brief description of the state-of-the-art studies using baseline sMRI data of ADNI-1 for AD classification (i.e., AD vs. NC) and MCI conversion prediction (i.e., pMCI vs. sMCI).

Reference	Methodology	Subject	AD vs. NC				pMCI vs. sMCI
			ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC
Hinrichs et al. [9]	Conventional classifiers (i.e., LPboosting, SVM) + voxel-level engineered features	183 (AD+NC)	0.82	0.85	0.80	0.88	-	-	-	-
Salvatore et al. [41]		162 NC + 76 sMCI + 134 pMCI + 137 AD	0.76	-	-	-	0.66	-	-	-
Koikkalainen et al. [45]	Conventional classifiers (i.e., linear regression, ensemble SVM) + region-level engineered features	115 NC + 115 sMCI + 54 pMCI + 88 AD	0.86	0.81	0.91	-	0.72	0.77	0.71	-
Liu et al. [17]		128 NC + 117 sMCI + 117 pMCI + 97 AD	0.93	0.95	0.90	0.96	0.79	0.88	0.76	0.83
Coupé et al. [19]	Conventional classifiers (i.e., linear discriminant analysis, hierarchical SVM, MIL model) + patch-level engineered features	231 NC + 238 sMCI + 167 pMCI + 198 AD	0.91	0.87	0.94	-	0.74	0.73	0.74	-
Liu et al. [21]		229 NC + 198 AD	0.92	0.91	0.93	0.95	-	-	-	-
Tong et al. [22]		231 NC + 238 sMCI + 167 pMCI + 198 AD	0.90	0.86	0.93	-	0.72	0.69	0.74	-
Suk et al. [50]	Deep Boltzmann machine [49] + patch-level engineered features	101 NC + 128 sMCI + 76 pMCI + 93 AD	0.92	0.92	0.95	0.97	0.72	0.37	0.91	0.73
Liu et al. [51]	Stacked auto-encoders [52] + region-level engineered features	204 NC + 180 AD	0.79	0.83	0.87	0.78	-	-	-	-
Shi et al. [66]	Deep polynomial network [67] + region-level engineered features	52 NC + 56 sMCI + 43 pMCI + 51 AD	0.95	0.94	0.96	0.96	0.75	0.63	0.85	0.72
Korolev et al. [68]	CNN + whole brain sMRI	61 NC + 77 sMCI + 43 pMCI + 50 AD	0.80	-	-	0.87	0.52	-	-	0.52
Khvostikov et al. [33]	CNN + hippocampal sMRI	58 NC + 48 AD	0.85	0.88	0.90	-	-	-	-	-
Our wH-FCN mehtod	Hierarchical FCN + automatic discriminative localizatoin	429 NC + 465 sMCI + 205 pMCI + 358 AD	0.90	0.82	0.97	0.95	0.81	0.53	0.85	0.78

6.2. Limitations and Future Work

While our proposed H-FCN method achieved good results in automatic discriminative localization and brain disease diagnosis, its performance and generalization capacity could be further improved in the future by carefully dealing with the following limitations or challenges.

First, in our current implementation, the size of input image patches was fixed for all location proposals. Considering the structural changes caused by dementia may vary across different locations, it is reasonable to extend our proposed method by using multi-scale image patches. To flexibly design sub-networks with shared-weights for multi-scale image patches, we could potentially modify our network architecture by including global pooling layers. Second, the network pruning strategy used in our current method may be too aggressive, since removed patches or regions will no longer be considered, while those pruned patches/regions could contain supplementary information (when combined with other distinctive patches/regions) for robust model training. Therefore, it is interesting to design a more flexible pruning strategy to re-use those removed patches/regions based on some criteria. Third, the non-linear registration step was required for establishing the voxel-wise anatomical correspondence across different subjects, which inevitably increased the computational complexity in the testing phase. To accelerate our proposed method for predicting unseen subjects, we could alternatively construct another automatic detection model (e.g., in [70]), using the training sMRIs and identified discriminative locations as the input and ground truth, respectively. Then, we could directly predict the identified discriminative locations for unseen subjects in the linearly-aligned image space, without using any time-consuming non-linear registration in the testing phase. Forth, in our current method, the location proposal module is isolated to the subsequent network. It should be a promising direction to further unify this important module into our current deep learning framework to automatically and specifically generate location proposals for each individual subjects. To this end, we could potentially develop a multi-task learning model. For example, we could include a weakly-supervised FCN (e.g., [35]) constructed on the whole brain sMRI to generate location proposals on high-resolution feature maps. Then, based on the location proposals and feature maps produced by this FCN, we could further construct our proposed H-FCN model for precise discriminative localization and brain disease diagnosis. Furthermore, it is worth mentioning that the datasets studied in this paper have different imaging data distributions due to the use of different scanners (i.e., 1.5T and 3T scanners) in ADNI-1 and ADNI-2. Hence, including domain adaptation [71] module into our current method could further improve its generalization capability.

7. Conclusion

In this study, a hierarchical fully convolutional network (H-FCN) was proposed to automatically identify multi-scale (i.e., patch- and region-level) discriminative locations in sMRI to construct the hierarchical classifier for AD diagnosis and MCI conversion prediction. On the two public datasets with 1,457 subjects, the effectiveness of our proposed method on joint discriminative localization and disease diagnosis has been extensively evaluated. Compared with several state-of-the-art CAD methods, our proposed method has demonstrated better or at least comparable classification performance, especially in the relatively challenging task of MCI conversion prediction.

Biography

Chunfeng Lian received the B.S. degree in Electronic and Information Engineering from Xidian University, Xi’an, China, in 2010, and the Ph.D. degree in Computer Science from Univiersite de Technologie de Compiègne, CNRS, Heudiasyc (UMR 7253), Compiègne, France, in 2017. He is currently a Post-Doctoral Research Associate with the Department of Radiology and BRIC, the University of North Carolina at Chapel Hill, Chapel Hill, USA. His current research interests include medical image analysis, pattern recognition, and machine learning.

Mingxia Liu received the B.S. and M.S. degrees from Shandong Normal University, Shandong, China, in 2003 and 2006, respectively, and the Ph.D. degree from the Nanjing University of Aeronautics and Astronautics, Nanjing, China, in 2015. Her current research interests include machine learning, pattern recognition, and neuroimaging analysis.

Jun Zhang was born in Shaanxi, China. He received the B.S. and Ph.D. degrees from Xidian University, Xi’an, China, in 2009 and 2014, respectively. His research interests include image processing, machine learning, pattern recognition, and medical image analysis.

Dinggang Shen (F’18) is Jeffrey Houpt Distinguished Investigator, and a Professor of Radiology, Biomedical Research Imaging Center (BRIC), Computer Science, and Biomedical Engineering in the University of North Carolina at Chapel Hill (UNC-CH). He is currently directing the Center for Image Analysis and Informatics, the Image Display, Enhancement, and Analysis (IDEA) Lab in the Department of Radiology, and also the medical image analysis core in the BRIC. He was a tenure-track assistant professor in the University of Pennsylvanian (UPenn), and a faculty member in the Johns Hopkins University. Dr. Shen’s research interests include medical image analysis, computer vision, and pattern recognition. He has published more than 900 papers in the international journals and conference proceedings, with H-index 83. He serves as an editorial board member for eight international journals. He has also served in the Board of Directors, The Medical Image Computing and Computer Assisted Intervention (MICCAI) Society, in 2012–2015, and will be General Chair for MICCAI 2019. He is Fellow of IEEE, Fellow of The American Institute for Medical and Biological Engineering (AIMBE), and also Fellow of The International Association for Pattern Recognition (IAPR).