Improving alignment in Tract-based spatial statistics: Evaluation and optimization of image registration

Abstract

Anatomical alignment in neuroimaging studies is of such importance that considerable effort is put into improving the registration used to establish spatial correspondence. Tract-based spatial statistics (TBSS) is a popular method for comparing diffusion characteristics across subjects. TBSS establishes spatial correspondence using a combination of nonlinear registration and a “skeleton projection” that may break topological consistency of the transformed brain images. We therefore investigated feasibility of replacing the two-stage registration-projection procedure in TBSS with a single, regularized, high-dimensional registration.

To optimize registration parameters and to evaluate registration performance in diffusion MRI, we designed an evaluation framework that uses native space probabilistic tractography for 23 white matter tracts, and quantifies tract similarity across subjects in standard space. We optimized parameters for two registration algorithms on two diffusion datasets of different quality. We investigated reproducibility of the evaluation framework, and of the optimized registration algorithms. Next, we compared registration performance of the regularized registration methods and TBSS. Finally, feasibility and effect of incorporating the improved registration in TBSS were evaluated in an example study.

The evaluation framework was highly reproducible for both algorithms (R² 0.993; 0.931). The optimal registration parameters depended on the quality of the dataset in a graded and predictable manner. At optimal parameters, both algorithms outperformed the registration of TBSS, showing feasibility of adopting such approaches in TBSS. This was further confirmed in the example experiment.

Introduction

Diffusion imaging of the brain provides insight into architectural properties, and developmental and degenerative processes of the white matter (Basser et al., 1994; Beaulieu, 2002; Lebel et al., 2010). Quantitative features derived from diffusion imaging, such as fractional anisotropy (FA) and mean diffusivity (MD), allow for comparison of diffusion properties across different subjects (Basser and Jones, 2002). This can be achieved in a number of ways, for example region of interest-based or voxel-based.

Voxel-based analyses offer a fast and automated means of analyzing diffusion data (Büchel et al., 2004; Buchsbaum et al., 1998; van Hecke et al., 2010). They do however require the images to be in a common space in which anatomical correspondence across subjects is assured. Establishing correspondence by bringing images into a common space is a non-trivial task, for which image registration techniques are commonly employed. However, image registration approaches in general do not achieve perfect anatomical correspondence due to anatomical variability. In an attempt to account for the residual misalignment, increase sensitivity and to satisfy the assumptions of parametric tests (if applied), voxel-based analyses often rely on smoothing. The extent of this smoothing ideally needs to be matched to the expected effect size, which can be spatially varying and not known a-priori (Jones et al., 2005). In 2006, an alternative approach for anatomical alignment of diffusion data was proposed. Tract-based spatial statistics (TBSS) (Smith et al., 2006, 2007) was introduced to mitigate the influence of residual misalignment in registration of diffusion data, and to overcome the need to set smoothing extent in voxel-based analyses. In TBSS, following an initial nonlinear registration step (of “medium” dimensionality), voxels that are local maxima for FA are mapped onto a skeleton composed of sheets of maximum FA voxels, and statistical analysis is performed on skeleton voxels. Constraining the analysis to the white matter skeleton results in a dimensionality reduction, ameliorating the issue of multiple testing. Over the past years, TBSS has been widely adopted, aided by its availability within FSL (Smith et al., 2004; Woolrich et al., 2009) and ease of use. The projection stage in TBSS however, is a spatially local operation, with the voxels containing locally maximal FA projected onto the skeleton independently; therefore it does not enforce spatial consistency of the warped images. This may result in an undesirable loss of anatomical topology of tracts in the projection stage. The main aim of this work is to investigate if it is feasible to replace the two registration + projection stages by a single regularized high-dimensional registration approach inside the TBSS method (while still aiming to carry out cross-subject voxelwise testing on the skeleton, to help minimize correspondence errors).

Since even small errors in correspondence may substantially influence results (Smith et al., 2006), considerable effort has been put in improving the registration of diffusion data (Jones et al., 2002; Park et al., 2003; van Hecke et al., 2007; Yap et al., 2009; Yeo et al., 2009; Zhang et al., 2006). In registration, a spatial transformation is determined by optimizing a similarity metric. For evaluating registration performance across algorithms, such as performed for diffusion imaging by Wang et al. (2011), or to optimize different registration parameters, a similarity metric must be employed as well. This is necessary since we do not know the ground truth anatomical correspondence of two images. To objectively measure registration performance however, we cannot use the same similarity metric that was optimized in the registration process, since this would bias the evaluation.

Similarity metrics in diffusion image registration can be based on scalar images such as FA or structural images. Metrics can, alternatively, be based on higher dimensional image features, e.g., on the full diffusion tensor or a number of its components. A third category of similarity metrics is defined on the results of white matter tractography. These three classes of similarity metrics have all been used in the objective functions of image registration approaches for diffusion images (Guimond et al., 2002; Park et al., 2003; Xu et al., 2003; Yeo et al., 2009; Zhang et al., 2006; Zvitia et al., 2010). Analogously, similarity metrics in all three categories have been employed in order to evaluate registration performance (Park et al., 2003; Wang et al., 2011; Yap et al., 2009; Yeo et al., 2009; Zhang et al., 2007; Zöllei et al., 2010).

An important advantage of a performance measure based on similarity of tractography results is that it is independent of any particular similarity metric, defined on a scalar or higher order image, which is employed in most registration approaches. Also, optimal white matter tract alignment is most closely linked to the eventual registration aim of obtaining anatomical correspondence in white matter (Lawes et al., 2008). We therefore developed a framework to evaluate scalar or higher-order similarity metric based registrations using tractography. Previous work using white matter tractography for this purpose was based either on whole brain tractography (Park et al., 2003) or only on a small selection of tracts (Jia et al., 2011; Xue et al., 2010; Yap et al., 2009; Zhang et al., 2006; Zöllei et al., 2010). Furthermore, all previous work depended on deterministic tractography, which has more difficulty in coping with complex fiber architecture (e.g., crossing fibers) and signal noise than probabilistic tractography (Behrens et al., 2007).

In this work, we extended the use of tractography for image registration evaluation to a broader range of white matter tracts, and we used a probabilistic model for tractography. Parameters for two nonlinear registration algorithms were optimized using similarity of different subjects' warped tracts as the registration performance measure. The optimization was performed on two datasets acquired at different institutions with different spatial resolution. Registration performance for these optimized approaches was then compared to the registration performance of the TBSS method on a white matter skeleton. We show that the optimized registration reproducibly improved the alignment of white matter structures compared to TBSS.

Methods

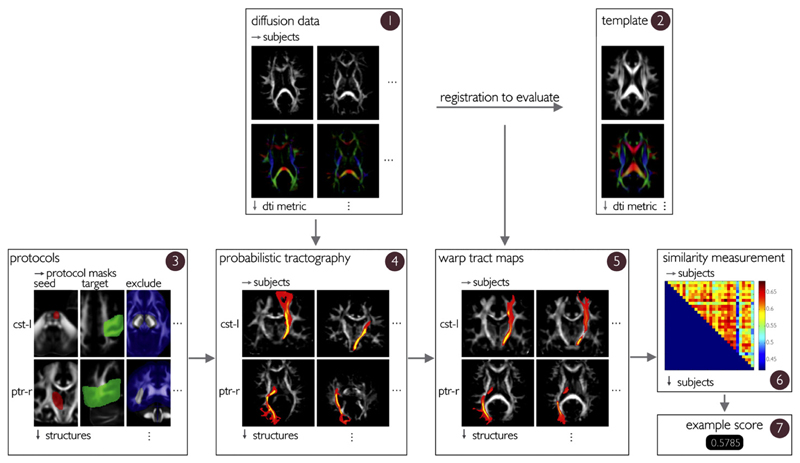
The evaluation framework consists of an automated approach to perform probabilistic tractography and a tract-based evaluation metric. A schematic overview of the process is provided in Fig. 1.

Fig. 1.

Schematic overview of the evaluation framework. Diffusion data in subject-native space (box 1) for N subjects are registered to an appropriate template image (box 2). This registration can be based on FA images, the full tensor, or on any other DTI metric. This set of N registrations obtained with a particular registration algorithm is the registration under evaluation. Separately, standard space seed, target, stop and exclusion masks (box 3) that initialize the probabilistic tractography are transformed to subject native space using a conservative nonlinear registration. Tractography for the total set of 23 structures is performed in subject native space (box 4). The registration under evaluation is used to warp the tract-density images to standard space for all N subjects (box 5). The similarity of the warped tract-density images in standard space is quantified via spatial correlation, for each structure and for each pair of subjects (NxN). The similarity is averaged over all structures (box 6), and then averaged over all subject pairs to yield the registration performance for the particular registration under evaluation (box 7).

Tractography

Tractography was performed with PROBTRACKX (Behrens et al., 2003, 2007), a Bayesian approach to probabilistic tractography available in FSL.

Tractography was initialized by defining standard space “seed”, “target”, “stop” and “exclusion” ROIs (masks). These masks were based on the protocols described by Mori et al. (2002), Stieltjes et al. (2001), and Wakana et al. (2004, 2007), but had to be adapted to cope with the more dispersing nature of probabilistic tractography. Most importantly, exclusion masks were added, e.g., the mid-sagittal slice was added in all but the commissural tracts. All masks were transferred to subject native space using nonlinear registrations obtained with FNIRT (Andersson et al., 2008) with default settings for FA images as available in FSL.

Tracts that could robustly be identified and which would lead to a reasonably uniform sampling across brain regions were selected. These tracts are listed in Table 1. Two tracts, the posterior thalamic radiation and the inferior fronto-occipital fasciculus, were excluded from the final set because of considerable overlap with other tracts. Exclusion of these tracts prevented uneven weighting of different regions in the registration evaluation. The final set therefore consisted of 23 tracts.

Table 1.

Overview of tracking protocols for different tracts in the evaluation framework. Tracts with left/right homologues are listed under ‘l/r’. If a stop mask is used, its relative location to the tract is given under the ‘stop’ column. The number of seed points per voxel is listed under ‘seed #’. Tracts that were generated twice with inverted target-seed regions are listed under ‘invert’. References (‘refs’) translate to a: Stieltjes et al. (2001), b: Wakana et al. (2004), c: Mori et al. (2002), d: Wakana et al. (2007).

	l/r	Stop	Seed # (*1000)	Inv.	Refs
Tracts in brainstem
Middle cerebellar peduncle	−		2	+	a,b
Medial lemniscus	+	Sup.	4	−	a,b
Projection fibers
Corticospinal tract	+		10	−	a,b,d
Acoustic radiation	+	Med.	10	+
Anterior thalamic radiation	+	Post.	2	−	b,c,d
Superior thalamic radiation	+	Inf.	2	−	b
Posterior thalamic radiation	+		30	−	b,c
Association fibers
Superior longitudinal fasciculus	+		2	+	b,c,d
Inferior longitudinal fasciculus	+	Ant.	2	−	b,c,d
Inferior fronto-occipital fasciculus	+		4	−	b,c,d
Uncinate fasciculus	+		4	−	b,c,d
Limbic system fibers
Cingulate gyrus part of cingulum	+	Ant. & post.	30	−	b,d
Parahippocampal part of cingulum	+	Sup. & inf.	4	−	b,d
Callosal fibers
Forceps minor	−		2	+	b,d
Forceps major	−		2	+	b,d

Tractography was performed in subject native space while recording tract density at a 1 mm³ resolution and using between 2000 and 30,000 samples per seed ROI voxel to account for differences in the number of seed voxels and tract geometry. These parameter settings were selected to aim for robust extraction of the tracts, and were based on the observed number of fiber-particles that were included in the tract together with visual inspection of tractography outputs. Commissural tracts and the middle cerebellar peduncle were tracked a second time (adding both runs) with inverted seed-target ROIs to ensure symmetry of the resulting tract. The acoustic radiations and the superior longitudinal fasciculus were also tracked in both directions to increase robustness. After tracking, the tract density image was normalized by dividing with the total number of particles.

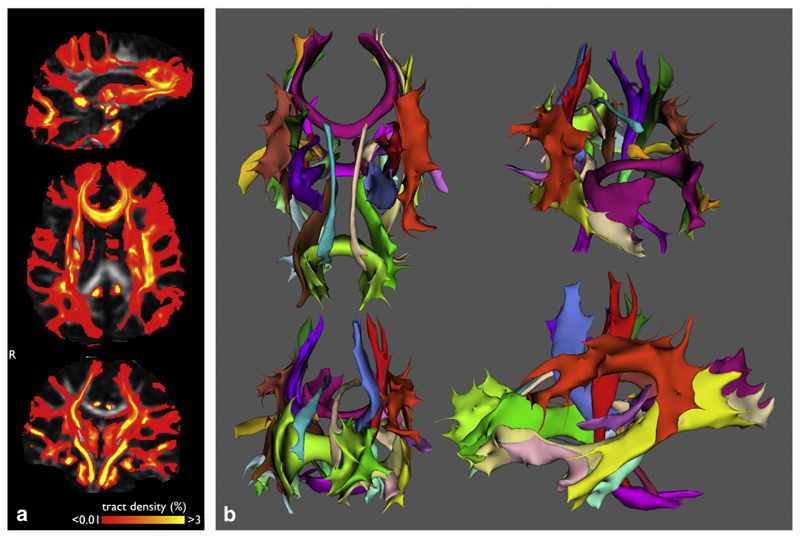
An example of an individual subject's tracking result, thresholded for the purpose of visualization, for all tracts is shown in Fig. 2. Tractography was performed for each subject and for each structure. The resulting maps of white matter structures reside in subject native space, and were used for all evaluations.

Fig. 2.

Automated tractography result for one individual in the Rotterdam dataset. The same subject is shown in seven different views. (a). Continuous probabilistic tractography output used in the evaluation for all structures combined. (b). Probabilistic tractography output thresholded for visualization purposes only. The threshold was applied on the normalized tract-density images, rejecting voxels containing less than 0.5% of the total number of tracts per structure.

Tract-based evaluation metric

The registration performance measurement was based on cross-subject similarity of the warped tract maps. Non-thresholded tract density images in subject native space were warped to common space, and then tract similarity was assessed.

To avoid differences in image characteristics between individual and group mean tract maps influencing the results, tract similarity was evaluated on a subject-to-subject basis. Tract similarity was assessed for each structure individually, and then averaged for all structures in each pair of subjects. In order to provide an even weighting over tracts in this averaging, similarity of left–right homologue structures was jointly given an equal weight as that of the commissural tracts and the middle cerebellar peduncle. If a particular tract could not be identified in one of the subjects with the automated tractography approach (i.e. no particles fulfilled the criteria imposed by the protocol masks), the tract was omitted in the aggregation of the subject–subject similarity score.

Similarity was assessed with the spatial correlation similarity metric,

$$C=\frac{{\displaystyle \sum _i{\mathbf{\text{J}}}_i{\mathbf{\text{K}}}_i}}{\sqrt{{\displaystyle \sum _i{\mathbf{\text{J}}}_i^2}}\sqrt{{\displaystyle \sum _i{\mathbf{\text{K}}}_i^2}}},$$

which is similar to the Pearson correlation coefficient, and provides a measure of voxelwise similarity of the continuous tract density image intensities (J and K) for two subjects, computed over all voxels (i), and is bound on a 0–1 scale. Similarity was calculated on the tract density images.

The probabilistic nature of tractography means that the intensity in the tract map varies; more support for the tract will translate into higher intensity. Increased uncertainty will conversely translate into lower tract-density. The information that is thereby encoded in the tract-density image is related to the anatomy of the tract. The similarity, as measured by the spatial correlation similarity metric, across two subjects therefore provides valuable feedback on alignment of the tracts in those subjects.

Evaluation on the skeleton

To investigate the feasibility of replacing the registration-projection in TBSS with a regularized, high-dimensional registration, we compared registration performance for both registration algorithms with the standard TBSS approach. The registration evaluation framework described above was therefore further tailored for both approaches to enable this comparison.

First, for the high-dimensional registrations, the registration performance measurement had to be constrained to the TBSS skeleton. Hence, the warped continuous tract-density images that resulted from the regularized high-dimensional registration were masked using the TBSS white matter skeleton mask, producing skeletonized tract density images for each structure, for each subject, which were used to evaluate registration performance.

Next, for assessing registration performance of TBSS, the measurement also needed to be constrained to the skeleton. Hence, the continuous tract density images for all structures were (separately) projected onto the white matter skeleton using the non-FA-image pipeline available within TBSS (Smith et al., 2006); this allows the initial registration and the skeleton projection, both derived from the FA data, to be applied to other scalar images starting in the same space as the FA data. This produced skeletonized tract density images for each structure, for each subject, which were used to evaluate registration performance.

Optimization experiments

Diffusion MRI data

Two sets of scans from two different MRI centers were used in the experiments. The first dataset represents a “low-end” diffusion acquisition; the second dataset is representative of a state-of-the-art, though still relatively “off-the-shelf”, high resolution, high signal-to-noise diffusion acquisition.

Lower resolution: Rotterdam data

The first dataset was derived from the Rotterdam Scan Study (Ikram et al., 2011), a neuroimaging study embedded in the larger, prospective population-based Rotterdam Study (Hofman et al., 2011) composed of middle aged and elderly subjects. The diffusion data is part of a multi-sequence MRI protocol on a 1.5 Tesla GE Signa Excite scanner. For DTI, single shot, diffusion-weighted spin echo-planar imaging data were acquired (repetition time (TR) = 8575 ms, echo time (TE) = 82.6 ms, field-of-view (FOV) = 210 × 210 mm, matrix = 96 × 64 (phase encoding) (zero-padded in k-space to 256 × 256) slice thickness = 3.5 mm, 35 contiguous slices). b-value was 1000 s/mm² in 25 non-collinear directions (number of excitations (NEX) = 1), and three volumes with no diffusion weighting were acquired. Acquisition time was 5 min. A sample of 30 subjects from the study population was rescanned on average 19.5 (SD 10.0) days after the baseline scan. These subjects were on average 76.7 years old (SD 4.8); 15 were female. The set of 30 baseline scans was used in the registration optimization experiments; the set of rescanned data (30 scans) was used to evaluate reproducibility of the evaluation framework. This dataset will be referred to as the Rotterdam data, with the time-points being labeled as “baseline” and “rescan”.

Higher resolution: Oxford data

The second dataset was acquired in healthy adults, described in Jbabdi et al. (2010). Scanning was performed on a 1.5 Tesla Siemens Sonata scanner. As described in Tomassini et al. (2007), diffusion-weighted data were acquired using echo planar imaging (72 × 2-mm-thick axial slices; matrix size, 128 × 104 (phase encoding); field of view, 256 × 208 mm; giving a voxel size of 2 × 2 × 2 mm). Diffusion weighting was isotropically distributed along 60 directions using a b-value of 1000 s/mm². For each set of diffusion-weighted data, five volumes with no diffusion weighting were acquired at evenly spaced points throughout the acquisition. Three sets of diffusion-weighted data were acquired for later averaging to improve the signal-to-noise ratio. The total scan time for the diffusion-weighted imaging protocol was 45 min. Data from 30 subjects were used. Mean age for this group was 32.0 years (SD 8.5); 12 were female. This dataset will be referred to as the Oxford data.

Diffusion data preprocessing

Diffusion data was preprocessed using the FDT toolbox included in FSL. Preprocessing included affine co-registration of all acquired volumes in order to compensate for subject motion and eddy currents. Non-brain tissues were removed with the Brain Extraction Tool. A tensor was fitted to log-transformed data using a linear least squares approach. The tensor image was then upsampled to 1 mm³ resolution, using cubic spline interpolation of the tensor components; note that upsampling of the tensor image is not currently done in TBSS. A high resolution FA image was then derived from the upsampled tensor image. Interpolating the tensor instead of the FA values allows the resulting FA image to contain more spatial detail that could aid the FA based registration algorithms, as visible in Figure 1b and e in Kindlmann et al. (2007). Higher registration accuracy (as measured with the evaluation framework) for the tensor-upsampled FA images was confirmed in preliminary experiments.

Separately, following the motion and eddy current correction, a probabilistic model of fiber orientations was fitted for each voxel using BEDPOSTX (Behrens et al., 2007). BEDPOSTX was run with default parameters, as a preprocessing step for the probabilistic tractography.

Registration algorithms

For two registration algorithms, FNIRT (Andersson et al., 2008) and Elastix (Klein et al., 2010), the evaluation framework was used for parameter optimization and performance comparison.

FNIRT (Andersson et al., 2008), the nonlinear image registration algorithm in FSL, optimizes a B-spline deformation field (Rueckert et al., 1999), and is specifically developed for brain imaging. The objective function is minimization of the sum of squared differences, and incorporates an intensity modulation term to compensate for intensity differences between the moving and reference images. FNIRT uses a multi-resolution strategy to increase robustness against local minima in the optimization. Following each resolution level, diffeomorphic warps are enforced. By concatenating multiple (each itself being multi-resolution) calls to FNIRT in a cascade, registration parameters can be varied over the course of the optimization. For evaluation, warp fields obtained with FNIRT were used to warp tract density images using the Applywarp utility in FSL. Tract density images were warped using cubic spline interpolation.

Elastix (Klein et al., 2010) (version 4.5) also includes B-spline based nonlinear deformations, and is based on the open source ITK platform. Elastix is designed to run in a cascade of resolutions, and offers the choice between multiple objective functions and multiple optimizers including an efficient adaptive stochastic gradient descent optimizer (Klein et al., 2009). When using the sum of squared differences (SSD) similarity metric, the intensity distributions of the moving and reference image are assumed to be equal. While FNIRT incorporates rescaling of the image intensities to compensate for differences, Elastix does not. In order to apply the SSD, we performed a linear intensity transformation as a preprocessing step. Based on the observed FA intensity histograms for each 30-subject dataset, we matched the 25 and 75 percentile points with those of the template image. Elastix furthermore offers the option to localize the behavior of the similarity metric by employing a regional sampling technique (Klein et al., 2008). Spatial transformations obtained with Elastix were applied to the tract density images with Transformix, which is distributed with Elastix. As with FNIRT, we used a cubic spline interpolation.

Optimization experiments

All registrations were performed with the subject FA images as moving image and with the FMRIB-58 FA template as reference image.

For both registration algorithms, the parameters to be optimized were varied in an exhaustive fashion. For FNIRT, the parameters varied in the optimization strategy are listed in Table 2; fixed parameters are listed in the parameter supplement, which is available as Supplementary material. All registrations with FNIRT contained some degree of regularization at all stages. The parameter space selected for the optimization resulted in a total of 63 settings of the algorithm.

Table 2.

Settings varied in the registration optimization of FNIRT. FNIRT is run as a cascade of three sets of parameters. Parameters are varied in one or two of these stages, as indicated. Stage 1 in itself contains a series of 4 substages, in which an initial regularization relaxation is performed. Warp field resolution is jointly varied in stages 2 and 3, and the final regularization level is varied in stage 3 alone.

Parameter	Stage 1	Stage 2	Stage 3
Number of substages	4	1	1
Warp field resolution (cubic)	10 mm	Varied in stages 2 and 3: 4; 2; 1 mm
Regularization at each substage	Varied: steep = 600, 125, 80, 40 medium = 300, 75, 50, 40 flat = 150, 60, 50, 40	Fixed (100)	Varied: 70–10 (steps of 10)

For the Elastix optimization, parameters and settings that were varied are listed in Table 3; again, a parameter supplement is available as Supplementary material. This parameter space resulted in a total of 576 settings of the algorithm.

Table 3.

Settings varied in the registration optimization of Elastix. Elastix is run as a single cascade of substages.

Parameter	Setting
Warp field resolution (cubic)	– 15 mm – 10 mm – 5 mm – 3 mm
Similarity metric	– Normalized cross correlation – Mutual information – Sum of squared differences
Multiresolution strategy (of the image data)	– None – Pyramidal downsampling moving image – Pyramidal downsampling both images
Regularization weight	– None, 1, 10 or 100
Optimizer	– Stochastic gradient descent – Adaptive stochastic gradient descent
Localized metric	Yes–no

All trials were performed on both datasets. Registration performance, as measured by the tract based similarity measure, was compared between the optimized registration settings for both registration algorithms. To statistically examine the difference between two different sets of registrations, we computed, for each subject, the average similarity to all other subjects in the dataset as defined in the Tract-based evaluation metric section. We then performed paired t-tests, pairing subjects across both algorithms (30 pairs).

To be able to interpret the registration performance measure, we investigated the relationship between warp distance and this measure. Hereto, we applied the (optimum) nonlinear transformation obtained with FNIRT, but scaled it by a fraction between 0.8 and 0.995, and computed the resulting impact on the registration performance. For each subject in the Rotterdam and Oxford datasets, the spline coefficients of the warp field were multiplied by the warp fraction, leaving the affine component of the transformation unchanged. All tract density images were transformed with these fractional warps. Then, for each subject, tract similarity was computed between the partially and fully warped tracts.

We also compared deformation fields obtained with both registration algorithms operating at optimal parameters. This was done to investigate the difference between the algorithms.

Reproducibility of the performance measurement

As optimization introduces the risk of overfitting to the specific data used in the optimization, we used the unseen rescan data, available for 30 subjects in the Rotterdam data, to test reproducibility of the evaluation framework. This evaluation involved running the pre-processing, the tractography, and the registrations for all settings of both algorithms, and all evaluations on this set of scans. Two tests were performed on these reproducibility measurements. First, for both algorithms we measured the correlation between the performance measurements on the two sets of scans. Second, we focused on the optimal settings for both registration algorithms, and compared the performance with the performance obtained on the rescan data.

Comparison with TBSS

To test feasibility and effect of replacing the registration-projection approach in TBSS (v1.2) with a regularized high-dimensional registration method, we performed three experiments. First we determined whether constraining the performance measurement to the white matter skeleton (as described in Evaluation on the skeleton) altered the behavior of the performance measure for the two registration approaches. Second, we compared the skeletonized registration performance to the TBSS performance on both datasets (Rotterdam and Oxford), and also between the registration algorithms. Third, we conducted an example analysis to investigate the influence of replacing the registration and projection stages with the improved registration, in a real-life study setting. For this experiment, we used MRI data of 50 female subjects from the Rotterdam Scan Study, aged 68–80 (mean 74.8, SD 2.9). These data were acquired and processed in a manner identical to the Rotterdam data that was used for the registration optimization but the subjects used for this example application were not included in the optimization experiment. We investigated the established (Sullivan and Pfefferbaum, 2006; Vernooij et al., 2008) association between age and FA, with head size as a confound regressor, with both TBSS and TBSS using the improved registration using FNIRT. Further details are provided in Supplementary Fig. 1.

Results

Optimization experiments

For optimization of the two registration algorithms, 639 registration settings (63 for FNIRT, 576 for Elastix) on both the Rotterdam data and Oxford data were performed and evaluated, adding up to a total of 639 sets of 60 registrations each. For Elastix, some combinations of parameters resulted in aborted registrations due to non-convergence for one or more subject images. In this case, the particular setting of the registration algorithm (30 for the Rotterdam data, 34 for the Oxford data) was completely excluded from the analysis. The resulting 1214 performance measurements therefore contained no cases of non-convergence, and are presented in three ways.

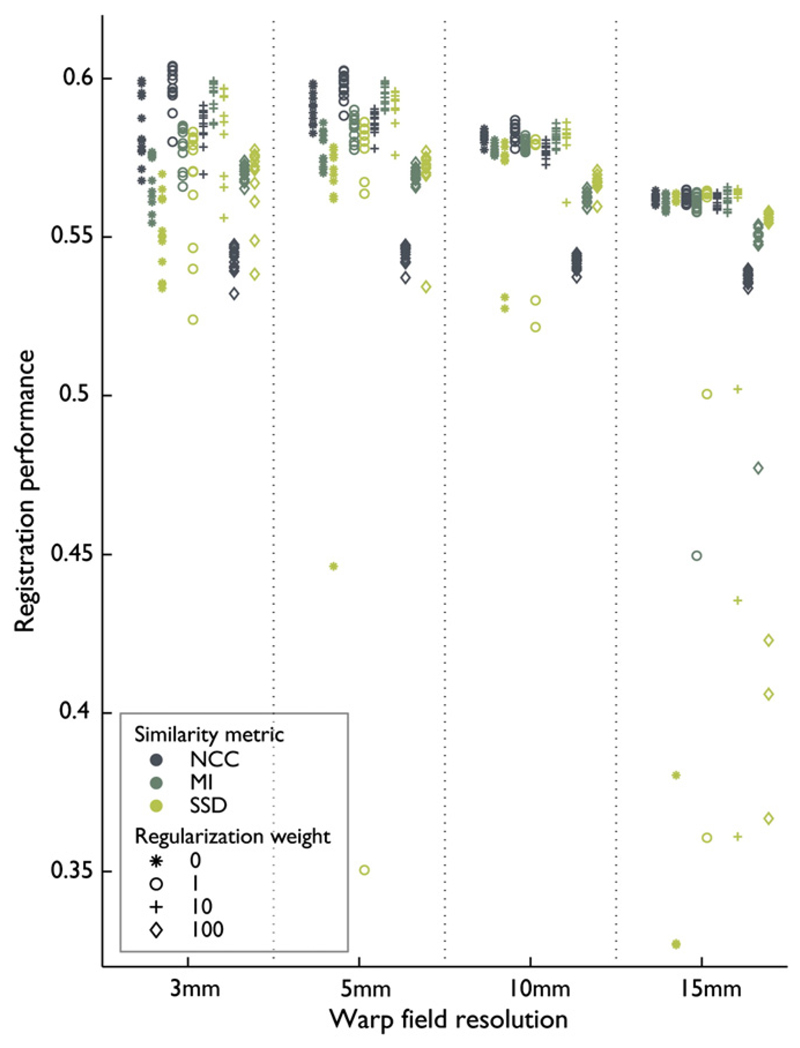
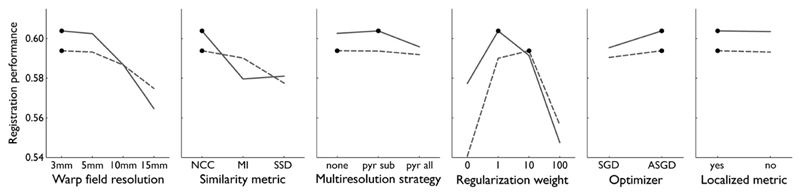
To illustrate the results of the optimization procedure for one of the four combinations of registration algorithm and dataset, the optimization of Elastix on the Oxford data, performance as a function of the most influential parameters is shown in Fig. 3. This graph shows all performance measurements for the combination of algorithm and dataset, as a function of the parameters that influenced registration performance most (three parameters are not discernible in this figure). Warp field resolution is presented on the horizontal axis, regularization is indicated with a symbol, and registration similarity metric is indicated by color. The graph shows that the optimal amount of regularization depended on the similarity metric. The graph also shows that robustness with respect to the indiscernible parameters (multiresolution strategy, optimizer and localization of the similarity metric) depended on warp field resolution, as indicated by the distribution of similar marks generally fanning out for increasing resolution. For conciseness, graphs for the other three combinations of registration algorithm and dataset are omitted and summarized results are presented in Figs. 4 and 5. To visualize parameter dependence, the marginal variation of the performance measurement when varying parameters around the optimum point is shown in Figs. 4 and 5. Based on the optimal registration parameters, these graphs show the influence of each of the parameters under investigation. These figures show that the warp field resolution, regularization, and, for Elastix, similarity metric were the most influential parameters in the optimization.

Fig. 3.

Scatterplot of registration performances for all settings evaluated on the Oxford data with the Elastix registration algorithm. Each point represents registration performance (vertical axis) on the entire Oxford dataset as a function of the most influential parameters: warp field resolution (horizontal axis), regularization weight (symbol) and similarity metric (color). Repeated appearance of the same symbol and color corresponds to variations in multiresolution strategy, optimizer and localization of the similarity metric.

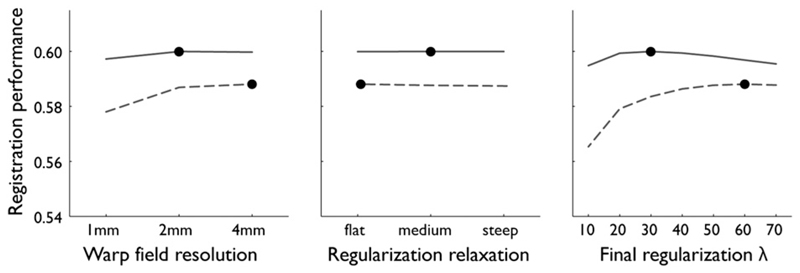
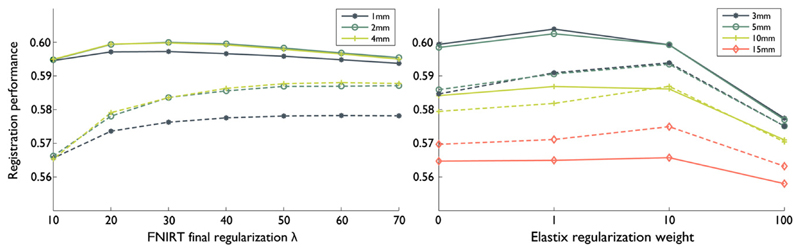
Fig. 4.

Registration performance (vertical axis) of FNIRT, for each of the parameters around the optimum parameter setting. Shown for the Rotterdam data (dashed) and the Oxford data (solid). The optimum points are indicated with dots. Registration performance is separately shown as a function of warp field resolution, regularization relaxation speed and final regularization (higher means more regularization).

Fig. 5.

Registration performance (vertical axis) of Elastix, for each of the parameters around the optimum parameter setting. Shown for the Rotterdam data (dashed) and the Oxford data (solid). The optimum points are indicated with dots. Registration performance is separately shown as a function of warp field resolution, similarity metric, multiresolution strategy, regularization weight, optimizer, and localization of the similarity metric.

Optimal registration parameters for FNIRT depended on the resolution of the data that was being registered (Fig. 4), even though the optimum settings for both datasets are located in relatively flat segments of the parameter-performance curves and the dependence is therefore fairly weak. For the Rotterdam data, optimal resolution for the final B-spline grid was 4 mm, compared to 2 mm for the higher-resolution Oxford data, although in both cases either choice would not result in a large change in performance. The optimal regularization at the last cascade of the registration was 60 for the Rotterdam data, compared to 30 for the Oxford data. The relaxation speed for the regularization was the least influential parameter, but was different for both datasets nonetheless; flat for the Rotterdam data compared to medium steep for the Oxford data.

Optimal registration parameters for Elastix also depended on the dataset being optimized. Two of the most influential parameters were the same for both datasets; warp field resolution was optimal at 3 mm and normalized cross correlation (NCC) was the optimal similarity metric. Optimal regularization weight depended on the dataset; for the Rotterdam data a weight of 10 was optimal, and for the Oxford data a weight of 1. Of the least influential parameters, two parameters had the same optimum for both datasets; the optimal optimizer (adaptive stochastic gradient descent), and localization of the similarity metric (yes). One parameter differed; for the Rotterdam data, the optimal multiresolution strategy was to not smooth any of the images, and for the Oxford data, decreasing smoothing for the subject image, with no smoothing of the template image, was the optimal strategy.

To center on the aforementioned optimization results, Fig. 6 shows the maximum performance as a function of the two most influential parameters (warp field resolution and regularization) for both datasets and both algorithms. Each point on these graphs represents the maximum performance across a set of 36 settings for Elastix, or three settings for FNIRT.

Fig. 6.

Maximum registration performance (vertical axis) for both algorithms and both datasets, as a function of regularization (horizontal axis) and warp field resolution (color). For each point on the graph, the maximum performance as a function of the other parameters is plotted. Performance for FNIRT is shown on the left, Elastix on the right. The dashed lines indicate Rotterdam data, the solid lines Oxford data.

The performances with optimal parameter settings are listed in Table 4. The table shows that optimal registration performance for Elastix was slightly higher than for FNIRT with a difference in performance of 0.004–0.006. Although the differences were very small, they were statistically significant (Table 4; p-values for all datasets < 10⁻⁴).

Table 4.

Registration performance for all datasets at the optimal registration parameters for both FNIRT and Elastix. Performance on the Rotterdam rescan data is computed using the registration settings determined to be optimal based on the Rotterdam baseline data. p-values listed are computed for paired t-tests, comparing the registration performance for all 30 subjects across both registration algorithms.

Algorithm	Rotterdam baseline	Rotterdam rescan	Oxford data
FNIRT	0.588	0.577	0.600
Elastix	0.594	0.583	0.604
FNIRT-Elastix (p-value)	−0.006 (<10−4)	−0.006 (<10−4)	−0.004 (<10−5)

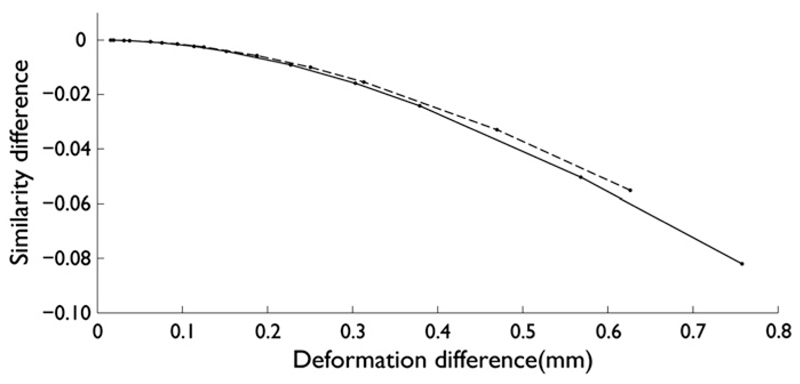
To be able to interpret these differences, the relationship between registration performance and deformation distance is shown in Fig. 7. A difference in performance of 0.01 translates to an average deformation difference of about 0.2 mm; this is twice the difference in registration performance between FNIRT and Elastix.

Fig. 7.

The relationship between tract similarity difference (based on spatial correlation between two aligned tract density images) and warp deformation difference for the Rotterdam data (dashed) and the Oxford data (solid), computed for FNIRT operating at optimum parameters for each dataset. The largest difference is obtained when scaling the warp with a factor of 0.8. This translates into a similarity drop between fully and partially warped tracts. Deformation difference is computed by taking the deformation difference (vector) image for each subject, comparing the full and partial warps. The deformation difference in the graph is then the median Euclidean deformation difference distance (vector length), averaged over all subjects in each dataset.

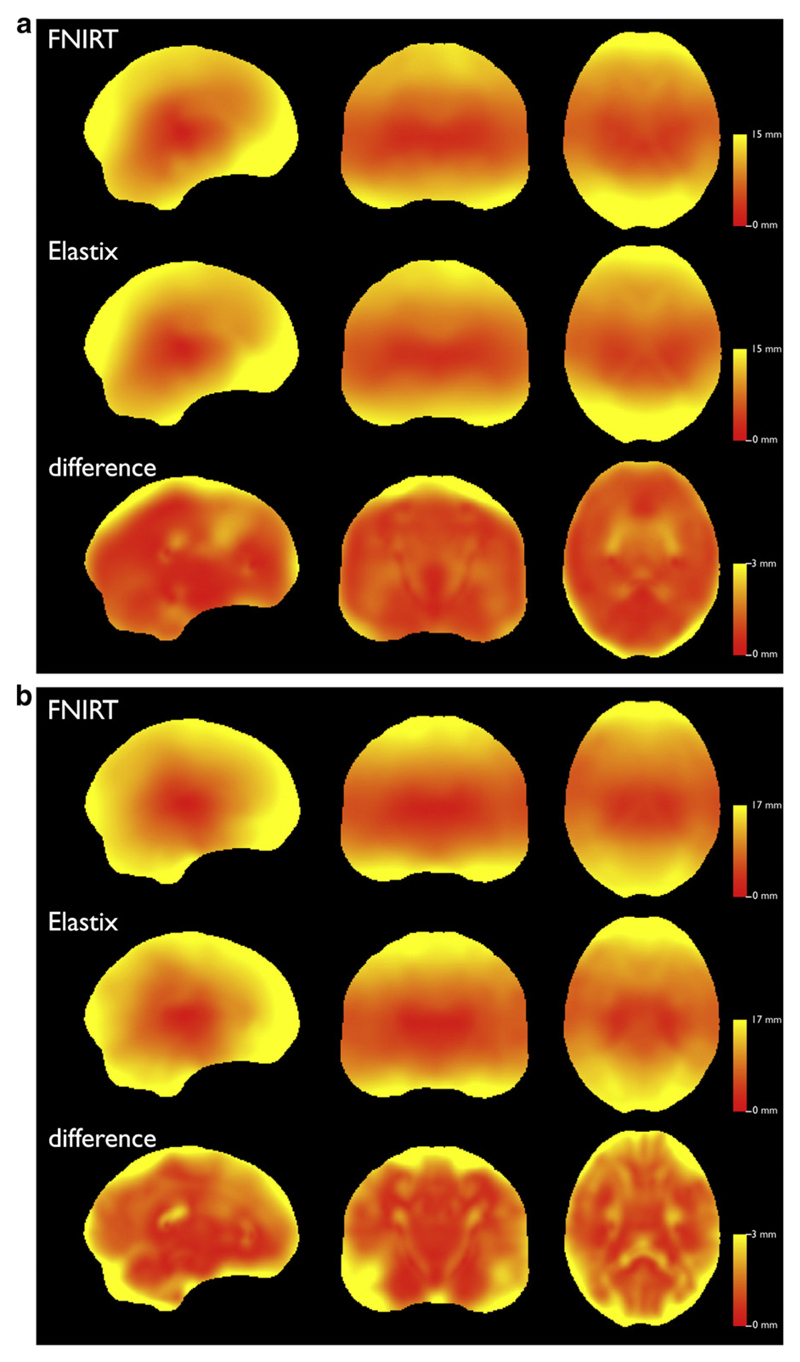
For both algorithms operating at the optimal parameters for both datasets, the mean deformation distance is shown in Fig. 8. For each dataset, the figure also shows the Euclidean difference between the optimal deformations of FNIRT and Elastix, including group wise differences in registration along white matter structures. The median difference for the Rotterdam data was 1.19 mm (IQR 0.91–1.71) and for the Oxford data 1.70 mm (IQR 1.14–2.52). Confined to the TBSS skeleton this corresponded to 1.10 mm (IQR 0.91–1.39) and 1.48 mm (IQR 1.03–1.98).

Fig. 8.

Average Euclidean deformation distance for the Rotterdam data (a) and the Oxford data (b). For each algorithm operating at the optimal parameters for each dataset, the individual deformation vector images are used to compute Euclidean deformation images, which are then averaged over all subjects to produce the images shown. For both algorithms we included the affine transformation in the deformation field, and then subtracted the mean displacement within the template image in order to account for differences in the coordinate definitions. The distance for both FNIRT and Elastix is shown in mm, the bottom panel in each graph shows the mean Euclidean deformation difference between both algorithms at their respective optimum settings.

Reproducibility of the performance measurement

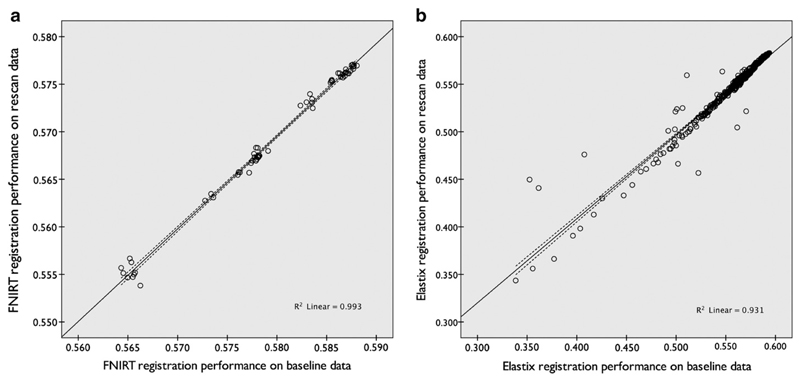
The optimization experiment was repeated on the rescan data. This resulted in a second, independent performance-measurement for each of the registration parameter settings of FNIRT and Elastix, calculated on a different set of scans of the same subjects. Scatterplots of performance measurements for both datasets are shown in Fig. 9. For FNIRT the scatterplot shows that the absolute performance on the rescan data was slightly reduced (mean difference 0.0105), but this difference was very consistent (SD 6.4 × 10⁻⁴), indicating a slightly lower data quality in the rescan data. Both measures showed an excellent correlation, which is reflected in the R² value of the OLS regression of 0.993. For Elastix the scatterplot shows that a similar performance difference was obtained (mean difference 0.0099), but at an increased variability (SD 8.9 × 10⁻³) which is reflected in a lower R² value of 0.931.

Fig. 9.

Reproducibility of the registration performance measurements for FNIRT (a) and Elastix (b) experiments on the Rotterdam data. Each point represents the registration performance for one registration parameter setting, as measured on two different sets of scans of the same subjects.

For the rescan data, registration performance was also measured for the optimal parameters determined on the baseline data. Performance measurements are listed in Table 4, showing that the small FNIRT — Elastix difference was exactly reproduced, albeit that the absolute performance measures for both algorithms were again slightly reduced.

Comparison with TBSS

Constraining the evaluation to the TBSS skeleton had little influence on the optimal parameters, especially around the optimal settings. While the optimal registration parameters evaluated on the whole tract did not exactly match the optimal parameters evaluated on the skeleton, this had very little influence on performance. The difference in registration performance between parameters obtained in the registration optimization (Optimization experiments), and the optimal registration according to a skeletonized optimization was at maximum 2.6 × 10⁻³.

To compare the performance of both FNIRT and Elastix to TBSS, Table 5 lists the registration performance for both DTI datasets restricted to the white matter skeleton. Performance differences between FNIRT or Elastix and TBSS were all significant and ranged from 0.038 to 0.046 (all p-values for paired t-tests between both nonlinear registration algorithms and TBSS were < 10⁻⁶). This indicates that registration performance was significantly better on the white matter skeleton for FNIRT and Elastix than for TBSS; the difference in performance between FNIRT and Elastix (in different directions in different datasets) was an order of magnitude smaller than the extent to which both performed better than TBSS.

Table 5.

Skeletonized performance at the optimum parameter settings for each dataset, compared to registration performance of TBSS. Performance on the Rotterdam rescan data is computed using the registration settings determined to be optimal based on the Rotterdam baseline data. p-values listed are computed for paired t-tests, comparing the registration performance for all 30 subjects across both registration algorithms and between registration algorithms and TBSS.

Algorithm	Rotterdam baseline	Rotterdam rescan	Oxford data
FNIRT	0.685	0.674	0.690
Elastix	0.689	0.677	0.686
TBSS	0.643	0.636	0.647
FNIRT–Elastix (p-value)	− 0.004 (0.002)	− 0.003 (0.01)	0.005 (<10−6)
FNIRT–TBSS (p-value)	0.04 (<10−6)	0.04 (<10−6)	0.04 (<10−6)
Elastix–TBSS (p-value)	0.05 (<10−6)	0.04 (<10−6)	0.04 (<10−6)

Table 5 also contains a comparison between FNIRT and Elastix in the skeletonized evaluation. For the Rotterdam data, Elastix reproducibly outperformed FNIRT, but for the Oxford data, FNIRT was significantly better than Elastix.

Supplementary Fig. 1 shows the results of the association between age and FA in the 50 aging female subjects, comparing TBSS to TBSS with improved registration using FNIRT. Replacing the registration-projection approach in TBSS with the improved registration yielded more symmetry in the clusters of significant association between higher age and lower FA. Also, clusters were larger and more clusters were found (50% more voxels) when using the improved registration. Bland–Altman plots of the t-values and the cluster enhanced t-values for both approaches (Supplementary Fig. 1) further show that at the cluster level, TBSS with improved registration rendered on average higher t-values than TBSS.

Discussion

We developed a method to determine the accuracy of established anatomical correspondence of white matter tracts between different subjects. Using this method, we optimized parameters for two registration algorithms, and showed that alignment in TBSS can be improved by using a regularized high-dimensional nonlinear registration approach rather than the registration-projection procedure.

We reproducibly observed substantially better alignment of white matter structures on the white matter skeleton with the optimized registration algorithms than with the current approach in TBSS. This indicates feasibility of replacing the registration-projection approach in TBSS with a finely optimized nonlinear registration. This replacement would improve alignment, but also topological consistency in white matter tracts, since this is explicitly preserved in the diffeomorphic registration of FNIRT, and almost always preserved by the regularized registration performed with Elastix.

The example analysis showed that TBSS with improved registration produced more symmetric, larger and more clusters of significant association between age and FA, and that clusters common to both approaches had smaller p-values using TBSS with improved registration. These observations do not prove that the improved registration yields higher sensitivity, as we do not know the ground-truth association in this experiment. However, the results are in line with the common notion of widespread degeneration of white matter with age (Sullivan and Pfefferbaum, 2006; Vernooij et al., 2008), and as such serve as an illustration of the potential benefit offered by the improved registration and maintained topological consistency, in the analysis of diffusion data in future studies.

There are several methodological considerations to be discussed. First, the optimization experiments showed that optimal registration parameters were different for both imaging datasets (low-end and high-resolution) used. Most notably the optimal regularization was different in both algorithms, for the Rotterdam data (low-end diffusion acquisition) this meant a higher final regularization of FNIRT and a larger regularization weight for Elastix compared to the Oxford data (high-resolution diffusion acquisition). For FNIRT this was coupled with a lower optimal warp field resolution for the Rotterdam data. With the quality of the Oxford data being higher than that of the Rotterdam data, this shows that there is a coherent relation between data quality and the optimal effective number of degrees of freedom of the registration, and that this relation can effectively be investigated with the registration evaluation framework presented here. The two datasets used for the optimization can be argued to encompass a large part of the range of diffusion data qualities commonly acquired. For a new dataset, interpolating optimal registration parameters with respect to e.g. acquisition time, allows making an informed decision on selecting optimal registration parameters. This allows future studies to benefit from improved registration accuracy without the need to redo the optimization for each new dataset.

The reproducibility of the registration, as measured with the evaluation on the rescan data shown in Fig. 9, is influenced by the individual reproducibility of the tractography, the registration, and the optimization/evaluation framework itself. The observed dispersion of the difference between performances calculated on baseline and rescan data is therefore a combination of variances. Assuming independence of the registration evaluation variance from the registration algorithm means that the excellent reproducibility of the registration performance measures for FNIRT (Fig. 9a) provides a lower bound for the reproducibility of the registration evaluation framework. It should be noted that the performance ranges for the two registration algorithms across the parameter ranges are nearly one order of magnitude apart. With Elastix spanning a larger performance range, this also means that part of the range is covering registrations that are so far away from optimal that reproducibility is less informative. Even so, it seems that reproducibility for FNIRT was slightly better than for Elastix.

It is interesting to see that for Elastix, the sum-of-squared-differences (SSD) similarity metric, which is the similarity metric implemented in FNIRT, was consistently outperformed by the mutual information (MI) and normalized cross correlation (NCC) metrics. This might have been caused by nonlinear intensity differences between subjects across tracts. With different tracts having slightly different intensity across subjects, the assumptions of the SSD cannot be met. This might explain the difference in registration performance between Elastix and FNIRT observed on the full tract evaluation.

Registration performance on the skeleton for both registration algorithms showed heterogeneous behavior amongst the datasets, with Elastix performing slightly better on the worse data, and FNIRT performing slightly better on the better data. Comparison of both algorithms using the whole tract evaluation showed Elastix to perform slightly better than FNIRT with absolute deformation differences in the order of 1–2 mm. These differences will be a composition of deformation differences that do, and deformation differences that do not translate into registration performance differences (think e.g. of two sets of transformations, each with an equal amount of different random perturbations). By scaling the optimal deformations, we found that the obtained difference in registration performance between optimal warp fields of both algorithms would translate to deformation differences in the order of 0.1 mm, had all deformation differences translated into registration performance differences. While performing slightly worse, FNIRT is diffeomorphic and therefore produces invertible warps. Invertibility of the warp field is a desirable property in a neuroscience context such as TBSS as this allows back-projecting points in standard space to subject-native space and preserves topological consistency of the whitematter through the transformation of native space to standard space.

The masks that initialize the probabilistic tractography (seed, target, exclusion, and stop) are defined in standard space, and transformed to subject space. The registration that is used for this transformation is obtained with a medium degree-of-freedom registration, i.e., the same registration that is used in the initial alignment of TBSS. This registration is inverted to obtain a standard space to subject transformation. The use of a registration inside a registration-evaluation framework can potentially bias the evaluation metric. However, this bias would favor transformations similar to the one used in the tractography initialization, i.e. conservative, medium degree-of-freedom transformations. It should also be noted that tractography is only run in a preprocessing stage, and that the same tract-sets are used to evaluate all different registration parameter settings. We therefore consider bias due to this registration step not to be a major factor in our results.

In this evaluation we have included two nonlinear registration algorithms that were developed in the groups that contributed to this study and for which primary developers were involved in the project. Though not the aim of this study, the developed framework may lend itself to a comprehensive comparison of more registration algorithms. Such a comparison of registration algorithms could e.g. include a broad selection of algorithms out-of-the-box, such as carried out in Wang et al. (2011), or could include a full optimization in which case we recommend involvement of developers of each algorithm to design the algorithm-specific optimization scheme. Such an optimization would inherently be very computationally intensive. Computing the registration performance for a single registration parameter setting, for a group of 30 subjects, took on average around 50 CPU-hours. This included the actual registration, warping the tract maps, and computing the spatial correlation. Computations were performed on the LISA cluster in Amsterdam (www.sara.nl/systems/lisa) and on a local cluster in Rotterdam. The optimal registrations of the Rotterdam data required on average 51 min (FNIRT), and 68 min (Elastix) of CPU time on 2.1 Ghz AMD Magny Cours processors, compared to 12 min for the registration + projection of TBSS. For the Oxford data this was 71 min for FNIRT, 71 min for Elastix, and 12 min for TBSS.

We used probabilistic tractography for fiber tracking and evaluated registration performance using a spatial correlation similarity metric. This is different from previous work that used fiber tracts to quantitatively measure registration performance (Park et al., 2003; Xue et al., 2010; Yap et al., 2009; Zhang et al., 2006; Zöllei et al., 2010), which were based on deterministic tractography. As a result, metrics for comparing similarity of warped tract maps in those methods were overlap-based, using similarity metrics such as the Dice, Jaccard and Cohen's Kappa metric (Stieltjes et al., 2001; Zhang et al., 2010), or distance-based metrics, related to the Hausdorff distance or the mean absolute surface distance (Park et al., 2003; Yap et al., 2009; Zhang et al., 2006; Zöllei et al., 2010). The near-continuous density information that results from probabilistic tractography is not so well suited for these similarity metrics. Most importantly, tract-density contains information about the tract, which would be lost if a thresholded, binary tract-mask was used. Secondly, setting a density threshold for binarization would introduce another parameter that requires setting. Spatial correlation as a similarity measure does not suffer from these drawbacks. Also, we have shown that when using the framework presented, based on multiple tracts identified with probabilistic tractography, using spatial correlation as similarity measurement allows for a precise and reproducible evaluation of registration quality. Investigating other evaluation metrics would be possible within this framework, but this is beyond the scope of the current research.

Registration performance measurements on the rescan data showed the difference between both nonlinear registration algorithms to be highly reproducible. Furthermore, performance measurements were highly reproducible themselves. This is an important observation, as it shows that using the tractography output to measure registration performance in the framework presented is not prone to overfitting registration parameters on the dataset that is used for training the registration parameters. This in turn allows one to train registration parameters without the explicit need to evaluate performance on a separate dataset that was not used in the optimization.

The optimized parameter sets that resulted from our experiments are available for both registration algorithms as Supplementary material. For Elastix, parameters can additionally be downloaded from the parameter file database on the Elastix wiki page (http://elastix.bigr.nl/wiki). For FNIRT, optimized parameter files will be distributed with FSL. Scripts and masks, developed for the automated tractography, will be made available for release with FSL.

Conclusions

In conclusion, firstly, we demonstrate that optimized nonlinear image registration algorithms produce better image alignment on the white matter skeleton than the registration-projection approach currently in TBSS.

Secondly, registration quality of diffusion imaging data can be assessed using probabilistic tractography and thus used for optimization of registration parameter settings and for comparison of registration algorithms. This evaluation is not in general biased towards any particular tensor or tensor metric based registration approach, and highly reproducible.

Thirdly, optimal registration parameters depend on the quality (resolution, number of averages etc.) of the diffusion dataset in a graded and predictable manner.

Future studies investigating cross-subject diffusion data with TBSS are expected to benefit from the improved anatomical alignment.

Supplementary Material

Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.neuroimage.2013.03.015.