Abstract
A paradigm shift for models of MT assembly is suggested by a recent cryo-electron microscopy study of microtubules (MTs). Previous assembly models have been based on the two-dimensional lattice of the MT wall, where incoming subunits can add with longitudinal and lateral bonds. The new study of McIntosh et al. concludes that the growing ends of MTs separate into flared single protofilaments. This means that incoming subunits must add onto the end of single protofilaments, forming only a longitudinal bond. How can growth of single-stranded protofilaments exhibit cooperative assembly with a critical concentration? An answer is suggested by FtsZ, the bacterial tubulin homolog, which assembles into single-stranded protofilaments. Cooperative assembly of FtsZ is thought to be based on conformational changes that switch the longitudinal bond from low to high affinity when the subunit is incorporated in a protofilament. This novel mechanism may also apply to tubulin assembly and could be the primary mechanism for assembly onto single flared protofilaments.
Significance
A recent study by cryo-electron microscopy contradicts assembly models in which tubulin subunits add to the microtubule lattice forming longitudinal and lateral bonds. McIntosh and colleagues found that the growing microtubule end consisted of separate flared protofilaments, where incoming subunits can only form a longitudinal bond. The bacterial tubulin homolog FtsZ may provide a model for how assembly of single protofilaments can be cooperative.
Main Text
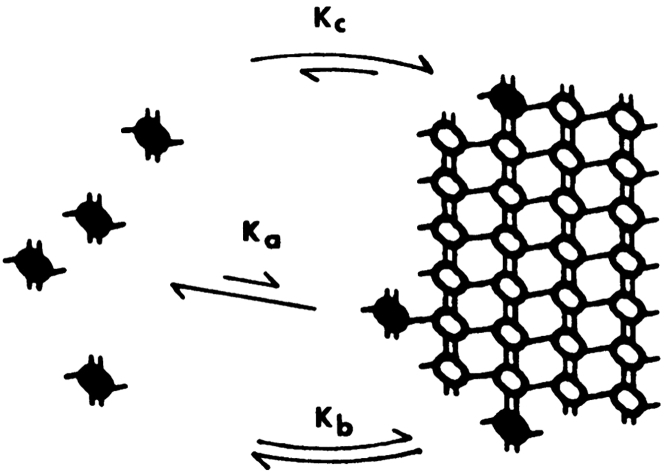
A recent study of the structure of microtubule (MT) ends by McIntosh et al. (1) may invoke a paradigm shift for models of MT assembly. Since the 1970s and 1980s, the MT has been pictured as a helical lattice of tubulin subunits that grow by adding subunits at the ends. Cooperative assembly could be explained by the cozy corner, where a subunit could simultaneously form a longitudinal and a lateral bond (Fig. 1) (2). Forming the two bonds together is orders of magnitude more favorable than forming either bond alone (3). However, the new study from McIntosh et al. (1) suggests that the cozy corner may not be relevant to the assembly of MTs.
Figure 1.
The classic cozy corner. Shaded subunits and arrows show the three ways subunits can add to the lattice: forming a single lateral bond with affinity Ka, a single longitudinal bond with affinity Kb, or both a lateral and longitudinal bond together with affinity Kc. With even a weak contribution from Ka, Kc can be orders of magnitude higher than Kb, as explained in detail in (3). The diagram is reprinted from (2) with permission.
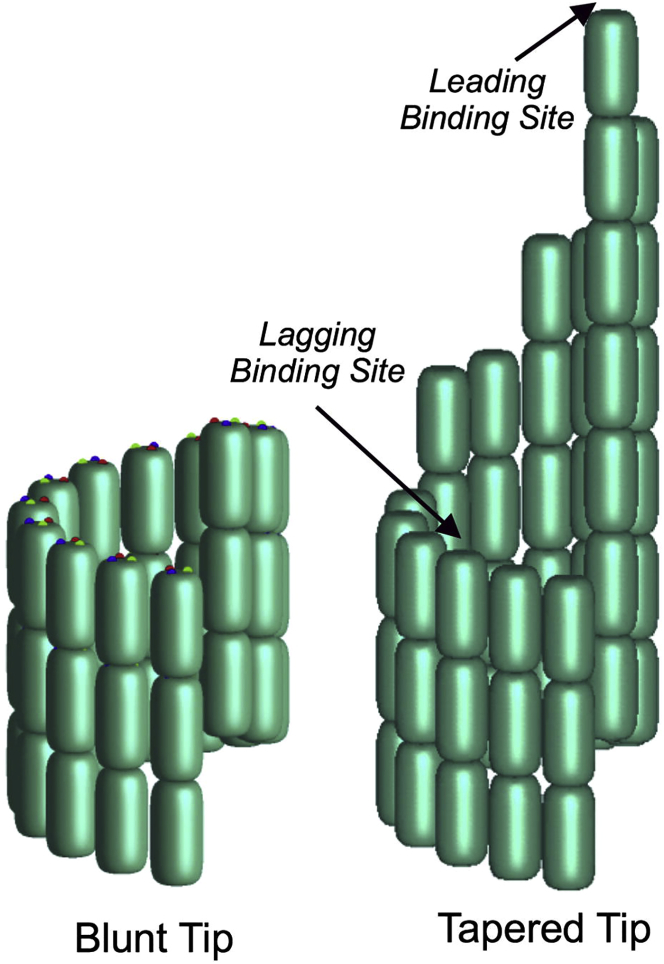
The early cozy corner paradigm pictured the MT to be a three-start helical lattice with up to three cozy corners, one at the end of each three-start helix (2). This simple picture was questioned when Chrétien et al. (4) obtained cryo-electron microscopy (cryoEM) images that showed thin, gently curved sheets of PFs projecting from the growing ends of MTs. These curved sheets gradually straightened and came together to make the cylindrical MT wall. This suggested that subunit addition occurs not just at cozy corners but must occur sometimes on the end of a protofilament (PF), forming a single longitudinal bond. Cozy corners could still be invoked on the projecting sheets (Fig. 2). A short PF on the edge of the sheet could add subunits at a cozy corner, with each new subunit making a longitudinal and a lateral bond, until it caught up with its neighbors. Once the PFs were all the same length, a subunit would have to be added by forming only a longitudinal bond, but then the row could be filled in by cozy corner addition. VanBuren et al. developed a comprehensive thermodynamic and kinetic model in which incoming subunits formed one longitudinal bond plus 2, 1, or 0 lateral bonds (5). Association of a subunit without a lateral bond could elongate a PF by forming only a longitudinal bond. This was a weaker association than the cozy corner association with a lateral bond, but it was essential to the model. This model was substantially extended by Castle and Odde (Fig. 2) (6), and by Gardner et al. (7).
Figure 2.
A model of a MT showing a blunt tip with a cozy corner and a tapered tip where projecting sheets of PFs provide sites for adding a subunit with a single longitudinal bond (leading binding site) and variations on a cozy corner. Reprinted from (6) with permission. To see this figure in color, go online.
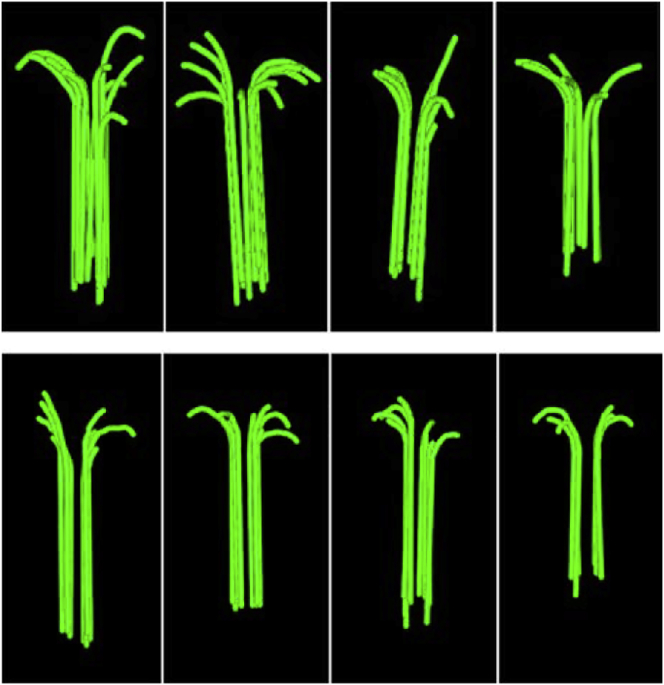
The revolutionary discovery of McIntosh et al. (1) is that the projections from the growing ends of MTs are not sheets of PFs. Each projection appears to be a single PF, completely separate from neighboring PFs. This new interpretation may be due to the imaging technique. Chrétien et al. interpreted structures from single projection images (4), whereas McIntosh et al. rotated the sections through multiple angles and recreated a three-dimensional image by tomography (1). The new, higher-resolution tomographic reconstructions convinced the authors that the projections are single PFs, not sheets (Fig. 3). In this structure, lateral bonds are important for joining PFs to make the MT wall, but they are formed 10–50 nm from the growing tip of the PF. Incoming tubulin dimers are only added at the end of the flared single PFs, forming a single longitudinal bond. This suggests that we might forget the cozy corner as a primary assembly site. This is a major paradigm shift.
Figure 3.
Models of flared PFs at the plus end of growing cytoplasmic MTs, reconstructed from cryoEM tomograms. The top row is from Chlamydomonas cells, the bottom row from PTK2 cells. Each green line is a single PF. Reprinted from (1) with permission. To see this figure in color, go online.
In contrast to the conclusions of McIntosh et al., another cryoEM tomography study showed MT ends as less flared and failed to resolve single PFs (8). However, that study was focused on determining the binding site of CAMSAP proteins and was not looking for new details of the structure of MT ends. McIntosh et al. were focused on resolving details of the flared projections that had been reported by Chrétien et al. This apparently required a considerable effort, such that the in vivo analysis was only achieved by one observer, Dr. McIntosh himself. “In vitro, the lack of cytoplasm made tracking somewhat easier, although the low signal-to-noise ratio of the low-dose images meant that tracking was still a challenge.” This is apparently at the limit of what can be achieved with the best current imaging technology and analysis. The interpretation may be debated and/or refined by future advances in cryoEM tomography. For the present, I will accept the conclusion of these skilled microscopists that the growth points at MT ends are single PFs.
Cooperative assembly of single-stranded PFs—Lessons from FtsZ
How can assembly of single-stranded PFs, with subunits connected only by longitudinal bonds, exhibit the characteristics of cooperative assembly? McIntosh et al. (1) provided a brief but important suggestion. “We infer that GTP-tubulin changes its properties upon addition to a PF, increasing its affinity for dimers in solution. The change is probably a subtle, binding-induced rearrangement in the tubulin fold.” Here, I expand on this suggestion, based on similar and more highly developed models for assembly of FtsZ, the bacterial tubulin homolog.
Several studies have provided convincing evidence that FtsZ assembly exhibits a critical concentration, a hallmark of cooperative assembly (9, 10, 11, 12). However, under many conditions in free solution, FtsZ assembles into PFs that are one subunit thick (13, 14), meaning subunits are connected only by longitudinal bonds. How can single-stranded PFs with only one type of bond exhibit cooperative assembly and a critical concentration?
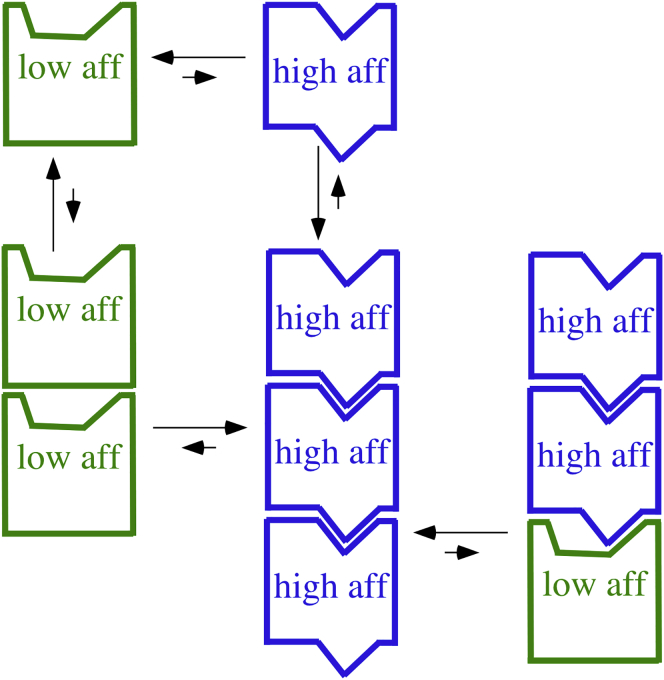
Several groups have suggested that this could be achieved if FtsZ had two conformations, one with high and one with low affinity for making the longitudinal bond (14, 15, 16, 17, 18). To explain cooperativity, the model proposes that FtsZ monomers are highly favored to be in the low-affinity conformation, whereas assembly into a PF switches the subunit to favor the high-affinity conformation. Some possible pathways encounter thermodynamic contradictions, but Miraldi et al. (18) provided a detailed analysis of pathways that are thermodynamically sound. Their analysis is somewhat complex, but the basic mechanism can be simply explained (see Fig. 4 for a diagram).
-
1.
Assume that the equilibrium constant for monomers switching from low affinity (L) to high (H) is Kconf = 1/4000. The free energy needed for this switch is ΔGconf = −RT ln(Kconf) = +5 kcal/mol, where the + indicates that it is unfavorable.
-
2.
Assume that the longitudinal bond for forming an LL dimer is −6.65 kcal/mol (this number is chosen to make the final critical concentration Cc = 1 μM). What is the free energy for forming an HH dimer? There are several pathways to go from L + L monomers to an HH dimer, but they all must have the same net free energy (18). Let us assume that we first switch one subunit to H, then form an HL dimer, and then switch the second subunit to H. Assume also that the free energy for the second switch is the same +5 kcal/mol as for the free monomer. The net free energy for forming an HH dimer would be ΔGHH = +5 − 6.65 + 5 = +3.35 kcal/mol, an unfavorable reaction. This does not give cooperative assembly.
-
3.
Now, assume that the H conformation alters the surfaces of the subunits that make the dimer interface so that they make a higher-affinity longitudinal bond. Assume, for example, that the H conformation doubles the surface area of the interface and therefore doubles the bond energy, so ΔGHH for forming an HH dimer is twice that of an LL dimer, ΔGHH = −13.3 kcal/mol. Then, the net free energy for forming the HH dimer is ΔGHH = +5 − 13.3 + 5 kcal/mol = −3.3 kcal/mol. This is favorable but still weak.
-
4.
The most important step is adding a third subunit. This now becomes highly favorable because it only costs one +5 kcal/mol to switch the its conformation to H, and it gains the −13.3 kcal/mol for the bond. The free energy for elongation is ΔGe = +5 − 13.3 = −8.3 kcal/mol. The third and all subsequent subunits add with the same elongation free energy. This generates the appearance of cooperative assembly, including a weak dimer nucleus and a critical concentration of Cc = 1/Ke = 1/exp(−ΔGe/RT) = 1 μM (where Ke is the association equilibrium constant for adding a subunit to the elongating PF).
Figure 4.
A diagram of the high- and low-affinity conformations. For monomeric subunits, the high-affinity conformation is highly disfavored, and the top and bottom surfaces form a poorly matched interface. In the high-affinity conformation, the top and bottom surfaces are rearranged so that they form a large and snugly fitting interface. The extra bond energy of this interface is sufficient to compensate for the free energy needed to switch to high affinity, so polymerization favors the switch to high affinity. The right-hand PF shows the process of elongation, in which a subunit is added in the low-affinity conformation and switches to high affinity. The high-affinity conformation involves internal rotations of the subdomains and movement of helix H7. These are not shown because the important switch is in the top and bottom interface surfaces. For simplicity, the diagram shows monomeric subunits, applicable to FtsZ. For dimeric tubulin, the conformational change would be transmitted across both α and β subunits, consistent with crystallography. To see this figure in color, go online.
Crystal structures show FtsZ in the high- and low-affinity conformations
Before 2012, there were numerous crystal structures of FtsZ from different bacterial species and having GTP, GDP, or nothing in the nucleotide-binding site. From these, it is clear that the bound nucleotide does not affect the conformation of the monomer. Oliva et al. (19) obtained crystal structures of GTP- and GDP-FtsZ from two species and found no significant structural change. More generally, crystal structures of FtsZ from a large number of species show a uniform structure regardless of nucleotide. Importantly, these structures are all of monomeric FtsZ, suggesting they would be the low-affinity conformation.
A major advance in the structure of FtsZ was achieved when two labs independently crystallized FtsZ from Staphylococcus aureus (SaFtsZ) and found that it crystallized in the form of long, straight PFs (20, 21). The FtsZ in these PFs showed a striking conformational change relative to the previous monomeric forms, in particular that of the closely related Bacillus subtilis (BsFtsZ). The globular domain of both FtsZ and tubulin is divided into two subdomains. The conformational change from BsFtsZ to SaFtsZ involved a large rotation (25–28°) of the C-terminal subdomain relative to the N-terminal subdomain. In addition to this rotation, the helix H7 moved downward one full turn. Importantly, this caused significant changes in the interfaces forming the longitudinal bond. This new structure of SaFtsZ assembled in straight PFs was an excellent candidate for the high-affinity conformation, whereas the monomeric BsFtsZ represented the low-affinity conformation. More recently, two groups have obtained structures of the low-affinity conformation of SaFtsZ, eliminating any concerns about comparison across different species (22, 23).
Matsui et al. (24) went on to crystalize SaFtsZ with mutations in the T7 loop, which is at the center of the interface. Remarkably, the mutants all crystallized in the form of straight PFs. However, for two mutants, the subdomain rotation was in the low-affinity conformation despite being assembled into PFs. These mutants had substantially reduced areas of contact at the interface: 740 and 810 Å2 for the mutants vs. 1230 Å2 for wild-type SaFtsZ. In a separate study, Fujita et al. found interface areas of 798 and 1168 Å2 for PFs of wild-type SaFtsZ in the low- and high-affinity conformations (22). This suggests that the smaller interfaces, although sufficient to assemble PFs at the high protein concentration for crystallization, do not provide sufficient bond energy to switch the subunit to the high-affinity conformation. These mutants lost virtually all GTPase activity (24) and are presumably not capable of cooperative assembly.
High- and low-affinity conformations of tubulin
A very similar rotation of subdomains and translation of helix H7 had already been observed in tubulin. A rotation similar to that of the SaFtsZ PF is seen in straight tubulin PFs (25, 26), whereas a rotation similar to BsFtsZ is seen in crystals of a curved tubulin PF (27, 28) and also in tubulin dimers blocked for assembly (29, 30). The subdomain rotation in tubulin is in the same direction as in FtsZ, but it is smaller in magnitude: 8–11° in tubulin vs. 25–28° in FtsZ.
I suggest that tubulin assembly at the ends of individual flared PFs may be based on the same transition from low- to high-affinity conformation as in FtsZ. Specifically, soluble tubulin dimers are highly favored to be low affinity, whereas assembly onto a PF favors their transition to high affinity. In this case, all of the subunits in the flared PFs will be high affinity. When a new tubulin dimer, initially low affinity, binds to the end of the PF, it will be induced to switch to high affinity.
In the tubulin field, the two conformations are usually designated straight and curved, corresponding to the shape of the PF where they have been identified. This designation may not match the new model of McIntosh et al. (1), in which growing and shrinking PFs have a very similar curvature. For this argument, the overall curvature is not important. The rotation of the subdomains and the shift of helix H7, which are the hallmarks to identify the conformations in crystal structures, are also minimally important. The important structural feature is how the conformations affect the top and bottom interfaces. This is diagrammed in Fig. 4. In the low-affinity conformation, the surfaces do not fit well together, and form an interface with a small contact area. In the high-affinity conformation, the surfaces are rearranged to provide a large and snugly fitting interface. The extra bond energy of this interface is sufficient to compensate for the unfavorable internal switch to the high-affinity conformation.
I will speculate that the tubulin subunits in the flared PFs are in the high-affinity conformation during both growth and shrinking. Because shrinking PFs have GDP in their interfaces, this can weaken the interfaces somewhat, but not enough to switch the internal subunits to low affinity or cause fragmentation. This applies to all internal subunits, which have a subunit below and above to stabilize their high-affinity conformation. However, the terminal subunit has a stabilizing bond only on one side. A GDP in this interface may weaken it further, letting the terminal subunit switch to low affinity and rapidly dissociate. This is discussed in the last section.
The role of lateral bonds in the new model
Lateral bonds are the links that bring PFs together to make the MT wall. In the splayed PF model, lateral bonds only form at a location several dimers below the tip where new dimers are being added. The relaxed single PF is curved, but it needs to straighten to enter the MT wall. The lateral bonds presumably provide enough energy to compensate for the mechanical strain to straighten the PF. As the PF straightens, subunits remain in the high-affinity conformation, as confirmed in high-resolution structures (25, 26). In this interpretation, the role of lateral bonds is to mold the PFs into the MT wall. They do not contribute to the primary MT assembly reaction, the association of tubulin subunits onto flared PFs.
If PF assembly does not require lateral bonds, one might ask why we never see isolated single PFs. A likely answer is that single PFs have multiple lateral bond sites, which would strongly favor association into pairs and sheets. Unassociated PFs would be rare. However, isolated tubulin PFs have actually been observed by atomic force microscopy (31, 32). In both atomic force microscopy studies, the PFs were adsorbed to mica. Most of the PFs were curved, suggesting that one lateral surface was in contact with the mica, blocking lateral association. Adsorption to mica may also have stabilized the PFs because they assembled at well below the critical concentration (32).
Lateral bonds are also probably important for the mechanisms of dynamic instability, discussed below.
Treadmilling and dynamic instability—The role of GDP
FtsZ assembly dynamics are now known to be based on treadmilling, both in vitro (33, 34) and in vivo (35, 36). Subunits add to the PF bottom and dissociate from the PF top, where the top is the GTP pocket (37, 38). When a subunit is added to the PF bottom, it is initially in the low-affinity conformation. It has some probability of coming off but a high probability of switching to high affinity. When it switches to high affinity, it remains in that conformation, awaiting the next subunit.
A seminal article by Albrecht Wegner pointed out that a treadmilling mechanism is not possible for a reversible assembly, but it can be achieved if assembly is accompanied by an irreversible step of nucleotide hydrolysis (39). In the current models of FtsZ treadmilling (23, 38), FtsZ with bound GTP is added to the bottom and undergoes hydrolysis with slow first-order kinetics. This establishes a nucleotide gradient, where subunits at the bottom have mostly GTP and subunits at the top mostly GDP.
Because FtsZ PFs do not fragment in the middle, we must assume that the high-affinity conformation maintains strong bonds within the PF even at interfaces with GDP. In fact, the original crystal of SaFtsZ PFs had GDP bound in all the PF interfaces (20). It is likely that interfaces with GDP are weaker than those with GTP but still strong enough to prevent significant fragmentation when they are stabilized by subunits above and below. However, the top subunit has no subunit above, which should weaken its interface below. We propose that if the penultimate subunit has a GDP, this interface is weakened enough to allow the terminal subunit to switch to low affinity and dissociate. Additional mechanistic details are required to meet Wegner’s thermodynamic constraints and will be discussed elsewhere (L.C. Corbin and H.P.E., unpublished data). The important conclusion is that GDP weakens the interface, but not enough to disrupt the high-affinity conformation, except for the terminal subunit.
In contrast to the treadmilling of FtsZ, MT assembly is characterized by dynamic instability, which is thought to be regulated by a GTP cap. The GTP cap is probably longer than the 10–50 nm length of the flared PFs (40). The fluctuations of cap size and the alterations that leads to catastrophe therefore take place within the MT lattice, involving lateral as well as longitudinal bonds. Rescue also likely involves the lattice (41). These mechanisms are outside the scope of this analysis. However, models should now consider that the actual subunit addition and loss occurs at the end of flared PFs, involving only a single longitudinal bond.
McIntosh et al. noted that the flared PFs had essentially the same length and curvature for growing and shrinking MT ends (1). Presumably the subunits in these flared PFs should have GTP when growing and GDP when shrinking. I speculate that subunits in both growing and shrinking flared PFs are in the high-affinity conformation. As noted above for FtsZ, GDP probably weakens the interface, but not enough to promote fragmentation at internal subunits. The terminal subunit, however, may be an exception. When there is no stabilizing subunit on one side, having a GDP on the other side may weaken its interaction and permit it to switch to low affinity and dissociate. Because the disassembling tubulin PF has all GDP, this would result in sequential loss of tubulin dimers, similar to the loss of FtsZ from the top end of the treadmilling PF. This would provide a unified assembly mechanism from treadmilling of FtsZ to dynamic instability of α-β tubulin.
The interpretation of McIntosh et al. (1) that the ends of MTs flare into single PFs is at the limit of current imaging and will likely be controversial and debated. Attempts by other laboratories to confirm or refute this model should be most welcome. However, it should be recognized that the conformational change from low to high affinity seems well established as the source of cooperative assembly of FtsZ. Even if lateral bonds are resurrected to have some role in the primary assembly of MTs, the contribution of the conformational change to assembly of longitudinal bonds should be considered as a paradigm shift in models of MT assembly.
Acknowledgments
Supported by National Institutes of Health grant R01-GM066014.
Editor: Brian Salzberg.
References
- 1.McIntosh J.R., O’Toole E., Gudimchuk N. Microtubules grow by the addition of bent guanosine triphosphate tubulin to the tips of curved protofilaments. J. Cell Biol. 2018;217:2691–2708. doi: 10.1083/jcb.201802138. [DOI] [PMC free article] [PubMed] [Google Scholar]; McIntosh, J. R., E. O’Toole, …, N. Gudimchuk. 2018. Microtubules grow by the addition of bent guanosine triphosphate tubulin to the tips of curved protofilaments. J. Cell Biol. 217:2691-2708. [DOI] [PMC free article] [PubMed]
- 2.Erickson H.P., Pantaloni D. The role of subunit entropy in cooperative assembly. Nucleation of microtubules and other two-dimensional polymers. Biophys. J. 1981;34:293–309. doi: 10.1016/S0006-3495(81)84850-3. [DOI] [PMC free article] [PubMed] [Google Scholar]; Erickson, H. P., and D. Pantaloni. 1981. The role of subunit entropy in cooperative assembly. Nucleation of microtubules and other two-dimensional polymers. Biophys. J. 34:293-309. [DOI] [PMC free article] [PubMed]
- 3.Erickson H.P. Co-operativity in protein-protein association. The structure and stability of the actin filament. J. Mol. Biol. 1989;206:465–474. doi: 10.1016/0022-2836(89)90494-4. [DOI] [PubMed] [Google Scholar]; Erickson, H. P. 1989. Co-operativity in protein-protein association. The structure and stability of the actin filament. J. Mol. Biol. 206:465-474. [DOI] [PubMed]
- 4.Chrétien D., Fuller S.D., Karsenti E. Structure of growing microtubule ends: two-dimensional sheets close into tubes at variable rates. J. Cell Biol. 1995;129:1311–1328. doi: 10.1083/jcb.129.5.1311. [DOI] [PMC free article] [PubMed] [Google Scholar]; Chretien, D., S. D. Fuller, and E. Karsenti. 1995. Structure of growing microtubule ends: two-dimensional sheets close into tubes at variable rates. J. Cell Biol. 129:1311-1328. [DOI] [PMC free article] [PubMed]
- 5.VanBuren V., Odde D.J., Cassimeris L. Estimates of lateral and longitudinal bond energies within the microtubule lattice. Proc. Natl. Acad. Sci. USA. 2002;99:6035–6040. doi: 10.1073/pnas.092504999. [DOI] [PMC free article] [PubMed] [Google Scholar]; VanBuren, V., D. J. Odde, and L. Cassimeris. 2002. Estimates of lateral and longitudinal bond energies within the microtubule lattice. Proc. Natl. Acad. Sci. USA. 99:6035-6040. [DOI] [PMC free article] [PubMed]
- 6.Castle B.T., Odde D.J. Brownian dynamics of subunit addition-loss kinetics and thermodynamics in linear polymer self-assembly. Biophys. J. 2013;105:2528–2540. doi: 10.1016/j.bpj.2013.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]; Castle, B. T., and D. J. Odde. 2013. Brownian dynamics of subunit addition-loss kinetics and thermodynamics in linear polymer self-assembly. Biophys. J. 105:2528-2540. [DOI] [PMC free article] [PubMed]
- 7.Gardner M.K., Charlebois B.D., Odde D.J. Rapid microtubule self-assembly kinetics. Cell. 2011;146:582–592. doi: 10.1016/j.cell.2011.06.053. [DOI] [PMC free article] [PubMed] [Google Scholar]; Gardner, M. K., B. D. Charlebois, …, D. J. Odde. 2011. Rapid microtubule self-assembly kinetics. Cell. 146:582-592. [DOI] [PMC free article] [PubMed]
- 8.Atherton J., Jiang K., Akhmanova A. A structural model for microtubule minus-end recognition and protection by CAMSAP proteins. Nat. Struct. Mol. Biol. 2017;24:931–943. doi: 10.1038/nsmb.3483. [DOI] [PMC free article] [PubMed] [Google Scholar]; Atherton, J., K. Jiang, …, A. Akhmanova. 2017. A structural model for microtubule minus-end recognition and protection by CAMSAP proteins. Nat. Struct. Mol. Biol. 24:931-943. [DOI] [PMC free article] [PubMed]
- 9.Mukherjee A., Lutkenhaus J. Dynamic assembly of FtsZ regulated by GTP hydrolysis. EMBO J. 1998;17:462–469. doi: 10.1093/emboj/17.2.462. [DOI] [PMC free article] [PubMed] [Google Scholar]; Mukherjee, A., and J. Lutkenhaus. 1998. Dynamic assembly of FtsZ regulated by GTP hydrolysis. EMBO J. 17:462-469. [DOI] [PMC free article] [PubMed]
- 10.Caplan M.R., Erickson H.P. Apparent cooperative assembly of the bacterial cell division protein FtsZ demonstrated by isothermal titration calorimetry. J. Biol. Chem. 2003;278:13784–13788. doi: 10.1074/jbc.M300860200. [DOI] [PubMed] [Google Scholar]; Caplan, M. R., and H. P. Erickson. 2003. Apparent cooperative assembly of the bacterial cell division protein FtsZ demonstrated by isothermal titration calorimetry. J. Biol. Chem. 278:13784-13788. [DOI] [PubMed]
- 11.González J.M., Jiménez M., Rivas G. Essential cell division protein FtsZ assembles into one monomer-thick ribbons under conditions resembling the crowded intracellular environment. J. Biol. Chem. 2003;278:37664–37671. doi: 10.1074/jbc.M305230200. [DOI] [PubMed] [Google Scholar]; Gonzalez, J. M., M. Jimenez, …, G. Rivas. 2003. Essential cell division protein FtsZ assembles into one monomer-thick ribbons under conditions resembling the crowded intracellular environment. J. Biol. Chem. 278:37664-37671. [DOI] [PubMed]
- 12.Chen Y., Bjornson K., Erickson H.P. A rapid fluorescence assay for FtsZ assembly indicates cooperative assembly with a dimer nucleus. Biophys. J. 2005;88:505–514. doi: 10.1529/biophysj.104.044149. [DOI] [PMC free article] [PubMed] [Google Scholar]; Chen, Y., K. Bjornson, …, H. P. Erickson. 2005. A rapid fluorescence assay for FtsZ assembly indicates cooperative assembly with a dimer nucleus. Biophys. J. 88:505-514. [DOI] [PMC free article] [PubMed]
- 13.Romberg L., Simon M., Erickson H.P. Polymerization of Ftsz, a bacterial homolog of tubulin. is assembly cooperative? J. Biol. Chem. 2001;276:11743–11753. doi: 10.1074/jbc.M009033200. [DOI] [PubMed] [Google Scholar]; Romberg, L., M. Simon, and H. P. Erickson. 2001. Polymerization of Ftsz, a bacterial homolog of tubulin. is assembly cooperative? J. Biol. Chem. 276:11743-11753. [DOI] [PubMed]
- 14.Huecas S., Llorca O., Andreu J.M. Energetics and geometry of FtsZ polymers: nucleated self-assembly of single protofilaments. Biophys. J. 2008;94:1796–1806. doi: 10.1529/biophysj.107.115493. [DOI] [PMC free article] [PubMed] [Google Scholar]; Huecas, S., O. Llorca, …, J. M. Andreu. 2008. Energetics and geometry of FtsZ polymers: nucleated self-assembly of single protofilaments. Biophys. J. 94:1796-1806. [DOI] [PMC free article] [PubMed]
- 15.Michie K.A., Löwe J. Dynamic filaments of the bacterial cytoskeleton. Annu. Rev. Biochem. 2006;75:467–492. doi: 10.1146/annurev.biochem.75.103004.142452. [DOI] [PubMed] [Google Scholar]; Michie, K. A., and J. Lowe. 2006. Dynamic filaments of the bacterial cytoskeleton. Annu. Rev. Biochem. 75:467-492. [DOI] [PubMed]
- 16.Dajkovic A., Lutkenhaus J. Z ring as executor of bacterial cell division. J. Mol. Microbiol. Biotechnol. 2006;11:140–151. doi: 10.1159/000094050. [DOI] [PubMed] [Google Scholar]; Dajkovic, A., and J. Lutkenhaus. 2006. Z ring as executor of bacterial cell division. J. Mol. Microbiol. Biotechnol. 11:140-151. [DOI] [PubMed]
- 17.Dajkovic A., Mukherjee A., Lutkenhaus J. Investigation of regulation of FtsZ assembly by SulA and development of a model for FtsZ polymerization. J. Bacteriol. 2008;190:2513–2526. doi: 10.1128/JB.01612-07. [DOI] [PMC free article] [PubMed] [Google Scholar]; Dajkovic, A., A. Mukherjee, and J. Lutkenhaus. 2008. Investigation of regulation of FtsZ assembly by SulA and development of a model for FtsZ polymerization. J. Bacteriol. 190:2513-2526. [DOI] [PMC free article] [PubMed]
- 18.Miraldi E.R., Thomas P.J., Romberg L. Allosteric models for cooperative polymerization of linear polymers. Biophys. J. 2008;95:2470–2486. doi: 10.1529/biophysj.107.126219. [DOI] [PMC free article] [PubMed] [Google Scholar]; Miraldi, E. R., P. J. Thomas, and L. Romberg. 2008. Allosteric models for cooperative polymerization of linear polymers. Biophys. J. 95:2470-2486. [DOI] [PMC free article] [PubMed]
- 19.Oliva M.A., Trambaiolo D., Löwe J. Structural insights into the conformational variability of FtsZ. J. Mol. Biol. 2007;373:1229–1242. doi: 10.1016/j.jmb.2007.08.056. [DOI] [PubMed] [Google Scholar]; Oliva, M. A., D. Trambaiolo, and J. Lowe. 2007. Structural insights into the conformational variability of FtsZ. J. Mol. Biol. 373:1229-1242. [DOI] [PubMed]
- 20.Matsui T., Yamane J., Tanaka I. Structural reorganization of the bacterial cell-division protein FtsZ from Staphylococcus aureus. Acta Crystallogr. D Biol. Crystallogr. 2012;68:1175–1188. doi: 10.1107/S0907444912022640. [DOI] [PubMed] [Google Scholar]; Matsui, T., J. Yamane, …, I. Tanaka. 2012. Structural reorganization of the bacterial cell-division protein FtsZ from Staphylococcus aureus. Acta Crystallogr. D Biol. Crystallogr. 68:1175-1188. [DOI] [PubMed]
- 21.Elsen N.L., Lu J., Lumb K.J. Mechanism of action of the cell-division inhibitor PC190723: modulation of FtsZ assembly cooperativity. J. Am. Chem. Soc. 2012;134:12342–12345. doi: 10.1021/ja303564a. [DOI] [PubMed] [Google Scholar]; Elsen, N. L., J. Lu, …, K. J. Lumb. 2012. Mechanism of action of the cell-division inhibitor PC190723: modulation of FtsZ assembly cooperativity. J. Am. Chem. Soc. 134:12342-12345. [DOI] [PubMed]
- 22.Fujita J., Harada R., Matsumura H. Identification of the key interactions in structural transition pathway of FtsZ from Staphylococcus aureus. J. Struct. Biol. 2017;198:65–73. doi: 10.1016/j.jsb.2017.04.008. [DOI] [PubMed] [Google Scholar]; Fujita, J., R. Harada, …, H. Matsumura. 2017. Identification of the key interactions in structural transition pathway of FtsZ from Staphylococcus aureus. J. Struct. Biol. 198:65-73. [DOI] [PubMed]
- 23.Wagstaff J.M., Tsim M., Löwe J. A polymerization-associated structural switch in FtsZ that enables treadmilling of model filaments. MBio. 2017;8:e00254-17. doi: 10.1128/mBio.00254-17. [DOI] [PMC free article] [PubMed] [Google Scholar]; Wagstaff, J. M., M. Tsim, …, J. Lowe. 2017. A polymerization-associated structural switch in FtsZ that enables treadmilling of model filaments. MBio. 8:e00254-17. [DOI] [PMC free article] [PubMed]
- 24.Matsui T., Han X., Tanaka I. Structural change in FtsZ Induced by intermolecular interactions between bound GTP and the T7 loop. J. Biol. Chem. 2014;289:3501–3509. doi: 10.1074/jbc.M113.514901. [DOI] [PMC free article] [PubMed] [Google Scholar]; Matsui, T., X. Han, …, I. Tanaka. 2014. Structural change in FtsZ Induced by intermolecular interactions between bound GTP and the T7 loop. J. Biol. Chem. 289:3501-3509. [DOI] [PMC free article] [PubMed]
- 25.Nogales E., Wolf S.G., Downing K.H. Structure of the α β tubulin dimer by electron crystallography. Nature. 1998;391:199–203. doi: 10.1038/34465. [DOI] [PubMed] [Google Scholar]; Nogales, E., S. G. Wolf, and K. H. Downing. 1998. Structure of the α β tubulin dimer by electron crystallography. Nature. 391:199-203. [DOI] [PubMed]
- 26.Alushin G.M., Lander G.C., Nogales E. High-resolution microtubule structures reveal the structural transitions in αβ-tubulin upon GTP hydrolysis. Cell. 2014;157:1117–1129. doi: 10.1016/j.cell.2014.03.053. [DOI] [PMC free article] [PubMed] [Google Scholar]; Alushin, G. M., G. C. Lander, …, E. Nogales. 2014. High-resolution microtubule structures reveal the structural transitions in αβ-tubulin upon GTP hydrolysis. Cell. 157:1117-1129. [DOI] [PMC free article] [PubMed]
- 27.Ravelli R.B., Gigant B., Knossow M. Insight into tubulin regulation from a complex with colchicine and a stathmin-like domain. Nature. 2004;428:198–202. doi: 10.1038/nature02393. [DOI] [PubMed] [Google Scholar]; Ravelli, R. B., B. Gigant, …, M. Knossow. 2004. Insight into tubulin regulation from a complex with colchicine and a stathmin-like domain. Nature. 428:198-202. [DOI] [PubMed]
- 28.Nawrotek A., Knossow M., Gigant B. The determinants that govern microtubule assembly from the atomic structure of GTP-tubulin. J. Mol. Biol. 2011;412:35–42. doi: 10.1016/j.jmb.2011.07.029. [DOI] [PubMed] [Google Scholar]; Nawrotek, A., M. Knossow, and B. Gigant. 2011. The determinants that govern microtubule assembly from the atomic structure of GTP-tubulin. J. Mol. Biol. 412:35-42. [DOI] [PubMed]
- 29.Pecqueur L., Duellberg C., Knossow M. A designed ankyrin repeat protein selected to bind to tubulin caps the microtubule plus end. Proc. Natl. Acad. Sci. USA. 2012;109:12011–12016. doi: 10.1073/pnas.1204129109. [DOI] [PMC free article] [PubMed] [Google Scholar]; Pecqueur, L., C. Duellberg, …, M. Knossow. 2012. A designed ankyrin repeat protein selected to bind to tubulin caps the microtubule plus end. Proc. Natl. Acad. Sci. USA. 109:12011-12016. [DOI] [PMC free article] [PubMed]
- 30.Ayaz P., Ye X., Rice L.M. A TOG:αβ-tubulin complex structure reveals conformation-based mechanisms for a microtubule polymerase. Science. 2012;337:857–860. doi: 10.1126/science.1221698. [DOI] [PMC free article] [PubMed] [Google Scholar]; Ayaz, P., X. Ye, …, L. M. Rice. 2012. A TOG:αβ-tubulin complex structure reveals conformation-based mechanisms for a microtubule polymerase. Science. 337:857-860. [DOI] [PMC free article] [PubMed]
- 31.Elie-Caille C., Severin F., Hyman A.A. Straight GDP-tubulin protofilaments form in the presence of taxol. Curr. Biol. 2007;17:1765–1770. doi: 10.1016/j.cub.2007.08.063. [DOI] [PubMed] [Google Scholar]; Elie-Caille, C., F. Severin, …, A. A. Hyman. 2007. Straight GDP-tubulin protofilaments form in the presence of taxol. Curr. Biol. 17:1765-1770. [DOI] [PubMed]
- 32.Hamon L., Panda D., Pastré D. Mica surface promotes the assembly of cytoskeletal proteins. Langmuir. 2009;25:3331–3335. doi: 10.1021/la8035743. [DOI] [PubMed] [Google Scholar]; Hamon, L., D. Panda, …, D. Pastre. 2009. Mica surface promotes the assembly of cytoskeletal proteins. Langmuir. 25:3331-3335. [DOI] [PubMed]
- 33.Loose M., Mitchison T.J. The bacterial cell division proteins FtsA and FtsZ self-organize into dynamic cytoskeletal patterns. Nat. Cell Biol. 2014;16:38–46. doi: 10.1038/ncb2885. [DOI] [PMC free article] [PubMed] [Google Scholar]; Loose, M., and T. J. Mitchison. 2014. The bacterial cell division proteins FtsA and FtsZ self-organize into dynamic cytoskeletal patterns. Nat. Cell Biol. 16:38-46. [DOI] [PMC free article] [PubMed]
- 34.Ramirez-Diaz D.A., García-Soriano D.A., Schwille P. Treadmilling analysis reveals new insights into dynamic FtsZ ring architecture. PLoS Biol. 2018;16:e2004845. doi: 10.1371/journal.pbio.2004845. [DOI] [PMC free article] [PubMed] [Google Scholar]; Ramirez-Diaz, D. A., D. A. Garcia-Soriano, …, P. Schwille. 2018. Treadmilling analysis reveals new insights into dynamic FtsZ ring architecture. PLoS Biol. 16:e2004845. [DOI] [PMC free article] [PubMed]
- 35.Bisson-Filho A.W., Hsu Y.P., Garner E.C. Treadmilling by FtsZ filaments drives peptidoglycan synthesis and bacterial cell division. Science. 2017;355:739–743. doi: 10.1126/science.aak9973. [DOI] [PMC free article] [PubMed] [Google Scholar]; Bisson-Filho, A. W., Y. P. Hsu, …, E. C. Garner. 2017. Treadmilling by FtsZ filaments drives peptidoglycan synthesis and bacterial cell division. Science. 355:739-743. [DOI] [PMC free article] [PubMed]
- 36.Yang X., Lyu Z., Xiao J. GTPase activity-coupled treadmilling of the bacterial tubulin FtsZ organizes septal cell wall synthesis. Science. 2017;355:744–747. doi: 10.1126/science.aak9995. [DOI] [PMC free article] [PubMed] [Google Scholar]; Yang, X., Z. Lyu, …, J. Xiao. 2017. GTPase activity-coupled treadmilling of the bacterial tubulin FtsZ organizes septal cell wall synthesis. Science. 355:744-747. [DOI] [PMC free article] [PubMed]
- 37.Redick S.D., Stricker J., Erickson H.P. Mutants of FtsZ targeting the protofilament interface: effects on cell division and GTPase activity. J. Bacteriol. 2005;187:2727–2736. doi: 10.1128/JB.187.8.2727-2736.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]; Redick, S. D., J. Stricker, …, H. P. Erickson. 2005. Mutants of FtsZ targeting the protofilament interface: effects on cell division and GTPase activity. J. Bacteriol. 187:2727-2736. [DOI] [PMC free article] [PubMed]
- 38.Du S., Pichoff S., Lutkenhaus J. FtsZ filaments have the opposite kinetic polarity of microtubules. Proc. Natl. Acad. Sci. USA. 2018;115:10768–10773. doi: 10.1073/pnas.1811919115. [DOI] [PMC free article] [PubMed] [Google Scholar]; Du, S., S. Pichoff, …, J. Lutkenhaus. 2018. FtsZ filaments have the opposite kinetic polarity of microtubules. Proc. Natl. Acad. Sci. USA. 115:10768-10773. [DOI] [PMC free article] [PubMed]
- 39.Wegner A. Head to tail polymerization of actin. J. Mol. Biol. 1976;108:139–150. doi: 10.1016/s0022-2836(76)80100-3. [DOI] [PubMed] [Google Scholar]; Wegner, A. 1976. Head to tail polymerization of actin. J. Mol. Biol. 108:139-150. [DOI] [PubMed]
- 40.Duellberg C., Cade N.I., Surrey T. The size of the EB cap determines instantaneous microtubule stability. eLife. 2016;5:e13470. doi: 10.7554/eLife.13470. [DOI] [PMC free article] [PubMed] [Google Scholar]; Duellberg, C., N. I. Cade, …, T. Surrey. 2016. The size of the EB cap determines instantaneous microtubule stability. eLife. 5:e13470. [DOI] [PMC free article] [PubMed]
- 41.Fees C.P., Moore J.K. A unified model for microtubule rescue. Mol. Biol. Cell. 2019;30:753–765. doi: 10.1091/mbc.E18-08-0541. [DOI] [PMC free article] [PubMed] [Google Scholar]; Fees, C. P., and J. K. Moore. 2019. A unified model for microtubule rescue. Mol. Biol. Cell. 30:753-765. [DOI] [PMC free article] [PubMed]