Computational Tool to Study Perturbations in Muscle Regulation and Its Application to Heart Disease

Abstract

Striated muscle contraction occurs when myosin thick filaments bind to thin filaments in the sarcomere and generate pulling forces. This process is regulated by calcium, and it can be perturbed by pathological conditions (e.g., myopathies), physiological adaptations (e.g., β-adrenergic stimulation), and pharmacological interventions. Therefore, it is important to have a methodology to robustly determine the impact of these perturbations and statistically evaluate their effects. Here, we present an approach to measure the equilibrium constants that govern muscle activation, estimate uncertainty in these parameters, and statistically test the effects of perturbations. We provide a MATLAB-based computational tool for these analyses, along with easy-to-follow tutorials that make this approach accessible. The hypothesis testing and error estimation approaches described here are broadly applicable, and the provided tools work with other types of data, including cellular measurements. To demonstrate the utility of the approach, we apply it to elucidate the biophysical mechanism of a mutation that causes familial hypertrophic cardiomyopathy. This approach is generally useful for studying muscle diseases and therapeutic interventions that target muscle contraction.

Significance

Pioneering work by McKillop and Geeves described an elegant approach to determine the equilibrium constants governing muscle regulation; however, the approach lacked a mechanism for error analysis or statistical hypothesis testing. This limitation makes it difficult to rigorously determine the effects of perturbations in muscle regulation, such as disease. Here, we provide an approach to measure the equilibrium constants that govern muscle activation with increased resolution, estimate uncertainty in these parameters, and statistically test the effects of perturbations. We provide a MATLAB-based computational tool for these analyses, along with easy-to-follow tutorials that make this approach accessible. Our tool opens the door for quantitative comparisons of the effects of perturbations in muscle regulation, including studies of muscle diseases and therapeutic interventions.

Introduction

Force production in cardiac and skeletal muscle is tightly regulated to ensure that contraction occurs in a controlled and concerted manner. Dysfunction of this regulation can lead to a wide array of diseases, including cardiomyopathies, and there are currently several therapies in development that target this regulation (1, 2, 3). Given the role of perturbations of muscle regulation in health and disease, there is an outstanding need for tools that can resolve statistically significant changes in this regulation.

At the molecular scale, force production in muscle is powered by the molecular motor myosin, which contracts the sarcomere by pulling thin filaments (i.e., actin filaments decorated with tropomyosin and the troponin complex) toward the M-line of the sarcomere. The interaction between myosin and the thin filament is regulated in a calcium-dependent manner, in which calcium influx into the cytoplasm leads to activation of the thin filament and subsequent muscle contraction. In their landmark work, McKillop and Geeves (4) used a battery of biochemical and biophysical techniques to demonstrate that thin-filament activation is a multistep process, requiring contributions from calcium binding to troponin as well as actomyosin binding. Their model is known as the “three-state model” (Fig. 1). In the absence of calcium, tropomyosin is primarily in the blocked state, obscuring the myosin-binding site on the thin filament and inhibiting muscle contraction. Calcium binding to the troponin complex causes tropomyosin to shift to the closed state on the thin filament, exposing part of the myosin-binding site. Tropomyosin can either move spontaneously to the open position, where it permits myosin strong binding, or it can be pushed there by myosin binding. Myosin first binds weakly to the thin filament, then isomerizes to a strongly bound, force-generating state. The binding of one myosin to the thin filament pushes tropomyosin into the open position, exposing adjacent myosin-binding sites and leading to cooperative activation. The three states of tropomyosin positioning along the thin filament were subsequently confirmed using structural techniques (5).

Figure 1.

Schematic of the three-state model of muscle regulation. Red, yellow, and green represent the blocked, closed, and open states of tropomyosin, respectively. The equilibrium constants K_B and K_T describe transitions between states of tropomyosin on the thin filament, whereas K_W and K_S describe myosin binding. To see this figure in color, go online.

The three-state model provides a useful framework to understand the mechanism of perturbations in skeletal and cardiac thin-filament regulation, such as drug treatments (1, 6), protein isoform changes (7), disease-causing mutations (8), and post-translational modifications (9, 10). The formalism laid out by McKillop and Geeves enables the determination of the equilibrium constants that govern transitions between states and thus the population of thin-filament regulatory units in each state (Fig. 1). However, it has been challenging to precisely define the values of these equilibrium constants, in part because of the number of free parameters in the model. Furthermore, the original McKillop and Geeves approach did not provide a methodology for assessment of uncertainty in parameter values or hypothesis testing. Such a methodology is necessary for the rigorous assessment of the effects of perturbations.

Here, we have modified the approach of McKillop and Geeves to better resolve the effects of perturbations in tropomyosin positioning along the thin filament. We provide a MATLAB-based computational tool and a user guide that enables users to determine the equilibrium constants that govern thin-filament activation, estimate uncertainty in these parameters, and statistically test the effects of perturbations. We demonstrate the utility of our approach by applying it to investigate the biophysical mechanism of a mutation in troponin T, ΔE160, that causes familial hypertrophic cardiomyopathy (HCM) (11). This approach allows for the robust determination of differences between WT and mutant proteins, which is an important step toward developing novel therapies to treat HCM and other devastating muscle diseases.

Materials and Methods

Determination of equilibrium constants using the McKillop and Geeves analysis

In the classic McKillop and Geeves analysis, the values of the equilibrium constants that govern muscle activation (Fig. 1) were determined from biochemical measurements. K_B was calculated based on stopped-flow measurements of the rates of myosin binding to regulated thin filaments (RTFs) at low (pCa 9) and high (pCa 4) calcium (see Supporting Materials and Methods for details). K_W, K_T, and nH (i.e., the size of the cooperative unit) were calculated from titrations of pyrene-labeled RTFs with myosin performed at saturating calcium (pCa 3; cal) and in the absence of calcium (2 mM EGTA; nocal) (see Supporting Materials and Methods for details). The relationship between the fraction of myosin-bound subunits, f([m]), and the fractional change in pyrene fluorescence upon myosin binding is given by the following equation (4):

$$\text{f}\left(\left[\text{m}\right]\right)=\frac{{\mathit{F}}_0-\mathit{F}}{{\mathit{F}}_0-{\mathit{F}}_{\infty }}=\frac{{\mathit{K}}_{\text{W}}\left[\text{m}\right]{\mathit{P}}^{\left(\text{nH}-1\right)}\left({\mathit{K}}_{\text{T}}{\left(1+{\mathit{K}}_{\text{S}}\right)}^{\left(\text{nH}\right)}+1\right)}{\left({\mathit{K}}_{\text{T}}{\mathit{P}}^{\left(\text{nH}\right)}+{\mathit{Q}}^{\left(\text{nH}\right)}+\frac{1}{{\mathit{K}}_{\text{B}}}\right){\left(1+{\mathit{K}}_{\text{S}}\right)}^{\left(\text{nH}-1\right)}},$$ (1)

where F is the measured pyrene fluorescence; F₀ and F_∞ are the pyrene fluorescence in the absence of myosin and at saturating myosin, respectively; [m] is the concentration of myosin; P = 1 + [m] × K_W(1 + K_S); and Q = 1 + [m] × K_W. K_B at high calcium and K_S were set to 20 and 18, respectively, based on (4). nH, K_W, and K_T were determined in the presence and absence of calcium by fitting each titration curve independently.

Modified fitting approach

To improve the resolution of the parameters extracted from fitting of the data, we modified the classic McKillop and Geeves approach:

• 1)For the calculations of K_T, K_W, and nH using steady-state fluorescence titrations, McKillop and Geeves examined two calcium concentrations (pCa 3 and 2 mM EGTA). Here, we perform an additional steady-state fluorescence titration at an intermediate calcium concentration (pCa 6.25; midcal) to improve our ability to resolve these parameters.
• 2)The data for curves collected at three different calcium concentrations are globally fitted using least-squares optimization, and the parameters that minimize the aggregate error in all three data sets are determined. In global fitting, individual parameters can be shared between data sets, reducing the number of free variables and increasing the power to precisely measure parameter values. Here, K_W and nH are shared parameters among all three curves; however, this approach does not require sharing these parameters. K_T depends on calcium, and thus three distinct K_T values (K_T-nocal, K_T-midcal, K_T-cal) are determined using this approach, one for each of the calcium concentrations used in the titrations (2 mM EGTA, pCa 6.25, and pCa 3, respectively).
• 3)We use a simulated annealing algorithm (simulannealbnd, included in the Global Optimization Toolbox of MATLAB (MathWorks, Natick, MA)) in our fitting procedure to avoid biasing the fit toward the initial guesses used in the fitting. The annealing routine ensures that the best-fit parameters are obtained from a global rather than local minimum.

Hypothesis testing and statistics

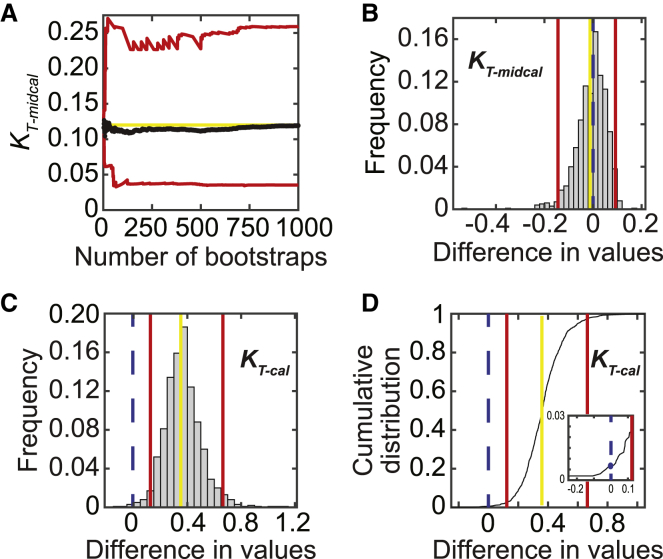
One limitation of the original formulation of the three-state model is that it lacks procedures for calculating uncertainties and statistical hypothesis testing. Here, we use the well-established technique of bootstrapping to calculate 95% confidence intervals (12, 13) for the parameter values determined by fitting Eq. 1 to the fluorescence titration data (see Fig. 4, B–D). This data set consists of the titration data collected at three calcium concentrations: 2 mM EGTA (nocal), pCa 6.25 (midcal), and pCa 3 (cal). In the bootstrapping method, the original data set is randomly resampled to generate synthetic data sets, each containing the same number of points as the original data set. Each synthetic data set is then fit to determine the best-fit values of the parameters for that data set. 95% confidence intervals are defined as the interval over which 95% of the simulated parameter values are found. Note that the number of bootstrapping simulations required will depend on the noise in the data as well as the number of sampled points. As such, one should empirically determine the number of simulations required for stable convergence of the confidence intervals. We find that for the experiments described here, 1000 rounds of bootstrapping simulations are sufficient (Fig. 2 A).

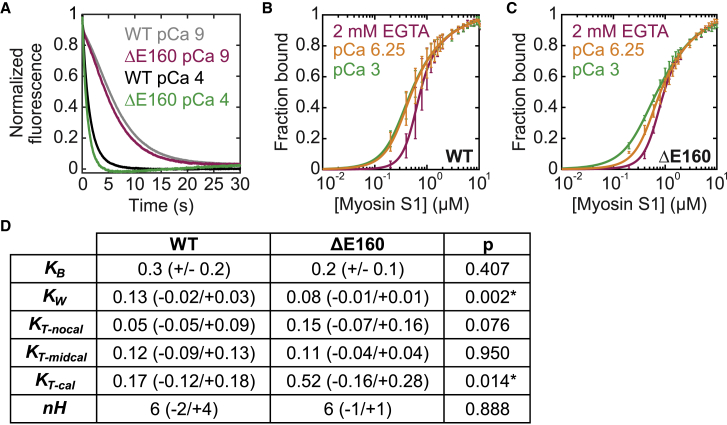
Figure 4.

Effects of the ΔE160 mutation in troponin T on thin-filament regulation. (A) Normalized stopped-flow fluorescence traces of myosin binding to RTFs. The pyrene fluorescence is quenched at a higher rate at high calcium (pCa 4, green/black) than at low calcium (pCa 9, magenta/gray). The traces for WT (black/gray; average of n = 6 curves each) and the ΔE160 mutant (magenta/green; average of n = 4 curves each) are similar at each calcium concentration. (B and C) Steady-state titrations of RTFs with myosin for the WT (B) or mutant (C) protein conducted at three distinct calcium concentrations: pCa 3 (cal, green), pCa 6.25 (midcal, orange), and 2 mM EGTA (nocal, magenta). Curves are fits to the data. Error bars show the SD of five technical replicates. (D) A table of parameter values obtained for WT and ΔE160 troponin complexes from stopped-flow measurements (for K_B) and using the computational tool (for all others) is given. Values in parentheses indicate the SD of six (WT) or four (ΔE160) replicates for K_B and 95% confidence intervals determined using the computational tool for all other parameters. Asterisks indicate statistical significance at the 95% confidence level. To see this figure in color, go online.

Figure 2.

Hypothesis testing. (A) Values of the average (black) and upper and lower bounds of the 95% confidence interval (red) for K_T-midcal for WT troponin are shown as a function of the number of bootstraps performed during error estimation. The yellow line marks the measured best-fit value. (B and C) Histograms of the test statistic (i.e., the difference in values between parameters determined for WT and ΔE160) for K_T-midcal (B) and K_T-cal (C) are given. Vertical lines represent the measured difference in values (yellow), the bounds of the 95% confidence interval (red), and the null hypothesis (blue dashed). The difference in parameter values is statistically significant at the 95% confidence level if the null hypothesis falls outside the 95% confidence interval, as in (C). (D) Cumulative distribution of the difference in values between WT and ΔE160 calculated from the bootstrapping simulations for K_T-cal is shown. Vertical lines are the same as in (C). Inset highlights the determination of the p-value from the value of the cumulative distribution at x = 0. This value is multiplied by two to make the test equivalent to a two-tailed test. To see this figure in color, go online.

For statistical hypothesis testing, we define a test statistic as the difference between parameter values in the perturbed and unperturbed systems (14). For example, to determine whether there is a statistically significant difference in the value of K_W for a mutant protein relative to the wild type (WT), the test statistic is H = K_W(WT) − K_W(mutant). The value of the test statistic is calculated for the real data and for pairs of K_W values drawn from the bootstrapping simulations of the data. The interval within which 95% of the test statistic values from the bootstrapped simulations fall is defined as the 95% confidence interval. If the null hypothesis (i.e., H₀ = 0) is not contained within the 95% confidence interval, then the null hypothesis is rejected, and K_W(WT) ≠ K_W(mutant) with a p-value < 0.05 (Fig. 2, B and C). The p-value can be calculated from a cumulative distribution of the test statistic by finding the largest interval that does not contain the null hypothesis (Fig. 2 D). This value is multiplied by two to make the test equivalent to a two-tailed test.

Results and Discussion

Here, we present a methodology and MATLAB-based computational tool for analyzing biochemical measurements of thin-filament positioning. This procedure builds on the formalism developed by McKillop and Geeves (4), extending it to allow for improved precision of parameter values, estimations of uncertainties, and statistical hypothesis testing. The basic workflow for the analysis follows:

• 1)Measure the value of the equilibrium constant between the blocked and closed states of the thin filament, K_B, using a stopped-flow kinetic technique (see Supporting Materials and Methods).
• 2)Perform steady-state fluorescence titrations measuring myosin binding to RTFs (see Supporting Materials and Methods). The titrations should be carried out at three separate calcium concentrations (i.e., low (nocal), high (cal), and intermediate (midcal) calcium concentrations). These data will be used in step 4 to determine the following parameters: K_T (the equilibrium constant between the closed and open states of the thin filament) at each calcium concentration, K_W (the equilibrium constant describing weak myosin binding), and nH (the size of the cooperative unit).
• 3)Use the provided script (Script_normalization_replicate.m) to normalize the data from each technical replicate (typically three curves: nocal, midcal, cal) before pooling the data.
• 4)Use the provided script (Script_global_fitting.m) to globally fit the pooled titration data set to determine the best-fit values and calculate confidence intervals from bootstrapping simulations for each parameter (K_T-nocal, K_T-midcal, K_T-cal, K_W, nH).
• 5)For a given perturbation, statistically test for differences between individual parameters obtained from the fitting using the provided script (Script_hypothesis_testing.m).

A detailed user guide describing how to perform each of these steps, along with the data used to generate the figures in this manuscript, is provided with the computational tool.

Results obtained using the traditional fitting procedure and the estimation of uncertainties

The individual equilibrium constants that define the positioning of cardiac tropomyosin along the thin filament were determined using tissue-purified porcine cardiac myosin and actin and recombinant human troponin and tropomyosin (see Supporting Materials and Methods). The equilibrium constant for the transition between the blocked and closed states, K_B, was determined by performing stopped-flow kinetic measurements. We measured K_B = 0.3 ± 0.2, in agreement with the previously determined value (4, 15). Although there is some variance between technical replicates for K_B, the values of parameters obtained from fitting of the titration data are relatively insensitive to small changes in the value of K_B.

The equilibrium constants for the transition between the closed and open states, K_T, and for myosin weak binding, K_W, were determined by performing titrations of RTFs with myosin at high (pCa 3) and low (2 mM EGTA) calcium. The titration curves were fit independently by Eq. 1 (4). To ensure that the fitting was not biased by the initial guesses of parameter values, we modified the fitting procedure described in (4) to incorporate an annealing routine that iteratively fits the data with altered initial guesses. The values obtained from these fits are shown in Fig. 3 A, and they are consistent with values obtained previously with skeletal and cardiac muscle proteins (15, 16, 17). The original formulation of the McKillop and Geeves model did not include a methodology for determining uncertainty in fitted parameters. We developed a procedure to calculate 95% confidence intervals via bootstrapping of the original data set (12, 13), and we applied this procedure to calculate the confidence intervals of the parameters calculated using the classic approach. With this procedure, we saw that the classic approach gave considerable uncertainty in the values of the fitted parameters. For example, for the data collected at low calcium, we obtained uncertainties much larger than the measured parameters for both K_W (0.13 (−0.03/+1.26)) and nH (6 (−2/+6)).

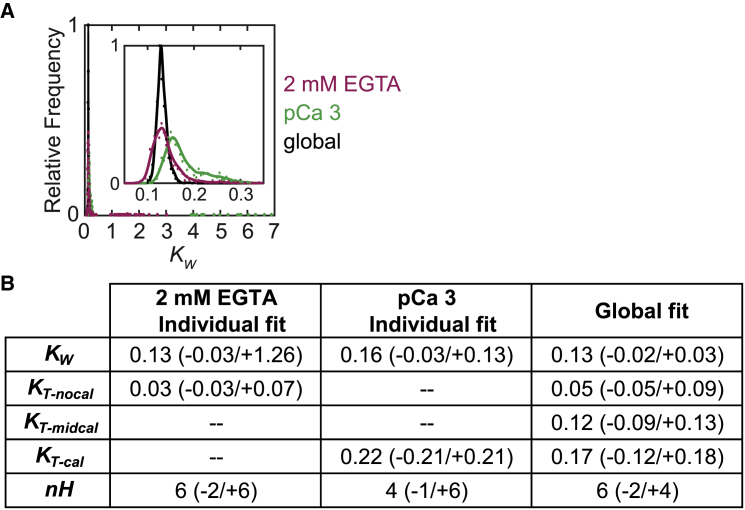
Figure 3.

Traditional versus global fitting of the three-state model to fluorescence titration data. (A) Histograms showing the frequency of K_W values determined from 1000 bootstrapping simulations are given. Points are the values from the global fitting (black) and from the individual fits of data collected at 2 mM EGTA (magenta) and pCa 3 (green). Lines are inserted to guide the eye. The inset shows the distributions near the mean values of K_W. These data demonstrate that global fitting reduces the uncertainty in the measurement. (B) A table of parameter values obtained from individual fits of data collected at 2 mM EGTA (nocal) or pCa 3 (cal) compared to those obtained from our global fitting method, which includes pCa 6.25 (midcal), is given. Values in parentheses indicate the 95% confidence intervals. To see this figure in color, go online.

Global fitting improves the resolution of fitted parameters

To improve the resolution of parameters derived from the fitting of the data, we adopted two modifications from the traditional approach. First, we performed an additional titration at pCa 6.25 (midcal). The inclusion of an additional titration curve at an intermediate calcium concentration is advantageous because some perturbations shift the calcium sensitivity at intermediate concentrations but not under fully activating or deactivating conditions (18). Second, titration curves collected at the three different calcium concentrations were fitted globally rather than individually. In the global fitting, the values of K_W, K_S, and nH were shared between the fits of all curves. Global fitting of the three curves (Fig. 3 A) yielded tighter 95% confidence intervals for both K_W and nH (Fig. 3). The confidence interval for K_W was 0.13 (−0.02/+0.03), compared to 0.13 (−0.03/+1.26) for the individually fitted curve at low calcium. Similarly, the confidence interval for nH for the individually fitted data was 6 (−2/+6), whereas the confidence interval for the globally fitted data was 6 (−2/+4). These data demonstrate the improved resolution of this approach.

Hypothesis testing and its application to determining the biochemical mechanism of a mutation that causes HCM

To demonstrate the utility of our approach for resolving the effects of molecular-based changes in cardiac thin-filament regulation, we examined a point mutation that causes familial HCM, ΔE160 in troponin T (11). Clinical studies have shown that this mutation causes pronounced ventricular hypertrophy and sudden cardiac death, with half of the patients not surviving past age 40 (11). Previous studies of the ΔE160 mutation in muscle fibers (19, 20), transfected myotubes (21), and purified proteins (22) have shown that the ΔE160 mutation causes increased activation of contractility. However, the biochemical mechanism of this activation is not well understood.

We applied our methodology to determine which transitions involved in thin-filament regulation (Fig. 1) are affected by the ΔE160 mutation. The goal of this analysis is not an exhaustive characterization of the mutant; rather, it is to demonstrate the utility of this approach for statistically assessing the effects of perturbations on thin-filament regulation. From stopped-flow kinetic measurements (Fig. 4 A), we obtained a K_B of 0.2 ± 0.1 for ΔE160, which is indistinguishable from the value obtained for WT troponin (0.3 ± 0.2; p = 0.41). We also performed fluorescence titrations (Fig. 4, B and C) to measure steady-state actomyosin binding and determine K_W, K_T, and nH. We used the computational tool to calculate parameter values and their corresponding uncertainties from global fitting of the titration curves (Fig. 4 D).

To determine whether there are statistically significant differences between the parameters for WT troponin and the ΔE160 mutant, we applied the hypothesis testing methodology described in the Materials and Methods. We found that the mutant showed a threefold increase in K_T at high calcium (0.17 (−0.12/+0.18) for WT vs. 0.52 (−0.16/+0.28) for ΔE160; p = 0.014). This threefold increase in K_T would result in an increased population of force-generating cross bridges at high calcium. We also found a slight but statistically significant decrease in K_W (0.13 (−0.02/+0.03) for WT vs. 0.08 (−0.01/+0.01) for ΔE160; p = 0.002). We saw that at low calcium, K_T was threefold larger for the mutant (p = 0.076); however, this difference was not significant at the 95% confidence level. We did not detect statistically significant differences in the values of nH (p = 0.89), K_B (p = 0.41), or K_T-midcal (p = 0.95). The net effect of these changes would be to increase activation, which is consistent with the hypercontractility associated with HCM. Taken together, these data demonstrate the power of this approach for hypothesis testing and for determining the biochemical mechanism of perturbations of thin-filament regulation. Moreover, determination of the specific steps of thin-filament activation affected by a perturbation provides a useful framework for interpreting results obtained from complementary methods (e.g., structural biology, muscle fiber mechanics), enhancing our understanding of muscle physiology and disease.

Relationship to other models of thin-filament regulation

Our method is based on the McKillop and Geeves approach, which significantly advanced our understanding of thin-filament regulation. The goal of this work is not to distinguish between this and other proposed models (23, 24); rather, it is to provide an improved framework for interpreting results obtained using the McKillop and Geeves formalism. In recent years, there have been additional modeling efforts to better refine the McKillop and Geeves model (25, 26, 27, 28, 29) and to extend its applicability to larger systems with more states. These efforts have enhanced our understanding of muscle contraction and have led to the development of systems that can recapitulate many of the salient features of muscle contraction in silico (28). However, these models are also significantly more complicated than the McKillop and Geeves model. The ability to assess the effect of perturbations on thin-filament regulation using the relatively simple three-state model is a major advantage of the approach and computational tool presented here.

Application of the hypothesis testing and uncertainty estimation to other systems

The computational tool for hypothesis testing and confidence interval estimation from bootstrapping simulations is not limited to analysis of fluorescence titrations but can be broadly applied to other data sets as well. We have supplied a standalone version of this section of the code for examining the mean and median values (i.e., data frequently used for single-cell measurements) so that others can apply it to their experimental system. This methodology is useful for data sets for which the form of the underlying distribution is either unknown or not normal, such as single-molecule data (30) and single-cell studies, as demonstrated in (18).

Conclusion

Here, we have demonstrated a method for extending the utility of the McKillop and Geeves (4) approach to understanding thin-filament regulation, and we have provided a well-documented, accessible computational tool to implement this methodology. Our approach extends the McKillop and Geeves approach to include a method for calculating confidence intervals and performing statistical tests. This methodology allowed us to resolve the molecular effects of a mutation that causes hypertrophic cardiomyopathy. This tool should be useful for studying physiological and pathological changes in muscle, as well as for testing new therapies that target muscle regulation.

The computational tool can be downloaded from GitHub at https://github.com/GreenbergLab/Thin_Filament_Fitting. The computational tool consists of a series of scripts that are executable in MATLAB. The software is compatible with at least versions of MATLAB 2017b to 2019a. Where we are aware of potential compatibility issues with previous versions of MATLAB, we provide suggestions for resolving these issues in the scripts. The scripts require the following MATLAB toolboxes: Optimization, Global Optimization, Statistics and Machine Learning. The Parallel Computing toolbox is recommended for the purposes of decreasing the time required to perform the fitting, but it is not strictly required to run the scripts. We also provide an in-depth user guide, along with the raw data used in the examples presented here. The MATLAB code is provided as an appendix to the user guide for users wanting to adapt the code to a different language.

Author Contributions

S.K.B. performed and analyzed the fluorescence experiments and developed code. S.R.C. helped with the early development and testing of the MATLAB code. L.G. generated mutant protein. M.J.G. oversaw the project and developed the early code for analyzing data. S.K.B. and M.J.G. wrote the first draft of the manuscript. All authors contributed to the final draft.

Editor: David Warshaw.

Supporting Citations

References (31, 32, 33, 34, 35, 36, 37) appear in the Supporting Material.