Nucleosome Crowding in Chromatin Slows the Diffusion but Can Promote Target Search of Proteins

Abstract

Dynamics of nuclear proteins in crowded chromatin has only been poorly understood. Here, we address the diffusion, target search, and structural dynamics of three proteins in a model chromatin using coarse-grained molecular simulations run on the K computer. We prepared two structures of chromatin made of 20 nucleosomes with different nucleosome densities and investigated dynamics of two transcription factors, HMGB1 and p53, and one signaling protein, ERK, embedded in the chromatin. We found fast and normal diffusion of the nuclear proteins in the low-density chromatins and slow and subdiffusional movements in the high-density chromatin. The diffusion of the largest transcription factor, p53, is slowed by high-density chromatin most markedly. The on rates and off rates for DNA binding are increased and decreased, respectively, in the high-density chromatin. To our surprise, the DNA sequence search was faster in chromatin with high nucleosome density, though the diffusion is slower. We also found that the three nuclear proteins preferred to bind on the linker DNA and the entry and exit regions of nucleosomal DNA. In addition to these regions, HMGB1 and p53 also bound to the dyad.

Significance

Chromatin is a highly crowded molecular environment, in which DNA-binding proteins, such as transcription factors, need to search for their recognition sequence from genomic DNA. This is apparently a formidable task for proteins. Thus, how nuclear proteins can move in crowded chromatin and search DNA sequence is an interesting question, but not much is known at molecular level. The study addresses this issue by coarse-grained molecular dynamics simulations. We investigated diffusional motions and target DNA search dynamics of nuclear proteins in small chromatin environment. To our surprise, we found that the crowded nucleosome environment slows the diffusional motion of proteins but can speed up the target search process.

Introduction

Chromatin accessibility regulates transcriptional activity in eukaryotic cells (1, 2). Often, chromatin accessibility is characterized at a genomic scale by DNase assays (3). However, these assays do not directly measure chromatin structures or diffusional dynamics of nuclear proteins. Recently, the diffusional dynamics of EGFPs and transcription factors (TFs) in interphase nuclei and mitotic chromosomes were observed via fluorescence correlation spectroscopy and live-cell imaging approaches (4) together with Monte Carlo simulation, elucidating the fluctuation of individual nucleosomes that enhances chromatin accessibility for TFs (5, 6). In these studies, both experiments and simulations have limited spatial resolutions, which precludes the precise characterization of the nuclear protein movements. For example, in the Monte Carlo simulation, nucleosomes and TFs were treated as hard spheres without intramolecular flexibility. The purpose of this study is to address the diffusional and the target search dynamics of nuclear proteins in chromatin using molecular dynamics (MD) simulations with intramolecular flexibility.

To investigate the dynamics of proteins in chromatin, we need chromatin models with a suitably large number of nucleosomes. Using modern supercomputers, we can perform MD simulations of increasingly large systems, such as an entire cytoplasm, with all of the 103 million atoms explicitly treated (7). However, the time that can be simulated is highly limited and not enough for the TFs and chromatin components containing disordered segments with long equilibration time. To overcome this issue, we performed coarse-grained MD simulations without explicitly treating all the atoms. Many coarse-grained MD simulations of chromatin have been performed using coarse-grained models with different resolutions (8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31).

In this study, we used coarse-grained models in CafeMol (32, 33), in which one particle represents each amino acid in proteins, whereas three particles represent sugar, phosphate, and base units of each nucleotide in DNA (32, 33). Using these models, one can approximate physicochemical interactions accurately in the flexible molecules and simulate long timescale dynamics within reasonable computation time. For proteins, we used the AICG2 + model, which incorporates interactions between atoms in the native structure into energy functions of the coarse-grained model (34). DNA was modeled by the 3SPN.1 model (19). This combination of coarse-grained models has been used for several protein-DNA complexes, including p53 dynamics along double-stranded DNA (22, 35), DNA unwrapping from the nucleosome (20), trinucleosome folding (23), and DnaA oligomerization in the bacterial DNA replication initiation complex (25). Notably, even with the coarse-grained model, the simulation of the protein dynamics in chromatin is challenging. In this study, using the K computer—a massively parallelized supercomputer—we simulated nuclear protein dynamics in chromatin that contains 20 nucleosomes (molecular weight ∼3199 kDa). The K computer involves more than 80,000 nodes and achieved over 10 peta-FLOPS in LINPACK benchmark in 2012, at which it was the top record (36). CafeMol is implemented with single instruction, multiple data to optimize for the K computer. By using CafeMol, the users can easily perform coarse-grained simulations of proteins and nucleic acids without detailed knowledge of models or coding.

In this work, we focus on the dynamics of three nuclear proteins: 1) a signaling protein ERK as an example of a non-TF; 2) a smaller TF, HMGB1; and 3) a larger TF, homotetrameric p53. Recent chromatin electron microscopy tomography (chromEMT) data elucidated that chromatin does not have a regular 30-nm fiber but takes an irregular folding structure (37), as was anticipated before (38, 39). As a model chromatin environment, simulating a 20-nucleosome array, we constructed irregular folding structures that mimic the chromEMT image. Simulating three nuclear proteins in the model chromatin environment, we found that the diffusion of the largest TF, p53, is slowed by high-density nucleosomes in a most dramatic way, but the DNA sequence search of it is faster.

Materials and Methods

Three nuclear proteins studied

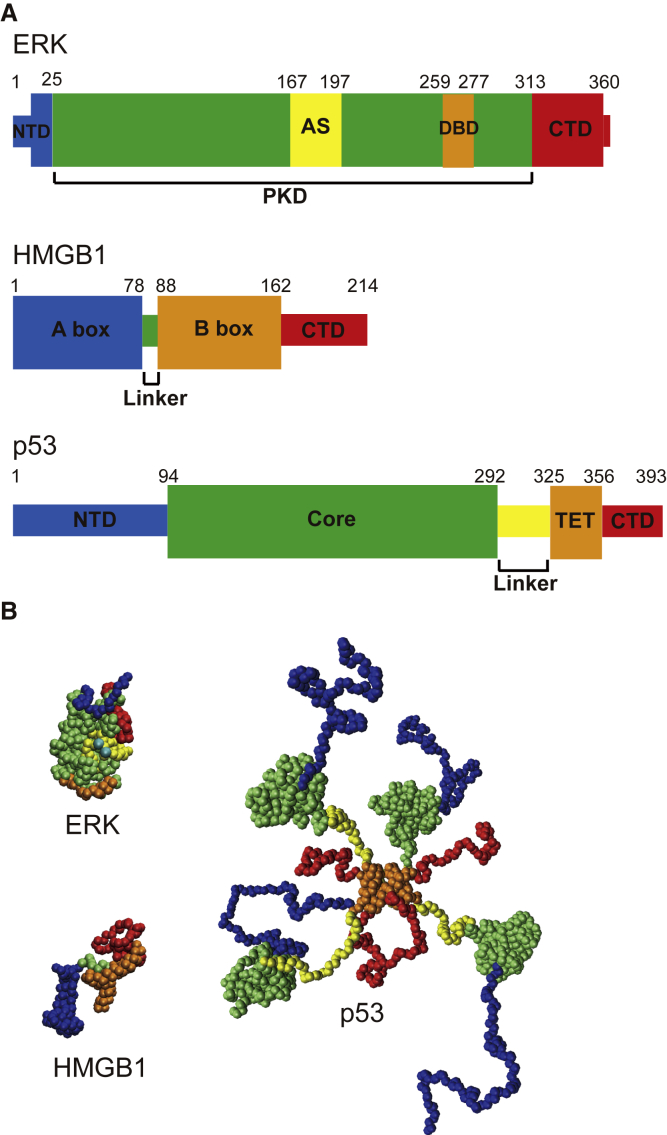
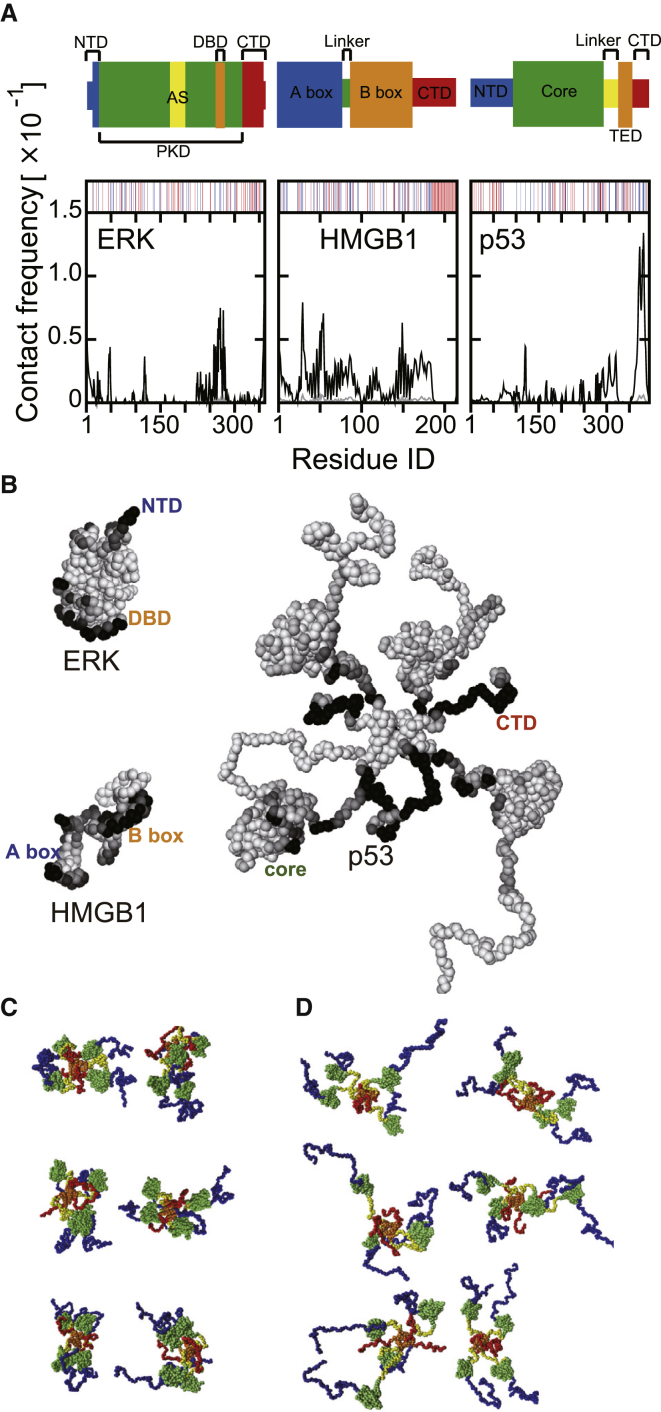
The domain maps and the molecular structures of our target TFs are shown in Fig. 1. The signaling protein ERK (Fig. 1 A: top, B: left-top) is a globular protein composed of three domains: NTD (N-terminal domain), PKD (protein kinase domain), and CTD (C-terminal domain) (40). PKD is the enzymatic domain containing the activation segment (AS) in which THR185 and TYR187 are phosphorylated by MEK protein (40). The phosphorylation of ASs makes ERK active. Then, the activated ERK moves into the nucleus and phosphorylate the downstream TFs such as c-Fos and Elk-1 (40). In our simulation, the charges for THR185 and TYR187 are set to −2, mimicking the activated state. Although, in this study, ERK is merely an example of non-TF proteins, the recent experiment (41) suggested that PKD in ERK has DNA-binding domains (DBDs): residues 259–277.

Figure 1.

The three nuclear proteins studied, ERK, HMGB1, and p53. (A) The domain compositions are shown. The thick bands stand for globular domains, and the thin bands correspond to linker and/or intrinsically disordered regions. (B) Snapshots of nuclear proteins sampled by coarse-grained simulations are given. Note that p53 is a homotetramer. The colors in the snapshots correspond to the colors in (A). Three snapshots are drawn with the same scales. NTD, N-terminal domain; CTD, C-terminal domain; PKD, protein kinase domain; AS, activation segment; DBD, DNA-binding domain; TET, tetramerization domain. To see this figure in color, go online.

HMGB1 (Fig. 1 A: middle, Fig. 1 B: left-bottom) is an example of a small TF. It contains 214 amino acids. In HMGB1, two structured domains—the A-box and B-box, which are responsible for DNA-binding—are connected by a flexible linker. Also, it has a disordered NTD that includes an acidic tail (42).

p53 (Fig. 1 A: bottom, Fig. 1 B: right) is a famous tumor suppressor that normally forms a homo-tetramer in living cells (43). p53 is the largest (1572 amino acids as the homotetramer) in our targets. Each monomer of p53 consists of four domains: NTD, core domain, tetramerization domain (TET), and CTD (44). Because the folded domains, core and TET, are connected by the intrinsically disordered regions, the entire p53 molecule stochastically takes various conformations (45). The core domain of p53 is responsible for specific DNA binding (46, 47), whereas CTD is responsible for nonspecific DNA-binding (48).

Model chromatin

The model chromatin system contains 20 nucleosomes connected by linker DNA strands of 20 basepairs. Each nucleosome is that from Xenopus laevis, of which the crystal structure is taken from the Protein Data Bank (PDB) entry of 1KX5. Each nucleosome is flanked by 10-basepair linker DNA: 5′-ACTTACATGC-[nucleosomal DNA]-ACTTACATGC-3′. This linker DNA length and sequence are from that in the tetranucleosome crystal structure (49). Twenty copies of this fragment are tandemly connected to form the 20-nucleosome array.

Coarse-grained models and energy functions

We used CafeMol and applied a coarse-grained model to investigate the dynamical behavior of the nuclear proteins in these nucleosomes. For proteins, each amino acid is represented by one bead, whereas each nucleotide in DNA is approximated by three beads, each representing sugar, phosphate, and base. Within each nucleosome, the globular part of histone octamers and nucleosomal DNA maintain their native interactions via the native-structure-based potential as in (20) (see Supporting Materials and Methods for more details). Interactions within globular proteins are residue-dependent and are mapped from atomic interactions in the reference nucleosome structure. Histone tails are treated as flexible polymers with sequence-based statistical potential for bond and torsion angles (50). The DNA model includes sequence-dependent basepair interactions, but the sequence dependence of the bending rigidity is not fine-tuned (19). The sum of electrostatic and excluded volume interactions approximated the other protein-DNA and protein-protein interactions. The electrostatic interactions for charged pairs take the Debye-Huckel formula with an ion strength of 0.21 M as in (22, 35). We assign +1e for ARG and LYS, −1e for GLU, ASP, and the phosphate in DNA, and −2e for the phosphorylated residues THR185 and TYR187 in the activation segment of ERK. For the acetylated LYS residues in p53, we set their charges to 0. In the excluded volume term, we used the radius parameter σ = 5.5 Å. Other main parameters were kept as the CafeMol 2.2 default values.

The reference structures for the globular domains of ERK, HMGB1, p53 core domain, and p53 TED were taken from PDB entries 2GPH, 2YRQ, 2XWR, and 1AIE, respectively. (See Supporting Materials and Methods for how to get full-length initial structures of HMBG1 and p53 tetramer.) For nucleosomes, we used 1KX5 as the reference structure.

Construction of the chromatin models and initial placement of nuclear proteins

Recent experiments clarified that chromatin does not form regular 30-nm-fiber structures but folds into irregular structures (37, 39). Here, we tried to model such irregular chromatin structures. First, we prepared a two-start helix configuration, one model of the 30-nm-fiber structure, by repeatedly connecting the first two nucleosome structures of the tetranucleosome (PDB: 1ZBB). Then, by biasing the radius of gyration of the two-start helix configuration, we conducted an expansion-and-shrink simulation. In this simulation, we alternately added the following biasing potential,

$$\pm k_{\mathrm{g}}{R}_{\mathrm{g}}^{\mathrm{Chro}},$$ (1)

where $R_{\mathrm{g}}^{\mathrm{Chro}}\left(t\right)$ is the radius of gyration of the chromatin system. Negative- and positive-signed potentials with k_g = 100 are alternately applied to the system 19 times to expand and shrink the model chromatin, respectively. Then, we applied the negative-signed potential to the chromatin once more to obtain an expanded structure. The time course and the snapshots of this simulation are depicted in Fig. S1. During the repeated expansion and shrink, the chromatin gradually lost the regular two-start helix configuration.

To investigate the dynamics of nuclear proteins in chromatin, we need to place the nuclear proteins inside chromatin. For this purpose, we put p53 near the COM of the chromatin in the most expanded structure after the expansion-and-shrink simulation. Subsequently, we slowly decreased the radius of gyration of the chromatin with a smaller positive potential (k_g = 10) for 5 × 10⁶ time steps, leading to the structures in which p53 is embedded into the chromatin with various nucleosome density. We used them as the initial structure of the p53 simulations. For the other targets, p53 in these structures was replaced with HMGB1 and ERK, respectively. By replacement, there could be some additional space. However, we found that contacts between the replaced proteins and DNAs are immediately recovered so that this replacement would not affect the subsequent simulations.

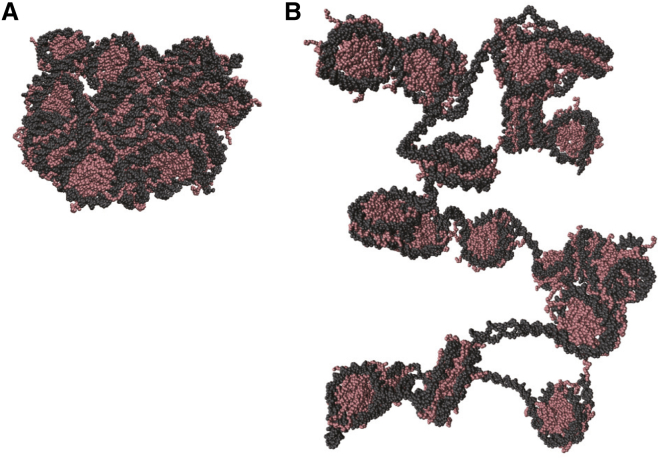
The nucleosome density in chromatin depends on genomic loci, phases of the cell cycle, and other regulatory factors. As chromatin models, we put 20 nucleosomes into the model with two distinct densities. For the high-density (nucleosome density ∼0.5 mM) structure, we set the maximal radius of the chromatin, R_max, to 261 Å based on the assumption that 20 nucleosomes uniformly distribute. This density roughly corresponds to that in compact clusters in the mitotic chromosome and likely corresponds to interphase heterochromatin (5). For the low-density (0.1 mM) structure, we set R_max to 458 Å. We chose 0.1 mM as a low density because this has been used in previous work (5). A rough estimate of the percentage occupied volumes for high and low densities is 10 and 2%, respectively. From the p53-embedded slow-shrink simulation, we picked up the structures with the target densities (Fig. 2).

Figure 2.

Two chromatin states used as an environment. Snapshots of the 20-nucleosome array in the high-density (A) and the low-density (B) chromatin environments are given. The DNA and the histone proteins are in gray and pink, respectively. (A) The high-density state with [nucleosome] ∼0.5 mM and (B) the low-density state with [nucleosome] ∼0.1 mM are shown. To see this figure in color, go online.

Time evolution by coarse-grained simulations

Here, we focus on the dynamics of three nuclear proteins, ERK, HMGB1, and p53, in chromatin with the high- and low-density nucleosomes. For each of these six setups, we conducted 20 Langevin dynamics simulations for 3 × 10⁷ time steps at a temperature of 300 K. We used a low friction coefficient value of 0.02 in CafeMol unit as in previous works (20). Our rough mapping in timescale suggests that one MD step corresponds to ∼1 ps (33). Thus, the duration of each trajectory is ∼30 μs. To prevent the change of nucleosome density, the harmonic potential (the spring constant is set to 500 kcal/mol Ų) restrained the center of mass (COM) of each nucleosome to its initial position, though this does nothing until the COM deviates ≥30 Å away from the initial position. Assumed here is that the added nuclear proteins would not change the overall topology or the nucleosome density of the chromatin.

Results

Dynamics of nuclear proteins in chromatin

First, we address the diffusional dynamics of nuclear proteins in the model chromatin environments. We used three nuclear proteins: a signaling protein ERK, a small TF HMGB1, and a larger TF p53. As the chromatin environments, we prepared the two states with distinct densities; the high-density state (Fig. 2 A) and the low-density state (Fig. 2 B) as described above. We embedded each of the three nuclear proteins near the COM of the two model chromatins (leftmost cartoons in Fig. 3, B–G), resulting in the six setups. For each of the six setups, we conducted 20 independent simulations with different stochastic forces.

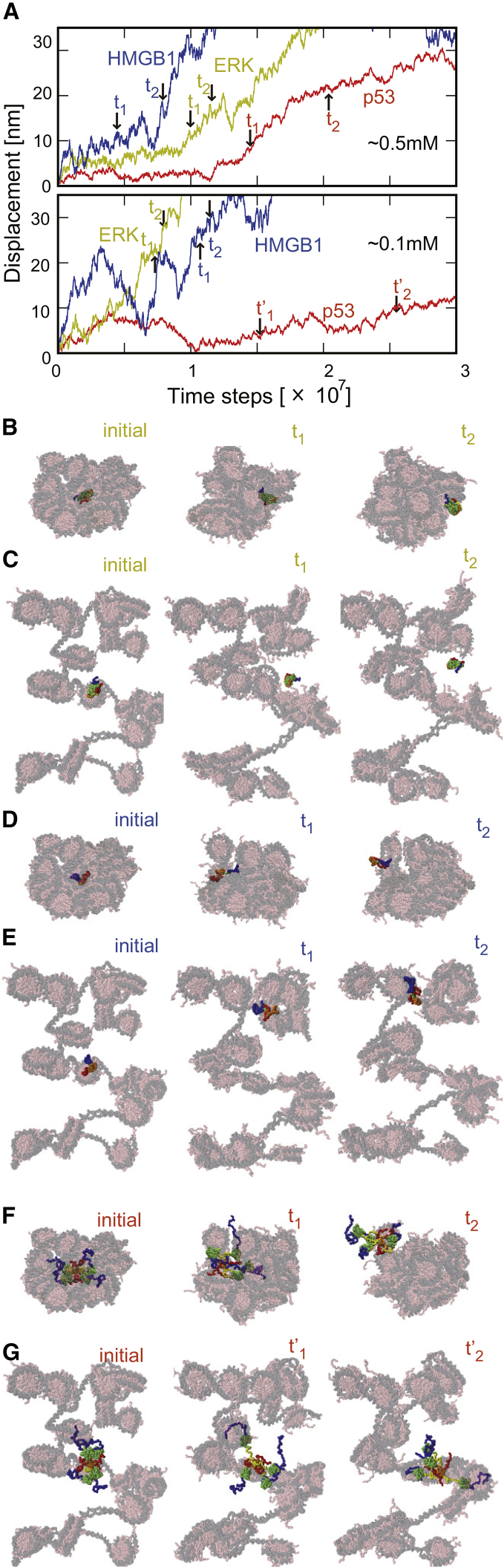
Figure 3.

Movements of nuclear proteins in chromatin environments. (A) Representative time courses of displacements for COMs of nuclear proteins in the high-density (upper panel) and the low-density (lower panel) chromatins are shown: ERK (yellow), HMGB1 (blue), and p53 (red). (B–G) Snapshots at three times are given: t = 0 (left), t₁ (middle), and t₂ (right). The times t₁ and t₂ are labeled in (A) with black arrows. For p53 in high-density chromatin, t₁′ and t₂′ are arbitrarily chosen. The snapshots in (B)–(G) are for ERK, HMGB1, and p53, respectively. (B), (D), and (F) are for the high-density cases, whereas (C), (E), and (G) are for the low-density cases. The color usage for nuclear proteins is the same as that in Fig. 1, and chromatin is drawn transparent to highlight the proteins. To see this figure in color, go online.

Fig. 3 A shows representative time courses of the COM displacements of nuclear proteins in chromatin from the initial position (see Fig. S2 for all the trajectories). Representative snapshots are depicted in Fig. 3, B–G (see the corresponding video files Video S1, S2, S3, S4, S5, and S6. Video S1 and S4 are for ERK, Video S2 and S5 are for HMGB1, and Video S3 and S6 are for p53 in high- and low-density chromatins, respectively).

In the case of high nucleosome density (Fig. 3 A, top), HMGB1 diffused most rapidly, which was followed by ERK. p53 showed the slowest diffusion. The higher the molecular weight is, the slower the diffusion is. We also note that the diffusion is relatively slow at the beginning and is accelerated in the middle of the time courses. The snapshots (Fig. 3, B, D, and F) suggest that the acceleration started when the nuclear protein reached the surface of the model chromatin. To clarify this event in the trajectories, we introduced a characteristic time t₁ when the nuclear protein touches the chromatin surface for the first time and another characteristic time t₂ when nearly the entire nuclear protein exits from the model chromatin environment (see the precise definition in Supporting Materials and Methods). We indicated these characteristic times in Fig. 3 A and depicted snapshots at these times in Fig. 3 B, D, and F for the high-nucleosome-density case.

In the case of the low-density chromatin environment (Fig. 3 A, bottom), we find qualitatively similar behavior. The diffusion was the fastest for HMGB1 and the slowest for p53 among the three proteins. In the case of p53, the molecule did not reach the surface of the model chromatin by the end of the simulation. Thus, we depicted two snapshots at arbitrarily chosen times indicated as t₁′ and t₂′ in Fig. 3 G.

We also note that irregular diffusion was observed for the time range [t₁:t₂] at which the target protein resides on the surface of the model chromatin (Fig. S3).

Quantifying the diffusion coefficient

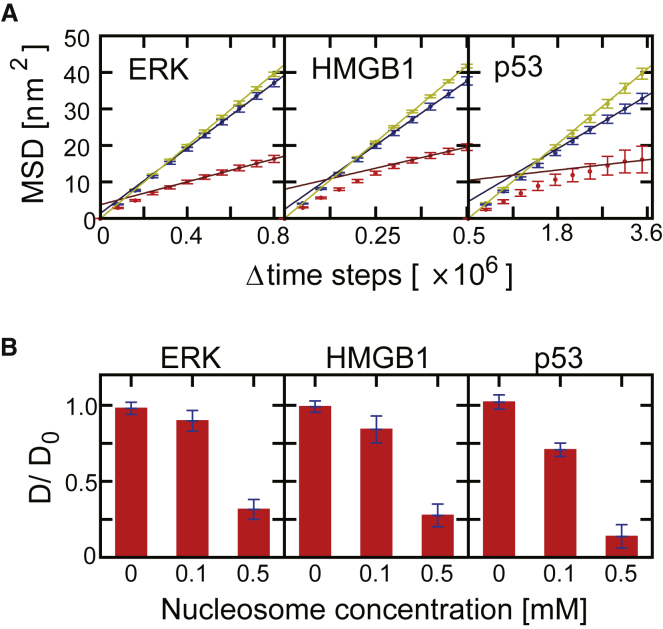
From the trajectories, we estimated the diffusion coefficients of the three nuclear proteins, ERK, HMGB1, and p53, in chromatin with high and low nucleosome densities. As a control, we also estimated the diffusion coefficients without nucleosome. We calculated the mean-square displacement (MSD) of the COM of nuclear proteins as a function of duration, Δtime steps (Fig. 4 A; Fig. S4). To reduce artifacts from the surface effect, we used the trajectory data up to t₁. (See Supporting Materials and Methods for the detailed explanation). We set the upper limit of Δtime steps so that the MSD without nucleosome does not exceed 40 nm² (yellow curves in Fig. 4 A).

Figure 4.

MSD and diffusion coefficients. (A) The mean-square displacement (MSD) is shown as a function of the time difference for three proteins. The yellow, blue, and red closed circles are for [nucleosome] ∼0.0, 0.1, and 0.5 mM, respectively, with error bars that are defined as standard errors. The straight lines represent the linear fit using the fourth quarter of the time window. (B) Relative diffusion coefficients estimated for three proteins in three environments relative to the solution environment are shown: [nucleosome] ∼0.0, 0.1, and 0.5 mM. The diffusion coefficient D is normalized by the analytical diffusion coefficient D₀ for each protein in free solution. To see this figure in color, go online.

Fig. 4 A shows that the low nucleosome density did not markedly affect the MSD of any targets (Fig. 4 A, blue curves). The MSD was approximately proportional to Δtime steps, which is a hallmark of the normal diffusion. In particular, the MSDs for ERK and HMGB1 in chromatin with low nucleosome density were nearly identical to those in the solution.

On the other hand, high nucleosome density significantly altered the MSD curves of all the three nuclear proteins (Fig. 4 A, red curves). The MSD plot as a function of Δtime steps was convex-shaped, which is consistent with the anomalous diffusion. Given the limited size of the model chromatin, flexible nature of nuclear proteins, and limited timescale of simulations, quantifying the diffusion coefficient is not trivial.

Visual inspection suggests that some parts of target proteins are often bound to nucleosomes and linker DNAs at a short timescale. At a longer timescale, the proteins dissociate from DNA and bind to neighboring DNA. Thus, we hypothesized that the diffusion of the proteins contains two distinct modes. In the short duration, although parts of the protein are bound to DNA, other unbound parts can move with restraint, resulting in the diffusion of the COM. The diffusion in the unbound parts is similar to that in solution and has a large diffusion coefficient. In the long duration mode, the diffusion coefficient is smaller because the proteins repeatedly dissociate from and associate to DNA. This two-mode model results in the convex MSD curves (see Fig. S5; Supporting Materials and Methods) and thus is consistent with the MSD plots obtained with high nucleosome density (red curves in Fig. 4 A). We note that the contribution of the first mode is larger for the cases of HMGB1 and p53 than for ERK, perhaps because the formers have flexible linkers at their central regions. Thus, we estimated the diffusion coefficient using the long duration part of the MSD curves. Using the fourth quarter of the duration range in Fig. 4 A, we obtained the diffusion coefficients by the linear fitting.

From this analysis, the question we asked is how the protein diffusion is retarded by the high nucleosome density. In Fig. 4 B, we showed the relative diffusion coefficients (D/D₀) for the three nuclear proteins in three environments, where D₀ is the analytical diffusion coefficient in the solution (see Supporting Materials and Methods).

In the low-density chromatin environment, the diffusion coefficient for ERK seems to be slightly smaller than D₀. The diffusion coefficients for the two TFs, HMGB1 and p53, were moderately smaller than D₀. Thus, the motion of ERK was not sensitive to the presence of chromatin, whereas the diffusion dynamics of other TFs tend to be retarded by sequence-nonspecific interactions to chromatin, primarily DNA.

In chromatin with high nucleosome density, the diffusion coefficients of all the three proteins were markedly reduced. In this condition, nucleosomes served as steric obstacles to some extent and thus retarded diffusion of all the proteins. Particularly, the diffusion of p53 was most strikingly slowed. Given that p53 is larger than the HMGB1, the size could be a reason for this difference. Alternatively, the stronger affinity of p53 to DNA than HMGB1 could make the diffusion of p53 slower than HMGB1 (51) (Fig. S6). These two factors are not mutually exclusive.

DNA sequence search by nuclear proteins in chromatin environment

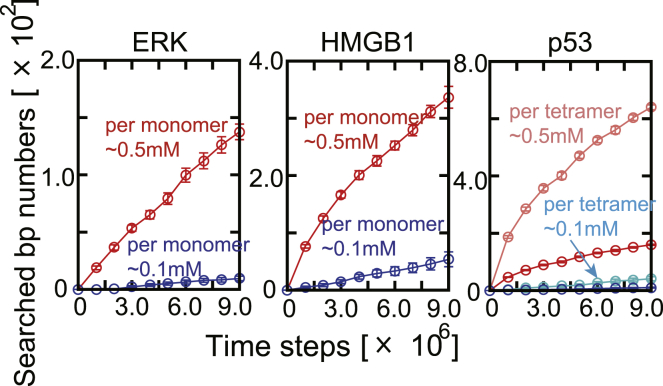
From the functional point of view, TFs need to search their target sequences efficiently in genomic DNA. We estimate the rate of sequence search by the three nuclear proteins. We counted the cumulative numbers of DNA basepairs that were “searched” by the protein as a function of time. Here, the “searched” is defined by the detected interactions between DNA particles and amino acids in the known DBDs: the DBD of ERK, the A-box and B-box of HMGB1, and the core and CTD of p53. The cutoff distance of the interaction between a bead of DNA and an amino acid in DBDs of proteins was set to 8.0 Å.

Of the two DBDs of p53, only the core domain is suggested to “recognize” the sequence. Here, for comparison, we used both domains of p53 in the analysis. Also, p53 remains as a homotetramer during the simulation. Thus, there can be two ways to count the searched basepairs: either per monomer or tetramer.

Fig. 5 plots the cumulative numbers of searched DNA basepairs averaged over 20 trajectories. Remarkably, for each of the target proteins, the number of searched basepairs increased more rapidly in the case of the high nucleosome density than low. This tendency is the opposite to the diffusion coefficient described above. In chromatin with high nucleosome density, DNA is more crowdedly packaged. Thus, the protein can search the DNA sequence more rapidly even though it diffuses slowly. This tendency is especially apparent for ERK and HMGB1: in the long time regime, the numbers of the searched basepair grow linearly, suggesting that the simulation reaches the stationary phase. In this phase, the numbers of the newly searched basepairs per time (the slope of the curves) were significantly more abundant in chromatin with high nucleosome density than low. Unexpectedly, the ratio of the slopes in high and low density is larger than the ratio of the density, i.e., 5, in the case of ERK. This result suggests that the ERK tends to bind to chromatin more stably with the high nucleosome density. This could be attributed to the macromolecular crowding effect that increased the nonspecific binding between the target protein and DNA. In the case of HMGB1, this effect could not be detected. Because HMGB1, as a TF, has higher affinity to DNA and nucleosome compared to ERK, as a signaling protein (Fig. S6), the macromolecular crowding effect may be weak.

Figure 5.

The cumulative number of DNA basepairs interacted with by nuclear proteins. Each panel shows the numbers of basepairs associated with DBDs of ERK, HMGB1, and p53 tetramer, respectively: the DBDs are the DBD of ERK, the A-box and B-box of HMGB1, and the core and CTD of p53. In each panel, red and blue symbols are for the number per monomer in high density and low density, respectively. For the number per tetrameric p53, we also plotted in light red and cyan symbols for the corresponding numbers in high- and low-density chromatins, respectively. Note that the scales in the vertical axes are different in the three proteins. The error bar for each symbol is defined as the standard error. To see this figure in color, go online.

For p53, the cumulative searched basepair numbers are clearly curved as a function of time in the short time regime, whereas in the long time regime, the asymptotic behavior seems to become linear-like.

In general, in a transcriptionally inactive heterochromatin state, one tends to assume that TFs cannot search the target sites efficiently. Interestingly, our simulation results do not support this assumption and suggest that the TFs in the crowded nucleosomes (0.5 mM) can search the target sites more efficiently than in the diluted nucleosomes (0.1 mM). We note that we have constructed the high-density chromatin structure by the expansion-and-shrink protocol, and the 0.5 mM nucleosome concentration is close to the achievable upper limit in the current coarse-grained model (Fig. S1). Even in the limit, there remains unoccupied space large enough for the target proteins to move around. Thus, proteins can search the DNA sequence more efficiently because of the high concentration of DNA in crowded chromatin. In reality, however, there are many other proteins and nucleic acids, in addition to nucleosomes, that may prevent diffusion of TFs.

Local DNA interaction profiles

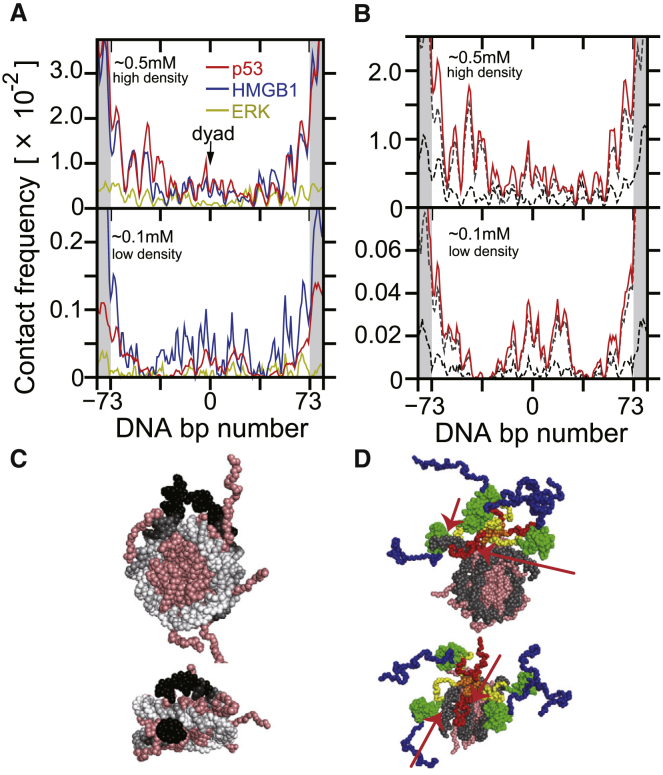
We next addressed which parts of the DNA segment interact with proteins during the simulations. Using snapshots before t₁, we calculated the contact frequency of each DNA basepair with the DBDs of the three nuclear proteins (Fig. 6 A). We excluded rarely observed unwrapped nucleosomes from the analysis because it could be a computational artifact (see Supporting Materials and Methods). We note that some DNA partial unwrapping from the histone core occurred in the expansion-and-shrink simulation. In the figure, the DNA segments were aligned using the dyad position (set to 0) as a reference. Thus, the nucleosomal DNA corresponds to basepair number (−73:73) (white in Fig. 6 A), whereas the linker DNA corresponds to basepair numbers (−83:−74) and (74:83) (gray in Fig. 6 A).

Figure 6.

Contact frequency at each DNA site with nuclear proteins. The upper and lower panels correspond to results for the high- and low-density chromatin. The DNA fragments for single-nucleosome regions were aligned by the dyad position of the nucleosome. The left and right ends with the gray shade (ID (−83:−74) and ID (74:83)) correspond to the linker DNA regions, whereas the central part (ID [−73:73]) corresponds to the nucleosomal DNA (the bp ID = 0 corresponds to the dyad). (A) The contact frequency of entire DBDs of ERK (yellow), HMGB1 (blue), and p53 (red) is shown. (B) The contact frequencies of the core and CTD of p53 and the entire region of p53 are shown by black dashed, gray dashed, and red solid curves, respectively. (C) Contact frequency is mapped on the nucleosome structure (side and top view) by grayscale. (D) Representative complex snapshots of p53 bound on a nucleosome (side and top view) are shown. The red arrow indicates the major contacts between linker and/or dyad of DNA and core and/or CTD of p53. To see this figure in color, go online.

The most apparent feature in Fig. 6 A is that the contact frequencies in high nucleosome density are an order of magnitude larger than those in low nucleosome density. This difference is in harmony with the macromolecular crowding effect that enhances the nonspecific binding. Another prominent feature is that the contact frequencies in linker DNAs are much higher than those in nucleosomal DNAs; the ratios of the average frequency in linker DNAs to that in nucleosomal DNA were ∼2 for ERK and ∼8 for HMGB1 and p53 (quantified in Fig. S7). This preferential contact to linker DNA is reasonable because the linker DNA may be more accessible for the nuclear proteins compared with the nucleosomal DNA that wrapped histone octamers. We also note that even though the length of the linker DNA affects the ratio of contacts, the comparison among the three proteins would remain the same.

Within nucleosomal DNA, the contact frequency profiles were not uniform but exhibited ∼10 bp periodicity at least for HMGB1 and p53 regardless of the nucleosome density. In the high-nucleosome-density case in which more data samples are available than the low-nucleosome-density case, we see that peaks are higher near the entrance and exit regions ([−73:−53] and [53:73]) than the center. Termini of nucleosomal DNA tend to partially unwrap (20) where the nuclear proteins can access them. Also, we found a faint high peak near the dyad region.

By comparing the contact frequencies of the three proteins, we found that the contact frequencies of HMGB1 and p53 (per monomer) were significantly higher than that of ERK. For p53, we also separately examined the contact frequencies of the CTD and the core domain (Fig. 6 B). As a result, we found that the peaks around the dyad are mainly due to contacts by the CTD, not by the core domain. This tendency is consistent with the fact that the CTD of p53 has more prominent roles in nonspecific DNA binding than the core domain (46, 47, 48).

In Fig. 6 C, the contact frequencies between p53 and each DNA basepair are mapped as grayscale onto the simulation snapshot. From this figure, we can see that the linker DNA and entrance and exit part of nucleosomal DNA have higher frequencies (almost black in Fig. 6 C) than the dyad region (dark gray). The snapshot sampled in MD simulations at the low-density chromatins shows that p53 can make a complex with a nucleosome with the CTD and core domain (Fig. 6 D).

Protein interaction profile

Next, we investigate which parts of the proteins interact with DNA. As expected, amino acids on the positively charged surface tend to have high probabilities to interact with DNA (Fig. 7 A), especially the highest peaks: residues 250–300 of ERK, residues 25–50 and around 150 of HMGB1, and residues near 125 and 350–393 of p53 agree with the experimentally suggested DBDs (41, 42, 46, 47, 48) (Fig. 7 B). For all the targets, the interaction surface patterns were indistinguishable between the low- and high-density chromatins (Fig. S8).

Figure 7.

Contact frequencies of protein residues with DNA. (A) The black and gray curves correspond to the results in the high- and low-density chromatin environments, respectively. The upper barcodes show positively (blue) and negatively (red) charged residues for each protein. (B) Contact frequencies in the high-density chromatin mapped on snapshots are shown. (C and D) Three representative snapshots of p53 in the high-density chromatin with two views are given: R_g of p53 in (C) and (D) corresponds to 60 ± 0.01 Å (near the minimal boundary of R_g distribution in Fig. S9) and 78 ± 0.01 Å (around peak of R_g distribution in Fig. S9), respectively. To see this figure in color, go online.

Binding and dissociation kinetics

We also investigated the kinetics of the nuclear protein-DNA binding and unbinding. First, we confirmed that the simple Poisson process with the single exponential functions well described the binding and unbinding processes (Fig. S6 A) except for the binding process in low-density chromatin. The on- and off-rate constants that are determined as the inverse of averaged duration times are depicted in Video S2. HMGB1 in Low-Density Chromatin, Video S5. HMGB1 in High-Density Chromatin. The crowded chromatin environment facilitates the nuclear protein binding (the on rate increased) and decelerates the unbinding (the off rate decreased). Notably, the on rate was accelerated by a factor ∼13–20, which is larger than the ratio of the density, i.e., 5.

Conformation of nuclear proteins in chromatin environment

In general, high-density crowding agents make flexible proteins more compact than in dilute solution because of the macromolecular crowding effects. Here, we investigated the conformational changes of the nuclear proteins in our model chromatin. We found that, although there was no marked change in the cases of ERK and HMGB1, p53 has a smaller radius of gyration $R_{\mathrm{g}}^{\mathrm{TF}}$ in chromatin with high nucleosome density than low nucleosome density (Fig. S9). The p53 snapshots with a smaller$R_{\mathrm{g}}^{\mathrm{TF}}$ (Fig. 7 C) differ from those with $R_{\mathrm{g}}^{\mathrm{TF}}$ (Fig. 7 D) at the peak of distribution in Fig. S9.

Effects of acetylation on the CTD of p53

It has been implicated that p53 needs to be acetylated in its CTD for activation (52). Acetylation sites include K373, K382, and so on (52). The functional roles of the acetylation have been addressed experimentally (53, 54) and computationally (22). In particular, using the same coarse-grained modeling approach as this work, we revealed that acetylation in the CTD of p53 remarkably reduces the sliding length so that the acetylated p53 tends to diffuse in three dimensions, whereas the unacetylated p53 can slide along DNA for a long duration (22, 35). Here, we investigated how the acetylation alters the dynamics of p53 in chromatin. Namely, we focus on the influence of acetylation on the MSD profile, the diffusion coefficient, DNA-bp searching speed, and the contact frequency with DNA.

For this purpose, we conducted 20 independent molecular simulations in which p53 with the K373 and K382 residues acetylated was embedded in chromatin with high and low nucleosome density. To mimic the acetylation, we just neutralized the charges of the corresponding two lysine residues of all four monomers, whereas the rest of the simulation setups are the same as before. Whereas the unacetylated p53 CTD contains +20 charges per a tetramer, the acetylated form has a reduced charge of +12, which reduces the affinity of the p53 CTD to DNA.

We plotted the MSD as a function of duration in Fig. S10 A and the diffusion coefficients in Video S2. HMGB1 in Low-Density Chromatin, Video S5. HMGB1 in High-Density Chromatin, comparing the acetylated p53 with the unacetylated p53. We found that the acetylation of p53 slightly weakened the crowding effect of chromatin on the diffusion, slowed the basepair searches (Video S1. ERK in Low-Density Chromatin, Video S2. HMGB1 in Low-Density Chromatin, Video S3. p53 in Low-Density Chromatin, Video S4. ERK in High-Density Chromatin, Video S5. HMGB1 in High-Density Chromatin, Video S6. p53 in High-Density Chromatin), and diminished the contact frequency between p53 and DNA, especially in the dyad (Document S1. Supporting Materials and Methods and Figs. S1–S10, Video S1. ERK in Low-Density Chromatin, Video S2. HMGB1 in Low-Density Chromatin, Video S3. p53 in Low-Density Chromatin, Video S4. ERK in High-Density Chromatin, Video S5. HMGB1 in High-Density Chromatin, Video S6. p53 in High-Density Chromatin, Document S2. Article plus Supporting Material). The effect on the search speed is more pronounced for the CTD rather than the core domain.

Discussion

Limitations in this study

In this study, we took a rather simple simulation setup that has many limitations.

First, we created structures of the chromatin with MD simulations without using experimental data. Recently, 3C-based experiments have provided structural restraints in the chromatin folding, which can be used to construct the chromatin structures (55).

Second, we employed simple Langevin dynamics without including hydrodynamic effects. Because the hydrodynamic effect is known to enhance the diffusion of large molecules, the diffusion coefficients evaluated by this study seem to give the lower limits (56). Notably, the hydrodynamic effect depends on the size of the proteins: the larger the protein, the more significant the impact of the hydrodynamics is. Thus, a quantitative comparison of the diffusion coefficients between p53 and HMGB1, for example, is inherently difficult in our work. However, qualitative comparison of the diffusion of the same proteins in different chromatin environments is likely to be less sensitive. Either way, including the hydrodynamic interaction is highly desired for the next step.

Third, real chromatin is much more complicated than just a polynucleosome array. Most notably, linker histones such as H1 bind on the nucleosome, which can affect binding and diffusion of nuclear proteins. Also, epigenetic marks such as histone acetylation would alter the chromatin structures and states greatly. These factors should be addressed in the future.

Fourth, our model does not approximate sequence-dependent protein-DNA interactions well. Nuclear proteins are attracted to DNA simply via the electrostatic interactions. Furthermore, the DNA model does not reflect the sequence-dependent bending rigidity, which could affect the model chromatin structure.

Future challenges

Some challenges could be addressed in the future by extending our model. We will describe these challenges in the following three paragraphs.

It has been revealed in previous studies that HMGB1 facilitates deformation of nucleosome by repeated association to and dissociation from DNA that unwraps from histone core complexes (57). Then, the deformation of nucleosome helps TFs bind to their specific binding sites in nucleosomes (51, 58). Also, the ability of HMGB1 to deform the nucleosome is regulated by the cysteine redox states (59). In experiments, the deformation requires a high concentration of HMGB1 (57). However, because only one HMGB1 molecule was included, the deformation could not be observed in our coarse-grained MD simulation. In the future, we will address the structural basis of nucleosome deformation activity of HMGB1 by simulating many HMGB1 molecules in chromatin.

As for the specific binding of p53 to its recognition site on DNA, rotational positioning of the site against histone core complexes regulates the binding (60, 61). Also, the previous simulation studies indicated that the CTD of p53 interacts with the DBD and regulates the binding, too (62). The DNA model did not contain any specific binding sites in our study because we focused on the search of specific binding sites. Because of this, the simulation trajectories did not include p53 dynamics on specific binding sites. In the future, we will address the structural basis of specific DNA binding of p53 in nucleosomes.

In various simulation studies, the effect of crowder molecules on the search has been investigated (63, 64, 65). These studies indicated that the crowder molecules increased the fraction of the molecules which slides along DNA and promoted intersegmental transfer. In this study, we did not model the various kinds of proteins in the nucleus that could have molecular crowding effects. Thus, we could not discuss the impact of crowder molecules on the search in a chromatin environment, which can be addressed by naturally extending our model (65).

Conclusions

We investigated diffusional dynamics, sequence search dynamics, and structures of two TFs, HMGB1 and p53, and a signaling protein, ERK, in chromatin with high and low nucleosome densities by coarse-grained MD simulations on the K computer, a massively parallelized supercomputer. Estimated diffusion coefficients in chromatin with a low nucleosome density were nearly the same as those in solution, whereas those in chromatin with a high nucleosome density were markedly reduced. Moreover, although the three nuclear proteins showed normal diffusion in chromatin with low nucleosome density, they exhibited anomalous subdiffusion in chromatin with high nucleosome density. Interestingly, we found that the rate of target search shows the opposite tendency: as the nucleosome density increases, the search rate increases. All the studied nuclear proteins preferred to contact with linker DNA rather than nucleosomal DNA. We also studied the acetylation effect of the CTD of p53.

Author Contributions

R.K.,T.T., and H.K. performed research and analyzed data. R.K., T.T., and S.T. conceived and designed the research. R.K. and S.T. wrote the manuscript. H.K. contributed simulation tools. All authors reviewed the final manuscript.

Editor: Tamar Schlick.