A Brownian Ratchet Model Explains the Biased Sidestepping of Single-Headed Kinesin-3 KIF1A

Abstract

The kinesin-3 motor KIF1A is involved in long-ranged axonal transport in neurons. To ensure vesicular delivery, motors need to navigate the microtubule lattice and overcome possible roadblocks along the way. The single-headed form of KIF1A is a highly diffusive motor that has been shown to be a prototype of a Brownian motor by virtue of a weakly bound diffusive state to the microtubule. Recently, groups of single-headed KIF1A motors were found to be able to sidestep along the microtubule lattice, creating left-handed helical membrane tubes when pulling on giant unilamellar vesicles in vitro. A possible hypothesis is that the diffusive state enables the motor to explore the microtubule lattice and switch protofilaments, leading to a left-handed helical motion. Here, we study the longitudinal rotation of microtubules driven by single-headed KIF1A motors using fluorescence-interference contrast microscopy. We find an average rotational pitch of $\simeq 1.5$μm, which is remarkably robust to changes in the gliding velocity, ATP concentration, microtubule length, and motor density. Our experimental results are compared to stochastic simulations of Brownian motors moving on a two-dimensional continuum ratchet potential, which quantitatively agree with the fluorescence-interference contrast experiments. We find that single-headed KIF1A sidestepping can be explained as a consequence of the intrinsic handedness and polarity of the microtubule lattice in combination with the diffusive mechanochemical cycle of the motor.

Significance

Efficient transport of organelles by molecular motors is essential in cells. Some kinesin motors are capable of sidestepping along the microtubule lattice, forming helical trajectories, a mechanism that has been proposed as a strategy to maneuver in the presence of obstacles. One such example is the kinesin-3 motor KIF1A, which is involved in the transport of synaptic vesicle precursors in neurons. Recently, the single-headed version of this motor was found to form helical membrane tubes in vitro. It was hypothesized that a diffusive state allows the motor to switch protofilaments and generate a left-handed helical motion. Here, we combine theory and experiments to test this hypothesis and show that this motor acts as a Brownian motor navigating the microtubule lattice.

Introduction

Molecular motors from the kinesin and dynein family move along microtubules, transducing the chemical energy of ATP hydrolysis into mechanical work (1). They perform a variety of mechanical functions in cells, which involve intracellular transport, flagellar beating, cell division, and cytoplasmic streaming (1, 2). Microtubule filaments are hollow cylindrical structures consisting of several protofilaments, providing a parallel array of tracks for the motors to move along (3). Interestingly, motors do not always follow single-protofilament tracks, but in some cases, they are capable of switching protofilaments in a consistent manner (4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15). Such biased off-axis motion leads to helical trajectories of the motors, with rotational pitches ranging from ∼0.3 to 3 μm. This phenomenon seems to be general, and it has been reported for a great variety of motors such as monomeric kinesin-1 (4), kinesin-2 (5), kinesin-5 (6), kinesin-8 (7, 8, 9), kinesin-14 (10, 11), axonemal dynein (12, 13, 14), and cytoplasmic dynein (8, 15). Despite numerous studies, the role and underlying mechanisms of such helical motions are still unclear. In the context of intracellular transport, it has been hypothesized that sidestepping might be a useful strategy to navigate the microtubule lattice and circumvent possible roadblocks (7, 16, 17, 18, 19, 20). What are the mechanisms enabling molecular motors to sidestep along the microtubule lattice in a biased manner and to generate torques? Diffusive search has been conjectured to be an important ingredient for such biased motion (4, 5), promoting lane-changing events (21, 22, 23), in contrast to the linear motion of motors that follow a single protofilament (e.g., dimeric kinesin-1 (24, 25)). Recently, the single-headed form of KIF1A (kinesin-3) was added to the list of motors that can generate helical movements (20). It was found that single-headed KIF1A motors were able to pull on membrane tubes and wind them around single microtubules in vitro (20). Several studies support the idea that the single-headed form of KIF1A acts as a prototype of a Brownian motor by virtue of a weakly bound diffusive state on the microtubule lattice (26, 27). In vivo, KIF1A is usually found in a dimeric form, eliciting large velocities (∼1 μm/s) (28), and it has been shown to switch between diffusive and processive states (29). This diffusive state makes the motor especially inefficient in its monomeric form, with velocities reported to be 10-fold lower (20, 27). At the same time, the diffusive state can also lead to cooperative force generation (30, 31, 32) and might be crucial for sidestepping on the microtubule lattice (20). However, the last hypothesis has not been carefully studied yet.

Here, we characterize the sidestepping motion of single-headed KIF1A by studying the longitudinal rotations of microtubules in gliding motility assays using fluorescence-interference contrast (FLIC) microscopy (8, 24). The average rotational pitch of microtubules is found to be $\simeq$ 1.5 μm, and surprisingly, it is highly robust to changes in the gliding velocity, ATP concentration, microtubule length, and motor density. This is in contrast to other recently studied kinesins such as Kip3/kinesin-8 (9) or Ncd/kinesin-14 (11), in which the rotational pitch is ATP dependent. To understand this phenomenon, we performed numerical simulations of Brownian motors exploring the microtubule lattice (26, 27, 30, 31). Such a simple model successfully reproduces the experimental observations in the FLIC experiments in terms of velocity, rotational pitch, and frequency of the gliding microtubules. We propose that the microtubule lattice geometry, together with the microtubule-motor interaction, determines the rotational pitch.

Materials and Methods

Protein expression and purification

Tubulin was purified from porcine brain (Vorwerk Podemus, Dresden, Germany) using established protocols as described previously (33). Single-headed KIF1A motor proteins (amino acids 1–382) with both a His-tag and a Cys residue at the C-terminus (27) were expressed in Escherichia coli, purified using a Ni-nitrilotriacetic acid column, and labeled with a sulfhydryl-reactive biotin before elution. The details of the purification procedure can be found in (20).

Polymerization of speckled microtubules

Guanylyl-(α, β)-methylene-diphosphonate (GMP-CPP), taxol-stabilized speckled microtubules were grown in a two-step process as described in (8). 25 μL of BRB80 solution (80 mM Pipes (Sigma-Aldrich, St. Louis, MO) (pH 6.9) with KOH (VWR), 1 mM EGTA (Sigma-Aldrich), and 1 mM MgCl₂ (VWR)) supplemented by 12 μM of porcine tubulin (98.8% unlabeled and 1.2% rhodamine-labeled (carboxytetramethylrhodamine; Thermo Fisher Scientific, Waltham, MA)), 1 mM GMP-CPP (Jena Bioscience, Jena, Germany), and 4 mM MgCl₂ were incubated on ice for 5 min and then for 25 min at 37°C to grow short, dimly labeled microtubule seeds. In parallel, an elongation mix consisting of 100 μL BRB80 solution supplemented by 0.8 μM of porcine tubulin (93.3% unlabeled and 6.7% rhodamine-labeled), 1 mM GMP-CPP, and 4 mM MgCl₂ was heated to 37°C for 30 s (after a 5 min incubation on ice). Afterwards, 10 μL of the dimly labeled seed solution was added to the elongation mix (resulting total tubulin concentration ∼2 μM) and incubated overnight at 37°C. Assembled speckled microtubules were centrifuged using a Beckman airfuge (Beckman, Brea, CA) at 100,000 × g for 5 min. The pellet was resuspended in a volume of 50–100 μL BRB80T (BRB80 supplemented with 10 μmM taxol (Sigma-Aldrich)). GMP-CPP, taxol-stabilized microtubules are mostly constituted of 14 protofilaments (∼95%; (34)), which provides them with a left-handed supertwist of 8.4 μm (8, 24). The rotational pitch and rotational frequency measures were corrected taking into account the aforementioned supertwist (8).

KIF1A gliding assays on silicon wafers

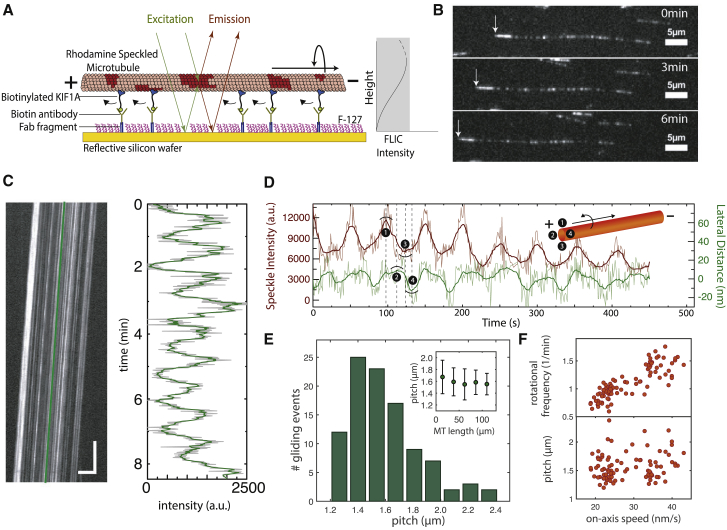
The gliding assays were performed in microfluidic flow chambers constructed by sealing 22 × 22 mm glass coverslips (#1.5; Menzel, Braunschweig, Germany) and 10 × 10 mm silicon wafers having a 30 nm thermally grown oxide layer (GESIM, Grosserkmannsdorf, Germany) with spacers of NESCO film (Azwell, Osaka, Japan). Both glass and wafer surfaces were coated with dichlorodimethylsilane to render the surface hydrophobic (35). The approximate dimension of each flow chamber was 10 × 1.5 mm × 100 μm. Flow chambers were flushed with solutions (15 μL each) in the following sequence: 1) Fab-fragment solution consisting of 100 μg/mL F(ab′)2 fragments (anti-mouse Immunoglobin G (fragment crystallizable region specific) antibody developed in goat; Sigma-Aldrich) in phosphate-buffered saline (PBS) that bind nonspecifically to the hydrophobic surface (incubation time 5 min); 2) Pluronic F127 (Sigma, 1% in PBS) to block the surface against unspecific protein adsorption (incubation time >60 min); 3) antibody solution consisting of 100 μg/mL anti-biotin mouse antibodies (Thermo Fisher Scientific) in PBS that bind specifically to the F(ab′)2 fragments (incubation time 5 min); 4) four times BRB40 buffer (40 mM Pipes (Sigma-Aldrich) (pH 6.84) with KOH (VWR), 1 mM EGTA (Sigma-Aldrich), and 4 mM MgCl₂ (VWR)) to remove excess F-127 in solution and exchange buffers; 5) motor solution consisting of 2 μM biotinylated KIF1A in motor dilution buffer (1 mM ATP (Roche, Basel, Switzerland), 0.1$\text{\%}$ Tween 20 (Sigma-Aldrich), 0.2 mg/mL casein (Sigma-Aldrich), and 0.2 mg/mL dithiothreitol (Sigma-Aldrich) in BRB40) to bind the KIF1A proteins specifically to the anti-biotin mouse antibodies (incubation time 5 min); 6) speckled-microtubule solution consisting of speckled microtubules in motor dilution buffer (incubation time 5 min); and 7) imaging solution containing the oxygen scavenger system (40 mM glucose (Sigma-Aldrich), 110 μg/mL glucose oxidase (SERVA Electrophoresis GmbH, Heidelberg, Germany), and 22 μg/mL catalase (Sigma-Aldrich)) in motor dilution buffer to remove excess microtubules. The gliding assay scheme is illustrated in Fig. 1 A, and microtubule polarity was determined from the gliding direction given that KIF1A motors are plus-end directed.

Figure 1.

Rotational motion of speckled microtubules gliding on single-headed KIF1A. (A) Schematic representation of a speckled microtubule gliding on a reflective silicon substrate coated with biotinylated KIF1A motors via anti-biotin mouse antibodies is shown. (B) Fluorescent image series of an example rhodamine-speckled microtubule (minus end marked by white arrow) gliding with a velocity of 22 nm/s (see Video S1) is shown. (C) Corresponding kymograph (space-time intensity plot) of the speckled microtubule in (B) (horizontal scale bar represents 5 μm; vertical scale bar: 1 min) and the FLIC intensity profile over time for one of the speckles (indicated by the green line in the kymograph) are shown. The rotational pitch for this microtubule was 1.1 μm. (D) Direction of rotation of the microtubules gliding on KIF1A: an individual speckle from a gliding speckled microtubule was tracked using FIESTA to obtain the lateral deviation of the speckle along with the variation in FLIC intensity over time. Raw data are indicated in light gray, and the smoothed data (rolling frame averaged over 20 frames) are indicated in green (lateral distance; positive values refer to the left) and brown (FLIC intensity). Inset: an illustration of the counterclockwise rotation of a microtubule in the direction of motion is given. (E) A histogram of rotational pitches showing a median pitch of 1.5 ± 0.2 μm (median ± SD, n = 100 gliding events) is given. Inset: Variation of rotational pitch with respect to microtubule length by binning the data (mean ± SD) is shown. (F) The rotational frequency (top) and rotational pitch (bottom) plotted with respect to the on-axis microtubule gliding velocity are shown. To see this figure in color, go online.

Image acquisition

Optical imaging was performed using an inverted fluorescence microscope (Zeiss Axiovert 200M; Carl Zeiss, Göttingen, Germany) with a 63× water immersion 1.2 NA objective (Zeiss) in combination with an Andor Ixon DV 897 (Andor Technology, Belfast, UK) EMCCD camera controlled by Metamorph (Molecular Devices, Sunnyvale, CA), providing a pixel size of 0.256 μm. A Lumen 200 metal arc lamp (Prior Scientific Instruments, Cambridge, UK) was used for epifluorescence excitation. Speckled microtubules gliding on the surface of the silicon wafer were imaged “through the solution” (i.e., on the far side of the flow channels) using a tetramethylrhodamine filter set (Ex 534/30×, DC BC R561, EM BL593/40; all Chroma Technology, Rockingham, VT) with an exposure time of 400 ms per frame. Images were recorded in time-lapse mode with a frame rate of 1 fps. The temperature was maintained at $\simeq 24$°C by fitting a custom-made hollow brass ring around the objective and connecting it to a water bath with a cooling/heating unit (F-25-MC Refrigerated/Heating Circulator; JULABO, Seelbach, Germany).

Image analysis

Kymographs (space-time intensity plots) for gliding speckled microtubules were generated in ImageJ (36). The kymographs were then analyzed with MATLAB (The MathWorks, Natick, MA), using the speckle analysis method described in (8), to obtain the rotational pitch and velocity corresponding to each gliding speckled microtubule. To obtain information regarding the direction of rotation, example speckles were tracked using FIESTA (37), and the tracks were averaged (rolling frame window of 2 μm) to get the estimated microtubule centerline. The perpendicular distance of a speckle track from the microtubule centerline at each point provided the lateral deviation of the speckle. In combination with the FLIC intensity variation, this information provided the direction of rotation (see Figs. 1 D and S2).

Two-dimensional Brownian motor model for single-headed KIF1A

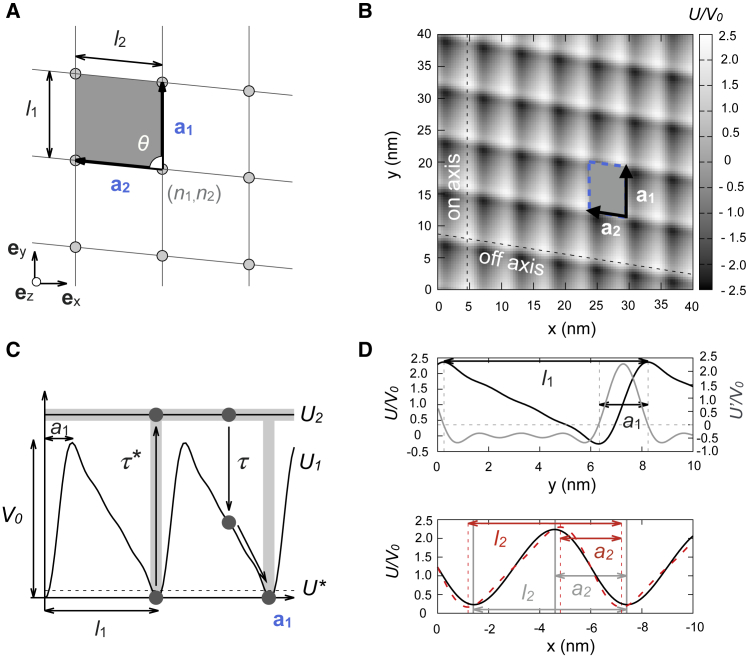
We define the position of a motor in Cartesian coordinates as r = xe_x + ye_y, where e_y corresponds to the microtubule axis direction (see Fig. 3 A). The microtubule lattice is treated as an oblique Bravais lattice with primitive vectors a_i, i = 1, 2, forming an angle θ > 0 (see Fig. 3, A and B). Hereinafter, Latin indices will be employed to label the primitive directions and Greek indices to label the Cartesian coordinates. The nodes of the lattice are defined as R(n₁, n₂) = n₁a₁ + n₂a₂, where n₁, n₂ denote integer numbers and correspond to the available binding sites for the motor. Hence, the set (n₁, n₂) indicates a given primitive cell. The two primitive vectors are a₁ = l₁e_y and a₂ = l₂(−sinθe_x + cosθe_y), where l_i, i = 1, 2 are the periodicities for each primitive direction (see Fig. 3, A and B). The reciprocal basis q_i reads

$${\mathbf{q}}_1=2\pi \frac{{\mathbf{a}}_2\times {\mathbf{e}}_y}{\left|{\mathbf{a}}_1\times {\mathbf{a}}_2\right|}=\frac{2\pi }{l_1}\left(\cot \theta {\mathbf{e}}_x+{\mathbf{e}}_y\right);{\mathbf{q}}_2=2\pi \frac{{\mathbf{e}}_y\times {\mathbf{a}}_1}{\left|{\mathbf{a}}_1\times {\mathbf{a}}_2\right|}=-\frac{2\pi }{l_2}\csc \theta {\mathbf{e}}_x.$$ (1)

Figure 3.

(A) Oblique Bravais lattice as a description of the microtubule lattice with primitive vectors a₁ and a₂ of sizes l₁ and l₂ respectively, forming an angle θ. The gray parallelogram corresponds to the primitive cell of the lattice, and the gray circles to the nodes of the lattice. (B) Two-dimensional microtubule-motor potential with N₁ = 4, N₂ = 2, and coefficients μ₁₁ = 1, μ₁₂ = 0.9, μ₁₃ = 0.65, μ₁₄ = 0.35, μ₂₁ = 1, and μ₂₂ = 0.085 is shown (see Materials and Methods). Dashed lines are directions along which 1d sections of the potential are plotted in (D). (C) Sawtooth linear potential along a₁ (N₁ = 4, μ₁₁ = 1, μ₁₂ = 0.9, μ₁₃ = 0.65, μ₁₄ = 0.35) for the motor-track interaction is shown. The gray regions depict the zones where excitations from U₁ to U₂ are allowed with exponentially distributed hydrolysis dwell times with mean τ^∗. Transitions from U₂ to U₁ are delocalized and occur with exponentially distributed decay times with mean τ. Dashed line: excitation time starts when the particle’s potential energy is lower than U^∗. (D) Top: potential section along a₁ is shown. Gray: partial derivative of the potential; its roots (intersections of the gray dashed lines) label the maxima and minima of the potential. l₁ = 7.9 nm, a₁ = 1.9 nm (a₁/l₁ = 0.24). Bottom: black marks a potential section along a₂; l₂ = 6.0 nm, a₂ = 2.8 nm (a₂/l₂ = 0.47). Red: potential section along a₂ when μ₂₂ = 0.4 (the rest being the same) is shown; l₂ = 6.0 nm, a₂ = 2.4 nm (a₂/l₂ = 0.4). To see this figure in color, go online.

We consider that the motor can be in two possible states: k = 1, 2. State k = 1 corresponds to a “strongly bound” state, in which the motor experiences a potential landscape U₁(x, y), describing the microtubule-motor interaction (see Fig. 3 C). In this state, the motor is not bound to an ATP molecule. After capturing an ATP molecule, hydrolysis takes place, and the motor excites to state k = 2, usually known as the “weakly bound” or ADP state, in which the motor can freely diffuse on the lattice (see Fig. 3 C). In this state, the motor experiences a flat potential. After the release of the ADP and P_i molecules, the motor decays from state k = 2 to the state k = 1. We consider that this process occurs with exponentially distributed decay times with mean τ. Decay processes are delocalized in space, whereas excitations are localized in the lattice nodes (U₁ potential minima). A transition to the weakly bound state k = 2 is only allowed if the potential energy in state 1 is below a certain threshold value U^∗, much smaller than the U₁ maxima. Again, an exponential distribution of exciting times is assumed, with mean time τ^∗. The potential U₁(x, y) must be asymmetric in the y component, reflecting microtubule polarity. A common choice is a sawtooth landscape potential. The reciprocal basis {q₁, q₂} is employed to build a periodic two-dimensional oblique sawtooth landscape, with periodicities l₁, l₂ along the primitive directions a₁, a₂, respectively. A simple choice is to define U₁ = V₁ + V₂, with V_i, i = 1, 2 being one-dimensional sawtooth functions in each primitive direction. The one-dimensional sawtooth functions may be expressed as Fourier series,

$$V_i(x,y)=V_0\sum _{j=1}^{N_i}\frac{{\mu }_{ij}}{j}\sin \left(j{\mathbf{q}}_i·\mathbf{r}\right);i=\mathrm{1,2}\text{.}$$ (2)

A simple choice of the coefficients μ_ij leads to a continuous smooth landscape (see Fig. 3, B–D). The two-dimensional ratchet may have two distinct asymmetries a_i along the directions a_i, i = 1, 2 (see Fig. 3, C and D). As previously mentioned, the polarity of a microtubule generates an asymmetry a₁ in the a₁ direction that has been estimated to be a₁/l₁ $\simeq$ 0.2 (30). In general, a second asymmetry $a_2/l_2\ne 1/2$ can exist along the a₂ direction. However, even in the symmetric case (a₂/l₂ = 1/2), the fact that $\theta \ne \pi /2$ and $a_1/l_1\ne 1/2$ is sufficient to generate a helical movement of the motor (data not shown). From Eq. 2, we see that the asymmetry is not a parameter itself in our model but is determined by the choice of the coefficients μ_ij. Two harmonics may be enough to generate an asymmetric landscape; however, the choice of a_i is limited because for μ_i2 ≥ 1, the potential displays a nondesirable second local minimum for each period. This problem can be overcome by using higher-order harmonics, as shown in Fig. 3, C and D. To match the experimental results, we choose the asymmetry parameters a₁/l₁ = 0.24 and a₂/l₂ = 0.47 (Figs. 4, E and F and 5). The dynamics of the motor follows Langevin dynamics in the overdamped limit,

$$\eta \dot{\mathbf{r}}=-{\delta }_{k1}\mathit{\nabla }{U}_1-\mathbf{F}+\mathit{\xi }\left(t\right),$$ (3)

where η is the friction coefficient fulfilling the Einstein’s relation D = k_BT/η (D is the diffusion coefficient), the nabla operator reads $\mathit{\nabla }\equiv \left({\partial }_x,{\partial }_y\right)$, F is a constant external force, and ξ is a random force vector with zero mean satisfying $\langle {\xi }_{\alpha }\left(t\right){\xi }_{\beta }\left(t\text{'}\right)\rangle$ = 2k_BTηδ_αβδ(t − t′), α, β = x, y where δ_k1, δ_αβ are Kronecker deltas. Finally, we define a useful quantity to study the randomness of the motor motion on the lattice (38, 39),

$$R_{\alpha }=\frac{\langle \mathit{\Delta }{r}_{\alpha }^2\left(t\right)\rangle -{\langle \mathit{\Delta }{r}_{\alpha }\left(t\right)\rangle }^2}{d_{\alpha }\langle \mathit{\Delta }{r}_{\alpha }\left(t\right)\rangle };\alpha =x,y,$$ (4)

where Δr_α(t) = r_α(t) − r_α(0) is evaluated at steady state, d_α is the motor step size—d_x = l₂sin(θ) along the x axis, d_y = l₁ along the y axis—and the angle brackets denote an ensemble average. The parameter R_α quantifies the temporal irregularity of the dynamics of the motor along the α axis. A perfect clocklike motor would display no stepping irregularity, R = 0, whereas a motor undergoing exponentially distributed steps would exhibit R = 1 (39).

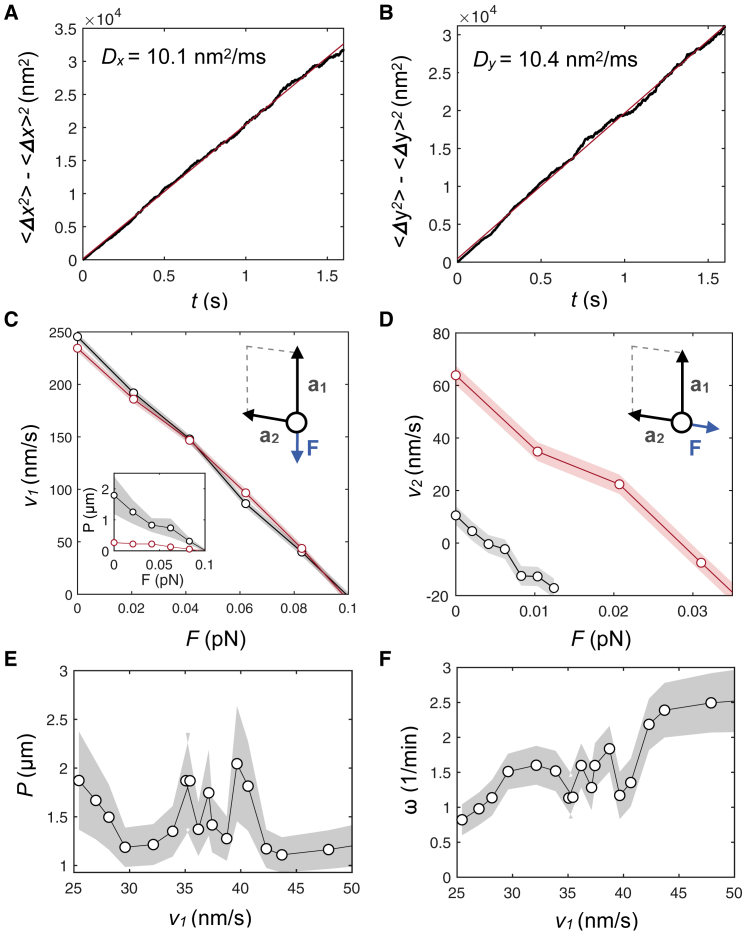
Figure 4.

Variance along the transversal (A) and longitudinal (B) axis obtained using an ensemble average with 10³ KIF1A trajectories and the landscape generated by Eq. 2, with μ₁₁ = 1, μ₁₂ = 0.9, μ₁₃ = 0.65, μ₁₄ = 0.35, μ₂₁ = 1, and μ₂₂ = 0.4. (C) Mean longitudinal velocity and rotational pitch (inset) for an ensemble of 10³ independent trajectories simulated in a landscape generated by Eq. 2 are shown, with asymmetries a₁/l₁ = 0.24, a₂/l₂ = 0.47 (gray) and a₁/l₁ = 0.24, a₂/l₂ = 0.40 (red). Horizontal axis corresponds to the absolute value of the force modulus applied along a₁, and force is applied toward −a₁. Simulation time, 1.6 s. (D) Mean lateral velocity for an ensemble of 10³ independent trajectories simulated in a landscape Eq. 2 is shown, with asymmetries a₁/l₁ = 0.24, a₂/l₂ = 0.47 (gray) and a₁/l₁ = 0.24, a₂/l₂ = 0.40 (red). Horizontal axis corresponds to the absolute value of the force modulus applied along a₂, and force is applied toward −a₂. The dwell time used in the simulations was τ^∗ = 4 ms. (E) Rotational pitch and (F) frequency of rotation for an ensemble of 10³ independent trajectories at zero load force in a landscape generated by Eq. 2 are shown, with asymmetry a₁/l₁ = 0.24, a₂/l₂ = 0.47 and varying dwell times in the range of τ^∗ = 36–72 ms, in 4 ms steps. Shaded error bars correspond to the standard error. To see this figure in color, go online.

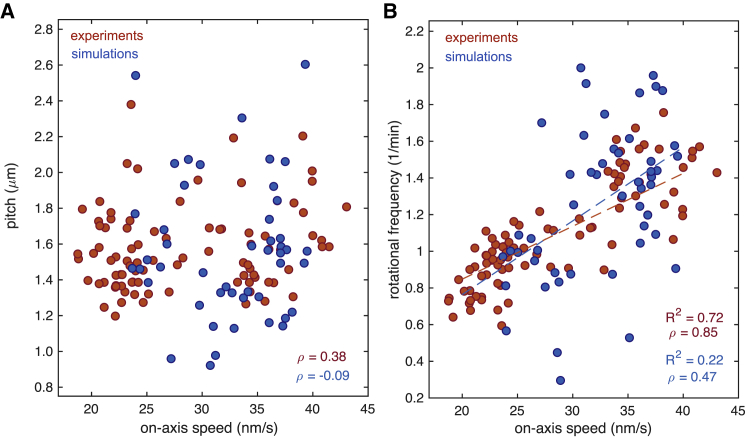
Figure 5.

(A) Rotational pitch and (B) the corresponding rotational frequency for the simulation results (blue circles) and the experimental data from Fig. 1F (red circles). The simulations are obtained for an ensemble of 10³ independent trajectories at zero load using a landscape generated according to Eq. 2, with asymmetry a₁/l₁ = 0.24, a₂/l₂ = 0.47 and varying the force applied in the direction of motion for τ^∗ = 46 ms (see Materials and Methods). The correlation of the pitch and the rotational frequency with the on-axis velocity is provided by the Pearson correlation coefficient ρ. The dashed lines correspond to fitted linear regressions with their corresponding coefficient of determination R². To see this figure in color, go online.

Simulation details

KIF1A trajectories were simulated by solving Eq. 3 using a second-order Euler method (Heun’s method), including a two-dimensional potential landscape given by Eq. 2. The numerical simulation of the stochastic part was carried out through a Gaussian random variate with null mean and variance equal to 1 according to the procedure developed in (40). To generate random numbers, we used the Mersenne Twister generator and the alternative Marsaglia-Tsang ziggurat and Kinderman-Monahan-Leva ratio methods (41). The discretization time step Δt was chosen as the smallest timescale of the system. In vitro experiments and previous studies (20, 26, 27, 30, 42) provided values for several parameters used in the simulation: D = 20 nm² ms⁻¹, τ = 4 ms, τ^∗ = 4–42 ms, θ = 0.45π, V₀ = 20k_BT, and U^∗ = 2V₀/100. The velocity at zero load was mainly modified by changing the dwell time τ^∗ (see Figs. 4 and 5).

Results

Experimental results

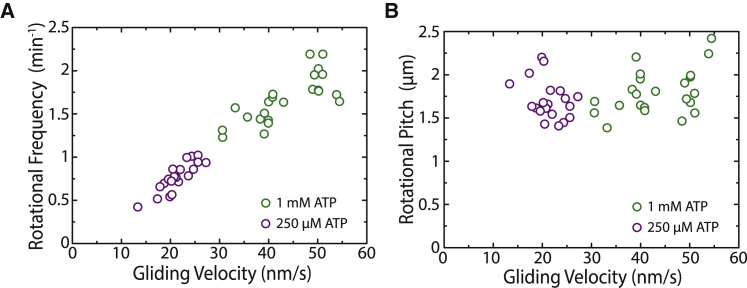
To investigate the longitudinal microtubule rotations driven by single-headed KIF1A motors, we performed gliding motility assays by 1) coating a reflective silicon surface with biotinylated KIF1A motors and 2) flushing in rhodamine-speckled microtubules (illustrated in Fig. 1 A). Biotinylated motors were linked to the surface via anti-biotin mouse antibodies, which in turn were bound to F(ab′)2 (or Fab) fragments coating the surface. Microtubules glided robustly with constant velocities in the range of 20–50 nm/s (see Fig. 1 B; Video S1). The velocities were found to be significantly lower compared to the case of KIF1A motors immobilized using anti-His antibodies (∼50–400 nm/s). However, because of the large spread in velocities in the latter case and for better comparison with the experiments in (20), we decided to immobilize the motors using anti-biotin antibodies. The microtubule gliding velocity did not vary with the concentration of Fab fragments, indicating no dependence on the motor density (see Fig. S1). This result is in agreement with theoretical studies predicting an early saturation of the velocity of KIF1A clusters with motor number (31). The reflective surface of the gliding assay enabled us to use FLIC microscopy to obtain rotational information in combination with forward motion for the gliding microtubules (7, 8, 24). As seen in Fig. 1 C, the recorded intensities of the speckles fluctuated periodically because of changes in speckle height with respect to the reflective surface. The periodicity of the intensity fluctuation provided us with the rotational pitch of the gliding microtubules. The mean rotational pitch was 1.5 ± 0.2 μm (mean ± SD, n = 100 gliding events; see Fig. 1 E), much shorter than the supertwist of GMP-CPP-grown taxol-stabilized microtubules (∼8 μm) (8, 24). To obtain the direction of rotation, several individual speckles from different microtubules were tracked using the tracking software FIESTA (37). In combination with the height information (obtained by FLIC), the sideways information revealed that the microtubules rotated counterclockwise in the direction of gliding motion (see Fig. 1 D and additional examples in Fig. S2). The rotational pitch did not vary significantly as a function of microtubule length (Fig. 1 E, inset). Furthermore, there was no significant dependence of the rotational pitch on the gliding velocity (Fig. 1 F, bottom). This implies that the rotational frequency, i.e., the number of motor sidesteps on the microtubule lattice per unit time, increases with increasing gliding velocity (Fig. 1 F, top). To investigate more carefully the dependence of the rotational pitch on the motor velocity, we varied the gliding velocity by changing the ATP concentration. Interestingly, we observed that a decrease in the ATP concentration reduced the gliding velocity but not the rotational pitch (Fig. 2, A and B). Hence, we conclude that the rotational pitch is remarkably robust to changes on the gliding velocity, ATP concentration, microtubule length, and motor density.

Figure 2.

Rotational frequency (A) and rotational pitch (B) plotted with respect to the gliding velocity for speckled microtubules gliding under low (250 μM) and high (1 mM) ATP conditions. The ATP concentration was switched in the same channel to keep all other parameters constant. A fourfold decrease in ATP concentration leads to an approximately twofold decrease of the gliding velocity, with a subsequent reduction on the frequency of rotation but no effect on the rotational pitch. To see this figure in color, go online.

Simulation results

To understand how KIF1A motors select the rotational pitch, we performed stochastic simulations of the dynamics of single KIF1A motors. Based on experimental observations and theoretical studies (20, 26, 27, 30, 31), we used a two-state Brownian ratchet model to simulate the dynamics of the motor on the microtubule lattice (see Fig. 3, A–D; Materials and Methods). Single KIF1A trajectories were found to be very noisy and followed a diffusive behavior at long timescales (Fig. 4, A and B). The motor movement was much more persistent in the longitudinal direction than in the transversal direction with randomness parameters $R_y\simeq 10$ and $R_x\simeq 300$, respectively (see Materials and Methods). The rotational pitch of a trajectory P and the frequency of rotation ω can be defined as P = v_y/ω and ω = v_x/(2πR_MT), where R_MT = 12.5 nm is the microtubule radius and v_x, v_y are the velocities in the transversal and longitudinal directions, respectively. Considering parameters extracted from the literature (see Simulation Details), at zero load, we obtained good agreement with experiments on the velocity and stall force of a single KIF1A motor (27, 30) as well as on the rotational pitch (see Fig. 4 C). Under on-axis loading (F = −Fa₁), the velocity-force curve remained unaltered for changes in the lateral asymmetry a₂, whereas the pitch exhibited a strong dependence (see Fig. 4 C, inset). Finally, under off-axis loading (F = −Fa₂), small changes in the lateral asymmetry had dramatic effects on the velocity-force relationship (Fig. 4 D). To test the robustness of the pitch to changes on the gliding velocities, we studied the pitch and the rotational frequency for different gliding velocities to compare the simulations with the experimental results in Fig. 1 F. There exist two main ways to change the gliding velocity in the simulations: 1) varying the ATP hydrolysis dwell time at zero load or 2) applying a certain force along the direction of motion. In the first case, we obtained that the pitch did not vary significantly as a function of the velocity of the motors, whereas the rotational frequency increased approximately linearly (see Fig. 4, E and F), in qualitative agreement with the experiments, by changing the ATP concentration (Fig. 2, A and B). In the second case, we changed the load along the direction of motion, and we kept the same value for the dwell time. This scenario mimics possible friction forces experienced by the motors during the gliding assay that might cause a dispersion on the velocities. The results obtained on the rotational pitch and frequency followed similar trends as for varying dwell times (Figs. 2, A and B and 4, E and F), and they quantitatively agreed with the experimental results (see Fig. 5, A and B). Altogether, we conclude that a Brownian ratchet description of single-headed KIF1A successfully explains the essential features observed experimentally.

Discussion

In this work, we have shown that the rotation of microtubules due to the action of single-headed KIF1A motors can be explained by a simple Brownian ratchet model on the microtubule lattice. Interestingly, the rotational pitch is independent on the gliding velocity, which implies that the frequency of rotation increases linearly with the velocity. These results are fundamentally different from recent studies on Kip3/Kinesin-8 or ncd/kinesin-14, in which the rotational pitch depends on the gliding velocity (9, 11). In the latter cases, an increase on the dwell time to hydrolyze an ATP molecule favors sidestepping with respect to forward stepping, whereas in our case, the dwell time affects both on-axis and off-axis movements, leaving the pitch unaffected. We find that both the experimental and theoretical pitch distributions are skewed (see Figs. 1 E and S3). We speculate that this is a consequence of the fact that the average value of the rotational frequency is similar to the magnitude of its fluctuations (Figs. 2 A and S3). Because the rotational pitch is inversely proportional to the rotational frequency (P ∼ 1/ω), a symmetric dispersion on ω leads to a nonsymmetric effect on the pitch, which translates into the skewness of the distribution.

The rotational pitch is found to be very similar to the one observed in tube-pulling experiments (20), in which KIF1A motors formed helical tubes around microtubules. This implies that both weak (membrane-bound) and strong (glass-bound) anchoring lead to similar results for the selection of the pitch. Our numerical simulations can reproduce such pitch values considering almost no lateral asymmetry $\left(a_2/l_2\simeq 0.47\right)$. In fact, even with a symmetric potential landscape along the off-axis direction (i.e., a₂/l₂ = 0.5), a spiraling motion can be obtained as a consequence of the handedness of the microtubule, which already breaks the left/right symmetry $\left(\theta \ne 0\right)$. The asymmetry parameter is likely to depend on the microtubule-motor interaction and thus be characteristic of each kinesin type. Slightly larger asymmetries $\left(a_2/l_2\simeq 0.4\right)$ lead to shorter pitch values ($\simeq 300$ nm), which could account for the observed pitch of other diffusive motors such as single-headed kinesin-1 (4, 6).

Finally, here, we compare the rotational pitch of microtubules in gliding assays to simulated data of the averaged rotational pitch of a single KIF1A motor. To what extent our single-motor description is valid to understand a multimotor process, such as the rotation of microtubules in a gliding assay, is unclear. Indeed, we cannot rule out the possibility that the observed pitch is different from the single-motor pitch. The simplest scenario is that collective effects only reduce the diffusivity (randomness) of the motors, leading to a more robust spiraling motion. However, a second possibility would be that the single-motor pitch is small, but collective effects play an important role and select a larger pitch, as proposed in (20), in which motors worked under loading conditions. To discern between these two possibilities, single-molecule tracking of the helical movement of single-headed KIF1A should in principle be performed, similarly as in (9, 43). However, the low processivity and high diffusivity of the motor seriously compromises this approach. Extending the numerical approach to groups of interacting motors could also shed some light into this point. Finally, our model can potentially explain the pitch of other weakly processive motors, such as single-headed kinesin-1 or kinesin-5, by changing the lateral asymmetry. Further work needs to be undertaken to confirm whether this mechanism also applies to other kinesin motors.

Author Contributions

A.M. performed experimental research. M.S. and D.O. performed theoretical research. D.O. and J.C. conceived the project. J.M.S., S.D., D.O., and J.C. directed the project. A.M., M.S., and D.O. wrote the manuscript. All authors approved the final version of the manuscript.

Editor: Steven Rosenfeld.