Cholesterol-Dependent Bending Energy Is Important in Cholesterol Distribution of the Plasma Membrane

Abstract

We consider the plasma membrane that contains a cholesterol molar fraction of 0.4 and ask how that cholesterol is distributed between the two leaves. Because of the rapid flip-flop of cholesterol between leaves, we assume that its distribution is determined by the equality of its chemical potentials in the two leaves. When we consider only the contributions of entropy and interactions to the cholesterol chemical potential in our model system, we find, not surprisingly, that the cholesterol is mostly in the outer leaf because of the strong attraction between cholesterol and sphingomyelin (SM), which is predominantly in that leaf. We find 72% there. We then include the contribution from the bending energy in each leaf that must be overcome to join the leaves in a flat bilayer. The product of bending modulus and spontaneous curvature is obtained from simulation. We find that the addition of cholesterol to the outer leaf reduces the spontaneous curvature, which is initially positive, until it passes through zero when the molar fraction of cholesterol in the outer leaf is 0.28. Additional cholesterol is driven toward the inner leaf by the sphingomyelin phosphatidylcholine mixture. This is resisted by the bending energy contribution to the inner leaf. We find, again by simulation, that the addition of cholesterol monotonically increases the magnitude of the spontaneous curvature of the inner leaf, which is negative. This increases its bending energy. We conclude that, as a result of these competing effects, the percentage of cholesterol in the outer leaf is reduced to ∼63 ± 6%.

Introduction

Despite the importance of the role of cholesterol in the mammalian plasma membrane (1), its distribution between the exoplasmic and cytoplasmic leaves is unknown. This is not because there have been no attempts to measure it. To the contrary, it has been measured many times, but the variation in the reported results is almost as large as it can possibly be: from a scant 8% in the cytoplasmic leaf (2) to a robust 90% in that leaf (3). There are about 10 other results scattered between. It is almost certain that the reported differences in the cholesterol distribution are due to the different probes and protocols used to measure it, and these have recently been comprehensively reviewed (4).

There has been much less theoretical work as to the distribution that might be expected. Because it is known that SM interacts strongly with cholesterol (5, 6, 7) and that over 90% of the SM in the plasma membrane is in the outer leaf (8), one might expect that most of the cholesterol in the plasma membrane would be in that leaf. That bending energy might be important to the cholesterol distribution was suggested by Giang and Schick (9). Noting that phosphatidylethanolamine (PE), which is found almost completely in the inner leaf, has a spontaneous curvature that is relatively large in magnitude, they suggested that cholesterol could be drawn to the inner leaf to relieve the stress caused by PE. They further hypothesized that the spontaneous curvature of PE could be reduced by cholesterol in a concentration-dependent manner. They predicted a distribution in which between 50 and 60% of the cholesterol would be in the inner leaf. Shortly thereafter, a very large molecular dynamics (MD) simulation of the plasma membrane (10), one which included 63 different lipid species, was carried out. Among other results, the authors obtained a distribution in which 46% of the cholesterol was found in the inner leaf. No explanation for the distribution obtained was provided.

Recently Courtney et al. (11) argued, on the basis of experiments carried out at 0°C and an MD simulation, that C24 SM in the outer leaf interdigitates with the chains of the inner leaf. Further, this causes defects in the chain packing, defects that draw cholesterol to the inner leaf to fill them. We leave a critique of their experimental protocol to the review of Steck and Lange (4), but the argument from the simulation does not seem plausible to us. The asymmetric bilayer simulated contained, in the inner leaf, cholesterol and almost equal amounts of dipalmitoylphosphatidylcholine and dioleoylphosphatidylcholine. Thus, the percentage of phospholipids with two saturated chains was nearly 50%. At this amount, the chains of the inner leaf would be sufficiently well ordered that an interdigitating chain could well create a defect in the packing. But this large percentage of saturated lipids does not at all reflect the composition of the inner leaf of the plasma membrane because it contains only on the order of a few percentage of them (8). The vast majority of unsaturated lipid tails are sufficiently disordered that the concept of an added defect caused by an interdigitating chain seems inapplicable.

In this article, we show that the SM in the outer leaf of the plasma membrane plays a hitherto unsuspected role in driving cholesterol toward the inner leaf of the plasma membrane. By simulating an outer leaf consisting of a 1:1 ratio (8) of C16 sphingomyelin (SM) to palmitoyloleoylphosphatidylcholine (POPC) and varying amounts of cholesterol, we show that the bending energy needed to bring such a leaflet into a flat bilayer depends upon the concentration of cholesterol. At small concentrations, the spontaneous curvature of the leaflet is positive, reflecting the contribution of SM. With the addition of cholesterol, the spontaneous curvature decreases and vanishes at a cholesterol molar (mol) fraction of 0.28. At this point, the bending energy contribution to the energy of the outer leaf is zero. Beyond this amount of cholesterol in the outer leaf, the spontaneous curvature becomes negative, and its magnitude increases with increasing cholesterol concentration. This increases the bending energy from the outer leaf. To reduce it, the SM POPC mixture drives cholesterol toward the inner leaf. This is resisted by the inner leaf, as we show by a simulation of an inner leaf with POPE, palmitoyloleoylphosphatidylserine (POPS), and POPC in a 5:3:1 ratio (8) at various cholesterol concentrations. We find that the spontaneous curvature of the inner leaf is negative and, in contradiction to the hypothesis of (9), its magnitude increases monotonically with cholesterol concentration. Employing, in addition, a simple regular solution free energy, assuming equal areas of the two leaves, and a mol fraction of cholesterol in the bilayer (12) of 0.4, we find that the chemical potentials of the cholesterol in the two leaves are equal when ∼37 ± 6% of the total cholesterol is in the inner leaf. This is similar to the result of (10) and provides an explanation for its value.

Methods

Theoretical model

We consider a model bilayer in which the outer leaf contains SM, POPC, and cholesterol, and the inner leaf contains POPE, POPS, POPC, and cholesterol. The system is shown schematically in Fig. 1.

Figure 1.

Schematic illustration of the model bilayer. It is composed of SM and POPC in a 1:1 ratio and cholesterol in the outer leaf and POPE, POPS, and POPC in a 5:3:1 ratio and cholesterol in the inner leaf. The mol fraction of cholesterol in the bilayer is 0.4.

The numbers of molecules of each component in the outer leaf are denoted $N_{SM}^O$, $N_{PC}^O$, and $N_C^O$, and those in the inner leaf are denoted $N_{PE}^I$, $N_{PS}^I$, $N_{PC}^I$, and $N_C^I$. The total number of molecules in the outer leaf is $N_{tot}^O$ and in the inner leaf is $N_{tot}^I$. It is convenient to work with the mol fractions of the components in each leaf;

$$y_{Co}\equiv \frac{N_C^O}{N_{tot}^O},y_{PCo}\equiv \frac{N_{PC}^O}{N_{tot}^O},y_{SM}\equiv \frac{N_{SM}^O}{N_{tot}^O},$$ (1)

$$y_{Ci}\equiv \frac{N_C^I}{N_{tot}^I},y_{PCi}\equiv \frac{N_{PC}^I}{N_{tot}^I},y_{PE}\equiv \frac{N_{PE}^I}{N_{tot}^I},y_{PS}\equiv \frac{N_{PS}^I}{N_{tot}^I}.$$ (2)

We consider the two leaves of the bilayer to be coupled only by the rapid interchange of cholesterol between them (13, 14, 15). Therefore, the free energy of the bilayer can be written in the form

$$F_{bi}=N_{tot}^O{f}^O\left(T,y_{Co},y_{PCo},y_{SM}\right)+N_{tot}^I{f}^I\left(T,y_{Ci},y_{PCi},y_{PE},y_{PS}\right),$$ (3)

where T is the temperature. The chemical potentials of cholesterol in the two leaves, then, are

$${\mu }_{Co}\left(T,y_{Co},y_{PCo},y_{SM}\right)=\frac{\mathit{\partial }{F}_{bi}}{\mathit{\partial }{N}_C^O}=f^O+\frac{\mathit{\partial }{f}^O}{\mathit{\partial }{y}_{Co}}-\sum _j{y}_j\frac{\mathit{\partial }{f}^O}{\mathit{\partial }{y}_j},$$ (4)

$${\mu }_{Ci}\left(T,y_{Ci},y_{PCi},y_{PE},y_{PS}\right)=\frac{\mathit{\partial }{F}_{bi}}{\mathit{\partial }{N}_C^I}=f^I+\frac{\mathit{\partial }{f}^I}{\mathit{\partial }{y}_{Ci}}-\sum _k{y}_k\frac{\mathit{\partial }{f}^I}{\mathit{\partial }{y}_k}.$$ (5)

Here, j = SM, PC_o, and C_o and k = PE, PS, PC_i, and C_i. We determine the cholesterol distribution by requiring that the chemical potentials of the cholesterol in the two leaves be equal,

$${\mu }_{Co}\left(T,y_{Co},y_{PCo},y_{SM}\right)={\mu }_{Ci}\left(T,y_{Ci},y_{PCi},y_{PE},y_{PS}\right).$$ (6)

For a given temperature, this is one equation in seven unknowns. Two other equations are, of course:

$$y_{Co}+y_{PCo}+y_{SM}=1,\text{and}$$ (7)

$$y_{Ci}+y_{PCi}+y_{PE}+y_{PS}=1.$$ (8)

Further, we shall specify the total concentration of cholesterol in the bilayer, x_c = 0.4 (12), which provides another equation:

$$x_c=\frac{\left(N_{tot}^I/N_{tot}^O\right)y_{Ci}+y_{Co}}{\left(N_{tot}^I/N_{tot}^O\right)+1}.$$ (9)

Specification of the system is completed by setting the ratios of SM to PC in the outer leaf to be 1:1 and the ratios of PE to PS to PC in the inner leaf to be 5:3:1, ratios that are all reasonable (8).

We begin with a system of two separated leaves that are each relaxed in that they have no bending energy. The leaves are then put together to form a flat bilayer. Our objective is to calculate the free energy of this bilayer, and we accomplish this in two steps. First, we focus on the contributions to the free energy from the intermolecular interactions and from the entropy and ignore the energy required to bend the leaves into the flat state. After this first step is taken, we add the bending energy contribution to the free energy in a second, distinct step.

To calculate the free energy of the assembled bilayer, there are two reasonable choices of ensembles: one in which the surface tensions of each of the two leaves are specified and their areas fluctuate, and the ensemble in which the areas of each leaf are specified and their surface tensions fluctuate. Average quantities in the two ensembles are the same, of course. For convenience, we choose the latter ensemble. We shall take the areas of the two leaves to be equal. Given that the fractional difference in their areas is of the order of the thickness of the plasma membrane to the size of a cell, a fractional difference on the order of 10⁻³, this is reasonable. In this ensemble, as one cholesterol molecule flips from the outer to the inner leaf, another cholesterol flips from the inner to the outer leaf. On the timescale of the cholesterol flipping, the phospholipids do not go from one leaf to the other.

We shall also consider the plasma membrane to be an incompressible fluid. As a consequence, the area A of each leaf is not an independent thermodynamic variable but is related to the number of molecules in the leaf as follows. Let the average area per phospholipid, 0.7 nm² (16), be denoted a, and the area of a cholesterol molecule, 0.42 nm² (17), be a_c. The ratio of the areas of cholesterol to phospholipid a_c/a will be denoted r and is equal to 0.6. We shall henceforth write ra for the area of a cholesterol molecule. The area of the leaves can now be written as follows:

$$A=a\left(N_{SM}^O+N_{PC}^O+r{N}_C^O\right)=a\left[N_{tot}^O-\left(1-r\right)N_C^O\right],$$ (10)

$$\text{with}{N}_{tot}^O\equiv N_{SM}^O+N_{PC}^O+N_C^O,$$ (11)

$$\text{A}=a\left(N_{PE}^I+N_{PC}^I+N_{PS}^I+r{N}_C^I\right)=a[N_{tot}^I-\left(1-r\right)N_C^I),$$ (12)

$$\text{with}{N}_{tot}^I\equiv N_{PE}^I+N_{PC}^I+N_{PS}^I+N_C^I.$$ (13)

Because the areas of the two leaves are equal and the leaves have different amounts of the smaller cholesterol, the numbers of molecules in the leaves are different. From the equality of the leaf areas, it follows that

$$\frac{N_{tot}^I}{N_{tot}^O}=\frac{1-\left(1-r\right)y_{Co}}{1-\left(1-r\right)y_{Ci}},$$ (14)

so that the total mol fraction of cholesterol x_c, Eq. 9, is

$$x_c\equiv \frac{N_C^I+N_C^O}{N_{tot}^I+N_{tot}^O}=\frac{y_{Ci}+y_{Co}-2\left(1-r\right)y_{Ci}{y}_{Co}}{2-\left(1-r\right)\left(y_{Ci}+y_{Co}\right)}.$$ (15)

Once we have determined the mol fraction of cholesterol in each leaf, y_Ci and y_Co, we obtain the central quantity of interest to us, the percentage of the total cholesterol that is in the inner leaf, F, from

$$\frac{F}{100}\equiv \frac{N_C^I}{N_C^I+N_C^O}=\frac{y_{Ci}}{2x_c}\frac{\left[1-\left(1-r\right)x_c\right]}{\left[1-\left(1-r\right)y_{Ci}\right]}.$$ (16)

To calculate the free energy of the bilayer ignoring any bending energy, we consider a model in which the bilayer consists of two triangular lattices, the inner one consisting of $N_{tot}^I$ sites and the outer of $N_{tot}^O$ sites. Each site of the inner lattice is occupied by a molecule, either of PE, PS, PC, or cholesterol. Similarly, each site of the outer lattice is occupied either by an SM, a PC, or a cholesterol molecule. The energy of a specific configuration is given by the following:

$$\begin{array}{c}{E}_{bi}=E_m^O\left(N_{SM}^O,N_{PC}^O,N_C^O\right)+E_m^I\left(N_{PE}^I,N_{PS}^I,N_{PC}^I,N_C^I\right),\\ E_m^O=\frac{1}{2}\sum _{i,j}\sum _{\beta }\sum _{\alpha }{g}_{\alpha ,\beta }{P}_{\alpha ,i}^O{P}_{\beta ,j}^O\\ =\frac{1}{2}\sum _{i,j}\sum _{\alpha }{g}_{\alpha ,\alpha }{P}_{\alpha ,i}^O{P}_{\alpha ,j}^O+\frac{1}{2}\sum _{i,j}\sum _{\beta \ne \alpha }\sum _{\alpha }{g}_{\alpha ,\beta }{P}_{\alpha ,i}^O{P}_{\beta ,j}^O\end{array}$$ (17)

where sites i and j are the nearest neighbors, g_α,β are interaction energies between nearest-neighbor α and β molecular species, the subscripts m and bi stand for monolayer and bilayer, respectively, and the statistical variables are as follows:

$$\begin{array}{ll}{P}_{\alpha ,i}^O=1\hfill & \text{if}\text{site}\text{i}\text{is}\text{occupied}\text{by}\text{a}\text{molecule}\text{of}\text{species}\alpha \hfill \\ =0\hfill & \text{otherwise}.\hfill \end{array}$$ (18)

Thus,

$$\begin{array}{cc}\sum _{\alpha }{P}_{\alpha ,i}^O=1,& \text{and}\sum _i{P}_{\alpha ,i}^O=N_{\alpha }^O.\end{array}$$ (19)

Similarly, the energy of a configuration of the inner layer is as follows:

$$E_m^I=\frac{1}{2}\sum _{i,j}\sum _{\gamma }{g}_{\gamma ,\gamma }{P}_{\gamma ,i}^I{P}_{\gamma ,j}^I+\frac{1}{2}\sum _{i,j}\sum _{\delta \ne \gamma }{g}_{\gamma ,\delta }{P}_{\gamma ,i}^I{P}_{\delta ,j}^I.$$ (20)

Using

$$P_{\alpha ,j}^O=1-\sum _{\beta \ne \alpha }{P}_{\beta ,j}^O$$ (21)

in the first term of the energy, Eq. 17, and the property g_α,β = g_β,α we can rewrite $E_m^O$ in the form

$$E_m^O=\sum _{ij}\sum _{<\alpha ,\beta >}\left[g_{\alpha ,\beta }-\frac{\left(g_{\alpha ,\alpha }+g_{\beta ,\beta }\right)}{2}\right]P_{\alpha ,i}^O{P}_{\beta ,j}^O+\frac{1}{2}\sum _{i,j}\sum _{\alpha }{g}_{\alpha \alpha }{P}_{\alpha ,i}^O=\sum _{i,j}\sum _{<\alpha ,\beta >}{\mathrm{\epsilon }}_{\alpha ,\beta }{P}_{\alpha ,i}^O{P}_{\beta ,j}^O+3\sum _{\alpha }{g}_{\alpha ,\alpha }{N}_{\alpha }^O,$$ (22)

where the sum over <α,β> denotes a sum over all distinct pairs of components. We have defined

$${\mathrm{\epsilon }}_{\alpha ,\beta }\equiv g_{\alpha ,\beta }-\frac{\left(g_{\alpha ,\alpha }+g_{\beta ,\beta }\right)}{2}.$$ (23)

Thus, the energy of a specific configuration of the bilayer can be written as follows:

$$\begin{array}{l}{E}_{bi}=\sum _{i,j}\sum _{<\alpha ,\beta >}{\mathrm{\epsilon }}_{\alpha ,\beta }{P}_{\alpha ,i}^O{P}_{\beta ,j}^O+3\sum _{\alpha }{g}_{\alpha ,\alpha }{N}_{\alpha }^O\\ +\sum _{m,n}\sum _{<\gamma ,\delta >}{\mathrm{\epsilon }}_{\gamma ,\delta }{P}_{\gamma ,m}^I{P}_{\delta ,n}^I+3\sum _{\gamma }{g}_{\gamma ,\gamma }{N}_{\gamma }^I.\end{array}$$ (24)

The free energy of the system is obtained, in principle, from

$$\text{exp}\left(-F_{bi}/k_{B}T\right)=Tr\exp \left(-E_{bi}/k_{B}T\right),$$ (25)

where the trace is over all the configurations of the statistical variables $P_{\alpha ,i}^O$ and $P_{\gamma ,n}^I.$

A good approximation to the exact free energy is provided by mean-field theory. Given that microstates are specified by the location of all molecules, although macrostates are specified only by the mol fractions of the components, mean-field theory approximates the exact free energy, a sum over all microstates, by the free energy of the most probable macrostate, the one compatible with the largest number of microstates. The approximation ignores all effects of fluctuations about the most probable macrostate. The mean-field approximation to the free energy of Eqs. 24 and 25 is known as the regular solution free energy, and can be written

$$F_{rs}=N_{tot}^O{f}_{rs}^O+N_{tot}^I{f}_{rs}^I,$$ (26)

with the free energies per particle

$$\begin{array}{l}{f}_{rs}^O=f_{int}^O+f_{same}^O+f_{ent}^O\hfill \\ f_{int}^O=6{\mathrm{\epsilon }}_{SM,PC}{y}_{SM}{y}_{PCo}+6{\mathrm{\epsilon }}_{SM,C}{y}_{SM}{y}_{Co}+6{\mathrm{\epsilon }}_{PC,C}{y}_{PCo}{y}_{Co}.\hfill \end{array},$$ (27)

$$f_{same}^O=3g_{SM,SM}{y}_{SM}+3g_{PC,PC}{y}_{PCo}+3g_{C,C}{y}_{Co},$$ (28)

$$f_{ent}^O=k_{B}T\left[y_{SM}\ln \left(y_{SM}\right)+y_{PCo}\ln \left(y_{PCo}\right)+y_{Co}\ln \left(y_{Co}\right)\right],$$ (29)

and

$$\begin{array}{c}{f}_{rs}^I=f_{int}^I+f_{same}^I+f_{ent}^I\\ f_{int}^I=6{\mathrm{\epsilon }}_{PE,PC}{y}_{PE}{y}_{PCi}+6{\mathrm{\epsilon }}_{PE,C}{y}_{PE}{y}_{Ci}+6{\mathrm{\epsilon }}_{PE,PS}{y}_{PE}{y}_{PS}\\ +6{\mathrm{\epsilon }}_{PS,PC}{y}_{PS}{y}_{PCi}+6{\mathrm{\epsilon }}_{PS,C}{y}_{PS}{y}_{Ci}+6{\mathrm{\epsilon }}_{PC,C}{y}_{PCi}{y}_{Ci},\end{array}$$ (30)

$$f_{same}^I=3g_{PE,PE}{y}_{PE}+3g_{PS,PS}{y}_{PS}+3g_{PC,PC}{y}_{PCi}+3g_{C,C}{y}_{Ci},$$ (31)

$$\begin{array}{l}{f}_{ent}^I=k_{B}T[y_{PE}\ln \left(y_{PE}\right)+y_{PCi}\ln \left(y_{PCi}\right)\\ +y_{PS}\ln \left(y_{PS}\right)+y_{C_i}\ln \left(y_{Ci}\right)],.\end{array}$$ (32)

The regular solution free energy has a form that is typical of mean-field theories; the entropy is simply that of an ideal mixture, whereas the energy is not ideal. An insight into the question of whether the neglect of composition fluctuations significantly affects our calculation of the cholesterol partitioning can be obtained by a comparison of the system of interest to an Ising model. In our case, a cholesterol molecule is either in the outer leaf or the inner leaf, just as an Ising spin is either up or down. The asymmetric composition of the two leaves is equivalent in the Ising system to the imposition of an external magnetic field. The relation we seek, that between the cholesterol distribution and the asymmetric composition of the leaves, is analogous to the relation between the magnetization of the Ising system and the external field. The effects of fluctuations on the thermodynamic properties of the two-dimensional Ising model are known from its exact solution (18). Their effects on nonuniversal properties, such as the temperature of the critical point, which is driven down by fluctuations, is significant. However, their effects on universal properties, such as that between the magnetization and an external field, are not large, except in the vicinity of a critical point. As there is no evidence that the temperature and composition of the mammalian plasma membrane place it close to a critical point, we conclude that the cholesterol distribution obtained in the absence of fluctuations should serve as a reliable approximation to the physical distribution.

Given the free energy per particle of the inner leaf, Eqs. 30, 31, and 32, one obtains the contributions of the interactions and of the entropy to the cholesterol chemical potential of the inner leaf:

$$\begin{array}{c}{\mu }_{C,rs}^I={\mu }_{C,int}^I+{\mu }_{C,same}^I+{\mu }_{C,ent}^I\\ \frac{{\mu }_{C,int}^I}{k_{B}T}=6\{\left[\frac{{\mathrm{\epsilon }}_{PS,C}}{k_{B}T}{y}_{PS}+\frac{{\mathrm{\epsilon }}_{PE,C}}{k_{B}T}{y}_{PE}+\frac{{\mathrm{\epsilon }}_{PC,C}}{k_{B}T}{y}_{PCi}\right]\left(1-y_{Ci}\right)\\ -\frac{{\mathit{\epsilon }}_{PE,PS}}{k_{B}T}{y}_{PS}{y}_{PE}-\frac{{\mathit{\epsilon }}_{PC,PS}}{k_{B}T}{y}_{PC}{y}_{PS}-\frac{{\mathit{\epsilon }}_{PE,PC}}{k_{B}T}{y}_{PCi}{y}_{PE}\}\end{array},$$ (33)

$$\frac{{\mu }_{same}^I}{k_{B}T}=3\frac{g_{C,C}}{k_{B}T},$$ (34)

$$\frac{{\mu }_{C,ent}^I}{k_{B}T}=\text{ln}\left(y_{Ci}\right).$$ (35)

Similarly, one obtains the contributions from the interactions and entropy to the chemical potential of the cholesterol in the outer leaf:

$$\begin{array}{l}{\mu }_{C,rs}^O={\mu }_{C,int}^O+{\mu }_{same}^O+{\mu }_{C,ent}^O\\ \frac{{\mu }_{C,int}^O}{k_{B}T}=6\{\left[\frac{{\mathrm{\epsilon }}_{SM,C}}{k_{B}T}{y}_{SM}+\frac{{\mathrm{\epsilon }}_{PC,C}}{k_{B}T}{y}_{PCo}\right]\left(1-y_{Co}\right),\\ -\frac{{\mathrm{\epsilon }}_{SM,PC}}{k_{B}T}{y}_{SM}{y}_{PCo}\}\end{array}$$ (36)

$$\frac{{\mu }_{same}^O}{k_{B}T}=3\frac{g_{C,C}}{k_{B}T},$$ (37)

$$\frac{{\mu }_{C,ent}^O}{k_{B}T}=\text{ln}\left(y_{Co}\right).$$ (38)

We note that the contributions ${\mu }_{same}^I$ and ${\mu }_{same}^O$ are constant, independent of the concentrations, and are equal to one another. Hence, when we obtain the cholesterol distribution by equating the cholesterol chemical potentials in the two leaves, these contributions will cancel, not affecting the cholesterol distribution. Thus, we shall subsequently ignore them.

To proceed, we must choose the relative pair-wise interactions ε_α,β of Eq. 23. Many of these interactions have been measured experimentally. The results have been tabulated by Almeida (19), who denotes them as ω_α,β. Were we to employ these values, however, any estimate of a miscibility transition temperature produced by our regular solution theory would be too high because of the exclusion of fluctuations, as noted above. Hence, to obtain experimental transition temperatures, we must decrease the values of the ε_α,β we employ. As shown in (9), we should take ε_α,β = 0.6 ω_α,β. For example, whereas Almeida quotes from experiment (20) for the SM, cholesterol pair the value ω_SM,C = −600 cal/mol at 37°C, or −0.97 k_BT, we must choose ε_SM,C = −0.58 k_BT.

The interactions fall naturally into two classes: those between a phospholipid and cholesterol and those between two phospholipids. Those in the first class are the larger, presumably because of the relatively rigid ring section of cholesterol. As noted above, we take ε_SM,C/k_BT = −0.58, which is the strongest of the interactions. For the others in this class we take ε_PE,C/k_BT = 0.28, ε_PC,C/k_BT = 0.20, and ε_PS,C/k_BT = −06. See the Appendix of (9) for the rationale of the choices for pair interactions that are not found in the table given by Almeida (19). The interactions between phospholipids are comparatively weak, presumably because the chains are relatively disordered. Indeed, for the interaction between SM and POPC, Almeida, citing an experiment at 37°C (20), quotes ω_SM,POPC = 0. This, of course, implies ε_SM,PC/k_BT = 0. We take all other such pair interactions, ε_PE,PC/k_BT = ε_PE,PS/k_BT = ε_PS,PC/k_BT to vanish also.

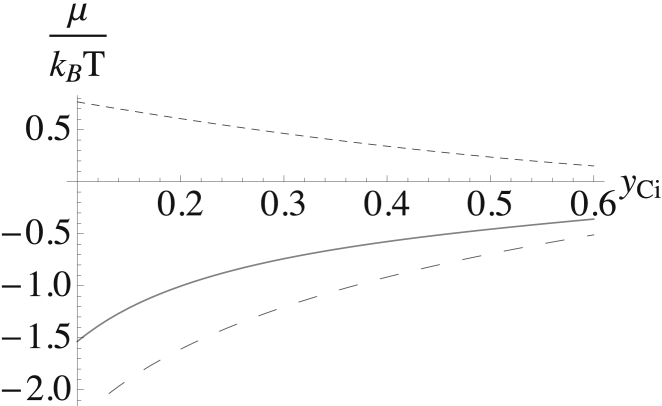
The two contributions to the cholesterol chemical potential of the inner leaf, ${\mu }_{C,int}^I$ and ${\mu }_{C,ent}^I$, and their sum are shown in Fig. 2 as a function of the mol fraction of cholesterol in the inner leaf, y_Ci. We note that the sum is an increasing function of the cholesterol content of the inner leaf, y_Ci, as it must be if the leaf is to be locally stable.

Figure 2.

Contributions to the chemical potential of the cholesterol in the inner leaf plotted versus the mol fraction of cholesterol in the inner leaf y_Ci. That from the interactions is shown by the smaller-dashed line; that from the entropy is shown by the larger-dashed line. The sum of the two is shown by the solid line.

In Fig. 3, we show the two contributions to the cholesterol chemical potential of the outer leaf and their sum. Note that the chemical potential in the outer leaf is a decreasing function of the amount of cholesterol in the inner leaf. But this is as it should be because, with a constant total cholesterol concentration in the bilayer, the concentration of cholesterol in the outer leaf decreases as that in the inner leaf increases. Hence, Fig. 3 shows that the chemical potential of the cholesterol in the outer leaf decreases with a decreasing concentration of cholesterol in that leaf. This demonstrates that the outer leaf is locally stable.

Figure 3.

Contributions to the chemical potential of the cholesterol in the outer leaf plotted versus the mol fraction of cholesterol in the inner leaf y_Ci. That from the interactions is shown by the smaller-dashed line; that from the entropy is shown by the larger-dashed line. The sum of the two is shown by the solid line.

Because the chemical potential of the cholesterol in the inner leaf increases with the mol fraction of cholesterol in the inner leaf, and the chemical potential of the cholesterol in the outer leaf decreases with it, the two chemical potentials are equal at some y_Ci. This determines the equilibrium distribution. The two chemical potentials are shown in Fig. 4 plotted versus y_Ci. They are equal at a value of y_Ci = 0.24. With a total mol fraction of cholesterol in the bilayer of 0.4, we find y_Co = 0.54 from Eq. 15 and then from Eq. 16, that this corresponds to F = 28% of the total cholesterol being in the inner leaf. As expected, the attractive interaction of cholesterol and SM in the outer leaf draws most of the cholesterol there.

Figure 4.

The chemical potentials of the cholesterol in the inner and outer leaves are shown as a function of the mol fraction of cholesterol in the inner leaf, y_Ci. The point at which they are equal determines the cholesterol distribution.

We now proceed to include the bending energy contribution to the free energy of the bilayer, that is, the energy that it takes to assemble the two monolayers into a bilayer. Because the natural, or spontaneous, curvatures of the two monolayers are nonzero in general, it does take energy to put the two monolayers together. This increases the internal energy of the bilayer. Regular solution theory does not encompass this bending energy because it treats the molecules as structureless particles so that its estimate of the free energy depends solely on the composition of the two leaves and not on their physical configuration (e.g., flat or curved). To include the contribution of the bending energy, one could utilize a more complete description of the molecules. In particular, one could specify their headgroups and the acyl chains because it is the interactions like hydrogen bonding involving the former and hardcore repulsions between the latter that bring about the curvature of the monolayer. Alternatively, one can add to the free energy a phenomenological bending term.

$$\frac{F_{bend}}{k_{B}T}=\frac{{\kappa }_m^I}{2k_{B}T}\int d{\mathbf{r}}^{\mathbf{I}}{\left[H\left({\mathbf{r}}^{\mathbf{I}}\right)-H_0^I\right]}^2+\frac{{\kappa }_m^O}{2k_{B}T}\int d{\mathbf{r}}^{\mathbf{O}}{\left[H\left({\mathbf{r}}^{\mathbf{O}}\right)-H_0^O\right]}^2,$$ (39)

where ${\kappa }_m^I$ is the bending modulus of the inner monolayer, H(r^I) is its local curvature, and $H_0^I$ is the spontaneous curvature of the leaf. Given that the spontaneous curvatures of the lipids that make up the membrane are on the order of inverse nanometers and that of the cell membrane itself is 1000 times smaller, we shall treat the bilayer as if it were flat. The bending energy per molecule of a monolayer in such a bilayer is, in units of k_BT, of the order of $\left(a{\kappa }_m/2k_{B}T\right)H_0^2$, where, again, a is the area per phospholipid. If this contribution to the free energy is to be comparable to that from the entropy, which in units of k_BT is of order unity, then the spontaneous curvature must be on the order of (aκ_m/2 k_BT)^−1/2. With a ≈ 0.7 nm² and taking the monolayer bending modulus to be 22 k_BT, which is one half that of a bilayer (21), one obtains an estimate of |H₀| ≈ 0.35 nm⁻¹. As the spontaneous curvature of POPE is −0.32 nm⁻¹ (22), it is reasonable to expect that the bending energy will play an important role in the cholesterol distribution, provided that the bending energy is cholesterol dependent (9). That it is so seems clear both from experiment (23) and theory (24). We also remark that the relative flatness of the plasma membrane is not due to equal spontaneous curvatures in its two leaves. The size of a cell, unlike the size of a lipid bilayer vesicle, is not mainly determined by its membrane’s spontaneous curvature but rather by its contents, the forces arising from the cytoskeleton and osmotic pressures, etc. Consequently, we do not expect that the magnitude of the spontaneous curvatures of the two leaves that result from the cholesterol distribution we find will necessarily be nearly identical.

The increase in the membrane free energy because of a spontaneous curvature in the outer leaf being part of a flat bilayer can be written as follows:

$$\begin{array}{l}\frac{F_{bend}^O}{k_{B}T}=A^O\frac{{\kappa }_m^O}{2k_{B}T}{\left(H_0^O\right)}^2=N_{tot}^O\frac{f_{bend}^O}{k_{B}T}\\ \frac{f_{bend}^O}{k_{B}T}=\frac{a{\kappa }_m^O}{2k_{B}T}\left[1-\left(1-r\right)y_{Co}\right]{\left(H_0^O\right)}^2.\end{array}$$ (40)

Similarly, the contribution from the inner leaf is as follows:

$$\begin{array}{l}\frac{F_{bend}^I}{k_{B}T}=A^I\frac{{\kappa }_m^I}{2k_{B}T}{\left(H_0^I\right)}^2=N_{tot}^I\frac{f_{bend}^I}{k_{B}T}\\ \frac{f_{bend}^I}{k_{B}T}=\frac{a{\kappa }_m^I}{2k_{B}T}\left[1-\left(1-r\right)y_{Ci}\right]{\left(H_0^I\right)}^2.\end{array}$$ (41)

From these expressions, one obtains the contributions from the bending to the cholesterol chemical potentials of the inner and outer leaves:

$$\frac{{\mu }_{C,bend}^I}{k_{B}T}=\frac{a}{2k_{B}T}\left\{r{\kappa }_m^I{\left(H_0^I\right)}^2+\left[1-\left(1-r\right)y_{Ci}\right]\left[\frac{\mathit{\partial }\left[{\kappa }^I{\left(H_0^I\right)}^2\right]}{\mathit{\partial }{y}_{Ci}}-\sum _k{y}_k\frac{\mathit{\partial }\left[{\kappa }_m^I{\left(H_0^I\right)}^2\right]}{\mathit{\partial }{y}_k}\right]\right\},$$ (42)

$$\frac{{\mu }_{C,bend}^O}{k_{B}T}=\frac{a}{2k_{B}T}\left\{r{\kappa }_m^O{\left(H_0^O\right)}^2+\left[1-\left(1-r\right)y_{Co}\right]\left[\frac{\mathit{\partial }\left[{\kappa }^O{\left(H_0^O\right)}^2\right]}{\mathit{\partial }{y}_{Co}}-\sum _j{y}_j\frac{\mathit{\partial }\left[{\kappa }_m^O{\left(H_0^O\right)}^2\right]}{\mathit{\partial }{y}_j}\right]\right\}$$ (43)

We remark that, in the usual convention, the spontaneous curvature of a lipid in the inner leaf has the opposite sign from that of the same molecule in the outer leaf. However, because the bending energy contribution to the cholesterol chemical potential is quadratic in the spontaneous curvature, we can, for clarity, ignore this convention. In this article, we shall employ the sign convention that, irrespective of the leaf in which it is located, the spontaneous curvature of a lipid is positive if its headgroup region is dilated and its tails compressed and is negative if the tail region is expanded and the heads compressed.

To proceed further, we note that the product of κ_mH₀ can be obtained for monolayers of various compositions by simulation methods. This is achieved by simulating a symmetric bilayer consisting of two copies of the monolayer of interest and evaluating the normal and transverse components of the pressure profile, p_N(z) and p_T(z). From them, one obtains (25, 26)

$$\frac{{\kappa }_m}{k_{B}T}{H}_0=\frac{1}{k_{B}T}\int z\left[p_T\left(z\right)-p_N\left(z\right)\right]dz,$$ (44)

where the integration is from the center of the bilayer, z = 0, to the top of the periodic cell.

Simulation methods

All MD simulations were run with the NAMD simulation package (27) version 2.12. The C36 CHARMM lipid all-atom model (28, 29) was used. For the purposes of computing the lateral pressure profile, some code modifications were required to achieve the same behavior obtained in previous works. The code modifications are available as a patch from GitHub.

The time step for dynamics integration was 2 fs. Bonds with hydrogen atoms were held rigid using the SETTLE algorithm. Nonbonded van der Waals forces were switched off between 1.00 and 1.20 nm. Electrostatics were computed, at each step, using the particle mesh Ewald method with interpolation order six. The grid size was at least one point per 0.1 nm. Systems were built with the CHARMM-GUI web system (30, 31) and downloaded scripts. Structures with bonds erroneously passing through cholesterol rings were rebuilt.

Unless otherwise specified, at least 300 ns of ensemble was acquired for each system in the Nγ$P_z$T ensemble. The temperature was controlled at 37°C using the Langevin thermostat with damping coefficient set to 1 ps⁻¹. Pressure was controlled using the Langevin piston method (32) with the piston period and decay set to 50 and 25 fs, respectively. The pressure along z, approximately normal to the membrane, was set to one atmosphere, whereas the lateral tension was set to zero.

The lateral pressure profile was computed with 250 slabs along the z coordinate. With the use of the NAMD reprocessing system, the Ewald contribution was recomputed with the grain set to 60, 60, and 72, along the x, y, and z dimensions. In addition to the Ewald contribution, the non-Ewald contribution to the lateral pressure profile was recomputed with the above code patches. For these calculations, configurations from the original ensemble were read in every 80 ps and run for 1 ps. For the recalculation of the nearly invariant Ewald contribution, configurations were run for a single time step on each of the same saved configurations of the original ensemble.

A water layer of 2.25 nm was applied above and below the bilayer. For systems with anionic lipids, this value was extended to 5.0 nm to allow for the anionic and cationic concentrations to converge. The CHARMM-GUI mechanism estimates the number of positive (K⁺) and negative (Cl⁻) ions required to achieve a bulk concentration of 150 mM. These estimates tended to be too low for our systems, equilibrating in the range of 140 mM at no cholesterol to 100 mM at 0.6 mol fraction cholesterol. Additional simulations using the CHARMM-GUI recommendation for 250 mM were executed, with the ensemble extending to at least 150 ns. Values of κ_mH₀ were then linearly interpolated to 150 mM. The maximal adjustment to κ_mH₀ was 0.195 k_BT/nm.

Snapshots from the simulation are shown in Figs. 5 and 6.

Figure 5.

Snapshot of the simulation of a bilayer with leaves of the same composition equal to that of the outer leaf of our model bilayer. The molecules are color coded as follows: SM are red, POPC are blue, and cholesterol is green. The ratio of SM:POPC is 1:1. The fraction of cholesterol is y_Co = 0.5.

Figure 6.

Snapshot of the simulation of a bilayer with leaves of the same composition equal to that of the inner leaf of our model bilayer. The molecules are color coded as follows: POPC are blue, POPE are purple, POPS are gray, and cholesterol is green. Their compositions are in the ratio POPE:POPS:POPC 5:3:1. The fraction of cholesterol is y_Ci = 0.3.

Results

By analyzing the values of κ_mH₀ obtained from simulation of symmetric bilayers containing up to three different phospholipids and cholesterol over the range 0 ≤ y_c ≤ 0.6 and the full range of mol fractions of the phospholipids, we noted two trends. First, for 0 ≤ y_c ≤ 0.25, the behavior of κ_mH₀ is not simple and typically depends nonlinearly on the mol fraction of cholesterol in the leaf, y_c. Second, for 0.25 ≤ y_c ≤ 0.6, the dependence of κ_mH₀ on mol fractions is well described by the functional form

$$\frac{{\kappa }_m{H}_0}{k_{B}T}=\frac{y_1}{y_1+y_2+y_3}\left(a_1-b_1{y}_C\right)+\frac{y_2}{y_1+y_2+y_3}\left(a_2-b_2{y}_C\right)+\frac{y_3}{y_1+y_2+y_3}\left(a_3-b_3{y}_C\right),0.25\le y_C\le 0.6,$$ (45)

where y₁, y₂, and y₃ are the mol fractions of the phospholipids in the leaf, and a₁,b₁, a₂,b₂, and a₃,b₃ are constants specific to each corresponding phospholipid and its mixture with cholesterol. For example, C16 SM-cholesterol mixtures are described by a_SM = 6.438 nm⁻¹ and b_SM = 18.58 nm⁻¹, whereas POPC-cholesterol mixtures are described by a_POPC = 1.341 nm⁻¹ and b_POPC = 9.267 nm⁻¹ It is clear from the above form that for fixed ratios y₂/y₁ and y₃/y₁, the quantity κ_mH₀ is linear in the amount of cholesterol, y_c, over the range 0.25 ≤ y_c ≤ 0.6. Also note that the cholesterol mol fraction never appears as simply a linear contribution to κ_mH₀ but is always multiplied by the mol fraction of one or another of the various phospholipids.

The bending contribution to the cholesterol chemical potential, Eqs. 42 and 43, is proportional to κ_m(H₀)² and its derivatives. However, the simulations yield the product κ_mH₀. Thus, we still lack sufficient information to determine the cholesterol dependence of the bending energy. To obtain it, we believe it is reasonable to assume that for flat asymmetric bilayers, the bending modulii of the two leaves can be taken to be equal and therefore one half the bending modulus of the bilayer. Further, as we are treating the total cholesterol mol fraction of the bilayer to be fixed at 0.40, we can ignore the variation of the bilayer bending modulus with cholesterol concentration. Based on the measurements of Evans (21) on mammalian red blood cells, we take ${\kappa }_m^I={\kappa }_m^O=22k_{B}T$ independent of the cholesterol distribution between leaves.

For the outer leaf, we have simulated a 1:1 mixture of 16 SM and POPC with varying amounts of cholesterol. We find that the product of the bending modulus and spontaneous curvature of this model outer leaf is indeed cholesterol dependent (24). It is well fit by the functional form

$$\begin{array}{cc}\frac{{\kappa }_m}{k_{B}T}{H}_0^O=3.895-13.909y_{Co}{\text{nm}}^{-1},& 0.25\le y_{Co}\le 0.6\end{array}.$$ (46)

There are two things to observe here. First, at the lower limit of the cholesterol concentration, the mixture of SM and POPC has a positive spontaneous curvature. This almost certainly contradicts the reported spontaneous curvature measurement (22) of POPC, −0.316 nm⁻¹, and of SM, −0.134 nm⁻¹. However, we note that in the measurement on SM, only a small mol fraction of it was soluble in the host PE (33). Thus, it is not at all obvious that the value reported is appropriate to a larger mol fraction. Further, a positive value for the spontaneous curvature of SM is consistent with experiments that showed that SM was preferentially absorbed in the outer leaflet of small spherical vesicles (34, 35). Equally interesting for our purposes is that, as can be seen from Eq. 46, the spontaneous curvature passes through zero for a mol fraction of cholesterol in the outer leaf of y_Co = 0.28. At this particular concentration, the bending energy of the outer leaf, which for small cholesterol concentrations is positive, vanishes. Hence, the SM/POPC mixture tends to draw cholesterol to the outer leaf if its concentration there is less than 0.28 and tends to expel it to the inner leaf if its concentration in the outer leaf is greater than 0.28. We note that if the mol fraction in the outer leaf were, in fact, as small as y_Co = 0.28, then in a bilayer of total cholesterol concentration of x_c = 0.4, most of the cholesterol would be driven to the inner leaf. One finds the inner leaf would have to have a mole fraction of y_Ci = 0.51, and the percentage of the total cholesterol in the inner leaf would be a rather large F = 67%. If as a result of our calculation, we find that the fraction of cholesterol in the inner leaf is, in fact, less than 67%, we must conclude that the bending free energy of the SM POPC mixture in the outer leaf tends to drive the cholesterol to the inner one.

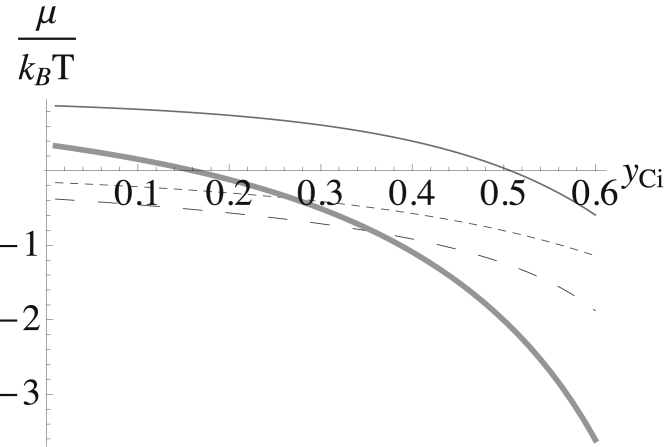
We next show that this contribution of the bending energy to the chemical potential of the cholesterol in the outer leaf is indeed comparable to the other contributions as we surmised earlier. This contribution, given in Eqs. 43 and 45, is shown together with those of the interaction and entropy as well as the sum of all three in Fig. 7. The contribution of the bending to the chemical potential of the outer leaf vanishes, as stated, at y_Ci = 0.51. It is positive, indicating that cholesterol is repelled from the outer leaf for smaller values of y_Ci.

Figure 7.

Contributions to the chemical potential of the cholesterol in the outer leaf plotted versus the mol fraction of cholesterol in the inner leaf y_Ci. That from the interactions is shown by the smaller-dashed line; that from the entropy is shown by the larger-dashed line; and that from the bending energy is shown as the thinner solid line. The sum of the three is shown by the thicker solid line.

The tendency of the cholesterol to be driven toward the inner leaf by the SM and PC in the outer leaf is resisted by the bending energy of the inner leaf, which is also cholesterol dependent. From a simulation of a model inner leaf containing POPE, POPS, and POPC in the ratio of 5:3:1 and varying amounts of cholesterol, we find that the product of the bending modulus and spontaneous curvature of the inner leaf is well fit by

$$\begin{array}{cc}\frac{{\kappa }_m}{k_{B}T}{H}_0^I=-\left(2.012+3.652y_{Ci}\right){\text{nm}}^{-1}& 0.25\le y_{Co}\le 0.6\end{array}.$$ (47)

Note that, because the bending modulus is positive, this says that the spontaneous curvature of the inner leaf is always negative (i.e., small heads, large tails) and becomes larger in magnitude with increasing amounts of cholesterol. Two observations are in order. First, this result is easily understood in terms of a simple polymer brush model of the hydrocarbon chains (36). Because the chains gain entropy by splaying out to sample more configurations, they will bend the hydrophobic-hydrophilic interface to do so, which results in a negative spontaneous curvature. This argument applies a fortiori to lipids with one unsaturated chain whose cis double bond produces a kink in the chain. Indeed, most of the unsaturated lipids of the plasma membrane have such a negative spontaneous curvature (22). The cholesterol easily intercalates between the disordered chains and increases the negative curvature. This argument is supported by the distribution of the cholesterol with respect to the phospholipids. This distribution, obtained from our simulation, is shown in Fig. 8 for the outer leaf at two different concentrations of cholesterol. One sees that the bulky ring of the cholesterol is well below the phospholipid headgroups. Hence, one expects an increasing negative curvature with an increasing cholesterol at these cholesterol concentrations. Our results for the inner leaf distribution are much the same and so are not shown.

Figure 8.

Distribution in the outer leaf of the cholesterol components are shown together with that of the phosphate of the lipid headgroups and of the lipid chains. Distributions are shown for two mol fractions of cholesterol, y_Co = 0.3 and y_Co = 0.5. There is a 1:1 ratio of SM to POPC.

The second observation to be made is that the behavior expressed in Eq. 47 contradicts the hypothesis of Giang and Schick (9). They based their hypothesis on the experimental observation (23) that for sufficiently large fractions of cholesterol in POPE, the cholesterol stabilized the lamellar phase with respect to the inverted-hexagonal one. The authors of (9) reasoned that this was due to the cholesterol ordering the chains of the POPE and driving the spontaneous curvature of PE from negative to positive. From our simulation of the above model inner leaf, this is not the case. An alternative explanation of the experimental data is that as cholesterol disorders the chains, the energy needed to stretch the chains to fill the interstices of the hexagonal lattice becomes greater and greater. Eventually, this phase becomes unstable.

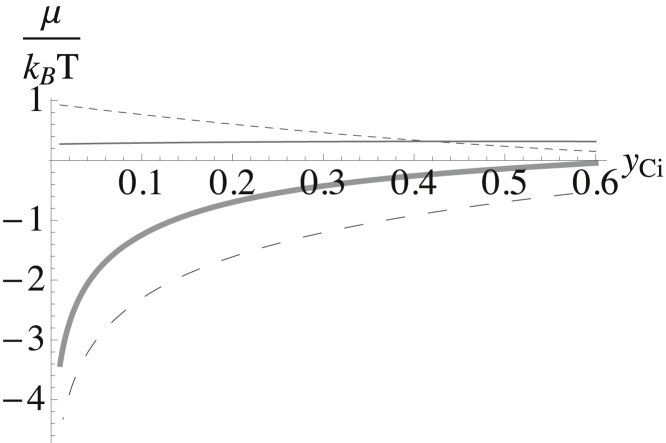
We show in Fig. 9 all three contributions to the chemical potential of the cholesterol in the inner leaf. Again, we assume a constant bending modulus κ_m/k_BT = 22. As anticipated, the contribution of bending to the chemical potential is comparable to the others.

Figure 9.

Contributions to the chemical potential of the cholesterol in the inner leaf plotted versus the mol fraction of cholesterol in the inner leaf y_Ci. That from the interactions is shown by the smaller-dashed line; that from the entropy is shown by the larger-dashed line; and that from the bending energy is shown as the thinner solid line. The sum of the three is shown by the thicker solid line.

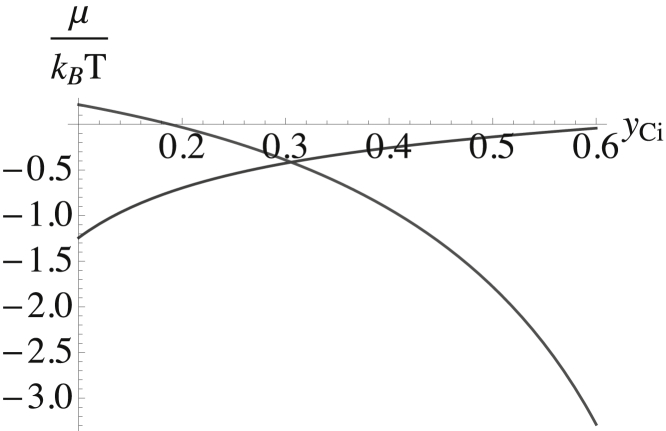
Having determined a result for the chemical potential of cholesterol in the outer leaf, Fig. 7, a result which contains the contribution from the bending energy and a similar result for the chemical potential of cholesterol in the inner leaf, Fig. 9, we can obtain the distribution of cholesterol between the two leaves as before. We compare the two chemical potentials and determine the distribution at which the two are equal. This comparison is shown in Fig. 10. The chemical potentials are equal at a cholesterol mol fraction in the inner leaf of y_Ci = 0.31. This corresponds to a mol fraction of cholesterol in the outer leaf of y_Co = 0.49 and to a F = 36.5% of the total cholesterol in the bilayer being in the inner leaf. The spontaneous curvatures of the outer and inner leaves are, from Eqs. 46 and 47, $H_0^O=-0.131$nm⁻¹ and $H_0^I=-0.142$nm⁻¹.

Figure 10.

The chemical potentials of the cholesterol in the inner and outer leaves are shown as a function of the mol fraction of cholesterol in the inner leaf, y_Ci. The point at which they are equal determines the cholesterol distribution.

Discussion

We have calculated the distribution of cholesterol in a model plasma membrane under the assumption that the membrane is in equilibrium with respect to the interchange of cholesterol between the leaves so that the chemical potentials of cholesterol in the leaves are equal. We have approximated these chemical potentials by calculating them from a mean-field, regular solution free energy augmented by the contribution of the bending energies needed to bring the two monolayers together into a flat bilayer. We found that, of the total cholesterol in the bilayer, about 37% was located in the inner leaf. We noted earlier that the mean-field approximation should be a reasonable one as the mammalian plasma membrane does not appear to be near a critical point. We have also assumed that the membrane is flat. This too is reasonable because the curvature of the cell membrane is on the order of a 1000 times smaller than that of the lipids that constitute it.

There are several parameters in our calculation that are uncertain to some degree, and we discuss how our results depend upon two of them. The first of these is the strength of the interaction between cholesterol and POPE. The strength of any repulsion can be bounded by the observation that cholesterol and POPE do not phase separate at temperatures of T = 35°C (37). This led us to choose a repulsive interaction of 0.28 k_BT. However, one experiment on mixtures of cholesterol and 1-stearoyl-2-linoleoyl-sn-glycero-3-phosphoethanolamine indicates that the interaction is strongly attractive. To determine the effect of a less repulsive interaction between PE and cholesterol, we have repeated our calculation for a vanishing interaction strength. The elimination of the repulsion between cholesterol and PE in the inner leaf naturally increases the percentage of total cholesterol in that leaf; it rises from F = 36.5% to F = 44.4%. The spontaneous curvatures of the inner and outer leaf change from $H_0^I=-0.14$nm⁻¹ to $H_0^I=-0.15$nm⁻¹ and $H_0^O=-0.13$nm⁻¹ to $H_0^O=-0.10$nm⁻¹.

A second parameter that we do not know well is the monolayer bending modulus κ_m. The modulus obtained from our simulations and measured spontaneous curvatures in one-component lipid layers is ∼11 k_BT. This is much smaller than can be inferred from one half the value measured in the bilayers of mammalian red blood cells (21), which would be 22 k_BT. If one increases the functional form of κ_mH₀ obtained from our simulations by a factor of (22/11), then the percentage of cholesterol in the inner leaf increases from F = 36.5% to F = 40.6%. Further, the spontaneous curvature of the inner leaf decreases from $H_0^I=-0.14$nm⁻¹ to $H_0^I=-0.29$nm⁻¹. Given the large fraction in the inner leaf of POPE, which has a spontaneous curvature of −0.32 nm⁻¹, this is quite reasonable. The spontaneous curvature of the outer leaf changes from $H_0^O=-0.13$nm⁻¹ to $H_0^O=-0.23$nm⁻¹. This increase in the magnitude of the spontaneous curvatures implies that the internal energy of the relatively flat cell membrane would also increase. This would put some additional stress on the forces that maintain the size of the cell, forces that are not simply due to lipid-lipid interactions.

Given the above uncertainties, we conclude that our calculations yield an amount of cholesterol in the inner leaflet of F = 37% ± 6%. This is in agreement with early measurements of the distribution (38, 39) and in disagreement with many others (4). It is also in satisfactory agreement with a large MD simulation of the plasma membrane (10).

To summarize, the favorable interaction with SM attracts cholesterol to the outer leaf. Further, cholesterol in the inner leaf increases the magnitude of the negative spontaneous curvature of that leaf, already large because of the presence of PE. This increases the bending energy and drives cholesterol toward the outer leaf. In concert, these two effects would cause an overwhelming majority of the cholesterol, some 79%, to be found in the outer leaf. However, these tendencies are mitigated by the fact that, as we found above, the addition of too much cholesterol to the outer leaf causes its spontaneous curvature to become increasingly large and negative, increasing its bending energy and therefore driving this cholesterol toward the inner leaf. The result of this competition, we predict, is that cholesterol in the outer leaf of the plasma membrane constitutes a majority of the total cholesterol, ∼63%, but it is not an overwhelming one.

Author Contributions

All authors contributed equally to this work.

Editor: Ana-Suncana Smith.