Homogeneous Nucleation in Polyethylene: Molecular Weight Dependence

Abstract

The droplet technique was used to obtain estimates of the isothermal rate of homogeneous crystal nucleation in highly supercooled melts of 8 characterized fractions of linear polyethylene (weight average molecular weights from 3,100 to 249,000). The data obtained from these experiments were analyzed in accord with current theories of homogeneous nucleation of chain folded crystals. Values for the quantity σ²σ_e, where σ and σ_e are the lateral and end-surface free energies of the crystal, were estimated as a function of molecular weight.

Sample 3.2 K was found to be anomalous in its nucleation behavior. When we assume that this sample crystallizes in the extended chain form and calculate σ³ instead of σ²σ_e the value for σ is found to be 10.57 ergs/cm² which is in reasonable agreement with the value 9.6 ergs/cm² found by other investigators for linear hydrocarbons. However, there remains the question as to whether sample 3.2 K ever underwent homogeneous nucleation.

For samples 9.70, 11.74, and 23.0 K, σ²σ_e was found to increase rapidly due to a decrease in the number of cilia per chain fold as the molecular weight increases. For higher molecular weights the value for σ²σ_e levels off and the average value of σ²σ_e for samples 23.0 to 249 K was found to be 19,000 ergs³/cm⁶.

The experimental value of the absolute nucleation frequency I₀, was found to differ from the theoretical value by approximately 1 × 10¹². If one assumes that the surface free energies are temperature dependent [i.e., $\sigma ={\sigma }_1(1+\overline{x}\text{Δ}T)$ and ${\sigma }_e={\sigma }_{e1}(1+\overline{y}\text{Δ}T)$ where $\overline{x}=-0.0073$ and $\overline{y}=0.014$] the average value of σ²σ_e> changes only slightly (to 19,800 ergs³/cm⁶) due to the compensating effects in the signs of the temperature corrections and I₀ is close to the theoretical value, 1 × 10³⁴ nuclei/cm³/s.

1. Introduction

For more than a decade there has been considerable interest in determining the magnitude of the lateral, σ, and end, σ_e, surface free energies for chain-folded polymer crystals. Measurements of spherulitic growth rates as a function of temperature provide values for the product, σσ_e, at temperatures near the melting point of the polymer. Studies of homogeneous nucleation provide important additional information concerning the surface free energies because the process depends on the product, σ²σ_e, at temperatures well below those accessible for growth studies. The temperature dependence of σ_e has been estimated [1]¹ from growth studies and the temperature dependence of σ can be estimated from the present homogeneous nucleation rate studies.

The original homogeneous nucleation rate studies for polyethylene were performed by Cormia, Price, and Turnbull, (CPT) [2] in 1962. The technique employed to suppress the effect of heterogeneities was that first used by Vonnegut [3], namely the bulk sample was subdivided into small droplets so that the heterogeneities were confined to a portion of the droplets, the remaining droplets being free to nucleate at rates governed by the molecular characteristics of the sample. CPT studied an unfractionated polyethylene sample (Marlex-50)² using a slow cooling technique. In 1967, Gornick, Ross, and Frolen (GRF) [4] repeated the nucleation studies on Marlex 50 under isothermal conditions, using essentially the same droplet preparation technique as CPT. In a later paper (1969) by Hoffman et al. [5] the nucleation studies on a fairly narrow fraction of polyethylene having a M_w=50,000 were reported. The results of all three studies were quite similar when calculated on the same basis, i.e., using the same melting point. In addition, in this later paper [5], the effect of a temperature dependence of the surface free energies was first explored.

In the present work, eight narrow molecular weight distribution linear polyethylene fractions were investigated using improved techniques for sample preparation. The goals of this study were threefold: (1) To determine the effects of molecular weight on the product, σ²σ_e, (2) To estimate the temperature dependence of σ and, (3) To investigate the effect of the temperature dependencies of σ and σ_e on the absolute nucleation rate constant, I₀·

2. Theory

Each determination of isothermal nucleation frequency was obtained by counting spots (i.e., crystallized frozen polethylene droplets) on successive frames of film exposed at known time intervals as discussed in section 3 of this paper. The nucleation rate, I, (nuclei cm⁻³s⁻¹) is related to the observed frequency of droplet freezing by the relationship,

$$n/n_0=\sum _{v=0}^{\infty }{N}_D\text{exp}\left(-K_{D}t\right)$$ (1)

where K_D = v_DI and v_D is the volume of a droplet of diameter D. Since for each fraction of polyethylene, the droplets which are in the homogeneous population have a constant diameter within our ability to measure (i.e., ±0.3 μm), the summation sign can be removed, resulting in the following expression:

$$n/n_0=\text{exp}(-Ivt).$$ (2)

The ratio (n/n₀) is the fraction of droplets of volume v, remaining unfrozen at time, t;n₀ is the total number of droplets which undergo the homogeneous nucleation act (population A) in any isothermal experiment. A plot of ln (n/n₀) versus time, t, results in a straight line having a slope of Iv. Since we can measure the value of v the value of I for each isothermal experiment can be calculated.

The temperature dependence of I is reflected in the following generalized relationship for homogeneous nucleation [6]:

$$I=I_0{}^{\prime }\text{exp}\left[-\text{Δ}{\varphi }^{*}/kT\right]$$ (3)

where Δϕ* is defined as the free energy change accompanying the formation of a nucleus of critical size. Following Fisher and Turnbull [7], we approximate Io′ by

$$I=I_0{}^{\prime }\text{exp}\left[-\text{Δ}{F}^{*}/RT\right]$$ (4)

where ΔF* is the activation energy for transport of the crystallizing molecules. Applying the reasoning of Hoffman et al. [5], we define

$$\text{Δ}{F}^{*}=\frac{U^{*}T}{\left(T-T_{\infty }\right)}$$ (5)

where T_x is defined as:

$$T_{\infty }\text{ = }{T}_g\text{−30}$$ (6)

and T_g is the glass transition temperature for the polymer. Now, combining eqs (3), (4), and (5), we have:

$$I=I_0\text{exp}\left[-U^{*}/R\left(T-T_{\infty }\right)\right]\exp \left(-\text{Δ}{\varphi }^{*}/kT\right).$$ (7)

Lauritzen and Hoffman [8] have shown that,

$$\text{Δ}{\varphi }^{*}=30.2{\sigma }^2{\sigma }_e/{(\text{Δ}f)}^2$$ (8)

where σ and σ_e are respectively the lateral and end surface free energies of the nucleus and — (Δf) is the thermodynamic driving force for the crystallization process. The factor 30.2 is obtained when one assumes that the homogeneous nucleus builds upon the orthorhombic unit cell. Hoffman and Weeks [9] have shown that (Δf) is best represented by

$$(\text{Δ}f)=\text{Δ}{h}_f\cdot \frac{\text{Δ}T}{T_m}\cdot f$$ (9)

where f is the correction term to the free energy and is equal to (2T/T_m + T). The correction factor, f, becomes increasingly important at high undercoolings. T_m is the equilibrium melting point, T is the experimental temperature and ΔT=T_m — T. (Δh_f) is the heat of fusion per unit volume of crystal.

Combining eqs (7), (8), and (9) we obtain the following relationship

$$I=I_0\text{exp}\left[-U^{*}/R\left(T-T_{\infty }\right)\right]\text{exp}\left[-30.2{\sigma }^2{\sigma }_e{T}_m^2/k{\left(\text{Δ}{h}_f\right)}^2{f}^{2}T\text{Δ}{T}^2\right].$$ (10)

Equation (10) assumes that the surface free energies, σ and σ_e, are temperature independent. However, Hoffman, et al. [5] have shown that it is more reasonable to assume that σ and σ_e vary with temperature and they suggested a dependence of the form

$$\sigma ={\sigma }_1(1+x\text{Δ}T)$$ (11)

and

$${\sigma }_{e(k)}={\sigma }_{e_1}(1+y\text{Δ}T)$$ (12)

where σ_e(k) is the kinetic value of the fold surface free energy [10]. Incorporating the temperature dependencies into eq (10), we then obtain the general nucleation relationship

$$I=I_0\text{exp}\left[\frac{U^{*}}{R\left(T-T_x\right)}\right]\text{exp}\left[\frac{-30.2{\sigma }_1^2{\sigma }_{e(k)}{T}_m^{°}}{k{\left(\text{Δ}{h}_f\right)}^2}\right]\left[\frac{{(1+x\text{Δ}T)}^2(1+y\text{Δ}T)}{f^{2}T{(\text{Δ}T)}^2}\right]$$ (13)

According to Fisher and Turnbull [7], I₀ can be defined in the following way,

$$I_0=\left(N/{\overline{V}}_m\right)(kT/h)$$ (14)

where N is Avogadro’s number and ${\overline{V}}_m$ (for polymers) is the molar volume of a sequence of chain segments whose length is approximately that of the crystal nucleus. (kT/h) is the usual frequency factor where k is Boltzman’s constant, T the_temperature, and h is Planck’s constant. Assuming ${\overline{V}}_m$ is equal to 140 times the molar volume of a single —CH₂— group, I₀ can be calculated and has a numerical value of approximately 1 × 10³⁴. It should be pointed out at this time that the theoretical value of I₀ differs from the experimentally determined I₀ by a factor of approximately 1 × 10¹². This discrepancy will be discussed in detail in the final section of this paper.

A careful analysis [1] of the crystal growth data for a number of polymers which crystallize by chain folding showed that the best value for U* is about 1500 cal/mol.³ and T_∞=Tg — 30 °C, where T_g, is the glass transition temperature. We assume these values for polyethylene. In addition for the particular case of polyethylene it was estimated that σ_e(k) and y were 93⁴ ergs/cm² and 0.014 deg⁻¹ respectively. The only other factor to be determined is the value of x and that can be established approximately with the homogeneous nucleation rate data. Lauritzen [11] has developed a theory for the behavior of σ based on a model where the presence of the lateral polymer crystal surface reduces the number of allowed configurations of the polymer molecule in the subcooled liquid adjacent to the crystal surface. In this treatment an entropy gradient exists in the surface zone whose magnitude increases with increasing temperature.

Under these circumstances, one would expect σ to increase with increasing temperature and consequently would expect x to be negative and considerably smaller than unity. The actual values determined for x will be discussed in detail in section 4 of this paper.

3. Experimental Detail

The nucleation behavior of eight fractions of linear polythylene was studied. Four of these (CE designation) were fractions from Marlex-50, which was obtained from the Phillips Petroleum Company. The fractions were prepared using a column extraction (CE) technique [12] with the solvent system described by Chiang [13]. The other four were fractions of the National Bureau of Standards linear polyethylene standard reference material, SRM 1475. These were fractioned by preparative gel permeation chromatography (GPC designation). GPC was used to analyze all of the fractions (table 1) using the column system and technique described in [14]. GPC instrumental broadening effects were estimated by measuring nearly pure samples of n — C₃₂H₆₆ and n — C₉₄H₁₉₀ for which M_w/M_n was known to be about 1.00. These samples gave M_w/M_n = 1.05 in the GPC analytical apparatus. Therefore, a correction of—0.05 was applied to the original data for the fractions characterized with the analytical GPC columns. In particular, the technique used in the preparation of samples 9.70 and 11.74 K was such that a true polydispersity of about 1.01 to1.02 was to be expected.

Table 1.

Sample designation	Mn	Mw	Mz	$T_m^{°}$ (°C) (calculated)b	Polydispersity (Mw/Mn)c	Method of Preparationd
3.2 K	2.140	3.160	4,530	131.7	1.43	CE
9.70 K	9.150	9.700	10.246	141.1	1.01	PGPC
11.74 K	10.970	1 1.740	12.431	142.0	1.02	PGPC
23.0 K	1 7.690	23.010	32,674	144.1	1.25	CE
30.6 K	25.710	30.600	36.659	144.6	1.14	PGPC
a49.9 K	36,370	49.890	69.850	145.2	1.32	CE
119 K	94.600	119,200	146.931	145.9	1.21	PGPC
249 K	178.500	248.560	348.000	146.2	1.34	CE

^aThis sample was treated as described in reference (4). The population of droplets which nucleated homogeneously contained 50–200 droplets as compared to present methods which produce 600–1000 droplets in the homogeneous population. Consequently, we feel that the results found for the other fractions are statistically more reliable than those obtained for Marlex-50 and CE-50.

^b

Calculated using the equation

$$T_m^0=\frac{T_m^{°}(\infty )(n-0.542)}{n+0.46\left\{7.667+1.987\text{ln}n+(5.6/n)-(0.25n-7)\left[1-\left(T_m^{°}/T_m^{°}(\infty )\right)\right]\right\}}$$

where n = M/ 14.026 is the number of carbon atoms in the polymer chain. This equation was derived from Broadhurst’s work (J. Res. NBS. 70A, 481 (1966)), by setting $T_m^{°}$ at n →∞ at $T_m^{°}(\infty )=419.7\cdot \text{K}={146.5}^{°}\text{C}$.

^cCorrected for instrumental broadening ettects (see text).

^dPGPC = preparative gel permeation chromatography; CE = column elution.

3.1. Droplet Preparation

In a crystallization process in the bulk there are two possible nucleation modes whereby a stable nucleus can be formed from the liquid phase. In heterogeneous nucleation the nucleus is formed on the surface of some extraneous solid existing in contact with the liquid, or at a liquid-liquid or liquid-solid interface. Homogeneous nucleation results from the spontaneous formation of a favorably oriented cluster of molecules (or a single molecule in the case of many polymers) without the aid of any substrate. Yonnegut [3] assumed that crystallization in bulk generally occurred by heterogeneous nucleation because of the large number of heterogenities per unit volume. However, he reasoned that by subdividing the bulk material into small particles, many of these particles would be free of heterogeneities (dirt). Therefore any nucleation occurring within such “clean” particles would occur via the homogeneous route. This is the rationale behind the droplet experiment.

Two ways for doing this subdivision are described in the literature. One method is to simply grind up the crystalline sample, using a grinder or blender. This technique was used by Turnbull and Cormia [15] in their homogeneous nucleation experiments with linear hydrocarbons. The other technique is to dissolve the sample in a suitable solvent, then to subdivide the solution into small portions, and subsequently to remove the solvent. Two different approaches have been used to achieve the latter. The first, described by Cormia, Price, and Turnbull (CPT) [2], made use of the consolute temperature portion of the polyethylenenitrobenzene phase relationship. If a solution of polyethylene in nitrobenzene is first heated to the boiling point of nitrobenzene and then allowed to cool, a new polyethylene-enriched liquid phase is produced. This new phase occurs as liquid droplets, approximately 5 μm in diameter. If the two-phase mixture is further cooled before the droplets of the enriched phase coalesce, the polyethylene in the droplets crystallizes, expelling the nitrobenzene and forming fairly uniform spheres approximately 1 to 2 μm in diameter. These polyethylene spheres can be separated from the nitro-benzene by either centrifugation or filtration. These polyethylene spheres are subsequently dispersed in a suitable dispersive media.

The second method is that employed by Koutsky, Walton, and Baer (KWB) [16]. The cells used in these experiments were heated microscope slides having shallow concavities containing silicone oil (a non-solvent) as a substrate. They sprayed a hot solution of polymer with atomizers onto the hot silicone oil substrate, volatilizing the solvent and leaving the finely divided polymer floating on or slightly below the silicone oil surface. No glass cover was used so the polyethylene droplets remained dispersed at the oil-air interface.

3.2. Sample Cleaning Techniques

The success of the homogeneous nucleation experiments is dependent upon producing a large number of polyethylene droplets which nucleate homogeneously and whose volumes are nearly identical. The CPT method of particle preparation was the one used, both in our previous work (GRF) [4], and the present studies. This method is only successful if all materials used are as free of extraneous matter as possible.

In order to render our starting solvents reasonably free of particulate matter, filtration, crystallization, distillation, and centrifugation were used. Starting materials were reagent grade xylene and nitrobenzene. First, each of these solvents was twice filtered through regenerated cellulose filters using only gravity flow; we had previously found that the higher flow rates which could be achieved by applying pressure to the filtration system were much less effective. Secondly, subatmospheric pressure distillation was used, wherein only the “center cut” was collected. This step was used both to chemically purify the solvent and to further reduce the concentration of particulates. After this treatment, analysis of both the nitrobenzene and xylene by gas-liquid chromatography indicated a purity in excess of 99.5 mol percent.

Crystallization was then used, not with the idea of further chemically purifying the solvents, but rather, as a means of further reducing the particulate count. The solutions were cooled somewhat below their melting point, and crystallization was induced. During this crystallization the solutions were vigorously stirred, producing a slurry of small crystals. These crystals were then removed from the remaining liquid by rapid filtration through a cooled filter. This crystallization process was performed twice, and analysis of both the nitrobenzene and xylene by light scattering indicated that suspended particulate matter was not present. This crystallization technique, sometimes referred to as “snowing out,” is quite effective in that the suspended particles usually act as crystallization nuclei, and hence they are scavenged by the crystals and are removed when the crystals and the remaining liquid are separated by filtration.

Originally we also employed ultracentrifugation, using only the middle portion of the solvent in the centrifuge tubes. Since subsequent experiments indicated that this technique did not seem to further reduce the particulate concentration, ultracentrifugation was not used for xylene and nitrobenzene.

For the final dispersion of the polyethylene droplets we used isooctylphenoxy-poly (ethyleneoxy)ethanol, furnished by the General Aniline and Film Company under the trade name of IGEPAL CA-630, as a suspending medium. Both CPT and GRF have experimentally verified that liquid and solid polyethylene are insoluble in this material. The IGEPAL was cleaned using the vacuum distillation and filtration procedures described for xylene and nitrobenzene. However, since the IGEPAL could not be crystallized we continued the use of ultracentrifugation as a final step.

Preliminary cleaning of the polyethylene samples was accomplished by dissolving them in hot xylene and filtering through 0.2 micrometer pore size filters in a heated filter assembly. The polyethylene was then allowed to crystallize and was separated from the xylene by filtration. This process was repeated three times per sample.

Initially we were of the opinion that all of the cleaning, preparation, and filling of the sample-containing cell should be done in clean-room facilities. In fact, while the procedures became much more difficult, no significant improvement was seen, and consequently we performed such experimental operations henceforth in a conventional laboratory area.

3.3. Sample Preparation

Each of the fractions of polyethylene was handled in an identical fashion. A concentrated solution of each was prepared by dissolving the previously cleaned fraction in hot, purified xylene. This solution was twice filtered through the 0.2 micrometer cellulose filters, and a small portion was then poured into nitrobenzene preheated to approximately 200 °C. Most of the zylene immediately boiled away, leaving solutions containing approximately 30 mg of polyethylene per 200 ml of nitrobenzene. Gas-liquid chromatography indicated that the amount of xylene left in the nitrobenzene solution was negligible.

With continuous shaking, the flask containing the hot polyethylene-nitrobenzene solution was immersed in tap water, ultimately producing a dispersion of frozen polyethylene droplets. The droplets were separated from the nitrobenzene by filtering through the cellulose filters. The nitrobenzene filtrate was saved, and the process of droplet preparation was repeated three times, each subsequent time using the same nitrobenzene. A small portion of the droplets collected in the fourth precipitation were redispersed in approximately 10 ml of the cleaned IGEPAL. The dispersion was achieved by ultrasonic agitation. One droplet of this dispersion was sufficient to fill the cell used for observation of homogeneous nucleation.

3.4. Preparation and Cleaning of the Cell

The cell used to contain the dispersion was formed by fusing a 0.2 mm thick glass washer with an inner diameter of 0.5 cm to an 18 mm square microscope cover glass. The sample was contained within the washer, and a disc made from a cover glass was used as the top. The cell and its cover were successively cleaned with chromic acid, distilled water, and ethanol. Prior to filling, the cell was ultrasonically scrubbed in distilled water. In a previous paper (GRF) [4], we described many treatments designed to change the nucleating effect of the glass surfaces of the cell, and came to the conclusion that little improvement could be made over the simple cleaning procedure just described.

3.5. Experimental Equipment

The disk-shaped cell containing the sample was fitted into an enclosed temperature environment on the stage of a polarizing microscope. This temperature stage was designed and constructed by us and will be described in a separate publication [17]. The cell temperature can be maintained to within ±0.02 °C for periods of weeks, and the absolute temperature in the cell is known to within ±0.1 °C. The temperatures are measured to ±0.005 °C, and temperature differences between a series of experiments on the same sample are accurate to ±0.01 °C.

The optics of the microscope were such that in a circular field of 200 μm radius, a 0.5 μm object could be identified from the resulting photographs. The experiments are conducted using crossed polarizers, and, in the liquid state, the droplets are invisible. Upon freezing they appear as small stars against the otherwise dark background. A xenon light source was used, and the sample was illuminated only during the actual film exposure.

Automatic time-lapse cinemicrophotography was used to record the nucleation, using a 16-mm motion picture camera. The camera framing rate was adjusted to obtain between 200 and 2000 pictures during a single experiment, but usally only 20 pictures were used in the actual analysis.

3.6. Preliminary Experiments

Prior to the final dispersion of the droplets, a small sample of droplets from each fraction was examined using both electron and optical microscopy. The electron micrographs were similar for all fractions, showing a few large diameter spheroids (diameters in excess of 20 μm), with the majority of the droplets having diameters between 2 and 1 μm. A peculiar characteristic of the droplet population was their occur-rence in clusters, held together by a thin, veil-like webbing (see fig. 1A). We assume that this webbing is polyethylene formed when the residual polyethylene in the nitrobenzene solution (not that in the concentrated droplet second phase) precipitates. When a dispersion is made of these droplets, the clusters are not completely broken up by mechanical agitation. Only ultrasonic agitation seems effective (see figs. 1B and 1C).

Figure 1.

Photographs of typical Polyethylene droplet populations.

(A) Electron micrograph of droplets as they are precipitated from nitrobenzene showing size distribution and veil as discussed in text; (B) droplet population dispersed in Igepal using only mechanical (shaking) agitation; and (C) droplet population in Igepal using ultrasonic dispersion. Note better uniformity and smaller droplet size.

The diameters of these spheres have been measured using two microscopical techniques. Using the optical microscope and a calibrated image-splitting device similar to that described by Dyson [18], we found that each polyethylene fraction formed droplets such that in a population of 2000, over 1800 had apparent diameters between 2 and 1 μm. This is in agreement with the less extensive measurements made using electron microscopy. Unfortunately, as was elegantly demonstrated by Saylor [19], it is extremely difficult to determine the absolute size of small particles. In these experiments on homogeneous nucleation of droplets, the size of the droplet has a direct relationship to the nucleation frequency (usually expressed in nuclei cm⁻³s⁻¹). We have attempted to minimize the effect of this uncertainty in absolute droplet radius by: (1) observing the same droplet population for a series of experiments with each fraction, and (2) by using the image-splitting device on each population to determine if there is a measurable difference between fractions. At best the apparent diameter can be determined to only±0.3 μm, and, we have found that all droplets assumed to be homogeneously nucleated in any given polyetnylene fraction have essentially the same diameter. Droplet size from fraction to fraction varies by no more than this same 0.3 μm limit. In general, it appears that the diameter of the droplet decreases slightly with increasing molecular weight.

Figure 1A is an electron micrograph of a small number of droplets. Figure 1B is an optical photo-micrograph of droplets dispersed by mechanical stirring, and figure 1C shows the effect of dispersion by ultrasonic agitation on the same sample.

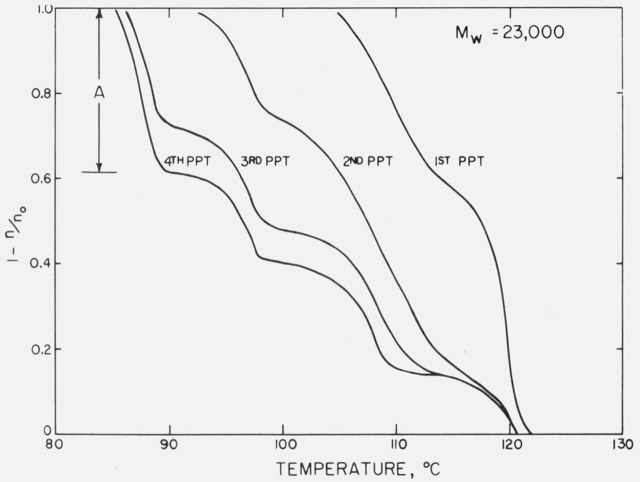
The reason for using only the polyethylene droplets prepared from nitrobenzene used for three previous preparations is shown in fig. 2. Here each of the four droplet preparations was dispersed in IGEPAL and its freezing (nucleating) behavior was recorded. The droplet size does not change, but the nucleating behavior changes dramatically. The first preparation produces droplets which freeze with relatively little super-cooling. The succeeding preparations freeze at progressively lower temperatures, forming well-defined subgroupings in respect to temperature. After the fourth preparation little or no change is observed. This tendency of the droplets to freeze at certain temperatures, forming subpopulations of droplets, is a characteristic of all of the fractions, although each fraction is unique in its temperature profile. We only show the behavior for sample 23.0 K, but in this discussion we will refer to the subpopulation nucleating at the lowest temperature (usually around 85 °C) as population A (this is assumed to be the homogeneous nucleation population), the next lowest in nucleating temperature (usually around 95 °C) as B, and so on. In the particular case shown, population D would be those droplets which nucleate around 125 °C. It is in this first freezing population that the larger droplets are invariably found. In the final preparations this population represents 10 percent or less of the total number of droplets. One interesting point of difference between the work of KWB [16] and our own work is that while we always observe a relatively large percentage of our droplet populations nucleating at temperatures around 95 °C. KWB finds no droplets nucleating in this temperature region. A possible explanation for this marked difference in droplet behavior is to be found in the following melting and freezing experiments.

Figure 2.

Nucleation of polyethylene fraction 23.0 K showing the effect of repeated droplet preparation using the same solvent.

1 — n/n₀ is the fraction of droplets nucleated as a function of temperature (cooling rate = 0.1°C/min). Population A is the droplet population prepared from the 4th precipitation which is assumed to be homogeneously nucleated.

One of the more interesting things which can be done is to compare the nucleating character of the droplet population with that of its melting character. Examples of this type of experiment are shown in figures 3 and 4. In figure 3 we have shown the nucleating and melting curves of sample 9.70 K. The freezing (nucleating) curve shows only three populations (A, B, and C). The first melting curve was produced by warming the sample at a nearly constant rate starting from 80 °C. The second melting curve was produced by first heating the sample at 115 °C for 5 h and then at 120 °C for another 48 h, prior to warming at a nearly constant rate. In general, those droplets which froze at the lower temperature are the same as those which melted at the lower temperatures. This tendency is seen throughout the total droplet population. Thus, we note that in both melting experiments those droplets in population A melt first and melt over a much wider range of temperature than the other populations. In addition, the annealing process produces melting of all droplets at higher temperatures.

Figure 3.

Curve (a). Nucleation of polyethylene fraction 9.70 K (cooling rate=0.1 °C/min.); Curve (b). Melting of the droplets whose crystallization profile is shown in curve (a) (warming rate0.5°C/min); Curve (c). The effect of annealing on the melting behavior of droplets whose crystallization profile is shown in curve (a).

The sample was heated to 115°C for 5 h then to 120°C for 48 h, followed by warming at a constant rate of 0.5 °C/min.

Figure 4.

Effect of heating the polyethylene droplet populations for sample 30.6 K to temperatures well above the melting point for long periods of time on nucleation and melting behavior.

Curve (a): Nucleation distribution of the same droplet population after heating to 150°C for 10 h (cooling rate = 0.1°C/min). Curve (b): Nucleation distribution of the droplet population shown in curve (a) after heating to 170° for 2 h. Curve (c): Melting behavior of the droplets crystallized in curve (b) (warming rate= 0.5°C/min).

Figure 4 shows that the same type of behavior is exhibited by sample 30.6 K. Here we show the freezing behavior of the droplet population when melted and heated to 150 °C for approximately 10 min (the usual type of pretreatment prior to running an actual nucleation experiment). Approximately 50 percent of the total population is in the subpopulation A. There are, in addition, at least three other populations. The sample was then heated to 170 °C for 2 h, and the experiment repeated. The results of freezing this sample are shown in the second freezing curve. There are two important differences. (1) Some of the droplets formerly freezing at the higher temperatures now freeze at lower temperatures. (2) Population A is being depleted forming a new population B. While not shown here, more prolonged heating at 170 °C or higher will completely annihilate that population originally called A. This is true for all of the samples which we have investigated. The melting curve shown in figure 4 is that obtained from melting the sample after the 170 °C treatment. Again we see a difference between population A and the rest of the droplet population. Qualitatively, with the possible exception of sample 3.2 K, all the samples behave similarly, namely that population A melts first and over a wider range of temperature, and that the entire droplet population shows the usual effects of annealing.

We are able to positively identify individual droplets as various melting-freezing cycles are examined, excepting occasionally a droplet seems to change its position, i.e., one droplet disappears and another appears near the position of the original one. When this is observed, the “old” and the “new” droplets may change from population A to population B. Under normal thermal treatment only two or three droplets will make this change, but upon more severe thermal conditioning, many droplets will go from population A to B. From the paper of KWB, we find that the top surface of their dispersions are not in contact with glass, i.e., the cells have no top or cover. To a droplet1 or 2 μm in diameter, the surface of the glass cover must appear to be far from smooth. It is therefore possible that our normal population B occurs as a result of heterogeneous nucleation by the glass surface of the cover, and that on occasion a droplet may move to a different position, either freeing itself from contact with the glass surface or becoming attached to it. Consequently, we could expect a large population of B, whereas KWB should not observe the phenomena.

4. Analysis of Data

From the 200 to 2000 pictures taken during an isothermal experiment, 20 pictures are selected with a time interval such that the homogeneous population (population A) is 80 percent frozen in the last frame. At the conclusion of each run the sample is cooled to 70 °C so that all droplets are frozen and the value for $n_0{}_{{}_{\text{exp}}}$, the total homogeneous population can be established. Using the first picture as a blank, succeeding pictures are compared one by one, giving the number of newly crystallized droplets, n_ij, which appear during each time interval, t_i.

The next step in the analysis is to plot the data as In ($n/n_0{}_{{}_{\text{exp}}}$) against t[(eq 2) in its logarithmic form].

This results in a linear plot having a slope equal to Iv. Figure 5 shows this type of analysis for sample 30.6 K at several isothermal temperatures. Since the volume, v, of the droplets is known, I, the nucleation rate can be calculated for each experimental temperature T_exp. n₀ is the total number of droplets in the homogeneous population A, i.e., the number of droplets which remain unfrozen at an arbitrarily chosen time, t_i, = 0.

Figure 5.

Typical isothermal homogeneous nucleation experiments showing the temperature dependence of the nucleation rate for polyethylene fraction 30.6 K.

n|n₀ is the fraction of droplets remaining not nucleated at any time, t.

A least squares analysis of In (n_i /n₀), t_i pairs done by first forcing the intercept through zero, using the experimentally determined n₀. Since the choice of t_i = 0 is completely arbitrary, the Iv is calculated first using all 20 n_i,t_i pairs; then the slope was redetermined using only the first 10 pairs and then the last 10 pairs. If there are no temperature fluctuations in the experiment, the three calculated slopes are identical. Experiments not meeting this test were discarded. The purpose of this test was only to show that the run was made under isothermal conditions; it tells nothing in respect to the constancy of volume of the droplet population.

The absolute correlation coefficients for the least squares fitting operations were of the order of 0.998 or greater, indicating that the droplet population was statistically well-behaved. Because the degree correlation was so high it was possible to perform a series of fitting tests.

First we refitted the data using the general relationship

$$\text{ln}n/n_0=a+bt$$ (15)

Wherein the intercept a was calculated. Without exception the calculated value of a was nearly equal to zero.

The value, n₀, can also be calculated. Using the absolute value of the correlation coefficient as the fitting criterion, we varied the value of n₀ highest absolute value of the correlation coefficient, using eq (15). From this we obtained calculated values of Iv, n₀ and a.

Thus, there are two final gates for establishing internal experimental consistency, namely that $n_0{}_{{}_{\text{exp}}}$ should nearly equal $n_{0_{\text{calc}}}$ and a should be nearly zero. If the calculated and experimental values of n₀ were not nearly equal, there would be strong evidence to suspect the validity of our basic assumption in regard to the constancy of droplet volume. As stated previously, the average number of droplets in the homogeneous population A was 600 and for all data used in this report $n_{0_{\text{calc}}}$ differed from $n_0{}_{{}_{\text{exp}}}$ by no more than 2 percent and a differed from zero by no more than ±0.01, (usually a was much smaller). It should be noted that the results reported for this current study are significantly more precise than those reported previously [5]. The actual values for I reported in this paper are those obtained using $n_{0_{\text{calc}}}$, although the results using $n_0{}_{{}_{\text{exp}}}$ are not significantly different.

The sets of values of I’s and T’s obtained in the above manner were next analyzed using eq (13) to determine the values for the surface-free energy product, σ²σ_e. In our original paper (GRF) [4] we assumed that these free energies were temperature independent, i.e., in eq (13) x = y=0. As a first step we again analyzed the data setting x = y= 0. The values for σ²σ_e and I₀ were determined by performing a least squares fit of

$$\text{ln}I+\frac{U^{*}}{R\left(T-T_{\infty }\right)}\text{ versus }\frac{{(1+x\text{Δ}T)}^2(1+y\text{Δ}T)}{f^{2}T{(\text{Δ}T)}^2},$$

using a value for U* of 1500 cal/mol. Plots of these functions for all the samples studied are shown in figure 6. Again we obtained values of nearly one for the absolute correlation coefficients. As in the previous work, the values obtained for σ²σ_e were reasonable but the values for I₀ differed from the theoretical value, 1 × 10³⁴, by approximately 1 × 10¹²·

Figure 6.

Graphical summary of the homogeneous nucleation experiments for all the polyethylene fractions studied except fraction 3.2 K which is anomolous.

See text for details.

As discussed in section 2, it is reasonable to assume that the surface-free energies are temperature dependent; consequently using y= 0.014 as the best value from crystallization studies, we sought a best value for x. This was done by reanalyzing the data with y= 0.014. Remembering that x should be negative and small, x was varied until the highest correlation coefficient was obtained. The value for x obtained in this way was —0.002. Using this value for I₀, the σ²σ_e values were low, and the value for I₀ was even higher than before.

As a final step we assumed that the theoretical value for I₀ might well be used as input information, and a value for x was determined by the fitting operation. Since the value for x should be nearly the same, at least for the higher molecular weight fractions, the calculated values for x were averaged and the value obtained was $\overline{x}=-0.0073$. As a result of the compensating effects of the small positive and negative temperature dependencies of σ_e and σ, the values for σ²σ_e calculated in this way are nearly identical to the values obtained when x and y are set equal to zero, and the value for I₀ is very close to the theoretical value [1].

Since other workers have also reported extremely high values of I₀, the discrepancy between theory and experiment does not appear to be a question of input data, and the introduction of the proper temperature dependencies does seem to resolve the problem in a simple way.

5. Results and Discussion

The results of our experiments for eight fractions of linear polyethylene are summarized in table 2. These samples can be divided into three molecular weight regions. Fraction 3.2 K is little more than a collection of high molecular weight hydrocarbons. Fractions 9.70, 11.74, and 23.0 K represent a region wherein T_m is rapidly changing with molecular weight and σ²σ_e is expected to show strong molecular weight effects. The remaining samples are in a region where T_m changes slowly and σ²σ_e should show little molecular weight dependence [20].

Table 2.

Sample	$T_m^b°\text{C}$	Experimental temperature range, °C	x = y = 0		y = 0.014 Log I0 = 34		Correlation coefficient
			σ2σe	Log I0	σ2σe	x
3.2 K	131.74	98.2–101.8	1,180	15.6	719	0.033	0.972
a9.70 K	141.09	85.0–87.5	12,400	37.9	11,100	−.0047	.994
a11.74 K	141.95	85.4–87.9	15,000	43.2	14,500	−.0063	.998
23.0 K	144.14	86.4–88.1	18,610	48.5	19,100	−.0073	.976
30.6 K	144.60	86.3–88.6	18,600	48.8	19,300	−.0074	.999
49.9 K	145.17	86.9–88.9	17,400	46.5	17,500	−.0069	.986
119.0 K	145.96	87.1–89.1	20,000	50.8	21,120	−.0077	.993
249.0 K	146.21	87.6–89.4	20.500	51.5	21,800	−.0077	.990
				Avg. 23,000–250,000 = 19,000 ergs3cm−6 (x = y = 0)
				Avg. 23,000–250,000 = 19,800 ergs3cm−6 (y = 0.014 Log I0 =34)

^aSpecial samples, estimated polydispersities between 1.01 and 1.02.

^bAssuming $T_m^{°}={146.5}^{°}\text{C}$. See reference [1] for details.

First, let us examine the unique results obtained for fraction 3.2 K. This sample is the first cut from the column elution of Marlex-50. As such it has a higher polydispersity than any of the other fractions contains a much higher percentage of terminating end groups per —CH₂— unit and although it was carefully purified, significant amounts of branched polymer, catalyst fragments, etc., might well remain.

For the moment, let us assume that homogeneous nucleation does occur in sample 3.2 K. The molecular weight of this sample is such that one might expect a stable nucleus containing one fold and two cilia to form. This nucleus would be expected to resemble an extended chain molecule more than a chain-folded nucleus. Assuming that one measures σ³ rather than σ ²σ_e the calculated value for σ is 10.57 ergs/cm² which is in good agreement although slightly higher than the 9.6 ergs/cm² value obtained by Turnbull and Cormia [15] for the linear hydrocarbons in their homogeneous nucleation experiments.

Although the calculated value for σ appears to be reasonable, there remains a question concerning the mechanism of nucleation in this sample. There is some evidence that the nucleation is heterogeneous rather than homogeneous. First, we note from table 2 that the lowest obtainable experimental temperature range is 15 degrees higher than that of 9.70 K although the calculated T_m is approximately 10 degrees lower. In addition, one notes that this is the temperature range in which the subpopulation B of all other fractions nucleate. When the kinetics of subpopulation B for the other fractions are analyzed the values for σ²σ_e and I₀ obtained are of the same magnitude as those calculated for 3.2 K.

We believe that the nucleation of population B is via a glass surface-polymer interaction. First of all, KWB [16], using no cover glass on their sample cell, do not obtain a B-type population. Second, if we subject our samples to harsh thermal treatment, there is an increase in population B at the expense of the homogeneous population. The lower molecular weight, thermally degraded sample has a lower viscosity than the original sample, consequently we postulate that the polymer wets the glass surface and henceforth nucleates heterogeneously on the glass surface of cell cover.

We therefore conclude that it is likely that the measurements on 3.2 K are really the results of heterogeneous rather than homogeneous nucleation.

Excluding fraction 3.2 K, table 2 shows a continuing increase in both σ²σ_e and log I₀ as the weight average molecular weight increases. For samples 9.70, 11.74, and 23.0 K one expects σ²σ_e to increase rapidly due to a decrease in the number of cilia per chain fold as the molecular weight increases [20]. This effect should be of much less importance in the higher molecular weight fractions. There is still a slight upward trend in σ²σ_e and I₀ even in the highest molecular weight fractions but in view of the experimental uncertainties the trend may not be statistically significant. One notes that the values of σ²σ_e and I₀ for fraction 49.9 K tend to be lower than those calculated for neighboring fractions. There are two reasons for this: (1) this fraction has a higher polydispersity than the other fractions, which may affect its nucleating character somewhat, and (2) this was the first fraction measured and the experimental techniques were greatly improved as the experiments progressed.

For the time being, if we regard σ²σ_e to be independent of temperature, the average value for the five highest molecular weight fractions is 19,000 erg³/cm⁶ and the value for log ₁₀I₀ is 49.4. The value of σ can be calculated in two ways from σ²σ_e: (1) σ²σ_e (homogeneous nucleation) σσ_e (growth) = 19,000/1280 = 14.8 ergs/cm², and (2) σ²σ_e (homogeneous nucleation) σ_e (T_m versus 1/l plot. = 19,000/93= σ²=205 and σ= 14.3 ergs/cm² [20]. Hoffman et al. [1] have shown that from all the information available it is reasonably certain that σ for polyethylene lies between 12 and 15 ergs/cm².

The question of the experimental [2, 4] value of I₀ is a more complicated one and does not appear to be a question of the input data. As discussed previously (sec. 4), it is reasonable to assume that both σ and σ_e are temperature dependent. The assignment of y= 0.014 appears to be experimentally justified. If we assume that the theoretical value for I₀, (i.e., log₁₀I₀ = 34) and calculate a value for x we obtain an average value of—0.0073. Applying these temperature dependencies to σ and σ_e we find that the average value of σ ²σ_e for the higher molecular weight fractions changes only slightly (to 19,800 erg³/cm⁶) due to the compensating effects in the signs of the temperature corrections and I₀ is the theoretical value. From these results we conclude that the theoretical value for I₀ should be included as input data in the homogeneous nucleation studies on other polymers.

With the exception of sample 3.2 K, we are satisfied that the nucleation mechanism in the measured fractions is homogeneous. First, nucleation has not been observed in a lower temperature range; second, the nucleation of population A is truly sporadic in nature and finally, the values calculated for σ using σ2σ_e from these studies and the values for σσ_e from the growth studies lie in a reasonable range. Hoffman et al. [20] have estimated the best values of σ and σ(∞) for polyethylene from several methods to be 14.2±0.4 ergs/cm² and 90.5 ergs/cm² respectively. The values obtained from the homogeneous nucleation studies presented here (i.e. σ =14.8 ergs/cm² and σ_e= 86.7 ergs/cm²) are in reasonable agreement.