The Impact of Melt Electrowritten Scaffold Design on Porosity Determined by X-Ray Microtomography

Abstract

Melt electrowriting (MEW) is an additive manufacturing (AM) technique using thermoplastic polymers to produce microscale structures, including scaffolds for tissue engineering. MEW scaffolds have, in general, high porosities and can be designed with different fiber diameters, spacings, and laydown patterns. The need for a reliable method for scaffold characterization is essential for quality assurance and research purposes. In this study, we describe the use of submicrometer X-ray tomography for the generation of local thickness maps of volume porosity of 16 different scaffold groups, comprising 2 diameter groups, 2 fiber spacing groups, and 4 different laydown patters (0/90°, 0/60/120°, 0/45/90/135°, and 0/30/60/90/120/150°), all made using a custom-built MEW printer with medical-grade poly(ɛ-caprolactone). The results showed a porosity range between 77.7% and 90.7% for all the scaffolds. Moreover, the influence of the scaffold regularity and flatness in the more regular pore shapes (0/90°, 0/60/120°) lead to the shift of the local thickness graph to one side, and thus the prevalence of one pore size. This nondestructive method for MEW scaffold characterization overcomes the limitations of microscopic methods of pore shape and size estimation.

Impact Statement

Melt electrowriting is an AM technology that bridges the gap between solution electrospinning and melt microextrusion technologies. It can be applied to biomaterials and tissue engineering by making a spectrum of scaffolds with various laydown patterns at dimensions not previously studied. Using submicrometer X-ray tomography, a “fingerprint” of porosity for such scaffolds can be obtained and used as an important measure for quality control, to ensure that the scaffold fabricated is the one designed and allows the selection of specific scaffolds based on desired porosities.

Introduction

Three-dimensional (3D) scaffolds are an important approach within tissue engineering and regenerative medicine (TERM).^1–3 There have been several fabrication methods to produce 3D porous scaffolds over many decades, however, in recent years the focus is on defined, reproducible, and sometimes customizable scaffolds made with additive manufacturing (AM). TERM scaffolds aim to mimic the composition of biological tissues, primarily by taking the temporary role of the extracellular matrix (ECM), which forms a complex and often fibrous network that regulates numerous biological functions and the formation of cell niches.^4,5 Understanding the complex relationship between a scaffold and tissue, particularly during healing, is a major research focus of TERM. The foreign body inflammatory reaction at the implant site^6,7 and subsequent cytokine secretion⁸ as well as vascularization^9,10 are all key aspects to consider for scaffold optimization.

There have been numerous methods to produce TERM scaffolds using traditional fabrication methods, for example, electrospinning, salt leaching, gas forming, or phase separation^11,12 or by AM approaches, for example, microextrusion,¹³ stereolithography,¹⁴ and selective laser sintering.¹⁵ The scaffold architecture influences parameters such as porosity, pore size, and interconnectivity as well as surface area of the scaffold,^12,16,17 and is often difficult to quantify. Despite this challenge, several methodologies for the quantification of a scaffold have been proposed,¹² although with resolution and feature size limits to each method.^16,18

Melt electrowriting (MEW) is a layer-by-layer AM fabrication technology that has a similar operation principle as microextrusion techniques; however, an applied high-voltage stabilizes the molten jet during direct-writing.^19,20 The result is precise and uniform direct-written scaffolds, with size features not typically attainable using conventional techniques, including submicrometer filaments.²¹ The typical fiber diameter of a MEW scaffold, however, ranges between 2 and 50 μm,^19,22 which bridges the divide between electrospinning and microextrusion. The ordered placement of small diameter fibers can have a significant impact on the mechanical properties, particularly when combined with hydrogel matrices.^23,24

The interplay between the fiber diameter, laydown pattern (through the computer-controlled collector movement), and interfiber spacing can produce MEW scaffolds with different porosities and pore shapes, in a reproducible manner. The 0/90° laydown pattern is by far the most used pattern for MEW,^25–28 while 0/60/120° has also been reported.^29,30 These laydown patterns lead to the generation of pores taking the regular shapes of squares or isosceles triangles, respectively (when the spacing is kept constant from one fiber to the next). While this is a symmetric and simple approach to produce architecture, it does not correspond to the complexity of the ECM where pores are heterogeneously arranged. MEW is particularly capable of fabricating scaffolds with different laydown patterns while maintaining a high porosity and therefore requires a method to describe and quantify the pore shape and size. This complexity is highlighted when a spectrum of different diameters is possible with single nozzles using MEW, which is distinct to melt microextrusion techniques.^22,31 To our knowledge, no one has previously reported a characterization comparison of regular and more complex MEW scaffolds, particularly with the 0/30/60/90/120/150° laydown pattern.

For the quantitative correlation between a scaffold design and the in vitro or in vivo response, the scaffold porosity is one fundamental measure. Traditional measurement methods based on imaging either generate two-dimensional images that are unsuitable for the analysis of complex 3D structures (scanning electron microscopy or SEM), or, like confocal microscopy, have a limited depth penetration.³² A promising technique to overcome these hurdles is the use of nondestructive X-ray microtomography (μCT) for the quantitative determination of volume porosity in MEW scaffolds.

The technique of μCT is capable of capturing the entire scaffold with micrometer accuracy within a field-of-view (FOV) of several cubic millimeters.³³ State-of-the-art volume image analysis provides the tools, not only for calculating the average porosity but also for quantifying the distribution of local pore spaces that are available for the cell infiltration.³⁴ Thereby, the research performed here attempts to establish a unique “fingerprint” for each MEW scaffold in four different laydown patterns, which can later be compared to results from in vitro or in vivo experiments or used as a nondestructive quality control for manufacture. This study derives quantitative structural parameters for porosity in highly ordered symmetric MEW scaffolds. Before establishing such a methodology, the current limit of spatially resolved microporous open structures required ascertaining. The accuracy of determining global porosity was verified, and finally, determining the influence of fiber laydown pattern, diameter and spacing on the characteristic porosity-related parameters of 16 different scaffold types were measured.

Materials and Methods

Scaffold design and fabrication

A custom-made MEW printer was used for the scaffold fabrication as previously described.²⁶ In brief, medical-grade poly(ɛ-caprolactone) (PCL), purchased from Corbion (PURASORB PC 12, lot no. 1412000249, March 2015, Gorinchem, The Netherlands) was heated to 73 ± 1°C in a plastic syringe with a 22 G spinneret (both from Nordson EFD Deutschland GmbH, Pforzheim, Germany) under computer-controlled pneumatic pressure. The PCL was carefully stored under dry, −80°C conditions as previously described.²⁶ A positive voltage was applied to the spinneret tip, while a negative one was supplied to the stainless-steel movable collector.

The scaffolds were designed to study the effect of fiber diameter, spacing, and laydown pattern. By adjusting the printer parameters, the target fiber diameter was either 10 μm (0.4 bar pneumatic pressure, 4.5 kV applied voltage, 2.5 mm collector distance and 600 mm/min collector speed) or 20 μm (1.2 bar pneumatic pressure, 6 kV applied voltage, 3.5 mm collector distance and 400 mm/min collector speed). To show the effect of pore size on the scaffold morphology, two fiber spacing values were selected, 125 and 250 μm. Finally, to demonstrate the effect of pore shape, scaffolds with fibers in four different laydown patterns, 0/90°, 0/60/120°, 0/45/90/135° and 0/30/60/90/120/150°, were printed (Fig. 1).

FIG. 1.

Computer-rendered images of the four different laydown patterns investigated: (A) 0/90° (2x5L), (B) 0/60/120° (3x4L), (C) 0/45/90/135° (4x3L), and (D) 0/30/60/90/120/150° (6x2L). Color images are available online.

The scaffold nomenclature is based on their architecture, with the first number indicating the targeted fiber diameter, the second number the fiber spacing, and the last two numbers are the number of fiber rotations in a single repeat of the scaffold and the number of repeats in the whole scaffold (e.g., 10-250-3x4L). Table 1 outlines the nomenclature of the 16 scaffold types investigated here and Figure 1 shows schematic illustrations of the four different laydown patterns. With the exception of the 2x5L scaffolds, the number of layers in the other scaffolds was kept at 12 layers in total.

Table 1.

Summary of the Scaffolds Used in the Experiments with the Corresponding Nomenclature Based on the Fiber Diameter, Spacing, and Laydown Pattern

Scaffold	Laydown pattern (°)	Target fiber diameter (μm)	Fiber spacing (μm)	Layer count
10-125-2x5L	0/90	10	125	2x5 layers
10-125-3x4L	0/60/120	10	125	3x4 layers
10-125-4x3L	0/45/90/135	10	125	4x3 layers
10-125-6x2L	0/30/60/90/120/150	10	125	6x2 layers
10-250-2x5L	0/90	10	250	2x5 layers
10-250-3x4L	0/60/120	10	250	3x4 layers
10-250-4x3L	0/45/90/135	10	250	4x3 layers
10-250-6x2L	0/30/60/90/120/150	10	250	6x2 layers
20-125-2x5L	0/90	20	125	2x5 layers
20-125-3x4L	0/60/120	20	125	3x4 layers
20-125-4x3L	0/45/90/135	20	125	4x3 layers
20-125-6x2L	0/30/60/90/120/150	20	125	6x2 layers
20-250-2x5L	0/90	20	250	2x5 layers
20-250-3x4L	0/60/120	20	250	3x4 layers
20-250-4x3L	0/45/90/135	20	250	4x3 layers
20-250-6x2L	0/30/60/90/120/150	20	250	6x2 layers

Scanning electron microscopy

A Zeiss Crossbeam 340 SEM (Carl Zeiss, Germany) was used to qualitatively and quantitatively visualize the scaffold structure and morphology. The scaffolds were mounted on stubs and sputter coated with 4 nm of platinum. Ten different scaffolds from each diameter group were imaged, and 10 fiber diameters were measured per scaffold from different, random points (n = 100).

X-ray μCT

The μCT scans were recorded on a detector-based submicrometer custom-built CT scanner, which is based on a liquid metal-jet anode and was previously described in detail.³⁵ Scaffolds were placed in a plastic sleeve to keep them from vibrating during the scan. The voxel sampling in all scans was 2.83 μm/voxel, the volume of interest was a cylinder of 6.1 mm in diameter and 7.2 mm in height. For simplicity, this scanning mode will be called medium resolution. For evaluating the accuracy of the present method, one scaffold was measured at a very high resolution: 0.53 μm/voxel sampling. However, the FOV at this resolution is much smaller: a cylinder that is only 1.2 mm in diameter and 1.4 mm in height.

The PCL fibers which are mostly transparent to the 9.25 keV X-ray energy were outlined by Fresnel propagation-based phase contrast, which is an inherent feature of these scanners. Following volume image reconstruction (back-projection) a volume phase retrieval filter was applied along with a Wiener deconvolution.³⁶ The Fourier-filter parameter for the phase retrieval (Paganin) kernel was 90, the deconvolution was modeled with a mixed point-spread function (σ = 1.7 and μ = 1.2 in units of pixel).

Volume image analysis

After scanning the area of interest in the scaffold, a high-resolution X-ray phase contrast image was generated. To transform into a binary volume image, a global threshold value had to be applied to the pixels, which are usually cast from floating point numbers to 16-bit gray values [0 … 65535]. The threshold was set to the 50% level between fibers and air and was checked for accuracy as mentioned below. The free and open-source software package distribution Fiji,³⁷ based on ImageJ v1.52c (National Institute of Health, USA), was used for the analysis and calculations. For the 3D renderings of the μCT scans, Avizo v9.0 (Thermo Fisher) was used.

Results

Scaffold characterization

The fiber diameter measured using SEM for the 10 μm target group was 11.15 ± 0.45 μm, while for the 20 μm one, it was 22.69 ± 0.52 μm. The direct-written structures were uniform throughout the scaffolds with no fiber pulsing observed due to the appropriate adjustment of the MEW printer parameters.²⁶ Figure 2 shows representative SEM images of all the 16 different scaffold groups with different laydown patterns, spacings, and diameters. With the exception of the 20-125-6x2L group, the fibers stacked well upon each other into walls. The accurate placement of fibers within the 20-125-6x2L sample was likely affected by electrostatic attractions toward fibers already deposited.

FIG. 2.

SEM images of the 16 investigated scaffolds with different laydown patterns, diameters, and fiber spacing. The nomenclature is fully described in Table 1. Scale bars are 100 μm. SEM, scanning electron microscope.

In general, the fibers were regular and round with a smooth surface. The more complex fiber laydown patters (4x3L and 6x2L) had a heterogenous distribution of pore sizes and shapes compared to the more regular ones (2x5L and 3x4L). The center point in the 6x2L scaffolds had the intersection point of the six fibers forming a single repetition (1L) of the scaffold and represented the most regular point.

The μCT imaging of the scaffold resulted in X-ray phase contrast images as shown in Figure 3. The data from these images are the basis for the further analysis of the scaffold morphology. In Figure 3, the 20-125-6x2L scaffold is shown from above and in a cross-sectional view, as an example of an X-ray phase contrast image. This scaffold, based on a dodecagonal unit design, represented the most dense and irregular scaffold.

FIG. 3.

X-ray phase contrast imaging. (A) HR X-ray phase contrast image of the 20-125-6x2L scaffold. (B) Axial slice image through the reconstructed volume (contrast is inverted for better visibility of the PCL fibers). Scale bar is 200 μm. HR, high resolution; PCL, poly(ɛ-caprolactone).

Figure 4 represents graphical renderings from the μCT data of the four laydown patterns in the 20-250 group. Through the rendering, it was possible to visualize the underlying fibers of the scaffolds and observe how they are stacking upon each other, especially in tilted views, which is also possible with the SEM but only to a certain depth. The 2x5L laydown pattern represented the most regular and reproducible pore shape, followed by the 3x4L one.

FIG. 4.

Rendering from μCT scans of the four investigated laydown patterns. (A) 2x5 layers, (B) 3x4 layers, (C) 4x3 layers, and (D) 6x2 layers. All pictures show samples with 20 μm intended fiber diameter and 250 μm fiber spacing (20-250 group). Scale bars are 500 μm. μCT, microtomography. Color images are available online.

Porosity calculation

Once the binary volume image is set, the part of the volume (V₀), which contains the fibers (V_F) and on which total porosity (P_tot) needs to be defined, can be calculated through the following:

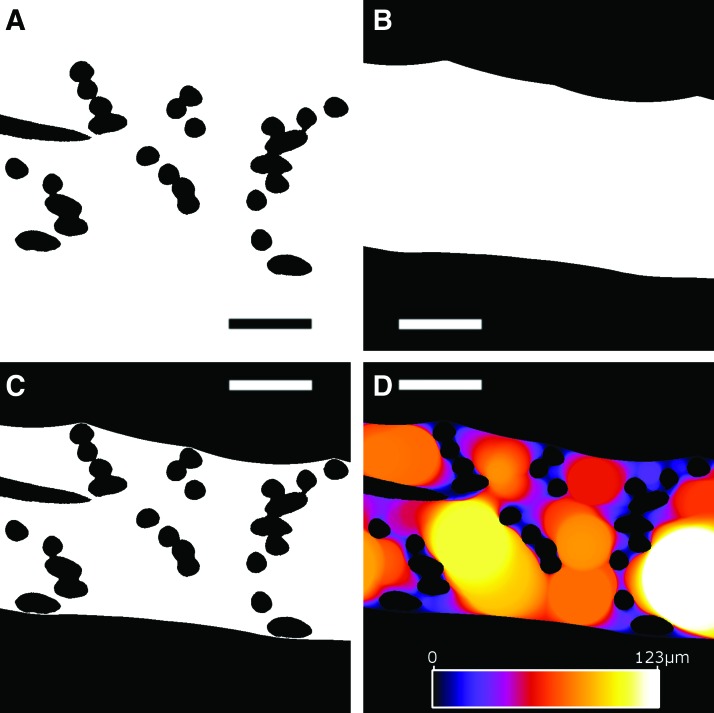
where V₀ is a volume mask and is defined by closing the space between the top most and lower most borders of the cross section of the PCL scaffold. For the sake of simplicity, this binary closing operation is applied as a two-step process. First, the Euclidian Distance Transform (EDT), which defines the exact distance to the nearest foreground voxel, is calculated on the background voxels. A closing radius (typically 100 pixels) is applied to the EDT resulting in a filled dilated mask (the sensitivity of this closing radius will be further examined below). Second, this dilated mask is eroded by performing the same procedure but with opposite sign on the mask voxels (EDT then closing radius then 100 pixels). The result of this process is illustrated in Figure 5, where the scaffold and surrounding space are shown, followed by the closing of the open spaces on the upper and lower borders of the scaffold and finally the generation of local thickness map.

FIG. 5.

(A) Binary volume image of fibers from the 20-125-6x2L scaffold; (B) mask created by binary closure; (C) pore volume; (D) local thickness map (color/brightness corresponds to local thickness in units of voxels). Scale bars are 100 μm and the color scale for local thickness is linear and ranges from 0 to 123 μm. Color images are available online.

P_tot of the different scaffolds

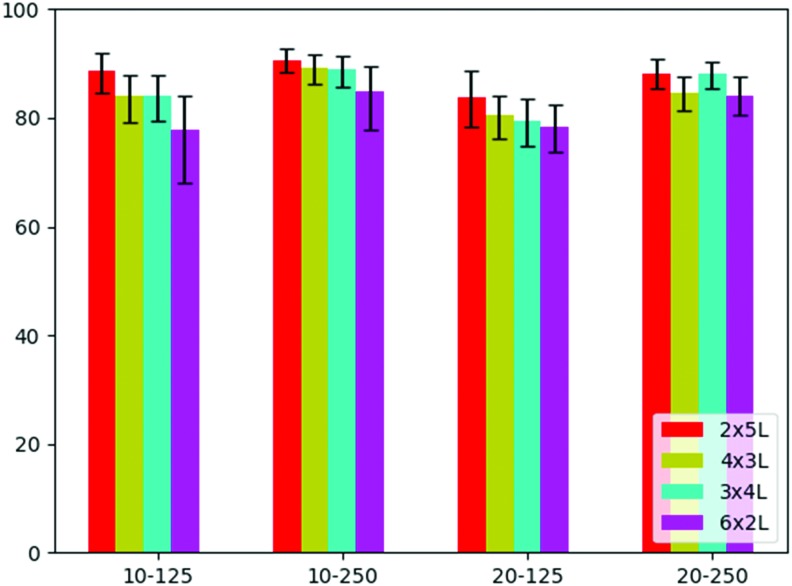
The variation in P_tot ranged between a maximum of 90.7% for the 10-250-2x5L scaffold and a minimum of 77.7% for 10-125-6x2L. To evaluate the sensitivity of these results on the choice of the gray value threshold (Fig. 6A) (which was selected as the middle gray value between the fibers and air), we changed the latter for all scaffolds by ±12.5% of the entire gray value interval, as an arbitrary number, and noted the relative changes in P_tot. The resulting change in P_tot, shown in the error bars in Figure 7, is to be regarded as the upper and lower limits, finding the middle gray value for thresholding is in fact much more precise. Nevertheless, this choice is the principle source of error.

FIG. 6.

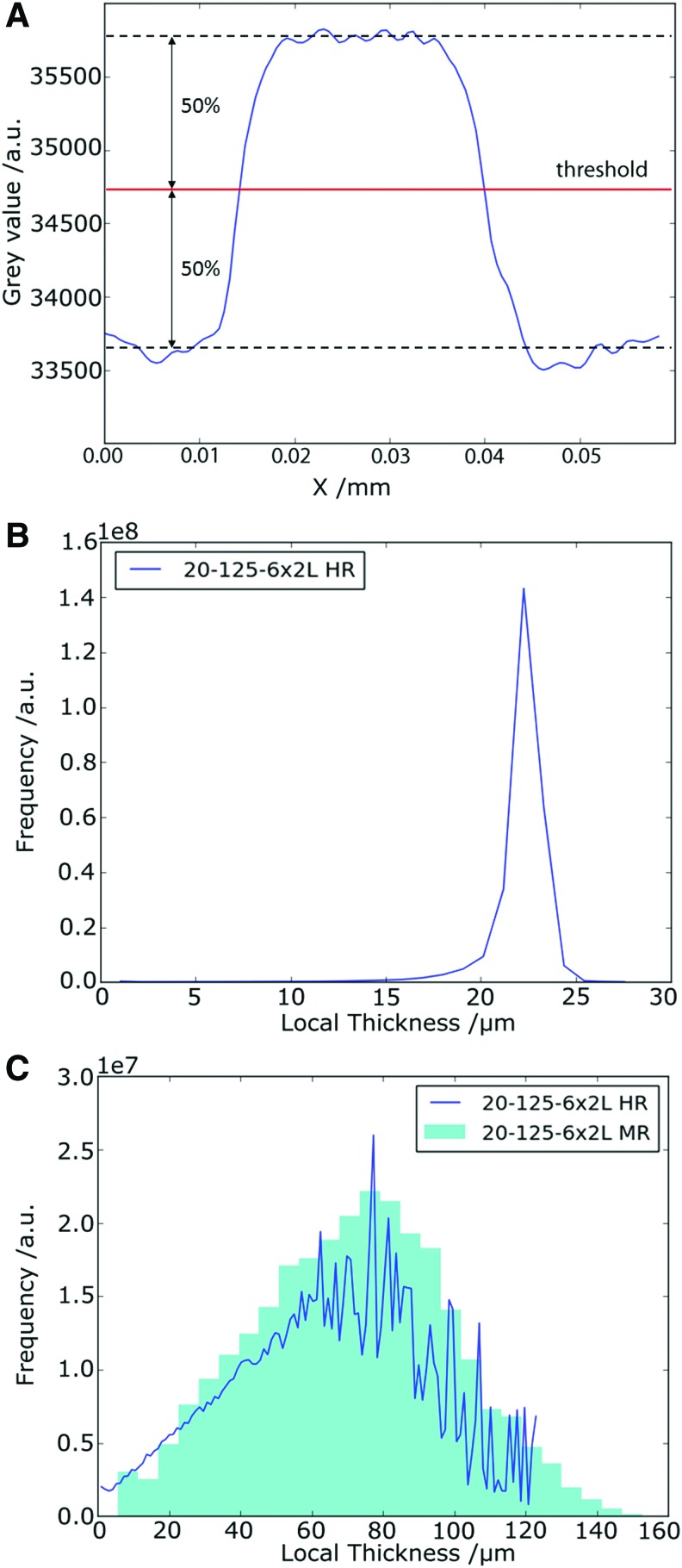
Analysis of local thickness of scaffolds and settings used. (A) Line plot over one PCL fiber. The gray value threshold for binary segmentation is set to 50%. (B) Fiber diameter of a fiber from the 20-125-6x2L scaffold scanned in HR mode where the local thickness of the fiber was measured instead of the pores. (C) Overlapping of the local thickness histograms of the 20-125-6x2L scaffold determined by HR scanning (line plot) on a MR scan (bar plot). MR, medium-resolution. Color images are available online.

FIG. 7.

Porosity for each of the 16 scaffold types. The error bars refer to the difference in porosity when the gray value threshold is changed by ±12.5% during calculation. Color images are available online.

Using the same test, but changing the radius of dilation and erosion during masking from 100, 150, to 200 pixels, we observe only variations <2% in P_tot (data not shown); for example, the values of P_tot of the 10-125-2x5L sample change between 87.8% (closing radius at 100 pixels) and 89.5% (closing radius at 200 pixels). Due to the smaller and larger fiber spacing and to avoid bumps in the pore mask (which might lead to an underestimation of P_tot), a radius of 100 pixels was applied to the 20-125 structures, 150 pixels to the 10-125 and 20-250 structures, and 200 pixels to the 10-250 structures.

Despite these uncertainties, Figure 7 shows that the least dense scaffolds (10-250 group) have the largest porosity, whereas the densest (20-125 group) have the lowest. In terms of laydown patterns, the most regular (2x5L) scaffolds have the largest values of P_tot, whereas the most complex structure (6x2L) yields the smallest value for every fiber spacing and fiber diameter groups. The two intermediate structures (4x3L and 3x4L) feature very similar values of P_tot between the two extremes with a slight tendency of 4x3L toward larger porosities in the 20-250 group.

Local thickness

The local thickness (T_loc) is computed on the pore volume as shown in Figure 5C, assigning to every pore the diameter of the largest sphere that could occupy the space where the pore is located (resulting in Fig. 5D). Plotting a number histogram of T_loc describes the number of voxels, hence the partial volume, which may be occupied by spheres of a certain size. The diameter of the spheres was changed from voxels to micrometers by multiplying the voxel value times 2.83 μm for medium-resolution scans and 0.53 μm for high-resolution scans.

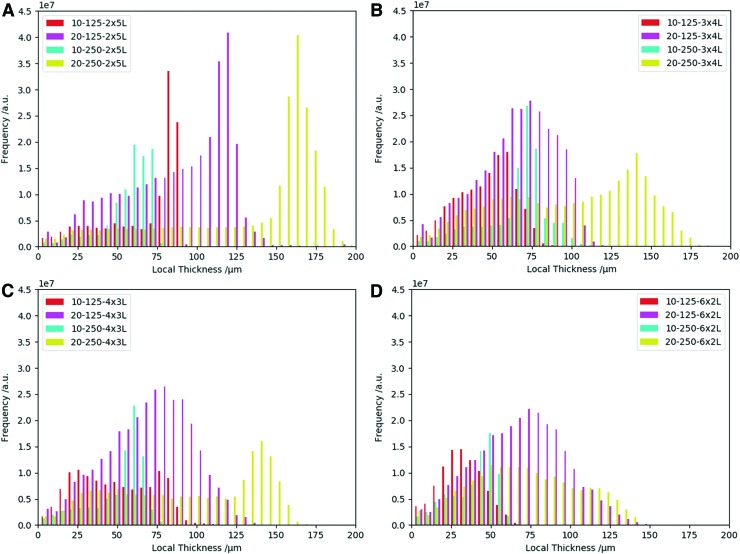
Next, we shall examine T_loc for each laydown pattern using data generated from the medium-resolution scan. Figure 8 displays histograms for the four examined laydown patterns (each including the different fiber diameters and spacings), previously shown in Figure 2, with the values of T_loc summarized in Table 2.

FIG. 8.

Local thickness for each symmetry; (A) 2x5L, (B) 4x3L, (C) 3x4L, and (D) 6x2L. Each plot shows four histograms, that is, different combinations of fiber diameters and fiber spacings (10-125, 10-250, 20-125, and 20-250). Color images are available online.

Table 2.

Summary of Calculated Porosity Values for the 16 Different Scaffold Types Using the Medium-Resolution Scans

			Local thickness (Tloc)
Group	Sample	Total porosity (Ptot)	Maximum (μm)	Mean (μm)	SD (μm)
2x5L	10-125-2x5L		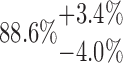96.22	69.01	24.54
	10-250-2x5L		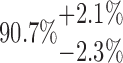85.09	58.95	14.98
	20-125-2x5L		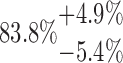200.03	88.26	32.73
	20-250-2x5L		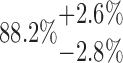198.75	135.19	47.98
3x4L	10-125-3x4L		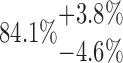96.39	48.05	17.95
	10-250-3x4L		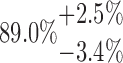119.40	66.75	20.42
	20-125-3x4L		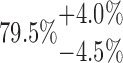131.16	65.99	23.72
	20-250-3x4L		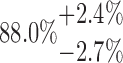185.14	99.33	43.55
4x3L	10-125-4x3L		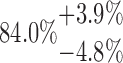131.16	50.86	24.25
	10-250-4x3L		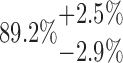82.41	52.73	16.74
	20-125-4x3L		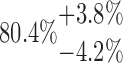135.84	70.02	26.34
	20-250-4x3L		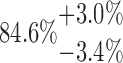169.23	95.67	44.36
6x2L	10-125-6x2L		79.24	33.26	13.47
	10-250-6x2L		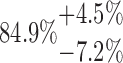90.21	40.69	14.22
	20-125-6x2L		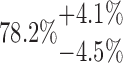154.49	68.84	27.64
	20-250-6x2L		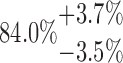144.75	73.01	32.87

Total porosity is additionally calculated for a change of ±12.5% in the gray value threshold.

The histograms of the box-shaped scaffolds (2x5L) (Fig. 8A) all feature a peak to the right-hand side of the distribution whereby those scaffolds with 10 μm fibers clearly have smaller pores than those with 20 μm fibers. From a visual inspection of the structure (compare with SEM images in Figure 2 or μCT renderings in Fig. 4) it appears that these peaks and their different positions stem from the different T_loc of the scaffolds. T_loc is hence dominated and limited by the flat square pores.

The impression that was obtained from the 3x4L structures (Fig. 8B) was similar to the 4x3L ones where there is a right-hand side peak of the distribution of T_loc for the 10-250 scaffolds. Unlike 10-250 and 20-250, the 20-125 scaffold appears to be unaffected by the flatness of the structure and, hence, provide a more varied distribution of T_loc. The mean pore diameter here is 66.0 ± 23.7 μm, while the largest pore is 131.2 μm. Furthermore, it appears that the distribution of T_loc for the 10-125 scaffold neatly follows the 20-125 structures up to a pore diameter of ∼60 μm, and then the distribution is reduced, most likely by flatness effects. The mean pore diameter of 10-125 is therefore 48.1 ± 17.9 μm and the largest pore 96.4 μm.

We observe the same trend for the 4x3L structures (Fig. 8C) where the distribution of T_loc for the 10-250 scaffold has the same pronounced peak. The 20-250 and the 10-125 structures, however, feature a bimodal histogram, and hence the local thickness of the pores is only partially limited by the flatness of the structure. The 20-125 scaffold finally shows a broad continuous distribution of (bulk) pores with little effects from the flatness of the structure. The mean pore diameter in this distribution is 70.0 ± 26.3 μm and the largest pore 135.8 μm.

Finally, the histograms of the 6x2L structures (Fig. 8D) support the impression that the pore space in more complex structures is less affected by the flatness of the scaffold. Only the 10-250 structure shows a right-handed peak in the distribution of T_loc. While the 20-250 distribution features a little hump, which is likely caused by the same effect, 10-125 and 20-125 appear to be entirely affected by this geometrical constrain. The distribution of 20-125 is the broadest of all, with mean pore diameter of 68.8 ± 27.6 μm and a maximum of 154.5 μm. On the contrary, the 10-125 scaffold features a mean pore diameter of 33.3 ± 13.5 μm and a maximum of 79.2 μm. Also, the 10-125 visibly features smaller pores than the 20-125 scaffold.

As mentioned before, the fibers in the 20-125-6x2L scaffold did not stack properly compared to the other scaffolds and this resulted in a more irregular fiber deposition. By scanning this scaffold with the high-resolution mode and then calculating the T_loc based on the new values, we find a broad continuous distribution (Fig. 6C) with a maximum of 123.2 μm (slightly smaller than the fiber spacing), a mean of 66.0 ± 29.3 μm. Applying the same calculations obtained from the high-resolution scan to the fiber diameter of this scaffold (20-125-6x2L) yielded a mean diameter of 22.6 ± 1.8 μm and a maximum of 27.8 μm (Fig. 6B).

Scan resolution

To compare the accuracy of the measurements taken from the medium-resolution scans, the 20-125-2x5L scaffold was also scanned by the high-resolution method. Figure 6C shows a comparison of the distribution of T_loc between both scan methods on the same scaffold. The sudden cutoff seen in the high-resolution scan after a T_loc value of 120 μm is probably caused by the narrow FOV of this scanning modality (Fig. 6C). The high-resolution method also was able to describe smaller pores in the scanned section, and this explains the difference in mean and standard deviation values between the high- and medium-resolution scans for the 20-125-6x2L scaffold, 66 ± 29.03 μm and 68.8 ± 27.6 μm, respectively.

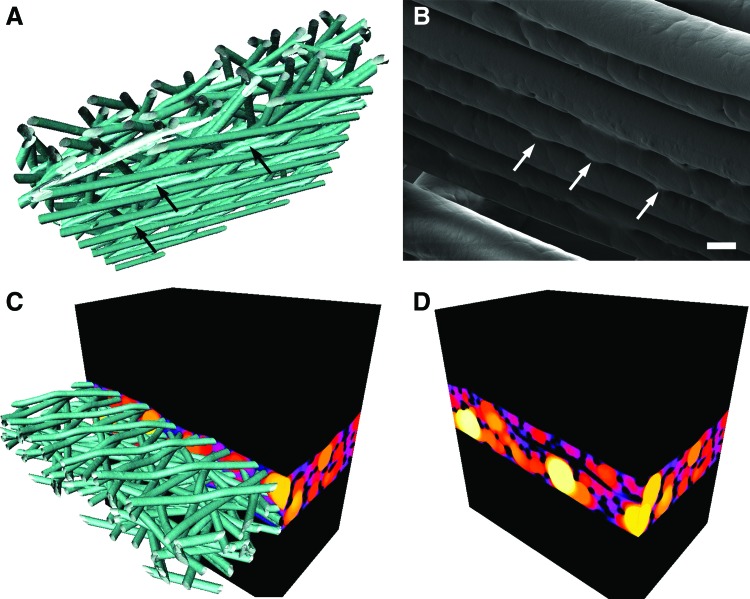
The high-resolution scan makes it possible to visualize the fibers, pores, and the surface of the fibers using video after 3D reconstruction of the μCT data. Supplementary Video S1 shows a graphical rendering of a high-resolution scan of the 20-125-6x2L scaffold with both the fiber surface and a scaffold cross section, showing the pores and the T_loc map. Screenshots from the Supplementary Video S1 such as Figure 9A depicts fine surface details such as the occasional fusion between two fibers before the upper one cools down and solidifies while being laid down on the second. These details could only be visualized with the SEM after significant tilting and/or cutting of the scaffold (Fig. 9B). The creation of a local thickness map (Fig. 9C) and the subsequent removal of the scaffold (Fig. 9D) in the Supplementary Video S1 provides a dynamic approach to visualizing a porous MEW scaffold. Additional videos such as Supplementary Video S2 can be generated using such data to demonstrate the regularity of MEW scaffolds (20-250-6x2L shown).

FIG. 9.

Precision of μCT scan in detection of scaffold imperfections. (A) 3D rendering of a high-resolution scan of a 20-125-6x2L scaffold showing partial fusion between two overlying fibers (black arrows). (B) A SEM image of 20-125-2x5L scaffold showing the same partial melting effect (white arrows); scale bar is 10 μm. It was practically hard to tilt a 20-125-6x2L scaffold sufficiently in an SEM to visualize such a fiber fusion effect. (C) A screenshot of Supplementary Video S1 depicting the local thickness map of the scaffold, while (D) shows another screenshot in the video where the scaffold fibers are removed (shown in black) to visualize the pores. 3D, three-dimensional. Color images are available online.

Discussion

PCL is a slowly degrading polymer that has been processed for much of the reported MEW literature for both in vivo and in vitro applications.^38–41 It is already in use for several medical devices produced through other AM approaches.^42,43 For the small diameter MEW scaffolds made with PCL, μCT could quantitatively characterize those of different fiber diameter, spacing, and laydown pattern. The total porosity calculation showed a clear trend indicating that larger values of fiber spacing lead to higher porosity. Concerning laydown patterns, less complex scaffolds (e.g., 2x5L) have higher porosity, whereas more complex structures (e.g., 6x2L) have a lower porosity. While the relative comparison of values of P_tot obtained in this study is accurate (the same measurement routine and data analysis were applied step-by-step to all samples), conclusions about absolute porosity have to be taken with care. Due to the very large specific surface of the layer-by-layer printed structures, changing the gray value threshold, which divides the space between air and PCL by 12.5%, can alter the porosity by ∼5% in total. This effect is 10 times more pronounced compared to changing the closing radius of the binary masking by 50% which is why the gray value threshold is the most prominent uncertainty in the presented method. By calculating the error bars of P_tot from all data sets, however, we found that the magnitude of the effect strongly depends on the scaffold structure: it can be as small as 2.1% (10-250-2x5L) or as large as 9.6% (10-125-6x2L) (Table 2).

The 3D nature of μCT scans further allowed for the histographical analysis of the pore space by calculating T_loc. Unlike calculations of P_tot, the analysis of T_loc takes a closer look at a design-influenced property: pore size. We have seen that for the less complex scaffolds (e.g., 2x5L, in particular, those printed with a target fiber diameter of 10 μm), the pore size is essentially limited by the flatness of the scaffolds, that is, the fiber spacing is larger than the height of the entire scaffold thickness. For the more complex structures (e.g., 6x2L) and for the scaffolds with a target fiber diameter of 20 μm, we found a bulk pore distribution that may be used as a morphological fingerprint for the 3D characterization of porosity.

The spatial resolution accuracy of this analysis can be addressed by comparing the distribution of T_loc in the 20-125-6x2L scaffold to a high-resolution scan that was recorded in addition to the medium resolution one. Figure 6C shows a superposition of both histograms, with a more jagged distribution toward the larger pores using the high-resolution scan due to the limited total volume which can be sampled by this method. Apart from this limited volume effect, both distributions show a congruent linear slope at the smaller pores, which is an indication that medium-resolution scans in this regime are equally valid, despite the lower spatial resolution, compared to the high-resolution scan. The maximum pore size of 80 μm for this sample is accurately reproduced from both scans (Fig. 6C).

Through MEW, it is possible to print precise scaffolds in a variety of geometric shapes and patterns,⁴⁴ using fiber diameters that span the gap between solution electrospinning and microextrusion techniques.²² However, the desire for perfect geometrical shapes might not represent the native ECM that the whole objective of scaffolds for TERM is to mimic. In this work, it was possible to observe the effect of the scaffold flatness on the local thickness in the 2x5L and 3x4L fiber laydown groups (and to some extent, the 10-250 group in the 4x3L and 6x2L fiber laydown groups). This disappears in the rest of the groups of the 4x3L and 6x2L, indicating that the pore size distribution is becoming more dependent on the complex geometrical shape of the scaffold.

While μCT analysis of MEW scaffolds was previously described for porosity estimation,⁴⁵ explanted MEW scaffolds as a tissue-engineered bone model,⁴⁶ analysis of particles in fibers,⁴⁷ and the creation of a finite element model for mechanical properties,^29,48 none so far analyzed the effect of the three scaffold properties we checked (fiber diameter, spacing, and laydown pattern) on the total porosity and local thickness distribution of the scaffold. By changing the laydown pattern and coupled with the possibility of changing the fiber diameter in a single print,²² the complexity of the scaffold can be tailored to fit a target structure. As it is possible to produce MEW scaffolds that are millimeters in thickness,²⁷ the local thickness analysis will help in the design of the scaffolds, for the potential biomedical application. For MEW scaffolds, these data may help in the design optimization and characterization of printed scaffolds, in the aim to optimize cellular infiltration by changing the scaffold porosity. Moreover, using the same method which we applied to the empty PCL scaffolds, one could thereby quantify the volume of deposited tissue (in vivo) or cells (in vitro) as part of TERM research. Recent research on the use of dynamic electric fields during MEW fabrication resulted in substantially thicker scaffolds; up to 7.1 mm in build height.²⁷ Under these circumstances, determining the morphology is challenging, and using μCT imaging becomes an essential tool for analysis.

Conclusion

With this work, we explored the nondestructive 3D quantitative analysis of microporosity in MEW scaffolds using μCT. The 3D analysis of porosity in thin fibrous scaffolds or in any other open porous structure is somewhat difficult compared to the analysis of closed pores (e.g., foams). First, a volume mask has to be defined which differentiates the structural porosity from the outside world. We achieved this with a two-step binary closing based on the exact EDT. Second, the resulting porosity cannot be simply subdivided into convex objects which would allow for labeling and morphological analysis of individual pores. We avoided this issue by calculating the local thickness of the entire pore space and analyzing its histographical distribution. Morphological parameters such as total porosity and pore size distribution of the scaffolds are obtained by this routine. From a high-resolution submicrometer CT scan, we showed that additional parameters can be calculated, for example, the fiber diameter, and it was possible to obtain values that are comparable to those obtained using the SEM.

The precision in calculating P_tot has been shown to depend on the accuracy of the gray value threshold, which separates voxels belonging to the scaffold from the surrounding air. Yet, within the accuracy of determining this value from the gray levels of both phases, we have shown that μCT accurately and quantitatively characterizes the volume porosity in all scaffolds, of 10 and 20 μm target fiber diameters as well as different laydown patterns and fiber spacing. From this preliminary study, we conclude that μCT is suited for analyzing and comparing volume porosity in PCL scaffolds, for example, for creating a unique fingerprint of their 3D structure. The nondestructive nature of μCT measurements could be used for MEW scaffold quality assurance, to verify that the additively manufactured structure is indeed the one that was designed, with a potential for using the same technique for scaffolds used in in vivo and in vitro experiments.

Disclosure Statement

No competing financial interests exist.

Supplementary Material

Supplementary Video S1

Supplementary Video S2