Generalization via superposition: combined effects of mixed reference frame representations for explicit and implicit learning in a visuomotor adaptation task

Abstract

Studies on generalization of learned visuomotor perturbations have generally focused on whether learning is coded in extrinsic or intrinsic reference frames. This dichotomy, however, is challenged by recent findings showing that learning is represented in a mixed reference frame. Overlooked in this framework is how learning appears to consist of multiple processes, such as explicit reaiming and implicit motor adaptation. Therefore, the proposed mixed representation may simply reflect the superposition of explicit and implicit generalization functions, each represented in different reference frames. Here we characterized the individual generalization functions of explicit and implicit learning in relative isolation to determine whether their combination could predict the overall generalization function when both processes are in operation. We modified the form of feedback in a visuomotor rotation task in an attempt to isolate explicit and implicit learning and tested generalization across new limb postures to dissociate the extrinsic/intrinsic representations. We found that the amplitude of explicit generalization was reduced with postural change and was only marginally shifted, resembling an extrinsic representation. In contrast, implicit generalization maintained its amplitude but was significantly shifted, resembling a mixed representation. A linear combination of individual explicit and implicit generalization functions accounted for nearly 85% of the variance associated with the generalization function in a typical visuomotor rotation task, where both processes are in operation. This suggests that each form of learning results from a mixed representation with distinct extrinsic and intrinsic contributions and the combination of these features shapes the generalization pattern observed at novel limb postures.

NEW & NOTEWORTHY Generalization following learning in visuomotor adaptation tasks can reflect how the brain represents what it learns. In this study, we isolated explicit and implicit forms of learning and showed that they are derived from a mixed reference frame representation with distinct extrinsic and intrinsic contributions. Furthermore, we showed that the overall generalization pattern at novel workspaces is due to the superposition of independent generalization effects developed by explicit and implicit learning processes.

INTRODUCTION

The details of how the motor system generalizes have been an issue of considerable interest in sensorimotor control because they can provide theoretical insights into the computational principles underlying motor learning (Poggio and Bizzi 2004; Shadmehr 2004). Specifically, the frame of reference according to which learning generalizes is critical for elucidating the internal representation of newly learned motor behavior.

Much has been learned about the internal representations of learning through adaptation tasks in which visual feedback of movement trajectories is distorted, such as that induced by a virtual device that rotates the normal relationship between the visually perceived and actual hand positions during reaching movements (Krakauer et al. 2000; Pine et al. 1996). In this approach, the reference frame associated with the representation is characterized by training participants to reach with the visuomotor perturbation in a single movement direction and examining generalization to different spatial positions and limb postures. The similarity with which generalization to the untrained limb posture is linked with the environment (i.e., extrinsic reference frame) or the state of the arm (i.e., intrinsic reference frame) defines the reference frame representation associated with the learning, since these two reference frames are necessary to span interaction between the body and the physical world (Buneo and Andersen 2012; McGuire and Sabes 2009; Sabes 2011; Sober and Sabes 2005).

Despite over two decades of studies employing this framework, there remains substantial disagreement regarding the characteristics of the internal representation. In visuomotor rotation tasks, Wang and Sainburg (2005) and Krakauer et al. (2000) have provided support for a representation based on movements extrinsic to the end effector. They found that the accuracy of reaching movements to the learned target direction from the novel posture was maintained despite requiring different joint rotations to attain the target. In contrast, others have reported patterns of generalization that are consistent with an intrinsic joint-based representation (de Rugy et al. 2009; Krakauer et al. 2006; Rotella et al. 2015). In an isometric visuomotor rotation task, Rotella et al. (2015) found that generalization was more complete to a target that was similar in terms of the learned joint torques and muscle activations than to a target that was consistent with the extrinsic movement direction at the new limb posture.

To complicate matters, Brayanov et al. (2012) showed that when generalization was probed across a wide distribution of movement directions at various limb postures, generalization was in fact most prominent in movement directions that were intermediate between the training directions defined according to extrinsic and intrinsic reference frames. This result was interpreted to indicate that learning is encoded in a gain-field combination of extrinsic and intrinsic movement representations. The authors further proposed that this gain-field combination can explain the apparently conflicting generalization patterns in previous studies.

At present, a mechanistic explanation for the apparent mixed reference frame underlying learning in visuomotor adaptation tasks is lacking. One possibility is that learning is not the result of a single process. Indeed, it has become increasingly clear that learning in visuomotor adaptation tasks is the result of multiple processes (Diedrichsen et al. 2010; Heuer and Hegele 2008, 2011; Huang et al. 2011; Izawa and Shadmehr 2011; Mazzoni and Krakauer 2006; Taylor et al. 2014). We have recently demonstrated that, by contrasting reports of subjects’ explicit reaiming directions with actual reaching directions, the adaptive response during a visuomotor rotation task is made up of at least two quantifiable components: explicit reaiming strategies that arise from awareness of the perturbation when large task performance errors are observed and an implicit motor adaptation process that is driven by sensory prediction error signals that reflect the difference between the intended and actual movement outcomes (Bond and Taylor 2015; McDougle et al. 2015, 2017; Poh et al. 2016; Taylor et al. 2014). Thus, given that the overall adaptive response during a visuomotor rotation task appears to consist of both explicit and implicit forms of learning, the ensuing generalization should carry signatures of both forms of learning, which may be very different.

The dual operation of explicit and implicit learning in a typical visuomotor rotation task makes for interesting interactions between these forms of learning, which may ultimately influence the pattern of generalization across different limb postures. Recent studies have suggested that the manner in which implicit learning generalizes to other movement directions, within a workspace, may be intimately linked to the locus of the explicit aiming direction (Day et al. 2016; McDougle et al. 2017; Schween et al. 2018). For example, McDougle et al. (2017) found that implicit learning was expressed maximally at the subject’s explicit aiming location, rather than the actual trained target location. If the locus of the explicit aim was maintained in extrinsic space across different limb postures, then appropriate generalization should be observed at the location of aim that is consistent in an extrinsic reference frame at the untrained limb posture. This would give the appearance of a generalization that is intermediate between extrinsic and intrinsic reference frames, as observed by Brayanov et al. (2012). This raises a more fundamental issue, that is, whether the generalization in the proposed mixed reference frame when examined across different limb postures is in fact a superposition of generalization effects driven by independent effects from both explicit and implicit forms of learning, each of which may operate in separate reference frames.

Multiple lines of evidence suggest that explicit and implicit forms of learning have different patterns of generalization, and accordingly different representations. For example, Heuer and Hegele (2008, 2011) showed that when subjects in a standard visuomotor rotation task are prompted that the perturbation is removed, aftereffects, a measure of implicit learning, generalize narrowly within the vicinity of the trained target. In contrast, explicit learning, which is quantified by a subject’s verbal reports of the direction of movement required to compensate for the perturbation, generalizes broadly to movements in all directions (Heuer and Hegele 2011; McDougle et al. 2017; Poh et al. 2016). Importantly, when generalization was probed across different limb postures, explicit reaiming displayed complete transfer to the novel limb posture, whereas implicit aftereffects were significantly reduced or hardly present (Heuer and Hegele 2011). This result shows that these forms of generalization have different attributes and thus in theory could be represented in different reference frames. However, given the broad generalization of explicit learning and the absence of implicit aftereffects at novel limb postures, the effects of generalization according to the extrinsic or intrinsic reference frame are indistinguishable. This presents a key obstacle in determining which reference frames contribute to the representation of explicit and implicit learning, and hence the question of which reference frame underlies both forms of learning has yet to be systematically addressed.

Here we designed a series of visuomotor rotation experiments to characterize and quantify the effects of explicit and implicit learning in relative isolation and then examined generalization across different limb postures to dissociate the extrinsic and intrinsic reference frames of representation. In an attempt to selectively engage explicit learning, subjects performed a visuomotor rotation task with delayed end-point feedback, which has been shown to severely disrupt development of implicit learning but not explicit reaiming strategies in a visuomotor rotation task (Brudner et al. 2016; Schween and Hegele 2017). This presents a particularly promising approach, in lieu of using verbal reaiming reports as a proxy for explicit learning, because it allows reaiming strategies to develop naturally in the task without visual cues or verbal instruction. What’s more, it may also allow for an unbiased estimate of the generalization function, as previous attempts to measure the generalization function have relied on visual cues or posttests that may warp the generalization function itself (Heuer and Hegele 2008, 2011; McDougle et al. 2017).

In an attempt to selectively engage implicit learning, we introduced a task-irrelevant visual error clamp in which the cursor followed an invariant trajectory regardless of the subject’s movement direction. Critically, the clamped visual feedback introduced a constant visuomotor discrepancy between angular hand position and visual feedback throughout training, which rendered the visual error signals observed irrelevant to the task. By emphasizing that the task goal is to reach for the target irrespective of the direction of the clamped visual feedback, this approach is thought to suppress explicit reaiming strategies, and any changes in behavior are presumed to reflect the signature of an implicit form of learning (Morehead et al. 2017). Behavior following exposure to such perturbations typically shows a change in reach direction opposite in sign to the visual feedback and saturates at a similar magnitude irrespective of the size of perturbation. Such adaptive response is consistent with observed patterns of implicit adaptation in visuomotor tasks designed to dissociate explicit and implicit contributions to motor learning and is thought to reflect implicit processes associated with sensory prediction errors—the discrepancy between the actual and expected sensory consequences of a motor command (Bond and Taylor 2015; Taylor et al. 2014).

The goal here was to try to isolate each learning process, characterize the generalization function across different limb postures, and then determine whether the combination of the independent generalization functions could predict the overall generalization function when both processes were in operation in a standard visuomotor rotation task. We hypothesized that explicit and implicit learning would display generalization in different reference frames and their superposition could account for the discrepancies between prior studies and the apparent mixture of reference frame representations. Contrary to our initial hypothesis, we found that both explicit and implicit learning result from mixed representations, but each form of learning had differing relative mixtures of extrinsic and intrinsic representation.

METHODS

Subjects

A total of 48 subjects (16 men, 32 women; age range: 18–32 yr) were recruited from the research participation pool of the Department of Psychology at Princeton University in exchange for course credit or money. The sample size was determined by a power analysis (α = 0.95), which sought to replicate the effect size of a relevant result (d = 1.6; shift of generalization pattern from workspace 1 to workspace 2 in experiment 1 in Brayanov et al. 2012). The required sample size was 15, but to counterbalance training target directions and rotation signs we recruited a sample of 16 subjects for each condition. All subjects were right-handed as verified with the Edinburgh handedness inventory (Oldfield 1971) and provided written informed consent before participation. The protocol was reviewed and approved by Princeton University’s Institutional Review Board.

Apparatus and Task

Subjects sat comfortably on a chair and made planar reaching movements while holding onto the handle of a two-link robotic manipulandum (KINARM End-Point; BKIN Technologies). The standard configuration of the robot’s handle was turned upside down, and the subject’s right arm was supported against gravity with a ceiling-mounted sling such that arm movements occurred predominantly in the horizontal plane. All visual stimuli were projected from a 47-in. 1,920 × 1,080-pixel resolution display (LG47LD452C; LG Electronics), which was horizontally mounted and inverted to face a mirror that was 6 cm above the robot’s handle. The mirror occluded the manipulandum as well as the hand and arm of the subject, preventing direct visual feedback of the hand location. Two-dimensional position of the hand location was sampled at 1,000 Hz.

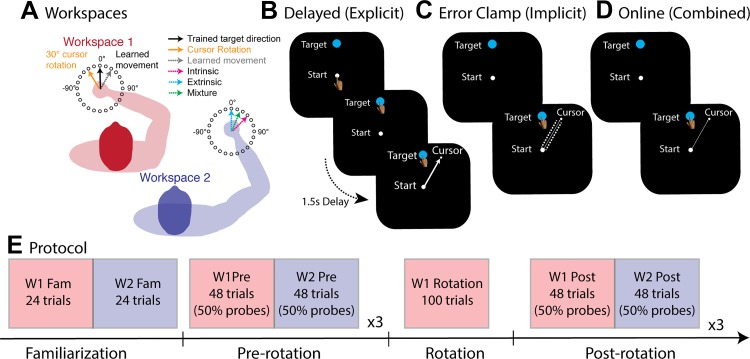
In all experiments, subjects performed 7.5-cm point-to-point reaching movements from two limb postures at the left, training workspace [workspace 1 (W1)] and the right, transfer workspace [workspace 2 (W2)] (Fig. 1A). These workspaces were uniquely defined for each subject based on his/her measured forearm and upper arm lengths. In W1, the subject’s shoulder and elbow angles were 75° and 90°, respectively. In W2, the subject’s elbow angle was maintained, but the shoulder angle was rotated clockwise 45°. Note that a greater angular separation between W1 and W2 allows for better dissociation between extrinsic and intrinsic reference frames; however, angles > 45° greatly affect the viewing angle and joint mobility. The reaching targets (24 target positions regularly spaced 15° around a circle) were located on the circumference of an invisible circle (radius 7.5 cm) centered on a starting location defined by W1 and W2.

Fig. 1.

Experimental setup and conditions. A: subjects learned to compensate for a 30° rotation at workspace 1 (W1) before generalization was tested to 24 targets in workspace 2 (W2). The 2 workspaces were separated by a 45° clockwise rotation of the shoulder to dissociate the extrinsic and intrinsic representations. B: in the explicit condition, subjects received delayed end-point feedback of their performance during training. C: in the implicit condition, the feedback cursor was clamped during training, such that it followed an invariant trajectory that was offset by ±30° regardless of the subject’s movement direction. D: in the combined condition, subjects learned to overcome the visuomotor rotation using online visual feedback. This approach has been shown to allow operation of both explicit and implicit forms of learning. E: training protocol.

Each trial began when the robotic manipulandum positioned the subject’s hand within a starting location (gray empty circle: radius 0.5 cm). When the hand was within the starting location, the gray circle turned white and a white cursor (white filled circle: radius 0.5 cm) representing the current hand position appeared. The two circles merged into a single filled start position circle. The hand had to remain in the starting location for 300 ms before a target (blue filled circle: radius 0.5 cm) appeared at 1 of 24 possible target locations (regularly spaced 15° around a circle). The presentation of each target coincided with a beep to initiate the trial, and subjects were instructed to make a ballistic movement that “sliced” through the target. Our intention for slicing movements was to minimize feedback-based corrections and discourage position coding (Scheidt and Ghez 2007). This approach should emphasize learning from, primarily, feedforward mechanisms.

Depending on the particular training condition in W1 (see below), subjects received delayed end-point feedback, clamped visual feedback, or continuous online feedback. For delayed end-point feedback trials, visual feedback of the cursor position was eliminated once movement velocity exceeded 5 cm/s. End-point feedback of the cursor appeared on the circumference of an invisible ring of radius 7.5 cm after 1.5 s. For clamped visual feedback, the cursor was visible throughout the outbound movement and followed an invariant trajectory that was offset by ±30° relative to the target, regardless of the subject’s movement direction. Once movement amplitude exceeded 7.5 cm, the cursor remained stationary for 1 s. For continuous online feedback trials, feedback of cursor location remained visible for the duration of the outbound movement. When radial movement amplitude exceeded 7.5 cm, the feedback cursor froze on the screen for 1 s. For both delayed end-point and online feedback conditions, the blue target changed to green if the feedback cursor overlapped any part of the target; otherwise the target turned red. In contrast, for clamped visual feedback, the target remained blue. After each trial, the target and cursor were extinguished and the robotic manipulandum repositioned the limb at a starting location defined by the training or transfer limb posture to start the next trial.

Experimental Procedures

Subjects were pseudorandomly assigned to one of three training conditions: explicit, implicit, and combined conditions. Specifically, the explicit (n = 16) and implicit (n = 16) conditions were aimed at characterizing the pattern of generalization for explicit and implicit forms of learning in relative isolation, which was accomplished by providing delayed end-point feedback and clamped visual feedback, respectively, during a visuomotor rotation task. The goal of the combined condition (n = 16) was to determine whether the generalization function that emerges in a standard visuomotor rotation task, when both implicit and explicit forms of learning are operating simultaneously, could be accounted for by the combination of separate implicit and explicit generalization functions obtained.

Each condition began with a brief familiarization phase, which consisted of a block of 24 trials (1 to each target location) in W1 and W2 (Fig. 1E). During these movements, subjects in the explicit condition received delayed end-point feedback of their movements, whereas subjects in the implicit and combined conditions received online cursor feedback. After familiarization, in the second prerotation phase, subjects completed 144 trials, divided into three blocks of 48 trials, in each workspace. During each block, visual feedback of the movements was only presented on 50% of the trials. Specifically, after every two trials with delayed end-point feedback in the explicit condition or online cursor feedback in the implicit and combined conditions, two probe trials without any visual feedback were presented to assess baseline performance at a workspace. We alternated between W1 and W2 after each block of 48 trials (24 feedback trials, 24 probe trials for each block). This resulted in three probe trials at each target location in both W1 and W2.

In the subsequent rotation phase, a 30° visuomotor rotation was introduced to a single training movement direction (selected from 8 possible locations: 0°, 45°, 90°, 135°, 180°, 225°, 270°, 315°; counterbalanced across subjects) for 100 trials at the training target in W1. The eight training targets were examined across all conditions to minimize movement irregularities arising from biomechanical constraints when moving in different directions, and thereby giving rise to nonsymmetrical generalization patterns. Note that the size of visuomotor rotation was chosen to match the perturbation used in a prior study (Brayanov et al. 2012). The direction of the 30° rotation was also counterbalanced across subjects.

Explicit condition.

For the explicit condition, subjects received rotated delayed end-point feedback of their performance (Fig. 1B). Critically, this approach has been shown to be effective in limiting the development of implicit learning and appears to result in predominantly explicit forms of learning during a visuomotor rotation task (Brudner et al. 2016; Schween and Hegele 2017).

Implicit condition.

For the implicit condition, subjects experienced clamped visual feedback (Fig. 1C): The cursor followed an invariant trajectory that was offset by ±30° (n = 8 clockwise; n = 8 counterclockwise) regardless of the subject’s movement direction (Morehead et al. 2017). Because subjects were instructed to ignore the clamped visual feedback and to move their hand directly to the target, this paradigm should suppress any explicit reaiming strategies since the visual error signals observed are irrelevant to the task. Thus any changes in behavior should reflect learning from implicit motor adaptation (Morehead et al. 2017). We note that our experimental approach of using delayed feedback and clamped feedback does not ensure the isolation of explicit and implicit processes, respectively, but based on prior findings these conditions should heavily suppress the undesired process.

Combined condition.

For the combined condition, subjects experienced rotated online visual feedback at the training target in W1 (Fig. 1D). This approach allows both explicit and implicit learning to operate during training (McDougle et al. 2015, 2017; Poh et al. 2016; Taylor et al. 2014).

Finally, to examine the pattern of generalization in the postrotation phase, subjects performed a total of 72 probe trials with no visual feedback at each limb posture (3 probe trials for each of the 24 movement directions). After every two trials with no visual feedback, the perturbed visual feedback was restored during movements made to the training target in W1 for the next two trials to maintain learning.

Data Analysis

Behavioral measures.

Terminal reach directions were computed as the direction of the vector connecting the subject’s hand location at movement onset to the point when movements passed a radial distance of 7.5 cm. Movement onset was defined when the movement speed threshold first exceeded a speed of 5 cm/s. For all trials, we computed the directional errors by calculating the angular difference between the direction of the target and terminal reach directions. To examine changes in movements made between W1 and W2, we subtracted the directional errors for each target during probe trials in the postrotation phase from the directional errors in the prerotation phase for each target to yield the change in hand angle from baseline for each target in each workspace. This was done to mitigate any potential performance biases due to biomechanical differences across workspaces and target locations. All performance measures are reported as means ± SE unless otherwise stated.

Measuring generalization.

To characterize the generalization pattern in W1 and W2, the changes in reach direction for each target location defined according to an extrinsic Cartesian reference frame were fit with Gaussian tuning functions (Brayanov et al. 2012; Tanaka et al. 2009):

$$g\left(\text{θ}\right)=k\cdot e^{-\frac{{(\text{θ}-{\text{θ}}_0)}^2}{2{\text{σ}}^2}}+h$$ (1)

The generalization function g(θ) is centered on the target direction eliciting the greatest change in reach direction (θ₀), has an amplitude of k, and is local with a width characterized by σ. The generalization function also contains a constant offset parameter, h, which has been thought to reflect the global (uniform) portion of motor adaptation (see Brayanov et al. 2012). The amplitude k of the fit, which excludes the offset (h, was constrained to the maximum change in reach direction at W1. We fit the Gaussian function to individual subjects’ data for each condition at the training and transfer limb postures to estimate the amplitude (k), center (θ), width (σ), and vertical offset (h) of the generalization at W1 and W2. The parameters of the generalization function were estimated with the least-squares method of the function “fit” in MATLAB.

Defining extrinsic and intrinsic space.

The purpose of this study was to examine how the extrinsic and intrinsic reference frames contribute to the internal representation of explicit and implicit forms of learning. To achieve this, we dissociated the extrinsic and intrinsic reference frames of representation by changing the limb postures relative to the training limb posture. It is important to note that our convention of reference frame was to express the general notion of a reference point according to which generalization is expressed. The reference frame has an origin but is agnostic to the specification of a metric for a coordinate representation within that frame (polar vs. Cartesian coordinate system). Indeed, recent studies have found that subjects can flexibly learn perturbations in either polar or Cartesian systems without addressing reference frames (Hudson and Landy 2012, 2016). However, the ability of our study to resolve the issue of reference frame does not depend on the coordinate specification, and thus we focused on the origin of the reference frame rather than the coordinate encoding.

To parameterize each movement with respect to the extrinsic and intrinsic reference frames for which we tested generalization, we adopted the framework of Brayanov et al. (2012), in which it is assumed that a movement can be defined according to reference frames that are either extrinsic or intrinsic relative to the spatial position of the limb. Briefly, in an extrinsic Cartesian reference frame, a straight point-to-point movement can be characterized by a vector that connects the movement starting and end points. Figure 2A shows the movement vectors in Cartesian space for all 48 target positions in the training and transfer limb postures. The start locations for each of the limb postures depicted in Fig. 2A were calculated based on the forearm and upper arm lengths averaged across all 48 subjects. In this conception, the relationship between any two straight movements with the same origin but ending at two different targets is defined by the angular distance between the movement vectors in Cartesian space. Correspondingly, the same two movements can be defined in an intrinsic joint-based reference frame as a pair of joint-space movement vectors that share a common origin. The joint-space angle separating the two vectors describes the angular separation between the two movements in an intrinsic joint-based reference frame. Figure 2B shows the intrinsic joint-based representations of the movements toward each target direction at both workspaces. Here, we computed the intrinsic joint-based trajectories using the inverse kinematics equations for a two-link robotic manipulandum (Spong et al. 2006). Note that all our calculations involving the intrinsic joint space were based on the relative joint angles. This framework was adopted from Brayanov et al. (2012), in which we seek to replicate all comparisons made previously when both explicit and implicit learning were combined (see Fig. 1 of Brayanov et al. 2012).

Fig. 2.

Defining intrinsic and extrinsic movement representations. A: extrinsic movement representations of ideal cursor movements. In this example, subjects adapted to a visuomotor rotation to the 0° target at workspace 1 (W1) (black arrow), and generalization was probed to an array of 24 targets (regularly spaced at 15°) at both W1 and workspace 2 (W2). The gray trajectories illustrate the ideal cursor movements to all targets in W1 and W2. In W2, the blue arrow illustrates the trained cursor movement in extrinsic Cartesian space, and the red arrow shows the trained cursor movement in intrinsic joint space. It is important to note that the parallel blue and black arrows in A indicate that these 2 movements require the same change in extrinsic Cartesian space. B: intrinsic movement representations of ideal cursor movements. Here, the x-axis represents the shoulder angle relative to the torso, and the y-axis represents the elbow angle relative to the torso. In W1, the black arrow represents the trained direction in joint space. Similarly, in W2, the blue arrow illustrates the trained cursor movement in extrinsic Cartesian space, and the red arrow shows the trained cursor movement in intrinsic joint space. In contrast to A, the black and red arrows are now parallel to each other, implying that these 2 movements require the same joint rotations. C: distance of the targets in extrinsic and intrinsic space. On the x-axis, the distance between different targets is calculated as the difference between that and the trained target in extrinsic Cartesian space. In comparison, the y-axis depicts the distance between each target and the trained one as the difference between that and the trained target in intrinsic joint space.

To determine the angular distance between the trained movement direction and any given movement direction in the extrinsic reference frame, we computed the difference between the trained and testing target locations in terms of the change in x-y coordinates:

$${\text{θ}}_{\text{E}}=\text{arctan}\left(\frac{\text{Δ}y}{\text{Δ}x}\right)$$ (2)

In comparison, the angular distance between the trained movement direction and any given movement in the intrinsic reference frame (θ_I) was defined in terms of the change in shoulder-elbow coordinates:

$${\text{θ}}_{\text{I}}=\text{arctan}\left(\frac{\text{Δshoulder angle}}{\Delta \text{elbow angle}}\right)$$ (3)

Figure 2C illustrates the two-dimensional extrinsic-intrinsic space employing the two reference frames as cardinal axes in a two-dimensional plot. This plot characterizes the distance in both the extrinsic and intrinsic reference frames between the trained movement and any given movement direction for which generalization was tested. Note that the trained target in the training limb configuration is located at the origin (0°, 0°). The limb posture manipulation in our study that resulted in a 45° rotation in the shoulder angle between W1 and W2 produced a 45° shift in the locus of the target locations defined in an intrinsic joint-based representation (Fig. 2C). This shift is such that the target location corresponding to the trained movement direction in intrinsic space is located at position (−45°, 0°), whereas the target location corresponding to the trained movement direction in extrinsic space is located at (0°, 45°).

Generalization predictions.

The manner in which the pattern of generalization is expressed at W2 depends on the reference frame according to which learning is represented. In our study, subjects learned to compensate for a visuomotor rotation in a single movement direction at W1, and generalization was tested at W2 with the shoulder angle rotated 45° clockwise. Based on the extrinsic-intrinsic space defined above, if learning mapped exclusively onto an intrinsic reference frame, the direction of peak generalization would be observed at the target direction rotated 45° clockwise relative to the trained target direction defined extrinsically at W2 (W2 − W1 ≈ 45°). In contrast, if learning is mapped exclusively onto an extrinsic reference frame, the pattern of generalization at W1 and W2 should be identical. In this case, the direction of peak generalization should remain invariant in extrinsic space, irrespective of limb posture (W2 ≈ W1). Additionally, we also considered the possibility that the representation involves a mixture of reference frames. Depending on the mixture ratios between extrinsic and intrinsic reference frames, this would cause the pattern of generalization to be shifted to an intermediate position between the trained target direction defined intrinsically and extrinsically (0 < W2 − W1 < 45°). The difference between estimated peak direction at W1 and W2 was tested with single-sample t-tests, with the test variable set at 0 or 45° in accordance with the pure extrinsic or pure intrinsic representation. Significance level for all tests was set at 0.05.

To further consider a mixed representation, we determined the relative contributions of extrinsic and intrinsic representations to the pattern of generalization, using the multiplicative gain-field combination model of Brayanov et al. (2012). This model posits that the generalization to a given target direction depends on combined distance across the extrinsic and intrinsic space from the trained direction.

$$g\left(\text{θ}\right)=k\cdot e^{\frac{-{({\text{θ}}_{\text{I}}-{\text{θ}}_{{\text{I}}^{\text{0}}})}^2}{2{\text{σ}}_{\text{I}}^{\text{2}}}}\cdot e^{\frac{-{({\text{θ}}_{\text{E}}-{\text{θ}}_{{\text{E}}^0})}^2}{2{\text{σ}}_{\text{E}}^{\text{2}}}}$$ (4)

where ${\text{σ}}_{\text{E}}=\text{σ}/\sqrt{s_{\text{E}}}$ and ${\text{σ}}_{\text{I}}=\text{σ}/\sqrt{s_{\text{I}}}$. The coefficients s_E and s_I, where s_E + s_I = 1, are included to allow for differential weighting of extrinsic and intrinsic components of the overall distance and allowed us to determine the extent to which extrinsic and intrinsic reference frames contribute to the generalization at W2. Note that we used the data from W1 to constrain the width of generalization. Furthermore, the offset term (h) is absent in this model to enable us to directly compare with that obtained in Brayanov et al. (2012).

Because the goodness of fit to the individual generalization functions is prone to variability inherent within each subject’s data, we performed a bootstrap test with 2,000 iterations to estimate the confidence intervals of the parameters estimated from the fit to the mean data from each condition. This approach allowed us to determine the variability associated with the parameters of the fit to the mean data. Specifically, on each iteration we selected 16 subjects with replacement from the respective condition and computed the generalization function and corresponding fits based on the data averaged across the selected subjects. The median and 95% confidence intervals were then estimated from the distribution of these fit parameters.

To statistically compare whether the distributions of the fitted parameters at W1 were different from those at W2, we used the P value computed from the bootstrap. That is, we first calculated the difference in the estimated parameters between the training and transfer limb postures on each iteration of the bootstrap. Using the distribution of bootstrapped differences, we estimated the number of samples in the distribution that are above the absolute value of the null hypothesis. This approach is advantageous because it allows us to create a full distribution of the sample (in this case 2,000 samples) and when computing the 95% confidence intervals we are looking at the two tails of the bootstrap for statistical evaluation (50 samples from the lower and upper ends of the bootstrap). The percentage of samples that are above the absolute value of the null hypothesis (0) constitutes the P value of the bootstrap (Fisher 1993). Significance level was set at 0.05.

RESULTS

Learning Delayed End-Point Feedback and Clamped Visual Feedback During Rotation Phase

We first set out to examine explicit and implicit forms of learning in relative isolation and characterize the generalization function across different limb postures. To do this, subjects learned to compensate for a 30° visuomotor rotation with delayed end-point or clamped visual feedback designed to isolate putative forms of explicit and implicit learning, respectively. Both groups displayed a rapid change in hand angle in response to the visuomotor rotation at the training posture (W1; Fig. 3), which is likely attributable to the fact that there is only one training target and is on par with previous studies (Bond and Taylor 2015; McDougle et al. 2015, 2017). Final performance in both explicit and implicit conditions, on average, reached asymptotic levels within the 20 trials. The asymptotic performance averaged over the last 10 trials was 26.2 ± 1.5° in the explicit condition versus 15.7 ± 2.2° in the implicit condition. Note that although not central to the primary goal of this study—characterizing the contribution of explicit and implicit learning to the pattern of generalization—we sought to compare the asymptotic level of learning between explicit and implicit learning. We found that although both explicit [t(15) = −2.73; P = 0.02] and implicit [t(15) = −6.4; P < 0.0001] conditions fall short of 30° required to fully compensate for the visuomotor rotation, the explicit condition resulted in significantly greater change in reach directions than the implicit condition (P < 0.001; independent-sample t-test). This difference between presumed explicit and implicit conditions is in line with previous studies that showed that explicit forms of learning can flexibly adjust and compensate for the size of rotation (Bond and Taylor 2015; Brudner et al. 2016; Taylor et al. 2014) whereas implicit forms of learning appear to asymptote at 15–20° (Bond and Taylor 2015; Morehead et al. 2017). This also suggests qualitatively different forms of learning when using clamped visual feedback and delayed end-point feedback during exposure to a visuomotor rotation.

Fig. 3.

Rotation training performance for explicit (Delay) and implicit (Clamp) conditions: mean change in reach directions when participant trained with a cursor that was aligned (Prerotation phase, no shading) or rotated 30° relative to hand movement (Rotation, light gray shading; Postrotation phase, dark gray shading). The vertical dashed lines indicate the transition between different phases. The red line corresponds to reach directions averaged across all participants in the explicit condition (Delay), and the blue line corresponds to reach directions averaged across all participants in the implicit condition (Clamp); shaded area represents SE.

Generalization of Explicit and Implicit Learning

In the subsequent postrotation phase, probe trials without visual feedback were used to assess the pattern of generalization at W1 and W2. To quantify the change in reach direction following rotation training, the directional errors from the prerotation phase were subtracted from the postrotation phase at each target location in each workspace. Subsequently, a Gaussian function with four free parameters (center position, amplitude, width, and vertical offset) was fit to each individual subject’s generalization data to approximate the pattern of generalization.

Figure 4 shows the generalization of rotation training, along with the Gaussian fit, averaged across subjects in the explicit (Fig. 4A) and implicit (Fig. 4D) conditions at W1 and W2. Contrary to previous studies, which have shown quite broad generalization functions for explicit learning (Heuer and Hegele 2008, 2011; McDougle et al. 2017), here we found it to be relatively narrow and Gaussian in shape. The generalization pattern for the explicit condition in W1 was centered near the 0° training direction {−2° [95% confidence interval (CI) = −13.2°, 8.5°]; Fig. 4B} and had an amplitude of 16.7° (95% CI = 11.3°, 21.7°; Fig. 4C), which falls short of the 30° required to fully compensate for the visuomotor rotation. Note that the average amplitude reported here is the amplitude of the Gaussian fit, but this excludes an offset of 4.4° (95% CI = 0°, 9.9°) that when combined provides a total offset of ~21.1°. Finally, the width of the generalization pattern associated with the explicit condition was 24.3° (95% CI = 17.5°, 34.7°).

Fig. 4.

Gaussian fits for the generalization pattern in the explicit (A) and implicit (D) conditions. The observed generalization pattern was the Gaussian fit to the data averaged across all participants in each condition at workspace 1 (W1) (red line) and workspace 2 (W2) (blue line). The shaded area represents mean ± SE. The vertical lines at 0° and 45° indicate the direction in which peak generalization at W2 would be observed for an exclusively extrinsic (cyan) or exclusively intrinsic (magenta) representation. B and C: box plots of the center of generalization (B) and amplitude (C) estimated by the Gaussian fit for each of the 2,000 bootstrap samples for the explicit condition at W1 and W2. E and F: box plots of the center of generalization (E) and amplitude (F) estimated by the Gaussian fit for each of the 2,000 bootstrap samples for the implicit condition at W1 and W2. Quartiles and confidence intervals (CI) are indicated on box plots. *Significant main effect following a bootstrap test at P < 0.05. n.s., Not significant.

Similarly, we found that the generalization function for the implicit condition at W1 was relatively narrow and well described by a Gaussian function, consistent with prior studies (McDougle et al. 2017; Morehead et al. 2017). As expected, the center location of the generalization pattern for implicit condition in W1 was near zero [−1.8° (95% CI = −14.9°, 11.2°); Fig. 4E] with an amplitude of 10.5° (95% CI = 7.4°, 15°; Fig. 4F) corresponding to ~35% compensation of the imposed visuomotor rotation. In addition, the width of the generalization pattern for implicit condition was 29.9° (95% CI = 22.4° 34.8°), and there appears to be no vertical offset [0.02° (95% CI = 0°, 1.2°)].

Comparison of the generalization patterns between explicit and implicit conditions at W1 revealed that the centers of the generalization pattern for the explicit (P = 0.37) and implicit (P = 0.39) conditions were not significantly different from training target direction at 0°, and they were also not different from one another (P = 0.49). Similarly, there was also no difference between the widths of the generalization pattern in the explicit and implicit conditions at W1 (P = 0.17). In contrast, the amplitude was significantly smaller for the implicit condition than for the explicit condition (P = 0.03). These results show that the presumed forms of explicit and implicit learning driven by delayed end-point feedback and clamped visual feedback, respectively, generalized locally at the trained movement direction but that the amplitude of generalization was significantly less for the implicit condition.

Furthermore, we note that the vertical offset in the generalization function for the explicit condition was larger than the generalization function associated with the implicit condition (P = 0.037). Such vertical offsets indicate that movements to all targets in the workspace were biased in the direction required to compensate for the visuomotor rotation. These vertical offsets were frequently observed in the measured generalization function in previous visuomotor adaptation studies (Krakauer et al. 2000; McDougle et al. 2017; Pearson et al. 2010; Taylor et al. 2013), and our findings imply that such vertical offsets in the generalization function appear to be primarily due to explicit and not implicit learning.

We then sought to determine whether the generalization functions associated with the explicit and implicit conditions changed when shifting to a different limb posture in W2. For the explicit condition, the generalization function was centered near 13.9° (95% CI = −7.7°, 35°) in W2 and appeared to be partially shifted toward the intrinsic training direction (i.e., phase shift). However, we found that the centers of generalization between W1 and W2 were not reliably different from one another (+15.8°; 95% CI = −7.7°, 39.3°; P = 0.09). On the other hand, the amplitude of generalization for the explicit condition at W2 was 9.5° (95% CI = 5.8°, 14.1°), which corresponded to a significant drop of −7.4° (95% CI = −13.6°, 0.4°; P = 0.03). Finally, the width and offset of the generalization function at W2 were 36.3° (95% CI = 18.2°, 74.3°; P = 0.1) and 0.8° (95% CI = 0°, 2.1°; P = 0.2) respectively, and they were both not reliably different from that in W1. Taken together, these results demonstrate that although the direction of peak generalization for the explicit condition appears to be maintained in an extrinsic reference frame, the amount of learning acquired in W1 was significantly reduced in W2.

For the implicit condition, the generalization function in W2 was centered at 22.7° (95% CI = 10.9°, 64.5°), which represents a median phase shift of +25.2° (95% CI = 7.3°, 70°) between W1 and W2. Interestingly, the median phase shift was approaching halfway between the zero phase shift predicted by a pure extrinsic representation (W2 − W1 ≈ 0°) and the 45° shift predicted by a pure intrinsic representation (W2 − W1 ≈ 45°). The center of the generalization function for the implicit condition at W2 was significantly different from that at W1 (P = 0.005). Next, the amplitude of the generalization function for implicit condition at W2 was 3.8° (95% CI = 0.1°, 7.3°), which was not significantly different from that in W1 (−3.3°; 95% CI = −8.7°, 1.3°; P = 0.08). Finally, the median width of the generalization function at W2 was 27.8° (95% CI = 17.7°, 66.9°), and the median offset was 0.8° (95% CI = 0°, 2.1°). Based on the bootstrap P values, both the median width (P = 0.38) and offset (P = 0.2) of the generalization function in W2 were not significantly different from those in W1. These results demonstrate that although the direction of peak generalization for the implicit condition is sensitive to limb posture, the degree of generalization is quite stable.

Next, we sought to directly address our hypothesis put forward in introduction, that is, explicit and implicit learning would generalize in different reference frames. To this end, we compared the changes in the direction of peak generalization (i.e., phase shifts), amplitude, widths, and offsets in the generalization pattern from W1 to W2 for the explicit learning condition with the corresponding implicit learning condition. We found that there were no significant differences in the change in direction of peak generalization (P = 0.27), the amplitude (P = 0.18), the width (P = 0.16), and the offset (P = 0.48) between the explicit and implicit conditions. In line with our preceding analysis, these results do not support our hypothesis that explicit and implicit learning generalize in different reference frames. Although our preceding analysis, which analyzed the peak of generalization for explicit and implicit conditions separately, suggested that the generalization for the explicit condition was more consistent with an extrinsic representation and the generalization for the implicit condition reflected a more mixed representation, the lack of a difference between the two generalization functions here suggests that the result is less clear. From visual inspection of Fig. 4, there is a shift on average for both generalization functions in W2, suggesting that both conditions likely have mixed representations but to differing degrees.

Finally, we analyzed the goodness of fits on the bootstrap samples. For the explicit condition, median R² were 0.84 (95% CI = 0.6, 0.93) and 0.62 (95% CI = 0.23, 0.85) in W1 and W2, respectively. For the implicit condition, median R² were 0.83 (95% CI = 0.64, 0.91) and 0.62 (95% CI = 0.23, 0.8) in W1 and W2, respectively. Taken together, these results suggest that the phase shifts in the pattern of generalization observed for the implicit condition, and the reduction in the amplitude for the explicit condition, were relatively robust.

Mixture of Extrinsic and Intrinsic Reference Frames for Explicit and Implicit Conditions

The preceding analysis of the direction of peak generalization revealed that the generalization patterns for explicit (+15.8° bootstrap median) and implicit (+25.2° bootstrap median) conditions displayed different amounts of phase shifts, suggesting that there could be differential contributions of extrinsic and intrinsic reference frames. To determine the mixture ratios of extrinsic and intrinsic reference frames for the pattern of generalization observed in the explicit and implicit conditions, we first fit the subject-averaged generalization pattern to the gain-field model of Brayanov and colleagues (Brayanov et al. 2012), which allows for differential weighting of extrinsic and intrinsic reference frames (Fig. 5).

Fig. 5.

Extrinsic and intrinsic contributions to the generalization patterns in the explicit and implicit conditions: different mixture ratios for explicit (A) and implicit (B) generalization in both conditions estimated by a gain-field model fit with varying extrinsic (s_E) and intrinsic (s_I) contributions to the data averaged across all subjects in workspace 1 (W1) (red line) and workspace 2 (W2) (blue line). Right: representation of the gain-field model arising from the combination of extrinsic and intrinsic representations.

Figure 5, A and B, illustrate the summation of the intrinsic and extrinsic components for the explicit and implicit conditions, respectively. By visual observation, generalization for the explicit condition has an “elliptical” shape, indicative of a wider generalization in intrinsic space and a narrower generalization in extrinsic space. In contrast, generalization for the implicit condition has a “round” shape, which suggests that the widths of generalization in extrinsic and intrinsic space are approximately equal. The observed differences in the contributions of extrinsic and intrinsic components to the gain-field model for each type of learning were confirmed by the differential weightings of extrinsic and intrinsic reference frames for the explicit and implicit conditions. We found that generalization for the explicit condition was characterized by a marginally greater contribution from the extrinsic reference frame (s_E = 0.7 and s_I = 0.3; Fig. 5A), whereas generalization for the implicit condition appeared to display an even mixture of extrinsic and intrinsic representations (s_E = 0.51 and s_I = 0.49; Fig. 5B).

We then compared the goodness of fit between the gain-field extrinsic-only (s_E = 1 and s_I = 0) and intrinsic-only (s_E = 0 and s_I = 1) models to the average data across all subjects, using the Bayesian information criterion (BIC). The BIC estimates whether one model is better than the other by introducing a penalty for every free parameter, which improves the goodness of fit.

$$\text{BIC}=n\cdot \ln \left({\text{σ}}_{\text{e}}^{\text{2}}\right)+k\cdot \ln \left(n\right)$$ (5)

Here ${\text{σ}}_{\text{e}}^{\text{2}}$ is the variance in residual errors of the fit, k is the number of free parameters, and n is the number of data points. A difference greater than ~4.6 between the BIC values of two models indicates that the model with the lower BIC value is generally favored (Jeffreys 1998).

For generalization in the explicit condition, fitting the extrinsic-only and intrinsic-only models to the generalization function yielded BIC values of 71.2 and 57.6, respectively. In contrast, the BIC value for the fit of the gain-field model to the generalization function was 49.1. Given that the difference in the BIC values of the models was >4.6, this result suggests that the gain-field model yielded a better fit to the generalization function in the explicit condition.

For generalization in the implicit condition, the BIC values for the extrinsic-only and intrinsic-only models were 47.6 and 49.2, respectively, whereas the BIC value for the gain-field model was 28.2. Similar to explicit learning, this result indicates that the gain-field model is superior compared with the extrinsic-only and intrinsic-only models. Taken together, these results are consistent with our conclusion that neither the generalization pattern in the explicit condition nor that in the implicit condition conforms to a simple interpretation in terms of encoding in either a pure extrinsic or pure intrinsic reference frame.

We then computed the 95% confidence intervals of s_E and s_I for both explicit and implicit conditions, using the bootstrap analysis. For the explicit condition, the median contributions of s_E and s_I were 0.7 (95% CI = 0.57, 0.9) and 0.3 (95% CI = 0.1, 0.42), respectively. In contrast, for the implicit condition, the median s_E and s_I contributions were 0.5 (95% CI = 0.39, 0.52) and 0.5 (95% CI = 0.48, 0.62), respectively. These results are consistent with the fits on the subject average data and show that the generalization pattern in each condition features distinct contributions from both intrinsic and extrinsic reference frames. Specifically, generalization in the explicit condition consisted of a marginally greater contribution from the extrinsic reference frame relative to the intrinsic reference frame, whereas generalization in the implicit condition had a different ratio that had a more even mixture of extrinsic and intrinsic reference frames.

Combination of Generalization Patterns for Explicit and Implicit Conditions Can Account for Generalization Pattern in Combined Condition

With the generalization functions associated with the explicit and implicit conditions characterized in isolation, we then sought to determine whether we could predict the generalization function when both explicit and implicit processes combine in a standard visuomotor rotation task. To this end, the combined condition was designed such that subjects learned to compensate for the visuomotor rotation with a combination of explicit and implicit learning. To accomplish this, subjects were trained to compensate for a visuomotor rotation using online visual feedback, akin to a standard visuomotor rotation task. Aside from the difference in the form of visual feedback, the workspace locations and the locations of testing targets were identical to the explicit and implicit conditions.

Subjects learned to compensate for the visuomotor rotation very well, displaying 26.9 ± 1.1° change in hand direction when averaged over the last 10 trials (Fig. 6A). The asymptotic performance was significantly different from zero [t(15) = 23.1, P < 0.0001] and the amount of rotation required to fully compensate for the visuomotor rotation [t(15) = −4.5, P < 0.0001].

Fig. 6.

Gaussian fit to the generalization pattern at workspaces 1 (W1) and 2 (W2) in the combined condition. A: mean change in hand angle when participant trained with a cursor that was aligned (Prerotation phase, no shading) or rotated 30° relative to hand movement (Rotation, light gray shading; Postrotation phase, dark gray shading) for the combined condition. Vertical dashed lines indicate the transition between different phases. B: Gaussian fits for the generalization pattern in the combined condition. The observed generalization pattern was averaged across all participants in each condition at W1 (red line) and W2 (blue line). Shaded area represents mean ± SE. C: estimated center of generalization for each of the 2,000 bootstrap samples at W1 and W2 for the combined condition. D: distribution of the amplitude of generalization for each of the 2,000 bootstrap samples at W1 and W2 for the combined condition. Quartiles and confidence intervals (CI) are indicated on the box plots. *Significant main effect following a bootstrap test at P < 0.05. E: the generalization in W2 is best accounted for by an equal weighted sum of implicit and explicit components according to the Bayesian information criterion (BIC). F: best fit to the subject averaged data when explicit and implicit weights are allowed to vary. G: best fit to the subject averaged data derived from a single-process model that arises from a combination of extrinsic and intrinsic representations. n.u., Normalized units; s_E, extrinsic contribution; s_I, intrinsic contribution.

The generalization function in the trained posture (W1) displays the typical Gaussian-like shape (Fig. 6B). Indeed, the generalization pattern at W1 was characterized by a single Gaussian with an amplitude of 20.3° (95% CI = 16.6°, 23.7°), a center location of 4.7° (95% CI = −2.5°, 10.3°) with respect to the 0° training target, a width of 29.8° (95% CI = 25°, 35.3°), and an offset of 0.32° (95% CI = 0°, 1.7°). When limb posture was rotated 45° to the transfer limb posture (W2), the generalization pattern maintained its characteristic Gaussian-like shape but with an apparent drop in the peak of generalization. We found that the generalization pattern had a peak that was centered at 26.4° (95% CI = 14.4°, 39.3°), with an amplitude of 14° (95% CI = 10.1°, 17.5°), a width of 14° (95% CI = 10.1°, 17.5°), and an offset of 0.4° (95% CI = 0°, 1.6°). Comparison of the generalization functions at W1 and W2 revealed that the amplitude of generalization was significantly reduced [−6.3°, 95% CI (−1.2, −11.5); P = 0.007] and had a shift of 21.7° (95% CI −8.8, −35.8; P = 0.0015) toward a pure intrinsic representation in W2. In addition, there were no significant differences in the width (P = 0.28) and vertical offset (P = 0.43) of the generalization function between W1 and W2.

Interestingly, the reduction in amplitude and the degree of phase shifts are similar to those observed in the explicit and implicit conditions, respectively. This raises the possibility that the generalization pattern found in the combined condition could be attributed to a combination of generalization patterns arising from explicit and implicit learning. To test this idea, we fit a simple model, in which the overall generalization function is the result of a linear combination of the individual explicit and implicit generalization functions obtained in the explicit and implicit conditions, to the data in the combined condition. Remarkably, we found that this model with no free parameters accounted for 83.4% of the variance in the generalization pattern at W2 for the combined condition (Fig. 6E). Next, we compared this model to alternative models in which the weighting of the explicit and implicit components was allowed to vary (Fig. 6F) or single-process models that arise from a combination of extrinsic and intrinsic representations using the BIC.

In this approach, the models in which the weighting of the explicit and implicit components was allowed to vary (BIC difference = 0.6; Fig. 6F) or single-process models that arise from a combination of extrinsic and intrinsic representations (BIC difference = 3.4; Fig. 6G) did not produce a significantly better fit. These results suggest that the generalization pattern in a typical visuomotor rotation task arises from a combination of explicit and implicit forms of learning with distinct extrinsic and intrinsic contributions.

DISCUSSION

The goal of our study was to identify the reference frames used for representing explicit and implicit forms of learning and to determine whether their simple combination could explain previous reports of mixed representations in standard visuomotor rotation tasks. First, we observed that when generalization was tested in W2 the amplitude of generalization in the explicit condition was reduced with postural changes and the phase of the function was only marginally shifted, resembling more of an extrinsic reference frame representation. In contrast, the generalization function for the implicit condition appeared to be phase shifted toward an intermediate position between the training target defined according to intrinsic and extrinsic reference frames when shifting to W2. Furthermore, generalization for the implicit condition did not reduce in amplitude when changing postures. These findings suggest that neither explicit nor implicit learning conforms to a simple interpretation in terms of encoding in either a pure extrinsic or a pure intrinsic reference frame. Thus, to gain further insights into this mixed representation, we fit a gain-field model that allows for varying contributions of extrinsic and intrinsic representations to explain the generalization function. We found that the generalization function for the explicit condition has a mixture ratio that consists of a marginally greater contribution from the extrinsic reference frame relative to the intrinsic reference frame, whereas generalization for the implicit condition appeared to display an even mixture of intrinsic and extrinsic representations. Finally, we showed that a simple composition model in which the overall generalization function is the result of a linear combination of explicit and implicit learning is able to account for nearly 85% of the variance associated with the generalization pattern due to learning in a typical visuomotor task, when both processes are operating. Taken together, these findings suggest that each form of learning makes distinct contributions from both extrinsic and intrinsic reference frames and the combination of these distinct features shapes the generalization pattern observed at novel limb postures.

Explicit and Implicit Generalization in Mixed Reference Frames

Several studies have examined how learning in visuomotor rotation tasks generalizes across different limb postures and have found conflicting evidence. For example, Wang and Sainburg (2005) and Krakauer et al. (2000) have shown that learned compensations to visuomotor rotations are transferred in an extrinsic reference frame, whereas others have found evidence that learning may be represented in an intrinsic reference frame (de Rugy et al. 2009; Krakauer et al. 2006; Rotella et al. 2015). There is also evidence that learning takes place in both extrinsic and intrinsic reference frames (Brayanov et al. 2012; Poh et al. 2017). Brayanov et al. (2012) probed generalization across a wide distribution of movement directions at various limb postures and showed that learning generalized most strongly to a target direction that is intermediate between the intrinsically and extrinsically defined training direction. This pattern of generalization was found to be most consistent with a multiplicative gain-field model with a mixture of extrinsic and intrinsic representations. We hypothesized that the failure to find a consistent representation is the result of the concurrent operation of explicit and implicit learning processes, each operating within a distinct representational space. As a consequence, different patterns of generalization in extrinsic, intrinsic, or mixed reference frames will arise depending on the relative contribution of generalization effects driven by independent effects from both explicit and implicit forms of learning (Heuer and Hegele, 2008, 2011; McDougle et al. 2017).

To assess this possibility, we measured the individual generalization functions associated with explicit and implicit learning in relative isolation, using a modified visuomotor rotation task. To this end, we hypothesized that explicit forms of learning may reflect a deliberate strategy to reaim movements toward the training target and thus be related to an extrinsic reference frame. In contrast, implicit forms of learning may depend more on an intrinsic reference frame since adaptive changes to motor output may be more related to limb posture and joint configurations. However, our behavioral results did not fit this view. Specifically, although learning in the explicit condition was expressed predominantly in an extrinsic reference frame, the amplitude of generalization decayed with modulations in limb posture, which complicates a pure extrinsic reference frame interpretation. In comparison, although the amplitude of generalization for the implicit condition did not decay substantially with changes in limb posture, the direction of peak generalization was phase shifted to an intermediate position between the extrinsically and intrinsically defined training directions, reflecting a mixed representation. These findings suggest that the representation underlying explicit and implicit learning may not rely on an easily categorizable extrinsic or intrinsic reference frame as we had initially theorized.

Implications for Explicit Learning

For learning in the explicit condition, we showed that changing limb posture did not strongly influence the direction in which learning was expressed; instead, the amplitude of generalization was reduced. This suggests that the amplitude of generalization is influenced by intrinsic limb position-based learning effects. One possible interpretation could be that limb posture might serve as a contextual cue that is coupled with the explicit learning such that generalization is reduced when limb posture is altered (Baraduc and Wolpert 2002; Gandolfo et al. 1996; Howard et al. 2012, 2013; Krakauer et al. 2006). The idea that the extent of generalization of learning between movements depends on the similarity of the underlying intrinsic joint-based requirements is reflected in previous studies that have shown that the extent of generalization is tied to specific muscles (de Rugy et al. 2009; Krakauer et al. 2006; Poh et al. 2017) and joint postures (Baraduc and Wolpert 2002) involved during training. Our findings are consistent with this work by showing that the intrinsic limb posture-dependent reduction in the amplitude of generalization is limited to explicit learning but not implicit learning.

It is important to note that our generalization task was designed to isolate explicit and implicit learning by using different visual feedback manipulations, which allowed us to independently examine how each form of learning generalizes to movements in the untrained limb posture. Our approach differs from other studies in which explicit estimations of the movement direction required to compensate for the visuomotor rotation were obtained to quantify the relative contributions of explicit and implicit forms of learning. For example, in the study by Heuer and Hegele (2011), after learning of the rotated visual feedback subjects verbally instructed the experimenter to rotate a guideline to align with their intended movement direction to compensate for the perturbation, and other studies have instructed participants to verbally state their aiming direction with reference to a numbered landmark during learning (Bond and Taylor 2015; McDougle et al. 2017; Taylor et al. 2014). Such reaiming strategies have been interpreted as an explicit form of learning that the motor system implements in parallel with implicit learning, and the difference between the direction of aim and the actual reach direction constitutes a measure of implicit learning. However, studies employing these approaches have often noted that explicit learning results in broad generalization across all movement directions (Heuer and Hegele 2008, 2011; McDougle et al. 2017). As such, it is challenging to determine which reference frames contribute to the representation of explicit learning because the learning is not direction specific and the generalization effects in extrinsic or intrinsic reference frames are indistinguishable at the untrained posture.

Unlike in those studies, here we have found relatively narrow generalization of explicit learning around the training direction in W1. When generalization was tested to W2, the pattern of explicit generalization was most consistent with an intermediate representation that is predominantly expressed in the extrinsic reference frame and the amplitude of generalization is modulated by changes in limb posture. The difference between our findings and prior approaches is intriguing and at present is unclear. One possible explanation is that explicit estimations of the aiming direction may encourage subjects to “solve” for the rotation by developing a strategy to reaim their movements in a direction opposite to the rotation for every target. Such a phenomenon may bear resemblance to the “observer expectancy effect” commonly observed in social psychology (Franke 1980; Franke and Kaul 1978). That is, by simply asking participants what they are doing, they necessarily change the way they respond. Thus it is unclear whether the broad generalization function of explicit aiming observed in previous studies reflects the true mark of explicit learning or an artifact of task instructions.

Implications for Implicit Learning

Our findings show that extent of generalization for the implicit condition was not modulated by the change in limb posture but the peak direction of generalization was shifted to an intermediate direction between the trained target location defined in an intrinsic and an extrinsic reference frame. This shift in the generalization pattern resembles the shift in the generalization pattern that was reported by Brayanov et al. (2012) and has been taken as evidence that learning is represented in a multiplicative gain-field combination of intrinsic and extrinsic movement representations. However, because the authors did not dissociate between explicit and implicit learning in their study, it was difficult to attribute the shift in the generalization pattern in the proposed mixed reference frame to either the explicit or the implicit form of learning. Given that we have designed our experiments to isolate effects of explicit and implicit forms of learning across different limb postures, the observed shifts in implicit generalization only suggest that the shift in the generalization in Brayanov et al. (2012) was likely due to an implicit form of learning. By this view, implicit learning could involve an integrated representation that combines both extrinsic and intrinsic reference frames. Taken together, the involvement of multiple reference frames in both explicit and implicit learning is consistent with previous modeling studies that suggest that learning might occur concomitantly in multiple reference frames. In this framework, the amplitude and shape of generalization expressed in a particular reference frame appear to be determined by how the motor system attributes errors to sensory signals in different reference frames (Berniker and Kording 2008, 2011).

However, although our results are compatible with the interpretation that the distinct patterns of generalization for explicit and implicit conditions arise because of different extrinsic and intrinsic reference frame contributions, several alternative explanations require consideration. First, visuomotor control of reaching movements involves both position and vectorial coding (de Grave et al. 2004; van den Dobbelsteen et al. 2001; van der Graaff et al. 2017). Given that our postural manipulations do not dissociate between learning that results from two different theories of visuomotor control—position coding, which is concerned with remapping between final limb position and the visually displayed target, and vectorial coding, which concerns remapping between the movement vector and the relative target vectors—it is possible that differences in position and vectorial remapping for explicit and implicit learning could account for our pattern of results when subjects are required to move to previously adapted targets from a new limb posture. However, we believe that the specific features of our experimental model render this alternative explanation unlikely.

In our study, participants were explicitly instructed to “shoot” through the target, which dissociates the spatial position of the limb from the position of the visually displayed target at the end of the movement. This dissociation is critical because there was no repetition of the required limb position during either the rotated or the baseline phase. This severely limits the capacity for the brain to remap position of a target and end-point limb position in accord with the position coding hypothesis. Thus the contribution from a position remapping model to the overall degree of learning is likely negligible.

Furthermore, although there is substantial literature on the contributions of both position and vector coding to visuomotor control (e.g., de Grave et al. 2004; van den Dobbelsteen et al. 2001; van der Graaff et al. 2017), it is not clear whether both mechanisms play a role in motor adaptation or learning. Indeed, learning during visuomotor rotation tasks has been shown to remap representations of movement vectors and not final positions of the limb (Krakauer et al. 2000; Paz et al. 2003; Tanaka et al. 2009; Wang and Sainburg 2005). The movement vector remapping hypothesis is further supported by evidence showing that rotation learning generalizes most strongly to movements with similar movement vectors, even when start and goal locations are altered (Brayanov et al. 2012; Krakauer et al. 2000; Wang and Sainburg 2005; Wu and Smith 2013). Taken together, given the absence of position remapping during rotation learning and the limited capacity for position remapping in our experimental task, it is unlikely that a mixture of position and vector remapping would have influenced the pattern of results.

Second, a single experimental task cannot be uniquely equated to a single cognitive/behavior mechanism (Jacoby 1991; Yonelinas and Jacoby 2012). This raises the possibility that at least some of the generalization effects for delayed (explicit) and clamped (implicit) conditions could be driven by mechanisms related to a mixture of explicit and implicit learning. For example, in our analysis for direction of peak generalization, the generalization pattern for delayed feedback (explicit) was shifted only by +15.8° toward an intrinsic reference frame representation, whereas the generalization pattern for clamped visual feedback (implicit) was shifted by +25.2°. With our hypothesis that extrinsic and intrinsic reference frames may be linked to explicit and implicit learning, respectively, this would imply that the reduced phase shifts for the delayed feedback condition might be attributed to enhanced explicit learning and impaired implicit learning relative to the clamped feedback condition. Although previous studies that have examined learning under delayed and clamped feedback have revealed very different learning characteristics and have linked these with explicit and implicit learning (Brudner et al. 2016; McDougle and Taylor 2019; Morehead et al. 2017; Schween and Hegele 2017), we cannot entirely rule out this possibility.

Conclusions

In conclusion, our results demonstrate that generalization of explicit and implicit learning did not conform to a simple interpretation in terms of encoding in a categorical extrinsic or intrinsic reference frame. Specifically, the amplitude of explicit generalization was reduced with postural change and was minimally phase shifted, resembling an extrinsic representation. In contrast, implicit generalization maintained its amplitude but was significantly phase shifted, resembling a mixed representation. Furthermore, we showed that a simple linear model in which the overall generalization function is the result of a linear combination of explicit and implicit generalization observed captures nearly 85% of the variance in the generalization pattern in a standard visuomotor rotation task, when the two processes are operating. These results suggest that multiple reference frames contribute to each form of learning and the combination of these distinct features shapes the generalization pattern observed at novel limb postures. Although our results suggest that the representation underlying explicit and implicit learning may not rely on an easily categorizable extrinsic or intrinsic reference frame, it remains an open question as to why both explicit and implicit learning arise from mixed representations. One intriguing possibility is that learning is not truly represented in an extrinsic or intrinsic reference frame but rather is learned in a higher-dimensional representation and we are simply observing low-dimensional projections from this higher representation (Shepard 1987).

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grant R01 NS-084948 and National Science Foundation Grant 1838462.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

E.P. and J.A.T. conceived and designed research; E.P. performed experiments; E.P. and J.A.T. analyzed data; E.P. and J.A.T. interpreted results of experiments; E.P. prepared figures; E.P. drafted manuscript; E.P. and J.A.T. edited and revised manuscript; E.P. and J.A.T. approved final version of manuscript.