Adapting the flow of time with dopamine

Abstract

The modulation of interval timing by dopamine (DA) has been well established over decades of research. The nature of this modulation, however, has remained controversial: Although the pharmacological evidence has largely suggested that time intervals are overestimated with higher DA levels, more recent optogenetic work has shown the opposite effect. In addition, a large body of work has asserted DA’s role as a “reward prediction error” (RPE), or a teaching signal that allows the basal ganglia to learn to predict future rewards in reinforcement learning tasks. Whether these two seemingly disparate accounts of DA may be related has remained an open question. By taking a reinforcement learning-based approach to interval timing, we show here that the RPE interpretation of DA naturally extends to its role as a modulator of timekeeping and furthermore that this view reconciles the seemingly conflicting observations. We derive a biologically plausible, DA-dependent plasticity rule that can modulate the rate of timekeeping in either direction and whose effect depends on the timing of the DA signal itself. This bidirectional update rule can account for the results from pharmacology and optogenetics as well as the behavioral effects of reward rate on interval timing and the temporal selectivity of striatal neurons. Hence, by adopting a single RPE interpretation of DA, our results take a step toward unifying computational theories of reinforcement learning and interval timing.

NEW & NOTEWORTHY How does dopamine (DA) influence interval timing? A large body of pharmacological evidence has suggested that DA accelerates timekeeping mechanisms. However, recent optogenetic work has shown exactly the opposite effect. In this article, we relate DA’s role in timekeeping to its most established role, as a critical component of reinforcement learning. This allows us to derive a neurobiologically plausible framework that reconciles a large body of DA’s temporal effects, including pharmacological, behavioral, electrophysiological, and optogenetic.

INTRODUCTION

The ability to accurately estimate time is crucial for survival and is critically intertwined with reinforcement learning (RL). To adequately learn the properties of its environment and respond to them as they change, an animal must learn the temporal information associated with both its environment and its own behavior (Allman et al. 2014; Buhusi and Meck 2005; Matthews and Meck 2014).

Over the past several decades, dopamine (DA) has emerged as a neural substrate with a central role in both RL and interval timing. In RL tasks, midbrain DA neurons communicate a “reward prediction error” (RPE), or the signed difference between received and expected reward (Schultz et al. 1997). This RPE serves as a teaching signal that instructs basal ganglia (BG) circuitry to update its estimates of incoming rewards until those rewards are well predicted (Eshel et al. 2015; Glimcher 2011; Niv and Schoenbaum 2008; Schultz et al. 1997; Steinberg et al. 2013). Hence, delivery of an unexpected reward elicits a DA burst, omission of an expected reward elicits a DA dip, and a fully predicted reward elicits no DA response. Subsequent work has shown that DA maps to the RPE term of temporal difference learning models particularly well (Schultz 2007), and we review this class of algorithms below.

On the other hand, decades of research have implicated DA and the BG in interval timing (Buhusi and Meck 2005). Timing dysfunction has been well documented in diseases of the DA system and the BG such as Parkinson’s disease (Malapani et al. 1998), Huntington’s disease (Rowe et al. 2010), and schizophrenia (Elvevåg et al. 2003). In Parkinson’s disease, dysfunction in timing is often ameliorated with DA agonists (Artieda et al. 1992; Jahanshahi et al. 2010; Malapani et al. 1998). This dysfunction has been recapitulated in healthy subjects pharmacologically (Arushanyan et al. 2003; Maricq and Church 1983) and through transgenic (Ward et al. 2009) and optogenetic (Soares et al. 2016) manipulation of the DA system in mouse models as well as by direct lesion of striatum in rats (Meck 2006).

Unlike its role as an RPE in RL tasks, however, a conceptual model of DA in timekeeping has been elusive, in part because of the recent emergence of conflicting evidence regarding its role. The pharmacological evidence, with notable exceptions, has tended to show that DA agonists result in behaviors consistent with a faster “internal clock” and DA antagonists with a slower clock (Cheng et al. 2007; Lake and Meck 2013; Maricq et al. 1981; Maricq and Church 1983; Meck 1986). On the other hand, recent photometric recordings and optogenetic manipulations have shown exactly the opposite effect (Soares et al. 2016). How to explain these seemingly conflicting results and, in fact, why DA would serve a role in modulating timekeeping in the first place remain open questions. Furthermore, whether and how the two seemingly disparate roles of DA in RL and timekeeping may be related remains unknown (Gershman et al. 2014; Petter et al. 2018).

We show in this article that viewing interval timing through an RL lens allows us to reconcile the conflicting evidence on the role of DA in timing tasks. To do so, we derive from first principles a local plasticity rule that describes how DA allows cortico-striatal circuits to learn the temporal structure of reward. This rule accounts for how the DA signal modulates the internal clock and shows that it can produce either a speeding or a slowing effect, depending on when during the task it occurs.

METHODS

For all simulations of experimental results, we have chosen μ_d = d for d ∈ {1,2,…, 80}, γ = 0.9, σ = 10, $\mathcal{T}$ = 40, τ = t^0.7, and α_η = 0.1, unless otherwise stated below.

Simulation of behavioral results.

Reinforcement density (RD) is the inverse of trial length. We have initialized baseline reward time to be T = 30. For high and low bias, we have selected T = 25 and T = 35, respectively, with subsequent return to the baseline condition T = 30 (see Fig. 5).

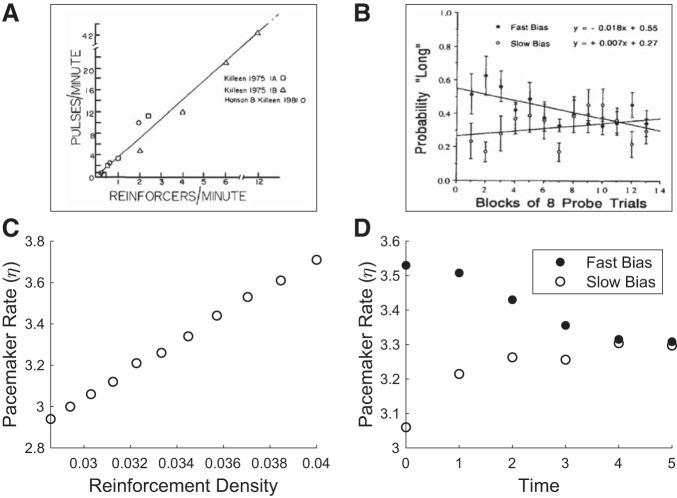
Fig. 5.

Results from behavioral experiments compared with model behavior. A: Killeen and Fetterman (1988) have found that the speed of the pacemaker is directly proportional to the rate of reinforcement. Reprinted from Killeen and Fetterman (1988). B: Morgan et al. (1993) have found that when exposed to high or low rates of reinforcement and returned to a baseline condition, pigeons’ behaviors were consistent with a faster or slower pacemaker, respectively. Reprinted from Morgan et al. (1993) with permission from Elsevier. C and D: model behavior, recapitulating observations in A and B, respectively. See methods for simulation details.

Simulation of electrophysiological results.

By visual inspection, we set σ = 30 and τ = t^0.6 (see Fig. 6).

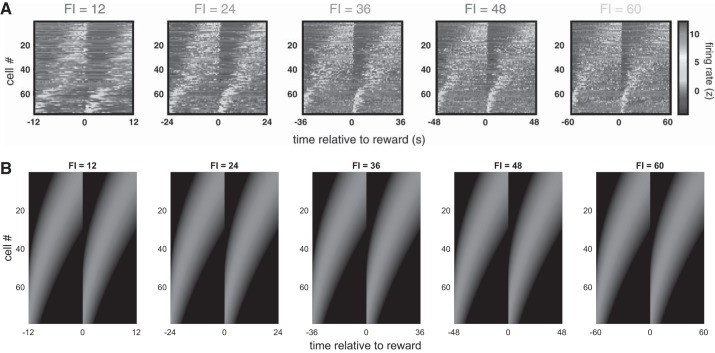
Fig. 6.

Results from electrophysiology compared with model behavior. A: in Mello et al. (2015), electrophysiological recordings in rat striatum during a timekeeping task identified medium spiny neurons that fired sequentially during the delay period and whose response profiles rescaled to reflect the timed duration [fixed interval (FI); note scaling of x-axis] but maintained their relative ordering. In addition, by visual inspection, the gradual increase in response profile widths across cells within each trial seems similar across different task durations, as would be suggested by the scalar property. Reprinted from Mello et al. (2015) with permission from Elsevier. B: our model recapitulates both phenomena. See methods for simulation details.

Simulation of pharmacological results.

Update over the course of a single trial occurred according to the approximation in Eq. 7. To visually match the deviation of responses in medicated conditions from those of placebo, we have arbitrarily scaled the total update by α_η = 20 (note that α_η need not be <1) and set σ = 5 and T_max = 35 for the placebo condition. For the temporal estimates, we have plotted x_t=7 and x_t=17. We take the end point of temporal reproduction to occur at the peak of V̂_τ. For administration of DA agonists, we have chosen a gain modulation of 5 for positive RPEs and 0.2 for negative RPEs; for administration of DA antagonists, we have chosen a gain modulation of 0.2 for positive RPEs and 5 for negative RPEs. Finally, we have fixed the veridical time estimate to correspond to the baseline condition of unitary modulation of all RPEs (see Fig. 7).

Fig. 7.

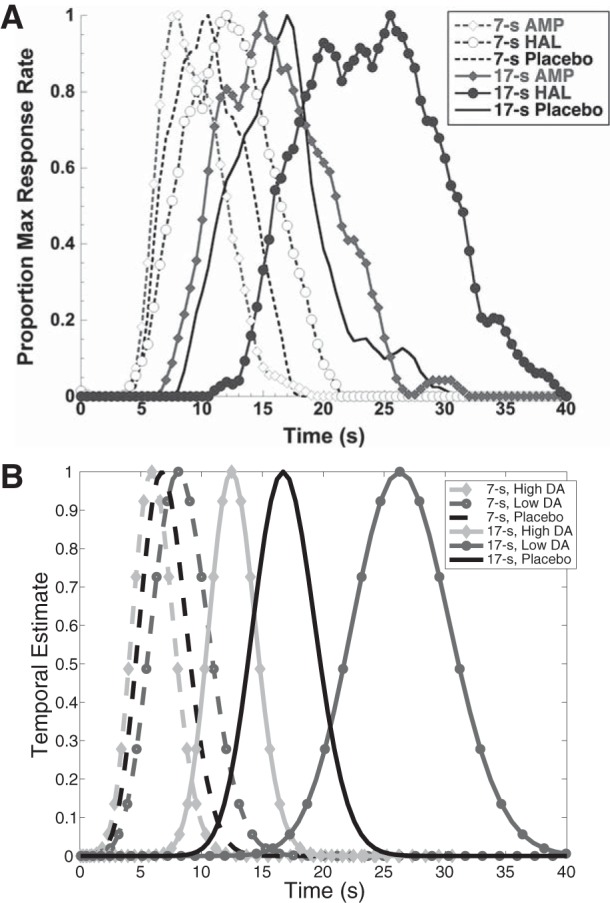
Results from pharmacology compared with model behavior. A: in Lake and Meck (2013), subjects reproduced previously learned 7-s and 17-s intervals after administration of the dopamine (DA) agonist amphetamine (AMP), the DA antagonist haloperidol (HAL), or placebo. In the majority of subjects, amphetamine reduced response time, whereas haloperidol delayed it. Reprinted from Lake and Meck (2013) with permission from Elsevier. B: our model recapitulates these effects. See methods for simulation details.

Simulation of optogenetic results.

To simulate the results of Soares et al. (2016), we have chosen α_η = 10 (α_η need not be <1). A mean of 1.5 and a temperature parameter of 0.2 in the softmax learning rule (Luce 1959; Shepard 1958) were used to generate the choices. For activation and inhibition, we have arbitrarily chosen δ_τ = +1 and δ_τ = −1, respectively (see Fig. 8). For the results of Toda et al. (2017), we have chosen α_η = 7 and T_max = 20 and set δ_τ = +1 (see Fig. 9).

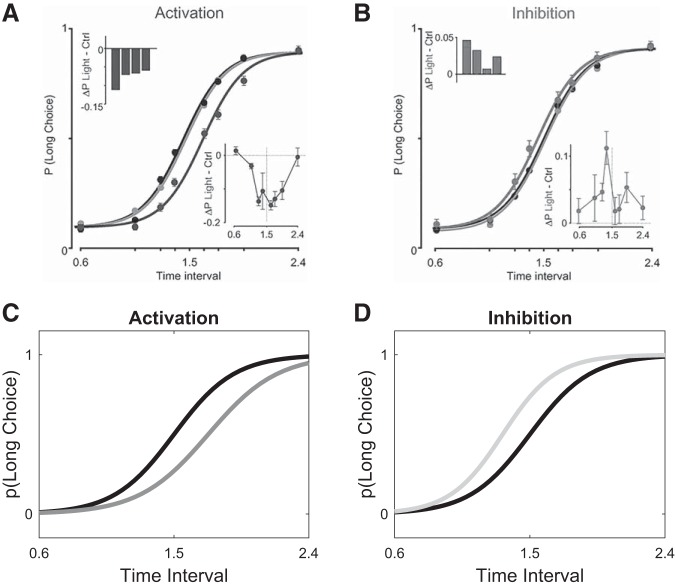
Fig. 8.

Results from optogenetic stimulation of midbrain dopamine neurons compared with model behavior. A and B: in Soares et al. (2016), mice were trained on a temporal discrimination task in which they had to judge intervals as either shorter or longer than 1.5 s, and psychometric functions were fit to the data (black curves in both panels). A: under optogenetic activation spanning the entire trial, the psychometric function shifted to the right (dark gray curve), consistent with a slower pacemaker. Insets show the average difference between the probability of selecting the long choice during activation trials vs. control trials per animal (top left) or per stimulus (bottom right). B: under optogenetic inhibition, the psychometric function shifted to the left (light gray curve), consistent with a faster pacemaker. Insets: same as in A, but for inhibition. A and B from Soares et al. Science 354: 1273–1277, 2016. Reprinted with permission from AAAS. C and D: our model recapitulates these effects. See methods for simulation details.

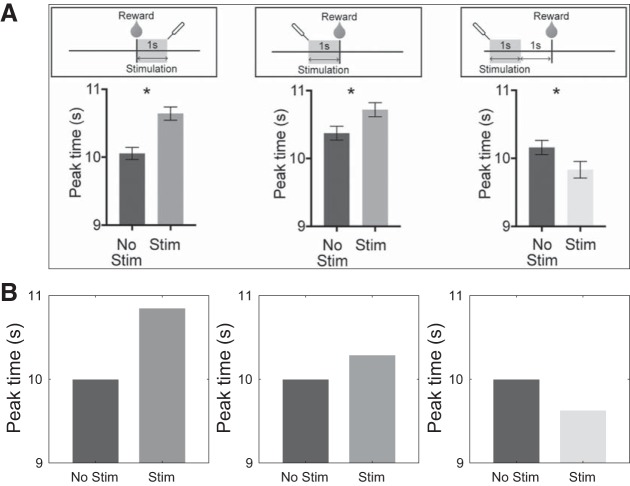
Fig. 9.

Results from optogenetic stimulation of basal ganglia output compared with model behavior. A, top: in Toda et al. (2017), mice were trained on a peak-interval licking task, and peak licking robustly reflected reward time. The nigrotectal pathway was optogenetically stimulated immediately after reward (left), immediately before reward (center), or 1 s before reward (right). Bottom: stimulation resulted in a shift in peak licking on the subsequent trial. The peak time occurred later when stimulation was delivered immediately after or immediately before reward (left and center), and it occurred earlier when stimulation was completed 1 s before reward (right). *P < 0.05. Reprinted from Toda et al. (2017) with permission from Elsevier. B: our model recapitulates these effects. See methods for simulation details.

Source code.

Source code for all simulations can be found at https://www.github.com/jgmikhael/flowoftime.

RESULTS

As our model endows interval timing frameworks with an RL architecture, we begin this section with a brief review of temporal difference learning algorithms.

Temporal difference learning in cortico-basal ganglia circuitry.

Perhaps the most successful account of DA function in the BG posits that phasic DA activity reports the RPE, or the difference between the received and expected reward (Glimcher 2011; Schultz 2007; Schultz et al. 1997). This account has been formalized in terms of the temporal difference (TD) learning algorithm (Sutton 1988), which we briefly review here.

For ease of exposition, we omit actions and assume that the agent traverses a series of “states” according to a Markov process. A state corresponds to some combination of relevant contextual cues, or features, that aid in predicting future rewards. For example, a state could denote proximity to a known food source or time until reward delivery. In the TD framework, the value of being in a state is defined as the expected discounted sum of current and future rewards:

$$V_t=\mathbb{E}\left[{\displaystyle \sum _{k=0}^{\infty }{\text{γ}}^k}{r}_{t+k}\right]$$ (1)

where t denotes time and indexes states, r_t is the reward received at time t, and γ ∈ [0,1) is a discount factor that decreases the weights of later rewards. Following previous work (Ludvig et al. 2008, 2012; Schultz et al. 1997), the agent estimates V_t by learning a linear weighting of the features:

$${\widehat{V}}_t={\displaystyle \sum _d{w}_d}{x}_{d,t}$$ (2)

where x_d,t is the dth feature at time t, and this feature is weighted by w_d. The weights are updated by gradient ascent to reduce the discrepancy between V_t and its estimate V̂_t:

$$w_d^{(t+1)}=w_d^{(t)}+{\text{αδ}}_t^{(t)}{\nabla }_{w_d}{\widehat{V}}_t^{(t)}$$ (3)

where α ∈ [0,1) denotes the learning rate, the superscript represents the learning step, ${\nabla }_{w_d}{\widehat{V}}_t^{(t)}=x_{d,t}$ is the gradient of ${\widehat{V}}_t^{(t)}$ with respect to the weight w_d and δ_t is the RPE:

$${\text{δ}}_t=r_t+\text{γ}{\widehat{V}}_{t+1}-{\widehat{V}}_t$$ (4)

For an intuition, the received reward r_t, together with the discounted expected value at the next step γV̂_t+1, can be thought of as a single sample of value V_t. RPE is then the difference between this sample and the current estimate V̂_t.

In mapping the TD framework onto cortico-BG circuitry, the features x_d,t represent cortical inputs to striatum, the weights w_d are encoded by the strengths of the cortico-striatal synapses (Houk et al. 1995; Montague et al. 1996), the error signal δ_t is communicated by the firing of midbrain DA neurons (Eshel et al. 2015; Glimcher 2011; Niv and Schoenbaum 2008; Schultz et al. 1997; Steinberg et al. 2013), and the estimated value V̂_t constitutes the output of the BG (Ratcliff and Frank 2012).

For a timekeeping task, a natural feature set arises from the recent experimental observation of “time cells,” or neurons that are sequentially activated during the timed interval and that predict the animal’s estimate of the interval (Mello et al. 2015; Wang et al. 2018). Remarkably, when the length of the required interval duration was experimentally manipulated, the response profiles of these cells rescaled to fit the newly timed duration as the animal learned the updated parameters of the task. This rescaling is an important attribute of our model, which we describe next.

Model description.

We adopt the approximation architecture outlined in Eq. 2, where the features x_d,τ and estimated value V̂_τ are indexed by subjective time τ. The features are encoded by time cells, and each time cell d is preferentially tuned to a subjective time μ_d, such that higher values of d correspond to cells that respond later. For simplicity, we take the features x_d,τ to be Gaussian in shape, centered at μ_d, and with tuning width σ, i.e.,

$$x_{d,\text{τ}}=\exp \left[-\frac{1}{2}{\left(\frac{\text{τ}-{\text{μ}}_d}{\text{σ}}\right)}^2\right]$$ (5)

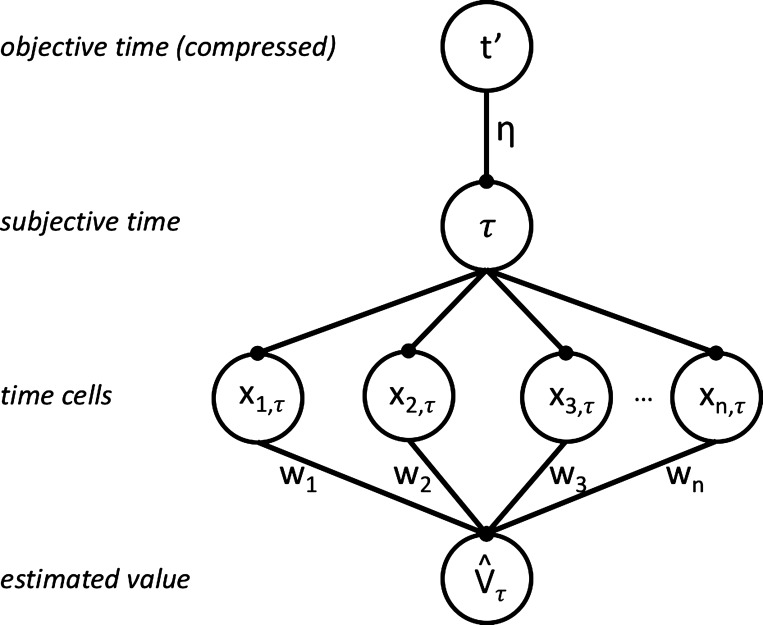
One simple neural circuit that implements this architecture is diagrammed in the bottom three layers of Fig. 1, where time cells are fed subjective time τ and their activations are weighted and summed to give the estimated value V̂_τ, as described in Temporal difference learning in cortico-basal ganglia circuitry.

Fig. 1.

Model architecture. The top layer denotes a compressive representation t′ of objective time t. t′ maps onto subjective time τ, weighted by the scaling factor η. Each time cell d is preferentially tuned to a time μ_d and responds with activation x_d,τ. The sum of the features x_d,τ, weighted by w_d, gives estimated value V̂_τ.

Let us now introduce our key addition to the linear approximation architecture, which derives from the observation that time cell responses rescale to reflect the properties of the external environment (Mello et al. 2015; Wang et al. 2018), as mentioned above. We implement this experimental finding with the parsimonious addition of a scaling factor η between t′ and τ, where t′ represents a compressive function of objective time t (see appendix for a comparison with alternative implementations) and t′ and τ are represented upstream of the time cells, presumably in cortex (Wang et al. 2018). Hence, η controls the mapping of objective time onto subjective time, where a higher η means a faster clock. In keeping with conventional terminology (Gibbon et al. 1997; Treisman 1963; Zakay and Block 1997), we also refer to the clock as a “pacemaker,” and hence refer to the parameter η as the pacemaker rate. The novelty of our account is the idea that the pacemaker rate, known to be modulated by DA as discussed in introduction, can be viewed as a parameter of the function approximation architecture. This parameter is thus updated by gradient ascent:

$${\text{η}}^{(t+1)}={\text{η}}^{(t)}+{\text{α}}_{\text{η}}{\text{δ}}_{\text{τ}}^{(t)}\frac{\text{τ}}{{\text{η}}^{(t)}}{\dot{\widehat{V}}}_{\text{τ}}^{(t)}$$ (6)

where α_η is the learning rate, ${\nabla }_{\text{η}}\widehat{V}=\frac{\partial \widehat{V}}{\partial \text{τ}}\frac{\partial \text{τ}}{\partial \text{η}}=\frac{\text{τ}}{\text{η}}{\dot{\widehat{V}}}_{\text{τ}}$ is the gradient of estimated value with respect to η, and ${\dot{\widehat{V}}}_{\text{τ}}$ denotes the time derivative of V̂_τ.

We have assumed a constant tuning width σ for all features against subjective time, but note that because subjective time is a compressive function of objective time, the widths of the features increase with the passage of objective time, as shown in Fig. 2. This compression will not be necessary for our results below but better reflects the universal observation that subjective estimates of elapsed duration become (linearly) more corrupted as the duration increases, a phenomenon known as the scalar property (Gibbon 1977). It also facilitates comparison of our features with those of the microstimulus model, which are also overlapping Gaussians of increasing tuning width (Ludvig et al. 2008), and the learning-to-time model (LeT) from the interval timing literature, which posits a sequential activation of behavioral states with associated learnable weights (Machado 1997).

Fig. 2.

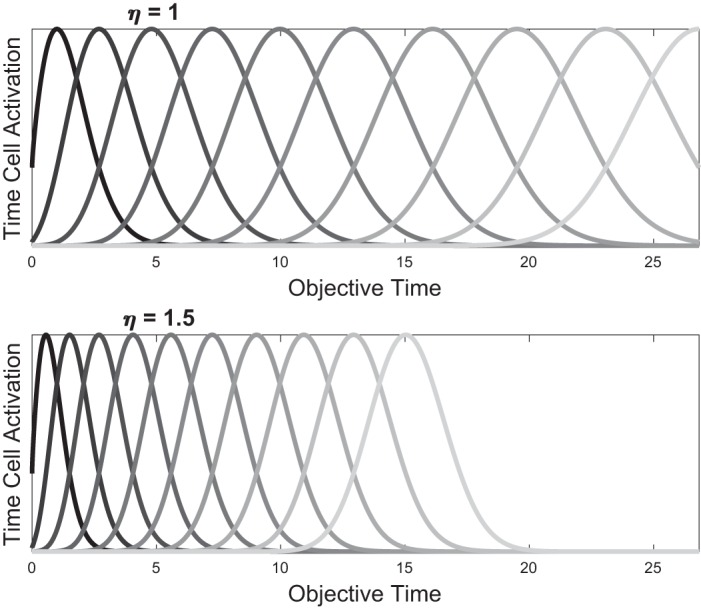
Effect of scaling η on activation of time cells. When measured against objective time t, higher η leads to more compressed time cell activations. Here, the same η for all features is learned. By Eq. 5, it is straightforward to show that all features move in tandem with a constant coefficient of variation, and no crossovers are produced during rescaling (appendix).

A bidirectional update rule governs η.

To examine the update rule in Eq. 6 more closely, let us restrict our analysis to the case of a single reward of magnitude 1 delivered after a delay of objective time T, which corresponds to subjective time $\mathcal{T}$. In this case, Eq. 1 reduces to $V_{\text{τ}}={\text{γ}}^{\mathcal{T}-\text{τ}}$ over the delay period (Fig. 3, top, dashed gray curve). Importantly, with an overlapping feature set, our architecture can never learn V_τ exactly. Instead, due to “smearing” across states, the estimate V̂_τ will resemble a smeared version of V_τ (Fig. 3, top, solid black curve). This in turn will result in an RPE that is not fully reducible even with extensive learning, as has been theoretically predicted (Ludvig et al. 2008) and experimentally suggested (Kobayashi and Schultz 2008). For instance, internal timing noise, which may be implemented by an overlapping feature set, precludes the exact time of reward from being perfectly estimated; hence, a small amount of “surprise” (or nonzero RPE) will be experienced even if the reward is delivered on time (Fig. 3, bottom, solid black curve). In addition, owing to the asymmetric shape of V_t about time T, the peak of the estimate V̂_τ occurs slightly before the true time of reward delivery T. We return to this point in a subsequent result.

Fig. 3.

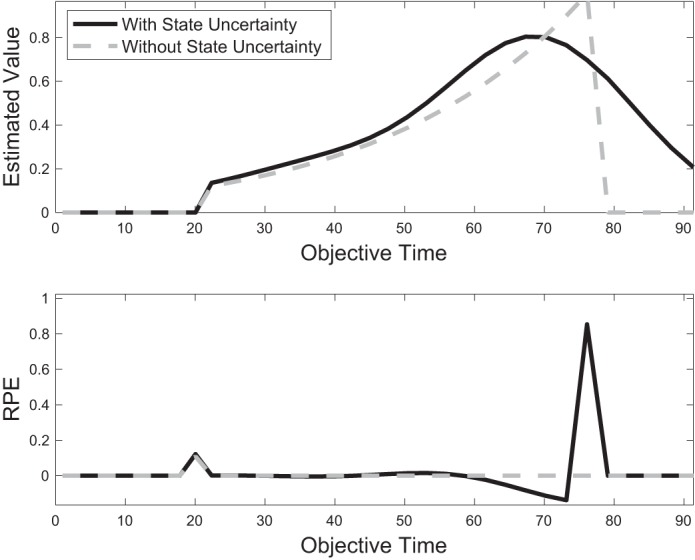
Effect of state uncertainty on value estimation and reward prediction error (RPE). With a perfectly learned value function (top, gray), δ_τ reduces to zero throughout the entire trial duration (bottom, gray). With state uncertainty, implemented by an overlapping feature set, value cannot be estimated perfectly (top, black), and δ_τ is nonzero even after extensive learning (bottom, black). (Figure for illustration only. For smaller T or larger γ, the initial phasic RPE can be larger than RPE at reward time, illustrated here at t = 20 and t = 75, respectively.)

There are two critical observations to be made about the update rule in Eq. 6. First, the synaptic weight encoding η has direct access to τ from its postsynaptic neuron (or its presynaptic neuron, as τ = ηt′), to δ_τ from the DA signal, and to ${\dot{\widehat{V}}}_{\text{τ}}$ from projections from the BG output nuclei (substantia nigra pars reticulata and globus pallidus interna) via the BG-thalamo-cortical loop (Utter and Basso 2008). Therefore, the learning rule for η is local. The update rule itself is a form of differential Hebbian learning (Klopf 1988; Kosko 1986), whereby changes in presynaptic activity are correlated with postsynaptic activity to determine the extent of update. Roberts (1999) has shown that this type of learning rule can be implemented by spike-timing-dependent plasticity (see also Rao and Sejnowski 2001). This update is effectively gated by the RPE, giving rise to a form of three-factor learning rule similar to what has been proposed to underlie plasticity at cortico-striatal synapses (Reynolds and Wickens 2002).

Second, it follows from Eq. 6 that the update of η produces a bidirectional learning rule, as illustrated in Fig. 4. Conceptually, just as the weights w_d will increase or decrease to allow V̂_τ to best approximate V_τ, so too will η. Whereas the weights w_d will change the magnitude of estimated value at different points of time, changes in η result in rescaling of estimated value against objective time. Hence, for η a reward that is delivered earlier than expected indicates that estimated value is not compressed enough, so η must increase. On the other hand, a reward that is delivered later than expected indicates that estimated value is too compressed, so η must decrease. For an intuition of how our derived update rule implements this bidirectionality, note that this rule relies on the product of ${\dot{\widehat{V}}}_{\text{τ}}$ and δ_τ. After learning, V̂_τ takes a monotonically increasing (and roughly convex) shape leading up to reward time $\mathcal{T}$, closely approximating $V_{\text{τ}}={\text{γ}}^{\mathcal{T}-\text{τ}}$, and then decreases quickly, but not instantaneously, to zero (Fig. 4, black curve, and Fig. 3, top, black curve). This more gradual decrease is due to the overlapping nature of our features, as late features accrue positive weights due to their contribution to the estimated value leading up to reward. The shape of V̂_τ implies that its derivative ${\dot{\widehat{V}}}_{\text{τ}}$ will be >0 before reward delivery, ∼0 zero at reward delivery, and <0 during a window afterward. Therefore, early reward will result in $\Delta \text{η}~{\dot{\widehat{V}}}_{\text{τ}}{\text{δ}}_{\text{τ}}>0$ and thus an increase in η and compression of the features against objective time. On the other hand, late reward will result in a negative RPE over $\text{τ}<\mathcal{T}$ when ${\dot{\widehat{V}}}_{\text{τ}}>0$, followed by a positive RPE when reward is delivered, at which point ${\dot{\widehat{V}}}_{\text{τ}}<0$; hence, $\Delta \text{η}~{\dot{\widehat{V}}}_{\text{τ}}{\text{δ}}_{\text{τ}}<0$ over both domains, so that η decreases and the features expand.

Fig. 4.

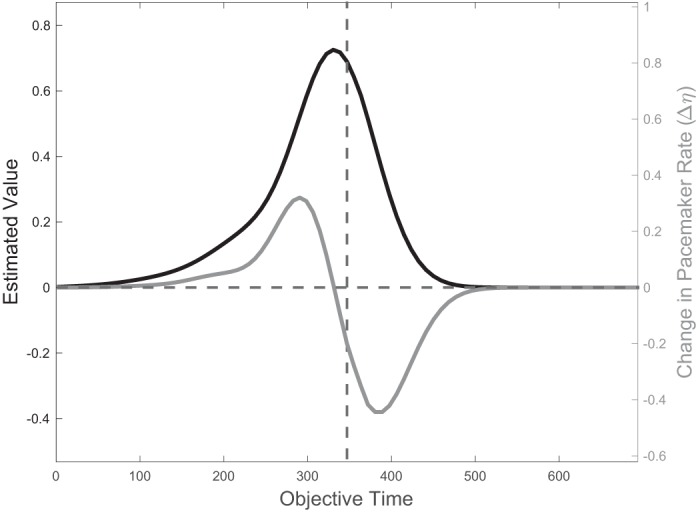
Bidirectional learning rule for η. Because of feature overlap, the learned value V̂ (black curve, plotted here against objective time) does not drop immediately to zero after reward time T (dashed vertical line). This gradual decrease allows its derivative $\dot{\widehat{V}}$ to be negative over a nonzero domain of time, which in turn allows the update rule for η in Eq. 6 to take negative values over that same domain. It follows that η increases if reward is delivered roughly before T and decreases if reward is delayed past T (gray curve).

In summary, Eq. 6 represents a local update rule of the pacemaker rate η, where DA can facilitate either an increase or a decrease in η to allow the estimated value V̂_τ to better approximate the true value V_τ.

Finally, having examined the role of phasic DA in communicating RPEs to update η, let us now consider how tonic DA levels influence the learning of η. Numerous studies have shown that higher levels of tonic DA enhance learning from positive RPEs, whereas low tonic DA levels enhance learning from negative RPEs (Cools et al. 2009; Frank et al. 2007, 2004; Shiner et al. 2012; Smittenaar et al. 2012). Assuming temporal reproduction occurs by timing until the peak of the estimated value function, over which ${\dot{\widehat{V}}}_{\text{τ}}>0$, it follows from Eq. 6 that higher tonic DA levels will result in a bias toward increases of η. Hence, the pacemaker will accelerate and the features will be compressed against objective time. Similarly, low tonic DA levels will decelerate the pacemaker and expand the features.

Relationship with experimental data.

A large body of experimental work in the interval timing literature is concerned with the modulation of timekeeping in healthy states and in disease. For instance, even in healthy states, timekeeping is biased by factors such as attention (Coull et al. 2004), motivation (Gable and Poole 2012), and emotion (Droit-Volet and Meck 2007), which may serve adaptive functions (Harrington et al. 2011; Matthews and Meck 2014; Meck 2003). To characterize these types of modulation, researchers have predominantly relied on either the peak-interval procedure (Roberts 1981) or the bisection task (Church and Deluty 1977). The peak-interval procedure is a reproduction task: Here, the animal is trained to respond maximally at a criterion duration to receive a reward. Occasionally, much longer, unreinforced probe trials are presented, and the peak response, a measure of the animal’s estimate of the time of reward delivery, is measured against the desired manipulation (e.g., administration of DA agonist). In this procedure, acutely increasing the speed of the pacemaker will result in underproduction of a timed interval. The bisection task, on the other hand, is an estimation task: Here, the animal is trained to respond differently to stimuli of either short or long duration, such as pressing a left lever when presented with a short interval and a right lever when presented with a long interval. In probe trials, unreinforced intervals of intermediate length are presented, and the animal must respond with either the “short” response or the “long” response. A psychometric function is fit against each of the control condition and the desired manipulation, and the two functions are then compared. A faster pacemaker will cause interval durations to be perceived as longer than they are, thus resulting in overestimation of intervals. Hence, acutely increasing the pacemaker rate will result in underproduction and overestimation. Similarly, acutely decreasing the pacemaker rate will lead to overproduction and underestimation.

Perhaps the main attraction of a bidirectional learning rule on η is that it allows our model to explain the seemingly conflicting effects of DA, and by extension unexpected rewards, on the pacemaker rate. Indeed, as discussed below, behavioral and pharmacological studies have found that higher reward rates and DA agonists result in behaviors consistent with a faster pacemaker, whereas optogenetic activation of midbrain DA neurons displays the opposite pattern. We show here that these results can be reconciled under the model behaviors derived above.

First, our model is consistent with results from the behavioral literature. In Morgan et al. (1993), pigeons were trained on a bisection task in which they had to discriminate between a 10-s and a 20-s duration and were then exposed to high or low rates of freely delivered reinforcers. When returned to the discrimination task, those returning from a richer context judged durations to be longer than those returning from a poorer context, consistent with a faster and slower pacemaker, respectively (Fig. 5B). Previously, Killeen and Fetterman (1988) had found that the speed of the pacemaker is directly proportional to the rate of reinforcement (Fig. 5A; see also MacEwen and Killeen 1991), similarly predicted by our model. These results are also consistent with studies of electrical brain stimulation of the medial forebrain bundle in mouse, an area that is involved in pleasure sensation and that supports self-stimulation (Olds 1958). Stimulation of this area resulted in a shift of timing behavior that is similarly consistent with a faster pacemaker (Meck 2014).

Second, the model is consistent with results from electrophysiology. As mentioned above, Mello et al. (2015) have shown that in a timekeeping task the response profiles of putative medium spiny neurons (MSNs) representing time cells undergo significant rescaling to reflect the temporal properties of the task at hand (Fig. 6). By construction, this is captured by our model: Here, DA modulates feature rescaling against objective time by exactly this mechanism, and this effect is unexplained by the existing TD and microstimulus models.

Third, the model is consistent with results from pharmacology. Pharmacological manipulations have shown that in a bisection task DA agonists such as methamphetamine predominantly shift the psychometric function to the left (or globally increase the probability of responding “long”), consistent with making the clock go faster, whereas DA antagonists like haloperidol shift it to the right, consistent with making it go slower (Maricq and Church 1983). Lake and Meck (2013) have demonstrated this effect on timekeeping with a peak-interval procedure, which our model recapitulates in Fig. 7.

Finally, our model is consistent with results from optogenetics. In Soares et al. (2016), successive optogenetic stimulation occurred over the duration of the entire trial, which corresponds in our model to sequentially updating η with every new traversed state in that trial by the increment Δη, determined by Eq. 6 and the gray curve in Fig. 4. Hence we may approximate the total change in η over the course of an entire trial as

$$\Delta \text{η}={\displaystyle \sum _{\text{τ}}{\text{α}}_{\text{η}}}\frac{\text{τ}}{\text{η}}{\dot{\widehat{V}}}_{\text{τ}}{\text{δ}}_{\text{τ}}$$ (7)

Importantly, the stimulation protocol covered both the early positive limb and the late negative limb of the gray curve in Fig. 4. Under our model, optogenetic activation (δ_τ > 0) therefore resulted in updates of η that first increased it (early stimulation, before the peak of the estimated value function) and then decreased it (late stimulation, after the peak). It is straightforward to show that for optogenetic activation the quantity in Eq. 7 is negative (see appendix for derivation). This can also be visually ascertained from Fig. 4, by noting that the negative limb of the gray curve is larger in area than the positive limb. Therefore, the net effect of this trial-long activation is to slow down the pacemaker. Similarly, trial-long inhibition (δ_τ < 0) will increase η, and the pacemaker will speed up (Fig. 8). Note here that, for convenience, we have taken the effects of optogenetic activation and inhibition to be equal and opposite (δ_τ = +1 and −1, respectively), but this need not be the case. In fact, the experimental data show a rather small effect for inhibition. In principle, this asymmetry may follow from differences in the stimulation protocol, from the asymmetric relationship of DA levels with positive and negative RPEs (Bayer et al. 2007), from the nonlinearity of behavior with equal and opposite changes in value (Luce 1959; Shepard 1958), or from other causes.

In Toda et al. (2017), mice were trained on a peak-interval licking schedule in which a drinking needle delivered sucrose solution every 10 s. Licking behavior was stereotyped, and peak licking occurred at approximately the expected reward time. The authors showed that although start and end times for licking tended to vary with satiety, the peak time was robust to such variations and continued to reflect the expected reward time. The authors then optogenetically stimulated the nigrotectal pathway, an output pathway of the BG, for a 1-s duration that occurred at different times during the trial. Interestingly, stimulation for 1 s immediately before or immediately after reward resulted in later peak responding on the subsequent trial, whereas stimulation ending 1 s before the reward led to earlier peak responding on the subsequent trial.

As illustrated in Fig. 9, this asymmetry follows from our model. Because the sign of ${\dot{\widehat{V}}}_{\text{τ}}$ changes at the peak of the estimated value function, which itself occurs before the true time of reward (Figs. 3 and 4), it follows from Eq. 6 that RPEs that occur after, or immediately before, reward time will have an opposite effect on the speed of the clock compared with those occurring sufficiently before reward time. Importantly, how the output of the BG, reflecting estimated value (Ratcliff and Frank 2012), is transformed and combined into the DA signal from midbrain has been ill defined, although various hints exist (e.g., Barter et al. 2015; Eshel et al. 2015). We assume here that increases in this output serve to increase δ_τ = γV̂_τ+1 − V̂_τ. This means that stimulation after, or immediately before, reward time will decrease η and lead to later responding on the next trial. On the other hand, stimulation that is early enough compared with reward time will increase η and lead to earlier responding.

DISCUSSION

The RPE hypothesis of DA is a compelling one, with a rich history of theoretical and experimental support (Eshel et al. 2015; Glimcher 2011; Montague et al. 1996; Niv and Schoenbaum 2008; Schultz 2007; Schultz et al. 1997; Steinberg et al. 2013). In this article, we consider one effect of DA that at first glance does not seem to relate to RPEs: the modulation of timekeeping estimates by DA.

We have shown in this work that, beyond updating the weights w_d of relevant features, the RPE interpretation may be generalizable to learning about other relevant parameters, including, for temporal tasks, the pacemaker rate. Given experimental evidence that DA modulates the pacemaker rate, and inspired by the recent discovery of scalable “time cells,” we have shown that the same RPE signal, when extended to the pacemaker rate η, reconciles a wide array of experimental observations, including some that may otherwise seem contradictory. Concretely, we derived from first principles a biologically plausible learning rule on η that facilitates either speeding or slowing the pacemaker, depending on the timing of the DA signal: When reward is presented earlier than expected, the function of η is to increase, thus compressing the estimated value function against objective time, which allows it to better match the true value. On the other hand, when reward is presented late, η must decrease to allow the estimated value to expand appropriately.

A learnable η, and hence a scalable feature set, allows similar numbers of features to participate in the timed interval independent of its length, thus maintaining time cells in the dynamic range of the relevant task. This carries implications for precision, whereby temporal estimates of shorter intervals can be resolved with higher granularity, and may account for the scalar property (Gibbon 1977). In fact, theoretical and experimental work has implicated DA in various measures of precision (Friston et al. 2012; Kroener et al. 2009; Manohar et al. 2015). Second, rescaling the features when the rate of reinforcement changes allows value functions to be rapidly updated without a need for relearning each weight w_d individually. This allows for fewer update steps to occur before convergence (as only a single parameter must now be updated), which paves the way for potentially faster convergence. In addition, we have limited our discussion to interval timing, but this rescaling may be extended to putative downstream representations, such as action velocity. For instance, Yin (2014) has proposed that DA may function as gain control on velocity reference signals, which may explain the bradykinesia of Parkinson’s disease and motor symptoms of Tourette syndrome. Indeed, under our formulation, a compression of time cells with high tonic DA will lead to a faster execution of learned action sequences, effectively implementing a type of gain control on executed velocity. Similarly, rescaling time cells to fit the task-specific dynamic range may carry implications for (upstream) cognitive control and attentional modulation, if these inputs exert their influence by operating at the level of the time cells themselves.

The key contribution of the present work—a bidirectional learning rule on the pacemaker rate that critically depends on the timing of DA—is conceptually in line with a number of observations from the broader BG literature. It has been well established that the modification of cortico-striatal weights occurs via a bidirectional, spike-timing-dependent plasticity mechanism (Song et al. 2000) that depends critically on dopaminergic modulation (Pawlak and Kerr 2008; Shen et al. 2008). Emerging experimental evidence furthermore supports the existence of bidirectional mechanisms for learning in striatum that depend on the timing of stimulation. Notably, Yttri and Dudman (2016) have found that optogenetically stimulating MSNs during an approach task can either increase or decrease the subsequent velocity of approach, depending on when during the task the stimulation occurs: Stimulation of D1 MSNs during the fastest phase of the animal’s motion in the task induced increases in velocity on both current and subsequent trials, whereas stimulation during the slowest phase of motion induced decreases in velocity. D2 MSNs, which are thought to act antagonistically to D1 MSNs in motor control (Albin et al. 1989; DeLong 1990; Kravitz et al. 2012; Smith et al. 1998), displayed the opposite effect (an increase in velocity following stimulation during the slowest phase and a decrease following stimulation during the fastest phase). For timekeeping in particular, it is the D2 receptor that seems to mediate the effects of DA. For instance, the discussed pharmacological effects on timekeeping relied on haloperidol (Fig. 7), which is a D2 antagonist, whereas these effects were not found with SCH-23390, a D1 antagonist (Drew et al. 2003). Transient overexpression of D2 in striatum has similarly been found to impair timing behaviors (Drew et al. 2007), although the understanding of the roles of D1 and D2 in interval timing is far from complete (see Coull et al. 2011 for a review).

Throughout this article, we have made a number of simplifying assumptions. First, for the optogenetic data, Soares et al. (2016) only observed the effects of dopaminergic modulation of temporal estimates in the currently evaluated trial, rather than in future trials in which modulation of synaptic weights is more likely to play a dominant role. The TD framework is untroubled by this limitation, as weights are not restricted to trial-level learning; rather, learning occurs across states, even within a single trial. Furthermore, as discussed above, in examining the effects of MSN stimulation on movement control, Yttri and Dudman (2016) have found that the time-dependent bidirectional effects on the current trial extended to future trials as well, presumably through plasticity-mediated changes. Second, for a canonical timekeeping model, our framework afforded us the convenience of examining the modulation of timekeeping with a single parameter. Alternative models, described below, can replace this framework with no effect on the bidirectionality of our update rule, which is determined by performing gradient ascent on V̂_τ independent of implementation. Third, for our canonical RL model, we have restricted learning to the case in which a nonzero value function has already been established and a change in the temporal dynamics of a simple reward distribution causes a subsequent initiation of learning. Hence, we have assumed that η is learned at a much faster rate than w_d. A series of behavioral papers have indeed shown rapid, nearly one-shot or two-shot learning of temporal duration in rats (Davis et al. 1989; Higa 1997; Meck et al. 1984), mice (Balci et al. 2008, with reanalysis in Simen et al. 2011, Supplemental Fig. 10), pigeons (Wynne and Staddon 1988), and humans (Simen et al. 2011). Recent theoretical work (Simen et al. 2011), discussed below, has taken these findings into account and developed learning rules that are particularly effective at rapid, single-exposure learning, compared with the TD models we have assumed, where learning is more gradual.

Finally, this work inherits the limitations of the existing literature on DA and interval timing. For instance, the present findings of DA’s role in timekeeping do not preclude the possibility of unanticipated off-target effects. Similarly, beyond influencing the internal clock, DA may affect motivation (Balcı 2014; Galtress et al. 2012), attention (Nieoullon 2002), and the role of context (Gu et al. 2015; Malapani et al. 1998; Shi et al. 2013) and may asymmetrically influence the encoding and decoding of temporal estimates in memory (Malapani et al. 2002). Although these are not novel concepts and timekeeping experiments have attempted to control for such factors (e.g., Lake and Meck 2013; Soares et al. 2016), the potential for confounds remains.

Experimental predictions.

Our model makes a number of novel experimental predictions. First, the model makes a strong claim on the bidirectional rule governing the update of η, as written in Eq. 6 and illustrated in Fig. 4. This claim can be experimentally verified with the paradigm of Soares et al. (2016): Correlating changes in pacemaker rate with DA levels preceding choice time by some increment Δt, for each increment independently, will recapitulate the gray curve in Fig. 4. In addition, direct optogenetic manipulation of DA levels over different intervals within a single trial will demonstrate this same relationship between DA levels and pacemaker rate, but with causality.

Second, as a result of feature rescaling, our model makes a strong claim about the conditioned stimulus (CS) response in classical conditioning tasks with fixed delay and in particular how it should change under different environmental or pharmacological conditions. Consider then the case in which animals are both trained and tested on timing tasks under either high or low tonic DA conditions. We have shown in results that high tonic DA leads to feature compression under our model. It follows that animals experiencing high-DA conditions will experience more states during the same delay period. This means that value at the CS will be of smaller magnitude than that of animals trained and tested under low-DA conditions (Fig. 10A). Hence, the phasic DA CS response will also be smaller under higher-DA conditions (Fig. 10B). This experiment can similarly be performed by varying reward rate environments rather than DA levels, with similar predicted results.

Fig. 10.

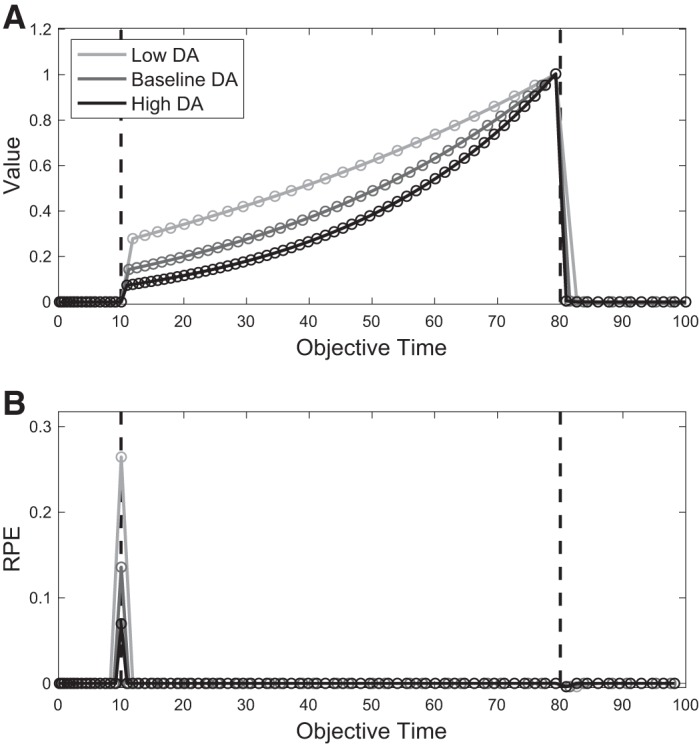
Simulated effect of tonic dopamine (DA) on value and reward prediction error (RPE) against objective time. A: in our model, higher-DA conditions lead to a faster pacemaker and more compressed features, which serve as states. By Eq. 4, this leads to a steeper slope in the value function when measured against objective time. B: DA response, computed by Eq. 4, and based on the corresponding value functions in A. Left and right dashed lines denote conditioned stimulus and reward time, respectively.

Third, our model asserts that the pacemaker rate and external reward rate are state functions. In other words, given a current average reward rate, η will converge to the same value regardless of reward history. As described in results, Morgan et al. (1993) studied the immediate effect of reward history on pigeons in a discrimination task and found that pigeons returning from a highly rewarding context initially judged duration to be longer than those returning from a poorer context, and these judgments in both groups slowly adjusted to the new environment. Our additional prediction, however, is that after overcoming this immediate effect the pacemaker rate in both conditions will converge to the same value (see Fig. 5B).

Fourth, our model makes a claim about the interaction between tonic and phasic DA levels, namely, that tonic DA functions to bias the pacemaker toward speeding up, whereas phasic DA functions to modulate the pacemaker in either direction depending on its timing. This interaction can be tested with combinations of experimental manipulations, for instance, by varying either the average reward rate or the type of optogenetic stimulation (activation vs. inhibition) against a background of either high or low tonic DA levels. The behavioral output of a categorization task similar to that of Soares et al. (2016) can address this prediction.

Relationship with other models.

As mentioned above, our key result, that a DA-dependent bidirectional rule controls time cell response scaling, can be incorporated into a large class of timing models, including pacemaker-accumulator (PA) models, sequential-state models, and striatal beat-frequency models.

In the influential PA model (Gibbon et al. 1997; Treisman 1963; Zakay and Block 1997), a pacemaker, representing the internal clock, emits pulses with approximately constant periodicity. When an interval is to be timed, an accumulator collects the pulses emitted during that interval, and the total number of accumulated pulses is subsequently stored in memory. To reproduce the stored interval, accumulation begins afresh and continues until the accumulated quantity closely matches the quantity stored in memory. This model, whose terminology we have borrowed, maps very naturally onto our framework: Here, the second layer of our neural circuit, encoding subjective time τ, represents the pacemaker, and the time cells, taken as an ordered set, represent the accumulator. The modulation of the pacemaker rate occurs by changing η.

Despite its abstract nature, perhaps the main attraction of the PA model is its intuitive implementation of timekeeping and its biases. For instance, acutely speeding the internal clock results in underproduction and overestimation of intervals. Under the PA model, this is intuitive: During reproduction of a previously stored interval, acutely increasing the speed of the pacemaker causes the accumulator to collect the desired number of pulses within a shorter time frame (underproduction). Alternatively, during a bisection task an acutely sped-up pacemaker will cause the accumulator to collect more pulses by the end of the presented interval than it otherwise would have, thus creating a bias toward selecting the “long” response (overestimation). Similarly, acutely slowing the pacemaker will lead to overproduction and underestimation.

Sequential-state models are similar to PA models but assume a population of cells that are connected in series (rather than in parallel) and thus sequentially activate each other with a time delay. These cells closely resemble the time cells in our model, and their activations serve to encode time (Buonomano and Merzenich 1995; Killeen and Fetterman 1988). For instance, in the behavioral theory of timing (BeT) (Killeen and Fetterman 1988), the cells correspond to behavioral states and the rate of transition across states is taken to be proportional to the reward rate. LeT (Machado 1997) is a descendant of BeT that further views these states as a basis set whose weighted sum constitutes the output layer. Although not a normatively justified RL model, LeT succeeds in proposing associative rules to govern these weights, which allow rewards to be correctly associated with early or late states. This is akin to the bottom two layers in our model and represents an early effort to use principles of RL in interval timing.

Finally, striatal beat-frequency models assume oscillatory neurons in cortex that fire and converge on MSNs in striatum. Timing information is stored in the cortico-striatal weights, gated by DA-dependent long-term potentiation and depression. Subsequent comparisons of time durations with the stored memory are then achieved by comparing the pattern of activation of the oscillatory neurons with the memory trace (Matell and Meck 2000, 2004). Although the architectures of the three presented models differ, it remains that a gradient ascent rule on a parameter controlling the rate of transitions between states, seeking to minimize the difference between the true value V_τ and estimated value V̂_τ, will qualitatively recapitulate the bidirectionality derived in Eq. 6.

With respect to the conflicting experimental evidence regarding the role of DA in timekeeping, we are not aware of any computational work that has sought to reconcile these observations. However, the idea of parameterized rescaling, interpreted broadly, is not novel in the interval timing literature, and whether DA may be related to these models is an open question. For instance, modulating drift rates for the purpose of learning to time is a key component of drift-diffusion models of interval timing (Luzardo et al. 2013; Rivest and Bengio 2011; Simen et al. 2011), and recent work has related these models with theories of classical conditioning (Luzardo et al. 2017). In the time-adaptive opponent Poisson drift-diffusion model (TopDDM) (Balcı and Simen 2016; Rivest and Bengio 2011; Simen et al. 2011), the ramping rate of neural integrators (or the drift) to a fixed threshold is controlled by the proportion of its active inputs, whose activations are in turn controlled by learning rules on their own input weights (see Komura et al. 2001 for a potential neural correlate of the integrator in sensory thalamus). A virtue of these update rules is that complete adaptation to a new duration can occur after a single exposure: If the timed duration ends before the ramp reaches the fixed threshold (late timing), then a “late learning” rule increases the input weights to the strength required for accurate timing of the new duration. On the other hand, if the threshold is reached before the end of the duration (early timing), a separate “early learning” rule begins to decrease the weights continuously until the timed duration ends. This occurs in such a way that the new drift will allow for accurate timing of the new duration. As discussed above, such learning rules, for either increasing or decreasing drift, are particularly adept at capturing rapid and one-shot learning.

Finally, there is a substantial literature within the study of interval timing that examines the effects of attentional control on timekeeping (Fortin 2003). It is conceivable that the different effects of DA may be explained by invoking differential attentional modulation, for instance, by reallocating the limited resource of attention either away from or toward the timekeeping system, depending on the experimental paradigm (Meck 1984). It is furthermore possible that attentional control works in tandem with the update mechanism proposed here, for instance, by modulating the compression t′ of objective time t or by other mechanisms. Our aim is not to refute these possibilities but instead to show how a single RPE interpretation can account for a wide range of seemingly conflicting results.

GRANTS

The project described was supported by National Institute of General Medical Sciences Grant T32 GM-007753 (J. G. Mikhael) and National Institute of Mental Health Grant CRCNS 1R01 MH-109177 (S. J. Gershman).

DISCLAIMERS

The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of General Medical Sciences or the National Institutes of Health.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.G.M. and S.J.G. conceived and designed research; J.G.M. analyzed data; J.G.M. prepared figures; J.G.M. drafted manuscript; J.G.M. and S.J.G. edited and revised manuscript; J.G.M. and S.J.G. approved final version of manuscript.

ENDNOTE

At the request of the authors, readers are herein alerted to the fact that additional materials related to this manuscript may be found at GitHub. These materials are not a part of this manuscript, and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.

APPENDIX

Alternative implementations of the pacemaker rate.

Rather than introducing a separate layer representing t′ in our circuit, it is possible to directly modulate the weights between τ and x_d,τ by η_d. This is a feasible alternative; however, without restricting the parameter space or introducing additional assumptions, such a neural circuit may result in crossovers of the time cell responses. For instance, if a large reward is delivered at τ = 3, the update of η₃ may be enough to cause x_3,τ to respond earlier than x_2,τ on the next trial. By restricting learning to a single η, our proposed circuit protects against this possibility. We can show this by rewriting x_d,τ as

$$\begin{array}{c}{x}_{d,\text{τ}}=\exp \left[-\frac{1}{2}{\left(\frac{\text{η}t\prime -{\text{μ}}_d}{\text{σ}}\right)}^2\right]\\ =\exp \left[-\frac{1}{2}{\left(\frac{t\prime -\frac{{\text{μ}}_d}{\text{η}}}{\frac{\text{σ}}{\text{η}}}\right)}^2\right]\end{array}$$

Hence, samples of x_d are drawn from $\mathcal{N}\left[\frac{{\text{μ}}_d}{\text{η}},{\left(\frac{\text{σ}}{\text{η}}\right)}^2\right]$ up to a constant, and the coefficient of variation is $\text{CV}=\frac{\text{σ}}{\text{η}}\frac{\text{η}}{{\text{μ}}_d}=\frac{\text{σ}}{{\text{μ}}_d}$, which is independent of η. In addition, the means for all features x_d are $\frac{{\text{μ}}_d}{\text{η}}$. Therefore the ordering of μ_d is maintained when scaling by η, and no crossovers occur.

Sequential activation of DA neurons over the course of an entire trial results in a net negative RPE.

Let us analytically derive this result. We begin by writing

$$\Delta \text{η}={\displaystyle \sum _{\text{τ}}{\text{α}}_{\text{η}}}\frac{\text{τ}}{\text{η}}{\dot{\widehat{V}}}_{\text{τ}}{\text{δ}}_{\text{τ}}$$ (A1)

over the duration of an entire trial. For a better intuition of the result we will derive below, let us extend our analysis to the continuous domain. The relationship in Eq. A1 thus becomes

$$\Delta \text{η}={\displaystyle {\int }_{\text{τ}}{\text{α}}_{\text{η}}}\frac{\text{τ}}{\text{η}}{\dot{\widehat{V}}}_{\text{τ}}{\text{δ}}_{\text{τ}}d\text{τ}$$ (A2)

Because the estimated value V̂_τ decays to zero after reward time $\mathcal{T}$, it follows that

$${\displaystyle {\int }_{\text{τ}}{\dot{\widehat{V}}}_{\text{τ}}}d\text{τ}=0$$ (A3)

Here, ${\dot{\widehat{V}}}_{\text{τ}}$, like Δη, has a positive limb, or a domain over which ${\dot{\widehat{V}}}_{\text{τ}}$ is >0, followed by a negative limb. Additionally, by Eq. A3, the integral over the positive limb is equal and opposite to that over the negative limb.

Since $\frac{\text{τ}}{\text{η}}=t\prime$ is monotonically increasing, it follows that

$${\displaystyle {\int }_{\text{τ}}\frac{\text{τ}}{\text{η}}}{\dot{\widehat{V}}}_{\text{τ}}d\text{τ}<0$$

Therefore, with optogenetic activation (δ_τ > 0), the integral in Eq. A2 is negative, so that η will decrease and the pacemaker will slow down. With a similar analysis for optogenetic inhibition, η will increase and the pacemaker will speed up.