Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 May 24;10(12):3217–3222. doi: 10.1021/acs.jpclett.9b00915

Observation of Distinct Carboxylic Acid Conformers in Aqueous Solution

Giulia Giubertoni 1, Oleksandr O Sofronov 1, Huib J Bakker 1,*
PMCID: PMC6589744  PMID: 31125521

Abstract

graphic file with name jz-2019-00915u_0006.jpg

We investigate the molecular geometry of the carboxyl group of formic acid in acetonitrile and aqueous solutions at room temperature with two-dimensional infrared spectroscopy (2D-IR). We found that the carboxyl group adopts two distinct configurations: a configuration in which the carbonyl group is oriented antiparallel to the hydroxyl (anti-conformer), and a configuration in which the carbonyl group is oriented at an angle of ∼60° with respect to the hydroxyl (syn-conformer). These results constitute the first experimental evidence that carboxyl groups exist as two distinct and long-living conformational isomers in aqueous solution at room temperature.

The chemical impact of conformational isomerism has been recognized for a long time.1−6 The conformation change of a relatively small molecular group can have a large impact on the macromolecular structure. For example, the cis/trans-isomerization of the amino acid proline determines the conformation of the folded protein.7−11 Carboxyl groups play an important role in this respect as they form strong inter- and intramolecular hydrogen bonds that govern and stabilize macromolecular structures.12,13 As a consequence, the conformational isomerism of carboxylic acids has been intensely studied with different calculation techniques.14−17 These studies predicted the existence of distinct conformational isomers of the carboxyl group in the gas phase and in aqueous solution.

Up to now, distinct carboxyl group conformers have only been experimentally observed in rare-gas matrices under cryogenic conditions.18−20 Under these conditions, the chemical reactivity of the carboxyl group was also observed to depend on its conformation.21 The carboxyl group adopts two distinct planar geometries in rare gas matrices at low temperatures, as illustrated in Figure 1.18,19,22−24 In the syn-conformer the O–H group is oriented at ∼60° with respect to the C=O and in the anti-conformer the O–H is antiparallel to the C=O. Molecular dynamics simulations showed that the high energy anti-conformer stabilizes under hydration, and that its equilibrium concentration in gas phase is negligible.16,17,25

Figure 1.

Figure 1

Open in a new tab

Schematic picture of syn- and anti-conformers. Orange and green arrows indicate the transition dipole moment of the carbonyl, and hydroxyl vibrations.

The anti- and syn-configurations were identified with linear infrared spectroscopy, which was enabled by the fact that the carbonyl and hydroxyl stretch vibrations of the carboxyl group have narrow absorption lines when the group is immersed in a rare-gas matrix at an extremely low temperature. In room-temperature solutions, in particular, in water, the carbonyl and hydroxyl stretch vibrations are strongly affected by the interactions with the surrounding solvent molecules, leading to a strong broadening of the absorption bands. In addition, at acid concentrations above ∼3 M, the vibrations will also be affected by dimer formation.26−28 These effects preclude the study of conformational isomerism of carboxylic acids in aqueous media at room temperature with conventional linear infrared spectroscopy.

Here we use two-dimensional infrared (2D-IR) spectroscopy to study the conformations of carboxyl group of formic acid molecules in room temperature solutions. We study the coupling between the carbonyl (C=O) and hydroxyl (O–D) stretch vibrations for deuterated formic acid dissolved in different solvents, including water. We found that the measurement of this coupling reveals the relative orientation of the carbonyl and the hydroxyl groups, and thus forms a unique experimental test of the existence of conformational isomerism of carboxylic acids under biorelevant conditions.

In Figure 2a and b we show the linear infrared spectra of formic acid dissolved in deuterated acetonitrile and heavy water (0.5 and 0.3 M, respectively) in the frequency regions of the carbonyl (∼1750 cm–1) and the O–D (∼2430 cm–1) stretching vibrations. Acetonitrile is a weakly polar and aprotic solvent, and the measured response of formic acid in this solvent may be similar to that in an inert gas matrix, which was used in previous experiments.18,22,23 Comparison of the response of formic acid in acetonitrile with the response in (heavy) water will reveal the effect of hydration on the carbonyl and hydroxyl stretch vibrations. For formic acid in acetonitrile the absorption spectrum shows two distinct bands at 1730 and 1754 cm–1. The similarity of this spectrum with that of a more dilute solution (SI Figure 1) indicates that one of the bands is not likely the result of dimer formation. In the O–D stretch region we observe a broad band around 2430 cm–1 with an additional peak at 2380 cm–1. The latter can be assigned to a Fermi resonance of the O–D stretch vibration with the overtone of the C–O stretch vibration.19,22,29 For formic acid in water (Figure 2b) we observe a broad band for the carbonyl vibration around 1700 cm–1 with a shoulder around 1724 cm–1. The absorption of the O–D vibrations is red-shifted in heavy water30 compared to acetonitrile solution. The actual band is broad and shows different subbands. Because of the strong absorption of the O–D stretch vibrations of D2O, we cannot resolve the full O–D stretch spectrum of formic acid. However, the spectrum shows a distinct band at 2050 cm–1 corresponding to the O–D stretch vibration. The full O–D stretch absorption spectrum of formic acid can be seen in dimethyl sulfoxide (DMSO) solution (SI Figure 3). The observed spectrum is broad (1900–2300 cm–1) and has multiple peaks due to combined excitations of the O–D stretch vibration and the O–D···O hydrogen bond. Since DMSO and water are hydrogen-bond acceptors of similar strength, the part of the formic O–D stretch absorption that we can observe in D2O corresponds to the low-frequency part of the formic O–D stretch absorption spectrum observed in DMSO.

Figure 2.

Figure 2

Open in a new tab

(a) Linear infrared absorption spectrum of a 0.5 M solution of formic acid in deuterated acetonitrile. The spectrum shows two distinct narrow bands at 1730 and 1754 cm–1, and a broad band around 2430 cm–1 with a shoulder at 2380 cm–1. (b) Linear infrared absorption spectrum of a 0.3 M solution of formic acid in D2O. The spectrum shows a C=O stretch band around 1700 cm–1 with a shoulder at 1724 cm–1, and a band at 2030 cm–1 that is part of the broad and structured absorption spectrum of the O–D stretch vibration of formic acid. The solvent background absorption is subtracted in both the cases.

We study the vibrational response of the carbonyl and hydroxyl stretch vibrations and their coupling with 2D-IR spectroscopy. The details of our 2D-IR setup can be found in the literature.31 In brief, we excite the carbonyl stretching vibrations with a strong femtosecond infrared pulse pair (∼100 fs, 6 μJ per pulse). This excitation induces transient absorption changes that are probed with a weaker (0.35 μJ) single femtosecond probing pulse that is delayed by a time Tw. In all experiments the excitation pulses are centered at 1720 cm–1 with a bandwidth of 200 cm–1, in resonance with the carbonyl vibrations. The probe pulse is centered at 2450 cm–1 to measure the response of the O–D stretch vibrations in deuterated acetonitrile, and at 2050 cm–1 to measure the response of the O–D stretch vibrations in heavy water solutions. The 2D-IR signal is recorded simultaneously with the probe in parallel and perpendicular polarizations with respect to the pump, which allows us to extract information on the relative orientation of the excited C=O vibration and the probed O–D vibration.

In Figure 3b and c, we show 2D-IR spectra of formic acid in acetonitrile. The blue colored regions correspond to negative transient absorption changes (bleaching) and the red-colored regions to positive transient absorption changes. The spectra contain several cross-peak signals corresponding to frequency shifts of the O–D stretch vibration that are induced by the excitation of the carbonyl vibration. In both the parallel and the perpendicular 2D-IR spectra, we observe cross-peak bleachings at 2380, 2423, and 2463 cm–1. We observe additional structure in the 2D-IR spectrum at probe frequencies below 2400 cm–1, namely, a decreased absorption near 2380 cm–1 and an enhanced absorption at 2340 cm–1. These signals result from the frequency shift and/or bleaching of the aforementioned Fermi resonance of the O–D stretch vibration and the overtone of the C–O vibration, following the excitation of the carbonyl vibrations. The 2423 cm–1 and the 2463 cm–1 represent O–D stretching modes. It is clearly seen that the low-frequency carbonyl vibration at 1754 cm–1 shows a more intense cross-peak (which we denote as A) with the 2463 cm–1 O–D stretch mode in parallel polarization (Figure 3b). Similarly, the low frequency carbonyl vibration at 1730 cm–1 shows a more intense cross-peak (which we denote as S) with the 2423 cm–1 O–D stretch mode in perpendicular polarization (Figure 3c).

Figure 3.

Figure 3

Open in a new tab

(a) Linear spectrum of a 0.5 M solution of formic acid in acetonitrile-d3 in the region of the carbonyl stretch vibration. (b,c) 2D-IR spectra at Tw = 1 ps of the same solution when exciting the carbonyl stretching modes and probing the O–D stretching modes in parallel and perpendicular polarization configuration, respectively. (d) Anisotropy of the A and S cross-peaks as a function of delay time between the excitation and detection pulses. Dashed lines are single exponential fits.

To better illustrate the polarization dependence of the signals, we plot the anisotropy of the two cross-peaks as a function of the time delay between the excitation and probing pulses. Figure 3d shows that at all time delays between 0.3 and 2 ps the anisotropy of the S-cross-peak is negative, indicating that the C=O at 1725 cm–1 is oriented at a large angle with respect to the O–D stretch vibration at 2423 cm–1. The A-cross-peak shows a positive anisotropy, indicating that the C=O vibration at 1754 cm–1 is oriented almost parallel to the O–D stretching vibrating at 2463 cm–1. The relative orientations indicate that there are two distinct species of formic acid in deuterated acetonitrile solution, with different relative orientations of the carbonyl and the O–D stretch modes.

The anisotropy signals of Figure 3d decay, probably as a result of the reorientation of the formic acid molecule. To extract the angle between the carbonyl and hydroxyl groups, we fit the anisotropy decays (Figure 3d) with a single exponential decay function. By extrapolating the fit to time delay zero, we determine the initial anisotropy R0, from which we calculate the angle with the following expression: 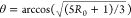Inline graphic. The two angles extracted from the anisotropy values (15 ± 5° and 65 ± 10°) match well with the molecular geometries of the anti and syn configurations, respectively (Figure 1). Thereby these results demonstrate that formic acid exists in distinct anti and syn configurations in room temperature solution. The extracted angles are affected by the fast inertial (librational) motion of O–D bond,32 which explains why the extracted angle for the anti-conformer is somewhat larger than expected (15° vs 0°).

We find that the syn-conformation of formic acid in deuterated acetonitrile has a low-frequency carbonyl vibration and a low frequency hydroxyl vibration, while the anti-conformation has a high-frequency carbonyl and high-frequency hydroxyl vibrations. This finding agrees with the observations for formic acid in a low-temperature rare-gas matrix. By comparing the linear infrared and 2D-IR spectra (see SI Figures 4–5), we find that the anti species accounts for 30% ± 5% of the total amount of carboxyl groups present in solution. The absence of a cross-peak signal between the different hydroxyl vibrations, which would indicate the transformation from syn to anti or vice versa, shows that the two species do not exchange within the lifetime of the vibrationally excited state (∼6–8 ps). This finding is supported by the results of an experiment in which we excite and probe the carbonyl vibrations, and in which we also do not observe a cross-peak signal of the two carbonyl vibrations (SI Figure 6). This outcome agrees with the results of molecular dynamics simulations that showed the presence of a large energy barrier (∼11 kcal/mol)24,25 between the two species.

In Figure 4b,c, we show 2D-IR spectra of formic acid in heavy water solution in the cross-peak region where the carbonyl stretching modes are excited and the O–D stretch modes around 2050 cm–1 are detected in a parallel and perpendicular polarization configuration with respect to the pump. The spectral features are much broader and not as distinct as in acetonitrile solution. However, we observe again that the cross-peak of the high-frequency shoulder of the carbonyl at 1724 cm–1 is stronger in parallel polarization (Figure 4b), while the cross-peak of the low-frequency carbonyl at 1694 cm–1 is stronger in perpendicular polarization (Figure 4c). An interesting observation is that the high-frequency carbonyl vibration now has a cross-peak with a lower frequency O–D vibration while the low-frequency carbonyl vibration has a cross-peak with a higher frequency O–D vibration. In Figure 4d we plot the anisotropy of the A and S cross-peaks in water, and we observe that the A cross-peak corresponds to a positive anisotropy value while the S cross-peak corresponds to a negative anisotropy. We thus find strong evidence of the existence of two molecular geometries of formic acid in aqueous solution: a configuration in which the carbonyl makes a small angle with the O–D vibration (A cross-peak and anti configuration), and a configuration where the carbonyl vibration makes a large angle with the O–D vibration (S cross peak and syn configuration).

Figure 4.

Figure 4

Open in a new tab

(a) Linear spectrum of a 0.3 M solution of formic acid in heavy water in the region of the carbonyl stretch vibration. (b,c) 2D-IR spectra at Tw = 1 ps of the same solution when exciting the carbonyl stretching modes and probing the O–D stretching modes in parallel and perpendicular polarization configuration, respectively. (d) Anisotropy of the A and S cross-peaks as a function of delay time between the excitation and detection pulses. For comparison also the results of Figure 3d are shown. Dashed and continuous lines are single exponential fits.

An interesting question is why the 1724 cm–1 carbonyl vibration shows a cross-peak with a lower frequency O–D stretch vibration, and the 1694 cm–1 carbonyl vibration with a higher frequency O–D stretch vibration. This finding clearly deviates from what was observed for formic acid in acetonitrile and in a rare-gas matrix at low temperature. This observation can be explained from the difference in the strength of the hydrogen bonds between the O–D group of formic acid and the surrounding water molecules in the two configurations. In the anti configuration these hydrogen bonds are stronger than in the syn configuration. As a result, the O–D vibration undergoes a stronger redshift in the anti configuration than in the syn configuration, which overcompensates the intrinsically higher frequency of the O–D stretch in the anti configuration that was observed for formic acid in deuterated acetonitrile and in a rare gas matrix. A similar reversal of the O–D stretch vibrational frequency is observed for a solution of formic acid in DMSO (which is a similarly strong hydrogen bond acceptor as water), as shown in SI Figure 6. This explanation is also supported by molecular dynamics simulations of acetic acid hydrates, that show that the anti-conformer is more strongly hydrated than the syn-conformer.25

In Figure 4d we compare the anistropy values obtained for formic acid in heavy water with the results obtained for formic acid in deuterated acetonitrile. We observe that the negative anisotropy of the S cross-peak does not show a significant change by changing the solvent while the positive anistropy of the A cross-peak is somewhat lower in heavy water than in deuterated acetonitrile. This difference likely results from the fact that the spectral features are much broader in heavy water than in deuterated acetonitrile. Hence, the signal observed in the region of the A cross-peak has some contribution of the stronger S cross-peak for which the anisotropy has a negative value. An additional effect may be that the stronger hydrogen bonding of the anti configuration to surrounding water molecules leads to larger conformational fluctuations and thus a larger net deviation from a perfect parallel arrangement of the carbonyl and O–D groups.

We estimate from the amplitudes of the cross peaks that 25 ± 10% of formic acid adopts an anti configuration in heavy water. Unfortunately, the precision of this estimation is lowered by the strong broadening of the carbonyl absorption band. The analysis of the more narrow carbonyl spectrum of formic acid in DMSO yields a similar fraction for the anti configuration of 30 ± 5%. It thus appears that the character of the solvent does not change significantly the concentration, and thus the relative stability of the two formic acid conformers. This result indicates that the stronger hydrogen bond donated by the formic acid O–D group in the anti configuration constitutes only a small contribution to the overall stabilization of this conformer, or that this contribution is compensated by counteracting solvation effects of other parts of the molecule.

In summary, using femtosecond 2D-IR spectroscopy we demonstrate that formic acid adopts two distinct, long-living conformations in deuterated acetonitrile and heavy water solutions, denoted as syn and anti (Figure 5). We observed that for formic acid in heavy water the frequency of the O–D stretch vibration is at a lower frequency in the anti configuration than in the syn configuration, which is opposite to what is observed for formic acid in deuterated acetonitrile. This difference indicates that the OD group of formic acid forms a stronger hydrogen bond to surrounding water molecules in the anti-conformer than in the syn-conformer. We observe that the fractions of the anti-conformer and the syn-conformer are 20–30% and 80–70%, respectively, both in deuterated acetonitrile and in heavy water solutions. The observation of distinct conformers of the carboxylic acid and their slow exchange at room temperature shows that these conformers are separated by high energy barriers. As a result, the presence of these conformers can have a large effect on the structure and dynamics of (bio)molecular systems.

Figure 5.

Figure 5

Open in a new tab

Illustration of the syn- and anti-conformers of formic acid in acetonitrile and in liquid water.

Methods

Sample Preparation

The samples were prepared in a glass vial by adding formic acid to deuterated acetonitrile, heavy water, and dimethyl sulfoxide to reach the desired concentration. All the solvents were provided by Sigma-Aldrich. Formic acid OD was purchased from Cambridge Isotope Laboratories.

FTIR

All linear absorption measurements were performed using a Bruker Vertex 80v FTIR spectrometer equipped with a liquid-nitrogen-cooled mercury–cadmium–telluride (MCT) detector. The spectra were recorded under nitrogen atmosphere at a wavelength resolution of 2 cm–1. For every spectrum 100 scans were averaged. In all the measurements, a standard sample cell with a path length of 100 or 50 μm was used. The reported spectra were corrected for the absorption of the solvent background.

2DIR

In the 2D-IR measurements, we perform two color experiments by pumping at 1720 cm–1 and probing at 2450 or 2050 cm–1. The home-built setup that we use has been described before.31 Briefly, the excitation is performed with a pair of femtosecond mid-infrared pulses, which are generated by a Mach–Zehnder interferometer. The pulses have a duration of approximately 100 fs and a pulse energy of 6 μJ The excitation pulse pair induces transient absorption changes that are monitored by a weaker probe pulse (0.35 μJ) that is delayed by a time Tw. After transmission through the sample, the separated parallel and perpendicular polarizations of the probe beam are sent into an infrared spectrograph and detected with two lines of an infrared mercury–cadmium–telluride (MCT) array detector, thus yielding the transient absorption spectrum as a function of the probe frequency. The dependence of the transient absoption spectrum on the excitation frequency is determined by measuring transient spectra for many different delay times between the two excitation pulses. By Fourier transformation of these spectra, we obtain the dependence of the transient absorption spectrum on the excitation frequency. By plotting the transient absorption spectrum as a function of the excitation and the probing frequency, we obtain a two-dimensional infrared (2D-IR) transient absorption spectrum for each delay time Tw.

Acknowledgments

This work is part of the research program of The Netherlands Organization for Scientific Research (NWO) and was performed at the NWO research institute AMOLF. This work is part of the industrial partnership program Hybrid Soft Materials that is carried out under an agreement between Unilever Research and The Netherlands Organization for Scientific Research (NWO). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No 694386).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.9b00915.

  • Experimental details; data analysis; infrared spectra of formic acid in D2O, in d-acetonitrile and in DMSO; anisotropy decay traces; 2D-IR of formic acid in d-acetonitrile (diagonal peaks and transient spectra); 2D-IR of formic acid in DMSO (PDF)

Author Contributions

‡ G. Giubertoni and O.O. Sofronov conceived the idea, designed and performed the experiments. G. Giubertoni, O.O. Sofronov, and H.J. Bakker discussed and interpreted the results and wrote the paper. All authors agree on the content. Giulia Giubertoni and Oleksandr O. Sofronov contributed equally.

The authors declare no competing financial interest.

Supplementary Material

jz9b00915_si_001.pdf (633.6KB, pdf)

References

  1. Seeman J. I. Effect of Conformational Change on Reactivity in Organic Chemistry. Evaluations, Applications, and Extensions of Curtin-Hammett Winstein-Holness Kinetics. Chem. Rev. 1983, 83, 83–134. 10.1021/cr00054a001. [DOI] [Google Scholar]
  2. Taatjes C. A.; Welz O.; Eskola A. J.; Savee J. D.; Scheer A. M.; Shallcross D. E.; Rotavera B.; Lee E. P. F.; Dyke J. M.; Mok D. K. W.; et al. Direct Measurements of Conformer-Dependent Reactivity of the Criegee Intermediate CH3CHOO. Science 2013, 340, 177–180. 10.1126/science.1234689. [DOI] [PubMed] [Google Scholar]
  3. Park S. T.; Kim S. K.; Kim M. S. Observation of Conformation-Specific Pathways in the Photodissociation of 1-Iodopropane Ions. Nature 2002, 415, 306–308. 10.1038/415306a. [DOI] [PubMed] [Google Scholar]
  4. Chang Y.-P.; Długołȩcki K.; Küpper J.; Rösch D.; Wild D.; Willitsch S. Specific Chemical Reactivities of Spatially Separated 3-Aminophenol Conformers with Cold Ca+ Ions. Science 2013, 342, 98–101. 10.1126/science.1242271. [DOI] [PubMed] [Google Scholar]
  5. Kim M.; Shen L.; Tao H.; Martinez T.; Suits A. Conformationally Controlled Chemistry: Excited-State Dynamics Dictate Ground-State Reaction. Science 2007, 315, 1561–1565. 10.1126/science.1136453. [DOI] [PubMed] [Google Scholar]
  6. Robertson E. G.; Simons J. P. Getting into Shape: Conforrmational and Supramolecular Landscapes in Small Biomolecules and Their Hydrated Clusters. Phys. Chem. Chem. Phys. 2001, 3, 1–18. 10.1039/b008225m. [DOI] [Google Scholar]
  7. Fischer G.; Wittmann-Liebold B.; Lang K.; Kiefhaber T.; Schmid F. X. Cyclophilin and Peptidyl-Prolyl Cis-Trans Isomerase Are Probably Identical Proteins. Nature 1989, 337, 476–478. 10.1038/337476a0. [DOI] [PubMed] [Google Scholar]
  8. Freedman R. Folding into the Right Shape. Nature 1987, 329, 196–197. 10.1038/329196a0. [DOI] [PubMed] [Google Scholar]
  9. Zosel F.; Mercadante D.; Nettels D.; Schuler B. A Proline Switch Explains Kinetic Heterogeneity in a Coupled Folding and Binding Reaction. Nat. Commun. 2018, 9, 3332. 10.1038/s41467-018-05725-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Lu K. P.; Finn G.; Lee T. H.; Nicholson L. K. Prolyl Cis-Trans Isomerization as a Molecular Timer. Nat. Chem. Biol. 2007, 3, 619–629. 10.1038/nchembio.2007.35. [DOI] [PubMed] [Google Scholar]
  11. Evans P. A.; Dobson C. M.; Kautz R. A.; Hatfull G.; Fox R. O. Proline Isomerism in Staphylococcal Nuclease Characterized by NMR and Site-Directed Mutagenesis. Nature 1987, 329, 266–268. 10.1038/329266a0. [DOI] [PubMed] [Google Scholar]
  12. Ilmain F.; Tanaka T.; Kokufuta E. Volume Transition in a Gel Driven by Hydrogen Bonding. Nature 1991, 349, 400–401. 10.1038/349400a0. [DOI] [Google Scholar]
  13. Alba K.; Bingham R. J.; Gunning P. A.; Wilde P. J.; Kontogiorgos V. Pectin Conformation in Solution. J. Phys. Chem. B 2018, 122, 7286–7294. 10.1021/acs.jpcb.8b04790. [DOI] [PubMed] [Google Scholar]
  14. Fausto R.; Batista de Carvalho L. A. E.; Teixeira-Dias J. J. C.; Ramos M. N. S-Cis and s-Trans Conformers of Formic, Thioformic and Dithioformic Acids. J. Chem. Soc., Faraday Trans. 2 1989, 85, 1945–1962. 10.1039/f29898501945. [DOI] [Google Scholar]
  15. Hirao H. Theoretical Study of Formic Acid: A New Look at the Origin of the Planar Z Conformation and C-O Rotational Barrier. Chem. Phys. 2008, 344, 213–220. 10.1016/j.chemphys.2008.01.003. [DOI] [Google Scholar]
  16. Pranata J. Relative Basicities of Carboxylate Lone Pairs in Aqueous Solution. J. Comput. Chem. 1993, 14, 685–690. 10.1002/jcc.540140609. [DOI] [Google Scholar]
  17. Sato H.; Hirata F. The Syn-Ranti-Conformational Equilibrium of Acetic Acid in Water Studied by the RISM-SCFrMCSCF Method. J. Mol. Struct.: THEOCHEM 1999, 461, 113–120. 10.1016/S0166-1280(98)00436-9. [DOI] [Google Scholar]
  18. Pettersson M.; Maçôas E. M. S.; Khriachtchev L.; Fausto R.; Räsänen M. Conformational Isomerization of Formic Acid by Vibrational Excitation at Energies below the Torsional Barrier. J. Am. Chem. Soc. 2003, 125, 4058–4059. 10.1021/ja0295016. [DOI] [PubMed] [Google Scholar]
  19. Maçôas E. M. S.; Khriachtchev L.; Fausto R.; Räsänen M. Photochemistry and Vibrational Spectroscopy of the Trans and Cis Conformers of Acetic Acid in Solid Ar. J. Phys. Chem. A 2004, 108, 3380–3389. 10.1021/jp037840v. [DOI] [Google Scholar]
  20. Maçôas E. M. S.; Khriachtchev L.; Pettersson M.; Fausto R.; Räsänen M. Rotational Isomerization of Small Carboxylic Acids Isolated in Argon Matrices: Tunnelling and Quantum Yields for the Photoinduced Processes. Phys. Chem. Chem. Phys. 2005, 7, 743–749. 10.1039/B416641H. [DOI] [PubMed] [Google Scholar]
  21. Khriachtchev L.; Domanskaya A.; Marushkevich K.; Räsänen M.; Grigorenko B.; Ermilov A.; Andrijchenko N.; Nemukhin A. Conformation-Dependent Chemical Reaction of Formic Acid with an Oxygen Atom. J. Phys. Chem. A 2009, 113, 8143–8146. 10.1021/jp903775k. [DOI] [PubMed] [Google Scholar]
  22. Marushkevich K.; Khriachtchev L.; Lundell J.; Domanskaya A. V.; Räsänen M. Vibrational Spectroscopy of Trans and Cis Deuterated Formic Acid (HCOOD): Anharmonic Calculations and Experiments in Argon and Neon Matrices. J. Mol. Spectrosc. 2010, 259, 105–110. 10.1016/j.jms.2009.12.001. [DOI] [Google Scholar]
  23. Marushkevich K.; Khriachtchev L.; Lundell J.; Domanskaya A.; Räsänen M. Matrix Isolation and Ab Initio Study of Trans-Trans and Trans-Cis Dimers of Formic Acid. J. Phys. Chem. A 2010, 114, 3495–3502. 10.1021/jp911515f. [DOI] [PubMed] [Google Scholar]
  24. Maçôas E. M. S.; Khriachtchev L.; Pettersson M.; Fausto R.; Räsänen M. Rotational Isomerization of Small Carboxylic Acids Isolated in Argon Matrices: Tunnelling and Quantum Yields for the Photoinduced Processes. Phys. Chem. Chem. Phys. 2005, 7, 743–749. 10.1039/B416641H. [DOI] [PubMed] [Google Scholar]
  25. Nagy P. I. The Syn-Anti Equilibrium for the COOH Group Reinvestigated. Theoretical Conformation Analysis for Acetic Acid in the Gas Phase and in Solution. Comput. Theor. Chem. 2013, 1022, 59–69. 10.1016/j.comptc.2013.08.017. [DOI] [Google Scholar]
  26. Génin F.; Quilès F.; Burneau A. Infrared and Raman Spectroscopic Study of Carboxylic Acids in Heavy Water. Phys. Chem. Chem. Phys. 2001, 3, 932–942. 10.1039/b008897h. [DOI] [Google Scholar]
  27. Chen J.; Brooks C. L.; Scheraga H. A. Revisiting the Carboxylic Acid Dimers in Aqueous Solution: Interplay of Hydrogen Bonding, Hydrophobic Interactions and Entropy. J. Phys. Chem. B 2008, 112, 242–249. 10.1021/jp074355h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Heyne K.; Huse N.; Dreyer J.; Nibbering E. T. J.; Elsaesser T.; Mukamel S. Coherent Low-Frequency Motions of Hydrogen Bonded Acetic Acid Dimers in the Liquid Phase Coherent Low-Frequency Motions of Hydrogen Bonded Acetic Acid Dimers in the Liquid Phase. J. Chem. Phys. 2012, 902, 902–913. [DOI] [PubMed] [Google Scholar]
  29. Lopes S.; Domanskaya A. V.; Fausto R.; Räsänen M.; Khriachtchev L. Formic and Acetic Acids in a Nitrogen Matrix: Enhanced Stability of the Higher-Energy Conformer. J. Chem. Phys. 2010, 133, 144507. 10.1063/1.3484943. [DOI] [PubMed] [Google Scholar]
  30. Kovács A.; Nyerges B.; Izvekov V. Vibrational Analysis of N-Acetyl-Alpha-D-Glucosamine and Beta-D-Glucuronic Acid. J. Phys. Chem. B 2008, 112, 5728–5735. 10.1021/jp710432d. [DOI] [PubMed] [Google Scholar]
  31. Selig O.; Siffels R.; Rezus Y. L. A. Ultrasensitive Ultrafast Vibrational Spectroscopy Employing the Near Field of Gold Nanoantennas. Phys. Rev. Lett. 2015, 114, 233004. 10.1103/PhysRevLett.114.233004. [DOI] [PubMed] [Google Scholar]
  32. Moilanen D. E.; Fenn E. E.; Lin Y.-S.; Skinner J. L.; Bagchi B.; Fayer M. D. Water Inertial Reorientation: Hydrogen Bond Strength and the Angular Potential. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 5295–5300. 10.1073/pnas.0801554105. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz9b00915_si_001.pdf (633.6KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES