A unified model for microtubule rescue

Abstract

How microtubules transition from depolymerization to polymerization, known as rescue, is poorly understood. Here we examine two models for rescue: 1) an “end-driven” model in which the depolymerizing end stochastically switches to a stable state; and 2) a “lattice-driven” model in which rescue sites are integrated into the microtubule before depolymerization. We test these models using a combination of computational simulations and in vitro experiments with purified tubulin. Our findings support the “lattice-driven” model by identifying repeated rescue sites in microtubules. In addition, we discover an important role for divalent cations in determining the frequency and location of rescue sites. We use “wash-in” experiments to show that divalent cations inhibit rescue during depolymerization, but not during polymerization. We propose a unified model in which rescues are driven by embedded rescue sites in microtubules, but the activity of these sites is influenced by changes in the depolymerizing ends.

INTRODUCTION

Transitions between microtubule polymerization and depolymerization involve major structural rearrangements at the microtubule end. During polymerization, incoming tubulin subunits first form longitudinal interactions to generate curved protofilaments that extend from the microtubule end, and then form lateral interactions with neighboring protofilaments to straighten into the coherent microtubule lattice (McIntosh et al., 2018). During depolymerization, protofilaments undergo the opposite transition; from the straight conformation of the lattice, to losing lateral interactions and sharply curling away from each other at the disassembling end (Mandelkow et al., 1991; Chrétien et al., 1995; McIntosh et al., 2018). Under some conditions, protofilaments at depolymerizing microtubule ends adopt a highly curled “ram’s horn” morphology that is not observed for polymerizing microtubules (Mandelkow et al., 1991; Chrétien et al., 1995). The outward curling of protofilaments during depolymeriza­tion is estimated to generate at least 19 pN∙nm of energy per tubulin subunit, and is thought to propagate strain along the protofilament that drives the straight-to-curled transition for subunits further down the lattice (Driver et al., 2017).

The transition from polymerization to depolymerization, known as catastrophe, must represent an intermediate state between the polymerizing and depolymerizing end structures. Current models posit that catastrophe may be caused by changes in the so-called “GTP cap” at the growing plus end, which would weaken subunit affinity for the lattice (Carlier and Pantaloni, 1981; Chen and Doxsey, 2012; Seetapun et al., 2012). Alternatively, catastrophe may be caused by the formation of asymmetric protofilament extensions during polymerization that lack stabilizing lateral interactions and lead to a weakening of the lattice (Coombes et al., 2013; Aher and Akhmanova, 2018). Both of these models imply that a quorum of stable lateral interactions is necessary to maintain polymerization, and catastrophe may represent a loss of quorum.

In contrast to catastrophe, the transition from depolymerization to polymerization, known as rescue, is poorly understood. In principle, rescue must represent an intermediate state between the depolymerizing and polymerizing end structures. This intermediate would need to overcome both the fast rate of subunit loss and the energy driving the outward curling of protofilaments. Rescue is a property intrinsic to tubulin, as it can be observed in experiments using purified tubulin (Dimitrov et al., 2008; Tropini et al., 2012; Aumeier et al., 2016). Importantly, this work showed that rescue frequency is largely independent of tubulin concentration, indicating that the mechanism is not simply kinetic (i.e., the subunit on rate does not overwhelm the subunit off rate during depolymerization [Walker et al., 1988; Gardner et al., 2013]). Instead, rescue may disrupt the depolymerizing end structure. Several conditions have been shown to promote rescue, including mechanical stress on the microtubule (de Forges et al., 2016), structural defects in the lattice (Aumeier et al., 2016), slowing GTP hydrolysis (Tropini et al., 2012), and extrinsic regulation by microtubule-binding proteins (Komarova et al., 2002; Arnal et al., 2004; Mimori-Kiyosue et al., 2005; Al-Bassam et al., 2010; Aher and Akhmanova, 2018; Hiremathad et al., 2018; Lindeboom et al., 2018). Nevertheless, we lack a basic understanding of the underlying mechanism.

A fundamental question is whether rescues are a predetermined property of the microtubule lattice or a state that may be sampled by the depolymerizing end. In the first model, “rescue sites” are formed in the lattice of a growing microtubule. After a subsequent catastrophe, when the depolymerizing end returns to a rescue site in the lattice, further depolymerization is inhibited and the microtubule end returns to a polymerizing state. This model is supported by several observations, including rescues near “GTP islands” that are detected in microtubule lattices, far from polymerizing ends (Dimitrov et al., 2008), and rescues near sites of mechanically induced damage, where subunits are thought to be lost from the lattice and new subunits may be incorporated (Aumeier et al., 2016). In the second model, changes in the structure of the depolymerizing microtubule end disrupt depolymerization and promote polymerization. This model is primarily supported by previous studies of proteins that bind to microtubules and promote rescue, including CLASP, CLIP-170, and Kip3/kinesin 8 (Komarova et al., 2002; Arnal et al., 2004; Bratman and Chang, 2007; Al-Bassam et al., 2010; Dave et al., 2018; Hiremathad et al., 2018; Lawrence et al., 2018; Lindeboom et al., 2018). It is unclear whether this is also a property of tubulin alone.

Here we tested these two models through a combined approach. First we developed Monte Carlo simulations to test simple predictions of each model. Then we validated the simulations experimentally using purified tubulin and found support for a combination of the two models. We find that regions of the microtubule lattice were capable of repeated rescues, which strongly supports the lattice-driven model. In addition, we observed that divalent cations are potent inhibitors of microtubule rescue, and used this to test whether conditions during lattice polymerization or depolymerization determine rescue. Our results support a combination of the two models wherein rescues are regulated through coordination between defined rescue sites in the lattice and changes at the depolymerizing end.

RESULTS

Microtubule rescue frequency is independent of tubulin concentration

We sought to investigate the mechanism of microtubule rescue that is intrinsic to tubulin. Using purified tubulin to study microtubule rescue in vitro has been historically challenging, because rescues occur infrequently, compared with catastrophes. Therefore, we developed an experimental protocol to address three limiting factors of studying rescue in vitro: 1) temporal resolution, 2) acquisition duration, and 3) microtubule number. Microtubules were assembled from purified porcine brain tubulin; determined to be >99% pure by Coomassie stain following SDS–PAGE separation (Figure 1A). This purified tubulin was mixed with 15–20% HiLyte 488–labeled tubulin to visualize microtubule polymerization from rhodamine-labeled GMPCPP seeds using total internal reflection fluorescence (TIRF) microscopy and standard polymerization conditions (5–10 µM tubulin in BRB80, 1 mM GTP, and oxygen scavenging buffer; Figure 1B; Gell et al., 2010; Fees and Moore, 2018). For these initial experiments, we brought the concentration of MgCl₂ in the reaction buffer to 5 mM, which represents the midpoint of the range of magnesium concentrations that we will examine later. We imaged thousands of microtubules at a 1-s time resolution for 15 min using a cMOS camera and processed the images into kymographs to measure microtubule dynamics using a custom MATLAB program (Fees and Moore, 2018). Measured rates of polymerization and depolymerization were used to determine the apparent tubulin association and dissociation constants, respectively (K_on: 5.28 subunits*µM⁻¹*s⁻¹; K_off: 567.30 subunits*s⁻¹; Figure 1, C and D). The catastrophe frequency (growing to shrinking) was calculated by dividing the number of transitions by the total polymerization time. We found no correlation between tubulin concentration and catastrophe frequency (Figure 1E). This experimental design allowed us to consistently detect rescues within the microtubule population and test models of the rescue mechanism.

FIGURE 1:

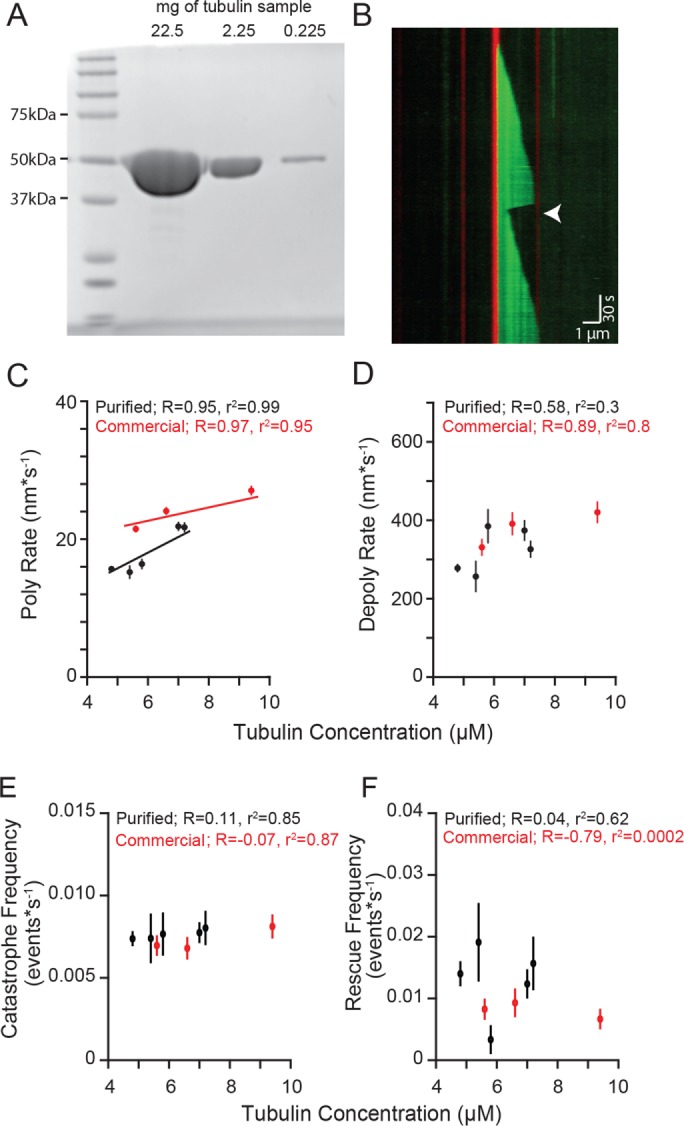
Microtubule rescue frequency is independent of tubulin concentration. (A) Purified tubulin sample separated by SDS–PAGE gel stained with Coomassie. Lane 1: protein ladder. Lanes 2–4: 10-fold serial dilutions of tubulin purified from porcine brain. Protein loads are ∼22.5–0.225 mg. (B) Representative kymograph of purified tubulin (green) polymerized from GMPCPP stabilized microtubule seeds (red), rescue event denoted (arrowhead). Images were collected at 1-s intervals. Tubulin concentration: 7.2 µM, vertical scale bar = 0.5 min and horizontal scale bar = 1 µm. (C) Polymerization rate plotted as a function of tubulin concentration. Protein purified from pig brain (black) compared with purchased protein purified commercially (red). Data points are mean ± 95% CI. (D) Depolymerization rate plotted as a function of tubulin concentration. (E) Catastrophe frequency plotted as a function of tubulin concentration. Catastrophe frequency defined as the number of events per sum of polymerization time for each concentration. Error bars represent SE of proportion (SEP). (F) Rescue frequency plotted as a function of tubulin concentration. Rescue frequency calculated as the number of rescues divided by total depolymerization time for each concentration. Error bars represent SEP. For C–F, at least 73 microtubules were analyzed for each tubulin sample, at each concentration.

We defined rescue as a transition from depolymerization to polymerization that occurred at least 150 nm from the GMPCPP-stabilized seed (Figure 1B, arrowhead). This definition ensures the distinction of rescues that occur in the dynamic microtubule lattice from those that occur at the stabilized seed, within the temporal and spatial resolution of our system. We measured rescues across a range of tubulin concentrations and found an average rescue frequency of 0.01 events per second of depolymerization time (95% confidence interval [CI]: 0.009–0.014 events*s⁻¹), with no clear dependence on tubulin concentration (Figure 1F). Overall, 18.7% of the 525 total seeds in these experiments nucleated microtubules that exhibited at least one rescue, and these rescued an average of 1.6 times per 15-min acquisition (CI: 1.4–1.7; Supplemental Figure 1, A and B).

We then validated the results from our purified porcine brain tubulin by conducting parallel experiments with commercially available porcine brain tubulin under the same reaction conditions. The commercially available tubulin exhibits similar polymerization and depolymerization rates as our purified tubulin (Figure 1, C and D), and similar frequencies of catastrophe and rescue (Figure 1, E and F). Importantly, neither set of experiments revealed a significant correlation between tubulin concentration, and therefore polymerization rate, and rescue frequency, consistent with previous findings (Walker et al., 1988; Gardner et al., 2013).

Computational simulations of microtubule rescue

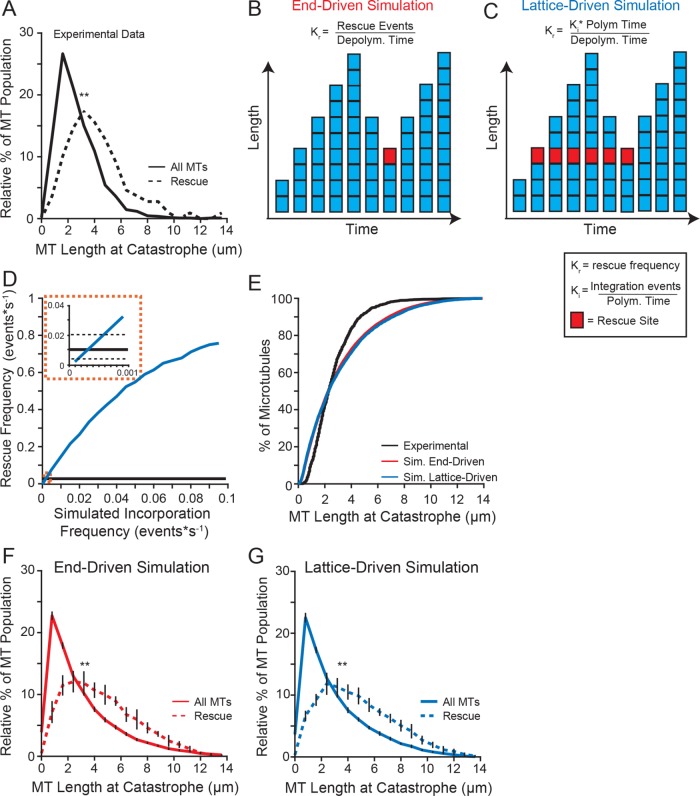
We considered two general models for how rescues might be triggered. First, an “end-driven” model in which the depolymerizing end of the microtubule stochastically switches to a stable state, resulting in rescue. Second, we considered a “lattice-driven” model in which rescue sites were integrated into the lattice before depolymerization and produced a rescue when the depolymerizing end reached that site in the lattice. Both models predict that longer microtubules would have a greater likelihood of rescue. Consistent with our prediction, we found that microtubules that rescue in our experiments were 51% longer at catastrophe than the population on average (mean = 3.68 µm, CI: 3.25–4.11 µm, compared with 2.44 µm, CI: 2.32–2.55 µm; Figure 2A).

FIGURE 2:

Longer microtubules are more likely to rescue. (A) Relative distribution of microtubule lengths at catastrophe leading to rescue (dashed line) compared with the entire population (solid line) of the experimental data under standard conditions (5 mM MgCl₂). Data represent 1127 microtubule lengths from 525 stabilized seeds, pooled from five separate experiments at the following tubulin concentrations: 4.8, 5.4, 5.8, 7.0, 7.2 µM. (B) Schematic of our end-driven simulation. Rescue site is denoted by a red square. Rescue frequency is defined as the number rescue events per depolymerization time. Rescues were triggered stochastically during depolymerization at the experimentally derived rescue frequency (0.01 events*depolymerization s⁻¹). (C) Schematic of our lattice-driven simulation. Rescue sites (denoted by a red square) are incorporated during polymerization, and always trigger rescue when the depolymerizing end returns to that site. (D) Simulated rescue frequency as a function of incorporation frequency. The simulated rescue frequency for each incorporation rate calculated from 1000 simulated microtubules. (E) Cumulative distribution of microtubule lengths at catastrophe under standard conditions (black) compared with end-driven simulation (red) and the lattice-driven simulation (blue). (F) Similar to A, using data from the end-driven simulation. Error bars represent SD from 10 separate simulations of 20,000 microtubule seeds. (G) Similar to A, using data from the lattice-driven simulation, with the incorporation frequency set to 0.0001 events*s⁻¹. Error bars represent SD from 10 separate simulations of 20,000 microtubule seeds. Significance determined by Kolmogorov-Smirnov test (F and G) or Mann-Whitney U test (A). **: p < 0.001.

We then developed computational models of microtubule rescue using Monte Carlo simulations of experimentally derived parameters (polymerization and depolymerization rates as well as transition frequencies; Table 1) to simulate a single filament with changes in length over time as the output. We modeled a microtubule as an individual linear filament, nucleated from a seed, which would grow and shrink at rates that were sampled according to frequencies observed in our experiments. The upper and lower limits of these rates were defined as the maximum and minimum of the experimentally observed rates, respectively. Time was calibrated to 1 s for these simulations. Simulated microtubule transition frequencies were similarly applied. The simulations sampled a range of tubulin concentrations (5–8 µM) to be consistent with experimental data.

TABLE 1:

Common simulation parameters.

Parameter	Value
Nucleation sites	1
Nucleation rate	0.02 * s−1
Time resolution	1 s
Duration	15 min
Microtubules per simulation	20,000
Total tubulin	5–8 µM
Kon (subunits*µM−1*s−1)	3.97
Vg (nm*s−1)	17.77 (17.28–18.27)
Vs (nm*s−1)	324.16 (313.65–334.69)
Kc (s−1)	0.0029 (0.0026–0.0032)
KR (s−1)	0.012 (0.009–0.014)
KI (s−1)a	0.001

aSpecific to the lattice-driven model.

For our “end-driven” simulation, rescue events were stochastically triggered during depolymerization, at a rescue frequency (K_r) that matched our experimental measurements (Figure 2B). For our “lattice-driven” simulation, rescue sites were incorporated during filament polymerization at a defined frequency (K_i). These sites would remain embedded in the lattice until, after catastrophe, the depolymerizing end reached the site and triggered a rescue event. Initially we set these sites as fully active—once incorporated into a filament, microtubules would rescue every time the depolymerizing end returned to that site (Figure 2C). This feature will be modified later in our study (see below). The K_i was computationally determined using our simulation to calculate the rescue frequency as a function of incorporation frequency (Figure 2D). The simulated rescue frequency intercepted the experimental values at an incorporation frequency between 0.0001 and 0.0006 events*depolymerization s⁻¹ (Figure 2D, inset).

We validated our end-driven and lattice-driven simulations first by comparing the lengths of microtubules at catastrophe to our experimental data. We found that both simulations accurately sample a similar range of microtubule lengths at catastrophe (Figure 2E). Of note, the simulated data were more normally distributed for microtubules that undergo catastrophe above 6 µm in length. We attributed this to a limitation of our experimental setup, specifically the inability to monitor longer microtubules that extend beyond the field of view. Both simulations were consistent with our experimental results showing that rescuing microtubules were significantly longer at catastrophe than the average distribution of lengths (Figure 2, F and G). We then sought to use these simulations to determine the mechanism of microtubule rescue by testing predictions from each model.

Effect of depolymerization rate on rescue

We began by testing whether depolymerization rates influenced rescue frequency. If rescue occurs through stochastic transitions at the depolymerizing end, then increasing the time spent in the depolymerizing state might promote rescue. We used our simulations to test this prediction across a range of experimentally derived depolymerization rates. We first determined whether our simple simulations could recapitulate the experimentally observed microtubules. The simulated microtubules could sample different depolymerization rates at an experimentally observed frequency with the range limited to the minimum and maximum observed rates (Figure 3A). We found that most (∼55%) of our simulated microtubules depolymerized for a time consistent with our experimental results (Figure 3B). We observed divergence from our experimental results at longer depolymerization times, which we attributed to the limited ability to track longer microtubules in our experiment (i.e., microtubules that extend beyond the field of view). Both simulations indicated that rescue location, if stochastic, should have a normal distribution (Figure 3C, red and blue lines). However, we observed that experimental microtubules rescue at a point more distal from the plus end (Figure 3C, black line).

FIGURE 3:

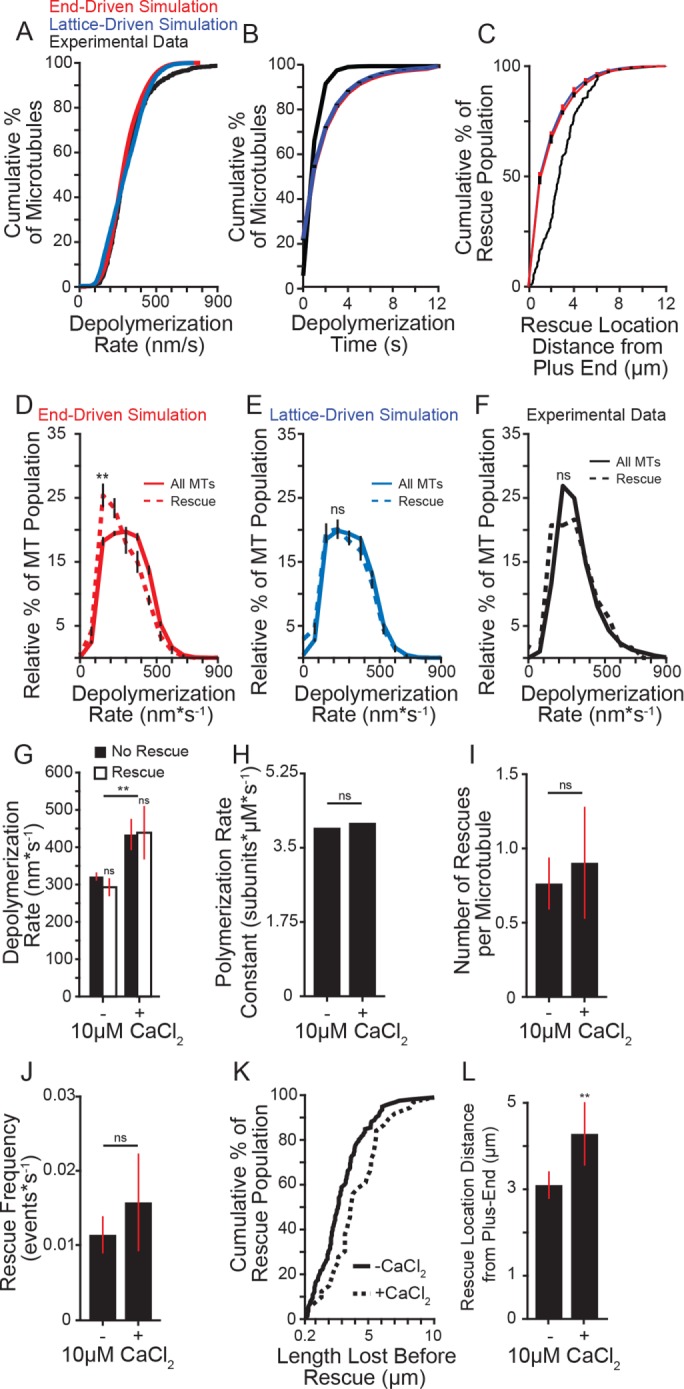
Effect of depolymerization rate on rescue. (A) Cumulative distribution of depolymerization rates of experimental data under standard conditions (5 mM MgCl₂; black) compared with the end-driven simulation (red) and the lattice-driven simulation (blue). (B) Cumulative distribution of microtubule depolymerization times (s) of experimental data under standard conditions (5 mM MgCl₂; black) compared with simulated microtubules from the end-driven and lattice-driven models (red and blue, respectively). Error bars represent SD from 10 separate simulations of 20,000 microtubule seeds. (C) Cumulative distribution of rescue location relative to the micro­tubule plus end of experimental data under standard conditions compared with the simulated models as in A and B. Error bars represent SD from 10 separate simulations of 20,000 microtubule seeds. (D) Relative distribution of depolymerization rates leading to rescue (dashed line) compared with entire population (solid line) of the end-driven simulation. Plot represents 10 separate simulations of 20,000 simulated microtubules per simulation. Error bars represent SD. (E) Relative distribution of depolymerization rates leading to rescue (dashed line) compared with entire population (solid line) of the lattice-driven model. Error bars represent SD. (F) Relative distribution of depolymerization rates leading to rescue (dashed line) compared with entire population (solid line) from experimental data under 5 mM MgCl₂ conditions. Rescue data represent 165 depolymerization events from 112 microtubules; solid line represents entire population data consisting of 1283 depolymerization events from 1164 microtubules from five separate experiments at the following tubulin concentrations: 4.8, 5.4, 5.8, 7.0, 7.2 µM. (G) Average depolymerization rates from experimental data of microtubules at 5 mM MgCl₂, with or without 10 µM CaCl₂, showing catastrophes terminating at the seed (No Rescue) compared with those terminating at a rescue site within the lattice (Rescue). Significance determined by comparing rescue to no rescue for each condition as well as rescue across conditions. Bars represent mean ± 95% CI, at least 230 depolymerization events from at least three experiments from at the following tubulin concentrations: -CaCl₂: 4.8, 5.4, 5.8, 7.0, 7.2 µM; + CaCl₂: 5.3, 6.4, 6.9 µM. (H) Average polymerization rate constants from experimental observations of at least 275 microtubules for each condition at tubulin concentrations listed for G. (I) Average number of rescues per microtubule with and without 10 µM CaCl₂. Bars represent mean ± 95% CI from at least 275 microtubules over at least three separate experiments for each condition at tubulin concentrations listed for G. (J) Average rescue frequency calculated as events per depolymerization time. Bars represent mean ± 95% CI from at least 275 microtubules over at least three experiments per condition at tubulin concentrations listed for G. (K) Cumulative distribution of the length lost before rescue with and without CaCl₂ at tubulin concentrations listed for G. (L) Mean ± 95% CI of the rescue position relative to the catastrophe site. Position defined as the difference of microtubule length at catastrophe and length at rescue. Bars represent at least 39 length measurements from 25 microtubules from at least three separate experiments at tubulin concentrations listed for G. **: p ≪ 0.001; ns: not significant. Significance determined by Mann-Whitney U test (F–L) or Kolmogorov-Smirnov test (B–E).

We then tested the prediction that slower depolymerization rates would promote an end-driven stochastic rescue. Consistent with this prediction, the end-driven simulation showed that rescue events were preceded by significantly slower depolymerization rates (mean = 250.7, CI: 240.3–261.1 nm*s⁻¹) than the rates exhibited by the total population (288.1, CI: 283.8–292.3 nm*s⁻¹; Figure 3D). In contrast, we tested the prediction that if rescue were caused by a site embedded in the lattice, then the rate of depolymerization would have no impact on rescue. Consistent with this prediction, the lattice-driven simulation showed no difference in depolymerization rates preceding a rescue event compared with the total population (Figure 3E). We then sought to determine which model best fit our experimental data and found no difference in the depolymerization rates preceding a rescue event compared with the total population (mean = 274.5, CI: 243.73–305.3 nm*s⁻¹, compared with 289.8, CI: 276.7–302.8 nm*s⁻¹; Figure 3F). In this case, our experimental data are more consistent with the lattice-driven model.

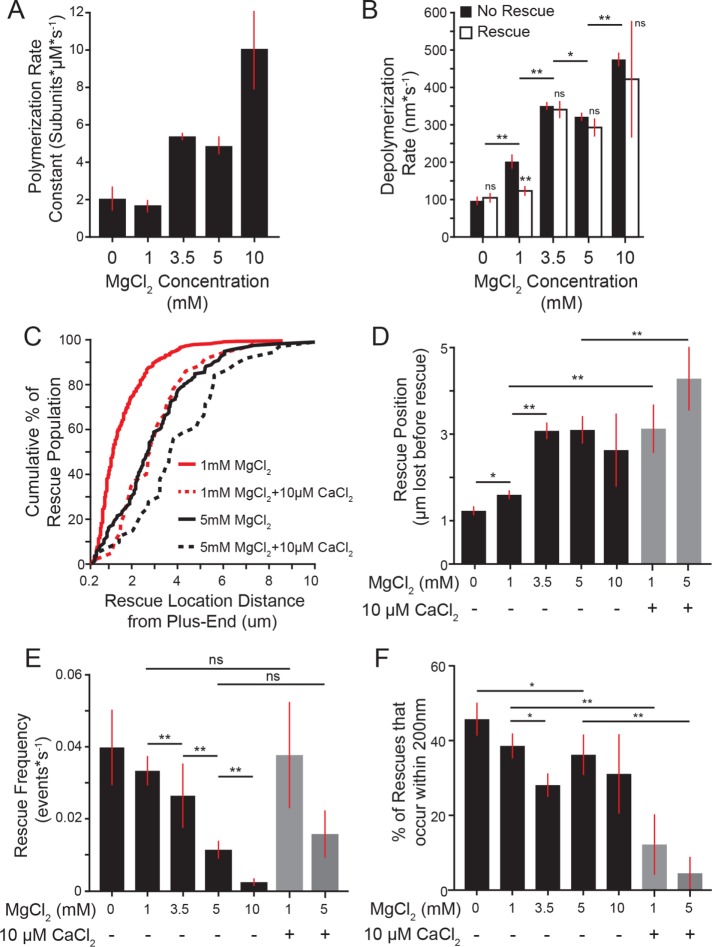
The results from our end-driven simulation showed that the average difference in depolymerization rates preceding rescue was ∼30 nm∙s⁻¹, which is at the edge of the detection threshold of our experiment. As an alternative approach, we tested the prediction that decreasing the time spent in depolymerization, by increasing the rate of depolymerization, would inhibit rescue. The divalent cation calcium (Ca²⁺) increases microtubule depolymerization rates (Rosenfeld et al., 1976; Herzog and Weber, 1977; Gal et al., 1988; O’Brien et al., 1997) without significantly altering polymerization rates (O’Brien et al., 1997). Adding 10 µM CaCl₂ to our experimental conditions significantly increased the depolymerization rate compared with control reactions (+CaCl₂: mean = 442.0, CI: 403.3–480.8 nm*s⁻¹ compared with no CaCl₂: 324.4, CI: 314.2 –334.9 nm*s⁻¹; Figure 3G), without altering the apparent polymerization rate constant (Figure 3H and Supplemental Figure 2). Under these conditions, we did not observe a significant change in the number of rescues per microtubule or the rescue frequency as a function of depolymerization time (Figure 3, I and J). However, we observed that more lattice was lost during depolymerization in the presence of 10 µM CaCl₂ before rescue occurred (Figure 3K). We calculated rescue position relative to catastrophe position as the difference of microtubule length at catastrophe and length at rescue, which we will refer to as rescue position. We found that adding CaCl₂ significantly shifted the position of rescue sites, causing more lattice loss before rescue (Figure 3L). These results suggest that depolymerization rate influences the position, but not the timing of rescue.

Rescues occur repeatedly at similar sites along the microtubule

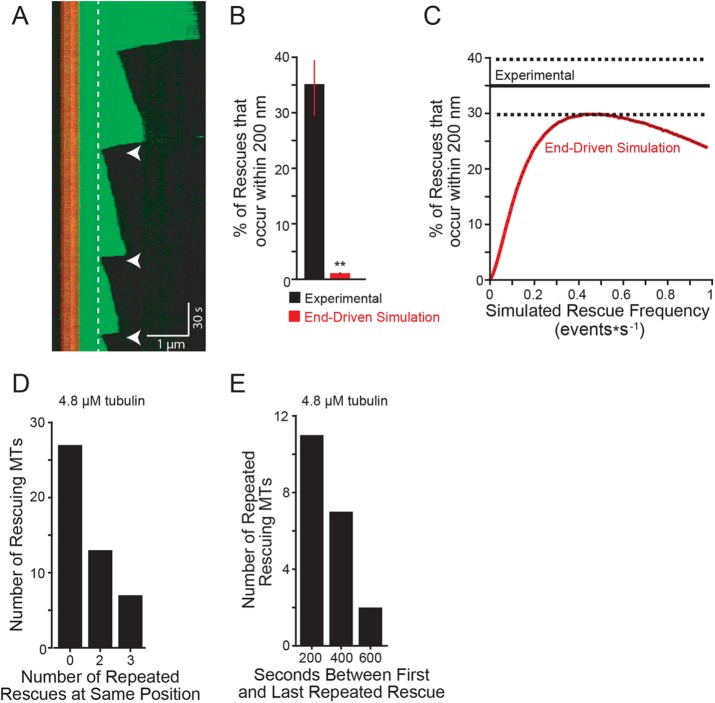
How might the position of rescue sites be determined? We predicted that if rescues were triggered by sites integrated into the lattice, then the same sites might exhibit multiple rescues in our experiments. Consistent with this prediction, we observed microtubules with multiple rescues at the same lattice position, as could be distinguished by our imaging system (i.e., ≤200 nm; Figure 4A, arrowheads). We termed these events “repeated rescues.” Applying this criterion to our experimental data, we determined that 34% of rescues will be followed by a repeated rescue, after the next catastrophe (Figure 4B). We used our simulation to test whether repeated rescues could be generated by an end-driven mechanism alone. Starting with our experimentally derived rescue frequency (0.01 events per second of depolymerization time), our end-driven simulation showed that <0.5% of rescues occurred within 200 nm of a previous rescue site (Figure 4B, red bar, and Table 2). We then asked what rescue frequency would be required to generate the repeated rescue behavior observed in our experiments. We ran multiple end-driven simulations, testing a range of rescue frequencies, and found that the overall rescue frequency must be ∼40× greater (i.e., 0.4 events per second of depolymerization time) to generate repeated rescue behavior that matches our experimental results (Figure 4C). This suggests that an end-driven model alone is highly unlikely to generate repeated rescues. The lattice is likely to play a determining role.

FIGURE 4:

Rescues occur repeatedly at similar sites along the microtubule. (A) Representative kymograph showing repeated rescue events (within 200 nm of previous rescue denoted with arrowheads. Dashed lines highlight the location of two separate rescue sites through time. Images were collected at 1-s intervals. Tubulin concentration: 5.6 µM using porcine brain tubulin purchased from Cytoskeleton; vertical scale bar: 30 s; horizontal scale bar: 1 µm. (B) Percent of rescues that occur within 200 nm of previous rescue site. Experimental data pooled from 105 total rescue events from five separate experiments at the following tubulin concentrations: 4.8, 5.4, 5.8, 7.0, 7.2 µM. Error bars are SEP. **: p ≪ 0.001; determined by Fishers exact test. (C) Percent of repeated rescues calculated with increasing rescue frequencies using the end-driven simulation (solid red line). Experimental data represented as mean (solid black line) ± SEP (dashed black lines). Sets of simulations were performed using 1000 microtubules per rescue frequency tested. Rescue frequencies were increased by 0.005 intervals between 0.01 and 0.99 events*s⁻¹. Plot represents the average percentage of microtubules with repeated rescue events from 10 separate simulation replicates of 20,000 microtubule seeds. Error bars in black represent SD; however, they are smaller than the mean line thickness. (D) Number of rescuing microtubules that exhibit zero, two, or three repeated rescues at the same lattice position. Experimental data are from microtubules assembled from 4.8 µM tubulin. (E) Observed time that repeated rescue sites persist during the image acquisition. Persistence time calculated by subtracting the time of the last observed rescue from the first rescue. Experimental data are from microtubules assembled from 4.8 µM tubulin.

TABLE 2:

Model simulation results.

Parameter	Lattice-driven model	End-driven model	Experimental
MTLength (µm)	3.0 (2.9–3.0)	3.1 (3.0–3.1)	2.8 (2.7–2.9)
% Repeated rescues	0.18	0.49	35

We then sought to characterize the persistence of repeated rescue sites. For this analysis we focused on data collected from microtubules assembled with 4.8 µM tubulin. Within this data set, 40% of microtubules that rescue go on to exhibit a second rescue at the same lattice position (Figure 4D). Furthermore, a subset of those microtubules went on to exhibit a third rescue at the same lattice position (Figure 4D). Our analysis also indicates that repeated rescue sites can be long-lived, with some events occurring up to 10 min after the first rescue at that lattice position (Figure 4E). Thus, specific regions of the microtubule lattice exhibit higher levels of “rescue activity,” which we simply define as the frequency at which depolymerizing microtubule ends are converted to a polymerizing state. This activity appears to decay on a timescale of minutes. Importantly, our experiments are limited to periods of 15-min image acquisition, and may therefore underestimate the longevity of repeated rescue sites.

Divalent cations suppress rescues

We next sought to identify factors that influence rescue sites. Recent work by Aumeier et al. (2016) reported microtubule rescues occurring closer to the site of catastrophe than we observed in our experiments thus far. An important difference between these experiments is the concentration of magnesium—whereas Aumeier et al. (2016) used polymerization buffer containing 1 mM MgCl₂, our polymerization buffer contains 5 mM MgCl₂. We therefore tested how changing the concentration of MgCl₂ impacts rescue. Consistent with previous studies, we find that rates of polymerization and depolymerization increase in proportion with the concentration of MgCl₂ in the reaction (Figure 5, A and B; Duellberg et al., 2016a; Fees and Moore, 2018). In addition, we find that rescues occur further from the site of catastrophe as magnesium concentration increases (1.4 ± 0.3 µm in 1 mM MgCl₂ compared with 3.0 ± 0.3 µm in 5 mM MgCl₂; mean ± 95% CI; Figure 5, C and D). In other words, higher magnesium increases the amount of the microtubule lattice that depolymerizes before rescue occurs. We further tested the impact of magnesium by titrating a range of MgCl₂ concentrations in the reaction buffer. Increasing MgCl₂ concentration inhibits rescue, as a function of both rescue position relative to the site of catastrophe and time in depolymerization (Figure 5, D and E). Adding 10 µM CaCl₂ also causes rescues to occur further from the site of catastrophe, even under low magnesium conditions (1 mM MgCl₂ + 10 µM CaCl₂; Figure 5, C and D); however, adding 10 µM CaCl₂ did not significantly alter rescue frequency as a function of depolymerization time (Figure 5E). This is likely attributable to differences in depolymerization rate, as 10 µM CaCl₂ increases the depolymerization rate by >150% (Figure 3G). These results suggest that divalent cations strongly influence the position of rescue sites.

FIGURE 5:

Divalent cations suppress rescues. (A) Polymerization rate constants for each concentration of magnesium tested. Plot represents mean ± 95% CI from pooled data of at least 32 polymerization events from at least 20 microtubules for increasing concentrations of tubulin from at least three separate experiments from the following tubulin concentrations: 0 mM MgCl₂: 5.3, 7.4, 10.5 µM; 1 mM MgCl₂: 4.4, 4.9, 5.0, 6.6, 7.1, 8.1, 8.8 µM; 3.5 mM MgCl₂: 5.2, 5.9, 7.1, 7.7 µM; 5 mM MgCl₂: 4.8, 5.4, 5.8, 7.0, 7.2 µM; 10 mM MgCl₂: 4.6, 5.1, 5.9, 6.9 µM. (B) Average depolymerization rate for each concentration of magnesium. Plots represent mean ± 95% CI. Data pooled from multiple tubulin concentrations listed for A. (C) Cumulative distribution of microtubule length lost before rescue. Lines are 5 mM MgCl₂ without (black) or with 10 µM CaCl₂ (black-dashed), and red lines are 1 mM MgCl₂ with and without 10 µM CaCl₂ (red and red-dashed, respectively). Each line represents at least 39 lengths from at least 25 microtubules pooled from at least three separate experiments from the following tubulin concentrations: 5 mM MgCl₂ − CaCl₂: 4.8, 5.4, 5.8, 7.0, 7.2 µM tubulin; 5 mM MgCl₂ + CaCl₂: 5.3, 6.4, 6.9; 1 mM MgCl₂ − CaCl₂: 4.4, 4.9, 5.0, 6.6, 7.1, 8.1, 8.8 µM tubulin; 1 mM MgCl₂ + CaCl₂: 4.8, 6.2, 8.8. (D) Rescue position relative to catastrophe site. Bars represent mean ± 95% CI from at least 39 length measurements from 25 microtubules, pooled from at least three separate experiments from the tubulin concentrations listed for A and C. (E) Rescue frequency as a function of depolymerization time. Bars represent mean ± SEP for each condition. Data pooled from at least 87 microtubules from at least three separate experiments from the tubulin concentrations listed for A and C. (F) Percent of rescues that occur repeatedly, as in Figure 4B. Bars represent mean ± SEP. (E) Significance determined by Fishers exact test. All other panels: significance determined by Mann-Whitney U test. *: p < 0.01; **: p ≪ 0.001; ns: not significant.

We then asked whether divalent cations alter repeated rescues in the lattice. We observed that increasing concentrations of MgCl₂ tends to decrease the frequency of repeated rescues (45% of rescues at 0 mM MgCl_2, compared with 25% of rescues at 3.5 mM MgCl₂; Figure 5F). Furthermore, adding 10 µM CaCl₂ strongly decreases the frequency of repeated rescues, even at low concentrations of MgCl₂ (Figure 5F). Together these results indicate that divalent cations suppress rescue.

Rescue activity is determined during depolymerization

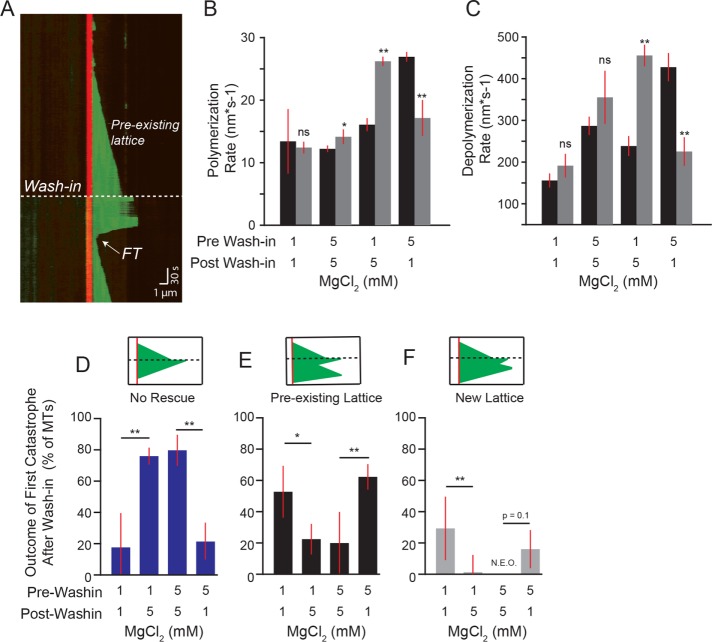
We reasoned that divalent cations could suppress rescue either by inhibiting the integration of rescue sites into the lattice or inhibiting their activity. To distinguish between these possibilities, we asked whether divalent cations influence rescues during the polymerization of the lattice or during depolymerization. We designed an experiment to isolate lattice polymerization from depolymerization by assembling microtubules under one set of reaction conditions, then rapidly exchanging the reaction buffer and testing how the preformed lattice behaves under different conditions (Figure 6A). These experiments differ from previously described “wash-out” experiments, in which the free tubulin was depleted from the reaction to halt further polymerization (Walker et al., 1988; Duellberg et al., 2016a; Fees and Moore, 2018). In contrast, our “wash-in” experiments maintain the same concentrations of tubulin, GTP, and oxygen scavenging buffer throughout the experiment; only the concentration of MgCl₂ is changed. Accordingly, we observed that after buffer exchange, microtubules continued to polymerize from the existing lattice at rates consistent with the present MgCl₂ concentration. Increasing or decreasing concentrations of MgCl₂ was sufficient to increase or decrease the polymerization and depolymerization rates, respectively (Figure 6, B and C). Control experiments where reaction buffers with the same concentration of MgCl₂ were washed in exhibited no difference in either polymerization or depolymerization rates (Figure 6, B and C).

FIGURE 6:

Rescue activity is determined during depolymerization. (A) Representative kymograph of wash-in experiment. Dashed line denotes the wash-in timepoint. Dashed line denotes the preexisting lattice before wash-in. The first termination site after wash-in (FT) denoted with arrow (see D–F). Image acquisition was paused during wash-in and resumed immediately afterward (see Materials and Methods). Images were collected at 1-s intervals. Tubulin concentration: 3.2 µM, pre-wash-in = 5 mM MgCl₂ and post-wash-in = 5 mM MgCl₂, vertical scale bar = 30 s and horizontal scale bar = 1 µm. (B) Polymerization rates of microtubules before (black bars) and after (gray bars) wash-in for each condition. Bars represent mean ± 95% CI of pooled data from at least 43 polymerization rates from 30 microtubules and a minimum of three separate experiments from the following tubulin concentrations: 5.3, 5.7, 5.9, 6.1, 6.3, 6.6, 6.9, 7.6, 8.0 µM. Significance denotes differences between rates before and after wash-in. (C) Depolymerization rates of microtubules before (black bars) and after (gray bars) wash-in for each condition from tubulin concentrations listed for B. (D) Percent of first catastrophes after wash-in that depolymerize to the stabilized seed and did not rescue. Bars in D–F represent mean ± SEP from data pooled from tubulin concentrations listed for B. (E) Percent of first catastrophes after wash-in that rescue within the preexisting lattice. (F) Percent of first catastrophes after wash-in that rescue within lattice added after wash-in. **: p ≪ 0.001; *: p < 0.05; ns: not significant. Significance determined by Fisher’s exact (D–F) and Mann-Whitney U test (B and C).

Using this experiment, we tested the prediction that if rescue is determined during the polymerization of the lattice, then microtubules grown under rescue-promoting conditions (1 mM MgCl₂) would be insensitive to the introduction of rescue-suppressing conditions (5 mM MgCl₂), and vice versa. We tested this prediction by examining the first catastrophe event after wash-in and asked whether and where along the lattice the microtubules rescue. Outcomes were classified into one of three groups: 1) no rescue, in which depolymerization reached the stabilized seed (Figure 6D); 2) rescue in a preexisting lattice, in which the microtubule rescued at a region of the lattice that was assembled before wash-in (Figure 6E); and 3) rescue in a new lattice, in which the microtubule rescued at a region of the lattice that was assembled after the wash-in (Figure 6F). Microtubules assembled in 1 mM MgCl₂ conditions (rescue-promoting) and then introduced to 5 mM MgCl₂ conditions (rescue-inhibiting) exhibited fewer rescues than controls that maintained 1 mM MgCl₂ (Figure 6D). In contrast, microtubules assembled in 5 mM MgCl₂ and then introduced into 1 mM MgCl₂ exhibited more rescues than controls that maintained 5 mM MgCl₂ (Figure 6D). Importantly, the majority of rescues after the introduction of 1 mM MgCl₂ occurred in regions of the lattice that were assembled before wash-in, in the presence of 5 mM MgCl₂ (Figure 6, E and F). Together these results suggest that rescue activity is not exclusively determined during the polymerization of the lattice.

DISCUSSION

In this study, we sought to elucidate the mechanisms of microtubule rescue by testing two models: 1) a lattice-driven model, in which rescue sites were integrated into the lattice, before depolymerization, and produced a rescue when the depolymerizing end returned to that site in the lattice; and 2) an “end-driven” model, in which the depolymerizing end of the microtubule stochastically switches to a stable state, resulting in rescue. Our data are consistent with rescue sites integrating into the lattice, supporting the lattice-driven model; however, we also found that changing the depolymerization conditions after lattice polymerization, by altering the concentration of divalent cations in the reaction buffer, was sufficient to alter rescue behavior. We therefore propose a unified model, in which the lattice contains defined sites that can promote rescue, but the activity of these sites may be regulated by conditions during depolymerization.

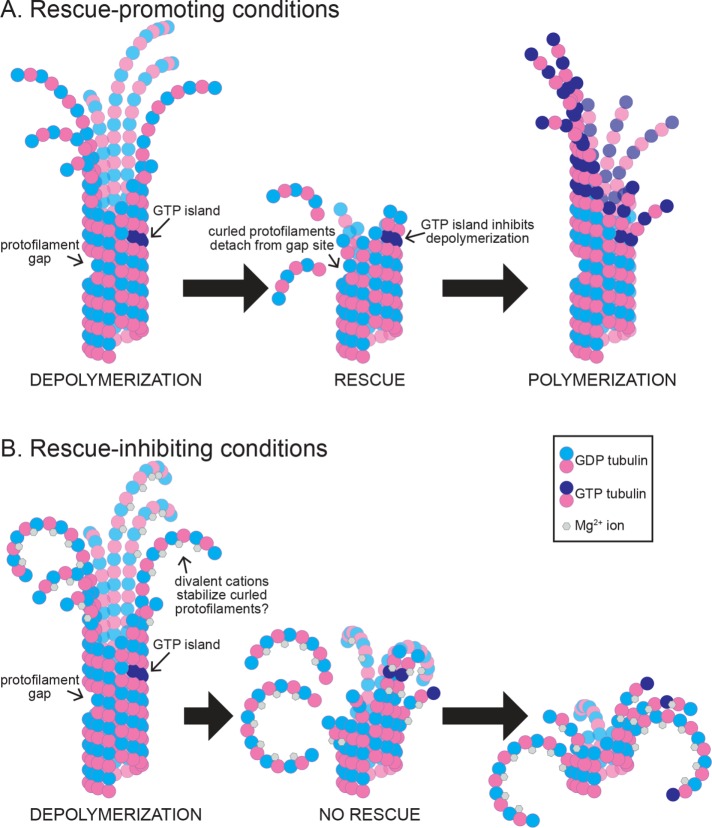
Figure 7 depicts models for how features of the lattice and depolymerizing end could stabilize an intermediate state of the microtubule end, between depolymerization and polymerization. We speculate that the depolymerizing microtubule end is a heterogeneous structure where individual protofilaments can visit different states of interactions with neighbors, curvature, and strain. In this model, states that enhance lateral interactions, reduce curvature, and/or reduce strain could lead to rescue. In addition, sites in the lattice could promote rescue by blocking the propagation of strain from the outwardly curled protofilament to the lattice. In this way, heterogeneous regions of existing microtubule lattice disrupt depolymerization and promote the return to a polymerizing state.

FIGURE 7:

Rescue activity is determined during depolymerization. (A) Under rescue-promoting conditions, depolymerization is inhibited by rescue sites in the microtubule lattice, and the microtubule end returns to a polymerizing state. These sites may include, but are not limited to, regions of missing subunits (i.e., “protofilament gaps”) and subunits that maintain GTP at the E-site (i.e., “GTP islands”). (B) Under rescue-inhibiting conditions, divalent cations promote depolymerization and inhibit the activity of rescue sites in the lattice. Here we depict a proposed role for magnesium ions in promoting the outward curling of protofilaments.

The lattice-driven model is supported by several lines of evidence from previous studies, including the observation of apparent “GTP islands”—regions of the lattice distal from the plus end that bind a GTP-tubulin–specific antibody (Dimitrov et al., 2008). These islands were shown to correlate with sites of rescue, suggesting that regions of incomplete GTP hydrolysis may stabilize the microtubule lattice to promote rescue (Dimitrov et al., 2008). Along these lines, Tropini et al. (2012) demonstrated that adding small amounts of a nonhydrolyzable GTP analogue (GMPCPP) to microtubules assembling in GTP could increase the frequency of rescues. Finally, recent work has shown that rescue events correlate with regions of microtubule repair, where new GTP-tubulin incorporates into sites along the lattice following mechanical damage (Aumeier et al., 2016). Our strongest evidence in support of the lattice-driven model comes from our observation of repeated rescue sites, which show successive rescues within the same region of lattice (Figure 4). Our simulations indicate that such behavior is not likely to arise from a stochastic rescue mechanism; therefore, the lattice at the repeated rescue site possesses a persistent, rescue-promoting activity. The exact nature of these repeated rescue sites in our experiments is uncertain, but clearly does not require the addition of nonhydrolyzable nucleotide analogues or the induction of mechanical damage to microtubules. Those conditions may increase rescues, but they are not necessary for rescues to occur.

An important question that has not been addressed by previous studies is how long rescue sites remain active and what are the requirements for activity. In an effort to measure the lifetime of repeated rescue sites, we attempted to quantify the period of time over which repeated rescues can occur; however, we were only able to capture the complete lifetime of a few microtubules with repeated rescue sites. Although sampling issues limit our ability to make general conclusions about the lifetime and activity of repeated rescue sites, two key points emerge from our observations. First, rescue sites do not always promote repeated rescues. Out of all rescue sites that we observed, only 35% exhibited a second rescue when a subsequent catastrophe returned the depolymerizing end to that same position (Figure 4). Furthermore, when we did observe two rescues at the same position, 43% of these microtubules went on to exhibit a third rescue while 57% failed to rescue again (Figure 4D). Second, rescue sites can promote repeated rescues over a relatively long period of time. We observed rescues occurring at a similar lattice site as soon as 30 s after a previous rescue, or up to 612 s later (Figure 4E). This indicates that sites can maintain high rescue activity over a period of time that is much longer than the expected lifespan of GTP at the exchangeable site (i.e., “E-site”) of tubulin under our reaction conditions. In addition, we observed rescues occurring all along the length of the lattice, without bias toward the GTP-rich plus end (Figure 5). These observations lead us to speculate that alternative lattice heterogeneities, independent of nucleotide state, could promote rescue activity. For example, previous work has shown that the microtubule lattice can transition between different numbers of protofilaments along its length, which could create a region of lattice where protofilaments are “missing” and the remaining protofilaments lack laterally bound neighbors (Chrétien et al., 1992). We speculate that such an environment could disrupt the depolymerizing end by uncoupling the strain of outwardly curling protofilaments from subunits in the lattice (Figure 7).

Although our results are consistent with the presence of rescue sites in the lattice, we also show that the formation of these sites is not sufficient to explain rescue activity. Our wash-in experiments provide the best evidence that depolymerization conditions determine rescue activity more strongly than lattice polymerization conditions. By observing the same microtubules under alternating rescue-promoting or -inhibiting conditions, we found that introducing rescue-promoting conditions during depolymerization is sufficient to recapitulate the rescue behavior of control microtubules that are constitutively exposed to rescue-promoting conditions (Figure 6). Thus, a preexisting microtubule can acquire higher rescue activity without assembling new lattice under rescue-promoting conditions. The key to these experiments was our finding that the divalent cations magnesium and calcium have potent effects on rescue activity. We conclude that the rescue activity of depolymerizing microtubules is strongly influenced by changes in the ionic environment.

We speculate that high concentrations of divalent cations alter the structure of the depolymerizing end to inhibit rescue. Divalent cations, like calcium and magnesium, are known to play important roles in microtubule dynamics. Magnesium promotes polymerization and depolymerization, and some of these roles are related to effects on GTP-binding and exchange (Huang et al., 1985; Correia et al., 1987; Lin and Hamel, 1987; O’Brien et al., 1990). However, magnesium also binds tubulin at additional sites outside of the GTP-binding pockets (Frigon and Timasheff, 1975; Lee and Timasheff, 1975; Lee et al., 1978; Na and Timasheff, 1986). Hence, magnesium may have additional roles in regulating tubulin activity. We have shown here that both magnesium and relatively small concentrations of calcium (estimated 1 nM free calcium; see Materials and Methods; Bers et al., 2010) can drastically increase depolymerization rates, consistent with previous work (O’Brien et al., 1997; Duellberg et al., 2016b; Fees and Moore, 2018). We also show that both cations are potent inhibitors of microtubule rescue (Figure 5). Although it is possible that divalent cations directly inhibit the activity of rescue sites within the lattice, we favor an alternative hypothesis, which is not mutually exclusive, that divalent cations inhibit rescue by altering how microtubules depolymerize. During depolymerization, the protofilaments of a microtubule curl away from the lattice (Mandelkow et al., 1991), which would bring the negatively charged regions on the outer surface of tubulin subunits into close proximity (Figure 7). Divalent cations could stabilize the outwardly curled conformation of the depolymerizing end by bridging the negatively charged side chains on the outer surface of tubulin (Figure 7). Consistent with this notion, previous work has shown that increased concentrations of magnesium and calcium promote greater protofilament curling by high-resolution cryo-EM (Tran et al., 1997). Interestingly, this finding is specific to divalent cations, as monovalent cations have no effect on protofilament curling, suggesting that multivalent ions may be acting as a bridge during depolymerization (Tran et al., 1997). Furthermore, we have shown previously that magnesium promotes depolymerization in a manner that requires the negatively charged C-terminal tail (CTT) domain of β-tubulin (β-CTT; Fees and Moore, 2018). Interestingly, we observed that removing the β-CTT slows depolymerization and also promotes microtubule rescue, mimicking the effect of low magnesium (unpublished data; Fees and Moore, 2018). Therefore, divalent cations may inhibit rescue by binding the negatively charged CTTs and promoting a conformation of the depolymerizing end that favors depolymerization. Further studies are needed to determine how CTTs could change the activity or abundance of rescue sites in the lattice.

Our findings on the intrinsic rescue behavior of tubulin proteins could be extended to cells, where extrinsic proteins may further regulate rescue by binding and selectively stabilizing structural intermediates at the depolymerizing end and/or rescue sites in the lattice. For example, CLASP proteins promote rescue and suppress catastrophe, however, with only a modest effect on polymerization and depolymerization rates (Lawrence et al., 2018). CLASP’s ability to promote rescue requires both binding along the microtubule lattice and its TOG domains (Bratman and Chang, 2007; Al-Bassam et al., 2010). It is possible that CLASP is facilitating rescue by binding the lattice and using its TOG domains to promote a conformational state of tubulin that favors rescue (Al-Bassam et al., 2010; Aher and Akhmanova, 2018; Lawrence et al., 2018). CLIP-170 proteins also promote rescue, and localize to both microtubule ends and to “GTP islands” in the microtubule lattice (Komarova et al., 2002; Arnal et al., 2004; de Forges et al., 2016). Interestingly, the N-terminal microtubule-binding domain of CLIP-170 is sufficient to promote rescues in vivo (Komarova et al., 2002). When combined with purified tubulin in vitro, the N-terminal domain promotes rescue and induces the formation of curved tubulin oligomers at microtubule ends and in solution, hinting that the rescue mechanism may be linked to the stabilization of specific protofilament structures (Arnal et al., 2004). Further investigations of how these and other regulators that promote rescue could yield important insights into the structure of a rescuing microtubule end, the nature of rescue sites in the lattice, and how these may be related.

MATERIALS AND METHODS

Chemicals and reagents were from Fisher Scientific (Pittsburgh, PA) and Sigma-Aldrich (St. Louis, MO), unless stated otherwise.

Tubulin purification

Tubulin was purified as previously described (Waterman-Storer, 1998). Briefly, porcine brain tissue was isolated, cleaned, and homogenized using a stainless-steel blender. The homogenized slurry was clarified by ultracentrifugation at 100,000 × g for 1 h. The tubulin heterodimers were purified by the well-characterized double-cycling protocol; microtubules were assembled at 37°C for 1 h and then the pellet was collected after centrifugation. The collected microtubule pellet was depolymerized on ice for 1 h after which the clarified supernatant was collected following another centrifugation. This process was performed twice. The double-cycled protein was further purified by liquid chromatography using a phosphocellulose anion-exchange column prepared as described previously (Waterman-Storer, 1998). We confirmed the activity of our purified protein by purchasing commercially available tubulin (Cytoskeleton, Denver, CO; Cat: T238P) and testing it under the same conditions.

In vitro microtubule dynamics assays

Assays to measure microtubule dynamics by TIRF microscopy were based on previously described methods (Gell et al., 2010; Fees and Moore, 2018). Double-cycled microtubule seeds were assembled by incubating 20 µM rhodamine tubulin (Cytoskeleton, Denver, CO) in BRB80 buffer (80 mM PIPES brought to pH 6.9 with KOH, 1 mM ethylene glycol tetraacetic acid [EGTA], 1 mM MgCl₂; minor pH adjustments were made with NaOH) with 1 mM GMPCPP at 37°C for 30 min. Sample was then centrifuged at 100,000 × g for 10 min at 30°C and the supernatant was removed. Pellet was suspended in 0.8× starting volume of ice-cold BRB80 buffer to depolymerize labile microtubules. An additional 1 mM GMPCPP was added and microtubules were polymerized at 37°C for 30 min and pelleted again. The pellet was suspended in 0.8× starting volume warm BRB80. The reaction was then gently pipetted 8–10 times to shear the microtubules, aliquoted into 1 µl volumes, and either used immediately or snap frozen and stored at −80°C.

Imaging chambers were assembled using 22 × 22 mm and 18 × 18 mm coverslips. The coverslips were cleaned and silanized as previously described (Gell et al., 2010; Fees and Moore, 2018). The prepared glass coverslips were stored in desiccators at room temperature until used. The coverslips were mounted in a custom fabricated stage insert and sealed with melted strips of parafilm. GMPCPP-stabilized microtubule seeds were affixed to coverslips using anti-rhodamine antibodies (Fisher Scientific; Cat# A-6397; diluted 1:50 in BRB80). Chambers were flushed with 1% pluronic-F127 in BRB80 to prevent other proteins from adhering to the glass and equilibrated with an oxygen scavenging buffer (40 mM glucose, 1 mM trolox, 64 nM catalase, 250 nM glucose oxidase, 10 mg/ml casein) before free tubulin addition. The imaging buffer consisting of unpolymerized tubulin (15–20% HiLyte 488–labeled tubulin [Cytoskeleton] and 80–85% unlabeled porcine brain tubulin), 5 mM MgCl₂, 1 mM GTP, the oxygen scavenging buffer, and BRB80–50 µl volume was then flowed into the imaging chambers. The chamber was sealed with VALAP (1:1:1 Vaseline, lanolin, paraffin wax) and warmed to 37°C using an ASI400 Air Stream Stage Incubator (Nevtek, Williamsville, VA) for 5 min before imaging. Temperature was verified using an infrared thermometer.

For experiments testing the impact of calcium on rescue activity, 10 µM CaCl₂ was added to the imaging buffer before chamber assembly. We used MaxChelator (maxchelator.stanford.edu) to estimate the concentration of free calcium in these reactions using theoretical values for ionic and chelator concentrations, pH, and temperature. At standard conditions plus calcium (5 mM MgCl₂, 10 µM CaCl₂, 1 mM EGTA, and 1 mM GTP at pH 6.9 and 37°C) it is estimated that more than 99.9% of the Ca²⁺ is bound to EGTA.

Images were collected on a Nikon Ti-E microscope equipped with a 1.49 NA 100× CFI160 Apochromat objective, TIRF illuminator, OBIS 488-nm and sapphire 561-nm lasers (Coherent, Santa Clara, CA), and an ORCA-Flash 4.0 LT sCMOS camera (Hamamatsu Photonics, Japan), using NIS Elements software (Nikon, Minato, Tokyo, Japan). Images were acquired using two-channel, single-plane TIRF, at 1-s intervals.

Image analysis

Images were analyzed using a custom-made MATLAB program as described previously (Fees and Moore, 2018). Briefly, seeds were identified by thresholding image intensity and used to segment the images along the axis of the microtubule. Images were then automatically cropped to 4 pixels above and below the microtubule axis and then the max intensity projection for each timepoint were stacked to generate kymographs for analysis.

Polymerization and depolymerization rates were calculated by measuring the changes in microtubule length and time from the first and last points of the individual polymerization and depolymerization events from the kymographs. Polymerization rate constants were estimated as the slope of the polymerization rate linear model. Depolymerization rate constants were determined similarly but using the median depolymerization rate (µm*min⁻¹) from all tubulin concentrations pooled.

Rescue and catastrophe frequencies were calculated as the quotient of the number of transitions and depolymerization or polymerization duration, respectively. Rescue abundance was determined by dividing the number of unique rescue events by the total length lost during depolymerization. Unique rescue events were defined as rescue sites separated by at least 200 nm from previous rescue sites on the microtubule lattice. Rescue position relative to the plus end was calculated as the difference between microtubule length at catastrophe and length at rescue.

Tubulin wash-in experiments

For wash-in experiments, GMPCPP-seeded imaging chambers were similarly assembled, but not sealed with VALAP. Imaging chambers were warmed on the stage for 3–5 min, allowing the temperature to equilibrate to 37°C, and then dynamic microtubules were imaged for 10 min before the imaging chamber was flushed with 4–5× chamber volumes of warm reaction buffer. Image acquisition was paused during the chamber flush and resumed immediately afterward. The average wash-in duration for all wash-in experiments was ∼60 s from time of acquisition pause to resumption.

Images were processed as described above, with the addition of postacquisition image stabilization that was used to reduce minor XY drift during image acquisition using the image stabilizer plug-in for ImageJ (Li, 2008).

Determining tubulin concentration

For each experiment, the tubulin concentration was determined by running a sample of the imaging buffer containing unpolymerized tubulin on a 10% bis-Tris SDS–PAGE gel, followed by staining with Coomassie blue. The concentration was determined by densitometry, directly compared with standard curve made from bovine serum albumin standards run on the same gel.

Monte Carlo simulations

Microtubule dynamics were simulated using a custom-made MATLAB program. Microtubules were modeled as an individual linear filament nucleated from a single “seed” that would grow and shrink consistent with experimental observations. The output of the simulation modeled changes in microtubule length over time. Time was calibrated to 1 s for these simulations. Simulated length changes were determined by confined random sampling of polymerization and depolymerization rates at experimentally observed frequencies. The upper and lower limits of these rates were defined as the max and min of the experimentally observed rates, respectively. Simulated microtubule transition frequencies were similarly applied. The simulations sampled a range of tubulin concentrations (5−8 µM) to be consistent with experimental data.

Rescues were simulated stochastically and differed slightly between the two models. For the end-driven model, rescue events were constrained to occur stochastically only during depolymerization at a frequency consistent with the experimentally observed rescue frequency. For the lattice-driven model, rescues were simulated as sites incorporated into the growing microtubule at an empirically derived frequency. Following catastrophe, a rescue event was triggered as the depolymerizing end approached the incorporation site within 100 nm. For simplicity, we modeled rescue sites to result in only a single rescue event per site once incorporated into the lattice. The simulated microtubule lengths were analyzed as experimental data.

Abbreviations used:

CI

confidence interval

CTT

carboxy-terminal tail

cryo-EM

cryo-electron microscopy

β-CTT

β tubulin carboxy-terminal tail

GMPCPP

guanosine-5’-[(α,β)-methyleno]triphosphate

GTP

guanosine triphosphate

K_c

catastrophe frequency

K_i

incorporation frequency

K_r

rescue frequency

TIRF

total internal reflection fluorescence

V_g

growth velocity

V_s

shrinking velocity