Lymphatic endothelial cell calcium pulses are sensitive to spatial gradients in wall shear stress

Abstract

Cytosolic calcium (Ca²⁺) is a ubiquitous second messenger that influences numerous aspects of cellular function. In many cell types, cytosolic Ca²⁺ concentrations are characterized by periodic pulses, whose dynamics can influence downstream signal transduction. Here, we examine the general question of how cells use Ca²⁺ pulses to encode input stimuli in the context of the response of lymphatic endothelial cells (LECs) to fluid flow. Previous work shows that fluid flow regulates Ca²⁺ dynamics in LECs and that Ca²⁺-dependent signaling plays a key role in regulating lymphatic valve formation during embryonic development. However, how fluid flow might influence the Ca²⁺ pulse dynamics of individual LECs has remained, to our knowledge, little explored. We used live-cell imaging to characterize Ca²⁺ pulse dynamics in LECs exposed to fluid flow in an in vitro flow device that generates spatial gradients in wall shear stress (WSS), such as are found at sites of valve formation. We found that the frequency of Ca²⁺ pulses was sensitive to the magnitude of WSS, while the duration of individual Ca²⁺ pulses increased in the presence of spatial gradients in WSS. These observations provide an example of how cells can separately modulate Ca²⁺ pulse frequency and duration to encode distinct forms of information, a phenomenon that could extend to other cell types.

INTRODUCTION

Calcium (Ca²⁺) is a universal secondary messenger that exerts profound effects on cell proliferation, contractility, migration, and transcriptional regulation (Clapham, 2007). In mammalian cells, cytoplasmic Ca²⁺ concentrations are kept low (100 nM) relative to the extracellular environment. In many cell types, Ca²⁺ release into the cytoplasm is transient, as pumps in the endoplasmic reticulum and plasma membrane continually remove Ca²⁺ from the cytoplasm (Clapham, 2007; Smedler and Uhlén, 2014). As a result, Ca²⁺ signaling is driven not only by changes in average cytosolic concentrations, but also by the frequency of individual Ca²⁺ pulses (Dolmetsch, Xu, and Lewis, 1998; Smedler and Uhlén, 2014). The rich temporal dynamics that characterizes Ca²⁺ signaling can in principle provide the cell with the opportunity to encode multiple forms of information in, for example, Ca²⁺ pulse frequency and duration. Whether this in fact occurs is, to our knowledge, little explored.

Fluid flow is thought to play a central role in patterning the developing blood and lymphatic vasculatures (Dixon et al., 2006; Sabine et al., 2012, 2015; Planas-Paz and Lammert, 2013; Baeyens et al., 2015; Jafarnejad et al., 2015; Kornuta et al., 2015; Sweet et al., 2015; Cha et al., 2016; Fatima et al., 2016). Lymphatic endothelial cells (LECs) line lymphatic vessels and experience a wide range of flow-induced wall shear stresses (WSSs) depending on the local vessel geometry. Previous work indicates that WSS may regulate both the growth of lymphatic vessels (lymphangiogenesis) and the deve­lopment of lymphatic valves (Dixon et al., 2006; Sabine et al., 2012, 2015; Planas-Paz and Lammert, 2013; Baeyens et al., 2015; Jafarnejad et al., 2015; Kornuta et al., 2015; Sweet et al., 2015; Cha et al., 2016; Fatima et al., 2016; Choi et al., 2017a,b). Interestingly both lymphatic and venous valves form preferentially near vessel constrictions and junctions, areas that feature large spatial variations in WSS, here termed WSS gradients (WSSGs) (Kampmeier and La Fleur Birch, 1927; Bazigou et al., 2009; Sabine et al., 2012; Planas-Paz and Lammert, 2013). However, how and whether WSSGs may act to regulate the timing and location of valve formation remains poorly understood.

Ca²⁺-dependent signaling provides a potential link between the physical stimulus provided by fluid flow and the regulation of lymphatic development (Sabine et al., 2012; Choi et al., 2017a,b). The Ca²⁺ release–activated channel (CRAC) ORAI1 is required for lymphangiogenesis in mouse embryos (Choi et al. 2017b), and inhibition of ORAI1 with SKF-96365 in LECs in vitro blocks activation of Klf2, a transcription factor that is both activated in response to WSS and required for cellular reorientation with WSS (Choi et al. 2017a). The activity of ORAI1 is subject to Ca²⁺-dependent feedback that is mediated in part by STIM1, a protein that senses Ca²⁺ levels in the endoplasmic reticulum (Soboloff et al., 2006; Choi et al. 2017a; Cai et al., 2018). Previous experiments indicate that WSS, and temporally varying WSS in particular, also leads to the activation of the Ca²⁺-dependent phosphatase calcineurin (Sabine et al., 2012). Calcineurin dephosphorylates the transcription factor Nuclear Factor of Activated T Cells cytoplasmic 1 (NFATc1), allowing it to accumulate in the nucleus (Clapham, 2007; Sabine et al., 2012), where it participates in the initiation of valvulogenesis (Dixon et al., 2006; Kulkarni et al., 2009; Vittet, 2014; Kornuta et al., 2015). NFAT-dependent transcriptional regulation can in turn potentially influence Ca²⁺ signaling: in hippocampal cells, Ca²⁺-mediated activation of NFATc4 triggers the transcription of inositol 1,4,5-trisphosphate (IP3) receptor type1 (IP3R1), further elevating cytoplasmic Ca²⁺ (Crabtree, 2001). Such feedback loops can in principle be rapid on the time scale of development: both NFAT and NF-κB, a transcription factor thah like NFAT is known to be sensitive to Ca²⁺ cytoplasmic levels (Dolmetsch et al., 1997; Smedler and Uhlén, 2014), relocalize to the nucleus in minutes in response to WSS (Yissachar, Sharar Fischler, et al., 2013; Zhao et al., 2018).

Although previous studies have examined Ca²⁺ signaling in LECs in response to spatially uniform WSS, little is known about how gradients in WSS may specifically regulate Ca²⁺ signaling. Further, to our knowledge, no previous study has characterized the dynamics of Ca²⁺ signaling in LECs at the individual cell level. Previously, we developed an impinging flow chamber (IFC) that imparts controlled WSSGs to adherent cells grown in a standard six-well tissue culture plate (Ostrowski et al., 2014, 2015; Nakayama et al., 2016; Surya et al., 2016; Chang et al., 2017). In this study, we used this device to determine how Ca²⁺ pulse dynamics in individual LECs respond to both the WSS magnitude and gradients in WSS. We found that both aspects of flow regulate Ca²⁺ pulse dynamics, and that WSSGs in particular increase Ca²⁺ pulse duration relative to uniform WSS. These and other observations indicate that both WSS magnitude and WSSGs can act as physical cues to regulate Ca²⁺ dynamics in LECs, suggesting that WSSGs provide a spatial cue that can potentially act to confine valvulogenesis to vessel constrictions and junctions.

RESULTS

Examination of Ca²⁺ pulse dynamics in human lymphatic microvascular endothelial cells subjected to a WSSG

In this study, we sought to investigate how WSS and WSSGs might modulate Ca²⁺ dynamics in LECs. To do so, we subjected human lymphatic microvascular endothelial cells (HLMVECs) to impinging flow, which generates a spatial WSSG that approximates the WSSGs found at a lymphatic vessel branch (Figure 1, A–C). LECs in vivo are likely exposed to 0–10 dyn/cm² (Dixon et al., 2006). To fully characterize the response of these cells to WSS and WSSGs, we employed WSSs ranging from 0 to 72 dynes/cm². We reasoned that characterizing the response of cells to as wide a range in WSSs as possible would be valuable in understanding their response to fluid flow: an analogy would be treating cells with a wide range of concentrations of a soluble signaling factor in order to understand how it influenced intracellular signal transduction.

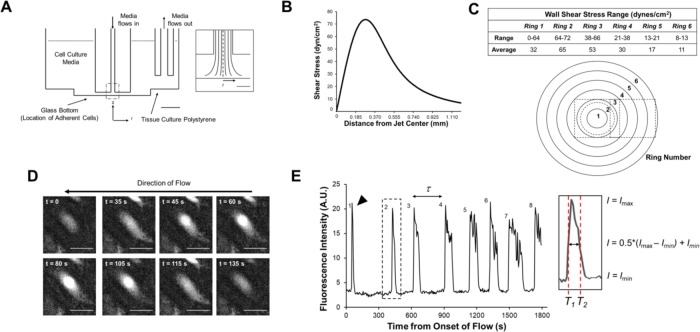
FIGURE 1:

Measuring Ca²⁺ pulse dynamics using the IFC. (A) A cross section showing to scale the location of the jet orifice, which is submerged in medium inside each well. Scale bar, 5 mm. Inset: The dashed region of impinging flow in A. The shear stress profile is axisymmetric about r = 0. Scale bar, 500 μm. Adapted from Ostrowski et al. (2015). (B) WSS is plotted as a function of distance from the jet center at a flow rate of 4.5 ml/min. (C) Cells are binned by their position into one of six concentric 185-μm rings. The table summarizes the range and average WSS values for each ring. On the schematic, the dashed circle represents the location of the maximum WSS (72 dyn/cm²) and the dashed squares represent the regions of image acquisition. (D) Fluorescence micrographs of a Ca²⁺ pulse for a representative HLMVEC (black triangle, E). In this example, a pulse begins soon after the onset of impinging flow (t = 0 s) and rises to a peak at t = 80 s. (E) Fluorescence intensity versus time for the cell shown in D, with the black triangle indicating the first observed pulse. The pulse count (i.e., how many pulses occur within the 30-min experimental time) and peak-to-peak period (τ, time between successive peaks) were determined for individual cells. The pulse duration was measured by calculating the full width at half maximum (FWHM) by measuring the difference in times T₁ and T₂ at half-maximum intensity.

In other systems, pulse frequency often reflects the strength of a Ca²⁺-activating stimulus; that is, increasing the external stimulus results in an increase in the Ca²⁺ pulse count (Smedler and Uhlén, 2014). In contrast, the pulse duration, here determined as the Ca²⁺ pulse full width at half maximum (FWHM), can reflect the signaling pathway(s) present in the cell that indirectly regulate Ca²⁺ influx and efflux (Smedler and Uhlén, 2014). The pulse duty cycle (DC), defined as the fraction of the time that cytosolic Ca²⁺ is above its baseline concentration, provides an alternate measure of the Ca²⁺ activation, with increasing DC values indicative of a stronger activation of Ca²⁺-dependent signal transduction. Here, we used live-cell recordings to quantify Ca²⁺ pulse count, peak-to-peak period, and pulse full width at half maximum (pulse duration; FWHM) for individual cells (Figure 1, D and E; Supplemental Movies S1–S4). These data were binned by position with reference to the center of the jet orifice (r = 0). We also examined whether exposure to impinging flow triggered the nuclear localization of NFATc1, an event that occurs in response to Ca²⁺-dependent signaling (Kulkarni et al., 2009; Norrmén et al., 2009; Sabine et al., 2012; Smedler and Uhlén, 2014). As expected, we observed that nuclear NFATc1 was higher in HLMVECs exposed to impinging flow than in cells under no flow, indicative of downstream signaling in response to flow-activated Ca²⁺ pulses (Supplemental Figure S1).

Movie S1.

Download video file ^{(5.1MB, mp4)}

HLMVEC Ca²⁺ dynamics in the IFC, recorded for 30 minutes starting from the onset of flow at t = 50 s. Regions corresponding to Rings 1 and 2 are shown, which have average WSSs of 32 and 65 dyn/cm², respectively. The flow direction is radially outward and symmetric about the jet center at the center of Ring 1. Frames were recorded every 5 seconds. Scale bar, 100 μm.

Movie S2.

Download video file ^{(5.1MB, mp4)}

HLMVEC Ca²⁺ dynamics as in Movie 1 for Rings 2 ‐ 6, which have average WSSs of 65, 53, 30, 17 and 11 dyn/cm². The flow direction is radially outward and here is roughly from left to right. Frames were recorded every 5 seconds. Scale bar, 100 μm.

Movie S3.

Download video file ^{(5.2MB, mp4)}

HLMVEC Ca²⁺ dynamics for cells exposed to uniform WSS (parallel plate flow), recorded for 30 minutes from the onset of flow at t = 50 s. Here, all HLMVECs experience a WSS of 50 dyn/cm². The flow direction is from the bottom of the video to the top. Frames were recorded every 5 seconds. Scale bar, 100 μm.

Movie S4.

Download video file ^{(5.2MB, mp4)}

HLMVEC Ca²⁺ dynamics under no flow conditions, recorded for 30 minutes. Frames were recorded every 5 seconds. Scale bar, 100 μm.

We found that Ca²⁺ pulse dynamics was heterogeneous: some cells pulsed repeatedly, while others either did not pulse or pulsed once in the 30-min observation window. For cells that pulsed, the first pulse often corresponded roughly to the onset of flow at the beginning of the experiment; this initial pulse was shorter for cells that went on to pulse multiple times (termed P or periodic cells) than for cells that only pulsed once in the 30-min observation window (termed NP or nonperiodic; see Supplemental Figure S2). For P cells, subsequent pulses were longer in duration than that initial pulse, but only in the presence of a WSSG (Figure 2). This trend held for the subset of P cells that pulsed three or more times, suggesting that the initial pulse was indeed distinct from subsequent ones, though only for cells exposed to a WSSG (Supplemental Figure S3). In contrast, there were no significant differences in the duration of initial vs. subsequent Ca²⁺ pulses in the absence of flow. Together, these findings suggest that Ca²⁺ dynamics are both WSS- and WSSG-sensitive.

FIGURE 2:

HLMVEC Ca²⁺ pulse durations are sensitive to WSS magnitude and WSSGs in cells that pulse repeatedly. Plots represent the cumulative distribution functions (CDFs) for individual pulse durations (measured as FWHM) for P cells. The initial pulse (first pulse, FP) is shown in red, while all subsequent pulses (second, third, etc., SP) are shown in black. Dotted lines are fits to the Weibull distribution (see text). Pulse duration distributions are portrayed for Rings 1–6 (A–F), spatially uniform WSS (parallel plate chamber, G), and no flow (H). The scale (β) and shape (κ) parameters for fits to the Weibull distribution and the average pulse durations (FWHM; μ) are presented at the bottom of each graph. Experiments were performed in triplicate. Asterisks indicate statistically significant differences in CDFs as determined using the Kolmogorov–Smirnov test (n.s., not significant; *, p < 0.05; **, p < 10^–4; ***, p < 10^–7).

Ca²⁺ pulse count scales with local WSS

Ca²⁺ pulse frequency is often used as a reporter for the strength of upstream signaling activators, with increasing pulse frequency being indicative of a stronger stimulus (Smedler and Uhlén, 2014). We therefore sought to determine the role of WSS and WSSGs in modulating Ca²⁺ pulse frequency. Of the models tested, we found that a hierarchical gamma (Γ) Poisson model provided the best fit to the cumulative distribution of the number of pulses produced by the total population of cells in a 30-min time window (Figure 3). This model functions analogously to a Poisson distribution, but with an average time between pulses that varies across individual cells according to a Γ distribution. Thus, this distribution can be used to characterize underlying heterogeneity that would be absent in a standard Poisson distribution.

FIGURE 3:

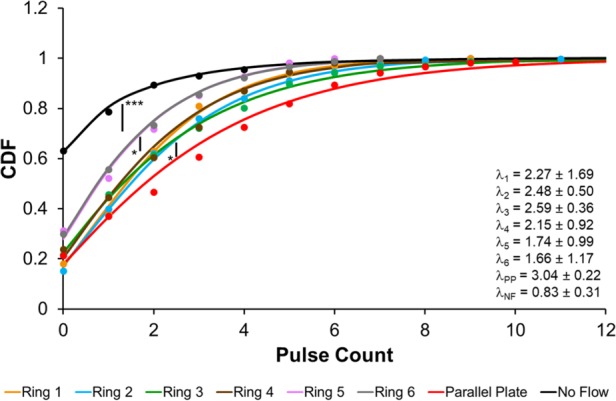
Ca²⁺ pulse count is WSS- and WSSG-dependent. CDF plots of Ca²⁺ pulse counts for HLMVECs exposed to either impinging flow (Rings 1–6), spatially uniform flow (parallel plate chamber; PP), or no flow (NF) for 30 min. HLMVECs are binned by location relative to the jet center (Figure 1, B and C). Dots indicate the measured CDF, while the solid line is a fit to a Γ-Poisson distribution. The parameter λ is the fit value for the average pulse count for the distribution and is presented in the lower right-hand corner. Experiments were performed in triplicate. Asterisks indicate statistically significant differences in CDFs as determined using the Kolmogorov–Smirnov test (n.s., not significant; *, p < 0.05; **, p < 10^–4; ***, p < 10^–7).

Cells exposed to WSSGs in the impinging flow cell had appreciably higher average pulse counts than cells observed under no flow, with an average pulse count λ that scaled roughly with the local WSS (Figure 3). In particular, the fraction of P cells increased with increasing WSS to a maximum of ∼0.6 (Table 1). These findings are in agreement with studies demonstrating that WSS is sufficient to trigger cytoplasmic Ca²⁺ release, including in HLMVECs (Shen et al., 1992; Okuda, Takahashi, et al., 1999; Jafarnejad et al., 2015), but expand on previous work by revealing an underlying population heterogeneity. We also compared the pulse count distributions arising from cells in Ring 3 of the IFC with that arising from cells experiencing an equivalent, spatially uniform WSS in a parallel-plate flow chamber. Cells exposed to spatially uniform WSS of 50 dyn/cm² exhibited a slightly hgher pulse count (λ = 3.1 vs. 2.5, p < 0.05). However, the overall similarity of the pulse counts observed for these two conditions lends support to the argument that pulse count scales primarily with local WSS.

TABLE 1:

Modeling parameters for the Ca²⁺ pulse count measurements in Figure 3.

	Average WSS (dyn/cm2)	μ	Fraction of P cells	α (shape)	β (interval)	λ = α/β
Ring 1	32	2.25	0.62	4.03	1.78	2.27 ± 1.69
Ring 2	65	2.45	0.60	2.80	1.13	2.48 ± 0.50
Ring 3	53	2.48	0.54	1.58	0.61	2.59 ± 0.36
Ring 4	30	2.19	0.56	2.63	1.22	2.15 ± 0.92
Ring 5	17	1.69	0.48	2.41	1.38	1.74 ± 0.99
Ring 6	11	1.68	0.45	2.20	1.32	1.66 ± 1.17
Parallel plate	50	3.07	0.63	1.64	0.54	3.04 ± 0.22
No flow	n/a	0.84	0.22	0.43	0.51	0.83 ± 0.31

The average WSS, experimental mean μ, fraction of P cells, and parameters from a fit to the hierarchical Γ-Poisson are listed from left to right. λ is the mean predicted from the fit to the Γ-Poisson distribution (modeled by the shape parameter, α, and the interval parameter, β).

The variability in timing between pulses is parameterized by the shape parameter α, with a larger α indicating a closer approximation to a standard Poisson distribution. By this metric, the time intervals between pulses were most irregular under no flow (α = 0.4), and most regular for cells near the center of the impinging flow (α = 4.0), where the elongational stresses (i.e., stretching forces due to fluid flow) were largest. This observation suggests that gradients in WSS, such as are found at sites of valve formation, may serve to regularize the time intervals between Ca²⁺ pulses.

We next sought to determine whether differences in pulse count were spatially correlated among neighboring LECs. To do so, we used the k-means clustering algorithm to identify clusters of cells for every condition presented on Figure 3. We then determined the fraction of P cells for each cluster (Supplemental Figure S4). To determine whether P cells indeed clustered, we then randomly reassigned the measured cell-by-cell pulse counts and repeated the clustering algorithm. The resulting fractions of P cells per cluster were statistically indistinguishable from those observed experimentally (Supplemental Figure S5). Thus, while we do not rule out some form of local coordination among cells, the data are most consistent with the idea that pulse counts are regulated on an individual cell level rather than on a cluster level.

Exposure to WSSGs results in increased Ca²⁺ pulse duration

We next examined the pulse duration (FWHM) for both the initial pulse and the subsequent pulses in P cells (pulse count > 1). To do so, we fitted each distribution of pulse durations to a Weibull distribution (Figure 2), which is commonly used to model time-to-termination distributions. The Weibull distribution consists of a stretched exponential distribution with shape (κ) and scale (β) parameters such that the probability distribution f for the duration T of a pulse is

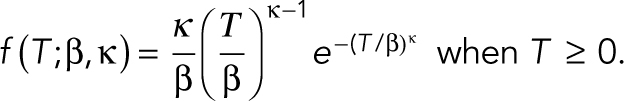The Weibull distribution reduces to an exponential distribution when the probability of a pulse terminating is constant in time following its initiation (κ = 1). We saw that κ changed from ≥1 for the initial pulse to <1 for the subsequent pulses in the presence of a WSSG with the exception of Ring 5, while it remained less than one under uniform flow and greater than one in the absence of flow. These differences are consistent with an increase in pulse duration with pulse number that occur in the presence of a WSSG but not spatially uniform WSS or the absence of flow (Supplemental Figure S3). Thus, WSSGs drove a gradual increase of Ca²⁺ pulse duration, whereas spatially uniform WSS did not.

WSSGs increase DC but not pulse frequency in P cells

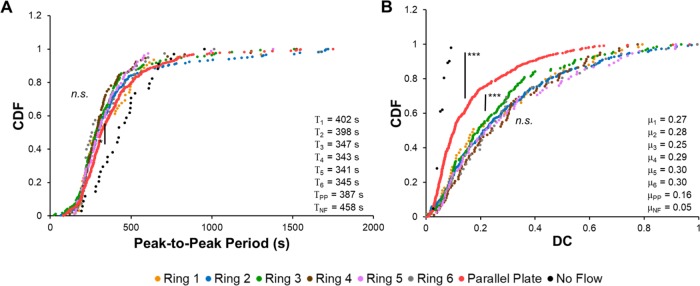
We also examined how WSS and WSSGs affected the DC, which we define here exclusively for P cells. We first sought to determine the time between consecutive pulses (peak-to-peak period), which would influence the DC. We observed that the time between consecutive pulses was shorter under flow conditions as compared with that in the absence of flow (Figure 4A). Interestingly, the peak-to-peak period was relatively constant in cells subjected to flow regardless of whether they experienced a gradient in WSS. To investigate this further, we examined the periodicity of repeatedly pulsing cells and observed little to no difference in the time between consecutive pulses (Supplemental Figure S6). In contrast, pulse durations for P cells exposed to WSSG, regardless of the absolute WSS magnitude, were twofold higher than those of P cells in the presence of a spatially uniform WSS, and four- to fivefold higher than those of P cells under no flow (Figure 2). In consequence, DCs measured for HLMVECs exposed to WSSGs were almost twofold higher than those measured for cells exposed to spatially uniform, 50 dyn/cm² WSS, and fourfold higher as compared with cells under no flow (Figure 4B). Thus, the presence of a WSSG increased the strength of Ca²⁺ activation relative to a spatially uniform WSS, regardless of the magnitude of WSS.

FIGURE 4:

WSSG modulates the Ca²⁺ pulse duty cycle but not the pulse period. CDF plots for the (A) average peak-to-peak period per cell and (B) duty cycle (DC) per cell for Ca²⁺ pulses in HLMVECs exposed to impinging flow, parallel plate flow, or no flow. The average period and DC for each distribution are presented in the lower right-hand corner of each graph. Experiments were performed in triplicate. Asterisks indicate statistically significant differences in CDFs as determined using the Kolmogorov–Smirnov test (n.s., not significant; *, p < 0.05; **, p < 10^–4; ***, p < 10^–7).

DC is influenced by both CRAC channel and calcineurin activity

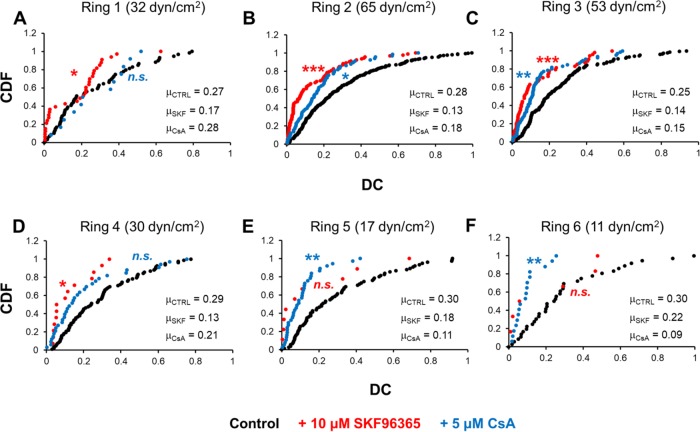
Previous studies identified roles for the CRAC channel ORAI1 and the Ca²⁺-dependent phosphatase calcineurin in lymphatic development (Kulkarni et al., 2009; Sabine et al., 2012; Choi et al. 2017a,b). We therefore examined whether either or both proteins might help to set Ca²⁺ pulse dynamics in response to WSS and/or WSSGs. We observed a significant decrease in the DC when HLMVECs were treated with either 10 μM SKF96365 (ORAI1 inhibitor, IC₅₀ = 10 μM) or 5 μM cyclosporin A (calcineurin inhibitor; CsA, IC₅₀ = 5 nM) for 1 h prior to the onset of impinging flow (Figure 5 and Supplemental Figures S7–S11). This decrease in DC appeared to be due in part to a decrease in pulse frequency for both inhibitors (Supplemental Figure S9). Also, inhibition of ORAI1 decreased pulse duration for P cells across Rings 2–5, while calcineurin inhibition decreased pulse duration in Rings 5 and 6 (Supplemental Figures S10 and S11). A plausible interpretation is that both ORAI1 and calcineurin are required for normal Ca²⁺ pulse dynamics, consistent with possible feedback mediated by both proteins. However, we cannot exclude the possibility that either or both inhibitors acted through alternative pathways in our experiments.

FIGURE 5:

Treatment with ORAI1 and calcineurin inhibitors decreases Ca²⁺ DC. HLMVECs were treated with either 10 μM SKF96365 or 5 μM CsA or left untreated and exposed to impinging flow. CDF plots of the average DC per cell are presented for each condition. The average DC for each distribution is presented at the lower right-hand corner of each graph. Experiments were performed in duplicate. Asterisks indicate statistically significant differences in CDFs with respect to the untreated control as determined using the Kolmogorov–Smirnov test (n.s., not significant; *, p < 0.05; **, p < 10^–4; ***, p < 10^–7).

DISCUSSION

Previous work has established that Ca²⁺-dependent activation of NFATc1 is essential for the formation of lymphatic valves (Kulkarni et al., 2009; Norrmén et al., 2009; Sabine et al., 2012; Planas-Paz and Lammert, 2013; Vittet, 2014). However, how exactly the activation of NFATc1 is confined to regions of valvulogenesis is unclear, as fluid flow is present throughout the lymphatic system. We found that both the fraction of P cells and the number of pulses scaled roughly with WSS, providing a mechanism by which LECs can encode the local WSS magnitude (Figure 3 and Table 1). This finding is consistent with and extends a previous report that the average cytoplasmic Ca²⁺ concentrations in HLMVECs increase with increasing WSS (Jafarnejad et al., 2015). Importantly, we also found that for P cells exposed to a WSSG, the DC was ∼0.3 regardless of the local WSS, and about twice that observed for LECs exposed to spatially uniform WSS (Figure 4B). A Ca²⁺ DC of 0.3 was previously shown to lead to maximal NFATc1 activation in Jurkat T-cells (Dolmetsch et al., 1997; Dolmetsch, Xu, and Lewis, 1998; Tsien et al., 1998; Smedler and Uhlén, 2014). We suggest that the marked increase in DC in the presence of a WSSG may provide a robust means of patterning valve formation by confining NFATc1 activation to regions that feature large gradients in WSS such as vessel constrictions and branches, precisely the regions where valve formation is favored.

Although Ca²⁺-mediated signaling in ECs in response to fluid flow has been examined (Ando et al., 1988; Schwarz et al., 1992; Shen et al., 1992; Helmlinger et al., 1996; Okuda, Takahashi, et al., 1999; Jafarnejad et al., 2015), to our knowledge a single-cell analysis of pulse kinetics such as we report here has not been performed previously. This analysis allowed us to distinguish between the responses of LECs to different input stimuli (spatially uniform WSS vs. WSSGs) and to infer that the Ca²⁺ signaling in response to the onset of flow differed from the response to sustained flow. We anticipate that the analysis approaches developed here may be useful for characterizing Ca²⁺ signaling in a variety of experimental systems.

Whether the cells that pulse repeatedly (P), once, or zero times reflect distinct subpopulations present in the primary cells used in our experiments is unclear. The fact that the fraction of cells that pulsed at least once varied with WSS magnitude argues that cells can convert between pulsing and nonpulsing states. On the other hand, we cannot definitively rule out that the ∼20% of cells that did not pulse in the observed time window even under the largest WSS may belong to a subpopulation of cells in which flow does not activate Ca²⁺ signaling.

The identity of the flow sensors that control the Ca²⁺ dynamics we describe is unclear. Endothelial cells have been proposed to sense flow via the activation of multiple transmembrane receptors and complexes, including the VEGFR2/PECAM-1/VE-Cadherin/VEGFR3 complex, G-protein coupled receptors (GPR68, Bradykinin B2), primary cilia, and stretch-activated ion channels (Tzima et al., 2005; Chachisvilis et al., 2006; Nauli et al., 2008; Li, Hou, et al., 2014; Ranade, Qiu, et al., 2014; Baeyens et al., 2015; Coon et al., 2015; Fotiou, Martin-Almedina, et al., 2015; Ellefsen, Chang, Nourse, et al., 2018; Xu et al., 2018). Several of these, including Bradykinin B₂, Piezo1 and VEGFR2 and -3 can potentially trigger downstream Ca²⁺ signaling through canonical signaling pathways (Tzima et al., 2005; Clapham, 2007; Baeyens et al., 2015). Which of these (or other) pathways are modulated specifically by WSSGs remains unknown, and an interesting topic for future investigations. Our observations suggest that calcineurin, whose activation lies downstream of cytosolic Ca²⁺, may in turn regulate Ca²⁺ pulse dynamics, suggestive of a positive feedback loop. Whether this indeed occurs, and whether it helps to drive LEC commitment to the valvular phenotype, is likewise a target for future work.

MATERIALS AND METHODS

Cell culture

HLMVECs (CC-2810) were purchased from Lonza Corporation (Walkersville, MD) and cultured in EGM-2 basal medium (Lonza CC-3156) with supplements and growth factors (Lonza CC-4147) containing 5% FBS (fetal bovine serum), hEGF, VEGF, hFGF-B, R3-IGF-1, hydrocortisone, and ascorbic acid. Penicillin (50 U/ml) and streptomycin (50 µg/ml; Life Technologies, Carlsbad, CA) were added to the medium. Cells used for experiments were between passages 6 and 8. Three to five days before the experiment, depending on the desired initial confluency, cells were plated onto a six-well cell culture dish with a #1.5 glass coverslip bottom (Cellvis, Sunnyvale, CA). These dishes were precoated with 0.2% gelatin (Sigma-Aldrich, Saint Louis, MO) for 1 h. Cells were plated at 0.5–1.5 × 10⁵ cells per dish and incubated at 37°C and 5% CO₂. We performed uniform WSS experiments using parallel plate flow chambers. The channels were also precoated with 0.2% gelatin. Cells were plated at 7.5 × 10⁴ cells per well on each chamber and incubated at 37°C and 5% CO₂.

For flow experiments, Leibovitz’s L-15 medium (Life Technologies) was used instead of EGM-2 to allow imaging independent of CO₂. The L-15 medium included 5% FBS, the endothelial growth factor kit from Lonza (CC-4147), 50 U/ml penicillin, and 50 μg/ml streptomycin (Life Technologies). LEC experiments were performed with cells at surface coverages (fractions of the coverslip covered by cells) of greater than 95% and confluency (fraction of maximum cell density) of 80% to ensure sufficient contact with neighboring cells.

Calcium dye treatment

Prior to the experiment, the EGM-2 media used to culture the HLMVECs were switched with the L-15 media (1.5 ml per well) described above. The plate containing the HLMVECs was then transferred to our custom-designed temperature-control chamber, used to keep the ambient temperature at 37°C during live-cell imaging. To perform live-cell imaging of Ca²⁺ dynamics, we used the Fluo-4 direct calcium assay kit (F10471; Thermo-Fisher Scientific, Waltham, MA). The kit contains three components: a Fluo4 Direct calcium assay reagent, a Fluo-4 Direct calcium assay buffer, and a proprietary water-soluble probenecid, which is added as described by Thermo-Fisher Scientific to prevent extrusion of the dye from cells. This custom formulation provides a stable and homogeneous fluorescence profile with low background fluorescence. A 250-mM stock solution probenecid was prepared by adding 1 ml of the supplied buffer to 77 mg of water-soluble probenecid. Resuspension and mixing through vortexing were performed until the reagent was completely dissolved. The dye formulation was made by adding 10 ml of the buffer to an entire bottle of the supplied dye and resuspending until dissolved; the resulting solution was dark red. Afterward, 200 μl of the prepared stock solution of probenecid was added to the prepared dye, and the resulting solution was vortexed thoroughly. The dye solution was then ready for use during flow experiments.

For Ca²⁺ imaging experiments, 500 μl of the prepared dye solution (optimized for HLMVEC flow experiments, 1:4 dilution in L-15) was incubated with the designated well of HLMVECs in the dark. Due to long–time scale cytotoxicity and the inevitable extrusion from the cells, the dye was added to each experimental well no more than 30 min before the beginning of imaging.

Fluid dynamics

Details of the fluid dynamics of the IFC have been reported previously (Ostrowski et al., 2015; Surya et al., 2016). Briefly, the IFC contains six submerged jet orifices that apply an impinging flow of cell culture media to a monolayer of adherent cells in standard glass-bottom six-well dishes. (Figure 1A). A nine-roller dampened peristaltic pump (Idex, Oak Harbor, WA) applied a flow of cell culture media at a flow rate of 4.5 ml/min. This flow rate provided a wide range of WSSs (0–72 dyn/cm²) to the monolayer of HLMVECs and maximized the WSSG experienced across Rings 1–6 (Figure 1, B and C). In addition, we have previously reported that this range triggers flow-mediated collective upstream migration in HLMVECs on a 24-h timescale and that the HLMVEC migratory response to a 0–72 dyn/cm² range in WSS was qualitatively similar to their migratory response to a range of 0–10 dyn/cm² in WSS (Ostrowski et al., 2014, 2015; Surya et al., 2016).

Before the cells were exposed to impinging flow, the IFC was prepared by adding 10 ml of L-15 medium to each of the six chambers in the absence of cells followed the removal of bubbles. Media was circulated through the device tubing. Once the tubing lines were filled, the device was stopped, and the remaining air was removed using a syringe attached to a side port. All flow experiments were performed for 30 min. Cleaning of the device after the conclusion of an experiment was performed analogously to the device preparation above and performed as detailed previously (Surya et al., 2016). All parallel plate experiments were performed with a uniform WSS of 50 dyn/cm² (comparable to the average WSS of Ring 3).

Fluorescence images were visualized using a Nikon Ti microscope (Nikon Corporation) with an Andor Neo Camera (Andor Technology, Belfast, UK), a Heliophor light engine providing excitation at 488 nm (89 North, Burlington, VT) and a 20× air objective (Nikon). A frame rate acquisition of once per 5 s was chosen based on prior in vitro studies demonstrating that the shortest observed Ca²⁺ pulses in ECs are ∼15 s in duration (Jafarnejad et al., 2015; Yokota et al., 2015). Two regions were recorded per sample condition to visualize all six rings (Figure 1C): one region contains the IFC jet center (at r = 0) and the entirety of Rings 1 and 2 (Jet Center, “JC”; ∼50 cells each ring) while the other was located in Rings 3 through 6 (Far Rings, “FR”; contains on average at least 25–30 cells per ring).

Inhibitor treatment

Our prior publications outline extensive inhibitor- and RNA interference–based studies using the IFC (Ostrowski et al., 2015; Surya et al., 2016). Each well of the six-well IFC is connected to a separate reservoir of cell culture medium, allowing six simultaneous, independent experiments. Generally, one JC and two FR measurements are performed per inhibitor experiment, along with the respective no-inhibitor control, subjected to identical flow conditions.

Stock concentrations of inhibitors were diluted in L-15 medium and added 1 h before the start of flow experiments. The inhibitor was also included in the recirculating medium to maintain its concentration throughout the experiment. SKF96365, a ORAI1 inhibitor, was purchased from Cayman Chemical (Ann Arbor, MI) (Item 10009312, CAS 130495-35-1) and a stock concentration was prepared in cell-culture grade dimethylsulfoxide (4–X; American Type Culture Collection, Manassas, VA), followed by dilution in L-15 to a final concentration of 10 μM. Cyclosporin A, a calcineurin inhibitor, was purchased from Sigma–Aldrich (Item 30024, CAS 59865-13-3) and a stock concentration was prepared in DMSO, followed by dilution in L-15 to a final concentration of 5 μM.

Immunofluorescence

At the end of the experiment, cells in the glass-bottom six-well dishes were fixed with 4% paraformaldehyde (43368, Alfa Aesar, Haverhill, MA) in PBS for 15 min, followed by two washes with PBS (2 min each), permeabilization for 10 min with 0.5% Triton X-100 (Sigma-Aldrich) and blocking for 1.5 h with 1% BSA in PBS. All these steps were performed at room temperature. Anti-human NFATc1 rabbit polyclonal antibody (1:250; ab25916, Burlingame, CA) and anti-human CD144 (1:500, VE-Cadherin) mouse antibody (555661, BD Pharmingen, San Jose, CA) were incubated overnight with the samples at 4°C. Secondary fluorescent antibodies anti-rabbit or mouse IgG Fab2 AlexaFluor Molecular Probes (4412S, 4410S, Cell Signaling Technology, Danvers, MA) were incubated with the samples for 1.5 h at room temperature in the dark (samples covered with aluminum foil). ActinRed 555 Ready Probes reagent (R37112, Thermo-Fisher Scientific) was used to stain actin and was incubated for 10 min at room temperature, followed by the addition of Hoechst (34580, Thermo-Fisher Scientific) to stain cell nuclei. Samples were visualized using the same Nikon Ti microscope, Andor Neo Camera, and 20× (air) objective as used for the calcium imaging experiments. Quantification of nuclear fluorescence intensity is presented in the Supplemental Information.

Analysis of calcium dynamics

Details of the analysis performed can be found in the Supplemental Information. Briefly, images were acquired in 16-bit format (2560 × 2160), binned, and downscaled to 8-bit format (640 × 540) before analysis using the Fiji (ImageJ) software. The available StackReg image stack registration macro was used to correct for minor stage drift. (Cells did not move appreciably over the course of the 30-min measurement.) A custom routine was created to track the total cellular fluorescence intensity per cell per frame, along with the cells’ initial positions. These data were imported into MATLAB for analysis of pulse frequency, duration, and periodicity (Figure 1E). Cumulative distribution function plots and modeling of the distributions of experimental data were performed using MATLAB. We employed a Weibull fit for pulse duration measurements (Figure 2), while a Γ-Poisson fit was used to describe pulse count distributions (Figure 3). The shape and rate parameters α and β determine the Γ-Poisson fit to each pulse count distribution and are determined through a negative binomial distribution fit via MATLAB and conversion to the Γ-Poisson parameters.

Abbreviations used:

Ca ²⁺

calcium

CRAC

calcium release activated channel

DC

duty cycle

FWHM

full width half maximum

IFC

impinging flow chamber

IP3

inositol 1,4,5-trisphosphate

IP3R1

inositol 1,4,5-trisphosphate receptor type1

LECs

lymphatic endothelial cells

NFATc1

Nuclear Factor of Activated T Cells cytoplasmic 1

NP

nonperiodic

P

periodic

WSS

wall shear stress

WSSG

wall shear stress gradient