Local, transient tensile stress on the nuclear membrane causes membrane rupture

Abstract

Cancer cell migration through narrow constrictions generates compressive stresses on the nucleus that deform it and cause rupture of nuclear membranes. Nuclear membrane rupture allows uncontrolled exchange between nuclear and cytoplasmic contents. Local tensile stresses can also cause nuclear deformations, but whether such deformations are accompanied by nuclear membrane rupture is unknown. Here we used a direct force probe to locally deform the nucleus by applying a transient tensile stress to the nuclear membrane. We found that a transient (∼0.2 s) deformation (∼1% projected area strain) in normal mammary epithelial cells (MCF-10A cells) was sufficient to cause rupture of the nuclear membrane. Nuclear membrane rupture scaled with the magnitude of nuclear deformation and the magnitude of applied tensile stress. Comparison of diffusive fluxes of nuclear probes between wild-type and lamin-depleted MCF-10A cells revealed that lamin A/C, but not lamin B2, protects the nuclear membranes against rupture from tensile stress. Our results suggest that transient nuclear deformations typically caused by local tensile stresses are sufficient to cause nuclear membrane rupture.

INTRODUCTION

Cell migration through narrow constrictions causes nuclear deformations (Wolf et al., 2013; Irianto et al., 2017). These deformations can be accompanied by local rupture of the nuclear membrane (Denais et al., 2016; Raab et al., 2016). Exposing nuclear contents to the cytoplasm causes DNA damage (Denais et al., 2016; Irianto et al., 2017) that may contribute to cancer progression. In these situations, increased intranuclear pressure resulting from compressive cytoskeletal forces is thought to cause the formation of micron-sized membrane blebs that separate from the lamina and eventually rupture (Denais et al., 2016; Hatch and Hetzer, 2016; Lammerding and Wolf, 2016). Such spontaneous membrane rupture occurs not only during cell migration in confined spaces but also in cultured cancer cells, likely due to actin confinement (Hatch and Hetzer, 2016).

Local tensile stresses can also cause nuclear deformations (Maniotis et al., 1997; Lammerding et al., 2006; Wang et al., 2009; Chancellor et al., 2010; Wu et al., 2014; Alam et al., 2015; Tajik et al., 2016; Lele et al., 2018). For example, extracellular stresses applied to integrin receptors on the cell membrane can be propagated to the nucleus through the cytoskeleton, causing local nuclear deformations, rotations, and translations (Maniotis et al., 1997; Wang et al., 2009; Tajik et al., 2016). Tensile stresses on the nuclear surface are also generated during cell migration, which can cause nuclear translations (Wu et al., 2014). Also, local cell membrane protrusions proximal to the nuclear surface have been shown to cause local nuclear deformations (Alam et al., 2015). Such tensile stresses are transmitted to the nuclear surface through molecular connections between nesprin proteins embedded in the outer nuclear envelope, which bind to the cellular cytoskeleton (Luxton and Starr, 2014; Uhler and Shivashankar, 2017; Kirby and Lammerding, 2018; Lee and Burke, 2018). Because nesprins are embedded in the cell membrane and bind to SUN proteins that are also in the inner nuclear membrane, it is possible that tensile stresses exerted on these proteins may cause rupture of the nuclear membranes. However, whether such deformations are accompanied by nuclear membrane rupture has not yet been examined.

Here, we applied local tensile stress on the nuclear membranes in living adherent cells using a direct force probe (Neelam et al., 2015; Zhang et al., 2018) and examined nuclear membrane integrity with previously established nuclear membrane rupture reporters (Denais et al., 2016). Our results suggest that transient nuclear deformations typically caused by local tensile stresses are indeed sufficient to cause nuclear membrane rupture.

RESULTS

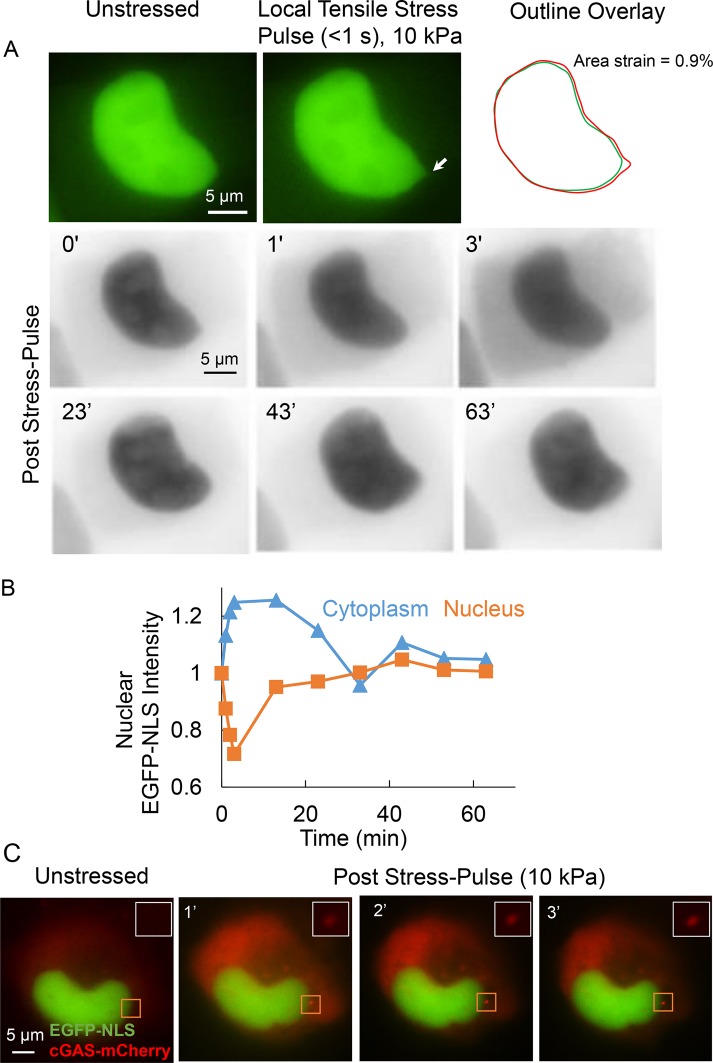
Using the direct force probe, we applied stress directly to the nuclear surface in an adherent living cell. The method involves suction-sealing a narrow micropipette to the nuclear surface.The suction pressure in the micropipette is known precisely (Neelam et al., 2015; Zhang et al., 2018). Moving the micropipette away from the nucleus deforms the nucleus locally. Eventually, the micropipette detaches when the restoring forces in the nucleus equal the applied suction pressure across the small nuclear membrane section. Using this method, we applied a short (<1 s; see Supplemental Movie 1) force pulse of 2 nN over a circular area (diameter 0.5 µm) of the nucleus of a normal mammary epithelial cell (MCF-10A cell) expressing an EGFP-NLS nuclear rupture reporter. This force corresponds to a (nearly normal) stress of 10 kPa. The nucleus transiently deformed at the force application site; the deformation resulted in a loss of nuclear membrane integrity (nuclear membrane rupture), as evidenced by the leakage of EGFP-NLS into the cytoplasm, resulting in a transient loss of nuclear EGFP-NLS fluorescence and a corresponding increase in the cytoplasmic EGFP-NLS signal (Figure 1, A, and corresponding intensities in B). By ∼60 min after the end of the force pulse, the nuclear and cytoplasmic EGFP-NLS intensities recovered back to preforce levels, indicating membrane repair and reimport of the EGFP-NLS reporter (Figure 1, A and B). These results confirm that the initial decrease in EGFP-NLS corresponded to an actual rupture event. For additional confirmation, we modified cells to express cGAS-mCherry, a cytoplasmic DNA-binding protein that accumulates at the site of nuclear envelope rupture where the genomic DNA is exposed to the cytoplasm (Denais et al., 2016). The rapid accumulation of cGAS-mCherry at the force application site indicated that the nuclear membrane rupture was local (Figure 1C; see inserts for an enlarged view).

FIGURE 1:

Local tensile stress applied to the nucleus in adherent cells can rupture the nuclear membranes. (A) Top: images show a representative MCF-10A nucleus expressing EGFP-NLS before application of stress (unstressed) and at the point of maximum deformation due to a local stress pulse of 10 kPa and duration of <1 s. The arrow indicates the location where the micropipette tip was attached to the nucleus. The outline overlay compares the outlines of the unstressed and deformed nucleus (right). Bottom: inverted time lapse fluorescent images of the nucleus probed above along with cytoplasm. The images show that the cytoplasmic intensity increases and the nuclear intensity decreases—the corresponding quantification of cytoplasmic and nuclear intensities (normalized to the corresponding initial intensity; stress pulse applied at time = 0) is shown in B—over the first several seconds, which indicates membrane rupture. Over longer times (∼30 min), both cytoplasmic and nuclear intensity are restored to levels before rupture indicating the nuclear membranes are repaired over time. (C) Images show cGAS-mCherry stably expressing MDA-MB-231 cell nucleus transfected with EGFP-NLS. Local tensile stress of 10 kPa (at the site indicated by rectangular box) causes the accumulation of cGAS cytoplasmic DNA binding protein near the site of stress application.

Movie S1.

Download video file ^{(141.5KB, avi)}

Time-lapse movie shows the short duration of the 10 kPa stress pulse applied to an MCF-10A nucleus expressing EGFP-NLS (corresponding to Figure 1A).

We tested whether the direct force probe causes consistent and reproducible rupture by analyzing the time-dependent decay in the nuclear EGFP-NLS intensity after the force pulse over several cells. Data pooled from several probed cells showed a consistent decrease in the nuclear intensity upon application of the stress pulse, an increase in cytoplasmic intensity, and a relatively small change in control cells (Figure 2A, control cells are unstressed, and in the same image as the stressed cell, which helps control for photobleaching effects). We quantified the extent of nuclear deformation by overlaying images of the nucleus before and at maximum deformation using the method in Neelam et al. (2015) (see Materials and Methods). A stress pulse of 10 kPa corresponded to an average area strain of 0.8% ± 0.1%. These data suggest that local tensile stresses, resulting in transient nuclear deformations of the degree typically caused by local tensile stresses (Maniotis et al., 1997; Lammerding et al., 2005; Lammerding and Lee, 2009; Alam et al., 2015; Tajik et al., 2016), consistently rupture the nuclear membranes of MCF-10A cells.

FIGURE 2:

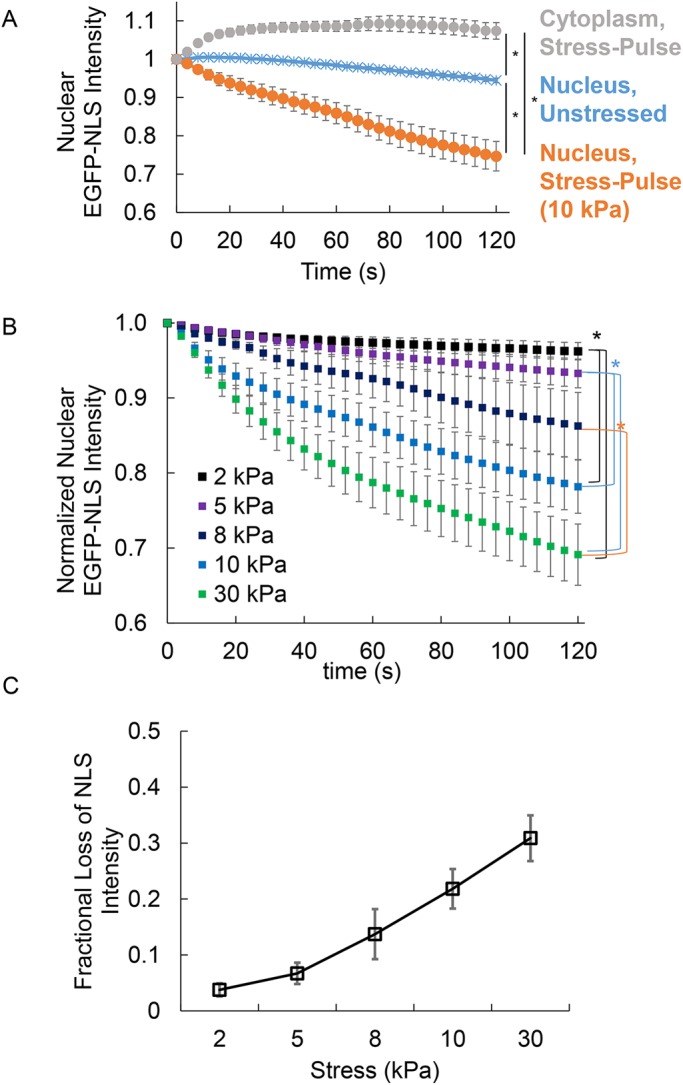
The extent of rupture of nuclear membranes scales with the magnitude of tensile stress. (A) The plot shows pooled measurements of cytoplasmic and nuclear EGFP-NLS fluorescence intensities (normalized to the initial intensity) at 120 s after a stress pulse was applied to the MCF-10A nucleus (gray and orange circles, respectively), along with EGFP-NLS fluorescence intensities in nuclei (blue; normalized to the initial intensity), which were present in the same field of view as the stressed nucleus, but which were not subjected to stress. The decrease in the fluorescence intensity of unstressed nuclei is due to photobeaching during image capture. The fluorescence intensity of stressed nuclei decreases consistently after application of the stress pulse. Data were pooled from 23 nuclei. The stress applied was 10 kPa. Error bars are SEM. Statistical differences were detected with two-way analysis of variance (ANOVA) (* represents p < 0.05). (B) Plot shows pooled mean values of normalized EGFP-NLS intensity from at least 20 nuclei per stress magnitude. Normalization involved correcting for effects of photobleaching by dividing stressed nuclear EGFP-NLS intensities with EGFP-NLS intensities in the unstressed control nucleus in the same field of view for each cell probed (see Materials and Methods for details on normalization). Rupture behavior is seen to change with the magnitude of the stress applied. Error bars are SEM (N ≥ 20). Statistical differences were detected with two-way ANOVA with Bonferroni correction (* represents p < 0.05/number of comparison). (C) Plot shows the fractional loss of nuclear EGFP-NLS intensity quantified from the data in B at 120 s after the stress pulse (see Materials and Methods for calculation). The data show that the extent of NLS loss is larger at a higher magnitude of stress. Error bars are SEM (N ≥ 20).

To test the hypothesis that the extent of rupture depends on the magnitude of tensile stress applied by the direct force probe, we repeated these experiments over a range of applied nuclear membrane stresses. Figure 2B shows pooled data for dynamic decrease in nuclear EGFP-NLS intensity at different stress levels. There was a measurable decrease in the nuclear EGFP-NLS intensity in the nucleus at stresses as low as 2 kPa. The maximum loss of nuclear EGFP-NLS intensity (measured as the intensity at 120 s after the stress pulse, i.e., long enough for the nuclear EGFP-NLS intensity to fully decay) scaled with the magnitude of the nuclear membrane stress applied (Figure 2C). Histograms of EGFP-NLS intensity at 120 s also show a clear trend toward higher means at larger stress values with only a minor effect on the probability of rupture (Supplemental Figure S1A). We confirmed a similar dependence of nuclear membrane rupture on applied membrane stress in mouse embryonic fibroblasts (MEFs) (Supplemental Figure S2), indicating that the findings are not specific to a single cell line or species.

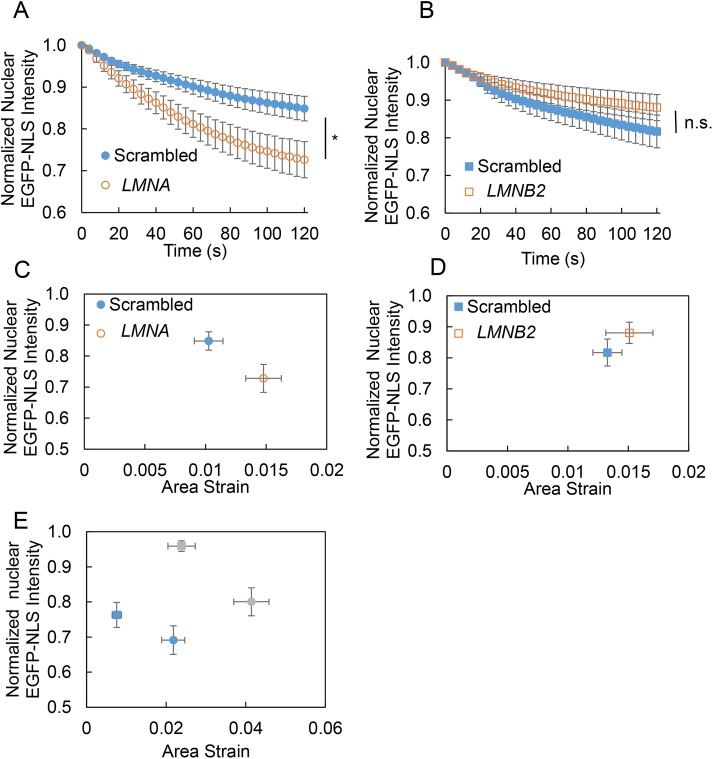
The underlying nuclear lamina may protect the nuclear membranes from rupture under tensile stress (Denais et al., 2016; Hatch and Hetzer, 2016). We therefore depleted nuclear lamins and examined the effect on nuclear membrane rupture. Depletion of lamin A/C by siRNA (small interfering RNA) (Supplemental Figure S3) resulted in a higher loss of nuclear EGFP-NLS (Figure 3A), whereas depletion of lamin B2 had no significant effect (Figure 3B). This was surprising, as previous studies with nuclear compression found that lamin B2 has a protective role in nuclear membrane rupture (Hatch et al., 2013; Bakhoum et al., 2018). Given that loss of of lamin A/C softens the nucleus (Broers et al., 2004; Lammerding et al., 2004; Pajerowski et al., 2007; Schäpe et al., 2009; Swift et al., 2013; Davidson et al., 2015; Stephens et al., 2017), we examined the effect of lamin depletion on nuclear deformation under transiently applied local nuclear membrane stress. Lamin B2 depletion had no effect on nuclear deformation (Supplemental Figure S4), consistent with previous studies (Lammerding et al., 2006), and correspondingly had no effect on rupture (Figure 3D), whereas lamin A/C depletion resulted in larger nuclear deformation (and a larger extent of membrane rupture) (Figure 3C). The loss in nuclear EGFP-NLS intensity after rupture scaled with the stress levels and with the extent of maximum nuclear deformation under stress for both MCF-10A cells and MEFs (Figure 3E).

FIGURE 3:

Effect of lamin depletion on nuclear membrane rupture caused by local tensile stress. Plots show pooled mean normalized nuclear EGFP-NLS intensity after a 10 kPa stress pulse was applied to the nucleus in MCF-10A cells transfected with (A) nontargeting siRNA (scrambled) and siRNA targeting LMNA and (B) siRNA targeting LMNB2 (N ≥ 22 for each condition). Statistical differences were detected with ANOVA (* represents p < 0.05). (C, D) Plots show the normalized nuclear EGFP-NLS intensity at 120 s after a 10 kPa stress pulse vs. the maximum nuclear deformation (quantified as area strain) in MCF-10A cells transfected with (C) nontargeting siRNA or siRNA targeting LMNA and (D) nontargeting siRNA or siRNA targeting LMNB2. Error bars are SEM (N ≥ 21). The EGFP-NLS intensity at the pseudosteady state of 120 s postrupture appears to correlate with the maximum deformation. (E) Plot shows the normalized nuclear EGFP-NLS intensity at 120 s poststress pulse vs. the maximum nuclear deformation (quantified as area strain) in MCF-10A cells (blue symbols; square corresponds to 10 kPa, and circle corresponds to 30 kPa), and MEFs (gray symbols; square corresponds to 10 kPa, and circle corresponds to 30 kPa). Error bars are SEM (N ≥ 17). For a given cell type, the pseudosteady fluorescence intensity of EGFP-NLS at 120 s postrupture scales inversely with the extent of deformation.

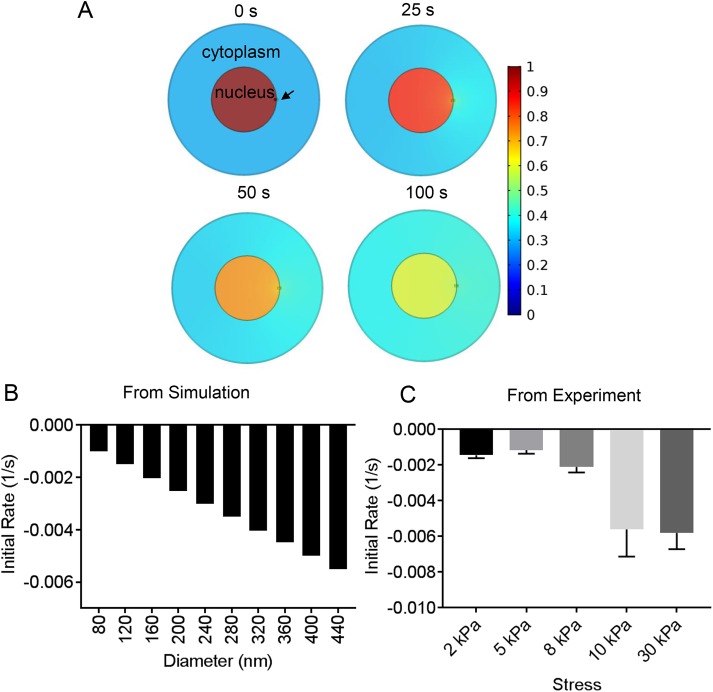
To estimate the size of the membrane defect during nuclear rupture, we used the quantitative kinetic data on the decrease of EGFP-NLS in the nucleus, combined with finite element modeling (FEM) of the diffusion of EGFP-NLS, through a small circular hole in the surface of the three-dimensional nucleus separating the nucleus and the cytoplasm (Figure 4A shows a two-dimensional projection of the three-dimensional nucleus and cell). Notably, the calculations estimate an ”effective size,” as it is possible that more than one smaller hole is created in the membranes, below the resolution limit of the light microscope. In this calculation, three-dimensional cell and nuclear geometric parameters were chosen based on our previously published measurements with MCF-10A cells (Neelam et al., 2016) (Table 1), and the diffusion coefficient of EGFP-NLS has been previously reported in both the cytoplasm and the nucleus (Wu et al., 2009) (Table 1). EGFP-NLS is reimported from the cytoplasm into the nucleus, and this reimport rate depends on the cytoplasmic concentration, the number of nuclear pores, and the efficiency of the nuclear transport mechanism (the latter are not easily measurable for a given cell). To avoid the complications of nuclear reimport, we modeled only the initial rates of loss of EGFP-NLS when the cytoplasmic intensity and hence the reimport rate are negligible. The FEM calculations yield the initial rate of NLS loss as a function of hole diameter (Figure 4B). Comparison between experimental and simulation data (Figure 4, B and C) allowed us to estimate the force-dependent effective hole size (Table 2). Our model indicates that these hole diameters are ∼100 nm (ranging from ∼96 nm at lower stresses to ∼465 nm at higher stresses), in agreement with similar pore sizes used by others (Deviri et al., 2017) and a previous estimate based on superresolution imaging (Denais et al., 2016).

FIGURE 4:

Experimental estimation of the hole size. (A) X-Y views of a finite element calculation of nuclear EGFP-NLS diffusion from a hole in the nucleus (marked by an arrow). The nucleus and cell are modeled as flat cylinders with geometrical parameters taken from experimental measurements in Neelam et al. (2016) and nuclear and cytoplasmic diffusion coefficients from Wu et al. (2009) (see Table 1). (B) Initial rate of EGFP-NLS diffusion from the nucleus into the cytoplasm through the nuclear hole as a function of hole size calculated from the finite element model in A (for details of how the initial rate was calculated from data, see Materials and Methods). (C) Plot shows experimental measurements of initial rate of nuclear EGFP-NLS decrease in the nucleus at different stress levels. Error bars are SEM N ≥ 22 for each stress.

TABLE 1:

Parameters used for finite element analysis in Figure 4.

	Nucleus	Cell		Nucleus	Cytoplasm
Height (μm)	4.2	4.2	Diffusion coefficient (μm²/s)	19	14
Radius (μm)	8.6	20	Initial intensity	1	0.3

TABLE 2:

Comparison between experimental and simulation data.

Simulation		Experimental
Initial rate (/s) × 1000	Hole size (nm)	Stress (kPa)	Initial rate (/s) × 1000	Hole size (nm)
−1.00	80	2	−1.46 ± 0.17	116 ± 14
−1.27	100	5	−1.21 ± 0.22	96 ± 17
−1.50	120	8	−1.96 ± 0.36	156 ± 27
−1.76	140	10	−5.62 ± 1.52	450 ± 119
−2.02	160	30	−5.82 ± 0.91	465 ± 72
−5.50	440
−5.76	460

Left column: initial rates of decrease in EGFP-NLS concentration in the nucleus calculated from the finite element analysis in Figure 4, for different hole sizes (diameter). The magnitude of the rate increases for increasing hole size as expected. Right column: initial rates (i.e., immediately after the stress pulse) estimated from experimental plots of EGFP-NLS intensity in the nucleus with time. Comparison with simulations was used to estimate the hole size, which is shown in the rightmost column.

DISCUSSION

Both compressive and tensile stress can cause nuclear deformation. Compressive stresses can cause rupture of the nuclear membrane, thereby exposing nuclear contents to the cytoplasm. Whether tensile stress–induced deformations similarly cause nuclear membrane rupture is currently unknown. Here we used the direct force probe to apply tensile stresses directly to the nuclear surface. Our results provide the first evidence that a tensile stress applied locally and transiently on the nuclear surface that elicits elastic nuclear deformation is sufficient to cause transient nuclear membrane rupture. The extent of nuclear deformation required for rupture under tensile stresses is relatively modest (<1% projected area strain) and is typical of what has been reported for nuclear deformations under tensile stress (Maniotis et al., 1997; Lammerding et al., 2005; Lammerding and Lee, 2009; Alam et al., 2015; Tajik et al., 2016).

Because the nuclear membrane is not a single membrane but consists of an outer and inner membrane fused to each other at several thousand nuclear pores, its mechanical rupture under stress is expected to be different from the well-studied situation of rupture of a single free-standing membrane. In addition, proteins that localize in the membrane mechanically couple the two membranes; these include SUN1/2 proteins embedded in the inner nuclear membrane that bind to nesprins embedded in the outer nuclear membrane. Also, proteins in the inner nuclear membrane (such as emerin and farnesylated lamins) tether the inner nuclear membrane to the underlying nuclear lamina and chromatin providing structural support (Foisner, 2001; Dahl et al., 2008; Isermann and Lammerding, 2013; Chang et al., 2015). The direct force probe allowed us to quantitatively compare rupture behavior between wild-type and lamin-depleted cells and also across cell types. Such comparisons are possible because the applied tensile stress is the same across these different conditions. We note here that although the applied stress is tensile (pulling), the mechanical response of nuclear components may be more complex, including possibly simultaneous compression of some elements and bending and expansion of others.

Depletion of lamin A/C, but not lamin B2, increased the loss in EGFP-NLS nuclear intensity under stress. The probability of rupture was not significantly altered upon depletion of lamin A/C (Supplemental Figure S1B), suggesting that the larger loss of intensity corresponded to a larger effective hole size. The hole size, estimated by comparison with the finite element calculations, was ∼433 nm for lamin A/C depletion (228 nm for the scrambled control) and ∼198 nm for lamin B2 depletion (223 nm for the scrambled control). This suggests that lamin A/C, but not lamin B2, plays a protective role in preventing rupture under tensile stresses.

The fact that the deformation scales with the applied stress (as we have previously reported [Neelam et al., 2015]) indicates that the rupture process itself does not cause detachment from the micropipette. If the small patch of nuclear membranes in contact with the pipette tip was being torn away from the nucleus due to pipette motion, then the pipette would detach when this rupture occurred, and nuclear deformation would be independent of the suction pressure. Further, applying suction alone to the nuclear membrane without pulling on it did not change the EGFP-NLS intensity in the nucleus (Supplemental Figure S6), arguing against the possibility that the applied suction pressure damages or opens nuclear pores.

Here we have reported nuclear deformation in terms of the projected area strain. The local strains near the pipette tip are likely higher than the projected area strain. It is desirable to measure the actual membrane area strain caused by application of the tensile stresses (the critical lipid membrane strain for rupture is of the order of 2% [Staykova et al., 2011]), but it is difficult to accurately quantify this strain in our live cell imaging experiments because the nuclear shape itself is changing locally (which involves translation of the membranes in addition to membrane strain).

In single-lipid bilayers, hole formation is determined by the energetic interplay between the surface tension in the bilayer and the line tension energy, which develops as a result of extreme bending of lipids at the pore interface (Gonzalez-Rodriguez et al., 2012; Akimov et al., 2017a,b). For such a system, there is a critical radius on the order of a few nanometers (Akimov et al., 2017a,b). If the holes in single bilayers exceed this critical radius, they are unstable and expand continually. If the holes are smaller than the critical radius, they spontaneously close. However, our experiments suggest that the holes are much larger (100 nm) and are stable over several seconds. The mechanism underlying this stability is not clear.

The fact that the leakage through nuclear holes would require rupture of both the nuclear membranes leads us to speculate that stable holes may be due to the creation of a donut-shaped hole between the ONM and the INM. After the initial rapid formation of the hole (<1 s), the hole may reach an equilibrium size over several seconds after hole formation. We explored this speculative picture by modeling the geometry of such donut holes by minimizing the bending energy. This approach is similar to the one we adopted previously to explain the separation of bilayers in the nuclear envelope (Torbati et al., 2016). It relies on the fact that a lipid bilayer is a two-dimensional elastic sheet, which is fluid in-plane, allowing lipids to diffuse freely, but resists out-of-plane bending deformations. We computed the equilibrium shapes of a donut hole for a prescribed membrane tension and appropriate boundary conditions (described under Materials and Methods). The calculation in Supplemental Figure S5A, top, shows a prediction of ∼60 nm three-dimensional donut-shaped holes corresponding to a membrane tension of ∼0.05 mN/m, which is comparable to our previous calculation of the resting tension in the nuclear membranes that explains the separation between these membranes (Torbati et al., 2016). At a lower resting tension of ∼0.01 mN/m, the hole diameter is predicted to be ∼240 nm (Supplemental Figure S5A, bottom). One possibility is that the lower stress pulses (Table 2) do not significantly perturb the resting tension in the nuclear membranes, whereas the higher-force pulses result in a larger loss of the resting tension, resulting in bigger hole sizes.

The above model is limited in that it accounts for only the intiation of pore formation and not the subsequent recruitment of membrane repair machinery, such as the ESCRT proteins, that occurs over minutes (Denais et al., 2016). These proteins can also apply physical forces onto the membranes (Chiaruttini et al., 2015), changing the geometry of the membranes and participating in resealing the hole. Further, hole establishment may be a process that is far from equilibrium and may be far more complex due to the many interactions among membrane-embedded proteins, the nuclear lamina, and the cellular cytoskeleton (Lele et al., 2018).

Our experimental results show that the direct force probe can be an effective tool to engineer ruptures in the nuclear membranes in adherent cells. The application of precise and known levels of stress to the nucleus allows comparisons of rupture behavior across cell types and across different types of perturbations to nuclear membranes. This probe could be valuable in understanding whether and how membrane components, such as LINC complex proteins that span the nuclear membranes, nuclear membrane composition, and membrane-embedded proteins, could contribute to nuclear membrane integrity under tensile forces.

MATERIALS AND METHODS

Cell culture

All cell types were maintained at 37°C in a humidified 5% CO₂ environment. MCF-10A cells were cultured in DMEM/F12 supplemented with 20 ng/ml EGF, 0.5 mg/ml hydrocortisone, 100 ng/ml cholera toxin, 100 µg/ml insulin, and 5% horse serum (Debnath et al., 2003). Human breast cancer cells (MDA-MB-231) and MEF cells were cultured in 4.5 g/l glucose DMEM supplemented with 10% DBS and 1% penicillin-streptomycin.

Plasmid transfection

Transient transfection of plasmids into cells was performed with Lipofectamine 3000 reagent (Life Technologies/Invitrogen, Carlsbad, CA) in OPTI-MEM media (Life Technologies/Invitrogen, Carlsbad, CA). EGFP-NLS was a kind gift of Alexander Ishov at the University of Florida (Negorev et al., 2001). Transfected cells were trypsinized and plated onto fibronectin-coated glass-bottomed dishes for micromanipulation and microscopy. The construction of cGAS-mCherry (pCDH-CMV-cGASE225A/D227A-mCherry2-EF1-blastiS) was described previously (Civril et al., 2013).

Immunostaining

Cells were fixed in 4% paraformaldehyde for 10 min, washed with phosphate-bufferered saline, and then permeabilized and blocked with 0.1% Triton X-100 in 1% bovine serum albumin solution for 45 min. The primary antibodies used in this study included rabbit anti–lamin B2 (Abcam; used at 1:500) and mouse anti–lamin A (Abcam; used at 1:1000). Cells were incubated with the primary antibody at 4°C overnight and secondary antibodies at room temperature for 1 h. Secondary antibodies used included goat anti-mouse Alexa Fluor 647 (Invitrogen; 1:500) and goat anti-rabbit Alexa Fluor 594 (Invitrogen; 1:500).

Micromanipulation

Micromanipulation was performed using an Eppendorf InjectMan micromanipulator system as described previously (Neelam et al., 2015; Zhang et al., 2018). In brief, a Femtotip micropipette tip (Eppendorf; 0.5-µm tip diameter) was mounted and connected to the Eppendorf microinjection system (InjectMan) by a tube. The cell membrane was penetrated with the micropipette tip, and the tip was brought next to the nuclear surface. The tube was then disconnected and opened to the atmosphere, which creates a known negative pressure that seals the micropipette tip to the ONM with a specified suction pressure (Neelam et al., 2015; Zhang et al., 2018). Nuclear deformation occurred when the pipette was translated away from the nucleus. When the resistance to nuclear motion and deformation balanced the applied suction force, there was a subsequent release from the tip (this process occured in less than a second, resulting in a short-stress pulse). The resisting stress on the ONM then is the suction stress at this point of detachment (calculated as suction pressure × area of tip). We have previously shown that the extent of nuclear motion and deformation depends on the suction force and is not due to nonspecific adhesion between the pipette tip and the membrane. Also, we have calculated negligible pressure drop due to flow through nuclear pores, such that the stress on the ONM is, for practical purposes, identical to the suction pressure (Neelam et al., 2015; Zhang et al., 2018). Time-lapse imaging was performed on a Nikon TE2000-inverted microscope with a 60× oil immersion objective and CCD camera (CoolSNAP; Photometrics, Tucson, AZ). Cells were maintained at 37°C at a 5% CO₂ level throughout imaging.

siRNA transfection

The siGENOME SMARTpool siRNA targeting LMNA and LMNB2 (Dharmacon) were used to deplete lamin A and lamin B2 proteins, respectively. The efficiency of siRNA depletion was confirmed by comparing the fluorescence intensity (confocal images, taken with the same imaging settings between scrambled group and transfected group) and the relative expression mRNA levels quantified with RT-qPCR (Supplemental Figure S3D). To perform RT-qPCR, whole cells were lysed 72 h posttransfection using the SingleShot Probes One-Step Kit (Bio-Rad). Lysates were then combined with complete RT-qPCR mix per the manufacturer’s protocol and predesigned fluorogenic probes targeting LMNA, LMNB2, or GAPDH (loading control; Bio-Rad). Reactions were processed on a CFX96 Real-Time PCR Detection System (Bio-Rad) using the following thermocycler conditions: 10 min at 50ºC, 3 min at 95ºC, followed by 40 cycles of 15 s at 95ºC and 30 s at 60ºC. All results were analyzed using the 2-∆∆Ct method and normalized against GAPDH expression and a scrambled siRNA negative control (Livak and Schmittgen, 2001).

Analysis

The NLS intensity of forced nuclei was normalized by the intensity of reference unforced nuclei in the same image to account for photobleaching effects as follows:

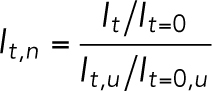(1)

where 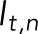is the normalized intensity at time t, 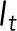is the fluorescence intensity of the stressed nucleus, and 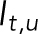is the fluorescence intensity of the unstressed nucleus quantified from images. The fractional loss of NLS intensity was calculated as 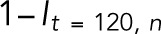corresponding to t = 120 s. The initial rate of loss of NLS intensity in the nucleus was estimated by fitting the normalized intensity data for the first 20 s with a fifth-order polynomial and then calculating the derivative by differentiating the polynomial and calculating the maximum rate. The area strain calculation was previously described in Neelam et al. (2015). Briefly, the nucleus at its maximum deformation was overlaid onto its unstressed shape and the nonoverlapping area was calculated. The area strain was calculated as the nonoverlapping area divided by the unstressed nuclear area.

Modeling

Finite element calculations of diffusion from a hole in the surface of the flat cylindrical nucleus into the flat cylindrical cytoplasm were performed in COMSOL. Zero flux boundary conditions were imposed everywhere else except at the hole, where continuity of concentration and mass flux was imposed. The predicted concentration in the nucleus was numerically averaged over the nuclear volume and normalized to the initial concentration. Initial rates were calculated from the time-dependent concentration profile in MATLAB by first fitting a polynomial to the time-dependent curve and differentiating this polynomial to calculate the initial rate. Next, hole size was varied, and initial rate dependence on hole size was calculated.

For mechanical calculations, the geometry of the membranes was modeled around a single donut-shaped pore as two-dimensional elastic sheets with the Helfrich–Canham relation:

(2)

where H is the mean curvature, K is the Gaussian curvature, and 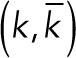are the bending moduli. The membranes were assumed to possess axisymmetry and reflection symmetry about the equatorial plane and hence, the geometry of only a single bilayer was simulated. The system is defined by the arclength s, the radial distance from the axis of revolution r(s), the elevation from a base plane z(s), and the angle which the tangent makes with the radial vector ψ(s) (see Supplemental Figure S5B). These parameters satisfy the geometric relation:

(3)

(4)

(5)

Here, ()’ is the partial derivative with respect to the arclength. These equations were integrated along with the force equilibrium equation, commonly referred to as the shape equation:

(6)

to compute the hole geometry. Here, λ is the surface tension and Δ is the surface Laplacian, and the transmembrane pressure was assumed to be zero. The integration was carried out with the following boundary conditions prescribed at the two ends of the simulated domain. The inner boundary is defined at the point where the membrane meets the equatorial plane at the hole site. Here we require z = 0, ψ = π/2, and rH^’ = 0. The last boundary condition imposes zero transverse shear, a condition that arises from reflection symmetry present in the geometry and allows the membranes to slide freely at the equatorial plane.The far boundary is assumed to lie at a distance of 200 nm from the center of the hole, midway between two typical adjacent holes (Belgareh and Doye, 1997; D’Angelo et al., 2006; Dultz and Ellenberg, 2010). Here we require Ψ = 0 and λ = λ₀, where λ₀ is the prescribed resting tension in the membranes. In addition, we assume that no membrane is lost during the process of hole creation and expansion. We therefore simulate different hole diameters with a conserved membrane area. We implemented this constraint by switching from the independent variable from the arclength (s) to the surface area (a) and use the geometric relation da = 2πrs ds to obtain the modified set of equations (Agrawal and Steigmann, 2009). We used the MATLAB solver BVP4C to perform numerical integration and computed the membrane geometry for different resting tensions.

Abbreviations used:

cGAS

cyclic GMP-AMP synthase

DBS

donor bovine serum

EGF

epidermal growth factor

FEM

finite element method

GFP

green fluorescent protein

INM

inner nuclear membrane

LINC

linker of nucleoskeleton and cytoskeleton

LMNA

lamin A/C

LMNB2

lamin B2

MEF

mouse embryonic fibroblast

NLS

nuclear localization sequence

ONM

outer nuclear membrane

RT-qPCR

reverse transcription quantitative PCR

SUN

Sad1 and UNC