Progress Towards Computational 3-D Multicellular Systems Biology

Abstract

Tumors cannot be understood in isolation from their microenvironment. Tumor and stromal cells change phenotype based upon biochemical and biophysical inputs from their surroundings, even as they interact with and remodel the microenvironment. Cancer should be investigated as an adaptive, multicellular system in a dynamical microenvironment. Computational modeling offers the potential to detangle this complex system, but the modeling platform must ideally account for tumor heterogeneity, substrate and signaling factor biotransport, cell and tissue biophysics, tissue and vascular remodeling, microvascular and interstitial flow, and links between all these sub-systems. Such a platform should leverage high-throughput experimental data, while using open data standards for reproducibility. In this chapter, we review advances by our groups in these key areas, particularly in advanced models of tissue mechanics and interstitial flow, open source simulation software, high-throughput phenotypic screening, and multicellular data standards. In the future, we expect a transformation of computational cancer biology from individual groups modeling isolated parts of cancer, to coalitions of groups combining compatible tools to simulate the 3-D multicellular systems biology of cancer tissues.

12.1. Introduction

Tumors cannot be understood without the context of their microenvironments. (See [1–3] and references therein.) Tumor cells depend upon growth substrates like oxygen, glucose, and growth factors for survival and proliferation. They release signaling factors that influence the behavior of other tumor cells and “normal” cells in the surrounding tissue (the stroma). Fibroblasts may respond to tumor-released signals by increasing motility and remodeling the extracellular matrix (ECM: a complex scaffolding that supports a tissue and its cells). Large populations of tumor cells directly alter the biochemical landscape through their uptake and depletion of growth substrates, creating gradients of these substrates that change the overall spatiotemporal distribution of substrates. When tumor cells experience low levels of oxygen (hypoxia), they may release factors (e.g., VEGF-A₁₆₅) that promote angiogenesis: endothelial cells detach from the existing blood vasculature, migrate, and proliferate to form new blood vessels [4]. Necrotic tumor cells (those that undergo uncontrolled death due to energy depletion—see our recent review [5]) and even viable tumor cells may release signaling factors that promote inflammatory responses, including infiltration by white blood cells and further matrix remodeling by stromal cells. All these cells cross-communicate in myriad, poorly understood ways.

The complexity of the tumor-tissue system is not merely biochemical. The ECM is a mixture of elastic fibers (e.g., collagen IV) and matrix-bound signaling factors [6]. Tissue remodeling (e.g., by fibroblasts, or by migrating tumor and endothelial cells) can release these matrix-bound factors, provoking new tumor and stromal cell responses. The mechanics of the ECM also plays a role: stiffer ECM can promote increased migration and proliferation, whereas softer matrices can down-regulate proliferation and motility [7]. Moreover, the stiffness and density of the ECM affect the speed of tumor cell migration. Even the geometry of the ECM matters: tumor cells use completely different migratory mechanisms on 2-D surfaces (e.g., basement membranes) and within 3-D matrix scaffolds [8]. Tumor cells can change their phenotype (current behavioral characteristics) based upon adhesive contact with 2-D or 3-D matrix and other cells [9].

Hence, a tumor is in constant, dynamical communication with the microenvironment through biochemical and biophysical processes. The microenvironment shapes tumor cell behavior, even while tumor cells reshape the microenvironment directly (e.g., by matrix remodeling) and indirectly (e.g., by secreted signals). Tumor growth cannot be understood in isolation—it must be studied as a 3-D multicellular system, in the presence of a dynamical biochemical and biophysical environment. In spite of recent advances in biomimetic materials, bioengineered tissues, and animal models, the complex tumor-tissue system is difficult to study solely through experiments.

Computational modeling, however, can provide a platform to ask questions and test new hypotheses on this complex system. To study cancer, a 3-D multicellular simulation platform should:

• simulate the birth, death, and motion of tumor cells,

• simulate biochemical microenvironments with multiple diffusing substrates,

• simulate the biomechanics of cells and the extracellular matrix,

• simulate the evolving blood vasculature,

• simulate interstitial and microvascular flow,

• integrate the above models, along with molecular-scale models to drive cell phenotype,

• integrate high-throughput experimental data to calibrate and validate models, and

• do so reproducibly, using interoperable data formats.

In this chapter, we shall discuss progress by our groups on these problems, and outline key steps for advancing from models of individual tumor and microenvironment subsystems, to true 3-D multicellular simulation systems that are adequate for attacking the complexity of cancer.

12.2. Progress Towards 3-D Multicellular Systems Biology

12.2.1. Simulating Tumor Growth in a Heterogeneous Microenvironment

Our earliest work with John Lowengrub and collaborators [10–14] focused on describing the evolving morphology of tumors, as driven by gradients of growth substrate. Building upon work by Cristini, Lowengrub and Nie [15], we developed a sharp interface model, where a well-defined tumor boundary Σ is represented with a level set function [16, 17] φ, satisfying φ < 0 inside the tumor, φ = 0 on the boundary, and φ > 0 outside the tumor. Tumor tissue was assumed incompressible with constant cell density. ∇ • u gives the net rate of tissue creation, where u is the tissue velocity field. The tumor boundary moved with normal velocity V= u•n. Cell proliferation was proportional to available growth substrate σ, which diffused from the tumor boundary. (See Sect. 12.2.2 below.) Wherever the growth substrate concentration was below a threshold σ_N, tumor cells became necrotic, giving one of the first detailed models of necrosis [11, 12].

We modeled tumor tissue mechanics with a tissue pressure p that obeyed Darcy’s law (porous flow), simulating tumor tissue as a fluid moving through the ECM. The Darcy coefficient μ modeled several biophysical effects, including cell-matrix adhesion and matrix stiffness. Combining Darcy’s law with the incompressibility assumption gave an elliptic partial differential equation (PDE) for the pressure; a curvature boundary condition (surface tension) modeled cell-cell adhesion. These level set models took the general form:

$$\nabla \cdot u=\{\begin{array}{cc}G(\sigma -A)& \text{inside}\text{the}\text{viable}\text{tumor}\\ -G_N& \text{in}\text{the}\text{necrotic}\text{core}\\ 0& \text{elsewhere}\end{array}$$

u = −μ∇p + chemotactic terms (where needed)

V = u · n on the tumor boundary, and

$$\frac{\partial \varphi }{\partial t}=-\tilde{V}|\nabla \varphi |,$$

where V is an extension of V off the tumor boundary Σ. In the work above, G is a “tumor aggressiveness” parameter that combines the effects of cell-cell adhesion and cell proliferation, A is the relative rate of tissue loss due to apoptosis, and G_N is the rate of tissue loss in necrotic regions [13]. Constitutive relations between the model parameters and microenvironmental factors could be used to model molecular-scale biological effects. See Sect. 12.2.3 for further discussion.

A typical simulation result can be found in Fig. 12.1a [15]. Our later work [10–14] improved the biological accuracy (by separately tracking the position of the tumor’s necrotic core [13] and allowing the substrate diffusivity and Darcy coefficient to vary spatially [14]) and numerical accuracy (a more robust curvature discretization [12], a more accurate jump boundary condition discretization, and a faster numerical solver for steady-state diffusion [14]). These improvements allowed simulation of tumor growth in complex tissues, such as brain tissues with white and grey matter, cerebrospinal fluid, and cranium [10, 14]. See Fig. 12.1b.

Fig. 12.1.

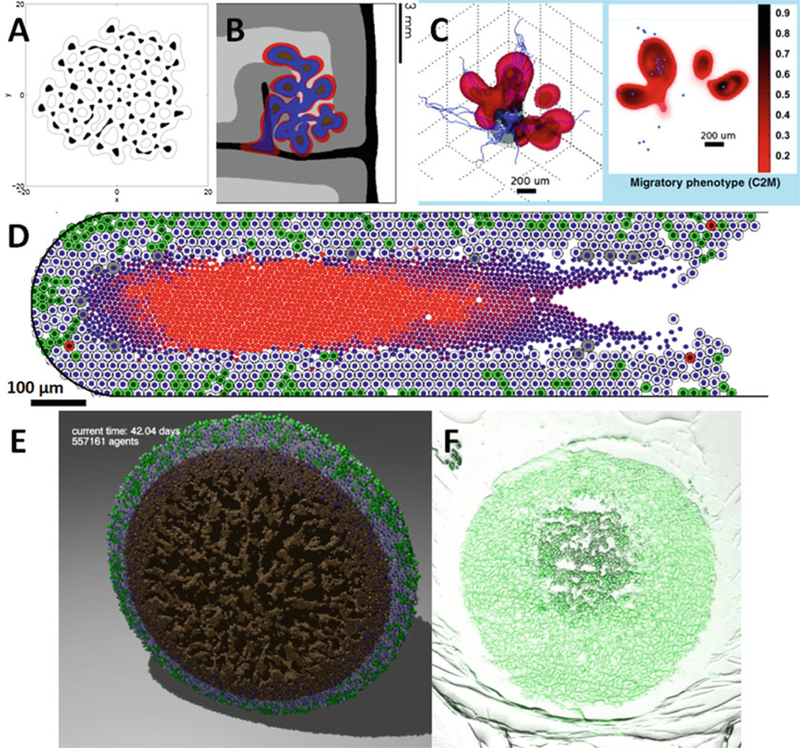
(a) A level set simulation of a tumor with viable regions (white) and necrotic tissue (black). The tumor shape can undergo complex topological changes, based upon the balance of growth and mechanics parameters (Adapted with permission from [11]). (b) Numerical refinements allowed simulation of growth in heterogeneous tissues, such as this simulated brain tumor. Red regions are proliferating, blue regions are hypoxic, and brown are necrotic. The brain tissue has white matter (light grey), grey matter (dark grey), cerebrospinal fluid (black), and cranium (white) (Adapted with permission from [52]). (c) A phase field simulation of a highly-motile subclone (red) emerging due to hypoxic signaling from a glioblastoma (grey) [7] (Adapted with permission from [7]). (d) Agent-based models—like this patient-calibrated simulation of ductal carcinoma in situ (DCIS) [19]—can simulate small-scale tissue mechanics, with more direct calibration to experimental and clinical data (Adapted with permission from [19]). (e) The agent-based model has been extended to 3D [29]. Here, we plot a cut-away view of a necrotic tumor spheroid. Green cells are proliferating, gray cells are quiescent, red cells are apoptotic, and brown cells are necrotic. Note the “crackly” structure in the necrotic core. (f) A hanging tumor drop spheroid (HCC827 non-small cell lung carcinoma) showing a similar structure in the necrotic center. Image courtesy Mumenthaler lab, Lawrence J. Ellison Institute for Transformative Medicine, University of Southern California

For improved modeling of tumor tissue mechanics, Wise, Lowengrub, Frieboes, Cristini, and others developed “phase field” or “mixture” models: each mesh site was modeled as a mixture of one or more cell types, matrix, and water [21, 22]. Each phase of this mixture was governed by conservation laws for mass and momentum; energy laws were used to govern mixing between the phases. The approach led to the introduction of Cahn-Hilliard equations of the form:

$$\frac{\partial {\rho }_i}{\partial t}+\nabla \cdot \left(u_i{\rho }_i+J_i\right)=S_i,i\in \{V,D,H\}.$$

The rate of change in the density ρ_i of cell species i (V: viable tumor; D: dead tumor; H: host) is determined by balancing net creation (S_i: proliferation minus cell death) with cell advection (∇ • (u_iρ_i)) by its velocity field u_i, and cell-cell and cell-ECM mechanical interactions (∇ • J_i), where the flux J_i generalized Fick’s law to include adhesion, cell incompressibility, chemotaxis, haptotaxis, and other biomechanical effects [21, 22].

The viable tumor cell density ρ_V increased through proliferation and decreased through apoptosis and necrosis. We assumed that normal host cells (ρ_H) do not proliferate but can apoptose (A) or necrose (N); the total dead cell density is ρ_D. These primarily affect tumor mass through water transport in the tissue; their solid fraction is neglected for simplicity [22]. Proliferation was assumed to increase with nutrient substrate σ above a threshold level σ_N [22], resulting in the creation of cells by removing the equivalent water volume from the interstitium. Cells experiencing a substrate level below σ_N were considered quiescent (e.g., due to hypoxia). Apoptosis transferred cells from the viable tumor and host cell species to the dead cell species, where cells degraded and released their water content. Necrosis occurred when the nutrient substrate concentration falls below the threshold σ_N and ultimately releases cell’s water content. The resulting model is

$$\begin{gathered} S_V=\left({\text{λ}}_{M,V}\left(\sigma -{\sigma }_N\right)-{\text{λ}}_{A,V}\right)H\left[\sigma -{\sigma }_N\right]{\rho }_V \\ -{\text{λ}}_{N,V}H\left[{\sigma }_N-\sigma \right]{\rho }_V \end{gathered}$$

$$\begin{array}{l}{S}_D=H\left[\sigma -{\sigma }_N\right]\left({\text{λ}}_{A,V}{\rho }_V+{\text{λ}}_{A,H}{\rho }_H\right)\\ +H\left[{\sigma }_N-\sigma \right]\left({\text{λ}}_{N,V}{\rho }_V+{\text{λ}}_{N,H}{\rho }_H\right)-{\text{λ}}_D{\rho }_D,\end{array}$$

Where λ_M,i, λ_A,i, and λ_N,i, are mitosis, apoptosis, and necrosis rates, λ_D is the cell degradation rate (with different values in apoptotic and necrotic tissue), and H is the Heaviside “switch” function.

Each cell species moves under the balance of proliferation-generated oncotic pressure, cell-cell and cell-ECM adhesion, chemotaxis (due to substrate gradients), and haptotaxis (due to gradients in the ECM density). The motion of cells and interstitial fluid through the ECM is modeled as flow of a viscous, inertialess fluid in a porous medium. We made no distinction between interstitial fluid hydrostatic pressure and mechanical pressure due to cell-cell interactions. Cell velocity is a function of cell mobility μ_i and tissue oncotic (solid) pressure (Darcy’s law); cell-cell adhesion is modeled with an energy approach from continuum thermodynamics [22]. For simplicity, the interstitial fluid is modeled as moving freely through the ECM at a faster time scale than the cells. These assumptions yield a constitutive relation for the tumor tissue velocity field u_i:

$$\begin{array}{l}{\rho }_i{u}_i+J_i=-{\mu }_i\left({\rho }_i,f\right)\left(\nabla p-\sum _j\frac{{\gamma }_j\delta E}{\delta {\rho }_j}\nabla {\rho }_j\right)\\ +{\chi }_{\sigma }\left({\rho }_i,f,\sigma \right)\nabla \sigma \\ +{\chi }_h\left({\rho }_i,f\right)\nabla f,i\in \{V,D,H\}.\end{array}$$

The variational derivative δE/δρ_i, combined with the remaining contributions to the flux J (due to pressure, haptotaxis, and chemotaxis; see [22]), yields a generalized Darcy-type constitutive law for the cell velocity u_i of a cell species i, determined by the balance of proliferation-generated oncotic pressure p, cell-cell and cell-ECM adhesion, chemotaxis (due to gradients in the cell substrates σ), and haptotaxis (due to gradients in the ECM density f). The Darcy coefficient μ_i is cellular mobility, reflecting the response to pressure gradients and cell-cell interactions by breaking integrin-ECM bonds and deforming the host tissue. γ_j is the cell adhesion parameter, and χ_σ and χ_h are the chemotaxis and haptotaxis coefficients, respectively.

Solving this system required sophisticated numerical techniques [23], but the work was worth-while: it allowed modeling new tissue biomechanics (see Sect. 12.2.3 below) to address drawbacks in the level set approach [11–14]. In particular, the phase field model could simulate mixed populations of tumor sub-clones without sharp boundaries between them. In [18], we simulated the 3-D growth of glioblastoma multiforme using the new phase field model. In the work, hypoxic tumor cells could mutate into a more motile subclone, modeled as a new phase in the phase field model. See Fig. 12.1c. In Sect. 12.2.3, we give another example of this model for simulating lymphoma [24]. Similar models were also developed to account for cell type and mechanical response heterogeneity of the solid and liquid tumor phases. See the review [25] for further discussion.

One difficulty for continuum models is that individual cell phenotypes (particularly for heterogeneous cell populations) cannot be fully resolved at the continuum scale. Allowing model parameters to vary at cell-scale resolution (e.g., 20 μm) and solving for the cell densities at cell-scale resolution rather than tissue-scale resolution (e.g., 100–200 μm) can result in small protrusions and other features that, while numerically accurate, are in violation of the models’ continuum hypotheses; these cannot be regarded as meaningful scientific results. Another difficulty for continuum models is matching to experimental and clinical data. Parameters such as μ in the models above incorporate multiple biophysical and biological effects, so calibration may require iteratively testing the model parameters until shape and other metrics match data at multiple time points. Such matching risks overfitting an underconstrained model, bringing scientific conclusions into doubt. “Bottom-up” calibration from direct cell-scale measurements can help overcome these problems, but direct mappings of such cell-scale measurements onto multiple-effect parameters are unclear. Both these difficulties can be addressed with cell-scale (discrete) models.

In [19], we developed an agent-based model of cancer, with application to ductal carcinoma in situ of the breast (DCIS). In this work, tumor cells in a duct (represented as a level set function) can be quiescent (Q), cycling (P), apoptotic (A), or necrotic (N) in regions of insufficient oxygen. Tumor cells obeyed conservation of momentum, with cell motion determined by a balance of adhesive and “repulsive” forces exchanged with other cells and the duct wall and fluid drag. The probability of changing state (Q, P, A, and N) depended upon the microenvironmental conditions. Cycling cells divided and regrew volume, apoptotic cells shrunk, and necrotic cells shrunk and calcified; this was the first model of calcifications in DCIS with comedonecrosis (a centralized core of necrotic material, which may be partially calcified) [5]. See Fig. 12.1d for a typical DCIS simulation. Individual cell phenotypes can be clearly observed and tracked (green cycling cells, gray quiescent cells, red apoptotic cells, and a central core of necrotic cells in varying states of degradation and calcification). A movie of this simulation can be found at [26].

We recently extended the model to 3D and increased its simulation capacity from thousands of cells to 10⁵ to 10⁶ cells on desktop workstations. The extended code (PhysiCell: physics-based cell simulator) is being prepared for a 2016 open source release [20]. See Fig. 12.1e for a PhysiCell simulation, showing a cross-section of a 3-D hanging drop spheroid with a necrotic core. The competing effects of the 3-D multicellular geometry, necrotic cell contraction (from water loss), and necrotic cell adhesion result in a fractured necrotic core structure, which can be observed in experimental data (Fig. 12.1f). For PhysiCell project updates, see http://PhysiCell.MathCancer.org. Several other open source model frameworks can simulate many cells in 3D, including Chaste [27], CompuCell3D [28], Morpheus [29], and iDynoMiCS [30]. In Sect. 12.2.5, we shall revisit the agent-based model in the context of direct calibration to experimental and pathology data.

12.2.2. Simulating the Chemical Microenvironment with Many Substrates

Substrate transport is critical to representing the tumor microenvironment. Growth substrates are released by the vasculature, transported within the tissue, and consumed by cells, which subsequently release metabolic waste products. Cells exchange diffusible signaling factors that alter phenotype. Apoptotic and necrotic cells may also release diffusing substrates that affect phenotype [5]. In our earliest work [11–14], we modeled substrate transport as quasi-steady, requiring a steady state solution after evolving the tumor morphology. Thus, we solved PDEs of the form

$$0=\nabla \cdot (D\nabla \sigma )-{\text{λ}}_{\text{background}}\sigma -\text{λ}(\text{cells})+\text{Sources}$$

with appropriate boundary conditions. In the first level set models [10–14, 31], we imposed a Dirichlet boundary condition on the tumor boundary to simulate growth into a well-vascularized tissue. Later, we embedded the evolving tumors into a larger domain with substrate diffusion and Dirichlet conditions as a far-field condition, to model growth into a locally-affected region [13]. We used a jump boundary condition to enforce continuity of substrate flux across the tumor boundary, using the ghost fluid method [11]. In 2D, the method yielded a banded linear system, which we solved with the stabilized biconjugate gradient method. (See the references in [11].) However, this technique was slow, not terribly robust, and difficult to extend to more accurate discretizations of the jump boundary conditions. In [14], we introduced a pseudotime τ:

$$\frac{\partial \sigma }{\partial \tau }=\nabla \cdot (D\nabla \sigma )-{\text{λ}}_{\text{backround}}\sigma -\text{λ}(\text{cells})+\text{Sources}$$

and solved to steady state using a semi-implicit finite difference scheme. The method was stable and second-order accurate in the steady-state solutions, but it could not (and was not designed to) capture the dynamics of the evolving substrate distribution. Many models (e.g., [32]) solve the time-dependent problem using explicit finite difference methods. While these methods are straightforward to implement and accurate, their stringent time step restrictions make them unfeasible for 3-D simulations or for simulating many substrates. Implicit methods like ADI (alternating directions implicit, method; see [33] for a model using this method) can remove the time step restrictions, but they often require linking to linear algebra libraries that can complicate cross-platform compatibility. (See the discussion in [34].) In [21, 22], Wise, Lowengrub, Frieboes, and co-workers took an alternative approach by using a fully adaptive, nonlinear multigrid/finite difference method to efficiently solve the equations [23].

One drawback of these approaches is that they do not scale very well to larger numbers of substrates, particularly in large 3-D domains. Each evolving substrate distribution requires solving a PDE. Most of these codes—including those above—solve the PDEs sequentially, and so simulating ten diffusing substrates requires ten times the computational effort of simulating one. This does not scale well as the number of substrates and the domain size are increased.

We recently addressed these problems by creating BioFVM (finite volume method for biological problems), an open source 3-D diffusion solver that was designed for both standalone simulations and for integration with existing simulation packages [34]. See http://BioFVM.MathCancer.org. BioFVM solves for a family of diffusing substrates vectorially:

$$\begin{array}{l}\frac{\partial \mathbf{p}}{\partial \text{t}}=\mathbf{D}\circ {\nabla }^2\mathbf{p}-\text{λ}\circ \mathbf{p}+\mathbf{S}\circ \left({\mathbf{p}}^{*}-\mathbf{p}\right)-\mathbf{U}\circ \mathbf{p}\\ +\sum _{\text{cells}i}\left({\mathbf{S}}_i\circ \left({\mathbf{p}}_i^{*}-\mathbf{p}\right)-{\mathbf{U}}_i\circ \mathbf{p}\right){\delta }_i{V}_i\end{array}$$

where p is a vector of diffusing substrates, D and λ are vectors of diffusion and decay constants (respectively), S and U terms are vectors of source and uptake rates (respectively), p* terms are vectors of saturation densities, and all products (°) are component-wise. Here, V_i is the volume of the i^th cell in a simulation environment, and δ_i is a Dirac delta function centered at its position.

By using a combination of operator splitting, vectorized operations, tailored ODE and Thomas solvers, specialized overloaded operators to reduce the memory-bound costs, and OpenMP parallelization, BioFVM can simulate diffusion of ten or more substrates on 3-D domains with a million or more voxels (enough to simulate diffusion in a 8 mm³ tissue at 20 μm resolution), using just a desktop computer. Simulating ten substrates requires only 2.6 times more effort than simulating one, and we have simulated up to 128 substrates. See Fig. 12.2 (top). The code is first-order accurate in time, second-order accurate in space, and numerically stable. Computational time scales linearly with the number of substrates, number of voxels, and the number of cell-based source/sink terms. In Fig. 12.2 (bottom), we simulate oxygen and VEGF transport in a 125 mm³ tissue (15,625,000 voxels) with over 2.8 million discrete source/sink terms, using a quad-core desktop workstation. Larger simulations are be feasible on individual HPC compute nodes, which often have 16 computational cores (32 virtual CPUs when including hyperthreading) and 32 GB of memory.

Fig. 12.2.

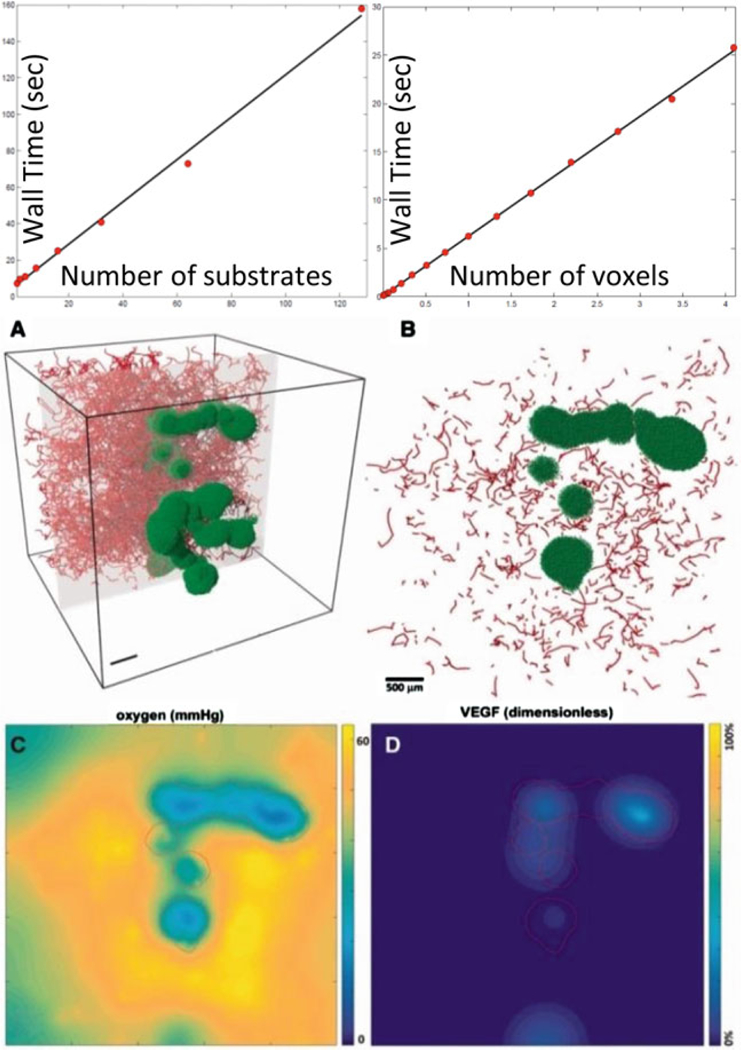
Top: BioFVM shows roughly Linear cost scaling with the number of substrates and voxels. (See the supplementary material in [34]). Bottom: Simulation of O₂ release by blood vessels (red line sources in a, b), diffusion, and consumption by tumor cells (green), and VEGF release by hypoxic tumor cells. (c, d) plot the pO₂ and VEGF distributions in the gray plane in (a) (Adapted with permission from [34])

12.2.3. Simulating the Physical Microenvironment

In [13], we performed our first investigations of the impact of the microenvironment on tumor shape. We enclosed the tumor in a larger circle of tissue where growth substrate σ diffused with coefficient D_tissue (the diffusion coefficient was set at D_tumor inside the tumor), and the mechanical pressure p dissipated with Darcy coefficient μ_tissue outside the tumor and μ_tumor inside the tumor. We assumed that the substrate was continuous across the tumor boundary Σ with no jump in flux (D_tumor∇σ•n – D_tissue∇σ•n = 0 on Σ). We modeled the mechanical pressure as solving p_tumor – p_tissue = k (an extension of the curvature-based cell-cell adhesion in [11, 12]), with no jump in the flux of the pressure across the tumor boundary (μ_tumor∇p•n – μ_tissue∇p•n = 0 on Σ). We varied by the microenvironmental conditions through the ratios

$$D=\frac{D_{\text{tissue}}}{D_{\text{tumor}}}\text{and}\mu =\frac{{\mu }_{\text{tissue}}}{{\mu }_{\text{tumor}}}.$$

Large values of D represented growth into a well-oxygenated tissue; large values of μ modeled growth into a soft, mechanically-compliant tissue. We found that the (D,μ) parameter space divided into three phases: tumors broke into small fragments when growing in poorly-oxygenated tissues (low D), whereas they developed invasive fingers in mechanically stiff, vascularized tissues (high D, low μ). In well-oxygenated, soft tissues (high D, high μ), relatively compact tumor shapes emerged. See Fig. 12.3a. These results were similar to cellular automaton model findings by Anderson and co-workers [32, 37], which examined the impact of oxygen heterogeneity and cell-cell adhesion upon tumor shape stability, but without modeling tissue mechanics.

Fig. 12.3.

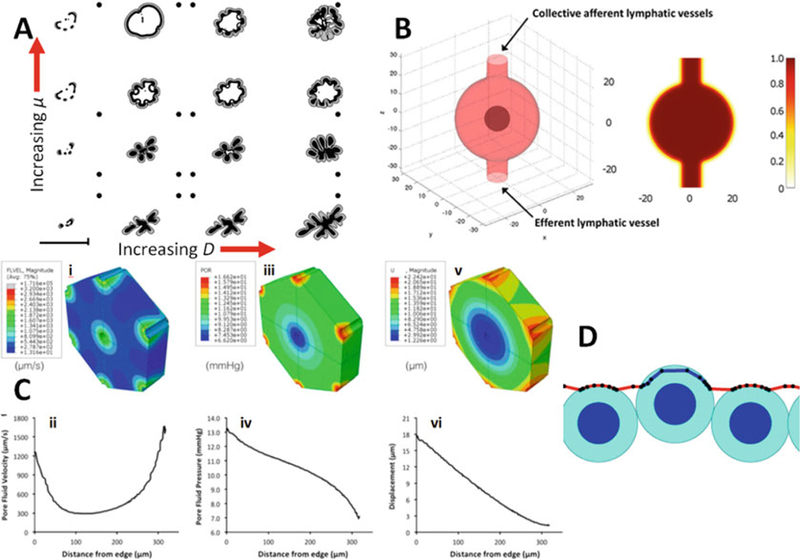
(a) A phase diagram of tumor shape (grey regions are viable; black regions are necrotic) of the (D,μ) parameter space [13]. Increasing D models increasing vascularization in the tissue surrounding the tumors; increasing μ models decreasing stiffness in the surrounding tissue. Three characteristic morphologies are seen: fragmenting (low D), fingering/invasive (high D, low μ), and compact growth (high D, high μ) (Adapted with permission from [13]). (b) Simulation of lymphoma in a lymph node [25], using the phase field method to represent the live and dead tumor cell populations, fluid, and the lymphatic vessel outer wall (Adapted with permission from [25]). (c) A poroviscoelastic (PVE) simulation of perfused liver tissue [66]. i,ii: pore fluid velocity. iii,iv: pore fluid pressure. v,vi: solid matrix deformation (Adapted with permission from [66]). (d) Discrete-scale models [13] can investigate smaller-scale tissue biophysics, such as this simulation of passive cell invasion through a weakened section of basement membrane (Adapted with permission from [13])

In [10, 14, 31], we extended the level set framework to let μ vary continuously across the tissue, as a model of mechanical variations. In our first such studies [10, 14] (tumors growing in brain tissue), the Darcy coefficient μ was set to a higher value (μ = 1.5) in relatively pliant white matter, a lower value (μ = 0.5) in stiffer grey matter, a high value (μ = 10) in cerebrospinal fluid, and a very low value (μ = 0.0001) in non-deformable cranium. In the simulations, tumor grew preferentially in regions of higher μ, and mechanical pressure built up between the growing tumor and the cranium. See Fig. 12.1b. In later work [31], we studied tissue remodeling by simulating the release of a diffusing matrix-degrading enzyme that removed ECM (E). Moreover, we introduced a constitutive relation between the ECM density and the Darcy coefficient:

$$\mu =\frac{{\mu }_0}{a+bE},$$

so that increasing ECM density decreased the Darcy coefficient, thus increasing the overall tissue stiffness and reducing its permeability to cells. Interestingly, this constitutive relation can be obtained mechanistically by considering the individual force terms in agent-based models discussed above, under the inertialess assumption that dissipative forces like fluid and ECM drag balance quickly with adhesive, motile, and other forces. (See the supplementary materials in [19].) A movie of an example simulation including the effects of tissue degradation and ECM-dependent cell mobility can be found at [38]. We note that later, higher-resolution studies of matrix degradation found that common reaction-diffusion type models cannot adequately model tissue remodeling without including the impact of activation factors and inhibitors (otherwise, they over-predict tissue degradation), and that the more common membrane-bound matrix metalloproteinases should not be modeled as diffusing species, even with very small diffusion coefficients [39].

While the level set models were able to simulate changing tumor shapes in heterogeneous, evolving microenvironments, they had several shortcomings. The tissue biomechanics were constrained by the constant cell density assumption. Cell-to-cell adhesion could not vary throughout the cell tissues (since it was modeled as a surface tension). Individual cell effects were difficult to include, particularly on smaller scales. While the sharp interface assumption was well-suited to strongly-adherent epithelial tumors, it could not model low-adhesion, highly motile cell species such as glioblastoma cells [40] and stromal cells [41]. Hence, the sharp interface tumor model could not readily apply to other cell types of interest in cancer biology, making it difficult to study the biomechanical dynamics of tissue remodeling and the impact on tumor growth. Even in cases where the sharp interface assumptions were valid, new cell populations could only be modeled by introducing new level set functions, with a large increase in computational cost.

Phase field/mixture models (see Sect. 12.2.1) can simulate sophisticated tissue biomechanics in more generalized cases where different cell types are mixed without sharp boundaries, or where the extracellular matrix itself must be evolved. For example, in [24], the lymph node was modeled as a surface Г that is stretched by the growing tumor, with membrane normal velocity proportional to the proliferation-generated pressure gradient. It was assumed that the tissue surrounding the organ can be deformed sufficiently to accommodate expansion [42]. The geometry is described by a phase field variable ψ governed by a modified Cahn-Hilliard equation:

$$\begin{gathered} \frac{\partial \psi }{\partial t}+v\cdot \nabla \psi =\nabla \cdot \left(B(\psi )\nabla {\mu }_{\psi }\right),\text{where}\psi (x,t) \\ =\{\begin{array}{l}1\text{inside}\text{the}\text{lymph}\text{node}\hfill \\ 0\text{outside}\text{the}\text{lymph}\text{node}\hfill \end{array} \end{gathered}$$

specifies the position of the interface Г through the narrow transition region characterized by a thickness parameter ε in the Cahn-Hilliard potential μ_ψ. B(ψ)=36 ψ²(1–ψ)² specifies the interfacial region [43, 44] where the Cahn-Hilliard potential takes effect. The surface Г is advected by the mechanical pressure (P) generated by tumor proliferation and the tissue surface tension [22]:

$$v=-\mu \left(\nabla P-\frac{\gamma }{ϵ}{\mu }_{\psi }\nabla \psi \right),$$

where γ specifies the strength of the surface tension, and μ is the tissue mobility in response to these exerted forces. In Fig. 12.3b, we show an example of simulating non-Hodgkin’s lymphoma in a lymph node from [24]. The phase ψ was used to represent the outer wall of the lymph node as discussed above, allowing later simulation of lymph node swelling—a common feature in lymphoma and metastatic carcinoma [45, 46].

The phase field mixture approach allows generalized modeling of a wide range of tissue mechanics, with separate constitutive relations and parameters for each phase of the simulated cell-ECM-fluid mixture. However, water was modeled as flowing freely through the simulated domain, and hence decoupled from the evolving ECM and cell phases. In some tissues, advective interstitial and microvascular flow couple significantly with the solid components of the tissue, causing deformation. Tissues in this flow regime can demonstrate viscoelastic properties [47].

Continuum models of flow through deformable porous media [48] are computationally efficient and do not require precise spatial and geometric information about every fiber or cell in a tissue [49]; hence they are well-suited for modeling perfusion in porous materials [50]. Similarly to the phase field model, poroviscoelastic (PVE) models use a continuum approximation to simulate both tissue mechanics and pore fluid behavior in tissue parenchyma. PVE is an extension of poroelastic or biphasic theory, to model material as a porous fluid-saturated linear elastic solid in which the fluid flows relative to the deforming solid [35, 48]. A poroviscoelastic model incorporates time-dependent (viscous) effects from two different sources: pore fluid movement through the matrix and intrinsic viscoelasticity of the solid matrix itself [51]. Thus, PVE models are well-suited for materials which exhibit significant viscoelastic behavior, such as liver [47], brain [52], or cartilage [51]. Since PVE models predict pore fluid pressure and velocity in addition to solid matrix stress, this modeling strategy is attractive for examining perfused tissue in both native and decellularized states [53, 54]. For example, we recently characterized the biomechanical response of perfused native and decellularized liver on both macroscopic and microscopic length scales via spherical indentation tests, then used PVE finite element models to extract the fluid and solid mechanical properties from the experimental data [53]. In another recent study, we used PVE modeling to predict lobule-scale stresses and deformations associated with experimental perfusion rates for native and decellularized livers [35]; the work was able to effectively predict flow rates and mechanical deformation in both decellularized and native liver tissues. See Fig. 12.3c. On the whole, PVE theory offers an effective technique for determining the tissue-scale spatial distribution of key microenvironmental variables related to ECM mechanics and interstitial flow.

Discrete models can simulate tissue mechanics while incorporating localized, micron-scale biology, particularly for thin basement membranes that cannot be accurately modeled with tissue-scale continuum models [39]. In [36], we developed a 2-D discrete plasto-elastic model of basement membrane. The membrane was written as a linked list of basement membrane agents centered at x_k, each of which was linked to two neighboring agents at x_k-1 and x_k+1. The total force F^k acting on the portion of basement membrane at x_k was modeled as:

$$F^k={\sum }_{\text{cells}i}\left(F_{\text{cba}}^{ik}+F_{\text{cbr}}^{ik}\right)+F_{\text{BM}}^k+F_{\text{ECM}}^k-v{v}_k,$$

where F_cba^ik and F_cbr^ik are the cell-BM adhesive and repulsive forces, respectively (modeled with potential functions as in [19]), F_BM^k is the force exchanged with neighboring portions of basement membrane, F_ECM^k is the elastic force between the portion of basement membrane and the nearby stroma, and υv_k is the dissipative, drag-like force acting against the basement membrane’s velocity v_k. We modeled F_BM^k as elastic:

$$\begin{gathered} F_{\text{BM}}^k=-\frac{K_{k+1}\left({\mathcal{l}}_{k+1}-{\mathcal{l}}_{k+1,0}\right)}{{\mathcal{l}}_{k+1}}\left(x_k-x_{k+1}\right) \\ -\frac{K_k\left({\mathcal{l}}_k-{\mathcal{l}}_{k,0}\right)}{{\mathcal{l}}_k}\left(x_k-x_{k-1}\right) \end{gathered}$$

where K_k is the elastic modulus of the basement membrane at x_k, and ℓ_k and ℓ_k,₀ are the current and resting lengths of the basement segment centered at x_k, respectively. We introduced additional constitutive relations to relate the elastic modulus K_k to the amount of material present in the basement membrane section at x_k and to the thickness of the basement membrane at that section; see [36] for further details. While the basement membrane is elastic over relatively short time scales, it can undergo plastic rearrangement over longer time scales as elastic fiber cross-links break and reform. We modeled this as an evolution of the resting length ℓ_k,0:

$$\frac{d{l}_{k,0}}{dt}=r{l}_k\text{max}(0,l_k-l_{k,0}-{\tau }_{\text{act}})$$

where τ_act is a threshold stress level above which ECM cross-links begin to break [55].

An example of this model can be seen in Fig. 12.3d. We were able to model small-scale interactions between basement membrane and cells. In particular, we found that if a small section of basement membrane is weakened (by reducing the amount of matrix material in the k^th BM agent, and then reducing its elastic modulus via the constitutive relation), then passive elastic forces alone can result in epithelial cell protrusion into the stroma (Fig. 12.3d) [36]. In [39], we used the framework to investigate the time scales of basement membrane degradation by matrix metalloproteinases, finding that realistic, 100 nm thick basement membranes can readily be penetrated in just 10–15 min. However, these models have proven difficult to implement efficiently in 3D. Moreover, solving basement membrane mechanics with micron-scale resolution is not scientifically meaningful when cell morphologies are not resolved, as in our present agent-based models. (These resolve cell position and volume, but not morphology.)

Other groups have addressed this problem by modeling extracellular matrix at the multicellular scale using modified agents. For example, to emulate the invasion of breast cancer from a duct to the surrounding stroma, Bani Baker and coworkers used small agents with different properties to model both basement membrane (BM) and extracellular matrix (ECM) [56]. Modeling ECM as a matrix of small particles allows changing the ECM structure by varying the number and type of interactions between matrix particles. For example, to model the ECM stiffening as the result of lysyl oxidase presence [57], one can increase the crosslinking between the particles.

12.2.4. Simulating the Evolving Microvasculature and Interstitial Flow

In [58–60], Anderson, Chaplain, and McDougall developed a sophisticated 2-D cellular automaton model of tumor-driven sprouting angiogenesis. In the model, each lattice site on a regular Cartesian mesh could contain ECM, a tumor cell, an endothelial cell, or a migrating sprout tip. Blood vessels released oxygen, which diffused through the tissue and was consumed by tumor cells. Hypoxic tumor cells released VEGF, which diffused through the tissue and could activate endothelial cells and “convert” them to migrating sprout tips. The sprout tips followed a random walk up gradients of VEGF (chemotaxis) and ECM (haptotaxis) to form new vessels by leaving a trail of endothelial cells behind them. They solved for blood flow in the connected network of endothelial cells, including the nonlinear effects of the plasma and solid hematocrit phases of the blood. Sheer stresses drove network remodeling.

In [31], we coupled the level set tumor growth model (see Sect. 12.2.1) to this angiogenesis model. As before, the vasculature released oxygen, but with an improved source function: oxygen release was proportional to hematocrit (as an indicator of flow) and the difference between the vascular and tumor pressure. Hypoxic tumor regions released VEGF, tumor tissue could remodel the ECM by secretion and degradation processes, and notably, regions of high tumor pressure could collapse vessels, thereby interrupting flow in the vascular network and creating new regions of hypoxia and renewed angiogenesis. See [31, 61] for a simulation movie. In [62], we extended the work to include interstitial fluid flow. See Fig. 12.4 left. This work provided key insights on coupling the biomechanics and biochemistry of the microenvironment, tumor growth, and angiogenesis. However, it had several drawbacks, most notably being restricted to 2D, and its reliance upon a non-physical Cartesian arrangement of blood vessels.

Fig. 12.4.

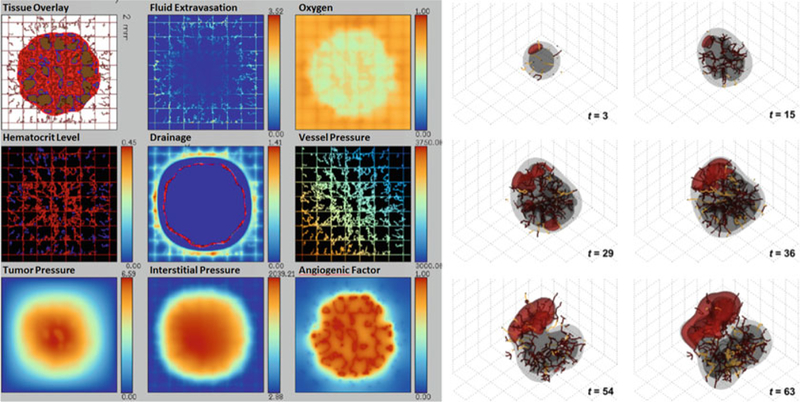
Left: Simulation of vascularized tumor growth and interstitial flow from [95], in which we extended our prior coupling [31] of a discrete angiogenesis model [4, 56, 57] with a level set tumor growth model [11–14] (Adapted from [95] with permission). Right: We later developed off-lattice, 3-D models of vascular growth [23] that included vascular pruning due to tumor-generated mechanical pressure (Adapted with permission from [23])

In [21], we built a 3-D lattice-free model of angiogenesis, building upon this earlier cellular automaton work [58–60] and refining off-lattice models by Plank and Sleeman [63, 64]. The model generates a vascular network dependent on tumor angiogenic factors [65] (e.g., VEGF), implemented via a single continuum variable c reflecting the net balance of pro- and anti-angiogenic regulators. Hypoxic tumor cells released c, which caused endothelial cells to proliferate and grow vessels towards the tumor by haptotaxis and chemotaxis [66]. Migrating endothelial sprout tips were assigned a fixed probability of branching at each time step of the simulation. Vessels were required to form loops (anastomose) before delivering growth substrates [67]; the vessels could connect if a leading endothelial cell crossed the trailing path of another vessel. Tumor proliferation-induced solid tissue pressure could cause vessels to spontaneously shut and regress [68]. We did not model microvascular blood flow or flow-induced changes in the vasculature (e.g., shear stress-induced branching). Instead, we focused on assessing the effect of local heterogeneity of growth substrates on the tumor species. A typical simulation can be seen in Fig. 12.4 right. We have used this model extensively in other investigations of 3-D tumor growth [18, 24].

The flow component in the PVE model (Sect. 12.2.3) is also well-suited to modeling interstitial flow in conjunction with these angiogenesis models. In [35] we used PVE models to create tissue-scale predictions of the distribution of interstitial fluid pressures and velocities across a decellularized hepatic lobule. Models were coupled to varying experimental perfusion flow rates [69]; results for trials at the 9 ml/min flow rate are highlighted here. Terminal and pre-terminal portal vein branches, located at the periphery of the lobular hexagonal prism (Fig. 12.3c) were used as the fluid inlets, and the central vein served as the fluid outlet. Prescribed pressures were applied to inlet and outlet vessel surfaces based on generation-specific pressures predicted by a previously developed electrical analog model of liver hemodynamics [35], for the appropriate flow rate. Poroviscoelastic material properties of perfused decellularized liver found in our previous work [53] were used as reported, while hydraulic conductivity was calculated from fluid properties (density, viscosity), vessel geometry, and void ratio data obtained from microscopy images of decellularized liver. Distributions of pore fluid pressure, pore fluid velocity, and ECM strain were then calculated from the finite element simulation. Average pore fluid pressure across the decellularized lobule (1.90 mmHg) agreed well with experimental interstitial fluid pressure for decellularized liver perfused at 9 mL/min (1.95 ± 1.16 mmHg, [69]). Fluid velocities ranged from 300 to 1700 μm/s over the decellularized lobule, with an average value of 618 μm/s. This result falls at the high end of the 100–750 μm/s plasma velocity range reported for in vivo native liver [70–73], as expected since vascular resistance is lower in decellularized liver compared to native [69]. It was also found that our native model pressure and velocity results for physiological flow rates were consistent with literature values [70–74].

12.2.5. Calibration to and Validation Against Clinical and Experimental Data

If multicellular systems modeling is to have an impact in explaining biological phenomena and predicting tumor growth dynamics, models must be calibrated to and validated against experimental and clinical data. If data are fitted by iteratively refining parameter values to obtain a match, then independent measurements must be used for model validation. In the level set and phase field models presented in Sect. 12.2.1, parameters such as G and μ incorporate multiple biophysical and biological effects. Early calibration efforts (e.g, [75]) calibrated a level set tumor model by (1) estimating the apoptosis and cell division time scales in the apoptosis parameter A, (2) fitting experimental tumor steady radius measurements to theoretical shape stability analyses [15] to constrain the tumor aggressiveness parameter G, and (3) matching growth curves. While the fitted models gave meaningful insights on tumor growth dynamics, we were motivated to move towards more direct calibration techniques. Using the agent-based model [19] described in Sect. 12.2.1, we took the approach of estimating or calibrating a larger set of simpler, biophysically meaningful parameters, most of which could be directly calibrated to cell-scale measurements.

In [19], we developed the first patient-specific calibration technique (for DCIS) that could fully constrain an agent-based model to pathology data from a single time point. After estimating cell cycle, apoptosis, and necrosis time scales, we coarse-grained the model to derive a system of differential equations for the fractions of apoptotic (AI) and proliferative (PI) cells in the viable rim:

$$\begin{gathered} \frac{d[\text{PI}]}{dt}=\langle {\alpha }_P\rangle (1-[\text{Al}]-[\text{Pl}]) \\ -\frac{1}{{\tau }_P}\left([\text{PI}]+{[\text{PI}]}^2\right)+\frac{1}{{\tau }_A}[\text{AI}][\text{PI}] \end{gathered}$$

$$\begin{gathered} \frac{d[\text{AI}]}{dt}=\langle {\alpha }_A\rangle (1-[\text{Al}]-[\text{PI}]) \\ -\frac{1}{{\tau }_A}\left([\text{AI}]-{[\text{AI}]}^2\right)+\frac{1}{{\tau }_P}[\text{AI}][\text{PI}] \end{gathered}$$

where ˱α_P˲ and ˱α_A˲ are the mean transition rates for quiescent cells to the proliferative and apoptotic states, respectively, and τ_P and τ_A are previously-estimated durations of the proliferative and apoptotic states. Assuming that the relative fractions of proliferative, apoptotic, and quiescent cells reach a balance after several days in a steady microenvironment [13], we solved the system above to steady state with patient measurements of PI (via Ki-67, a standard nuclear immunohistochemical marker for cell proliferation [76]) and AI (via cleaved Caspase-3, a cytoplasmic marker for apoptosis [77]) to obtain patient-specific estimates of ˱α_P˲ and ˱α_A˲. We used a similar approach to calibrate cell-cell mechanical interactions: published experimental data on cell mechanical relaxation were used to estimate the overall cell mechanics timescale, and we used patient-specific measurements of cell density to calibrate the mean cell volume and equilibrium spacing between cell centers. We set the cell-cell adhesive force parameter by setting cell adhesion and repulsion in equilibrium at the mean cell-cell spacing. We estimated oxygen boundary conditions by matching steady-state, radially-symmetric solutions of the oxygen transport equations to the patient’s (mean) ductal geometry. We later refined this calibration protocol to better account for cell confluence, and the fact that Ki-67 stains positive not only in cells preparing to divide, but also those in G₁ state immediately after division [78].

We seeded a 2-D section of a patient’s breast duct with calibrated DCIS cells and simulated 45 days of growth along a 1.5 mm length of the duct. After several days, a viable rim and necrotic core emerged (See Fig. 12.1d) with sizes consistent with our calibration data. We tracked the leading viable and calcified cells: these positions advanced linearly in time, due to the balance between substrate-limited growth in the viable rim and tissue volume loss in the necrotic center. Moreover, the simulated growth curve predicted that DCIS grows along the ducts at approximately 1 cm/year, similar to prior clinical measurements [79, 80]. The model also predicted a linear mammography-pathology size correlation, and after extrapolating this relationship over two orders of magnitude, the mammography-pathology correlation was consistent with an earlier clinical study [81]. Hence, a “bottom-up” calibration to cell-scale data can yield meaningful tissue-scale predictions. In later work [82], we matched the equations in the coarse-grained agent-based model to the level set model of tumor growth in [15], allowing us to directly calibrate A to pathology-scale data without fitting. We then used prior theoretical results [15] to compute the steady-state DCIS resection area, with successful predictions (as validated against post-mastectomy pathology size measurements not used in the calibration process) in 14 of 17 patients.

In [24], we extended the calibration technique to simulation studies of non-Hodgkin’s lymphoma. The work aimed to attain a deeper understanding of lymphoma growth in the inguinal lymph node and transport barriers to effective treatment. Cell-scale data were obtained by fine sectioning across whole tumors within lymph nodes, yielding 3-D cell-scale information. After calibrating the phase field model (Sects. 12.2.1 and 12.2.3) to these cell-scale data for two different lymphoma cell lines, the simulations correctly predicted tissue-scale, in vivo observations of growth dynamics and tumor size, without fitting to the data. This work also gave new insights on the physical causes for drug therapy failure in resistant Eμ-myc Arf−/− lines: it found that the cells were more densely packed in the lymph nodes than sensitive lines, thus exacerbating drug delivery gradients. This is a critical consideration when attempting to quantify and predict the treatment response.

These examples demonstrate that computational models can be successfully calibrated to experimental and clinical data, and used to make scientifically and clinically useful predictions. However, most of this work required substantial manual coding to make use of the measurements, which themselves required custom image analysis routines. For multicellular modeling to be both useful and widespread, it must transition from single-use, custom-built prototypes to a generalized workflow that can automatically extract model parameters from high-throughput data.

We have developed experimental platforms to characterize cell phenotype (cell birth and death rates, motility, and other parameters) in controlled microenvironmental conditions. Using the Operetta high content screening (HCS) platform and Harmony image analysis software (PerkinElmer), we can convert cell-based images into detailed quantitative phenotypic information across different timescales, environmental contexts, and in high-throughput. Our automated image analysis protocol can rapidly generate single-cell data for millions of cells. Cells can be identified and segmented at the nuclear level to determine live and dead cell counts over time using specific nuclear and dead cell stains. Filter criteria, including nuclear size and nuclei clustering, are used to identify individual cells, and must be optimized for each cell type. The dead cell stain intensity (e.g. PI, TO-PRO-3, or DRAQ7) is subsequently calculated for each cell, and a threshold is defined to identify cells with stain intensities indicative of cell death. Thus, for any set of microenvironmental conditions, we can obtain live and dead cell counts at several time points, which can then be used to determine context-dependent birth and death rates [83, 84].

At the population level, it is important to not only characterize mean phenotype, but also phenotypic heterogeneity across the population [33]. We can address this by tracking individual cell nuclei with nuclear fusion proteins (e.g., histone-2B-GFP) across time. Readouts from these experiments include changes in total cell count and motility parameters (e.g., speed, direction, displacement). Using this high-throughput imaging platform, we can assess the impact of a heterogeneous tumor microenvironment on cellular dynamics and treatment response in real-time. Such a comprehensive view of cellular behavior under the unique control of individual and co-occurring gradients of environmental factors is a considerable improvement over current models based on qualitative in vitro experiments/assays.

Lastly, cell count and other high-throughput measurements must be analyzed to obtain biophysical parameters. We recently have developed CellPD (cell phenotype digitizer), which gives a user-friendly interface to input cell count data (as an Excel spreadsheet), obtains best-fit parameters and uncertainty estimates for several “canonical” mathematical forms (e.g., exponential and logistic growth), ranks the fits, and summarizes the results (parameter values and publication-quality plots) as user-friendly HMTL pages [85, 86]. CellPD will be open sourced in 2016.

12.2.6. Data Standards and Reproducibility

High-throughput screening platforms can generate many cell phenotype parameters under a variety of microenvironmental conditions, and for many cell types. This can yield a vast collection of phenotype parameters, but they cannot be used by mathematical models without systematic recording. Similarly, mathematical models output quantitative data on cell positions, phenotypes, and substrate distributions, but many papers ultimately discard these outputs in favor of simplified analytics (e.g., tumor size vs. time) and visualizations. Even when the data are stored and disseminated, each model tends to use a customized data format. This vastly complicates replication studies and new analyses of prior works. Moreover, using different formats for simulation and experimental data hinders efforts to directly compare simulation and validation datasets.

We are working to overcome these difficulties. While good standardizations exist for subcellular data (e.g., the Gene Ontology (GO) [87] is used for annotating genomics data), few exist for multicellular data. In [19], we introduced MultiCellXML (multicellular extensible markup language) to describe the model outputs of our agent-based model. The key data elements for MultiCellXML described biophysical cell agent parameters that are common to many discrete models: cell position, volume, phenotypic state (e.g., cycling, apoptotic, or quiescent), and elapsed time in the state. Indeed, many of these key data elements were incorporated into the Cell Behavior Ontology (e.g., the Boolean data element IsApoptotic) [88]. In 2014, we expanded this effort to form the MultiCellDS (multicellular data standard) Project. After assembling a multidisciplinary panel of biologists, clinicians, mathematicians, and computer scientists, we set out to form a data standard that was complementary to most ontology efforts: a method to systematically record microenvironment-dependent phenotype data (digital cell lines), and a method to consistently report continuum and discrete simulation data (digital snapshots). To accelerate the project, we are incorporating data elements from existing ontologies (e.g., Cell Behavior Ontology (CBO) [88] and Chemical Entities of Biological Interest (ChEBI) [89]) when they are available. Much of this work focuses on giving a logical, hierarchical structure to the diverse set of phenotype and biochemical descriptors in use today. By focusing on data interchange, we hope to improve the cross-model compatibility, encourage data sharing, and ease the creation of configuration, analysis, and visualization software. We note that the same standard can be used for segmented experimental and clinical data. Visit http://MultiCellDS.org for up-to-date project information.

A standardized, model-independent recording of simulation output data is key to reproducibility and open science. To reproduce a modeling result, both the same computational model and independent models or implementations should simulate the same physical system, and their outputs should be directly compared, either voxel-by-voxel (for continuum models) or on a statistical basis (for stochastic, agent-based models). However, even if model outputs are made openly available as part of a publication (i.e., as open data), this step is either complicated or impossible if the simulation inputs are model-dependent. Hence, today it is difficult to use a lattice-free model (e.g., Chaste [27]) to reproduce a cellular Potts result (e.g., from CompuCell3D [28]).

Lastly, we note that for work to be truly reproducible and open, the underlying computational code should be distributed as open source. Otherwise, version-dependent bugs are difficult to eliminate when replicating simulation results. Moreover, non-open licensing can prevent scientists from fully stating their method. For example, BioCellion [90] can simulate millions to billions of cells on supercomputers, but its non-OSI [91] academic license [92] is very restrictive: it stipulates internal non-commercial use only, with no distribution of source code (e.g., as a method section) or sublicensing without written permission; this hampers reproducibility [93].

12.3. Next Steps and Closing Thoughts

We have seen great strides in building simulation platforms to understand 3-D multicellular systems in complex, dynamical microenvironments. Tumor growth models can simulate millions of cells with individual cell effects, or large masses of mixed cell populations. Simulations can include detailed tissue biomechanics, coupled to the fluid mechanics of interstitial and microvascular flow. Simulated tumors can alter the mechanical and vascular landscape, with feedback loops affecting tumor cell phenotype. We have seen that models can be calibrated to experimental and clinical data to give meaningful insights, which can be shared and replicated with open data and open source codes. We have seen an emerging consensus on the need to document and share data and models, and new ontologies and data standards are emerging to accomplish the task.

But key ingredients are missing. The work we described focused on the biophysics of the tumor and the microenvironment; however, molecular-scale effects (cell signaling, mutation networks, metabolic/energy models, etc.) still need to be integrated. This can be achieved by integrating fast ordinary differential equation solvers for systems biology, such as libRoadrunner [94]. For better efficiency, tumor growth models should combine both discrete cell models and continuum models, with mass and force exchange between the discrete and continuum cells [25].

Perhaps more notably, the models presented in this paper (and most in the field) only couple two or three key components, often by manually combining the codes. No one simulator brings to bear all these aspects in a single platform. It is impractical to expect any single simulator to model all biochemical and biophysical aspects of cancer and the microenvironment well, from sub-cellular effects to tissue-scale dynamics and coupled vascular networks. Even if there were such a monolithic platform, it would be scientifically risky: a single bug could undermine scores of papers built upon it. And investment (and “sunk costs”) in a single simulator may well discourage development of “competing” simulation engines for independent replication studies.

Instead, we need modular software infrastructures for combining open source models. Multiple groups could contribute tumor growth, vascularization, diffusion, and other modules, which read and modify shared data structures through standardized protocols (similarly to message passing in MPI, or TCIP/IP packets in networks). To encourage the widest possible participation, such a platform needs to support many programming languages (e.g., C++, Python, Java, Julia), rather than require compiler-level binary linking. With standardized data structures (e.g., MultiCellDS) now emerging, such a development effort is feasible.

The community will require better shared data resources. As sophisticated multiphysics models emerge, we will need correspondingly sophisticated validation datasets, including information on cell phenotype and distribution, substrate distribution, tissue mechanics, and interstitial flow, with sufficient time resolution to validate model dynamics as well as steady-state behavior. We will need further advances in novel bioengineered and biomimetic models (such as organoids grown in bioreactors and “organ-on-a-chip” systems [95]) that can drive development and validation of tumor-vasculature interaction models. These data sets must be released openly with standardized formats, so that all modelers may test their models and contribute to the community. As open data become more widespread, centralized, searchable repositories will be needed to help make data discoverable. To ensure research quality, these repositories will need to be curated, based upon (as yet undetermined) community standards for assessing quality and deciding when a newly-submitted measurement should replace an existing measurement.

No group can do this alone. Individual models of tumor growth and the microenvironment are growing to such sophistication that no one group could hope to develop a model of everything. Experiments, too, are requiring large efforts that are better realized through teams. We expect that in the future, computational systems biology will make the leap from isolated, single-lab efforts to coalitions of scientists working with open source codes and open, standardized data, allowing us to take the best of each and grow beyond the sum of the parts.