The use of prognostic scores for causal inference with general treatment regimes

Tri‐Long Nguyen; Thomas PA Debray

doi:10.1002/sim.8084

. 2019 Jan 16;38(11):2013–2029. doi: 10.1002/sim.8084

The use of prognostic scores for causal inference with general treatment regimes

Tri‐Long Nguyen ^1,^2,³, Thomas PA Debray ^1,^4,^5,^6,^✉

PMCID: PMC6590249 PMID: 30652333

Abstract

In nonrandomised studies, inferring causal effects requires appropriate methods for addressing confounding bias. Although it is common to adopt propensity score analysis to this purpose, prognostic score analysis has recently been proposed as an alternative strategy. While both approaches were originally introduced to estimate causal effects for binary interventions, the theory of propensity score has since been extended to the case of general treatment regimes. Indeed, many treatments are not assigned in a binary fashion and require a certain extent of dosing. Hence, researchers may often be interested in estimating treatment effects across multiple exposures. To the best of our knowledge, the prognostic score analysis has not been yet generalised to this case. In this article, we describe the theory of prognostic scores for causal inference with general treatment regimes. Our methods can be applied to compare multiple treatments using nonrandomised data, a topic of great relevance in contemporary evaluations of clinical interventions. We propose estimators for the average treatment effects in different populations of interest, the validity of which is assessed through a series of simulations. Finally, we present an illustrative case in which we estimate the effect of the delay to Aspirin administration on a composite outcome of death or dependence at 6 months in stroke patients.

Keywords: causal inference, multiple treatment exposures, observational study, prognostic score

1. INTRODUCTION

In clinical research, experimental studies are generally considered as the gold standard for inferring causal effects of interventions.1 The most common form is the randomised trial, which involves randomised allocation of a subject's treatment. Unfortunately, the conduct of randomised trials is not always feasible, as there may be operational, financial, or even ethical constraints to administer a certain treatment. In addition, many randomised trials adopt very narrow enrolment criteria and fail to address the impact of studied interventions in clinical practice.2, 3, 4 For this reason, observational studies may sometimes be regarded as alternative sources for assessing the relative effect of medical interventions.

Evidently, it may come as no surprise that inferring causal effects from nonrandomised data is no easy task. Foremost, confounding bias is likely to occur because treatment exposure usually depends on patient characteristics and preferences of care givers. This implies that substantial efforts are needed to handle the presence of systematic differences in covariate distributions across treated individuals. A common framework to address confounding bias is to mimic randomisation by propensity score analysis, which aims to restore the balance in the subjects' baseline covariate distributions across the different treatment exposures.5 The prognostic score analysis is a related method that seeks to balance the subjects' baseline prognosis, rather than their covariates per se.6

Although both propensity and prognostic score analyses share similar assumptions (ie, stable treatment unit value and absence of hidden bias),5, 6 a major advantage of the latter is that it relaxes the positivity assumption,6 This assumption requires to have observations for all exposures at every value of the observed confounders, which might be hardly feasible in the presence of multiple exposures. Further, because the positivity assumption of propensity score analysis is rarely evaluated in practice,7, 8 prognostic score analysis appears as an appealing alternative to study causal effects in the presence of multiple treatment exposures.

The growing demand for real‐world evidence and large amounts of (high quality) observational data expose the need for more advanced statistical methods for analysing relative treatment effects. In particular, patients in routine care often present substantial variation in treatment dosage or drugs for a therapeutic class, and thus, researchers may often be interested in treatment effect estimation for these multiple exposures. Although the theory of propensity score has been extended to general treatment regimes, its implementation is not very straightforward as it involves estimation of different propensity models given the treatment exposure distribution.9, 10, 11

In this article, we aim to extend the framework of prognostic scores for causal inference to the case of general treatment regimes. We present a theoretical framework in Section 2, which is complemented by a simulation study reported in Section 3, and a study case in Section 4. To illustrate the (potential) advantages of our method, we compare its performance to the propensity score analysis framework.

2. THEORY AND METHODS

2.1. Causal framework

Using Rubin's notations for causal inference,12 let Y_i be the actual (observed) outcome, $X_{i} \in A$ a vector of measured subject‐level covariates and $Z_{i} \in Z$ the treatment status. Further, let $Z = \{z_{1}, …, z_{T}\}$ represent the treatment space for the exposures. A common notion in causal inference is the concept of “potential outcomes” (or “counterfactuals”), which refers to the outcomes that would be observed if the individuals were—contrary to the fact—to receive each treatment exposure. Hence, to any exposure z_t then corresponds a potential outcome Y_(t)i. Note that according to this formulation, one of the potential outcomes (but no more) is always observed. We can formulate the observed outcome Y_i as an amalgamation of these potential responses to the various possible treatment exposures

Y_{i} = \sum_{t = 1}^{T} I (Z_{i} = z_{t}) Y_{(t) i},

where I(Z_i = z_t) is the indicator function for actually receiving treatment z_t. Setting Z_i = z_t leads to observing Y_i = Y_(t)i which refers to consistency.

Causal inference requires the stable treatment unit value assumption (SUTVA); that is, the distribution of potential outcomes for one individual is independent from the treatment assigned to any other unit.13

Setting z_r as the “reference” treatment (eg, standard care), the treatment effect (henceforth TE) caused by any other treatment z_s (∀ s ≠ r) for a given subject is defined as

{TE}_{(z_{s} z_{r}) i} = Y_{(s) i} - Y_{(r) i} .

However, it may be clear that ${TE}_{(z_{s} z_{r}) i}$ is nonidentifiable in practice because individual subjects cannot simultaneously experience z_s and z_r, and thus, either Y_(s)i or Y_(r)i will obviously remain unobserved. This issue refers to the “fundamental problem of causal inference” and is equally relevant for randomised and nonrandomised studies.14

Although the lack of counterfactual evidence obfuscates any causal inference at the subject level, treatment effect estimates can, in fact, be obtained for specific (sub)populations. In this regard, a common quantity of interest is the average effect caused by treatment z_s over z_r. Depending on which population the causal effect is to be inferred, different estimands can be defined—among these, the most commonly used are the average treatment effect in the entire population (ATE), the average treatment effect in the treated population (ATT), and the average treatment effect in the “reference” population (ATR). Given that potential outcomes are averaged over (sub)populations, the index i is to be suppressed in the following equations:

\begin{matrix} {ATE}_{z_{s}, z_{r}} & = E (Y_{s} - Y_{r}) = E (Y_{s}) - E (Y_{r}) \\ {ATT}_{z_{s}, z_{r}} & = E (Y_{s} - Y_{r}| Z = z_{s}) = E (Y_{s}| Z = z_{s}) - E (Y_{r}| Z = z_{s}) \\ {ATR}_{z_{s}, z_{r}} & = E (Y_{s} - Y_{r}| Z = z_{r}) = E (Y_{s}| Z = z_{r}) - E (Y_{r}| Z = z_{r}) . \end{matrix}

(In case of binary treatments where Z ∈ {0, 1}, taking Z = 0 as reference, the ATR is often referred to as “average treatment effect in the untreated/control population.”)

Similarly, one can define the effects caused by any other treatment z_t over z_r, ∀t ≠ s ≠ r (ie, multiple treatment exposures), as

\begin{matrix} {ATE}_{z_{t}, z_{r}} & = E (Y_{t} - Y_{r}) = E (Y_{t}) - E (Y_{r}) \\ {ATT}_{z_{t}, z_{r}} & = E (Y_{t} - Y_{r}| Z = z_{t}) = E (Y_{t}| Z = z_{t}) - E (Y_{r}| Z = z_{t}) \\ {ATR}_{z_{t}, z_{r}} & = E (Y_{t} - Y_{r}| Z = z_{r}) = E (Y_{t}| Z = z_{r}) - E (Y_{r}| Z = z_{r}) . \end{matrix}

It is important to note that ATEs and ATRs are transitive estimands, in the sense that

\begin{matrix} {ATE}_{z_{s}, z_{r}} - {ATE}_{z_{t}, z_{r}} & = E (Y_{s}) - E (Y_{r}) - E (Y_{t}) + E (Y_{r}) \\ = E (Y_{s}) - E (Y_{t}) \\ = {ATE}_{z_{s}, z_{t}} \end{matrix}

and

\begin{matrix} {ATR}_{z_{s}, z_{r}} - {ATR}_{z_{t}, z_{r}} & = E (Y_{s}| Z = z_{r}) - E (Y_{r}| Z = z_{r}) - E (Y_{t}| Z = z_{r}) + E (Y_{r}| Z = z_{r}) \\ = E (Y_{s}| Z = z_{r}) - E (Y_{t}| Z = z_{r}) \\ = {ATR}_{z_{s}, z_{t}} . \end{matrix}

This property allows the average effects caused by z_t and z_s, with respect to z_r, to be directly compared and as such to make inferences on their relative efficacy.

Similarly, transitivity of ATTs requires that ${A T T}_{z_{s}, z_{r}} - {A T T}_{z_{t}, z_{r}} = {A T T}_{z_{s}, z_{t}}$ . This property, however, generally does not hold when multiple treatment exposures are available for a certain population. In particular, in nonrandomised studies, treatment allocation is often influenced by multiple covariates, such that the populations eligible to receive z_t and z_s are likely to differ in terms of covariate distribution. In other words, the expression E (Y_s | Z = z_s) − E (Y_r | Z = z_s) − E (Y_t | Z = z_t) + E (Y_r | Z = z_t) is unlikely to collapse to E (Y_s | Z = z_s) − E (Y_t | Z = z_s) because, usually, E (Y_r | Z = z_s) ≠ E (Y_r | Z = z_t) and E (Y_t | Z = z_t) ≠ E (Y_t | Z = z_s).

For this reason, we argue that ATEs and ATRs might be preferable estimands in case of multiple treatment exposures.

2.2. Prognostic score

For causal inference, Hansen formalised the use of the prognostic score that can be regarded as the “prognostic analogue of the propensity score.”6 While the propensity score analysis seeks to ensure propensity balance on e_s(X) = Pr (Z = z_s | X),5 the prognostic score analysis is aimed at securing a prognostic balance across the treatment arms.6 The framework of propensity scores demands major assumptions: SUTVA, absence of hidden bias given the set of measured covariates (ie, $Y_{(\cdot)} ⊥ Z ∣ X, X \in A$ ), and positivity (ie, $0 < \Pr (Z \in Z ∣ X)$ with certainty).5, 9 (Note, the contraction of the latter two is also called “strong ignorability of treatment assignment.”) Similarly, the framework of prognostic scores requires SUTVA, absence of hidden bias, and a relaxed form of positivity.

Let ψ_r(X) be a prognostic score such that Y_r ⊥ X ∣ ψ_r(X), $X \in A$ , $A$ being any measurable set.6 In that sense, ψ_r(X) is sufficient for Y_r, which does not necessarily imply it is for Y_s—in particular, when effect modification exists, such that Pr(Y_s | Y_r, X) ≠ Pr(Y_s| Y_r).6 In presence of any effect modifier denoted m_s,r(X), then {ψ_r(X), m_s,r(X)} is sufficient for Y_s (ie, Y_s ⊥ X ∣ ψ_r(X), m_s,r(X)).6

Hansen's proposition 3 showed that, under the assumption of no hidden bias, $Y_{r} ⊥ Z ∣ X, X \in A$ (ie, the measurable set includes all relevant confounders), conditioning on ψ_r(X) deconfounds the potential response Y_r from treatment assignment, that is, Y_r ⊥ Z ∣ ψ_r(X).6 In the absence of effect modifier, it also deconfounds the potential response to z_s from treatment assignment, that is, Y_s ⊥ Z ∣ ψ_r(X); otherwise, Y_s ⊥ Z ∣ ψ_r(X), m_s,r(X).6 Should there be no hidden bias, then conditioning on the prognostic score (and effect modifier) allows one to estimate causal effects.

2.3. Identification of causal effects

2.3.1. Average treatment effect in the treated population

Suppose that Y_r ⊥ Z ∣ ψ_r(X) and Pr{0 < Pr(Z = z_r ∣ ψ_r(X))} = 1, then

{A T T}_{z_{s}, z_{r}} = E (Y_{s} - Y_{r}| Z = z_{s}) = E_{ψ_{r} (X) ∣ Z = z_{s}} \{E (Y | Z = z_{s}, ψ_{r} (X)) - E (Y | Z = z_{r}, ψ_{r} (X))\},

where $E_{ψ_{r} (X) ∣ Z = z_{s}}$ denotes the expectation with respect to the distribution of ψ_r(X) in the treated population Z = z_s.

This corresponds to Hansen's proposition 4,6 the proof of which is the following.

Therefore,

\begin{matrix} E (Y | Z = z_{s}, ψ_{r} (X)) - E (Y | Z = z_{r}, ψ_{r} (X)) & = E (Y_{s} | Z = z_{s}, ψ_{r} (X)) - E (Y_{r} | Z = z_{s}, ψ_{r} (X)) \\ = E (Y_{s} - Y_{r} | Z = z_{s}, ψ_{r} (X)) \end{matrix}

from which follows

\begin{matrix} E_{ψ_{r} (X) ∣ Z = z_{s}} \{E (Y | Z = z_{s}, ψ_{r} (X)) - E (Y | Z = z_{r}, ψ_{r} (X))\} \\ = E_{ψ_{r} (X) ∣ Z = z_{s}} \{E (Y_{s} - Y_{r} | Z = z_{s}, ψ_{r} (X))\} = E (Y_{s} - Y_{r} Z = z_{s}) ▪ \end{matrix}

Hereto, conditioning on solely ψ_r(X) allows the estimation of ${A T T}_{z_{t}, z_{r}}$ , regardless of whether there be effect modification.

2.3.2. Average treatment effect in the reference population

Suppose in presence of some effect modifier m_s,r(X), Y_s ⊥ Z ∣ ψ_r(X), m_s,r(X) and Pr{0 < Pr(Z = z_s | ψ_r(X), m_s,r(X))} = 1; otherwise, in absence of effect modifier, suppose Y_s ⊥ Z | ψ_r(X) and Pr{0 < Pr(Z = z_s | ψ_r(X))} = 1. Then,

(1)
In presence of an effect modifier m_s,r(X),
$\begin{matrix} {A T R}_{z_{s}, z_{r}} & = E (Y_{s} - Y_{r} Z = z_{r}) \\ = E_{ψ_{r} (X), m_{s, r} (X) ∣ Z = z_{r}} \{E (Y | Z = z_{s}, ψ_{r} (X), m_{s, r} (X)) - E (Y | Z = z_{r}, ψ_{r} (X), m_{s, r} (X))\} . \end{matrix}$
(2)
Otherwise, in the absence of effect modifier,
$\begin{matrix} {A T R}_{z_{s}, z_{r}} & = E (Y_{s} - Y_{r} Z = z_{r}) \\ = E_{ψ_{r} (X) ∣ Z = z_{r}} \{E (Y | Z = z_{s}, ψ_{r} (X)) - E (Y | Z = z_{r}, ψ_{r} (X))\} . \end{matrix}$

Here, $E_{ψ_{r} (X), m_{s, r} (X) ∣ Z = z_{r}}$ and $E_{ψ_{r} (X) ∣ Z = z_{r}}$ denote expectations with respect to the distribution of {ψ_r(X), m_s,r(X)} and ψ_r(X), respectively, in the reference population Z = z_r.

Certainly, E (Y | Z = z_s, ψ_r(X), m_s,r(X)) = E (Y_s | Z = z_s, ψ_r(X), m_s,r(X)) and E (Y | Z = z_r, ψ_r(X), m_s,r(X)) = E (Y_r | Z = z_r, ψ_r(X), m_s,r(X)). The initial assumptions imply that E (Y_s | Z = z_s, ψ_r(X), m_s,r(X)) = E (Y_s | Z = z_r, ψ_r(X), m_s,r(X)).

Therefore,

$\begin{matrix} E (Y | Z = z_{s}, ψ_{r} (X), m_{s, r} (X)) - E (Y | Z = z_{r}, ψ_{r} (X), m_{s, r} (X)) \\ = E (Y_{s} | Z = z_{r}, ψ_{r} (X), m_{s, r} (X)) - E (Y_{r} | Z = z_{r}, ψ_{r} (X), m_{s, r} (X)) \\ = E (Y_{s} - Y_{r} | Z = z_{r}, ψ_{r} (X), m_{s, r} (X)) \end{matrix}$

from which follows

$\begin{matrix} E_{ψ_{r} (X), m_{s, r} (X) ∣ Z = z_{r}} \{E (Y | Z = z_{s}, ψ_{r} (X), m_{s, r} (X)) - E (Y | Z = z_{r}, ψ_{r} (X), m_{s, r} (X))\} \\ = E_{ψ_{r} (X), m_{s, r} (X) ∣ Z = z_{r}} \{E (Y_{s} - Y_{r} | Z = z_{r}, ψ_{r} (X), m_{s, r} (X))\} \\ = E (Y_{s} - Y_{r} Z = z_{r}) . \end{matrix}$

Should there be no effect modifier, then m_s,r(X) vanishes from (1), and (2) follows.

2.3.3. Average treatment effect in the entire population

Suppose simultaneously the assumptions announced in Sections 2.3.1 and 2.3.2, and then,

(1)
In presence of an effect modifier m_s,r(X),
$\begin{matrix} {A T E}_{z_{s}, z_{r}} & = E (Y_{s} - Y_{r}) \\ = E_{ψ_{r} (X), m_{s, r} (X)} \{E (Y | Z = z_{s}, ψ_{r} (X), m_{s, r} (X)) - E (Y | Z = z_{r}, ψ_{r} (X), m_{s, r} (X))\} . \end{matrix}$
(2)
Otherwise, in the absence of effect modifier,
${A T E}_{z_{s}, z_{r}} = E (Y_{s} - Y_{r}) = E_{ψ_{r} (X)} \{E (Y | Z = z_{s}, ψ_{r} (X)) - E (Y | Z = z_{r}, ψ_{r} (X))\} .$

Here, $E_{ψ_{r} (X), m_{s, r} (X)}$ and $E_{ψ_{r} (X)}$ denote expectations with respect to the distribution of {ψ_r(X), m_s,r(X)} and ψ_r(X), respectively, in the entire population.

Certainly, E (Y | Z = z_s, ψ_r(X), m_s,r(X)) = E (Y_s | Z = z_s, ψ_r(X), m_s,r(X)) and E (Y | Z = z_r, ψ_r(X), m_s,r(X)) = E (Y_r | Z =z_r, ψ_r(X), m_s,r(X)).

Assuming Y_r ⊥ Z ∣ ψ_r(X), m_s,r(X) and Pr{0 < Pr(Z = z_r | ψ_r(X), m_s,r(X))} = 1 entails that E (Y | Z = z_r, ψ_r(X), m_s,r(X)) =E (Y_r | ψ_r(X), m_s,r(X)). Similarly, assuming Y_s ⊥ Z | ψ_r(X), m_s,r(X) and Pr{0 < Pr(Z = z_s | ψ_r(X), m_s,r(X))} = 1 entails that E (Y | Z = z_s, ψ_r(X), m_s,r(X)) = E (Y_s | ψ_r(X), m_s,r(X)).

Therefore,

$E (Y | Z = z_{s}, ψ_{r} (X), m_{s, r} (X)) - E (Y | Z = z_{r}, ψ_{r} (X), m_{s, r} (X)) = E (Y_{s} | ψ_{r} (X), m_{s, r} (X)) - E (Y_{r} | ψ_{r} (X), m_{s, r} (X))$

from which follows

$\begin{matrix} E_{ψ_{r} (X), m_{s, r} (X)} \{E (Y | Z = z_{s}, ψ_{r} (X), m_{s, r} (X)) - E (Y | Z = z_{r}, ψ_{r} (X), m_{s, r} (X))\} \\ = E_{ψ_{r} (X), m_{s, r} (X)} \{E (Y_{s} | ψ_{r} (X), m_{s, r} (X)) - E (Y_{r} | ψ_{r} (X), m_{s, r} (X))\} \\ = E (Y_{s} - Y_{r}) . \end{matrix}$

Should there be no effect modifier, then m_s,r(X) vanishes from (1), and (2) follows.

Note that, in case of binary treatment, $Z \in Z = \{z_{s} z_{r}\}$ , this corresponds to Hansen's proposition 5,6 which assumes Pr{0 < Pr(Z = z_s | ψ_r(X))} = 1 and Pr{Pr(Z = z_s | ψ_r(X)) < 1} = 1. However, for multiple treatment exposures, Pr{Pr(Z = z_s | ψ_r(X)) < 1} ≢ Pr{0 < Pr(Z = z_r | ψ_r(X))}.

2.4. Estimation of prognostic scores

For prognostic score analysis involving multiple exposures, the term “reference population” can be defined in multiple ways. One option is to define the reference population from a pragmatic perspective by taking the population with the largest sample size for fitting a prognostic score model. On the other hand, one could also define the reference population as the patients who receive the standard treatment, primarily indicated in a given disease. Note that these two potential reference populations generally coincide, as often the largest group of treated patients in observational studies will be those receiving the standard care.

In practice, ψ_r(X) is unknown and therefore needs to be estimated from data at hand. The corresponding model can be parametric, such that $\hat{ψ_{r}} (X) = E (Y_{r} | X, \hat{β})$ . According to the outcome type (eg, continuous, binary, categorical, or time‐to‐event), relevant regression models are to be considered (eg, linear, logistic, multinomial logistic, or proportional hazards regression models). To fit $\hat{ψ_{r}} (X)$ , it is common to use only the reference arm of the data set that includes the multiple exposures alongside, which is referred to as “same‐sample estimation.” Alternatively, $\hat{ψ_{r}} (X)$ can be derived from a historical cohort of control subjects or from previously published prognostic models. Regardless of this choice, it is important to fit a prognostic score to reference subjects only, that is, not to include individuals under other exposures.6 Otherwise, one would no longer estimate ψ_r(X).

In practice, the propensity score $\hat{e_{s}} (X) = \Pr (Z = z_{s} X, \hat{α})$ is often derived from maximum likelihood estimation. This strategy is not to transpose to prognostic score modelling without precautions. Indeed, $\hat{ψ_{r}} (X) = E (Y_{r} X, \hat{β})$ is to be extrapolated to the different treatment exposure groups and thus requires that predictions from the prognostic score are well calibrated in the corresponding subjects. Poorly calibrated prognostic scores may lead to improper matches, thereby introducing confounding bias. In general, problems with calibration may arise when prognostic associations are biased (eg, due to overfitting or systematic measurement error), misspecified (eg, failure to account for nonlinear effects or interactions) or omitted. It is therefore important to adopt robust estimation methods (eg, penalised regression) and to ensure that prognostic scores properly account for prognostic factors that are likely to differ (eg, in distribution or measurement method) across treatment exposures.

2.5. Conditioning on prognostic scores

For estimating causal effects, conditioning on propensity or prognostic scores often relies on subclassification or matching methods.

2.5.1. Subclassification

As in propensity score analysis, one can condition on the prognostic score (and effect modifier) by performing subclassification.6, 15, 16 In this approach, individuals are parted into subclasses S ∈ {1,…,Q}, within which the estimated score $\hat{ψ_{r}} (X)$ is roughly similar. Precedents have shown that subclassification by quintiles (ie, Q = 5) removed 90% of confounding bias when using propensity scores for binary treatments.15 After subclassification, one can approximate the distribution of the potential outcomes as weighted means, with weights defined after the proportions of individuals falling into subclasses.9 Let S_i be the subclass of individual i. The average potential outcome Y_s is estimated as

{\{\sum_{s = 1}^{Q} W_{s}\}}^{- 1} \sum_{s = 1}^{Q} \{W_{s} \frac{\sum_{i = 1}^{N} I (S_{i} = s) I (Z_{i} = z_{s}) Y_{i}}{\sum_{i = 1}^{N} I (S_{i} = s) I (Z_{i} = z_{s})}\} .

W_s denotes the subclass weight, which is calculated as

W_{s} = \{\frac{\sum_{i = 1}^{N} I (S_{i} = s) f}{\sum_{i = 1}^{N} f}\} \{\frac{\sum_{i = 1}^{N} I (Z_{i} = z_{s})}{\sum_{i = 1}^{N} I (S_{i} = s) I (Z_{i} = z_{s})}\} .

To estimate the average potential outcome Y_s in the entire population, the treated population (Z = z_s), and the reference population (Z = z_r), we set f = 1, ƒ= I (Z_i = z_s) and f = I(Z_i = z_r), respectively.

Estimating the potential responses across the multiple treatment exposures translates into dose‐response relationships in case of ordinal or continuous exposures. (Note that, in the latter, the use of a smoothing function might be of interest.) We believe this approach to be robust because nonparametric and saved from model dependence.

In case of generalised propensity score analysis, subclassification depends on the treatment distribution and, thus, on the propensity score models. For instance, for categorical treatments, estimated propensity scores can be derived from multinomial logit or probit regression models.9, 10, 17 Each treatment arm z_s is then subclassified—separately—on the corresponding propensity score, $\hat{e_{s}} (X) = \hat{P r} (Z = z_{s} X)$ .16, 18 Note that other treatments arms (Z ≠ z_s) are also to be subclassified on $\hat{e_{s}} (X)$ in case one wants to estimate the distribution of Y_s that would be observed if those populations were, contrary to the fact, to receive z_s. Using generalised prognostic score analysis, all treatment arms are to be subclassified on a same prognostic score $\hat{ψ_{r}} (X)$ . Note, to estimate ATEs or ATRs in the presence of an effect modifier m(X), the subclassification has to be made concurrently upon $\hat{ψ_{r}} (X)$ and m(X). For instance, in case of a binary effect modifier, this would require to double the number of subclasses.

2.5.2. Matching

In comparison to rough subclassification, matching methods aim to pair units that are “similar” with regard to the estimated score. Previous works have presented reviews as to the role of matching for causal inference.19, 20, 21 Here, we focus on matching methods that minimise a distance metric by sampling subjects without replacement. These methods may, however, allow more than one individual per exposure arm to be involved in the matching. This implies that a paired set could, for instance, consist of several (rather than one) control matches for a treated subject.

Let match(·) be a matching function of treatment exposure Z and distance D, and ‖·‖ be a generic metric function. The function match(z_s, d) indexes by M = m, M ∈ {1,…,K}, the individuals with exposure z_s and minimal distance metric d

match (z_{s} d) = arg \min_{m : Z_{m} = z_{s}} ‖D_{m}‖ .

Note that applying match(z_s, d) to units under other exposures (Z ≠ z_s) leads to indexing them as if they were to receive z_s. As in subclassification, this procedure is necessary to estimate the distribution of the potential outcome Y_s that would be observed in the other arms were they to be allocated z_s. In the matching function, the distance refers to the “closeness” between individuals within matched pair m and can be defined on the covariates X as

D_{m} = |X_{m} - x| .

The generic metric function ‖·‖ depends on the matching method. For instance, when performing covariate exact matching on the covariates,

‖D_{m}‖ = \{\begin{matrix} 0, if X_{m} = x \\ \infty, if X_{m} \neq x, \end{matrix}

Other common distance metrics are described in the literature, such as the Mahalanobis distance metric. If the distance is instead defined as a scalar (eg, prognostic score $\hat{ψ_{r}} (X)$ or propensity score $\hat{e_{s}} (X))$ , then D becomes D. Generally, ‖D_m‖ is taken as ‖D_m‖ = D_m. For instance, using prognostic scores

‖D_{m}‖ = D_{m} = |\hat{ψ_{r}} (X_{m}) - \hat{ψ_{r}} (x)| .

Matching can be achieved upon a same prognostic score $\hat{ψ_{r}} (X)$ in generalised prognostic score analysis, while using generalised propensity scores requires individuals under exposure z_s be matched on the corresponding propensity score $\hat{e_{s}} (X)$ .16 Note, however, that in the presence of an effect modifier m(X), matching only on $\hat{ψ_{r}} (X)$ is no longer sufficient for estimating the ATE and ATR: One must then match on the combined set $\{\hat{ψ_{r}} (X), m (X)\}$ , which could in fact be scaled on a propensity score $\hat{e_{s}} (X) = \hat{P r} (Z = z_{s} \hat{ψ_{r}} (X), m (X))$ (sometimes called “prognostic propensity score”). Notice that, instead of using the scores themselves, particular functions can be used—eg, the logit of the propensity score.22

As when using subclassification, the distribution of the potential outcomes can then be approximated as weighted means, with weights defined after the proportions of individuals falling into matched pairs. If M_i denotes the matched pair unit i belongs to, then the average potential outcome Y_s is estimated as

{\{\sum_{m = 1}^{K} W_{m}\}}^{- 1} \sum_{m = 1}^{K} \{W_{m} \frac{\sum_{i = 1}^{N} I (M_{i} = m) I (Z_{i} = z_{s}) Y_{i}}{\sum_{i = 1}^{N} I (M_{i} = m) I (Z_{i} = z_{s})}\} .

W_m defines the pair weight

W_{m} = \{\frac{\sum_{i = 1}^{N} I (M_{i} = m) f}{\sum_{i = 1}^{N} f}\} \{\frac{\sum_{i = 1}^{N} I (Z_{i} = z_{s})}{\sum_{i = 1}^{N} I (M_{i} = m) I (Z_{i} = z_{s})}\} .

To estimate the average potential outcome Y_s in the entire, the treated (Z = z_s) and the reference (Z = z_r) populations: ƒ= 1, ƒ= I (Z_i = z_s) and f = I(Z_i = z_r), respectively. Should we be interested in estimating the average potential outcome Y_s in the population receiving another exposure (Z = z_t, ∀ t ≠ s ≠ r), then f = I(Z_i = z_t).

Again, a “pair” can comprise many individuals of same exposure arms as far as the specified distance is minimised. Here, we focus on optimal full matching, the use of which is of great interest in case of binary treatment.23, 24, 25 Briefly, this method involves the formation of “pairs” (or “strata”) consisting of either a single treated subject and one or more control subjects, or a single control subject and one or more treated subjects. Subjects are paired such that their matched sets are optimally balanced with regard to the distance metric.26 A key advantage of optimal full matching is that all subjects are preserved in the analysis, thereby avoiding bias due to incomplete matching (which may, for instance, occur when adopting 1:1:1 matching methods or callipers).

Because estimation of ATTs and ATRs requires conditioning on the prognostic score (and, if applicable, effect modifier) across the reference and relevant exposure arms (ie, two paired arms), ATTs and ATRs can be estimated fairly straightforward in the presence of multiple treatment exposures as in binary treatments. However, to estimate the ATEs, one must condition on the prognostic score (and effect modifier) with respect to its distribution in the entire population—that is, perform an optimal full matching across all treatment arms. To the best of our knowledge, no such approach has yet been described in the literature. We therefore propose to apply optimal full matching to the estimation of ATE in presence of multiple treatment arms, as follows: Individuals under exposure z_s are to be matched as would be those exposed to others (Z ≠ z_s)—regardless of the distinction between z_t and z_r (∀t ≠ s ≠ r)—were they to receive z_s. Hence, each individual i falls into a matched pair within which the distance in prognostic score $\hat{ψ_{r}} (X)$ (or relevant propensity score $\hat{e_{s}} (X))$ is optimally minimised. For each unit i and matched pair m, I(M_i = m) is identifiable, and relevant weights W_m can therefore be computed. Thus, one can estimate the distribution of Y_s that would be observed if all treatment arms were to receive z_s.

To estimate the distribution of the other potential outcomes under the different treatment exposures, the same approach is to be used as described for Y_s in this section. Using subclassification and optimal full matching, we conducted generalised prognostic score analyses in comparison to generalised propensity score analyses to estimate causal effects through a series of simulations.

3. SIMULATION STUDY

In this section, we illustrate the use of prognostic scores for causal inference with multiple treatment exposures.

3.1. Data generation

We generated 10 independent variables X₁,…, X₁₀, with X₁,…, X₅ ∼ N(0, 1); X₅,…, X₈∼Binomial(0.3) and X₉, X₁₀∼Binomial(0.5). We considered three treatment exposures A (“reference”), B, and C, and we generated the potential outcomes (binary) as follows:

\begin{matrix} \Pr (Y_{A} X) & = {[1 + \exp \{- (- 0.5 X_{1} + 0.5 X_{3} + 1.2 X_{4} + 1.5 X_{5} + 0.5 X_{6} - 0.7 X_{7} - X_{8} - 1.2 X_{9} - 0.5 X_{10})\}]}^{- 1} \\ \Pr (Y_{B} X) & = {[1 + \exp (- 0.25 + 1.15 \log \{\Pr (Y_{A} | X)\})]}^{- 1} \\ \Pr (Y_{C} X) & = {[1 + \exp (- 0.5 + 0.65 X_{10} \log \{\Pr (Y_{B} | X)\})]}^{- 1} . \end{matrix}

Y_A = 1, Y_B = 1 and Y_C = 1, if their respective probability was greater than a random number u, drawn from a Uniform distribution U(0, 1). Note that equation for Pr(Y_C | X) included an effect modifier (X₁₀) of C with respect to B and thus also to A.

To mimic nonrandomised studies, we assigned the treatment exposure Z according to the covariates

\begin{matrix} L_{A} = 0.9 + 0.30 X_{1} + 0.50 X_{2} + 0.70 X_{3} + 0.90 X_{4} \\ L_{B} = 0.2 + 0.10 X_{1} + 0.20 X_{2} + 0.30 X_{3} + 0.40 X_{9} \\ \Pr (Z = A X) = \frac{\exp (L_{A})}{1 + \exp (L_{A}) + \exp (L_{B})} \\ \Pr (Z = B X) = \frac{\exp (L_{B})}{1 + \exp (L_{A}) + \exp (L_{B})} \\ \Pr (Z = C X) = \frac{1}{1 + \exp (L_{A}) + \exp (L_{B})} . \end{matrix}

Using their respective probability, we sampled A, B, and C with replacement to allocate the treatment. The actual outcome was then generated using the equation:

Y = I (Z = A) Y_{A} + I (Z = B) Y_{B} + I (Z = C) Y_{C} .

Reiterating this process, we generated 1000 observational studies for the analyses, each including 2000 subjects. “True values” of treatment effects were obtained from an independently drawn “superpopulation” including 5 000 000 subjects.

3.2. Analysis

In each observational study, we estimated the prognostic score by fitting a parametric logistic regression to the “reference” arm, including all covariates X = (X₁,…, X₁₀)

\hat{ψ_{A}} (X) = \Pr (Y Z = A, X, \hat{β}) = \frac{1}{1 + \exp \{- ({\hat{β}}_{0} + \sum X_{p} {\hat{β}}_{p})\}} .

This model was extrapolated to the other arms to predict the potential outcome that would have been observed, had they received the reference exposure A. We then used two methods for conditioning: subclassification (by quintiles) and optimal full matching (see Section 2.5). On the one hand, we conditioned on $\{\hat{ψ_{A}} (X), X_{10}\}$ ; on the other hand, we conditioned on $\hat{ψ_{A}} (X)$ only.

Using formulae described in Section 2.3, we estimated the effects of treatment exposures Z = B and Z = C, with reference to Z = A, as ATEs, ATTs, and ATRs (all on an absolute risk difference scale). Given the property of transitivity of ATEs and ATRs (Section 2.1), we also computed the effect of Z = B in comparison to Z = C, as ${\hat{A T E}}_{B, C} = {\hat{A T E}}_{B, A} - {\hat{A T E}}_{C, A}$ and ${\hat{A T R}}_{B, C} = {\hat{A T R}}_{B, A} - {\hat{A T R}}_{C, A}$ .

In comparison to generalised prognostic score analysis, we conducted generalised propensity score analysis.9, 10 Having a categorical treatment, we fit a parametric multinomial logistic regression to estimate the propensity scores10, 17

\begin{matrix} {\hat{e}}_{A} (X) = \Pr (Z = A | X, \hat{α}) = \frac{1}{1 + \exp ({\hat{α}}_{B 0} + \sum X_{p} {\hat{α}}_{Bp}) + \exp ({\hat{α}}_{C 0} + \sum X_{p} {\hat{α}}_{Cp})} \\ {\hat{e}}_{B} (X) = \Pr (Z = B | X, \hat{α}) = \frac{\exp ({\hat{α}}_{B 0} + \sum X_{p} {\hat{α}}_{Bp})}{1 + \exp ({\hat{α}}_{B 0} + \sum X_{p} {\hat{α}}_{Bp}) + \exp ({\hat{α}}_{C 0} + \sum X_{p} {\hat{α}}_{Cp})} \\ {\hat{e}}_{C} (X) = \Pr (Z = C | X, \hat{α}) = \frac{\exp ({\hat{α}}_{C 0} + \sum X_{p} {\hat{α}}_{Cp})}{1 + \exp ({\hat{α}}_{B 0} + \sum X_{p} {\hat{α}}_{Bp}) + \exp ({\hat{α}}_{C 0} + \sum X_{p} {\hat{α}}_{Cp})} . \end{matrix}

We performed subclassification (by quintiles) and optimal full matching to condition on the propensity scores.

3.3. Results

On average, the prevalence to exposures Z = A, Z = B and Z = C was equal to 49.3%, 29.1%, and 21.6%, respectively. The outcome prevalence within each arm was equal to 40.2%, 13.3%, and 24.4%, respectively. (The naïve estimates corresponded to the mere differences between these values.) All estimates of causal effects using the generalised propensity score and the generalised prognostic score are reported in Table 1. Empirically, the estimators proposed in Section 2.3 allowed unbiased estimation of the causal effects. As described in Section 2.3, conditioning on relevant effect modifiers, in addition to the prognostic score, is necessary to estimate the ATEs and ATRs without bias. The property of transitivity held when estimating these two treatment effects. (Note, for the internal validity of our simulations, we computed, along with the transitive estimates of ATEs and ATRs, the corresponding matching/subclassification estimates; this resulted in a perfect agreement. See Appendix 1 in Supplementary Material.) Generally, optimal full matching yielded higher mean squared error (but lower bias) than subclassification. In this series of simulations, the use of generalised prognostic scores outperformed that of generalised propensity scores in terms of bias, variance, and mean squared error (Table 1). The mean squared errors obtained by generalised propensity score analysis was on average 149.9% higher than those obtained by generalised prognostic score analysis, when conditioning on $\{\hat{ψ_{A}} (X), X_{10}\}$ .

Table 1.

Results of simulation study, when including all covariates in analysis. Bias (standard deviation, SD) and mean squared error (MSE) of estimates

	Generalised Propensity Score Analysis				Generalised Prognostic Score Analysis
	Subclassification		Full Matching		Effect Modifier Included				Effect Modifier (Wrongfully) Ignored
					Subclassification		Full Matching		Subclassification		Full Matching
	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE
	(SD)	×1000	(SD)	×1000	(SD)	×1000	(SD)	×1000	(SD)	×1000	(SD)	×1000
ATE_B,A	−0.009	0.5630	0.000	0.8365	−0.005	0.4758	−0.001	0.6147	−0.005	0.4711	−0.001	0.6287
	(0.022)		(0.029)		(0.021)		(0.025)		(0.021)		(0.025)
ATE_C,A	−0.006	0.9801	0.000	1.4452	−0.004	0.7696	0.002	1.3742	−0.001	0.7462	0.005	1.3731
	(0.031)		(0.038)		(0.027)		(0.037)		(0.027)		(0.037)
ATE_B,C	−0.002	0.9894	0.000	1.6867	−0.001	0.7523	−0.004	1.601	−0.004	0.7587	−0.006	1.6521
	(0.031)		(0.041)		(0.027)		(0.040)		(0.027)		(0.040)
ATT_B,A	−0.025	1.0862	−0.012	1.0001	−0.009	0.4613	0.000	0.546	−0.009	0.4552	0.000	0.5148
	(0.022)		(0.029)		(0.020)		(0.023)		(0.020)		(0.023)
ATT_C,A	0.001	0.9062	0.017	1.6601	−0.009	0.8816	−0.001	0.9786	−0.009	0.8593	0.000	1.0116
	(0.030)		(0.037)		(0.028)		(0.031)		(0.028)		(0.032)
ATT_B,C ^*	‐	‐	‐	‐	‐	‐	‐	‐	‐	‐	‐	‐
ATR_B,A	−0.005	0.9296	0.000	1.6029	−0.004	0.6137	−0.003	1.0326	−0.004	0.6086	−0.002	1.0608
	(0.030)		(0.04)		(0.025)		(0.032)		(0.024)		(0.033)
ATR_C,A	−0.004	1.8233	−0.003	2.7686	−0.002	0.9367	0.003	2.0917	0.003	0.9225	0.009	2.1526
	(0.042)		(0.053)		(0.031)		(0.046)		(0.030)		(0.046)
ATR_B,C	−0.001	2.1482	0.003	3.8504	−0.002	1.0113	−0.005	2.8026	−0.007	1.0396	−0.010	2.8889
	(0.046)		(0.062)		(0.032)		(0.053)		(0.031)		(0.053)

Open in a new tab

Due to nontransitivity, ATT_B,C was not estimated.

Figure 1 depicts the estimated average potential outcomes under treatment exposures A, B, and C after subclassifying on both the prognostic score and the effect modifier with respect to their distribution in the entire population (ie, condition for estimating ATEs). This allowed us to directly assess the potential responses of the entire population to the three treatment exposures; computing the average treatment effects was done by merely calculating the relevant differences across these. Alternatively, we could have defined exposures A, B, and C as ordinal to visualise a dose‐response relationship.

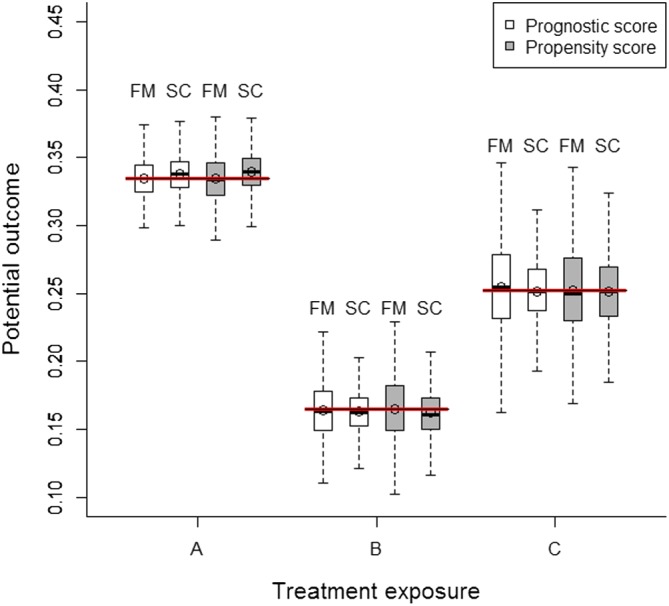
sim8084-fig-0001 — Distribution of estimated potential outcomes after conditioning on the prognostic score and effect modifier, and the propensity score. Red bold lines (ie, reference values) correspond to the expected values of potential outcomes obtained in an independent “superpopulation” including 5 000 000 individuals. FM, full matching; SC, subclassification [Colour figure can be viewed at wileyonlinelibrary.com]

Results of additional simulations are reported in Tables 2 to 4, describing the impact of omitting some variables in prognostic score modelling (eg, introduction of hidden bias) on the treatment effect estimation. Further simulations were conducted in small samples, with results provided in Appendix 2 (Supplementary Material).

Table 2.

Results of simulation study, when omitting X₃ (“true confounder,” ie, related to both exposures and potential outcomes) from all analysis. Bias (standard deviation, SD) and mean squared error (MSE) of estimates

	Generalised Propensity Score Analysis				Generalised Prognostic Score Analysis
	Subclassification		Full Matching		Effect Modifier Included				Effect Modifier (Wrongfully) Ignored
					Subclassification		Full Matching		Subclassification		Full Matching
	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE
	(SD)	×1000	(SD)	×1000	(SD)	×1000	(SD)	×1000	(SD)	×1000	(SD)	×1000
ATE_B,A	−0.027	1.1794	−0.020	1.1397	−0.024	1.0117	−0.020	1.0287	−0.024	1.0108	−0.020	1.0046
	(0.022)		(0.027)		(0.021)		(0.025)		(0.021)		(0.025)
ATE_C,A	−0.024	1.3804	−0.019	1.6438	−0.022	1.2041	−0.018	2.1513	−0.020	1.1351	−0.015	2.4085
	(0.028)		(0.036)		(0.027)		(0.043)		(0.027)		(0.047)
ATE_B,C	−0.003	0.8301	0.000	1.3966	−0.002	0.7148	−0.001	1.9575	−0.004	0.7208	−0.005	2.3173
	(0.029)		(0.037)		(0.027)		(0.044)		(0.027)		(0.048)
ATT_B,A	−0.046	2.5693	−0.037	2.2180	−0.029	1.2797	−0.022	1.0215	−0.029	1.2739	−0.022	1.0043
	(0.021)		(0.029)		(0.020)		(0.023)		(0.020)		(0.023)
ATT_C,A	−0.034	2.0128	−0.024	1.8702	−0.046	2.9076	−0.041	2.7115	−0.046	2.8738	−0.041	2.6661
	(0.029)		(0.036)		(0.028)		(0.032)		(0.028)		(0.031)
ATT_B,C ^*	‐	‐	‐	‐	‐	‐	‐	‐	‐	‐	‐	‐
ATR_B,A	−0.015	0.9734	−0.009	1.4521	−0.015	0.7847	−0.013	1.1850	−0.015	0.7770	−0.013	1.1310
	(0.027)		(0.037)		(0.024)		(0.032)		(0.023)		(0.031)
ATR_C,A	−0.009	1.3518	−0.009	2.2235	−0.007	0.8858	−0.006	2.8341	−0.003	0.8345	0.001	3.3665
	(0.036)		(0.046)		(0.029)		(0.053)		(0.029)		(0.058)
ATR_B,C	−0.005	1.5374	0.000	2.9242	−0.008	0.9284	−0.007	3.3145	−0.012	0.9931	−0.013	3.9591
	(0.039)		(0.054)		(0.029)		(0.057)		(0.029)		(0.061)

Open in a new tab

Due to nontransitivity, ATT_B,C was not estimated.

Table 4.

Results of simulation study, when omitting X₂ (“instrumental variable,” ie, related only to exposures) from all analysis. Bias (standard deviation, SD) and mean squared error (MSE) of estimates

	Generalised Propensity Score Analysis				Generalised Prognostic Score Analysis
	Subclassification		Full Matching		Effect Modifier Included				Effect Modifier (Wrongfully) Ignored
					Subclassification		Full Matching		Subclassification		Full Matching
	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE
	(SD)	×1000	(SD)	×1000	(SD)	×1000	(SD)	×1000	(SD)	×1000	(SD)	×1000
ATE_B,A	−0.008	0.5453	0.000	0.7973	−0.005	0.4742	−0.001	0.6139	−0.005	0.4701	−0.001	0.6341
	(0.022)		(0.028)		(0.021)		(0.025)		(0.021)		(0.025)
ATE_C,A	−0.007	0.9263	−0.001	1.3437	−0.004	0.7590	0.002	1.2912	−0.001	0.7366	0.005	1.3531
	(0.030)		(0.037)		(0.027)		(0.036)		(0.027)		(0.036)
ATE_B,C	−0.002	0.9305	0.000	1.5498	−0.001	0.7497	−0.003	1.5167	−0.004	0.7570	−0.006	1.5963
	(0.030)		(0.039)		(0.027)		(0.039)		(0.027)		(0.040)
ATT_B,A	−0.022	0.9290	−0.009	0.8251	−0.009	0.4550	0.000	0.5000	−0.009	0.4478	0.000	0.5061
	(0.021)		(0.027)		(0.020)		(0.022)		(0.019)		(0.023)
ATT_C,A	−0.001	0.8189	0.013	1.5119	−0.009	0.8570	−0.001	0.9676	−0.009	0.8344	0.000	0.9533
	(0.029)		(0.037)		(0.028)		(0.031)		(0.028)		(0.031)
ATT_B,C ^*	‐	‐	‐	‐	‐	‐	‐	‐	‐	‐	‐	‐
ATR_B,A	−0.006	0.8355	−0.001	1.4711	−0.004	0.6121	−0.002	1.0467	−0.004	0.6059	−0.002	1.0727
	(0.028)		(0.038)		(0.024)		(0.032)		(0.024)		(0.033)
ATR_C,A	−0.005	1.5473	−0.004	2.5417	−0.002	0.9275	0.002	1.9736	0.003	0.9174	0.009	2.1754
	(0.039)		(0.050)		(0.030)		(0.044)		(0.030)		(0.046)
ATR_B,C	−0.001	1.8331	0.002	3.4033	−0.002	1.0085	−0.004	2.6074	−0.007	1.0342	−0.011	2.8121
	(0.043)		(0.058)		(0.032)		(0.051)		(0.031)		(0.052)

Open in a new tab

Due to nontransitivity, ATT_B,C was not estimated.

Table 3.

Results of simulation study, when omitting X₆ (“prognostic variable,” ie, related only to potential outcomes) from all analysis. Bias (standard deviation, SD) and mean squared error (MSE) of estimates

	Generalised Propensity Score Analysis				Generalised prognostic score analysis
	Subclassification		Full Matching		Effect Modifier Included				Effect Modifier (Wrongfully) Ignored
					Subclassification		Full Matching		Subclassification		Full Matching
	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE
	(SD)	×1000	(SD)	×1000	(SD)	×1000	(SD)	×1000	(SD)	×1000	(SD)	×1000
ATE_B,A	−0.009	0.5702	0.000	0.8103	−0.005	0.4787	−0.002	0.6485	−0.005	0.4742	−0.001	0.6368
	(0.022)		(0.028)		(0.021)		(0.025)		(0.021)		(0.025)
ATE_C,A	−0.006	0.9832	0.000	1.4841	−0.004	0.7793	0.001	1.2774	−0.001	0.7520	0.005	1.3421
	(0.031)		(0.039)		(0.028)		(0.036)		(0.027)		(0.036)
ATE_B,C	−0.002	0.9811	0.000	1.6842	−0.001	0.7598	−0.003	1.4801	−0.004	0.7625	−0.006	1.5943
	(0.031)		(0.041)		(0.028)		(0.038)		(0.027)		(0.039)
ATT_B,A	−0.025	1.0852	−0.012	0.9704	−0.009	0.4608	0.000	0.5505	−0.009	0.4541	0.000	0.5192
	(0.022)		(0.029)		(0.020)		(0.023)		(0.019)		(0.023)
ATT_C,A	0.001	0.9042	0.016	1.6300	−0.009	0.8740	−0.001	0.9912	−0.009	0.8486	0.000	1.0268
	(0.030)		(0.037)		(0.028)		(0.031)		(0.028)		(0.032)
ATT_B,C ^*	‐	‐	‐	‐	‐	‐	‐	‐	‐	‐	‐	‐
ATR_B,A	−0.009	0.5702	0.000	0.8103	−0.005	0.4787	−0.002	0.6485	−0.005	0.4742	−0.001	0.6368
	(0.022)		(0.028)		(0.021)		(0.025)		(0.021)		(0.025)
ATR_C,A	−0.006	0.9832	0.000	1.4841	−0.004	0.7793	0.001	1.2774	−0.001	0.7520	0.005	1.3421
	(0.031)		(0.039)		(0.028)		(0.036)		(0.027)		(0.036)
ATR_B,C	−0.002	0.9811	0.000	1.6842	−0.001	0.7598	−0.003	1.4801	−0.004	0.7625	−0.006	1.5943
	(0.031)		(0.041)		(0.028)		(0.038)		(0.027)		(0.039)

Open in a new tab

Due to nontransitivity, ATT_B,C was not estimated.

4. STUDY CASE

As an illustrative case, we performed a subgroup analysis of the International Stroke Trial (IST), the data of which have been made available in open access by the investigators.27 This trial included 19 435 patients across 36 countries and aimed to estimate the effect of Aspirin (compared to non‐Aspirin) on a primary composite outcome of death or dependence at 6 months in stroke patients (binary outcome).28 Further details on the data set can be found elsewhere.27, 28 Though the IST was a randomised controlled trial, in this study case, we focused on the Aspirin arm only (9720 patients) as we were interested in estimating the effect of the delay to Aspirin administration on the primary outcome. This delay varied from 1 to 48 hours from symptoms and likely depends upon clinical covariates (eg, stroke subtype, consciousness, executive function deficits). Differences in these clinical characteristics are depicted in Figure 2, using standardised mean differences (SMD). At each time point, we calculated the covariate mean (approximated by p the proportion of the class, for categorical/binary variables), which was then divided by the standard deviation (approximated by $\sqrt{p (1 - p)}$ for categorical/binary variables) obtained in the whole sample (ie, Aspirin arm). We computed SMDs, as the absolute differences in those ratios (ie, standardised means), taking a delay of 24 hours as “reference.” As depicted in Figure 2, strong imbalance (SMD > 0.25) occurred at very low or high delays, suggesting that patients receiving Aspirin very early or very lately were likely to differ from those who received the treatment around 24 hours, in terms of clinical characteristics.

sim8084-fig-0002 — Difference in baseline characteristics expressed in standardised mean differences against delay (reference: 24‐hour delay). Each colour line denotes a covariate. Red bold dotted lines refer to common thresholds for considering imbalance [Colour figure can be viewed at wileyonlinelibrary.com]

We performed both a generalised prognostic score analysis and a generalised propensity score analysis to estimate the effect of the delay to Aspirin administration on the primary outcome.

For prognostic score analysis, we first derived a logistic regression model by maximum likelihood estimation as to the risk of death or dependence at 6 months after Aspirin administration at 24 hours. We took this delay as “reference,” since it included the largest sample size (809 patients), with 483 outcomes. We considered the following relevant confounders to be entered into the model: age, systolic blood pressure, sex, consciousness, previous computerised tomography (CT‐scan), visible infarct at CT‐scan, stroke subtype, atrial fibrillation, Aspirin intake within the previous 3 days, and all function deficits. We transposed the obtained prognostic score to other delay arms to predict the potential outcomes that would have been observed, had all individuals received Aspirin at 24 hours. Using methods described in Section 2.5, we subclassified and conducted an optimal full matching on the prognostic score to estimate the ATE. For matching, we considered 48 treatment exposures, each corresponding to their respective delay (in hours) of Aspirin administration. This enabled us to investigate the entire function of treatment exposure. As described in Section 2.5.2, the prognostic score was matched separately for each exposure group: we matched the individuals who received Aspirin at 1 hour to all the others; then, those who received it at 2 hours to all the others; and so on. This allowed us to reweight all the treatment exposure groups, as though they had similar distribution of the prognostic score as in the entire sample. We considered no effect modifiers in this analysis.

In comparison, we performed a generalised propensity score analysis. Considering the delay as a continuous variable, we derived a linear model by maximum likelihood estimation, including the same set of covariates as in the prognostic score. Though the scalar returned by this linear model, $\hat{θ}$ , does not represent the conditional probability of treatment delay (ie, propensity score), Imai and van Dyk showed that, since the propensity function is characterised by $\hat{θ}$ , conditioning on it allows one to condition on the propensity score.9 As for the generalised prognostic score, we conducted subclassification and optimal full matching. Note that here, as opposed to ordinal or categorical multi‐exposures which require to match/subclassify on the respective propensity scores, all individuals are to be conditioned on $\hat{θ}$ , regardless of the actual delay.

In prognostic and propensity scores, continuous variable (age and systolic blood pressure) were modelled using a restricted cubic spline with three knots. To address missing data (1067 missing values with regard to the outcome and relevant covariates), we performed multiple imputation by chained equations, setting m = 10. Hereby, we adjusted for the observed outcome and covariates used in the prognostic and propensity models. Furthermore, we adopted the strategy recommended by Leyrat et al29: for each imputed dataset, we derived a prognostic score and a propensity score, matched and subclassified on the scores, estimated the potential outcome distribution at each delay and the treatment effect (ie, mean change to potential outcome across all delays, expressed in absolute risk difference); finally, we applied Rubin's rules to average the estimates across the 10 data sets.

As depicted in Figure 3, the generalised prognostic and propensity score analyses yielded similar results. Using both methods, we found no evident effect of the delay to Aspirin administration on the risk of death or dependence at 6 months in stroke patients. Like in the simulation study, subclassification resulted in less variance than optimal full matching, regardless of the scores. Indeed, matching estimates were particularly scattered, as compared with those obtained by subclassification. This poor performance was likely due to the substantial number of treatment exposures (ie, 48 time points), which were to be matched separately.

sim8084-fig-0003 — Estimated risk of death or dependence at 6 months, given delay to Aspirin administration in stroke patients, by propensity and prognostic score analyses. ARD, absolute risk difference per hour of delay [Colour figure can be viewed at wileyonlinelibrary.com]

5. DISCUSSION

In this article, we describe the theory of the prognostic score for causal inference with general treatment regimes and propose estimators for different estimands of interest (Section 2), the validity of which is empirically verified through a series of simulations (Section 3) and then illustrated in a study case (Section 4).

We extend Hansen's formalisation of prognostic scores6 to allow investigation of multiple treatment exposures. The proposed methods can be applied to compare multiple treatments using nonrandomised data, a topic of great relevance in contemporary evaluations of clinical interventions. Similarly to the propensity score, the prognostic score reduces the dimension of multiple subject covariates into a single, summarising score that can be used for matching or subclassification. While the primary purpose of the propensity score is to balance the covariate across the treatment arms as would do a randomised experiment,5 conditioning on a prognostic score aims to approximate an experimental design in which subjects would share similar potential responses to treatments at baseline.6 The use of the propensity score for causal inference with general treatment regimes has been defined elsewhere,9, 10 yet not the use of the prognostic score. In the pharmacoepidemiology literature, a previous simulation study attempted to compare the performance of multivariable regression, propensity, and prognostic scores in case of multiple treatment exposures.30 However, it remained unclear—to the best of our understanding—which estimand was of interest (ATE, ATT, ATR, marginal or conditional effect) and how the performance, related to a true causal effect, was measured. Nor was it evident to us why the authors chose to fit a prognostic model to the overall sample, instead of deriving it from reference subjects only, as recommended.6 In his article, Hansen clearly cautioned against the fitting of a model to the entire sample (including both reference and treated subjects), for it does no longer allow the estimation of the true prognostic score ψ_r(X) but a mixture of propensity and prognostic scores influenced by potential outcomes under nonreference exposures.6

In the present article, we show that the framework of prognostic scores can easily be transposed to multiple treatment exposures, by relating to the propositions and assumptions applicable to the case of binary treatments. In multiple treatment exposures, the generalised propensity score involves either the estimation of the multivariate conditional density of Z given X, or the fitting of a parametric model (depending on the treatment exposure distribution), which requires the assumption of uniquely parameterised propensity function.9 In contrary, the generalised prognostic score is estimated in a way akin to the case of binary treatment, regardless of the exposure distribution—be it categorical, ordinal, or continuous. A prognostic model is still to be fitted to some reference subjects (originating from same sample as treated or from historical cohorts), before being extrapolated to subjects receiving different treatment exposures. In addition, the positivity assumption required for generalised propensity score analysis is relaxed in generalised prognostic score analysis: The former requires $\Pr (Z \in Z X) > 0$ for all $X \in A$ ,9 while the latter demands $\Pr (Z \in Z | ψ_{r} (X), m (X)) > 0$ . Note that this relaxation is even stronger in case of multiple treatment exposures, since positive measures are necessitated in ${dim}_{Z} (Z) \times {dim}_{A} (X)$ dimensions for generalised propensity score, compared to ${dim}_{Z} (Z) \times (1 + F)$ dimensions for generalised prognostic score (F being the number of effect modifiers). Thus, the generalised propensity score is likely to suffer more from the curse of dimensionality. In that sense, the generalised prognostic score offers advantages over the generalised propensity score from an analytic perspective.

As shown in Section 2.5, conditioning on the generalised prognostic score via subclassification or matching is straightforward as in the case of binary treatments. Each exposure arm is to be subclassified (or matched) on a same prognostic score, as opposed to subclassification (or matching) on the generalised propensity score, which must be done on the relevant, corresponding exposure propensity score. An alternative offered to the generalised propensity score analysis, which is not directly applicable to the generalised prognostic score, is weighting on the inverse probability of treatment exposure.17 However, a recent simulation study demonstrated that this approach offers no substantial advantages over subclassification or matching.16 Empirical results reported in Section 3 suggest that—using the same variable set in score modelling and the same methods for conditioning (subclassification or full matching)—the generalised propensity score analysis generally leads to higher variance in treatment effect estimations than does the generalised prognostic score analysis. This might be due to the fact that, in case of a binary outcome and T treatment arms, a multinomial logistic propensity score model fits T − 1 equations and is therefore likely to consume much more degrees of freedom (ie, (T − 1)(k + 1) d.f., for 1 intercept and k regression coefficients) than a binary logistic prognostic model (ie, (k + 1) d.f.). (Note that this does not hold in case of continuous treatment regimes, as in the study case, for it is sufficient for propensity score analysis to condition on the scalar, $\hat{θ}$ , estimated by linear regression using (k + 1) d.f.) Furthermore, the generalised propensity score suffers from an additional issue that is not relevant when dealing with two treatment exposures. In binary treatment exposures (ie, Z ∈ {0, 1}), subclassifying/matching on $\hat{e_{1}} (X) = \hat{P r} (Z = 1 X)$ is similar to subclassifying/matching on $\hat{e_{0}} (X) = \hat{P r} (Z = 0 X)$ , since $\hat{e_{1}} (X) = 1 - \hat{e_{0}} (X)$ . This does not hold in case of multiple treatment exposures, where subclassification/matching relies on propensity scores that are “extrapolated” to predict the exposure probability in the corresponding, but also in the different treatment arms. In this sense, the generalised propensity score presents no advantage over the prognostic score as it does in binary treatment arms. Further studies are thus needed to compare the relative performance between generalised propensity score analysis and its prognostic analogue in scenarios in which—albeit relatively uncommon in clinical practice—the exposures would be limited to but a few treatment arms and the outcome would include numerous categories. (Note, in this case, the prognostic scores would be no longer scalar but multidimensional.)

A common approach to estimating treatment effects is to adopt “traditional” regression adjustment methods. Although this strategy is relatively straightforward, its implementation may be problematic in practice because treatment effect estimates are directly affected by changes in model specification (eg, interaction or continuous variable functional specification). For instance, Ho et al showed that adjusting for a continuous confounder could lead to conflicting estimated treatment effects (ie, positive or negative effects), depending on whether the analyst chose a linear or a quadratic model.31 Propensity score and prognostic score methods rely on a different paradigm: They aim to restore a form of balance which is sufficient for causal inference, such that treatment effect estimation requires no model specification but a mere marginal difference in observed outcomes. This balance is attained by minimising a distance—namely, propensity or prognostic distance—between individuals under different exposures. In this sense, propensity and prognostic scores limit model dependence for they do not allow the analyst to directly specify the relationship between the treatment effect and the outcome.

In practice, balance of the propensity score can be assessed in the entire sample. Conversely, for the prognostic score, balance is merely assumed, as it is impossible to assess whether individual predicted potential outcomes for nonobserved treatment exposures are correct. A recent study has investigated the use of “dry‐run” analysis to address this issue.32 In the predictive modelling literature, it is known that applying a prognostic model to an external population might lead to a decreased predictive accuracy when differences in covariate distributions or in predictor‐outcome associations occur.33 In nonrandomised studies, it is most likely that subjects receiving alternative (eg, experiential) treatments differ from those assigned to the reference (eg, standard care). It is thus of uttermost importance to build prognostic models that account for the relevant covariates (ie, assumption of no hidden bias) but at the same time avoid overfitting. Otherwise, such an approach would be reduced back to model dependence, the issue of which matching and propensity score analysis are specifically aimed at avoiding.31 Since the prognostic score has to be fitted to a reference group, deriving a same‐sample model may become difficult in the presence of many exposure arms (eg, continuous treatments). In such cases, prognostic models derived on historical cohorts of reference subjects may be regarded as an interesting alternative. According to a few simulation studies,6, 34, 35, 36, 37 the latter is deemed as more robust an approach than the former, even in case of binary exposures, in the sense that—being less concerned by overfitting—it might enable a better extrapolation of $\hat{ψ_{r}} (X) = E (Y_{r} | X, \hat{β})$ to the treated arms, thereby allowing a more desirable prognostic balance. The development of advanced prognostic models might further be improved by considering evidence synthesis, either using patient‐level data or (previously published) aggregate data from multiple studies.33, 38, 39, 40, 41, 42, 43 We will investigate these strategies in the near future.

To the absence of hidden bias also required in propensity score analysis, the prognostic score analysis entails an additional assumption in estimating the ATEs and ATRs: One must be able to identify all effect modifier(s), since conditioning on them along with the prognostic score is necessary. This seems of particular importance, for ATEs and ATRs are transitive estimands which allow direct comparisons of nonreference treatment effects. In contrary, estimating the ATTs does not require conditioning on any effect modifiers; yet it provides limited interpretation on causal effects that are inferred upon different populations across which comparisons are unlikely to be relevant. However, as discussed by some authors, it is sometimes of great interest to estimate the treatment effect in those for whom the treatment was intended44; situations for which the use of prognostic scores appears most appealing.

In response to these issues, further research is needed to improve the practical use of the generalised prognostic score. First, one should investigate whether robust regression methods, eg, involving penalisation, improve the predictive performance of prognostic score models when applied to new (ie, treated) subjects. Second, extending the joint use of propensity and prognostic scores45 to general treatment regimes might be of interest as it would enable the causal effect estimation to rely on the accuracy of, at least, only one of the two components (“double robustness”). Note, conditioning on the propensity score e_s(X) = Pr(Z = z_s | X) would result in Y_s ⊥ Z | e_s(X), if Y_s ⊥ Z | X (ie, in the absence of unmeasured confounders related to Y_s and Z). Hence, as suggested by a reviewer, the joint use of ψ_r(X) and e_s(X) would enable the estimation of ATRs and ATEs by ensuring that (Y_r, Y_s) ⊥ Z | (ψ_r(X), e_s(X)). Similarly, ATRs and ATEs could be estimated by conditioning on two (rather than one) prognostic scores ψ_r(X) = E(Y_r | X) and ψ_s(X) = E(Y_s | X). This would then result in (Y_r, Y_s) ⊥ Z | (ψ_r(X), ψ_s(X)), if additionally to Y_r ⊥ Z | X we had Y_s ⊥ Z | X. In both cases, the joint use of several scores demands additional modelling steps and a slightly stronger form of the assumption of no unmeasured confounders. Finally, further research is needed to allow direct estimation of standard errors of estimated treatment effects. These estimates are particularly relevant when comparing causal effects across nonreference exposures, as allowed by the property of transitivity of ATEs and ATRs. Although we did not evaluate this here, one (rather time‐consuming) common approach might be to adopt bootstrapping—the limitations of which have been discussed for matching estimators.46

Since several precautions have been raised, one should carefully weigh up the pros and cons of performing the generalised prognostic score over the generalised propensity score analysis. On the one hand, the prognostic score seems more appealing when facing a large number of exposures as it enables the estimation of ATEs, ATRs, and notably, ATTs, while being less dependent on the positivity assumption. (Note, as raised by a reviewer, since the prognostic score assumes Y_r ⊥ X ∣ ψ_r(X), it may require that Pr(Y_r ∈ ·| X) > 0, that is, another form of positivity). Deriving a prognostic score for a common reference treatment can, however, be challenging as it may dramatically reduce the effective sample size. A second limitation of generalised prognostic score is that estimation of ATEs and ATRs is difficult in the presence of multiple (continuous) effect modifiers. For this reason, the generalised prognostic score may be more appealing when ATTs are of primary interest, or when there is limited evidence of effect modification. In general, we believe that both methods should be regarded as complementary rather than exclusive, which warrants the need for further research to extend their combined use to general treatment regimens (“generalised prognostic propensity score analysis”).

In conclusion, this article presents an extension of the framework proposed by Hansen, on the use of prognostic scores for causal inference in binary treatments,6 to the case of general treatment regimes.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

Supporting information

SIM_8084‐Supp‐0001‐SIM_20180924_Nguyen_Appendix1_R1.docx

Click here for additional data file.^{(55.1KB, docx)}

SIM_8084‐Supp‐0002‐SIM_20180924_Nguyen_Appendix2_R1.docx

Click here for additional data file.^{(1.2MB, docx)}

ACKNOWLEDGEMENTS

We would like to thank two anonymous reviewers for their constructive feedback during the review of this manuscript. Thomas P.A. Debray was supported by the Netherlands Organization for Scientific Research (91617050 and 91215058).

Nguyen T‐L, Debray TPA. The use of prognostic scores for causal inference with general treatment regimes. Statistics in Medicine. 2019;38:2013–2029. 10.1002/sim.8084

REFERENCES

1. Concato J, Shah N, Horwitz RI. Randomized, controlled trials, observational studies, and the hierarchy of research designs. N Engl J Med. 2000;342(25):1887‐1892. [DOI] [PMC free article] [PubMed] [Google Scholar]
2. Eichler H‐G, Abadie E, Breckenridge A, et al. Bridging the efficacy‐effectiveness gap: a regulator's perspective on addressing variability of drug response. Nat Rev Drug Discov. 2011;10(7):495‐506. [DOI] [PubMed] [Google Scholar]
3. Najafzadeh M, Schneeweiss S. From trial to target populations—calibrating real‐world data. N Engl J Med. 2017;376(13):1203‐1205. [DOI] [PubMed] [Google Scholar]
4. Vickers AJ. Clinical trials in crisis: four simple methodologic fixes. Clinical Trials. 2014;11(6):615‐621. [DOI] [PMC free article] [PubMed] [Google Scholar]
5. Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70(1):41‐55. [Google Scholar]
6. Hansen BB. The prognostic analogue of the propensity score. Biometrika. 2008;95(2):481‐488. [Google Scholar]
7. Petersen ML, Porter KE, Gruber S, Wang Y, van der Laan MJ. Diagnosing and responding to violations in the positivity assumption. Stat Methods Med Res. Feb 2012;21(1):31‐54. [DOI] [PMC free article] [PubMed] [Google Scholar]
8. Westreich D, Cole SR. Invited commentary: positivity in practice. Am J Epidemiol. 2010;171(6):674‐677; discussion 678‐681. [DOI] [PMC free article] [PubMed] [Google Scholar]
9. Imai K, van Dyk DA. Causal inference with general treatment regimes. J Am Stat Assoc. 2004;99:854‐866. [Google Scholar]
10. Imbens GW. The role of the propensity score in estimating dose‐response functions. Biometrika. 2000;87(3):706‐710. [Google Scholar]
11. Lopez MJ, Gutman R. Estimation of causal effects with multiple treatments: a review and new ideas. 2017. arXiv:1701.05132.
12. Rubin DB. Estimating causal effects of treatments in randomized and nonrandomized studies. J Educ Psychol. 1974;66(5):688‐701. [Google Scholar]
13. Rubin DB. Randomization analysis of experimental data: the fisher randomization test comment. J Am Stat Assoc. 1980;75(371):591‐593. [Google Scholar]
14. Holland PW. Statistics and causal inference. J Am Stat Assoc. 1986;81(396):945‐960. [Google Scholar]
15. Rosenbaum PR, Rubin DB. Reducing bias in observational studies using subclassification on the propensity score. J Am Stat Assoc. 1984;79(387):516‐524. [Google Scholar]
16. Yang S, Imbens GW, Cui Z, Faries DE, Kadziola Z. Propensity score matching and subclassification in observational studies with multi‐level treatments. Biometrics. 2016;72(4):1055‐1065. [DOI] [PubMed] [Google Scholar]
17. Feng P, Zhou X‐H, Zou Q‐M, Fan M‐Y, Li X‐S. Generalized propensity score for estimating the average treatment effect of multiple treatments. Statist Med. 2012;31(7):681‐697. [DOI] [PubMed] [Google Scholar]
18. Zanutto E, Lu B, Hornik R. Using propensity score subclassification for multiple treatment doses to evaluate a national antidrug media campaign. J Educ Behav Stat. 2005;30(1):59‐73. [Google Scholar]
19. Stuart EA. Matching methods for causal inference: a review and a look forward. Stat Sci Rev J Inst Math Stat. 2010;25(1):1‐21. [DOI] [PMC free article] [PubMed] [Google Scholar]
20. Hirano K, Imbens GW. The propensity score with continuous treatments. In: Gelman A, Meng X‐L, eds. Applied Bayesian Modelling and Causal Inference from Missing Data Perspectives. New York, NY: Wiley; 2004. [Google Scholar]
21. Imbens GW, Rubin DB. An Introduction to Causal Inference in the Statistical, Biomedical and Social Sciences. Cambridge, UK: Cambridge University Press; 2015. [Google Scholar]
22. Rubin DB, Thomas N. Matching using estimated propensity scores, relating theory to practice. Biometrics. 1996;52(1):249‐264. [PubMed] [Google Scholar]
23. Austin PC, Stuart EA. Estimating the effect of treatment on binary outcomes using full matching on the propensity score. Stat Methods Med Res. 2017;26(6):2505‐2525. [DOI] [PMC free article] [PubMed] [Google Scholar]
24. Austin PC, Stuart EA. Optimal full matching for survival outcomes: a method that merits more widespread use. Statist Med. 2015;34(30):3949‐3967. [DOI] [PMC free article] [PubMed] [Google Scholar]
25. Hansen BB. Full matching in an observational study of coaching for the SAT. J Am Stat Assoc. 2004;99(467):609‐618. [Google Scholar]
26. Rosenbaum PR. A characterization of optimal designs for observational studies. J Royal Stat Soc Ser B Methodol. 1991;53(3):597‐610. [Google Scholar]
27. Sandercock PA, Niewada M, Czlonkowska A, International stroke trial collaborative Group . The international stroke trial database. Trials. 2011;12:101 [DOI] [PMC free article] [PubMed] [Google Scholar]
28. International Stroke Trial Collaborative Group . The International Stroke Trial (IST): a randomised trial of aspirin, subcutaneous heparin, both, or neither among 19435 patients with acute ischaemic stroke. Lancet. 1997;349(9065):1569‐1581. [PubMed] [Google Scholar]
29. Leyrat C, Seaman SR, White IR, et al. Propensity score analysis with partially observed covariates: how should multiple imputation be used? Stat Methods Med Res. 2017;096228021771303 [DOI] [PMC free article] [PubMed] [Google Scholar]
30. Cadarette SM, Gagne JJ, Solomon DH, Katz JN, Stürmer T. Confounder summary scores when comparing the effects of multiple drug exposures. Pharmacoepidemiol Drug Saf. 2010;19(1):2‐9. [DOI] [PMC free article] [PubMed] [Google Scholar]
31. Ho DE, Imai K, King G, Stuart EA. Matching as nonparametric preprocessing for reducing model dependence in parametric causal inference. Polit Anal. 2007;15(3):199‐236. [Google Scholar]
32. Wyss R, Hansen BB, Ellis AR, et al. The “dry‐run” analysis: a method for evaluating risk scores for confounding control. Am J Epidemiol. 2017;185(9):842‐852. [DOI] [PMC free article] [PubMed] [Google Scholar]
33. Debray TPA, Koffijberg H, Nieboer D, Vergouwe Y, Steyerberg EW, Moons KGM. Meta‐analysis and aggregation of multiple published prediction models. Statist Med. 2014;33(14):2341‐2362. [DOI] [PubMed] [Google Scholar]
34. Glynn RJ, Gagne JJ, Schneeweiss S. Role of disease risk scores in comparative effectiveness research with emerging therapies. Pharmacoepidemiol Drug Saf. 2012;21(S2):138‐147. [DOI] [PMC free article] [PubMed] [Google Scholar]
35. Kumamaru H, Gagne JJ, Glynn RJ, Setoguchi S, Schneeweiss S. Comparison of high‐dimensional confounder summary scores in comparative studies of newly marketed medications. J Clin Epidemiol. 2016;76:200‐208. [DOI] [PubMed] [Google Scholar]
36. Kumamaru H, Schneeweiss S, Glynn RJ, Setoguchi S, Gagne JJ. Dimension reduction and shrinkage methods for high dimensional disease risk scores in historical data. Emerg Themes Epidemiol. 2016;13(1):5 [DOI] [PMC free article] [PubMed] [Google Scholar]
37. Wyss R, Ellis AR, Brookhart MA, et al. Matching on the disease risk score in comparative effectiveness research of new treatments. Pharmacoepidemiol Drug Saf. 2015;24(9):951‐961. [DOI] [PMC free article] [PubMed] [Google Scholar]
38. Debray TPA, Koffijberg H, Vergouwe Y, Moons KGM, Steyerberg EW. Aggregating published prediction models with individual participant data: a comparison of different approaches. Statist Med. 2012;31(23):2697‐2712. [DOI] [PubMed] [Google Scholar]
39. Debray TPA, Vergouwe Y, Koffijberg H, Nieboer D, Steyerberg EW, Moons KGM. A new framework to enhance the interpretation of external validation studies of clinical prediction models. J Clin Epidemiol. 2015;68(3):279‐289. [DOI] [PubMed] [Google Scholar]
40. Cai T, Gerds TA, Zheng Y, Chen J. Robust prediction of t‐year survival with data from multiple studies. Biometrics. 2011;67(2):436‐444. [DOI] [PMC free article] [PubMed] [Google Scholar]
41. Martin GP, Mamas MA, Peek N, Buchan I, Sperrin M. Clinical prediction in defined populations: a simulation study investigating when and how to aggregate existing models. BMC Med Res Methodol. 2017;17(1):1. [DOI] [PMC free article] [PubMed] [Google Scholar]
42. Royston P, Parmar MKB, Sylvester R. Construction and validation of a prognostic model across several studies, with an application in superficial bladder cancer. Statist Med. 2004;23(6):907‐926. [DOI] [PubMed] [Google Scholar]
43. Steyerberg EW, Eijkemans MJC, Van Houwelingen JC, Lee KL, Habbema JDF. Prognostic models based on literature and individual patient data in logistic regression analysis. Statist Med. 2000;19(2):141‐160. [DOI] [PubMed] [Google Scholar]
44. Pirracchio R, Carone M, Rigon MR, Caruana E, Mebazaa A, Chevret S. Propensity score estimators for the average treatment effect and the average treatment effect on the treated may yield very different estimates. Stat Methods Med Res. 2016;25(5):1938‐1954. [DOI] [PubMed] [Google Scholar]
45. Leacy FP, Stuart EA. On the joint use of propensity and prognostic scores in estimation of the average treatment effect on the treated: a simulation study. Statist Med. 2014;33(20):3488‐3508. [DOI] [PMC free article] [PubMed] [Google Scholar]
46. Abadie A, Imbens GW. On the failure of the bootstrap for matching estimators. Econometrica. 2008;76(6):1537‐1557. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SIM_8084‐Supp‐0001‐SIM_20180924_Nguyen_Appendix1_R1.docx

Click here for additional data file.^{(55.1KB, docx)}

SIM_8084‐Supp‐0002‐SIM_20180924_Nguyen_Appendix2_R1.docx

Click here for additional data file.^{(1.2MB, docx)}

[sim8084-bib-0001] 1. Concato J, Shah N, Horwitz RI. Randomized, controlled trials, observational studies, and the hierarchy of research designs. N Engl J Med. 2000;342(25):1887‐1892. [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0002] 2. Eichler H‐G, Abadie E, Breckenridge A, et al. Bridging the efficacy‐effectiveness gap: a regulator's perspective on addressing variability of drug response. Nat Rev Drug Discov. 2011;10(7):495‐506. [DOI] [PubMed] [Google Scholar]

[sim8084-bib-0003] 3. Najafzadeh M, Schneeweiss S. From trial to target populations—calibrating real‐world data. N Engl J Med. 2017;376(13):1203‐1205. [DOI] [PubMed] [Google Scholar]

[sim8084-bib-0004] 4. Vickers AJ. Clinical trials in crisis: four simple methodologic fixes. Clinical Trials. 2014;11(6):615‐621. [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0005] 5. Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70(1):41‐55. [Google Scholar]

[sim8084-bib-0006] 6. Hansen BB. The prognostic analogue of the propensity score. Biometrika. 2008;95(2):481‐488. [Google Scholar]

[sim8084-bib-0007] 7. Petersen ML, Porter KE, Gruber S, Wang Y, van der Laan MJ. Diagnosing and responding to violations in the positivity assumption. Stat Methods Med Res. Feb 2012;21(1):31‐54. [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0008] 8. Westreich D, Cole SR. Invited commentary: positivity in practice. Am J Epidemiol. 2010;171(6):674‐677; discussion 678‐681. [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0009] 9. Imai K, van Dyk DA. Causal inference with general treatment regimes. J Am Stat Assoc. 2004;99:854‐866. [Google Scholar]

[sim8084-bib-0010] 10. Imbens GW. The role of the propensity score in estimating dose‐response functions. Biometrika. 2000;87(3):706‐710. [Google Scholar]

[sim8084-bib-0011] 11. Lopez MJ, Gutman R. Estimation of causal effects with multiple treatments: a review and new ideas. 2017. arXiv:1701.05132.

[sim8084-bib-0012] 12. Rubin DB. Estimating causal effects of treatments in randomized and nonrandomized studies. J Educ Psychol. 1974;66(5):688‐701. [Google Scholar]

[sim8084-bib-0013] 13. Rubin DB. Randomization analysis of experimental data: the fisher randomization test comment. J Am Stat Assoc. 1980;75(371):591‐593. [Google Scholar]

[sim8084-bib-0014] 14. Holland PW. Statistics and causal inference. J Am Stat Assoc. 1986;81(396):945‐960. [Google Scholar]

[sim8084-bib-0015] 15. Rosenbaum PR, Rubin DB. Reducing bias in observational studies using subclassification on the propensity score. J Am Stat Assoc. 1984;79(387):516‐524. [Google Scholar]

[sim8084-bib-0016] 16. Yang S, Imbens GW, Cui Z, Faries DE, Kadziola Z. Propensity score matching and subclassification in observational studies with multi‐level treatments. Biometrics. 2016;72(4):1055‐1065. [DOI] [PubMed] [Google Scholar]

[sim8084-bib-0017] 17. Feng P, Zhou X‐H, Zou Q‐M, Fan M‐Y, Li X‐S. Generalized propensity score for estimating the average treatment effect of multiple treatments. Statist Med. 2012;31(7):681‐697. [DOI] [PubMed] [Google Scholar]

[sim8084-bib-0018] 18. Zanutto E, Lu B, Hornik R. Using propensity score subclassification for multiple treatment doses to evaluate a national antidrug media campaign. J Educ Behav Stat. 2005;30(1):59‐73. [Google Scholar]

[sim8084-bib-0019] 19. Stuart EA. Matching methods for causal inference: a review and a look forward. Stat Sci Rev J Inst Math Stat. 2010;25(1):1‐21. [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0020] 20. Hirano K, Imbens GW. The propensity score with continuous treatments. In: Gelman A, Meng X‐L, eds. Applied Bayesian Modelling and Causal Inference from Missing Data Perspectives. New York, NY: Wiley; 2004. [Google Scholar]

[sim8084-bib-0021] 21. Imbens GW, Rubin DB. An Introduction to Causal Inference in the Statistical, Biomedical and Social Sciences. Cambridge, UK: Cambridge University Press; 2015. [Google Scholar]

[sim8084-bib-0022] 22. Rubin DB, Thomas N. Matching using estimated propensity scores, relating theory to practice. Biometrics. 1996;52(1):249‐264. [PubMed] [Google Scholar]

[sim8084-bib-0023] 23. Austin PC, Stuart EA. Estimating the effect of treatment on binary outcomes using full matching on the propensity score. Stat Methods Med Res. 2017;26(6):2505‐2525. [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0024] 24. Austin PC, Stuart EA. Optimal full matching for survival outcomes: a method that merits more widespread use. Statist Med. 2015;34(30):3949‐3967. [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0025] 25. Hansen BB. Full matching in an observational study of coaching for the SAT. J Am Stat Assoc. 2004;99(467):609‐618. [Google Scholar]

[sim8084-bib-0026] 26. Rosenbaum PR. A characterization of optimal designs for observational studies. J Royal Stat Soc Ser B Methodol. 1991;53(3):597‐610. [Google Scholar]

[sim8084-bib-0027] 27. Sandercock PA, Niewada M, Czlonkowska A, International stroke trial collaborative Group . The international stroke trial database. Trials. 2011;12:101 [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0028] 28. International Stroke Trial Collaborative Group . The International Stroke Trial (IST): a randomised trial of aspirin, subcutaneous heparin, both, or neither among 19435 patients with acute ischaemic stroke. Lancet. 1997;349(9065):1569‐1581. [PubMed] [Google Scholar]

[sim8084-bib-0029] 29. Leyrat C, Seaman SR, White IR, et al. Propensity score analysis with partially observed covariates: how should multiple imputation be used? Stat Methods Med Res. 2017;096228021771303 [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0030] 30. Cadarette SM, Gagne JJ, Solomon DH, Katz JN, Stürmer T. Confounder summary scores when comparing the effects of multiple drug exposures. Pharmacoepidemiol Drug Saf. 2010;19(1):2‐9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0031] 31. Ho DE, Imai K, King G, Stuart EA. Matching as nonparametric preprocessing for reducing model dependence in parametric causal inference. Polit Anal. 2007;15(3):199‐236. [Google Scholar]

[sim8084-bib-0032] 32. Wyss R, Hansen BB, Ellis AR, et al. The “dry‐run” analysis: a method for evaluating risk scores for confounding control. Am J Epidemiol. 2017;185(9):842‐852. [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0033] 33. Debray TPA, Koffijberg H, Nieboer D, Vergouwe Y, Steyerberg EW, Moons KGM. Meta‐analysis and aggregation of multiple published prediction models. Statist Med. 2014;33(14):2341‐2362. [DOI] [PubMed] [Google Scholar]

[sim8084-bib-0034] 34. Glynn RJ, Gagne JJ, Schneeweiss S. Role of disease risk scores in comparative effectiveness research with emerging therapies. Pharmacoepidemiol Drug Saf. 2012;21(S2):138‐147. [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0035] 35. Kumamaru H, Gagne JJ, Glynn RJ, Setoguchi S, Schneeweiss S. Comparison of high‐dimensional confounder summary scores in comparative studies of newly marketed medications. J Clin Epidemiol. 2016;76:200‐208. [DOI] [PubMed] [Google Scholar]

[sim8084-bib-0036] 36. Kumamaru H, Schneeweiss S, Glynn RJ, Setoguchi S, Gagne JJ. Dimension reduction and shrinkage methods for high dimensional disease risk scores in historical data. Emerg Themes Epidemiol. 2016;13(1):5 [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0037] 37. Wyss R, Ellis AR, Brookhart MA, et al. Matching on the disease risk score in comparative effectiveness research of new treatments. Pharmacoepidemiol Drug Saf. 2015;24(9):951‐961. [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0038] 38. Debray TPA, Koffijberg H, Vergouwe Y, Moons KGM, Steyerberg EW. Aggregating published prediction models with individual participant data: a comparison of different approaches. Statist Med. 2012;31(23):2697‐2712. [DOI] [PubMed] [Google Scholar]

[sim8084-bib-0039] 39. Debray TPA, Vergouwe Y, Koffijberg H, Nieboer D, Steyerberg EW, Moons KGM. A new framework to enhance the interpretation of external validation studies of clinical prediction models. J Clin Epidemiol. 2015;68(3):279‐289. [DOI] [PubMed] [Google Scholar]

[sim8084-bib-0040] 40. Cai T, Gerds TA, Zheng Y, Chen J. Robust prediction of t‐year survival with data from multiple studies. Biometrics. 2011;67(2):436‐444. [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0041] 41. Martin GP, Mamas MA, Peek N, Buchan I, Sperrin M. Clinical prediction in defined populations: a simulation study investigating when and how to aggregate existing models. BMC Med Res Methodol. 2017;17(1):1. [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0042] 42. Royston P, Parmar MKB, Sylvester R. Construction and validation of a prognostic model across several studies, with an application in superficial bladder cancer. Statist Med. 2004;23(6):907‐926. [DOI] [PubMed] [Google Scholar]

[sim8084-bib-0043] 43. Steyerberg EW, Eijkemans MJC, Van Houwelingen JC, Lee KL, Habbema JDF. Prognostic models based on literature and individual patient data in logistic regression analysis. Statist Med. 2000;19(2):141‐160. [DOI] [PubMed] [Google Scholar]

[sim8084-bib-0044] 44. Pirracchio R, Carone M, Rigon MR, Caruana E, Mebazaa A, Chevret S. Propensity score estimators for the average treatment effect and the average treatment effect on the treated may yield very different estimates. Stat Methods Med Res. 2016;25(5):1938‐1954. [DOI] [PubMed] [Google Scholar]

[sim8084-bib-0045] 45. Leacy FP, Stuart EA. On the joint use of propensity and prognostic scores in estimation of the average treatment effect on the treated: a simulation study. Statist Med. 2014;33(20):3488‐3508. [DOI] [PMC free article] [PubMed] [Google Scholar]

[sim8084-bib-0046] 46. Abadie A, Imbens GW. On the failure of the bootstrap for matching estimators. Econometrica. 2008;76(6):1537‐1557. [Google Scholar]

PERMALINK

The use of prognostic scores for causal inference with general treatment regimes

Tri‐Long Nguyen

Thomas PA Debray

Abstract

1. INTRODUCTION

2. THEORY AND METHODS

2.1. Causal framework

2.2. Prognostic score

2.3. Identification of causal effects

2.3.1. Average treatment effect in the treated population

2.3.2. Average treatment effect in the reference population

2.3.3. Average treatment effect in the entire population

2.4. Estimation of prognostic scores

2.5. Conditioning on prognostic scores

2.5.1. Subclassification

2.5.2. Matching

3. SIMULATION STUDY

3.1. Data generation

3.2. Analysis

3.3. Results

Table 1.

Figure 1.

Table 2.

Table 4.

Table 3.

4. STUDY CASE

Figure 2.

Figure 3.

5. DISCUSSION

CONFLICT OF INTEREST

Supporting information

ACKNOWLEDGEMENTS

REFERENCES

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases