Joint models for longitudinal and time‐to‐event data in a case‐cohort design

Abstract

Studies with longitudinal measurements are common in clinical research. Particular interest lies in studies where the repeated measurements are used to predict a time‐to‐event outcome, such as mortality, in a dynamic manner. If event rates in a study are low, however, and most information is to be expected from the patients experiencing the study endpoint, it may be more cost efficient to only use a subset of the data. One way of achieving this is by applying a case‐cohort design, which selects all cases and only a random samples of the noncases. In the standard way of analyzing data in a case‐cohort design, the noncases who were not selected are completely excluded from analysis; however, the overrepresentation of the cases will lead to bias. We propose to include survival information of all patients from the cohort in the analysis. We approach the fact that we do not have longitudinal information for a subset of the patients as a missing data problem and argue that the missingness mechanism is missing at random. Hence, results obtained from an appropriate model, such as a joint model, should remain valid. Simulations indicate that our method performs similar to fitting the model on a full cohort, both in terms of parameters estimates and predictions of survival probabilities. Estimating the model on the classical version of the case‐cohort design shows clear bias and worse performance of the predictions. The procedure is further illustrated in data from a biomarker study on acute coronary syndrome patients, BIOMArCS.

1. INTRODUCTION

Longitudinal measurements are becoming increasingly popular in clinical research, particularly in studies where patients are followed up to an event of interest. By repeatedly collecting and analyzing measurements on patients, their progress is monitored more closely and temporal trends in the disease progress can be estimated, leading to improved prediction of outcomes.1 In these kinds of studies two types of outcomes are collected: the longitudinal outcome (often a biomarker) and the time‐to‐event outcome, eg, death. When interest lies in using temporal patterns of the longitudinal response to estimate the event of interest, both outcomes can be modeled together by using the joint modeling approach.2 To increase prediction even further, instead of one biomarker, a set of multiple markers can be measured.

The motivation for the current paper comes from the longitudinal “BIOMarker study to identify the Acute risk of a Coronary Syndrome” (BIOMArCS), in which acute coronary syndrome (ACS) patients were examined in different medical centers in the Netherlands to study the association between (multiple) biomarkers and a recurrent ACS event (primary endpoint).3, 4 Multiple biomarkers were identified to be of interest, measured in blood samples taken regularly during one year of follow‐up. A downside of collecting multiple biomarkers is the rising costs due to the numerous biomarker measurements, since costs are associated with the ascertainment of each biomarker measured. This can cause such a project to become infeasible in practice. On top of the burden of costs, the BIOMArCS study turned out to have a low event rate, with only 5% of the patients reaching the primary endpoint. This means that the overwhelming majority of biomarker measurements belong to the censored patients where low additional information from the longitudinal patterns is expected. This gave motivation to opt for a case‐cohort design, which enables analysis of the relevant subset of patients, while largely maintaining statistical power.

In the case‐cohort design,5 a random sample of patients from the full cohort is taken, defined as the subcohort ( $\mathcal{A}\cup \mathcal{B}$ in Figure 1). For every patient in the full cohort, the failure status is known. The complete longitudinal biomarker information, however, is only measured in the patients who experienced the study endpoint (the cases) and the random subcohort ( $\mathcal{A}\cup \mathcal{B}\cup \mathcal{C}$ in Figure 1). The advantage the case‐cohort design has over the more popular case‐control design is that the same random subcohort can be used to study different endpoints. The disadvantage, and the main reason why the case‐cohort design is not as popular is that the appropriate analysis becomes more complicated. The case‐cohort design is also known (early on) as “case‐base design” or “hybrid‐retrospective design”.5 These designs were described by Kupper et al6 and Miettinen.7 Prentice was the first to introduce the design in an failure‐time setting and used a pseudolikelihood estimation approach to obtain unbiased estimates for the hazard of the event.5 In this approach, cases outside the subcohort are only included in the risk‐set right before experiencing the endpoint. Other researchers followed and extended this approach by considering other types of weighting schemes.8, 9, 10, 11, 12, 13

Figure 1.

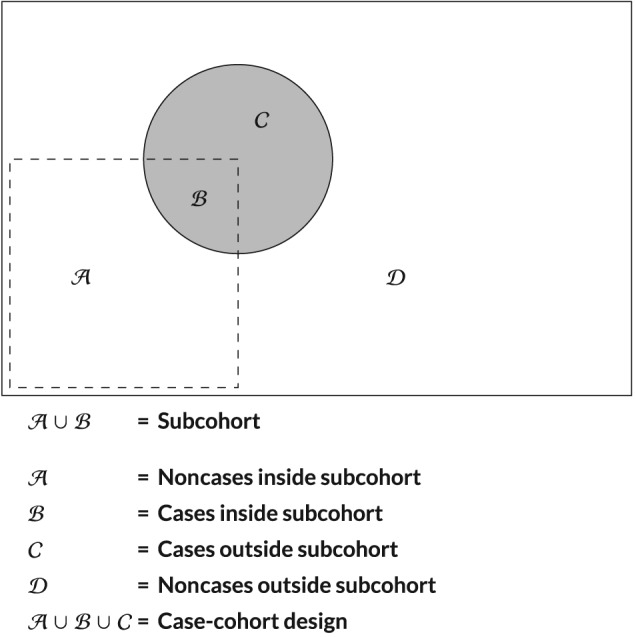
A graphical representation of the case‐cohort design

Motivated by BIOMArCS, the aim of our paper is twofold: first, to extend the estimation framework of joint models for longitudinal and survival data in the context of case‐cohort designs and, second, to assess how dynamic predictions and their accuracy perform in this setting. As mentioned above, the previously developed strategies for case‐cohort designs have been based on pseudolikelihood ideas. However, in joint models, a full specification of the joint distribution of the two outcomes is required, making the use of these approaches complicated. Hence, to appropriately account for the selection bias in the case‐cohort design, we approach the fact that we do not have longitudinal information for a subset of the patients as a missing data problem. This, theoretically, should provide unbiased estimates if the appropriate models are used and only requires small modification in the formulation of the likelihood of the model. With regard to our second goal, we focus on how the accuracy of dynamic predictions for the survival outcome is influenced by the case‐cohort design. The evaluation is based on standard measures of predictive accuracy, such as the time‐varying area under the receiver operating characteristic curves and time‐varying squared prediction errors (PEs). The remainder of this paper is organized as follows. Section 2 presents the joint model used throughout this paper. Section 3 describes the general scenario of estimating a joint model, as well as our proposed modification to avoid biased estimates in relation to the case‐cohort design. Methods to measure the predictive accuracy of the models will be discussed in Section 4. A simulation study to verify our method is performed in Section 5, whereas Section 6 shows the application to the real‐life BIOMArCS data. Finally, in Section 7, results will be discussed and conclusions are made.

2. MODEL SPECIFICATION

We consider here a basic joint model for a continuous longitudinal outcome and a time‐to‐event outcome. More specifically, let y _i(t) be the longitudinal measurement for the ith patient at time t. The longitudinal outcome y _i(t) is modeled by a mixed effects submodel. The design vector for the fixed effects is denoted by x _i(t) and the design vector for the random effects by z _i(t). The time‐to‐event outcome is modeled by a proportional hazards submodel. Both submodels are of the form

$$\left\{\begin{array}{cc}{y}_i(t)& =m_i(t)+{\epsilon }_i(t)\\ & =x_i^{\top }(t)\beta +z_i^{\top }(t)b_i+{\epsilon }_i(t)\\ \\ h_i(t)& =h_0(t)\exp \left\{{\gamma }^{\top }{w}_i+\alpha m_i(t)\right\}.\end{array}\right.$$ (1)

The vector β in the longitudinal submodel denotes the parameters for the fixed effects and b _i the random effects for patient i, which are assumed to follow a normal distribution with mean 0 and variance‐covariance matrix D. The error terms are denoted by ε _i(t) and are also assumed to be normally distributed with mean 0 and variance σ ². Real‐life studies often shown nonlinear trends in the longitudinal patterns, which can be incorporated in the design vectors for the fixed and random effects parts (x _i(t) and z _i(t)). Furthermore, let $T_i^{\ast }$ be the true event time, C _i the censoring time, and $T_i=\min (T_i^{\ast },C_i)$ the observed event time. For each patient, the event indicator is given by δ _i, taking the value of 1 when $T_i^{\ast }\le C_i$ and 0 otherwise. Baseline covariates used in the survival submodel are denoted by w _i. The hazard for the survival outcome (T _i,δ _i) is modeled with a proportional hazards model h _i(t) defined in (1). Here, we assume m _i(t) is the true and unobserved value of longitudinal outcome for patient i at time t, modeled by the longitudinal submodel. The baseline hazard is given by h ₀(t) and is modeled in a flexible manner by B‐splines. Finally, α denotes the association between the longitudinal and time‐to‐event outcome.

3. ESTIMATION

3.1. Bayesian estimation in a standard full cohort

In this study, the Bayesian framework will be used for estimation. The parameters of the model will be estimated using Markov chain Monte Carlo (MCMC) methods. The contribution of patient i to the posterior distribution of the joint model is defined as

$$p(\theta ,b_i|T_i,{\delta }_i,y_i)\propto p(T_i,{\delta }_i|b_i,\theta )p(y_i|b_i,\theta )p(b_i|\theta )p(\theta ),$$

where θ denotes the vector of all parameters. The contribution of patient i to the likelihood of the survival submodel is written as

$$\begin{array}{ll}p(T_i,{\delta }_i|b_i,\beta ,{\theta }_t)& =h_i{\{T_i|{\mathcal{M}}_i(T_i),{\theta }_t\}}^{{\delta }_i}{S}_i\{T_i|{\mathcal{M}}_i(T_i),{\theta }_t\}\\ & ={\left[h_0(T_i|{\gamma }_s)\exp \left\{{\gamma }^{\top }{w}_i+\alpha m_i(T_i)\right\}\right]}^{{\delta }_i}\times \\ & \exp \left\{-{\int }_0^{T_i}{h}_0(s|{\gamma }_s)\exp \{{\gamma }^{\top }{w}_i+\alpha m_i(s)\}ds\right\},\end{array}$$

where θ _t = (γ _s,γ,α) and $m_i(t)=x_i^{\top }(t)\beta +z_i^{\top }(t)b_i$. Additionally, ${\mathcal{M}}_i(T_i)$ denotes the complete history of longitudinal marker for patient i. The contribution of patient i to the likelihood of the longitudinal submodel is given by

$$p(y_i|b_i,{\theta }_y)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left\{-\frac{{\displaystyle {\sum }_{j=1}^{n_i}}{\left(y_{ij}-x_{ij}^{\top }\beta -z_{ij}^{\top }{b}_i\right)}^2}{2{\sigma }^2}\right\},$$

with θ _y = (β,σ) and $\theta ={({\theta }_y^{\top },{\theta }_t^{\top })}^{\top }$.

Uninformative normal priors are used for the β, γ, and α parameters, as well as the parameters for the B‐splines in the baseline hazard (γ _s). For the elements of the variance‐covariance matrix of the random effects (D), an inverse Wishart prior is used and a gamma prior is used for the variance of the errors of the longitudinal outcome (σ ²). Initial values for the parameters of the prior distribution are obtained from estimations based on fitting the longitudinal and time‐to‐event submodels separately. The joint models are analyzed with JAGS software, using Gibbs sampling to execute the MCMC methods.

3.2. Bias in a case‐cohort design

If a study follows a case‐cohort design, estimation with the abovementioned standard likelihood will result in bias, due to the outcome dependent missingness in the data. The bias occurs, because in the case‐cohort design, only a selection of the censored or nonevent patients is used in the analysis, along with all the event patients. As a consequence, the event rate in the case cohort is higher than the event rate in the original full cohort.

In a standard full cohort, the observed data is ${\mathcal{F}}_n=\{y_i,T_i,{\delta }_i;i=1,\text{…},n\}$ and is fully observed for each patient. In the case‐cohort design, additionally, we have S _i as the indicator for the randomly drawn subcohort with a pre‐specified size z (eg, z = 1/3) ( $\mathcal{A}\cup \mathcal{B}$ in Figure 1) and CC _i denoting the indicator for being included in the case‐cohort design ( $\mathcal{A}\cup \mathcal{B}\cup \mathcal{C}$ in Figure 1), whereby

$$C{C}_i=\left\{\begin{array}{cc}1,& \text{if}{\delta }_i=1\text{or}{S}_i=1,\\ \\ 0,& \text{if}{\delta }_i=0\text{and}{S}_i=0\end{array}\right.$$

or CC _i = δ _i + (1 − δ _i)S _i. The full set of observed data is now ${\mathcal{F}}_n=\{S_i,C{C}_i,y_i,T_i,{\delta }_i;i=1,\text{…},n\}$. There are four distinct groups a patient in the case‐cohort design can belong to as defined in Figure 1. In each group, the following data is collected:

$$\begin{array}{ll}\mathcal{A}& =\left\{S_i=1,C{C}_i=1,y_i^o,T_i,{\delta }_i=0\right\},\\ \mathcal{B}& =\left\{S_i=1,C{C}_i=1,y_i^o,T_i,{\delta }_i=1\right\},\\ \mathcal{C}& =\left\{S_i=0,C{C}_i=1,y_i^o,T_i,{\delta }_i=1\right\},\\ \mathcal{D}& =\left\{S_i=0,C{C}_i=0,y_i^m,T_i,{\delta }_i=0\right\},\end{array}$$

where $y_i^o$ are the observed longitudinal measurements and $y_i^m$ the unascertained longitudinal measurements. In the standard version of the case‐cohort design, only patients belonging to $\mathcal{A}\cup \mathcal{B}\cup \mathcal{C}$ are included in the analysis. CC _i can be seen as selection indicator and the missing data in the case‐cohort design (patients in $\mathcal{D}$) can be interpreted as missing due to selection bias. Since these missings depend on unobserved data, the missing data mechanism will be missing not at random (MNAR). The different event rates between the full cohort and the case‐cohort design will result in a misspecification of the baseline hazard. This, in turn, will lead to bias both in the estimation of the parameters of the model and the estimation of survival probabilities.

3.3. Unbiased estimation using survival information from entire cohort

The bias caused by the outcome‐dependent missings can be circumvented by utilizing the survival information of the entire cohort, which has to be available due to the nature of the case‐cohort design, as argued by Dong et al.14 Since the random subcohort ( $\mathcal{A}\cup \mathcal{B}$) is supplemented with the remaining cases outside the random subcohort ( $\mathcal{C}$), it follows that the patients left out are all event free and therefore censored patients ( $\mathcal{D}$).

If all survival information is used in the analysis, the missing data only comes from missing longitudinal measurements in $\mathcal{D}$. In this case, these missing values are missing depending on observed information (survival status) and are therefore missing at random (MAR). The probability that the longitudinal response is missing, which is the same as the probability that the patient belongs to group ${\mathcal{D}}_i$, can be written as

$$p\left({\mathcal{D}}_i|{\delta }_i,y_i^o,y_i^m,\psi \right)=p({\mathcal{D}}_i|{\delta }_i,\psi ),$$ (2)

where ψ is the vector of parameters describing the missingness model. In the version of the case‐cohort design used throughout this manuscript, this is simply the probability of not being drawn by the random subcohort ( p = 1 − z). To obtain unbiased estimates for the joint model, we have to estimate the full distribution of all processes, including ${\mathcal{D}}_i$. When the complete survival information is taken into account (so patients in $\mathcal{D}$ are included in the analysis), the full distribution can be decomposed as

$$p\left(T_i,{\delta }_i,y_i^o,{\mathcal{D}}_i|b_i,\theta ,\psi \right)=\int p\left(T_i,{\delta }_i,y_i^o,y_i^m|b_i,\theta \right)\times p\left({\mathcal{D}}_i|b_i,{\delta }_i,y_i^o,y_i^m,\psi \right)d{y}_i^m.$$

Under (2), this becomes

$$p\left(T_i,{\delta }_i,y_i^o,{\mathcal{D}}_i|b_i,\theta ,\psi \right)=p\left(T_i,{\delta }_i,y_i^o|b_i,\theta \right)\times p({\mathcal{D}}_i|b_i,{\delta }_i,\psi ).$$ (3)

Because of the decomposition, the distribution of CC _i does not depend on $y_i^m$ but only on observed data δ _i. Additionally, since ψ and δ are distinct, the missing data caused by ${\mathcal{D}}_i$ is ignorable and analysis on the observed data gives unbiased results. This decomposition does not hold when patients in $\mathcal{D}$ are excluded from the analysis, where, as a result, ${\mathcal{D}}_i$ depends on unobserved data.

In the newly proposed version of the case‐cohort design, all patients will be included in the analysis, but not all patients supply the same amount of information. The posterior distribution stated earlier, will be different for certain patients. For the patients in the case‐cohort design (CC _i = 1), all information is available and the posterior distribution remains equal. For the censored patients outside the subcohort (CC _i = 0), the longitudinal information is not measured and therefore missing. However, the values are imputed by the model and the posterior distribution of longitudinal submodel is replaced by imputed values ( $y_i^m$). The values are based on the posterior predictive distribution of the missing data, which is

$$p\left(y_i^m|T_i,{\delta }_i=0,{\mathcal{F}}_n\right)=\int p\left(y_i^m|T_i,{\delta }_i=0,\theta \right)p(\theta |{\mathcal{F}}_n)d\theta ,$$

where the first term of the integral can be expressed as

$$\begin{array}{ll}p\left(y_i^m|T_i,{\delta }_i=0,\theta \right)=\int p\left(y_i^m|b_i,\theta \right)p(b_i|T_i,{\delta }_i=0,\theta )d{b}_i.& \end{array}$$

Based on the observed data and averaged over the posterior distribution of the parameters and random effects estimated by the model, this distribution is available. For each patient, the missing values of y can be obtained directly, and this occurs during estimation of the model. Aside from the survival information, any available covariate measurements taken on baseline can also be included for these patients. The posterior distribution for all patients in the cohort will therefore be given by

$$p\left(\theta ,b_i,y_i^m|T_i,{\delta }_i,y_i^o\right)\propto \left\{\begin{array}{cc}p(T_i,{\delta }_i|b_i,\theta )p\left(y_i^o|b_i,\theta \right)p(b_i|\theta )p(\theta ),& \text{if}C{C}_i=1,\\ \\ p(T_i,{\delta }_i|b_i,\theta )p\left(y_i^m|b_i,\theta \right)p(b_i|\theta )p(\theta ),& \text{if}C{C}_i=0.\end{array}\right.$$

4. PREDICTIVE PERFORMANCE

In clinical studies, it is often of interest to use the estimated model to predict survival probabilities for (a) new patient(s). Therefore, we need to assess the performance of the model in terms of predictive accuracy of the survival outcome. In general, a joint model fitted on the data sample ${\mathcal{F}}_n=\{T_i,{\delta }_i,y_i;i=1,\text{…},n\}$ is used to make survival predictions for a new patient j, with longitudinal measurements ( ${\mathcal{Y}}_j(t)$) up to time t. The information that the new patient provided longitudinal measurements up to t is used to postulate that the patient was event free at t and interest lies in events taking place in a medically relevant time interval (t,t + Δt]. The probability that the patient survives this time window is

$${\pi }_j(t+\mathrm{\Delta }t|t)=\mathrm{Pr}\left(T_j^{\ast }\ge t+\mathrm{\Delta }t|T_j^{\ast }>t,{\mathcal{Y}}_j(t),{\mathcal{F}}_n\right).$$ (4)

This probability can be estimated based on the posterior predictive distribution given by

$${\pi }_j(t+\mathrm{\Delta }t|t)=\int P\left(T_j^{\ast }\ge t+\mathrm{\Delta }t|T_j^{\ast }>t,{\mathcal{Y}}_j(t),\theta \right)p(\theta |{\mathcal{F}}_n)d\theta ,$$

where the first part of the integrand can be rewritten as

$$\begin{array}{ll}P\left(T_j^{\ast }\ge t+\mathrm{\Delta }t|T_j^{\ast }>t,{\mathcal{Y}}_j(t),\theta \right)& =\int P\left(T_j^{\ast }\ge t+\mathrm{\Delta }t|T_j^{\ast }>t,b_j,\theta \right)p\left(b_j|T_j^{\ast }>t,{\mathcal{Y}}_j(t),\theta \right)d{b}_j\\ & =\int \frac{S_j\{t+\mathrm{\Delta }t|{\mathcal{M}}_j(t+\mathrm{\Delta }t,b_j),\theta \}}{S_j\{t|{\mathcal{M}}_j(t,b_j),\theta \}}p\left(b_j|T_j^{\ast }>t,{\mathcal{Y}}_j(t),\theta \right)d{b}_j.\end{array}$$

Based on these equations and the posterior distribution of the parameters for the original data ${\mathcal{F}}_n$ obtained by the MCMC samples, Monte Carlo estimates of π _j(t + Δt | t) can be obtained by a new simulation scheme. More details on this procedure can be found in the works of Rizopoulos et al.2, 15

In this paper, we will assess the accuracy of the predictions in terms of discrimination and calibration. A model shows good discrimination if the estimated longitudinal biomarker profile can discriminate well between patients with and without the study endpoint. A model is calibrated well if the estimated longitudinal patterns can predict a future endpoint with high accuracy. In the situation of a case‐cohort design, the data used to fit the joint model is ${\mathcal{F}}_n=\{S_i,C{C}_i,T_i,{\delta }_i,y_i;i=1,\text{…},n\}$, where, for a set of the patients, y _i is missing, as discussed earlier. For these patients, ${\mathcal{Y}}_j(t)$ is not observed, and therefore, the corresponding survival probability in (4) cannot be estimated. In this paper, the predictive measures will be calculated only on patients from the random subcohort (S _i = 1), so the event rate corresponds to the full cohort while no missing data occurs in the patients. To assess the discrimination of the model, the area under the ROC curve (AUC) can be estimated, using longitudinal information up to time t for a new (set of) patient(s) and then calculate the AUC up to Δt.

With c in [0,1], a patient is labeled as event free if π _j(t + Δt | t) > c and as experiencing the endpoint if π _j(t + Δt | t) ≤ c. The AUC, calculated for a pair of randomly chosen patients {i,j}, is therefore

$$\text{AUC}(t,\mathrm{\Delta }t)=\mathrm{Pr}\left[{\pi }_i(t+\mathrm{\Delta }t|t)<{\pi }_j(t+\mathrm{\Delta }t|t)|\left\{T_i^{\ast }\in (t,t+\mathrm{\Delta }t]\right\}\cap \left\{T_j^{\ast }>t+\mathrm{\Delta }t\right\}\right].$$

This means that we would assign a higher survival probability to patient j than to patient i, if patient i experiences the endpoint in the time window t + Δt and patient j does not.

However, since $T_i^{\ast }$ is not observed for all patients due to censoring, this equation cannot be solved directly. Therefore, the estimated AUC is decomposed as

$$\widehat{\text{AUC}}(t,\mathrm{\Delta }t)={\widehat{\text{AUC}}}_1(t,\mathrm{\Delta }t)+{\widehat{\text{AUC}}}_2(t,\mathrm{\Delta }t)+{\widehat{\text{AUC}}}_3(t,\mathrm{\Delta }t)+{\widehat{\text{AUC}}}_4(t,\mathrm{\Delta }t).$$ (5)

The first part ( ${\widehat{\text{AUC}}}_1(t,\mathrm{\Delta }t)$) refers to the pairs without censoring, so, for which, the event times can be ordered directly, and the remaining parts refer to the patient pairs where censoring occurs.15 The full specification of the AUC is given in the supplemental material.

The calibration of the model is measured by the PE, where, based on all available information of a patient j, the estimated survival probability (π _j(t + Δt | t)) is compared to the observed survival ( $I(T_j^{\ast }>t+\mathrm{\Delta }t)$). The expected PE is then as follows:

$$\text{PE}(t+\mathrm{\Delta }t|t)=E\left[{\left\{I\left(T_j^{\ast }>t+\mathrm{\Delta }t\right)-{\pi }_j(t+\mathrm{\Delta }t|t)\right\}}^2\right].$$

Lower values of PE indicate smaller differences between the observed and predicted survival and therefore a better calibrated model. An appropriate estimator for time‐to‐event data is proposed by Henderson et al16 and is given in the supplemental material.

For the real life application, an internal validation of the model was applied to evaluate the predictive performance of the model.17 Since the same data is used for fitting the model and evaluating the performance of the model, optimistic predictions can occur. This holds particular importance when the data set is small. In this paper, corrections for the optimism will be done by a bootstrap method developed by Harrell et al.18 This method works in several steps.

1. First, fit the model on the data and calculate the apparent predictive measures (here, the AUC and PE), denoted by AUC_app and PE_app.

2. Take a bootstrap sample of the data. Refit the model on the bootstrap sample and calculate the apparent predictive measures, denoted by AUC_b,boot and PE_b,boot.

3. Thirdly, calculate the predictive measures on the original data from the model fitted on the bootstrap sample, called AUC_b,orig and PE_b,orig.

4. Then, calculate the optimism in this bootstrap sample by O _AUC,b = AUC_b,boot − AUC_b,orig and O _PE,b = PE_b,boot − PE_b,orig.

5. Repeat steps 2‐4 B times. Harrell recommends to use a B between 100‐200.

6. After the optimism is calculated for all B bootstrap samples, correct the apparent predictive measure with each optimism (AUC_cor,b = AUC_app − O_AUC,b and PE_cor,b = PE_app + O _PE,b).

7. In the last step, take the average of all these corrected predictive measures to obtain the for optimism adjusted AUC and PE (AUC = $B^{-1}{\sum }_B{\text{AUC}}_{\mathrm{cor},b}$ and PE = $B^{-1}{\sum }_B{\text{PE}}_{\mathrm{cor},b}$). Additionally, the 2.5% and 97.5% percentiles of the bootstrapped samples can be obtained as an indication of the spread of the estimator.

5. SIMULATION STUDY

5.1. Design

A simulation study was carried out to verify that the proposed model results in unbiased estimates and shows good predictive performance. Data sets representing the full cohort were simulated, and from these data sets, a case‐cohort design was imitated by drawing a random set of patients and supplementing the cases to this. The submodel for the simulated longitudinal outcome is defined as

$$y_i(t)={\beta }_1+{\beta }_{2}t+{\beta }_3{t}^2+{\beta }_4{\mathrm{G}}_i+b_{1i}+b_{2i}t+b_{3i}{t}^2+{\epsilon }_i(t),$$ (6)

where the β's define the average population trajectory, and the b's define subject‐specific deviations from this trajectory and are assumed to be normally distributed ( $b_i\sim \mathcal{N}(0,D)$). The variance‐covariance matrix of the random effects (D) is left unstructured. G is a binary covariate, drawn from a binomial distribution with probability 0.5. A quadratic term for time was added to the fixed and random effects to imitate nonlinear trajectories often found in real‐life longitudinal studies. The survival times are generated by

$$h_i(t)=h_0(t)\exp \{\gamma {\mathrm{G}}_i+\alpha m_i(t)\}.$$ (7)

Here, m _i(t) is assumed to be the true longitudinal outcome at time t. The baseline hazard h ₀(t) was generated with a Weibull distribution with a shape parameter (ϕ) of 2. The scale of the Weibull model is $\exp \{\gamma {\mathrm{G}}_i+\alpha m_i(t)\}$ and the hazard function can therefore also be written as $h_i(t)=h_0(t)\exp \{\gamma {\mathrm{G}}_i+\alpha m_i(t)\}=\varphi t^{\varphi -1}\exp \{\gamma G_i+\alpha m_i(t)\}$. The association parameter α was set equal to 1. The remaining parameter settings were β ₁ = 1, β ₂ = 0.3, β ₃ = 0.1, β ₄ = 0.1, γ = −2, σ ² = 1. Data sets were simulated with 2000 subjects and 25 planned measurements per subject. The mean of the exponential distribution for the censoring mechanism varied and the maximum follow‐up time was 15.

5.2. Analysis

Two versions of the case‐cohort design were generated from the simulated data sets. In the first version, the survival information of all patients was retained and only the biomarker values for the unselected patients were put to missing. The second version (also called the classical case‐cohort) only uses information from the patient in the case‐cohort design and completely removes the remaining patients for analyses. The same joint model was fitted on all three data sets, where the results from the full cohort were viewed as the golden standard. Four different scenarios with varying event rates and varying sizes of the random subcohort were simulated 200 times. In scenario 1, the mean value of censoring time was set at 3.2 and the coefficient of the intercept of the Weibull regression at −7.5, which resulted in a 20% event rate. Here, 1/3 of the cohort was randomly sampled as subcohort. In scenario 2, the event rate was kept at 20%, but now, the size of the subcohort was 1/6 of the full cohort. For scenarios 3 and 4, the event rate was set to 5% using a mean censoring time of 2.5 and an intercept coefficient of −9.5. The sizes of the random subcohort in scenarios 3 and 4 were 1/3 and 1/6, respectively. For the predictive performances of the models, a validation data set was simulated with 1000 subjects using the same scenario as the data on which the model was fitted. Time‐dependent AUC and PE were calculated on two intervals during follow‐up, where the intervals depended on the simulation scenario.

5.3. Results

Table 1 shows the characteristics of the simulated data in the four different scenarios. Apart from the number of biomarker measurements, the dimensions of the data sets for the full cohort (FC) and the case‐cohort (CCI) are the same. In the classical case‐cohort design (CCII), additionally, the number of patients and event rate differs from the FC. It is clear that a different event rate, together with the size of the drawn subcohort, has a large impact on the size of the remaining case‐cohort data set. For scenario 4, the resulting event rate in the classical case‐cohort data set is 5 times as high (25%) as it was in the FC. The results of the model estimation are shown in Table 2. For each scenario, the association parameter (α) is given, along with the bias (the difference between the mean estimate of the simulation and the simulated parameter value) and the coverage rate. The coverage rate is calculated as the percentage of times the true simulated value of α falls in the credible interval of each simulation. For all four scenarios, the bias of α in the CCI is small and close to the estimate of α based on the FC (the difference between mean α _FC and α _CCI ≤ 0.023). This is also the case for the coverage rate, which is similar for the FC and the CCI. The CCII, on the other hand, shows a clear downward bias (mean bias between 0.15‐0.35) and low coverage rates between 0% and 13%. For the scenario's with a low event rate, all three models give an underestimation of the true parameter value of α; however, the FC and CCI give similar performances compared to CCII. Table 2 additionally shows the estimated parameters of the longitudinal submodel (β's) and the parameter of the survival submodel (γ). These parameters indicate the same results; the estimates for the FC and the CCI are very similar, and clear bias is found for the CCII. The bias, percentiles, and coverage rates of these parameters can be found in the supplemental material.

Table 1.

Characteristics of the simulated data sets based on 200 replications of each scenario

			Size Subcohort: 1/3				Size Subcohort: 1/6
% Events		Scenario				Scenario
			FC	CCI	CCII		FC	CCI	CCII
20%	patients, n	1	2000	2000	900	2	2000	2000	700
	events, n		400	400	400		400	400	400
	event rate, %		20%	20%	40%		20%	20%	60%
	measurements, n		15 000	7000	7000		19 000	6000	6000
5%	patients, n	3	2000	2000	700	4	1900	1900	400
	events, n		100	100	100		100	100	100
	event rate, %		5%	5%	15%		5%	5%	25%
	measurements, n		11 000	4500	4500		9000	2000	2000

Abbreviations: CCI, case‐cohort design, retain all survival information; CCII, case‐cohort design, classical version; FC, full cohort.

Table 2.

Results from estimating a joint model on simulated data based on 200 replications per scenario

			Size Subcohort: 1/3				Size Subcohort: 1/6
% Events		Scenario				Scenario
			FC	CCI	CCII		FC	CCI	CCII
20%	α	1	0.975	0.971	0.849	2	0.976	0.966	0.799
	bias		−0.025	−0.029	−0.151		−0.024	−0.034	−0.201
	(2.5%‐97.5%)		(0.89‐1.07)	(0.88‐1.07)	(0.76‐0.94)		(0.89‐1.07)	(0.88‐1.06)	(0.71‐0.89)
	coverage		92%	91%	13%		92%	88%	4%
	β 1		1.003	0.996	1.087		1.004	0.986	1.139
	β 2		0.319	0.331	0.558		0.324	0.357	0.713
	β 3		0.110	0.104	0.142		0.109	0.097	0.154
	β 4		0.104	0.105	0.092		0.102	0.099	0.092
	γ		−1.979	−1.987	−1.774		−1.979	−1.978	−1.676
5%	α	3	0.856	0.845	0.727	4	0.858	0.835	0.649
	bias		−0.144	−0.155	−0.273		−0.142	−0.165	−0.351
	(2.5%‐97.5%)		(0.74‐0.99)	(0.72‐0.98)	(0.61‐0.86)		(0.74‐0.99)	(0.71‐0.97)	(0.53‐0.78)
	coverage		38%	33%	1%		39%	32%	0%
	β 1		1.003	0.993	1.062		1.005	0.990	1.127
	β 2		0.331	0.343	0.474		0.334	0.371	0.638
	β 3		0.108	0.099	0.127		0.106	0.087	0.146
	β 4		0.101	0.103	0.055		0.100	0.107	0.023
	γ		−2.730	−2.760	−2.421		−2.771	−2.806	−2.238

The bias indicates the difference between the simulated parameter value and the estimated value by each of the models. The coverage is calculated by the percentage of times the true simulated values falls in the credible interval of each simulation.

Simulated values of the parameters: α = 1, β ₁ = 1, β ₂ = 0.3, β ₃ = 0.1, β ₄ = 0.1, γ = −2.

Abbreviations: CCI, case‐cohort design, retain all survival information; CCII, case‐cohort design, classical version; FC, full cohort.

The performance of the predictive accuracy of the models is assessed by evaluating the AUC and PE on two different time points during the simulation follow‐up. The time points depend on the follow‐up time in the data and can therefore differ per scenario. The outcomes are shown for scenario 2 by the boxplots in Figure 2. The boxplots for the other scenarios can be found in the supplemental material. The CCI performs very similar compared to the FC in terms of predictive accuracy, however only slightly worse (as demonstrated by a smaller AUC and a higher PE). The CCII analysis demonstrates a decidedly worse performance in prediction, particularly in terms of calibration. The other scenarios show a similar result, although less pronounced.

Figure 2.

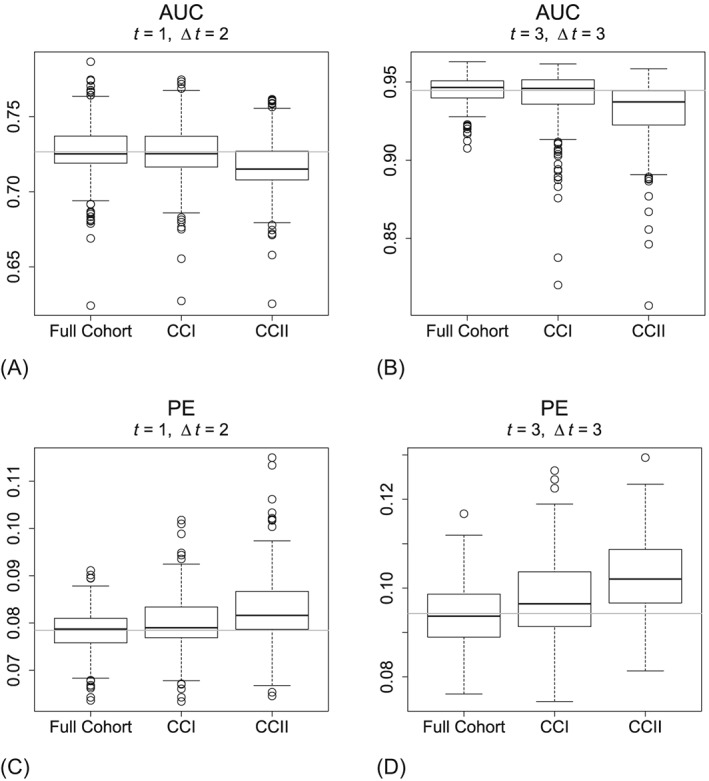
Predictive accuracy measures from scenario 2 (event rate: 20%; size subcohort: 1/6). AUC, area under the ROC curve; CCI, case‐cohort design, retain all survival information; CCII, case‐cohort design, classical version; PE, prediction error

An additional simulation study was performed to evaluate the method in smaller data sets (n = 500). The results can be found in the supplemental material and are in line with the other simulations.

6. APPLICATION TO BIOMARCS STUDY

6.1. Study design

We illustrate the use of our findings on data from the BIOMArCS study. In this multicenter study, patients admitted for ACS at several Dutch hospitals in the Netherlands were enrolled between January 1, 2008 and September 1, 2014. Patient follow‐up ended at September 1, 2015. Patients were followed for the first year after their initial cardiac event. They were invited back to the hospital on regular occasions, where blood samples were collected. The first blood sample was collected during hospitalization for the index event. Subsequent blood samples were collected every two weeks for the first 6 months of follow‐up and once a month during the last 6 months of follow‐up. The goal of BIOMArCS was to study the association between longitudinal patterns of multiple biomarkers and the primary endpoint. In total, 839 patients were included with a median of 17 blood samples per patient. The primary endpoint was a composite of cardiovascular mortality, nonfatal ACS or unplanned coronary revascularization due to progressive angina pectoris during 1‐year follow‐up. In total, 45 patients were identified as having the primary endpoint (5.4% of the entire cohort). The low event rate combined with the high number of biomarker measurements led to the decision to only ascertain biomarker values in a subset of the patients using the case‐cohort design. A random sample of 150 patients was selected ( $\mathcal{A}\cup \mathcal{B}$ in Figure 1). Of these, 142 patients were event free at the end of follow‐up and 8 patients had experienced the primary endpoint. The subcohort of 150 was supplemented with the remaining 37 event patients outside the subcohort ( $\mathcal{C}$ in Figure 1) reaching a total of 187 patients in the case‐cohort design.

6.2. Analysis BIOMArCS

It is of interest to model how strongly Cardiac Troponin‐I (TnI), a well established cardiovascular biomarker,19 is related to the hazard of the primary endpoint. The distribution of TnI is heavily skewed, so a log ₂ transformation was applied. On top of that, the TnI values were transformed to z‐scores, for potential head‐to‐head comparison between different biomarkers. Patients showed nonlinear evolutions due to a stabilization period after the index event, which were modeled by a piecewise linear regression model, with the breakpoint at 30 days. The longitudinal submodel used to fit TnI on the BIOMArCS data is of the form

$$z{\text{TnI}}_i(t)={\beta }_1+{\beta }_{2}t+{\beta }_3{(t-30)}_{+}+{\beta }_4{\text{Sex}}_i+b_{1i}+b_{2i}t+b_{3i}{(t-30)}_{+}+{\epsilon }_i(t),$$ (8)

where (·)₊ denotes (A)₊ = A if A > 0 and 0 elsewhere. Sex is a covariate that denotes the gender (1 = female and 2 = male) of the patient. The variance‐covariance matrix of the random effects (D) is left unstructured. The survival submodel is given by

$$h_i(t)=h_0(t)\exp \{\gamma {\text{Sex}}_i+\alpha m_i(t)\}.$$ (9)

The baseline hazard h ₀(t) is modeled with cubic B‐splines, with five knots placed based on the percentiles of the observed event times (67, 338, 359, 368, and 382 days). Since the FC is unknown in the BIOMArCS data, for this application, we can only estimate and compare the two versions of the case‐cohort design. The predictive performance of the models is again assessed by calculating the AUC and PE. These measures are calculated on a subset of the data that consists only of the random subcohort (S _i = 1) because, in this subcohort, the event rate is equal to the event rate in the FC and longitudinal measurements are available for all patients. A downside of using this subset of the data is that the random subcohort only has eight endpoints, which can lead to unstable estimates of the predictive accuracy. For the calculation of the AUC and PE, longitudinal information from the first 60 days was used to calculate the respective diagnostic measurements at time 100 (Δt = 40 days). This interval was chosen by the distribution of the event times of the 8 events in the BIOMArCS subcohort. To account for the fact that these validation measures are estimated on the same data set as the model was developed, they are corrected with Harrell's optimism measure using the bootstrap method.18

6.3. Results BIOMArCS

Applying a case‐cohort design to the BIOMArCS data has a large consequence on the number of patients used in the analyses. In the FC and therefore also in newly proposed version of the case‐cohort design (again denoted by CCI), there were 839 patients, where the classical case‐cohort design (denoted by CCII) only uses 187 patients. This also leads to a substantial difference in event rate which is 24% in CCII, compared to 5% in CCI. Both versions of the case‐cohort design use 1492 TnI measurements and, additionally, in CCI, there is a large number of missing TnI values (9829) corresponding to the unascertained TnI measurements from the patients outside the case‐cohort design. The results from the model estimates are presented in Table 3. The parameter estimates are very similar for both models. The α parameter, denoting the association between the longitudinal marker TnI and the composite endpoint, is 0.30 (95% credible interval: 0.10‐0.50) and 0.33 (95% credible interval: 0.14‐0.53) for the new and classical case‐cohort design, respectively. The remaining parameters are also very similar. The predictive accuracy measures, corrected for optimism, are presented in the last part of Table 3. CCI performs slightly better in predicting new events by showing larger AUC (0.551 vs 0.533) and smaller PE (0.014 vs 0.017).

Table 3.

Results from estimating a joint model for repeated TnI values and the combined study endpoint on two versions of the case‐cohort design in the BIOMArCS data

		CCI		CCII
Longitudinal submodel		Mean	95% CI	Mean	95% CI
β 1	Intercept	8.87	(7.98, 9.66)	8.98	(8.26, 9.78)
β 2	Slope (t < 30 days)	−6.35	(−7.15, −5.56)	−6.34	(−7.07, −5.63)
β 3	Δ Slope(t < 30, t ≥ 30)	−6.77	(−7.55, −5.97)	−6.76	(−7.46, −6.08)
β 4	Sex	0.54	(0.15, 0.93)	0.48	(0.11, 0.88)
Survival submodel		Mean	95% CI	Mean	95% CI
α	Association	0.30	(0.10, 0.50)	0.33	(0.14, 0.53)
γ	Sex, survival	−0.43	(−1.04, 0.21)	−0.44	(−1.07, 0.15)
Predictive accuracy		Estimate	(2.5%‐97.5%)	Estimate	(2.5%‐97.5%)
AUC	t = 60,Δt = 40	0.551	(0.420‐0.695)	0.533	(0.438‐0.633)
PE	t = 60,Δt = 40	0.014	(0.007‐0.031)	0.017	(0.011‐0.032)

β ₃ indicates the difference between the slope estimates before and after 30 days. The coefficient for the slope after 30 days is given by (β ₂ + β ₃).

The area under the ROC curve (AUC) and prediction error (PE) are calculated using longitudinal measurements up to t = 60 (days) to predict events in (60, 100]. The measures are corrected with Harrell's optimism and shown with the 2.5% and 97.5% confidence limits.

Abbreviations: AUC, area under the ROC curve; CCI, case‐cohort design, retain all survival information; CCII, case‐cohort design, classical version; CI, credible interval; PE, prediction error.

7. DISCUSSION

Longitudinal studies following patients over time are becoming increasingly more popular in clinical research, since they can incorporate dynamic patterns reflecting disease progress and thus improve prediction of events. If longitudinal studies are extended further to include multiple markers, different aspects of the disease can be modeled, which, in turn, leads to additional improvement of the model. A severe downturn is the increasing costs associated with ascertaining large numbers of biomarker measurements. To ensure practical use of these studies, new methods are necessary so that unbiased results and optimal efficiency are warranted when only utilizing a subset of the measurements. A case‐cohort design can help in cost reduction, by measuring all patients who experienced the study endpoint and only a subset of the patients without the endpoint. However, the overrepresentation of the cases causes bias, interpreted as selection bias, in estimation of the model parameters and when predictions for a new patient are made. By incorporating survival information of all patients, the problem is solved and models will show unbiased estimations. The simulation study we performed showed that, by incorporating all survival information, the case‐cohort design performs very similar to the FC in terms of unbiased estimation and predictive accuracy. When the classical case‐cohort is applied for comparison, in general, the model will show biased estimates and worse predictive accuracy.

The difference in estimates between the two versions of the case‐cohort design, however, was not found in the real‐life application. Possibly, this is due to the smaller size of association parameter in the BIOMArCS study (0.3), compared to value of the parameter in the simulated data (which was 1). The difference in event rate also had a modest impact on predicting new events as shown by the corrected predictive accuracy methods. The newly proposed version of the case‐cohort design performed slightly better in terms of discrimination and calibration than the classical case‐cohort design. It should be noted, however, that, although corrected for optimism, these measures were calculated on a subset of the data with only eight events (the random subcohort). New methods are necessary to incorporate the complete survival information in these functions in a similar manner as we incorporated them in the model estimation.

The findings throughout this paper combined, we can conclude that, for studies with large amounts of longitudinal measurements, costs can be saved while results remain reliable, by applying a case‐cohort design and incorporating the survival information from the complete cohort in the models. This work can be extended to find the optimal selection of longitudinal measurements taken while retaining unbiased estimates and high values of predictive accuracy and developing new methods to efficiently estimate the predictive accuracy.

Supporting information

SIM_8113‐Supp‐0001‐Supplemental_material.pdf

Baart SJ, Boersma E, Rizopoulos D. Joint models for longitudinal and time‐to‐event data in a case‐cohort design. Statistics in Medicine. 2019;38:2269–2281. 10.1002/sim.8113