Training and Interpreting Machine Learning Algorithms to Evaluate Fall Risk after Emergency Department Visits

Abstract

Background:

Machine learning is increasingly used for risk stratification in healthcare. Achieving accurate predictive models does not improve outcomes if they cannot be translated into efficacious intervention. Here we examine the potential utility of an automated risk-stratification and referral intervention to screen older adults for fall risk after ED visits.

Objective:

This study evaluated several machine learning methodologies for the creation of a risk stratification algorithm using electronic health record (EHR) data, and estimated the effects of a resultant intervention based on algorithm performance in test data.

Methods:

Data available at the time of ED discharge was retrospectively collected and separated into training and test datasets. Algorithms were developed to predict the outcome of return visit for fall within 6 months of an ED index visit. Models included random forests, AdaBoost, and regression-based methods. We evaluated models both by area under the receiver operating characteristic curve (AUC) and by projected clinical impact, estimating number needed to treat (NNT) and referrals per week for a fall risk intervention.

Results:

The random forest model achieved an AUC of 0.78, with slightly lower performance in regression-based models. Algorithms with similar performance when evaluated by AUC differed when placed into a clinical context with the defined task of estimated NNT in a real-world scenario.

Conclusion:

The ability to translate the results of our analysis to the potential tradeoff between referral numbers and NNT offers decisionmakers the ability to envision the effects of a proposed intervention prior to implementation.

Introduction:

Falls among older adults are a major public health concern, with significant morbidity and mortality.(1, 2) Despite guidelines(3) and quality measures,(4) screening for fall risk remains inconsistent in the primary care setting.(5, 6) Emergency department (ED) patients are generally at higher risk of outpatient falls than the general population,(7-9) making the ED an important additional setting to identify high risk patients. While guidelines recommend screening for fall risk in the ED,(10-12) this practice has not been widely implemented for many reasons, including the effort burden of screening in the high intensity, high volume ED setting and limited availability of referrals for intervention.(13) Despite previous efforts, no existing screening tools satisfy the need for a scalable, adaptable, and measurable instrument suitable for widespread implementation.(14)

One potential solution to increase screening rates without requiring significant additional resources in the ED is through the development and implementation of an algorithm to screen patients using information present in the electronic health record (EHR) at the time of an ED visit. Recently, healthcare has seen a sharp rise in the implementation of machine learning derived algorithms for predicting risk across a broad range of clinical scenarios.(15-18) Often, performance of these algorithms is evaluated by comparing the area under a receiver operating characteristic (ROC) curve, using the terms area under the curve (AUC) or C-statistic, with the concept that algorithms offering superior classification based on AUC are suitable for implementation.(19, 20) AUC as a single number may do a poor job of conveying an algorithm’s performance for a predictive task in a clinical context which may require a particular balance of sensitivity and specificity.(21, 22) Clinicians are generally interested in applying an algorithm to aid in risk-stratification for a particular scenario, such as ruling out a rare disease, confirming a particular diagnosis, or reducing population risk via an intervention—in this case, referral for a fall risk reduction intervention.

Such an intervention already exists at our institution in the form of a multidisciplinary falls clinic. Based on prior literature, we estimate a relative risk reduction of 38% for future falls for patients enrolled in such a program.(23) Currently, very few referrals are made to the falls clinic from the ED. Prior to initiating an automated referral program, decisionmakers must understand both the anticipated number of referrals generated and the effectiveness of such referrals in preventing future falls. To do so, decisionmakers may be better served by extrapolations of a model’s performance in a given population than by test characteristics such as AUC. This information would allow a clinical site to select the most appropriate risk-stratification algorithm, and most appropriate threshold point, to maximize patient benefit within the constraints of available resources and acceptable effectiveness. In this study, we developed several machine learning models to predict six month fall risk after an ED visit. We evaluated these models both using AUC analysis and by interpreting model performance to describe potential clinical tradeoffs more concretely in terms of referrals per day and numbers needed to treat (NNT) for prevention of a fall.

Methods:

Study Design and Setting:

We performed a retrospective observational study using patient EHR data at a single academic medical center ED with level 1 trauma center accreditation and approximately 60,000 patient visits per year. The goal of developing the models was to create an alert at the time of an ED visit suggesting referral of patients who are at heightened risk of fall for an existing multidisciplinary falls intervention. In our case, based on discussions with our falls clinic, an estimated 10 referrals per week was seen as operationally feasible. Using the available EHR data, we created risk-stratification models for fall-revisits to the ED. Our outcome of interest was a fall visit to the same ED in the 6 months after an index visit. While this paper focuses on predicting fall revisits, the methodology we describe is robust and lends itself to any clinical risk-stratified prediction task.

Data Selection and Retrieval:

EHR data for patients aged 65 years and older who visited the study ED were acquired for a duration of 43 months starting January 2013, with an additional six months of followup data collected for outcome determination. Available EHR features were evaluated for inclusion under the conceptual framework of the Andersen Behavioral Model of Health Services Use, a well-established model which provides a context for characterizing the many factors which lead to healthcare utilization.(24-27) This model has been used to frame numerous prior studies involving ED use and falls among older adults.(28, 29) For each visit, discrete data available within the EHR at the time of the ED visit were collected to create data features including patient demographics, historical visits and visit patterns and diagnoses, as well as visit-specific information including timing, lab tests performed and results thereof, vital signs, chief complaint, and discharge diagnoses. Features were selected based on their availability, clinical relevance, and potential to provide predictive value for fall-revisit risk estimation. Another important criteria for feature selection was to exclude attributes that contained information obtained after an index visit.

The data were organized and analyzed at the level of an ED visit (as opposed to patient level) since our objective was to stratify risk for a fall-revisit based on index visit data alone. Visits by patients who were transferred from other healthcare facilities were rejected as part of our primary exclusion criteria. We excluded visits that resulted in hospital admissions, as our algorithm would only be implemented for patients who were discharged from the ED. Finally, we excluded patients who did not have a primary care provider (PCP) in our network, as our intervention was specifically aimed towards referring in-network patients. At the end of the exclusion procedures, we were left with 10,030 records.

Feature Preparation:

The encoding process for features depended on whether they were numerical or categorical in nature. Numerical features such as age, vital signs during the index ED visit, duration of the index visit, and number of primary care or hospital visits in the six months prior to the index visit were treated as continuous values. Attributes related to Elixhauser comorbidity index, Hendrich II score, patients’ demographics, medications, and lab results were treated as categorical variables. In the case of numerical features, we dropped records that had missing values due to the relatively small number of records that were incomplete in this regard, which left us with 9,687 records. However, for categorical variables, missing values were considered as a separate category – in general the absence of most categorical features could be potentially informative for decision making by the predictive models. At the end of the feature engineering process, we obtained our final dataset which was comprised of 725 features. The feature preparation phase was completely independent of outcome status.

Model Development:

Once our features were selected and prepared, we created predictive models from the data. We tested several regression-based methodologies, including thresholded linear regression and logistic regression, both unregularized and including lasso(30) and ridge(31) penalties. We also included two tree-based methodologies: random forests(33) and AdaBoost.(34) Appendix A provides a nontechnical description of the methods used. Models were generated using the Scikit-learn package in Python.(35) The dataset created at the end of feature preparation was split into training and test sets in a 3:1 ratio. We split data chronologically, with the final 25% of visits kept as a holdout test set, and the earliest 75% of data retained as a training set. The training set was further split, again chronologically in a 2:1 ratio, to create a tuning set for interim validation.

Models were initially trained on the smaller training set, where tunable parameters were varied using a grid search pattern to achieve best results within the tuning set. Finally, we picked the six models that performed best on the tuning set, and trained one model of each type on the entire training set. These models were then evaluated on the test data that had been held out during the previous phase. Since our dataset was skewed, with more patients who did not fall than those who did, we up-sampled the positive class records while training models to provide a weighting effect to incentivize correct classification of fall cases. This was achieved by randomly duplicating positive cases in the training set until their frequency equaled that of negative cases. Up-sampling was carried out only after the training set had been split into a tuning set, to ensure that no duplicate records created as a result of up-sampling on the entire training set were members of both the training and tuning set. Further, the tuning validation set was not subjected to any up-sampling, to maintain the true population distribution in the evaluation set to simulate performance assessment on future data.

Model Evaluation:

Our initial evaluation of the trained models involved comparing the AUC. 95% confidence intervals were generated in STATA (College Station, TX) using a nonparametric bootstrapping with the Rocreg command and 1,000 iterations.(36) We then generated classification statistics for each model at each potential threshold value, consisting of performance within the evaluation set in terms of true positives (TP), false positives (FP), true negatives (TN) and false negatives (FN). We were able to use these data to extrapolate both referrals per week and NNT.(37) Estimated referrals per week were calculated by taking the total percentage of TP and FP results (all patients flagged “positive”) at a given threshold from each model and multiplying by the weekly visit volume. NNT was estimated by assuming that the falls reduction clinic would provide a relative risk reduction of 38% (95%CI 21%−52%) based on the results of the PROFET randomized clinical trial which studied a similar intervention in practice and found the percentage of fallers decreased from 52% to 32% in a high risk cohort of patients discharged from the ED.(23) Relative risk reduction and confidence intervals were generated from the reported PROFET data using STATA. The absolute fall risk for a population of patients above a given risk threshold in our models was calculated as the ratio of true positives (patients we predicted would fall who did go on to fall) as compared to all model identified positives for all patients at or above the risk threshold in the test dataset (TP/TP+FP). This absolute risk was multiplied by the relative risk reduction of 0.38 to estimate an absolute risk reduction, and the inverse of the absolute risk reduction was taken to generate the number needed to treat.(37) For instance; if the absolute fall risk in the flagged positive group was 60%, the estimated NNT was 1/(0.38* 0.6) = 4.4 referrals per fall prevented. These projected performance measures were used to create plots that visually described the tradeoff between risk reduction gained per referral and number of referrals expected per day.

RESULTS:

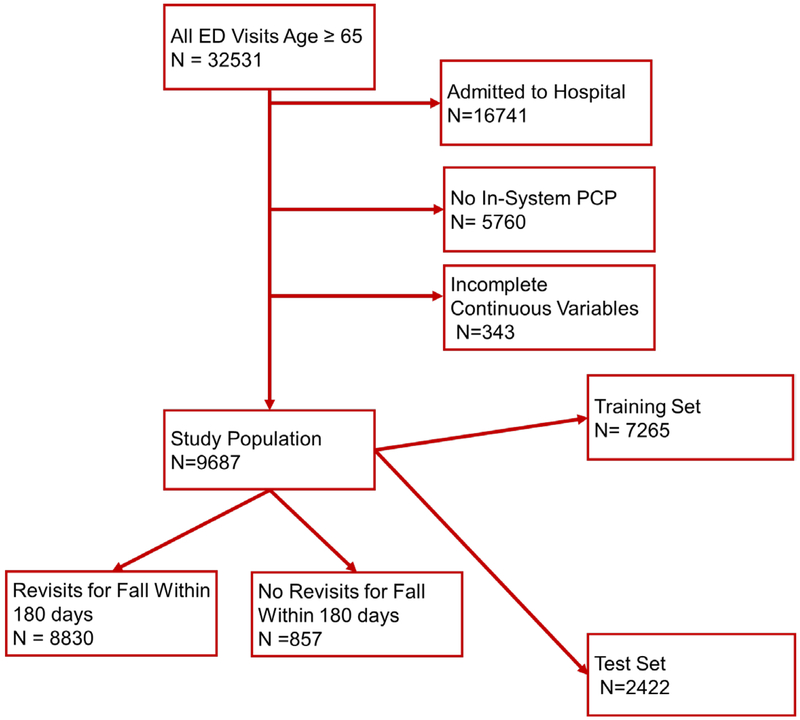
We had 32,531 visits to the ED during the study period by adults aged 65 and older, of which 9,687 were both discharged and had a PCP in our network and full numerical data, making up our study population (Figure 1). Within this population, 857 patients returned within 6 months for a fall-related visit; the overall return rate for fall within 6 months was 8.8%. Demographics of patients by outcome are presented in Table 1. As compared to patients who did not return for falls, those with falls were similar with regards to gender and insurance status, but were older, more likely to have fallen on their index visit, and more likely to have been brought to the ED by an ambulance.

Figure 1:

Patient allocation. Once the study population was defined; it was split at a 3:1 ratio into training and test sets. The training set was further split to create an intermediate tuning set.

Table 1:

Characteristics of analyzed visits.

	All Analyzed Visits	Visits without 180- day return for fall	Visits with 180 day return for fall.
N (%)	9687	8830	857
Mean Age (sd)	76.0(8.4)	75.7(8.3)	79.3(8.9)
Female (%)	5863(60.5%)	5286(59.9%)	577(67.3%)
White Race (%)	8980(92.7%)	8187(92.7%)	793(92.5%)
Insurance Status
Medicare	8444(87.2%)	7705(87.3%)	739(86.2%)
Commercial/Worker’s Comp	1210(12.5%)	1095(12.4%)	115(13.4%)
Other/Self Pay	26(0.3%)	23(0.3%)	3(0.4%)
Mode of Arrival
Family or Self	6641(68.6%)	6263(70.9%)	378(44.1%)
EMS or Police	30(31.4%)	2567(29.1%)	479(55.9%)
Fall at Index Visit	1543(15.9%)	1267(14.4%)	272(31.7%)

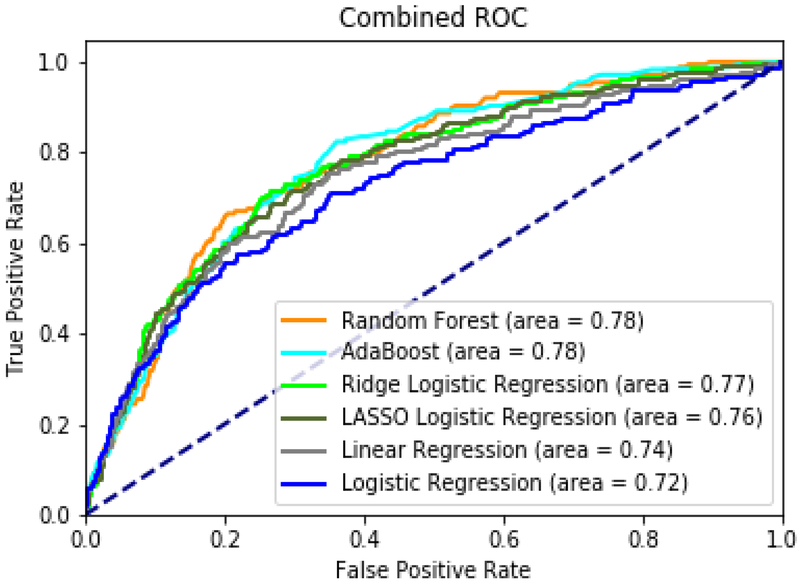
When comparing models based on AUC, the random forest model achieved an AUC of 0.78 (95%CI 0.74–0.81), and AdaBoost also had an AUC of 0.78 (95%CI 0.74–0.81). These tree based models were the highest performers, followed by ridge-penalized logistic regression at 0.77 (95%CI 0.73–0.80), lasso-penalized logistic regression at 0.76 (95%CI 0.73–0.80), unpenalized linear regression at 0.74 (95%CI 0.71–0.78), and unpenalized logistic regression at 0.72 (95%CI 0.68–0.76). Figure 2 shows AUC plots for all tested machine learning models. Appendix B describes model parameters and variable importance.

Figure 2:

Area under Receiver-Operating Characteristic Curves (AUC) for random forest, elastic net regression, lasso regression, AdaBoost, ridge regression, linear regression.

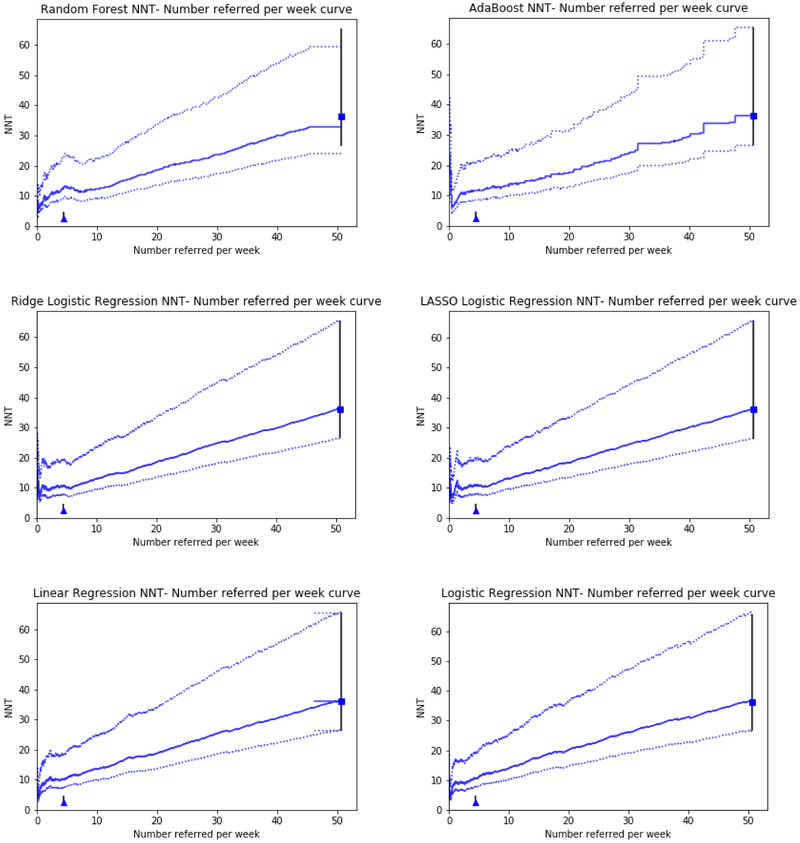
Models were further characterized by estimating both number of referrals per week from the study ED, and NNT of referred patients. Figure 3 shows these plots. In this analysis, we present the relationship between increasing the number of patients referred, and the decrease in effectiveness per referral as the threshold for defining “high risk” is lowered. The plots additionally contain two fixed points for reference: a “refer all patients” scenario in which all patients are marked as high risk, and a “perfect model” scenario, in which the model predicts with 100% accuracy which patients would go on to fall without the intervention and refers only these patients. In our case, the maximum achievable NNT is 2.6, in the case where a 38% relative risk reduction is applied to a population at 100% risk of falling. Table 2 illustrates model performance in terms of predicted NNT at various referrals per week. At the predefined threshold of 10 referrals per week (setting a high risk threshold), the random forest model outperformed the other models, generating an NNT of 12.4. At other thresholds, ridge regression and AdaBoost outperformed the Random Forest model. The lasso and non-penalized regression models had poorer performance across the spectrum of anticipated referrals.

Figure 3:

NNT vs. Anticipated Referrals per week. This line shows the tradeoff between rising number needed to treat and a rising number potential referrals as a lower threshold for risk is selected within the model. The square represents a potential scenario in which all patients are referred regardless of model risk. The triangle represents the performance of a model with perfect discrimination (one which only refers patients who would definitely fall in the future and no one else). Error bars represent the 95% confidence interval of the relative risk estimation.

Table 2:

Model performance at various referrals per week thresholds. Asterisks indicate the best performing model (lowest NNT) at each referral per week threshold.

Referrals per Week Threshold	Random Forest	AdaBoost	Ridge Logistic Regression	Lasso Logistic Regression	Linear Regression	Logistic Regression
5	12.74	11.94	10.03*	10.70	10.70	11.08
10	12.41*	13.82	13.13	13.13	13.70	14.01
15	15.36	15.49	15.24*	15.75	17.18	17.50
20	18.65	17.40*	18.52	18.38	18.79	20.15
25	21.28	20.76	21.27*	21.71	22.32	22.97
30	23.60*	24.00	24.68	24.52	25.52	26.22
35	26.96*	27.21	27.19	27.02	28.06	28.79
40	29.91	29.44*	29.79	30.14	30.51	31.27

DISCUSSION:

The various machine learning models tested in this study differed in their ability to predict falls, with the random forest and AdaBoost models offering the best overall performance with an AUC of 0.78. Based on AUC alone, penalized regression-based models including ridge-penalized logistic regression offered similar performance with an AUC of 0.77. This result is consistent with other studies evaluating the performance of tree-based algorithms alongside regression-based methodologies.(16, 18, 38-40) As opposed to traditional methods, tree-based methodologies have an improved ability to deal with complex variable interactions and nonlinear effects in large databases, which may explain their advantage in these instances.(41)

When translating the models into potential deliverable performance at individual thresholds, the random forest-based approach offers the best performance in terms of NNT versus Referrals in the proposed operational scenario, offering the ability to refer 10 patients per week at an NNT of 12.4 referrals to reduce the risk of an ED revisit for fall. While these data are technically inferable based on the shape of the ROC curves, the degree of distinction between the models would likely not be apparent based on visual inspection alone to a reader not already expert in machine learning or statistics.

Algorithms derived by machine learning have become increasingly common in medicine, with significant excitement surrounding their potential to improve the ability to risk-stratify patients.(42, 43) Unfortunately, gaps still exist between the ability to predict a potentially avoidable event and specific actionable interventions.(44) In the majority of studies evaluating machine learning techniques, model performance is reported based on AUC or test characteristics such as sensitivity and specificity.(45) These test characteristics may be useful for establishing predictive performance generally, but may be misleading when not set into clinical context.(21) Once AUC curves have been generated for a given risk stratification model in test data, calculating additional information including NNT and anticipated referrals requires only an algebraic transformation of the data, as long as a proposed intervention has been identified along with an estimated effectiveness. The curves generated for this study communicate this tradeoff to policymakers, and provide a basis for comparison of anticipated “real world” effects of model performance.

For any particular harm-reduction intervention, there is a tradeoff when choosing a risk cutoff for referral. The most total harm-reduction would be accomplished by simply referring all patients in a given population, however such nonspecific referral would be costly in terms of time and resource use, and inefficient as many low risk patients would receive minimal benefit, or potentially be exposed to risks of an intervention. At the same time, selecting only those patients who are at extremely high risk of harm reduces the overall potential benefit of a risk-reduction strategy by not offering it to a large proportion of patients who will go on to have the outcome of interest. In our example, where a set number of referral slots per week was available, and the task was to select the highest risk patients to fill those slots, the random forest algorithm was the best performer. If there had been only 5 referral spots available however, the ridge penalized logistic regression model would have been the top performer, despite an overall slightly lower AUC, had better performance in selecting those 5 patients at highest risk, achieving an NNT of ~10 vs. ~12 for the tree based models. If the intervention tied to the algorithm were a referral to a less resource-intensive community-based falls prevention program with more availability, policymakers may be looking in a region of higher referrals per week and higher NNT - in this region, model performance was generally similar between the various models.

The projections of performance generated in this study were based on model performance on a set of test data which immediately followed the training data chronologically. While these projections are expected to help policymakers envision potential operational performance, they are not intended to replace evaluation of performance during and after implementation. Machine learning models are tuned to specific population parameters, and subject to calibration drift as patient and data characteristics change over time,(46) necessitating continued postimplementation monitoring to ensure effective results.

To our knowledge, three ED specific fall screening instruments have been examined: Carpenter et al examined a number of factors for association with future falls, proposing a screen of 4 independent factors, reporting a 4% probability of falling in their lowest risk group and 42% among the highest.(7) Tiedemann et al developed and externally validated a screening instrument with an AUC of 0.70,(9) and Greenberg et al utilized a modified CAGE criteria but did not report fall outcomes in their pilot.(47) As compared to these prior efforts, the machine learning-derived algorithms here offer improved performance in terms of test characteristics, and the advantage of not requiring the devotion of scant ED resources to in-person screening. (43)

Limitations:

When generating our NNT; we assumed that the relative risk reduction generated by our proposed intervention would remain constant across varying absolute risks. This assumption, while broadly made in medical decision making literature, is a simplification that is often, but not always, true.(48, 49) Furthermore, for the sake of simplifying our calculations we assumed that all patients referred for fall intervention would attend the required intervention. If an estimate of likelihood of completed referral were available, it could be taken into account in the NNT calculation.

We presented our NNT vs. Anticipated referrals per week curves with error bars based on the effectiveness estimate from the PROFET trial. PROFET measured the effectiveness of an intervention similar to our own falls clinic, but on a somewhat different outcome (any reported fall vs. ED visit for fall) and with somewhat different inclusion criteria (only selected older adults reporting to the ED for fall as opposed to all older adults). Given the relatively wide confidence interval of the PROFET results, we feel the included error bars provide a reasonable estimate of uncertainty, however these could be widened to incorporate estimated impact of other sources of potential variation in predicted effectiveness.

During model development, we chose to censor visits which were missing data features encoded as continuous variables (categorical variables were encoded to allow a “missing” category). While the inclusion of only complete records has the potential to introduce bias,(50) only 343 (3%) of records were dropped for incompleteness, suggesting minimal potential for change in algorithm performance if this data were imputed.

Our model was trained on an outcome of return visits to our emergency department for falls. Patients who fell may in some instances have presented to other emergency departments, in which case they were not captured by our definition. We limited our analysis to patients with a PCP in our system, and only analysed patients who presented to our emergency department in an index visit in an attempt to minimize this risk.

CONCLUSIONS:

In this analysis, we developed an algorithm which had an AUC of 0.78 for prediction of return visit to the ED for fall within 6 months of an index visit. Placed in the clinical context of harm reduction, this offered the ability to refer 10 patients per week to our fall clinic with a predicted NNT of 12 referrals to reduce the risk of a single fall. Our ability to translate the results of our analysis to the potential tradeoff between referral numbers and NNT offers decisionmakers the ability to envision the effects of a proposed intervention prior to implementation.