Abstract
Here we have developed a cell-level systems PK-PD model to characterize the bystander effect of ADCs. Cytotoxicity data generated following incubation of Trastuzumab-vc-MMAE in cocultures of high HER2 expressing N87 and low HER2 expressing GFP-MCF7 cells were used to build the model. Single cell PK model for ADC was used to characterize the PK of Trastuzumab-vc-MMAE and released MMAE in N87 and GFP-MCF7 cells. The two cell-level PK models were mechanistically integrated to mimic the coculture condition. MMAE induced intracellular occupancy of tubulin was used to drive the efficacy of ADC, and improvement in the tubulin occupancy of GFP-MCF7 cells in the presence of N87 cells was used to drive the bystander effect of Trastuzumab-vc-MMAE. The ‘dual’ cell-level PK-PD model was able to capture the observed data reasonably well. It was found that similar and high occupancy of tubulin by MMAE was required to achieve the cytotoxic effect in each cell line. In addition, estimated model parameters suggested that ~60% improvement in the tubulin occupancy was required to attain half of the maximum bystander killing effect by the ADC. The presented model provides foundation for in vivo systems PK-PD model to characterize and predict the bystander effect of ADCs.
Keywords: Antibody-drug conjugates, bystander effect, cellular disposition, single-cell PK-PD model, Trastuzumabvc-MMAE, microtubule inhibitors
Introduction
To overcome the dose-limiting toxicities and narrow therapeutic index associated with the conventional chemotherapy (1), cancer treatment has advanced towards targeted immunotherapies that can achieve tumor selectivity (2). Antibody-Drug Conjugates (ADCs) are one of those targeted immunotherapies that leverages the targeting potential of a monoclonal antibody (mAb) to deliver highly potent cytotoxic agents (payloads) to antigen-rich tumor cells (3), with the goal of achieving a wider therapeutic index (4). The last decade has witnessed an exponential growth in the clinical pipeline of ADCs (5, 6), with more than 70 molecules currently in the development (7). With the recent approvals of Besponsa® (Inotuzumab Ozogamicin) (8) and Mylotarg® (Gemtuzumab Ozogamicin) (9), there are now four FDA-approved ADCs in the market. While proven to be successful, the overall therapeutic potential of ADCs has been continuously challenged by dose-limiting toxicities (10), poor tumor penetration (11), and translation failures. Our long term goal is to develop mechanistic pharmacokinetic-pharmacodynamic (PK-PD) models that can address the critical questions pertaining to the efficacy and toxicity of ADCs, and ultimately facilitate their successful preclinical-to-clinical translation (12–16).
Cellular processing of ADCs is very important for their pharmacological effect. Upon binding to antigen-overexpressing tumor cells, ADC molecules are internalized and eventually degraded in the endosomal/lysosomal space. Based on the chemistry of the linker, the drug molecules are released in endosome/lysosome, and binds to the intracellular target (e.g. tubulin or DNA) to exert cell-cytotoxicity. The released drug molecules can also efflux out of the antigen expressing cells and diffuse into the nearby (i.e. bystanding) cells to exert their cytotoxicity. This additional mechanism for ADC efficacy is known as the ‘bystander effect’, and it is a desirable attribute to improve the overall efficacy of ADC in a heterogeneous tumor environment (17). In fact, bystander effect has been experimentally validated in both in-vitro and in-vivo settings (18–23). Both, ADC-specific (e.g. presence of a cleavable linker) and system-specific (e.g. antigen expression profile) parameters, can contribute towards the bystander effect. However, there is a lack of quantitative framework that can help in understanding how these parameters interact with each other, and how to manipulate them to attain an optimal and sustained bystander effect.
In the past we have used trastuzumab-vc-MMAE as a tool ADC, and in-vitro coculture system containing high HER2 (Ag-high, N87) and low HER2 (Ag-low, GFP-MCF7) expressing cells, to generate experimental data that can help in building a quantitative framework for the bystander effect (17). In fact, we have used this data to develop an empirical PK/PD model that can characterize the bystander killing of Ag-low cells in the presence of increasing percentage of Ag-high cells in a coculture. However, while building the empirical model it became obvious that a more comprehensive understanding of the cellular disposition of ADC and the released drug is required to develop a robust PK/PD model that can effectively predict the bystander effect of ADCs in vitro and in vivo.
Subsequently, a detailed cellular disposition study was conducted using T-vc-MMAE in N87 and GFPMCF7 cell-lines (14). Multiple analytes were measured and quantitatively integrated to develop a novel single-cell PK model for ADC. Here, we have presented an application of the cellular PK model for characterizing the bystander effect of ADCs. A ‘dual’ cell-level PK-PD model is developed, which can characterize the exchange of released drug molecules between Ag-high and Ag-low cells, and uses intracellular occupancy of the pharmacological target (i.e. tubulin) by released drug molecules (i.e. MMAE) to drive the cytotoxicity and bystander effect of the ADC.
Materials and Methods
Cell lines and tool ADC:
The two HER2-expressing cells used for the present investigation included GFP-MCF7 cells (breast cancer cells stably transfected with green fluorescent protein (GFP)) and NCI-N87 cells (human gastric carcinoma cells). GFP-MCF7 cells are reported to have a low expression of HER2 receptors (HER2 0/+1) whereas N87 cells overexpress HER2 receptors (HER2 3+), making them suitable Ag-low and Ag-high cell lines respectively. Trastuzumab-vc-MMAE, a tool ADC, was synthesized and characterized in-house. Vc-MMAE drug-linker was conjugated to humanized anti-HER2 antibody trastuzumab (Herceptin®, Genentech) using a random conjugation method. This method results in a heterogeneous formulation of ADC with an average drug: antibody ratio (DAR) of ~4.5. Detailed cell culture conditions and T-vc-MMAE synthesis and characterization procedures have been published before (14, 17).
In-vitro experiments to investigate T-vc-MMAE mediated direct cytotoxicity and bystander killing:
Effect of T-vc-MMAE on the viability of GFP-MCF7 (Ag-low) and N87 (Ag-high) cells was first investigated individually, where growth of each cell line was monitored following incubation with a range of T-vc-MMAE concentrations (0.1 pM - 1μM). Based on these experiments a threshold T-vc-MMAE concentration (100 nM) was identified, which enabled complete killing (>IC90) of N87 (Ag-high) cells and minimal killing (<IC50) of GFP-MCF7 (Ag-low) cells. Subsequently, coculture experiments were conducted to quantify the bystander killing of GFP-MCF7 (Ag-low) cells by T-vc-MMAE (at the threshold concentration) in the presence of varying percentage of N87 (Ag-high) cells. Detailed methodology of these experiments has been published before (17).
Simulations of intracellular target occupancy following T-vc-MMAE exposure:
Simulations of tubulin occupancy in GFP-MCF7 and N87 monocultures:
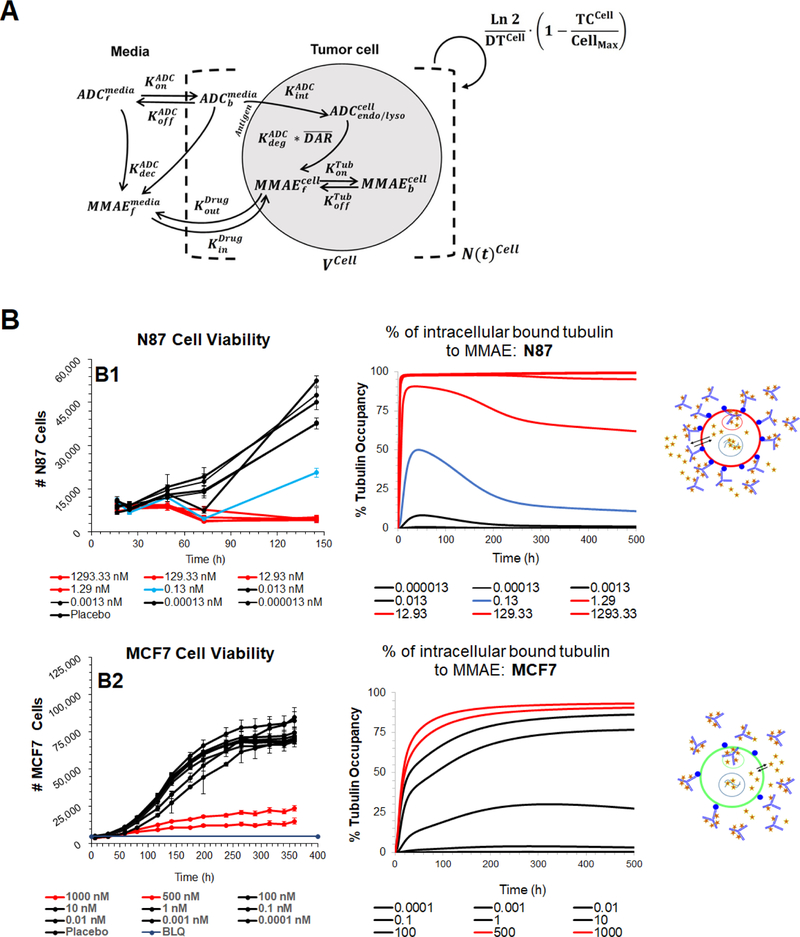
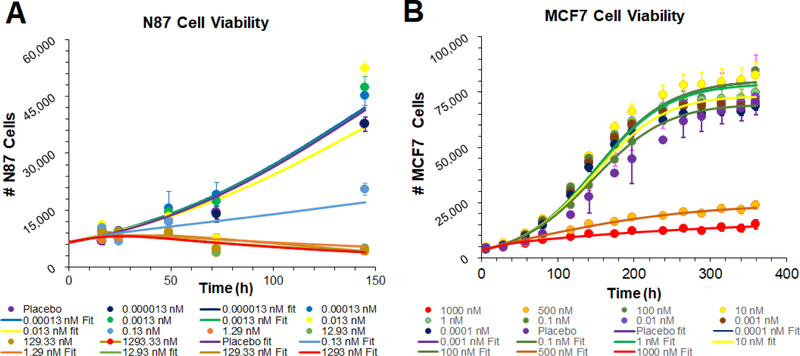
Previously published single-cell PK model for T-vc-MMAE (Fig. 1A) (14) was used to simulate the time course of percentage of tubulin molecules occupied with the released MMAE molecules inside the cell. All drug and system-specific parameters were fixed to the values used in the published model (14), and tubulin occupancy was explored at a range of T-vc-MMAE concentrations (0.1 pM - 1μM). The simulated tubulin occupancies for each cell-type were compared with the observed in vitro cytotoxicity data obtained at the same ADC concentrations (17), where simulated profiles associated with efficacious concentrations were color-matched to enable comparison.
Figure 1.
(A) Schematic of the single cell-level PK model for T-vc-MMAE ADC. (B) Comparison of model simulated MMAE induced intracellular tubulin occupancy at various T-vc-MMAE concentrations (in nM) with the observed cell cytotoxicity (17) at similar concentrations. B1 represents N87 cells and B2 represents GFP-MCF7 cells. Lines have been color coded to visually segregate the groups that show different extent of cytotoxicity and % tubulin occupancy.
Simulations of tubulin occupancy in GFP-MCF7 and N87 cocultures:
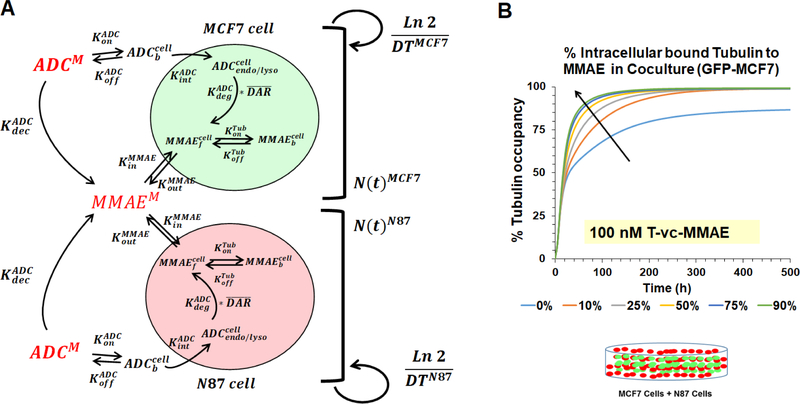
To mimic the coculture conditions, two cell-level PK models (specific to each cell line) were mechanistically integrated to develop a ‘dual’ cell-level PK model (Fig. 2A), which enables the disposition of T-vc-MMAE and released MMAE molecule in and across each cell type. All the equations associated with a ‘dual’ cell-level PK model are described below, and the list of state-variables and parameter values used in the equations is provided in Table-1 and Table-2 respectively. Mechanistic processes associated with the cellular disposition of ADCs were kept the same as our previous publications (12–16). Briefly, two distinct population of tumor cells were assumed which were growing at their respective growth rates in the media space. The ADC molecules incubated in the media were allowed to distribute simultaneously in both the cell-types using drug-specific binding ( and ) and internalization () processes. Once internalized in a cell, the ADC molecules were assumed to catabolize (), leading to release of unconjugated drug molecules () in the cytoplasmic space. In addition, non-specific deconjugation of ADC molecules in the media () was also incorporated, resulting in the generation of unconjugated drug molecules directly in the media, which could influx into either cancer cell-type. Once inside the cell, unconjugated drug molecules were either assumed to interact with the intracellular target (i.e. tubulin) to form the bound drug molecules (), or efflux out of the tumor cells. In order to conserve the mass-balance within the system, it was also assumed that with each cell-division, the intracellular content (either intact ADC or released drug) is distributed equally among the two daughter cells, resulting in a dilution rate equal to the growth rate () of each cell line.
Figure 2.
(A) Schematics of the ‘dual’ cell-level PK model, which integrates N87 and GFP-MCF7 cell models to represent the coculture system. (B) Simulations using the ‘dual’ cell-level PK model for intracellular occupancy of tubulin in GFP-MCF7 cells with varying percentage of N87 cells in the coculture.
Table 1:
The list of state variables used in the differential equations for the model, and their definitions.
| Variable Name | Definition |
|---|---|
| The number of tumor cells for each cell-type in a cell-distribution phase | |
| ADCM | Concentration (nM) of T-vc-MMAE in the media space |
| MMAEM | Amount (nMoles) of unconjugated MMAE in the media space |
| Number of molecules of HER2-bound T-vc-MMAE on surface of a single cell | |
| Number of molecules of T-vc-MMAE internalized in endosomal/lysosomal space of a single cell | |
| Number of molecules of ‘free’ unconjugated MMAE in the intracellular space of a single cell | |
| Number of molecules of ‘tubulin bound’ unconjugated MMAE in the intracellular space of a single cell | |
| Average Drug: Antibody Ratio of T-vc-MMAE at a given time |
Table 2:
The list of parameters utilized to build the ‘dual’ cell-level PK-PD model for ADC.
| Parameters | Description | Units | Value (CV%) | Source |
|---|---|---|---|---|
| SF | Scaling factor to convert the number of molecules to nanomoles | Unitless | Fixed | |
| MV, , | Volumes of media, single N87 and MCF7 cell | μL, pL, pL | 100, 3.12, 8.14 | (14) |
| DTN87, DTMCF7 | Doubling times for N87 and MCF7 cells | h | 40.1, 33.6 | (14, 17) |
| , | Maximum achievable cell-count in a culture well for N87 and GFP-MCF7 cells | Number | 80, 500, 105,00 | (17) |
| TubTotal | Total concentration of intracellular tubulin in each cell | nM | 65 | Previously estimated (12) |
| , | Second-order association and first-order dissociation rates of MMAE binding to tubulin | 1/nM/h, 1/h | 0.0183, 0.545 | (13,38,39) |
| , | Second-order association and first-order dissociation rates of T-vc-MMAE binding to HER2 | 1/nM/h, 1/h | 0.03, 0.014 | (13, 14) |
| First-order net antibody-HER2 complex internalization rate | 1/h | 0.11 | (13, 14) | |
| First-order non-specific deconjugation rate of MMAE from ADC | 1/h | ~0 | Previously estimated to a low value (14) | |
| DAR | Initial drug: antibody ratio of T-vc-MMAE | Unitless | 4.5 | Experimentally measured (17) |
| , | Number of HER2 receptors on N87 and GFP-MCF7 cells | Unitless | 950,000, 52,000 | Determined in-house (14) |
| First-order rate of proteases-induced intracellular ADC degradation and MMAE release | 1/h | 0.353 | (14) | |
| , | First-order influx and efflux rate constants for MMAE from extracellular space to intracellular space | 1/h | 8.33, 0.199 | (14) |
| , | First-order killing rates ofMMAE in N87and GFP-MCF7 cells | 1/h | 0.03 (12.3 %), 0.021 (4.1%) | Estimated |
| , | Mean intracellular occupancy to tubulin () required to achieve 50% cytotoxicity | percentage | 98.3 % (19.3%), 96.1% (5.5%) | Estimated |
| , | Within-cell variability in KC50 values associated with N87 and GFP-MCF7 cells | Percentage | 19.2% (31%), 17.9 % (10.9%) | Estimated |
| τN87, τMCF7 | Transit time parameter associated with the cell distribution model for N87 and GFP-MCF7 cells | h | 0.32(18%), 5.0 (12.3%) | Estimated |
| γN87, γMCF7 | Curve fitting parameter that determines the steepness of the occupancy-response relationship for each cell line | Unitless | 1.1 (18.2%), 3.1(21.9%) | Estimated |
| Percentage improvement in occupancy (“ƛ”) that results in 50% of maximum bystander killing | Percentage | 59% (12.6%) | Estimated | |
| τƛ | Transit time parameter associated with the delay between bystander killing signal and observed bystander effect response | h | 37 (41%) | Estimated |
Below are the equations associated with the growth of each cell type in the coculture:
| (1) |
| (2) |
Above, “i” refers to the cell type, and can be N87 or MCF7. Initial condition for equation 2 corresponds to the initial cell-seeding density in an experiment.
Equations associated with the concentration of T-vc-MMAE in the media (ADCM) and amount of unconjugated MMAE in the media (MMAEM), following incubation of the ADC in MCF7 and N87 coculture system, are provided below:
| (3) |
| (4) |
The initial condition for equation 3 is the concentration of T-vc-MMAE in the media used for the experiment, and the initial condition for equation 4 is zero.
Equations associated with the cellular disposition of ADC, in the form of number of molecules of a given ADC analyte in a single cell, are provided below:
| (5) |
| (6) |
| (7) |
| (8) |
Above, “i” refers to the cell type, and can be N87 or MCF7. Initial conditions for equations 5–8 are zero.
Equation associated with the non-specific deconjugation of MMAE from T-vc-MMAE in the media is described below:
| (9) |
Initial condition for equation 9 is the initial DAR value of the ADC in the formulation.
Percent occupancy of tubulin by MMAE inside each cell type “i” () was calculated by dividing the number of tubulin-bound MMAE molecules with the number of total tubulin molecules inside each cell:
| (10) |
To facilitate the assessment of the bystander effect, the model was used to simulate intracellular occupancy of tubulin in GFP-MCF7 (Ag-low) cells in the presence of varying amounts of N87 (Ag-high) cells in different cocultures.
Development of a cell-level PK-PD model to link intracellular tubulin occupancy to cell cytotoxicity:
In vitro cytotoxicity data generated following the incubation of T-vc-MMAE with GFP-MCF7 and N87 monocultures (Figure 1B) (17) was utilized to develop an in vitro PK-PD relationship for each cell type. The cell-level PK model for T-vc-MMAE (Figure 1A) was used to simulate intracellular occupancy of tubulin by MMAE (), and the tubulin occupancy was in turn used to drive the cytotoxicity of ADC using a non-linear killing function, since the relationship between tubulin occupancy and cell cytotoxicity was not always linear. The cell killing was characterized using the ‘cell-distribution model’, which shuttles growing cells into non-growing phases using transit compartments to account for the apparent delay between ADC exposure and observed cell-death. It was assumed that the cellular disposition of T-vc-MMAE remains active for growing or non-growing populations of cells. To conserve the mass-balance, it was assumed that upon death of each cell the intracellular content (i.e. intact ADC or unconjugated drug) is released back into the extracellular (media) space. Figure 3 describes the full schematic of the cell-level PK-PD model used for each cell line.
Figure 3.
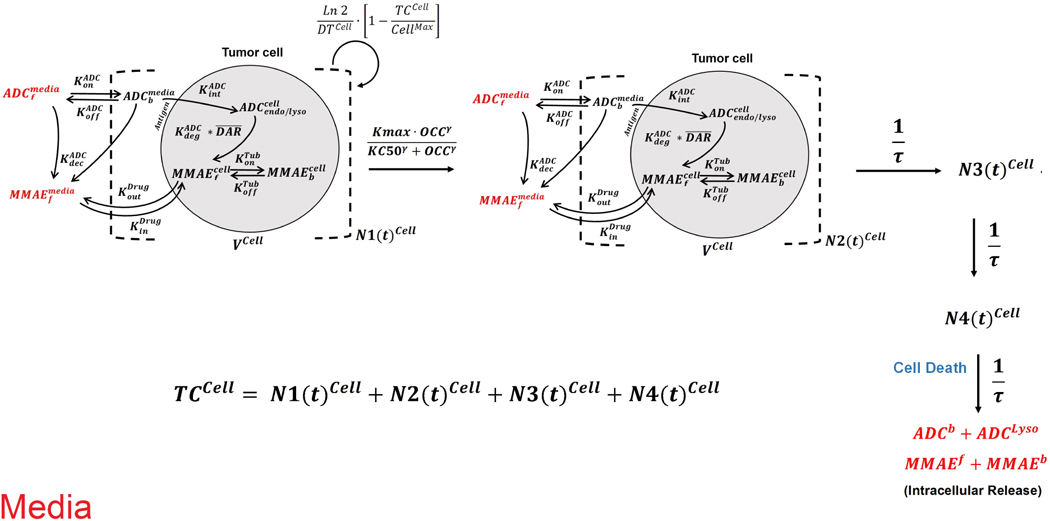
Schematic of the single cell level PK-PD model for T-vc-MMAE ADC. The model incorporates growing (N1) and non-growing (N2–N4) populations of cells. The cellular disposition of T-vc-MMAE was assumed to be active in all populations of cells, where intracellular occupancy of tubulin with released unconjugated MMAE shuttles the cells from growing to non-growing phases using transit compartments leading to cell death. Upon the death of each cell, the intracellular content was assumed to release in the media and could freely exchange with other cells.
Equations describing the growth and killing of each cell type “i” (where “i” refers to MCF7 or N87 cells) are provided below, along with population of cells in each transit compartment “j” (where “j” ranges from 2 to 3):
Growth function:
| (11) |
Kill function:
| (12) |
| (13) |
| (14) |
| (15) |
The total number of cells for each cell type (Ni) can be calculated using the following expression:
| (16) |
Initial condition for equation 13 corresponds to the initial cell seeding density of each cell type in an experiment whereas, the initial conditions for equations 14 and 15 are zero.
Equations associated with the cellular disposition of ADC and the released drug for each cell-type were kept the same as described earlier (i.e. equations 5–8). However, the equations pertaining to the concentrations of T-vc-MMAE in the media and amounts of unconjugated MMAE in the media for each cell type were modified to have inputs from the intracellular content of dead cells (i.e. the last transit compartment ). The modified media equations are listed below:
| (17) |
| (18) |
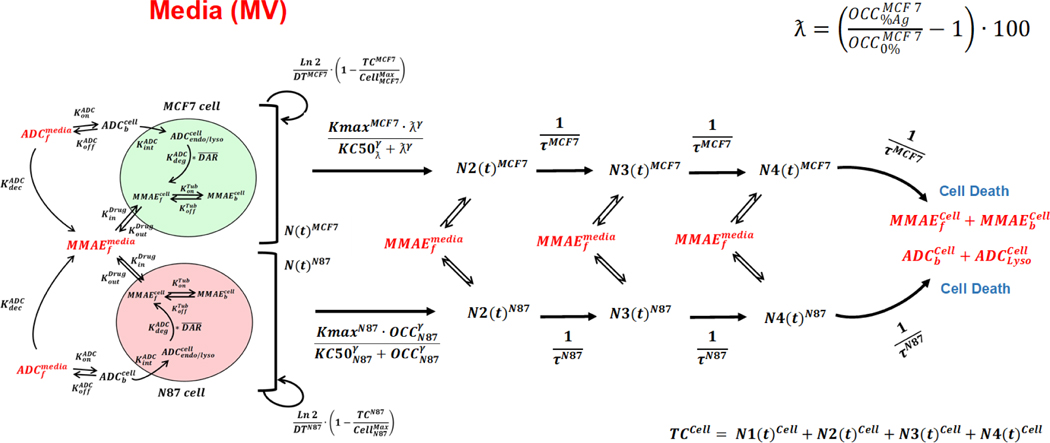
Development of a ‘dual’ cell-level PK-PD model to link increased tubulin occupancy with the bystander killing:
Once the cell-level PK-PD model was developed for each cell-type, the two models were mechanistically integrated as described in Figure 2A to facilitate the bystander effect. The schematic of the final ‘dual’ cell-level PK-PD model is described in Figure 4. It was assumed that cellular disposition of T-vc-MMAE in each cell-type remains active for both growing and non-growing population of cells. In addition, it was assumed that when a cell dies the intracellular content (i.e. ADC or released drug) becomes part of the media space. The model also accounted for the exchange of unconjugated drug molecules between different growing and non-growing populations of two cell-types. As such, the presence of higher proportion of N87 (Ag-high) cells in a coculture will lead to an increased production of unconjugated MMAE in the media, which will then diffuse into GFP-MCF7 (Ag-low) cells and lead to an increase in its tubulin occupancy. The dynamics of T-vc-MMAE induced N87 (Ag-high) cell killing was described using the PK-PD relationship detailed earlier (equations 11–15). However, a novel non-linear killing function was incorporated in the cell-distribution model of GFP-MCF7 cells (i.e. equation 12), which utilized the ‘improvement in tubulin occupancy’ (“ƛ”) as a driver for bystander killing of the cells. Incorporation of this expression facilitated isolation of the direct killing of GFP-MCF7 from the bystander killing induced by neighboring N87 (Ag+) cells. The following expression describes “ƛ”:
| (19) |
Figure 4.
Schematic of the ‘dual’ cell-level PK-PD model that is used to characterize T-vc-MMAE induced bystander effect in GFP-MCF7 and N87 coculture system.
Equation 19 calculates the percentage improvement in tubulin occupancy () by unconjugated MMAE in GFP-MCF7 (Ag-) cells in the presence of different cocultures with increasing percentages of N87 (Ag+) cells. Here, () depicts tubulin occupancy in GFP MCF7 cells when there are no N87 cells within the coculture system. Whereas () (10%, 25%, 50%, 75% or 90%) depicts tubulin occupancy in the presence of different N87 cell ratios. This expression was later used within a non-linear killing function (eq. 20), to characterize the bystander killing of ADC and obtain parameters (Kmax and KC50) specific to the bystander effect.
| (20) |
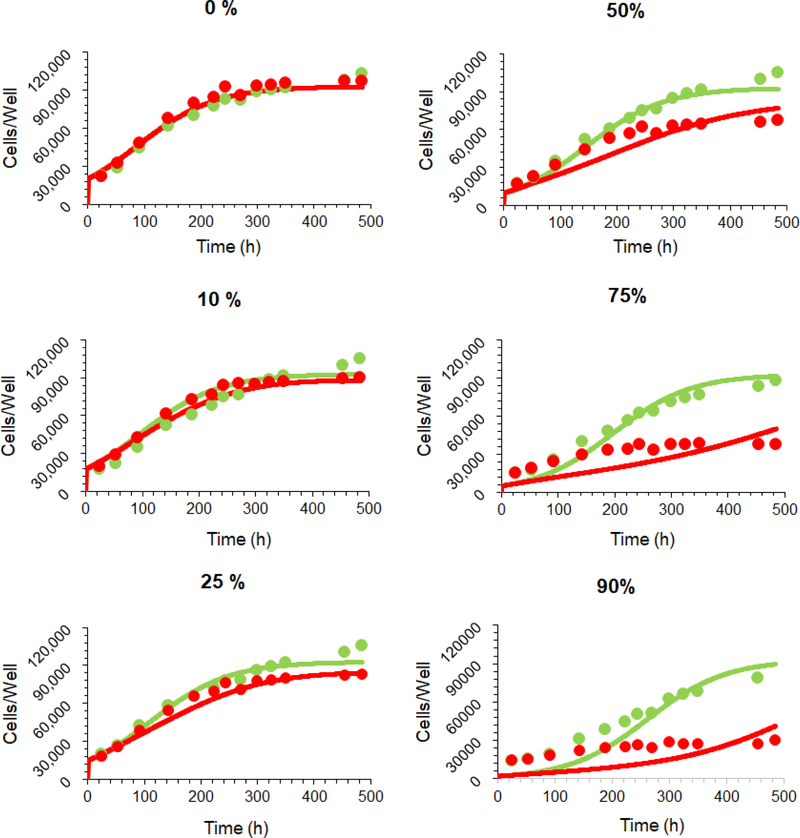
The ‘dual’ cell-level PK-PD model was used to fit the dataset describing the bystander killing of GFPMCF7 (Ag-low) cells in the presence of increasing % of N87 (Ag-high) cells, following an incubation with 100 nM T-vc-MMAE (17). The model predicted cell numbers were then overlaid with the experimentally observed values (Figure 6).
Figure 6.
Observed and model-fitted cell-viability profiles for GFP-MCF7 cells in the presence of varying percentage of N87 cells in the coculture. The fittings were obtained using the ‘dual’ cell-level PK-PD model shown in Figure 4. Green profiles are control profiles with no ADC, and red profiles were generated following 100 nM T-vc-MMAE exposure.
Parameter Estimation, Model Fitting, and Simulation:
The parameters associated with the cellular PK of T-vc-MMAE as well as the growth rates of each cell line were fixed to the values previously reported by us (14, 17), while simulating the intracellular tubulin occupancy. The model fitting and parameter estimation was performed sequentially, where initially, the efficacy parameters associated with the in vitro PK-PD relationships (i.e. , , , τi and γi) for individual cell-type were estimated by fitting the model to in-vitro cytotoxicity data (Figure 1B). In the subsequent step, ‘dual’ cell-level PK-PD model was utilized to fit the bystander killing dataset (Figure 6) to obtain the estimates for and τƛ, while keeping the rest of parameters fixed to known or prior estimated values.
All models were initially built and simulated in Berkeley Madonna (University of California at Berkeley, CA) whereas data fitting was performed using maximum likelihood (ML) estimation method of ADAPT-5 software (BMSR, CA) (24). To obtain the estimates for the within-cell variability (WCV) in the potency parameter() for each cell line, maximum likelihood expectation maximization (MLEM) method was chosen with an assumption of log-normal distribution in values. For the model fitting, following variance model (Var(t)) was used, where σintercept refers to the additive error and σslope refers to the proportional error associated with the model prediction (Y (t)).
| (21) |
Results
Simulations of intracellular target occupancy following T-vc-MMAE exposure:
Simulations of tubulin occupancy in GFP-MCF7 and N87monocultures:
Figure 1B shows the simulated tubulin occupancy () profiles for each cell-type following incubation with varying concentrations of T-vc-MMAE (0.1 pM - 1μM). The profiles associated with the observed cytotoxicity of T-vc-MMAE in each cell line at the respective ADC concentrations is also shown for comparison. Overall, there was a positive correlation between the extent of cytotoxicity and corresponding tubulin occupancy. Model simulations revealed that the extracellular ADC concentrations that led to complete killing of N87 (Ag-high) cells (Fig. 1B1, profiles in red), were also able to accomplish almost complete occupancy of intracellular tubulin. The extracellular T-vc-MMAE concentration which led to ~50% cytotoxicity in N87 cells (0.13 nM, profile in blue), was able to accomplish ~50% tubulin occupancy. In addition, all the non-efficacious concentrations of T-vc-MMAE (profiles in black) resulted in an insignificant occupancy of tubulin in N87 cells. While the exposure-response relationship for T-vc-MMAE in GFP-MCF7 (Ag-low) cells was very steep, a much gradual change in tubulin occupancy was observed following incubation with different ADC concentrations (Figure 1B2). However, similar to N87 cells, there was a trend towards higher cytotoxicity with higher tubulin occupancy. The two efficacious T-vc-MMAE concentrations (0.5 and 1 μM) resulted in maximum tubulin occupancy (profiles in red). These results suggest that different cell lines may have their unique pharmacodynamic relationship between tubulin occupancy and cell cytotoxicity.
Simulations of tubulin occupancy in GFP-MCF7 and N87 cocultures:
Figure 2B shows the simulated tubulin occupancy () profiles for GFP-MCF7 (Ag-low) cells in the presence of varying percentage of N87 (Ag-high) cells, following incubation with 100 nM T-vc-MMAE concentration. Model simulations revealed that increasing percentage of N87 cells in a coculture led to an improvement in the intracellular tubulin occupancy by unconjugated MMAE in GFP-MCF7 (Ag-low) cells.
Development of a cell-level PK-PD model to link intracellular tubulin occupancy to cell cytotoxicity:
Figure 5 shows observed and model fitted ‘cell number vs. time’ profiles obtained following incubation with different concentrations (0.1 pM - 1μM) of T-vc-MMAE in monocultures of N87 (Fig. 5A) and GFP-MCF7 (Fig. 5B) cells. The in vitro cell-level PK-PD model was able to characterize all the cytotoxicity data reasonably well. The estimated values of parameters associated with ADC efficacy are provided in Table 2. All the predicted profiles were found to be within 2-fold of the observed profiles (based on percentage predictive error calculations). Interestingly, modeling analysis revealed that the parameters associated with T-vc-MMAE induced efficacy () were very similar between GFP MCF7 (Ag-low) and N87 (Ag-high) cells.
Figure 5.
Observed and model-fitted cell-viability profiles for (A) N87 and (B) GFP-MCF monocultures in the presence of different T-vc-MMAE concentrations. The fittings were obtained using the single cell PK-PD model shown in Figure 3.
Development of a ‘dual’ cell-level PK-PD model to link increased tubulin occupancy with the bystander killing:
Figure 6 shows observed and model fitted ‘cell number vs. time’ profiles of GFP-MCF7 cells in the presence of varying percentage of N87 cells, following incubation with (red profile) or without (green profile) 100 nM T-vc-MMAE (17). While there were slight deviations between model predictions and observed profiles at initial time points in cocultures with high percentage of N87 cells, overall, the ‘dual’ cell-level PK-PD model was able to predict the observed bystander effect of ADC in the coculture system reasonably well with a precise estimation of ‘’, which revealed that 59% increase in tubulin occupancy will lead to 50% of the maximum bystander killing.
Discussion
With the emergence of continuously expanding clinical pipeline, bystander effect has been considered as an advantageous attribute of an ADC design for solid tumors (16, 25–28). While ADCs can selectively reach solid tumors using overexpressed target antigens, its overall efficacy can still be limited due to several other factors (28). For example, inter- and intra-tumor heterogeneity in antigen expression levels has been shown to limit the efficacy of many targeted therapeutics in the clinic (29). In addition, alterations in tumor microenvironment and antigen expression profile over time can also render many patients resistant to the targeted therapies over time (29, 30). Moreover, because of the binding-site-barrier, there is a heterogeneous distribution of targeted molecules like monoclonal antibodies and ADCs around perivascular regions, which limits their distribution to the deeper portions of tumor tissues (11). It is believed that these challenges related to heterogeneous antigen expression and ADC distribution can be overcome to a certain extent by designing ADCs with the ‘bystander effect’ (17, 31), which can promote more homogeneous distribution of the released drug inside solid tumor.
The importance of bystander effect in improving the overall efficacy of ADCs has been qualitatively demonstrated by several groups in both in-vitro and in-vivo settings (18, 19, 23). More recently, we have described a quantitative characterization of the bystander effect using T-vc-MMAE as a tool ADC and cocultures of GFP-MCF7 (Ag-low) and N87 (Ag-high) cell lines (17). One of the important findings from our work was the apparent delay in the onset of bystander effect in the coculture system. While this delay may stem from the time taken in cellular processing of the ADC, in the absence of cellular PK at the time, extracellular (media) ADC concentrations were used as a forcing function to mathematically characterize T-vc-MMAE induced direct and bystander killing. Although the developed semi-mechanistic PD model could characterize the rate and extent of bystander killing, successful in-vitro to in-vivo translation (13) of observed bystander effect required more mechanistic characterization of the determinants that influence the exchange of released unconjugated drug (MMAE) across two cell types. Based on our previously proposed preclinical-to-clinical translation strategy (12, 15, 16), cellular disposition is the most integral component of a multi-scale PK-PD model, which is conserved while transitioning across discovery, preclinical and clinical development. This prompted us to mechanistically characterize the cellular disposition of T-vc-MMAE in GFP-MCF7 (Ag-low) and N87 (Ag-high) cell lines (14). Subsequently, comprehensive dataset with multiple bioanalytical measurements was generated, and a single cell-level PK model was developed to quantitatively characterize all the data simultaneously. The model was able to capture the relationship between extracellular T-vc-MMAE concentration and released MMAE exposure within a single cell (14). Here we have utilized this single cell PK model to develop a more mechanistic PK-PD relationship for the bystander effect of ADCs.
Since the mechanism-of-action of MMAE involves inhibition of cell-division by binding to intracellular tubulin (32), occupancy to tubulin () was utilized as the main driver of cell cytotoxicity. Upon simulating the intracellular tubulin occupancy () with varying extracellular concentrations of T-vc MMAE (0.1 pM - 1μM), it was observed that the cell cytotoxicity was significantly correlated with the extent of MMAE-induced tubulin occupancy in each cell line. While we have used 65 nM concentration of total tubulin to simulate intracellular tubulin occupancies () in each cell line, it is important to note that this is an estimated value obtained via modeling of unconjugated MMAE PK in L540cy tumor bearing xenografts. This value was deemed necessary to capture intracellular binding of MMAE and sustained exposure of MMAE within tumors (12). While we have validated this value via extensive in vitro and in vivo modeling and simulation work (14), experimental validation of this tubulin concentration remains to be done. Based on the observed correlation between cell cytotoxicity and MMAE-induced tubulin occupancy, the cell-level PK model (14) was mechanistically integrated with the cell-distribution PD model (17, 33) (as shown in Figure 3) to link the intracellular tubulin occupancy values with cell killing. The model was able to characterize in-vitro cytotoxicity data obtained from monocultures very well (Figure 5). In addition, the estimated ADC efficacy parameters () for each cell line (i.e. MCF7 and N87) were much closer to each other when compared with the estimates obtained using previously published empirical model (17). This is because the empirical model uses media ADC concentrations to drive the efficacy and the cell-level PK-PD model uses intracellular MMAE occupied tubulin concentrations to drive the efficacy. When the ability of higher antigen expressing cells to bring more drug in a cell compared to the low antigen expressing cells is ignored, the empirical model suggests that the T-vc-MMAE ADC has higher potency in N87 (Ag-high) cells compared to GFP-MCF7 (Ag-low) cells. However, when the differential antigen expression is accounted for by using the cellular PK model, it results in very similar estimations of killing rate () and potency () values for MMAE occupied tubulin concentrations. These results suggest that once inside the cells MMAE has the same efficacy for both the cell lines, which needs to be proven experimentally. Nonetheless, our results are in line with what is reported by Maass et al. (34), who demonstrated that similar number of doxorubicin molecules are required in the intracellular space to inhibit the proliferation of different cancer cell lines. Our results also suggest an important correlation between antigen expression levels and ADC efficacy, which is widely presumed but not fully validated.
Incorporation of cell-level ADC PK also allowed us to eliminate additional signal transduction steps, which are typically incorporated within the empirical PK-PD model (35). This is mainly because the timespan associated with the processing of ADC and attainment of desired target occupancy may have significantly contributed towards the observed delay in the onset of ADC mediated cell-killing. However, incorporation of cell-distribution transit compartments (35) was still necessary to account for the remaining delay in the killing of cells. It is important to note that while performing our modeling analysis we estimated a minimal extent of within-cell variability (WCV). Literature reports have also suggested that there can be notable variability in the intracellular exposure and cell cytotoxicity between different cells due to cell-to-cell differences in drug delivery and PD responses (34, 36). Therefore, we recommend that going forward a more stochastic approach should be favored over the deterministic approach to translate these results in vivo. Nonetheless, the observation that very similar and high extent of tubulin occupancy by MMAE (Table 2) is required to achieve cytotoxic effects in each cell line still holds true.
Once the cell-level PK-PD relationships were established for monocultures, the models for each cell-type were combined mechanistically to mimic the coculture situation and characterize the bystander effect of ADC (Figure 2). The ‘dual’ model was able to simulate an improvement in MMAE induced intracellular tubulin occupancy of GFP-MCF7 (Ag-low) cells in the presence of N87 (Ag-high) cells. Increased percentage of N87 cells in a coculture led to an increase in the percentage of tubulin occupancy in GFPMCF7 cells, suggesting the presence of mechanism driven bystander effect (17). Consequently, percentage improvement in tubulin occupancy (“ƛ”) was used as the main driver for characterizing the bystander effect of ADC. Since there was a time lag observed between the improvement in tubulin-occupancy and enhancement in bystander effect driven cytotoxicity (compare Figures 2B and 6), transit compartments were introduced in the model (Figure 4) to characterize the delay (35). The final dual cell-level PK-PD model was able to capture the observed bystander effect data reasonably well (Figure 6). The estimates of the potency parameter associated with the bystander killing () suggested that ~59% improvement in the tubulin occupancy will lead to 50% of maximum bystander killing (Table 2). Although this conclusion is specific for the underlying system (i.e. coculture of N87 and GFP-MCF7 cells), it provides an estimate for extension of the ‘dual’ cell-level PK-PD model to other coculture/heterogeneous tumor systems, so one can a priori predict the bystander effect of relevant ADCs. Of note, there was a slight deviation between model predicted and observed profiles at initial time points in cocultures with high percentage of N87 cells. This may stem from the use of semi-mechanistic transit compartment model to characterize the delay in the PD effect, which may stem from a more complex underlying system. Furthermore, cocultures at higher percentages of N87 cells (75% and 90%) inherently had lower percentages of GFP-MCF7 cells, and hence our fluorescent-based analytical method (described in (17)) could have been less sensitive at these lower numbers of GFP-MCF7 cells. As such, the discrepancy between the observed and model predicted profiles may stem from model misspecification or experimental issues.
It is important to note that mechanistic vigilance will be required while translating results from in vitro bystander effect data to in vivo settings. While there is a ‘well-mixed’ population of two cell-types in the examined coculture system, within a solid tumor there is a significant intra-tumoral heterogeneity and the composition of different cell types can significantly vary across different regions of the tissue (29). Additionally, based on our previous work that investigated the role of different pathways in bringing the drug inside a cell following in-vitro and in-vivo ADC administration, (13), the extent of in-vivo bystander effect can be dampened by diffusion of the released drug out of the tumor into the systemic circulation (7). In fact, Khera et al. (7) have recently presented a theoretical analysis of ADC bystander effect with similar conclusion, suggesting payloads with physicochemical properties that allow them to be taken up by cells rapidly compared to the tumor washout rate would demonstrate the maximum in vivo bystander effect. As such, one should develop in vivo systems PK model by incorporating cell-level coculture models like the one developed here to obtain realistic insight into ADC induced in vivo bystander effect.
In summary, to facilitate the development of a translational PK-PD model that can characterize and predict ADC induced bystander effect in vivo, here we have presented the development of a ‘dual’ cell-level PK-PD model that can characterize ADC induced bystander effect in vitro. The presented model is the first attempt on characterizing the PK and PD effects of ADC on a single cell-level and employs tubulin occupancy to drive ADC-induced cytotoxic effect. In addition, the single-cell framework also allows the flexibility to incorporate more than two populations and multiple cell-types (e.g. immune cells) in the coculture, to investigate ADC induced other pharmacological effects (e.g. immunogenic cell-death, ICD) and the interaction of ADC with other therapeutics (e.g. immune-oncology agents). The presented cell-level models can be integrated with the tumor disposition model of ADC (37) to characterize and predict ADC induced bystander effect in vivo.
Supplementary Material
Acknowledgements
This work was supported by the Centre for Protein Therapeutics at University at Buffalo. D.K.S is supported by NIH grant GM114179 and AI138195. Authors would also like to thank Dr. David D’Argenio (USC) for his continuous support and discussions on implementation of complex models in ADAPT 5 software.
List of Abbreviations:
- ADC
Antibody-drug conjugate
- T-vc-MMAE
Trastuzumab-valine-citrulline-monomethyl auristatin E
- PK-PD
Pharmacokinetics-pharmacodynamics
- GFP
Green fluorescent protein
- DAR
Drug: Antibody Ratio
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Joo WD, Visintin I, Mor G. Targeted cancer therapy--are the days of systemic chemotherapy numbered? Maturitas. 2013;76(4):308–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Vanneman M, Dranoff G. Combining immunotherapy and targeted therapies in cancer treatment. Nat Rev Cancer. 2012;12(4):237–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lambert JM, Berkenblit A. Antibody-Drug Conjugates for Cancer Treatment. Annu Rev Med. 2018;69:191–207. [DOI] [PubMed] [Google Scholar]
- 4.Valeur E, Knerr L, Olwegard-Halvarsson M, Lemurell M. Targeted delivery for regenerative medicines: an untapped opportunity for drug conjugates. Drug Discov Today. 2017;22(6):841–7. [DOI] [PubMed] [Google Scholar]
- 5.Vezina HE, Cotreau M, Han TH, Gupta M. Antibody-Drug Conjugates as Cancer Therapeutics: Past, Present, and Future. J Clin Pharmacol. 2017;57 Suppl 10:S11–S25. [DOI] [PubMed] [Google Scholar]
- 6.Govindan SV, Sharkey RM, Goldenberg DM. Prospects and progress of antibody-drug conjugates in solid tumor therapies. Expert Opin Biol Ther. 2016;16(7):883–93. [DOI] [PubMed] [Google Scholar]
- 7.Khera ECC, Bhatnagara S, Thurber GM. Computational transport analysis of antibody-drug conjugate bystander effects and payload tumoral distribution: implications for therapy. Mol Syst Des Eng. 2018;3(1):73–88 [Google Scholar]
- 8.Pfizer Receives U.S. FDA Approval for BESPONSA® (inotuzumab ozogamicin) [press release]. 2017.
- 9.PFIZER RECEIVES FDA APPROVAL FOR MYLOTARG™ (GEMTUZUMAB OZOGAMICIN) [press release]. Friday, September 1, 2017 2017.
- 10.Masters JC, Nickens DJ, Xuan D, Shazer RL, Amantea M. Clinical toxicity of antibody drug conjugates: a meta-analysis of payloads. Invest New Drugs. 2018;36(1): 121–35. [DOI] [PubMed] [Google Scholar]
- 11.Cilliers C, Guo H, Liao J, Christodolu N, Thurber GM. Multiscale Modeling of Antibody-Drug Conjugates: Connecting Tissue and Cellular Distribution to Whole Animal Pharmacokinetics and Potential Implications for Efficacy. AAPS J. 2016;18(5):1117–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shah DK, Haddish-Berhane N, Betts A. Bench to bedside translation of antibody drug conjugates using a multiscale mechanistic PK/PD model: a case study with brentuximab-vedotin. J Pharmacokinet Pharmacodyn. 2012;39(6):643–59. [DOI] [PubMed] [Google Scholar]
- 13.Singh AP, Maass KF, Betts AM, Wittrup KD, Kulkarni C, King LE, et al. Evolution of Antibody-Drug Conjugate Tumor Disposition Model to Predict Preclinical Tumor Pharmacokinetics of Trastuzumab-Emtansine (T-DM1). AAPS J. 2016;18(4):861–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Singh AP, Shah DK. Measurement and Mathematical Characterization of Cell-Level Pharmacokinetics of Antibody-Drug Conjugates: A Case Study with Trastuzumab-vc-MMAE. Drug Metab Dispos. 2017;45(11):1120–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Singh AP, Shah DK. Application of a PK-PD Modeling and Simulation-Based Strategy for Clinical Translation of Antibody-Drug Conjugates: a Case Study with Trastuzumab Emtansine (T-DM1). AAPS J. 2017;19(4):1054–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Singh AP, Shin YG, Shah DK. Application of Pharmacokinetic-Pharmacodynamic Modeling and Simulation for Antibody-Drug Conjugate Development. Pharm Res. 2015;32(11):3508–25. [DOI] [PubMed] [Google Scholar]
- 17.Singh AP, Sharma S, Shah DK. Quantitative characterization of in vitro bystander effect of antibody-drug conjugates. J Pharmacokinet Pharmacodyn. 2016;43(6):567–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kovtun YV, Audette CA, Ye Y, Xie H, Ruberti MF, Phinney SJ, et al. Antibody-drug conjugates designed to eradicate tumors with homogeneous and heterogeneous expression of the target antigen. Cancer Res. 2006;66(6):3214–21. [DOI] [PubMed] [Google Scholar]
- 19.van der Lee MM, Groothuis PG, Ubink R, van der Vleuten MA, van Achterberg TA, Loosveld EM, et al. The Preclinical Profile of the Duocarmycin-Based HER2-Targeting ADC SYD985 Predicts for Clinical Benefit in Low HER2-Expressing Breast Cancers. Mol Cancer Ther. 2015;14(3):692–703. [DOI] [PubMed] [Google Scholar]
- 20.Golfier S, Kopitz C, Kahnert A, Heisler I, Schatz CA, Stelte-Ludwig B, et al. Anetumab ravtansine: a novel mesothelin-targeting antibody-drug conjugate cures tumors with heterogeneous target expression favored by bystander effect. Mol Cancer Ther. 2014;13(6):1537–48. [DOI] [PubMed] [Google Scholar]
- 21.Li JY, Perry SR, Muniz-Medina V, Wang X, Wetzel LK, Rebelatto MC, et al. A Biparatopic HER2-Targeting Antibody-Drug Conjugate Induces Tumor Regression in Primary Models Refractory to or Ineligible for HER2-Targeted Therapy. Cancer Cell. 2016;29(1): 117–29. [DOI] [PubMed] [Google Scholar]
- 22.Tolcher AW, Ochoa L, Hammond LA, Patnaik A, Edwards T, Takimoto C, et al. Cantuzumab mertansine, a maytansinoid immunoconjugate directed to the CanAg antigen: a phase I, pharmacokinetic, and biologic correlative study. J Clin Oncol. 2003;21(2):211–22. [DOI] [PubMed] [Google Scholar]
- 23.Ogitani Y, Hagihara K, Oitate M, Naito H, Agatsuma T. Bystander killing effect of DS-8201a, a novel anti-human epidermal growth factor receptor 2 antibody-drug conjugate, in tumors with human epidermal growth factor receptor 2 heterogeneity. Cancer Sci. 2016;107(7):1039–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.David Z D’Argenio AS, Xiaoning Wang. ADAPT 5 User’s Guide: Pharmacokinetic/Pharmacodynamic Systems Analysis Software Biomedical Simulations Resource, Los Angeles: 2009. [Google Scholar]
- 25.Staudacher AH, Brown MP. Antibody drug conjugates and bystander killing: is antigen-dependent internalisation required? Br J Cancer. 2017;117(12):1736–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Perrino E, Steiner M, Krall N, Bernardes GJ, Pretto F, Casi G, et al. Curative properties of noninternalizing antibody-drug conjugates based on maytansinoids. Cancer Res. 2014;74(9):2569–78. [DOI] [PubMed] [Google Scholar]
- 27.Thudium K, Bilic S, Leipold D, Mallet W, Kaur S, Meibohm B, et al. American Association of Pharmaceutical Scientists National Biotechnology Conference Short Course: Translational Challenges in Developing Antibody-Drug Conjugates: May 24, 2012, San Diego, CA. MAbs. 2013;5(1):5–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lambert JM, Morris CQ. Antibody-Drug Conjugates (ADCs) for Personalized Treatment of Solid Tumors: A Review. Adv Ther. 2017;34(5):1015–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Seol H, Lee HJ, Choi Y, Lee HE, Kim YJ, Kim JH, et al. Intratumoral heterogeneity of HER2 gene amplification in breast cancer: its clinicopathological significance. Mod Pathol. 2012;25(7):938–48. [DOI] [PubMed] [Google Scholar]
- 30.Kittaneh M, Montero AJ, Gluck S. Molecular profiling for breast cancer: a comprehensive review. Biomark Cancer. 2013;5:61–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cilliers C, Menezes B, Nessler I, Linderman J, Thurber GM. Improved Tumor Penetration and Single-Cell Targeting of Antibody-Drug Conjugates Increases Anticancer Efficacy and Host Survival. Cancer Res. 2018;78(3):758–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Waight AB, Bargsten K, Doronina S, Steinmetz MO, Sussman D, Prota AE. Structural Basis of Microtubule Destabilization by Potent Auristatin Anti-Mitotics. PLoS One. 2016;11(8):e0160890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shah DK, Loganzo F, Haddish-Berhane N, Musto S, Wald HS, Barletta F, et al. Establishing in vitro-in vivo correlation for antibody drug conjugate efficacy: a PK/PD modeling approach. J Pharmacokinet Pharmacodyn. 2018. [DOI] [PubMed] [Google Scholar]
- 34.Maass KF, Kulkarni C, Quadir MA, Hammond PT, Betts AM, Wittrup KD. A Flow Cytometric Clonogenic Assay Reveals the Single-Cell Potency of Doxorubicin. J Pharm Sci. 2015;104(12):4409–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Yang J, Mager DE, Straubinger RM. Comparison of two pharmacodynamic transduction models for the analysis of tumor therapeutic responses in model systems. AAPS J. 2010;12(1): 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Spencer SL, Gaudet S, Albeck JG, Burke JM, Sorger PK. Non-genetic origins of cell-to-cell variability in TRAIL-induced apoptosis. Nature. 2009;459(7245):428–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Shah DK, King LE, Han X, Wentland JA, Zhang Y, Lucas J, et al. A priori prediction of tumor payload concentrations: preclinical case study with an auristatin-based anti-5T4 antibody-drug conjugate. AAPS J. 2014;16(3):452–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bhattacharyya B, Wolff J. Maytansine binding to the vinblastine sites of tubulin. FEBS Lett. 1977;75(1):159–62. [DOI] [PubMed] [Google Scholar]
- 39.Maass KF, Kulkarni C, Betts AM, Wittrup KD. Determination of Cellular Processing Rates for a Trastuzumab-Maytansinoid Antibody-Drug Conjugate (ADC) Highlights Key Parameters for ADC Design. AAPS J. 2016;18(3):635–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.