Multivariate approaches improve the reliability and validity of functional connectivity and prediction of individual behaviors

Abstract

Brain functional connectivity features can predict cognition and behavior at the level of the individual. Most studies measure univariate signals, correlating timecourses from the average of constituent voxels in each node. While straightforward, this approach overlooks the spatial patterns of voxel-wise signals within individual nodes. Given that multivariate spatial activity patterns across voxels can improve fMRI measures of mental representations, here we asked whether using voxel-wise timecourses can better characterize region-by-region interactions relative to univariate approaches. Using two fMRI datasets, the Human Connectome Project sample and a local test-retest sample, we measured multivariate functional connectivity with multivariate distance correlation and univariate connectivity with Pearson’s correlation. We compared multivariate and univariate connectivity estimates, demonstrating that relative to univariate estimates, multivariate estimates exhibited higher reliability at both the edge-level and connectome-level, stronger prediction of individual differences, and greater sensitivity to brain states within individuals. Our findings suggest that multivariate estimates reliably provide more powerful information about an individual’s functional brain organization and its relation to cognitive skills.

Introduction

Functional connectivity and network-based analyses of neuroimaging data have gained popularity as methods to uncover large-scale brain organization at the group level. More recently, studies have further demonstrated that functional connectivity is closely related to cognition and behavior at the level of the individual. Finn et al. (2015) introduced the concept of connectome fingerprinting, demonstrating that an individual’s functional connectome, or whole-brain pattern of functional connectivity, is unique, and can therefore be used to distinguish individuals from one another (Finn et al., 2015; Miranda-Dominguez et al., 2014). This has led to a proliferation of studies demonstrating that patterns of functional connectivity can predict individual differences in a wide variety of cognitive abilities and behaviors (Beaty et al., 2018; Rosenberg et al., 2016), personality traits (Hsu et al., 2018; Nostro et al., 2018), as well as dysfunction in brain disorders (Emerson et al., 2017; Lin et al., 2018). Furthermore, complementary work has added evidence that the connectome is stable across time (i.e., multiple imaging sessions) (Laumann et al., 2015; Noble et al., 2017b) and cognitive states (i.e., engagement in distinct tasks and rest) (Cole et al., 2014; Finn et al., 2015).

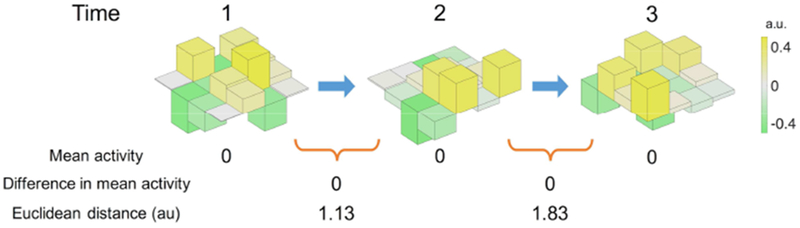
The majority of functional connectivity studies compare univariate fMRI signals, that is, by correlating activity timecourses from the average of all constituent voxels within each region. While this approach provides straightforward estimates of functional connectivity, it overlooks the spatial patterns of voxel-wise signals within individual regions. Although node-wise averaging, essentially a spatial smoothing operation, can increase the signal-to-noise ratio (Parrish et al., 2000), it may obscure informative voxel-wise spatial activity patterns (Haynes and Rees, 2006; Sundermann et al., 2014). For example, multivariate pattern analysis can decode detailed information about mental processes and cognitive states difficult to discover from averaged activity, such as the task in which a subject is engaged or the stimulus that they are perceiving (see for reviews, Haxby et al., 2014; Tong and Pratte, 2012). Individual brain parcels contain heterogeneous activity patterns that would be lost when relying on a single representative timecourse for the node (Geerligs et al., 2016). Further biological or engineering factors also contribute to heterogeneity, such as individual variance in the brain structure and functional organization, and imperfect coregistration of MR images (Gordon et al., 2015; Kong et al., 2018; Sohn et al., 2015), making it arbitrary to define boundaries between brain parcels, and missing distinct functional sub-regions within each parcel. To minimize these issues, recent studies have proposed using uni- and multi-modal neuroimaging data to improve parcellations of the human brain (Eickhoff et al., 2018; Glasser et al., 2016; Gordon et al., 2017; Shen et al., 2010). However, even if all these factors are carefully controlled at the subject-level, each brain parcel could still contain heterogeneous sets of voxels. That is, because of the brain’s complex hierarchical modular structure, any given node within a brain atlas can potentially be further divided into smaller regions (Igelström et al., 2015; Meunier et al., 2010; Sohn et al., 2012). Thus, given that each node of a brain atlas may not reflect the smallest “true” functional unit of a neural population, considering within-node patterns in addition to mean node activity timecourse may better characterize region-by-region functional interactions and representational content (Figure 1).

Figure 1. Example of mean activity difference (univariate) and Euclidean distance (multivariate) between time-points.

This conceptual illustration presents an example of multi-voxel timecourses. In this illustration, a region consists of 16 voxels across time points 1 to 3, and their activities are represented by color and height. Across time, the mean activity of these voxels remains the same, but they have distinct patterns of activity. Multivariate functional connectivity is used to capture the timecourse of this multi-voxel activity pattern.

Multivariate distance correlation, a measure of multivariate dependency between two sets of variables, was recently introduced in the field of statistics (Székely et al., 2007), and a few studies have applied this measure to estimate fMRI connectivity (Geerligs et al., 2016, 2017). It offers a theoretical advantage over Pearson’s correlation in that it can handle inhomogeneity within nodes, whereas univariate approaches utilize the mean signal of nodes with inhomogeneous voxels. Previous work empirically showed that distance correlation better captures the relationship between regions comprised of more than one homogeneous subset of voxels (Geerligs et al., 2016), demonstrating higher reliability than univariate connectivity measured with Pearson’s correlation (Geerligs et al., 2016).

The following questions, however remain unanswered and are investigated in this study i) whether multivariate estimates of functional connectivity are consistently more reliable, ii) whether multivariate connectivity is more strongly predictive of behavior at the individual level, and iii) whether multivariate connectivity is more sensitive and specific to cognitive states. We first demonstrated the utility of multivariate functional connectivity in two ways using Human Connectome Project data: we assessed the identifiability of individuals’ multivariate functional connectivity patterns using a connectome fingerprinting approach (Finn et al., 2015), and then we used multivariate functional connectivity to predict an individual’s fluid intelligence using connectome-based predictive modeling (Finn et al., 2015; Rosenberg et al., 2016; Shen et al., 2017). In these analyses, we tested whether multivariate connectivity estimates outperform a standard univariate measure of functional connectivity, Pearson’s correlation (Finn et al., 2015; Noble et al., 2017b). We next assessed the test-retest reliability of multivariate connectivity using a dataset previously used to evaluate the reliability of functional connectivity estimated with Pearson’s correlation (Noble et al., 2017b). In doing so, we compared the edge-wise and connectome-wise reliability of multivariate and univariate connectivity calculated with varying amounts of resting-state fMRI data. Finally, we investigated the sensitivity and specificity of the multivariate connectome to the brain states manipulated by tasks and compared them with those of the univariate connectome. By doing so, we demonstrated that compared to univariate estimates, multivariate estimates of functional connectivity are more reliable, strongly predictive of behaviors, and sensitive to cognitive states. Thus, we propose that multivariate estimates may offer a more powerful, reliable measure of functional connectivity.

Methods

We used 2 independent fMRI datasets in the current study.

HCP dataset: Human Connectome Project’s S1200 release

Data were obtained from the S1200 release of the Human Connectome Project (HCP). The S1200 release originally contained 1113 individuals with nine fMRI scans (7 tasks [emotion, gambling, language, social, motor, working memory, and relational] and 2 rest scans over 2 days). Our analyses were limited to 563 subjects who completed all nine fMRI scans, exhibited low head motion in all task and resting fMRI runs (<3 mm translation, <3° rotation, and <0.15 mm mean frame-to-frame displacement), and had behavioral scores of fluid intelligence.

The length of the 9 fMRI scans ranged from 176 TRs (EMOTION) to 1,200 TRs (REST1 and REST2). We controlled for effects of scan duration by restricting all analyses to the first 160 volumes (≈2 min) of each run. This restriction allowed us to rule out the effects of scan length throughout this study.

Additional preprocessing steps were applied to the minimally preprocessed HCP data. The first 15 volumes of each scan were discarded, and then nuisance covariates were regressed from the data for each run using custom scripts in MATLAB R2016b. Nuisance covariates included 24 motion-related parameters (6 translational and rotational motions, 6 derivatives, and their squares), 3 mean signals (global, white matter and cerebro-spinal fluid), and linear and quadratic trends.

TRT dataset: Test-retest reliability cohort

Twelve healthy individuals (mean age = 40 years; range = 27–56 years; 6 female) with no history of any psychiatric illness were recruited to participate in a previous study (Noble et al. 2017b). All participants gave informed consent. Each individual underwent 4 fMRI sessions approximately one week apart (mean 9.4 days, SD 5.3 days), with all sessions completed within 1.5 months. Of 4 scanning sessions, 2 were completed on one scanner and 2 were completed on another in the same MRI facility. The order of scanner visits was counterbalanced across subjects. At each session, six 6-min resting-state functional runs were collected. In total, 144 min of data were obtained for each participant (4 sessions/participant × 6 runs/session × 6 min/run).

MR data were acquired on 2 identically configured 3T MR scanners (Siemens 3T Tim Trio system equipped with a 32-channel head coil) at Yale University (Noble et al. 2017b). High-resolution T1-weighted 3D anatomical, T1-weighted 3D anatomical, and functional images were acquired in this order. High-resolution anatomical scans were acquired using a magnetization prepared rapid gradient echo sequence with the following parameters: repetition time (TR) = 2400 ms, echo time (TE) = 1.18 ms, flip angle = 8°, acquisition matrix = 256 × 256, in-plane resolution = 1 mm × 1 mm, 208 slices in the sagittal plane, slice thickness = 1 mm. Next, T1-weighted scans were acquired using a fast low angle shot sequence with the following parameters: TR = 440 ms, TE = 2.61 ms, flip angle = 70°, acquisition matrix = 256 × 256, in-plane resolution = 2 mm × 2mm, 75 slices in the axial plane, slice thickness = 2 mm. Functional images were acquired in the same slice location as the axial T1-weighted scan using a multiband echo-planar imaging sequence with the following parameters: TR = 1000 ms, TE = 30 ms, flip angle = 55°, acquisition matrix =110 × 110, in-plane resolution = 2 mm × 2 mm, 75 slices in the axial plane, slice thickness = 2 mm. During functional scans, subjects were instructed to remain still while keeping their gaze on a fixation cross.

Functional images were preprocessed using Biolmage Suite (Joshi et al., 2011), with the exception of motion-correction, which was performed using SPM5. Preprocessing included motion-correction, iterative spatial smoothing, regression out of nuisance covariates, temporal smoothing with Gaussian filter, generation of group-specific template, and transformation of individual fMRI into the group template. Detailed information regarding preprocessing procedures is described in Noble et al. 2017b.

Functional connectome

Network nodes were defined with a 268-node whole-brain gray matter atlas covering the cortex, subcortex and cerebellum (Shen et al., 2013). Voxel-wise timecourses were extracted for each node and used to calculate functional connectivity matrices for each run. In this study, we used “univariate” and “multivariate” to refer to the number of variables (here timecourses) in each node. When voxel-wise timecourses were averaged to yield one representative timecourse for a node, we used “univariate”. When we used multiple voxel-wise timecourses, we used “multivariate”. The same usage of these terms can be found in previous work (Geerligs et al., 2016).

pCor: Univariate approach by Pearson’s correlation

Voxel-wise timecourses were averaged within each node. Pearson’s correlation between the mean timecourses of every pair of nodes was calculated as univariate functional connectivity. This provided a 268×268 full connectome matrix constructed using Pearson’s correlation (pCor).

dCor: Multivariate approach by multivariate distance correlation

Compared to Pearson’s correlation, which is a univariate measure of the linear dependency of two signals, multivariate distance correlation is a more general measure of the dependency of two sets of signals. Distance correlation (dCor) captures both linear and non-linear relationships (Székely et al., 2007). Throughout the paper, “distance correlation” refers to the multivariate version of distance correlation described here. One major difference between distance correlation and univariate measures, including Pearson’s correlation, is that distance correlation uses all voxel-wise timecourses within a node rather than averaging them. Note that distance correlation, like Pearson’s correlation, is insensitive to the order of time points.

To calculate the distance correlation between two regions, the regions must have the same number of time points but may have different numbers of voxels. For example, regions A and B had t time-points, and v_A and v_B voxels, respectively. First, each voxel’s timecourse was z-scored using its mean and variance. Then, the Euclidean distance between each pair of time points was computed for each region. The Euclidean distance, d_A:t1,t2 and d_B:t1,t2, between time points t1 and t2 of regions A and B is defined as follows:

$$d_{A:t1,t2}=\sqrt{{\sum }_{v=1}^{v_A}{(A_{v,t1}-A_{v,t2})}^2}\forall t1,t2=1,\dots ,t$$ (1)

$$d_{B:t1,t2}=\sqrt{{\sum }_{v=1}^{v_B}{(B_{v,t1}-B_{v,t2})}^2}\forall t1,t2=1,\dots ,t$$ (2)

U-centering is applied to set row and column means to zero.

$$D_{A:t1,t2}=\{\begin{array}{cc}{d}_{A:t1,t2}-\frac{1}{t-2}{\sum }_{p=1}^t{d}_{A:t1,p}-\frac{1}{t-2}{\sum }_{q=1}^t{d}_{A:q,t2}+\frac{1}{(t-1)(t-2)}{\sum }_{p,q=1}^t{d}_{A:q,p},\hfill & t1\ne t2\hfill \\ 0,\hfill & t1=t2\hfill \end{array}\phantom{\}}$$ (3)

The distance correlation, dCor, is then computed as follows:

$$\mathit{dCor}(A,B)=\{\begin{array}{cc}\sqrt{\mathit{dCov}(A,B)∕\sqrt{\mathit{dVar}(A)\mathit{dVar}(B)}},\hfill & \mathit{dCov}(A,B)>0\hfill \\ \hfill 0,\hfill & \mathit{dCov}(A,B)\le 0\hfill \end{array}\phantom{\}}$$ (4)

where dCov and dVar are distance covariance and distance variance respectively.

$$\mathit{dCov}(A,B)={}^1∕_{t(t-3)}{\sum }_{t1,t2=1}^t{D}_{A:t1,t2}{D}_{B:t1,t2}$$ (5)

$$\mathit{dVar}(A)={}^1∕_{t(t-3)}{\sum }_{t1,t2=1}^t{D}_{A:t1,t2}^2$$ (6)

dCor was calculated for every pair of regions in the 268-node atlas, generating a whole-brain dCor matrix. In the current study, all datasets include more than one fMRI run for every individual. Hence, a full matrix of dCor and a full matrix of pCor were constructed for each run and averaged across runs. In the HCP sample, one connectivity matrix was constructed for each of two runs with different phase encoding directions (L-R and R-L) of the same state (e.g., REST1), and the two matrices with different phase encoding directions were averaged to generate one connectivity matrix for the state.

To investigate the relationship between univariate and multivariate functional connectivity patterns, we assessed the spatial similarity of participants’ dCor and pCor. Similarity was quantified using Pearson’s spatial correlation between the 35,778 edges of dCor and 35,778 edges of pCor (i.e., the edge values in the lower triangular of the matrices).

With in-subject similarity of multivariate distance correlation (HCP dataset)

We first investigated within- and between-subject similarity of the whole-brain functional connectome using two resting runs, REST1 and REST2, in the HCP sample. Within-subject similarity was assessed as the Pearson’s spatial correlation between each participant’s dCor calculated from REST1 data and dCor calculated from REST2 data. Between-subject similarity was assessed with the Pearson’s spatial correlation between every pair of 563 participants for each of REST1 and REST2.

Utility of the whole-brain connectome constructed with multivariate distance correlation (HCP dataset)

Fingerprinting for identification

Connectome-based fingerprinting analysis (Finn et al., 2015) was performed to assess the reliability and distinctiveness of whole-brain connectivity matrices measured with dCor. Fingerprinting analysis, which aims to distinguish a participant from a group of individuals based on his or her unique functional connectivity pattern, was applied to every pair of rest and task scans in the HCP sample. Fingerprinting analysis requires two functional connectivity matrices from each individual: one to serve as the ‘target’ and the other to serve as the ‘database’.

An individual is considered successfully identified if their target matrix is more similar to their own database matrix than to the database matrix of every other participant in the sample. In other words, participant i is considered successfully identified if

$$r_{\mathit{ii}}>r_{\mathit{ij}},\forall \text{subject}j\ne i$$

where r_ij is Pearson’s spatial correlation between participant i’s connectome in one data pool (target) and subject j’s connectome in the other pool (database).

Fingerprinting accuracy was measured with identification success rate as follows:

$$\frac{\text{The number of individuals successfully identified}}{\text{The total number of individuals}(=563)}\times 100$$

Identification success rate was computed twice for each pair of scans with the opposite target-database pairs.

Predicting individual fluid intelligence

A second test of utility was to use CPM to predict individual differences in fluid intelligence (Finn et al., 2015; Shen et al., 2017). For dCor to be a useful measure of functional brain organization, it should capture individual differences in cognitive abilities such as fluid intelligence.

The goal of CPM is to predict individual differences in behavior from whole-brain connectomes. In this study, two different connectomes, a matrix of dCor and a matrix of pCor, were used to construct two different CPMs for predicting individuals’ fluid intelligence scores. We tested a range of fMRI scan lengths (160, 300, and 500 TRs) in building CPM models. Since the inclusion of related individuals across the training and testing sets could inflate prediction accuracy, we additionally excluded subjects only for this prediction analysis. From each family, all but one member were randomly selected and excluded. This procedure resulted in 316 unrelated individuals, reduced from 563 individuals. CPM models were trained and tested using 10-fold cross-validation. Predictive models were trained on 9 folds of the data (90% or 284-285 subjects) and tested in the left-out fold (10% or 31-participants32 participants) iteratively for all 10 folds. Then, model performance was assessed by correlating predicted and observed fluid intelligence. This 10-fold validation procedure was performed 5,000 times with random assignment of the 316 individuals into 10 folds to provide reliable statistics for model performance. To evaluate whether predictive power significantly differed between dCor-based and pCor-based models, we obtained a distribution of the prediction difference between dCor-based and pCor-based models from the 5,000 permutations. We compared this distribution with 0, which corresponds to the null hypothesis that there is no difference in predictive power (significance defined as p < 0.01). We further validated the significance of the difference in predictive power by using the corrected repeated k-fold cross-validation test (Bouckaert and Frank, 2004)

Test-retest reliability analysis (TRT dataset)

Edge-wise reliability

Using our TRT dataset, we examined edge-wise test-retest reliability of participants’ dCor values using the generalizability theory framework. This framework was previously adopted to assess the test-retest reliability of functional connectivity (Forsyth et al., 2014; Gee et al., 2015; Noble et al., 2017a, 2017b). To estimate reliability, variance components were first estimated for all factors with a 3-way ANOVA model. Factors were the “object” of measurement (here, people), “facets” of measurement (here, sessions and runs) and their interactions, and modeled as random to maximize generalizability. Then, the residual component contains variance due to the 3-way interaction and residual error. In estimating variances, any negative variance components were set to 0, as in previous work (Noble et al., 2017b). The model of variance is as follows,

$${\sigma }^2={{\sigma }_p}^2+{{\sigma }_s}^2+{{\sigma }_r}^2+{{\sigma }_{\mathit{ps}}}^2+{{\sigma }_{\mathit{pr}}}^2+{{\sigma }_{\mathit{sr}}}^2+{{\sigma }_{\mathrm{psr},e}}^2$$ (7)

where p is person, s is session, r is run, and e is residual.

Test-retest reliability was then estimated using the estimated variance components. Here, we computed a dependability coefficient, representing the absolute agreement of measurements. The dependability coefficient is a form of the intraclass correlation coefficient (Shrout and Fleiss, 1979) that reflects a (marginal) measurement error model. The dependability coefficient (Φ_u) was calculated for each edge as follows,

$${\Phi }_u(e)=\frac{{{\sigma }_p}^2(e)}{{{\sigma }_p}^2(e)+\frac{{{\sigma }_s}^2(e)}{n_s}+\frac{{{\sigma }_r}^2(e)}{n_r}+\frac{{{\sigma }_{\mathit{ps}}}^2(e)}{n_s}+\frac{{{\sigma }_{\mathit{pr}}}^2(e)}{n_r}+\frac{{{\sigma }_{\mathit{sr}}}^2(e)}{n_s\ast n_r}+\frac{{{\sigma }_{\mathit{psr},e}}^2(e)}{n_s\ast n_r}}$$ (8)

where e represents a single edge and n is the number of conditions of the facet used for an average measurement. Φ_u can range from 0 to 1 and can be interpreted as follows: poor for <0.4, fair for 0.4–0.59, good for 0.60–0.74, and excellent for >0.74 (Cicchetti and Sparrow, 1981). Mean Φ_u across all edges was used to summarize all edges. Note that the treatment of facets as possibly similar across subjects yet randomly selected from a larger population makes this Φ_u of the form intraclass correlation coefficient (2,1) (cf. Webb et al., 2006).

This formulation enables the construction of a decision study. A decision matrix can be used to determine a combination of measurements from each facet of measurement to achieve the desired level of test-retest reliability. The decision matrix was acquired by calculating Φ_u with varying n_p, n_s, and n_r. Increasing n in the calculation of the Φ_u is akin to assessing the test-retest reliability of connectivity matrices averaged over multiple sessions or runs. For example, Φ_UV obtained from n_s = 1 and n_r = 1 is the projected edge-wise test-retest reliability of the connectivity obtained from a single 6-min run, whereas Φ_u obtained from n_s = 5 and n_r = 4 is the projected reliability of the connectivity obtained from the average of matrices over five sessions of four 6-min runs (5 sessions of 24 min/session).

Connectome-wise reliability

We next investigated the reliability of individuals’ whole-brain functional connectivity patterns. To assess connectome-wise test–retest reliability, a single reliability coefficient was calculated as described by Shou et al. (2013) as follows,

$${\Phi }_m=\frac{{\sum }_e{{\sigma }_p}^2(e)}{{\sum }_e\left({{\sigma }_p}^2(e)+\frac{{{\sigma }_s}^2(e)}{n_s}+\frac{{{\sigma }_r}^2(e)}{n_r}+\frac{{{\sigma }_{\mathit{ps}}}^2(e)}{n_s}+\frac{{{\sigma }_{\mathit{pr}}}^2(e)}{n_r}+\frac{{{\sigma }_{\mathit{sr}}}^2(e)}{n_s\ast n_r}+\frac{{{\sigma }_{\mathrm{psr},e}}^2(e)}{n_s\ast n_r}\right)}$$ (9)

In accordance with Shou et al. (2013), the image intraclass correlation coefficient approach represents an image measurement error model because these combined variance components reflect the true overall image variance.

Connectome-based Discriminability

Discriminability was assessed by the identification rate and the perfect separation rate (cf. Noble et al., 2017b). The connectivity matrix was calculated for each run, and then matrices of runs within a session were averaged. Therefore, in calculating the identification rate and the perfect separation rate, each subject had a total of four matrices, one for each session. The identification rate and the perfect separation rate were calculated 6 times to assess the effect of data amount (1, 2, 3, 4, 5, and 6 six-min runs).

In this identification analysis, each of the 48 sessions (12 subjects of 4 sessions/subject) served as a ‘target’ while the other 47 sessions served as a ‘database’. If a ‘target’ session had maximum correlation with a matrix from the same subject, then the ‘target’ was considered successfully identified. The identification rate was calculated as follows,

$$\frac{\text{The number of individuals successfully identified}}{\text{The total number of individuals}(=48)}\times 100$$

The perfect separation rate describes whether all within-subject correlations exceeded all between-subject correlations. Again, each of the 48 sessions was used as the ‘target’. For each ‘target’ session, if all three correlations between the ‘target’ and the three sessions’ matrices from the same subject exceeded all correlations between the ‘target’ and the other 44 sessions’ matrices in ‘database’, then the ‘target’ session was considered successfully separated. Then the perfect separation rate was calculated as follows,

$$\frac{\text{The number of individuals successfully separated}}{\text{The total number of individuals}(=48)}\times 100$$

Sensitivity and specificity of multivariate functional connectivity to task-defined brain states (HCP dataset)

We next investigated the sensitivity of dCor to different brain states defined by 7 tasks in HCP dataset. Two resting connectomes from REST 1 and REST2 were first averaged to represent one resting connectome for each subject. Then, all individual edges from each of the seven tasks were compared to all edges in resting state using a paired t-test. A range of statistical thresholds (p-value of 1×10⁻³ to 1×10⁻⁷ without correction) was applied here to minimize arbitrary selection of thresholds. Once the edge-wise significance of the difference between one of the seven tasks and the rest was determined under a selected p-value threshold, a binary matrix was created with ‘one’ representing a significant difference and ‘zero’ representing no difference for each task, resulting in seven binary matrices. Then, the seven binary matrices were summed to provide one integrative matrix with integer weights ranging from zero to seven, yielding the number of tasks in which each edge was significantly modulated from the resting state.

We also tested the sensitivity of dCor to each brain state by counting the number of edges exhibiting a statistically significant difference in each state compared to the resting state (p=0.05, Bonferroni corrected. This corresponds to p≈1.4×10⁻⁶ without correction) and compared with the sensitivity of pCor.

Modularity analysis (HCP dataset)

Finally, we investigated the modular structure of the whole-brain connectome constructed using dCor. Community detection was used to determine the optimal modular structure of a dCor matrix by clustering nodes into non-overlapping communities that maximize within-module functional connectivity and minimize between-module connectivity. The Louvain method implemented in the Brain Connectivity Toolbox was used to detect community partition of a dCor matrix. In this analysis, we used a range of sparseness (for every 2% from 4% to 30%) in thresholding the connectivity matrix. The results from the 15% sparsity matrix were presented as representative since similar results were obtained across the range of sparsity. We then investigated how dCor’s modular structure differs from pCor’s modular structure by estimating the quantitative overlap between modules from dCor and from pCor. For each module from dCor, we estimated the ratio of the number of nodes in common with each module from pCor to the total number of nodes in the dCor module.

Results

Whole-brain univariate and multivariate functional connectivity

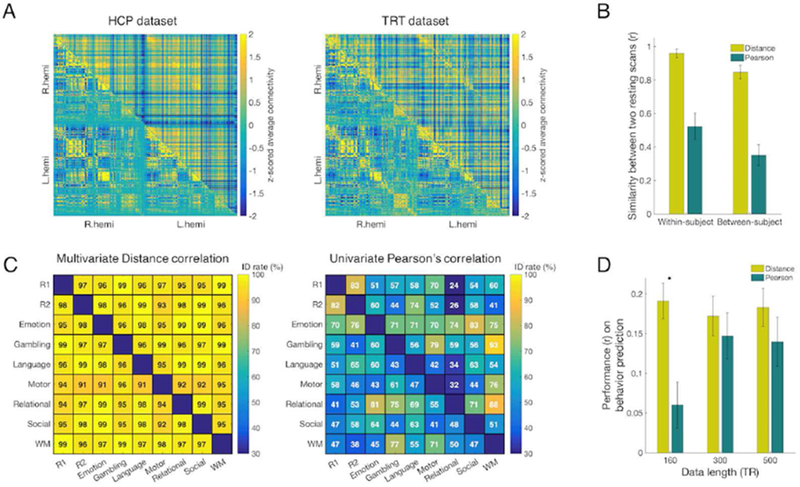
The average resting-state connectomes constructed with distance correlation (dCor) and Pearson’s correlation (pCor) are presented in Figure 2A. Although the overall pattern of dCor is distinct from that of pCor, they were statistically similar with a spatial correlation of r = .201 in the HCP sample and r = .250 in the TRT sample (p < 1×10⁻⁵ for both, group average). Within-subject similarity between the two connectomes was, on average, r = .148 (s.d. = .035) in HCP and r = .217 (s.d. = .029) in TRT.

Figure 2. The whole-brain functional connectome shows both similar and distinct features across multivariate and univariate connectivity estimates.

A) Left: Group-averaged resting-state connectomes constructed by multivariate distance correlation (upper triangle) and by Pearson’s correlation (lower triangle) in the Human Connectome Project (HCP) dataset. Connectomes were first constructed for each run for each subject, and then averaged across runs and subjects to generate the group average. Right: The same resting-state connectome in the test-retest (TRT) dataset. B) Within- and between-subject similarity in the HCP set. All similarity values (error bar=standard deviation) assessed with Pearson’s spatial correlation are significant (p < 1×10⁻⁵). Similarity via multivariate connectivity is significantly different than and similarity via univariate connectivity (p < 1×10⁻⁵). Between-subject similarity was estimated twice, once for each of the two resting scans, and then averaged. C) Identification with connectome fingerprinting in the HCP dataset. In each matrix plot, the lower triangular and upper triangular represent opposite directions of a ‘target’-‘database’ pair. Since two directions of a ‘target’-‘database’ pair give different identification results, the identification success rate matrices are asymmetric. Distance correlation connectomes provided identification success rates of 96.6% and 97.5% between two resting scans. In comparison, Pearson’s correlation connectomes gave identification success rates of 83.3% and 81.5% between the same two resting scans. Across all pairs of brain states, the identification success rates of distance correlation ranged from 91% to 99%, whereas the identification success rates of Pearson’s correlation ranged from ~30% to 93%. For every pair of fMRI scans, connectomes constructed using distance correlation (left) showed higher identification success rates than connectomes generated with Pearson’s correlation (right). R1 and R2 represent the 1^st and the 2^nd resting scans, respectively. WM represents the working memory task scan. This analysis was performed within the HCP sample. D) Prediction of individual fluid intelligence using different fMRI scan lengths (160, 300, 500 TRs) in the HCP dataset. CPM models were built using multivariate or univariate connectivity. Model performance is assessed as the Pearson correlation between predicted and observed fluid intelligence scores. Error bar represents standard deviation from 5,000 iterations of randomly assigned 10-fold cross validation. (*significant difference with p<0.01)

With in-subject similarity of resting-state functional connectivity

Within-subject similarity between each HCP participant’s two resting scans was estimated. dCor showed significantly higher within-subject similarity (Figure 2B) and also had higher between-subject similarity. Within- and between-subject similarity values among different brain states (two rest runs and seven task runs) are provided in Supplementary Figure S1, S2.

Identification with connectome fingerprinting

As the first utility test of our novel multivariate functional connectivity measure, identification via connectome-based fingerprinting was performed. Fingerprinting was applied between every pair of nine scans (two rest and seven task). Between the two resting scans, dCor achieved a higher identification rate than pCor (Figure 2C). Across all pairs of fMRI states, dCor also provided a higher identification rate than pCor.

Connectome-based prediction of fluid intelligence

As a second test of the utility of dCor as a multivariate functional connectivity measure, we used dCor to predict individual differences in fluid intelligence with connectome-based predictive modeling (CPM). When applied to a small amount (160 TRs) of data, a CPM model based on dCor was significantly better at predicting individual differences in fluid intelligence than a model based on pCor (Figure 2D, Supplementary Figure S3; p < 0.01 with 5,000 permutations). This significance was also confirmed with a corrected repeated k-fold cross-validation test (p < 0.01). For longer periods of data, there was no significant difference betewen dCor and pCor models. The predictive power of CPM models with different feature selection thresholds and with combined features of multivariate and univariate estimates are provided in Supplementary Figure S4.

Test-retest reliability of connectivity measures

Edge-wise test-retest reliability

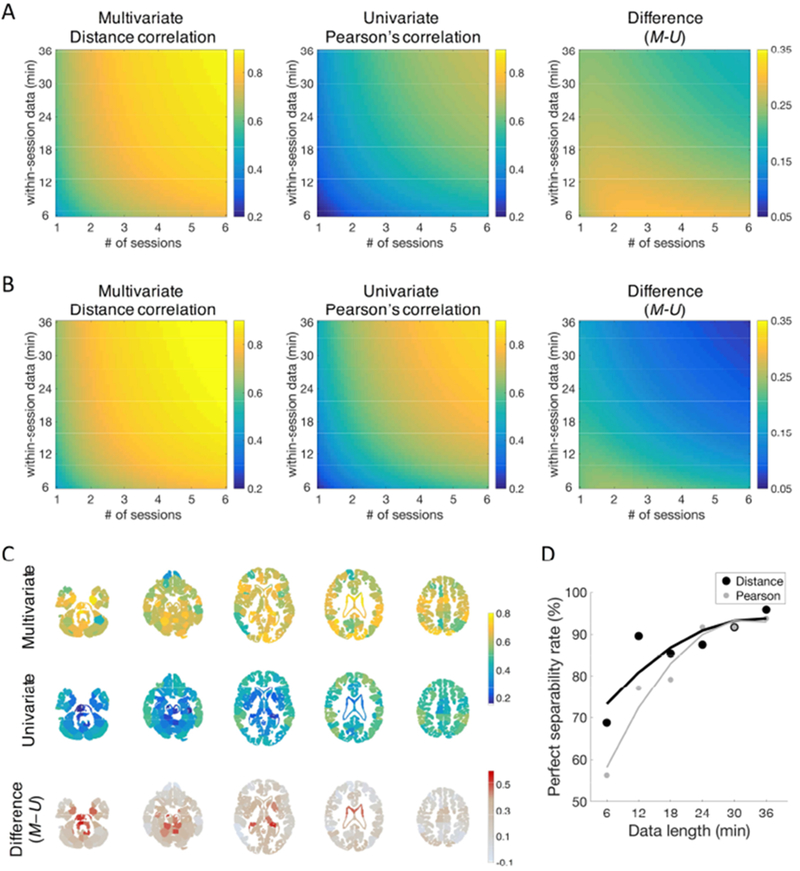
For a single session 6 min in length, edge-wise test-retest reliability of dCor across all edges was shown to be fair (Φ_u = 0.43 ± 0.13, Figure 3A). In comparison, test-retest reliability of pCor was poor (Φ_u = 0.18 ± 0.13). Compared to the variance components from pCor, a larger contribution of the person component (43.1% versus 18.3%) and smaller contribution of the residual (35.2% versus 66.2%) were obtained when using dCor (Supplementary Table S1, Figure S5). Similar to pCor, all other variance components from dCor were relatively small (<2%) except the person by session interaction (16.3%).

Figure 3. Test-retest reliability of distance and Pearson’s correlation.

Test–retest reliability is categorized as follows: poor < 0.4, fair = 0.4–0.59, good = 0.6–0.74, excellent ≥ 0.74 (Cicchetti and Sparrow, 1981). A) Edge-wise test-retest reliability of distance and Pearson’s correlation. Absolute reliability (Φ_u) was estimated as a function of length of scan and number of sessions. Distance correlation (left) achieved fair test-retest reliability with a single 6-min session, whereas Pearson’s correlation (middle) provided poor reliability for the same amount of data. The difference between these maps (right) is higher with lower amounts of data. Excellent test-retest reliability is obtained only by distance correlation (e.g., at five 6-min sessions). B) Connectome-wise test-retest reliability of distance and Pearson’s correlation. Connectome-wise absolute test-retest reliability (Φ) was estimated as a function of length of scan and number of sessions. Distance correlation (left) exhibited excellent test-retest reliability with four 6-min sessions, whereas Pearson’s correlation (middle) provided excellent reliability with longer data, four 22-min sessions The difference between these maps (right) is higher with lower amounts of data. In distance correlation, excellent test-retest reliability is obtained with four 6-min sessions, whereas Pearson’s correlation exhibits excellent reliability with four 22-min sessions. C) Edge-wise test-retest reliability of edges organized by nodes. Test-retest reliability (Φ_u) of connectivity was averaged within each node. For each node, the mean test–retest reliability of all edges of the node was calculated for a single 36-min session. In distance correlation (top), subcortical nodes exhibited comparable test-retest reliability to cortical nodes, whereas in Pearson’s correlation (middle) cortical nodes exhibited higher reliability than subcortical nodes. Difference between distance and Pearson’s correlation (bottom) is most distinctive in subcortical areas. D) Perfect separation rates with different scan length in TRT dataset. The perfect separation rate measures whether, for each reference scan, all within-subject correlations exceed all between-subject correlations. Two rigid lines represent fitted curves, one for the perfect separation rate of distance correlation (black) and another for that of Pearson’s correlation (gray). The fitted curve shows that distance correlation’s separation rate is higher than Pearson’s rate.

A Decision Study map was estimated using test-retest reliability for different combinations of sessions and runs (Figure 3A). This map represents the influence of data quantity on test-retest reliability. Compared to pCor, which does not achieve excellent (≥0.74) test-retest reliability within this map, using dCor provides excellent reliability with various combinations of measurements, including five 6-min sessions. The reliability difference between the two correlation measures was larger when the amount of data was small, especially within a single session. The difference between the two correlation measures became smaller as more data were acquired.

Node-wise reliability of dCor showed a pattern distinct from that of pCor (Figure 3C). First, overall reliability of dCor was higher than that of pCor. Second, reliability for dCor in subcortical areas was comparable to cortical areas, whereas reliability for pCor in subcortical areas was lower than cortical areas.

Connectome-wise test-retest reliability

The Decision Study map for connectome-wise test-retest reliability is shown in Figure 3B. For a single 6-min session, connectome-wise test-retest reliability of dCor was higher than overall edge-wise reliability, but still shown to be fair (Φ_m = 0.45). Across all combinations of numbers of sessions and runs, dCor’s reliability was consistently higher than its overall edge-wise reliability, but the differences were small (mean = 0.027, s.d. = 0.003, min. = 0.017, max. = 0.033). In dCor, excellent connectome-wise test-retest reliability could be obtained with four 6-min sessions, whereas excellent pCor reliability needed four 22-min sessions, connectome-wise reliability of dCor was higher than that of pCor across all the combinations of numbers of sessions and runs. However, the differences between dCor’s and pCor’s connectome-wise reliabilities were smaller compared to the differences in their edge-wise reliability values.

Connectome-based discriminability

The identification rate with dCor was perfect (100%), even with 6 min of data from one scan, whereas 8.3% of cases were still misidentified when using pCor with 6 min of data (Table 1). The perfect separation rate with dCor was 69% with 6 min of data from one scan and increased to 96% with all of 36 min from six scans in a session (Figure 3D). The fitted curve shows that dCor’s separation rate is higher than pCor’s rate across scan lengths with converging at longer scan.

Table 1.

Identification success rates (%) in the TRT dataset with different amounts of data.

Scan length (min)	6	12	18	24	30	36
Distance correlation	100	100	100	100	100	100
Pearson’s correlation	91.7	100	100	100	100	100

Sensitivity and specificity of multivariate connectivity to task-defined brain states

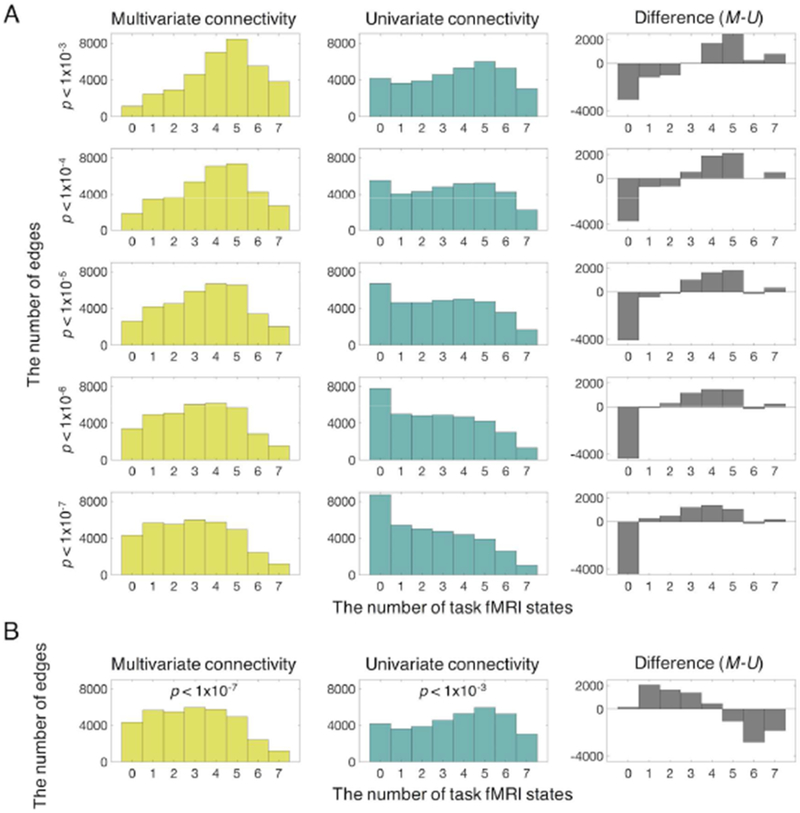
By comparing task-manipulated and resting-state connectivity, we found that dCor shows a larger number of edges modulated by task compared to pCor (Figure 4A, Supplementary Figure S6). In other words, dCor was more sensitive to ongoing cognitive state. Across a range of statistical thresholds, dCor consistently exhibited higher sensitivity compared to pCor. In addition, dCor shows higher sensitivity to 5 of 7 states (Emotion, Language, Motor, Relational, and Social), while univariate estimate shows higher sensitivity to 2 states, Gambling and Working Memory (p < 0.05, Bonferroni corrected). In summary, dCor is more sensitive than pCor to the majority of states measured by HCP tasks, but not every state.

Figure 4. Edges involved in different numbers of brain states.

All individual edges from each of seven tasks were statistically compared to all edges in resting state, and counts are provided for the number of tasks in which each edge is significantly modulated from resting state. A) Given the same statistical threshold, distance correlation exhibited a larger number of edges modulated by task compared to Pearson’s correlation, and Pearson’s correlation had a larger number of edges unchanged in all of tasks, suggesting that distance correlation is more sensitive to ongoing cognitive state. B) The left bar graph (yellow) represents results from distance correlation (p = 1×10⁻⁷) and the middle bar graph (bluish green) shows results from Pearson’s correlation (p = 0.001). Given similar numbers of edges that were not modulated by any task between distance and Pearson’s correlation, distance and Pearson’s correlation shows distinct involvement of their edges in multiple tasks (gray). A larger number of edges defined by distance correlation were involved in the smaller number of tasks (1~3 tasks), showing specificity. In contrast, a larger number of edges defined by Pearson’s correlation were modulated by the majority of tasks (5~7 tasks), showing generality.

By matching the number of edges that remained unchanged across 7 tasks, (Figure 4B, e.g., dCor threshold: p < 1×10⁻⁷; pCor threshold: p < 1×10⁻³), we could estimate the ratio of edges modulated by different numbers of tasks to all significantly changed edges, representing task-specificity and task-generality. More edges defined by dCor were involved in fewer tasks (1~3), showing specificity (Figure 4B). In contrast, more edges defined by pCor were modulated by the majority of tasks (5~7 tasks), showing generality.

Distinct modular structure of the whole-brain connectome from multivariate connectivity estimates

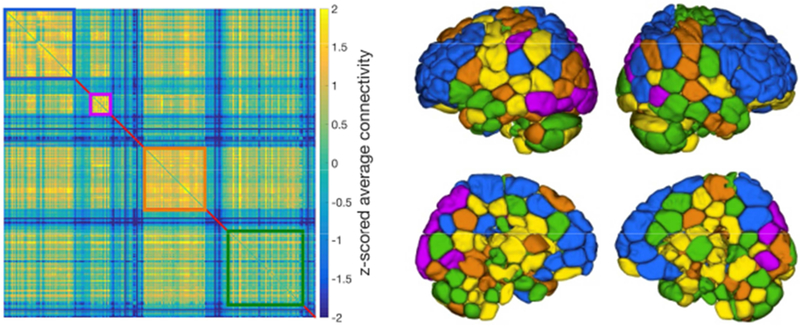
Four modules were uncovered from dCor. Subnetworks of modules are shown in Figure 5. The community structure of dCor was distinct from that of pCor, which better reflects well known traditional resting-state networks (Supplementary Figure S7). Using dCor, we found one module that consists of fronto-parietal regions as well as regions of the default mode network (a module in blue in Figure 5). Another module included visual areas and a region in left parietal cortex (a module in purple in Figure 5). The other two modules were comprised of distributed regions across the cortex, subcortex and cerebellum (two modules in orange and green in Figure 5). Some subcortical and periventricular regions did not form in any cluster (regions in yellow in Figure 5). Quantitative overlap between dCor-based modules and pCor-based modules is provided in Supplementary Table S2.

Figure 5. Subnetwork of modules in the whole brain connectome constructed using distance correlation.

Optimal structure with 4 modules was obtained by Louvain community detection methods on 15% sparsity, weighted matrix. A module of regions in blue consists of fronto-parietal regions and default mode network regions. Another module in purple consists of visual areas and left parietal cortex. The other two modules in orange and green contain distributed regions across cortex, subcortex and cerebellum. Yellow depicts regions not included in any of 4 modules.

Discussion

In this study, we examined whether a multivariate measure of similarity, which preserves voxel-level information, could be used to improve estimates of brain functional connectivity. We assessed the reliability of multivariate functional connectivity measured with distance correlation, and confirmed that, at both the edge- and connectome-wise level, multivariate connectivity is more reliable than traditional univariate connectivity estimated with Pearson’s correlation. Fingerprinting analysis revealed that an individual’s multivariate connectome was more stable over time and more distinct from the group. Moreover, multivariate connectivity patterns were more reliably modulated by task states, and models based on multivariate functional connectivity better predicted individual differences in fluid intelligence. Our findings suggest that multivariate dependency is a sensitive and reliable measure of functional connectivity, providing more powerful information about an individual’s unique functional brain organization, ongoing cognitive processes, and cognitive abilities.

Multivariate estimates improve the reliability of functional connectivity measurements

Multivariate functional connectivity achieved not only high edge-wise reliability, but also high connectome-wise reliability. Using a decision study, we demonstrated that the multivariate connectome is more reliable than the univariate connectome, when calculated with anywhere from 6 to 216 min of resting-state data, at both the edge-level and the full connectome-level. Overall, edge-wise reliability of multivariate estimates was high, producing excellent reliability with ~30 min of data (5 sessions × 6 min/session), whereas univariate estimates did not yield excellent reliability within protocol, even with over 3.5 hours of data (6 sessions × 36 min/session). Previous studies using univariate estimates have shown similarly that individual resting-state functional connections have low reliability, and do not reach to a good reliability with 30 minutes of fMRI data (Noble et al., 2017b; Pannunzi et al., 2017). Given the importance of replicability in scientific research (Baker, 2016) including neuroimaging studies (Poldrack et al., 2017), the high test-retest reliability of multivariate functional connectivity is a significant benefit.

Fair reliability from a small amount of data: the conventional 5-min resting-state scan

The difference in reliability between multivariate and univariate functional connectivity estimates was more pronounced at shorter scan lengths, demonstrating that multivariate estimates are more robust to scan length limitations. In fact, many studies use a conventional 5-min resting-state fMRI scan; at this duration univariate connectivity has poor edge-wise reliability (Noble et al., 2017b; Pannunzi et al., 2017). In contrast, individual multivariate connections have fair edge-wise reliability when calculated with the same amount of data. The dramatic reduction in the amount of data required to achieve fair to excellent reliability with multivariate compared to univariate functional connectivity suggests that multivariate connectivity may be superior for both practical and clinical applications.

Reliable estimation of subcortical connectivity

It is also worth noting that subcortical connectivity is estimated more reliably with multivariate than with univariate connectivity measures. We found that the anatomical profile of multivariate estimate’s reliability was distinct from that obtained with univariate estimates (Figure 3C). Although previous studies using univariate connectivity estimates have consistently reported that subcortical connectivity is much less reliable than other regions (Noble et al., 2017b), multivariate connectivity estimates produced highly reliable subcortical connections. Researchers have attributed this low reliability of subcortical areas to their small size and anatomical location, which cause low signal-to-noise ratio (Noble et al., 2017b; Shah et al., 2016). However, we found that using the voxels’ signals within subcortical nodes improves the reliability of subcortical connectivity estimates.

Better discrimination of individuals

Using a connectome fingerprinting approach, we found that an individual’s multivariate functional connectome is more identifiable—that is, more distinct and consistent across scans—than their univariate functional connectome. In the HCP dataset, multivariate functional connectivity patterns could identify individuals with a high success rate (mean identification rate between scan pairs = 97%) even with very short scan periods (160 TRs, Figure 2B). In contrast, univariate estimates showed much lower identification rates (58%), similar to previous reports (Finn et al., 2017, 2015). Given that multivariate connectivity patterns show higher between-subject similarity than univariate connectivity patterns, our finding of high discriminability from multivariate estimate is somewhat surprising. Individual identification could be credited to the high reliability of multivariate functional connectivity estimates, which, in turn, is reflected in high within-subject similarity. Importantly, however, the observed identification results depend on interactions between both within- and between-subject similarity. That is, while within-subject similarity increases individual identifiability, between-subject similarity reduces it. In our data, variation of within- and between-subject similarity by multivariate estimates was consistently smaller than that by univariate (mean deviation = 0.01 versus 0.04, Supplementary Figure S1, S2), indicating more robust differences between within- and between-subject similarity across pairs of subjects. This also partially explains the high reliability of the multivariate connectome, leading to its powerful identification rates.

Variance in multivariate connectivity is explained by individual differences

Test-retest reliability analyses of the Noble et al. (2017b) dataset support the finding that multivariate connectivity estimates improve individual discrimination. In particular, these results demonstrate that a larger proportion of inter-individual variance (“Person” factor) is explained by multivariate than univariate functional connectivity patterns (43% vs. 18%). In addition, residual variance was 35% in the multivariate estimate, whereas it was 66% in the univariate estimate (Noble et al. 2017b), resulting in 31% points lower residual variance in the multivariate estimate. Thus, differences in the amount of variance and residual explained by individual differences likely contribute to the high individual discriminability of the multivariate connectome.

Multivariate functional connectivity better predicts fluid intelligence

Using a CPM approach (Finn et al. 2015; Rosenberg et al. 2016; Shen et al. 2017), we demonstrated that multivariate connectivity estimates better predict individuals’ fluid intelligence than univariate connectivity estimates. In our previous work using three univariate connectivity measures—Pearson’s correlation, accordance, and discordance—to predict individual differences in attention, all three models showed similar predictive power and none consistently outperformed the others (Yoo et al. 2018). However, in the present study, functional connectivity estimated with distance correlation provides better predictions of fluid intelligence than functional connectivity estimated with Pearson’s correlation. Distance correlation differs from Pearson’s correlation in two ways: first, it is a multivariate measure, and second, it captures nonlinear associations between a pair of variables (Székely and Rizzo, 2009). Therefore, our results indicate that multivariate relationships between voxel-wise activity patterns may index individual differences in cognitive abilities.

Sensitivity and specificity to ongoing task context: intra-individual differences

Multivariate functional connectivity is more sensitive to cognitive state

Our results suggest that multivariate functional connectivity is more sensitive to task context than univariate functional connectivity. Across liberal to conservative statistical thresholds, more multivariate than univariate functional connections were modulated by cognitive states (rest and 7 unique tasks). Together with the high within-subject similarity of the multivariate connectome across rest and task engagement, our finding that multivariate connectivity is highly context-dependent may indicate the existence of a small but consistent effect of task state across individuals.

Despite the accumulating evidence that patterns of functional connectivity may serve as reliable personalized markers of individuals’ symptoms and behavior, connectome-based predictive models have not yet been applied in patient care settings. One potential reason may be that the degree to which functional connectivity patterns represent stable traits versus transient states remains unclear. That is, if an individual’s functional connectome is overly rigid and does not flexibly reflect changes in mental states, behavior, or symptoms, connectome-based models may be of little practical or clinical value. Rather, models will be most useful if they are based on features that are both reliable (i.e., stable) and sensitive to changes in context and behavior (i.e., flexible).

Flexibility can describe both long-term changes, such as aging or transitions between healthy and disease states, and short-term changes, such as fluctuations in ongoing cognitive processing. Although the majority of published studies focus on longer-term connectivity changes, recent work has begun to examine the reliability of connectivity measures within single subjects and their sensitivity to relatively short-term fluctuations in cognitive state and ongoing task context. This is under debate; some studies suggest that functional connectivity is flexible and dynamic, mirroring ongoing mental states (Calhoun et al., 2014; Shine et al., 2016), while other studies claim that functional connectivity measures are not able to sensitively track the fast transition of brain states (Gratton et al., 2018; Laumann et al., 2017).

The sensitivity and flexibility of the functional connectome to brain states may have been limited by univariate estimates of connectivity that average voxel-wise signals within a region, diluting the detailed information distributed across the voxels. Thus, mirroring the success of multivariate approaches to extract meaningful information from spatial patterns of voxel-wise activity to decode different task states (Haynes and Rees, 2005), we demonstrate that multivariate estimates of connectivity can also incorporate spatially distributed information and may therefore show greater sensitivity to distinct brain states within single individuals.

Multivariate functional connectivity has higher specificity to ongoing brain states

Although previous work has investigated the reliability of functional connectivity patterns and their sensitivity to cognitive state, the specificity of functional connectivity strength has received less attention. Here we demonstrated that multivariate functional connections are more state-specific than univariate functional connections. Whereas multivariate connections exhibit task-specificity, univariate connections exhibit generality. Our results are consistent with previous work showing that univariate functional connectivity patterns are mainly non-specific to different brain states, revealing a task-general pattern of connectivity during task engagement (Cole et al., 2014; Gratton et al., 2018, 2016). Functional connectivity requires specificity to differentially represent ongoing task contexts or transient cognitive states (e.g., dynamic connectivity). To the best of our knowledge, this study was the first to investigate the specificity of multivariate functional connectivity, demonstrating that multivariate estimates offer greater brain-state specificity than univariate estimates.

Community structure of multivariate connectivity

We found that the community organization of multivariate connectivity features differs from that of univariate connectivity features. Although the multivariate connectivity occipital module has 88.2% of its nodes in common with univariate occipital module (Supplementary Table S2), other multivariate connectivity modules include regions that are distributed across different univariate modules. For example, multivariate connectivity yields a module including both fronto-parietal and default mode network regions (blue in Figure 5). In contrast, as observed previously (Fox et al., 2006, 2005), fronto-parietal and default mode regions compose two separate, anticorrelated modules in the univariate connectome (Supplementary Figure S7). The origin of these differences in community structure, however, remains unclear. Future work should address whether differences in community composition originate from the multivariate nature of regional interactions, or whether they are a consequence of (the lack of) negative correlations since distance correlation provides only positive values and 0.

Further considerations

The primary advantage of multivariate connectivity over univariate connectivity is that it appears to be more robust to smaller amounts of data. Univariate approaches likely require longer data acquisition because they inevitably blur fMRI signals by spatial averaging in each node, resulting in the loss of information (Gardumi et al., 2016; Schaefer et al., 2018). One limitation however, is that multivariate connectivity’s prediction performance levels off with increasing data. The reasons for this are unclear, but it is possible that because multivariate approaches deal with single voxels, requiring one-to-one correspondence across the time domain, they may be more vulnerable to noise such as head motion (Coutanche and Thompson-Schill, 2012; Gardumi et al., 2016). Nevertheless, multivariate connectivity was more reliable than univariate connectivity at all data lengths tested in this study. An additional disadvantage or limitation of distance correlation is that, like Pearson’s correlation, it is insensitive to the order of time points. This means that distance correlation might not take advantage of information in the temporal structure of fMRI signals, revealing the likelihood of transitions from one state to another. In other words, considering the order of time points may improve measures of such temporal dependencies, and help assess the directionality or dynamics in regional couplings (Calhoun et al., 2014; Stephan and Roebroeck, 2012). Certainly, one must be cautious about utilizing and interpreting temporal information from fMRI signals, given temporal delays and blurring confounds in hemodynamic fMRI signals (Smith, 2012).

Conclusion

In conclusion, we demonstrated that multivariate connectivity estimates provide more powerful information about an individual’s unique brain organization and cognitive abilities. Multivariate functional connectivity was more reliable than univariate functional connectivity, and better predicted individual differences in fluid intelligence. Furthermore, multivariate connectivity estimates were more sensitive and specific to ongoing cognitive state. Based on our findings, we propose that future connectome studies incorporate multivariate approaches to better characterize functional brain organization and its relationship to behavior.

Highlights.

1. Multivariate connectivity is calculated using all voxels’ timecourses in each region.

2. Multivariate connectivity estimates are more reliable than univariate estimates.

3. Multivariate estimates better predict individuals’ fluid intelligence.

4. Multivariate estimates have higher sensitivity to cognitive states within individuals.