Self-compensation in chlorine-doped CdTe

Abstract

Defect energetics, charge transition levels, and electronic band structures of several Cl-related complexes in CdTe are studied using density-functional theory calculations. We investigate substitutional chlorine (Cl_Te and Cl_Cd) and complexes formed by Cl_Te with the cadmium vacancy (Cl_Te-V_Cd and 2Cl_Te-V_Cd) and the Te_Cd antisite (Cl_Te-Te_Cd). Our calculations show that none of the complexes studied induce deep levels in the CdTe band gap. Moreover, we find that Cl_Te-V_Cd and Cl_Te are the most stable Cl-related centers in n-type and p-type CdTe, under Te-rich growth conditions, showing shallow donor and acceptor properties, respectively. This result suggests that the experimentally-observed Fermi level pinning near midgap would be originated in self-compensation. We also find that the formation of the Cl_Te-Te_Cd complex passivates the deep level associated to the Te antisite in neutral charge state.

Introduction

Cadmium telluride (CdTe) is a II-VI chalcogenide semiconductor with a band gap energy of ∼1.5 eV at room temperature, being one of the few that can be relatively easily doped p- and n-type. CdTe has been actively investigated for more than 70 years for photovoltaics^1–3, room-temperature γ- and x-ray radiation detection^4–7, as well as medical imaging⁸. Due to its high stability (formation enthalpy ∼100 kJ mol⁻¹), high absorption coefficient (>5 × 10⁵ cm⁻¹), and near optimum band gap for visible absorption, CdTe is very suitable material for use as absorber layer in thin-film solar cells. In fact, single-junction CdTe-based solar cells have recently reached conversion efficiencies as high as 22.1%⁹. Additionally, its low manufacturing cost and the continuing improvement on its conversion efficiency have positioned CdTe among one of the most promising materials alternative to crystalline silicon, which dominates the global photovoltaic market¹⁰.

In addition, the large CdTe band gap allows its use in γ- and x-ray detectors, operating at room temperature with modest cooling¹¹, as opposed to germanium-based detectors that require cryogenic temperatures to operate. Moreover, high-quality radiation detectors require an intrinsic high resistivity to reduce dark currents, a high mobility-lifetime product of electrons (μτ), and a high atomic weight¹². The former property can be achieved in CdTe by self-compensation of intrinsic point defects during the crystal growth, while the latter are guaranteed by its good charge transport properties and large atomic number of its constituents.

It is widely known that native defects usually play an important role by limiting the p- or n-type conductivity in a semiconductor^13–17, which may be achieved by extrinsic doping^18,19. Due to its importance and the complexity of the problem, understanding the effect of self-compensation in CdTe is a major focus of current research in the field^15,20–23. Moreover, in the case of CdTe, group IV elements can be used as extrinsic dopants to achieve a semi-insulating material^24–27. However, these impurities normally introduce deep levels in the band gap, which may act as non-radiative Shockley-Read-Hall recombination centers^28,29 with a deleterious effect on the performance of the detector. This does not apply to chlorine doping of CdTe, which results in a high-resistive material with good carrier transport properties^30,31, suitable for γ- and x-radiation detection^32,33; still, the origin of its electric properties is not well understood and remains as an open issue³⁴.

The dominant compensation model for detector-grade CdTe:Cl is based on the existence of one compensating deep level located at ∼0.725 eV above the valence band maximum (VBM)^12,34, which might be responsible for the Fermi level pinning near midgap. This model is supported by experimental observations, but it cannot be explained by theory. In this context, several theoretical works have suggested that compensation between shallow donors and acceptors, rather than one deep level, should be responsible for the Fermi level pinning in CdTe:Cl^35,36. However, other works have concluded that high-resistivity in CdTe:Cl cannot be explained by shallow defect levels alone³⁷.

In this work, we set out to determine the origin of the high-resistivity experimentally observed in detector-grade CdTe:Cl. In that aim, we calculate from ab-initio the formation energies, electronic structure, and transition states of three chlorine-related defects in CdTe: (i) the isolated substitutional chlorine, that is Cl occupying a Te site (Cl_Te) and a Cd site (Cl_Cd); (ii) the two complexes formed by Cl_Te nearest neighbor to the cadmium vacancy (V_Cd). The first one contains one Cl_Te neighboring to the vacancy (Cl_Te-V_Cd), which is commonly known as the A-center, while the second one contains two Cl_Te neighboring to the vacancy (2Cl_Te-V_Cd); and (iii) the complex formed by the Cl_Te impurity nearest neighbor to the Te_Cd antisite (Cl_Te-Te_Cd). Our results show that Cl_Te-V_Cd is the most stable Cl-related complex in n-type CdTe, that together with Cl_Te, the most stable Cl impurity in p-type CdTe, would play a key role in the self-compensation mechanism. Indeed, our results support the hypothesis that compensation between shallow donors and acceptors alone can explain the good electron mobility and high-resistivity of CdTe:Cl, in agreement with experimental observations.

Results and Discussion

Substitutional chlorine in CdTe

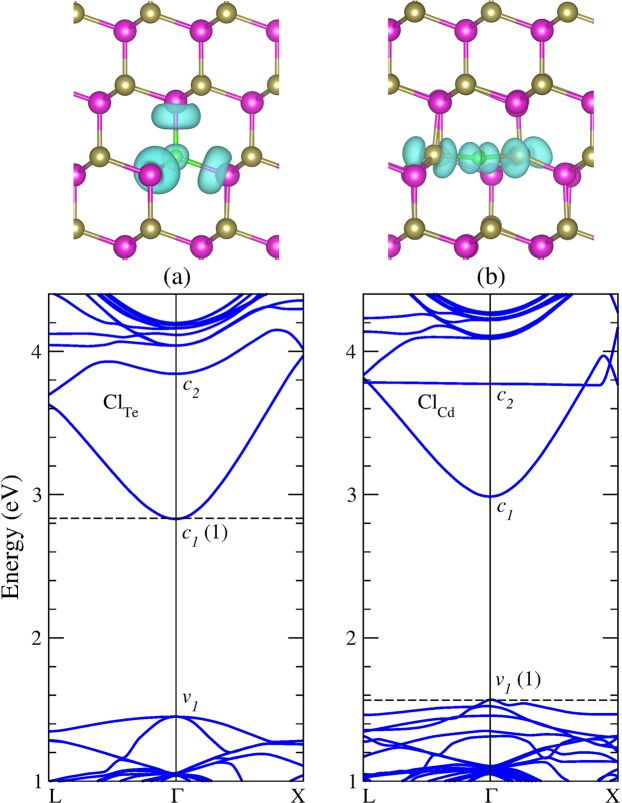
As an isolated substitutional impurity, chlorine can occupy only a Cd site or a Te site in CdTe. Our initial model was simply substitute a lattice atom with the neutral Cl impurity and left the system to relax. Figure 1(a) shows the equilibrium geometries and band structure of substitutional chlorine in CdTe in the neutral charge state. Our results for chlorine occupying a Te site (Cl_Te) indicate a four-fold coordinated impurity with almost undistorted geometry, preserving the T_d symmetry. The Cd atoms next to the impurity relax outwards by about 3%, resulting in a Cd-Cl bond distance of 2.936 Å. The same configuration is observed in single positive charge state. The electronic properties indicate that Cl_Te is a shallow donor, introducing an impurity level resonant in the conduction band (c₂). The squared wavefunction, or simply the charge density, corresponding to this level indicates a Cl-Cd antibonding character, as shown Fig. 1(a). The electronic structure shows a band gap of 1.40 eV, close to that calculated for pristine CdTe (1.44 eV).

Figure 1.

Equilibrium geometry and band structure calculations of substitutional chlorine in the neutral charge state. (a) Cl_Te, and (b) Cl_Cd. The dashed line indicates the Fermi energy. Charge density isosurface of the impurity level (c₂) of Cl_Te and Cl_Cd are plotted for ρ = 0.001 and 0.005 e/ų, respectively. Violet, brown, and green balls represent Cd, Te, and Cl atoms, respectively.

Figure 1(b) shows the equilibrium geometries and band structure of chlorine occupying a Cd site (Cl_Cd), revealing a strong relaxation from the T_d symmetry. In the neutral charge state, the impurity has two-fold coordination, forming a bridge-like structure between two Te atoms. The Te-Cl bond distances are found to be of 2.627 Å with a Te-Cl-Te bond angle of 169°. Whereas, the two other Te atoms become three-fold coordinated at a distance of 3.75 Å from the Cl atom. The same configuration is observed in single negative charge state. It is interesting to note that the Cl_Cd equilibrium configuration is similar to that expected for the V_Cd-Cl_i complex. The electronic properties of Cl_Cd show that it is a shallow acceptor that introduces a strong perturbation on the top of the valence band. These states are associated with the three-fold coordinated Te atoms next to the Cl atom. In addition, an impurity level with an antibonding character (c₂) is found to be resonant in the conduction band, as shown Fig. 1(b).

The stability of substitutional chlorine in CdTe is obtained through formation energy calculations, as shown in Fig. 2. Our results indicates that Cl_Te is the most stable impurity for both Cd-rich and Te-rich growth conditions. Moreover, the Cl_Te impurity is a shallow donor with a ε(+/0) transition level at VBM + 1.29 eV, while Cl_Cd is a shallow acceptor that introduces a ε(0/−) transition level at VBM + 0.15 eV. However, Cl_Cd shows a high formation energy in comparison with Cl_Te, suggesting that it would be unlikely to form at relevant concentrations.

Figure 2.

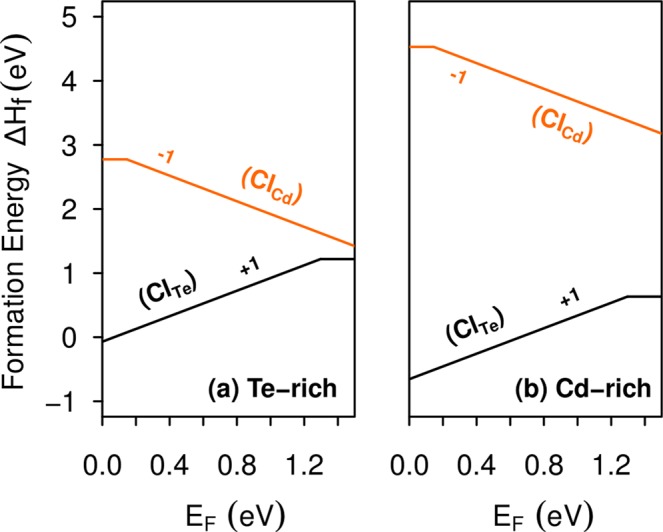
Formation energies of substitutional chlorine in CdTe, Cl_Te and Cl_Cd, as a function of the Fermi level, under (a) Te-rich condition and (b) Cd-rich condition. The slopes of the formation energy lines indicate the charge states and changes in its slopes indicates defect transition states.

The Cl_Te-V_Cd complex in CdTe

The Cl_Te-V_Cd complex in CdTe is formed when a Cl atom replaces a Te atom nearest neighbor to a Cd vacancy³⁸. Previous DFT calculations have identified the isolated Cd vacancy as the dominant intrinsic acceptor in CdTe^39–41. We found that V_Cd is stable in T_d, D_2d, and C_2v symmetries, being the V_Cd(C_2v) configuration the global minimum. We also found that V_Cd is stable in C_3v symmetry in the single-negative charge state, which is stabilized by a hole polaron, in good agreement with previous calculations⁴¹. In the neutral charge state, V_Cd(T_d) and V_Cd(D_2d) are 0.64 and 2.11 eV higher in energy than V_Cd(C_2v), respectively. The V_Cd(C_2v) structure is characterized by the formation of a Te-Te dimer between two undercoordinated Te atoms neighboring to the vacancy. Our results show that this dimer has a bond distance of 2.773 Å, while the others Te atoms remain three-fold coordinated and are displaced inward the vacancy by about 0.24 Å with respect to their perfect crystal positions. Interestingly, the V_Cd(C_2v) in the neutral charge state exhibits a ground-state configuration with all the valence band filled and all the conduction bands empty. This result is in close agreement with recent DFT-HSE06 calculations, although the formation of the Te-Te dimer was not reported⁴². On the other hand, the V_Cd(D_2d) structure reveals the formation of two Te-Te dimers with bond distances of 2.765 Å, while its electronic structure indicates a double donor character.

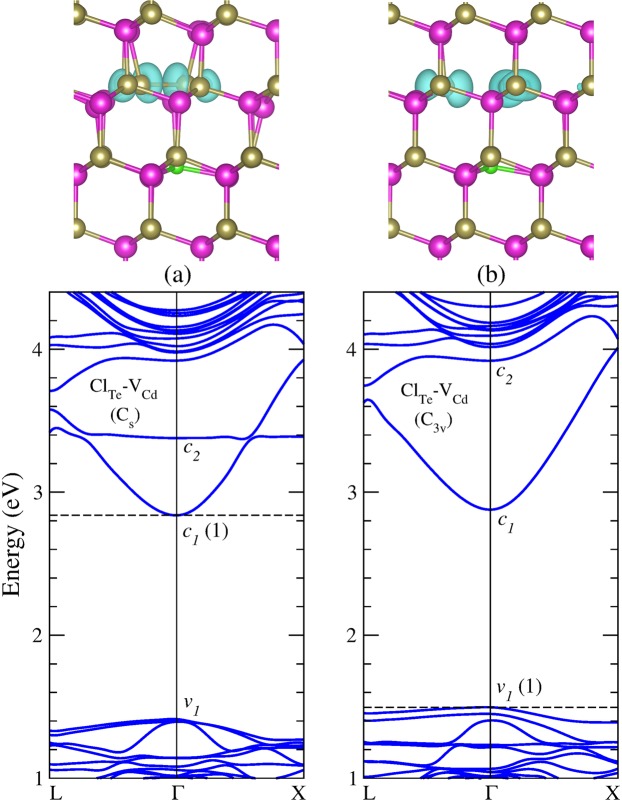
Next, we investigate the formation of the Cl_Te-V_Cd complex starting from the V_Cd(T_d) geometry by substituting a neighboring Te atom by a Cl atom. Our results for the electronic band structure and the equilibrium geometry are shown in Fig. 3(b). We find that the neutral complex is stable in C_3v symmetry [hereafter referred as (Cl_Te-V_Cd)(C_3v)], where the Cl_Te impurity moves outward the vacancy by 0.5 Å, while the three-fold coordinated Te atoms relax inward by 0.29 Å with respect to their perfect crystal positions, as shown in Fig. 3(b). Moreover, neutral (Cl_Te-V_Cd)(C_3v) has a hole at the VBM, indicating a shallow acceptor character in good agreement with previous theoretical^35,43,44 and experimental³² results.

Figure 3.

Equilibrium geometry and band structure calculations of the complexes (a) (Cl_Te-V_Cd) (C_s), and (b) (Cl_Te-V_Cd)(C_3v) in the neutral charge state. The dashed line indicates the Fermi energy. Charge density isosurfaces for the impurity level (c₂) in (a) and the level at VBM (v₁) in (b) are plotted for ρ = 0.005 e/ų and ρ = 0.001 e/ų, respectively.

By taking into account the high stability of the V_Cd(C_2v) structure that form the Te-Te dimer, we construct another complex by substituting an under-coordinated Te atom by a Cl atom. Our results for the band structure and equilibrium geometry of this complex are shown in Fig. 3(a). We find that the new complex geometry preserves the Te-Te dimer of the V_Cd(C_2v) configuration with a bond distance of 2.771 Å. Moreover, we found that the substitutional chlorine moves outward the Cd vacancy by 0.5 Å. This complex has C_s symmetry with only one symmetry plane [hereafter referred as (Cl_Te-V_Cd)(C_s)], which is 0.73 eV higher in energy than the (Cl_Te-V_Cd)(C_3v) structure in the neutral charge state. It is worth noting that the Cl_Te-V_Cd complex was recently studied by Lindström et al., using DFT-HSE06 calculations³⁶. They found two equilibrium geometries for this complex, which is stable in both C_s and C_3v symmetries, in the neutral and in the negative charge state, respectively. Although the two configurations of the complex agree with our calculations, the equilibrium geometry of the neutral (Cl_Te-V_Cd)(C_s) differs from our results. We find the formation of a Te-Te dimer, while Lindström et al.³⁶ found only a small approach between the same Te atoms, suggesting that its configuration may be a metastable state.

Our results shows that the (Cl_Te-V_Cd)(C_s) complex has a shallow donor property, in contrast to the (Cl_Te-V_Cd)(C_3v) complex, which is a shallow acceptor, as shown Fig. 3. Although with a higher formation energy, the (Cl_Te-V_Cd)(C_s) complex is likely to form in the single-positive charge state, which is a ground state configuration with all the valence band filled and all the conduction bands empty. Indeed, for the Fermi energy close to the VBM the [(Cl_Te-V_Cd)(C_s)]⁺ configuration has much lower energy than the [(Cl_Te-V_Cd)(C_3v)]⁻ polaronic configuration found in ref.³⁶, which acts as a harmful electron trap.

Figure 4 shows the formation energies of (Cl_Te-V_Cd)(C_s) and (Cl_Te-V_Cd)(C_3v), indicating that both complexes can coexist for the Fermi energy close to VBM + 0.33 eV, the energy at which their formation energies are equal, as indicated by the arrow. As the transition between the C_3v and C_s geometries involves the formation of a Te-Te dimer, we want to know the energy needed to overcome the barrier between them, that is the activation energy, and if this process is likely to occur at the operational conditions. To do that, we calculate the minimum energy path (MEP) of neutral Cl_Te-V_Cd moving from C_3v to C_s geometries, using the climbing-image nudged elastic band (NEB) method⁴⁵. This method finds the MEP between two local minima previously obtained, by optimizing intermediate geometries called images. Then, the activation energy is obtained by calculating the difference between the lowest minimum and the saddle point. In our calculations we obtain the MEP using GGA-PBE functional, considering a 128-atom supercell with all atoms free to relax, and ten images between the C_3v and C_s local minima. We obtain an activation energy of 0.64 eV, as shown in Fig. 5.

Figure 4.

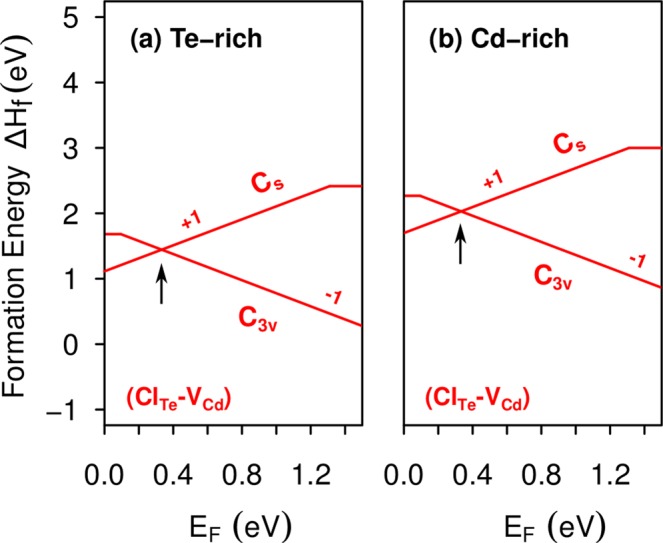
Formation energies of the Cl_Te-V_Cd complex in C_s and C_3v symmetries, as a function of the Fermi level, under (a) Te-rich condition and (b) Cd-rich condition.

Figure 5.

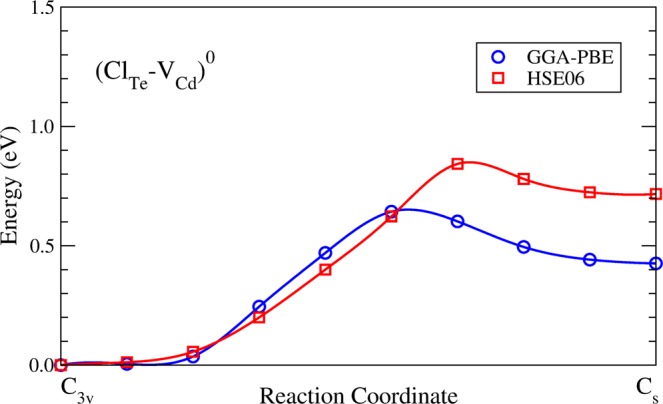
Minimum energy paths for transition of the neutral complex Cl_Te-V_Cd from C_3v to C_s symmetries, as calculated with GGA-PBE and HSE06 functionals.

To estimate the MEP using the hybrid HSE06 functional, which is the functional used throughout this work, we re-evaluated the GGA-PBE images previously found using now the HSE06 functional without allow the system to relax (single-point energy). It is important to note that NEB calculations using directly the HSE06 functional are not possible due to the huge computational time required. Our results show an activation energy of 0.85 eV, as shown in Fig. 5. The difference between both minimum energy paths is partially attributed to a residual strain in the single-point calculation and the inclusion of the fraction of exact exchange due to the hybrid functional. It is interesting to note that the larger difference between MEPs is obtained when the Te-Te dimer becomes to form. We believe that a realistic activation energy for transition between the C_3v and C_s geometries should be something between GGA-PBE and HSE06 calculations. Experiments have measured activation energies for the chlorine diffusion in CdTe to be of 0.63 and 1.32 eV for a temperature range between 200 and 700 °C⁴⁶. Therefore, the activation energy for the C_3v to C_s transition in the neutral Cl_Te-V_Cd complex lies in the range of 0.64 to 0.85 eV, suggesting that it is likely to occur.

However, the activation energy for the inverse transition C_s to C_3v, which would be the most probable direction, is just of 0.15 eV. Therefore, at the HSE06 level of calculation, the formation of the Cl_Te-V_Cd complex would start with a neutral V_Cd vacancy with C_2v geometry. If a Cl impurity occupies the position of one of the two three-fold coordinated Te atoms surrounding the vacancy, a neutral (Cl_Te-V_Cd)(C_s) complex would form. According to Fig. 3(a), this complex is a shallow donor being likely to lose an electron, changing to the (Cl_Te-V_Cd)(C_3v) geometry after overcoming an energy barrier of 0.15 eV.

The 2Cl_Te-V_Cd complex in CdTe

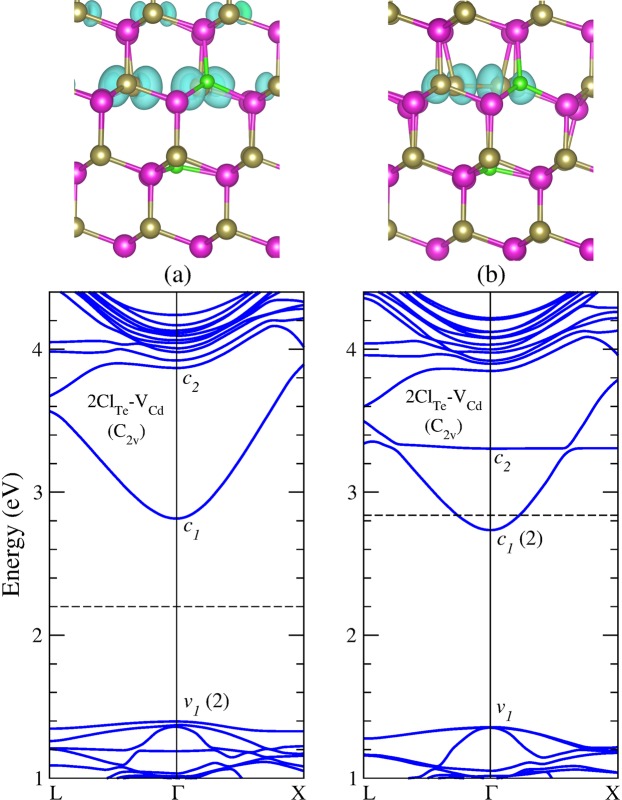
We subsequently investigate the possibility of a new complex consisting of two Cl atoms substituting two of the four undercoordinated Te atoms nearest neighbors to a Cd vacancy (hereafter referred as 2Cl_Te-V_Cd). This complex was predicted in 1974 by Canali et al.⁴⁷, suggesting that it would be likely to be found in high-resistivity donor-doped CdTe. After substituting the second Te atom by a Cl atom in (Cl_Te-V_Cd)(C_3v) as shown in Fig. 3(b), we observe that the system relaxes to the 2Cl_Te-V_Cd configuration shown in Fig. 6(a), exhibiting C_2v symmetry. The inclusion of the second chlorine fills the hole that (Cl_Te-V_Cd)(C_3v), shows at the VBM, stabilizing the (2Cl_Te-V_Cd)(C_2v) complex in neutral charge state. Moreover, the electronic structure of this complex shows that the neutral charge state is a ground-state configuration, that is with all the valence bands filled and all the conduction bands empty.

Figure 6.

Equilibrium geometry and band structure calculations of the neutral 2Cl_Te-V_Cd complex in the two stable configurations (a) with Te atoms separated, and (b) with the Te atoms forming a dimer. The dashed line indicates the Fermi energy. Charge density isosurfaces for the level at the VBM (v₁) in (a) and the impurity level (c₂) in (b) are plotted for ρ = 0.001 e/ų and ρ = 0.005 e/ų, respectively.

In addition, we find a second configuration for the 2Cl_Te-V_Cd complex, where the two adjacent undercoordinated Te atoms form a Te-Te dimer with a bond length of 2.771 Å, preserving the C_2v symmetry. In the neutral charge state, this complex has two excess electrons in the conduction bands, as shown in Fig. 6(b), indicating that 2Cl_Te-V_Cd is a double donor that would tend to transfer its excess electrons to uncompensated acceptors such as the V_Cd. In this way, the ground-state configuration [2Cl_Te-V_Cd]²⁺ should be stabilized.

Figure 7 shows the calculated formation energies for the two configurations of the 2Cl_Te-V_Cd complex as a function of the Fermi level, under both Te-rich and Cd-rich growth conditions. We find that the Te-Te dimer configuration, which will be referred as (2Cl_Te-V_Cd)(d), has the lowest formation energy for the Fermi level close to the VBM (n-type CdTe), being likely to be found under this condition. Whereas for other Fermi level positions, the complex configuration with the separated Te atoms is the most stable. Thus, the crossing point of formation energy lines, indicated by arrows in Fig. 7, shows that 2Cl_Te-V_Cd introduces a shallow transition level ε(2 + /0) at VBM + 0.1 eV. Interestingly, this complex exhibits the same defect formation energies under both Te-rich and Cd-rich growth conditions.

Figure 7.

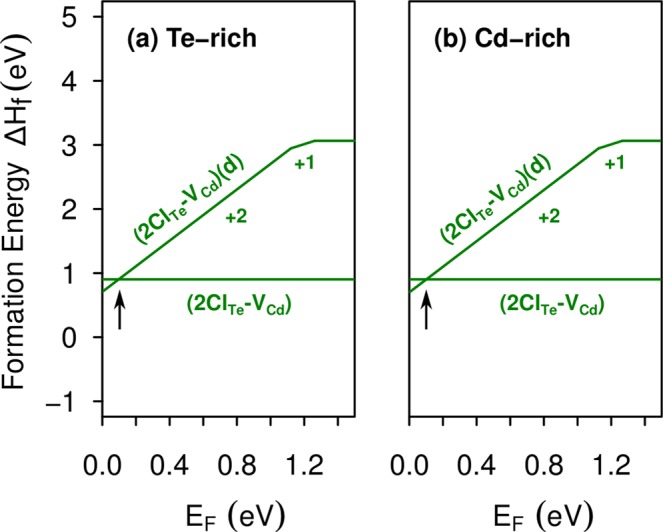
Formation energies of the 2Cl_Te-V_Cd complex as a function of the Fermi level, under (a) Te-rich condition and (b) Cd-rich condition. The neutral charge state represents the complex with separated Te atoms and the positive charge states represent the complex with a Te dimer.

The Cl_Te-Te_Cd complex in CdTe

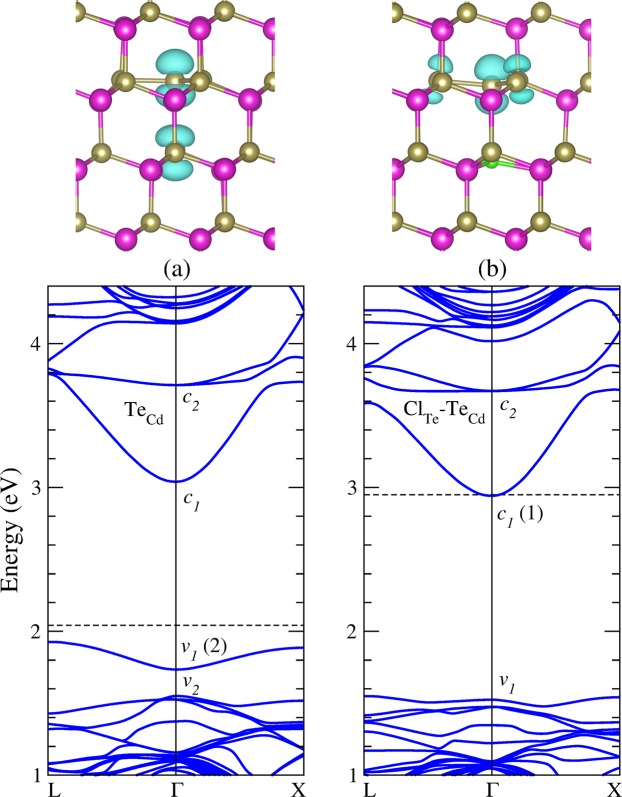
We now turn to examine the complex formed by the substitutional chlorine (Cl_Te) nearest neighbor to the Te antisite (Te_Cd). Previous DFT calculations have extensively studied the Te_Cd antisite because is one of the most abundant native defect under Te-rich growth conditions^{7,35,40,48–52}. Lindström et al.⁵² using the hybrid functional HSE06 have reported three charge states for this defect: ${\mathrm{Te}}_{\mathrm{Cd}}^{2+}$, ${\mathrm{Te}}_{\mathrm{Cd}}^0$, and ${\mathrm{Te}}_{\mathrm{Cd}}^{2-}$, which are stable in T_d, C_3v and C_s symmetries, respectively. We found similar results, but according to our formation energy calculations only ${\mathrm{Te}}_{\mathrm{Cd}}^{2+}$ and ${\mathrm{Te}}_{\mathrm{Cd}}^0$ would be stable, as shown in Fig. 8. The discrepancy can be attributed to finite size effect, as the authors of ref.⁵² applied a potential alignment scheme in a 128-atom supercell, in contrast to our formation energy calculations performed with a larger 250-atom supercell. It is interesting to note that Te_Cd shows higher formation energies than Cl_Te for all values of the Fermi energy in the band gap, as can be seen by comparing Figs 8 and 2, suggesting that the chlorine impurity would be energetically favorable over any native defect. Moreover, the Te_Cd defect exhibits a negative-U behavior, where the single-positive charge state is never stable, in agreement with previous calculations^40,50,52,53. Hence, the Te_Cd defect shows a ε(2 + /0) transition level at VBM + 0.4 eV. However, in a previous work using accurate quasiparticle DFT + GW calculations we found this state at VBM + 1.0 eV⁵³. The electronic structure of ${\mathrm{Te}}_{\mathrm{Cd}}^{2+}$ shows an empty t₂ level in the higher part of the CdTe band gap. After capturing two electrons, the defect experiences a Jahn-Teller distortion, which is characterized by the breaking a Te-Te bond, lowering the symmetry from T_d to C_3v. In this way, the t₂ level split into a fully-occupied a₁ level and an empty e level, which are represented by v₁ and c₂ levels in the ${\mathrm{Te}}_{\mathrm{Cd}}^0$ band structure, shown in Fig. 9(a).

Figure 8.

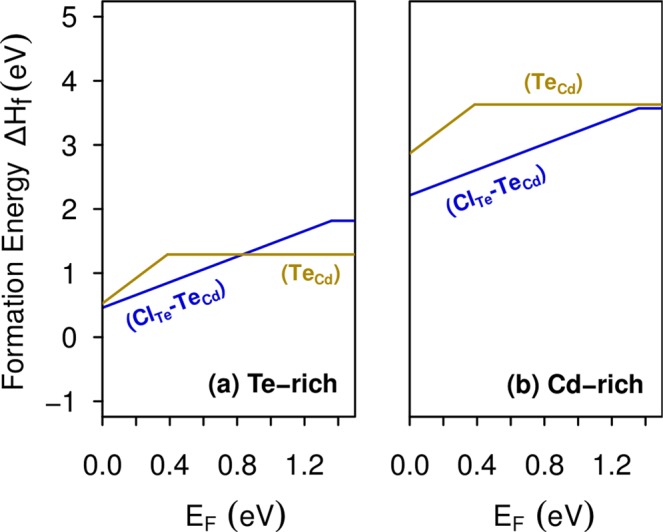
Formation energies of the Te_Cd antisite and the Cl_Te-Te_Cd complex as a function of the Fermi level, under (a) Te-rich condition and (b) Cd-rich condition.

Figure 9.

Equilibrium geometry and band structure calculations of (a) the Te_Cd antisite, and (b) the Cl_Te-Te_Cd complex, in the neutral charge state. The dashed line indicates the Fermi energy. Charge density isosurfaces of the occupied level in the band gap (v₁) in (a) and the VBM level (v₁) in (b) are plotted for ρ = 0.005 e/ų and ρ = 0.001 e/ų, respectively.

Concerning Cl_Te-Te_Cd, our results suggests that this complex only exists in single positive charge state with similar formation energy than the Te_Cd antisite, as shown Fig. 8. Figure 9(b) shows the band structure calculations of this complex, indicating a shallow donor character, without exhibiting deep levels in the band gap. This result suggests the passivation of the fully-occupied a₁ level of ${\mathrm{Te}}_{\mathrm{Cd}}^0$ after the formation of the Cl_Te-Te_Cd complex, providing an additional explanation to the beneficial effect of the chlorine treatment as experimentally reported.

Interstitial chlorine in CdTe

In an earlier paper⁵⁴, we discussed the role of interstitial chlorine in CdTe (Cl_i). In that study we found that Cl_i is stable in at least five distinct interstitial sites with close formation energies. Moreover, this impurity introduces shallow energy levels that may lead to a donor-acceptor compensation mechanism. Nevertheless, the dominant configurations of Cl_i have a formation energies higher than Cl_Te and the 2Cl_Te-V_Cd complex for values of the Fermi level near midgap, under both Te-rich and Cd-rich growth conditions. We refer the interested reader to ref.⁵⁴, the work of Lindström et al.³⁶, and the topical review of  Yang et al.⁴⁴.

Self-compensation in chlorine-doped CdTe

Figure 10 summarizes the formation energies Cl-related defects in CdTe, which are likley to be formed due to their low formation energies. For values of the Fermi level in the lower part of the band gap (n-type CdTe), we observe that (Cl_Te)⁺ is the most relevant defect under both Te-rich and Cd-rich growth conditions, acting as the dominant donor. Whereas, for the Fermi level in the higher part of the band gap (p-type CdTe), the relevant defect is the complex [(Cl_Te-V_Cd)(C_3v)]⁻, which is the dominant acceptor. Therefore, in the Te-rich limit, the closed-shell (Cl_Te)⁺ donor would be compensated by the [(Cl_Te-V_Cd)(C_3v)]⁻ acceptor after transferring its electron in excess, leading to the Fermi level pinning at VBM + 0.92 eV, as indicate the arrow in Fig. 10(a).

Figure 10.

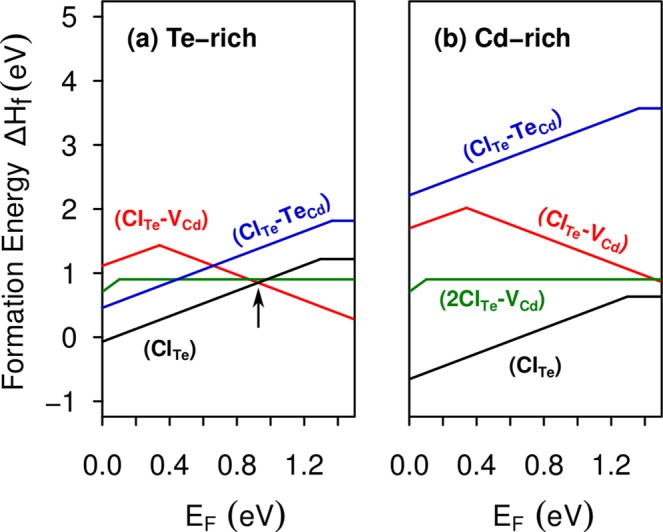
Formation energies of most stable Cl-related defects in CdTe, as a function of the Fermi level, under (a) Te-rich condition and (b) Cd-rich condition.

Interestingly, at the crossing point between (Cl_Te)⁺ and [(Cl_Te-V_Cd)(C_3v)]⁻ in Te-rich CdTe, the complex 2Cl_Te-V_Cd is only 0.05 eV higher in energy [see Fig. 10(a)]. Thus, the existence of 2Cl_Te-V_Cd complexes will contribute to stabilize the charge neutrality condition, allowing the Fermi level pinning in CdTe:Cl without introducing a compensating deep level at variance of the cases of CdTe:Sn²⁷ and CdTe:Ge⁵⁵. These results are in good agreement with the earlier work of Höschl et al.⁵⁶, who suggested that Cl_Te-V_Cd and 2Cl_Te-V_Cd dominate (59% and 40%) over Cd vacancies as compensating acceptors in semi-insulating CdTe:Cl. Moreover, Lindström et al.³⁶ also suggested the possible formation of a tricomplex consisting of two Cl ions and one Cd vacancy. An alternative explanation for the deep level observed by spectroscopy methods³⁴ could be the possible formation of chlorine complexes with Te antisites, which are the dominant recombination centers in CdTe⁵³. However, our results for the Cl_Te-Te_Cd complex do not show any deep levels in the band gap. In addition, our calculations show that Cl_Te is the dominant defect in the Cd-rich limit for any value of the Fermi energy, suggesting that chlorine can be used as an effective n-type dopant under these conditions. For instance, the incorporation of Cl under controlled Cd partial pressures might help to populate the intermediate band in CdTe:Sn²⁷.

Summary

In summary, we have investigated the electronic structure, formation energies, and transition states of substitutional chlorine Cl_Te and Cl_Cd, and the complexes formed by Cl_Te with the most probable defects found in Te-rich CdTe, namely the Cd vacancy and the Te antisite. We find that the Cl_Te-V_Cd complex can exist in two geometries, with C_s and C_3v symmetries, showing shallow donor and acceptor properties, respectively. We also identify a second complex containing two substitutional chlorine neighboring to the cadmium vacancy 2Cl_Te-V_Cd, which also can exist in two geometries, both with C_2v symmetry. The latter is found stable only in double positive charge state for n-type CdTe, while the former exhibits a ground-state configuration. Concerning the Cl_Te-Te_Cd complex, our results suggest that it is stable only in single positive charge state with similar formation energy than the Te_Cd antisite. For a Fermi energy close to the middle of the CdTe band gap, the three complexes show formation energies of around 1 eV under Te-rich condition, as shown in Fig. 10(a), suggesting that they are equally likely to be found. Table 1 compares the formation energy values for all the Cl-related defects studied under Te-rich and Cd-rich conditions for the Fermi energy at the VBM.

Table 1.

Formation energy (in eV) of the Cl-related defects in CdTe under study. The Fermi energy is set at the valence band maximum. Lower values for the formation energy, in general less than 1 eV, indicates the most likely defects to be found.

Defect	ΔHf (Te rich)	ΔHf (Cd rich)
(ClTe)1+	−0.07	−0.65
(ClTe)0	1.22	0.63
(ClCd)1−	2.92	4.68
(ClCd)0	2.82	4.57
[(ClTe-VCd) (Cs)]1+	1.11	1.70
[(ClTe-VCd) (Cs)]0	2.42	3.00
[(ClTe-VCd) (C3v)]1−	1.78	2.36
[(ClTe-VCd) (C3v)]0	1.68	2.27
[(2ClTe-VCd) (d)]2+	0.71	0.71
[(2ClTe-VCd) (d)]1+	1.81	1.81
[(2ClTe-VCd) (d)]0	3.06	3.06
[(2ClTe-VCd)]0	0.90	0.90
(TeCd)2+	0.53	2.87
(TeCd)0	1.29	3.63
(ClTe-TeCd)1+	0.46	2.21
(ClTe-TeCd)0	1.82	3.57

Finally, we find that neither the complexes under study nor the substitutional Cl impurity induce deep level in the CdTe band gap. Therefore, our calculations suggest that self compensation between Cl-induced shallow donors and acceptors should be responsible for the high resistivity observed in detector-grade CdTe:Cl, usually grown in a Te-rich environment, in agreement with previous hypothesis³⁵. Particularly, the (Cl_Te)⁺ shallow donor would be compensated by the [(Cl_Te-V_Cd)(C_3v)]⁻ shallow acceptor, leading to the Fermi level pinning at VBM + 0.92 eV. In addition, our results show that the formation of the Cl_Te-Te_Cd complex passivates the deep level associated to the Te antisite (Te_Cd), confirming to some extent the beneficial effect of chlorine in CdTe.

Methods

We performed first-principles calculations based on the density functional theory (DFT)^57,58, as implemented in the Vienna Ab Initio Simulation Package (VASP)⁵⁹. We used the Heyd-Scuseria-Ernzerhof (HSE06)^60,61 hybrid functional with the standard mixing parameter α = 25%, a plane-wave basis set with a cutoff energy of 285 eV. The core-valence interaction is described by the projector augmented-wave mathod⁶². Our calculations were performed using large 250-atom supercells, which were fully relaxed until the forces on each atom were less than 0.025 eV/Å. Our computational approach improves previous theoretical works in which smaller 64-atom supercell were used^36,44,63, despite the fact that the convergence of hybrid functionals with respect to the supercell size may be slower than its local and semi-local counterparts^15,64,65. Additionally, due to the high computational cost of the HSE06 calculations, only the Γ point was used for the Brillouin zone sampling, whereas band structures calculations were performed using a 128-atom supercell.

The formation energy (ΔH_f) of a defect in charge state q can be written as a function of the Fermi level (E_F) and the chemical potentials of the atomic species (μ_i) as follows⁶⁶:

$$\mathrm{\Delta }{H}_f[E_F]=E_{tot}[X^q]-E_{tot}[\mathrm{bulk}]-\sum _i{n}_i{\mu }_i+q(E_F+E_{\mathrm{VBM}}),$$ 1

where E_tot[X^q] and E_tot[bulk] are the total energy of the system with a defect in charge state q and the pristine system, respectively. E_VBM is the energy of the valence band maximum. n_i is the number of atoms of type i that have added or removed from a pristine system. For instance, in the case of Cl substituting a Cd atom in the charge state q, the formation energy can be obtained as:

$$\mathrm{\Delta }{H}_f[E_F]=E_{tot}\left[{({\mathrm{Cd}}_{n-1}{\mathrm{Te}}_n\mathrm{Cl})}^q\right]-E_{tot}[{\mathrm{Cd}}_n{\mathrm{Te}}_n]+{\mu }_{\mathrm{Cd}}-{\mu }_{\mathrm{Cl}}+q(E_F+E_{\mathrm{VBM}}),$$ 2

where E_tot(Cd_nTe_n) is the total energy of a supercell containing n primitive cells of CdTe and E_tot(Cd_n−1Te_nCl)^q is the energy of the same supercell with one Cd atom replaced by a Cl atom with q electrons removed. For Cl substituting a Te atom in charge state q (${\mathrm{Cl}}_{\mathrm{Te}}^q$), the same procedure is applied, just exchanging Te by Cd in Eq. (2).

The chemical potentials in Eq. (2) are defined as:

$${\mu }_{\mathrm{X}}=E_{\mathrm{X}}+\mathrm{\Delta }{\mu }_{\mathrm{X}},\mathrm{with}\mathrm{X}=\{\mathrm{Cd},\mathrm{Te},\mathrm{Cl}\},$$ 3

where E_X is the energy per atom of bulk-phase Cd and Te, and gas-phase Cl (Cl₂). In addition, the thermodynamic equilibrium requires the following restrictions to the chemical potentials:

$$\mathrm{\Delta }{\mu }_{\mathrm{Cd}}\le \mathrm{0,}\mathrm{\Delta }{\mu }_{\mathrm{Te}}\le \mathrm{0,}\mathrm{\Delta }{\mu }_{\mathrm{Cl}}\le \mathrm{0,}$$ 4

$$2\mathrm{\Delta }{\mu }_{\mathrm{Cl}}+\mathrm{\Delta }{\mu }_{\mathrm{Cd}}\le \mathrm{\Delta }H({\mathrm{CdCl}}_2)=-3.59\mathrm{eV},$$ 5

$$\mathrm{\Delta }{\mu }_{\mathrm{Cd}}+\mathrm{\Delta }{\mu }_{\mathrm{Te}}=\mathrm{\Delta }H(\mathrm{CdTe})=-1.17\mathrm{eV}.$$ 6

Inequalities (4) and (5) represent necessary conditions to avoid that elements and compounds segregate, whereas Δμ_Cd = 0 and Δμ_Te = 0 represent Cd-rich and Te-rich conditions, respectively. ΔH(CdCl₂) and ΔH(CdTe) are the heats of formation of CdCl₂ and CdTe. The numerical values of heats of formation are obtained from HSE06 calculations. Relations (4) and (6) impose that both Δμ_Cd and Δμ_Te are larger than ΔH(CdTe). Others expressions like (5) can be set to avoid the formation of other compounds like TeCl₄ and Te₃Cl₂, but in practice (5) sets the maximum possible value for Δμ_Cl in equilibrium with CdTe. E_tot(Cd_nTe_nCl)^q in Eq. (2) includes size corrections for electrostatic interactions between nearest-neighbor images in the supercell calculation⁶⁷. No additional corrections for band filling are needed⁶⁷, as we used only the Γ point for the Brillouin zone sampling.

Author Contributions

The research and manuscript were led by authors W.O. and M.A.F.; W.O. conducted the band structure calculations and created Figures 1, 3, 5, 6, and 9; E.M.P. and M.A.F. conducted the formation energy calculations; M.A.F. created Figures 2, 4, 7, 8, and 10. All authors analysed the results and reviewed the manuscript.

Competing Interests

The authors declare no competing interests.