Abstract
An Experimental Thermodynamic Equation (ETE) temperature scale valid from 0.2 to 2.0 °K has been calculated for He3. The scale is based on new comparisons, (P3, P4),of He3 and He4 vapor pressures above 0.9 °K; on the 1958 He4 temperature scale; and on the best available data for several thermodynamic properties of He3 from 0.2 to 2.0 °K.
The T62 Full-Range Working Equation (FWE) scale,
fits the ETE scale and the (P3, T58) data and is therefore valid for use from 0.2 to the critical point, 3.324 °K. The maximum deviation from the ETE scale is 0.4 mdeg and the standard deviation from the input data is 0.25 mdeg. The fit to the seven recalculated isotherms of Keller in the range of the 1962 He3 scale can be determined by converting Keller’s P4’s to equivalent P3’s, using direct P4 to P3 interpolation equations. The fit of the 1962 He3 scale is as good as the fit of the 1958 He4 scale to the same isotherms, the average displacements of the two scales both being 1.5 mdeg below the isotherms. The average standard deviations for (T62−Tiso) and for (T58−Tiso) are 1.2 and 1.0 mdeg, respectively, for these seven isotherms
1. Introduction
At the time He3 was first liquified [39]2 a comparison of its vapor pressures, P3, with those of He4, P4, was given, along with a careful determination of its critical pressure, Pc, which was found to be 875 mm Hg. Subsequently, Abraham, Osborne, and Weinstock (AOW) presented [5] more accurate (P3, P4) comparisons, additional critical point data in agreement with ref. [1], and an empirical temperature scale, TK, based on a modification [5] of the 1948 He4 scale [41]. They found it possible to fit all their data, ranging from 0.011 (Pc (1.02 °K) up to Pc, to an equation for log (P/T5/2)having only three fitted powers of T.
In 1953, Chen and London [42] criticised the form of the TK equation and attempted to fit the same (P3,P4) data of AOW to an equation having a proper theoretical form for extrapolation to 0 °K. Although they fitted coefficients of five powers of T, and omitted data at pressures above 0.4 Pc, the fit of their equation was not satisfactory above 0.1 Pc.
In 1957 Sydoriak and Roberts [9] extended the measured range of pressures and temperatures down to 0.000074 Pc and 0.45 °K using two different paramagnetic salts calibrated against He3 above 1° for the temperature measurement. At that time two newer He4 temperature scales were in use, so two He3 scales were calculated: the TE He3 scale, based on the 1955lE He4 scale [43], and the TL He3 scale, based on the 1955L He4 scale [25].
Only by abandoning attempts to retain an analytical expression of proper theoretical form for extrapolation to 0 °K did Sydoriak and Roberts find it possible to get a good fit to their data in combination with those of AOW. To cover the four orders of magnitude range in P3 only four fitted powers of T were needed.
Following the adoption of the 1958 He4 scale [2] the present authors made a proposal [1] to the Seventh International Conference of Low Temperature Physics held at the University of Toronto in 1960 for a new He3 vapor pressure scale to be based on the 1958 He4 scale and on various thermodynamic properties of He3. The proposed procedure was similar to that used for the existing TE and TL scales except that newly available specific heat data [3, 4] could now be included instead of using a calculated “spin entropy” [44] term. In addition, a different magnetic temperature conversion was being studied for the paramagnetic salt data [9] intended to be used to extend the scale below 1 °K.
The proposal was favorably received by members of the conference, with some reservations as to the feasibility of including vapor pressure data obtained with an iron alum thermometer.
We have subsequently abandoned incorporation of any paramagnetic salt data into the scale derivation except for measurements of specific heat using a cerium magnesium nitrate thermometer [3].
An alternative procedure for establishment of the low-temperature end of the new He3 scale has been thoroughly discussed [10] in a report to the Fourth Symposium on Temperature, its Measurement and Control in Science and Industry, Columbus, Ohio, March 1961. In this method the thermodynamic consistency of the (P,T) data can be examined point by point. The method showed [45] that the AOW data could not be combined with the 1958 He4 scale to yield a thermodynamically consistent scale in the range from 1 to 2 °K. A detailed discussion of the inconsistency, which is equivalent to several milli-degrees, is given in a companion paper [7] to this one, hereafter referred to as Part III. Because of this inconsistency new (P3,P4)comparisons were undertaken [45] in an improved apparatus designed to mininize errors due to He4 film reflux. The results are reported in detail in another companion paper [46] to this one, hereafter referred to as Part I.
Since the measurements reported in Part I provide an explanation for the thermodynamic inconsistency, below Tλ, of a scale based on the AOW data, we have used only (P3,P4)data given in Part I in deriving the 1962 He3 scale, reserving the AOW data above Tλ for the purpose of checking the final scale.
The second and third virial coefficients of He3 are needed to establish the low-temperature end of the present scale. For this purpose Keller’s isotherm data [12] has been reanalyzed, using the method of multiple variable least squares [47, 48]. For a further discussion of the method and results we refer to Part III, in which the scale derived below is examined for consistency with isotherm, paramagnetic salt, and latent heat data.
2. The High-Temperature Working Equation Scale
The three steps required to arrive at a full range equation are those discussed in detail for a Method I derivation in ref. [10].
The first step is to derive a working equation scale by which one can interpolate between the(P3,P4)data points of Part I converted to a(P3,T58) table of data. The primary use of this scale is for making small corrections to experimental quantities of second order importance which enter into the thermodynamic treatment of the (P3,T58) data. It will suffice to state that we used a working equation scale which fits the (P3,T58) data with a variance of 0.25 mdeg and a maximum deviation of 0.6 mdeg. (In other He3 scale derivations a high-temperature working scale was considerably more important, since it was also used in the determination of paramagnetic salt calibration equations [9] and to assign temperatures to He3 latent heat data [10].)
3. The Experimental Thermodynamic Scale
The second step is to derive an analytical expression for the thermodynamic vapor pressure equation (see eqs (2) and (4) of ref. [10]) which can be written as follows, putting on the left those terms which can be evaluated from existing thermodynamic data:
| (1) |
The values of P3 and T58 used are given in table 1, which is a portion of the data of Part I, excluding the lowest three data points, at P4<40μ, because the calculated He4 film reflux pressure drop was excessive.
Table 1. He3 vapor pressure dataa used in deriving the 1962He3 scale.
P3 is the measured He3 vapor pressure in mm Hg at 0 °C and standard .gravity, δP3 the estimated maximum error in P3, and δT62 the temperature error equivalent to δP3. Temperature T58 is obtained from the measured He4 vapor pressure. P4, and the 1958 He4 temperature scale. δT58 is the estimated maximum error in T58 equivalent to the maximum estimated error in our measurement of P4, excluding possible errors in the 1958 He4 scale itself. The last column showing the deviations of the 1962 He3 scale from the input data, exhibits a random scatter above 2 °K. At lower temperatures there appears to be some small regularity in the misfit.
In fitting the coefficients of the equation for the 1962 He3 scale, the weight given to each data point was a function of both δP3 and δT58.bAs expected, for almost all of the data points (T62−T58)<(δT62+δT58), since the right side of the inequality is the estimated maximum error. On average (δ T62+δT58)was 1.7 times (T62−T58)
The last entry in the table is the measured value of the critical point.a In addition to the pressure measurement error listed, there is an uncertainty of ±1.5 mm Hg in the location of the critical point.
| P3 | ± δP3 | ± δT62 | T58 | ± δT58 | T62−T58 |
|---|---|---|---|---|---|
| mm Hg | mm Hg | mdeg | deg | mdeg | mdeg |
| 5.254 | 0.003 | 0.11 | 0.89848 | 0.78 | –0.2 |
| 6.671 | .003 | .09 | .94311 | .56 | –.2 |
| 8.692 | .004 | .10 | .99612 | .39 | .3 |
| 10.176 | .004 | .09 | 1.03014 | .48 | .3 |
| 11.041 | .004 | .08 | 1.04850 | .41 | .2 |
| 13.487 | .005 | .09 | 1.09572 | .42 | .0 |
| 20. 001 | .008 | .11 | 1.19772 | .27 | .0 |
| 28.395 | .011 | .12 | 1.30024 | .09 | .1 |
| 38.512 | .014 | .13 | 1.39994 | .68 | .0 |
| 50.234 | .018 | .13 | 1.49553 | .58 | .1 |
| 66. 069 | .027 | .17 | 1.60410 | .53 | –.3 |
| 81. 978 | .060 | .32 | 1.69703 | .48 | –.6 |
| 82.515 | .028 | .15 | 1.69980 | .48 | –.5 |
| 102.75 | . 060 | .28 | 1.80113 | .18 | –.0 |
| 103.65 | .060 | .28 | 1.80548 | .18 | –.2 |
| 103.81 | .060 | .28 | 1.80627 | .05 | –.2 |
| 124.23 | .070 | .29 | 1.89616 | .06 | –.5 |
| 125.86 | .060 | .25 | 1.90300 | .05 | –.6 |
| 151.88 | .070 | .26 | 2.00293 | .11 | –.1 |
| 153.49 | .035 | .13 | 2.00845 | .11 | .2 |
| 181.58 | .048 | .16 | 2.10432 | .11 | .2 |
| 196.61 | .045 | .14 | 2.15174 | .10 | .2 |
| 203.29 | .055 | .17 | 2.17207 | .10 | .1 |
| 205.83 | .055 | .16 | 2.17945 | .10 | .4 |
| 214.47 | .080 | .23 | 2.20521 | .09 | .0 |
| 227.21 | .059 | .17 | 2.24144 | .09 | .1 |
| 248.77 | .080 | .21 | 2.30010 | .08 | –.1 |
| 288.86 | .090 | .22 | 2.40069 | .07 | –.1 |
| 333.14 | .090 | .20 | 2.50157 | .06 | .0 |
| 381.81 | .110 | .22 | 2.60250 | .06 | .3 |
| 433.39 | .100 | .18 | 2.70121 | .05 | .1 |
| 491.85 | .110 | .19 | 2.80389 | .05 | .0 |
| 555.00 | .110 | .17 | 2.90588 | .04 | .0 |
| 617.09 | .130 | .19 | 2.99913 | .04 | –.3 |
| 657.11 | .109 | .16 | 3.05549 | .08 | –.1 |
| 657.78 | .110 | .16 | 3.05632 | .07 | .0 |
| 658.95 | .110 | .16 | 3.05792 | .07 | .0 |
| 721.41 | .114 | .15 | 3.14129 | .07 | .1 |
| 729.70 | .114 | .15 | 3.15203 | .07 | .1 |
| 738.63 | .116 | .15 | 3.16356 | .07 | .0 |
| 804.98 | .120 | .14 | 3.24556 | .06 | –.1 |
| 806.35 | .120 | .14 | 3.24724 | .06 | –.1 |
| 853.73 | .140 | .16 | 3.30238 | .06 | .3 |
| 873.00 | .300 | .34 | 3.3240 | .47 | .6 |
The second term is
| (2) |
where i is the chemical constant, i = 5.31733.
For the remaining terms on the left we write the thermodynamic function and its empirical equivalent as follows. The calculable part of the specific heat term is
| (3a) |
where Csat is the specific heat of saturated liquid He3. Smoothed values of the Csat data of Brewer, Sreedhar, Kramers, and Daunt [3] and data points of Wein-stock, Abraham, and Osborne [4] are shown in table 2, and are used to obtain an empirical equation for Csat,
| (3b) |
for 0.2<T<2°. In this and the following equations and tables the subscript, x, is used to designate either an empirical function of T fitted to a thermodynamic quantity or an experimental interpolation equation.
Table 2. Values at selected temperatures, T, of the specific heat functiona, f(Csat,T) appearing in the thermodynamic equation for In P3.
The function is evaluated by means of an explicit equationb, Csat,x, fitted to smoothed Csat data of Brewer, Sreedhar, Kramers, and Daunt c below 1 °K and plotted data points of Weinstock, Abraham, and Osborned above 1 °K. The misfit of the equation, ΔC=Csat,x–Csat,obs, is seen to have a random scatter.
| T | Csat,x | ΔCsat | fx(Csat,T) |
|---|---|---|---|
| deg | cal mole–1 deg–1 | mcal mole–1 deg–1 | |
| 0.2 | 0.652b | 8c | 0.000 |
| .3 | .706 | −8 | .0243 |
| .4 | .752 | −5 | .0665 |
| .5 | .793 | 0 | .1109 |
| .6 | .831 | 8 | .1539 |
| .7 | .870 | 3 | . 1946 |
| .8 | .911 | .2329 | |
| .9 | .957 | .2691 | |
| 1. 0 | 1.009 | .3034 | |
| 1.1 | 1.069 | −4, −9d,e | .3362 |
| 1.2 | 1.136 | +1, −9, +4 | .3675 |
| 1.3 | 1.211 | +6,+4 | .3977 |
| 1.4 | 1.294 | +5,–1 | .4269 |
| 1.5 | 1.385 | −6 | .4553 |
| 1.6 | 1.482 | –13,+14 | .4831 |
| 1.7 | 1.585 | +2 | .5104 |
| 1.8 | 1. 692 | +16, −4 | .5372 |
| 1.9 | 1. 800 | −20, +2 | .5637 |
| 2.0 | 1.908 | +5 | .5899 |
The lower limit of the fit, 0.2 °K, was arbitrarily selected within the range of measured values of Csat. By this choice the lower limit of reliability of the 1962 He3 scale is chosen to be 0.2 °K. By inserting eq (3b) , the exact theoretical expression (3a) is converted to the experimental interpolation equation for Tm=1.0° and 0.2<T<2°:
| (3c) |
For convenience we have taken Tm to be 1.0 °K, although any other temperature in the range of eq (3b) could as well have been selected. The effect of the specific heat term on the ETE scale below 1 °K is easier to identify with this choice of Tm.
The vapor volume term is
| (4a) |
For the vapor volume, VG, we used the inverse volume expansion form of the equation of state
| (4b) |
For the second and third virial coefficients of He3 we used the equations found in Part III in the multiple parameter least squares analysis of Keller’s isotherm data [12],
| (4c) |
and
| (4d) |
Since a high-speed calculator was available, it was possible to use the implicit form (4a), with P3 being taken from the (P3,T58) data of table 1. Table 3 shows values of the term and of its component parts. The liquid volume term is
| (5a) |
or
| (5b) |
The coefficients of (5b) were evaluated by fitting the next to last column of table 4, which is calculated from the smoothed [49] VL data of Taylor and Kerr [50] and of Sherman and Edeskuty [51] and from the working equation (for ΔP3).
Table 3. The vapor volume terma, ϵ, in the equation for In P3, as evaluated by an iterative procedure, using a highspeed digital computer.
For their general usefulness the table also shows solutions of the cubic equationb for the vapor volume Vg, and values of the secondc and thirdd vir-coefficients, B and C, based on reanalysise of the isotherms of Kellerf.
| T | VG | B | C | ϵ |
|---|---|---|---|---|
| deg | cm3/mole | cm3/mole | (cm3/mole)2 | |
| 0.2 | 1.03×109 | –1350 | 6409 | 0.0000 |
| .3 | 9.97×106 | –898.3 | 5233 | .0001 |
| .4 | 8.87×105 | –672. 5 | 4532 | .0008 |
| .5 | 1.95×105 | –537. 0 | 4053 | . 0027 |
| .6 | 6.83×104 | –446. 7 | 3700 | .0065 |
| .7 | 3.123×104 | –382.2 | 3426 | .0122 |
| .8 | 1.692×104 | –333.8 | 3204 | .0195 |
| .9 | 1.028×104 | –296. 2 | 3021 | .0284 |
| 1.0 | 6780 | –266. 0 | 2866 | .0384 |
| 1.1 | 4747 | –241. 4 | 2732 | .0495 |
| 1.2 | 3478 | –220. 9 | 2616 | .0613 |
| 1.3 | 2640 | –203. 5 | 2513 | .0738 |
| 1.4 | 2061 | –188.6 | 2422 | .0868 |
| 1.5 | 1646 | –175.7 | 2340 | . 1003 |
| 1.6 | 1339 | –164.4 | 2266 | . 1141 |
| 1.7 | 1106 | –154.5 | 2198 | .1282 |
| 1.8 | 925.6 | –145.6 | 2136 | . 1427 |
| 1.9 | 782.8 | –137.7 | 2079 | .1574 |
| 2.0 | 667.9 | –130.6 | 2027 | .1723 |
Table 4. The liquid volume term, f (VL, P3, T), in the equation for In P3 is calculated by numerical integration at selected temperatures, T, using smoothed values a, VL, of liquid volume data of Kerr and Taylorb and Sherman and Edeskuty. c.
For P3 the high-temperature working equation is used. Column 3 shows valuesd calculated from a power series in Tn fitted to column 2. The last two columns show the mismatch and its equivalent in millidegrees.
| T | f(VL,P3,T) | fx(VL,P3,T) | fx−f | ΔT |
|---|---|---|---|---|
| deg | mdeg | |||
| 0.2 | 0.0000 | 0.0000 | 0.0000 | 0.0 |
| .4 | .0000 | .0004 | .0004 | .0 |
| .6 | .0005 | .0012 | .0007 | .1 |
| .8 | .0021 | .0029 | .0008 | .1 |
| 1.0 | .0052 | .0057 | .0005 | .1 |
| 1.2 | .0099 | .0099 | –.0000 | –.0 |
| 1.4 | .0163 | .0158 | –.0005 | –.2 |
| 1.6 | .0244 | .0238 | –.0006 | –.2 |
| 1.8 | .0342 | .0341 | –.0001 | –.0 |
| 2.0 | .0459 | .0470 | .0011 | .6 |
On the right side of eq (1) we have those terms of the thermodynamic equation which cannot be adequately calculated from existing data on He3:
| (6) |
and
| (7) |
where Lo is the value of the latent heat of vaporization at absolute zero, and SL(Tm) is the liquid entropy at Tm.
Using the ordinary method of least squares analysis and weighting each data point equally in this step of the derivation of the 1962 He3 scale, we find
| (8a) |
and
| (8b) |
By combining all the above functions we obtain an experimental thermodynamic equation scale (ETE) which is valid from 0.2 to 2.0 °K.
Because of the complexity of the ETE equation, and the fact that it is implicit in the pressure, iterative solutions were obtained with the aid of an electronic digital computer. A table in steps of 1 mdeg was prepared for comparison with the work-ins; equation scale.
4. The 1962 He3 Full-Range Working Equation Scale
To obtain an expression valid over the full range from 0.2 °K to the critical point we now fit selected portions of eq (1) to a power series in Tn, using as input pressures all of the (P3,T58) data of table 1. Using the method of multiple variable least squares analysis [47, 48] we fit
| (9a) |
Note that in this fitting the vapor and liquid volume terms are expected to be fitted by the power series. To be acceptable it will therefore be necessary to demonstrate not only that the scale fits the input data but also that the scale of (9a) agrees with the ETE scale below the range of the input data, i.e., below P3 = 5.254 mm.
The solution of the analysis, combining coefficients of identical powers of T, is the full range working equation scale, FWE,
| (9b) |
The upper limit is the critical point temperature consistent with the redetermination of the critical pressure found in Part I to be at 873.0 mm Hg.
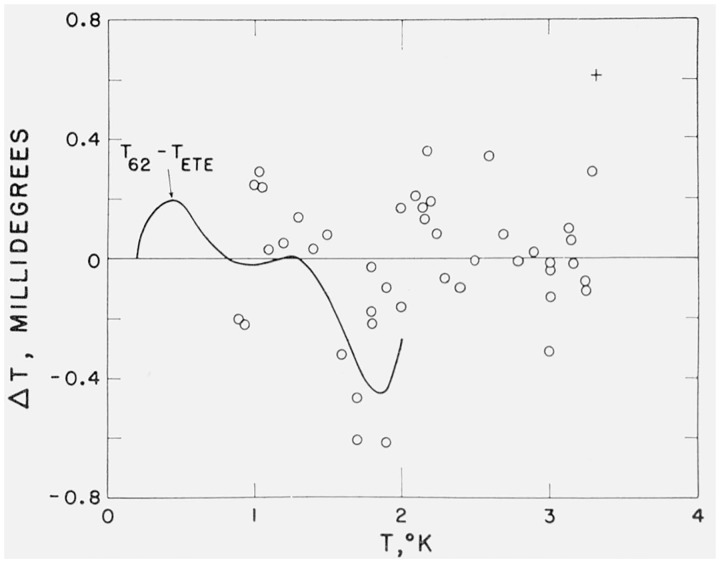
As shown in figure 1, a comparison of the two tables we generate from the ETE scale and the FWE scale shows excellent agreement: nowhere below 2 °K do the scales differ by more than 0.4 mdeg. Equation (9b) is therefore in effect an experimental thermodynamic scale from 0.2 to 2.0 °K and an empirical scale above 2 °K.
Figure 1. The solid line is the deviation of the 1962 He3 scale (i.e., the Full-range Working Equation, eq 9b) from the Experimental Thermodynamic Equation (ETE) scale in the range of validity of the ETE scale.
Plotted points are deviations of the 1962 He3 scale from the (P3,P4) input data: T62(P3)— T58(P4). The + represents data at the critical point.
A comparison of the fit of the 1962 He3 scale to the input (P3,T58) data is given in table 1 and figure 1. The standard deviation of the data from the scale is 0.25 mdeg.
The He4 lambda point occurs at P4,λ=37.80 mm Hg (corrected to 0 °C and standard gravity). On the 1958 He4 scale this corresponds to 2.1720 °K. In Part I a direct interpolation procedure is described by which the value of P3 which corresponds to P4,λis 203.25 mm Hg. Hence T62,λ=2.1721 °K, for P3=203.25 in good agreement with the value of this fixed point on the 1958 He4 scale of temperatures.
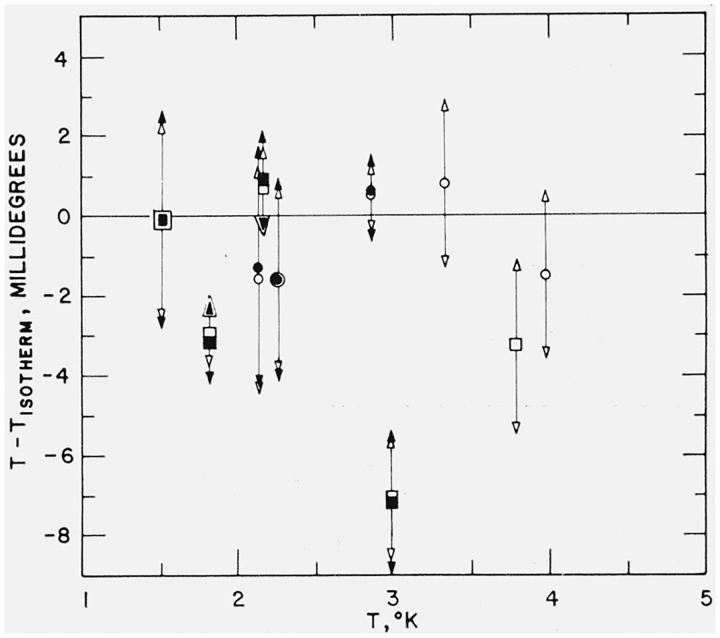
The most fundamental test which can be given to the 1962 He3 scale is its fit to He3 and He4 isotherm data, of which those of Keller [11, 12] are the most complete and accurate. Although Keller used a He4 thermometer in most of his isotherms, his observed P4’s can be related to P3’s by the direct interpolation equations described in Part I. In Part III Keller’s isotherms have been reanalyzed by the method of multiple variable least squares. Results of the comparison with the 1962 He3 and with the 1958 He4 scales are shown in figure 2. We note that the weighted average of TN, 62 is 1.52 mdeg below Tiso, whereas for the same isotherms TN, 58 averages 1.50 mdeg below Tiso. Since for these isotherms Tn,62—Tiso and TN,62—Tiso have average standard deviations of 1.2 mdeg and 1.0 mdeg, respectively, we conclude that not much would be gained by basing a He3 scale more directly on the isotherm data. In other words, the 1958 He4 scale, which is itself fundamentally based on these isotherm data, has evidently been an adequate interpolation parameter for fitting the He3 data to these isotherms.
Figure 2. Deviations of temperature scales from Keller’s (ref. [11, 12]) isotherm temperatures.
Tiso, as reanalyzed in Part III (ref. [7]). ● (T62—Tiso) for He4 isotherms; ■ (T62—Tiso) for He3 isotherms; ◯, ☐ (T58—Tiso) for He4 and He3 isotherms, respectively. To get T62, Keller’s He4 vapor pressure thermometer readings are converted to equivalent P3’s by means of direct P4−to−P3 interpolation equations derived in Part I (ref. [46]). Lengths of bars for the 1958 He4 scale deviations are equal to the standard deviation for Tiso as calculated in the analysis of the isotherm data. For 1962 He3 scale deviations we add on the standard deviation of the conversion from P4 to equivalent P3. The T62 and T58 bars terminate in solid and open triangles respectively.
Table 5 shows vapor pressures calculated from eq (9b) in steps of 10 mdeg. In table 6 we show dP/dT and T62—Tx in 0.1 deg steps, where T62 corresponds to eq (9b) and Tx to the various He3 scales in use in the past. We also have included on the far right the two He4 scale differences (TL55—T58) and (T55E—T58), as given in the NBS Monograph 10 “The 1958 He4 Scale of Temperatures” [2]. In a few recent publications an attempt has been made to “correct” the TL and TE He3 scales by adding these He4 scale “correction” terms. To convert these temperatures to the 1962 He3 scale it is necessary to apply the sum of columns 3 and 6 (or 4 and 7) to the “corrected TL” or “corrected TE” scales.
Table 5. He3 vapor pressures on the 1962 He3 scale at 0 °C and standard gravity, 980.665 cm/sec2.
The units of pressure are microns (10–3 mm) of mercury below 1 °K and millimeters of mercury at higher temperatures
| T | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0. 20 | 0.012 | 0. 024 | 0.046 | 0.084 | 0.144 | 0.239 | 0. 382 | 0. 592 | 0. 891 | 1.308 |
| 0.30 | 1.877 | 2. 636 | 3. 633 | 4. 921 | 6. 561 | 8. 619 | 11.173 | 14. 304 | 18.105 | 22. 673 |
| 0. 40 | 28.11 | 34. 54 | 42.08 | 50. 86 | 61.01 | 72.68 | 86. 02 | 101.17 | 118. 31 | 137. 61 |
| 0.50 | 159.2 | 183.3 | 210.1 | 239.8 | 272.5 | 308.5 | 347.9 | 391.1 | 438.0 | 489.1 |
| 0.60 | 544.4 | 604.3 | 668.9 | 738.4 | 813.0 | 893.0 | 978. 7 | 1070.1 | 1167. 6 | 1271.4 |
| 0.70 | 1381 | 1498 | 1622 | 1753 | 1892 | 2038 | 2192 | 2355 | 2525 | 2704 |
| 0.80 | 2892 | 3089 | 3295 | 3511 | 3736 | 3971 | 4216 | 4472 | 4739 | 5016 |
| 0. 90 | 5304 | 5603 | 5914 | 6237 | 6572 | 6918 | 7277 | 7649 | 8034 | 8431 |
| 1.00 | 8.842 | 9. 267 | 9.704 | 10.156 | 10. 622 | 11.102 | 11. 597 | 12.106 | 12. 631 | 13.170 |
| 1.10 | 13. 725 | 14. 295 | 14. 881 | 15. 484 | 16.102 | 16. 737 | 17. 388 | 18.056 | 18. 741 | 19.443 |
| 1.20 | 20.163 | 20. 900 | 21. 655 | 22. 428 | 23.220 | 24.029 | 24. 857 | 25. 704 | 26. 571 | 27. 456 |
| 1.30 | 28.360 | 29. 285 | 30. 229 | 31.193 | 32.177 | 33.181 | 34. 206 | 35.252 | 36. 319 | 37. 407 |
| 1.40 | 38. 516 | 39. 646 | 40.799 | 41.973 | 43.169 | 44. 388 | 45. 629 | 46. 893 | 48.179 | 49. 489 |
| 1.50 | 50.822 | 52.178 | 53. 558 | 54. 961 | 56.389 | 57.840 | 59. 316 | 60.817 | 62. 342 | 63.892 |
| 1.60 | 65.467 | 67.068 | 68. 694 | 70.345 | 72.022 | 73. 726 | 75. 455 | 77. 211 | 78. 993 | 80.802 |
| 1.70 | 82. 638 | 84. 501 | 86.391 | 88. 309 | 90.254 | 92. 228 | 94. 229 | 96. 258 | 98.315 | 100.402 |
| 1.80 | 102. 516 | 104. 660 | 106. 833 | 109.035 | 111.266 | 113. 527 | 115. 818 | 118.138 | 120. 489 | 122.870 |
| 1. 90 | 125.282 | 127. 724 | 130.197 | 132. 701 | 135.236 | 137. 803 | 140. 401 | 143.031 | 145. 692 | 148.386 |
| 2.00 | 151.112 | 153. 870 | 156. 661 | 159. 485 | 162.342 | 165. 232 | 168.155 | 171.112 | 174.102 | 177.126 |
| 2.10 | 180.184 | 183. 276 | 186. 403 | 189.564 | 192. 760 | 195. 990 | 199. 256 | 202. 557 | 205. 894 | 209.266 |
| 2. 20 | 212. 673 | 216.117 | 219.597 | 223.113 | 226.665 | 230. 255 | 233. 881 | 237. 544 | 241. 244 | 244.982 |
| 2. 30 | 248. 757 | 252. 570 | 256. 420 | 260. 309 | 264. 236 | 268. 202 | 272. 206 | 276. 249 | 280. 331 | 284. 452 |
| 2. 40 | 288. 613 | 292. 813 | 297.053 | 301.333 | 305. 653 | 310.013 | 314. 414 | 318.855 | 323.337 | 327. 861 |
| 2.50 | 332.425 | 337.031 | 341. 679 | 346. 368 | 351.100 | 355. 874 | 360. 690 | 365. 549 | 370. 450 | 375.395 |
| 2. 60 | 380.383 | 385. 414 | 390. 489 | 395. 608 | 400. 771 | 405. 978 | 411. 230 | 416. 526 | 421. 868 | 427. 254 |
| 2.70 | 432.686 | 438.164 | 443. 687 | 449. 256 | 454. 872 | 460. 534 | 466. 242 | 471. 998 | 477. 801 | 483. 651 |
| 2. 80 | 489. 549 | 495. 495 | 501.488 | 507. 531 | 513. 622 | 519. 762 | 525. 951 | 532.189 | 538. 477 | 544.815 |
| 2. 90 | 551. 203 | 557. 642 | 564.131 | 570.672 | 577.264 | 583. 907 | 590. 602 | 597.349 | 604.149 | 611.002 |
| 3.00 | 617.907 | 624. 866 | 631. 879 | 638. 945 | 646.066 | 653. 241 | 660. 472 | 667. 757 | 675.098 | 682. 496 |
| 3.10 | 689. 949 | 697. 459 | 705.026 | 712. 650 | 720.332 | 728.072 | 735. 871 | 743.728 | 751. 644 | 759. 620 |
| 3.20 3. 30 | 767.656 851.406 | 775. 753 860.130 | 783. 910 868. 918 | 792. 128 877. 773 | 800.408 | 808. 750 | 817.155 | 825. 622 | 834.153 | 842. 747 |
Table 6. The temperature derivative dP3/dT62 and deviations of various He3 temperature scales from the present 1962 He3 scale.
Columns 3,4, and 5 give differences of the TE, TL and TK He3 scales respectively from the 1962 He4 scale in the form (T62–Tx) expressed in millidegrees. In Columns 6 and 7 are reproduced the deviations of the 1955 He4 scales from the accepted 1958 He4 scale as these deviations have been utilized by some investigators in an attempt to “update” the TE and TL He3 scales.
| T | dP3/dT62 | T62−TLa | T62−TEa | T62−Tkb | (TL55−T58)c | (T55E−T58)c |
|---|---|---|---|---|---|---|
| °K | mm Hg/°K | mdeg | mdeg | mdeg | mdeg | mdeg |
| 0.2 | 0.001 | |||||
| .3 | .066 | −5.0 | −6.3 | |||
| .4 | .592 | −5.8 | −7.4 | |||
| .5 | 2.283 | −6.2 | −8.1 | |||
| .6 | 5.756 | −6.2 | −8.3 | |||
| .7 | 11.362 | −5.8 | −8.2 | –1.1 | 1.0 | |
| .8 | 19.234 | −5.2 | −7.8 | –1.2 | 1.1 | |
| .9 | 29.379 | −4.4 | −7.3 | –1.3 | 1.2 | |
| 1.0 | 41.745 | −3.6 | −6.7 | −4.0 | –1.5 | 1.3 |
| 1.1 | 56.26 | −2.9 | −6.1 | −3.7 | –1.6 | 1.4 |
| 1.2 | 72.84 | −2.1 | −5.4 | −3.2 | –1.7 | 1.5 |
| 1.3 | 91.44 | –1.5 | −4.9 | −2.5 | –1.8 | 1.5 |
| 1.4 | 111.99 | −0.9 | −4.4 | –1.6 | –1.9 | 1.6 |
| 1.5 | 134.45 | –.4 | −3.9 | −0.7 | −2.0 | 1.6 |
| 1.6 | 158.78 | .0 | −3.4 | 0.2 | −2.1 | 1.5 |
| 1.7 | 184.94 | .3 | −3.1 | 1.1 | −2.1 | 1.4 |
| 1.8 | 212.92 | .5 | −2.8 | 2.0 | −2.2 | 1.1 |
| 1.9 | 242.68 | .7 | −2.4 | 2.7 | −2.2 | 0.8 |
| 2.0 | 274.22 | .9 | −2.0 | 3.4 | −2.2 | 0.6 |
| 2.1 | 307.51 | 1.1 | –1.6 | 3.9 | −2.2 | 0.6 |
| 2.2 | 342.57 | 1.4 | –1.1 | 4.3 | −2.2 | 0.8 |
| 2.3 | 379.40 | 1.6 | −0.6 | 4.5 | −2.1 | 0.5 |
| 2.4 | 418.03 | 1.9 | 0.0 | 4.5 | −2.0 | 0.0 |
| 2.5 | 458.53 | 2.2 | 0.6 | 4.4 | –1.9 | −0.4 |
| 2.6 | 500.96 | 2.5 | 1.3 | 4.1 | –1.8 | −0.7 |
| 2.7 | 545.46 | 2.7 | 1.9 | 3.5 | –1 5 | −0.9 |
| 2.8 | 592.18 | 2.9 | 2.4 | 2.7 | –1.3 | –1.1 |
| 2.9 | 641.34 | 2.8 | 2.7 | 1.5 | −0.9 | –1.1 |
| 3.0 | 693.22 | 2.5 | 2.9 | 0.0 | −0.6 | –1.1 |
| 3.1 | 748.16 | 1.9 | 2.6 | −2.0 | −0.2 | –1.1 |
| 3.2 | 806.61 | 0.6 | 1.7 | −4.7 | 0.2 | −0.9 |
| 3.3 | 869.11 | –1.3 | 0.1 | −8.0 | 0.7 | −0.7 |
Detailed (P,T) and (T,P) tables have been published [8] by the Los Alamos Scientific Laboratory and in Part IV of this series.
In order to make the advantages of He3 as a vapor pressure thermometer more widely accessible, specially purified He3 is being made available for purchase3 for thermometry through the United States Atomic Energy Commission isotopes program.
If it were possible the authors would acknowledge in detail the aid given by numerous cryogenists in the course of the development and evaluation of the 1962 He3 scale of temperatures and the discussions concerning the scale by the Advisory Committee on Thermometry of the International Committee on Weights and Measures. We are especially indebted to F. G. Brickwedde, B. M. Abraham, H. van Dijk, M. Durieux, R. I. Joseph, W. E. Keller, D. W. Osborne, and J. H. van Vleck. Since our correspondence ran to several dozen letters it would be impractical to specify all of the participants and to elaborate on their various contributions.
Footnotes
This list of references applies to papers I, II, III, and IV of this series. For completeness and convenience, it is reproduced in its entirety at the end of each, paper.
Work performed under the auspices of the United States Atomic Energy Commission.
Figures in brackets indicate the literature references at the end of thir paper.
References*
- [1].Sydoriak S. G., Roberts T. R., and Sherman R. H., Proc 7th Intern. Conf. Low Temperature Physics, ed. Graham G. M. and Hollis-Hallett A. C. (Univ. of Toronto Press, Toronto, 1961), ch. 30, p. 717. [Google Scholar]
- [2].Brickwedde F. G., van Dijk H., Durieux M., Clement J. R., and Logan J. K., J. Res. NBS 64A (Phys. & Chem.), 1 (1960). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Brewer D. F., Sreedhar A. K., Kramers H. C., and Daunt J. G., Phys. Rev. 115, 836(1959). [Google Scholar]
- [4].Weinstock B., Abraham B. M., and Osborne D. W., Nuovo Cimento Suppl. 9, 310(1958). [Google Scholar]
- [5].Abraham B. M., Osborne D. W., and Weinstock B., Phys. Rev. 80, 366(1950). [Google Scholar]
- [6].Sydoriak S. G., Roberts T. R., and Sherman R. H., Paper II of this series. [Google Scholar]
- [7].Roberts T. R., Sherman R. H., and Sydoriak S. G., Paper III of this series. [Google Scholar]
- [8].Sherman R. H., Sydoriak S. G., and Roberts T. R., Paper IV of this series See also Los Alamos Scientific Lab. Rept. LAMS; 2701 (July 1962). [Google Scholar]
- [9].Sydoriak S. G. and Roberts T. R., Phys. Rev. 106, 175(1957). [Google Scholar]
- [10].Roberts T. R., Sydoriak S. G., and Sherman R. H., Proc. 4th Symp Temperature, Its Measurement and Control in Science and Industry, ed. Herzfeld C. M. (Reinhold Publ. Corp., New York, 1962), Vol. 3, pt. 1, p. 75. [Google Scholar]
- [11].Keller W. E., Phys. Rev. 97, 1 (1955); 100, 1790(1955). [Google Scholar]
- [12].Keller W. E., Phys. Rev. 98, 1571(1955). [Google Scholar]
- [13].Hoare F. E. and Zimmerman J. E., Rev. Sci. Instr. 30, 184(1959); [Google Scholar]; Swim R. T., Advances in Cryogenic Engineering, ed. Timmerhaus K. D. (Plenum Press, Inc., New York, 1960), Vol. 5, pp. 498–504. [Google Scholar]
- [14].Plumb H. H., Proc 10th Intern. Congr. Refrigeration, Copenhagen, 1959, ed. Jul M. and Jul A. M. S. (Pergamon Press, Paris, 1960), Vol. 1, pp. 184–187. [Google Scholar]
- [15].Durieux M., Thermometry at Liquid Helium and Liquid Hydrogen Temperatures, Thesis, Leiden Univ. (16 Mar. 1960). [Google Scholar]
- [16].Brickwedde F. G., Report on the Conference Agreement on the Helium Vapor-Pressure Scale of Temperatures, Conf. Physique des Basses Temperatures, Paris, 2–8 Septembre 1955, pp. 608–610. [Google Scholar]
- [17].Bleaney B. and Simon F., Trans. Faraday Soc. 35, 1205(1939). [Google Scholar]
- [18].Bleaney B. and Hull R. A., Proc. Roy. Soc. (London) 178A, 74(1941). [Google Scholar]
- [19].de Boer J. and Cohen E. G. D., Physica 17, 993(1951). [Google Scholar]
- [20].Becker E. W. and Misenta R., Phys. Rev. 93, 244(1954). [Google Scholar]
- [21].Becker E. W., Misenta R., and Schmeissner F., Z. Physik 137, 126(1954). [Google Scholar]
- [22].Mendelssohn K. and White G. K., Proc. Phys. Soc. (London) A63, 1328(1950). [Google Scholar]
- [23].Bowers R. and Mendelssohn K., Nature 163, 870(1949); [DOI] [PubMed] [Google Scholar]; Proc. Phys. Soc. (London) A63, 1318(1950). [Google Scholar]
- [24].Taconis K. W., Progress in Low Temperature Physics, ed. Gorter C. J. (North Holland Publ. Co., Amsterdam, The Netherlands, 1961), Vol. 3, p. 154. [Google Scholar]
- [25].van Dijk H. and Durieux M., Physica 24, 1(1958). [Google Scholar]
- [26].Sydoriak S. G. and Sommers H. S. Jr., Rev. Sci. Instr. 22, 915(1951). [Google Scholar]
- [27].Kapitza P., Phys J.. (U.S.S.R.) 4, 181(1941). [Google Scholar]
- [28].Fairbank H. A. and Wilks J., Proc. Roy. Soc. (London) A231, 545(1955). [Google Scholar]
- [29].Challis L. J., Dransfeld K., and Wilks J., Proc. Roy. Soc. (London) A260, 31(1961). [Google Scholar]
- [30].Kuang Wey-Yen, Zh Experim. i Teor. Fiz. (U.S.S.R.) 42, 921(1962); [Google Scholar]; Soviet Phys. JETP (English Transl.) 15, 635(1962). [Google Scholar]
- [31].Khalatnikov I.M., Zh. Experim. i Teor. Fiz. (U.S.S.R.) 22, 687(1952). [Google Scholar]
- [32].Sydoriak S. G. and Roberts T. R.. Phys. Rev. 118, 901(1960). [Google Scholar]
- [33].Mills R. L., Grilly E.R., and Sydoriak S. G., Ann. Phys. 12, 41(1961). [Google Scholar]
- [34].Cawood W. and Patterson H. S., Trans. Faraday Soc. 29, 522(1933). [Google Scholar]
- [35].Kistemaker J., Leiden Commun. 268d (1944); [Google Scholar]; Physica 11, 277(1944–1946); [Google Scholar]; Blaisdell B. E., J. Math. Phys. 19, 186(1940). [Google Scholar]
- [36].Brombacher W. G., Johnson D. P., and Cross J. L., Mercury Barometers and Manometers, NBS Mono. 8 (U.S. Govt. Printing Office, Washington, 1960). [Google Scholar]
- [37].Roberts T. R. and Sydoriak S. G., Phys. Rev. 103, 304(1956). [Google Scholar]
- [38].Esel’son B. N. and Berezniak N. G., Zh. Experim I Teor. Fiz. (U.S.S.R.) 30, 628(1956); [Google Scholar]; Soviet Phys. JETP (English Transl.) 3, 568(1956). [Google Scholar]
- [39].Sydoriak S. G., Grilly E. R., and Hammel E. F., Phys. Rev. 75, 303(1949). [Google Scholar]
- [40].Peshkov V. P., Zh. Experim i Teor. Fiz. (U.S.S.R.) 33, 833(1957); [Google Scholar]; Soviet Phys. JETP (English Transl.) 4, 645(1958). [Google Scholar]
- [41].van Dijk H. and Shoenberg D., Nature 164, 151(1949). [Google Scholar]
- [42].Chen T. C. and London F., Phys. Rev. 89, 1038(1953). [Google Scholar]
- [43].Keller W. E., Nature 178, 883(1956); [Google Scholar]; Clement J. R., Low Temperature Physics and Chemistry (Univ. of Wisconsin Press, Madison, 1958),p. 187 [Google Scholar]; (Proc. 5th Intern. Conf. Low Temperature Physics and Chemistry, Madison, Wis., 1957). [Google Scholar]
- [44].Goldstein L., Phys. Rev. 496, 155(1954); [Google Scholar]; Phys. Rev. 102, 1205(1956). [Google Scholar]
- [45].Sherman R. H., Roberts T. R., and Sydoriak S. G., Supplement au Bulletin de l’Institut International du Froid, Annexe 1961–5, p. 125(Proc. Meeting of Commission I of the International Institute of Refrigeration, London, 1961). [Google Scholar]
- [46].Sydoriak S. G. and Sherman R.H., Paper I of this series. [Google Scholar]
- [47].Deming W. E., Statistical Adjustment of Data (John Wiley & Sons, New York, 1943). [Google Scholar]
- [48].Roberts T. R., Sydoriak S. G., and Sherman R. T., see ref. [45], p. 115.
- [49].Grilly E. R. and Hammel E. F., Progress in Low Temperature Physics III (1961), pp. 113–152. [Google Scholar]
- [50].Kerr E. C. and Taylor R. D., Proc. 7th Intern. Conf. Low Temperature Physics, ch. 24, pp. 605–608, ed. Graham G. M. and Ilollis-IIallett A. C. (Univ. of Toronto Press, Toronto, 1961). [Google Scholar]
- [51].Sherman R. H. and Edeskuty F. J., Ann. Phys. 9, 522(1960). [Google Scholar]
- [52].Roberts T. R., Sherman R. H., Sydoriak S. G., and Brickwedde F. G., Progress in Low Temperature Physics IV, ch. 10 (North Holland Publ. Co., Amsterdam, The Netherlands, 1964), p. 480 [Google Scholar]
- [53].Mood A. M., Introduction to the Theory of Statistics, p. 299(McGraw-Hill, New York, N.Y., 1950). [Google Scholar]
- [54].Durieux M., Proces-Verbaux du Comite Consultatif de Thermometrie aupres du Comite International des Poids et Mesures, 6e Session, 1962 (Gauthier- Villars, Paris, France, 1964), p. 190. [Google Scholar]
- [55].Osborne D. W., private communication.
- [56].Berman R. and Mate C. F., Phil. Mag. 3, 461(1958). [Google Scholar]
- [57].JI van Dijk, Progr. Cryog. 2, p. 125(Academic Press, Inc., New York, N.Y., 1962). [Google Scholar]
- [58].Catalaud and G. Plumb H.H., Proc. 8th Intern. Conf. Low Temperature Physics, London, Sept. 16–22, 1962, ed. Davies R. O. (Butterworths, Washington, D.C., 1963), pp. 439–40. [Google Scholar]
- [59].Kerr E. C., Phys. Rev. 96, 551(1954). [Google Scholar]
- [60].Kerr E. C. and Taylor R. D., Ann. Phys. 20, 450(1962). [Google Scholar]
- [61].Anderson A. C., Salinger G. L., Steyert W. A., and Wheatley J. C., Phys. Rev. Letters 6, 331(1961); [Google Scholar]; Anderson A. C., Reese W., and Wheatley J. C., Phys. Rev. 130, 495(1963). [Google Scholar]
- [62].Strongin M., Zimmerman G. O., and Fairbank H. A., Phys. Rev. 128, 1983(1962). [Google Scholar]
- [63].Abraham B. M., Osborne D. W., and Weinstock B., Phys. Rev. 98, 551(1955). [Google Scholar]
- [64].drove G. R. and Haubach W. J. Jr.; see ref. [58], p. 441 For further information, write Gaseous Isotope Sales, Montsanto Research Corporation, Mound Laboratory, Miamisburg, Ohio. [Google Scholar]
- [65].Edwards D. O. and Daunt J. G., Phys. Rev. 124, 640(1961). [Google Scholar]
- [66].Sydoriak S. G., Roberts T. R., and Sherman R. H.; see ref. [58], pp. 437–8.
- [67].Hall J. A., Sixieme Rapport du Comite Consultatif de Thermometrie au Comite International des Poids et Mesures; see ref. [54]. [Google Scholar]
- [68].Stimson H. F., NBS Tech. News Bull. 47, No. 2, 30(February 1963); [Google Scholar]; Nature 197, 1055(1963). [Google Scholar]
- [69].Brickwedde F. G., Phys. Today 16, 24(1963). [Google Scholar]
- [70].Weber S., Commun. Kamerlingh Onnes Lab. Univ. Leiden; Suppl. 71b (1932), 264b and 264d (1936). [Google Scholar]
- [71].Weber S. and Schmidt G., Commuj. Kamerlingh Onnes Lab. Univ. Leiden; 264c (1936). [Google Scholar]
- [72].Chase C. E., Maxwell E., and Whitney W. M., Physica 26, 160(1960); [Google Scholar]; Chase C. E., Maxwell E., and Millctt W. E., Physica 27, 1129(1961). [Google Scholar]
- [73].Moore R. H. and Zcigler R. K., Trans. Am. Nuclear Soc. 1, 128–9 (1958); [Google Scholar]; The Solution of the General Least Squares Problem with Special Reference to High-Speed Computers, Los Alamos Scientific Lab. Rept. LA-2367 (March 4, 1960). [Google Scholar]
- [74].Roberts T. R. and Swartz B. K., Proc. 2d Symp. Liquid and Solid Helium Three, ed. Daunt J. G. (Ohio State Univ. Press, Columbus, 1960), p. 163. [Google Scholar]