Abstract
Diffusion kurtosis imaging (DKI) is a diffusion MRI (dMRI) technique to quantify brain microstructural properties. While DKI measures are sensitive to tissue alterations, they are also affected by signal alterations caused by imaging artifacts such as noise, motion and Gibbs ringing. Consequently, DKI often yields output parameter values (e.g. mean kurtosis; MK) that are implausible. These include implausible values that are outside of the range dictated by physics/biology, and visually apparent implausible values that form unexpected discontinuities, being too high or too low comparing with their neighborhood. These implausible values will introduce bias into any following data analyses (e.g. between-population statistical computation). Existing studies have attempted to correct implausible DKI parameter values in multiple ways; however, these approaches are not always effective. In this study, we propose a novel method for detecting and correcting voxels with implausible values to enable improved DKI parameter estimation. In particular, we focus on MK parameter estimation. We first characterize the relation between MK and alterations in the dMRI signal including diffusion weighted images (DWIs) and the baseline (b0) images. This is done by calculating MK for a range of synthetic DWI or b0 for each voxel, and generating curves (MK-curve) representing how alterations to the input dMRI signals affect the resulting output MK. We find that voxels with implausible MK values are more likely caused by artifacts in the b0 images than artifacts in DWIs with higher b-values. Accordingly, two characteristic b0 values, which define a range of synthetic b0 values that generate implausible MK values, are identified on the MK-curve. Based on this characterization, we propose an automatic approach for detection of voxels with implausible MK values by comparing a voxel’s original b0 signal to the identified two characteristic b0 values, along with a correction strategy to replace the original b0 in each detected implausible voxel with a synthetic b0 value computed from the MK-curve. We evaluate the method on a DKI phantom dataset and dMRI datasets from the Human Connectome Project (HCP), and we compare the proposed correction method with other previously proposed correction methods. Results show that our proposed method is able to identify and correct most voxels with implausible DKI parameter values as well as voxels with implausible diffusion tensor parameter values.
1. Introduction
Diffusion kurtosis imaging (DKI) (Jensen et al., 2005) is a clinically feasible extension to diffusion tensor imaging (DTI) (Basser et al., 1994), providing additional important microstructural information (Cheung et al., 2009). DTI relies on an assumption that the probability density function of water molecule displacement follows a Gaussian distribution. However, the diffusion of water molecules in biological tissues such as the human brain, can deviate considerably from a Gaussian distribution due to restriction and hindrance (e.g., cellular membranes) (Jensen et al., 2005), and due to partial volume effects, where multiple microstructural compartments reside in the same voxel (Westin et al., 2016; Yang et al., 2012). DKI uses a diffusion model that extends DTI to characterize non-Gaussian water molecule diffusion by estimating the excess kurtosis of the probability density function (Jensen et al., 2005). Changes in kurtosis are believed to reflect microstructural changes that alter molecular restrictions and tissue heterogeneity (Steven et al., 2014).
In DKI, a typical approach is to parameterize the diffusion MRI (dMRI) data by a diffusion tensor and by a kurtosis tensor (Tabesh et al., 2011). Therefore, in addition to the standard diffusion tensor parameters such as mean diffusivity (MD) and fractional anisotropy (FA) (Pierpaoli and Basser, 1996), DKI estimates kurtosis-tensor-specific parameters including mean kurtosis (MK), axial kurtosis (AK) and radial kurtosis (RK) (Hui et al., 2008; Jensen et al., 2005; Lu et al., 2006). These additional DKI parameters have been suggested to indicate the complexity of the microstructural environment of different brain tissues (Steven et al., 2014), and have been found useful in the identification and characterization of neurological changes in aging (Falangola et al., 2008; Grinberg et al., 2017), in rodent brain maturation (Cheung et al., 2009), as well as in neurological disorders, such as brain tumors (Raab et al., 2010), Alzheimer’s disease (Benitez et al., 2014), traumatic brain injury (Zhuo et al., 2012), and many more, as described in two recent reviews (Marrale et al., 2016; Steven et al., 2014).
DKI parameter maps (e.g. MK) that are calculated directly from the dMRI data, with no additional processing, often have implausible values. Physical considerations and empirical evidence from biological tissue indicate that MK should be positive and lower than 3 (Jensen et al., 2005; Tabesh et al., 2011). A broader definition of implausible voxels includes voxels with visually implausible MK values, which are defined here as voxels with too high or too low values that form unreasonable spatial patterns with neighboring voxels from the same brain tissue. Most visually implausible voxels have MK values that are outside of the expected range of 0–3. However, many of the visually implausible voxels are within the empirically set range, and still appear as very dark or very bright comparing with their neighborhood. Most common are implausibly low values which in their extreme case appear as very dark voxels within brain tissue. Typically, the number of voxels with visually appearing implausible values is considerable (as demonstrated in Figure 1a). If not corrected, these implausible values would introduce large biases in the processing of DKI parameters, incorrectly describing the true tissue microstructure, and affect any following DKI data analyses such as between-population statistical comparisons (Shaw and Jensen, 2017a). Resolving voxels with implausible values is therefore an important preprocessing task for any DKI analyses.
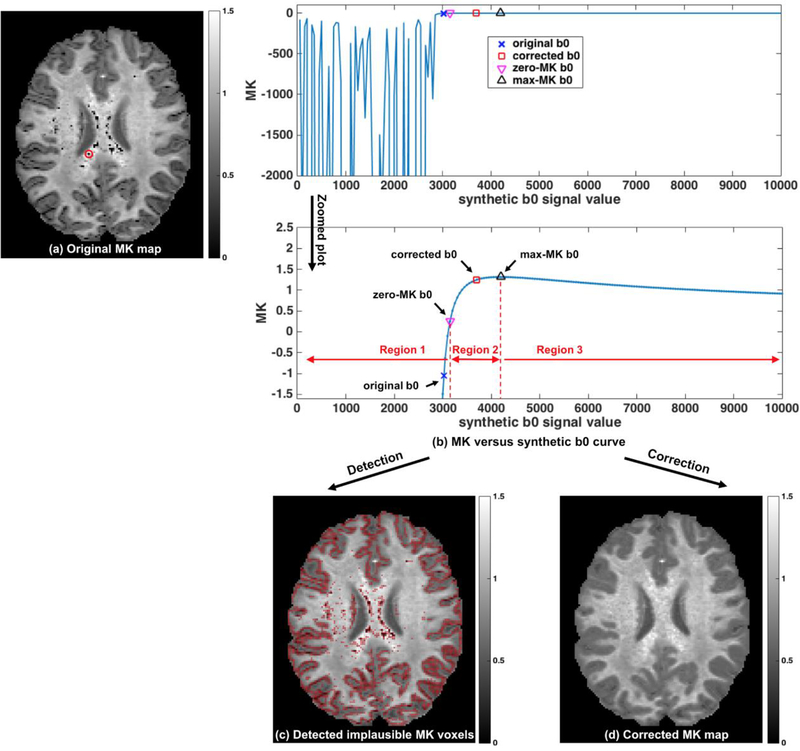
Figure 1. Method overview:
Implausible MK values are clearly visible in the initial MK map (a) as dark voxels. To characterize the relation between MK and b0, we construct the MK-curve (MK versus synthetic b0 as shown in (b); here, the MK-curve of one example voxel annotated in (a) is displayed). The curve identifies a range of low b0 values that generate unstable MK values, reaching to extremely low (and in some cases extremely high) MK values (left plot in b). In the stable MK region (right plot in b) we identify and calculate two characteristic b0 values of the MK-curve: the point where MK crosses 0 (zero-MK b0), and the point it reaches maximum (max-MK b0). These characteristic b0 values split the curve into three regions, where Region 1 is unstable with negative MK, Region 2 is a transition phase with positive MK, and Region 3 is stable with positive MK. Detection is performed by marking all voxels where the original b0 is lower than a voxel-specific threshold b0 value computed from the voxel’s zero-MK b0 and max-MK b0 (c). The detected voxels coincide with the visually apparent implausible MK values. Detected voxels are corrected by replacing their b0 value with the voxel-specific threshold b0, and recalculating MK (d). The resulting MK maps no longer show visually apparent implausible MK values.
Not all causes for implausible DKI parameter values are known yet, but they include image artifacts such as Gibbs ringing (Perrone et al., 2015; Veraart et al., 2016a), noise and subject motion (Shaw and Jensen, 2017a; Tabesh et al., 2011). These factors typically have more effect on DKI than DTI (Perrone et al., 2015; Shaw and Jensen, 2017a; Tabesh et al., 2011). Previously proposed approaches to resolve implausible parameter values mainly include imposing constraints during the model fitting and performing signal denoising. In the constrained fit approach, the empirically expected range is enforced during the model fit (e.g., constrained linear least squares (Tabesh et al., 2011)). As a result, when estimated by constrained fit, the DKI parameter values of all voxels are within the predefined parameter range. However, this approach does not correct visually apparent implausible values that are within the allowed range (e.g. positive values of MK that are near zero). Another common approach to resolve implausible parameter values is signal denoising, which is typically based on spatial operators that are applied on the dMRI data. For example, Gaussian smoothing has been applied to reduce the variability between neighboring voxels (Tabesh et al., 2011). More advanced signal denoising methods have applied techniques such as non-local formulation filtering (Chen et al., 2017; Zhou et al., 2015) and principal component analysis (PCA) (Manjón et al., 2013; Veraart et al., 2016c), as reviewed by Shaw and Jensen (Shaw and Jensen, 2017a). Denoising increases the signal-to-noise-ratio (SNR) in dMRI data, which could improve kurtosis/diffusion tensor parameter estimation and is expected to reduce the occurrence of implausible values. However, denoising is normally applied on the entire image, which also affects voxels where the parameter values do not require altering. This could reduce the contrast variability and remove subtle spatial details that may be of clinical/neurological importance. In addition, most denoising methods assume that neighboring voxels are from the same brain structure and thus share similar dMRI information. This assumption is not valid for voxels at tissue boundaries, whose neighbors include multiple brain structures. Other approaches reduce the occurrence of implausible kurtosis values by specifically reducing the effect of Gibbs ringing (Kellner et al., 2016; Perrone et al., 2015; Veraart et al., 2016a). However, these approaches are less effective in voxels where the implausible values are not directly caused by Gibbs ringing. While applying the above mentioned approaches reduces the occurrence of implausible parameters in DKI, they are not effective enough to resolve it completely.
In this study, we propose a novel method for detecting and correcting voxels with implausible DKI parameters, focusing on MK. We characterize the relation between artifactual alterations to the input dMRI signals in a single image (i.e., the baseline (b0) or a diffusion-weighted image (DWI)) and the resulting output MK values. To do so, we perform voxel-wise experiments where we synthetically alter one value (either b0 or DWI) and recalculate MK. These synthetic alterations include a large range of possible values to encompass possible alterations due to effects like noise, Gibbs ringing, motion, etc. As a result, we obtain a curve representing MK as a function of synthetic DWI or b0 (the MK-curve) for each image voxel.
We identify that implausible MK values are more likely caused by artifacts in the b0 images than artifacts in DWIs with higher b-values. Further, we identify two characteristic b0 values on the synthetic b0 MK-curve for each voxel, which help us identify a range of synthetic b0 values that generate implausible MK values. Based on this characterization, we propose an automatic approach to detect voxels with implausible MK values, and we demonstrate successful detection performance in in-vivo human dMRI data. Finally, based on the characterization of the MK-curve we propose a correction approach, where the original b0 in each detected implausible MK voxel is replaced with a synthetic b0 value computed from the curve.
Instead of changing the entire dMRI volume, our proposed method minimally changes the dMRI data by correcting only the b0 signals of those voxels that were detected to have implausible MK values. Moreover, the proposed detection and correction method is voxel-specific, based on the actual measurements of each voxel from its MK-curve without requiring any global constraints (e.g. empirically set range of MK values) or spatial neighborhood information. We evaluate the method on a DKI phantom dataset (Kuder et al., 2012) and on 10 dMRI datasets from the Human Connectome Project (HCP) (Van Essen et al., 2013), and we compare the quality of the correction with other previously proposed correction methods.
2. Methods
2.1. DKI model fit, computation of DKI parameters, and evaluation datasets
The DKI model expresses the DW signals as (Tabesh et al., 2011):
| (1) |
where S(n, b) is the DW signal of a voxel given the diffusion weighting b along the gradient direction n=[n1, n2, n3], S0 is the non-DW b0 signal, Dij and Kijkl are the elements of the diffusion tensor D and the kurtosis tensor K, respectively, and D= trace(D) / 3 is the mean diffusivity. A weighted linear least square (WLLS) fitting (Veraart et al., 2013) was applied to compute the kurtosis tensor K and the diffusion tensor D. MK was computed as the average of the directional kurtoses derived from K (Tabesh et al., 2011). In addition to MK, we computed two other kurtosis tensor parameters: axial kurtosis (AK), which is the kurtosis in the direction of the highest diffusion, and radial kurtosis (RK), which is the mean diffusional kurtosis perpendicular to the direction of the highest diffusion (Tabesh et al., 2011); as well as two diffusion tensor parameters derived from D: mean diffusivity (MD) and fractional anisotropy (FA) (Pierpaoli and Basser, 1996).
The proposed method for detection and correction of voxels with implausible MK values is evaluated with in-vivo human multi-shell dMRI datasets from the Human Connectome Project (HCP) (Van Essen et al., 2013). 10 HCP datasets (age: 29.1 ± 4.0 years; gender: 5 females and 5 males) were randomly selected from the HCP repository1. The HCP datasets were acquired with a high quality image acquisition protocol using a customized Connectome Siemens Skyra scanner and were processed following the HCP minimum processing pipeline (Glasser et al., 2013), which includes brain masking, motion correction, eddy current correction and EPI distortion correction. The acquisition parameters used for the diffusion MR data were TE = 89.5 ms, TR=5520 ms, phase partial Fourier = 6/8, and voxel size =1.25×1.25×1.25 mm. A total of 288 images were acquired in each dMRI dataset (acquired in both AP and PA phase encoding, to correct for EPI distortions), including 18 baseline images with a low diffusion weighting b = 5 s/mm2 and 270 diffusion weighted images evenly distributed at three shells of b=1000/2000/3000 s/mm2. An average b0 image across the 18 b0 images was computed for the DKI model fit. The HCP-provided brain masks were used to exclude background voxels (e.g. from the skull and non-brain regions).
We also performed experimental evaluation on a DKI phantom dataset (Kuder et al., 2012) to quantify difference from ground truth values, and to help in tuning parameters of the proposed method. (Kuder et al., 2012) phantom consists of parallel polyester fibers wound on a circular spindle immersed in agarose gel. Full description of this phantom is available in (Laun et al., 2009) and in (Kuder et al., 2012). Water molecule displacement is restricted between the densely packed fibers, yielding diffusivity and kurtosis levels similar to those of white matter. The gel region is isotropic and has low kurtosis, resembling cerebrospinal fluid (CSF). Diffusion data of the phantom was downloaded from the open source project: “Fiber Phantom for Kurtosis Imaging”2. The data acquired on a 3T MR scanner (Magnetom Trio; Siemens Healthcare, Erlangen, Germany) using a single-shot, twice refocused spin-echo echo-planar imaging diffusion sequence. The acquisition parameters were TE = 165 ms, TR = 2000 ms, partial Fourier = 6/8, single slice with voxel size = 2.5×2.5×2.5 mm, and 16 b-values from 0 to 10,000 s/mm2. In our study, we used the images from b=0/1000/2000/3000 s/mm2 to be consistent with the in-vivo human data. The fiber and agarose gel regions were segmented based on the computed MD map (using a threshold at 0.001 mm2/s) using the SlicerDMRI extension (http://dmri.slicer.org) (Norton et al., 2017) in 3D Slicer (www.slicer.org).
Finally, our proposed method was also applied on an additional dataset with a more conventional DKI acquisition parameters, that are more likely to be used in clinical studies. This data was acquired on a 3T MR scanner (Magnetom Verio; Siemens Healthcare, Erlangen, Germany) and acquisition parameters were TE = 109 ms, TR = 15800 ms, phase partial Fourier = 6/8, voxel size = 2×2×2 mm3, 5 b0 images, and two shells of b=1000/3000 s/mm2, with the same 30 directions in each shell. An average b0 image across the 5 b0 images was used for DKI model fit of this data. This data was acquired with approval of the local ethics board. We used this data to demonstrate the performance of the proposed method on data that was expected to have more imaging artifacts than the HCP data that was acquired using a high quality imaging protocol and processed using a more sophisticated pipeline.
2.2. Method overview
Below we propose a processing approach that is designed for detection and correction of voxels with implausible MK values to enable improved DKI parameter estimation. The method includes (see Figure 1 for an overview) an automatic approach for detection of voxels with implausible MK values, followed by a voxel-specific correction strategy for these detected voxels. The computational steps are listed in the pseudocode in Algorithm 1 and are detailed in the next two sections.
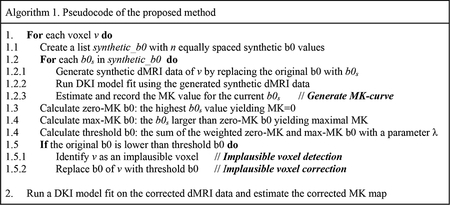
2.3. Generating the MK-curve
To detect voxels with implausible MK values, we first characterized the relation between alterations in the dMRI signal (b0 or DWIs) and their resulting MK value. The characterization took place by generating novel MK-curves: “MK versus synthetic b0” and “MK versus synthetic DWI” curves. The MK-curves synthetically simulate all possible values that a single acquired dMRI signal (either b0 or DWI) may have. Therefore, the MK-curve represents all possible artifactual MK values that could be caused by a change to a single b0 or DWI value.
To generate the MK versus b0 curve, for each voxel we replaced the original b0 value with a range of synthetic values while not altering any DWIs. To generate synthetic b0 values, we used 200 equally spaced values in the range of 0.1 to 2 times the average b0 (calculated from the entire volume, within the brain mask). This synthetic b0 range was large enough to include very small and very large b0 values that could possibly result from any imaging artifacts. We used a weighted linear least square (WLLS) fitting (Veraart et al., 2013) to estimate MK (as described in Section 2.1) for each synthetic data experiment. As a result, we could plot the MK value for each synthetic b0 signal (Figure 1b). The MK versus synthetic DWI curve was similarly generated by replacing a single DWI with a range of synthetic values and calculating MK for each synthetic dataset. As demonstrated below in the Results, in certain ranges, slight b0 differences yielded dramatically variable MK values, whereas differences in DWIs only led to small MK variability, which suggests that noise or artifacts in the b0 are more likely to cause voxels with implausible MK values than noise or artifacts in the DWIs.
The MK versus synthetic b0 curves have a similar shape for all brain tissue/regions (see Figure 1b for the MK-curve from one example voxel; see Figure 2 for the MK-curves from multiple voxels): Looking from right to left, and starting from the maximal synthetic b0, as the synthetic b0 value decreases, the MK values slightly increase until reaching a peak, which we define as a characteristic b0 value and call max- MK b0. The curve then continues with a sharp decrease in the MK value, which crosses MK=0 (i.e., zero mean kurtosis) at another characteristic b0 value that we define and call zero-MK b0. Then, when the synthetic b0 value is further reduced, the MK value enters an unstable phase where MK fluctuates dramatically, often reaching extreme low and high values, where very small changes in the b0 value cause very large changes in the MK value. As a comparison, for the MK versus synthetic DWI curves (Supplementary Figure S1), voxels had different MK-curve shapes, and there was not a typical unstable region on the curves.
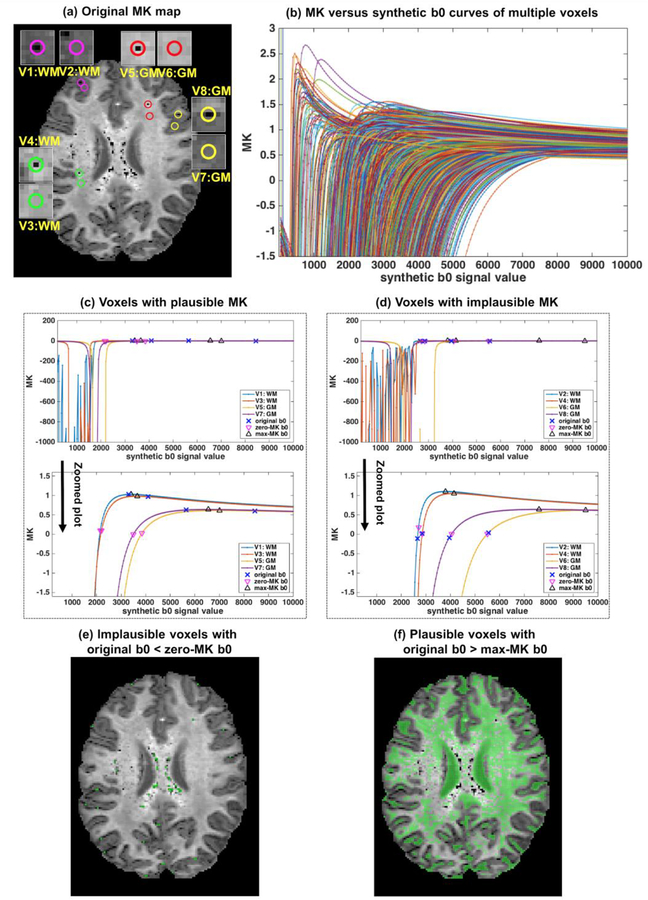
Figure 2. Characterization of MK using the MK-curve.
MK versus synthetic b0 curves from all voxels on the example image slice (a) have a similar shape (b), allowing the definition of zero-MK b0 and max-MK b0. The definition is demonstrated for 8 example voxels shown as circles in (a), including 4 that are visually plausible (V1, V3, V5 and V7 with MK-curves in (c)) and 4 that are visually implausible (V2, V4, V6 and V8 with MK-curves in (d)), from white and gray matter. Over the entire slice, voxels whose original b0 value was lower than the zero-MK b0 values (colored in green as shown in (e)) had visually implausible MK values. Voxels whose original b0 value was higher than the max-MK b0 values (colored in green as shown in (f)) had visually plausible MK values.
2.4. Detection and correction of voxels with implausible MK using the MK-curve
The two identified characteristic b0 values, i.e., zero-MK b0 and max-MK b0, divide the MK-curve into three regions (Figure 1b) that help in detecting which voxels have implausible values. The leftmost region (Region 1), with b0 values below the zero-MK b0 value, is an unstable region where small changes in the synthetic b0 result in erratic MK changes reaching extreme values. This region is characterized by having very low or negative diffusion tensor eigenvalues. Therefore, all voxels whose original b0 was in this range were defined as implausible, even if by chance the MK fluctuations resulted in positive values. The rightmost region (Region 3) is a stable region (i.e., small changes in b0 yield small changes in MK) with b0 values higher than the max-MK b0 value. MK values in this region are always positive and within the plausible range. Therefore, all voxels whose original b0 was higher than max-MK b0 were identified as plausible. The remaining region on the MK-curve is in the range between the zero-MK and max-MK b0 values (Region 2). MK and diffusion tensor eigenvalues in this range are always positive. However, many voxels that had an original b0 within this range visually appear as implausibly low.
To determine the implausibility of MK values in voxels whose original b0 was within Region 2, we set a threshold on the MK-curve for each voxel, and we defined its MK value as implausible if its original b0 was below this threshold. The threshold is defined as a function of the zero-MK b0 and the max-MK b0, as:
| (2) |
Where λ ∈ [0, 1] is a weighting parameter (the suggested range for λ is 0.3–0.5 see below). Since the computed b0threshoid is voxel-specific, each voxel can have a different range of values which are defined as implausible, rather than setting a global MK threshold for all voxels.
Then, all voxels that were identified to have implausible values were corrected by replacing their original b0 with their voxel-specific b0threshoid. In this way, we could make the smallest change to the b0 image, while correcting MK to a value that will no longer be detected as implausible.
2.5. Quantitative evaluation
The definition of implausible values is based on visual inspection, and as such many of the evaluations are qualitative rather than quantitative. However, the availability of the phantom data allows for a more quantitative evaluation approach. The ground truth MK values of the phantom data are not known. However, due to the construction of this phantom it is reasonable to assume that the MK values in the polyester fiber area would be homogenous, and higher than the MK values in the isotropic agarose gel area. Therefore, and assuming no systematic bias in MK, we can expect that noise and other image artifacts would generate a distribution that is centered at the real MK value. The expected underlying MK value was thus identified by plotting the histogram of MK of all voxels from the fiber region, versus those from the gel region, verifying that the peak of the distribution in the fiber region is higher than that of the gel region, and assigning the peaks as the “ground truth” MK value for the fiber region and for the gel region (see Figure 3). To quantify deviation from the ground truth we then calculated for each voxel, v, its absolute bias: | MKv - MKpeak | / MKpeak and then calculated the mean and standard deviation (std) of the absolute bias across all voxels in a region (fiber region or gel region). Using the mean and std of the absolute bias we can then compare the performance of our algorithm for different λ values, as well as compare with other correction methods, or with the uncorrected raw data.
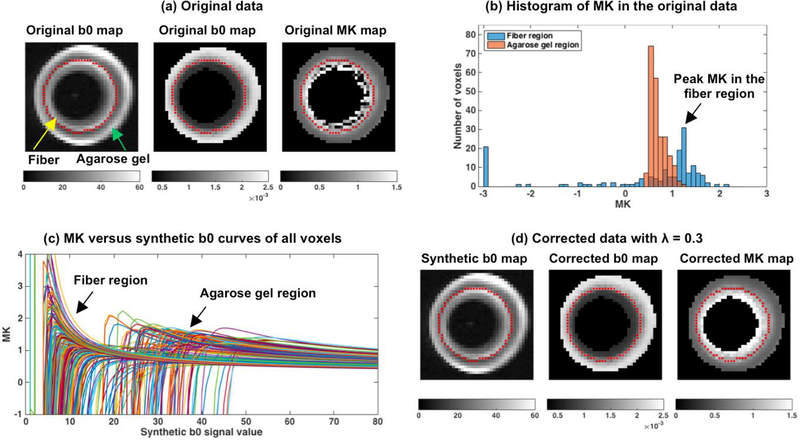
Figure 3. Detection and correction of implausible MK voxels on DKI phantom data.
The phantom consists of a fiber region and an agarose gel region (a). Homogenous and high MK is expected in the fiber region, however many voxels on the original MK map in this region have very low values. In the agarose gel region MK values appear homogeneous. Histogram of the MK values in the original data (b) shows a wide distribution of MK values in the fiber region extending to low or negative values that overlap with the distribution of MK values in the agarose gel region. The peak of the MK distribution in the fiber region (b) is selected as a reference point (“ground truth” MK value) to which bias is estimated (see Figure 4). MK versus synthetic b0 curves from all voxels were computed (c), showing the characteristic shape of the MK-curve. After correction (using λ = 0.3 which had the lowest mean absolute bias - Figure 4), the MK map appears homogeneous and with values that are higher than the agarose gel values (d). The b0 and MD maps after correction are visually similar to the original data.
2.6. Comparison with other correction methods
We compared the proposed method (referred to as the MK-curve method in the rest of the paper) with four correction approaches that are currently used in leading DKI implementation packages: 1) The Gaussian smoothing method (Tabesh et al., 2011) to average signals of neighboring voxels (implemented in the Dipy package3), 2) The constrained fit method (Tabesh et al., 2011), which imposes constraints on minimum and maximum kurtosis values to ensure physically and/or biologically plausible parameter estimates (implemented in the NYU-DiffusionMRI repository via the Diffusion-Kurtosis-Imaging package4), 3) The Gibbs removal method (Kellner et al., 2016) that is designed to remove Gibbs ringing based on local subvoxel-shifts (implemented in the unring package5), and 4) The Marchenko-Pastur-BasedPCA (MPPCA) method (Veraart et al., 2016c) that exploits data redundancy by estimating spatial noise level in a local neighborhood of each voxel (implemented in the NYU-DiffusionMRI repository via the mppca_denoise package6). Tuning parameters for each method were set to those suggested by the software packages. Quantitative comparisons were made on the DKI phantom data, and qualitative visual comparisons were made on the in-vivo data. We note that MPPCA could not be applied on the DKI phantom data, since it requires more than a single slice. For the in-vivo data, the different methods were applied on the already preprocessed HCP data. This is not optimal for the MPPCA, Gibbs removal and Gaussian smoothing methods which should ideally be applied prior to any preprocessing. On the other hand, the constrained fit method and our proposed MK-curve method are model-based approaches that require fitting the DKI model, which is more accurate as a step that follows any image corrections and preprocessing. Nevertheless, additional experiments (see Supplementary Figure S2) showed that the order of application made little difference to the ability to correct implausible MK values.
3. Results
In this section, we first demonstrate how the MK-curve characterizes voxels with implausible MK values, we then select the free parameter λ, followed by showing the detection and correction results on the test datasets. Finally, we quantitatively and visually compare the proposed MK-curve method with other correction methods.
3.1. Characterization of voxels with implausible MK values
To characterize the relation between dMRI signals (b0 or DWI) and MK values, we constructed MK versus synthetic b0 curves and MK versus synthetic DWI curves. Plotting the MK versus synthetic b0 curves for all the voxels within an example image slice of a single subject (Figure 2a) shows that all curves had a similar shape. The similar shape leads to the definition of the zero-MK b0 and max-MK b0 of the curve (see Section 2.2). We note that these two characteristic b0 value can be identified for all voxels, except for some background noise voxels that entered the brain mask. At b0 values below zero- MK b0, the curves had an erratic behavior, fluctuating between extreme MK values (see Figure 2b). To demonstrate the features of the MK versus b0 curve we chose 8 example voxels that their unprocessed MK values were visually plausible or visually implausible (Figure 2a), from either white or gray matter. The curves show that in some b0 ranges, altering the b0 value leads to large changes in MK. In voxels with originally plausible MK (Figure 2b), changing the b0 may lead to implausible MK values. In voxels with originally implausible MK (Figure 2c), changing the b0 may lead to plausible values.
As explained in the Methods (Section 2.2), the two identified characteristic b0 values divide the MK versus synthetic b0 curve into three regions. All voxels with original b0 that is lower than zero-MK (Region 1) had visually apparent implausible MK values (Figure 2e). All voxels with b0 higher than max- MK (Region 3) had visually plausible MK values (Figure 2f). The remaining voxels in the region between zero-MK and max-MK b0 values (Region 2) had both apparent plausible and apparent implausible MK values.
Unlike the synthetic b0, the MK versus synthetic DWI curves do not show common patterns (Supplementary Figure S1). Changes of the synthetic b=1000, b=2000 or b=3000 values in voxels that originally had visually plausible MK values did not have much effect on the MK value, and did not lead to implausible MK values. This suggests that an artifact in a single DWI would only subtly change the MK value, and is not typically sufficient to cause implausible MK values. In voxels that originally had visually implausible MK voxels, changing the DWI signal did not always map the MK value back to the plausible range, and when it did, it often required a very large increase in the signal value. This suggests that altering a single DWI is less likely to provide a sufficient solution for correcting voxels with implausible MK values.
3.2. Detecting and correcting voxels with implausible MK values
Applying the MK-curve detection and correction method requires a selection of a λ value. To select a λ value we quantitatively compared the bias measure on the DKI phantom, and qualitatively compared the results of the in-vivo data for varying λ values.
Similar to the in vivo data, the DKI phantom data displayed many voxels with visually implausible MK values (“black holes”), all in the fiber region (see Figure 3a). These implausible values appeared despite the high quality of the acquisition, and despite the lack of motion artifacts. Plotting the histogram of the MK values in the fiber region and in the gel region identified a peak value of MK = 0.6 for the gel region, and MK = 1.3 for the fiber region. In the uncorrected data the distribution of the MK values in the fiber area had a long tail towards small and negative values (Figure 3b), which yielded a mean absolute bias of 0.759 with std of 1.100, reflecting the visually implausible MK values and the inhomogeneous appearing MK map. In the gel region, the distribution of the MK was relatively homogeneous, yielding a bias measure of 0.188 with std of 0.129. All voxels in the fiber and gel regions showed the distinctive shape of the MK versus synthetic b0 curves (Figure 3c), which enables the application of the MK-curve method. Following the application of the MK-curve detection and correction algorithm, the mean and std bias scores for varying λ values show improvement comparing with the raw data for all λ values (Figure 4a). The lowest mean absolute bias was 0.122 with std of 0.120 at λ = 0.3. Across the different λ values, the range between 0.2 to 0.5 resulted with a similar mean absolute bias values that were lower than that of the gel region. The low bias scores in this range of λ is aligned with a visual inspection (Figure 4b), showing that after correction all visually implausible MK values were no longer implausible. Histograms of the corrected MK values under λ = 0.3 and 0.5 in the fiber region show that after correction the MK values of all fiber voxels are mapped to values larger than MK=1, while the peak MK value of the corrected data remains the same as the peak MK value of the original data. However, with a lower λ value (e.g. λ = 0.1), visually implausible MK voxels were not sufficiently corrected; on the other hand, with a larger λ value (e.g. λ = 0.7 and 0.9), the peak MK value of the histogram of the corrected MK values deviated from the peak MK value of the original data, suggesting over estimation. Our method did not detect, and therefore did not change any voxels in the agarose gel region regardless of λ selection. Of note, in this phantom dataset RK had a similar pattern of implausible values as MK (Supplementary Figure S3), and following correction (using λ = 0.3), had much reduced bias. AK, FA, and MD did not show clear implausible values on the original images. Still, the computed mean absolute bias was slightly improved following the application of the MK-curve method. The histogram of values preserved its peak, and the maps look very similar to the uncorrected maps (Supplementary Figure S3).
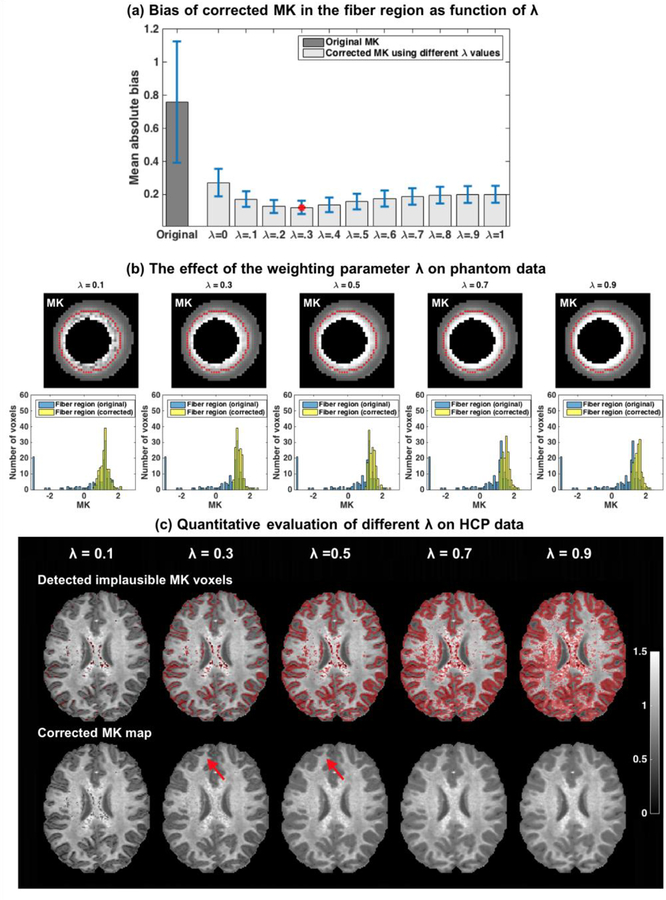
Figure 4: The effect of the weighting parameter λ.
Evaluating the mean and std absolute bias in the fiber region of the DKI phantom for varying λ values shows that the mean absolute bias was always lower than the original mean absolute bias on the raw data, suggesting that MK estimation is improved for all λ values (error bars in (a) represent std/3). The lowest bias was for λ = 0.3, although similar values were found in the range of 0.2 to 0.5. The corrected MK maps show that with a lower λ value (e.g. λ = 0.1), visually implausible MK voxels were not sufficiently corrected. The histograms suggest that for a larger λ value (e.g. λ = 0.7 and 0.9) MK was overestimated. The in-vivo data provided best results for λ = 0.5 and λ = 0.3 (c), although λ = 0.5 was more inclusive in the identification of implausible voxels in the interface between gray and white matter (red arrows). For λ = 0.1 not all visually implausible MK voxels were detected. Higher λ values (λ = 0.7 and 0.9) resulted in overinclusive detection of voxels that visually appeared to be plausible.
In the in vivo human data, which has a larger distribution of underlying MK values than the DKI phantom (due to multiple tissue types, partial volume effects, etc.), we do not have a ground truth measure to compare with, and therefore we visually compared the results for varying λ values. For λ = 0.1, many voxels with apparently low MK values were not detected. For λ = 0.3 and λ = 0.5, almost all visually implausible voxels were detected and corrected. λ = 0.5 resulted with slightly better performance compared to λ = 0.3 for voxels in the interface between white and gray matter region (see arrows in Figure 4c). As λ increases to 0.7 and 0.9, more voxels were identified as implausible including many that originally appeared to be plausible.
Taken together, the phantom and in vivo experiments suggest that 0.3 to 0.5 is a preferred range for the selection of λ. This range provides a balance in detecting and correcting as many as possible voxels with visually implausible MK values, while avoiding changing voxels that appeared to have visually plausible values. The fiber area in the phantom resembles white matter areas in the brain, however, it appears that a higher lambda is more efficient in the interface between gray and white matter, which was not appropriately modeled in the phantom experiment. Therefore, in the following in-vivo experiments we used λ = 0.5.
Applying our detection and correction algorithm on the 10 HCP datasets (Figure 5) shows that all voxels with visually apparent low MK values (dark voxels) and visually apparent high MK values (a small number of bright voxels, typically outside the brain boundary) in the original MK maps were successfully identified by the detection method as implausible MK voxels. The locations of identified voxels were in highly organized white matter structures (e.g., the corpus callosum) and at the gray/white matter interface. The detection of voxels with implausible MK values delineated the gray/white matter interface. All of the voxels with MK values outside the plausible range of 0 to 3 were identified as implausible, except for a very small number of voxels outside the brain, where an overinclusive mask caused some background voxels to be analyzed (less than 0.001% of the voxels). After correction, voxels that initially had implausible MK values appeared to now have visually plausible values, no longer appearing as too dark or too bright.
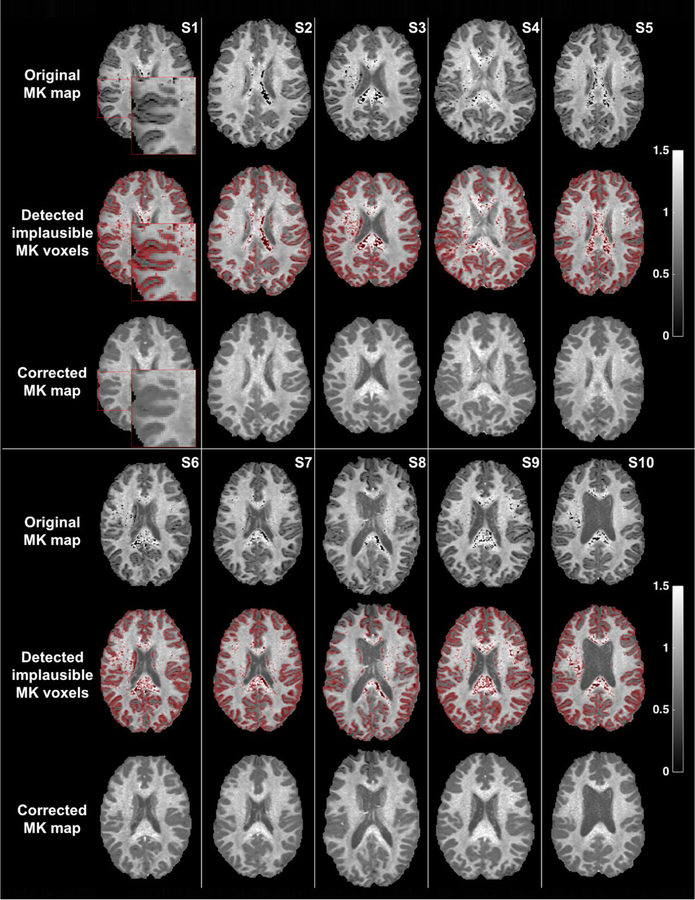
Figure 5. Detection and correction of voxels with implausible MK values on each of the 10 datasets.
An inset image for Subject-1 enlarges part of the image, showing that in this high resolution data the gray/white matter interface is visually implausible. Accordingly, the detected voxels almost perfectly delineate the gray/white matter interface, in addition to voxels in deep white matter structures that are detected as having implausible MK values.
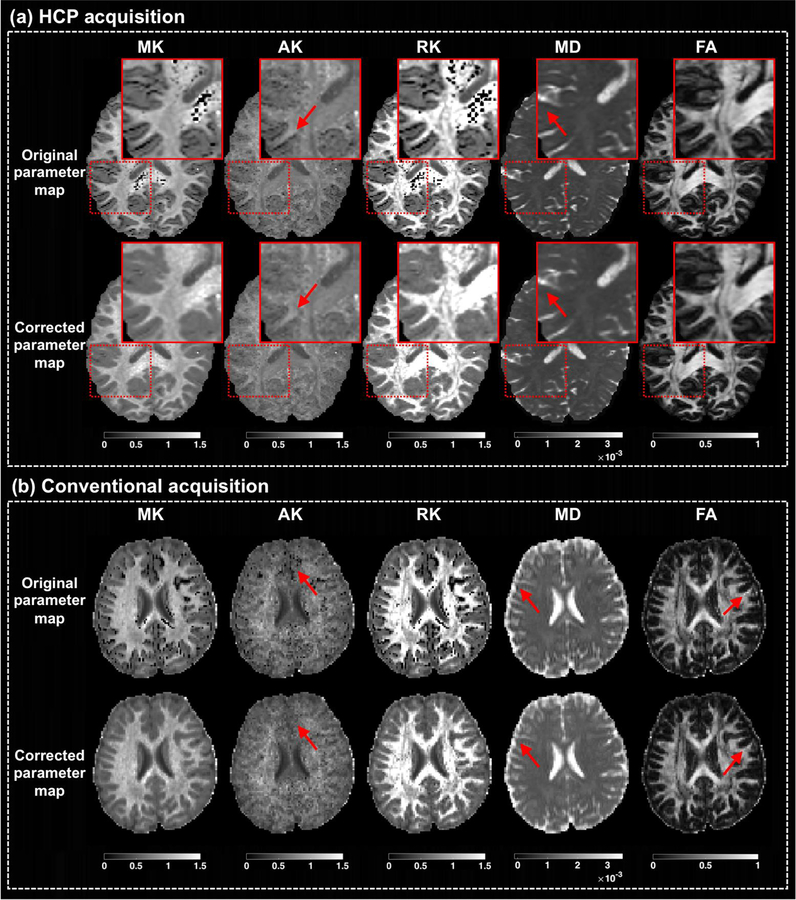
Similar to the DKI phantom (Supplementary Figure S3), the MK-curve correction resulted also in improved RK on the human data, where many implausible values were visible on the original map, and no longer appeared implausible on the corrected map (Figure 6). Changes in AK, MD and FA are more subtle (Figure 6). The effect of the correction methods on AK was similar to that on MK and RK, i.e., the original maps had apparently implausible values (dark voxels), while the corrected maps appeared to be plausible after correction. There were only a few voxels with implausible MD (dark voxels) and FA (bright voxels) values on the original maps, and most of them appeared to be plausible after corrections. These voxels with implausible MD and FA are more visible in the data obtained with conventional acquisition, and were associated with negative diffusion tensor eigenvalues. Even though our algorithm did not directly aim to detect and correct voxels with implausible DTI parameters, all voxels with negative diffusion tensor eigenvalues across all datasets under study were detected as implausible (see Supplementary Figure S4c for a visualization), and all of these voxels except for some background voxels (less than 0.001%) were corrected to a plausible range with positive diffusion tensor eigenvalues (see Supplementary Table S1). Of note, in the original b0 image of the datasets included in this study (see Supplementary Figure S4d for an example), the detected (and the visually appearing) implausible MK voxels did not have visually implausible b0 values. Composing maps from the voxel-wise computed zero- MK b0 and max-MK b0 (Supplementary Figures S4f and S4g) shows that in the white matter the contrast of these maps is very similar, and close to the original b0 image, demonstrating again that slight b0 differences can cause large MK changes. Comparing with white matter voxels, voxels with CSF appear much darker on both the zero-MK b0 and max-MK b0 maps, and these values were much lower than the actual original b0 values in the same voxels. This means that the actual b0 values of all CSF voxels were in the rightmost region on the MK-curve (i.e., Region 3 where MK values are plausible; see Figure 1), suggesting that CSF voxels (low anisotropy and high diffusivity) are less likely to show implausible MK values, similar to the agarose gel region in the DKI phantom that did not show any implausible MK values.
Figure 6: Correction of additional DKI and DTI parameters.
The output of the MK-curve approach is compared with the original images for the mean kurtosis (MK), axial kurtosis (AK), and radial kurtosis (RK), as well as two diffusion tensor parameter maps: mean diffusivity (MD) and fractional anisotropy (FA). For each parameter map, the values are truncated to the range displayed on the colorbar. For demonstration purposes, results are shown in randomly selected subjects, although similar results were observed for all subjects. Images are shown from the high quality HCP data and from a dataset with more conventional DKI acquisition protocol, in which the derived DKI and DTI parameters are more affected.
3.3. Comparison with other correction methods
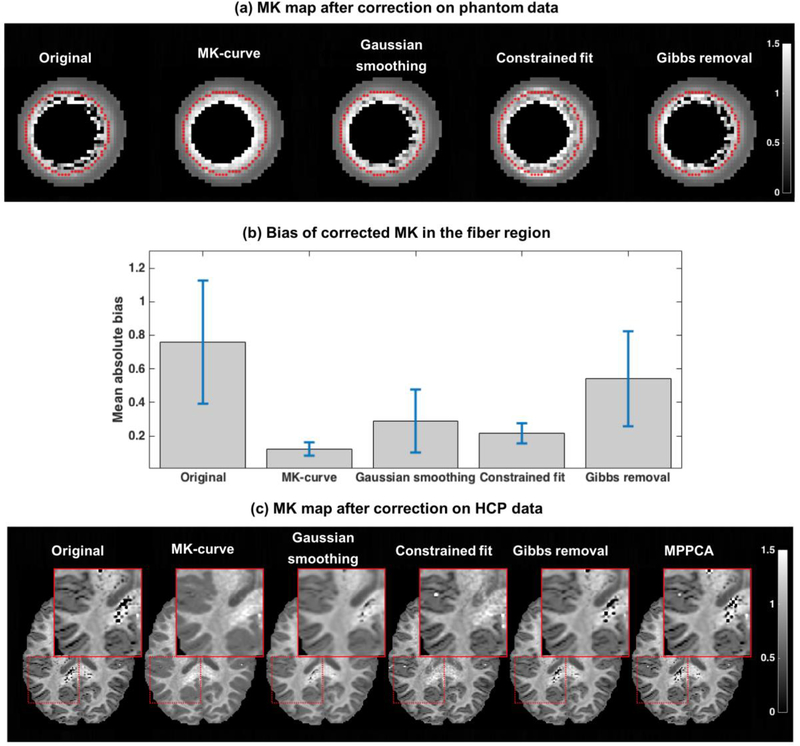
Quantitative comparison of the bias measure on the DKI phantom data for the different correction methods shows that all methods improved the bias measure versus the original uncorrected data, which had mean absolute bias of 0.759 with std of 1.10 (Figure 7b). Of the four methods compared (MPPCA could not applied since it required more than one slice) our proposed MK-curve method had the lowest mean absolute bias (0.122 with std of 0.120). Visually comparing the corrected MK maps on the phantom data (Figure 7a) agrees with the quantitative bias measure, ranking the MK-curve resulted MK map as having the least remaining visually implausible voxels, followed by the constrained fit method, Gaussian smoothing and finally the Gibbs removal approach which resulted with the most remaining visually implausible voxels. The differences between the correction methods can also be appreciated with a visual comparison of an example HCP dataset (Figure 7c). In the white matter, MK-curve and constrained fit resolve most if not all implausible voxels. Most differences are visible in the white-gray matter interface, where many of the dark MK voxels remain dark following the constrained fit but appear plausible following the MK-curve correction. The MK-curve also performed well in eliminating negative diffusion tensor eigenvalues comparing with the other methods (Supplementary Table S1). Similar to the phantom dataset, the MK-curve correction yielded MK distributions that were more aligned with the expected, i.e., did not have long tails that reached to extreme values, and was concentrated around the biological/physical expected ranges of 0–3 (Supplementary Figure S5).
Figure 7: Comparison between correction methods.
The corrected MK map computed from the phantom data using each correction method is shown in (a), and the mean and std of the absolute bias after correction is reported in (b)(error bars in (b) represent std/3). The MK maps of one example HCP dataset is presented in (c) following application of the various correction methods. The inset focuses on deep white matter and on white matter/gray matter interface where most implausible MK values are located.
4. Discussion
By generating the MK-curve that characterizes the relation between the b0 and MK values we were able to propose a novel method to detect and correct voxels with implausible MK values.
We showed that variations in the b0 (e.g., caused by noise or artifacts) are more likely to result in implausible MK values, when compared to variations in the DWIs. Changes in the b0 might have large effects on the MK since the b0 image is used to normalize the DWIs, and thus noise in the b0 propagates to all normalized DWIs. In addition, some imaging artifacts (e.g., Gibbs ringing) have more effect on the images when the b-value is lower (Perrone et al., 2015; Veraart et al., 2016a). Contrary to changes to the b0, we show that even extreme changes in the value of a single DWI do not change the computed MK noticeably (Supplementary Figure S1). This may be due to the fact that there are many DWIs, and the effect of noise on a single DWI averages out during the model fitting. Therefore, in our approach we chose to modify the b0 alone, without altering the DWIs. While changing the b0 helps to correct implausible MK values, it may introduce bias to the b0 image itself; however, our experiments show that if such bias exists, its effect is small as compared to the improvement to the MK image. Nevertheless, we recognize that even though it is less likely, some of the implausible parameter values might be caused by artifacts in the DWIs. For example, if several DWIs were affected simultaneously, or if there were specific DWIs that were more sensitive to changes than others. We note, however, that such voxels are probably very few, since the b0 correction corrected almost all voxels with implausible MK values.
Our experiments reveal several advantages of our method. First, the MK-curve approach had excellent visual and quantitative results, effectively reducing the number of voxels with apparent implausible MK values and the number of voxels with negative MK and negative DTI eigenvalue, as well as other DKI and DTI parameters. Second, the MK-curve based correction only changes MK values in voxels that are detected as implausible, thus minimally changing the dMRI data. Third, our correction approach only requires the MK versus b0 curve, which is derived from the actual measurements of each voxel. Therefore, our method avoids potential partial volume effects introduced when the neighboring voxels are from different brain tissues. This is unlike some of the previous denoising methods that are based on local neighborhoods (Manjón et al., 2013; Shaw and Jensen, 2017b; Veraart et al., 2016b), in which case adaptive smoothing is required (Tabelow et al., 2015). We note that advanced adaptive smoothing approaches could be considered as an alternative correction method that could be applied on voxels identified as implausible, e.g., using the MK-curve for detection. Disadvantages of our method, as discussed below, include heuristically selected parameters and potential bias that may be introduced when parameters are inappropriately selected.
Our detection method requires setting a threshold to determine what b0 values are considered to be too low. Setting a threshold on the b0 is translated to an adaptive MK threshold, that is different in each voxel. This is different from methods such as the constrained fit, which enforce the same MK range on all voxels. Nevertheless, setting a threshold that is higher than the zero-MK b0 also means that voxels with true positive MK values that are close to zero (but lower than the threshold) would be wrongly identified as implausible. In practice, while low kurtosis values may be expected in a perfectly Gaussian signal, it appears that no such voxels can be found in the brain. For example, in the CSF as well as in the agarose gel, where the diffusion propagator should be close to a Gaussian, the (uncorrected) MK is significantly higher than zero. Setting λ to a lower value would reduce the number of false positives, but it would also increase the number of false negatives. Our experiments suggest that there is a range of λ values that is appropriate for analysis. On the phantom data that has a very narrow distribution of MK values (similar to white matter), we identified that λ=0.3 resulted in the lowest mean absolute bias. However, on the in-vivo data that has a broader distribution of MK values it appears that slightly higher value of λ=0.5 provides better identification of visually implausible values.
The selected λ = 0.5 resulted in the b0 threshold to be midway between the zero-MK and max-MK b0 values, providing a balance in detecting and correcting as many as possible visually implausible MK voxels, while avoiding changing voxels that appeared to be plausible. We have selected λ = 0.5 heuristically based on our experiments. Setting the threshold to a higher value would over-identify implausible MK voxels. This, however, would only slightly affect the correction, considering that changes in MK are more subtle when the synthetic b0 used for correction is closer to the max-MK b0. Setting λ to a lower value, i.e., a synthetic b0 close to the zero-MK b0, increases the number of voxels with implausible MK values that are not detected.
Our phantom and in-vivo experiments suggest that the optimal λ value might depend on the underlying true diffusivity and kurtosis. In our experiments any selection of λ appeared to improve the quantitative and visual results comparing with the uncorrected data. Nevertheless, as the underlying diffusivity and kurtosis may be different across brain regions, the selection of a single λ value might introduce bias in some regions in the brain for which the chosen λ is inappropriate. Additional studies are thus required to further optimize the selection of λ. For example, λ could be determined based on tissue type (e.g., white matter, white matter/gray matter interface, or a specific pathology), and take into account acquisition parameters such as resolution and signal to noise ratio. We note that the phantom we use requires assumptions of homogeneity and lack of systematic bias in order to achieve a ground truth experiment. Therefore, future studies could benefit from additional realistic ground truth experiments, either phantoms that have pre-known MK distributions that are more similar to in-vivo distributions, or simulations that are able to correctly model sources of variability that are expected in vivo (Kristoffersen, 2011). Currently, without such experiments, and without an analytic proof for the correction properties, our method may be considered a useful heuristic, especially since the mechanism for the MK-curve based method is not yet fully understood.
As a result of our detection approach, we found that most voxels with implausible MK values were on the gray/white matter interface. Potential explanations for artifacts in the interface areas could include partial volume effects (Westin et al., 2016; Yang et al., 2012) and Gibbs ringing (Perrone et al., 2015; Veraart et al., 2016a). Some of these voxels may be false positives; however, visual inspection of the gray/white matter interface clearly shows implausibly low values in many interface areas. In the context of partial volume effects, it is interesting to note that previous studies (e.g., Jbabdi et al., 2012) also noticed that gray/white matter partial volume effects are a major cause of model fitting issues, which might be the reason for the implausible MK values observed there. Analyses based on bi/multi exponential models may shed some light on the mechanism behind it. While other correction methods specifically target artifacts caused by Gibbs ringing (Perrone et al., 2015; Veraart et al., 2016a), our approach effectively corrects almost all implausible DKI parameter values regardless of if they were caused by Gibbs ringing or by other image artifacts. Nevertheless, since our method is applied on the dMRI signal itself, combining methods can be easily achieved. For example, it is possible to first directly correct for noise and Gibbs artifacts and then apply our method as a second step, which would improve the resulted MK map (see Supplementary Figure S2d for an example). Similarly, since our correction method is applied on the raw dMRI signal, the corrected data may be used for other analyses beyond DKI, although this should be validated for each additional parameter. Although in this sense, our detection method is limited to datasets that support the fitting of the MK model, i.e., multi-shell data with sufficiently high b0 (Jensen et al., 2005; Jensen and Helpern, 2010; Lu et al., 2006).
We detected a large number of voxels with implausible MK values. While these high numbers might reflect overinclusive detection, the high frequency of implausible MK voxels is clearly visible upon inspection of the MK maps, demonstrating the sensitivity of the DKI acquisition to artifacts. This is despite the fact that the HCP datasets were acquired using a high quality imaging protocol and processed using a sophisticated pipeline. The number of artifacts is increased as the acquisition protocol is of lesser quality, resembling conventional DKI acquisitions (see Figure 6b and Supplementary Figure S2d). The high occurrence of implausible MK values stresses the need for a robust correction method. While the quantitative assessment suggests that our method corrected more implausible MK voxels than the other correction methods, this kind of evaluation may be considered circular, since the amount of detected implausible voxels is directly affected by our detection method (e.g., the selection of λ), which favors our correction method over the other correction approaches. Nevertheless, our quantitative evaluations also showed that our method corrected almost all negative diffusivity and MK voxels (Supplementary Table S1). The performance is similar to the constrained fitting method that is a more principled method to fix negative kurtosis values. This suggests that the approach may be applicable to datasets with a range of data qualities.
Currently, our approach requires many repeated DKI model fits (e.g., 200 fits for each voxel) in order to delineate the MK-curve of all voxels from the entire brain (taking about 30 minutes to calculate on a standard Mac computer using parallel computing). These repeated DKI model fits are required to get sufficient sampling of the MK-curve to accurately find its two characteristic b0 values. We point out that while the zero-MK b0 can be analytically identified without generating the curve, we do not yet know whether there is an analytic expression for the max-MK b0 point. Here we chose to generate many synthetic b0 values in order to demonstrate the full shape of the MK-curve and to provide accurate estimations of the two characteristic b0 values using exhaustive search. However, future applications may dramatically reduce the number of synthetic b0 values (and the resulting runtime) either by analytically solving for zero-MK b0 and max-MK b0, or by applying more sophisticated search approaches that take into account the now known shape of the MK curve, and search for a peak point to identify max-MK b0. The range of synthetic b0 that forms the search space for max-MK b0 and zero-MK b0 could also be optimized by, for example, limiting the range to b0 values that result in positive diffusion tensor eigenvalues, or by setting a different search space for each individual voxel. Estimating the zero-MK and max-MK b0 values in each voxel forms new b0 maps that potentially have meaningful contrasts (Supplementary Figure S4). However, a thorough characterization of the maximal MK as well as the max-MK b0 contrast is left for future work.
We note that there are subtle differences in the shape of the MK versus synthetic b0 curve of voxels from different brain tissues (Figure 2), e.g., gray matter, white matter and CSF. A future work could include investigation of the MK-curve characteristics in different brain structures, as well as in brains with lesions such as tumors or edema. Such work would require further validation for the MK value ranges that are expected in pathologies. Furthermore, future work could explore the applicability of the proposed method to other diffusion kurtosis estimation approaches such as the fast diffusion kurtosis imaging (Hansen et al., 2016, 2013) and the generalized kurtosis (Ning et al., 2015).
Supplementary Material
ACKNOWLEDGMENT:
The authors would like to thank the NYU Diffusion MRI group (WLLS DKI model fit, constrained fit and MPPCA), Dr. Marco Reisert (Gibbs removal), and the Dipy community (Gaussian smoothing) for making code used in this study available online, and Dr. Kuder and Dr. Laun for making the DKI phantom data available online. We gratefully acknowledge funding provided by the following NIH grants: P41EB015902, P41EB015898, R01MH108574, R01MH085953, R01MH074794, R03 NS088301, U01CA199459, R21MH115280.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES:
- Basser PJ, Mattiello J, LeBihan D, 1994. MR diffusion tensor spectroscopy and imaging. Biophysical Journal 66, 259–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benitez A, Fieremans E, Jensen JH, Falangola MF, Tabesh A, Ferris SH, Helpern JA, 2014. White matter tract integrity metrics reflect the vulnerability of late-myelinating tracts in Alzheimer’s disease. Neuroimage: Clinical 4, 64–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen G, Dong B, Zhang Y, Shen D, Yap P-T, 2017. Neighborhood Matching for Curved Domains with Application to Denoising in Diffusion MRI In: Medical Image Computing and Computer Assisted Intervention (MICCAI). pp. 629–637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung MM, Hui ES, Chan KC, Helpern JA, Qi L, Wu EX, 2009. Does diffusion kurtosis imaging lead to better neural tissue characterization? A rodent brain maturation study. NeuroImage 45, 386–392. [DOI] [PubMed] [Google Scholar]
- Falangola MF, Jensen JH, Babb JS, Hu C, Castellanos FX, Di Martino A, Ferris SH, Helpern JA, 2008. Age-related non-Gaussian diffusion patterns in the prefrontal brain. Journal of Magnetic Resonance Imaging 28, 1345–1350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, Van Essen DC, Jenkinson M, WU-Minn HCP Consortium, 2013. The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grinberg F, Maximov II, Farrher E, Neuner I, Amort L, Thönneßen H, Oberwelland E, Konrad K, Shah NJ, 2017. Diffusion kurtosis metrics as biomarkers of microstructural development: A comparative study of a group of children and a group of adults. NeuroImage 144, 12–22. [DOI] [PubMed] [Google Scholar]
- Hansen B, Lund TE, Sangill R, Jespersen SN, 2013. Experimentally and computationally fast method for estimation of a mean kurtosis. Magnetic Resonance in Medicine 69, 1754–1760. [DOI] [PubMed] [Google Scholar]
- Hansen B, Shemesh N, Jespersen SN, 2016. Fast imaging of mean, axial and radial diffusion kurtosis. NeuroImage 142, 381–393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hui ES, Cheung MM, Qi L, Wu EX, 2008. Towards better MR characterization of neural tissues using directional diffusion kurtosis analysis. NeuroImage 42, 122–134. [DOI] [PubMed] [Google Scholar]
- Jbabdi S, Sotiropoulos SN, Savio AM, Graña M, Behrens TEJ, 2012. Model-based analysis of multishell diffusion MR data for tractography: How to get over fitting problems. Magn. Reson. Med 68, 1846–1855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen JH, Helpern JA, 2010. MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR in Biomedicine 23, 698–710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K, 2005. Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine 53, 1432–1440. [DOI] [PubMed] [Google Scholar]
- Kellner E, Dhital B, Kiselev VG, Reisert M, 2016. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magnetic Resonance in Medicine 76, 1574–1581. [DOI] [PubMed] [Google Scholar]
- Kristoffersen A, 2011. Statistical assessment of non-Gaussian diffusion models. Magn. Reson. Med 66, 1639–1648. [DOI] [PubMed] [Google Scholar]
- Kuder TA, Stieltjes B, Bachert P, Semmler W, Laun FB, 2012. Advanced fit of the diffusion kurtosis tensor by directional weighting and regularization. Magn. Reson. Med 67,1401–1411. [DOI] [PubMed] [Google Scholar]
- Laun FB, Huff S, Stieltjes B, 2009. On the effects of dephasing due to local gradients in diffusion tensor imaging experiments: relevance for diffusion tensor imaging fiber phantoms. Magn. Reson. Imaging 27, 541–548. [DOI] [PubMed] [Google Scholar]
- Lu H, Jensen JH, Ramani A, Helpern JA, 2006. Three-dimensional characterization of non-gaussian water diffusion in humans using diffusion kurtosis imaging. NMR in Biomedicine 19, 236–247. [DOI] [PubMed] [Google Scholar]
- Manjón JV, Coupé P, Concha L, Buades A, Collins DL, Robles M, 2013. Diffusion weighted image denoising using overcomplete local PCA. PLoS One 8, e73021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrale M, Collura G, Brai M, Toschi N, Midiri F, La Tona G, Lo Casto A, Gagliardo C, 2016. Physics, Techniques and Review of Neuroradiological Applications of Diffusion Kurtosis Imaging (DKI). Clinical Neuroradiology 26, 391–403. [DOI] [PubMed] [Google Scholar]
- Ning L, Westin C-F, Rathi Y, 2015. Estimating diffusion propagator and its moments using directional radial basis functions. IEEE transactions on medical imaging 34, 2058–2078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norton I, Essayed WI, Zhang F, Pujol S, Yarmarkovich A, Golby AJ, Kindlmann G, Wassermann D, Estepar RSJ, Rathi Y, Pieper S, Kikinis R, Johnson HJ, Westin C-F, O’Donnell LJ, 2017. SlicerDMRI: Open Source Diffusion MRI Software for Brain Cancer Research. Cancer Research 77, e101–e103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perrone D, Aelterman J, Pizurica A, Jeurissen B, Philips W, Leemans A, 2015. The effect of Gibbs ringing artifacts on measures derived from diffusion MRI. NeuroImage 120, 441–455. [DOI] [PubMed] [Google Scholar]
- Pierpaoli C, Basser PJ, 1996. Toward a quantitative assessment of diffusion anisotropy. Magnetic Resonance in Medicine 36, 893–906. [DOI] [PubMed] [Google Scholar]
- Raab P, Hattingen E, Franz K, Zanella FE, Lanfermann H, 2010. Cerebral gliomas: diffusional kurtosis imaging analysis of microstructural differences. Radiology 254, 876–881. [DOI] [PubMed] [Google Scholar]
- Shaw CB, Jensen JH, 2017a. Recent Computational Advances in Denoising for Magnetic Resonance Diffusional Kurtosis Imaging (DKI). Journal of the Indian Institute of Science 1–14. [Google Scholar]
- Shaw CB, Jensen JH, 2017b. Recent Computational Advances in Denoising for Magnetic Resonance Diffusional Kurtosis Imaging (DKI). Journal of the Indian Institute of Science 1–14. [Google Scholar]
- Steven AJ, Zhuo J, Melhem ER, 2014. Diffusion kurtosis imaging: an emerging technique for evaluating the microstructural environment of the brain. American Journal of Roentgenology 202, W26–33. [DOI] [PubMed] [Google Scholar]
- Tabelow K, Voss HU, Polzehl J, 2015. Local estimation of the noise level in MRI using structural adaptation. Medical Image Analysis 20, 76–86. [DOI] [PubMed] [Google Scholar]
- Tabesh A, Jensen JH, Ardekani BA, Helpern JA, 2011. Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging. Magnetic Resonance in Medicine 65, 823–836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TEJ, Yacoub E, Ugurbil K, WU-Minn HCP Consortium, 2013. The WU-Minn Human Connectome Project: an overview. NeuroImage 80, 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart J, Fieremans E, Jelescu IO, Knoll F, Novikov DS, 2016a. Gibbs ringing in diffusion MRI. Magnetic Resonance in Medicine 76, 301–314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart J, Fieremans E, Novikov DS, 2016b. Diffusion MRI noise mapping using random matrix theory. Magnetic Resonance in Medicine 76, 1582–1593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart J, Novikov DS, Christiaens D, Ades-Aron B, Sijbers J, Fieremans E, 2016c. Denoising of diffusion MRI using random matrix theory. NeuroImage 142, 394–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart J, Sijbers J, Sunaert S, Leemans A, Jeurissen B, 2013. Weighted linear least squares estimation of diffusion MRI parameters: strengths, limitations, and pitfalls. NeuroImage 81, 335–346. [DOI] [PubMed] [Google Scholar]
- Westin C-F, Knutsson H, Pasternak O, Szczepankiewicz F, Özarslan E, van Westen D, Mattisson C, Bogren M, O’Donnell LJ, Kubicki M, Topgaard D, Nilsson M, 2016. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. NeuroImage 135, 345–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang AW, Jensen JH, Hu CC, Tabesh A, Falangola MF, Helpern JA, 2012. Effect of cerebral spinal fluid suppression for diffusional kurtosis imaging. Journal of Magnetic Resonance Imaging 37, 365–371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou M-X, Yan X, Xie H-B, Zheng H, Xu D, Yang G, 2015. Evaluation of non-local means based denoising filters for diffusion kurtosis imaging using a new phantom. PLoS One 10, e0116986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhuo J, Xu S, Proctor JL, Mullins RJ, Simon JZ, Fiskum G, Gullapalli RP, 2012. Diffusion kurtosis as an in vivo imaging marker for reactive astrogliosis in traumatic brain injury. NeuroImage 59, 467–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.