Chemical exchange saturation transfer fingerprinting for exchange rate quantification

Abstract

Purpose:

There is an increased interest to determine the exchange rate using CEST to provide pH information. However, current CEST quantification methods require lengthy scan times and do not address magnetization transfer effects. The purpose of this work was to apply the magnetic resonance fingerprinting (MRF) concept to CEST to achieve more efficient and accurate exchange rate quantification.

Methods:

The proposed CEST fingerprinting method used varying saturation powers and saturation times to create unique signal evolutions for different exchange rates. The acquired signal was matched to a predefined dictionary to determine the exchange rate. The magnetization transfer effects were also addressed in the framework of CEST fingerprinting: The simulated dictionary could predict the signal curves without magnetization transfer effects, and comparing the dictionary to the acquired signals allowed the correction of the magnetization transfer effects. The CEST fingerprinting method was compared with the conventional pulsed quantitative CEST method using omega plots in the creatine phantom study.

Results:

The CEST fingerprinting method has a significantly reduced scan time (10 minutes versus 50 minutes) while providing more accurate exchange rate quantification using literature values as the reference.

Conclusion:

In this study, we demonstrate that CEST fingerprinting is more efficient (5 times faster) compared with pulsed quantitative CEST. It is also shown that the results of the proposed CEST fingerprinting technique are much closer to the literature values than pulsed quantitative CEST at 3 T.

1 |. INTRODUCTION

Chemical exchange saturation transfer imaging is based on the chemical exchange between solute protons and water protons, which is affected by pH.¹ Previous studies have used CEST imaging to detect acidosis-based ischemic penumbra^2–4 and tumor acidosis.^5–7 However, CEST contrast can be affected by multiple confounding factors, including solute concentration and water relaxation parameters T₁ and T₂. These parameters can also have considerable changes in diseases, resulting in multiple origins for CEST signal changes.^8,9

Attempts have been made to quantify the CEST effects by measuring the exchange rate and proton fraction ratio (the ratio of solute protons and water protons). These methods repeat the CEST experiment multiple times with different CEST saturation times or CEST saturation powers, then fit the exchange rate and proton fraction ratio to the Bloch-McConnell equations. Due to the complexity of the equation, fitting to the numerical solutions can be computationally expensive. Methods based on approximate analytical solutions have been developed, including QUEST and QUESP,¹⁰ ratiometric CEST,^11–13 and quantitative CEST with omega plots.^14–17 These methods have been applied in preclinical studies.^14,18,19

However, challenges remain to accurately and efficiently quantify the CEST effects. First, current methods require long scan times due to the long TR needed for full longitudinal magnetization recovery and long CEST saturation time needed for the chemical exchange to reach steady state to approximate the analytical solution. Second, in clinical scanners Gaussian-shaped pulses are commonly used rather than continuous-wave pulses due to hardware constraints.^16,20 The varying B₁ amplitudes make it more challenging to determine the analytical solutions of the Bloch-McConnell equations. Approximations are needed to simplify the mathematical model of the 2-pool CEST system using Gaussian-shaped saturation pulses,^16,20 which may introduce errors. Third, the accuracy of current CEST quantification methods will be affected by the competing MT effects.^10,16 The conventional MT correction methods use multipool Lorentzian fitting to separate MT effects from CEST effects, which is quite challenging because the multiparametric fitting has a strong dependence on image quality, initial values, and boundaries.^21,22 Magnetization transfer correction remains a problem in CEST quantification.

Magnetic resonance fingerprinting (MRF) is a new method that provides an alternative way to perform multiparametric mapping.²³ Instead of using a repeated, serial acquisition of data, it uses a pseudorandomized acquisition to create unique signal evolutions for tissues with different properties. The acquired signal is matched to a predefined dictionary of simulated signal curves to determine the best-fit parameters, enabling the quantification of a complex multiparametric system without equation fittings.

The MRF concept can be applied to CEST imaging, in which CEST saturation times and saturation powers are pseudorandomized to generate unique CEST signal evolutions. The acquired signal can be matched to a predefined dictionary instead of fitting to the Bloch-McConnell equations. This method addresses the challenges mentioned previously. First, scan time can be significantly reduced because CEST fingerprinting is not based on the analytical solution, which eliminates the need for long TR and CEST saturation times. Second, CEST fingerprinting can be applied in clinical MR systems with improved accuracy, because the RF pulse profile can be incorporated in the dictionary generation and the signal matching process, which avoids errors caused by Gaussian-shaped pulse approximations. Third, the MT effects can be estimated in the framework of CEST fingerprinting by simulating a dictionary without MT effects and comparing this dictionary to the acquired signal, enabling MT correction.

In this work, we propose a CEST fingerprinting framework for exchange rate quantification in the presence of MT effects. This technique uses CEST saturations with varying saturation powers and saturation times to create unique signal evolutions for different exchange rates. Exchange rates were quantified in creatine phantoms using the proposed CEST fingerprinting and the pulsed quantitative CEST (qCEST) techniques. The pulsed qCEST serves as a benchmark for comparison, as it is the only method that has been validated for measuring the exchange rates of creatine protons on clinical scanners.²⁴ The exchange rate values reported by Goerke et al. using water-exchange spectroscopy²⁵ were used as the reference.

2 |. METHODS

2.1 |. Pulse sequence design

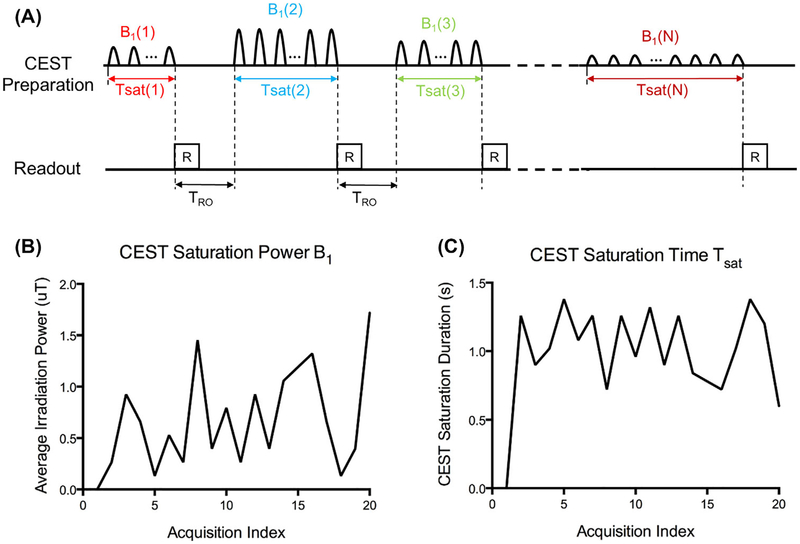
Figure 1A illustrates the sequence diagram for CEST fingerprinting. Each acquisition block consists of a CEST preparation module and a 2D single-shot readout module. Images from each acquisition block were reconstructed separately. In each subsequent acquisition block, identified by acquisition index, the CEST preparation parameters (CEST saturation power B₁ and CEST saturation time T_sat) were varied in a pseudorandom pattern. The duration of the readout module, T_RO, was fixed. In this study, 20 images were collected from 20 corresponding acquisition blocks and T_RO was set to be 1000 ms to avoid specific absorption rate (SAR) issues.

FIGURE 1.

The CEST fingerprinting sequence pattern. A, Acquisition sequence diagram. In each subsequent acquisition block, CEST saturation powers B₁ and CEST saturation times T_sat are varied in a pseudorandom pattern. B,C, Examples of average CEST saturation power B₁ and CEST saturation time T_sat series used in this study

The acquisition parameters B₁ and T_sat change in a pseudorandom pattern for each acquisition index, as shown in the examples in Figure 1B,C. B₁ ranges from 0 uT to 2 uT, whereas T_sat ranges from 0 seconds to 1.5 seconds. The B₁ and T_sat series were optimized for the amine protons of creatine (+2.0 ppm) at a field strength of 3 T. For any molecule or field strength, the sequence parameters can be determined with the following process: First, B₁ was randomly chosen in the range with minimal spillover effect; then for each acquisition index, according to the corresponding B₁, T_sat was determined as when the CEST signal has reached a certain ratio (e.g., 50%) of the steady-state CEST signal. This process ensures efficient CEST signal generation because the CEST signal grows most rapidly in the beginning of the CEST saturation.

To show the generality of CEST fingerprinting, Gaussian-shaped saturation pulses are used in this study. However, CEST fingerprinting can also be easily applied to continuous-wave saturation pulses, which are more commonly used in small-animal scanners.

2.2 |. Dictionary

The dictionary was generated following the 2-pool Bloch-McConnell equations as follows²⁶:

$$\frac{d}{dt}\left[\begin{array}{c}{M}_{xw}\\ M_{yw}\\ M_{zw}\\ M_{xs}\\ M_{ys}\\ M_{zs}\end{array}\right]=\left[\begin{array}{cccccc}-\frac{1}{T_{2w}}-k_{ws}& \mathrm{\Delta }{\mathrm{\omega }}_w& & k_{sw}& & \\ \mathrm{\Delta }{\mathrm{\omega }}_w& -\frac{1}{T_{2w}}-k_{ws}& -{\mathrm{\omega }}_1& & k_{sw}& \\ & -{\mathrm{\omega }}_1& -\frac{1}{T_{2w}}-k_{ws}& & & k_{sw}\\ k_{ws}& & & -\frac{1}{T_{2s}}-k_{sw}& \mathrm{\Delta }{\mathrm{\omega }}_s& \\ & k_{ws}& & \mathrm{\Delta }{\mathrm{\omega }}_s& -\frac{1}{T_{2s}}-k_{sw}& -{\mathrm{\omega }}_1\\ & & k_{ws}& & -{\mathrm{\omega }}_1& -\frac{1}{T_{2s}}-k_{sw}\end{array}\right]\left[\begin{array}{c}{M}_{xw}\\ M_{yw}\\ M_{zw}\\ M_{xs}\\ M_{ys}\\ M_{zs}\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ \frac{M_{0w}}{T_{1w}}\\ \\ \\ \frac{M_{0s}}{T_{1s}}\end{array}\right]$$ (1)

where M_x,y,zw and M_x,y,zs represent the x, y, and z magnetization of the water protons (w) and solute protons (s), respectively, with T_1w, T_2w, T_1s and T_2s being their longitudinal and transverse relaxation rates; f_r is the labile proton fraction ratio with respect to bulk water, which can be defined as f_r=M_0s/M_0w; k_sw and k_ws are the exchange rates from solute pool to water pool and vice versa, and k_ws=f_rk_sw; ω₁ is the RF irradiation amplitude; and Δω_w and Δω_s correspond to the differences between the CEST saturation frequency offset, Δω, and the water and solute proton resonant frequencies, δ_w and δ_s, respectively.

Two dictionaries were generated: a label dictionary at the solute proton resonant frequency (Δω= δ_s) and a reference dictionary at the opposite resonant frequency (Δω= −δ_s). The CEST dictionary was generated using asymmetry analysis by subtracting the label dictionary from the reference dictionary. The labile proton fraction ratio f_r is a scaling factor in the CEST dictionary, as shown in the Supporting Information and can be set as a constant. In the dictionary generation, T_1w and T_2w were determined from additional relaxation mapping measurements. The value of T_1s was set to be the same as T_1w, and T_2s was set according to literature values. The RF profile ω₁ was extracted from the customized CEST fingerprinting sequence. In this study, the label dictionary consisted of 60 entries per pixel with k_sw ranging from 10 s²¹ to 600 s⁻¹ with an interval of 10 s⁻¹ using corresponding T₁ and T₂ values from the separate mapping measurements and f_r was set to 0.001. Because the reference dictionary has negligible CEST effects, it was generated with k_sw = 0 and f_r = 0.

2.3 |. Magnetization transfer correction

The label signal was defined as the signal acquired at the solute proton resonant frequency (Δω= δ_s). The reference signal was defined as the signal acquired at the opposite resonant frequency (Δω= −δ_s). The acquired signals I were normalized by the signal without CEST saturation I₀. Similarly, the dictionary curves were normalized by the signal simulated without CEST saturation using the same tissue parameters and readout parameters.

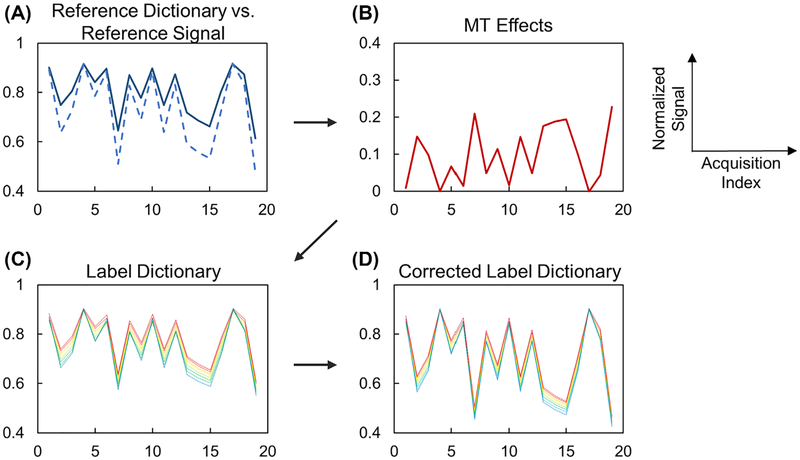
Figure 2 illustrates the framework for MT correction with CEST fingerprinting. Figure 2A compares the reference dictionary and the reference signal. In an ideal water-solute 2-pool system, the reference signal matches the reference dictionary generated with corresponding T₁ and T₂ values. However, due to the existence of MT effects, the normalized reference signal shows signal dropouts compared with the reference dictionary. The signal attenuation due to MT effects can be estimated by comparing the reference signal and reference dictionary (Figure 2B). Assuming that the MT effects are symmetric, the corrected label dictionary with the MT effects can be generated (Figure 2D) by adding the estimated MT signal to the dictionary with varying exchange rates k_sw (Figure 2C). The mathematical representation of the MT correction method is described in the Appendix.

FIGURE 2.

Framework of magnetization transfer (MT) correction. A, Reference dictionary (solid) and reference signal (dashed) are different in the presence of MT effect. B, Signal attenuation due to MT effect can be estimated by comparing the reference dictionary and reference signal. C, The label dictionary is generated by simulating 2-pool Bloch-McConnell equations with known T₁ and T₂ values. D, The corrected label dictionary can be generated by adding the MT effect (B) to the dictionary (C)

2.4 |. Signal matching

Signal matching was performed between the CEST signal and dictionary, both of which were calculated by asymmetry analysis. The CEST signals were calculated by subtracting the label signal (Δω= +δ_s) from the reference signal (Δω= −δ_s).²⁵ Similarly, the MT-corrected CEST dictionary was calculated by subtracting the MT-corrected label dictionary (Δω= +δ_s) from the MT-corrected reference dictionary (Δω= −δ_s).

For each pixel, the CEST signal was matched to its corresponding CEST dictionary. The CEST dictionary entry with the highest vector dot-product was selected as a match. Because f_r is a scaling factor, it does not affect the matching process.

2.5 |. Numerical simulation

Numerical simulations were performed to evaluate the effect of T₁ and T₂ errors on the accuracy of the exchange rate estimation in the proposed CEST fingerprinting scheme. The relaxation parameters used were as follows: T_1w = 1000 ms, T_2w = 200 ms, T_1s = 1000 ms, T_2s = 20 ms. The sequence parameters matched the phantom imaging protocol. The signal curves were simulated using varying CEST saturation power B₁ and saturation time T_sat (Figure 1B,C) with fast low-angle-shot readout (flip angle: 15°, number of segments: 48, TE: 1.5 ms) using a 3-pool model with the following MT parameters (T_1mt = 1000 ms, T_2mt = 10 μs, k_mtW = 40 Hz, f_mt = 0.05).

The CEST signals were simulated for different exchange rates using the same relaxation parameters. The CEST dictionary was generated using a variety of T₁ and T₂ errors using a 2-pool model. The MT correction and signal matching were performed as described previously to determine the exchange rate.

2.6 |. Phantom preparation

The CEST fingerprinting method was tested in creatine phantoms. Three groups of phantoms containing creatine monohydrate (Sigma-Aldrich, St. Louis, MO) were prepared. For group 1, pH was varied in each vial and other parameters were kept constant. For group 2, agarose was added to each vial to induce MT effects. For group 3, the relaxation parameters T₁ and T₂ and the creatine concentration were also varied. The details of the phantoms are listed in Table 1. T₁ and T₂ were varied by adding nickel chloride (Sigma-Aldrich) and agarose (Sigma-Aldrich).

Table 1.

Composition of the 3 phantom groups

Group	T1 (ms)	T2 (ms)	Agarose	Creatine concentration (mM)	pH
1	786	709	0	60	6.96
1	1299	1099	0	60	6.85
1	902	875	0	60	6.45
1	974	774	0	60	7.27
1	1226	1133	0	60	6.76
2	1037	136	1.5%	60	6.70
2	1059	133	1.5%	60	7.18
2	1056	136	1.5%	60	7.10
2	1022	140	1.5%	60	6.77
2	1035	130	1.5%	60	7.49
3	1721	140	1.5%	60	6.96
3	1389	143	1.5%	60	6.94
3	1042	116	2%	60	6.72
3	449	137	1%	60	7.45
3	1069	133	1.5%	100	7.06
3	1071	135	1.5%	30	7.06

2.7 |. Magnetic resonance imaging acquisition

Phantom experiments were performed at 20°C on a 3T clinical scanner (Magnetom Verio; Siemens Healthineers, Erlangen, Germany) with standard 32-channel head receiver coils. The exchange rates were quantified using CEST fingerprinting and pulsed qCEST techniques. The results were compared with the exchange rate values reported by Goerke et al as in Ref 25. For both methods, images were acquired with saturation frequency offsets at ± 2.6 ppm, ± 2.3 ppm, ± 2.0 ppm, ± 1.7 ppm, and ±1.4 ppm. All images were acquired with a slice thickness of 5 mm, FOV of 150 × 150 mm², resolution of 2.3 × 2.3 mm², and imaging matrix of 64 × 64. The B₀ field was corrected using the water saturation shift referencing method.

The scan time for CEST fingerprinting was approximately 10 minutes. Images were acquired with a 2D single-shot, fast low-angle-shot readout (flip angle: 15°; iPAT: 2; number of segments: 48; number of averages: 1; TE: 1.5 ms) in one slice. The duration of the readout block T_RO was fixed to be 1000 ms to avoid SAR issues. The CEST preparation module consisted of 30-ms non-selective Gaussian saturation pulses (flip angle ranging from 100° to 1500°) with a 50% duty cycle with equivalent B_1rms ranging from 0.13 μT to 1.98 μT. For each CEST saturation frequency offset, 20 images with varying CEST saturation power B₁ and saturation time T_sat (as shown in Figure 1B,C) were acquired. This was repeated for all different CEST saturation frequency offsets. The scan time for 1 frequency offset was approximately 50 seconds.

The scan time for the pulsed qCEST method was approximately 50 minutes. Images were acquired with single-shot turbo spin-echo (TSE) readout (flip angle: 180°; iPAT: 2; echo train length: 48; number of averages: 3; TR: 16 000 ms; TE: 7 ms). The CEST preparation module consisted of 50 80-ms Gaussian-shaped pulses with a 50% duty cycle (total saturation time of 8000 ms). The CEST experiments were repeated for 4 different saturation flip angles: 900°, 1500°, 2100°, and 2800°.

T₁ maps were calculated using T₁-weighted images acquired with an inversion-recovery TSE sequence with 10 different TIs (50, 150, 300, 600, 900, 1200, 1500, 1800, 2100, and 2500 ms; TR/TE = 6000/12 ms). T₂ maps were calculated using T₂-weighted images acquired with a TSE sequence with 10 different TEs (12, 25, 50, 100, 150, 200, 250, 300, 350, and 400 ms; TR = 6000 ms). The TSE-based T₂ mapping method may be biased by stimulated echoes.²⁷ However, a more accurate spin-echo measurement would take too much time. As described later, the CEST fingerprinting method is not very sensitive to T₂ errors. Therefore, the TSE sequence was used for T₂ mapping in this study.

2.8 |. Data analysis

Postprocessing was performed with custom-written programs in MATLAB (The MathWorks, Natick, MA). The T₁ maps and T₂ maps were obtained by pixel-wise logarithmic fit of the signal equations. The resonant frequency of creatine protons is +2.0 ppm. The reference signal (−2.0 ppm) and label signal (+2.0 ppm) were interpolated from the signal acquired at multiple frequency offsets with corrected B₀ field. The signal curves were then normalized with a reference image acquired with no CEST saturation pulses. The dictionary was simulated with T_1w and T_2w from the acquired T₁ and T₂ maps. For amine protons of creatine, T_1s was set to be the same as T_1w, and T_2s was set to be 20 m.¹⁵ The MT correction and signal matching were performed as described previously to determine the exchange rate k_sw. These calculations were performed both pixel-wise and by region of interest.

3 |. RESULTS

3.1 |. Numerical simulation

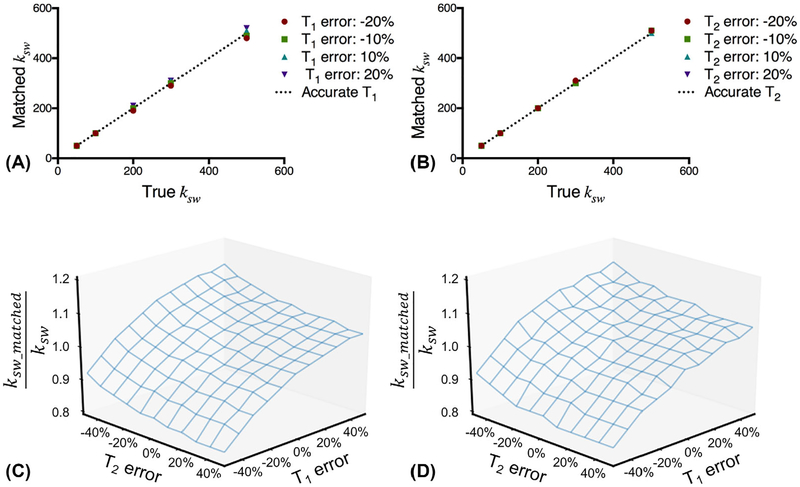
The simulation process was consistent with the acquisition and postprocessing scheme used in the phantom study. Figure 3A,B shows the matched k_sw as a function of the true k_sw with T₁ and T₂ errors, respectively. There are fewer than 5% errors in the matched k_sw with up to 20% errors in T₁ or T₂. The exchange rate accuracy was evaluated in the case of both T₁ and T₂ errors for k_sw = 150 s⁻¹ (Figure 3C) and k_sw = 500 s⁻¹ (Figure 3D). With up to 50% errors in both T₁ and T₂, there are fewer than 20% errors in the matched k_sw. The accuracy of the exchange rate using the proposed CEST fingerprinting is not very sensitive to T₁ and T₂ errors.

FIGURE 3.

Impact of T₁ and T₂ errors on exchange rate accuracy. The matched exchange rate k_sw as a function of true exchange rate k_sw with T₁ error (A) or T₂ error (B). The normalized exchange rate k_{sw_matched}/k_sw as a function of T₁ error and T₂ error for k_sw = 150 s⁻¹ (C) and k_sw = 500 s⁻¹ (D)

3.2 |. Phantom study

The scan time for the CEST fingerprinting method was approximately 10 minutes, whereas the scan time for the pulsed qCEST method was approximately 50 minutes.

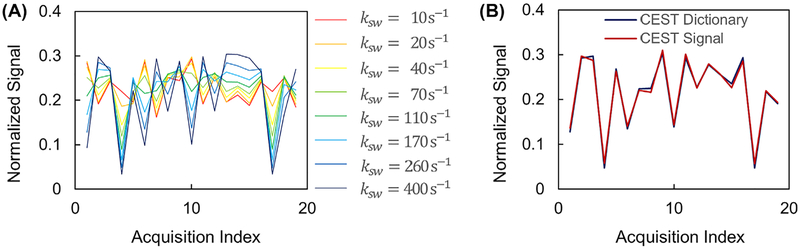
Figure 4A shows the simulated CEST signals with different exchange rates ranging from 10 s⁻¹ to 400 s⁻¹ for tissues with T₁ of 1000 ms and T₂ of 120 ms using the sequence patterns shown in Figure 1B,C. Figure 4B shows an acquired CEST signal curve from one of the phantom vials and its match to the CEST dictionary.

FIGURE 4.

Signal properties and matching results from the phantom study. A, Simulated CEST signal with different exchange rates. B, Measured CEST signal and the corresponding dictionary match. Note the signal curves are normalized in this figure

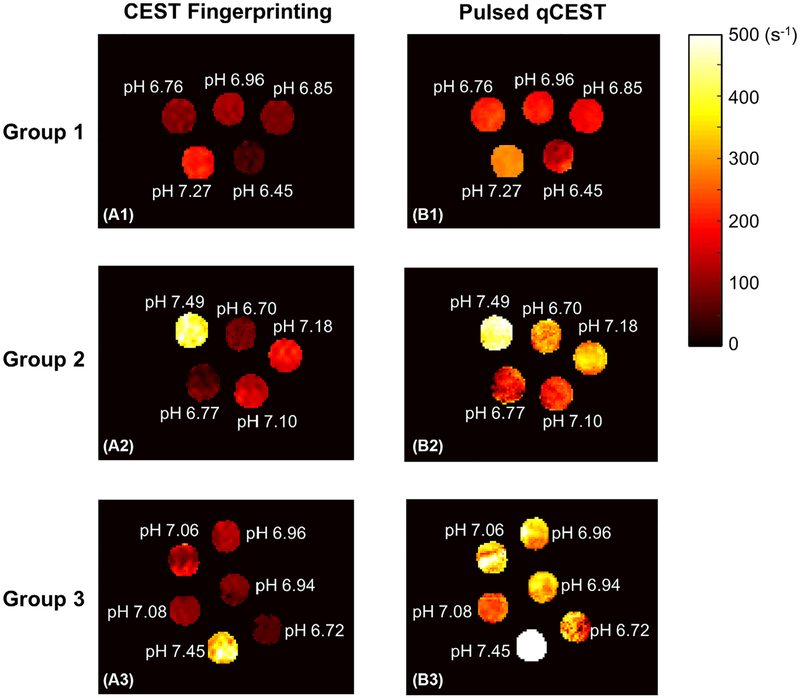
Pixel-wise mapping of the chemical exchange rate k_sw for all phantom groups is shown in Figure 5. For group 1, both CEST fingerprinting and pulsed qCEST methods provided homogenous exchange rate maps. However, for groups 2 and 3 with MT effects, more variations can be observed within each vial in the exchange rate maps generated with the pulsed qCEST method compared with the CEST fingerprinting method. This is because long CEST saturation pulses used in the pulsed qCEST method will cause large MT effects. For groups 2 and 3, the CEST-weighted images acquired with the pulsed qCEST method have reduced SNR because of the MT effects. This makes the qCEST method more sensitive to errors from the B₀ map and T₁ map.

FIGURE 5.

Exchange rate maps of the phantom study. In group 1, pH was varied in each vial and other parameters were kept constant. There was no MT effect. For group 2, agarose was added to each vial to introduce the MT effect. For group 3, the relaxation parameters T₁ and T₂ and the creatine concentration were also varied

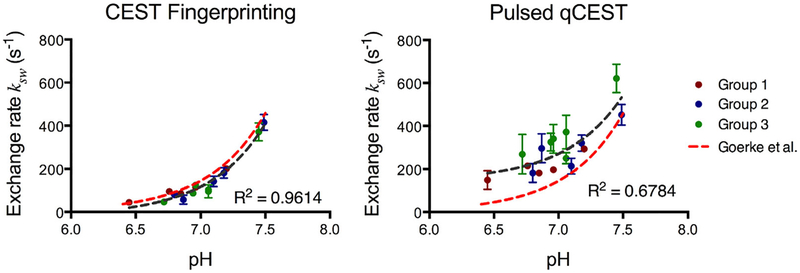
The relationship between exchange rate k_sw and pH is shown in Figure 6 for both CEST fingerprinting and pulsed qCEST methods. All phantom vials are presented, with group 1 in red, group 2 in blue, and group 3 in green. The error bars represent the SD of the exchange rates within the region of interest of each tube. The dark gray dashed lines in Figure 6 represent the fitted curve of exchange rate as a function of pH. For the CEST fingerprinting method, the exchange rate can be described as k_sw=1:35×10^pH−5218:14 (R² = 0.9614). For the pulsed qCEST method, the exchange rate can be described as k_sw=1:25×10^Ph−5+145:70 (R² = 0.6784). The results were compared with the exchange rates reported by Goerke et al using water-exchange spectroscopy, shown as the red dashed lines in Figure 6.²⁵ The exchange rates measured by the CEST fingerprinting method appear to be very close to the literature values.

FIGURE 6.

Chemical exchange rate as a function of pH. The error bars represent the SD of the exchange rate within the region of interest of each tube. The dark gray dashed line represents the fitted curve of the exchange rate as a function of pH. The exchange rates reported by Goerke et al at 20°C shown in red dashed lines²⁵ serve as the reference

4 |. DISCUSSION

In this work, the MRF concept was introduced to quantify exchange rates in CEST imaging. The phantom study demonstrated that CEST fingerprinting can measure the exchange rate more efficiently and more accurately compared with the pulsed qCEST method. The pulsed qCEST method was tested previously and validated in phantoms with no MT effects on clinical scanners.¹⁶ Therefore, it was used as a benchmark for comparison in this study. However, it has been shown that pulsed qCEST tends to overestimate lower exchange rates at 3 T.²⁴ This explains the systematic bias observed in the pulsed qCEST results, even in group 1 where there were no MT effects.

4.1 |. Chemical exchange saturation transfer fingerprinting

In the CEST fingerprinting framework, CEST saturation powers B₁ and saturation times T_sat were varied in the CEST preparation module. The pseudorandom pattern of CEST saturation parameters was chosen based on early MRF papers.^23,28 However, it has been shown recently that optimized flip-angle patterns for MRF have a nonrandom appearance.²⁹ The CEST saturation parameters should be further optimized based on the applications. In addition, the oscillatory signal curve contains more informative points under different B₁ powers at different stages of the chemical exchange.

Dictionary generation and signal matching is another key element of the CEST fingerprinting framework. In conventional CEST quantification methods, the acquired signals are fitted to the approximated analytical solution of the Bloch-McConnell equations. However, this adds certain restrictions to the CEST experiments. A long saturation time is required for the chemical exchange to reach steady state and a long TR is required for full longitudinal recovery. However, by directly matching the signal curve to a predefined dictionary, these restrictions can be removed. In this study, the CEST saturation time ranged from 1000 to 2000 ms and TR was 2000 to 3000 ms, whereas in conventional CEST quantification methods the CEST saturation time was at least 4000 ms and TR was 8000 ms or more. The much shorter TR explains the increased efficiency of CEST fingerprinting compared with the conventional CEST quantification methods.

Previous studies have used varying CEST saturation parameters^30,31 or the concept of dictionary generation and signal matching in CEST imaging.³² However, no quantification was performed to obtain the exchange rates. By incorporating both elements in the proposed CEST-fingerprinting framework, we were able to achieve efficient CEST quantification.

The CEST fingerprinting has subtle signal changes compared with MRF, due to the nature of CEST imaging. In most in vivo studies with endogenous CEST agents, the CEST signal is less than 5%, which means CEST fingerprinting is more sensitive to noise as compared with MRF. In addition, it takes longer to acquire 1 image for CEST fingerprinting (2000−3000 ms) compared with MRF (< 20 ms). Therefore, in the CEST fingerprinting framework, a highly undersampled image acquisition was not adopted and the sequence parameters were optimized to enhance CEST signal so that the number of images that need to be acquired is in a feasible range.

The long CEST saturation pulses in the conventional CEST quantification methods were designed to make sure the chemical exchange between water protons and solute protons has reached steady state. However, MT effects were also increased at the same time. In most cases, with long CEST saturation time, MT becomes the dominant effect. Therefore, long CEST saturation pulses reduce the SNR significantly when MT effects are present. As shown in Figure 5B, for the pulsed qCEST method, the exchange rate maps for groups 2 and 3 (with agarose) have more variations within the vials than the exchange rate map of group 1 (without agarose). In CEST fingerprinting, because the CEST saturation times are in the moderate range (1000–2000 ms), the effects from MT are not as significant.

T₁ and T₂ maps need to be acquired as an input for dictionary generation in CEST fingerprinting. With recent improvements in MRI relaxometry techniques, simultaneous T₁ and T₂ mapping can be achieved in less than 20 seconds using MRF.²³ In a practical situation, the entire protocol will include B₀ mapping, CEST fingerprinting, and T₁ and T₂ mapping.

In this study, slice profile was not included in dictionary generation because the proposed CEST fingerprinting method was not sensitive to slice profile imperfections, as shown in Supporting Information Figure S1. This is mostly because the CEST signal is generated by subtracting the label signal from the reference signal and the slice profile imperfections could be canceled out, as shown in Supporting Information Figure S2. However, it has recently been shown that failing to include the slice profile in the dictionary may lead to substantial errors in MRF for T₁ and T₂ mapping.^33,34 In future studies, when CEST signal is generated in a different way, the effects of slice profile imperfections should be taken into careful consideration.

4.2 |. Magnetization transfer correction

In this study, MT correction was performed using the dictionary as a no-MT reference. The MT signal was estimated by comparing the reference signal and the reference dictionary. Without CEST effects, the difference between the reference signal and the reference dictionary is from MT effects, meaning the signal attenuation due to MT effects can be estimated. With the assumption of symmetric MT effects, the MT signal estimated at −δ_s can be used to correct the MT effects at +δ_s.

There are also other ways to perform MT corrections without the need for reference data. These methods use wide-offset data (|Δω| > 7 ppm) to fit for the MT model. The fitted parameters were used to correct for MT effects at the solute resonant frequency.^35,36 There have also been attempts to correct for MT effects using 3-pool CEST fingerprinting.³⁷ However, these methods all require multiparametric fitting/matching. Due to the complexity of the model, the fitting/matching process could be challenging and multiple points at different frequency offsets are acquired for MT correction.

4.3 |. Potential impact

In this work, we presented the proof-of-concept implementation of CEST fingerprinting. This framework can also be extended to quantify other proton chemical exchange contrast mechanisms, including chemical exchange sensitive spin-lock,^38–40 balanced SSFP with detection of chemical exchange,⁴¹ and MT.⁴² The sequences of these techniques are similar to CEST sequences in the way that they all use off-resonance saturation pulses. More broadly, the framework presented in this study can serve as an example of how to apply the MRF concept to contrast mechanisms that use preparation pulses to achieve the contrast, such as diffusion. By varying the preparation parameters and matching the signal to a predefined dictionary, the efficiency can be improved by acquiring more informative points in a faster way.⁴³

4.4 |. Moving to in vivo studies

There are several major challenges to quantifying pH in vivo using CEST, including long scan times and complex in vivo environments. Currently, most in vivo studies are in preclinical animal models due to the long scan times.^14,18 To address the issue of complex in vivo environments, exogenous CEST agents with resonant frequency offsets higher than +4.0 ppm, such as Iopromide and Iohexol, were used commonly to enhance the sensitivity to pH-dependent exchange rate.^6,44 It avoids the complex 2-ppm to 4-ppm region that includes CEST pools from multiple protons, such as amide protons (+3.5 ppm) and amine protons (+3.0 ppm) and the nuclear Overhauser enhancement effects (−3.5 ppm).

The proposed CEST fingerprinting method can significantly reduce the scan time compared to previous methods. In addition, the MT correction scheme allows more accurate exchange rate quantification. When applying CEST fingerprinting in in vivo studies using protons that resonate between +2 ppm to + 4 ppm, nuclear Overhauser enhancement effects and multiple-pool CEST effects need to be taken into consideration during postprocessing. Exogenous CEST agents, such as Iopromide and Iohexol, have been used to enhance exchange rate quantification. To address the in vivo MT asymmetry, the signal curves acquired before the injection can serve as reference signal and the signal curves acquired after the injection can serve as label signal.

5 |. CONCLUSIONS

In this work, CEST fingerprinting was proposed for exchange rate quantification. The phantom study demonstrated that CEST fingerprinting was more efficient (5 times faster) for exchange rate quantification compared with pulsed qCEST. We also have shown that the results of the proposed CEST fingerprinting technique are much closer to the literature values than pulsed qCEST at 3 T.

Supplementary Material

Supporting Information

FIGURE S1 Impact of slice profile correction on exchange rate accuracy. The matched exchange rate k_sw as a function of true exchange rate k_sw with (A) and without (B) slice profile correction. The average errors of the results with and without slice profile correction are 2.53% and 2.97%, respectively. This shows that the proposed CEST fingerprinting method is not very sensitive to slice profile imperfections. The experiment was performed as follows. The signal curves were simulated with incorporated slice profile using exchange rates k_sw randomly chosen in the range of 100 s⁻¹ to 500 s⁻¹. The relaxation parameters and MT parameters are the same in the numerical simulation in the main manuscript. The dictionary was generated with and without slice profile correction. The MT correction and signal matching were performed as described in the main manuscript. The error is defined as |matched k_sw–true k_sw|/true k_sw.

FIGURE S2 Simulated signal with and without slice profile correction. Some differences are observed between the simulated signal without (A) and with (B) slice profile correction. However, in the normalized CEST signal curves simulated without (C) and with (D) slice profile correction, only small differences can be observed. This is because the CEST signal is generated by subtracting the label signal from the reference signal and the errors caused by the slice profile imperfections are canceled out.

APPENDIX: MATHEMATICAL REPRESENTATION OF MT CORRECTION

Mathematically, the MT correction scheme is based on Equation A1.⁴⁵ The normalized signal intensity I/I₀ is affected by CEST, MT, and direct water saturation (DWS) effects and can be described as the probability distribution of the union of CEST, MT, and DWS effects.

$$\frac{I}{I_0}=1-\left(\sum _{i=\text{CEST},\text{MT},\text{DWS}}{L}_i-\sum _{i,j=\text{CEST},\text{MT},\text{DWS},i\ne j}\left(L_i\times L_j\right)+\prod _{i=\text{CEST},\text{MT},\text{DWS}}{L}_i\left(\mathrm{\Delta }\mathrm{\omega }\right)\right)$$ (A1)

where L_CEST; L_MT, and L_DWS refer to the Lorentzian distributions for the CEST, MT, and DWS effects, respectively.

MT correction can be separated into the following steps:

Step 1: Estimate the DWS effects. With known T₁ and T₂ values, the distribution of the DWS effect (L_DWS) can be simulated using the Bloch equations at Δω=−δ_s in the same way as the reference dictionary.

Step 2: Estimate the MT effects. The reference signal has negligible CEST effects and can be described by Equation A2. The value of L_MT can be calculated because the normalized reference signal I_ref /I₀ and L_DWS are known.

$$\frac{I_{ref}}{I_0}=1-\left(\left(L_{\text{MT}}+L_{\text{DWS}}\right)-L_{\text{MT}}\times L_{\text{DWS}}\right)$$ (A2)

Step 3: Estimate the CEST effects. The label dictionary has no MT effects and can be described by Equation A3. The value of L_CEST can be calculated because the label dictionary Dictlabel and L_DWS are known.

$${\text{Dict}}_{\text{label}}=1-\left(\left(L_{\text{CEST}}+L_{\text{DWS}}\right)-L_{\text{CEST}}\times L_{\text{DWS}}\right)$$ (A3)

Step 4: Generate the corrected dictionary by combining L_CEST, L_MT, and L_DWS determined from the previous steps following Equation A1.