Extraction of the cardiac waveform from simultaneous multislice fMRI data using slice sorted averaging and a deep learning reconstruction filter.

Abstract

Cardiac signal contamination has long been a confound to analysis of blood-oxygenation-level-dependent (BOLD) functional magnetic resonance imaging (fMRI). Cardiac pulsation results in significant BOLD signal changes, especially in and around blood vessels. Until the advent of simultaneous multislice echo-planar imaging (EPI) acquisition, the time resolution of whole brain EPI was insufficient to avoid cardiac aliasing (and acquisitions with repetition times (TRs) under 400–500 ms are still uncommon). As a result, direct detection and removal of the cardiac signal with spectral filters is not possible. Modelling methods have been developed to mitigate cardiac contamination, and recently developed techniques permit the visualization of cardiac signal propagation through the brain in undersampled data (e.g., TRs > 1s), which is useful in its own right for finding blood vessels. However, both of these techniques require data from which to estimate cardiac phase, which is generally not available for the data in many large databases of existing imaging data, and even now is not routinely recorded in many fMRI experiments.

Here we present a method to estimate the cardiac waveform directly from a multislice fMRI dataset, without additional physiological measurements, such as plethysmograms. The pervasive spatial extent and temporal structure of the cardiac contamination signal across the brain offers an opportunity to exploit the nature of multislice imaging to extract this signal from the fMRI data itself. While any particular slice is recorded at the TR of the imaging experiment, slices are recorded much more quickly – typically from 10–20 Hz - sufficiently fast to fully sample the cardiac signal. Using the fairly permissive assumptions that the cardiac signal is a) pseudoperiodic b) somewhat coherent within any given slice, and c) is similarly shaped throughout the brain, we can extract a good estimate of the cardiac phase as a function of time from fMRI data alone. If we make further assumptions about the shape and consistency of cardiac waveforms, we can develop a deep learning filter to greatly improve our estimate of the cardiac waveform.

Introduction

Cardiac signal contamination has long been a confound to analysis of blood-oxygenation-level-dependent (BOLD) functional magnetic resonance imaging (fMRI). Cardiac pulsation results in significant changes in the observed BOLD signal, especially in and around blood vessels. Until the advent of simultaneous multislice echo-planar imaging (EPI) acquisition, the time resolution of whole brain EPI was insufficient to avoid cardiac aliasing (and the required acquisitions with repetition times (TRs) under 400–500 ms are still uncommon). As a result, direct detection and removal of the cardiac signal with spectral filters is not possible. A number of advanced modelling methods and tools have been developed to mitigate cardiac and respiratory contamination [1–9]. However, the most effective of these require an estimate of the cardiac waveform (for example from an ECG or plethysmogram), which is generally not available for the data in many large databases of existing imaging data, and even now not routinely recorded in many fMRI experiments. More recently, Voss’ hypersampling technique [10] permits the visualization of the propagation of the pseudoperiodic cardiac signal through the brain in undersampled data (e.g., TRs > 1s); however this, too, relies on an externally recorded cardiac signal to determine cardiac phase. Finally, higher order properties of the cardiac waveform itself, such as heart rate variability, can be used to probe autonomic nervous system function and emotional responding [11], which can add depth to the interpretation of fMRI data.

The pervasive spatial extent and temporal structure of the cardiac contamination signal, however, offers an opportunity – we can exploit the nature of multislice imaging to extract this signal from the fMRI data itself. While any particular slice is recorded at the TR of the imaging experiment, slices are usually recorded much more quickly – at the maximum image acquisition rate allowed by the gradient hardware, typically from 10–20 Hz - sufficiently fast to fully sample the cardiac signal (0.66–3 Hz). Using the fairly permissive assumptions that the cardiac signal is a) pseudoperiodic, b) somewhat coherent within any given slice, and c) is similarly shaped throughout the brain, we can extract a good estimate of the cardiac signal as a function of time from fMRI data alone (i.e., without peripheral physiological data).

In addition, this cardiac signal estimate can be improved upon significantly. If we further assume that the shape and frequency of the cardiac waveform varies only slowly over time, we can develop a deep learning filter to greatly improve our estimate of the cardiac waveform by reducing noise (by which we mean making the estimate more closely resemble the ground truth plethysmogram data). We do not know exactly how the shape of the cardiac waveform in any voxel of the fMRI data compares to the shape of the plethysmogram recorded at the fingertip, but machine learning methods, in particular deep learning architectures, do not require us to specify a particular model to define this relationship a priori. We need only propose a very general parametrized function to mathematically relate the input and output data. In deep learning, this parametrized function is learned by iteratively adjusting the connection weights between elements of a neural network. Given sufficient data, the parameters of the function are learned through an optimization procedure, and the deep learning filter incorporates prior knowledge of the structure of plethysmogram waveforms through its training. The crucial point is that we need to have large amount of input/output pairs. This was the case in our study. We used a convolutional neural network (CNN) architecture, which has found a number of applications in computer vision in general [12–16] and medical imaging in particular [17, 18], as well as for time series analysis [19, 20]. Once trained on the matched fMRI derived waveforms and plethysmogram data, this deep learning filter can transform our noisy estimate of the cardiac waveform to a much better estimate of the actual driving cardiac waveform. This estimate can then be used as input to cardiac noise modelling and removal algorithms. We note that ours is not the first work to retrospectively infer physiological signals from fMRI data for the purpose of noise removal; Ash, et al. [21] used a support vector machine approach to estimate cardiac and respiratory phase volume-wise from fMRI data. Our method differs in that we seek to estimate cardiac phase slice-wise, which offers increased accuracy due to increasing the sampling rate. Furthermore, we regenerate an estimate of the actual cardiac waveform, which can be used for additional purposes, such as heart rate variability analysis.

We start with one observation and three assumptions regarding the cardiac signal in the fMRI dataset. Our premises are:

1. Observation: While any given voxel is only sampled once per TR, slices (or groups of slices in the case of multiband (MB) acquisitions) within a TR are being acquired at a much higher rate – typically 10–20 Hz – a rate sufficient to adequately represent the cardiac signal.

2. Assumption 1: The cardiac signal will be sufficiently coherent within a given slice that the normalized timecourses of all the voxels in the slice can be averaged. While this assumption is obviously not strictly true, it is mostly true for the vessel signals that dominate the slice average (however, restricting the averaging to the vessels does improve the estimate, as shown below).

3. Assumption 2: The effect of the cardiac signal across slices is similar enough that the individual slice timecourse averages can be combined with proper delays accounting for the slice acquisition offset, filtering to remove noise, and timecourse normalization, to derive a single timecourse merging information from the whole-brain at a higher effective sample rate to yield an initial estimate of the cardiac waveform.

4. Assumption 3: Prior knowledge of the characteristics of pulsatile cardiac signals (most notably that they are pseudoperiodic with a slowly changing frequency) can be encoded into a deep learning filter and can be used to regularize the initial waveform estimate.

Subsequently, we verified the validity of these assumptions by comparing cardiac waveforms generated by our procedure with the actual plethysmogram signals recorded in vivo in multiple datasets spanning a range of acquisition parameters.

Methods

This method was developed and evaluated using resting state data from the Human Connectome Project 1200 Subjects Release (HCP) [22] (TR=0.72 seconds, MB factor=8), and was further tested on data from the Myconnectome project [23] (TR=1.16 seconds, MB factor=4), and on data from the Discovery Science Study of the Enhanced Nathan Kline Institute – Rockland Sample (NKI-RS) (TR=0.645, 1.4, and 2.5 seconds, with MB factors=4, 4, and 1, respectively) [24]. In the HCP protocol, a large cohort of healthy 22–37 year old participants each underwent four ~14.4-minute resting state scans: data was collected in two sessions on subsequent days, REST1 and REST2; each session consisted of two runs alternating between a left-right (LR) and a right-left (RL) phase encode direction, resulting in 4 resting state scans per participant. Our analysis was only performed on participants with complete data for both LR and RL runs and both REST1 and REST2 sessions. Of the 1113 unique participants in the release, 1009 met this criterion, yielding 4036 datasets. We used data from the first 100 participants numerically in a list of 339 unrelated subjects that were present in the HCP 900 Subjects release as the training dataset. All HCP fMRI data had simultaneously recorded fingertip plethysmogram waveforms for each run. In the Myconnectome dataset, all 90 10-minute resting state runs (collected longitudinally on a single participant over ~2 years) were used for evaluation. This dataset does not have plethysmogram data, but heart rate was measured before and after each scan. The NKI-RS group comprised 67 participants between 22 – 37 years of age (to match the HCP 1200 Subjects release cohort) who had complete fMRI and concurrent fingertip plethysmogram data from three resting state scans (detailed above), two visual checkerboard (TR=0.645 and 1.4 seconds, both with MB factor=4) scans, and one breath-hold (TR=1.4 seconds, MB factor=4) scan.

In order to take advantage of the high effective sampling rate of multislice fMRI data, the exact acquisition time of each voxel must be known. As noted by Voss [10], the extraction of the cardiac information from the fMRI data must be done on the raw and completely unprocessed 4- D fMRI data (which are provided in all three studies utilized in the present manuscript) so that exact time each voxel was recorded is known. Slice timing information is encoded in the DICOM header of most datasets, and various conversion programs such as dcm2niix can be used to extract it [25]. Common preprocessing steps such as motion correction and gradient distortion correction destroy the ability to uniquely assign acquisition time based on image coordinate, as voxels may move from one slice to another. Similarly, slice time correction explicitly shifts data in time to align with the TR; this is only valid for signals with frequencies at or below the Nyquist frequency, which the cardiac signal is not (the resting human heart rate usually ranges from ~40– 140BPM; capturing even the fundamental of a 40BPM heartbeat requires a sample time of 0.75 seconds or shorter). While the HCP data is not slice time corrected, most preprocessing streams perform this correction.

Simultaneous plethysmography and respiratory belt data were recorded for the HCP scans at 400 Hz – the pulse plethysmogram data for each run is used as the target to train the deep learning reconstruction filter, and as the ground truth for performance evaluation, since this is the waveform typically used as a starting point for cardiac noise removal and phase estimation. The plethysmograms in the NKI-RS data have a 62.5Hz sample rate.

Initial cardiac waveform generation

The procedure we use to derive the initial cardiac waveform is simple, and is summarized as follows:

1. Determine the time at which each slice is acquired relative to the start of each TR period, and the effective sampling rate. The effective sample rate is the conventional sample rate (1/TR), multiplied by the number of unique slice acquisition times during a TR (NS / MB), where NS is the number of slices, and MB is the multiband factor (1 for non-multiband acquisitions). The initial derived cardiac waveform therefore has number of volumes × NS / MB timepoints, equally spaced in time at the effective sample rate.

2. Mask the 4-D BOLD data to limit the analysis to voxels where the mean over time exceeds a certain percentage of the robust maximum (the 98^th percentile of values) over all voxels. We selected 10% for this analysis to only include voxels with a high signal to noise ratio (SNR).

3. Detrend each voxel’s timecourse (we use a 3^rd order polynomial here) and normalize each voxel’s timecourse by converting it to its fractional variation around the voxel mean over time (divide by the mean over time and subtract 1). BOLD contrast is the product of mean voxel intensity (not of interest for our purposes) and the effect of nearby hemodynamic fluctuations (which is the effect we are looking for). This normalization removes the effect of the former while preserving the latter.

4. Select the voxels to be used to calculate the cardiac waveform. The simplest version of the procedure simply uses all voxels that pass the threshold in step 2. However, restricting the selection to voxels in or close to blood vessels will improve the quality of the estimate. This is discussed in more detail below in “fMRI data analysis”.

5. Average the normalized timecourses from all voxels within the mask in each slice. The result is a set of time samples spaced by the TR, offset in time by the slice acquisition offset.

6. Normalize each average slice time course. We divided each slice time course by its median absolute deviation (MAD) over time. By using the MAD, we make the variance in each slice equivalent in a manner that is immune to spikes or other artifacts such as sudden motion, which are of limited duration.

7. Combine these samples into the estimated cardiac regressor, starting at the offset of the slice acquisition time in the first TR, with a sample stride equal to the number of unique sample times. If multiple slices are acquired at a particular time offset, their timecourses are averaged.

8. Although not truly part of the cardiac waveform calculation, we then resample the derived waveform to 25 Hz (independent of the effective sample rate). This decouples the later signal denoising and reconstruction steps from any particulars of the data acquisition. As a result, regardless of the number of slices, TR, or MB factor (all of which determine the effective sample rate at which we calculate the cardiac waveform), the derived waveform is resampled to 25 Hz. All of the training, and performance evaluations of the deep learning filter, are done using the 25 Hz waveforms. This makes the denoising step independent of acquisition parameters.

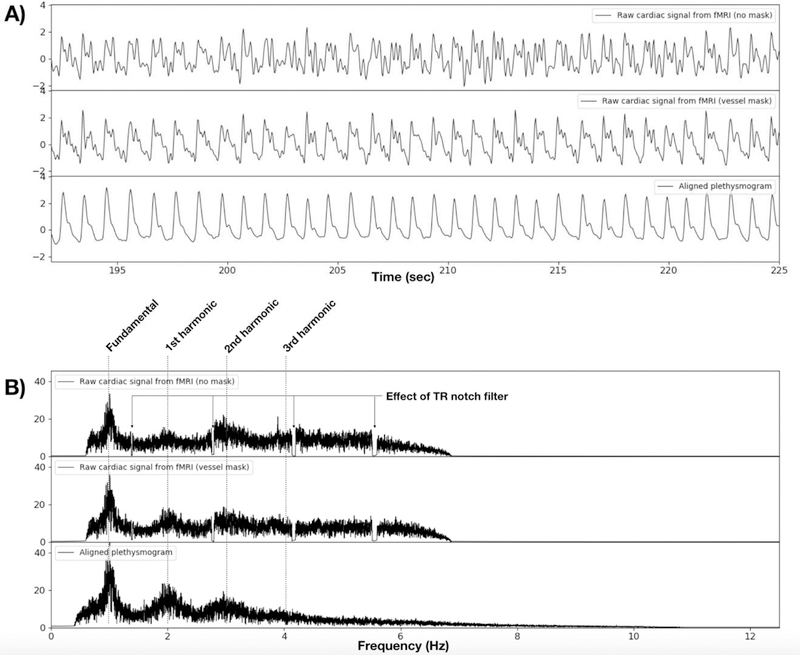
The resulting signal is the initial estimate of the cardiac waveform. This raw signal, calculated both with no masking (top trace) and using a vessel mask (middle trace), and their power spectra, are shown and compared to the ground truth plethysmogram data (bottom trace) from a single scan in Figure 1. The characteristic pattern of peaks at the fundamental cardiac frequency and its harmonics is clearly visible. It is worth noting that even this initial waveform represents at least the fundamental frequency of the plethysmogram waveform quite well. However, as described below we can further improve this estimate by additional processing.

Figure 1.

A) A magnified portion of the raw cardiac signal estimate, using no masking (upper trace) from a typical fMRI dataset (HCP participant 100206, REST1, RL), compared to raw cardiac signal estimate from voxels in a vessel mask (middle trace), and to the ground truth plethysmogram data from the same scan (lower trace). B) Shows the signal spectra from the timecourses above. The spectra of the raw signals show the fundamental and harmonics of the cardiac waveform, but with different relative strengths than the plethysmogram waveform. Using a vessel mask visibly increases the quality of the derived cardiac waveform, showing the risetime more clearly in the time domain, and the harmonic structure is closer to that of the plethysmogram than with the unmasked waveform. The effect of the TR harmonic notch filter can clearly be seen in the top two spectra. The middle trace shows that the spectral characteristics of the plethysmogram are more accurate in the vessel masked waveform estimate. Note that the effective sampling frequency of the HCP data is 12.5 Hz (72 slices, multiband (MB) factor of 8, TR of 0.72s), so there is no spectral energy over the Nyquist frequency of 6.25Hz in the raw cardiac estimates.

Signal filtration

While the normalization of individual slice waveforms (step 6 above) helps to smooth the derived cardiac waveform at the effective sample rate, there will be unavoidable differences in the amplitude and/or offset of the cardiac waveform between slices, since each slice is sampling different parts of the brain. This results in the high-resolution waveform being modulated by a repeating pattern with a period equal to the TR of the acquisitions reflecting differences between the individual slices. The resulting spectral components (at the reciprocal of the TR and harmonics) can be large, and can interfere with estimates of the cardiac fundamental frequency, especially for TR’s around the average human heart rate of one beat per 833 ms. In order to remove this component, we use a Fast Fourier Transform (FFT) filter with notches at the reciprocal of the TR and its harmonics up to ½ the effective sampling frequency; each notch has a width of 1.5% of the frequency being removed (see Fig 1B for effects of the notch filter).

In addition to notch filtration, the data is also high pass filtered at 0.66Hz. This eliminates low frequency noise and respiratory signals, while preserving any heartbeat signal over 40 BPM (the low end of the normal adult heart rate, with allowance for the slightly lower heart rates seen in recumbent participants and athletes). We preserve higher order harmonics of the plethysmogram waveform where possible by not aggressively lowpass filtering, as these harmonics contain information about the vasculature[26]. However we limit the search range for the peak cardiac frequency over the range of 40–140Hz. The frequency range is adjustable for individual participants that may fall outside this range or have other, structured noise in the signal due to motion or other factors.

fMRI data analysis.

All data were processed using the cardiac signal extraction procedure described above in “Initial cardiac waveform generation”, in addition to performing Voss’ hypersampling through analytic phase projection technique [10]. We implemented both procedures in a python program called “happy” (Hypersampling by Analytic Phase Projection – Yay!), now part of the rapidtide analysis suite [27]. As noted above, all cardiac waveform extractions were performed on the unprocessed resting state scans from the Human Connectome Project 1200 participants release, the Myconnectome dataset, and the NKI-RS dataset. For the HCP data, we used the fully “unprocessed” data rather than the “minimally processed”, “fix”, or “fix-extended” data (names for HCP datasets which have undergone various levels of preprocessing) for the reasons stated above.

As described above, in order to develop a generalized reconstruction filter, we added a final step which is not truly part of the cardiac waveform calculation. Regardless of the number of slices, TR, or MB factor (all of which determine the effective sample rate at which we calculate the cardiac waveform), the derived waveform is resampled to 25 Hz. All of the training, and performance evaluations, are done using the 25 Hz waveforms.

Vessel maps for improved cardiac waveform estimation

While estimation of the cardiac waveform can be performed with no masking, the intensity of cardiac contamination in fMRI data varies widely throughout the brain, being strongest near blood vessels. Limiting the estimation procedure to the voxels with the largest expected cardiac variance should improve the quality of the waveform estimate. Unfortunately, vessel maps are rarely recorded in functional imaging studies. However, the hypersampling method described above provides a nice workaround. We can run the estimation procedure on all brain voxels, and use this initial cardiac waveform as input to Voss’ method; this will produce cardiac waveform maps throughout the brain (this is described in more detail below in “Results - Cerebral Pulse Waves”.) By selecting the voxels with the largest variance in these waveform maps over a cardiac cycle, we can produce a rough vessel map (this is output during an initial run of happy). We can then repeat the estimation procedure from the beginning, using the vessel map to select the voxels used for cardiac waveform estimation for a noticeable boost in signal accuracy.

Delay

On average, the HCP plethysmogram signal lags the brain derived cardiac signal by ~132 ± 301ms. At first, we attributed this to instrumentation delays. However, if this were the case, the delay would be constant. Upon closer inspection, we found that the delays varied widely between participants, so it is likely that this reflects differences in individual vasculature, which leads to different relative propagation times of the cardiac wave to the brain and the finger. To remove this additional source of variance (for filter training, or when using the plethysmogram for further analyses), each participant’s plethysmogram data was aligned to the raw cardiac signal by calculating the peak crosscorrelation time and timeshifting the plethysmogram prior to training. This procedure makes the simplifying assumption that the delay time is constant over the length of the experiment.

Deep learning cardiac waveform filter – structure.

The candidate signal for the cardiac waveform initially derived from the fMRI data is noisy, distorted and contains spikes (most likely due to uncompensated motion, not traditional EPI “spiking”). To remove these artifacts, we used a convolutional neural network (CNN) architecture noise removal/signal reconstruction filter implemented in Keras [28]. CNNs are frequently used for noise removal and feature extraction tasks, as they are flexible and can be trained rapidly. Most current work in CNNs is in images, where the data is in matrix form; CNNs are used to extract salient features from spatial “regions” of various sizes. In our case our input is time domain data, so it is in vector form, and the local regions are time windows[29].

As a result of the hyperparameter search to optimize parameters (see “Deep learning cardiac waveform filter – training and optimization” below, as well as “Results”), we selected a vector of 60 contiguous time points from the raw cardiac waveform (which corresponds to 2.4 seconds of data at 25Hz) for the input layer of the CNN, and a deep network architecture with 19 hidden convolution layers, containing 50 channels with a 5 sample convolution kernel for each hidden CNN layer. We used a Rectified Linear Unit (ReLU) as the nonlinear activation function. The final, output layer is composed of a single channel of the same size as the input layer which contains the reconstructed plethysmogram waveform, typically used as a starting point for cardiac noise removal and phase estimation. Deriving plethysmogram data from the input is a regression problem. Hence, we used mean square error (MSE) as the typical loss function.

Deep learning cardiac waveform filter – training and optimization.

As mentioned above, we used the resting state data from the first 100 participants numerically from the HCP to train and test our deep learning filter. The resting state fMRI data were processed as described above to generate initial cardiac waveform estimates at the common frequency of 25 Hz. An intermediate frequency of 25 Hz was chosen to allow this filter to be used independent of the image acquisition frequency. The target of the CNN architecture was the plethysmogram waveforms recorded during each scan, downsampled to 25 Hz from the native 400 Hz (using a common, lower sampling rate simplifies the structure of the network and reduces the number of parameters to train). Input and output waveforms were normalized to have zero mean and unit variance. This allowed us to detect bad data regions, by rejecting runs of points with normalized magnitudes exceeding 4 standard deviations (which we classified as an “outlier point”). We used this extremely stringent threshold to ensure that we used only the highest quality datasets for training. Similarly, runs with “bad” plethysmogram data were excluded (some participants’ data had low SNR, and some had structured noise, and some were missing entirely). Of the 400 runs examined (4 runs each for 100 participants), 47 runs (11.75%) had bad plethysmogram data, leaving 353 runs for analysis. We discarded the first 200 time points and trimmed both the 25Hz fMRI-derived and plethysmography waveforms to 21399 time samples. We demeaned and normalized each timecourse to unit variance. We further excluded any runs that had outliers in the normalized fMRI timecourse (values exceeding +/−4), leaving 258 subjects for training. Subsequently, we chunked the data into 60-point windows (2.4 s), sliding the window one timepoint in each subsequent window (this window shift is a tunable parameter – for larger training datasets it can be increased to keep training time manageable). This yielded a training set composed of 5505720 input output pairs of 60 time points each. We took the first 80 % (4404576 pairs) as training data set and the last 20% (1101144 pairs) as the validation set. As this was a regression problem, rather than a classification problem, we used mean squared error (MSE) as the loss function. We used the ADAM optimizer in Keras for the optimization of the MSE loss function.

We optimized the final deep learning filter architecture detailed above after a hyperparameter search of the several parameters. For ease of the training, we started with 5 hidden layers. After that, we performed a hyperparameter search for channel size among the set (1, 2, 3, 4, 5,10, 50, 100, 150, 200). Finding the optimal channel size, we swept the hidden layer numbers by incrementing from 1 to 29. Each network was trained for 5 epochs. The parameters which gave the lowest validation MSE loss at the epoch number with minimum loss for each training session were selected.

Deep learning cardiac waveform filter - Filter implementation

To apply the filter to a raw timecourse, the input timecourse is segmented into overlapping windows, as during training. The deep learning filter is applied to each segment, and a weighted average of all the overlapped prediction segments is calculated to generate the full, filtered timecourse. This procedure is implemented in happy, which includes a copy of the trained CNN model described above. This is the timecourse we then used for all performance calculations.

Data and code availability statement

All source data comes from publicly available datasets – the Human Connectome Project (www.humanconnectome.org), the Myconnectome project (myconnectome.org), and the enhanced NKI-RS dataset (fcon_1000.projects.nitrc.org/indi/enhanced/). “happy”, the program for extracting and filtering cardiac waveforms from fMRI, and the trained deep learning reconstruction model, are included as part of the open source rapidtide package (https://github.com/bbfrederick/rapidtide). Extracted cardiac waveforms (raw and filtered) for all resting state scans in the Myconnectome dataset will be available at openneuro.org, or from the authors by request.

Results

HCP data

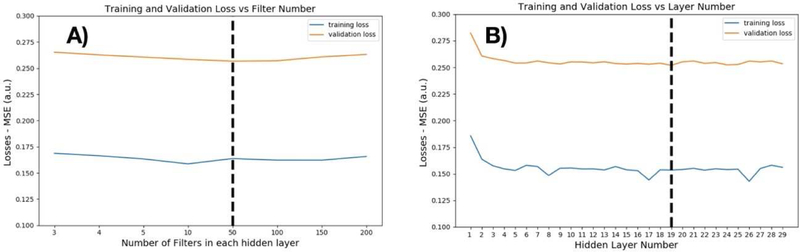
As described in the Methods section, we performed a simple hyper-parameter search for the parameters with the lowest validation loss during training. We swept the number of filters in each hidden layer among the values 1, 2, 3, 4, 5, 10, 50, 100, 150, 200. The optimum number of filters was 50, as shown in Figure 2A. Fixing the filter number at 50, we then swept the hidden layer number between 1 to 29. The optimal hidden layer number was found to be 19, as shown in Figure 2B. Training was performed on the O2 High Performance Compute Cluster, supported by the Research Computing Group, at Harvard Medical School (http://rc.hms.harvard.edu) using a single M40 GPU. For 19 hidden layers consisting of 50 filters and 5 epochs of training, total time was 29 minutes 2 seconds.

Figure 2.

A) Hyper-parameter search for optimum number of filters. We selected 50 filters as the optimum point in the hyper-parameter search. For every layer, we used the same number of filters. Increasing the number of filters past 50 did not improve performance on the validation set. B) Hyper-parameter search for the optimum number of layers: After choosing the number of filters, we tested different numbers of hidden layers. There was no improvement in validation performance after 19 hidden layers.

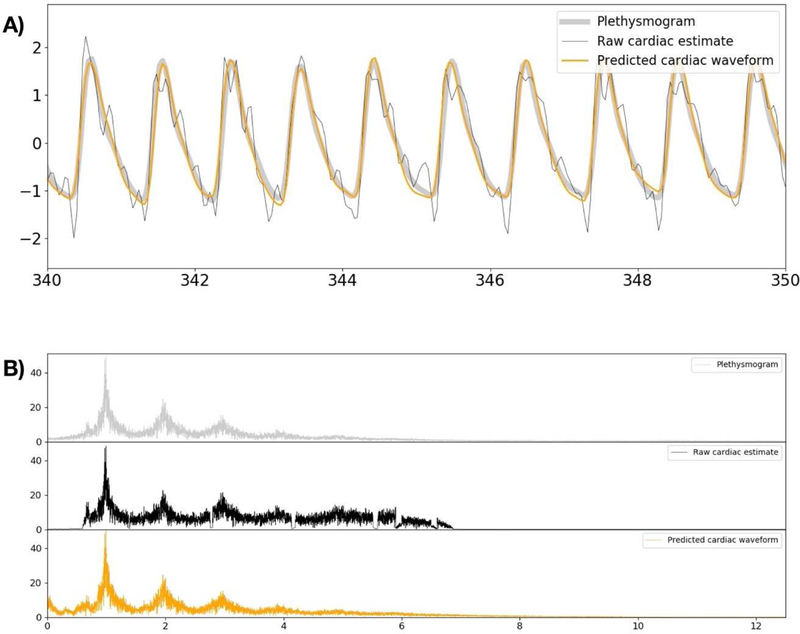
For this set of CNN model parameters, the MSE of the raw signal timecourse with respect to plethysmogram data was 0.518 in the validation set. This is compared to an error of only 0.264 for the deep learning prediction (~49% noise reduction). As the next step, we tested the filter performance in the data which include spikes. This analysis used 94 sessions which had been excluded from the training and validation dataset due to the presence of spikes in the fMRI generated waveforms. In this second experiment, the MSE of the raw signal estimate is 0.675, whereas the MSE of the deep learning prediction is 0.315 (~53% noise reduction). Figure 3 shows the typical graph which includes the raw cardiac signal estimate, the CNN filter prediction, and the ground truth plethysmogram data for one of the validation participants. As shown from this Figure, the raw signal estimation is rather noisy and distorted version of the ground-truth data. The CNN output is a denoised and jitter-corrected version of the raw signal estimate.

Figure 3.

Comparison of the initial raw signal estimate, the CNN filter prediction, and the ground-truth plethysmogram data. A) shows a magnified section of the timecourse from a typical scan, with the signals overlayed for ease of comparison. The raw cardiac estimate shows the cardiac periodicity, and can be used to estimate cardiac phase, but the signal itself is noisy and distorted. The CNN output is de-noised and much closer to the ground truth. B) Shows the spectra of the same signals.

While the visual appearance of the cardiac signal is greatly improved, the most important metric of the filter performance is the instantaneous cardiac phase of the signal, as this is the actual quantity used for most cardiac noise removal methods. As the next step, we therefore calculated the estimated cardiac phase for all timepoints for all three signals using Voss’ method of phase extraction [10] – after detecting the average cardiac frequency with an FFT, we bandpass filter the estimated cardiac waveform to isolate the fundamental of the cardiac oscillation, and then use the Hilbert transform to perform analytic extension and generate a complex waveform. The instantaneous phase is calculated from this waveform using the “angle” function in Python. In the majority of the data, the phase error obtained from the CNN filter output relative to the plethysmogram data was significantly lower than that from the raw signal estimate. Figure 4 shows the ratio of the mean square phase error of the deep learning filter output relative to that of the raw signal estimate.

Figure 4.

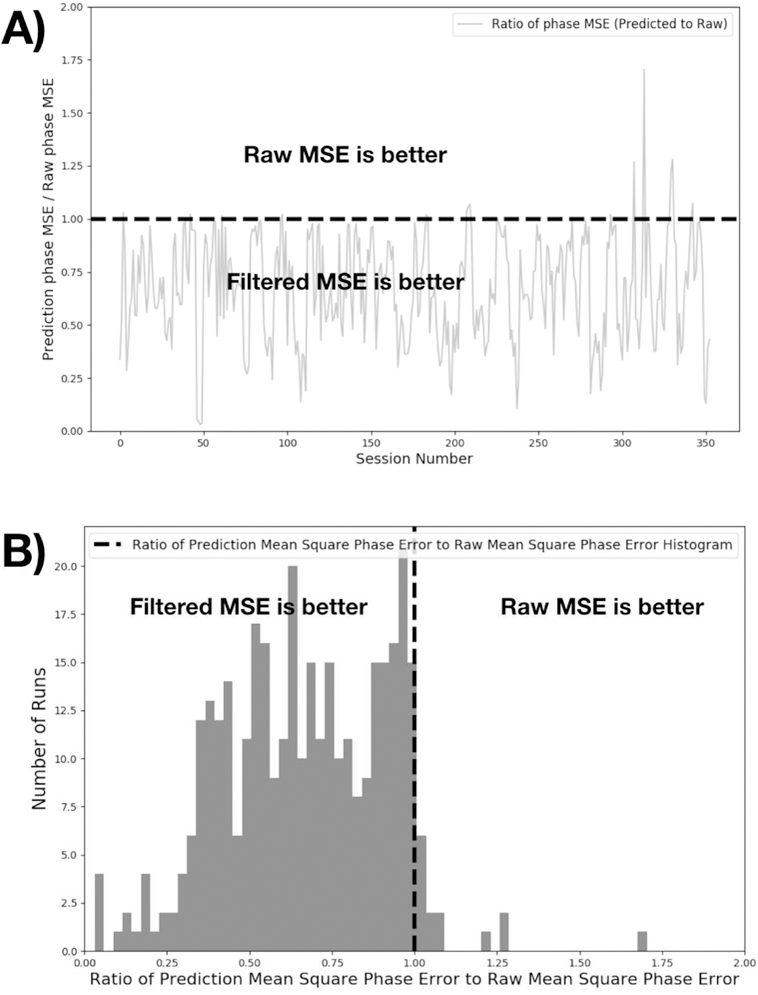
This figure shows phase error comparison of CNN versus the raw cardiac signal. For 353 sessions, we calculated the phase error for both CNN and raw cardiac signals. Analytic phase projection algorithm can result in outliers in some period of the time sequence. We include datapoints up to the 99.9th percentile of the phase errors to exclude outliers in the data. Mean square phase errors relative to the ground truth plethysmogram are calculated and presented as a ratio. In the majority of the cases, phase calculated from CNN output was better compared to Stage 2 output. A) shows the error ratios for individual runs, B) presents the same data as a histogram. The top 2 outliers were found to be high frequency plethysmogram data (cardiac rate of ~120 BPM) which was outside of the typical training range of the dataset.

As a more concrete test of the performance of the extracted waveform, we assessed the cross correlation of the estimated waveforms with the recorded plethysmograms. Figure 5 summarizes these results, comparing the cross-correlation values of the plethysmogram with the raw and filtered cardiac estimates, both in the initial run and in the second run where the cardiac estimates were limited to voxels in the vessel map produced by the first run.

Figure 5.

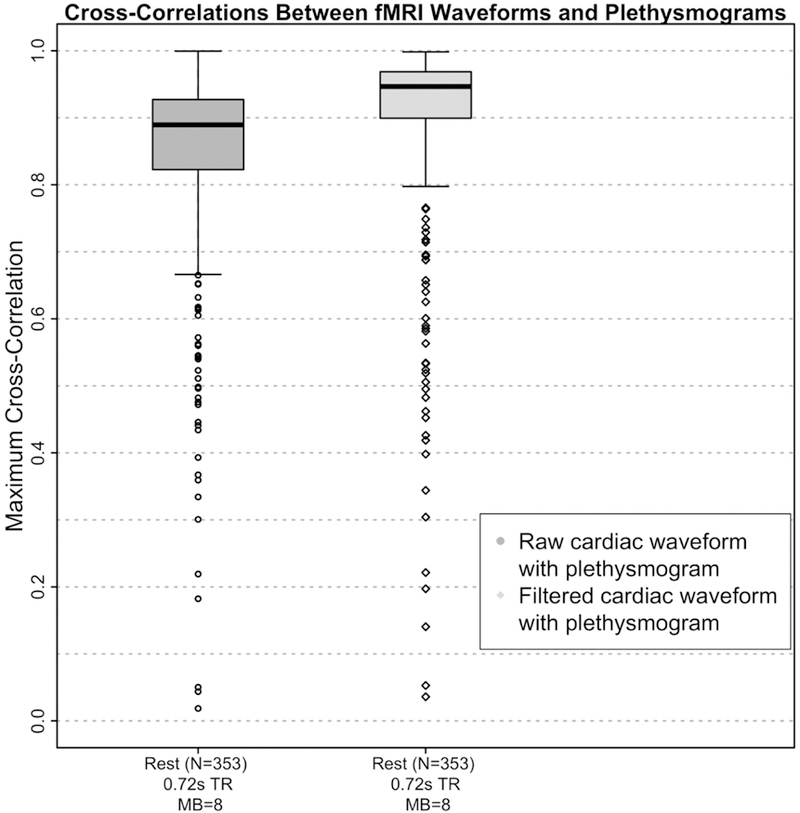
Boxplots of maximum cross-correlation values between the fMRI derived cardiac waveforms and the simultaneously acquired plethysmograms before (“raw”) and after (“filtered”) application of the deep learning reconstruction filter for the Human Connectome Project (HCP) data. The fMRI and plethysmogram data were obtained from the HCP 1200 Subjects Release. 4 scans each from the first 100 subjects numerically in the “339 unrelated subjects” list were included in the dataset. Of the 400 runs, 47 were eliminated due to unusable plethysmograms, leaving 353 runs in the correlation analysis.

Finally, we compared the average heart rate over each run measured from the plethysmogram to that measured using the extracted and filtered waveform for 353 scans with usable plethysmogram data. The results are presented as a Bland-Altman plot [30] in Figure 6. The correlation between the measurements is 0.988 with p < 1.543e-286.

Figure 6.

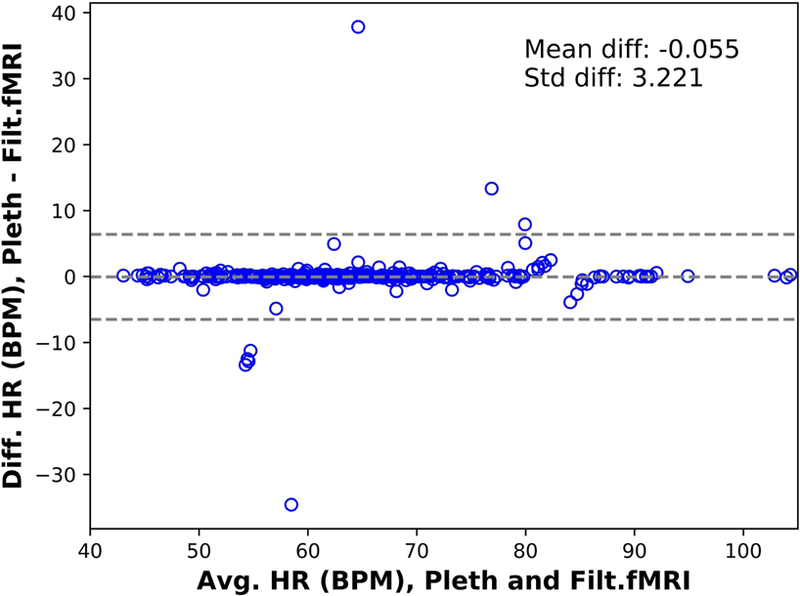
Bland-Altman plot of the average (Avg) heart rate (HR) in beats per minute (BPM) estimated from the plethysmogram (pleth) and the rate estimated from the signal extracted from the MR data, after applying the deep learning filter (Filtered fMRI) vs their difference (Diff) for the Human Connectome Project (HCP) participants for the 353 runs with quantifiable plethysmogram data (see “Plethysmogram data quality”). The correlation coefficient between the estimates is 0.988 with p < 1.543e-286.

In order to evaluate the practical consequences of the differences between the waveforms, we evaluated the utility of each waveform in removing cardiac noise with RETROICOR [1]. We first translated the raw and unfiltered cardiac waveform estimates, and the plethysmogram, into R- waves using the PhysIO toolbox [9], which uses a template matching approach to find the cardiac peaks. We then used each waveform to perform denoising using the AFNI implementation of RETROICOR [31] on the first scan of each participant in our HCP data subset (N=54). Comparing the cardiac phase generated by RETROICOR with the raw estimate, deep learning estimate and the plethysmogram data, we found high correlations (median=0.8–0.85) (Figure 7A). In addition, we evaluated the reduction in variance in the grey matter between the estimates and the plethysmogram data. Although we found only a small reduction in grey matter variance in agreement with prior research on high temporal resolution fMRI data [32], we found, surprisingly, that the deep learning estimate removed more variance than the plethysmogram (p < 0.0038) (Figure 7B). A possible explanation can be found below in “Plethysmogram data quality”.

Figure 7.

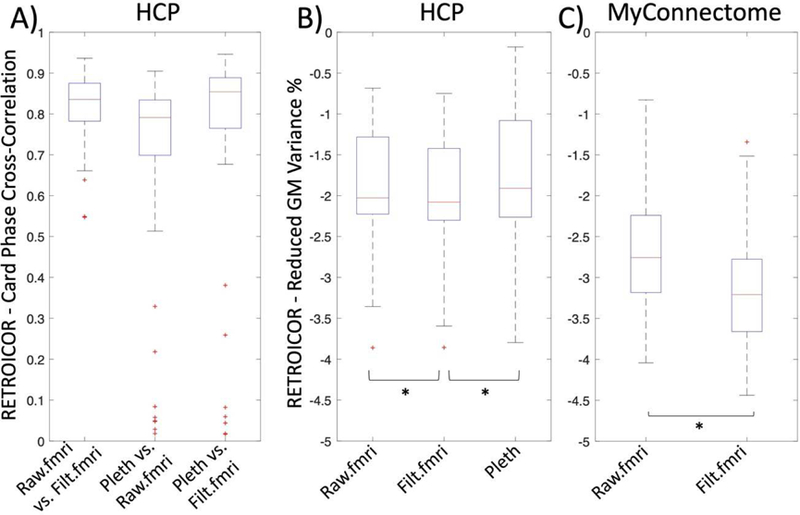
A) High correlation (r=0.8–0.85) between the timecourse of the cardiac phase derived by using RETROICOR for all methods of deriving the cardiac waveform. B) and C) show the reduced variance in the grey matter for Human Connectome (HCP) and MyConnectome data, respectively. The deep learning estimate performed better than both the raw signal estimate (Raw.filt, p=7.1881e-08) or the plethysmogram data (Pleth, p=0.0038) in the HCP data (B) as well as better than the raw signal estimate (Raw.filt, p= 1.7275e-15) in the MyConnectome data (C).

Because the PhysIO toolbox finds the cardiac peak locations to high accuracy, one additional use of the plethysmogram is to calculate heart rate variability (HRV), the variation in beat to beat timing, which holds information about autonomic nervous system function. From the R-wave locations, it is simple to construct the RR interval (RRI) waveform (the interval between successive peaks), from which the HRV can be calculated. This requires accurate peak location, as the variation in peak timing is in the 10s of milliseconds. Figure 8 compares the RRI waveforms from the raw cardiac signal, the filtered cardiac signal, and the plethysmogram for the first scan in the HCP dataset numerically (subject 100206, REST1, LR). The raw cardiac waveform shows a great deal of spurious variability in peak location relative to the plethysmogram, leading to a noisy RRI waveform. The filtered version, however, tracks the plethysmogram very closely, demonstrating that the extracted cardiac waveform can be used for more than noise removal.

Figure 8.

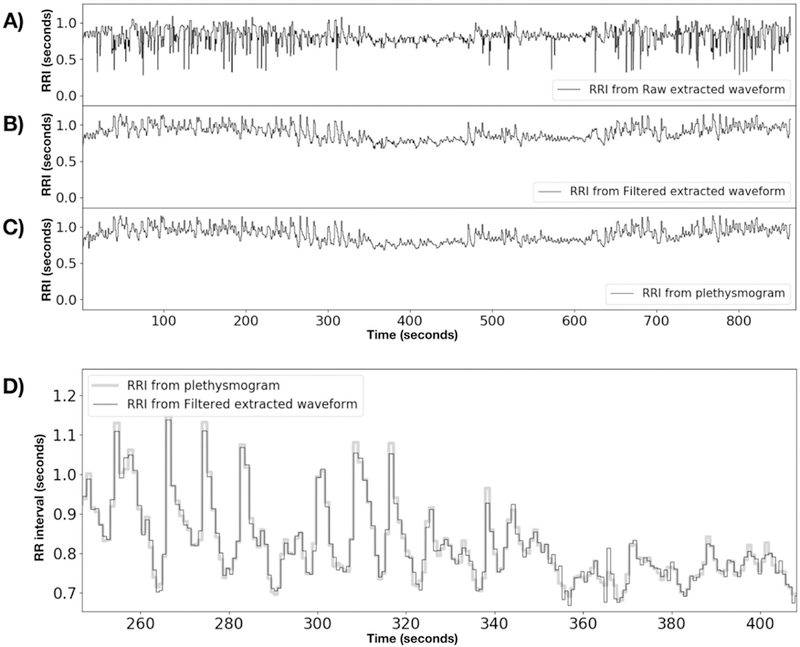
RR interval timecourses for HCP subject 100206, REST1, LR. A) is derived from the raw fMRI extracted timecourse, B) is from the deep learning filtered timecourse, and C) is from the simultaneous plethysmogram. D) Shows a magnified portion of the RRIs from the plethysmogram with the filtered fMRI RRI trace overlaid to show the match. All R-wave timecourses were obtained using the PhysIO toolbox to process the raw waveforms.

Plethysmogram data quality

During the course of constructing the training data set, and the evaluation of filter performance, it became apparent that the failure rate for plethysmogram recordings in the HCP data was higher than anticipated. Plethysmogram recordings can fail for a number of reasons (bad sensor placement, participant movement, poor peripheral circulation, nail polish on finger where the sensor was placed, or in some cases, instrument malfunction). Of 400 data runs, 47 (11.75%) were found to have unusable plethysmograms using the automated procedure described below. Manual screening of the plethysmograms was a tedious procedure; however, we developed an automated checking method that detects problem recordings. Since the deep learning filter was designed to regenerate high quality plethysmogram data from noisy estimates, we reasoned that if a high quality plethysmogram were used as input to the filter, it would not be substantially changed, therefore the input and output waveforms should have a high cross-correlation. Correlating the input to filter with its output, we found the distribution of correlation coefficients shown in Figure 9. There is a clear discontinuity – correlation coefficients below 0.7 were all visually verified to correspond to unusable plethysmogram data. This highlights another use case for our procedure – even when plethysmogram data is collected, the collection can fail – the deep learning filter can be used to assess data quality, and the fMRI generated waveform can be used as a backup to replace unusable recordings. The fact that some of the recorded HCP plethysmograms are bad is likely the reason that the fMRI derived waveform slightly outperformed the plethysmogram data in RETROICOR cardiac noise removal (the RETROICOR analysis was performed on sequential subjects, without checking for bad plethysmograms). This highlights the utility of this method in compensating for deficits in physiological data that arise even in high quality, curated datasets.

Figure 9.

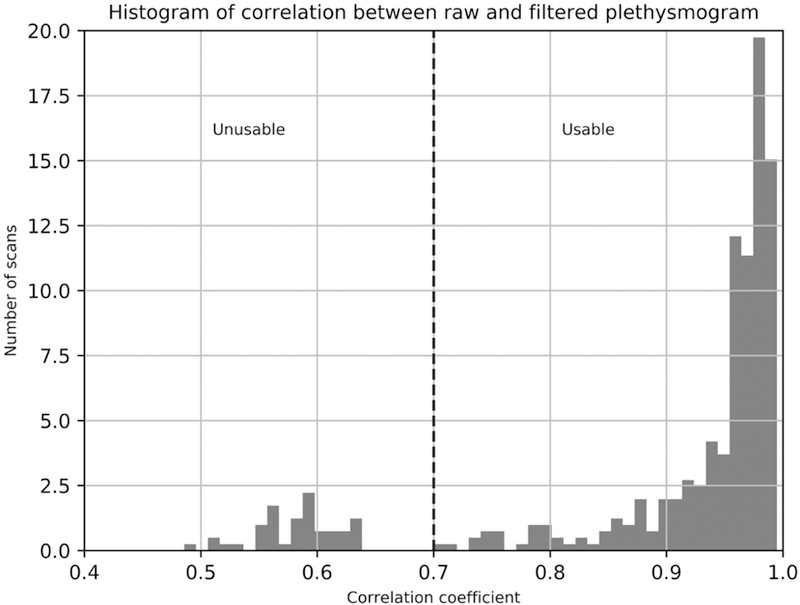
Histogram of crosscorrelation values between plethysmogram waveforms before and after application of the deep learning filter. High quality plethysmograms are not significantly changed by the filter, but signals without a strong cardiac waveform are. “Unusable” plethysmograms were visually verified to have either no signal, extremely poor SNR, strong artifacts, or distorted cardiac waveforms. 47 of 400 runs (11.75%) were found to be unusable.

Myconnectome data

As a second test, we used the Myconnectome dataset to generate cardiac waveforms for datasets that did not have ground truth data (a situation which would be substantially more useful). While the Myconnectome data did not record cardiac signals during the fMRI sessions, heart rate before (“Morning”) and after (“After”) the scanning sessions were recorded, so we do have a method to evaluate data quality, by comparing the rates from the synthetic timecourses we generated with our method from the fMRI data (“Deep Learning Prediction”, or DLP) with these recorded values. The Myconnectome dataset also allows us to test the generalizability of the method. Myconnectome data were collected with a lower spatial resolution (2.4mm isotropic as opposed to 2mm isotropic for the HCP), with a longer TR (1.16 vs. 0.72 seconds), a lower MB factor (4 vs. 8), and between 64 and 68 slices (compared to 72 for the HCP). This corresponds to an effective sampling rate of 13.79–14.66Hz at 55.17–58.62 slices per second (compared to 12.5Hz at 100 slices per second for the HCP).

The results of the comparisons are shown in Figure 10. There was substantially more variance between the fMRI derived heart rate and the values measured outside the scanner in the Myconnectome data than between the heart rate estimates from the HCP fmri data and plethysmograms. Aside from possible differences in estimating the heart rate from a cardiac waveform (which is a fairly straightforward procedure), there are some systematic differences between the measurements. There is a substantial difference between the “Morning” and “DLP” numbers – the “DLP” numbers are 3.998 BPM lower on average than their matched “Morning”. “DLP” is 0.743 BPM lower than the “After” measurement. However, this is consistent with expected physiology – a participant lying on their back during a resting state scan would be expected to have a lower heart rate than when they are sitting up, either having walked into a prep room or just gotten up out of the scanner. In fact, the “After” measurements are on average 3.239 BPM lower than the matched “Morning” measurements.

Figure 10.

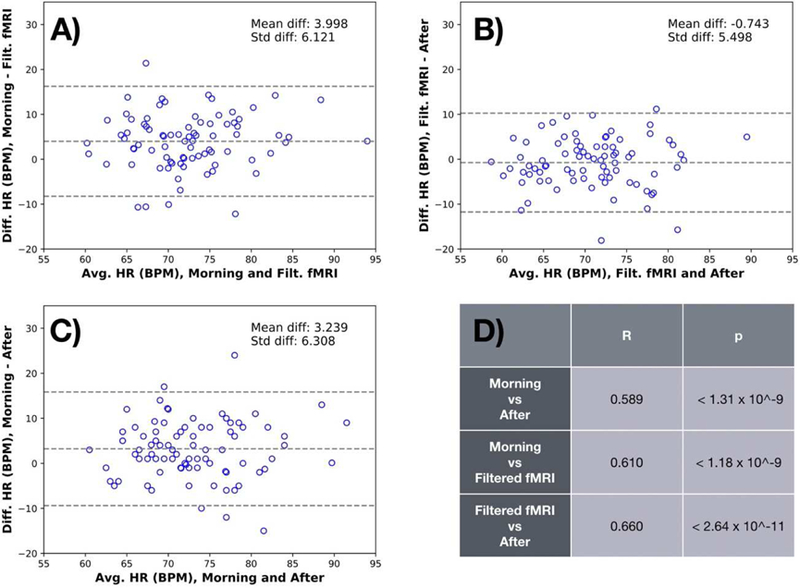
Bland-Altman plots characterizing the relationship of the measured heart rate (HR) estimated before (“Morning”) and after (“After”) the MR imaging session with the rate estimated from the signal extracted from the MR data, after applying the deep learning filter for the Myconnectome dataset (“Deep Learning Prediction”). It is noteworthy that the correlation coefficient both between the “Morning” and “Deep Learning Prediction” (R=0.610, p<1.18e-9, panel A) and the “Deep Learning Prediction” and “After” (R=0.660, p<2.64e-11, panel B) are higher than the correlation between the “Morning” and “After” measurements (R=0.589, p<1.31e- 9, panel C). Correlations are summarized in panel D. This highlights the fact that heartrate measured outside of the scanner is variable, and may not truly reflect the heart rate during the fMRI scan. Again, the plot shows no bias or dependence on heart rate.

The more important metric here is the correlation coefficient. The correlation coefficient both between the “Morning” and “DLP” (R=0.610, p<1.18e-9) and the “DLP” and “After” (R=0.660, p<2.64e-11) are higher than the correlation between the “Morning” and “After” measurements (R=0.589, p<1.31e-9) which are being used as ground truth. This highlights the fact that heart rate measured outside of the scanner is variable, and may not truly reflect the heart rate during an fMRI scan. The heart rate measured directly from the fMRI data itself is likely more accurate.

As above, we used RETROICOR to evaluate the utility of the extracted regressors. As discussed before, we found in general a higher reduction of grey matter variance (N=97, p=3.3361e-15) in the Myconnectome data with TR=1.16s (Median Reduced variance = −3.2%) than in the HCP data with TR=0.72s (Median Reduced variance = −2.8%) (Figure 7b). In addition, the deep learning estimate (Figure 7c, Filt.fMRI) showed a higher reduction in grey matter variance in comparison to the raw signal estimate (Figure 7c, Raw.fMRI).

NKI-RS data

The NKI-RS dataset has three resting state acquisitions per participant: 1) TR of 0.645s, 900 volumes, 40 slices with a MB factor of 4, 3mm isotropic resolution, 2) TR of 1.4s, 404 volumes, 64 slices, with a MB factor of 4, 2mm isotropic resolution, and 3) TR of 2.5s, 120 volumes, 38 slices, no MB, 3×3×3.3 mm resolution. This corresponds to effective sampling rates of 15.50, 11.43, and 15.20Hz and 62.02, 45.71, and 15.20 slices per second respectively. Furthermore, the first two effective sampling rates also apply to the visual checkerboard scans and the second one to the breath hold scan. We calculated the maximum cross-correlation coefficients between both the raw and filtered fMRI derived waveform and the simultaneously recorded plethysmogram data. The distribution of the cross-correlation results are summarized in Figure 11.

Figure 11.

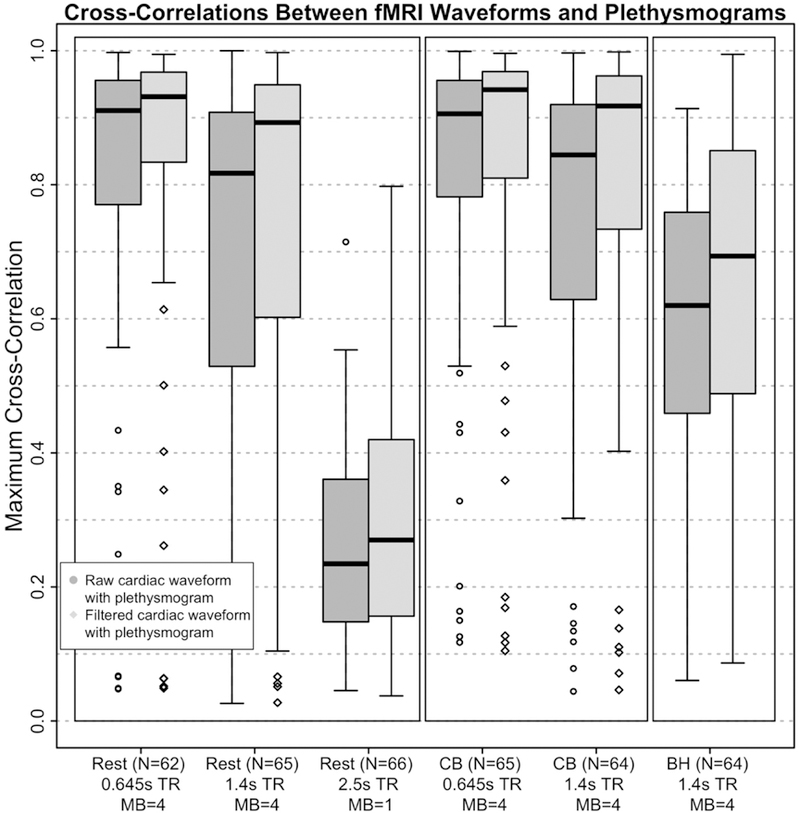
Boxplots of maximum cross-correlation values between the fMRI derived cardiac waveforms and the simultaneously acquired plethysmograms before (“raw”) and after (“filtered”) application of the deep learning reconstruction filter for the three resting state (Rest) scans in the left-most panel, the two visual checkerboard (CB) scans in the middle panel, and one breath hold (BH) scan in the right-most panel. The fMRI and plethysmogram data were obtained from the Discovery Science Study of the Enhanced Nathan Kline Institute – Rockland Sample (NKI-RS) dataset. Participants (out of N=67) included in this figure met the threshold of maximum cross- correlation of the filtered cardiac waveform with its associated plethysmogram >0.70. TR=repetition time, s=seconds, and MB=multiband factor.

Analogously to the HCP results, the application of the deep learning reconstruction filter produces a clear increase in the cross-correlation magnitudes from the raw fMRI derived cardiac waveform with the plethysmogram and the filtered fMRI derived cardiac waveform with the plethysmogram for all three resting state scan parameter choices (Figure 11). As expected, the maximum cross-correlations were highest at the shortest TRs/MB factor=4. More specifically, this was the case for the 62 of 67 (~92.5%) participants in the TR=0.645 seconds acquisition condition with usable plethysmogram data as well as the 65 of 67 (~97%) participants for the TR=1.4 seconds acquisition. Both scan types had a MB factor=4. While there was also a noticable increase in cross-correlation magnitude in the TR=2.5 seconds/MB factor=1 acquisition condition (66 of 67, or 98.5% with usable plethysmograms), the average crosscorrelation values of ~0.25 indicate that performance on this data was quite poor. This suggests that the effective sampling rate, which is roughly comparable between the TR=0.645 seconds/MB factor=4 and TR=2.5 seconds/MB=1 scans (effective sample rates=15.50 and 14.8Hz, respectively), alone does not provide a clear indicator of exactly how well the derived the cardiac waveform corresponds to the ground truth (with or without the application of the deep learning filter). The factors that determine performance of the algorithm likely include not only effective sample rate, but also total number of slices, slices per second, spatial resolution, and multiband factor, and will require further work to fully characterize.

The results from the visual checkerboard and breath hold scans corroborate and extend the findings from the resting state to task fMRI. We observed similar high correlations between the plethysmogram and the derived cardiac waveforms in the TR=0.645 (N=65 of 67, 97%) and TR=1.4 (64 of 67, 95.5%) checkerboard acquisitions (Figure 11). The checkerboard scans have equivalent scan parameters to the resting state scans, and as such, can be directly compared. The fact that these cross-correlation results are so similar suggests that even a strong task activation does not perturb the cardiac extraction process. In contrast, the breath hold scan has the same scan parameters as the other TR-1.4 second scans, and the correlations between the fMRI derived cardiac waveform (both raw and filtered) and the plethysmogram is much lower than for the equivalent resting state and checkerboard scans; we suspect uncompensated motion from the breathhold may be partially responsible for the decrease in the accuracy of the reconstructed cardiac waveform (Figure 11).

Cerebral Pulse Waves

As a final demonstration of the quality of the fMRI derived waveforms, we used the Deep Learning Prediction cardiac waveforms from both HCP and Myconnectome to generate Cerebral Pulse Wave movies [10] from typical datasets. Using Voss’ hypersampling technique, a full cycle of the average cardiac waveform in each voxel is estimated in happy by regridding each timepoint in each voxel’s timecourse to its appropriate location in the cardiac cycle. This requires knowledge of acquisition time of each voxel relative to the start of the TR, and a good estimate of cardiac phase over time. Without the cardiac phase estimate, the cardiac portion of the fMRI signal will not average coherently, degrading the estimation of the voxel waveforms. Frames from the movie of the cardiac waveform for a typical HCP and Myconnectome dataset are shown in Figure 12. The full videos are included in the supplemental material.

Figure 12.

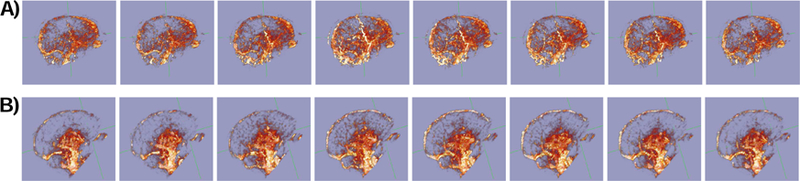
Frames from cardiac pressure wave movies generated using phase projections using cardiac phase from the deep learning filtered cardiac regressor extracted from typical fMRI data for a run in A) the HCP dataset (participant 100307 REST1 LR) and B) the Myconnectome dataset (run 060). Frames are equally spaced in phase across a single cycle of the cardiac waveform. Full movies can be found in the supplemental material.

Discussion

We have implemented and tested a simple algorithm for extracting the cardiac waveform from nominally undersampled fMRI data on three different datasets, and found good agreement between the calculated waveform and external cardiac metrics (plethysmogram data in the case of the HCP and NKI-RS datasets, and pre and post imaging heart rate for the Myconnectome data). As we have previously demonstrated with low frequency signals [33–35], the pervasive nature of hemodynamic signals in the brain means that they can be isolated and quantified in fMRI data by exploiting their spatial extent and temporal structure. This capability will permit flexible retrospective noise removal from fMRI data [1, 5, 6, 8, 9] and visualization of the cardiac waveform [10], as these methods, which require a cardiac waveform as input, can now be performed on data where no such information was collected at scan time, or if the data recorded was of poor quality. We evaluated the algorithm’s ability to recover the cardiac signal from fMRI data in three large and publicly available datasets (the HCP, Myconnectome and NKI-RS studies). Of note, the results from the NKI-RS analyses replicated the HCP findings, yielding high cross-correlations between fMRI derived cardiac waveforms with ground truth plethysmograms, and importantly, extended those results to task fMRI (i.e., the visual checkerboard and breath hold scans). This is meaningful also as the deep learning reconstruction filter was trained on resting state data with different scan parameters. In addition, the cross- correlation results for the breath hold scan, while not as strong as observed for the resting state and visual checkerboard scans, are encouraging. Characterization of the cardiac waveform will likely improve in breath hold data when scans are acquired using a shorter TR and with a MB factor >1; this would be useful, as the cardiac waveform might reveal aspects of cerebrovascular health with implications for studies in aging populations. In the future, we will include more variable datasets (in terms of tasks and scan parameters) in the training of the deep learning reconstruction filter as this might further improve its performance. This could be particularly important for physiological scans like breath hold tasks, as those have a very different BOLD signal shape compared to resting state data. Further work remains to be done to determine how the recovered waveform quality depends on fMRI acquisition parameters (TR, MB factor, slice acquisition order, spatial resolution, different fMRI tasks, etc.)

While the raw signal generated from the data contains sufficient information to determine cardiac phase and heart rate, the time domain CNN noise removal filter described here provides a significant improvement in the signal – increasing SNR, recovering signal harmonics and patching data dropouts where the fMRI generated waveform fails due to motion or other factors. In contrast to simple spectral filters, the CNN filter is a better candidate to recover the ground- truth waveform shape, as it incorporates prior knowledge of the structure of plethysmogram waveforms through its training. We saw substantial improvement after applying multiple layers with multiple filters. Tailoring a simple spectral filter to transform the noisy, distorted input waveform to a complex target waveform is arduous. However, the deep learning filter deduces the best filter coefficients by using the training input and output data for a wide range of signal shapes and frequencies. As a comparison, we compared the deep learning filter performance to that of the best single spectral filter, found by dynamically optimizing the filter coefficients, to map the same training input to training output data. The MSE error performance of the spectral filter was far worse than even a single layer CNN architecture.

MSE reduction in both spike and non-spike data is significant compared to the raw signal estimates (49–53% noise reduction). For non-spike data the CNN based filter can be used as denoiser and jitter remover. When there are spikes in the raw data set, the spikes were also removed and signal was often recovered in the spike regions.

Deep learning architectures work best when they can be trained on sufficiently large datasets. In our case, by subdividing the timecourses into overlapped, chunked windows we had more than 5 million input/output pairs. We observed that the dataset is large enough that optimization reached a steady state in very few epochs - usually 1 to 4 passes through the dataset were enough. Deep learning approaches are most beneficial when it is difficult to model the input and output relation or when there is much uncertainty in models. In fact, we initially tried a model based (Kalman filter/smoother) approach (results not shown). This required system identification of the model parameters. However, the models frequently diverged in the real, noisy data sets. In contrast, the CNN filter was robust in a wide range of datasets with varying levels of noise.

Limitations

Three of the test datasets for this analysis, the HCP and Myconnectome dataset, and one of the NKI-RS datasets, were acquired with MB acquisitions at relatively short TRs (0.72, 1.16, and 0.645 seconds, respectively). While these sampling frequencies are insufficient to fully record the cardiac waveform in any given slice (even in HCP data, the fundamental could only be properly recorded for heart rates at or below 41.6 BPM), performance on datasets with longer TRs may be significantly worse. The NKI-RS comprised datasets with 0.645, 1.4, and 2.5 second TRs. Despite the fact that a 1.4 second TR will ensure aliasing of the cardiac waveform, performance on this dataset was good. In contrast, the cardiac signal could not be recovered well from the 2.5 second dataset (which had a small number of slices, low resolution, and no MB acquisition). Further testing will be needed to determine what combination of spatial and temporal resolution, brain coverage, and MB factor are necessary for this algorithm to perform adequately. However, MB acquisition and short TRs are becoming far more common with time, so this is likely to become less of a problem going forward.

The CNN filter we implemented here uses only very local information (a 2.4 second window). Given the pseudoperiodic nature of the cardiac signal, a larger time window, or a recurrent architecture, which capitalized on the repetition of the cardiac waveform, would likely provide additional benefits. However, in this case we found that even this simple architecture provided significant performance gains, and the CNN filter can be trained quickly and calculated efficiently. While a GPU was used during the training phase to keep training time reasonable, application of the filter can performed quickly using only the CPU.

Conclusions

By combining time corrected multi-slice summation of slice voxel averages with a convolutional neural network filter, we have successfully estimated the cardiac signal from resting state fMRI data itself. While the raw estimate can be used for phase estimation, and cardiac frequency measurement, and generation of cardiac propagation maps, applying a CNN filter trained to regenerate simultaneously recorded plethysmogram data from the raw data significantly improves both the waveform shape and instantaneous phase performance. Mean square error reduction was 49% in the validation set, and was 53% in a larger dataset including very poor quality, spiky data. In this dataset, in addition to denoising and jitter removal, spikes were also significantly attenuated. Analytic phase projections accuracies were also compared. In the vast majority of cases, deep learning output results were significantly better in phase accuracy. The reconstructed cardiac signal can be used for noise removal, physiological state estimation and analytic phase projection to construct vessel maps, even in cases where no physiological data was recorded during the scan.