Emergent Modular Neural Control Drives Coordinated Motor Actions

Abstract

A remarkable feature of motor control is the ability to coordinate movements across distinct body parts into a consistent, skilled action. To reach and grasp an object, “gross” arm and “fine” dexterous movements must be coordinated as a single action, but how the nervous system achieves this coordination is currently unknown. One possibility is that, with training, gross and fine movements are co-optimized to produce a coordinated action; alternatively, gross and fine movements may be modularly refined to function together. To address this question, we recorded neural activity in primary motor cortex (M1) and dorsolateral striatum (DLS) during reach-to-grasp skill learning in rats. During learning, the refinement of fine and gross movements was behaviorally and neurally dissociable. Furthermore, inactivation of M1 and DLS had distinct effects on skilled fine and gross movements. Our results indicate that skilled movement coordination is achieved through emergent modular neural control.

Introduction

The deceptively simple act of reaching and grasping an object requires the precise coordination of both “gross” movements of the arm and “fine” movements of the fingers. Each body part plays a different role in the action with distinct complexities in its control^1,2. How, then, does the nervous system coordinate such movements to produce a unified skilled action? It has been suggested that such coordination is achieved by globally optimizing movements with respect to biologically relevant task goals^3,4. For example, in reaching and grasping, fine and gross movements may be jointly optimized to achieve task success while minimizing parameters such as effort. Little is known, however, about the emerging neural basis of such coordination during skill learning.

While many tasks have been used to study the neural basis of skill learning (e.g. reaching and grasping^5–7, lever pressing^8,9, accelerating rotarod^10–12), learning is often measured using global task parameters rather than by changes in movements (however, see Kawai, et al., 2015, Rueda-Orozco, et al., 2015, Li, et al., 2017). For example, while rodent reach-to-grasp skill learning requires the coordination of both fine and gross movements², learning is commonly assessed by overall success rate⁵. Thus, a key goal of this study was to establish how changes in parameters such as success rate are achieved through changes in the underlying movements involved and to determine the neural basis for the emergence of such skilled movements.

One possibility is that changes in success rate are achieved through the co-optimization of both fine and gross movements. In this case, during reach-to-grasp skill learning, we would expect a pattern of neural activity linked to both fine and gross movements to emerge as fine and gross movements are refined concurrently. Alternatively, coordination may be achieved in a distributed fashion. In this case, we would expect modular patterns of neural activity to emerge independently that represent the control of fine or gross movements specifically.

Here, we report emerging modular neural control of fine and gross movements as a coordinated motor action was learned. We recorded neural activity in primary motor cortex (M1) and dorsolateral striatum (DLS), the primary striatal target of M1^12,13, throughout learning of a reach-to-grasp skill in rats. We observed emerging coordinated low-frequency activity across M1 and DLS that was linked to the emergence of fast and consistent gross movements. Surprisingly, the emergence of skilled fine movements was independent of this activity, evolved over a longer timescale, and displayed a stronger cortical reliance. Consistent with these results, inactivation of M1 and DLS had distinct effects on skilled fine and gross movements. Together, our results indicate that skilled movement coordination can be achieved through emergent modular neural control.

Results

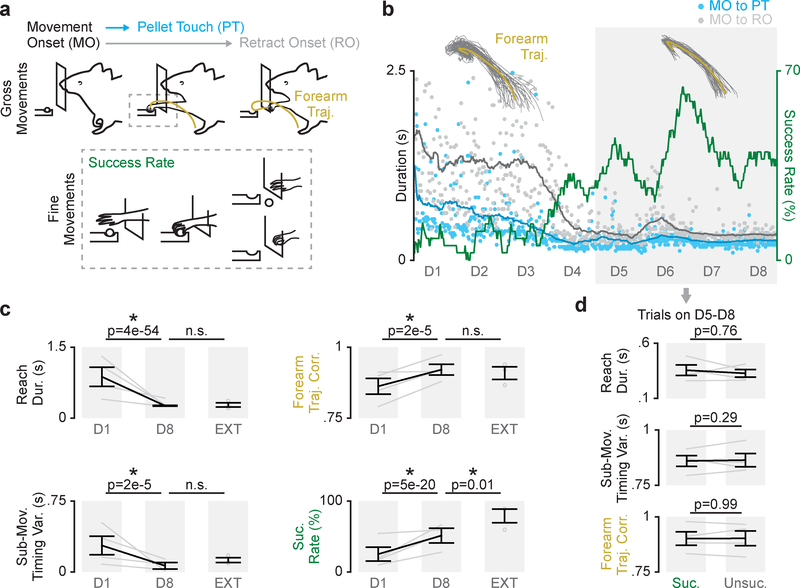
We recorded neural signals, including single-unit activity and local field potentials (LFP) in M1 and DLS (Supp. Fig. 1; Supp. Fig. 2) as rats (n = 4 animals) learned a reach-to-grasp skill. Rats were trained for eight days in automated behavioral boxes, performing 75–150 trials each day¹⁴. Refinement of both “gross” movements of forearm, for an accurate reaching action, and “fine” movements of the digits, to successfully grasp the pellet, are required to learn this skill (Fig. 1a). Consistent with past results^5,6, over eight days of learning, success rate increased and movements became faster and more consistent (Fig. 1b&c; reach duration: 874 ± 203ms on day one to 262 ± 10ms on day eight, mean ± SEM across animals hereafter, mixed-effects model: t(913) = −16.6, P = 3.6×10^–54; sub-movement timing variability: 281 ± 97ms to 66 ± 34ms, mixed-effects model: t(913) = −4.4, P = 1.7×10^–5; forearm trajectory consistency: 0.86 ± 0.02 to 0.92 ± 0.02 mean correlation value, mixed-effects model: t(516) = 4.4, P = 1.5×10^–5; success rate: 25.2 ± 9.9% to 51.4 ± 10.3%, mixed-effects model: t(913) = 9.4, P = 5.1×10^–20).

Figure 1. Refinement of skilled fine and gross movements is dissociable during reach-to-grasp skill learning.

a. Diagram of skilled reach-to-grasp task and measures of learning including duration from movement onset (MO) to pellet touch (PT), duration from movement onset to retract onset (RO), forearm trajectory correlation, and success rate. b. Example time course of learning (dots represent individual trials, lines are averaged over 30 trials; forearm trajectories are shown from day one and day eight, individual trial trajectories in grey and mean trajectory in yellow). c. Difference in reach duration, sub-movement timing variability, forearm trajectory correlation, and success rate between day one (D1) and day eight (D8) of training in learning cohort (n = 4 animals), and performance from an extended training cohort (EXT; n = 3 animals). Grey lines represent individual animals from learning cohort on day one and day eight, grey dots represent individual animals in extended training cohort, and black lines represent mean and SEM across animals. P values are from mixed-effects models. d. Differences in reach duration, sub-movement timing variability, and forearm trajectory correlation between successful (Suc.) and unsuccessful (Unsuc.) trials on days 5–8 (n = 4 animals). Grey lines represent mean values from each animal in learning cohort and black lines represent mean and SEM across animals. P values are from mixed-effects models.

Refinement of skilled fine and gross movements is dissociable during skill learning

We first sought to determine how changes in success rate were related to changes in fine or gross movements. During learning, we observed that success rate and changes in gross forearm movements, measured by reach duration, sub-movement timing variability, and forearm trajectory consistency, evolved on different timescales. While measures of gross forearm movements reached a plateau within eight days, success rate remained variable (Fig. 1b, D5-D8 in gray box). This dissociation suggested that gross movements may stabilize while the fine movements of the digits remain variable, resulting in variable success rate. In fact, we observed that differences in forearm movements did not account for success on days five through eight of learning, as we found no significant differences between reach duration, sub-movement timing variability, or forelimb trajectory consistency for successful and unsuccessful trials on these days (Fig. 1d; reach duration: 355 ± 48ms for successful trials and 327 ± 35ms for unsuccessful trials, mixed-effects model: t(1310) = 0.3, P = 0.76; sub-movement timing variability: 101.1 ± 24.7ms and 100.6 ± 34.9ms, mixed-effects model: t(114) = 1.1, P = 0.29; forearm trajectory consistency: 0.92 ± 0.02 and 0.92 ± 0.01 mean correlation value, mixed-effects model: t(301) = −0.001, P = 0.99). Furthermore, success rate did not covary with measures of gross movements on these days (Supp. Fig. 3; reach duration: Pearson’s correlation r = 0.11, P = 0.21; sub-movement timing variability: Pearson’s correlation r = 0.10, P = 0.26).

Importantly, the control of skilled fine movements continued to evolve over a longer time scale. In a separate “extended training” cohort (n = 3 animals), performing ~2500 trials over 4 weeks, average success rate reached a significantly higher rate than our “learning cohort” reached in eight days, while reach duration, sub-movement timing variability, and forearm trajectory consistency were not significantly different between cohorts (Fig. 1c; reach duration: 262 ± 10ms for learning cohort and 279 ± 39ms for extended training cohort, mixed-effects model: t(714) = 0.49, P = 0.62; sub-movement timing variability: 66 ± 34ms and 125 ± 22ms, mixed-effects model: t(135) = 1.5, P = 0.12; forearm trajectory consistency: 0.92 ± 0.02 and 0.91 ± 0.01 mean correlation value, mixed-effects model: t(460) = 0.07, P = 0.94; success rate: 51.4 ± 10.3% and 78.9 ± 8.4%, mixed-effects model: t(714) = 2.5, P = 0.01). Altogether, this indicated that the refinement of skilled fine and gross movements was dissociable during reach-to-grasp skill learning.

Coordinated movement-related activity emerges across M1 and DLS during skill learning

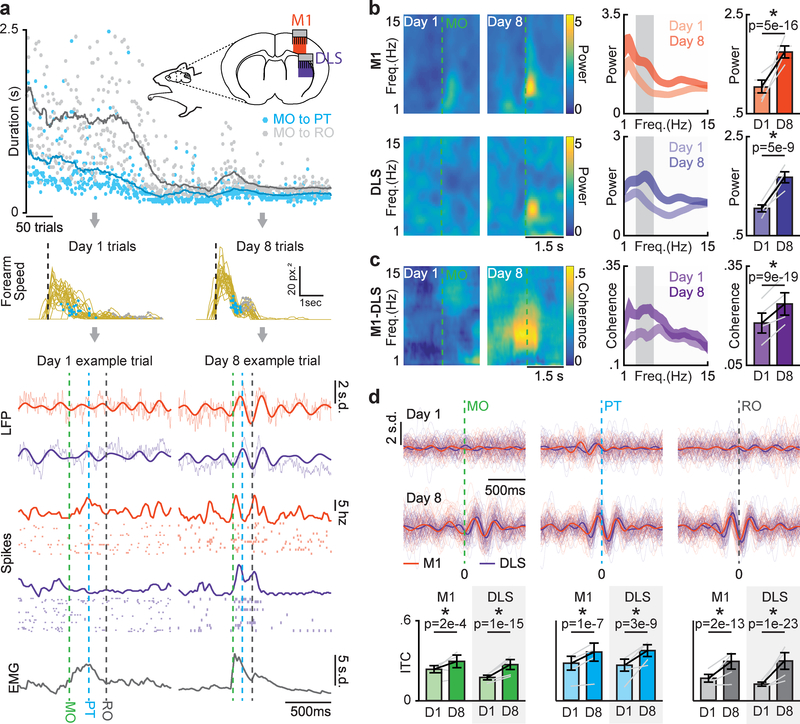
With learning, reaching sub-movements became consistently timed and the velocity profile of the forearm developed a multiphasic profile (Fig. 2a, top/middle). Strikingly, we observed that coordinated low-frequency (~3–6Hz) activity emerged during movement across M1 and DLS that was closely related to the consistent timing of sub-movements and forearm muscle activity, which also displayed a similar low-frequency component (Fig. 2a, bottom).

Figure 2. Coordinated movement-related activity emerges across M1 and DLS during skill learning.

a. Diagram of emerging low-frequency dynamics across forearm speed profile, neural activity in M1 and DLS, and forearm muscle activity during reach-to-grasp skill learning. Top: Illustration of recoding scheme and example time course of learning for duration from movement onset to retract onset (gray) and movement onset to pellet touch (blue; dots represent individual trials, lines are averaged over 30 trials). Middle: Forearm speed profiles for all trials on day one and day eight with timing of pellet touch (blue dots) and retract onset (grey dots) overlaid for example animal. Bottom: neural activity and forearm muscle activity for representative successful trials from day one and day eight. b. Left: Spectrograms from example M1 and DLS LFP channels. Middle: Mean M1 and DLS LFP power spectrums across animals (n = 4 animals; width denotes mean ± SEM). Right: Difference in 3–6Hz M1 and DLS LFP power from day one to day eight. Grey lines represent mean power from individual animals (n = 4 animals) and black lines represent mean and SEM across animals. P values from mixed-effects models. c. Left: Coherograms from example M1-DLS LFP channel pair. Middle: Mean coherence spectrum across animals (n = 4 animals; width denotes mean ± SEM). Right: Difference in 3–6Hz M1-DLS LFP coherence from day one to day eight. Grey lines represent mean coherence from individual animals (n = 4 animals) and black lines represent mean and SEM across animals. P values from mixed-effects models. d. Top: 3–6Hz filtered LFP from example M1 and DLS channels time locked to sub-movements, individual trials with mean signal overlaid. Bottom: Changes in inter-trial coherence (ITC). Grey lines represent mean inter-trial coherence from individual animals (n = 4 animals) and black lines represent mean and SEM across animals. P values from mixed-effects models.

The emergence of coordinated low-frequency activity across M1 and DLS was clearly observed in movement-related LFP signals. Movement-related LFP power between 3–6Hz increased from day one to day eight in both M1 and DLS (Fig. 2b; M1: 1.0 ± 0.13 baseline normalized power on day one to 1.74 ± 0.1 on day eight, mixed-effects model: t(146) = 9.1, P = 5.0×10^–16; DLS: 1.0 ± 0.7 to 1.67 ± 0.1, mixed-effects model: t(94) = 6.4, P = 5.1×10^–9). Movement-related LFP coherence between M1 and DLS LFP also increased in the 3–6Hz frequency range (Fig. 2c; 0.18 ± 0.03 coherence on day one to 0.24 ± 0.03 on day eight, mixed-effects model: t(870) = 9.1, P = 9×10^–19). Movement-related 3–6Hz LFP phase lag between high-coherence M1 and DLS channels was consistent with the connectivity between M1 and DLS and inconsistent with volume conducted signals¹⁵ (Supp. Fig. 4). Additionally, increases in LFP power and coherence were not solely a byproduct of faster and more consistent movements, as LFP power and coherence increased for behaviorally-matched trials early and late in learning (Supp. Fig. 5).

With training, reaching sub-movements became precisely phase-locked to 3–6Hz LFP signals in both M1 and DLS, consistent with what we would expect if this activity was involved in generating sub-movements^16,17 (Fig. 2d; significant increase in inter-trial coherence (ITC) of M1 LFP locked to movement onset: mixed-effects model: t(102) = 3.8, P = 2×10^–4, pellet touch: mixed-effects model: t(102) = 4.7, P = 1×10^–7, and retract onset: mixed-effects model: t(102) = 8.5, P = 2×10^–13; DLS LFP locked to movement onset: mixed-effects model: t(96) = 9.6, P = 1×10^–15, pellet touch: mixed-effects model: t(96) = 6.6, P = 3×10^–9, and retract onset, mixed-effects model: t(96) = 12.4, P = 1×10^–23). Additionally, the peak frequency of LFP coherence covaried with movement duration on day eight (Supp. Fig. 6), further suggesting that coordinated low-frequency activity across M1 and DLS was closely linked to skilled gross movements.

Coordinated spiking activity emerges across M1 and DLS during skill learning

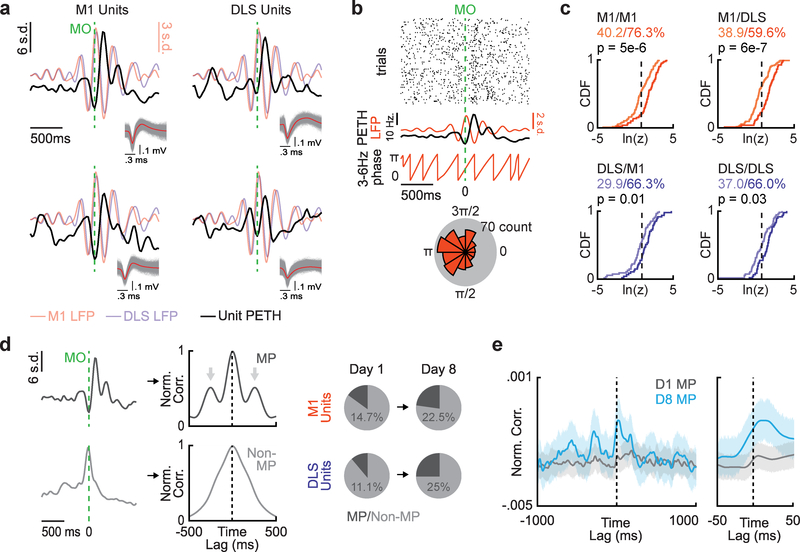
The emergence of coordinated low-frequency activity across M1 and DLS was also clearly observed in movement-related spiking activity across M1 and DLS. Peri-event time histograms (PETHs) of M1 and DLS units displayed movement-related multiphasic activity locked to 3–6Hz LFP activity (Fig. 3a). We quantified phase-locking of movement-related M1 and DLS spikes to low-frequency LFP signals by generating polar histograms of the LFP phase at which each spike occurred for a single unit and LFP channel (Fig. 3b). The non-uniformity of these histograms (indicating phase-locking) was quantified using a Raleigh test of circular non-uniformity. We compared all M1 and DLS units on day one and day eight to the same LFP channel in M1 and DLS and observed an increase in the percentage of M1 and DLS units phase-locked to both M1 and DLS LFP signals with training (Fig. 3c; black vertical dotted lines correspond to the P=0.05 significance threshold of the natural log of the z-statistic; M1 unit - M1 LFP pairs: 40.2% day one to 76.3% day eight, P = 5×10^–6, Kolmogorov-Smirnov test; M1 unit - DLS LFP pairs: 38.9% to 59.6%, P = 6×10^–7, Kolmogorov-Smirnov test; DLS unit - M1 LFP pairs: 29.9% to 66.3%, P = 0.01, Kolmogorov-Smirnov test; DLS unit – DLS LFP pairs: 37.0% to 66.0%, P=0.03, Kolmogorov-Smirnov test). We did not observe any clear timing differences in the average responses of phase-locked and not phase-locked units (Supp. Fig. 7i&j).

Figure 3. Coordinated spiking activity emerges across M1 and DLS during skill learning.

a. Example Peri-Event Time Histograms (PETH) from units in M1 (left) and DLS (right) displaying multiphasic activity locked to 3–6Hz LFP activity. b. Diagram of spike-LFP phase locking. Top: Raster plot of example M1 unit spiking activity during movement aligned to movement onset (MO). Middle: Example unit PETH with M1 LFP activity overlaid and extracted 3–6Hz LFP phase. Bottom: Polar histogram of LFP phases at which spikes occurred. c. Cumulative density functions of z-statistics for every unit-LFP pair across and within each region (vertical dotted lines denote significance threshold of z-statistic at p<0.05, % of respective unit-LFP pairs greater than threshold noted, lighter color is day one; n = 107 M1 unit-LFP pairs on day one, n = 80 M1 unit-LFP pairs on day eight, n = 54 DLS unit-LFP pairs on day one, n = 47 DLS unit-LFP pairs on day eight). P values from Kolmogorov-Smirnov test. d. Left: PETHs from example unit displaying multiphasic activity and example unit not displaying multiphasic activity and corresponding autocorrelations used for classifying multiphasic (MP; arrows denote “bumps” used for classification, see methods) and non-multiphasic units (Non-MP). Right: Percentage of units in M1 and DLS on day one and day eight that display multiphasic activity. e. Mean cross-correlation between all multiphasic M1 and DLS units on day one (grey; n = 46 cross-correlations) and day eight (blue; n = 104 cross-correlations). Grey and blue lines represent mean deviation across cross-correlations and width of shaded region depicts mean ± SEM).

The percentage of units displaying movement-related multiphasic activity in the 3–6Hz range also increased with learning (Fig. 3d). We classified units as “multiphasic” based on the shape of each unit’s autocorrelation, providing an LFP-independent measure of movement-related low-frequency activity (47.1% of M1 multiphasic units were also phase-locked to M1 LFP on day eight, compared to 42.1% on day one; 53.9% DLS multiphasic units were also phase-locked to DLS LFP on day eight, compared to 50% on day one). Strikingly, the mean cross correlation of all M1 multiphasic units to all DLS multiphasic units displayed a short-latency peak consistent with the connectivity of M1 and DLS, as well as secondary peaks corresponding to a 3–6Hz rhythm. This spiking relationship was not observed on day one (Fig. 3e). These results further suggest that coordinated low-frequency activity emerges across M1 and DLS during skill learning.

Coordinated M1 and DLS activity is specifically linked to skilled gross movements

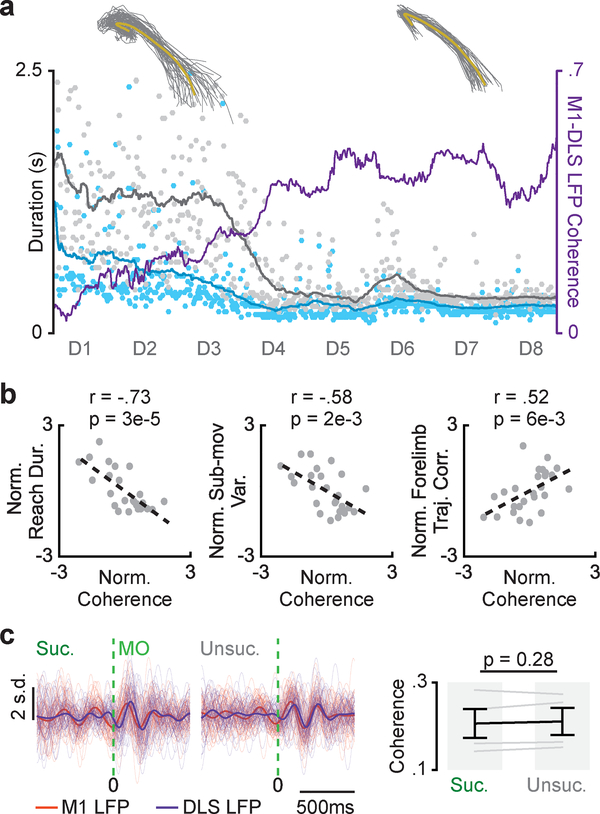
If coordinated low-frequency activity across M1 and DLS is involved in generating skilled gross movements, we expect their emergence to coincide during learning. In fact, we found that increases in movement-related M1-DLS 3–6Hz LFP coherence coincided with the transition to fast and consistent gross movements (Fig. 4a). Across animals, we observed a significant correlation between each day’s average movement-related 3–6Hz M1-DLS LFP coherence and average reach duration, sub-movement timing variability, and forearm trajectory correlation (Fig. 4b; reach duration: Pearson’s r = −0.73, P = 3× 10^–5; sub-movement timing variability: Pearson’s r = −0.58, P = 2×10^–3; forelimb trajectory correlation: Pearson’s r = 0.52, P = 6×10^–3, n = 25 sessions across 4 animals).

Figure 4. Coordinated M1 and DLS activity is specifically linked to skilled gross movements.

a. Time course of movement-related 3–6Hz LFP coherence from example M1-DLS channel pair over training period overlaid with timing of sub-movements and forearm trajectories from day one and day eight. b. Scatterplots of each session’s mean movement-related 3–6Hz M1-DLS LFP coherence and mean reach duration, sub-movement timing variability, and forelimb trajectory correlation, each normalized per animal (n = 25 sessions across 4 animals; Pearson’s r). c. Filtered LFP (3–6Hz) signals from example M1 and DLS channels for successful and unsuccessful trials on days 5–8, individual trials overlaid with mean signal (left) and difference in M1-DLS LFP coherence for successful and unsuccessful trials on days 5–8 (right; n = 4 animals). Grey lines represent mean coherence from individual animals (n = 4 animals) and black lines represent mean and SEM across animals. P values from mixed-effects model.

We next tested whether coordinated low-frequency activity across M1 and DLS was also related to changes in success rate. We compared movement-related 3–6Hz M1-DLS LFP coherence between successful and unsuccessful trials after the stabilization of gross movements (i.e., days five through eight of learning; e.g., Fig. 1b, D5-D8 in gray box) and found no significant difference (Fig. 4a&c; 0.20 coherence ± 0.03 for successful trials and 0.21 ± 0.03 for unsuccessful trials, mixed-effects model: t(2558) = 1.1, P = 0.28). As we attribute variability in success rate during this period to differences in fine movements, these results suggested that coordinated low-frequency activity across M1 and DLS specifically linked to skilled gross movements.

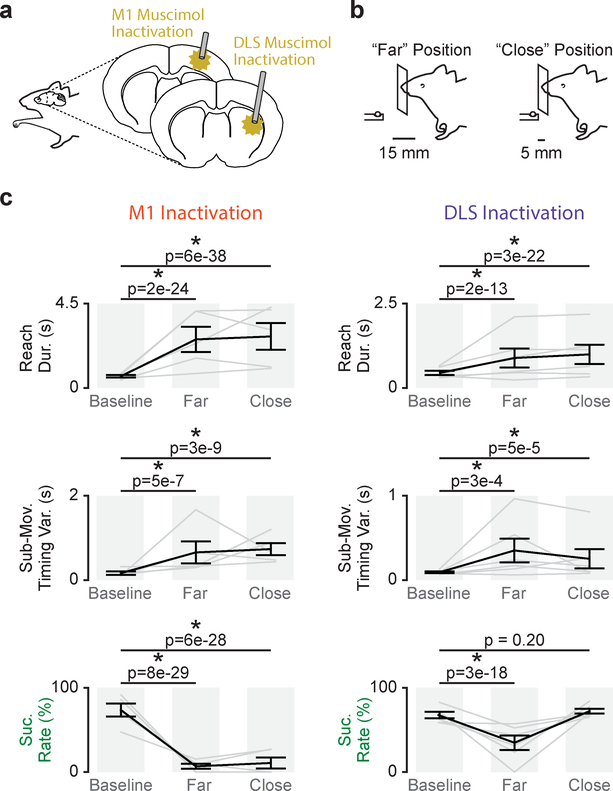
M1 and DLS inactivation have differential effects on skilled fine and gross movements

To causally test the role of M1 and DLS activity in producing skilled fine and gross movements, we implanted a separate well-trained cohort (n = 5 animals) with infusion cannulas in both M1 and DLS to acutely inactivate either M1 or DLS by muscimol infusion (Fig. 5a). To dissect impairments of either skilled fine or gross movements we developed a novel reach-to-grasp task design in which the pellet is either placed at the “far” position (same position used for training) or a “close” position (Fig. 5b). The close position generated a reaching condition in which the reliance on skilled gross movements for success was reduced, while skilled fine movements were still required to successfully grasp the pellet. Differential effects of region inactivation on success rate for the close and far position indicate differences in skilled fine and gross movement impairment.

Figure 5. M1 and DLS inactivation have differential effects on skilled fine and gross movements.

a. Illustration of M1 and DLS muscimol inactivation. b. Illustration of two-position reach-to-grasp task design with a “far” pellet and “close” pellet position. c. Differences in reach duration, sub-movement timing variability, and success rate between trials before muscimol infusion (Baseline), trials after muscimol infusion reaching to the far pellet position (Far), and trials after muscimol infusion reaching to the close pellet position (Close) for M1 infusions (n = 5 sessions across 3 animals; left) and DLS infusions (n = 6 sessions across 5 animals; right). Grey lines represent mean values from individual sessions and black lines represent mean and SEM across sessions. P values from mixed-effects models.

Both acute M1 and DLS inactivation disrupted gross movements, consistent with our conclusion that coordinated activity across both M1 and DLS is closely linked to skilled gross movements. (Fig. 5c; M1 inactivation/far position: reach duration: 662 ± 63ms baseline and 2.6×10³ ± 667ms post-infusion, mixed-effects model: t(311) = 11.2, P = 2×10^–24; sub-movement timing variability: 121 ± 35ms and 586 ± 228ms, mixed-effects model: t(53) = 5.7, P = 5×10^–7; M1 inactivation/close position: reach duration: 662 ± 63ms and 2.7×10³ ± 711ms, mixed-effects model: t(312) = 14.8, P = 6×10^–38; sub-movement timing variability: 121 ± 35ms and 641 ± 89ms, mixed-effects model: t(54) = 7.0, P = 3×10^–9; DLS inactivation/far position: reach duration: 448 ± 63ms baseline and 889 ± 279ms post-infusion, mixed-effects model: t(725) = 7.5, P = 2×10^–13; sub-movement timing variability: 74 ± 8ms and 237 ± 77ms, mixed-effects model: t(136) = 3.7, P = 3×10^–4; DLS inactivation/close position: reach duration: 448 ± 63ms and 995 ± 284ms, mixed-effects model: t(735) = 10.0, P = 3×10^–22; sub-movement timing variability: 74 ± 8ms and 195 ± 82ms, mixed-effects model: t(138) = 4.2, P = 5×10^–5).

Intriguingly, while both M1 and DLS inactivation also impaired success rate to the far position, only M1 inactivation impaired success rate at the close position, suggesting that while skilled gross movement rely on activity across M1 and DLS, skilled fine movements display a stronger cortical reliance. (Fig. 5c; M1 infusion/far position: 73.6 ± 7.7% baseline and 6.8 ± 3% post-infusion, mixed-effects model: t(311) = −12.4, P = 8×10²⁹; M1 infusion/close position: 73.6 ± 7.7% and 10.8 ± 6.6%, mixed-effects model: t(312) = −12.1, P = 6×10^–28; DLS infusion/far position: 67.5 ± 3.8% and 34.7 ± 8.6%, mixed-effects model: t(725) = −8.95, P = 3×10^–18; DLS infusion/close position: 67.5 ± 3.8% and 72.2 ± 2.9%, mixed-effects model: t(735) = −1.3, P = 0.20). No changes in behavior were observed with saline infusions (M1 and DLS saline infusion sessions combined; saline/far position: reach duration: 269 ± 43ms baseline and 279 ± 53ms post-infusion, mixed-effects model: t(817) = 1.5, P = 0.13; sub-movement timing variability: 135 ± 27ms and 140 ± 34ms, mixed-effects model: t(817) = 0.93, P = 0.35; success rate: 64.6 ± 2% and 66.5 ± 7.2%, mixed-effects model: t(817) = 0.77, P = 0.44).

When reaching to the far position, reach amplitude was decreased with DLS inactivation, but increased with M1 inactivation (DLS infusion: 1 ± 1×10^–16 normalized reach amplitude baseline to 0.99 ± 5×10^–3 normalized reach amplitude post-infusion, mixed-effects model: t(593) = −4.1, P = 6×10^–5; M1 infusion: 1 ± 1×10^–16 to 1.01 ± 0.02, mixed-effects model: t(322) = 6.1, P = 3×10^–9). This is consistent with work implicating the striatum in movement vigor^18–23 and suggested that decreased reach amplitude may account for the decrease in success rate at the far position with DLS inactivation. In fact, when we compared DLS inactivated, post-infusion trials with “normal” reach amplitude (i.e., greater or equal to the average reach amplitude during pre-infusion baseline trials) to pre-infusion baseline trials, success rate was not significantly different (74.4 ± 4.4% baseline to 75.33 ± 11.8% post-infusion “normal” reach amplitude trials, mixed-effects model: t(670) = 1.5, P = 0.12). This further suggested that DLS inactivation impairs gross movements involved in transporting the paw to the pellet rather than the fine movements involved in grasping. Body posture at the time of movement onset was not significantly different after DLS inactivation compared to pre-infusion baseline trials (Supp. Fig. 8).

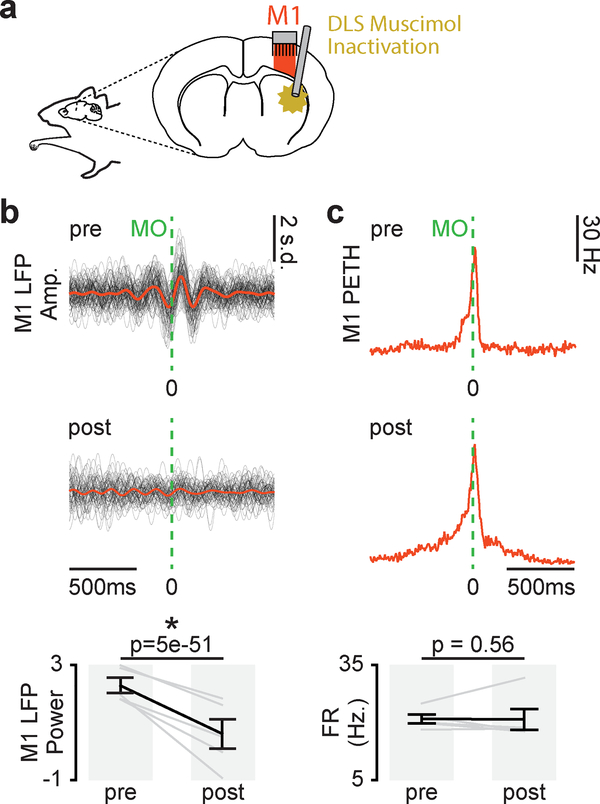
Off-target effects of DLS inactivation

To examine the possibility of off-target effects of DLS inactivation, we implanted infusion cannulas in DLS and electrodes in M1 in a separate well-trained cohort (n=3 animals) to acutely inactivate DLS by muscimol infusion and observed the effects on M1 activity (Fig. 6a). Movement-related 3–6Hz M1 LFP power decreased with DLS inactivation (Fig. 6b; mixed-effects model: t(318) = 18.1, P = 5×10^–51). This suggested that DLS is required for movement-related low-frequency activity in M1. Importantly, this change was not attributable to a general suppression of M1 activity as movement-related firing rates in M1 were not changed with DLS inactivation (Fig. 6c; mixed-effects model: t(318) = 18.1, P = 0.56). No changes in movement-related M1 LFP power or firing rate were observed after saline infusion (LFP power, mixed-effects model: t(190) = 1.3, P = 0.20; movement-related firing rate, mixed-effects model: t(168) = 0.36, P = 0.72).

Figure 6. DLS inactivation decreases movement-related low-frequency M1 activity.

a. Illustration of DLS muscimol infusion and M1 recording. b. Left: 3–6Hz filtered LFP aligned to movement onset from example M1 channel for trials before and after DLS inactivation, individual trials overlaid with mean signal. Right: Difference in movement-related 3–6Hz LFP power in M1 before and after DLS inactivation (n = 5 sessions across 3 animals). Grey lines represent mean power values from individual sessions and black lines represent mean and SEM across sessions. P values from mixed-effects model. c. Left: PETH from example M1 unit for trials before and after DLS inactivation. Right: Difference in movement-related firing rate before and after DLS inactivation (n = 5 sessions across 4 animals). Grey lines represent mean firing rate across units from individual sessions and black lines represent mean and SEM across sessions. P values from mixed-effects model.

Skilled movement impairments with chronic DLS lesion

To test whether acute off-target effects of DLS inactivation may be causing behavioral impairments, we performed excitotoxic lesions centered on DLS that lesioned DLS as well as small portions of surrounding cortex (n = 3 animals). Consistent with previous work²⁴, we observed increased reach duration, sub-movement timing variability and decreased success rate two weeks post-lesion (Supp. Fig. 9; reach duration: 428 ± 56ms baseline and 631 ± 114ms post-lesion, mixed-effects model: t(620) = 4.7, P = 3×10^–6; sub-movement timing variability: 106 ± 13ms and 296 ± 90ms, mixed-effects model: t(620) = 4.2, P = 4×10^–5; success rate: 63 ± 4.3% and 40.7 ± 2.9%, mixed-effects model: t(620) = −5.5, P = 5×10^–8). This indicated that acute off-target effects do not fully account for the disruptions in skilled gross movements observed with acute DLS inactivation. Importantly, fine grasping movements appeared preserved two-weeks post lesion (Supp. Video 1).

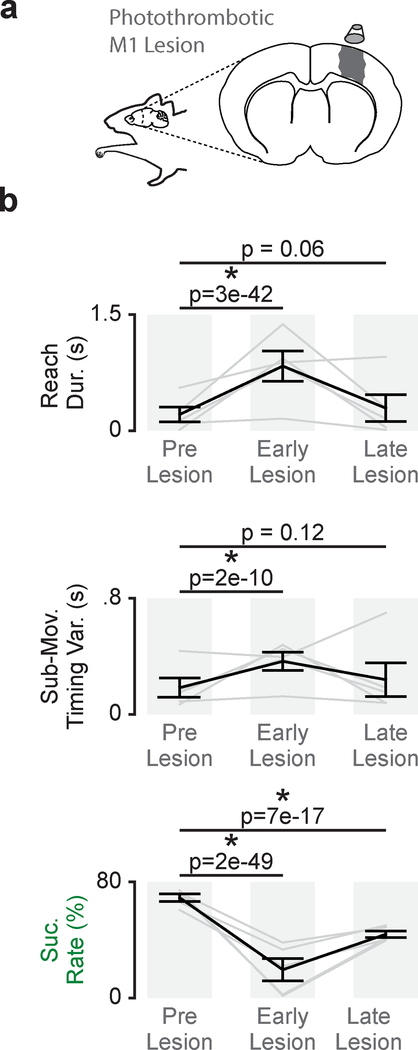
Skilled movement impairments with chronic M1 lesion

To further determine the role of M1 in skilled movements we tested performance after chronic M1 lesions. In a well-trained cohort (n = 5 animals), we generated photothrombotic lesions centered on M1 (Fig. 7a). In the first training session post-lesion (within 8 to 13 days post-lesion), reach duration and sub-movement timing variability were increased and success rate was decreased (Fig. 7b; reach duration: 339 ± 63ms baseline and 756 ± 130ms early post-lesion, mixed-effects model: t(806) = 14.5, P = 3×10^–42; sub-movement timing variability: 183 ± 66ms and 365 ± 63ms, mixed-effects model: t(195) = 6.7, P = 2×10^–10; success rate: 69.1 ± 2.5% and 19.4 ± 7.65%, mixed-effects model: t(808) = −15.84, P = 2×10^–49). With training, gross movement metrics recovered while success rate remained disrupted. Comparing pre-lesion performance to performance once all behavioral performance measures had plateaued (within 15 to 73 days post-lesion), reach duration and sub-movement timing variability were not significantly different than pre-lesion performance, but success rate remained significantly decreased (Fig. 7b; reach duration: 339 ± 63ms baseline and 394 ± 115ms late post-lesion, mixed-effects model: t(927) = 1.9, P = 0.06; sub-movement timing variability: 183 ± 66ms and 238 ± 1117ms, mixed-effects model: t(225) = 1.6, P = 0.12; success rate: 69.1 ± 2.5% and 43.9 ± 2.25%, mixed-effects model: t(929) = −8.5, P = 7×10^–17). The differential recovery of skilled fine and gross movements further suggested skilled fine movements have a strong cortical reliance.

Figure 7. Persistent disruption of skilled fine movements after M1 lesion.

a. Illustration of photothrombotic M1 lesion. b. Differences in reach duration, sub-movement timing variability, and success rate between trials before M1 lesion (Pre Lesion), trials during the first reaching session post- lesion (Early Lesion), and trials once a performance plateau had been reached (Late Lesion; n = 5 animals). Grey lines represent mean values from individual animals and black lines represent mean and SEM across animals. P values from mixed-effects models.

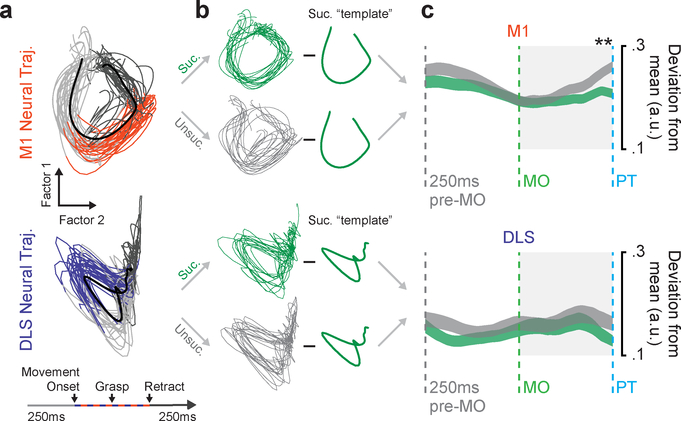
Skilled fine movement representation in M1

Lastly, we explored the representation of skilled fine movements in M1 and DLS. We used gaussian-process factor analysis (GPFA) to find low-dimensional neural trajectory representations of population spiking activity in M1 and DLS on individual trials²⁵ (Fig. 8a) and then compared trajectories for successful and unsuccessful trials on days five through eight, during the period of learning after gross movements had stabilized (e.g., Fig. 1b, D5-D8). As we attribute whether trials were successful during this period to the control of skilled fine movements of the digits, we expected to find a difference in movement-related neural signals between successful and unsuccessful trials only if a region encodes the control of skilled fine movement.

Figure 8. Skilled fine movement representation in M1.

a. GPFA neural trajectories for trials on day eight for M1 (top) and DLS (bottom) from example animal. b. Illustration of method for calculating deviation from the mean successful template for successful and unsuccessful trials. c. Mean deviation from successful template for successful and unsuccessful trials from 250ms before movement onset to pellet touch, across animals (n = 10 sessions across 4 animals; width depicts mean deviation across sessions ± SEM; * = P<0.05, P value from mixed-effects model w/Bonferroni correction for multiple comparisons).

We observed a difference between trajectories for successful and unsuccessful trials in M1 but not DLS. To compare successful and unsuccessful trials we subtracted the mean neural trajectory for successful trials, i.e., the “successful template”, from each individual trial’s neural trajectory (Fig. 8b) and calculated the mean absolute value of the deviation during each time point from 250ms before movement onset until pellet touch. We focused on this period as it includes the fine movements involved in shaping the digits for contact with the pellet but does not include differences in retraction or reward between successful and unsuccessful trials. As trials differed in the duration of this period, we interpolated trajectories such that they were all the same length. M1 neural trajectories for unsuccessful trials had significantly higher deviation than successful trials starting after movement onset (Fig. 8c, top; * = P<0.05, mixed effects model w/Bonferroni correction for multiple comparisons). DLS neural trajectories for successful and unsuccessful trials did not differ (Fig. 8c, bottom), providing further evidence for the strong cortical reliance of skilled fine movements.

Discussion

In summary, we found that skilled fine and gross movements were behaviorally and neurally differentiable during reach-to-grasp skill learning. Coordinated low-frequency activity emerged across M1 and DLS, linked to the emergence of skilled gross movements, while the emergence of skilled fine movements was independent of this activity, evolved over a longer timescale, and displayed a stronger cortical reliance. Consistently, inactivation of either M1 or DLS disrupted gross movements, while only inactivation of M1 disrupted fine movements. This work provides evidence that coordinated skills can emerge from the modular refinement of movements.

The role of M1 in skill learning and execution

Primary motor cortex has been ascribed multiple roles in learning and executing motor skills²⁶. A critical determinant for the role of M1 is whether the skill involves dexterous movements²⁶. Our results indicate that distinct patterns of M1 activity emerge independently during skill learning related to the dexterous component (fine) and non-dexterous (gross) component. This suggests that M1 plays dual, but separable, roles in learning a skill composed of both dexterous and non-dexterous components.

Motor cortex is known to play a critical role in the production of dexterous movements^27,28. Motor cortical projections to brainstem and spinal cord are thought to mediate this role^29–31. Lesions to cortex disrupt this pathway and lead to chronic impairments in dexterous movements^32,33. Interestingly, non-dexterous movements have been shown to recover after motor cortical lesion^32,33, suggesting a greater ability for gross movements to be generated subcortically. Our results are broadly consistent with this literature. While, both acute and chronic lesions disrupted skilled fine movements, aspects of gross movements recovered with chronic M1 lesion (Fig. 5; Fig. 7). The disruption of skilled gross movements with acute M1 inactivation raises the possibility for off-target effects³⁴.

The role of motor cortex in non-dexterous movements can evolve with learning. A recent study found that bilateral lesions of premotor and motor cortex after learning did not impair performance of complex motor skill composed of non-dexterous movements. However, similar lesions before learning prevented skill acquisition⁹. This has led to the notion that non-dexterous skills are “transferred” to downstream structures and that motor cortex plays a “tutor” role in skill learning, i.e., is required for learning but not execution of a motor skill⁹. What may allow non-dexterous control in the absence of M1? Skill learning is commonly associated with plasticity in corticostriatal projections^8,11,12 and it has therefore been theorized that the striatum and thalamostriatal inputs may be critical downstream producers of these learned skills^9,35,36. Our results suggest that corticostriatal plasticity is indeed important to learn motor skills (Fig. 2–4). Additionally, it is possible that the observed coordinated activity across M1 and DLS is a neurophysiological substrate for the motor cortical tutor signal, providing a mechanism through which M1 activity patterns induce long-term plasticity in the DLS. Modeling has shown that temporally patterned inputs to the striatum can drive inter-striatal plasticity³⁶.

Importantly, in our work, recovery of aspects of gross movements after motor cortical lesion occurred over time with training. This is different from Kawai, et al., 2015, in which full recovery was observed after a period of 10 days with no further training. This discrepancy may be due to differences in task (e.g., the reach-to-grasp contains both dexterous and non-dexterous components) or differences in training. In Kawai, et al., 2015, the complex motor skill was learned over a long period of training (~20,000 training trials over ~30 days); it remains possible that an action containing dexterous movements may be realized by downstream circuitry after cortical lesions with enough prior training.

The role of DLS in skill learning and execution

The striatum’s role in producing skilled movements is also multifaceted. Receiving widespread cortical innervation, the striatum is positioned to play a central role in motor function as is evidenced by the motor dysfunction caused by basal-ganglia disorders³⁷. Cortical innervation of the striatum projects back to cortex via basal-ganglia output nuclei and the thalamus, forming a corticostriatal “loop”. The precise role of this loop in the production of motor skills remains unclear, although it has been shown that striatal activity can influence motor cortical activity with low-latency³⁸ (<200ms). It has also been shown in a Brain Machine Interface (BMI) task in which animals learn to modulate cortical activity to achieve reward that plasticity in corticostriatal projections is required, suggesting that cortex may require striatum to generate stereotyped patterns of activity³⁹. Consistent with this notion, we found disrupted movement-related LFP activity in M1 with DLS inactivation (Fig. 6). Altogether, this suggests that the striatum may play a role in modulating cortical activity during skill learning.

Recent work has also championed a role of the striatum in controlling movement vigor^18–23. One such model focuses on the feed-forward convergent pathway of motor cortical neurons that project to “premotor” brainstem regions and their collaterals that project to the dorsal striatum, that in turn projects to the same premotor brainstem regions through basal ganglia output nuclei²³. This pathway through the striatum is theorized to play a role in controlling the gain of descending motor commands based on previous experience. One prediction of this “history-dependent gain” model (for details see Yttri & Dudman, 2018) posits that the striatum is active during the acceleration and deceleration phases of a movement, which was confirmed in a joystick²⁰ and locomotor²¹ task. Similarly, we find that striatal units are active throughout the reaching action (Fig. 2; Fig. 3; Supp. Figure 7). Additionally, we found evidence that disrupting striatal activity effects movement vigor, as reach amplitude was decreased with DLS inactivation. Altogether, our results support the notion that DLS may play a role in both modulating cortical activity and controlling movement vigor for skilled gross movements. Our finding that DLS activity is linked to skilled gross movements in the rodent is consistent with work in the monkey⁴⁰ and human⁴¹ basal ganglia, demonstrating a greater representation of proximal, compared to distal, portions of the limb.

What kind of “skill” is the reach-to-grasp task?

The term “motor skill” can describe a vast range of behaviors characterized by fast, accurate, and consistent movements. One group of skills has been formalized using the speed-accuracy tradeoff⁴². Learning such skills typically involves optimizing speed while maintaining accuracy. For example, one can play a series of notes on the piano consistently and accurately on the first day of learning if the movements are performed slowly enough. Learning therefore involves optimizing speed. Other skills require optimizing accuracy without constraints on than speed (e.g., shooting a free throw). The rodent reach-to-grasp skill falls under this latter type of learning. Interestingly, while there were no explicit constraints on speed, we still observed a significant decrease in movement duration. This may be because the brain’s motor network, in general, biases toward faster skills to increase rewards per unit time⁴³. Another possibility is that coordinated low-frequency activity between M1 and DLS is critical for consistent and accurate movements, and that speed is simply a byproduct of network dynamics. There is evidence that increases in speed are required to maximize efficiency or maintain consistency⁴⁴.

Coordination across the motor network

It has been suggested that oscillatory or rhythmic activity is central to multi-region communication^45–47. Intriguingly, a growing body of work has also proposed that transient oscillatory activity is central to motor function^16,48,49. In fact, modeling has suggested that low-frequency activity may be an essential feature of neural activity that generates descending commands to muscles⁵⁰. Our work suggests that coordinated low-frequency activity is present beyond cortex in the motor network and that such rhythmic activity may allow for the coordination of activity across regions. Further work exploring multi-region interactions will be essential to understanding the interplay between cortex and striatum, and the greater motor network, during motor skill learning.

Methods

Animal Care and Surgery

All procedures were in accordance with protocols approved by the Institutional Animal Care and Use Committee at the San Francisco Veterans Affairs Medical Center. Male Long-Evans rats between 3–4 months old and 250–300 grams were used in this study. Animals were kept under controlled temperature and a 12–h light, 12–h dark cycle with lights on at 06:00 A.M.

All surgical procedures were performed using sterile technique under 2–4% isoflurane. For electrode and/or cannula implantation, surgery involved exposure and cleaning of the skull, preparation of the skull surface (using cyanoacrylate), and then implantation of skull screws for referencing and overall head-stage stability. Reference screws were implanted posterior to lambda, contralateral to the neural recordings. Ground screws were implanted posterior to lambda, ipsilateral to the neural recordings. Craniotomy and durectomy were performed, followed by implantation of neural probes or cannulas. Neural probes (32- or 64-channel Tucker-Davis Technologies (TDT) 33 μm polyimide-coated tungsten microwire electrode arrays) or infusion cannulas (PlasticsOne) were implanted in the forelimb area of M1, centered at 3.5mm lateral and 0.5mm anterior to bregma and implanted in layer 5 at a depth of 1.5mm, and the dorsolateral striatum, centered at 4mm lateral and 0.5mm anterior to bregma and implanted at a depth of 4.5mm. Final location of electrodes was confirmed by electrolytic lesion (Supp. Fig. 1). Muscimol localization was performed by infusing a fluorescent muscimol (Supp. Fig. 10; BODIPY, TMR-X Conjugate) prior to perfusion and histology. The forearm was implanted with a pair of twisted electromyography (EMG) wires (0.007” single-stranded, teflon-coated, stainless steel wire; A-M Systems, Inc.) with a hardened epoxy ball (J-B Weld) at one end preceded by 1–2 mm of uncoated wire under the ball. Wires were inserted into the muscle belly and pulled through until the ball came to rest on the belly. EMG wires were braided, tunneled under the skin to a scalp incision, and soldered into headstage connectors. Fascia and skin incisions were closed with a suture. The post–operative recovery regimen included administration of buprenorphine at 0.02 mg/kg and meloxicam at 0.2 mg/kg. Dexamethasone at 0.5 mg/kg and Trimethoprim sulfadiazine at 15 mg/kg were also administered post–operatively for 5 days. All animals recovered for 14 days prior to start of behavioral experiments.

For photothrombotic lesion surgery, the protocol was the same as for electrode and cannula implantation up to the craniotomy. After the craniotomy, rose bengal dye was injected into the femoral vein using an intravenous catheter. Next, the surface of the brain was illuminated with white light (KL-1500 LCD, Schott) using a fiber optic cable for 20 min. We used a 4-mm aperture for lesion induction (centered on the M1 coordinates reported above) and covered the remaining cortical area with an aluminum foil mask to prevent light penetration. After lesion induction the craniotomy was covered with a layer of silicone (Quiksil), followed by dental cement. The same post-operative recovery regimen as electrode and cannula implantation surgery was then implemented. After all experiments, rats were anesthetized and transcardially perfused with 0.9% sodium chloride, followed by 4% formaldehyde. The harvested brains were post-fixed for 24 h and immersed in 20% sucrose for 2 days. Coronal cryostat sections (40-μm thickness) were then mounted and imaged for lesion and muscimol localization.

Behavior

For learning, rats naïve to any motor training were first tested for forelimb preference. This involved presenting approximately ten pellets to the animal and observing which forelimb was most often used to reach for the pellet. One-week later rats underwent surgery followed by a recovery period. Rats were then trained using an automated reach-box, controlled by custom MATLAB scripts and an Arduino micro-controller. This setup required minimal user intervention, as described previously¹⁴. Each trial consisted of a pellet dispensed on the pellet tray followed by an alerting beep indicating that the trial was beginning and then the door opening. Animals had to reach, grasp and retrieve the pellet. A real-time “pellet-detector” using an IR sensor centered over the pellet was used to determine when the pellet was moved, indicating the trial was over, and the door was closed. All trials were captured by video through a camera placed on the side of the behavioral box, which was synced with electrophysiology data using an Arduino digital output. Two types of cameras were used, Microsoft LifeCams which captured videos at 30Hz, and Basler Cameras which captured videos at 75Hz. Behavioral scoring, including timing of sub-movements and reconstruction of the forelimb trajectory, was performed manually. Such behavioral scoring was not performed blind but results were validated across multiple scorers. For inactivation experiments, a second camera was placed above the behavioral box to capture body posture during reaching. The learning paradigm consisted of 100–150 trial sessions performed each day for 8 consecutive days. Rats had 15 seconds in each trial to execute a reach before a 10 second inter-trial-interval in which the door was closed, which led to ~75–150 trials performed (i.e., trials where the pellet was displaced) each day. For the “extended training” cohort, a separate cohort of animals was trained more extensively using the same paradigm for 4 weeks, resulting in ~2500 trials performed. No statistical methods were used to pre-determine cohort sizes, but our sized are similar to those reported in previous publications^{5–8,10–12} (4–9 animals per group). Furthermore, randomizations were not used in the organization of experiments and no animals were excluded.

Behavioral Analysis

Learning was assessed using four metrics (Fig. 1): (1) reach duration defined as the time from the onset of movement (movement onset) to when the paw is fully retracted off of the pellet tray (retract onset), (2) sub-movement timing variability defined as the standard deviation across trials of the duration between paw touching the pellet (pellet touch) and when the paw is fully retracted off of the pellet tray (retract onset), (3) success rate defined as the percentage of reaches that resulted in retrieval of the pellet into the box, and (4) forelimb trajectory consistency defined as the average correlation between each individual trial’s forelimb trajectory and the mean forelimb trajectory calculated over all trials in that session (computed separately in each of the two dimensions). These metrics were chosen as they measured changes in both gross movements of the forelimb involved in producing a consistent reach and fine movements of the fingers involved in successful grasping. For the scatter plots comparing changes in reach duration, sub-movement timing variability, and forelimb trajectory consistency across learning to changes in movement-related 3–6Hz M1-DLS LFP coherence (Fig. 4b), normalized values of reach duration, sub-movement timing variability, and forelimb trajectory consistency were computed by z-scoring the eight mean values corresponding to the eight days of training for each animal separately, then combining the normalized values across animals. To determine body posture with DLS inactivation we used a top camera and manually determined the body axis from nose to center of the body (Supp. Fig. 8). We defined posture variability as the mean of the absolute value of the distance across all trials from the middle of the body to the average middle of the body position. We defined lateral bias as the mean distance in the x-axis across all trials from the middle of the body to the average middle of the body position.

Inactivation Experiments

We performed two sets of inactivation experiments. For both experiments, rats were first tested for forelimb preference, then underwent either dual cannula surgery (M1 and DLS cannula implantation) or cannula and electrode implantation surgery (DLS cannula and M1 electrode implantation). Following the recovery period, rats were trained for 10 days (100 trials/day). Following this training, inactivation experiments began. For each session, baseline performance was calculated from 100 trials performed before muscimol infusion. For M1/DLS inactivation experiments (Fig. 5), infusion consisted of anesthetizing the rat (w/isoflurane) and infusion of 250nl of 1ug/ul muscimol (Tocris) in saline (0.9% sodium chloride) at a rate of 100nl/min in either M1 or DLS. After the two-and-a-half-minute infusion and a five-minute waiting period with the infusion cannula inserted, the rat was taken off anesthesia and allowed to recover for 2 hours. A 200 trials block was then performed alternating between 10 trials to the “close” position (5mm from pellet center to slot opening in behavioral box) and 10 trials to the “far” position (15mm from pellet center to slot opening in behavioral box). For DLS inactivation experiments (Fig. 6), infusion protocol was the same except a volume of 1ul of muscimol was infused. After the ten-minute infusion and a five minute waiting period, a 100-trial block was performed at the “far”/normal pellet position to examine effects of DLS inactivation on movement-related M1 activity.

Lesion Experiments

For photothrombotic lesion experiments (Fig. 7), rats were first tested for forelimb preference, then trained for 10 days (100–150 trials/day). Pre-lesion performance was measured before animals underwent photothrombotic lesion surgery. Post-lesion, animals began performing reaching trials at variable times, so “early” lesion performance was defined as the performance during the first session that animals were completing trials (within 8 to 13 days post-lesion). Animals underwent reach training until a performance plateau was reached, which was defined as “late” lesion performance (within 15 to 73 days). Photothrombotic lesion size was determined with immunohistochemistry (see below). For excitotoxic lesion experiments (Supp. Fig. 11), rats were first tested for forelimb preference, then trained for 10 days (100 trials/day). Pre-lesion baseline performance was then measured. Excitotoxic lesions were then implemented with 500nl infusions of 10ug/ul ibotenic acid (7.4 pH; Abcam) at an infusion rate of 100nl/min at the same DLS coordinates as referenced above. The animals recovered for two weeks, then performance post-lesion was measured. Excitotoxic lesion position and size was determined with immunohistochemistry (see below).

In Vivo Electrophysiology

Units, LFP, and EMG activity were recorded using a TDT-RZ2 system (Tucker-Davies Technologies). Spike data were sampled at 24414 Hz and LFP/EMG data at 1017 Hz. ZIF-clip-based analog headstages with a unity gain and high impedance (∼1 GΩ) were used. Behavior-related timestamps (i.e., trial onset, trial completion) and video timestamps (i.e., frame times) were sent to the RZ2 analog input channel using an Arduino digital board and synchronized to neural data.

Neural Data Analysis

Analyses were conducted using a combination of custom-written scripts and functions in MATLAB 2015a/2017a (MathWorks), along with functions from the EEGLAB toolbox (http://sccn.ucsd.edu/eeglab/) and the Chronux toolbox (http://chronux.org/).

LFP analysis

Pre-processing steps for LFP analysis included: artifact rejection (manually removing noisy/broken channels), z-scoring entire recording session, and common-mode referencing using the median signal (at every time-point, the median signal across all channels in a region was calculated. This median signal was subtracted from every channel to decrease common noise and minimize volume conduction. Common-mode referencing was performed independently for the channels in each region, i.e., M1 and DLS.

In several instances we filtered LFP signals to isolate and display the low-frequency (3–6Hz) component of the signal (Fig. 2a&d; Fig. 3a&b; Fig. 4c; Fig. 6b; Supp. Fig. 4a; Supp. Fig. 6a). Filtering was performed using the EEGLAB function eegfilt. In addition to display purposes, we also used filtered LFP to characterize phase-locking of spiking activity specifically to low-frequency LFP signals. For this we used the Hilbert transform (MATLAB) to extract the phase information from low-frequency filtered LFP signals (Fig. 3b&c). We also used filtered LFP and phase extraction to determine the movement-related phase lag between M1 and DLS LFP signals (Supp. Fig. 4).

To quantify changes across frequencies in the amplitude of rhythmic activity in LFP signals we calculated movement-related LFP spectrograms and power spectrums within each region (Fig. 2b; Fig. 6b; Supp. Fig. 5). For learning comparisons, power was measured and compared for the same channels on day one and day eight across all channels (except those removed due to noise). This was carried out using wavelets with the EEGLab function newtimef⁵¹.To quantify phase-locking of LFP signals to specific sub-movements (movement onset, pellet touch, and retract onset) we calculated inter-trial coherence (ITC) of LFP signals across trials time-locked to these sub-movements (Fig. 2d). ITC was measured and compared for the same channels on day one and day eight across all channels (except those removed due to noise). ITC was computed using the EEGLab function newtimef⁵¹.

To characterize coordination of activity across regions we measured changes in movement-related spectral coherence between LFP channels in M1 and DLS (Fig. 2c; Fig. 4; Supp. Fig. 5; Supp. Fig. 6). For learning comparisons, coherence was measured for the same channels on day one and day eight, and specifically for channels with an increase in power of one baseline normalized unit from day one to day eight. Strong coherence in a specific frequency band indicates a constant phase relationship in that frequency between two signals and is theorized to indicate increased communication between regions^46,47. Spectral coherence was computed using chronux function cohgramc⁵². All comparisons of “movement-related” LFP power or coherence used power and coherence values generated from signals between 250ms before movement onset to 750ms after movement onset and trial averaging over relevant trials (e.g., all trials on day one or day eight).

To determine whether the emergence of coordinated low-frequency activity during training was attributable solely to faster and more consistent movements, we compared LFP power and coherence between “fast” trials (trials with a movement duration between 200 and 400ms) and trials with high forelimb trajectory correlation values (correlation values > 0.9) on days one and two vs. days seven and eight (Supp. Fig. 5).

For the scatter plots comparing changes in reach duration, sub-movement timing variability, and forelimb trajectory consistency across learning to changes in movement-related 3–6Hz M1-DLS LFP coherence (Fig. 4b), normalized values of LFP coherence were computed by z-scoring the eight mean values corresponding to the eight days of training for each animal separately, then combining the normalized values across animals.

Spiking analysis

Thresholds for spiking activity were set online using a standard deviation of 4.5 (calculated over a one-minute baseline period using the TDT-RZ2 system), and waveforms and timestamps were stored for any event that crossed that threshold. Spike sorting was performed using Plexon OfflineSorter v4.3.0 (Plexon Inc.) with a PCA-based clustering method followed by manual inspection. We accepted units based on waveform shape, clear cluster boundaries in PC space, and 99.5% of detected events with an ISI>2ms. All units were analyzed and not sorted into cell type based on waveform shape. Average firing rates were consistent with what has been previously reported for M1 and DLS units⁸ (Supp. Fig. 7). Peri-event time histograms (PETHs) were generated by averaging spiking activity across trials in a session, locked to movement onset and binned at 25ms, then fitting a smoothing spline using MATLAB function fit (Fig. 3a&b&d; the smoothing spline was not applied to PETHs presented in Fig. 6c). These PETHs were used to generate average movement-related spiking plots (Supp. Fig. 7e–j). To investigate spiking activity relative to movement phase (Supp. Fig. 7g&h), we interpolated spiking activity binned at 25ms during movement (from movement onset to retract onset) for each trial such that the resulting spiking activity from each trial was normalized to the same length and then averaged across trials. We also used PETHs to classify task-related units (Supp. Fig. 7). We defined a unit as task-related if during movement its activity was greater than one standard deviation or less than one standard deviation away from its baseline activity.

To characterize low-frequency spiking activity, we generated histograms of the LFP phases at which each spike occurred for a single unit to a single LFP channel filtered in the 3–6Hz band in a one-second window around movement (−250ms before to 750ms after movement onset) across all trials of a session (Fig. 3b). For learning comparisons, all units were compared to the same selected M1 and DLS LFP channel on day one and day eight. These histograms were generated for each unit-LFP channel pair both within and across regions. For every pair we then calculated the Rayleigh’s z-statistic for circular non-uniformity. These z-statistics were then used to calculate the percentage of significantly non-uniform distributions across unit-LFP pairs with a significance threshold P=0.05 (Fig. 3c). A significantly non-uniform distribution signifies phase preference for spikes of a unit to an LFP signal.

To further characterize low-frequency spiking activity, we determined the percentage of units that displayed low-frequency (3–6Hz) quasi-oscillatory activity. To do this, we computed autocorrelations on each unit’s PETH. If a unit’s autocorrelation had a “peak” between 166–333ms time lag (corresponding to 3–6Hz activity) the unit was considered quasi-oscillatory. A “peak” was defined as a higher average value between 166–333ms than between 100–166ms (Fig. 3d).

To characterize spiking interactions between M1 and DLS we calculated the mean cross-correlation of movement-related spiking across regions for all M1 and DLS quasi-oscillatory units on day one and day eight (Fig. 3e). To do this we concatenated spiking activity for all trials between −250ms to 750ms from movement onset for each M1 and DLS quasi-oscillatory unit and then computed the cross correlation for each M1 and DLS quasi-oscillatory unit pair using the MATLAB function xcorr.

To determine the effects of DLS inactivation on M1 spiking activity we compared movement-related firing rates from pre-infusion baseline trials and post-infusion trials. Movement-related firing rates were calculated by averaging the firing rate from −250ms before to 500ms after movement on each trial of the session (Fig. 6c).

To characterize single-trial representations of population spiking activity we used Gaussian process factor analysis (GPFA)²⁵ to find low-dimensional neural trajectories for each trial (Fig. 8; Supp. Fig. 12). GPFA analyses were carried out using MATLAB based GUI DataHigh⁵³, 25ms time bins, and a dimensionality of 5. The first two factors were used for analysis as they accounted for >90% of shared variance explained in both M1 and DLS on each session. We found that the consistency of these trajectories, calculated by averaging the correlation of every trial’s neural trajectory to the mean neural trajectory of that session (performed in each dimension independently) provided a robust measure neural consistency as this measure increased in both M1 and DLS during learning (Supp. Fig. 12b; M1: mixed-effects model: t(1789) = 6.9, P = 7×10^–12; DLS: mixed-effects model: t(766) = 4.8, P = 2×10^–6). We also determined the magnitude of deviation for each individual trial trajectory from the mean trajectory across all successful trials by taking the absolute value of the difference between the trajectory of each trial and the mean trajectory across all trials (Fig. 8b&c; computed in each dimension independently). This was performed specifically for the time period between 250ms before movement onset until pellet touch. As this duration varied across trials, we interpolated each trial such that every trial was the same length (100 values) and then calculated the average deviation.

Statistics

Linear mixed-effects models were used to test the significance of differences across both behavioral and neural measures. Using these models accounts for the fact that units, channels or trials from the same animal are more correlated than those from different animals and is more stringent than computing statistical significance over all units, channels or trials⁵⁴. For example, to test for learning-related changes in reach duration across all trials from training day one to all trials from day eight, we implemental a linear mixed-effects model (using MATLAB fitlme) with random intercepts/effects for each rat (n = 4) and reported the P values for the regression coefficients associated with day one and day eight. Similar models were used to test for changes in other behavioral or neural measures, including LFP power, LFP coherence, and LFP/sub-movement phase-locking. Two-sample Kolmogorov-Smirnov tests were used to test whether spike-LFP phase locking values on day one and day eight of learning came from the same distribution. Pearson’s r was used to test linear correlations between behavioral and neural measures. No normality tests were carried out, but individual data points have been included in figures to display distributions.

Viral Injection

We performed two sets of viral injections in separate cohorts of rats to label anterograde projections from M1 and retrograde projections from DLS. To label anterograde projections from M1 we injected 750nl of AAV8-hsyn-JAWs-KGC-GFP-ER2 virus into two sites (1.5mm anterior, 2.7mm lateral to bregma, at a depth of 1.4mm and 0.5 posterior, 3.5mm lateral to bregma, at a depth of 1.4mm). To label retrograde projections from DLS we injected 750nl of retrogradeAAV-hsyn-JAWs-KGC-GFP-ER2 virus at one site (4mm lateral and 0.5 mm anterior to bregma at a depth of 4mm). Two weeks after injection rats were anesthetized and transcardially perfused with 0.9% sodium chloride, followed by 4% formaldehyde. The harvested brains were post-fixed for 24 h and immersed in 20% sucrose for 2 days. Coronal cryostat sections (40-μm thickness) were then mounted and imaged with a fluorescent microscope.

Immunohistochemistry

Cryostat sections (40-μm thickness) were pre-incubated with blocking buffer (2% goat serum, 0.1% bovine serum albumin and 0.3% Triton X-100 in 0.1 M PB) at room temperature, and then incubated with mouse anti-NeuN (1 mg/ml; Millipore, Temecula, CA) overnight. After washing, the sections were incubated with biotinylated anti-mouse IgG secondary antibody (5 mg/ml; Vector laboratories, Burlingame, CA) for 2 hrs. Sections were visualized by the DAB method, using ABC reagents using a Vector ABC kit (Vector laboratories) and peroxidase substrate solution (Vector laboratories). For fluorescence images, sections were incubated with Alexa Fluor 594-conjugated donkey anti-mouse IgG (Life Technologies Corporation, Grand Island, NY; 1:1000).

Reporting Summary

Further information on experimental design is available in the Nature Research Reporting Summary linked to this article.